An active contour model based on local fitted images for image segmentation

Abstract

Active contour models are popular and widely used for a variety of image segmentation applications with promising accuracy, but they may suffer from limited segmentation performances due to the presence of intensity inhomogeneity. To overcome this drawback, a novel region-based active contour model based on two different local fitted images is proposed by constructing a novel local hybrid image fitting energy, which is minimized in a variational level set framework to guide the evolving of contour curves toward the desired boundaries. The proposed model is evaluated and compared with several typical active contour models to segment synthetic and real images with different intensity characteristics. Experimental results demonstrate that the proposed model outperforms these models in terms of accuracy in image segmentation.

1. Introduction

Since the introduction by Kass et al. [12], active contour models [8] have become very popular in the field of image segmentation in the past years, and can yield closed and smooth contours of the desired objects with promising accuracy [4]. These models are in general characterized by a predefined energy functional with intensity and/or gradient information based on the intrinsic properties of images. This energy functional can be minimized by using the level set method [17], where contour curves are represented implicitly as the zero level set of higher dimensional function. This energy minimization procedure is effective [6] to drive the motion of contour curves towards the boundaries of target objects and achieve satisfactory segmentation results for images with different intensity characteristics.

In the past, a variety of active contour models have been proposed for image segmentation purpose [1,2,7]. They can be coarsely categorized into the edge- [18,45] and region-based models [13–15,19,20,25,29] according to image information used in the energy functional. Edge-based active contour models usually utilize intensity gradients to approximate the target boundaries and attract contour curves toward desirable boundaries [11]. This type of models is efficient but sensitive to image noise and the initial curve placement due to the local characteristic of image gradients. Different from this type of models, region-based models employ a great deal of image information, such as pixel intensities, shape and texture features in global or local regions, to make contour curves accurately converge to desirable target boundaries. The region-based models are in general more robust to image noise, less sensitive to the initial contour curve placement, and more capable of dealing with weak boundaries and intensity inhomogeneity owing to the use of more image information, which in turn causes more segmentation time.

Among region-based models, the Chan–Vese (CV) model [2] has been widely used for many image segmentation tasks. It assumes that images to be processed have homogeneous intensities and can be partitioned into several disjoint subregions according to intensity characteristics. However, this model may not work well for images with intensity inhomogeneity due to the mere use of global intensity averages. To accurately segment inhomogeneous images, a number of region-based models [14,15] have been developed by constructing a proper energy functional to drive the evolution of contour curves. Li et al. [14] and Zhang et al. [44] improved the CV model by using the local binary fitting (LBF) energy and local image fitting (LIF) energy, respectively. Ali et al. [1] developed a variational model from multiplicative and difference images to handle intensity inhomogeneity, which turned out to outperform the CV model and its many variants [36]. Mabood et al. [21] proposed an absolute median deviation based model for noisy images, which was accurate and efficient as compared to the local Chan–Vese (LCV) model [36]. More models can be found in [9,16,30,32] by defining energy functional with other information, such as texture features [22,46], prior shape information [3,23,40] and local patch [35]. With proper initialization, these models are able to successfully extract the desirable objects depicted on images, but typically need complicated estimation strategies [10,31].

Another strategy to accurately segment the objects in an image is to incorporate feature information into the energy functional to reduce the adverse influence of intensity inhomogeneity. There are a variety of feature information [5,7,21] used in segmentation, but most of them are not applicable for inhomogeneous images and cannot effectively highlight desirable objects located in inhomogeneous regions. Hence, it is desirable to design novel information for accurate segmentation.

In this study, we proposed to construct a local hybrid image fitting (LHIF) energy functional for accurate image segmentation by leveraging the strength of both LBF and LIF models. Specifically, a novel local fitted image was derived from the LBF and LIF models, aiming to approximate the square of local image and called square fitted image (SFI). Using this SFI image, a novel local intensity fitting energy was constructed, together with a regularization term of level set function. Minimizing this energy functional in a variational level set formulation will drive contour curves toward the boundaries of desirable objects in an optimal way. The developed model was validated using a number of synthetic and real images as well as medical images. A comparison with several typical active contour models was also performed.

2. Related work

2.1. CV model

The CV model can be viewed as a variant of the Mumford–Shah model [16] based on the assumption of image homogeneity. It partitions a given image into two disjoint subregions with an initial contour curve C (i.e., inside and outside regions of C, expressed as C_in and C_out, respectively). The initial curve evolves to the desired boundaries according to the following energy functional:

$$E^{CV}={\lambda }_1{\int }_{C_{in}}{\mid I(x)-c_1\mid }^{2}dx+{\lambda }_2{\int }_{C_{\mathit{out}}}{\mid I(x)-c_2\mid }^{2}dx+\upsilon \mid C\mid$$ (1)

where constants c₁ and c₂ are the average intensities for the regions C_in and C_out, respectively; I(x) denotes the pixel intensity in the position of x. λ₁ and λ₂ are weighting parameters for intensity fitting terms, which play a major role in driving the motion of the contour curve; while υ is the weighting parameter for length penalty term |C|. In calculus of variations, the level set formulation of the CV model is obtained by minimizing this energy functional with respect to the level set function ϕ and given by as follows:

$$\frac{\partial \varphi }{\partial t}=\delta (\varphi )\left[-{\lambda }_1{(I(x)-c_1)}^2+{\lambda }_2{(I(x)-c_2)}^2+\upsilon ·\mathit{div}\left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)\right]$$ (2)

where δ(·) is the Dirac function; div(·) and ∇ are the divergence and gradient operator, respectively. c₁ and c₂ are computed according to the following formulations:

$$c_i=\frac{\int I(x)H_i(\varphi (x))dx}{\int H_i(\varphi (x))dx},i=1,2$$ (3)

where H₁(ϕ) = H(ϕ) and H₂(ϕ) = 1 − H(ϕ) are used to identify the internal and external regions of ϕ; $H(\varphi )=\frac{1}{2}[1+\frac{2}{\pi }arctan(\frac{\varphi }{\epsilon })]$ is the smooth Heaviside function [39] with a small positive constant ε, and its derivative is the Dirac function $\delta (\varphi )=\frac{1}{\pi }\frac{\epsilon }{{\epsilon }^2+{\varphi }^2}$.

In the CV model, the differences between c₁ and c₂ should be large enough to attract contour curves to the desired boundaries according to the assumption of image homogeneity. When image intensities are not homogeneous, c₁ may be approximately equal to c₂ in certain regions, which means that the model loses the capability of identifying the desired objects and image background, together with boundary leakages and inadequate segmentation.

2.2. LBF model

To overcome the drawbacks of the CV model, the LBF model [14] was proposed by introducing a binary fitting energy in a local region specified by a Gaussian kernel, and this LBF energy can be given by:

$$E^{\mathit{LBF}}={\lambda }_1{\iint }_{C_{in}}{K}_{\sigma }(x,y){\mid I(y)-f_1(x)\mid }^2\mathit{dydx}+{\lambda }_2{\iint }_{C_{\mathit{out}}}{K}_{\sigma }(x,y){\mid I(y)-f_2(x)\mid }^2\mathit{dydx}$$ (4)

where $K_{\sigma }(x,y)=\frac{1}{\sqrt{2\pi }\sigma }\mathit{exp}(-\frac{{(x-y)}^2}{2{\sigma }^2})$ is a Gaussian kernel with standard deviation σ and used to define a local region centered at x; y is a pixel coordinate in this local region; f₁(x) and f₂(x) are spatially varying intensity averages for the internal and external regions of contour curve C, which are quite different from constants c₁ and c₂ of the CV model due to the introduction of K_σ(x, y). The other symbols have the same meanings as those mentioned above in the CV model.

The presence of Gaussian kernel K_σ(x, y) enables the LBF model to identify small intensity differences in local regions and have the capability of handling intensity inhomogeneity. Meanwhile, this model can avoid the time-consuming reinitialization step by introducing a new regularization term to penalize the deviation from a signed distance function [18]. However, this model relies on the initial curve placement to avoid the local minimums of the energy functional in the presence of severe intensity inhomogeneity due to the localization property of Gaussian kernel and simple intensity statistical estimation.

2.3. LIF model

The LIF model [44] was proposed by introducing the local image fitting energy with the local intensity averages m_i, i=1,2 based on the piecewise-smooth assumption that image I can be simply reconstructed by the internal region of m₁ and the external region of m₂ in a local region. The LIF energy can be regarded as a constraint of the differences between the local fitted image and the original image, and expressed as:

$$E^{\mathit{LIF}}=\frac{1}{2}{\int }_{\mathrm{\Omega }}{\left(I(x)-I^{\mathit{LIF}}(x)\right)}^{2}dx$$ (5)

$$I^{\mathit{LIF}}=m_1{H}_1(\varphi )+m_2{H}_2(\varphi )$$ (6)

$$\{\begin{array}{l}{m}_1=\mathit{mean}(I\in (\{x\in \mathrm{\Omega }\mid \varphi (x)<0\}\cap W_k(x)))\hfill \\ m_2=\mathit{mean}(I\in (\{x\in \mathrm{\Omega }\mid \varphi (x)>0\}\cap W_k(x)))\hfill \end{array}$$ (7)

where Ω is the whole image region; I^LFI denotes the local fitted image (LFI) for the approximation of the image I in a local region; m₁ and m₂ are intensity averages in this region defined by Gaussian window W_k with the stand deviation of σ and the radius of k. This model is able to achieve similar segmentation accuracy as the LBF model, and needs less computational time due to the presence of Gaussian smoothing for the level set function ϕ. However, the LIF model tends to ignore some details in the segmentation of small objects, because of the usage of the Gaussian smoothing filter, and thereby may suffer from inadequate image segmentation in the presence of intensity inhomogeneity.

3. Proposed method

To obtain reasonable segmentation performances for inhomogeneous images, we proposed to construct a novel energy functional by incorporating other valuable information. We noticed that a local region can not only be divided into two disjoint parts with f_i(x) in the LBF model, but also reconstructed approximately with m_i in the LIF model. This means that the LBF and LIF models can be combined together for image segmentation purpose. The combination will result in a novel local fitted image, called square fitted image (SFI) and quite different from the LFI image, and a novel active contour model, constructed by defining a local hybrid image fitting (LHIF) energy based on images I^SFI, I^LFI and I. The SFI image and LHIF energy are explained in detail in the following.

3.1. The SFI image

In the LIF model, a local region can be approximated by a local fitted image with the formulation of I^LFI(x) = m₁H₁(ϕ) + m₂H₂(ϕ), where m₁ and m₂ are intensity averages in the local neighborhood specified by Gaussian window. The average m_i equals to f_i(x) in the LBF model (i.e., m₁ = f₁(x) and m₂ = f₂(x)) when setting the same Gaussian parameters, by which image I^LFI can be incorporated into the LBF model. To this end, we set the same Gaussian parameters for m_i and f_i(x), with λ₁ = λ₂ = 1, and then the LBF fitting energy can be expanded as:

$$\begin{gathered} E^{\mathit{LBF}}=\sum _{i=1}^2\iint K_{\sigma }(x,y){\mid I(y)-f_i(x)\mid }^2{H}_i(\varphi )\mathit{dydx} \\ =\sum _{i=1}^2\iint K_{\sigma }(x,y)\left[I^2(y)-2I(y)m_i+m_i^2\right]H_i(\varphi )\mathit{dydx} \\ =\iint K_{\sigma }(x,y)\left[I^2(y)-2I(y)I^{\mathit{LFI}}(x)+m_1^2{H}_1(\varphi )+m_2^2{H}_2(\varphi )\right]\mathit{dydx} \end{gathered}$$ (8)

The minimization of the LBF fitting energy is equivalent to approximately minimizing the formulation of $I^2(y)-2I(y)I^{\mathit{LFI}}(x)+m_1^2{H}_1(\varphi )+m_2^2{H}_2(\varphi )$ in a local neighborhood centered at x, largely ignoring the effect of Gaussian kernel K_σ(x, y), which is mainly used to specify a local neighborhood. Due to I ≈ I^LFI in a local region, this approximation formulation can be further expressed as $m_1^2{H}_1(\varphi )+m_2^2{H}_2(\varphi )-I^2(x)$, leading to another fitted image $m_1^2{H}_1(\varphi )+m_2^2{H}_2(\varphi )$, called square fitted image I^SFI. Hence, the minimization of the LBF fitting energy can be obtained when local intensity average m_i satisfying the following two conditions, i.e., I(x) ≈ I^LFI(x) and I²(x) ≈ I^SFI(x).

3.2. The LHIF fitting energy

To take advantage of two local fitted images I^SFI and I^LFI, a local hybrid image fitting (LHIF) energy was proposed by quantifying the image differences between original image I and its two approximated versions, i.e., I^SFI and I^LFI in terms of Kullback–Leibler divergence, which can be expressed as:

$$E^{\mathit{LHIF}}={\lambda }_1\int \left[I(x)log\left(\frac{I(x)}{I^{\mathit{LFI}}(x)}\right)+I^{\mathit{LFI}}(x)log\left(\frac{I^{\mathit{LFI}}(x)}{I(x)}\right)\right]dx+{\lambda }_2\int \left[I^2(x)log\left(\frac{I^2(x)}{I^{\mathit{SFI}}(x)}\right)+I^{\mathit{SFI}}(x)log\left(\frac{I^{\mathit{SFI}}(x)}{I^2(x)}\right)\right]dx$$ (9)

$$I^{\mathit{SFI}}(x)=m_1^2{H}_1(\varphi )+m_2^2{H}_2(\varphi )$$ (10)

where λ₁ and λ₂ are the weighting parameters for the first and second integral terms; I^LFI(x) and I^SFI(x) are used to approximate images of I and I², respectively.

Note that images I and I² can be expressed as

$$\{\begin{array}{c}I(x)=I^{\mathit{LFI}}(x)+D^{\mathit{LFI}}(x)\\ I^2(x)=I^{\mathit{SFI}}(x)+D^{\mathit{SFI}}(x)\end{array}$$ (11)

where D^LFI(x) and D^SFI(x) are the residual errors for the approximations of I and I² and correlated according to the formulation

$$I^2(x)={(I^{\mathit{LFI}}(x)+D^{\mathit{LFI}}(x))}^2=I^{\mathit{SFI}}(x)+D^{\mathit{SFI}}(x)$$ (12)

Here, we do not focus on the relationship between these two errors, but on how to minimize the LHIF fitting energy because when both D^LFI(x) and D^SFI(x) are small enough and approach zero, this energy functional can be successfully minimized in theory.

To obtain smooth contour curves, two commonly used regularization terms $P(\varphi )=\frac{1}{2}\int {(\mid \nabla \varphi \mid -1)}^{2}dx$ and L(ϕ) = ∫|∇H(ϕ)|dx [18] were introduced into our model, resulting in the final fitting energy functional given by:

$$E(\varphi )=E^{\mathit{LHIF}}+\mu P(\varphi )+\upsilon L(\varphi )$$ (13)

where μ and υ are the weighting parameters for the signed distance function P(ϕ) and the length of level set function L(ϕ), respectively.

This energy functional is minimized by standard gradient descent [41,42]: for a fixed ϕ, E(ϕ) is minimized with respect to f_i(x) or m_i, which is given by:

$$f_i(x)=m_i=\frac{\int K_{\sigma }(x,y)I(y)H_i(\varphi (y))dy}{\int K_{\sigma }(x,y)H_i(\varphi (y))dy},i=1,2$$ (14)

For fixed f_i(x), E(ϕ) is minimized with respect to ϕ based on the gradient descent flow (see Appendix A)

$$\frac{\partial \varphi }{\partial t}=\delta (\varphi )({\lambda }_1{e}_1+{\lambda }_2{e}_2)+\mu \left({\nabla }^2\varphi -\mathit{div}\left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)\right)+\upsilon \delta (\varphi )\mathit{div}\left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)$$ (15)

$$e_1=(f_1(x)-f_2(x))\left(\frac{I(x)}{I^{\mathit{LFI}}(x)}-1-log\frac{I^{\mathit{LFI}}(x)}{I(x)}\right)$$ (16)

$$e_2=(f_1^2(x)-f_2^2(x))\left(\frac{I^2(x)}{I^{\mathit{SFI}}(x)}-1-log\frac{I^{\mathit{SFI}}(x)}{I^2(x)}\right)$$ (17)

4. Experiments

To demonstrate the performance of the developed mode, we applied it to segment both synthetic and real images in a variational level set framework. ϕ was initially set to a positive constant c₀ outside a region and −c₀ inside; and then computed iteratively by: ϕⁿ⁺¹ = ϕⁿ + Δt · Δϕⁿ; where Δt is time-step and n is iteration number. Gaussian kernel K_σ was truncated by a (2k + 1)(2k + 1) window, where k has been recommended for the smallest odd number no less than 2σ [14,15,34]. Other parameters were set by default as follows: σ = 3, c₀ = 2, λ₁ = 1.0, λ₂ = 0.1, Δt = 0.1, μ = 1, ε = 0.1 and υ = 0.001 × 255 × 255. The tests were conducted in Matlab R2013a programming environment on a PC with 3.3 GHz Intel Core system and 8GB RAM.

4.1. Segmentation of synthetic and real images

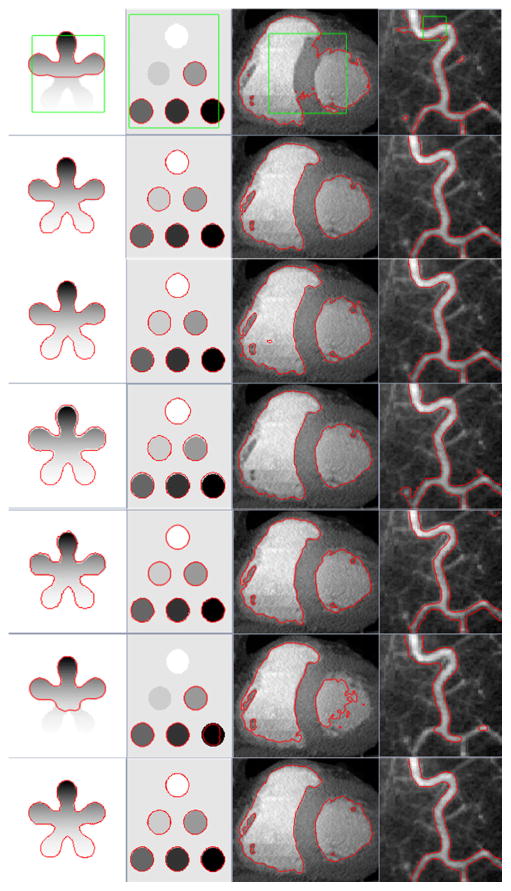
Fig. 1 shows the segmentation results of the proposed model for both synthetic and real images, which are inhomogeneous. Three randomly chosen initial rectangular contour curves shown in the first row, can evolve successfully to the boundaries of the desired objects with different sizes and shapes. According to these evolution results, it can be seen that our proposed model is capable of accurately segmenting the desired objects from noisy and inhomogeneous images. Also, our model needs relatively few iterations to drive the contours to desirable boundaries.

Fig. 1.

The segmentation results of the proposed model for both synthetic and real images displayed in different columns by changing default parameter values (i.e., σ = 5, Δt = 0. 01, ε = 1. 0 and υ = 0.0085 × 255 × 255 for the first image; σ = 5 and ε = 5 for the second image, λ₂ = 0.05, σ = 7, Δt = 0.01 and ε = 7 for the third image). Row 1: initial rectangle contours and their final evolutions. Row 2 and Row 3: intermediate results with 50 and 100 iterations, respectively.

4.2. Segmentation of medical images

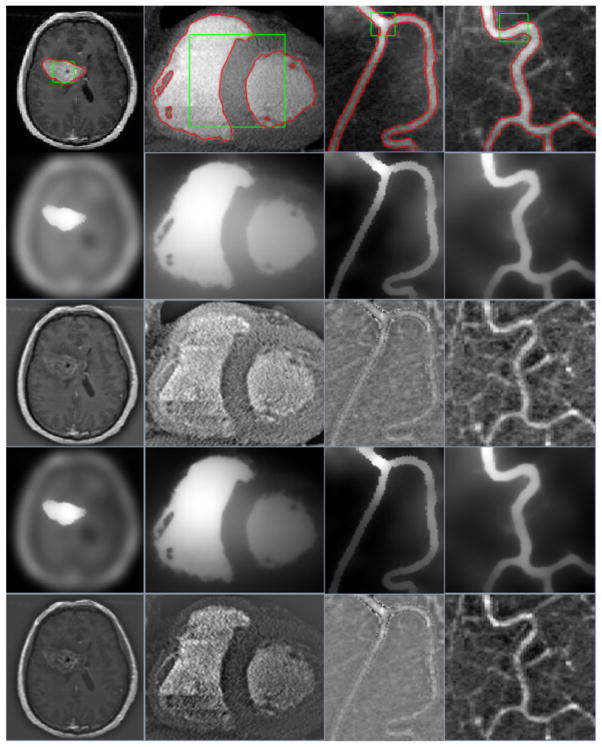
Fig. 2 shows the segmentation results when applying the developed model to four clinically medical images with both intensity inhomogeneity and complex image background. As demonstrated by these examples, our proposed model can accurately identify the boundaries of all targeted objects based on randomly chosen rectangle initial curves, while successfully excluding a great deal of undesired background information due to the existence of two different local information from images I^LFI and I^SFI. Both of these two fitted images are capable of effectively highlighting the desirable objects with different texture characteristics, and significantly reduces the adverse influence of complicated image background in image segmentation. I^SFI demonstrates a unique strength in emphasizing the intensity differences between the foreground and background of images to be segmented, which can be partly verified according to the two estimated images of D^LFI and D^SFI.

Fig. 2.

The segmentation results of our proposed model for four medical images by replacing several default parameter values from left to right (i.e., λ₂ = 0.07, σ = 5, Δt = 0.01 and ε = 1.0 for the first image; σ = 19, Δt = 0.01 and ε = 7 for the second image; σ = 5, Δt = 0.35 and ε = 1 for the third image; and σ = 8, Δt = 0.01 and ε = 1 for the last image). Row 1: initial rectangle contours and their final evolutions. Row 2 and Row 3: fitted images I^LFI and D^LFI. Row 4 and Row 5: fitted images I^SFI and D^SFI.

4.3. Comparative evaluation

We also compared the developed model with region-based active contour models ¹ (i.e., the CV model, LBF model, LIF model, local Gaussian distribution fitting (LGDF) model [33], local region-based CV model (LRCV) [20] and cross entropy based model (CEM) [27]) to display their performance differences. The comparison of these models was presented in Fig. 3, where the initial green contour curves and their final evolution results were displayed in different rows, respectively. These segmentation results can effectively demonstrate their performances in terms of handling severe intensity inhomogeneity, extracting multiple target objects, and excluding complex image background. Specifically, the CV and CEM models cannot handle intensity inhomogeneity and had the worst segmentation performances among these models; and the LBF, LIF, LGDF, and LRCV models can, to some extent, extract the desirable objects from those regions with severe intensity inhomogeneity, but had the inadequate or excessive segmentation problems in the neighborhood nearby the target boundaries. Different from above these models, our proposed model achieved better segmentation performances in terms of accuracy for all these four images based on the same initial contour curves.

Fig. 3.

Comparisons of the CV, LBF, LIF, LGDF, LRCV, CEM and our models for the segmentation of four images displayed in different columns based on the same initial green contour curves. Row 1 to Row 7: results of the CV, LBF, LIF, LGDF, LRCV, CEM and our models, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

We also quantitatively assessed the performance of these models using the Dice Similarity Coefficient (DSC) [31] as defined as:

$$\mathit{DSC}(A,B)=\frac{2N(A\cap B)}{N(A)+N(B)}$$ (18)

where ∩ is the intersection operator; N (·) is the number of pixels enclosed set. A is segmentation results of a given algorithm; B is the ground truths, which in general approximately replaced by the manual segmentation. The value of DSC ranges from 0 to 1, and the higher the value of DSC is, the more accurate the result of the algorithm is. According to this metric, the segmentation results of these models, based on images displayed in Figs. 1 and 2, were quantified and shown in Tables 1 and 2, respectively.

Table 1.

Comparison of our proposed model with the CV, LBF, LIF, LGDF, LRCV and CEM models based on DSC for synthetic and real images shown in Fig. 1.

Models	Image1	Image2	Image3	Mean
CV	0.533	0.813	0.935	0.760
LBF	0.969	0.949	0.972	0.963
LIF	0.972	0.940	0.966	0.959
LGDF	0.970	0.948	0.948	0.955
LRCV	0.883	0.934	0.891	0.903
CEM	0.672	0.611	0.797	0.693
LHIF	0.987	0.959	0.981	0.976

Table 2.

Comparison of our proposed model with the CV, LBF, LIF, LGDF, LRCV and CEM models based on DSC for clinically medical images shown in Fig. 2.

Models	Image1	Image2	Image3	Image4	Mean
CV	0.412	0.904	0.754	0.752	0.705
LBF	0.898	0.976	0.951	0.979	0.951
LIF	0.890	0.955	0.956	0.951	0.938
LGDF	0.909	0.948	0.964	0.977	0.950
LRCV	0.796	0.962	0.963	0.954	0.919
CEM	0.451	0.827	0.783	0.705	0.692
LHIF	0.919	0.981	0.969	0.981	0.963

The quantitative assessments demonstrate that our model has the largest values of DSC for all test images, the CV and CEM models have the lowest values of this measure due to absence of local image information. Although the LBF, LIF, LGDF and LRCV models can segment the desired objects in the presence of intensity inhomogeneity, they are less accurate than our proposed model. In addition, the computational cost of these models in our experiments were given in Table 3 for images displayed in Fig. 1. Although our model need more segmentation time than the CV model for these images due to the existence of various local information, it is more efficient than the LBF, LIF, LGDF and LRCV models. As for the CEM model, it is based on the same global information as the CV model, but its segmentation time varies dramatically with images. In summary, our model has better segmentation performances than the global and local region-based models, considering both computational time and accuracy.

Table 3.

Comparison of our model and the CV, LBF, LIF, LGDF, LRCV and CEM models in terms of iterations (Iter) and CPU time for synthetic and real images given in Fig. 1.

Models	Image1		Image2		Image3
	96 × 127 pixels		75 × 79 pixels		93 × 118 pixels
	Iter	Time(s)	Iter	Time(s)	Iter	Time(s)
CV	100	0.438	50	0.235	100	0.420
LBF	200	1.689	600	2.392	200	2.454
LIF	1000	2.510	800	1.859	200	3.056
LGDF	400	7.329	400	7.315	200	2.509
LRCV	800	9.932	360	4.217	100	4.462
CEM	500	2.945	400	2.214	150	0.889
LHIF	300	1.649	150	0.825	300	1.942

We further compared our developed model with available local region-based models (i.e., the LBF, LIF, LGDF, and LRCV models) based on publicly available Berkeley segmentation data set 500 (BSDS500) [24,28]. This dataset consists of a number of natural images and their ground truth manually generated by different individuals. The performance was quantitatively evaluated using the probabilistic rand index (PRI) [26], which was given by:

$$\mathit{PRI}(A,B)=\frac{2}{N(N-1)}\sum _{i,j;i<j}[s_{ij}{q}_{ij}+(1-s_{ij})(1-q_{ij})]$$ (19)

where B = {B₁, B₂, ···, B_M} is M ground truths, A = {x₁, x₂, ···, x_N} is the result of a specified algorithm where a subscript indexes one of N pixels. s_ij is a membership function, and set to 1 when pixels i and j belong to the same cluster, and otherwise to 0. q_ij is the ground truth probability of pixels i and j belonging to the same cluster. The PRI takes a value between 0 and 1, with a higher value representing a more accurate segmentation. With the PRI, the comparative results of all models were displayed in Table 4. ² As demonstrated by the results, our model has the highest PRI values for 12 images, along with highest mean of the PRI.

Table 4.

Comparison of our model and the LBF, LIF, LGDF, and LRCV models in terms of PRI for randomly chosen 15 images from BSDS500 data set.

Image ID	LBF	LIF	LGDF	LRCV	LHIF
15088	0.773	0.858	0.862	0.797	0.876
28096	0.920	0.951	0.969	0.941	0.971
35070	0.659	0.776	0.754	0.713	0.793
66075	0.707	0.790	0.801	0.749	0.859
80099	0.802	0.826	0.888	0.911	0.924
108004	0.773	0.768	0.850	0.713	0.817
113044	0.605	0.601	0.723	0.701	0.788
135069	0.987	0.986	0.988	0.986	0.987
147091	0.735	0.755	0.863	0.724	0.869
175043	0.835	0.805	0.797	0.803	0.832
196027	0.810	0.843	0.885	0.829	0.891
207056	0.735	0.701	0.755	0.747	0.805
227092	0.796	0.779	0.750	0.755	0.810
296059	0.738	0.854	0.827	0.742	0.865
317080	0.784	0.791	0.787	0.777	0.839
Mean	0.777	0.806	0.833	0.793	0.862

5. Discussion

5.1. Parameters analysis

Although our proposed model demonstrated a relatively high performance in image segmentation, it is not easy to achieve an optimal tradeoff among different weighting parameters. Most of these parameters have been analyzed and discussed in previous studies [33] in detail. Here, we only focus on parameters λ₁ and λ₂, which are mainly used in our model to keep a tradeoff between the two intensity integral terms derived from I^LFI(x) and I^SFI(x), respectively. The first integral term tends to segment the objects with different intensity characteristics, including certain background regions nearby the desired boundaries; while the second term highlights to some extent the differences of image intensities in local regions, consequently making it difficult to extract undesired background regions. To correctly segment desired foreground and avoid undesired background, it is advisable to set proper values for λ₁ and λ₂ according to the characteristics of the image itself, including intensity inhomogeneity, noise level and image contrast. For example, (λ₁, λ₂) are set to (0.85, 0.1), (1.0, 0.1) and (1.0, 0.25) respectively for the segmentations of images shown in Fig. 4. Their segmentation results demonstrate that our proposed model is relatively stable when solely changing the parameter λ₁ in a small range, but unstable when changing the parameter λ₂ under the condition of fixing the other parameters. This means that the first integral term plays greater important part in image segmentation than the second term; and is more tolerant for the changes of its corresponding weighting parameter.

Fig. 4.

The segmentation results of our model by merely changing (λ₁, λ₂) to (0.85, 0.1), (1.0, 0.1) and (1.0, 0.25) for images shown in different columns.

5.2. Sensitivity to initialization and noise

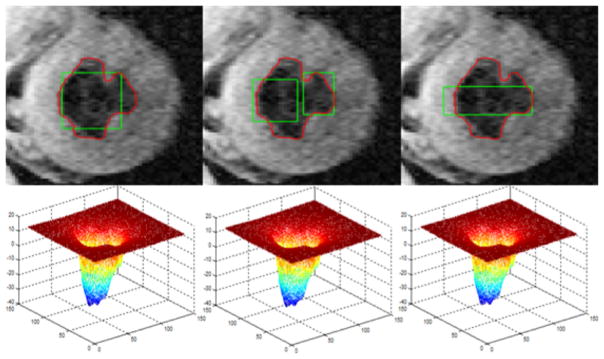
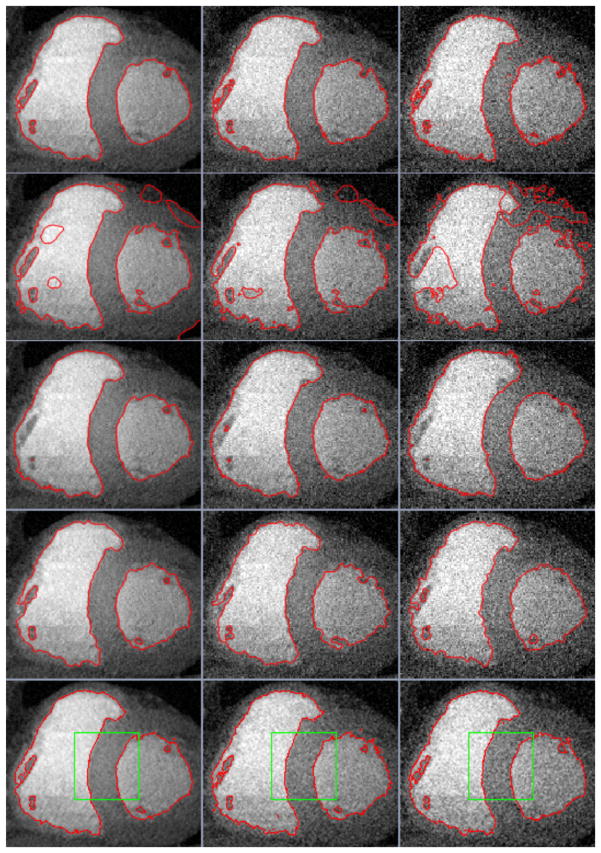
To estimate our model in terms of sensitivity to initial curve placements and robustness against noise, it was tested, by keeping all the parameters fixed, for a medical image displayed in Fig. 5 with different initial curves; and then compared with the LBF, LIF, LGDF and LRCV models based on the same initial curve for another medical image shown in Fig. 6, which was normalized and corrupted by Gaussian white noise with zeros mean and variances of 0.005, 0.01, and 0.015, respectively. The red evolution results presented in Fig. 5 demonstrate that our model has nearly the same results for different initial curves, and deteriorated performances as noise variances increase according to Fig. 6. These noises cause some undesirable regions are extracted, together with ignoring small details of target objects; but these adverse segmented components of our model are tiny compared with the whole segmentation results. This means that our model is insensitive to initial curve placements due to the local information from both I^LFI and I^SFI, and robust to some extent against Gaussian white noise in segmentation, relative to other existing models shown in Fig. 6.

Fig. 5.

The segmentation results of our models for a real image based on different initial contour curves. Row 1: initial rectangle contours and their final evolutions. Row 2: the estimated level set functions.

Fig. 6.

Comparison of the LBF, LIF, LGDF, LRCV and our models based on the same green initial curves for the image corrupted by Gaussian white noise with variances of 0.005, 0.01, and 0.015, respectively. Rows 1–5: the results of the LBF, LIF, LGDF, LRCV and our models, respectively. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)

6. Conclusions

In this study, a novel region-based active contour model was developed for accurate image segmentation. Its novelty lies in the introduction of a novel local hybrid region intensity fitting energy based on the LBF and LIF models, and this energy functional was constructed by using the original image and its two local fitted versions drawning upon the concept of Kullback–Leibler divergence, and minimized in a variational level set framework to drive the motion of the contour curves to desirable boundaries. Experiments demonstrate that our proposed model is capable of segmenting synthetic and real images, as well as clinically medical images, and has a relatively higher performance as compared to available region-based models.

Appendix A. Derivation of the gradient flow

The minimization of energy functional E(ϕ) is equal to search for the steady-state solution of the following gradient flow formulation:

$$\frac{\partial \varphi }{\partial t}=-\frac{\partial E}{\partial \varphi }$$

where $\frac{\partial E}{\partial \varphi }$ is the Gateaux derivative [37,38,43] of E(ϕ) with respect to ϕ. In our proposed model, the derivations of regularization terms of ϕ in Eq. (12) have been already analyzed in previous paper [33], we only need to solve the derivative of E^LHIF in the manner: ϕ̃ = ϕ + ηϱ with a small variation η. Fixing f_i(x), i = 1, 2 and letting ϱ → 0, we have

$$\begin{gathered} \frac{\partial E^{\mathit{LHIF}}}{\partial \varphi }=\underset{\varrho \to 0}{lim}\frac{d}{d\varrho }\int {\lambda }_1\left[I(x)log\left(\frac{I(x)}{I^{\mathit{LFI}}(x)}\right)+I^{\mathit{LFI}}(x)log\left(\frac{I^{\mathit{LFI}}(x)}{I(x)}\right)\right]+{\lambda }_2\left[I^2(x)log\left(\frac{I^2(x)}{I^{\mathit{SFI}}(x)}\right)+I^{\mathit{SFI}}(x)log\left(\frac{I^{\mathit{SFI}}(x)}{I^2(x)}\right)\right]dx \\ =\underset{\varrho \to 0}{lim}\eta \delta (\stackrel{\sim }{\varphi })\int {\lambda }_1(f_1(x)-f_2(x))\left(1-\frac{I(x)}{I^{\mathit{LFI}}(x)}+log\left(\frac{I^{\mathit{LFI}}(x)}{I(x)}\right)\right)+{\lambda }_2\left(f_1^2(x)-f_2^2(x)\right)\left(1-\frac{I^2(x)}{I^{\mathit{SFI}}(x)}+log\left(\frac{I^{\mathit{SFI}}(x)}{I^2(x)}\right)\right)dx \end{gathered}$$

Thus the corresponding Euler–Lagrange equation can be given by:

$${\lambda }_1(f_1(x)-f_2(x))\left(1-\frac{I(x)}{I^{\mathit{LFI}}(x)}+log\left(\frac{I^{\mathit{LFI}}(x)}{I(x)}\right)\right)+{\lambda }_2(f_1^2(x)-f_2^2(x))\left(1-\frac{I^2(x)}{I^{\mathit{SFI}}(x)}+log\left(\frac{I^{\mathit{SFI}}(x)}{I^2(x)}\right)\right)=0$$

The Gateaux derivative of E^LHIF is derived as follows

$$\frac{\partial E^{\mathit{LHIF}}}{\partial \varphi }={\lambda }_1(f_1(x)-f_2(x))\left(1-\frac{I(x)}{I^{\mathit{LFI}}(x)}+log\left(\frac{I^{\mathit{LFI}}(x)}{I(x)}\right)\right)+{\lambda }_2(f_1^2(x)-f_2^2(x))\left(1-\frac{I^2(x)}{I^{\mathit{SFI}}(x)}+log\left(\frac{I^{\mathit{SFI}}(x)}{I^2(x)}\right)\right)$$

Combining the derivative of all the three terms in our proposed model, the total variational formulation of ϕ is as below

$$\frac{\partial \varphi }{\partial t}=-\frac{\partial E^{\mathit{LHIF}}}{\partial \varphi }+\mu \left({\nabla }^2\varphi -\mathit{div}\left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)\right)+\upsilon \delta (\varphi )\mathit{div}\left(\frac{\nabla \varphi }{\mid \nabla \varphi \mid }\right)$$