APPROACHING ULTIMATE INTRINSIC SIGNAL-TO-NOISE RATIO WITH LOOP AND DIPOLE ANTENNAS

Abstract

Purpose

Previous work with body-size objects suggested that loops are optimal MR detectors at low fields, whereas electric dipoles are required to maximize signal-to-noise ratio (SNR) at ultra-high fields (≥7T). Here we investigated how many loops and/or dipoles are needed to approach the ultimate intrinsic (UI) SNR at various field strengths.

Methods

We calculated the UISNR inside dielectric cylinders mimicking different anatomical regions. We assessed the performance of various arrays with respect to the UISNR. We validated our results by comparing simulated and experimental coil performance maps.

Results

Arrays with an increasing number of loops can rapidly approach the UISNR at fields up to 3T, but are suboptimal at ultra-high fields for body-size objects. The opposite is true for dipole arrays. At 7T and above, 16 dipoles provide considerably larger central SNR than any possible loop array, and minimal g factor penalty for parallel imaging.

Conclusion

Electric dipoles can be advantageous at ultra-high fields because they can produce both curl-free and divergence-free currents, whereas loops are limited to divergence-free contributions only. Combining loops and dipoles may be optimal for body imaging at 3T, whereas arrays of loops or dipoles alone may perform better at lower or higher field strengths, respectively.

INTRODUCTION

Analytic electrodynamic simulations enable rapid modeling of electromagnetic (EM) effects in simple object geometries (1,2). For example, mode expansions with dyadic Green’s functions (DGF) have been used to express the full-wave EM field in a dielectric sphere (3,4) and cylinder (3,5) for simulated magnetic resonance (MR) experiments. The EM field was employed to compute signal-to-noise ratio (SNR) and specific absorption rate (SAR), both for specific coil geometries and for the ultimate intrinsic (UI) case, which is independent from any particular coil design. UISNR and UISAR, which can be calculated also with other approaches (6–10), are absolute metrics that enable to predict coil performance in simulation (11–13) or to rigorously assess the performance of actual coil prototypes (14). Although they use simplified geometries to model anatomical regions, DGF simulations can provide useful physical insights, which have already led to novel coil designs for ultra-high-field (UHF) MR imaging (15–18).

Previous work, using either DGF simulations (11) or other methods (19), showed that finite coil arrays can approach the UISNR at the center of a head-size spherical object and achieve a significant fraction of it at intermediate voxel positions. Only one previous study investigated array performance with respect to the UISNR for cylindrical geometries (13). This study showed that an array of loop coils encircling a dielectric cylinder mimicking the human body could approach UISNR for a central voxel at low fields, whereas the performance was considerably lower at UHF (≥ 7 T). In subsequent work, we demonstrated that, in fact, loop coils could not approach the UISNR at UHF, because they can capture only divergence-free currents, whereas there is a significant contribution of curl-free currents to the UISNR at UHF (3). This observation suggested that electric dipoles, which can produce curl-free current contributions but had traditionally been viewed as inefficient MR detectors and transmitters, could improve central SNR at UHF, paving the way for novel coil designs in recent years (15–18,20,21). Some designs combined loop and dipole elements to improve SNR (17,20,21), but the optimal choice of loops, dipoles, or mixed arrays remains an open question for a variety of anatomical targets.

In the current work, we extended the DGF framework for cylindrical geometries to model electric dipoles, in addition to “cylindrical window” loop coils (3). We computed absolute SNR performance in a uniform cylinder for arrays of loops, electric dipoles, and combinations of these two coil types. We investigated array performance for different sample dimensions and electrical properties, main magnetic field strengths, imaging planes and acceleration factors. To validate our DGF simulations, we modeled an existing 3 T loop array prototype and compared the predicted performance with the corresponding experimental performance. In Appendix A and in Supporting Note 1, we detail all the equations needed to reproduce the results of this paper. Preliminary results of this work were presented at the 2016 UHF Workshop of the International Society for Magnetic Resonance in Medicine (22).

THEORY

The UISNR is the largest possible SNR allowed by electrodynamics, independent of particular coil geometry. It can be calculated as an SNR-optimizing weighted combination of contributions from a basis of surface current modes (3). If we consider a uniform infinite cylinder of radius r_a, we can define a basis of current modes on a concentric cylindrical surface with radius r_b:

$${\mathit{K}}_n(m,\phi ,z)=W_n^{(M)}(m)\mathit{\nabla }\times e^{in\phi }{e}^{\mathit{imz}}\widehat{\mathit{r}}+W_n^{(E)}(m)\mathit{\nabla }{e}^{in\phi }{e}^{\mathit{imz}}.$$ [1]

Here, m and n are mode indices, $i=\sqrt{-1}$ is the imaginary unit, φ and z are the azimuthal and axial coordinates, respectively, $W_n^M(m)$ and $W_n^{(E)}(m)$ are coefficients for divergence-free and curl-free surface currents, respectively. According to the surface equivalent theorem (23), the basis in Eq. [1] can generate all possible EM field distributions within the sample, since it includes both magnetic and electric surface current densities. The net EM field generated by the current modes inside the cylinder can be calculated using the appropriate DGF (Appendix A):

$$\begin{array}{l}\mathit{E}(\mathit{r})=-\frac{\omega {\mu }_0}{8\pi }{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }[{\mathit{M}}_{n,\gamma }(m,\mathit{r})V_n^M(m)+{\mathit{N}}_{n,\gamma }(m,\mathit{r})V_n^N(m)]dm\\ \mathit{B}(\mathit{r})=-\frac{i{k}_{in}{\mu }_0}{8\pi }{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }[{\mathit{N}}_{n,\gamma }(m,\mathit{r})V_n^M(m)+{\mathit{M}}_{n,\gamma }(m,\mathit{r})V_n^N(m)]dm\end{array}$$ [2]

Here, ω is the angular frequency, μ₀ is the magnetic permeability of free space, $k_{in}=\sqrt{{\omega }^2{\epsilon }_r{\epsilon }_0{\mu }_0-i\omega {\mu }_0\sigma }$ is the complex wave number inside the cylinder, where ε_r and σ are the relative permittivity and the electric conductivity, respectively, and ε₀ represents the electric permittivity of free space. M_n,γ(m,r) and N_n,γ(m,r) are vector wave functions used to construct the DGF, whereas $V_n^M(m)$ and $V_n^N(m)$ are weighting coefficients derived by multiplying the current coefficients by a transformation matrix T, which accounts for boundary conditions both at r_b and at the location (r_c) of the conductive shield surrounding both the object and the current patterns. All these quantities are defined in Appendix A. Note that harmonic time variation is assumed for all fields and currents, although the common factor e^+iωt is omitted from the equations for convenience.

If we employ the current modes as hypothetical elements of an infinite coil array, we can construct a sensitivity matrix, S, which contains the complex-valued receive sensitivities associated with each mode at the target position r₀ (as well as all the aliased positions r in the case of parallel imaging), and a noise covariance matrix Ψ_mode that accounts for interactions between the modes’ electric fields. We can then calculate the UISNR per unit bandwidth as (3,11):

$$\stackrel{\sim }{\xi }({\mathit{r}}_0)=\frac{{\omega }_0{M}_0}{\sqrt{4k_B{T}_S{\left(\mathit{S}{(\mathit{r})}^H{\mathbf{\Psi }}_{\mathit{mode}}^{-1}\mathit{S}(\mathit{r})\right)}_{0,0}^{-1}}}$$ [3]

Here M₀ is the equilibrium magnetization, ω₀ is the Larmor frequency, k_B is the Boltzmann constant, T_S is the absolute temperature of the sample, and the “0,0” subscript indicates the diagonal element of the matrix in parenthesis with an index associated with the target position r₀.

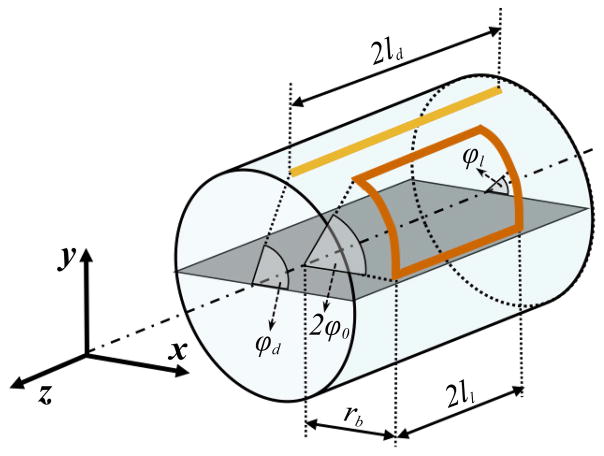
The SNR of particular radiofrequency (RF) antennas can be calculated within the same DGF theoretical framework by applying appropriate weighting coefficients to the basic modes. The current weights for a cylindrical window loop coil with angular aperture 2φ₀ and axial length 2l_l (Figure 1) were derived in (3) as

Figure 1. Schematic representation of the cylindrical sample, a cylindrical window coil (orange) and a z-directed electric dipole (yellow).

The coil elements were modeled on a cylindrical surface concentric with the sample, which was surrounded by the conductive shield of the system (not shown).

$$\begin{array}{l}{W}_n^{\mathit{loop},(M)}(m)=-\frac{{\phi }_0{l}_l}{{\pi }^2}\mathit{sinc}(n{\phi }_0)\mathit{sinc}(m{l}_l)e^{-in{\phi }_l}{e}^{im\mathrm{\Delta }z}\\ W_n^{\mathit{loop},(E)}(m)=0\end{array}$$ [4]

where φ₁ and Δz are the azimuthal and axial offset of the loop from φ = 0 and z = 0, respectively. (Note that Eq. [4] multiplies the corresponding expression in (3) by a factor of −1/2π² to achieve the desired normalization). For the current work, we have derived (Appendix A) the current weights for a straight filamentary electric dipole of length 2l_d along the z direction (Figure 1), carrying current $I(z)=cos\left(\frac{\pi z}{2l_d}\right)$ to model an actual dipole with a central feed point:

$$\begin{array}{l}{W}_n^{\mathit{dipole},(M)}(m)=\frac{i}{4{\pi }^2}\frac{\frac{n{l}_d}{{(r_b)}^2}\left\{\mathit{sinc}\left(m{l}_d-\frac{\pi }{d}\right)+\mathit{sinc}\left(m{l}_d+\frac{\pi }{2}\right)\right\}}{\frac{n^2}{r_b}+m^2}{e}^{-in{\phi }_d}{e}^{-im\mathrm{\Delta }z}\\ W_n^{\mathit{dipole},(E)}(m)=\frac{-i}{4{\pi }^2}\frac{\frac{m{l}_d}{r_b}\left\{\mathit{sinc}\left(m{l}_d-\frac{\pi }{d}\right)+\mathit{sinc}\left(m{l}_d+\frac{\pi }{2}\right)\right\}}{\frac{n^2}{r_b}+m^2}{e}^{-in{\phi }_d}{e}^{-im\mathrm{\Delta }z}\end{array}$$ [5]

where φ_d is the angular position of the dipole around the circumference of the cylinder, and Δz accounts for the axial offset as in the previous equation. Eq. [5] shows that typical electric dipoles combine divergence-free and curl-free surface current components (24), whereas the current patterns of loop coils are always divergence-free (Eq. [4]).

The receive sensitivity and the noise covariance matrix elements for finite arrays of cylindrical window loop coils and/or electric dipoles are obtained by applying the combination weights in Eqs. [4] and [5], respectively, to the corresponding mode expressions:

$$\begin{array}{l}\mathit{S}(\mathit{r})\to {\mathit{W}}^T\mathit{S}(\mathit{r})\hfill \\ {\mathbf{\Psi }}_{\mathit{mode}}\to {\mathit{W}}^T{\mathbf{\Psi }}_{\mathit{mode}}{\mathit{W}}^{\ast }\hfill \end{array}.$$ [6]

The vector W includes the coefficients for both divergence-free and curl-free modes:

$$\mathit{W}=\left(\begin{array}{l}{W}_n^{\mathit{loop}/\mathit{dipole},(M)}(m)\hfill \\ W_n^{\mathit{loop}/\mathit{dipole},(E)}(m)\hfill \end{array}\right)$$ [7]

The SNR of the array is then calculated as for the ultimate case, but replacing the quantities in Eq. [3] with those in Eq. [6]. In addition to the intrinsic thermal noise due to the presence of the sample (sample noise), coil conductor losses (coil noise) can be included in the SNR calculation as an extra term added to the diagonal elements of the coils’ covariance matrix (Appendix A).

METHODS

Simulations

The SNR of encircling arrays of cylindrical window loops and z-directed dipoles, as well as the UISNR associated with the same cylindrical geometry, were calculated using azimuthal and axial mode expansion orders of n = −48:1:47 and m = −150:1:149 (57,600 total surface current modes), respectively, to ensure convergence (Supporting Figure S1). We approximated three anatomical regions as homogeneous dielectric cylinders with different radii: head (r_a = 9 cm), body (r_a = 17 cm) and extremities (r_a = 6 cm). These sample dimensions, as well as the corresponding electrical properties (Table 1), were extracted as average values from the Virtual Family (Duke) dataset (IT’IS Foundation, Zurich, Switzerland) (25). The current distribution (Eq. [1]) was defined on a surface concentric with the sample at r_b = r_a + 0.5 cm, whereas the system conductive shield was modeled at a fixed distance of r_c = 34.25 cm. UISNR and SNR of finite arrays were simulated for different main magnetic field strength (B₀), voxel position, acceleration factor, and number of elements. For each array, all coil elements of the same type (cylindrical window loop or z-directed dipole) had the same dimensions. To assess array performance with respect to the number of loops, for each case the coil elements were uniformly distributed in multiple rows. The total axial length of the loop arrays was 22 cm, 30 cm, and 20 cm, for head, body and extremities, respectively. Electric dipoles were symmetrically distributed around the cylinder in a single row. For each magnetic field strength and sample size, the length of the electric dipoles (2l_d) was optimized for maximum SNR at the center, by repeating the calculation over a range of lengths (Table 1). Annealed copper conductivity (58×10⁶ S m⁻¹) and conductor thickness equal to skin depth at the operating frequency were assumed to compute coil noise. All calculations were implemented in Matlab (MathWorks, Natick, MA).

Experimental validation

In order to validate our simulations, we used the DGF framework to model a 24-element 3 T prototype array of encircling cylindrical window coils, which had been previously constructed at our research center (Figure 2). Coil elements were made of wire conductors, with axial and azimuthal length equal to 14.08 cm and 14.05 cm, respectively, and were uniformly distributed on a cylindrical former with radius = 15.75 cm. They were arranged in three rows of eight coils each, with adjacent elements overlapped by 10% along both the axial and the azimuthal directions, and with the middle row staggered by half the coil aperture (φ₀). We used a mode expansion order of n = −48:1:47 and m = −800:1:799 to approximate as closely as possible in DGF the width of the unrolled surface of the wires, and we calculated a correction factor for the coil noise term to account for the remaining differences (Supporting Note 1). We calculated the UISNR and the SNR of the 24-element array for a transverse plane at the center of a uniform cylinder modeled after a phantom available at our institution. The phantom had radius = 14.61 cm, length = 120 cm, electric conductivity and relative permittivity equal to 0.52 S m⁻¹ and 80.7, respectively.

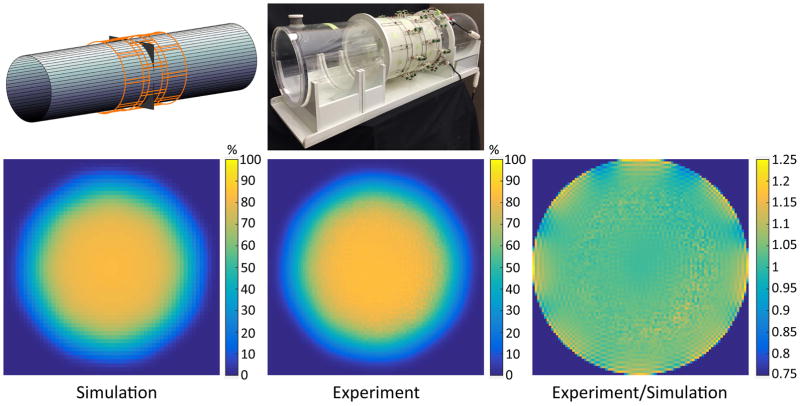
Figure 2. Simulated vs. experimental coil performance maps at 3 T, for a transverse plane at the center of a cylindrical phantom.

DGF simulations (left) provided an accurate prediction of the absolute performance, i.e., SNR as a percentage of the UISNR, of the actual array (center). The two maps were practically identical, except near the edge of the sample (right).

The cylindrical phantom was scanned on a 3 T MR scanner (TIM Trio, Siemens Healthineers, Erlangen, Germany) using the 24-element array and the same image plane as for the simulations. A single proton density weighted two-dimensional gradient echo image (GRE) was obtained with parameters TR = 2000 ms, TE = 5 ms, slice thickness = 3 mm, 128×128 matrix, FOV = 400 mm, and receiver bandwidth = 46.1 kHz (line bandwidth = 180 Hz/pixel). The flip angle distribution was mapped by fitting a sinusoid model of image intensity to each image pixel across eight body coil reference images, acquired with identical pulse sequence parameter values but with increasing transmit voltages (14). Individual coil GRE images were then normalized voxel-by-voxel by the sine of the measured flip angle, and these normalized maps were then used as an approximation of the receive sensitivity profiles S(r). Note that this is a valid approximation, because the phantom contained no internal structure. We acquired a noise reference measurement by recording complex-valued data with the coil array using the same pulse sequence used for the image acquisition but with no RF excitation. The noise covariance matrix, Ψ, was calculated from the statistics of the noise samples scaled by the noise equivalent bandwidth (26). An experimental SNR map was obtained using S and Ψ, following the general procedure outlined by Kellman and McVeigh (26), and was cropped to a size of 92×92 to produce a tight FOV around the phantom.

A predicted coil performance map, which provides a measure of coil efficiency as a function of position inside the sample of interest, was synthetically generated by dividing, voxel-by-voxel, the simulated array SNR map by the UISNR map. An experimental coil performance map was then generated by dividing experimental SNR values by suitably scaled UISNR values. Specifically, for comparison with experimental values, the UISNR values were scaled to account for the specific pulse sequence parameters and system characteristics (14):

$${\stackrel{\sim }{\xi }}^{\prime }({\mathit{r}}_0)=\stackrel{\sim }{\xi }({\mathit{r}}_0)\frac{V_{\mathit{voxel}}\sqrt{N_{\mathit{acq}}{N}_{\mathit{ave}}}\mathit{sin}(\theta )}{F\sqrt{\mathrm{\Delta }f}}$$ [8]

where V_voxel is the volume of the voxel, N_acq is the number of the acquired k-space samples (256×128 in this case including oversampling in the frequency readout), N_ave is the number of signal averages, θ is the flip angle (sin(θ)=1 in this case as the experimental maps were normalized), F is the system noise factor and Δf is the receiver bandwidth. (Note that we corrected a typographical error in the original equation in Ref. (14), where F is written inside the square root.) F was obtained experimentally (14), and was equal to 1.14. Other factors used in Eq. [3] were M₀ = 9.03×10⁻³ A·m⁻¹, T_S = 295 K, ω₀ = 2π×123.2 rad·MHz, and k_B = 1.381×10⁻²³ J·K⁻¹. Predicted and experimental coil performance maps were then compared.

RESULTS

Predicted and experimental performance maps of the 24-element loop array were in close agreement, except for small regions near the surface of the cylinder (Figure 2), where both UISNR and experimental SNR measurements are known to be difficult to stabilize. This finding represents an indirect validation of other DGF simulation results presented here.

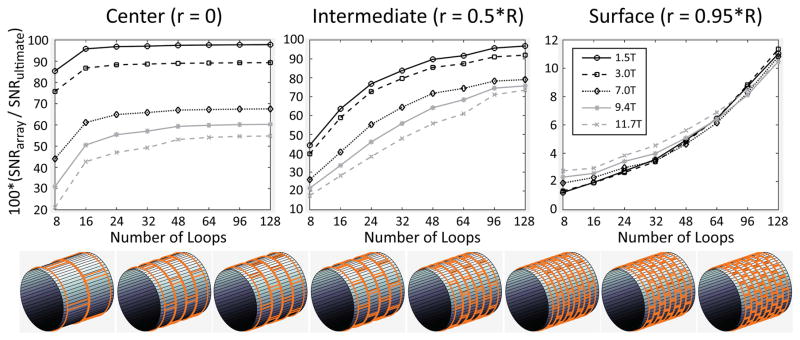
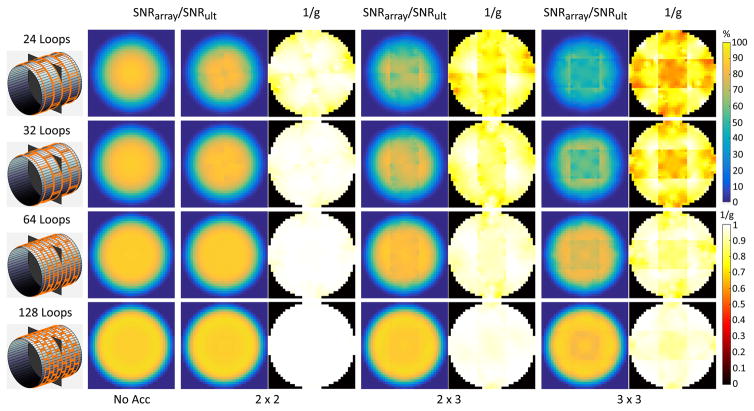
Figure 3 shows that at 1.5 T and 3 T it was possible to approach the UISNR for interior regions of the body with finite arrays of loop coils encircling the sample. For a central voxel, array performance rapidly converged to an asymptotic value for increasing number of coils. The rate of convergence depended on the size and properties of the sample, and it was faster for the body-mimicking object (Figure 3 vs. Supporting Figure S2). Loop performance was considerably lower at UHF, except in the case of the extremities, for which it exceeded 90% at 7 T (Supporting Figure S2). For an intermediate voxel, loop performance was more similar among field strengths, and it increased monotonically as a function of the number of coils without reaching a plateau, even with 128 coils. As expected (11), large arrays still resulted in low performance for a voxel close to the surface of the cylinder. Even larger numbers of small elements would be required in this case. However, Figure 4 shows that the superficial region of low performance became narrower with more coils. Larger arrays also enabled higher acceleration factors, and the 128-element “body” array had almost no g factor penalty for 9-fold (R = 3×3) acceleration at 3 T.

Figure 3. Coil performance as a percentage of the UISNR vs. number of loops in the array, for different values of main magnetic field strength and voxel position.

Results are shown for samples with average size and electrical properties of the human body. For fields up to 3T, a small number of loops was sufficient to approach the UISNR closely at the center, whereas for an intermediate voxel a large array was needed to obtain a similar performance. At ultra-high field, even with a large number of loops, only a limited performance can be achieved.

Figure 4. Coil performance with respect to UISNR and inverse g-factor maps on a transverse plane for increasing number of array elements and acceleration factors at 3 T.

The sample had average size and electrical properties of the human body (Table 1). Coil performance increased and approached the UISNR over a wider portion of the FOV for larger arrays, which can also enable higher acceleration factors with reduced parallel imaging artifacts.

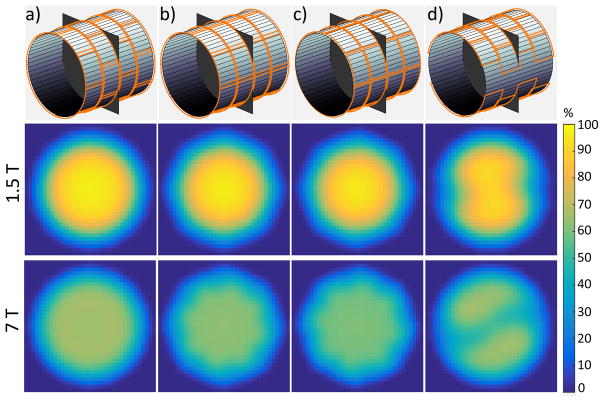
Different geometrical arrangements for a 32-loop array are compared in Figure 5. Staggering, overlapping or separating the loop coils had a negligible effect on array performance. On the other hand, when the elements did not fully encircle the object, performance decreased near the regions not covered with coils, and the central SNR dropped, especially at 7 T.

Figure 5. Coil performance maps for different 32-element array designs for a transverse plane.

In design a) the coil elements were overlapped by 10%, in both the azimuthal and axial directions, and staggered by 50%. In b) the coils were only overlapped, in c) they were separated (i.e., neither staggered nor overlapped), whereas in d) they were staggered and overlapped, but did not completely encircle the object. Staggering and overlapping the coil elements had a minor effect on coil performance, whereas SNR was severely penalized in the case of the non-fully-encircling design, especially at 7 T, where central SNR dropped by approximately 15% without a fully-encircling design. The sample had average size and electrical properties of the human body.

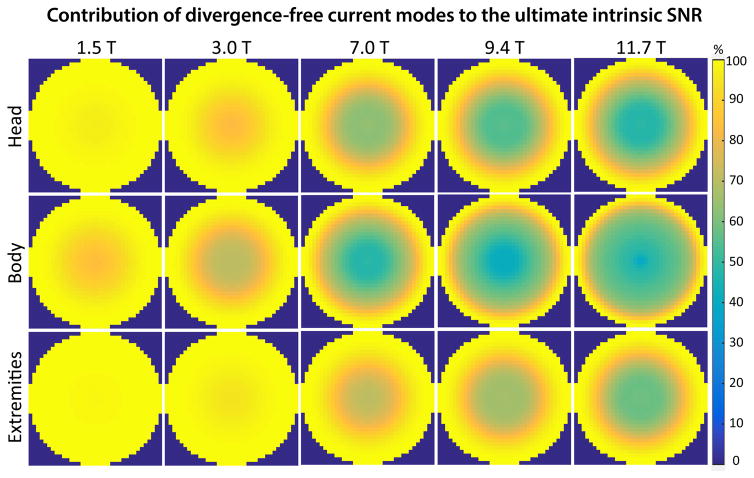
The DGF framework allows UISNR contributions to be separated into divergence-free and curl-free surface current modes (Eq. [1]). Figure 6 shows that the divergence-free currents saturated the total UISNR at low field, but contributed less as B₀ increased. While they dominated near the surface at all field strengths, divergence-free currents did not capture more than 50% of the optimum performance in the central region of the body-size object at 7 T or above. These results confirm that the performance of loops is limited for body-size cylindrical samples at UHF, since they can produce only divergence-free currents. Although Figure 6 shows that curl-free currents accounts for a non negligible portion of the UISNR at UHF in the head-mimicking cylinder, previous work based on a spherical model of the head showed that divergence-free currents saturate UISNR at the center and curl-free currents are only needed to approach UISNR at intermediate voxel positions (4). When the sample is small, as in the case of the narrow cylinder mimicking extremities, divergence-free currents remain the main contributor to the UISNR throughout the FOV also at UHF.

Figure 6. Contribution of divergence-free current modes to the UISNR on a transverse plane vs. main magnetic field strength, for different sample size and properties.

At low field, divergence-free current modes were sufficient to capture nearly 100% of the best possible SNR. As the main magnetic field strength increased, divergence-free contributions accounted for a lower percentage of the UISNR, especially for larger sample size, suggesting that it is not possible to approach the optimal performance with loop arrays.

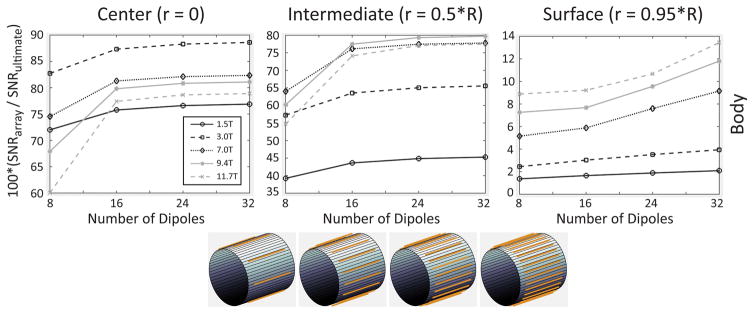
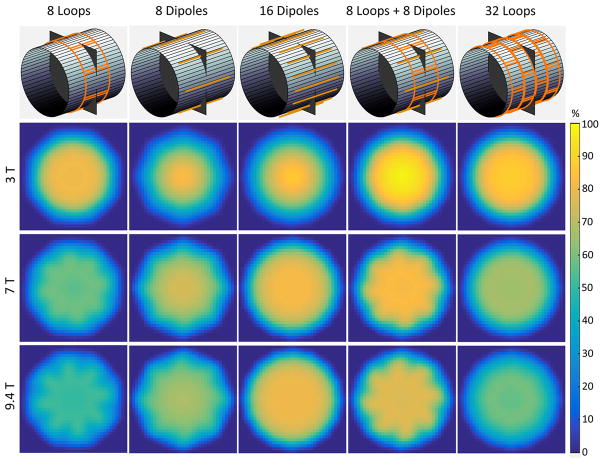
For these reasons, in Figure 7, we investigated the performance of electric dipole arrays, which capture both divergence-free and curl-free currents, only for the body-like object. While in the case of loops it was possible to approach the UISNR closely for a central voxel at 1.5 T (Figure 3), 32 electric dipoles converged to a maximum performance of only 75% in the body-like cylinder at 1.5 T. However, the largest array performance observed for a central voxel increased from 65% to 82%, from 55% to 80%, and from 50% to 78% at 7 T, 9.4 T and 11.7 T, respectively, when using arrays of 32 dipoles instead of 128 loops for the body-like object (Figure 7 vs. Figure 3). A similar trend with respect to B₀ was observed for an intermediate voxel: the main difference was that the performance rapidly reached a plateau for an increasing number of electric dipoles, whereas it grew monotonically between 8 and 128 loops. Note that 16 dipoles were sufficient to outperform 128 loops at UHF for the body-like object, which was true also for the central voxel. In fact, Supporting Figure S3 shows that the central SNR of the 16-dipole array exceeded that of the 128-loop array for B₀ > 3.2 T and surpassed the UISNR achievable using either only curl-free or only divergence-free current modes for B₀ > 3.45 T, until approximately 10.5 T. Figure 8 shows that the performance of the 16-dipole array for a body-like object was larger than 80% for most of the FOV at UHF. However, at 3 T the combination of 8 electric dipoles and 8 loops achieved overall higher performance than either 16 dipoles or 32 loops. The array with 16 electric dipoles had almost no g factor penalty for 6-fold (R = 2×3) accelerations and, in general, dipoles seemed to be advantageous compared to loops for parallel imaging (Figure 9).

Figure 7. Coil performance as a percentage of the UISNR vs. number of z-directed electric dipoles in the array, for different values of main magnetic field strength and voxel position.

Results are shown for a sample with average size and electrical properties of the human body. A smaller number of dipoles compared to loops could achieve an SNR close to the UISNR. Since electric dipoles combine divergence-free and curl-free current modes, performance was higher at ultra-high field, where the latter contribute considerably to the total UISNR.

Figure 8. Coil performance maps on a central transverse plane at different magnetic field strength for different array designs.

16 encircling electric dipoles provided the highest performance at ultra-high field, whereas the configuration with 8 loops and 8 dipoles achieved the largest performance at 3 T. Arrays with only loop coils resulted in low performance at ultra-high field. The sample had average size and electrical properties of the human body.

Figure 9. Inverse g-factor maps on a transverse plane vs. acceleration factor for different array designs at 3 T.

Although the array with 8 loops and 8 dipoles resulted in the highest SNR in the unaccelerated case, the array with 16 dipoles can enable larger acceleration factors in a central transverse plane.

DISCUSSION

We showed that the UISNR can be approached in the center of a body-sized cylinder with a comparatively small number of loops at 1.5 T and 3 T, whereas large loop arrays provide less than 65% of the UISNR at higher field strengths. Previous work reported similar values for different sample size and electrical properties (13). Large loop arrays yielded similar performance both at the center and at intermediate voxel positions. In fact, an array with many small coils surrounding the sample has the flexibility to act comprehensively as a large loop for optimal SNR at depth or as a small loop for voxels closer to the surface. However, loops can produce only divergence-free currents, which intrinsically limits their performance at UHF. In fact, Figures 3 and 6 suggest that an infinite loop array cannot provide high performance in the center of the body. On the other hand, we showed that as few as 16 dipoles could achieve high performance in the center at UHF (Supporting Figure S3). That is consistent with the fact that ideal current patterns for a central voxel resemble z-directed electric dipoles at UHF (3,24). Note that loops remain optimal for voxels near the surface at any field strength, because they can maximize signal sensitivity while receiving noise only from a localized region.

The efficiency of dipoles depends on B₀, object dimensions and electrical properties. Our simulations suggest that dipoles could be effectively used for imaging the abdomen at UHF. That is in agreement with a recent simulation study, which showed that large arrays of z-directed dipoles could approach the UISNR at the center of a body-size cylinder at 7 T (27). While we confirmed that loop arrays are extremely efficient at fields up to 3 T (Figure 3), we also showed that dipole arrays could achieve as much as 75% and 88% of ideal central performance at 1.5 T and 3 T, respectively (Figure 7). These results speak to the fact that electric dipoles can produce both curl-free and divergence-free currents, since the latter represent the dominant contribution to the UISNR at 1.5 T and 3 T (Figure 6). At first glance, it is tempting to assume that a simple line-segment electric dipole coil is curl-free, since it is by definition non-closed. That this is not in fact true is relatively straightforward to see by application of Stokes’ Law: drawing a path that branches off into current-free space after following the current filament results in a non-vanishing line integral and corresponding curl. Nor is an electric dipole divergence-free, which can be seen by applying Gauss’ law for a surface surrounding one end or the other of the dipole. This dual nature of electric dipoles (24) also explains why 16 dipoles could achieve higher SNR than 128 loop coils and outperform the UISNR calculated using either only curl-free or only divergence-free current modes (Supporting Figure S3). Recent work by Chen et al. based on numerical simulations at 7 T confirmed the near optimality of a 16-element dipole array, showing that it resulted in 12% more SNR at the center than a 48-element array with three rows of 16 loops (27). Note that our investigation is limited to loops and dipoles, but other coil elements have been proposed for UHF MRI. An interesting example is the strip line coil (28–30), in which the return current pattern is out-of-plane with respect to the strip conductor, effectively forming a loop orthogonal to the surface of the imaging sample. Modeling a strip line element in DGF would require projecting such current pattern onto a surface concentric with the object and expressing it as a weighted combination of basis modes. Note that the resulting surface current pattern could include both curl-free and divergence-free currents, which could explain the high efficiency reported for strip line coils at UHF (29, 30). Traveling wave coils have also been proposed for 7 T imaging (31) and they could be modeled directly with the DGF formalism (32), since all basis elements (Eq. [1]) are already traveling wave modes. Since a traveling wave coil has no restriction along the z direction, its SNR is expected to be lower than for loops or dipoles, because the integrated E field, i.e., the sample noise, would be considerably higher.

Although simulations suggest that fewer dipoles than loops may be needed to maximize SNR for UHF body imaging, the construction of dipole arrays presents additional challenges. For example, electric dipoles cannot be overlapped to remove mutual inductance, and one may have to rely exclusively on preamplifier decoupling, which may reduce SNR. A practical solution for dense dipole arrays could involve staggering the elements in the z direction, so that the central feeding points of neighboring dipoles would be distant, and interactions would be concentrated toward the dipole extremities where the current is very low. Staggering adjacent dipoles would also improve coverage (27). While this approach could be practical for body arrays, it would be difficult to implement in head coils, since the limited space would require a substantial shortening of the dipole elements. This represents an additional design consideration in general, since self-resonant dipoles are not necessarily optimal or practical, so inductors, or meanders, would be required to shorten the elements, introducing resistance into the array that may reduce SNR. However, this effect may be relevant only for large dipole arrays (27). Raaijmakers et al. showed that introducing inductors between segments of fractionated dipole antennas in an 8-dipole array could reduce SNR at depth by 6%, although improving the specific absorption rate (SAR) by 20% if the same array were used for transmission (33). They also showed that capacitively shortened dipoles improve SNR near the surface, but would increase SAR considerably if used for transmission.

An intriguing solution to improve SNR efficiency for both superficial and deep regions would be to combine loops and dipoles in the same array. An array integrating 8 dipoles and 8 loops was first proposed by Wiggins et al., who showed that such an arrangement could achieve approximately 22% higher central SNR than either 8 or 16 loops (17). We evaluated a similar coil design and showed that the performance of the mixed array was larger than for both loop-only and dipole-only arrays everywhere in the FOV, even if the dipole elements were optimized for maximum SNR only at the center (Figure 8). Another advantage of the mixed array is that loop and dipole pairs that share the same central axis are intrinsically orthogonal, which eliminates coupling that can practically limit dense dipole arrays. Erturk et al. reported more than 25% improvement in transmit efficiency and SNR for prostate imaging when using an array with 8 loops and 8 dipoles, compared to using 16 loops (21). Voogt et al. combined 8 dipoles for transmission with 64 loops for reception and showed good performance in simulation and phantom experiments, although in vivo performance was less promising (34).

We showed that dipole arrays could be used with parallel imaging. In fact, we found that an encircling array with 16 dipoles (Figure 9) had a similar g factor of an array with 64 loops (Figure 4) for 2×3 acceleration in a transverse plane. However, dipoles would need to be optimally arranged in multiple rows to achieve a similar performance for accelerations also in the z direction. For a transverse plane, 16 dipoles had larger performance than 32 loops at 7 T and 9.4 T, (Figure 8). A 32-loop array remains nevertheless a good option for body imaging at 3 T, since it provides high performance within a large portion of the volume encircled by the coil elements. We observed that fully surrounding the object with coils is critical to maximizing SNR, while staggering or overlapping the loop elements had only a minor effect on array performance, (Figure 5). This agrees with previous simulation work that showed large arrays of overlapping and gapped loop elements had similar g-factors for R ≤ 3 along one dimension (11,35). Note that these results could change for actual arrays if inductive coupling between adjacent elements becomes strong enough to change considerably the current distribution on the conductors, which both in our model and in Refs. (11,35) was assumed to be uniform and identical for all array elements.

Although this work provides the first extensive investigation of the performance of loop and dipole arrays in MRI, it has some intrinsic limitations. For example, we modeled anatomical regions as dielectric cylinders, in order to be able to calculate the EM field analytically. We believe that overall this represents a minor limitation, since this study did not focus on a specific array for a particular clinical application, but was rather aimed at providing general physical insights for coil design. Nevertheless, while a cylindrical geometry is a straightforward model for body and extremities, it may provide a less accurate representation of the head. A recent article showed that the UISNR distribution inside a realistic heterogeneous head model is similar to that in a uniform sphere (10), suggesting that the latter is a reliable approximation for the human head. While a comparable result would probably hold for a transverse slice at the center of a uniform head-size cylinder, the UISNR distribution for sagittal and coronal planes would not resemble the case of the realistic head model at positions away from the center, since our model is based on an infinite cylinder (with sufficiently separated periodic repetitions of the EM field), where the current can flow only on the lateral surface. Despite this limitation, we chose to include a head-mimicking cylindrical sample in our investigation because arranging loops on an open cylindrical former, without surrounding the top, is a possible design option for head arrays.

Another limitation is that we were necessarily constrained in the number of different cases we could simulate. For example, for each field strength, we optimized the length of the dipoles for maximum SNR at the center, whereas other dimensions could be optimal for different voxel positions (36). Since the EM field of the dipole we modeled decays along its length, an optimal arrangement of the array elements could exist that achieves similar performance over multiple transverse slices, as well as along coronal and sagittal FOV’s. However, optimizing dipole array design was beyond the scope of this work. Our coil noise model accounted only for conductor losses, whereas actual dipole and loop antennas may also include lossy lumped elements and decoupling circuits. However, note that resistance correction factors can be obtained from bench measurements and incorporated in the simulations. Although our DGF simulation framework does not explicitly account for inductive coupling between array elements, the effect of coupling on the calculated array performance is expected to be minimal, because we included the noise covariance matrix in the optimal SNR coil combination (37). However, since the calculation of the noise covariance matrix is based on an assumed current distribution on the conductors, simulated array performance could deviate from experiments if inductive coupling is strong enough to change the current distribution considerably. In this work, we validated our DGF simulation framework for a loop array, showing good agreement between simulated and experimental coil performance maps. A similar comparison was previously attempted for a spherical phantom, but the actual array was only qualitatively modeled in DGF, yielding approximate results (14). Here we showed that we could accurately predict the performance of a 24-element array by carefully calibrating DGF simulations (Figure 2). Simulated and experimental maps were different only near the edge of the phantom, where both UISNR and experimental SNR measurements are difficult to stabilize. Coil noise was only approximately 3% of sample noise because the array closely fitted the phantom, providing good loading; therefore adding the coil noise correction factor (Supporting Note 1) was not critical for our results. However, estimating coil noise correctly is important when the array is at some distance from the sample (38,39), and in general when loading is poor. While our analytic simulation results showing the performance benefits of electric dipoles for body imaging at UHF agree with previous numerical simulations and experiments (17,27), rigorous experimental validation would require the construction of a dipole array prototype, which is beyond the scope of this work. Note, however, that a coil noise calibration procedure has recently been proposed to account for resistive losses in the inductors used to shorten electric dipoles (27) and could be employed in future work.

One additional fundamental question underlying this work relates to why curl-free current contributions and z-directed electric dipole character become significant at ultra-high fields as opposed to low fields. Preliminary work connecting this behavior to the topology of the current-bearing surface, and introducing a so-called “optimality principle” by which to understand ideal current patterns, was presented at the 2016 meeting of the International Society for Magnetic Resonance in Medicine (24). Further elaborations of this principle are currently underway (40).

CONCLUSION

This work investigated the performance of loop and dipole antennas in MRI. Our results confirmed previous observations that dipole antennas are efficient MR coils near a dielectric load, although their typical radiation pattern is omnidirectional in free space (36). While loops produce only divergence-free current patterns, dipoles additionally capture curl-free current patterns, which are responsible for a significant portion of the UISNR for body-size samples at UHF. As a result, large arrays of cylindrical window coils can approach the UISNR only at low to moderate fields, whereas electric dipoles are needed for high performance in body imaging at UHF. Future work will include investigating optimal element arrangement in dipole arrays, and in mixed arrays including loops and dipoles for improved performance over large FOV’s.

Supplementary Material

Supp info

Supporting Figure S1. Convergence of the Ultimate Intrinsic SNR (UISNR) calculations.

UISNR was calculated using azimuthal and axial mode expansion orders of n = − 48:1:47 and m = −150:1:149, which correspond to a basis with 57,600 surface current modes, equally divided between curl-free and divergence-free types. This ensured convergence of the calculations. The zoomed views on the right show that calculations converged also for the case of a voxel near the surface of the cylinder, although the discretization of the plots seems to suggest the contrary. In fact, UISNR changes only by 0.3% when the number of modes is increased from 57,232 to 57,624.

Supporting Figure S2. Coil performance as a percentage of the UISNR vs. number of loops in the array, for different values of main magnetic field strength and voxel position.

Results are shown for samples with average size and electrical properties of the head (top) and extremities (bottom). Results for samples with average size and electrical properties of the human body are shown in Figure 3.

Supporting Figure S3. UISNR and SNR of finite arrays at the center vs. main magnetic field strength (a).

Array geometries for a body-size sample are shown in (b). The SNR of the array with 16 dipoles exceeded that of the array with 128 loops for B₀ > 3.2 T and the UISNR achievable using either only curl-free or only divergence-free current modes for 3.45 T < B₀ < ~10.5 T (c). The array with 128 loops approached the UISNR closely only at low field.

APPENDIX A

Mode expansion of the EM field inside an infinite dielectric cylinder

We can construct the DGF for a dielectric cylinder using the method of superposition (41):

$$\overline{\mathit{G}}(\mathit{r},{\mathit{r}}^{\prime })=\{\begin{array}{ll}{\overline{\mathit{G}}}_{\mathbf{0}}(\mathit{r},{\mathit{r}}^{\prime })+{\overline{\mathit{G}}}_s^{(1)}(\mathit{r},{\mathit{r}}^{\prime })\hfill & r\ge r_a\hfill \\ {\overline{\mathit{G}}}_s^{(2)}(\mathit{r},{\mathit{r}}^{\prime })\hfill & r\le r_a\hfill \end{array}$$ [A.1]

Where, (r′ = r_b, φ′, z′) is the location of the current source, r_a is the radius of the cylinder and r is the position at which the EM field is calculated. In the presence of a conductive shield surrounding the cylinder at r_c > r_b ≥ r_a, ${\overline{\mathit{G}}}_{\mathbf{0}}(\mathit{r},{\mathit{r}}^{\prime })+{\overline{\mathit{G}}}_s^{(1)}(\mathit{r},{\mathit{r}}^{\prime })$ in Eq. [A.1] are valid for r_a ≤ r < r_c, and the free-space and the scattered DGF can be calculated as:

$${\overline{\mathit{G}}}_{\mathbf{0}}(\mathit{r},{\mathit{r}}^{\prime })=\frac{-i}{8\pi }{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }dm\frac{1}{{\eta }^2}\{\begin{array}{ll}{\mathcal{A}}_{n,\eta }(m,\mathit{r}){\mathit{M}}_{n,\eta }(m,{\mathit{r}}^{\prime })+{\mathcal{B}}_{n,\eta }(m,\mathit{r}){\mathit{N}}_{n,\eta }(m,{\mathit{r}}^{\prime })\hfill & \mathit{r}\ge {\mathit{r}}^{\prime }\hfill \\ {\mathit{M}}_{n,\eta }(m,\mathit{r}){\mathcal{A}}_{n,\eta }(m,{\mathit{r}}^{\prime })+{\mathit{N}}_{n,\eta }(m,\mathit{r}){\mathcal{B}}_{n,\eta }(m,{\mathit{r}}^{\prime })\hfill & \mathit{r}\le {\mathit{r}}^{\prime }\hfill \end{array}$$ [A.2]

$${\overline{\mathit{G}}}_s^{(1)}(\mathit{r},{\mathit{r}}^{\prime })=\frac{-i}{8\pi }{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }dm\frac{1}{{\eta }^2}\left\{\begin{array}{l}[a_n(m){\mathcal{A}}_{n,\eta }(m,\mathit{r})+b_n(m){\mathcal{B}}_{n,\eta }(m,\mathit{r})]{\mathcal{A}}_{n,\eta }(m,{\mathit{r}}^{\prime })\hfill \\ +[c_n(m){\mathcal{A}}_{n,\eta }(m,\mathit{r})+d_n(m){\mathcal{B}}_{n,\eta }(m,\mathit{r})]{\mathcal{B}}_{n,\eta }(m,{\mathit{r}}^{\prime })\hfill \end{array}\right\}$$ [A.3]

$${\overline{\mathit{G}}}_s^{(2)}(\mathit{r},{\mathit{r}}^{\prime })=\frac{-i}{8\pi }{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }dm\frac{1}{{\eta }^2}\left\{\begin{array}{l}[e_n(m){\mathit{M}}_{n,\gamma }(m,\mathit{r})+f_n(m){\mathit{N}}_{n,\gamma }(m,\mathit{r})]{\mathcal{A}}_{n,\eta }(m,{\mathit{r}}^{\prime })\hfill \\ +[g_n(m){\mathit{M}}_{n,\gamma }(m,\mathit{r})+h_n(m){\mathit{N}}_{n,\gamma }(m,\mathit{r})]{\mathcal{B}}_{n,\eta }(m,{\mathit{r}}^{\prime })\hfill \end{array}\right\}$$ [A.4]

Here $\eta =\sqrt{{\omega }^2{\epsilon }_0{\mu }_0-m^2}=\sqrt{k_0^2-m^2},\gamma =\sqrt{k_{in}^2-m^2}$, and the quantities M,N are orthonormal vector wave functions, defined as

$$\begin{array}{ll}{\mathit{M}}_{\gamma ,n}(m,\mathit{r})\hfill & =\mathbf{\nabla }\times J_n(\gamma r)e^{in\phi }{e}^{\mathit{imz}}\widehat{\mathit{z}}=\left(i\frac{n}{r}{J}_n(\gamma r)\widehat{\mathit{r}}-\gamma J_n^{\prime }(\gamma r)\widehat{\mathit{\phi }}\right)e^{in\phi }{e}^{\mathit{imz}}\hfill \\ {\mathit{N}}_{\gamma ,n}(m,\mathit{r})\hfill & =\frac{1}{k_{in}}\mathbf{\nabla }\times {\mathit{M}}_{\gamma ,n}(m,\mathit{r})=\left(i\frac{\gamma m}{k_{in}}{J}_n^{\prime }(\gamma r)\widehat{\mathit{r}}-\frac{nm}{k_{in}r}{J}_n(\gamma r)\widehat{\mathit{\phi }}+\frac{{\gamma }^2}{k_{in}}{J}_n(\gamma r)\widehat{\mathit{z}}\right)e^{in\phi }{e}^{\mathit{imz}}\hfill \end{array}$$ [A.5]

where J_n(γr) is a Bessel function of integer order n and $J_n^{\prime }(\gamma r)=\partial J_n(\gamma r)/\partial (\gamma r)$. The same definition applies for M_ηn and N_ηn with the substitution γ → η and k_in → k₀. It is important in practice to select the appropriate sign for γ and η, which are defined as square roots: for large m, both γ and η acquire a substantial imaginary component, and the square root branches which yield 𝒥m(γ) < 0 and 𝒥m(η) < 0 must be chosen independently for each value of m. This selection insures that the Bessel functions with argument γr or ηr – and hence the electromagnetic fields associated with each mode – remain appropriately bounded with increasing radius. The modified wave functions 𝓐, 𝓑 guarantee that the tangential component of the electric field vanishes at the location of the conductive shield (3):

$$\begin{array}{ll}{\mathcal{A}}_{\eta ,n}(m,\mathit{r})\hfill & ={\mathit{M}}_{\eta ,n}^{+}(m,\mathit{r})-\frac{{H_n^{(2)}}^{\prime }(\eta r_c)}{J_n^{\prime }(\eta r_c)}{\mathit{M}}_{\eta ,n}(m,\mathit{r})\hfill \\ {\mathcal{B}}_{\eta ,n}(m,\mathit{r})\hfill & ={\mathit{N}}_{\eta ,n}^{+}(m,\mathit{r})-\frac{H_n^{(2)}(\eta r_c)}{J_n(\eta r_c)}{\mathit{N}}_{\eta ,n}(m,\mathit{r})\hfill \end{array}$$ [A.6]

Here ${\mathit{M}}_{\eta ,n}^{+}$ and ${\mathit{N}}_{\eta ,n}^{+}$ take precisely the same form as M_ηn and N_ηn, with the additional substitutions $J_n(\gamma r)\to H_n^{(2)}(\eta r)$ and $J_n^{\prime }(\gamma r)\to {H_n^{(2)}}^{\prime }(\eta r)$, where $H_n^{(2)}(\eta r_c)$ is the Hankel function of the second kind of order n evaluated at the shield radius, and ${H_n^{(2)}}^{\prime }(\eta r_c)$ is its first derivative with respect to ηr. Note that, in the absence of the conductive shield, 𝓐 = M⁺ and 𝓑 = N⁺ as in Ref. (5).

The coefficients a, b, c, d, e, f, g, h are found by applying boundary conditions requiring continuity of the electric and magnetic fields at the cylinder surface, which results in the following conditions on the DGF in the unprimed coordinate system (5):

$$\begin{array}{l}\widehat{\mathit{r}}\times {\left({\overline{\mathit{G}}}_{\mathbf{0}}+{\overline{\mathit{G}}}_s^{(1)}\right)}_{\mathit{r}={\mathit{r}}_{\mathit{a}}^{+}}=\widehat{\mathit{r}}\times {\left({\overline{\mathit{G}}}_s^{(2)}\right)}_{\mathit{r}={\mathit{r}}_{\mathit{a}}^{-}}\\ \widehat{\mathit{r}}\times \mathbf{\nabla }\times {\left({\overline{\mathit{G}}}_{\mathbf{0}}+{\overline{\mathit{G}}}_s^{(1)}\right)}_{\mathit{r}={\mathit{r}}_{\mathit{a}}^{+}}=\widehat{\mathit{r}}\times \mathbf{\nabla }\times {\left({\overline{\mathit{G}}}_s^{(2)}\right)}_{\mathit{r}={\mathit{r}}_{\mathit{a}}^{-}}\end{array}$$ [A.7]

Eq. [A.7] results in the following system of equations, which allows one to calculate the coefficients:

$$\mathcal{P}·\left[\begin{array}{c}{a}_n\\ b_n\\ e_n\\ f_n\end{array}\right]=\left[\begin{array}{c}\eta J_n^{\prime }(\eta r_a)\\ 0\\ \chi J_n(\eta r_a)\\ {\eta }^2{J}_n(\eta r_a)\end{array}\right]\mathcal{P}·\left[\begin{array}{c}{c}_n\\ d_n\\ g_n\\ h_n\end{array}\right]=\left[\begin{array}{c}\frac{\chi }{k_0}{J}_n(\eta r_a)\\ \frac{{\eta }^2}{k_0}{J}_n(\eta r_a)\\ k_0\eta J_n^{\prime }(\eta r_a)\\ 0\end{array}\right]$$ [A.8]

with χ = nm/r_a and:

$$\mathcal{P}=\left[\begin{array}{cccc}-\eta \left({H_n^{(2)}}^{\prime }(\eta r_a)-\frac{{H_n^{(2)}}^{\prime }(\eta r_c)}{J_n^{\prime }(\eta r_c)}{J}_n^{\prime }(\eta r_a)\right)& \frac{-\chi }{k_0}\left(H_n^{(2)}(\eta r_a)-\frac{H_n^{(2)}(\eta r_c)}{J_n(\eta r_c)}{J}_n(\eta r_a)\right)& \gamma J_n^{\prime }(\gamma r_a)& \frac{\chi }{k_{in}}{J}_n(\gamma r_a)\\ 0& \frac{-{\eta }^2}{k_0}\left(H_n^{(2)}(\eta r_a)-\frac{H_n^{(2)}(\eta r_c)}{J_n(\eta r_c)}{J}_n(\eta r_a)\right)& 0& \frac{{\gamma }^2}{k_{in}}{J}_n(\gamma r_a)\\ -\chi \left(H_n^{(2)}(\eta r_a)-\frac{{H_n^{(2)}}^{\prime }(\eta r_c)}{J_n^{\prime }(\eta r_c)}{J}_n(\eta r_a)\right)& -k_0\eta \left({H_n^{(2)}}^{\prime }(\eta r_a)-\frac{H_n^{(2)}(\eta r_c)}{J_n(\eta r_c)}{J}_n^{\prime }(\eta r_a)\right)& \chi J_n(\gamma r_a)& k_{in}\gamma J_n^{\prime }(\gamma r_a)\\ -{\eta }^2\left(H_n^{(2)}(\eta r_a)-\frac{{H_n^{(2)}}^{\prime }(\eta r_c)}{J_n^{\prime }(\eta r_c)}{J}_n(\eta r_a)\right)& 0& {\gamma }^2{J}_n(\gamma r_a)& 0\end{array}\right]$$ [A.9]

The electric field generated by the surface current K in Eq. [1] inside the cylinder can be calculated using the DGF valid for r ≤ r_a:

$$\mathit{E}(\mathit{r})={\iiint }_{V^{\prime }}{\overline{\mathit{G}}}_s^{(2)}(\mathit{r},{\mathit{r}}^{\prime })·\mathit{J}({\mathit{r}}^{\prime })d{V}^{\prime }=r_b{\iint }_{{\phi }^{\prime },z^{\prime }}{\overline{\mathit{G}}}_s^{(2)}(\phi ,z,{\phi }^{\prime },z^{\prime })·\mathit{K}({\phi }^{\prime },z^{\prime })d{\phi }^{\prime }d{z}^{\prime }$$ [A.10]

Using $\mathit{B}(\mathit{r})=\frac{i}{\omega }\mathbf{\nabla }\times \mathit{E}(\mathit{r})$ results in the expression for the EM field in Eq. [2], where the weighting coefficients are defined as:

$$\begin{array}{l}\mathit{V}=\left(\begin{array}{l}{V}_n^M(m)\hfill \\ V_n^N(m)\hfill \end{array}\right)=\\ -i\frac{4{\pi }^2{r}_b}{{\eta }^2}\left\{\begin{array}{c}\left[{H_n^{(2)}}^{\prime }(\eta r_b)-\frac{{H_n^{(2)}}^{\prime }(\eta r_c)}{J_n^{\prime }(\eta r_c)}{J}_n^{\prime }(\eta r_b)\right]\left(\begin{array}{ll}{e}_n(m)\eta m\hfill & e_n(m)\eta n/r_b\hfill \\ f_n(m)\eta m\hfill & f_n(m)\eta m/r_b\hfill \end{array}\right)\\ +\left[H_n^{(2)}(\eta r_b)-\frac{H_n^{(2)}(\eta r_c)}{J_n(\eta r_c)}{J}_n(\eta r_b)\right]\left(\begin{array}{ll}{g}_n(m)n{k}_0/r_b\hfill & g_n(m)(m/k_0)({(n/r_b)}^2-{\eta }^2)\hfill \\ h_n(m)n{k}_0/r_b\hfill & h_n(m)(m/k_0)({(n/r_b)}^2-{\eta }^2)\hfill \end{array}\right)\end{array}\right\}·\left(\begin{array}{l}{W}_n^{(M)}(m)\hfill \\ W_n^{(E)}(m)\hfill \end{array}\right)\\ ={\mathit{T}}^{\mathit{T}}·\mathit{W}\end{array}$$ [A.11]

Calculation of the ultimate intrinsic SNR

The modes’ electric and magnetic fields are used to calculate the relevant quantities in the expression for the UISNR (Eq. [3]). The electric field is used to compute the noise equivalent resistance:

$${\mathbf{R}}_{\mathit{mode}}=\mathit{\sigma }{\iiint }_{\mathit{V}}\mathit{E}(\mathit{r})·\mathit{E}{(\mathit{r})}^{\ast }dV={\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }\left(w_n^{(M)}(m)W_n^{(E)}(m)\right){\mathbf{\Psi }}_{\mathit{mode}}{\left(\begin{array}{l}{W}_n^{(M)}(m)\hfill \\ W_n^{(E)}(m)\hfill \end{array}\right)}^{\ast }dm$$ [A.12]

in which the modes’ noise covariance matrix Ψ_mode = TR_LT*^T can be constructed using the matrix in Eq. [A.9] and:

$${\mathit{R}}_{\mathit{L}}=\mathit{\sigma }{\left(\frac{\omega {\mu }_0}{4}\right)}^{\mathbf{2}}\frac{{\mid \gamma \mid }^2}{2}\left(\begin{array}{cc}{F}_{n-1}+F_{n+1}& \frac{m}{k_{in}^{\ast }}[F_{n-1}-F_{n+1}]\\ \frac{m}{k_{in}}[F_{n-1}-F_{n+1}]& {\left|\frac{m}{k_{in}}\right|}^2\left[F_{n-1}+F_{n+1}+2{\left|\frac{\gamma }{m}\right|}^2{F}_n\right]\end{array}\right)$$ [A.13]

where

$$F_n={\int }_0^{r_a}{J}_n(\gamma r)J_n({\gamma }^{\ast }r)\mathit{rdr}=\frac{{\gamma }^{\ast }{r}_a{J}_{n-1}({\gamma }^{\ast }{r}_a)J_n(\gamma r_a)-\gamma r_a{J}_{n-1}(\gamma r_a)J_n({\gamma }^{\ast }{r}_a)}{{\gamma }^2-{\gamma }^{\ast 2}}.$$ [A.14]

The integral in Eq. [A.14] was solved using the recurrence relations of the Bessel functions (see Eqs. [7.4] and [7.5] in Ref. (41)). The magnetic field is used to calculate the matrix S in Eq. [3], which contains the complex signal sensitivities of all modes at the target position r₀ (and at all aliased positions if parallel imaging is used):

$$\begin{array}{l}{B}_x(\mathit{r})-i{B}_y(\mathit{r})={\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }\left(V_n^{(M)}(m)V_n^{(E)}(m)\right)\left(\frac{\gamma {\mu }_0}{8\pi }{J}_{n-1}(\gamma r)e^{i(n-1)\phi }{e}^{\mathit{imz}}\left[\begin{array}{c}m\\ k_{in}\end{array}\right]\right)dm=\\ {\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{\mathit{W}}^{\mathit{T}}\mathit{TX}(\mathit{r})dm={\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{\mathit{W}}^{\mathit{T}}\mathit{S}(\mathit{r})dm\end{array}$$ [A.15]

The ultimate intrinsic SNR can be calculated with Eq. [3] using the previous definitions.

Current weights for cylindrical window loop coils

The current density distribution for an ideal cylindrical window coil centered at φ = 0 and z = 0 (Figure 1), with angular aperture 2φ₀ and axial length 2l_i, carrying current I on each leg is:

$${\mathit{K}}^{\mathit{loop}}(\phi ,z)=I\left\{\begin{array}{c}\left(\delta (z+l_l)-\delta (z-l_l)\right)\left(\theta (\phi -{\phi }_0)-\theta (\phi +{\phi }_0)\right)\widehat{\mathit{\phi }}\\ +\frac{1}{r_b}\left(\delta (\phi -{\phi }_0)-\delta (\phi +{\phi }_0)\right)\left(\theta (z-l_l)-\theta (z+l_l)\right)\widehat{\mathit{z}}\end{array}\right\}$$ [A.16]

Here θ(φ − φ₀) is the step function with a positive step from 0 to 1 at φ = φ₀. The factor 1/r_b in the z component arises from the requirement of uniform current around the loop. We can express Eq. [A.16] as an inverse Fourier transform:

$$\begin{array}{l}{\mathit{K}}^{\mathit{loop}}(\phi ,z)=I{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }\left\{\begin{array}{c}\frac{1}{2\pi }\left(e^{im{l}_l}-e^{-im{l}_l}\right)\frac{1}{2\pi }\left(-2\frac{\mathit{sin}(\eta {\phi }_0)}{n}\right)e^{in\phi }{e}^{\mathit{imz}}\widehat{\mathit{\phi }}\\ +\frac{1}{r_b}\frac{1}{2\pi }\left(e^{-in{\phi }_0}-e^{in{\phi }_0}\right)\frac{1}{2\pi }\left(-2\frac{\mathit{sin}(m{l}_l)}{m}\right)e^{in\phi }{e}^{\mathit{imz}}\widehat{\mathit{z}}\end{array}\right\}dm=\\ I{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }\frac{-1}{{\pi }^2}\frac{\mathit{sin}(m{l}_l)}{m}\frac{\mathit{sin}(n{\phi }_0)}{n}\left(im\widehat{\mathit{\phi }}-\frac{in}{r_b}\widehat{\mathit{z}}\right)e^{in\phi }{e}^{\mathit{imz}}dm\end{array}$$ [A.17]

where the factors 1/2π derive from incorporating 2π in our definitions of m and n. Since the cylindrical window loop coil allows only divergence-free currents, we can express its current density using Eq. [1] with $W_n^{(E)}=0$:

$$\begin{array}{l}{\mathit{K}}^{\mathit{loop}}(\phi ,z)=I{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{W}_n^{\mathit{loop},(M)}(m)\mathit{\nabla }\times e^{in\phi }{e}^{\mathit{imz}}\widehat{\mathit{r}}=\\ I{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{W}_n^{\mathit{loop},(M)}(m)\left(im\widehat{\mathit{\phi }}-\frac{in}{r_b}\widehat{\mathit{z}}\right)e^{in\phi }{e}^{\mathit{imz}}dm\end{array}$$ [A.18]

By comparing Eqs. [A.17] with [A.18] and accounting for the effects of rotation or translation of the coil on the cylindrical surface, we obtain the expression in Eq. [4], where we have assumed unit current I = 1.

Current weights for electric dipoles directed along the z-axis

As for the case of the loop coil, we can express the current density distribution for a straight electric dipole of length 2l_d along the z direction centered at φ = 0 and z = 0 and carrying current $I(z)=I\text{cos}\left(\frac{\pi z}{2l_d}\right)$ as an inverse Fourier transform:

$$\begin{array}{l}{\mathit{K}}^{\mathit{dipole}}(\phi ,z)=\frac{1}{r_b}I\text{cos}\left(\frac{\pi z}{2l_d}\right)\left(\theta (z-l_d)-\theta (z+l_d)\right)\widehat{\mathit{z}}\\ =\sum _{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }\frac{1}{4{\pi }^2}\frac{l_d}{r_b}I\left\{\mathit{sinc}\left(m{l}_d-\frac{\pi }{2}\right)+\mathit{sinc}\left(m{l}_d+\frac{\pi }{2}\right)\right\}{e}^{in\phi }{e}^{\mathit{imz}}\widehat{\mathit{z}}dm\end{array}$$ [A.19]

Let us compare the previous expression with the general expression in Eq. [1]:

$$\mathit{K}(\phi ,z)=I{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }\left\{W_n^{(M)}(m)\left(im\widehat{\mathit{\phi }}-\frac{in}{r_b}\widehat{\mathit{z}}\right)+W_n^{(E)}(m)\left(\frac{in}{r_b}\widehat{\mathit{\phi }}+im\widehat{\mathit{z}}\right)\right\}{e}^{in\phi }{e}^{\mathit{imz}}dm$$ [A.20]

We see that, for the two equations to match, the φ̂ component in Eq. [A.20] must cancel at all points in space. The only way to accomplish this is by using a combination of divergence-free and curl-free basis functions:

$$\begin{array}{l}{W}_n^{\mathit{dipole},(M)}(m)=\frac{n}{r_b}{W}_n(m)\\ W_n^{\mathit{dipole},(E)}(m)=-m{W}_n(m)\end{array}$$ [A.21]

Substituting the previous expression in Eq. [A.20] we obtain

$$\mathit{K}(\phi ,z)=I{\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{W}_n(m)\left(-\frac{i{n}^2}{r_b}-i{m}^2\right)e^{in\phi }{e}^{\mathit{imz}}\widehat{\mathit{z}}dm$$ [A.22]

Comparison with Eq. [A.19] yields:

$$W_n(m)=\frac{i}{4{\pi }^2}\frac{\frac{l_d}{r_b}\left\{\mathit{sinc}\left(m{l}_d-\frac{\pi }{2}\right)+\mathit{sinc}\left(m{l}_d+\frac{\pi }{2}\right)\right\}}{\frac{n^2}{r_b}+m^2}$$ [A.23]

We can obtain Eq. [5] by substituting the last expression into Eq. [A.21] and accounting for the effects of rotation or translation of the dipole on the cylindrical surface.

Coil noise

If only sample noise is considered, the optimal SNR for loops and dipoles can be calculated with the substitutions in Eq. [6]. The DGF formalism allows one also to account for coil noise contributions in a straightforward manner, by adding resistive power losses in the coil conductors to the diagonal of the noise covariance matrix, which becomes Ψ_mode = TR_LT*^T+R_A, where R_A is calculated by integrating the current distribution:

$$\begin{array}{l}\hfill \frac{r_b}{{\sigma }_c{d}_c}\underset{{\phi }^{\prime },z^{\prime }}{\iint }\mathit{K}({\phi }^{\prime },z^{\prime })·{\mathit{K}}^{\ast }({\phi }^{\prime },z^{\prime })d{\phi }^{\prime }d{z}^{\prime }=\hfill \\ {\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }\left(W_n^{(M)}(m)W_n^{(E)}(m)\right)\frac{r_{b}4{\pi }^2}{{\sigma }_c{d}_c}\left(m^2+{\left(\frac{n}{r_b}\right)}^2\right)\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right){\left(\begin{array}{c}{W}_n^{(M)}(m)\\ W_n^{(E)}(m)\end{array}\right)}^{\ast }=\\ {\sum }_{n=-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }\left(W_n^{(M)}(m)W_n^{(E)}(m)\right){\mathbf{R}}_A{\left(\begin{array}{c}{W}_n^{(M)}(m)\\ W_n^{(E)}(m)\end{array}\right)}^{\ast }\end{array}$$ [A.24]

Here σ_c and d_c are the electric conductivity and the thickness of the coil material, respectively.