Abstract
Purpose
To determine the intracellular water preexchange lifetime, τi, the “average residence time” of water, in the intracellular milieu of neurons and astrocytes. The preexchange lifetime is important for modeling a variety of MR datasets, including relaxation, diffusion-sensitive, and dynamic-contrast-enhanced.
Methods
Herein, τi in neurons and astrocytes is determined in a microbead-adherent, cultured cell system. In concert with thin-slice-selection, rapid flow of extracellular media suppresses extracellular signal, allowing determination of the transcytolemmal-exchange-dominated, intracellular T1. With this knowledge, and that of the intracellular T1 in the absence of exchange, τi can be derived.
Results
Under normal culture conditions, τi for neurons is 0.75 ± 0.05 s vs. 0.57 ± 0.03 s for astrocytes. Both neuronal and astrocytic τi's decrease within 30 min after the onset of oxygen-glucose deprivation, with the astrocytic τi showing a substantially greater decrease than the neuronal τi.
Conclusion
Given an approximate intra- to extracellular volume ratio of 4:1 in the brain, these data imply that, under normal physiological conditions, an MR experimental characteristic time of less than 0.012 s is required for a non-exchanging, two-compartment (intra- and extracellular) model to be valid for MR studies. This characteristic time shortens significantly (i.e., 0.004 s) under injury conditions.
Keywords: magnetic resonance, relaxation, rat, cerebral cortex, cultured cells
Introduction
Water exchange across cell membranes plays a fundamental role in cell physiology and pathophysiology (1-4). Various biophysical parameters have been employed to describe the characteristics of transcytolemmal water exchange, including osmotic water permeability, diffusional water permeability, and Arrhenius activation energy (1,2). Among these parameters, the intracellular water preexchange lifetime, τi, reflects the “average residence time” of water in the intracellular space. More precisely, τi is the exponential time constant (inverse of the rate constant, kie, vide infra) characterizing transcytolemmal water exchange in the intra-to-extracellular direction (5-7). It is the time required for 63% (i.e., 1-e-1) of the intracellular water to exchange.
If intracellular water can be considered as “well mixed” (i.e., cell dimensions are small relative to the diffusion-driven, water root-mean-square displacements that occur over the characteristic time of a given measurement), Fick's laws of diffusion for water transiting across the cell membrane relate τi directly to the diffusional water permeability, Pd, according to Eq. [1]:
| [1] |
Here Vi is the volume of intracellular water and A is the surface area of the cell membrane (8,9). While it is generally assumed that transcytolemmal water exchange is purely diffusive (i.e., thermally driven by Brownian motion), recent reports have also implicated energy-dependent ion channels as significant “active transport” vehicles for this exchange (4,10,11). τi describes the accumulated total flux of all active and passive exchange processes.
All physical measurements have an associated characteristic time, and τi sets a limit (vide infra) on the characteristic time over which the tissue water MR signal can be modeled as separable, compartment-specific, water signals from intra- and extracellular compartments, rather than being a compartment-inseparable signal resulting from exchange (mixing) between the compartments. Indeed, it is difficult, if not impossible, to construct a meaningful biophysical model for tissue water MR measurements, such as T1 (12) or apparent diffusion coefficient (ADC) (13), without knowledge of τi. For example, to address the biophysical mechanism(s) underlying the rapid and remarkable decrease in brain-water ADC upon ischemic stroke (14,15), various hypotheses invoke the two-compartment — intracellular and extracellular — diffusion model, and hence require assignment of values for compartment-specific ADC's (reviewed in (16-18)). However, strategies to measure compartment-specific ADC's and changes therein in response to injury, a subject of considerable debate, generally require knowledge of τi (6,13,19).
Considerable effort has focused on measuring τi using different MR strategies, including T2-based methods (20-22), T1-based methods (6,10,12,23), and diffusion-based methods (3,19,24-26). A rather wide range of τI values in mammalian cells has been reported, from ∼10 ms in erythrocytes (20,21) to ∼1 s in rat skeletal muscle (12) and ∼2 s in human white matter (3). Of greatest relevance to this study, there are three reports of τi in central nervous system (CNS) tissue (3,6,19) and one report of τi in cultured glioma cells (24). Derived τi values vary substantially across these reports: 1.25–2.5 s (3), 0.55 s (6), 0.3 s (19), and 0.05 s (24).
In this study, we determine the intracellular water preexchange lifetime for microbead-adherent neurons and glia (astrocytes), respectively, using a thin-slice-selection, inversion-recovery, spin-echo (IRSE) MR spectroscopy (MRS) method in concert with rapid flow of the extracellular perfusing media (Fig. 1) (7). The microbead-adherent cell culture is modeled as a two-compartment (intra- and extracellular water) system with first-order transcytolemmal water exchange at equilibrium, which is often regarded as a “two-site-exchange” system (5,7,12). At equilibrium/steady-state (static-cell volume), the intra- and extracellular water volume fractions (fi and fe, respectively) and water exchange rate constants (or preexchange lifetimes) are related by Eq. [2],
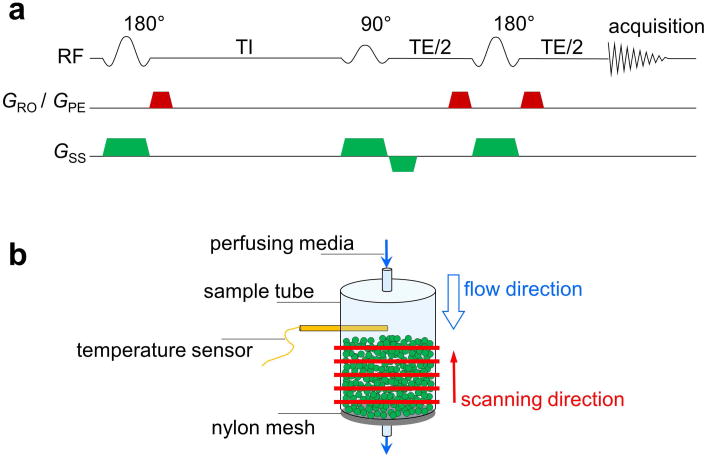
Figure 1. Perfused MRS experiment.
(a) Slice-selective IRSE spectroscopy sequence. Slice-selection gradients (green trapezoids) were applied along the vertical flow direction and the crusher gradients (red trapezoids) were applied along the other two orthogonal directions (read-out and phase-encode). (b) Perfusion unit and MRS scanning scheme. Cell-attached microbeads (green spheres) were stabilized on an 80-μm nylon mesh inside the sample tube (inner diameter 7.8 mm).
| [2a] |
| [2b] |
Here kie is the first-order water exchange rate constant in the intra-to-extracellular direction, the inverse of which is the intracellular water preexchange lifetime, τi. Likewise, kei is the first-order water exchange rate constant in the extra-to-intracellular direction, the inverse of which is the extracellular water preexchange lifetime, τe.
For simplicity, relaxation rate constants, R, rather than relaxation time constants, T (R = 1/T), are used in the following description. If the extracellular media flows sufficiently fast, and if thin (∼100 μm) slices are interrogated via a standard, slice-selective, spin-echo MR measurement (Fig. 1), the effective/apparent R1 and R2 of the flowing extracellular media, and , will be flow-dominated and large relative to the intrinsic R1 of intracellular water, R1,i (i.e., that which would be measured in the absence of transcytolemmal exchange). Under such conditions, the R1 measurement in this two-site-exchange system will be in the slow exchange limit (Eq. [3a]) (12).
| [3a] |
Given the perfused, low density, mircobead-adherent, cell-culture conditions employed herein, fe ≫ fi. Thus, it follows from Eq. [2] that kie ≫ kei and Eq. [3a] simplifies to
| [3b] |
Presaging what follows, the conditions of our perfused cell system are, conservatively, such that , and kie∼1–5 s-1. Thus, the system can be considered to be in, or approaching, the slow-exchange limit. In this situation, the inversion-recovery time course will be bi-exponential, including a rapidly-recovering component, principally reflecting extracellular water and characterized by flow-dominated , and a slowly-recovering component, principally reflecting intracellular water and characterized by exchange-dominated , vide infra, Eq. [4]. Further, the thin-slice, spin-echo acquisition, in concert with the time-of-flight, flow-induced large , will result in substantial suppression of signal from extracellular water. (Note that the longitudinal relaxation rate constant for the intracellular water in the presence of transcytolemmal exchange is identified as , to distinguish it from the intrinsic rate constant in the absence of transcytolemmal water exchange, R1,i)
Modeling the IRSE time course as bi-exponential yields the rate (or time) constant and amplitude for each of the two components of the water 1H longitudinal-magnetization recovery. The relaxation rate constant, , measured under the conditions of this experiment (thin slice, rapid flow, IRSE), reflects two parallel kinetic processes: (i) relaxation due to transcytolemmal exchange and (ii) intrinsic relaxation that would occur in the absence of exchange. Since it is the associated rate constants that are additive for parallel kinetic processes, in the slow exchange limit
| [4a] |
Rearranging and writing in terms of time constants, the inverse of the intracellular preexchange lifetime can be expressed as (7),
| [4b] |
With knowledge of and T1,i, τi can be estimated. T1,i itself can be estimated via IRSE measurement in cell pellets after removing the majority of the extracellular water.
Methods
All animal experiments were approved by the Washington University Institutional Animal Care and Use Committee.
Cell Culture: Microbead-Adherent Cells and Cell Pellets
Neurons and astrocytes from rat cerebral cortex were dissociated with papain, as previously described (27). In brief, cortical hemispheres from two Long Evans newborn rats, age 1–5 days, were cut into 500-μm slices using a Mcilwain tissue chopper and then incubated at 30–35 °C for 90 min under 95% O2 and 5% CO2 in Earl's buffered salt solution (EBSS, in mM: 117 NaCl, 5.3 KCl, 1 NaH2PO4, 26.2 NaHCO3, 1.5 CaCl2, 1 MgCl2) containing 200 units of papain, 1 mM cysteine and 0.5 mM EDTA. Slices were rinsed twice with EBSS containing 1 mg/mL BSA and ovomucoid (Sigma-Aldrich, St. Louis, MO, USA) and then dissociated by trituration through a fire polished Pasteur pipette.
To prepare cell pellets, suspended cells were transferred into a 4.5-mm inner diameter glass tube and were centrifuged at 3000 g for 2 min. After the supernatant was removed, the volume of the condensed cells was ∼0.3 mL.
To prepare microbead-adherent cultures, suspended cells were mixed with polystyrene microbeads fabricated to have a net positive surface charge (125–212 μm in diameter; 3 mL in volume, settled by gravity; Pall/SoloHill, Port Washington, NY, USA). The microbeads were previously sterilized by autoclaving in double-distilled water, then incubated for 24–48 hours with 3 μg/mL laminin (Sigma-Aldrich), washed twice with sterile distilled water, once with EBSS, and finally suspended in serum-free Neurobasal medium (Invitrogen, Carlsbad, CA, USA). Both the positive surface charge and the laminin coating are known to promote attachment of many cell types including neurons and astrocytes.
The mixture of cells and microbeads (∼15 mL) was dispensed into six Petri plates (60-mm diameter) that were coated with 0.15% agarose (Sigma-Aldrich) to minimize cell adhesion. Mixed neuron and astrocyte cultures were maintained for 1–2 weeks at 37 °C in a humid atmosphere of 95% air and 5% CO2 in complete growth medium (CGM) consisting of Eagle's MEM (Invitrogen) containing 0.5 mM glutamine, 20 mM glucose, penicillin and streptomycin (50 units and 50 μg/mL, respectively; Invitrogen) and 5% rat serum (28). In most cases, CGM was added 4–5 hours after cell dissociation to allow for attachment to the microbeads. Several days after cell preparation, 10 μM 1-γ-D-arabinofuranosyl cytosine (ARA-C) was added to the cultures to halt proliferation of non-neuronal cells. For some experiments, mature mixed cultures, enriched for astrocytes, were prepared by excitotoxic depletion of neurons using 200 μM N-methyl-D-aspartate one week after cell dissociation. For other experiments, cultures enriched for neurons were prepared by extending the period between dissociation and addition of CGM to ∼16 hours and adding ARA-C, together with CGM, after this 16-hour period in serum-free medium.
Immunofluorescence
The appearance of the cells on the surface of microbeads was visualized by immunofluorescence. Mixed cultures of microbead-adherent neurons and astrocytes were rinsed using warm Tyrode's solution (in mM: 150 NaCl, 4 KCl, 2 CaCl2, 2 MgCl2, 10 glucose, 10 HEPES, pH to 7.4 with NaOH) and then immersed for 30 min in 0.12 M sodium phosphate, pH 7.4, containing 4% depolymerized paraformaldehyde and 0.1% glutaraldehyde. After three washes using Tris-buffered saline, pH 7.4, cultures were incubated for 15 min in blocking solution: phosphate buffered saline (PBS), pH 7.4, containing 1% normal goat serum and 0.1% Triton X-100. Rabbit anti-neuronal β-3-tubulin (1:1000; Covance, Princeton, NJ, USA) and mouse anti-glial fibrillary acidic protein (GFAP) (1:200; Sigma-Aldrich) primary antibodies were diluted in blocking solution and applied for 18–24 hours. After three washes using PBS, fluorescently-tagged goat anti-mouse and anti-rabbit secondary antibodies were applied for 1–2 hours at 1:200 dilution in blocking solution. After three PBS washes, labeled cells were visualized by epi-illumination and Z-stacks of images collected using a Photometrics CCD camera on a Nikon Eclipse E600 microscope with 10× and 40× objectives (0.3 and 0.8 numerical apertures (NA), respectively).
General MR Experimental Setting
MR experiments were performed on an Agilent/Varian DirectDrive™ MRI system (Agilent/Varian, Santa Clara, CA, USA) with an 11.74-T, 26-cm-diameter, clear-bore horizontal magnet (Agilent/Varian/Magnex, Santa Clara, CA, USA). The system was equipped with an actively shielded gradient and shim-coil assembly (8-cm inner diameter), driven by Analogic/Copley gradient amplifiers (Analogic/Copley, Peabody, MA, USA), providing a maximal gradient of 120 G/cm with a rise time of ∼300 μs. A lab-made, two-turn solenoid coil was used for RF transmission and reception. The 1H inversion-recovery experiments were conducted using a slice-selective IRSE spectroscopy sequence (Fig. 1a).
IRSE Experiments with Perfused Microbead-Adherent Cells
A sample of microbead-adherent cells (∼2–3 mL), enriched for either neurons or astrocytes, was loaded into a lab-built perfusion system, and Tyrode's solution (media) was perfused through the sample at 36.5 °C with a volumetric flow rate of 30–45 mL/min (Fig. 1b). The media temperature was maintained using a glass heat exchanger upstream of the sample tube and was monitored by a fiber-optic temperature sensor (FISO, Quebec, QC, Canada) located ∼5 mm above the sample. The volumetric flow rate of the media was measured using a flow meter (Cole-Parmer, Vernon Hills, IL, USA) downstream of the sample tube. IRSE spectroscopy data were collected from five 100-μm slices spanning across the sample (red bars in Fig. 1b), with a 500-μm inter-slice gap. The scan parameters include: echo time (TE) 35 ms, duration of both 90° and 180° pulses 4 ms, acquisition time 140 ms, eight or sixteen total averages, and fifteen empirically-derived, approximately logarithmically-spaced inversion times (TI's) (5.5, 11, 15, 21, 27, 36, 48, 70, 100, 170, 350, 780, 1800, 3000, and 5000 ms, respectively). For each TI, the IRSE cycle (Fig. 1a) proceeded from the bottom of the sample incrementally to the top (red arrow in Fig. 1b), which was against the direction of media flow (blue arrow in Fig. 1b). This ensured the flow of fully equilibrium-magnetized perfusate water, unperturbed by preceding inversion pulses, into each slice. A 3-s delay was inserted after each bottom-to-top multislice acquisition to recover magnetization equilibrium in the sample. The bottom-to-top scan was repeated four times (four “sub-averages”) with the same TI before proceeding to the next TI, which enabled the use of a four-step phase cycle in the pulse sequence. The scan time for a 4-sub-average acquisition block employing all fifteen TI's was 7.5 min. Thus, the total scan time for an 8- (16-) total-average measurement, which included two (four) 4-sub-average blocks, was 15 (30) min. In this way, the full TI array spread across the total scan time.
Experimental timing was referenced (t = 0) to loading of the sample into the perfusion system. Generally, the first ∼15 min were used for experiment setup and then four (two) consecutive 8- (16-) total-average IRSE measurements were conducted, which made the entire experimental time period ∼75 min. Immediately following the final IRSE measurement, the sample was unloaded and prepared for quality-assurance assessment. An overview of the experimental schema is shown in Supporting Fig. S1.
For MR experiments under normal conditions, the perfusion media was oxygenated Tyrode's solution. Under oxygen and glucose deprivation (OGD) conditions, modified Tyrode's solution was used from the beginning of system setup, in which glucose (10 mM) was replaced with 2-deoxy-D-glucose (10 mM; Sigma-Aldrich) and the media was saturated with nitrogen gas instead of oxygen. OGD conditions were maintained throughout the 75-min MR experimental time period.
Cell Viability Assurance
Cell viability was confirmed via calcein fluorescence staining. (Live cells stain green when calcein acetoxymethyl (AM) is transported into the cells and converted to calcein through intracellular acetoxymethyl ester hydrolysis.) Before loading the sample for MR experiments, a portion (∼1 mL) was collected as control and was separately maintained in a Petri plate at 36.5 °C. After MR experiments, both the sample and the control were rinsed three times using Tyrode's solution containing 15 μM Calcein AM (Life Technologies, Carlsbad, CA, USA) and then maintained in this media at 36.5 °C for 45 min. Fluorescence images of the calcein-stained live cells were acquired using a Photometrics CCD camera (Photometrics, Tucson, AZ, USA) on a Nikon Eclipse 80i fluorescence microscope (Nikon Instruments, Melville, NY, USA) with 4×, 10×, and 20× objectives (0.2, 0.3, and 0.5 NA, respectively). The quantity and morphology of live cells in the post-experiment sample were visually compared with those in the control to confirm viability.
IRSE Experiments with Cell Pellets
The sample tube containing the condensed cell pellet was mounted inside the same solenoid coil that was used for perfusion experiments. The ambient temperature around the sample was maintained at 36.5 °C via circulating, temperature-controlled water. IRSE data were acquired using the pulse sequence in Fig. 1a, and one 10-mm slice was selected to cover the entire sample. Other parameters include: TE 2.8 ms, duration of both 90° and 180° pulses 500 μs, acquisition time 500 ms, four averages, and fifteen empirically-determined, approximately logarithmically-spaced TI's (0.2, 0.4, 0.6, 0.9, 1.2, 1.5, 1.9, 2.3, 2.8, 3.5, 4.4, 5.8, 9.2, 13, 20 s, respectively). The delay time after each IRSE cycle was 15 s, and the scan time for a 4-average measurement was 15 min. Four consecutive measurements were conducted, which resulted in a total scan time of 1 hr.
Data Analysis
MRS data were modeled using a lab-developed “Bayesian Data-Analysis Toolbox” software suite (bayesiananalysis.wustl.edu). Student's t-test was employed to assess statistical significance (MATLAB R2015a: The MathWorks Inc., Natick, MA, USA). Results are reported as mean ± SD, unless otherwise noted.
The slice-selective, MRS water 1H time-domain signal was modeled as a single, exponentially-decaying sinusoid, and the signal amplitude was estimated for each slice. The signal amplitude was then averaged across all slices for each TI to form a fifteen-point, inversion-recovery dataset (signal amplitude vs. TI). Inversion-recovery datasets were modeled as mono- and bi-exponentials (Eqs. [5a] and [5b]), and model parameters were estimated.
| [5a] |
| [5b] |
Here , , and are the observed relaxation rate constants. The constant c = s(∞) is the signal amplitude at TI = ∞. The longitudinal-magnetization-differential Δ = s(0) – s(∞) is the extent to which the inversion pulse perturbs the magnetization from its equilibrium value. Under conditions of idealized inversion, Δ = −2s(∞). The respective component fractional amplitudes are: f, fA, and fB, where f = 1 and fB = 1 – fA.
As will be described, is equated with and should, ideally, be the same for all samples of a given cell type (i.e., neuron vs. astrocyte). In contrast, is equated with and, in early developmental experiments, was found to be moderately dependent upon the sample-specific, microbead packing arrangement within the sample tube.
Special Notes on Sample Size
In this study, an IRSE determination can be associated with different identifiers/types of sample size, n. First, each cultured cell batch consisted of cells from two rat pups. Second, each batch was evenly divided into six samples, and each sample was subject to an individual/independent MR study. Third, during each MR study, a replicate series of IRSE measurements was performed on a given sample. Accordingly, results are identified with three sample size types: npup, nsample, and nmeasurement. The nsample and nmeasurement indicate the number of samples (individual/independent MR studies) and IRSE measurements included in a dataset, respectively, while npup shows the number of rat pups that contributed cells to the dataset. The sample sizes are summarized in Table 1.
Table 1. Summary of Sample Sizes.
| Neurons | Astrocytes | ||
|---|---|---|---|
| Perfused Cells (duplicate, 16-total-average measurements) | nsample = 6 (npup = 4) | nsample = 7 (npup = 8) | |
| Perfused Cells (quadruplicate, 8-total-average measurements) | Normal | nsample = 3 (npup = 2) | nsample = 7 (npup = 8) |
| OGD | nsample = 3 (npup = 2) | nsample = 5 (npup = 6) | |
| Cell Pellets | nsample = 4 (npup = 4) | nsample = 3 (npup = 4) | |
Results
Immunofluorescence
Immunofluorescence micrographs of the microbead-adherent cells are shown in Fig. 2. The images were taken from a mixed culture of neurons and astrocytes, and were chosen for the best visualization of cell morphology. The neurons were stained in green for class III β-tubulin, the astrocytes in red for glial fibrillary acidic protein, and the nuclei in blue using Hoechst 33342. As shown in Fig. 2a, the microbeads were usually “glued” into clusters by the cells that grew across different microbeads. The shapes of neurons and astrocytes on the surface of a single microbead are shown in Fig. 2b and Fig. 2c, respectively, with the dendritic branching clearly visualized.
Figure 2. Immunofluorescence micrographs of microbead-adherent neurons and astrocytes.
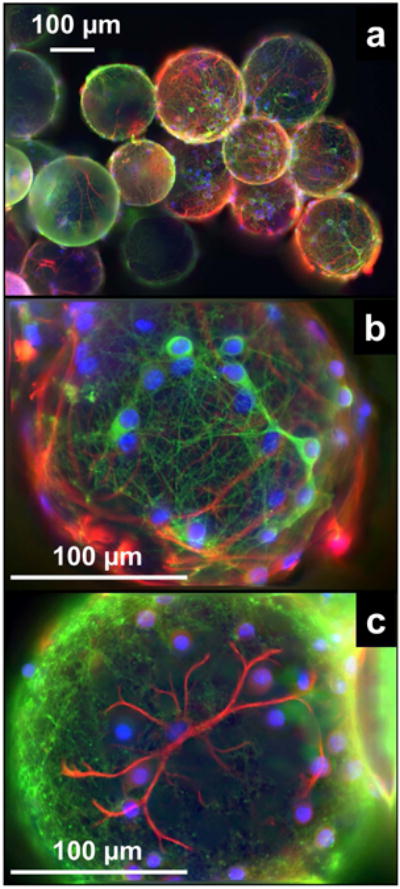
The neurons were stained for class III β-tubulin (green), the astrocytes for glial fibrillary acidic protein (red), and the nuclei were counterstained using Hoechst 33342 (blue). The images were collected from a mixed culture of neurons and astrocytes.
Cell viability Assurance
An example of the cell-viability assay in a neuron culture is presented in Fig. 3. The shapes of the cells, particularly the dendritic structures, can be clearly seen in the examples marked by yellow arrows and are consistent with those observed by immunofluorescence (Fig. 2). The yellow circles highlight examples of cells that grew between microbeads. The high-intensity areas marked by yellow boxes are example locations of cells that were out of focus in the given captured photo-plane due to the significant dimensions of the spherical microbeads.
Figure 3. Fluorescence micrographs of viability staining in (a–d) a control sample and (e–h) a post-experiment sample from a culture of neurons.
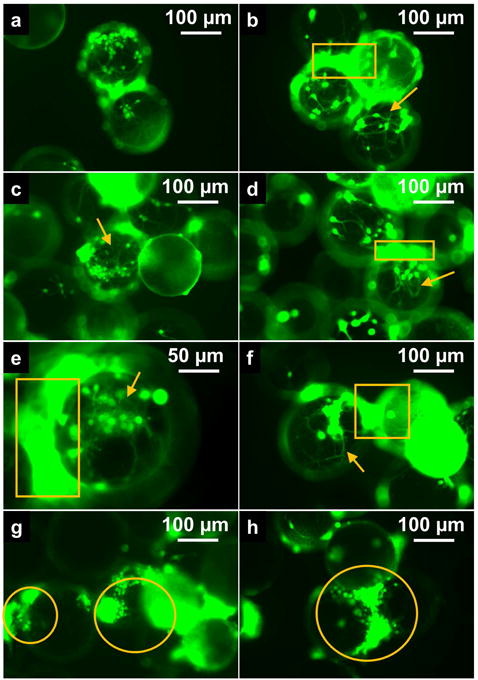
Live cells are stained in green. Examples of dendrites are marked by yellow arrows. Examples of cells that had grown between the microbeads are marked by yellow circles. The high-intensity areas, marked by yellow boxes, are examples of locations where cells were out of focus in the given micrograph plane.
IRSE Experiments with Perfused Microbead-Adherent Cells
The thin-slice, spin-echo portion of the IRSE sequence provides substantial time-of-flight suppression of the otherwise dominant signal from the flowing extracellular media. Suppression would be complete at very high flow velocity, as previously shown with microbead-adherent HeLa cells (7,29). CNS cells are far less robust to flow-induced mechanical forces (vide infra), limiting the flow rate and, thus, also the flow-enabled suppression of the extracellular water signal. The observed IRSE signal will therefore be the sum of signals from the two (intra- and extracellular) compartments, with the signal from the flowing extracellular media substantially, but not completely, suppressed.
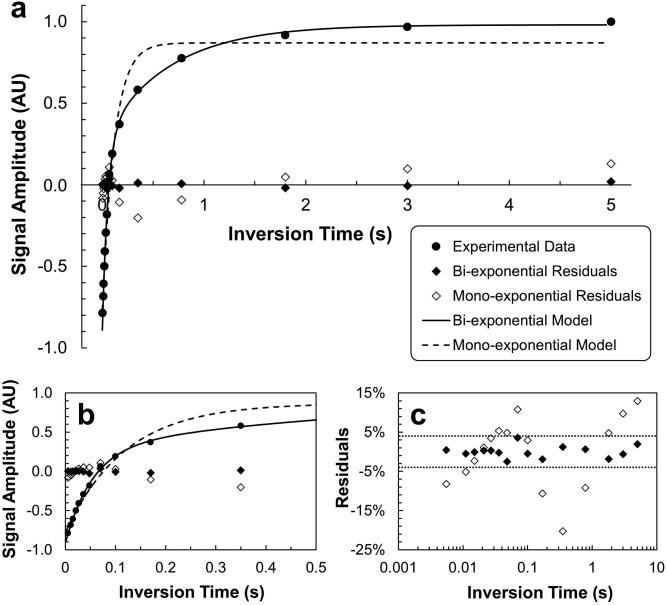
IRSE data from perfused cell experiments were modeled as mono- and bi-exponential, respectively (Eq. [5]). A representative example is shown in Fig. 4, in which a dataset from a neuron sample is modeled. The mono-exponential (Eq. [5a]) failed to model the data well, as suggested by the large systematic residuals. In contrast, the bi-exponential (Eq. [5b]) modeled the data well, leaving residuals of less than 4% of the maximum signal amplitude (amplitude at TI = 5 s). Bayesian-based model selection (30) estimated the probability for the bi-exponential model to be essentially 100% for this dataset. These two competing models were tested on every IRSE dataset from perfused-cell experiments, and the bi-exponential model was substantially more probable (probability > 90%) than the mono-exponential model in all cases.
Figure 4. Mono- and bi-exponential modeling of inversion-recovery data collected from a perfused IRSE measurement in neurons. (a, b, & c).
The three panels share the same legend scheme. Experimental data (filled circles) were obtained in the first IRSE measurement (15–30 min under perfusion) of the 75-min MRS experiment. (c) The values of residuals were converted to percentages relative to the maximum signal amplitude in the experimental data (amplitude at TI = 5 s). The dotted horizontal lines mark the residual level of ± 4%.
Bi-exponential modeling of IRSE data revealed two distinct relaxation components with relaxation time constants and . Relaxation time constant was identified with the relatively-slowly-relaxing component and with the rapidly-relaxing component. Considering individual cell preparations (under normal perfusion conditions) during the 15–45 min period when cells are most viable, derived values for neuron ranged between ∼0.45–0.7 s and those for astrocyte between ∼0.3–0.7 s. For both cell types, was only ∼0.05 s, an order-of-magnitude difference. The amplitude ratio of relaxation components, fA/fB, was ∼1:3 for both types of cells. Control perfusion experiments were performed with cell-free microbeads, which pack more uniformly/consistently than the clumping-prone, cell-attached microbeads. IRSE control perfusion experiments with cell-free microbeads yielded a of ∼0.01 s (via mono-exponential modeling (31)), which is of the same order as . Early experiments developing the thin-slice IRSE protocol showed that increased with either decreasing flow rate or increasing slice thickness, consistent with flowing perfusate time-of-flight effects. Importantly, a slowly relaxing component was never observed under any control experiments with perfused cell-free microbeads. Finally, only was affected by exposing the cell-attached microbeads to OGD conditions, vide infra. Based on these findings, is assigned to the intracellular-water component ( ) and to the extracellular-water component ( ).
IRSE Experiments with Cell Pellets
IRSE data from cell pellets were well modeled as mono-exponential (Eq. [5a]). The estimated T1 was 3.32 ± 0.01 s for neurons (nsample = 4, npup = 4) and 3.06 ± 0.01 s for astrocytes (nsample = 3, npup = 4) at 36.5 °C. These results are used as estimates for the intrinsic T1 of intracellular water, T1,i (Eq. [4b]), to calculate the value of τi.
τi under Normal Conditions
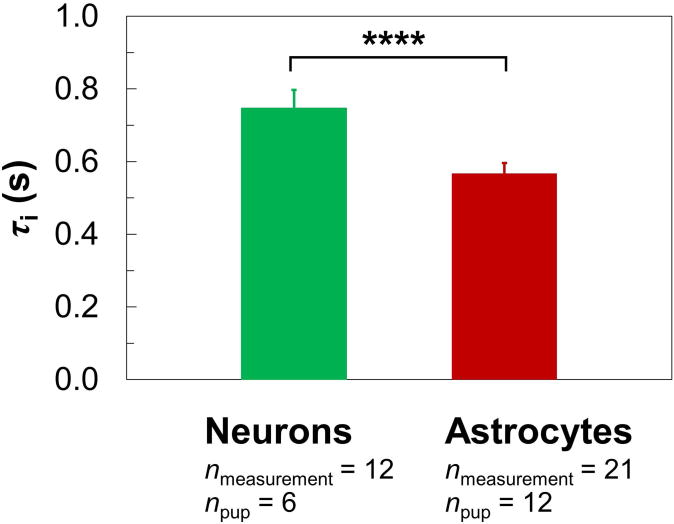
Representative τi values under normal conditions (Fig. 5) were estimated via Eq. [4] by considering all the IRSE datasets acquired 15–45 min under perfusion (i.e., during the first-half of the 1-hr MR experiment, when cells are expected to be most viable; see also Supporting Fig. S1). The estimated τi is 0.75 ± 0.05 s for neurons (nmeasurement = 12, npup = 6) and 0.57 ± 0.03 s for astrocytes (nmeasurement = 21, npup = 12), values that are statistically different (P < 0.0001).
Figure 5.
The τi in neurons and astrocytes under normal conditions (mean ± SD). Representative τi's (colored columns) were derived via Eq. [4], which involved all 8- and 16-total-average IRSE measurements acquired 15–45 min under perfusion (see also Supporting Fig. S1). The neuron database includes a total of 12 measurements (nmeasurement = 12) from 3 batches of cells (npup = 6) while the astrocyte database includes 21 measurements (nmeasurement = 21) from 6 batches of cells (npup = 12). There is a significant difference (**** for P < 0.0001) between the neuronal and astrocytic τi's.
τi under Oxygen and Glucose Deprivation Conditions
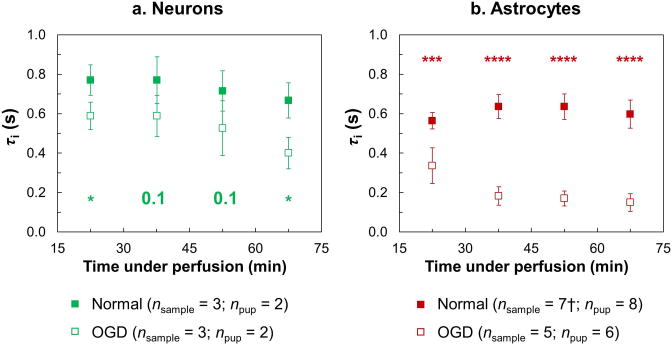
A time-course analysis of τi and its response to OGD treatment are presented in Fig. 6. The results only include data from the 8-total-average IRSE measurements, yielding a 1-hour tracking of τi under both normal and OGD conditions with a time resolution of 15 min. Recall, the onset of OGD preceded the first MR data acquisition time block by 15 min. Within the first 30 min after the onset of OGD (measurement #1), τi in both neurons and astrocytes had decreased significantly from that measured under normal conditions (P < 0.05 for neurons and P < 0.001 for astrocytes). This drop in τi became more evident for astrocytes after 30 min under OGD conditions (measurements #2–4, P < 0.0001). For neurons, the difference in τi between the control and the OGD group is not significant at measurements #2 and #3 because of a slight decreasing trend in τi in the control group across measurements #1–4, a decrease that was not observed in the control group of astrocytes. It is noteworthy that, during the progression of the decrease in τi under OGD conditions, the neuronal and astrocytic τi's are different, not only from their normal values, respectively (except for measurements #2 and #3 in neurons), but also from each other at each measurement (P < 0.01). The largest difference between the neuronal and astrocytic τi's under OGD conditions was observed at 45 min post-OGD onset (measurement #2), at which time τi was 0.6 ± 0.1 s for neurons (nsample = 3, npup = 2) and 0.18 ± 0.05 s for astrocytes (nsample = 5, npup = 6).
Figure 6. Time-course analysis of τi in (a) neurons and (b) astrocytes (mean ± SD).
τi's measured under both normal (filled squares) and OGD (open squares) conditions are plotted versus experiment time (“time under perfusion”) for each cell type (green for neurons and red for astrocytes). Sample sizes are indicated in the legend. The numbers and/or asterisks along the bottom or top of the panels mark the P-values comparing τi under normal conditions vs. the OGD-induced τi (* for P < 0.05; *** for P < 0.001; **** for P < 0.0001). † Measurement #4 in astrocytes under normal conditions contains only six datasets due to a leak in the sample tube in one of the seven experiments.
Discussion
The determination of intracellular water preexchange lifetime from a population of cultured cells requires a method for differentiating between the water in intra- and extracellular compartments (5). In MR measurements, this can be achieved by establishing an inter-compartment contrast in resonance frequency (32-34), relaxation time constants (T2 (20-22) or T1 (6,10,12,23,35)), or ADC (24-26,36,37). Many of these methods employ paramagnetic compounds to generate the corresponding contrasts (6,10,12,20-23,32-35). This laboratory previously developed a method using perfusion media flowing at high velocity, in concert with thin-slice, spin-echo MRS, for selectively acquiring and analyzing the intracellular-water 1H signal with microbead-adherent HeLa cells (7,29). Herein, we have modified application of this method, albeit at lower perfusion rates, to microbead-adherent CNS cells. Microbead-adherent HeLa cells showed excellent robustness in the face of perfusion flow rates as high as 125 mL/min, thus achieving ∼100% suppression of extracellular-water signal (7). Microbead-adherent CNS cells, however, proved far less flow resistant in pilot experiments, where substantial cell loss was observed via the cell-viability assay at perfusion flow rates higher than ∼50 mL/min, thus necessitating a substantially lower perfusion flow rate (30–45 mL/min) for the current study. One additional consideration is the influence of a hydrostatic pressure gradient between the intra- and extracellular spaces (2) on the apparent cell-membrane water permeability. However, such a hydrostatic contribution to the apparent permeability would be negligible, as the cell membranes are not sufficiently stiff to support such a gradient.
The microbead-adherent CNS cells tend to grow across different microbeads, thus “gluing” the microbeads into small clusters (Fig. 2a). This impedes the flow-driven replenishment of bulk fluid inside the clusters compared to that in the “free space” outside the clusters. In concert with significantly reduced perfusion-flow rate (compared to earlier studies with HeLa cells), this resulted in incomplete suppression of the 1H signal from extracellular water following the slice-selective IRSE acquisition (Fig. 1a). While suppression of the 1H signal from extracellular water was substantial (> 95%), the residual was not negligible, its amplitude being ∼3× that of the intracellular water signal, as suggested by the amplitude ratio fA/fB. Nevertheless, the resulting IRSE signals from intra- and extracellular water yielded a bi-exponential inversion-recovery curve with relaxation time constants differing by an order of magnitude. Importantly, T1,i determined from cell-pellet experiments (∼3.1-3.3 s for both neurons and astrocytes) was ∼65× longer than the short, flow-driven (∼50 ms). This difference in relaxation rate constant, , provides access to the MR slow-exchange condition, Eq. [3b]. At 11.74 T and 36.5 °C, T1,i is similar to the 1H T1 measured in bulk Tyrode's solution, ∼3.0 s, at the same temperature, but is longer than the overall T1 (∼2 s) reported for rat brain in vivo (38).
Because of the substantial difference between and T1,i, the derivation of τi via Eq. [4] is not particularly sensitive to the value estimated for T1,i. Further, the assignment of (∼50 ms) as is conservative. Measurements with packed, cell-free microbeads suggest the major extracellular-water fraction, whose signal is highly suppressed by the thin-slice, IRSE microbead perfusion method, has a . This value would yield and provide even more rigorous achievement of the MR slow exchange condition, Eq. [3b].
This study employed rapidly flowing perfusate in the presence of thin-slice selection to generate rapid apparent extracellular relaxation, as characterized by short apparent extracellular longitudinal and transverse relaxation time constants. In principle, this effect could also be realized through the use of slowly flowing perfusate doped with paramagnetic relaxation (contrast) agent. However, to achieve a perfusate relaxation time of ∼50 ms, as achieved herein via thin-slice selection and rapid perfusate flow, would require doping the perfusate with, for example, ∼5 mM Gd-BOPTA (Bracco, Monroe Township, NJ, USA). In preliminary experiments, this approach resulted in a strong magnetic-susceptibility differential between the plastic microbeads, the relaxation-agent-doped perfusate, and the relaxation-agent-free intracellular water, which substantially increased the intracellular water linewidth, thus, obviating quantitative signal analysis (data not shown).
The τi values measured under normal (healthy) conditions, ∼0.8 s for neurons and ∼0.6 s for astrocytes, represent an average over complex and diversified cell morphologies (Figs. 2b and c) and fall within the range of several reported values measured in vivo in rat brain (mostly gray matter; ∼0.6 s (6) and ∼0.2 s (39)) and human brain (∼0.3 s in corticospinal tracts (19); ∼2 s in white matter (3)). However, this is the first time that near-direct MR measurement of τi has been achieved separately in neurons and astrocytes.
The transcytolemmal water exchange in glial cells (mainly astrocytes) has been hypothesized to be fast (3,40) and, in modeling the MR signal, glial intracellular water is, in some cases, considered part of the extracellular milieu (41,42). However, the τi in astrocytes determined herein, while statistically different, is not greatly dissimilar from that measured in neurons. Glial cells compose ∼65% of total cells in the mouse brain and ∼90% in the human brain (43,44). Therefore, the MR signal contribution from glial cells and their neuron-approximating τi suggest that glia should be considered separately from the extracellular compartment in the interpretation of in vivo brain MR data. Given the complex, highly dendritic morphology of CNS cells, it is difficult to calculate the cell volume and surface area and, thus, the diffusional cell-membrane water permeability in these cells using Eq. [1]. Making the very rough approximation that neurons can be considered as having ∼10-μm diameter spherical cell bodies, as suggested by Fig. 2, and ignoring dendritic branching, the diffusional water permeability Pd is ∼2 × 10-3 mm/s.
Oxygen and glucose deprivation is a widely accepted model for ischemic injury in CNS cell cultures (45-47). By removing oxygen and glucose from the media, energy-dependent mechanisms of water (and ion) transport across the cell membrane are subject to decline. In the 75-min time-course experiments (15 min set up, 4 × 15 min measurements; Fig. 6), τi for both neurons and astrocytes significantly decreased within 30 min post-onset of OGD (measurement #1), compared with τi, measured during the same time window, in control-state neurons and astrocytes. As the perfusion period lengthened beyond 30 min (measurements #2–4), τi for the control-state neurons decreased slightly, eliminating the statistical difference in τi between OGD and control-state neuron groups (measurements #2 and #3). Such was not the case for astrocytes under control-state conditions. We speculate that neurons are less robust, relative to astrocytes (45), in the presence of continuous shear stress from media flow.
This study was not designed to identify the biophysics behind the reduction in τi associated with OGD, and the factors influencing τi for neurons and astrocytes are not fully understood. Nevertheless, it is possible to identify some potential mechanisms. The period over which the OGD-induced decrease in τi (increase in the apparent cell-membrane water permeability) was detected corresponds well with that for other effects, including change in the intracellular Na+ concentration (46,47), cell swelling (48), and cell death (49), which have all been shown to occur under similar hypoxia-ischemia protocols. For astrocytes, the water channel protein aquaporin-4 (AQP4) plays a major role in regulating transcytolemmal water transport (50). The water permeability of AQP4 increases in association with a reduction in intracellular pH (51), which may occur with OGD. Further, increased astrocyte cell volume (due to swelling) following cerebral ischemia is associated with increased expression of AQP4, as quantified early (1 hr (52)) and late (24 hrs (53)) after injury onset. Under OGD conditions, an increase in the water permeability of AQP4 or its over-expression would cause increased apparent cell-membrane water permeability (decreased τi). Decreased expression of AQP4 has the opposite effect, as, for example, a seven-fold decrease in the osmotic water permeability was observed in primary astrocyte cultures from AQP4-depleted mice (54). For astrocytes, the result reported herein (OGD-induced decrease in τi) is consistent with the observation of intracellular pH effects (51) or increased expression of AQP4 following OGD (52), but does not preclude the possibility of other mechanisms that have not yet been identified. While neurons in the brain do not typically express aquaporins (50,55), neuronal τi also decreased in response to OGD, suggesting the additional presence of an aquaporin-independent mechanism(s). It is interesting to note that astrocytes, which showed a greater reduction in τi than neurons, also responded more quickly to osmotic stress than neurons, possibly as a consequence of the presence of AQP4 (56).
This study was motivated by a desire to elucidate the characteristic time for transcytolemmal water exchange, in the context of MR-based measurements in vivo (e.g., relaxation, diffusion, dynamic contrast enhanced). Every MR measurement has an experimental characteristic time(s). For diffusion-sensitive MR measurements, a keen interest of our laboratory, the experimental characteristic time is the diffusion encoding time, τdiff, the time between the diffusion encoding gradient pulse pair(s), in the narrow gradient-pulse limit. If τdiff is sufficiently long compared to the characteristic time for transcytolemmal water exchange, the diffusion signal is not separable into intra- and extracellular components and the diffusion measurement yields a single (average) ADC. If τdiff is sufficiently short compared to the characteristic time for transcytolemmal water exchange, the diffusion signal can, in principle, be separated into intra- and extracellular components, assuming the component ADC values are sufficiently different. Assuming that τi determined herein is a reasonable approximation to the in vivo case, particularly for gray matter, the question of how short τdiff must be to place the presumed two-compartment (intra- and extracellular) measurement in the slow-exchange limit can be addressed. Specifically, how short must τdiff be, such that the diffusion signal can be separated into that from the intracellular and extracellular compartments? Here the extracellular water preexchange lifetime, τe, also must be taken into account. In the brain, the intra- to extracellular water volume ratio is ∼4:1 (6,57). Therefore, for equilibrium transcytolemmal water exchange (Eq. [2]), τe is one fourth that of τi. Using the astrocyte τi (∼0.6 s; kie ∼1.7 s-1) as the more conservative (shortest) estimate for CNS cell preexchange lifetime, τe is ∼150 ms (kei ∼7 s-1) under normal (healthy) conditions. The relevant metric defining whether the MR diffusion measurement time is sufficiently short relative to the characteristic time of transcytolemmal water exchange is (6)
| [6a] |
where the metric is dominated by kei. Accordingly, to differentiate between the diffusion properties of intra- and extracellular water in normal (healthy) brain, the diffusion time of an MR measurement should be on the order of 12 ms (10% of 115 ms) or less.
After 30 min of OGD treatment, τi decreased for both neurons and astrocytes. Again, using the astrocyte τi (∼0.2 s; kie ∼5 s-1) as the most conservative (shortest) estimate for CNS cell preexchange lifetime, τe reduces to ∼50 ms (kei ∼20 s-1) for brain in vivo. Repeating the above analysis for OGD conditions,
| [6b] |
Thus, again extrapolating to brain in vivo, to differentiate between the diffusion properties of intra- and extracellular water under injury conditions, the diffusion time of an MR measurement should be on the order of 4 ms (10% of 40 ms) or less.
The slow-exchange limit criteria for the MR diffusion time deduced herein (τdiff < 12 ms for healthy brain, and τdiff < 4 ms for injury conditions) are consistent with recent MR diffusion studies employing oscillating magnetic-field gradients. Short diffusion times (τdiff < 5 ms) were required to reliably characterize intracellular water ADC (58,59) and cell size (59) in various leukemia cells, which have similar τi and cell-body dimensions as the CNS cells in this work.
The validity of these conclusions regarding characteristic experimental times depends on the extent to which the microbead-adherent, CNS cell-culture system captures the essential water exchange features of CNS cells in vivo. As myelin is absent from this cell-culture preparation, it more closely approximates gray matter than white matter.
Further, the measured parameter, τi, is accurate to the extent that the thin-slice, IRSE microbead perfusion method has achieved the MR slow-exchange limit for intracellular water. This depends on achieving conditions expressed by Eq. [3b], which is facilitated by short We assigned (∼50 ms) as . As noted earlier, this is a conservative assignment for , as measurements with packed, cell-free microbeads suggest the major water fraction, whose signal is highly suppressed by the thin-slice, IRSE microbead perfusion method, has a . Nevertheless, under normal (healthy) conditions, the slow-exchange limit is achieved, or closely approximated, in the conservative case ( ) where for both neurons and astrocytes. However, for astrocytes under OGD conditions, the conservative case ( ) yields (≈ 10 kie for neurons). Here, the τi derived for OGD astrocytes would be a lower estimate, the true value being somewhat longer. If is the more accurate assignment, then the slow exchange limit is also achieved, or closely approximated, for OGD astrocytes.
Conclusion
The intracellular water preexchange lifetimes for microbead-adherent cultured neurons and astrocytes under normal and oxygen-glucose-deprivation conditions have been determined. Intracellular ↔ extracellular water exchange was brought into (or close to) the “MR-relaxation slow exchange limit” through the combined use of rapid perfusion and thin-slice-selective MRS. For neurons under normal (healthy) conditions, τi was estimated to be 0.75 ± 0.05 s and, for astrocytes, 0.57 ± 0.03 s (P < 0.0001). Within 30 min after the onset of oxygen-glucose-deprivation, τi in both neurons and astrocytes decreased significantly from its value in normal (healthy) cells, with astrocytic τi showing a substantially greater decrease than neuronal τi. To the extent that the microbead-adherent, CNS cell-culture system captures the essential water exchange features of CNS cells in vivo, particularly gray matter, valid application of the slow-exchange-limit, two-compartment (intra- and extracellular) model to diffusion MR data in the brain under normal (healthy) conditions requires that the diffusion time be on the order of 12 ms or less, and under injury conditions, 4 ms or less.
Supplementary Material
Supporting Figure S1. Overview of perfused IRSE experiments. IRSE measurements with 8- and 16-total-averages are represented by short, and long colored bars, respectively (dark green for neurons under normal conditions, light green for neurons under OGD conditions, dark red for astrocytes under normal conditions, light red for astrocytes under OGD conditions). Gray bars indicate where IRSE data were not collected. An experiment on each sample includes either two consecutive (duplicate), 16-total-average measurements (two long bars) or four consecutive (quadruplicate), 8-total-average measurements (four short bars). Data from normal perfusion condition measurements acquired during the first-half of each experiment (15–45 min under perfusion) were used to estimate τi's displayed in Fig. 5. All 8-total-average measurements were used for time-course analysis of τi under normal and OGD conditions (Fig. 6).
* n stands for nsample.
Acknowledgments
Support from NIH/NIBIB grant R01-EB002083 (JJN) and NIH/NINDS grant R01-NS030888 (JEH) is gratefully acknowledged.
References
- 1.Verkman AS, van Hoek AN, Ma T, Frigeri A, Skach WR, Mitra A, Tamarappoo BK, Farinas J. Water transport across mammalian cell membranes. Am J Physiol. 1996;270:C12–30. doi: 10.1152/ajpcell.1996.270.1.C12. [DOI] [PubMed] [Google Scholar]
- 2.Verkman AS. Water permeability measurement in living cells and complex tissues. J Membr Biol. 2000;173:73–87. doi: 10.1007/s002320001009. [DOI] [PubMed] [Google Scholar]
- 3.Nilsson M, Latt J, van Westen D, Brockstedt S, Lasic S, Stahlberg F, Topgaard D. Noninvasive mapping of water diffusional exchange in the human brain using filter-exchange imaging. Magn Reson Med. 2013;69:1573–1581. doi: 10.1002/mrm.24395. [DOI] [PubMed] [Google Scholar]
- 4.Springer CS, Li X, Tudorica LA, et al. Intratumor mapping of intracellular water lifetime: metabolic images of breast cancer? NMR Biomed. 2014;27:760–773. doi: 10.1002/nbm.3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kirk K. NMR methods for measuring membrane transport rates. NMR Biomed. 1990;3:1–16. doi: 10.1002/nbm.1940030102. [DOI] [PubMed] [Google Scholar]
- 6.Quirk JD, Bretthorst GL, Duong TQ, Snyder AZ, Springer CS, Ackerman JJH, Neil JJ. Equilibrium water exchange between the intra- and extracellular spaces of mammalian brain. Magnet Reson Med. 2003;50:493–499. doi: 10.1002/mrm.10565. [DOI] [PubMed] [Google Scholar]
- 7.Zhao L, Kroenke CD, Song J, Piwnica-Worms D, Ackerman JJ, Neil JJ. Intracellular water-specific MR of microbead-adherent cells: the HeLa cell intracellular water exchange lifetime. NMR Biomed. 2008;21:159–164. doi: 10.1002/nbm.1173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stein WD, Lieb WR. Transport and diffusion across cell membranes. Orlando: Academic Press; 1986. pp. 1–68. [Google Scholar]
- 9.Chen ST, Springer CS. Ionophore-catalyzed cation-transport between phospholipid inverted micelles manifest in DNMR. Biophys Chem. 1981;14:375–388. doi: 10.1016/0301-4622(81)85041-7. [DOI] [PubMed] [Google Scholar]
- 10.Zhang YJ, Poirier-Quinot M, Springer CS, Balschi JA. Active trans-plasma membrane water cycling in yeast is revealed by NMR. Biophys J. 2011;101:2833–2842. doi: 10.1016/j.bpj.2011.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Rooney WD, Li X, Sammi MK, Bourdette DN, Neuwelt EA, Springer CS. Mapping human brain capillary water lifetime: high-resolution metabolic neuroimaging. NMR Biomed. 2015;28:607–623. doi: 10.1002/nbm.3294. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Landis CS, Li X, Telang FW, Molina PE, Palyka I, Vetek G, Springer CS. Equilibrium transcytolemmal water-exchange kinetics in skeletal muscle in vivo. Magnet Reson Med. 1999;42:467–478. doi: 10.1002/(sici)1522-2594(199909)42:3<467::aid-mrm9>3.0.co;2-0. [DOI] [PubMed] [Google Scholar]
- 13.Lee JH, Springer CS., Jr Effects of equilibrium exchange on diffusion-weighted NMR signals: the diffusigraphic “shutter-speed”. Magn Reson Med. 2003;49:450–458. doi: 10.1002/mrm.10402. [DOI] [PubMed] [Google Scholar]
- 14.Moseley ME, Cohen Y, Mintorovitch J, Chileuitt L, Shimizu H, Kucharczyk J, Wendland MF, Weinstein PR. Early detection of regional cerebral ischemia in cats: comparison of diffusion- and T2-weighted MRI and spectroscopy. Magn Reson Med. 1990;14:330–346. doi: 10.1002/mrm.1910140218. [DOI] [PubMed] [Google Scholar]
- 15.Warach S, Chien D, Li W, Ronthal M, Edelman RR. Fast magnetic-resonance diffusion-weighted imaging of acute human stroke. Neurology. 1992;42:1717–1723. doi: 10.1212/wnl.42.9.1717. [DOI] [PubMed] [Google Scholar]
- 16.Neil JJ, Duong TQ, Ackerman JJ. Evaluation of intracellular diffusion in normal and globally-ischemic rat brain via 133Cs NMR. Magn Reson Med. 1996;35:329–335. doi: 10.1002/mrm.1910350310. [DOI] [PubMed] [Google Scholar]
- 17.Duong TQ, Ackerman JJ, Ying HS, Neil JJ. Evaluation of extra- and intracellular apparent diffusion in normal and globally ischemic rat brain via 19F NMR. Magn Reson Med. 1998;40:1–13. doi: 10.1002/mrm.1910400102. [DOI] [PubMed] [Google Scholar]
- 18.Ackerman JJH, Neil JJ. The use of MR-detectable reporter molecules and ions to evaluate diffusion in normal and ischemic brain. NMR Biomed. 2010;23:725–733. doi: 10.1002/nbm.1530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nilsson M, Latt J, Nordh E, Wirestam R, Stahlberg F, Brockstedt S. On the effects of a varied diffusion time in vivo: is the diffusion in white matter restricted? Magn Reson Imaging. 2009;27:176–187. doi: 10.1016/j.mri.2008.06.003. [DOI] [PubMed] [Google Scholar]
- 20.Conlon T, Outhred R. Water diffusion permeability of erythrocytes using an NMR technique. Biochim Biophys Acta. 1972;288:354. doi: 10.1016/0005-2736(72)90256-8. [DOI] [PubMed] [Google Scholar]
- 21.Benga G. Comparative studies of water permeability of red blood cells from humans and over 30 animal species: an overview of 20 years of collaboration with Philip Kuchel. Eur Biophys J. 2013;42:33–46. doi: 10.1007/s00249-012-0868-7. [DOI] [PubMed] [Google Scholar]
- 22.Nouri-Sorkhabi MH, Chapman BE, O'Loughlin E, Li Z, Kuchel PW, Gaskin KJ. NMR measurements of the diffusional permeability of water in cultured colonic epithelial cancer cells. Cell Biol Int. 2005;29:441–448. doi: 10.1016/j.cellbi.2005.01.006. [DOI] [PubMed] [Google Scholar]
- 23.Bacic G, Alameda JC, Jr, Iannone A, Magin RL, Swartz HM. NMR study of water exchange across the hepatocyte membrane. Magn Reson Imaging. 1989;7:411–416. doi: 10.1016/0730-725x(89)90490-6. [DOI] [PubMed] [Google Scholar]
- 24.Pfeuffer J, Flogel U, Dreher W, Leibfritz D. Restricted diffusion and exchange of intracellular water: theoretical modelling and diffusion time dependence of 1H NMR measurements on perfused glial cells. NMR Biomed. 1998;11:19–31. doi: 10.1002/(sici)1099-1492(199802)11:1<19::aid-nbm499>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 25.Roth Y, Ocherashvilli A, Daniels D, Ruiz-Cabello J, Maier SE, Orenstein A, Mardor Y. Quantification of water compartmentation in cell suspensions by diffusion-weighted and T2-weighted MRI. Magn Reson Imaging. 2008;26:88–102. doi: 10.1016/j.mri.2007.04.013. [DOI] [PubMed] [Google Scholar]
- 26.Åslund I, Nowacka A, Nilsson M, Topgaard D. Filter-exchange PGSE NMR determination of cell membrane permeability. J Magn Reson. 2009;200:291–295. doi: 10.1016/j.jmr.2009.07.015. [DOI] [PubMed] [Google Scholar]
- 27.Huettner JE, Baughman RW. Primary culture of identified neurons from the visual-cortex of postnatal rats. J Neurosci. 1986;6:3044–3060. doi: 10.1523/JNEUROSCI.06-10-03044.1986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Segal MM, Baughman RW, Jones KA, Huettner JE. Mass cultures and microislands of neurons from postnatal rat brain. In: Banker G, Goslin K, editors. Culturing Nerve Cells. Cambridge, MA: MIT Press; 1998. pp. 309–338. [Google Scholar]
- 29.Zhao L, Sukstanskii AL, Kroenke CD, Song J, Piwnica-Worms D, Ackerman JJ, Neil JJ. Intracellular water specific MR of microbead-adherent cells: HeLa cell intracellular water diffusion. Magn Reson Med. 2008;59:79–84. doi: 10.1002/mrm.21440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Bretthorst GL, Hutton WC, Garbow JR, Ackerman JJH. Exponential model selection (in NMR) using Bayesian probability theory. Concept Magn Reson A. 2005;27A:64–72. [Google Scholar]
- 31.Lee JH, Li X, Sammi MK, Springer CS. Using flow relaxography to elucidate flow relaxivity. J Magn Reson. 1999;136:102–113. doi: 10.1006/jmre.1998.1629. [DOI] [PubMed] [Google Scholar]
- 32.Naritomi H, Kanashiro M, Sasaki M, Kuribayashi Y, Sawada T. In vivo measurements of intra- and extracellular Na+ and water in the brain and muscle by nuclear magnetic resonance spectroscopy with shift reagent. Biophys J. 1987;52:611–616. doi: 10.1016/S0006-3495(87)83251-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Eleff SM, McLennan IJ, Hart GK, Maruki Y, Traystman RJ, Koehler RC. Shift reagent enhanced concurrent 23Na and 1H magnetic resonance spectroscopic studies of transcellular sodium distribution in the dog brain in vivo. Magn Reson Med. 1993;30:11–17. doi: 10.1002/mrm.1910300104. [DOI] [PubMed] [Google Scholar]
- 34.Galons JP, Lope-Piedrafita S, Divijak JL, Corum C, Gillies RJ, Trouard TP. Uncovering of intracellular water in cultured cells. Magn Reson Med. 2005;54:79–86. doi: 10.1002/mrm.20565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sobol WT, Jackels SC, Cothran RL, Hinson WH. NMR spin-lattice relaxation in tissues with high concentration of paramagnetic contrast media: evaluation of water exchange rates in intact rat muscle. Med Phys. 1991;18:243–250. doi: 10.1118/1.596722. [DOI] [PubMed] [Google Scholar]
- 36.van Zijl PCM, Moonen CTW, Faustino P, Pekar J, Kaplan O, Cohen JS. Complete separation of intracellular and extracellular information in NMR-spectra of perfused cells by diffusion-weighted spectroscopy. P Natl Acad Sci USA. 1991;88:3228–3232. doi: 10.1073/pnas.88.8.3228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pilatus U, Shim H, Artemov D, Davis D, van Zijl PCM, Glickson JD. Intracellular volume and apparent diffusion constants of perfused cancer cell cultures, as measured by NMR. Magnet Reson Med. 1997;37:825–832. doi: 10.1002/mrm.1910370605. [DOI] [PubMed] [Google Scholar]
- 38.de Graaf RA, Brown PB, McIntyre S, Nixon TW, Behar KL, Rothman DL. High magnetic field water and metabolite proton T1 and T2 relaxation in rat brain in vivo. Magnet Reson Med. 2006;56:386–394. doi: 10.1002/mrm.20946. [DOI] [PubMed] [Google Scholar]
- 39.Prantner AM. Re-evaluation of transmembrane water exchange in the rat brain [Dissertation] Washington University; St. Louis: 2008. p. 165. [Google Scholar]
- 40.Badaut J, Ashwal S, Adami A, Tone B, Recker R, Spagnoli D, Ternon B, Obenaus A. Brain water mobility decreases after astrocytic aquaporin-4 inhibition using RNA interference. J Cereb Blood Flow Metab. 2011;31:819–831. doi: 10.1038/jcbfm.2010.163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nilsson M, van Westen D, Stahlberg F, Sundgren PC, Latt J. The role of tissue microstructure and water exchange in biophysical modelling of diffusion in white matter. Magn Reson Mater Phy. 2013;26:345–370. doi: 10.1007/s10334-013-0371-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Assaf Y, Freidlin RZ, Rohde GK, Basser PJ. New modeling and experimental framework to characterize hindered and restricted water diffusion in brain white matter. Magnet Reson Med. 2004;52:965–978. doi: 10.1002/mrm.20274. [DOI] [PubMed] [Google Scholar]
- 43.Allen NJ, Barres BA. Neuroscience: Glia - more than just brain glue. Nature. 2009;457:675–677. doi: 10.1038/457675a. [DOI] [PubMed] [Google Scholar]
- 44.Herculano-Houzel S. The glia/neuron ratio: how it varies uniformly across brain structures and species and what that means for brain physiology and evolution. Glia. 2014;62:1377–1391. doi: 10.1002/glia.22683. [DOI] [PubMed] [Google Scholar]
- 45.Lange SC, Bak LK, Waagepetersen HS, Schousboe A, Norenberg MD. Primary cultures of astrocytes: Their value in understanding astrocytes in health and disease. Neurochem Res. 2012;37:2569–2588. doi: 10.1007/s11064-012-0868-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Goldberg MP, Choi DW. Combined oxygen and glucose deprivation in cortical cell-culture: calcium-dependent and calcium-independent mechanisms of neuronal injury. J Neurosci. 1993;13:3510–3524. doi: 10.1523/JNEUROSCI.13-08-03510.1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Rose CR, Waxman SG, Ransom BR. Effects of glucose deprivation, chemical hypoxia, and simulated ischemia on Na+ homeostasis in rat spinal cord astrocytes. J Neurosci. 1998;18:3554–3562. doi: 10.1523/JNEUROSCI.18-10-03554.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rutkowsky JM, Wallace BK, Wise PM, O'Donnell ME. Effects of estradiol on ischemic factor-induced astrocyte swelling and AQP4 protein abundance. Am J Physiol-Cell Ph. 2011;301:C204–C212. doi: 10.1152/ajpcell.00399.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bondarenko A, Chesler M. Rapid astrocyte death induced by transient hypoxia, acidosis, and extracellular ion shifts. Glia. 2001;34:134–142. doi: 10.1002/glia.1048. [DOI] [PubMed] [Google Scholar]
- 50.Papadopoulos MC, Verkman AS. Aquaporin water channels in the nervous system. Nat Rev Neurosci. 2013;14:265–277. doi: 10.1038/nrn3468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Kaptan S, Assentoft M, Schneider HP, Fenton RA, Deitmer JW, MacAulay N, de Groot BL. H95 Is a pH-Dependent Gate in Aquaporin 4. Structure. 2015;23:2309–2318. doi: 10.1016/j.str.2015.08.020. [DOI] [PubMed] [Google Scholar]
- 52.Ribeiro MD, Hirt L, Bogousslavsky J, Regli L, Badaut J. Time course of aquaporin expression after transient focal cerebral ischemia in mice. J Neurosci Res. 2006;83:1231–1240. doi: 10.1002/jnr.20819. [DOI] [PubMed] [Google Scholar]
- 53.Badaut J, Ashwal S, Tone B, Regli L, Tian HR, Obenaus A. Temporal and regional evolution of aquaporin-4 expression and magnetic resonance imaging in a rat pup model of neonatal stroke. Pediatr Res. 2007;62:248–254. doi: 10.1203/PDR.0b013e3180db291b. [DOI] [PubMed] [Google Scholar]
- 54.Solenov E, Watanabe H, Manley GT, Verkman AS. Sevenfold-reduced osmotic water permeability in primary astrocyte cultures from AQP-4-deficient mice, measured by a fluorescence quenching method. Am J Physiol-Cell Ph. 2004;286:C426–C432. doi: 10.1152/ajpcell.00298.2003. [DOI] [PubMed] [Google Scholar]
- 55.Iacovetta C, Rudloff E, Kirby R. The role of aquaporin 4 in the brain. Vet Clin Path. 2012;41:32–44. doi: 10.1111/j.1939-165X.2011.00390.x. [DOI] [PubMed] [Google Scholar]
- 56.Risher WC, Andrew RD, Kirov SA. Real-Time Passive Volume Responses of Astrocytes to Acute Osmotic and Ischemic Stress in Cortical Slices and In Vivo Revealed by Two-Photon Microscopy. Glia. 2009;57:207–221. doi: 10.1002/glia.20747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Silva MD, Omae T, Helmer KG, Li FH, Fisher M, Sotak CH. Separating changes in the intra- and extracellular water apparent diffusion coefficient following focal cerebral ischemia in the rat brain. Magnet Reson Med. 2002;48:826–837. doi: 10.1002/mrm.10296. [DOI] [PubMed] [Google Scholar]
- 58.Li H, Jiang XY, Xie JP, McIntyre JO, Gore JC, Xu JZ. Time-dependent influence of cell membrane permeability on MR diffusion measurements. Magn Reson Med. 2016;75:1927–1934. doi: 10.1002/mrm.25724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Jiang LiH, Xie X, Gore J, Xu JCJ. Impact of transcytolemmal water exchange on estimates of tissue microstructural properties derived from diffusion MRI. Magn Reson Med. 2016 doi: 10.1002/mrm.26309. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Figure S1. Overview of perfused IRSE experiments. IRSE measurements with 8- and 16-total-averages are represented by short, and long colored bars, respectively (dark green for neurons under normal conditions, light green for neurons under OGD conditions, dark red for astrocytes under normal conditions, light red for astrocytes under OGD conditions). Gray bars indicate where IRSE data were not collected. An experiment on each sample includes either two consecutive (duplicate), 16-total-average measurements (two long bars) or four consecutive (quadruplicate), 8-total-average measurements (four short bars). Data from normal perfusion condition measurements acquired during the first-half of each experiment (15–45 min under perfusion) were used to estimate τi's displayed in Fig. 5. All 8-total-average measurements were used for time-course analysis of τi under normal and OGD conditions (Fig. 6).
* n stands for nsample.