Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2018 Jan 5.
Published in final edited form as: J Child Neurol. 2013 Aug 21;29(11):1460–1466. doi: 10.1177/0883073813494265

Speed-accuracy testing on the Apple iPad® provides a quantitative test of upper extremity motor performance in children with dystonia

Matteo Bertucco 1, Terence D Sanger 2
PMCID: PMC5754271  NIHMSID: NIHMS927763  PMID: 23965400

Abstract

The only currently available scales for quantitative measurement of the severity of childhood dystonia require human observer ratings and provide poor granularity in the scores for individual limbs. The recent availability of low-cost high-quality touchscreens suggests that these devices could be used for quantification of upper extremity severity. In this study we evaluated the use of an Apple iPad® for testing speed and accuracy in a simple pointing task. We compared the abilities or thirteen healthy adults, fifteen healthy children, and sixteen children with primary or secondary dystonia. The linear relation described by Fitts’ Law held for all the groups. The movement time and the information transmitted were age and severity related. Our results provide evidence for the usability and validity of using Fitts’ Law as a quantitative diagnostic tool in children with dystonia. Furthermore, testing on touch-screen tablets may help to guide the design of user interfaces to maximize communication rate for children who depend upon assistive communication devices.

Keywords: Dystonia, Fitts’ Law, reaching, iPad®, human-computer interaction, transmission of information

Introduction

Childhood dystonia is defined as “a movement disorder in which involuntary sustained or intermittent muscle contractions cause twisting and repetitive movements, abnormal postures, or both” (Sanger el al., 2003). Dystonia is particularly common in children with dyskinetic cerebral palsy (CP), which has an estimated prevalence of 25,000 children in the United States (Hagberg and Olow, 1975; Kyllerman et al., 1982; Kyllerman, 1982; Hagberg et al., 1989). Children with CP often must interact with the outside world through augmented and assistive communication (AAC) devices such as programmable touch screens. Thus, such children are dependent upon their sensory-motor abilities to activate the buttons on the screen.

The quantitative evaluation of dystonia is a critical aspect of clinical care, both during the first assessment and at follow-up visits, in order to evaluate medical treatment, physical therapy, and surgical interventions. Currently the sensory-motor abilities of patients with dystonia as well as severity are assessed by clinical scales, such as the Gross Motor Function Classification System (GMFCS) (Palisano et al., 1997), Burke-Fahn-Marsden dystonia rating scale (BFM) (Burke el al., 1985), the Barry-Albright Dystonia rating scale (BAD) (Barry et al., 1999) and the Unified Dystonia Rating Scale (UDRS) (Comella et al., 2003). The ease of use and immediate results are important features of these scales. However they are ordinal scales with a component of subjective interpretation, particularly for severity. Hence, adding a quantitative and objective test could be a very important adjunct for the sensory-motor assessment of childhood movement disorders, including dystonia.

In 1954 Paul Fitts (Fitts, 1954) proposed the first mathematical model to describe the trade-off between speed and accuracy. Derived from Shannon’s information theory (Shannon and Weaver, 1949), Fitts hypothesized that the speed-accuracy relationship was due to a limitation of information transmission in the human motor system. He showed that movement time (MT) to reach a target increases with distance (D) and decreases as target size increases (W), such that MT = a + b log2 (2D/W), wherein a and b are empirical constants for each subject, and log2 (2D/W) represents the index of difficulty (ID) (Fitts, 1954; Fitts and Peterson, 1964). This relationship predicts that at a constant 2D/W ratio, MT will remain unchanged. Hence, MT is directly proportional to the ID, which may have the same value for different combinations of movement parameters D and W. The law has been validated in different experimental conditions, populations and devices (see Plamondon and Alimi, 1997 for a review). It has been shown that also children with congenital spastic hemiplegia obey Fitts’ Law despite their limitations in fine motor control (Smits-Engelsman et al., 2007). Notwithstanding an increased signal dependent noise, Sanger and colleagues (2005) showed that children with dystonia could scale the movement speed with the target size as expected for the Fitts’ speed-accuracy tradeoff.

Fitts’ law was originally proposed as a test for the manual skill of factory workers, and it continues to be useful to measure the speed-accuracy abilities of healthy adults. Therefore, it seems that Fitts’ Law might be a suitable test to evaluate the sensory-motor abilities in children with dystonia or other movement disorders, and a very useful diagnostic clinical aid for physicians.

Over the last thirty years, Fitts’ law has been extremely successful in human computer interaction (HCI) to measure and characterize the performance of various input systems (for a review see Soukoreff and MacKenzie, 2004). The Fitts model has allowed comparing and evaluating novel pointing devices through the Index of Performance (IP), expressed by the inverse of the linear equation slope (1/b) (Fitts and Peterson, 1964), such that the higher its value, the less MT is affected by increases in ID. Later, ISO 9241-9 (ISO, 2002; MacKenzie and Soukoreff, 2003) has introduced the Throughput (TP) in HCI design as a further metric in quantifying input system performance (see Methods for mathematical description). Fitts’ law has recently been applied in optimizing the layout of AAC devices for children with CP using a mathematical model for information based on the relationship between movement time and buttons size (Sanger and Henderson, 2007).

The availability of the latest generation of touch screen tablets has changed the concept of using AAC devices in children with speech and motor impairments. These devices are extremely portable, easy to manage, and the screen layouts are relatively simple to program. Thus there is a need to analyze and compare the capability of these “input” devices for transmitting information from the user to the computer, and a need to optimize the communication rate for children.

This study tests two hypotheses: 1) Fitts’ Law applies to targets on touch-screen tablets, in typical children and in children with movement disorders. 2) Fitts’ index of performance (IP) can assess and compare the sensory-motor abilities between children with dystonia and control subjects.

Therefore, we designed an experiment using custom software on the Apple iPad® to test the Fitts’ Law paradigm in healthy adults, healthy children, and children with dystonia. The Index of Performance and Throughput were compared between groups to measure the extent of information transmitted by using the iPad® and to test its efficiency as an assisted communication device for children with speech and motor impairments (Sanger and Henderson, 2007).

Methods

Participants

16 children with a clinical diagnosis of either primary or secondary dystonia affecting one or both hands (13.7 ± 4.2 SD years old), 15 healthy children (9.7 ± 2.5 SD years old) and 13 healthy adults (28.5 ± 2.8 SD years old) participated. The children with dystonia were recruited from the movement disorders clinic at Children’s Hospital of Los Angeles (CHLA). Their characteristics are outlined in Table 1.

Table 1.

Characteristics of children with dystonia

Participant Age Gender Diagnosis Left arm BAD score Right arm BAD score Preferred arm Arm used for the task
P1 14 F Primary dystonia; DYT1- 2 3 Left Left
P2 18 M Secondary generalized dystonia; vitamin E deficiency 1 1 Right Right
P3 18 M Secondary generalized dystonia; cerebral palsy 3 3 Left Left
P4 7 M Secondary generalized dystonia; cerebral palsy 1 1 Left Left
P5 16 F Secondary generalized dystonia; Glutaric acid urea type 1 3 3 Left Left
P6 18 M Primary dystonia; DYT1+ 1 1 Left Left
P7 11 M Primary dystonia; DYT1+ 0 1 Left Right
P8 11 M Secondary generalized dystonia; cerebral palsy 1 1 Left Left
P9 16 F Secondary generalized dystonia; right hemiplegia 0 3 Left Right
P10 9 M Primary dystonia; DYT1+ 2 2 Left Left
P11 11 M Primary dystonia; DYT1+ 3 2 Right Right
P12 19 F Secondary generalized dystonia; cerebral palsy 2 2 Right Right
P13 9 M Secondary generalized dystonia; cerebral palsy 2 2 Right Right
P14 18 F Secondary generalized dystonia; cerebral palsy 3 1 Right Right
P15 16 M Dystonic tremor 2 1 Right Right
P16 8 M Secondary generalized dystonia; cerebral palsy 2 3 Left Left
Open in a new tab

BAD, Barry-Albright Dystonia Scale

Participants were excluded if there was clinical evidence of spasticity or corticospinal injury in the upper extremities, including hyper-reflexia, a spastic catch, or weakness. The University of Southern California Institutional Review Board approved the study protocol. All healthy adults and children’s parents gave informed written consent for participation, and all children gave written assent. Authorization for analysis, storage, and publication of protected health information was obtained from parents according to the Health Information Portability and Accountability Act (HIPAA).

Experimental setting

Each participant attended a single experimental session of approximately one hour. All dystonic participants were previously rated on the Barry-Albright Dystonia scale (BAD) (Barry et al., 1999).

Participants sat in a chair or their own wheelchair in front of a table whose surface height was adjusted at the midpoint between the hip and the Xiphoid process. They placed the hand that was not used for the task on their lap.

An iPad® (Apple Inc, Cupertino, CA, USA) was located on the table in portrait mode in front of the participants at a distance that ranged between 40 to 55 cm. An adjustable metal bookstand supported the iPad® to allow the participants a comfortable screen view. The size of the screen was 19.5 × 14.6 cm. Custom software was developed for the experimental task (XCode 3.2 development environment, iOS 4.2 operating system; Apple Inc, Cupertino, CA, USA).

Task

The subjects were required to touch targets on the iPad® screen with the index finger of their preferred (less-affected) arm. Two children with dystonia (P7 and P9) were asked to perform the task with their non-preferred arm since the preferred was not affected by dystonia (BAD score equal to 0, see Table 1). Subjects were asked to maintain their trunk posture upright without touching the table or the bookstand with their pointing arm. Each trial was initiated by touching a 4 × 4 cm “start” button centered on the screen. The experimental task consisted of 180 targets divided in 4 blocks: 45 targets each block with a one-minute interval between trials to avoid fatigue. Targets appeared at one of nine different locations on the screen, and subjects moved their finger sequentially from one target to the next. The targets were square with an image of three blue bubbles. Subjects were asked to touch and “burst the bubbles”. Subsequent targets appeared in a sequential manner on the screen at a random interval between 0.7 and 1.2 s and disappeared at the instant when the next one appeared. The subject was required to maintain contact with the last target until the next target appeared without returning to the start button position (Fig.1A). In all, six target distances (D = 4.5, 6.6, 8.0, 9.1, 13.2, and 16.0 cm) and five target widths (W = 1, 2, 3 cm) were used, yielding 18 different target conditions with different Indices of Difficulty, ID = log2 (2D/W) (Fitts, 1954), varying from 1.60 to 4.99 bits. This resulted in 10 trials for each target condition, namely for each ID. The locations of the targets were chosen to match the six experimental distances and the 18 target conditions (ID) were shown in a pseudo-random order throughout the 180 trials, which resulted in nine Cartesian coordinates displayed in a rectangular grid (see Fig.1B). Subjects were encouraged to maintain motion close to the plane of the iPad® without an excessive displacement in perpendicular direction. However, sliding the finger along the iPad to the next target was not permitted, and success required that the first contact with the finger on the screen be within the desired target.

Figure 1.

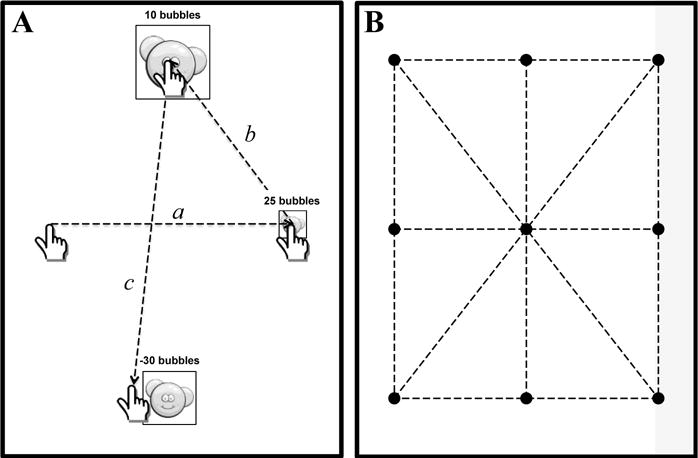
Figure 1

Open in a new tab

A) A representative sequence of three consecutive trials (a-b-c) with different target distance and target width. The score at each trial was based on the speed of the movement and the actual ID; note the values displayed in the figure were chosen only for demonstrative purpose. In case a target was missed, as the last move (c) in the figure shows, a penalty of 30 bubbles was deducted from the Total Score (TS, see Methods) at the end of the a block of 45 sequential targets. B) The nine locations of the targets on the screen (black circles) are shown; the dashed lines indicate the movement distances between targets.

The software was programmed to avoid target locations that could be hidden by the hand or forearm. A score, rewarded in number of bubbles, was visually provided at each touch, just above of the target, based on the movement time and actual ID; it was computed as follows: Score (S) = (2.5 × ID)/MT, where MT is the Movement Time, ID is the index of difficulty and 2.5 a constant term in order to return a tangible and reasonable score of the performance. At the end of each block of 45 sequential targets, the iPad® displayed the Total Score (TS, [45 × S]) showing the “total number of bubbles” achieved. In order to ensure attempts at accuracy, a penalty of thirty bubbles was given for each missed target. The penalties were, in that case, subtracted from the TS at the end of each block. The actual instruction to the subjects was: “Touch and burst the bubbles as fast as you can to get the highest score, if you miss the target you will lose thirty bubbles”. Different auditory feedback was played for a hit or a missed target. The entire experimental test required less than 30 minutes for each subject.

Data Analysis and Statistics

Custom software computed the Movement Time (MT) and the endpoint at the target for each movement. Later, the data were transferred to a desktop computer and analyzed using Matlab 7.10 software (Mathworks Inc., Natick, MA, USA). The MT was determined as the time interval between release of the index finger from the screen and the next contact with the screen. The location of the touch (and whether or not it fell within the target) was determined from the operating system pointer location.

In order to test Fitts’ Law, linear regressions were performed by the method of least squares, and the correlation coefficient was used to indicate the goodness of the fit of MT as a function of IDs. The index of performance (IP) was calculated by 1/b, where b was the slope of the linear regression equations (Fitts and Petterson, 1964) and the Throughput (TP) was defined as following (MacKenzie and Soukoreff, 2003):

TP=1N∑i=1NIDi/MTi

Where N=18 is the number of ID conditions.

The intercept a of the linear regression equations and the fraction of successful touches (S = successful touches / 180) were also calculated. A two-way ANOVA was performed to test the effects of the groups (three levels; Group) and the Index of Difficulty (eighteen levels, ID) on the MT. In addition one-way ANOVAs were performed to test differences between the three groups for the other dependent variables: intercept a, slope b, S, IP and TP. The Levene’s test was used to test the homogeneity of variance and Tukey’s HSD (Honestly Significant Difference) tests were run as post hoc comparisons. The Games-Howell post-hoc test was used in case the population variances were unequal. Means and standard deviations were computed for outcome variables. For each participant, we also identified 95% confidence intervals. We used a criterion of p<0.05 in tests of significance. The statistical analysis was performed using SPSS 16.0 (SPSS Inc, Chicago, IL, USA).

Results

No subject withdrew from the study and there were no complaints of fatigue or any adverse events.

The one-way ANOVA showed a significant effect of group on S (successful pointing fraction) [F(2,43) = 7.358, p = 0.002]. Post-hoc comparisons of the three groups indicated that children with dystonia (μ = 0.88 ± 0.11, 95% CI [0.82, 0.94]) had lower success than healthy children (p = 0.031, μ = 0.96 ± 0.19, 95% CI [0.95, 0.97]) or adults (p = 0.019, μ = 0.97 ± 0.20, 95% CI [0.95, 0.98]). Comparison of success between healthy children and adults was not statistically significant (p > 0.05). On average the control groups completed the test with an error rate no more than 5%, while children with dystonia had an average error rate of 12%.

The two-way ANOVA showed a significant effect for both Group and ID factors [F(2,41) = 860.61, P<0.001 and F(17,697) = 26.90, P<0.001, respectively], with no significant interaction [F(34,697) = 1.01, P=0.452]. Children with dystonia were on average (μ = 0.611 ± 0.116 s, 95% CI [0.561, 0.660]) slower than healthy children (p < 0.001, μ = 0.438 ± 0.100 s, 95% CI [0.387, 0.489]) or adults (p < 0.001, μ = 0.251 ± 0.632 s, 95% CI [0.196, 0.305]) (Fig.2). Between controls, adults were faster than healthy children (p < 0.001).

Figure 2.

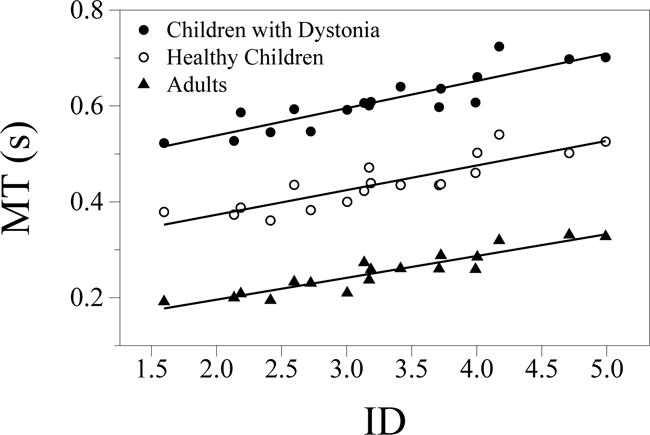
Figure 2

Open in a new tab

Mean movement time (MT) for all subjects as a function of the index of difficulty (ID). The straight lines show the best fits by the least squares method for each group (● - Children with dystonia, ○ - Healthy Children and ▲ - Adults).

MT showed a significant linear regression on ID for children with dystonia (r = 0.89, 95% CI [0.49, 0.70], F(1,17) = 63.694, p < 0.001), healthy children (r = 0.88, 95% CI [0.54, 0.71], F(1,17) = 52.971, p < 0.001), and adults (r = 0.93, 95% CI [0.54, 0.71], F(1,17) = 104.008, p < 0.001), see Fig.2. The correlation coefficients were 0.56 ± 0.20, 0.63 ± 0.16 and 0.81 ± 0.06 for children with dystonia, healthy children, and adults respectively. Correlation coefficients were not significantly different if we instead fitted MT against the ID computed using the effective information capacity formulation of Shannon and Weaver (1949): ID = log2 ((D/W)+1), as proposed by Soukoreff and MacKenzie (2004) (r = 0.90, 0.88 and 0.93). Moreover the MT showed a significant linear correlation with the BAD score in children with dystonia: r = 0.329, F(1,15) = 8.368, p < 0.05, 95% CI [0.024, 0.159] (Fig.4).

Figure 4.

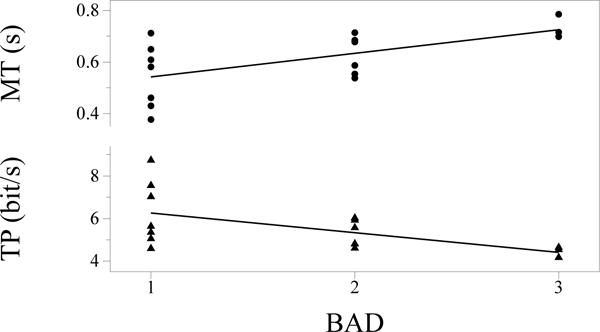
Figure 4

Open in a new tab

Movement time (MT,top) and Throughput (TP, bottom) averaged across subjects as functions of the Barry Albright Dystonia (BAD) rating. Each data point represents one child with dystonia. The straight lines show the best fits by the least squares method.

There were significant differences in the coefficients of the regression of MT on ID, including both intercept “a” [F(2,43) = 24.731, p < 0.001] and slope “b” [F(2,43) = 4.687, p = 0.015]. Post hoc tests showed a significant higher intercept in children with dystonia (μ = 0.425 ± 0.156 s, 95% CI [0.342, 0.508]) compared to healthy children (p = 0.010, μ = 0.270 ± 0.114 s, 95% CI [0.206, 0.333]) and adults (p < 0.001, μ = 0.111 ± 0.559 s, 95% CI [0.077, 0.145]). Healthy children had a higher intercept than adults (p < 0.001). The slope “b” was significantly higher in children with dystonia (μ = 0.068 ± 0.023 s/bit, 95% CI [0.056, 0.081]) compared to adults (p = 0.013, μ = 0.042 ± 0.011 s/bit, 95% CI [0.036, 0.050]) but not when compared to healthy children. There was no significant difference of slope between healthy children and adults (μ = 0.051 ± 0.030 s/bit, 95% CI [0.35, 0.068]).

We calculated the index of performance (IP) and the Throughput (TP) to compare the touchscreen tablet with other input devices used to transmit information between humans and computers, as well as to investigate the suitability of using touchscreen tablets to assess and compare dexterity between healthy population and subjects with movement disorders. One-way ANOVA revealed a significant effect of group on IP [F(2,43) = 6.253, p = 0.004]. Post-hoc comparisons of the three groups indicated that children with dystonia (μ = 16.36 ± 6.18 bit/s, 95% CI [13.06, 19.64]) had lower IP than healthy children (p = 0.027, μ = 23.14 ± 8.26 bit/s, 95% CI [18.57, 27.72]) and adults (p = 0.006, μ = 24.91 ± 6.32 bit/s, 95% CI [21.10, 28.74]). Comparisons between healthy children and adults were not statistically significant (p = 0.782). There was also a significant effect of TP among groups [F(2,43) = 48.488, p < 0.001]. Post-hoc comparisons of the three groups indicated that children with dystonia (μ = 5.56 ± 1.26 bit/s, 95% CI [4.89, 6.23]) had lower TP than healthy children (p = 0.018, μ = 7.88 ± 2.03 bit/s, 95% CI [6.76, 9.00]) and adults (p < 0.001, μ = 13.71 ± 3.25 bit/s, 95% CI [11.73, 15.67]). Adults had higher TP than healthy children (P<0.001) (Fig.3). The TP showed an inverse linear correlation with the BAD score in children with dystonia: r = 0.278, F(1,15) = 6.761, p < 0.05, 95% CI [−1.691, −0.162] (Fig.4).

Figure 3.

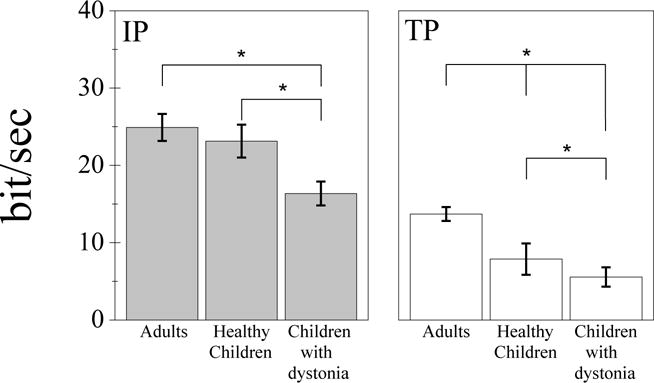
Figure 3

Open in a new tab

Plot showing the means and standard errors of the Index of Performance (IP, left panel) and the Throughput (TP, right panel) for the three groups.

Discussion

In the last thirty years Fitts’ Law had been validated using a large variety of input devices, including mouse, trackball, joystick and touchpad (see MacKenzie, 1992 and MacKenzie and Soukoreff, 2003 for reviews). Given the recent widespread availability of high quality touch-screen tablets, it is worthwhile to validate whether Fitts’ Law using these inputs devices might result in a useful clinical tool to assess motor skills in patients with sensory-motor disabilities, such as dystonia. It may also be a helpful tool for the selection and programming of assistive communication devices.

In this study we tested two hypothesis: 1) Fitts’ Law applies to targets on a touch-screen tablet in healthy subjects and in children with dystonia, and 2) Fitts’ index of performance (IP) can be used to differentiate between children with dystonia and control subjects. Both hypotheses are supported by our results. The movement time to point at the targets scaled with the index of difficulty in the three groups. The correlation coefficients (0.93, 0.88, 0.89 for Adults, Children and Dystonic respectively) lie in a range of coefficients of Fitts’ Law previously tested with different input devices (MacKenzie, 1992). Furthermore, there were significant differences between children with dystonia and both healthy children and healthy adults, with almost no overlap between the performance measures of individual subjects within the healthy and dystonic groups.

Fitts’ Law has been validated for different age populations (Hay, 1981; Brogmus, 1991) and for children with motor-sensory disabilities (Sanger et al., 2005; Smits-Engelsman et al., 2007). In particular Hay (1981) found that as children develop, their movement speed increases. This has been explained as a maturation of the CNS (Sporns and Edelman, 1993; Schneiberg et al., 2002) that leads the motor system to process more quickly the information necessary for motor skills. In our results, adults performed faster than children. In children with sensory-motor impairments, Fitts’ Law holds despite limitations of motor function, including increased signal-dependent noise and slower movements compared to typical age-matched children (Sanger el al., 2005).

Children with dystonia showed a significantly lower index of performance than healthy children and adults, resulting in lower information transfer rate. In other words, at the same index of difficulty children with dystonia perform the task more slowly. This agrees with the hypothesis that slower movement compensates for increased variability due to increased signal-dependent noise (Sanger et al., 2005; Sanger, 2006). Thus, dystonic children are constrained to reduce the velocity, namely the motor output, to contain the movement variability in order to accomplish accuracy-dependent tasks (Harris and Wolpert, 1998). This is further confirmed by relationships between movement time and throughput, and the BAD scale in children with dystonia. Ultimately, the limited amount of information transmitted through a pointing movement on the iPad® closely reflects the reduced communication rate, (measured as words or items produced per minute), in children with CP (Sanger and Hendenrson, 2007).

To summarize, we have shown that Fitts’ Law applies to rapid pointing movements on a touch-screen tablet, and the Index of Performance can be used to differentiate between children with dystonia and healthy subjects. We hope that our results will be useful for the development of future quantitative measurement tools for children with movement disorders, and that they may also help to guide the design of touch-screen user interfaces to maximize communication rate for children who depend upon assistive communication devices.

Acknowledgments

We thank Rebecca Sheehan-Stross and Andrea Mogollon Carrillo for assistance with recruitment. We thank Diana Ferman, Physician Assistant, for assistance with neurological examinations. Custom iPad® software was written by Matteo Bertucco. This research was performed at the University of Southern California and the Children’s Hospital Los Angeles. Preliminary results were presented at the Neural Control of Movement Annual Meeting in San Juan, Puerto Rico, in April 2011.

Funding

This research was supported in part by grants from the Don and Linda Carter Foundation, the Crowley-Carter Foundation, the National Institutes of Health (NS064046), and the University of Southern California Department of Biomedical Engineering.

Footnotes

Author contributions

Matteo Bertucco: conceived the experiment, developed apparatus and methods; performed the experiment; designed, performed, and reviewed statistical analysis; wrote first draft and reviewed manuscript.

Terence D. Sanger: conceived the experiment; clinically evaluated participants; designed and reviewed statistical analysis; and reviewed manuscript.

Declaration of conflicting interests:

No potential conflicts of interest in the conduct of the study, interpretation of results, or preparation of the manuscript.

Ethical Approval

The University of Southern California Institutional Review Board approved the study protocol. All parents gave informed written consent for participation and authorization for use of protected health information. All children gave written assent.

References

  1. Barry MJ, VanSwearingen JM, Albright AL. Reliability and responsiveness of the Barry-Albright Dystonia Scale. Dev Med Child Neurol. 1999;41:404–411. doi: 10.1017/s0012162299000870. [DOI] [PubMed] [Google Scholar]
  2. Brogmus GE. Effects of age and sex on speed and accuracy of hand movements: And the refinements they suggest for Fitts’ Law. Proceedings of the Human Factors and Ergonomics Society Annual Meeting. 1991;35(3):208–212. [Google Scholar]
  3. Burke RE, Fahn S, Marsden CD, et al. Validity and reliability of a rating scale for the primary torsion dystonias. Neurology. 1985;35:73–77. doi: 10.1212/wnl.35.1.73. [DOI] [PubMed] [Google Scholar]
  4. Comella CL, Leurgans S, Wuu J, et al. Rating scales for dystonia: A multicenter assessment. Mov Disord. 2003;18:303–312. doi: 10.1002/mds.10377. [DOI] [PubMed] [Google Scholar]
  5. Fitts PM, Peterson JR. Information capacity of discrete motor responses. J Exp Psychol. 1964;67:103–112. doi: 10.1037/h0045689. [DOI] [PubMed] [Google Scholar]
  6. Fitts PM. The information capacity of the human motor system in controlling the amplitude of movement. J Exp Psychol. 1954;47(6):381–391. [PubMed] [Google Scholar]
  7. Hagberg B, Hagberg G, Olow I, von Wendt L. The changing panorama of cerebral palsy in Sweden. V. The birth year period 1979–82. Acta Paediatr Scand. 1989;78:283–290. doi: 10.1111/j.1651-2227.1989.tb11071.x. [DOI] [PubMed] [Google Scholar]
  8. Hagberg G, Hagberg G, Olow I. The changing panorama of cerebral palsy in Sweden 1954–1970. II. Analysis of the various syndromes. Acta Paediatr Scand. 1975;64(2):193–200. doi: 10.1111/j.1651-2227.1975.tb03821.x. 1975. [DOI] [PubMed] [Google Scholar]
  9. Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394(6695):780–784. doi: 10.1038/29528. [DOI] [PubMed] [Google Scholar]
  10. Hay L. The effect of amplitude and accuracy requirements on movement time in children. J Mot Behav. 1981;13(3):177–186. doi: 10.1080/00222895.1981.10735247. [DOI] [PubMed] [Google Scholar]
  11. ISO. Ergonomic requirements for office work with visual display terminals (VDTs)—Part 9—Requirements for non-keyboard input devices (ISO 9241-9) International Organization for Standardization; 2002. Reference Number: ISO 9241-9:2000(E) (Vol. February 15, 2002) [Google Scholar]
  12. Kyllerman M, Bager B, Bensch J, et al. Dyskinetic cerebral palsy. I. Clinical categories, associated neurological abnormalities and incidences. Acta Paediatr Scand. 1982;71:543–550. doi: 10.1111/j.1651-2227.1982.tb09472.x. [DOI] [PubMed] [Google Scholar]
  13. Kyllerman M. Dyskinetic cerebral palsy. II. Pathogenetic risk factors and intra- uterine growth. Acta Paediatr Scand. 1982;71:551–558. doi: 10.1111/j.1651-2227.1982.tb09473.x. [DOI] [PubMed] [Google Scholar]
  14. MacKenzie IS. Fitts’ Law as a Research and Design Tool in Human-Computer Interaction. Human-Comp Interaction. 1992;7(1):91–139. [Google Scholar]
  15. MacKenzie IS, Soukoreff RW. Card, English, and Burr (1978)-25 years later. Proceedings of the Extended Abstracts of the ACM Conference on Human Factors in Computing Systems-CHI. 2003:760–761. [Google Scholar]
  16. Palisano R, Rosenbaum P, Walter S, Russell D, Wood E, Galuppi B. Development and reliability of a system to classify gross motor function in children with cerebral palsy. Dev Med Child Neurol. 1997;39:214–23. doi: 10.1111/j.1469-8749.1997.tb07414.x. [DOI] [PubMed] [Google Scholar]
  17. Plamondon R, Alimi AM. Speed/accuracy trade-offs in target-directed movements. Behav Brain Sci. 1997;20(2):279–303. doi: 10.1017/s0140525x97001441. [DOI] [PubMed] [Google Scholar]
  18. Sanger TD, Delgado MR, Gaebler-Spira D, Hallett M, Mink JW. Classification and Definition of Disorders Causing Hypertonia in Childhood. Pediatrics. 2003;111(1):e89–e97. doi: 10.1542/peds.111.1.e89. [DOI] [PubMed] [Google Scholar]
  19. Sanger TD, Henderson J. Optimizing Assisted Communication Devices for Children With Motor Impairments Using a Model of Information Rate and Channel Capacity. IEEE Trans Neural Syst Rehabil Eng. 2007;15(3):458–468. doi: 10.1109/TNSRE.2007.903969. [DOI] [PubMed] [Google Scholar]
  20. Sanger TD, Kaiser J, Placek B. Reaching Movements in Childhood Dystonia Contain Signal-Dependent Noise. Journal of Child Neurology. 2005;20(6):489–496. doi: 10.1177/088307380502000604. [DOI] [PubMed] [Google Scholar]
  21. Schneiberg S, Sveistrup H, McFadyen B, McKinley P, Levin MF. The development of coordination for reach-to-grasp movements in children. Exp Brain Res. 2002;146(2):142–154. doi: 10.1007/s00221-002-1156-z. [DOI] [PubMed] [Google Scholar]
  22. Shannon CE, Weaver W. The Mathematical Theory of Communication. Urbana, IL: University of Illinois Press; 1949. [Google Scholar]
  23. Smits-Engelsman BCM, Rameckers EAA, Duysens J. Children with congenital spastic hemiplegia obey Fitts’ Law in a visually guided tapping task. Experimental Brain Research. 2006;177(4):431–439. doi: 10.1007/s00221-006-0698-x. [DOI] [PubMed] [Google Scholar]
  24. Soukoreff R, MacKenzie I. Towards a standard for pointing device evaluation, perspectives on 27 years of Fitts’ law research in HCI. International Journal of Human-Computer Studies. 2004;61:751–789. [Google Scholar]
  25. Sporns O, Edelman GM. Solving Bernstein’s problem: a proposal for the development of coordinated movement by selection. Child Dev. 1993;64(4):960–981. [PubMed] [Google Scholar]

RESOURCES