Hydrophobicity of proteins and nanostructured solutes is governed by topographical and chemical context

Significance

Numerous biological self-assembly processes, from protein folding to molecular recognition, are driven by hydrophobic interactions, yet characterizing hydrophobicity at the nanoscale has remained a major challenge, because it requires understanding of the strength of protein–water interactions and the ease with which they can be disrupted. Water near a protein responds to its chemistry and topography in a manner that is collective and complex and cannot be captured by commonly used surface area models or hydropathy scales. We demonstrate that water density fluctuations near proteins can characterize protein hydrophobicity and reveal its dependence on curvature and chemical patterns at the nanoscale. Our approach opens new avenues for understanding and efficient characterization of biomolecular interactions.

Abstract

Hydrophobic interactions drive many important biomolecular self-assembly phenomena. However, characterizing hydrophobicity at the nanoscale has remained a challenge due to its nontrivial dependence on the chemistry and topography of biomolecular surfaces. Here we use molecular simulations coupled with enhanced sampling methods to systematically displace water molecules from the hydration shells of nanostructured solutes and calculate the free energetics of interfacial water density fluctuations, which quantify the extent of solute–water adhesion, and therefore solute hydrophobicity. In particular, we characterize the hydrophobicity of curved graphene sheets, self-assembled monolayers (SAMs) with chemical patterns, and mutants of the protein hydrophobin-II. We find that water density fluctuations are enhanced near concave nonpolar surfaces compared with those near flat or convex ones, suggesting that concave surfaces are more hydrophobic. We also find that patterned SAMs and protein mutants, having the same number of nonpolar and polar sites but different geometrical arrangements, can display significantly different strengths of adhesion with water. Specifically, hydroxyl groups reduce the hydrophobicity of methyl-terminated SAMs most effectively not when they are clustered together but when they are separated by one methyl group. Hydrophobin-II mutants show that a charged amino acid reduces the hydrophobicity of a large nonpolar patch when placed at its center, rather than at its edge. Our results highlight the power of water density fluctuations-based measures to characterize the hydrophobicity of nanoscale surfaces and caution against the use of additive approximations, such as the commonly used surface area models or hydropathy scales for characterizing biomolecular hydrophobicity and the associated driving forces of assembly.

Hydrophobic interactions drive many important biological and colloidal self-assembly processes (1–6). During such assembly, the hydration shells of the associating solutes are disrupted, replacing hydrophobic–water contacts with hydrophobic–hydrophobic ones. Characterizing how strongly water adheres to a given solute is, therefore, directly relevant to the strength of hydrophobic interactions between solutes. Macroscopically, surface–water adhesion is quantified by measuring the water droplet contact angle on a surface. However, such characterization does not translate usefully to proteins and other nanoscale solutes. Indeed, characterizing how strongly or weakly a protein surface or a specific patch on it adheres to water (i.e., its hydrophobicity) is incredibly challenging and has necessitated the use of simplifying assumptions.

To this end, simple surface area (SA) models have been used to estimate the driving force for assembly, $\mathrm{\Delta }G=\gamma \mathrm{\Delta }A$, where $\mathrm{\Delta }A$ is the nonpolar SA buried upon assembly and $\gamma$ is an appropriate surface tension (7–9). However, the value of $\gamma$ used in popular models is nearly an order of magnitude lower than the oil–water surface tension (10), and its temperature dependence is at odds with that of biological assembly (11), reducing it to a fitting parameter. Moreover, not just the magnitude but even the sign of the best-fit $\gamma$ can depend on the class of solutes used to estimate it (12). As a result, for certain complex solutes the burial of nonpolar SA can even be unfavorable, rendering such models ill-suited for characterizing the driving forces of nanoscale assembly (13).

Other approximate approaches that use hydropathy scales (or scoring functions) (14–18) assign an index (or a score) to an amino acid residue based on some measure of its aversion to water (e.g., water to oil transfer free energy) and estimate the hydrophobicity of a protein patch as a sum of the hydrophobicities of constituent amino acids (14). Many hydropathy scales exist, and they differ significantly from each other (19, 20). Importantly, while such methods can efficiently extract information from large protein databases and classify them into meaningful groups, they fail to predict the driving forces in specific situations (21–23). Here we trace the failure of such approaches to the assumption that the hydrophobicity of a protein patch can be decomposed into a sum of its constituent parts (i.e., additivity), and that a unique hydrophobicity can be assigned to each residue; our results contribute to the growing consensus that the hydrophobicity of a residue is not unique but depends in a nontrivial manner on its chemical and topographical context in a protein.

To study context-dependent hydrophobicity we use molecular dynamics (MD) simulations coupled with enhanced sampling methods (24, 25) to systematically displace water molecules from the solute hydration shell and quantify the corresponding free energetic cost. The free energetics of interfacial water density fluctuations, and especially the rare ones that result in opening of a cavity adjacent to the solute, then serve to quantify hydrophobicity. Density fluctuations are enhanced and correspondingly it is easier to create a cavity near a hydrophobic surface (26–29), consistent with the weaker surface–water adhesion. Theory of inhomogeneous liquids connects water density fluctuations to other quantities, such as water compressibility, transverse water density correlations, and the free energy of cavity formation, all of which can also serve as molecular measures of context-dependent hydrophobicity (24, 26–35). Such measures have been used previously to study aspects of context-dependent hydrophobicity of nanoscale surfaces (35–48).

Here, we build on this work by characterizing the hydrophobicity of surfaces with systematic variations in curvature and the chemical patterns they display. We show that concave nonpolar surfaces are more hydrophobic than convex ones. We also show that hydrophobic patches with variations in chemical pattern and topography, whether on self-assembled monolayers (SAMs) or on the surface of a protein, hydrophobin-II, can display significantly different hydrophobicity. Our work highlights the power of water density fluctuations-based measures to characterize hydrophobicity of nanoscale surfaces and cautions against the use of additive approximations, such as the commonly used SA models, hydropathy scales, and similar scoring functions, for characterizing biomolecular hydrophobicity and the associated driving forces of assembly.

Results and Discussion

Effect of Nanoscale Curvature on Surface Hydrophobicity.

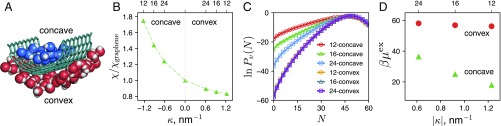
How curvature influences the hydration of spherical hydrophobic solutes is known. Highly curved solutes smaller than $R_{\mathrm{c}}\approx 1$ nm are hydrated without significantly perturbing water’s hydrogen bond network, whereas hydrating larger solutes requires the energetically unfavorable breaking of hydrogen bonds (5, 49, 50). Although typical proteins are larger than $R_{\mathrm{c}}$, their surfaces include bumps and crevices with different curvatures. To understand how protein hydrophobicity is influenced by both the magnitude and the sign of its local curvature we first study surfaces with homogeneous chemistry and well-defined curvatures, hemicylindrical nanotubes (Fig. 1A), which allows us to set one principal curvature to zero and systematically vary the other, $\kappa$.

Fig. 1.

Effect of nanoscale curvature on hydrophobicity. (A) Simulation snapshot of a (16,16) hCNT in water. Only the water molecules in observation volumes, $v$, near the concave (blue and white) and the convex (red and white) surfaces are shown for clarity. hCNT–water interactions are scaled by $\lambda =0.5$. (B) Compressibility of water in the first hydration shell normalized by its value near a flat graphene sheet, $\chi /{\chi }_{\text{graphene}}$, as a function of the surface curvature, $\kappa$. (C) Water density fluctuations, $P_v(N)$, in cylindrical-shell volumes on the concave and convex sides of hCNTs computed using the INDUS method (25). (D) Excess chemical potential, $\beta {\mu }_v^{\mathrm{ex}}=-\ln P_v(0)$, for creating a cavity of size and shape $v$ near various hCNTs. These results show that concave nonpolar surfaces are more hydrophobic than convex ones. Surface hydrophobicity is sensitive to and increases substantively with nanoscale curvature of concave surfaces but is rather insensitive to curvature for convex surfaces (51).

To sample concave ($\kappa <0$) and convex ($\kappa >0$) curvatures we performed MD simulations of hemicylindrical open-ended $(n,n)$ armchair carbon nanotubes (hCNTs) with $n$ = 12, 16, and 24, as well as flat graphene sheets ($\kappa =0$) in water. We systematically varied the strength of surface–water attractions using a scaling factor $\lambda$, as described in SI Appendix. For $\lambda =0.5$, the wettability of the reference graphene surface is similar to that of a CH₃-terminated SAM surface, in that they both have similar water droplet contact angles (SI Appendix). Fig. 1 shows results for systems with $\lambda =0.5$; results for other $\lambda$-values are included in SI Appendix.

Fig. 1B shows the isothermal compressibility of interfacial water near the curved hCNT surfaces, obtained by performing MD simulations over a range of pressures and taking the pressure derivative of the average number of waters, $⟨N_v⟩$, in an interfacial observation volume, $v$, using $\chi \equiv -{\left(\partial \ln ⟨N_v⟩/\partial P\right)}_T$ (see SI Appendix for details). To compare different curvatures on the same footing we deliberately selected subvolumes $v$, such that they contain about the same number of water molecules, $⟨N_v⟩$, on average. The hydration water near the concave surface of the (12,12) hCNT is almost twice as compressible as that near a flat graphene sheet. The hydration shell compressibility decreases monotonically with $\kappa$ as the surface becomes less concave, and then increasingly convex, suggesting that concave nonpolar surfaces are more hydrophobic than convex surfaces of the same curvature.

Our results for the convex surfaces are consistent with those of Sarupria and Garde (34), who showed that the hydration shell compressibility is the lowest near methane-sized hydrophobic solutes and increases monotonically with increasing solute size (decreasing curvature). For convex surfaces, results in Fig. 1B are also in good agreement with those of Jabes et al. (52), who found that hydration shell compressibility reduces by about 22% near a hydrocarbon-coated cylinder with $\kappa =1.13$ ${\text{nm}}^{-1}$, relative to that near a flat plate. Our results highlight an asymmetric dependence of hydration shell compressibility on the sign of nanotube curvature. In particular, compressibility is more sensitive to concave curvatures (i.e., the absolute value of slope $|\frac{\partial \chi }{\partial \kappa }|$ is higher for $\kappa <0$ than for $\kappa >0$). We note that this asymmetry in slopes depends on the exact definition of curvature. As shown in SI Appendix, Fig. S5 and discussed in SI Appendix, section I-F, defining $\kappa$ based on the curvature of liquid water interface reduces the asymmetry; nevertheless, the observation that compressibility of hydration water is higher near concave surfaces compared with convex ones holds true. This observation suggests that introduction of both positive and negative curvatures (of equal magnitude) on an otherwise flat surface ought to increase its hydrophobicity. Our assertion that a rugged nonpolar surface is more hydrophobic than a flat one is supported by Mittal and Hummer (42), who find that the interfacial free energy of a sinusoidal hydrophobic surface increases with its amplitude.

Fig. 1C shows probability, $P_v(N)$, of observing $N$ water molecules in an interfacial observation volume, $v$. To compare the various curved surfaces on an equal footing we varied the axial length of $v$, such that they all contain roughly the same number of waters on average, $⟨N_v⟩\approx 49$. The $P_v(N)$ distributions, for all of the surfaces obtained using the INDUS method (25), are Gaussian (parabolic) near the mean but display prominent non-Gaussian low-$N$ tails. Patel et al. (24, 27) have shown that such low-$N$ fat tails serve as an excellent signature of surface hydrophobicity; the fatter the tail, the more hydrophobic the surface. In qualitative agreement with the data for compressibility (Fig. 1B), Fig. 1C shows that while the low-$N$ tails of $P_v(N)$ are rather insensitive to curvature for convex surfaces, curvature significantly influences the tails, and thereby the hydrophobicity of concave surfaces.

These low-$N$ tails in $P_v(N)$ are directly connected to the work required to create a cavity of the size and shape of $v$ near the surface (26, 28) through $\beta {\mu }_v^{\text{ex}}=-\ln P_v(0)$. Fig. 1D shows the dependence of $\beta {\mu }_v^{\text{ex}}$ on the absolute curvature of the hCNT. It is far easier to create a cavity in the vicinity of concave surfaces compared with convex ones, suggesting that concave nonpolar surfaces are more hydrophobic and ought to bind hydrophobic solutes more strongly than convex surfaces, consistent with the results of Setny (53). These results point to an important shortcoming of SA models, which assume that the thermodynamic driving forces for burying concave and convex hydrophobic areas are identical.

Surfaces with the Same Chemistry but Different Patterns Can Have Widely Varying Hydrophobicities.

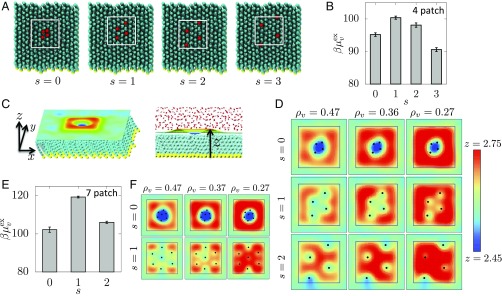
Flat SAMs provide excellent systems to analyze the effects of chemical patterns on hydrophobicity without being encumbered by the effects of surface topography (40, 54, 55). We study SAM surfaces with $n$ hydrophilic sites (–OH head groups) in a background of hydrophobic sites (–CH₃ head groups) (see SI Appendix for details). We hold $n$ constant but vary the separation, $s$, the number of CH₃ sites between adjacent OH sites (Fig. 2A). We studied seven patterns with $n$ = 4 ($s=0,1,2,3$) and $n=7$ ($s=0,1,2$) and monitored water density fluctuations in cuboidal volumes, $v$, of width 0.3 nm placed above a square 3-nm $\times$ 3-nm surface patch containing the chemical patterns (Fig. 2A).

Fig. 2.

How chemical patterns influence surface hydrophobicity. (A) Top views of a CH₃-SAM containing $n=4$ -OH head groups (red) separated by $s=0,1,2,$ and 3 CH₃ head groups (cyan), respectively. A $3\times 3\times 0.3$-nm³ observation volume, $v$ (white), is placed above the patches. (B) Free energies of emptying $v$ near the four patches in A. (C) Snapshot of the $n=4$, $s=0$ SAM surface (space-filled) illustrating the SAM–water interface, $z(x,y)$, for a biased simulation that displaces all but a fraction, ${\rho }_v=0.27$, of waters from $v$. $z$ is the vertical distance from the bottom of the SAM surface. (D) Top views of the interfaces for $n=4$ and $s=0,1,$ and 2 for partially wet configurations (${\rho }_v=0.47,0.36,0.27$ from left to right). (E) Same as B for $n=7$, and $s=0,1,$ and 2. (F) Same as D for $n=7$, and $s=0$ and 1.

Which of the four patches in Fig. 2A is the most hydrophobic and which is the most hydrophilic? Additive models would predict that all patterns are equally hydrophobic; however, the answer is both nonintuitive and nontrivial. Fig. 2B shows the hydrophilicity of the $n=4$ patterns, as quantified by the reversible work, ${\mu }_v^{\mathrm{ex}}$, required to empty the interfacial volume, $v$; the higher the ${\mu }_v^{\mathrm{ex}}$, the more hydrophilic the patch. Although the number of hydrophobic and hydrophilic sites is the same in the four patches, ${\mu }_v^{\mathrm{ex}}$ is different and varies nonmonotonically with $s$. The $s=1$ patch with –OH groups separated by one methyl group is the most hydrophilic of the four. Thus, embedding a given number of –OH groups in a hydrophobic background decreases hydrophobicity most effectively not when the –OH groups are adjacent to one another in a cluster ($s=0$), but when they are separated by a methyl group ($s=1$).

What leads to such a nonmonotonic response to the chemical context presented by the patch? To answer this question, we visualize dewetting of the patches by following the average water density field in INDUS simulations, where biasing potentials are used to dewet $v$. For example, consider a biased simulation of the $n=4$, $s=0$ SAM surface, which displaces all but a fraction, ${\rho }_v=0.27$, of waters in $v$ on average; in Fig. 2C we show the corresponding SAM–water interface, $z(x,y)$ [SI Appendix includes details of the interface calculation (56)].

As $v$ is dewetted for the $s=0$ pattern (Fig. 2D, top row) the interface detaches from the patch at the borders but remains pinned to the central cluster, forming a doughnut-shaped cavity above the patch. The $s=1$ pattern (Fig. 2D, middle row) pins the interface over a larger area, even when the observation volume is significantly dewetted, indicating the difficulty of dewetting the region in its vicinity. Indeed, the work of cavity creation ${\mu }_v^{\mathrm{ex}}$ is several $k_{\mathrm{B}}T$ larger for the $s=1$ pattern than for $s=0$. Interestingly, as the –OH groups are further separated ($s=2$) the interface depins from the space between the hydrophilic sites, making cavity formation easier, as reflected in lower ${\mu }_v^{\mathrm{ex}}$ (Fig. 2B). The $s=2$ pattern facilitates interface formation between the OH sites as well as pins the interface outside $v$; thus, the patch defined by $v$ does not bear the full brunt of the pinning by the hydrophilic sites. Therefore, $v$ can be emptied more easily, leading to the nonmonotonic dependence of hydrophobicity on $s$. Patterns with seven –OH sites also display similarly context-dependent hydrophobicity that varies nonmonotonically with $s$ (Fig. 2 E and F).

Collectively, these results highlight that even for simple flat surfaces, surface–water adhesion strength depends on chemical patterns in a manner that is complex and not anticipated by additive models. Our results are consistent with previous work on the hydration of patterned surfaces. For example, Luzar and Leung (57) showed that in confined geometry a regularly spaced distribution of hydrophilic sites is much more effective in slowing the formation of vapor tubes that trigger the evaporation process. Vanzo et al. (58) also found that uniformly distributing charges (rather than segregating them) in a hydrophobic surface makes the surface significantly more hydrophilic.

Protein Hydrophobicity Is Context-Dependent and Nonadditive.

We use water density fluctuations-based measures to characterize the hydrophobicity of a protein, hydrophobin II (Protein Data Bank ID code 2B97) (59), which is a small globular ($\approx 7$ kDa) fungal protein secreted in the extracellular environment. It displays a relatively large hydrophobic patch that makes the protein amphiphilic and surface active at the vapor–liquid interface of water, enabling the formation of hydrophobic coatings and sheaths that cover fungal spores (59). We note that when viewed from the atomic-level hydrophobicity scale perspective of Kapcha and Rossky (60) the patch appears actually quite heterogeneous (SI Appendix). Acharya et al. (40) interrogated the hydrophobin-II surface using binding of small methane-like nonpolar solute probes present in an aqueous solution, which revealed the hydrophobic patch referred to above. We have also used the INDUS method to characterize the hydrophobicity of hydrophobin-II using larger benzene-shaped probe volumes. While the benzene-shaped probes also identified the large hydrophobic patch, interestingly, we found that protein hydrophobicity can also depend on the size and shape of probe itself (29).

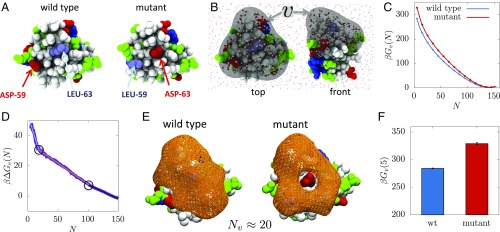
Here we study how altering the local context affects the hydrophobicity of the patch. To this end, we created a swap mutant by switching the positions of residues Asp-59 and Leu-63 in the wild-type protein to Asp-63 and Leu-59 in the mutant (Fig. 3A). Such a swap places a charged residue from the edge to the center of the patch but does not perturb the overall structure of the protein; there are four disulfide bonds in the protein, and the backbone root mean square deviation between equilibrium wild-type and mutant structures are within thermal fluctuations (see SI Appendix for simulation details). To study the collective response of water to the swap we defined an observation volume, $v$, of width 0.3 nm that envelopes a contiguous region of nine nonpolar residues and Asp-59 (Fig. 3 A and B) and contains roughly 140 waters on average. We calculated the free energetics of water density fluctuations, $\beta G_v(N)=-\ln P_v(N)$, near the wild-type and the swap mutant proteins (Fig. 3C), allowing comparisons between two patches with the same number and type of amino acids but having different geometrical arrangement. It is clear that over the entire range of water numbers one expends more work to dewet the patch in the swap mutant compared with that in the wild-type protein, highlighting the decreased hydrophobicity of the patch in the swap mutant.

Fig. 3.

Protein hydrophobicity is nonadditive. (A) Wild-type hydrophobin-II shown in space-fill representation (white, nonpolar; green, polar; red, anionic; blue, cationic). Two residues, Leu-63 (gray, at the center) and Asp-59 (red, at the periphery of the patch), were swapped to create the mutant (Right). (B) Top and front views of hydrophobin-II are shown along with the observation volume, $v$, that covers the hydrophobic patch and Asp-59. (C) The free energetics, $\beta G_v(N)=-\ln P_v(N)$, of observing $N$ waters in $v$, is shown for wild type and swap mutant in units of the thermal energy, ${\beta }^{-1}=k_{\mathrm{B}}T$. (D) The difference in $G_v(N)$ for wild-type and mutant proteins is shown; the three lines are fits over the ranges 5–20, 30–100, and 110–150, respectively. (E) Interface encompassing dewetted region (orange mesh) near wild-type and mutant proteins for a dewetted state with $\approx 20$ (waters hidden for clarity). (F) $\beta G_v(N=5)$ is significantly larger for the mutant than for the wild type, highlighting the diminished hydrophobicity of the patch on the swap mutant.

The additional work, $\mathrm{\Delta }{G}_v(N)$, required to dewet the swap mutant relative to the wild type (Fig. 3D) shows three approximately linear regimes. The one at high $N$ arises from the slightly different number of average water molecules in the volumes near the two patches, whereas the differences in the low-$N$ fat tails are visible in the $N$ range from 20 to 120 and reflect the increased hydrophilicity of the mutant patch. Further depletion in water numbers encroaches directly on the hydration shell of the charged Asp-63 in the swap mutant, which is costly, leading to the steep linear region for $N<20$. Instantaneous interfaces encompassing the dewetted regions near the wild-type and the mutant proteins with roughly 20 water molecules in $v$ (Fig. 3E) show that a large cavity develops near the patch in both cases (see SI Appendix for details). However, the cavity shape near the wild-type hydrophobin-II is contiguous, whereas that near the swap mutant is doughnut-shaped in that water remains pinned to the central Asp-63. Importantly, it costs nearly 30 $k_{\mathrm{B}}T$ less to displace all but five waters from $v$ and open the cavity near the wild-type patch (Fig. 3F), consistent with the larger hydrophobicity of the patch in the wild-type protein. Given that the number and types of amino acid residues are identical in the two patches, their disparate hydrophobicities are not be anticipated by additive models.

Conclusions and Outlook

Characterizing the hydrophobicity of heterogeneous nanoscale surfaces has remained a major challenge. Additive and context-independent descriptions of hydrophobicity are frequently used by computational drug design approaches and implicit solvent methods to estimate the hydrophobic contribution to association (61). We showed that molecular measures based on water-density fluctuations effectively capture the collective response of water to complex surfaces and serve as robust nanoscale measures of hydrophobicity. We used these measures to show that the hydrophobicity of proteins and nanostructured solutes is strongly influenced by their chemistry and topography in a manner that cannot be captured by additive approaches.

In particular, by studying hemicylindrical nonpolar surfaces we showed that concave nonpolar surfaces are more hydrophobic compared with flat or convex surfaces, as reflected in the higher water compressibility, larger water density fluctuations, and easier cavity formation in the vicinity of concave surfaces. The relative ease of displacing water from a concave region suggests an important role for concave features (e.g., clefts or pockets) in binding to hydrophobic solutes. Molecular details of water density fluctuations in a concave interfacial region and how they are coupled to an approaching ligand are also known to be important in ligand binding kinetics (62).

The asymmetric dependence of hydrophobicity of nonpolar surfaces on curvature implies that introducing nanoscale topographical features on an otherwise flat nonpolar surface would increase its hydrophobicity. Such features may be integral parts of the structure of proteins and other macromolecules, or they may appear fleetingly through conformational changes of a flexible molecule or surface, suggesting that flexible nonpolar surfaces ought to be more hydrophobic than rigid ones. This expectation is consistent with the results of Andreev et al. (63), who showed that flexible nanotubes are more hydrophobic, expel water from their interior, and reduce the flow of water through them. Enhanced hydrophobicity as a result of flexibility should also influence water phase behavior and evaporation rates under nonpolar confinement. Indeed, Altabet and Debenedetti (64) and Altabet et al. (65) have shown that water confined between flexible nonpolar surfaces is less stable and evaporates significantly faster relative to water confined between the corresponding rigid surfaces.

We also showed that patches with the same chemical composition but different geometrical arrangements, either on SAM surfaces or on proteins, can display significantly different hydrophobicities. Specifically, we showed that hydrophilic sites are most effective in increasing the hydrophilicity of a nonpolar surface not when they are clustered together but when they are separated from each other by one hydrophobic site. Favorable direct (electrostatic) interactions between polar or charged sites and water can pin water molecules not only in direct contact with the site but also in subsequent hydration shells. Thus, polar sites separated by $\sim 1$ nm can pin water effectively in the region between them, and, similarly, a polar or charged site has a larger impact on hydrophobicity and interactions when placed at the center of a hydrophobic patch instead of at its periphery. Such context dependence will play an important role in protein engineering [for example, in engineering of antibodies to optimize both affinity and specificity (66)] as well as in materials design.

Finally, our work suggests that context-dependent hydration of protein surfaces can be characterized effectively using water-density fluctuations and associated quantities. Such characterization captures many-body effects that are missing in additive models, which presents an important advantage, especially with regard to developing predictive approaches. The success of bioinformatic approaches in predicting protein structure from sequence has relied on the availability of protein sequence–structure information in the Protein Data Bank (67). The sequence–structure relationship is nonadditive and complex, similar to the relationship between chemistry and topography, and hydrophobicity. If extensive data on the hydration of diverse proteins were available, we speculate that data analytics approaches could be applied to estimate the hydrophobicity of protein surfaces. Such information about hydration is not available in the Protein Data Bank, which contains information about only the strongly localized crystal waters. However, our approach using water-density fluctuations-based characterization of hydrophobicity combined with advances in high-performance computing provides a route to developing an extensive “protein hydration data bank,” which could not only support development of nonadditive predictive approaches but also help efficient prediction of biomolecular interactions in complex systems.