Microscopic dynamics of charge separation at the aqueous electrochemical interface

Significance

Aqueous electrode interfaces serve as the backdrop for many important chemical processes in nature and technology. These interfaces continually garner much interest due to their ability to facilitate and even catalyze certain electrochemical reactions. Charge separation is a fundamental step in nearly all catalytic processes that occur at metal interfaces. Traditional electrochemical measurements are able to observe the consequences of charge separation but are limited in their ability to reveal direct molecular details. By studying detailed molecular models of charge transfer at water metal interfaces, we have uncovered the microscopic dynamics of this fundamental process. Elucidating the altered thermodynamics and kinetics of charge separation at water–metal interfaces and identifying their molecular underpinnings will inform the interpretation of macroscopic measurements and the design of better catalysts.

Abstract

We have used molecular simulation and methods of importance sampling to study the thermodynamics and kinetics of ionic charge separation at a liquid water–metal interface. We have considered this process using canonical examples of two different classes of ions: a simple alkali–halide pair, Na⁺I⁻, or classical ions, and the products of water autoionization, H₃O⁺OH⁻, or water ions. We find that for both ion classes, the microscopic mechanism of charge separation, including water’s collective role in the process, is conserved between the bulk liquid and the electrode interface. However, the thermodynamic and kinetic details of the process differ between these two environments in a way that depends on ion type. In the case of the classical ion pairs, a higher free-energy barrier to charge separation and a smaller flux over that barrier at the interface result in a rate of dissociation that is 40 times slower relative to the bulk. For water ions, a slightly higher free-energy barrier is offset by a higher flux over the barrier from longer lived hydrogen-bonding patterns at the interface, resulting in a rate of association that is similar both at and away from the interface. We find that these differences in rates and stabilities of charge separation are due to the altered ability of water to solvate and reorganize in the vicinity of the metal interface.

In aqueous solution, the association or dissociation of oppositely charged ions requires the collective rearrangement of surrounding water molecules (1, 2), which solvate bound ion pairs differently than individual ions (3–6). The solvent fluctuations that enable these collective rearrangements drive the dynamics of ion pairing and unpairing and therefore play a fundamental role in many chemical reactions. Near the surface of an electrode, these collective solvent fluctuations can differ significantly from that of the bulk liquid (7, 8), and these differences can affect the rates and mechanisms of aqueous electrochemical reactions. In this work, we use molecular simulation to investigate the microscopic processes of aqueous ion pairing when it takes place near, but not in direct contact with, an extended metallic electrode. We identify the specific effects of the electrode interface by comparing our results to those generated in the environment of the bulk liquid. We find that the presence of an electrode has little effect on the mechanistic details of ionic charge separation, but can significantly influence the thermodynamics and kinetics of the process. We highlight that this influence is different for simple monovalent salts like ${\mathrm{Na}}^{+}$ and ${\mathrm{I}}^{-}$, whose transport is limited by the mobility of an aqueous solvation shell (9), than it is for water ions, like ${\mathrm{H}}_3{\mathrm{O}}^{+}$ and ${\mathrm{OH}}^{-}$, whose transport is limited by the concerted hopping of protons along hydrogen-bonding chains (10). This fundamental difference is controlled by the microscopic details of electrode–water interactions and thus has implications for the nanoscale design of aqueous electrochemical systems.

When described in terms of a chemical reaction,

$${\mathrm{A}}_{(\mathrm{aq})}^{+}+{\mathrm{B}}_{(\mathrm{aq})}^{-}\rightleftharpoons {\mathrm{AB}}_{(\mathrm{aq})},$$

the process of aqueous ion association (forward reaction above) or dissociation (reverse reaction above) is deceptively simple. The expression omits the cooperative role of solvent, which must restructure to accommodate transitions between the associated and dissociated states (2, 11). This restructuring, which is driven by thermal fluctuations, is both collective (extending beyond the first solvation shell) and fleeting (12–14). These microscopic processes are difficult to probe experimentally (15), so atomistic simulation has played an important role in revealing their molecular-level details. Simulations based on state-of-the-art quantum chemical methods reveal important information about the structure and energetics of these systems; however, without additional importance sampling or embedding, they are too computationally demanding to characterize collective room-temperature dynamics (16–19). Classical simulations overcome this limitation by treating some interactions empirically, thereby enabling the characterization of the equilibrium dynamics of extended molecular systems. The tools of modern statistical mechanics, combined with computational techniques for efficiently sampling reactive trajectories (20), enabled a detailed characterization of the reaction mechanism, thermodynamics, and kinetics of these processes. These tools have been previously applied to investigate ion pair dissociation in the bulk liquid, which has revealed that the dissociation of classical ions and water ions are both crucially driven by electrostatic fluctuations of the aqueous environment (2, 6). The characteristics of these electrostatic fluctuations are similar between the two types of ion pairs, despite the fact that their solvation structures differ significantly.

When simple classical ions are solvated in aqueous solution, they are dressed by a solvation shell of water molecules whose orientations are polarized in response to the ionic charge. Similarly, bound pairs of ions are dressed by water molecules whose orientations are polarized in response to the electric dipole of the bound ion pair. In order for a bound pair of ions to separate, this dipolar solvation shell must be deconstructed and transformed into two separate and oppositely polarized ionic solvation shells. This solvent reorganization has been identified as the rate-limiting step for aqueous ion dissociation, and numerous efforts have been aimed at quantifying water’s role in this process (1–4, 14). These efforts have revealed that, although the overall process of aqueous ion dissociation is usually thermodynamically favorable, solvent reorganization leads to the emergence of a free-energy barrier that is on the order of typical thermal energies, $k_{\mathrm{B}}T$, where $k_{\mathrm{B}}$ is Boltzmann’s constant and $T$ is the temperature.

Water ions, specifically hydroxide and hydronium, are the products of proton transfer to and from an individual water molecule. These ions can easily integrate into the aqueous hydrogen-bonding network and leverage the Grotthuss-like shuttling of protons for delocalized and rapid transport (6). This feature leads the solvation properties of water ions to differ from those of similarly sized monovalent ions (21). The solvent’s role in mediating the separation of water ions is thus different from that of simple monovalent salts. It has been shown with ab initio simulation that the dissociation of bound water ions, a process known as autoionization, requires the well-timed coordination of solvent-induced electric field fluctuations and the making/breaking of hydrogen bonds. These correlated fluctuations result in a near-spontaneous relocation of a proton from a neutral water molecule to a newly formed hydronium (${\mathrm{H}}_3{\mathrm{O}}^{+}$) (6, 12), leaving behind a negatively charged hydroxide ion (${\mathrm{OH}}^{-}$).

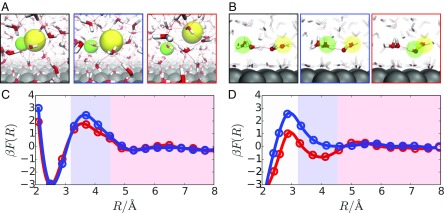
Because the water-mediated separation of water and classical ions occurs via different mechanisms, they can be affected differently by changes in the aqueous environment. In this work, we consider specifically the environmental changes that are associated with an electrochemical interface of an extended platinum electrode. A unique feature of these interfaces is the way that water binds to them, with its oxygen centered on the top site and its dipole pointing along the plane of the surface (22, 23). The partial chemical bond formed is typically strong and leads to the formation of an electrode-adsorbed water monolayer (24, 25). This monolayer can be hydrophobic, exhibiting molecular relaxation dynamics that are orders of magnitude slower than that of the bulk liquid (8). Snapshots taken along charge separation trajectories near the electrode interface are shown in Fig. 1 A and B. This slowly evolving water monolayer affects the structure and dynamics of the adjacent bulk liquid (26). For pure water systems, this effect is subtle in comparison with the dramatic slowdown of the monolayer itself; however, ions at this liquid interface can incorporate part of the monolayer into their solvation shell and thus couple directly to the slow dynamics of adsorbed water.

Fig. 1.

A and B contain typical snapshots going from a recombined state (black-bordered panel) to a dissociated state (red-bordered panel) for classical ions and water ions, respectively. The positive ion is highlighted in green, and the negatively charged ion is highlighted in yellow. C and D contain plots of the free-energy profile as a function of $R$, the interionic separation for classical ions and water ions, respectively. The data plotted in red correspond to ions in the bulk, and the data plotted in blue correspond to ions at the electrode interface.

Simulating Rare Events in Heterogeneous Environments

To study ion dynamics at the aqueous electrode interface, we performed atomistic simulations of liquid water in contact with the (111) surface of an extended platinum electrode. We used two different model systems: The first was designed to study the dissociation of a classical ion pair, ${\mathrm{Na}}^{+}$ and ${\mathrm{I}}^{-}$, and the second was designed to study the recombination of water ions, ${\mathrm{H}}_3{\mathrm{O}}^{+}$ and ${\mathrm{OH}}^{-}$. In the first model system, we describe the aqueous solution using classical force fields. Specifically, we describe water using the SPC/E model (27), and we describe the ions similarly, as spherically symmetric point charge particles. This efficient combination has been demonstrated to accurately reproduce the molecular structure and dynamics of liquid water as well as experimental measures of ion hydration and mobility. Although we studied this particular ion pair, previous studies on the adsorption free energies and mobilities of other alkyl halides have shown consistent qualitative changes between behaviors at and away from the electrode (26). Unfortunately, this classical nondissociative model is inadequate to describe the dynamics of water ions, whose transport is facilitated by the making and breaking of covalent OH bonds. Thus, in the second model system, we used an ab initio model of water based on density functional theory (6).

For both model systems, the electrode and its interaction with water molecules is described following the model of Siepmann and Sprik (28). In this model, each electrode atom includes a fluctuating partial charge that varies to maintain a constant potential condition. In this way, fluctuations in the charge distribution of the aqueous environment induce corresponding fluctuations in the electronic polarization of the electrode. These fluctuations mimic the electrostatic contributions of image charges and are consistent with a textbook description of a metal in that they obey the Johnson–Nyquist relation (29). As found in other studies (30–32), this description of the electrostatic environment results in an electrostatic potential that is rapidly varying near the electrode, but homogeneous in the bulk, with concomitant Gaussian electric field fluctuations (24). Other electronic degrees of freedom, such as those that determine the details of water–platinum binding, are described implicitly by using empirical interaction potentials. This electrode model captures important aspects of molecular physics that are unique to electrode interfaces, such as electronic polarization and site-specific water adsorption, at a fraction of the computational cost associated with an ab initio description of the metal.

We analyzed charge separation in terms of both thermodynamics and kinetics. We quantified the thermodynamics by computing the free energy along the microscopic coordinate that characterizes transitions between the bound and charge separated states. For the classical ion system, we computed this free energy using standard umbrella sampling techniques (33), and we computed the dissociation rate constant from the side–side correlation function (34). These methods are direct and accurate but they are too computationally demanding to be applied to the water-ion system, which relies on relatively expensive ab initio molecular dynamics simulations. Thus, for water-ion recombination, we used our limited ensemble of trajectories to construct a Markov state model (MSM), and we analyzed this model to infer the thermodynamics of charge recombination (35). To construct this model, we discretized the charge separation order parameter defined in SI Appendix into a series of metabasins, and then we used these metabasins as a basis for a MSM. The MSM was parameterized by specifying the transition rates between metabasins, which we computed directly from our trajectory ensemble. This MSM framework allowed us to infer the thermodynamic consequences associated with subtle difference between simulations carried out in the bulk and at the electrode interface. We analyzed the kinetics of water-ion pairs by analyzing the statistics of recombination times as derived from simulation data and an associated model of charge recombination dynamics.

Thermodynamics of Interfacial Charge Separation

The thermodynamics of aqueous charge separation can be evaluated by considering the free energy, or reversible work, to separate two oppositely charged particles in solution, such as plotted in Fig. 1 C and D. As this figure illustrates, the free energy to separate water ions and the free energy to separate classical ions bear a similar general structure. That is, both systems exhibit a stable free-energy basin at small interionic spacing, which we identify as the bound state, and a plateau-like region at larger interionic spacing, which we identify as the charge-separated state. In both cases, these two states are separated by a transition region that includes a small ($\sim 2k_{\mathrm{B}}T$) free-energy barrier in the direction of association.

The thermodynamics of charge separation depends significantly on the solvation free energy of the ion pair. This free energy is shaped by the properties of the aqueous environment through two primary contributions. The first contribution is due to differences in the solvation free energy between the bound and charge separated states. This free-energy difference controls the relative heights of the bound basin and the charge separated plateau. The second contribution is due to distortions in the ionic solvation shell that arise in response to the changes in interionic distance that occur during transitions between the bound and charge separated states. These distortions determine characteristics such as the size and shape of the free-energy barrier.

As indicated in Fig. 1, aqueous contributions to the free energy depend on both the identity of the charged particles and also on the details of the aqueous environment. We focused on the latter by comparing the charge separation free energy for ions at the electrode interface to that of ions in the bulk liquid. We observed that near an electrode, both water ions and classical ions faced an increased free-energy barrier for recombination. However, this barrier increase was larger for water ions than it was for classical ions. This differing influence of the electrode on the charge separation free energy of classical ions and water ions reflects water’s differing role in the charge separation mechanism for these two systems. That is, the electrode’s influence on charge separation is determined by water’s specific role in the microscopic process. To understand this influence more thoroughly, we now describe the mechanistic details for each case separately, focusing specifically on the indirect role of the electrode on the water-mediated aspects of charge separation.

The Mechanism of Charge Separation for Simple Ions

The mechanism of ionic charge separation involves an interplay between ion and water dynamics. To understand this interplay and how it is affected by the electrode interface, we first identified the reaction coordinate that encodes the microscopic details that are relevant to the dynamical process. An appropriate reaction coordinate must be capable of (i) distinguishing between the bound and charge separated states, and (ii) properly characterizing the transition state ensemble (TSE), which are those configurations that have equal probability of committing to either the bound or charge separated state (1). The one-dimensional coordinate of Fig. 1 accomplishes the former, but not the latter. It omits the fundamental role of the solvation environment in facilitating transitions between the bound and charge separated states.

The configuration of water molecules in the system determines the electrostatic environment of an ion pair. Collective rearrangements of water molecules control the electrostatic variations that drive the process of ionic charge separation. We can quantify these variations by computing the solvent-induced electrostatic potential, also known as the Madelung potential,

$${\psi }_{\pm }=\frac{q_{\pm }}{4\pi {ϵ}_0}\sum _i^{N_{{\mathrm{H}}_2\mathrm{O}}}\frac{q_i}{|{𝐫}_i-{𝐫}_{\pm }|},$$ [1]

where the summation is taken over all of the atoms that belong to water molecules, $q_i$ and ${𝐫}_i$ is the charge and position of the $i^{th}$ water atom, $q_{+}$ and ${𝐫}_{+}$ are the charge and position of the ${\mathrm{Na}}^{+}$ ion, and ${ϵ}_0$ is the vacuum permittivity. This quantity reports directly on water’s collective contribution to the electrostatic environment of the ${\mathrm{Na}}^{+}$ ion, and similarly the analogous quantity for ${\mathrm{I}}^{-}$, ${\psi }_{-}$, reports on collective water fluctuations around it. Their sum, $\psi ={\psi }_{+}+{\psi }_{-}$, is thus the total electrostatic potential acting on the ionic pair, from the surrounding solvent; for convenience, we report it in units of $1/\beta =k_{\mathrm{B}}T$.

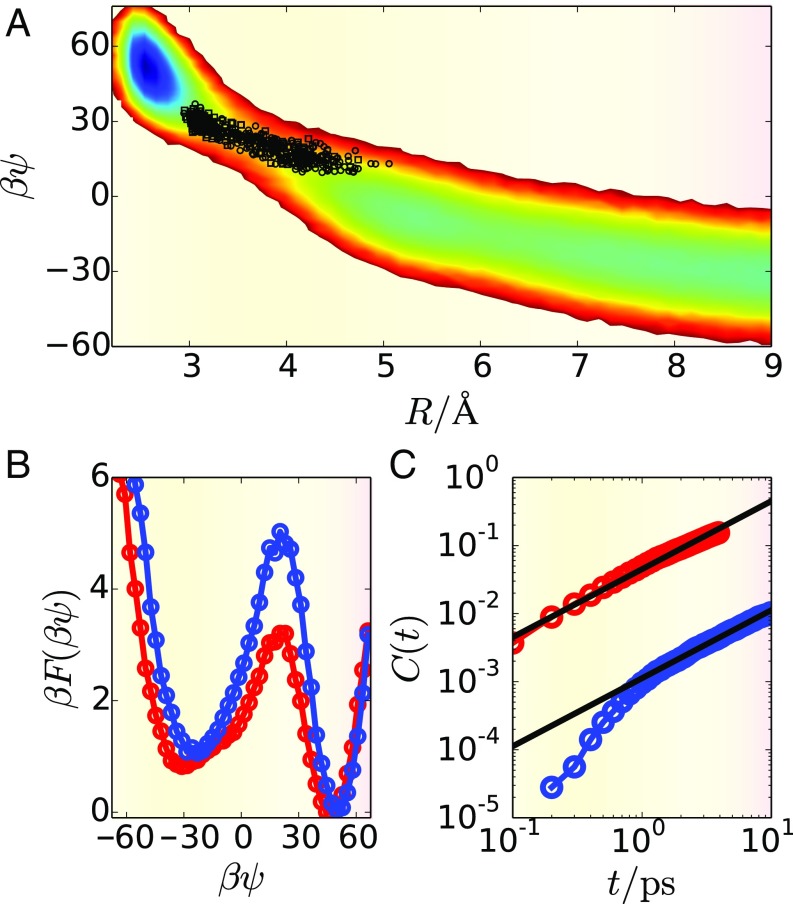
The quantity $\psi$ exhibits different statistics when the ions are in their bound state compared with when they are independently solvated. This result can be seen in Fig. 2, which contains a plot of the charge separation free energy as a function of $\psi$ and $R$. When resolved in these coordinates, the bound and charge separated states are connected via a pathway that is mutually elongated in both $\psi$ and $R$, clearly indicating the importance of collective water fluctuations in ionic charge separation. Furthermore, members of the TSE harvested with transition path sampling are distributed along this free-energy path, suggesting that the 2D coordinate of $(\psi ,R)$ satisfies the criteria to be a suitable reaction coordinate. We have confirmed this suitability by performing commitor analysis across members of the TSE (SI Appendix).

Fig. 2.

Mechanism of ion pair dissociation for NaI. (A) Free energy as a function of interionic separation, $R$, and the total Madelung potential, $\psi$, shown in the contour plot. Members of the TSE are shown as black points on this surface. (B) Free energy as a function of the Madelung potential for the bulk (red) and interface (blue). (C) Side–side correlation function for the classical ions for the bulk (red) and interface (blue), with linear fits shown in black.

We isolated water’s contribution to the charge separation process by projecting the free energy onto the coordinate $\psi$. The result, plotted in Fig. 2B, reveals that the free-energy cost for solvent reorganization is larger at the electrode interface, by $\sim \mathrm{\hspace{0.17em}1.5}{k}_{\mathrm{B}}T$, than it is in the bulk liquid—a consequence of constraints imposed on the liquid by the presence of the electrode. This difference in barrier height is expected to have consequences for the relative dissociation kinetics. Based on transition state theory, identical systems with a barrier height difference of $1.5k_{\mathrm{B}}T$ are predicted to have rates that differ by a factor of $\exp (1.5)\approx \mathrm{\hspace{0.17em}4.5}$. That is, based on barrier height alone, we expect $k_{\mathrm{elec}}\approx \mathrm{\hspace{0.17em}0.2}{k}_{\mathrm{bulk}}$. However, when dissociation rates are computed directly, via the side–side correlation function shown in Fig. 2C, we find that $k_{\mathrm{elec}}\approx \mathrm{\hspace{0.17em}0.02}{k}_{\mathrm{bulk}}$, a full order of magnitude different. The resolution to this apparent discrepancy is that the bulk environment is not identical to that of the electrode interface and that these differences affect the flux over the barrier in the free-energy surface.

Water dynamics are more sluggish at the electrode interface than they are in the bulk liquid (8). Strong water–electrode interactions lead to the formation of an adsorbed water monolayer, and molecules within this monolayer experience slow orientational relaxation dynamics. For ions near the electrode, the charge separation process couples to this slowly evolving monolayer, which significantly increases the timescale governing dynamics in $\psi$. Together, this reduced diffusion and the increase in free-energy barrier height combine to yield the anomalously large difference in dissociation rate between the bulk and electrode interface.

The influence of the electrode on the dissociation of ions is mediated by the interfacial aqueous environment. This influence is controlled by water’s specific role in driving the dynamics of ion pairs and how that role is affected by the presence of the electrode. For the simple classical ions described above, electrode-induced constraints on the collective reorientations of water molecules lead to a significant slowdown in dissociation rates. The electrode’s influence is fundamentally different for water ion pairs, which do not require such large collective water reorientations.

The Mechanism of Charge Separation for Water Ions

The bound state of ${\mathrm{H}}_3{\mathrm{O}}^{+}$ and ${\mathrm{OH}}^{-}$ is simply a pair of neutral water molecules. This exceptionally stable state dissociates reluctantly and is thus difficult to simulate, even with the help of rare event-sampling techniques. We therefore chose to focus on the time-reversed process of charge recombination, which is both rapid and spontaneous. The recombination process occurs through the concerted transfer of protons along a chain of hydrogen bonds that connect the ${\mathrm{H}}_3{\mathrm{O}}^{+}$ and ${\mathrm{OH}}^{-}$ (6). During this process, a large electric field fluctuation drives the shuttling of an excess proton from the ${\mathrm{H}}_3{\mathrm{O}}^{+}$ to the ${\mathrm{OH}}^{-}$ via the participation of two or three intermediate water molecules. An illustration of this process at the electrode interface is shown in Fig. 1B.

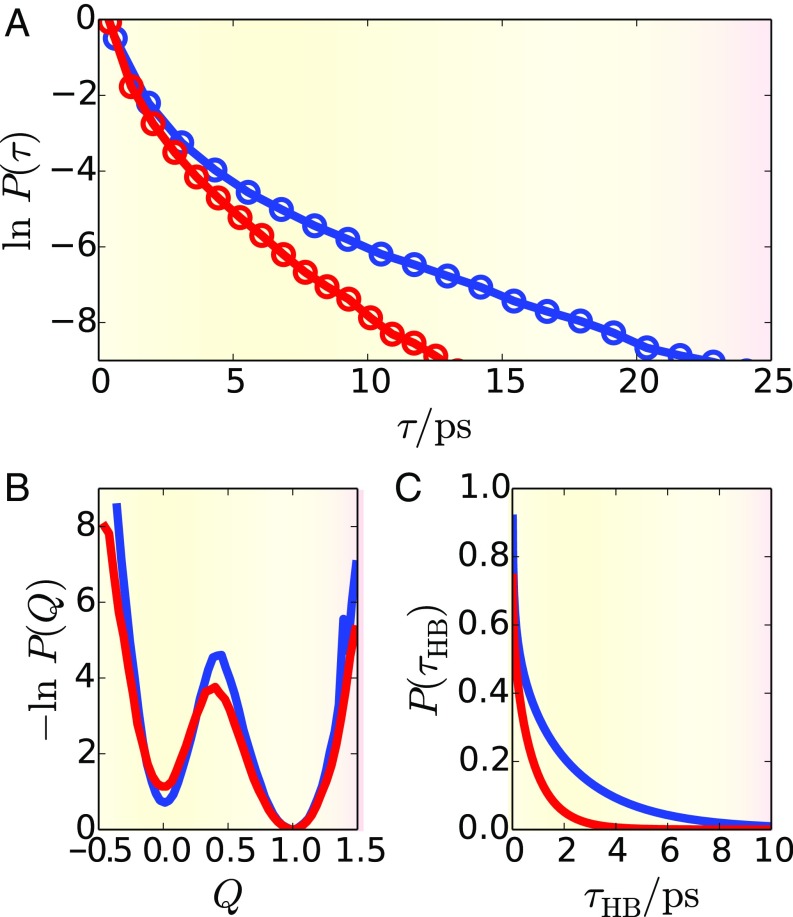
We began by considering the kinetics of water ion recombination, which we quantified by computing the time, $\tau$, for initially separated water ions to reach the bound state. Because $\tau$ depends sensitively on the initial separation of the ions, we only compared trajectories initialized from an ensemble of configurations that have been equilibrated with a fixed hydronium–hydroxide separation of $5\AA$. From the free-energy function in Fig. 1D, this distance is sufficiently large that the ions are not already committed to the bound basin. Starting from larger distances affects the quantitative time to recombine, but that time is just that associated with diffusion to the barrier. Water ion pairs separated by $5\AA$ are typically bridged by chains of three consecutive hydrogen bonds via two intermediate water molecules. These hydrogen bond chains facilitate rapid charge recombination, with average recombination times of ${\tau }_{\mathrm{bulk}}=\mathrm{\hspace{0.17em}0.35}$ ps and ${\tau }_{\mathrm{elec}}=\mathrm{\hspace{0.17em}0.40}$ ps for ions in the bulk liquid and at the electrode interface, respectively. Notably, and unlike the case of monovalent salts, the presence of the electrode has little effect on the average recombination dynamics of water ions. However, we observed that the electrode had a subtle effect on the statistics of $\tau$.

We quantified the electrode’s effect on the recombination time statistics by computing $P(\tau )$, the probability that a given trajectory with initial ion separation of $5\AA$ will have a recombination time of $\tau$. Comparing $P(\tau )$ for ions in the bulk and the electrode interface revealed discernible differences in the large-$\tau$ tails of the distributions. However, as shown in SI Appendix, these differences are difficult to quantify due to poor statistics (our simulation data includes $\approx 200$ independent trajectories). We thus improved statistics with the use of a simplified model of water ion recombination derivable from this coarse data. This model, described in more details within SI Appendix, is designed to efficiently predict the value of $\tau$ given the positions of ${\mathrm{H}}_3{\mathrm{O}}^{+}$, ${\mathrm{OH}}^{-}$, their surrounding water molecules, and the connectivity of the hydrogen bond network. The model describes charge recombination in terms of two types of dynamic events. First, a single proton can hop along a hydrogen bond to the ${\mathrm{OH}}^{-}$ or from the ${\mathrm{H}}_3{\mathrm{O}}^{+}$. This proton hopping results in an exchange of positions of a water ion and neighboring water molecule. Second, the charges can recombine, via a concerted mechanism, through short chains of hydrogen bonds. The rate for this process is a function of the number of hydrogen bonds in the chain. We simulated charge recombination with a kinetic Monte Carlo (KMC) algorithm for fixed configurations of the hydrogen bond network. We computed the rates of the processes in the KMC model directly from our simulation data.

Fig. 3A contains a plot of $P(\tau )$ computed by applying our KMC model across the ensemble of initial conditions used in our ab initio simulations. We observed that recombination in the bulk and at the electrode interface have similar mean behavior, but differ in the tails of their recombination time distributions. Specifically, it is more likely that an ion pair at the electrode interface has an abnormally long recombination time. This large difference involves very low probability events, and thus does not manifest itself in the mean behavior. We attribute the difference in these curves to subtle differences in the topology of the hydrogen-bond network between the bulk and the interface. Proton dynamics in our model are constrained by the hydrogen-bond network and thus especially sensitive to the details of network structure. Specifically, the interfacial hydrogen-bond network is distorted along the plane of the interface. This distortion leads to a slight reduction in the relative number of hydrogen-bond chains along which recombination can occur (see SI Appendix for details). This reduction is balanced by an increase in the probability that a proton transfer will increase the separation between the ions, thus leading to an increase in recombination time.

Fig. 3.

Mechanism for water ion association for bulk (red) and the interface (blue). (A) The distributions of recombination times, $\tau$. (B) Distribution function of the net system charge. (C) Distribution of hydrogen bond lifetimes.

The electronic and nuclear rearrangements that accompany water ion recombination are driven by electrostatic fluctuations of the aqueous environment. These fluctuations are reflected in the distribution of electronic charge in the system, which is different for the bound and charge separated states. One way to quantify this difference is to compute the imbalance of electronic charge between the hydroxide and the hydronium species, as given by,

$$Q=\frac{1}{2}\left[\sum _{i\in {\mathrm{H}}_3\mathrm{O}+}{q}_i-\sum _{j\in {\mathrm{OH}}^{-}}{q}_j\right],$$ [2]

where the two summations are taken over all of the atoms belonging to the hydronium or hydroxide ion, respectively, and $q_i$ is the Mulliken charge on the $i$th atom. We define the hydroxide and hydronium based on nuclear coordinates by first associating each hydrogen with its nearest oxygen, as described in SI Appendix, and then identifying an oxygen with only one associated hydrogen as a hydroxide center and an oxygen with three associated hydrogens as a hydronium center. These water-ion centers and their associated hydrogens are thus included in the summations in Eq. 2*. This continuously varying quantity was formulated so that $Q=\mathrm{\hspace{0.17em}1}$ when the hydronium and hydroxide are fully charged and $Q=\mathrm{\hspace{0.17em}0}$ when the two species are charge neutral. By analyzing the statistics of $Q$, sampled over an ensemble of recombining trajectories, we can compute the free energy for charge recombination.

Fig. 3B shows the probability distributions for $Q$ for water ion recombination in the bulk and at the electrode interface, computed directly from the ensemble of recombination trajectories^†. These profiles reveal that the barrier height to recombination is slightly larger at the electrode interface than it is in the bulk liquid. This barrier height difference is ∼$1.5k_{\mathrm{B}}T$, similar to that found in the case of the classical ions described above. However, the kinetic consequences of this observation are not apparent when comparing the recombination times, which are nearly identical near and away from the electrode interface. We can thus conclude that the kinetic effect of an increased barrier height is compensated by an increase in flux along the coordinate $Q$.

We explain the molecular origins of the enhanced flux in $Q$ in terms of the equilibrium dynamics of hydrogen bonding. The concerted proton hops that drive recombination are directed along chains of multiple hydrogen bonds. This process is therefore contingent on the stability of these chains. Fluctuations that destabilize or sever hydrogen-bond chains will have a negative effect on recombination. Along a liquid water interface, such fluctuations are suppressed due to geometric constraints that lead to more stable and longer lived hydrogen bonds (36, 37). The consequences of these constraints can be quantified by computing the distribution of hydrogen-bond lifetimes, $P({\tau }_{\mathrm{HB}})$. In Fig. 3C, we see that the hydrogen-bond lifetimes are larger at the electrode interface than they are in the bulk. Hydrogen-bond chains at the interface are thus longer lived, which allows more time for the environmental fluctuations to induce the electronic reorganization associated with charge recombination.

Implications for Electrochemistry

The aqueous environment of an electrode interface differs from that of the bulk liquid. These differences affect the microscopic processes that underlie many electrochemical applications. In this work, we have highlighted specifically the microscopic process of ionic charge separation and shown that the electrode’s influence can depend significantly on the identity of the ionic species. This dependence is controlled by water’s specific role in mediating ion pair dynamics. We find that for ions comprising monovalent salts, charge separation is slowed near an electrode interface by over an order of magnitude; however, the analogous process for water ions is barely affected. Understanding and accounting for these effects, and their dependence on ion type, is important for the design of electrochemical systems.

Importantly, the dominant influence of the electrode on the separation of ion pairs is dynamical. Electrode-water interactions alter the equilibrium properties of the aqueous environment, such as the timescales that govern molecular fluctuations, which couple to the microscopic dynamics of ionic charge separation. The details of the electrode–water interactions thus control these dynamical effects. In these results, we use a platinum(111) electrode; however, an electrode made of a different metal, such as gold or copper, or with a different surface geometry and water-binding energy may have a different influence on the dynamics of charge separation (22, 38, 39). Notably, these dynamical effects are not apparent in the thermodynamics and are thus difficult to predict without a model that explicitly describes the interplay between ions, their solvation shell, and the aqueous dynamics at the electrode interface. Traditional continuum models (40) are thus insufficient to predict these significant interfacial effects.

Methods

All simulations were performed in an ensemble with a constant number of particles, volume, temperature, and applied electrode potential. The classical simulations were set up with simulation cell sizes $3\times \mathrm{\hspace{0.17em}3}\times \mathrm{\hspace{0.17em}6}$ nm, and the ab initio simulations with cell sizes $1\times \mathrm{\hspace{0.17em}1}\times \mathrm{\hspace{0.17em}2}$ nm. The latter used the PBE functional with D3 dispersion correction and GTH pseudopotentials. More details can be found in SI Appendix.