Molecular characterization of water and surfactant AOT at nanoemulsion surfaces

Significance

Nanoemulsions provide exciting opportunities for a wide range of biological, scientific, and industrial applications. The interfacial structure of nanoemulsions is crucial to their stabilization, but molecular factors contributing to their surfactant stabilization are far from understood for most systems. Much more is known about the molecular properties of their smaller micellar counterparts where model systems using surfactants such as dioctyl sodium sulfosuccinate (AOT or Aerosol-OT) have been illuminating. The studies described herein provide details about the bonding and structure of water and surfactant AOT at regular and reverse nanoemulsion curved surfaces as well as at the corresponding planar oil–water interface. This is accomplished with vibrational sum-frequency spectroscopy in its scattering and reflection geometries.

Abstract

Nanoemulsions and microemulsions are environments where oil and water can be solubilized in one another to provide a unique platform for many different biological and industrial applications. Nanoemulsions, unlike microemulsions, have seen little work done to characterize molecular interactions at their surfaces. This study provides a detailed investigation of the near-surface molecular structure of regular (oil in water) and reverse (water in oil) nanoemulsions stabilized with the surfactant dioctyl sodium sulfosuccinate (AOT). Vibrational sum-frequency scattering spectroscopy (VSFSS) is used to measure the vibrational spectroscopy of these AOT stabilized regular and reverse nanoemulsions. Complementary studies of AOT adsorbed at the planar oil–water interface are conducted with vibrational sum-frequency spectroscopy (VSFS). Jointly, these give comparative insights into the orientation of interfacial water and the molecular characterization of the hydrophobic and hydrophilic regions of AOT at the different oil–water interfaces. Whereas the polar region of AOT and surrounding interfacial water molecules display nearly identical behavior at both the planar and droplet interface, there is a clear difference in hydrophobic chain ordering even when possible surface concentration differences are taken into account. This chain ordering is found to be invariant as the nanodroplets grow by Ostwald ripening and also with substitution of different counterions (Na:AOT, K:AOT, and Mg:AOT) that consequently also result in different sized nanoparticles. The results paint a compelling picture of surfactant assembly at these relatively large nanoemulsion surfaces and allow for an important comparison of AOT at smaller micellar (curved) and planar oil–water interfaces.

We are all familiar with the adage that “oil and water do not mix,” but of course, it depends upon the definition of “mix.” Emulsions are an important special case, where the oil is dispersed as tiny droplets in the aqueous phase, taxonomically called a regular emulsion, or where the water is dispersed as tiny droplets throughout the oil phase, called a reverse emulsion. Because both emulsions are thermodynamically unstable, overcoming this requires an emulsifying agent such as a surfactant. Recently, there has been interest in surfactant-stabilized emulsions with droplet diameters in the nanoscale range for unique applications in drug delivery (1, 2) and oil recovery (3, 4) and as nanoreactors to produce materials ranging from polymers to quantum dots (5). Regular or reverse emulsions with droplet diameters in the range of 10–1,000 nm are called nanoemulsions. Little is known about the processes or molecular structures that result in their stability via surfactants. Even less is known about the structure–function relationship, which is crucial to determine the best surfactant for a given nanoemulsion application. Their utility hinges on a molecular-level understanding of the structure and bonding interactions present at the surface of these soft nanoparticles. This study provides a molecular snapshot of reverse and regular nanoemulsions stabilized by dioctyl sodium sulfosuccinate (AOT or Aerosol-OT).

One might expect that formation of these larger nanoemulsions would be similar to smaller micellar (e.g., microemulsion) systems. Such is not the case, and in fact, they can behave quite differently, often for reasons that are not yet fully understood (6). Nanoemulsions do not form spontaneously, and overcoming surface tension on their scale requires an external shear beyond that used to create smaller micelles (7–10). Once formed, they can be quite stable, a desirable attribute in products and applications requiring a long shelf life.

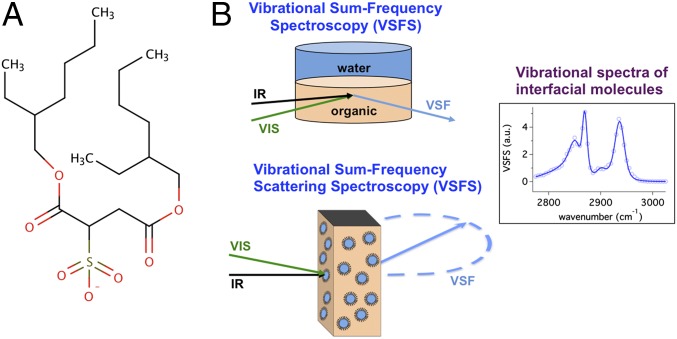
AOT was selected for these studies of nanoemulsion surfaces for several reasons. It is used in a range of applications including as an oil spill dispersant, a pesticide, and even as a laxative. As with microemulsions, AOT also has the ability to form both regular and reverse nanoemulsions without a cosurfactant (7). Its efficacy at forming reverse emulsions is attributed to its wedge-like shape (8) and enhanced aqueous solubility (9). AOT (Fig. 1) is composed of two branched alkyl chains and a charged sulphonate head group that make up the hydrophobic and hydrophilic portions of the molecule, respectively. Extensive studies of AOT in microemulsions have been conducted using techniques such as NMR spectroscopy, small-angle neutron scattering, X-ray scattering, theoretical calculations, and ultrafast laser methods (11–13). Few molecular-level studies have been conducted on nanoemulsion interfaces with none involving AOT, largely due to the experimental challenges in probing spherical interfaces of this size with surface specificity.

Fig. 1.

(A) The chemical structure of AOT. (B) A diagram of the planar and particle VSF experimental geometries, both involving an overlap of the incoming visible and IR beams at the planar interface (Top) in a TIR geometry or the center of a cuvette composed of a CaF₂ front window with a quartz back window and an optical path length of 200 µm (Bottom). (See Supporting Information for more details.)

In recent years, much research has focused on developing different methods to make nanoemulsions and determining what factors contribute to their stability. Ultimately, it is the intermolecular forces between neighboring molecules that govern surfactant packing at the interface, and this depends on its molecular structure (10), the organic phase (14), and the electrostatics of the interface (15). The studies described herein are aided by prior work at neat oil–water interfaces as examined by vibrational sum-frequency spectroscopy (VSFS) and computational studies on planar interfaces (16–18). What has been learned from these and related studies is that weak bonding interactions between interfacial water and various hydrophobic oils is a general trait for these oil–water systems, which results in significant molecular ordering and structuring of both solvent phases near the interfacial region. The electric field at the oil–water interface has been shown to facilitate the adsorption of simple electrolyte ions at the interface (17), surfactant adsorption (19), the ordered assembly of polyelectrolytes (20), and 2D peptoid nanosheets (21).

One of the unique aspects of this study is the ability to compare the interfacial molecular structure, bonding, and orientation of AOT and interfacial water at the nanoemulsion surface with its behavior at the planar oil–water interface using compatible solvents. Included in this comparison is the examination of the effect of a change in the interfacial water and AOT as the counterion is varied (i.e., Na:AOT, K:AOT, and Mg:AOT). Because AOT can form both types of nanoemulsions, this allows a comparison of the degree of alkyl chain ordering with the chains directed into the interior (regular) and exterior (reverse) of the nanodroplets. Additional studies show the invariance in alkyl chain ordering as the nanoemulsions grow with time via Ostwald ripening. All AOT studies described below are with Na:AOT unless specified otherwise.

Experimental Approach

Vibrational sum-frequency spectroscopy is the primary tool used to examine AOT at the oil–water nanodroplet and planar interfaces. The droplet spectroscopy, pioneered by the Roke group (22–26), is conducted in a scattering geometry [vibrational sum-frequency scattering spectroscopy (VSFSS)], and the comparative planar surface studies (VSFS) are conducted in a total internal reflection geometry (TIR) as in previous work from this laboratory (16, 18, 27, 28).

The interfacial specificities of both VSFSS and VSFS allow the vibrational modes of the relatively small number of oriented molecules at an interface to be detected despite the presence of many more bulk molecules (29, 30). Different polarization schemes for incident and detected beams allow for the selection of specific vibrational dipole net orientations. In spectra reported here the polarization scheme used was sum-frequency, visible, infrared (SSP), which measures frequencies associated with changing dipole moments whose orientations are perpendicular to the interface.

The nanodroplet spectroscopic studies of interfacial AOT and water molecules at the CCl₄–D₂O and hexadecane-d₃₄–D₂O interfaces were measured using a femtosecond broadband laser system (Supporting Information) at a scattering angle of θ = 60°. The VSFS planar studies were conducted using a picosecond laser system with experimental parameters similar to previous studies from this laboratory (Supporting Information) (19, 20, 31). In all cases, spectra were taken of the C–H and S–O vibrational stretching modes of AOT and the O–H stretching modes of water. In selected C–H studies, D₂O was chosen to replace H₂O to remove the spectral interference of overlapping H₂O modes with the blue side of the C–H stretching modes (27, 32, 33). Likewise, hexadecane-d₃₄ and CCl₄ were chosen as the oil phases for regular and reverse nanoemulsion systems, respectively, because of their optical transparencies.

VSFSS measurements were performed on 200-nm reverse and regular nanoemulsions with a bulk solution AOT concentration of 1.0 mM to ensure full coverage of the droplet interfaces (6). Free surfactants residing in the bulk as monomers or aggregates can attenuate the incoming IR beam. To minimize this loss an optical cuvette with a path length of 200 µm was used. Reverse nanoemulsions were made by ultrasonicating 1.0 mM AOT dissolved in CCl₄ with 1% D₂O using a Branson S-250A ultrasonicator for 2 min. Regular nanoemulsions were prepared in an identical manner, except with 1.0 mM AOT dissolved in D₂O with 1% hexadecane-d₃₄. Samples were used the day they were prepared, except in the reverse nanoemulsion growth experiments where the same sample was used over the course of several days.

Dynamic light scattering (DLS) methods are used to determine particle size. Interfacial pressure measurements, conducted using the pendant drop method, provide a more quantitative measure of surface coverage than VSF methods and assist when there is ambiguity as to whether a change in the VSF signal arises from a change in surface population or net orientation. The regular and reverse nanoemulsion systems are composed of mixtures of hexadecane-d₃₄–D₂O and CCl₄–D₂O, respectively, with CCl₄–D₂O for the planar interface. The CCl₄–D₂O system is chosen to allow maximal penetration of the incident infrared light to the interface for the planar studies conducted in TIR geometry.

Surface Coverage of AOT at Planar and Droplet Surfaces

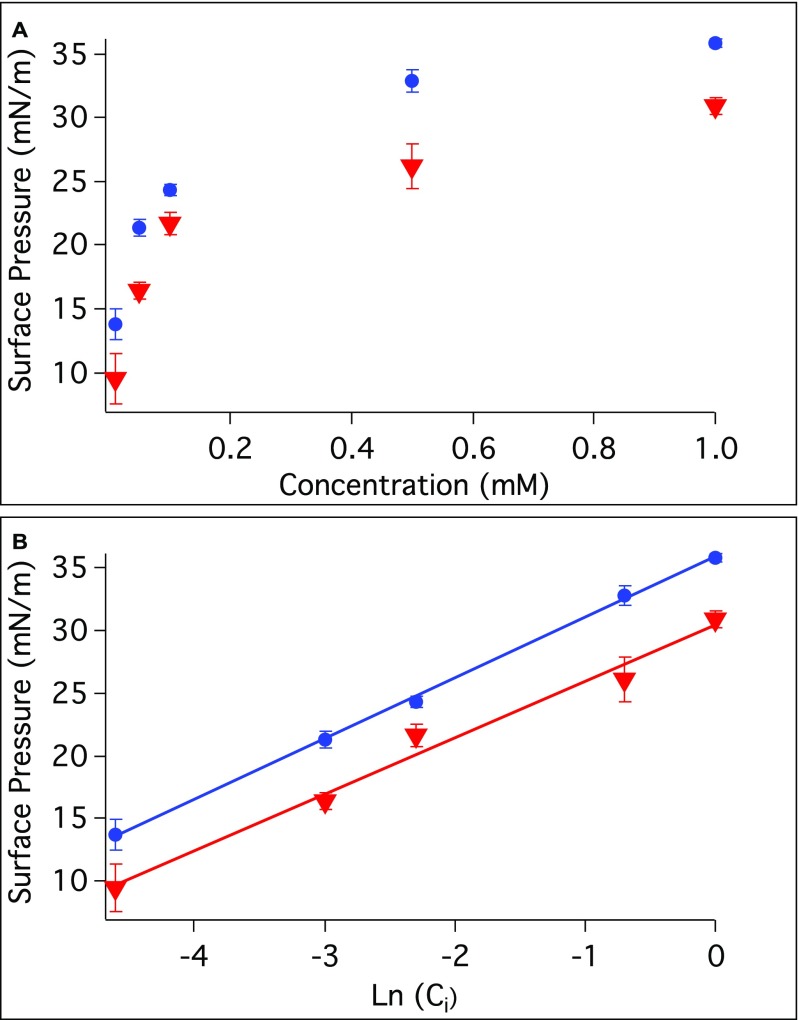
Estimation of the surface coverage of AOT at the nanoemulsion surface was aided by interfacial pressure measurements conducted with planar CCl₄–H₂O and hexadecane–H₂O interfaces for bulk AOT concentrations from 0.01 to 1.0 mM (Fig. S1). From these measurements the maximum surface excess of AOT was calculated to be 1.3 × 10⁻¹⁰ (±0.1 × 10⁻¹⁰) and 1.1 × 10⁻¹⁰ (±0.1 × 10⁻¹⁰) mol/cm² for the CCl₄–H₂O and hexadecane–H₂O, respectively (34). This gives calculated interfacial head group areas of 131 (±20) and 151 (±23) Ų/molecule, respectively. These are consistent with measurements of AOT at the air–water interface reported in neutron reflectivity studies (78–132 Ų/molecule) (35, 36). Using the calculated head group area (6), the minimum bulk surfactant concentration necessary to cover a 200-nm diameter nanoemulsion droplet in this study is estimated to be 0.4 and 0.3 mM for the CCl₄ and hexadecane systems, respectively.

Fig. S1.

(A) A plot of the surface pressure vs. bulk AOT concentration at the CCl₄–H₂O interface (red) and at the hexadecane–H₂O interface (blue) is shown with a sigmoidal dependence. (B) A linear fit of the surface pressure vs. the natural logarithm of AOT concentration for the CCl₄–H₂O interface (red) and at the hexadecane–H₂O interface (blue).

Hydrophobic Chain Ordering of AOT at Planar and Curved Surfaces

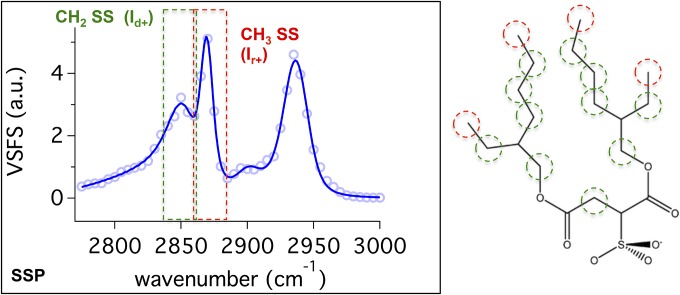
The vibrational spectrum of the C–H stretching region for AOT at the planar oil–water interface (Fig. 2) provides a starting point for discussion of the spectroscopic results. The VSFS spectrum corresponds to C–H modes with dipole moments with a component perpendicular to the interface by use of the SSP polarization scheme. AOT has two branched alkyl chains with potential contributions from a number of C–H groups [4CH₃ (red), 11CH₂ (green), and 3CH]. The strong signal from the C–H modes indicates that AOT is surface active and highly oriented at the planar CCl₄–D₂O interface.

Fig. 2.

VSFS SSP spectra in the C–H stretch region for 1 mM AOT at the planar CCl₄–D₂O interface. Contributions from methylene (CH₂) and methyl (CH₃) symmetric stretches are highlighted in green and red, respectively.

The spectrum is fit to four peaks of known C–H vibrational frequencies (33, 37, 38). The peaks at 2,856 ± 2 cm⁻¹ and 2,869 ± 2 cm⁻¹ are assigned to the methylene symmetric stretch (CH₂–SS) and methyl symmetric stretch (CH₃–SS), respectively. The peaks at 2,908 ± 2 cm⁻¹ and 2,932 ± 2 cm⁻¹ correspond to the methine stretch (C–H) and the Fermi resonance splitting between the CH₃–SS and bending overtone, respectively (25, 33, 39, 40). The spectra are fit with a relatively broad CH₂–SS peak, which is justified as the intensity arises from numerous CH₂ moieties on different parts of the AOT molecule (green sites in Fig. 2) that occupy different chemical environments and orientations. These spectral assignments are consistent with vibrational sum-frequency literature in the C–H region (19, 32, 40).

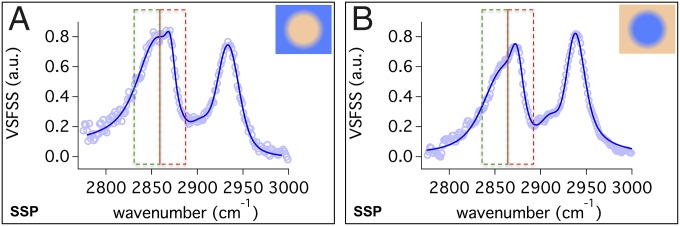
The VSFSS spectra for AOT at the regular and reverse nanoemulsion surfaces are shown in Fig. 3 A and B, respectively. For AOT at the regular nanoemulsion interface, the CH₂–SS (2,866 ± 1 cm⁻¹), CH₃–SS (2,872 ± 1 cm⁻¹), and methine (C–H) (2,905 ± 2 cm⁻¹) modes are measured along with the Fermi resonance splitting of the CH₃–SS and bending overtone modes at 2,933 ± 1 cm⁻¹. The reverse nanoemulsion interface yields very similar peak positions at 2,863 ± 2 cm⁻¹, 2,871 ± 1 cm⁻¹, 2,908 ± 1 cm⁻¹, and 2,931 ± 1 cm⁻¹, respectively, with the same assignments.

Fig. 3.

VSFSS SSP spectra in the C–H stretch region for 1 mM AOT at the (A) regular hexadecand-d₃₄-D₂O and (B) reverse CCl₄–D₂O nanoemulsion droplet interface.

In comparison, all three C–H spectra are remarkably similar. The independently fit planar and nanoemulsion spectra have the same peak assignments due to very similar peak positions and phases. However, there is a noticeable difference in the relative intensities of the methylene and methyl modes that is most relevant to understanding differences in the chain ordering. The higher resolution of the picosecond system used in the planar studies (2 cm⁻¹) versus the scattering experiments (8 cm⁻¹) is responsible for the somewhat sharper spectral features for the planar studies.

The measured intensity ratio of the methylene (I_d+) SS and methyl (I_r+) SS is often used as a measure of the degree of alkyl chain disorder or gauche structure along a hydrocarbon chain (28, 41). The smaller the ratio, the more trans configuration along an alkyl chain. In addition to eight sets of alkyl chain methylene C–H modes from the primary chains, there are three additional sets of methylene C–H modes on side chains and near the head group. Hence, determining whether AOT chains are gauche or trans is not strictly possible using I_d+/I_r+ ratios; however, a relative comparison of I_d+/I_r+ can give some insight when comparing AOT at different interfaces (19, 41). For the regular and reverse nanoemulsions, I_d+/I_r+ was found to be 2.8 ± 0.4 and 2.4 ± 0.3, respectively, indicating that the alkyl chains at these two interfaces show similar conformational order.

AOT at the planar interface shows significantly more ordering with a corresponding I_d+/I_r+ ratio of 0.9 ± 0.1 due to the increased intensity of the CH₃–SS peak at 2,869 cm⁻¹. This ordering at the planar oil–water interface is consistent with lamellar structures formed at solid–liquid and air–liquid interfaces (42). Less alkyl ordering of AOT at both nanoemulsion droplet interfaces found here is consistent with VSFSS studies of SDS at the droplet interface for regular nanoemulsions (25).

To determine whether surface concentration could be a factor in the difference in alkyl ordering between the droplet and planar interfaces, the I_d+/I_r+ ratio was examined as the AOT surface concentration at the planar interface was varied for bulk AOT concentrations between 0.01 and 2.0 mM, a range well above and below the bulk solution concentration necessary to achieve the calculated maximum surface coverage for regular (0.4 mM) or reverse (0.3 mM) nanoemulsions. The results show that although the overall signal amplitude increases with concentration, no change is observed in the spectral profile or corresponding I_d+/I_r+ ratio. Assuming that the contributions from the C–H modes along the small side chains are minimal, this indicates that there is no significant change in the AOT alkyl chain conformation as the density of surfactants increases at the interface. We conclude that the steric hindrance caused by the branched alkyl chains of AOT do not allow tight packing or the transformation into a more trans configuration at the planar interface with increasing concentration, contrary to what is found with many single alkyl chain surfactants with smaller head group areas. This conclusion also appears operative for AOT at the nanoemulsion surface (28).

Does Size Matter?

For AOT in a CCl₄–H₂O reverse nanoemulsion, droplet diameters were determined by DLS measurements to grow over time, eventually leading to phase separation. This natural growth facilitates the examination of how the AOT alkyl structure and I_d+/I_r+ varies with nanoparticle size and surface curvature. Ostwald ripening is found to contribute to this size growth as the particle volume (r³) shows a linear relationship with time with a measured rate of 360 ± 20 nm³/s. The regular nanoemulsion size was found to be stable over the same period due to the differences in droplet solubility in the continuous phase of the hexadecane–H₂O vs. CCl₄–H₂O system, consistent with the Ostwald ripening mechanism.

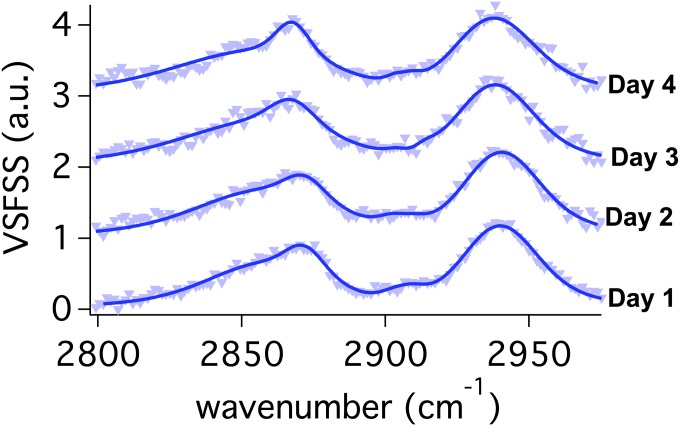
VSFSS measurements of the C–H region were taken during a 4-day period while monitoring the (increasing) reverse nanoemulsion diameters of 200, 584, 595, and 643 nm from day 1 to day 4, respectively. As the reverse nanoemulsions become larger, there are no changes observed in the amplitude or spectral features of the C–H modes of AOT (Fig. S2). The Ostwald ripening process is not typically described as being interfacially dependent. During growth, as water molecules transit the interface, one might expect a perturbation of the interfacial AOT structure, but none is seen here on a timescale of ∼20 min per scan. As with the planar AOT studies where there appears to be an optimum geometry for the alkyl chain conformation that is largely invariant with surface concentration, AOT alkyl conformations are invariant as the surface curvature changes over the size range examined here.

Fig. S2.

VSFSS SSP spectra in the C–H stretching region for 1 mM Na:AOT at the reverse CCl₄–D₂O nanoemulsion droplet interface taken each day over the course of 4 days. Spectra have been vertically offset for comparison.

What can explain the difference found for the higher degree of ordering for the planar compared with the nanoemulsion surface? Mason et al. (6) suggest that the surfactant surface density equilibrium and interfacial head group area differ for nanoemulsion interfaces compared with planar interfaces. However, even when the planar studies are conducted over a range of surface concentrations that include the surface concentration at the nanoemulsion interface, the alkyl ordering never achieves the higher degree of order found for AOT at the droplet interface. We conclude that this difference in ordering is intrinsic to adsorption of AOT at the droplet surface. For example, at the nanodroplet interface, AOT has the potential to adopt a larger angular distribution of the methyl groups (relative to the planar geometry) with respect to the interface. Hydrophobic alkyl chains, their lengths, their conformations, and their interactions with neighboring molecules have been suggested to play a significant role in the stabilization of emulsions including in the formation of different shapes and sizes of nanoemulsions (43, 44).

Orientation and Solvation of the AOT Head Group

Understanding the molecular structure and solvation of the ionic head group of a surfactant such as AOT is important because of its presence directly at the junction (19, 31). Its position in the interface and its interaction with neighboring water molecules and neighboring charged head groups is dependent in large part on the electrostatic interaction with its counterion and its solvation shell. This has certainly been shown to be true for the sulfonate head group of reverse micelles (45, 46).

Described below are studies investigating the spectroscopy of the charged sulfonate head group region and surrounding water molecules of Na:AOT, K:AOT, and Mg:AOT at the reverse nanoemulsion and planar interfaces. The counterions were exchanged using previously published methods (47), with the surfactants and counterion identities verified using ¹H NMR and ²³Na NMR. Reverse nanoemulsions were made by dissolving enough M:AOT (M = Na⁺, K⁺, and Mg²⁺) in CCl₄ to create a 1 mM AOT concentration and sonicated with a 1% aqueous phase. Under the same sonication conditions DLS measurements showed that nanodroplet diameters were dependent on the counterion identity, with sizes of 210, 320, and 590 nm for Na⁺, K⁺, and Mg²⁺, respectively. Previous studies indicate that Mg²⁺ has a higher degree of water association with ratios of water molecules/counterion found to be 0.002, 0.6, and 2.7 for Na⁺, K⁺, and Mg²⁺, respectively. The ¹H NMR showed this water association with the ion is also present for Mg:AOT in microemulsions (48).

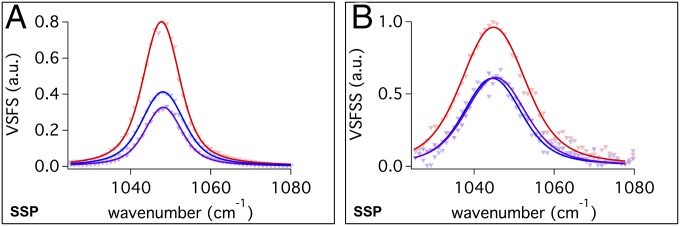
Fig. 4 compares the SSP vibrational spectra of the symmetric stretch of the sulphonate mode of M:AOT/CCl₄–D₂O mixtures for the (A) planar interface and (B) reverse nanoemulsions. The strong sulfonate signal found for all systems indicates that the dipole moment of the sulfonate group of AOT has a high degree of orientation perpendicular to the interface with frequencies of 1,048 cm⁻¹ and 1,045 cm⁻¹ for the planar and reverse nanoemulsion interfaces, respectively. This peak is assigned to the symmetric stretch of a highly hydrated sulfonate group, consistent with previous IR and Raman studies of AOT that place the peak at 1,045 cm⁻¹ and 1,048 cm⁻¹, respectively (46). The small differences measured here in frequency and bandwidth are within experimental uncertainty and difference in laser resolution for the planar and nanoemulsion systems (49). The absence of any peak broadening or spectral shifts found here between the monoatomic and diatomic cations indicates that the hydration of the AOT head groups is similar between counterion samples and interfacial geometries (45).

Fig. 4.

VSF SSP spectra of the S–O symmetric stretch of Na:AOT (blue), K:AOT (purple), and Mg:AOT (red) at the (A) planar isooctane/D₂O interface and the (B) CCl₄/D₂O reverse nanoemulsion interface.

For both the planar and the reverse nanoparticle surfaces, Mg:AOT has a higher intensity than Na:AOT and K:AOT. Two factors could contribute to this response: a higher surface concentration of Mg:AOT relative to the other ion complexes and/or a stronger net surface orientation. Looking at surface tension data for similar bulk concentrations, the maximum surface excess for Mg:AOT is 1.59 × 10⁻¹⁰ mol/cm², ∼15% more than what is found for either Na:AOT and K:AOT that have very similar surface excesses. This larger surface concentration is in the range of the observed increase in the VSF signal of the sulfonate mode when the nonlinearity in the response is taken into account. A larger droplet surface concentration for the Mg:AOT nanoparticles is likely contributing to the observed larger nanoparticle size relative to the other two cations. What is quite striking in these studies is that whereas the hydrophobic chains show sensitivity to planar versus the nanodroplet assembly, the most polar portion of the molecule does not.

Interfacial Water Orientation and Bonding

Further understanding of interfacial water molecules in the presence of AOT and different counterions can be gleaned from studies of the O–H stretch modes of water in the 3-μm region as has been done for many other surfactants (18, 19, 50). Changing the counterion associated with AOT has been shown to have an effect on water bonding in the interior of the micelle (48, 51).

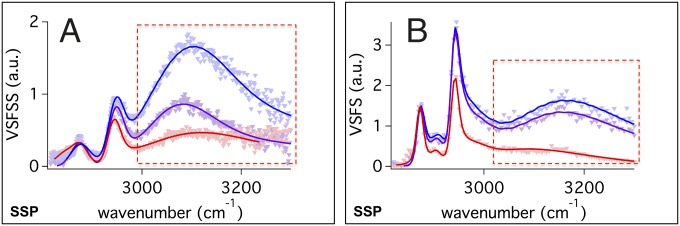
Shown in Fig. 5A is the VSF O–H stretch region for AOT at the reverse nanoemulsion interface with different counterions. The comparable data for the planar interface (Fig. 5B) show very similar spectral features and trends. The spectral region corresponding to the O–H modes is highlighted. Water at the interface is clearly oriented as seen by the strong and broad O–H stretching modes of highly coordinated water that appear from ∼3,000 to 3,400 cm⁻¹. This is apparent for both the droplet and planar interface. The C–H modes are also observed in all spectra and have similar intensities and frequencies once fitting routines are applied to remove the O–H contributions. Further exploration of the C–H modes from AOT at the reverse nanoemulsion and planar oil–water surface that use D₂O as the solvent to minimize O–H and C–H stretch spectral interferences show no significant difference in C–H frequency, intensity, or I_d+/I_r ratio as the counterion is changed (Fig. S3).

Fig. 5.

VSF SSP spectra of the C–H and O–H stretch modes for Na:AOT (blue), K:AOT (purple), and Mg:AOT (red) at the (A) CCl₄–H₂O at the reverse nanoemulsion interface and (B) the planar interface. The O–H stretch modes of highly coordinated water are highlighted in the red box.

Fig. S3.

VSFSS SSP spectra of the C-H stretching region for Na:AOT (blue), K:AOT (purple), and Mg:AOT (red) at the reverse CCl₄–D₂O nanoemulsion droplet interface. Spectra have been vertically offset for clarity.

Interfacial water contributions are from oriented water solvating AOT and its counterion but also from water oriented by the electric field created by charge separation at the interface. In fact, because of the larger volume of water oriented by this field relative to the water molecules directly solvating AOT, the majority of water signal in the 3,000–3,400 cm⁻¹ region is highly coordinated water that is oriented by the interfacial field created by the AOT charged head group. Both the planar and nanodroplet interfaces indicate the lowest degree of field-oriented water for Mg:AOT and the most for Na:AOT.

The overall picture obtained from AOT at the surface of a reverse nanoemulsion and also the planar interface is that the dipole moments of the hydrated sulfonate head group and neighboring water molecules in the interfacial region are highly oriented perpendicular to the surface (Fig. 6). The surface concentration and possibly the degree of sulfonate alignment varies for different AOT counterions studied and follows the trend of Mg:AOT > K:AOT ∼ Na:AOT, mirroring the size of the solvation spheres and counterion proximity. The interfacial water orientation follows the opposite trend with the highest degree of water orientation found for the less hydrated Na⁺ ion and a significantly reduced water alignment found when the highly hydrated Mg²⁺ ion complexes at the surface with AOT. Previous ¹H NMR studies show that the Mg²⁺ counterion is more tightly coordinated to the sulphonate head group followed by K⁺ and Na⁺ (45). We attribute this difference in water orientation to the higher degree of charge screening of the sulfonate head group that results in a reduction of the field that orients interfacial water molecules and reduces the VSF response. Even with this difference in water orientation, no significant difference is observed in the frequency or bandwidth of the sulfonate as the counterion is changed, indicative of similar levels of head group hydration.

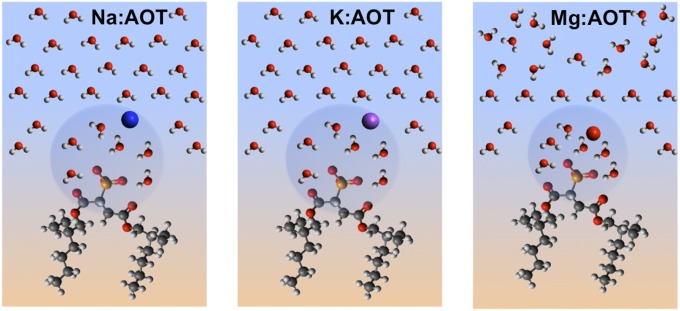
Fig. 6.

Illustration of Na:AOT, K:AOT, and Mg:AOT at the reverse emulsion surface.

Further comparison of the differences in the magnitude of the O–H intensities relative to the C–H stretches in the planar versus the nanoemulsion studies suggests that the water for the nanoemulsion surface is somewhat more tightly coordinated/oriented than at the planar interface. However, from our past experience with many charged surfactants at planar oil–water interfaces, this difference is well within the realm of experimental uncertainty due to small differences in AOT surface concentration for the nanoparticle versus planar interface. For example, the somewhat larger water intensity for the M:AOT systems could be indicative of a slightly higher AOT surface concentration (and hence higher field effects) at the nanodrop versus the planar interface under the conditions of identical M:AOT bulk concentrations.

Summary

The growing use of nanoemulsions in a variety of applications makes understanding the molecular characteristics of surfactants contributing to their stabilization of high importance. This study examines the bonding and ordering of the prevalent surfactant AOT at the surface of both reverse and regular nanoemulsions and compares these characteristics with AOT at a planar oil–water interface. Although many insightful studies have been conducted with AOT on micellar systems, this study examines its behavior for larger nanoemulsions surfaces with the unique sensitivity to surface molecular structure and orientation that the recently developed VSFSS provides.

Comparative VSFS and VSFSS spectra of the branched hydrophobic chains of AOT at the planar, reverse, and regular nanoemulsion interfaces provide interesting and important insights. The C–H spectroscopy and degree of the alkyl chain ordering of AOT for both types of nanoemulsions are nearly identical even though regular emulsions have chains pointing inward, whereas reverse emulsions have them pointed outward. This result indicates that the AOT chains have minimal interaction with each other or the two different organic solvents that could potentially cause them to adopt different conformations whether pointing internally or externally. Further evidence for this comes from the planar concentration studies that show that even as the surface population of AOT goes from very low to very high surfactant congestion, and within the region of our estimated nanoparticle AOT surface concentration, there is essentially no change in the alkyl ordering. Clearly, the bulky nature of AOT and the relatively large head group area does not allow for hydrophobic chain–chain interactions that are seen in many simpler charged alkyl chain surfactants that become more ordered with increasing surface concentration (28). This lack of chain–chain interaction is also apparent in the Ostwald ripening studies that show that as nanodroplets vary in curvature from diameters of 200 to 650 nm, no variation in alkyl chain ordering is observed. Such is also the case when the substitution of different counterions alters the size of the nanoparticle. Surfactant congestion with decreased size and increased curvature does not result for AOT in the kind of neighboring hydrophobic interactions one might expect when considering smaller droplets in the micellar range or single chain surfactants.

What then is responsible for the different alkyl ordering found for the planar and spherical surfaces? That the degree of alkyl chain disorder found for the nanoparticles cannot be reproduced in the planar studies at comparable droplet surface concentrations eliminates surface concentration as a major cause and also, as discussed above, eliminates the surface curvature. It is more likely due to the different surface orientational geometries and possible surface energetics inherent to the nanodroplet system. Hydrophobic alkyl chains, their lengths, and their interactions with neighboring organic solvents can play a significant role in the stabilization of emulsions as shown in recent studies that indicate their importance in the formation of different shapes and sizes of nanoemulsions (43, 44).

The polar and charged sulfonate head group portion of AOT displays a high degree of solvation and net dipole orientation perpendicular to the interface in both reverse nanoemulsion and planar interfaces. The stronger sulfonate spectral signal found for Mg:AOT compared with K:AOT and Na:AOT nanodroplets is attributed primarily to a higher surface concentration that is enabled by higher charge screening caused by the more tightly bound magnesium ion. It is likely that this higher surface concentration and charge screening are responsible for the larger size of the Mg:AOT nanoparticles relative to K:AOT and Na:AOT. The size variation with counterion is fairly well understood for micelles, but it is largely unknown for nanoparticles of this size.

Interfacial water at the reverse nanoparticle surface can be characterized as strongly hydrogen bonding to neighboring water molecules and highly oriented with their dipoles perpendicular to the interface. The similarity in the water spectra and intensity trends for the oil–water planar and nanoemulsion interfaces in the presence of the three different M:AOT surfactants are indicative of very similar water bonding and orientation for both large curved and planar interfaces. In all cases, the VSF water signal is dominated the highly oriented and strongly bonded water molecules within the double layer region that is created by the interfacial charge separation of the sulfonate head group and counterion. There is no evidence of the type of confinement effects that are prevalent in the much smaller reverse micelles where the ratio of water molecules to surfactant molecule is less than ∼10 compared (13) to greater than 1,000 in these studies.

Given the growing use of nanoemulsions in the energy, food, health, and technology sectors, understanding the factors that contribute to nanoemulsion formation and stabilization as thoroughly as has been achieved for smaller micellar systems is very important. This report provides insights into some of the key interfacial molecular details for understanding and utilizing surfactant stabilized nanodroplets used in a variety of applications.

Sample Preparation

All glassware used was rigorously cleaned by soaking in H₂SO₄ (98%) and NOCHROMIX (Godax Labs, Inc.) oxidizer for a minimum of 12 h and then rinsed with Nano pure H₂O (18.2 MΩ resistivity). All carbon tetrachloride (CCl₄) (HPLC grade, ≥99.9%), used was purchased from Sigma-Aldrich and doubly distilled. Hexadecane-d₃₄ (98.6 atom % D) was purchased from CDN Isotopes and used without further modification. Dioctyl sodium sulfosuccinate (AOT) (≥99%) was purchased from Sigma-Aldrich and used without further modifications. AOT was stored in a dry vacuum chamber to minimize water absorption.

Interfacial Tension Measurements and Particle Surface Coverage

Interfacial tension measurements were performed using the drop shape analysis technique with a pendant drop tensiometer (KSV). Droplets of aqueous surfactant solution were suspended from the tip of a Hamilton Gastight syringe in a cuvette filled with ∼5 mL of CCl₄. Interfacial tension was measured by recording photographs of the droplets every 10 s until the interfacial tension remained constant. Instrumental software fit the droplet shape using the Laplace–Young equation to determine the surface tension.

The interfacial pressure, π, is the difference between the interfacial tensions, γ, of the neat oil–H₂O interface and AOT at the oil–H₂O interface. Interfacial pressures of the CCl₄–H₂O and hexadecane–H₂O interfaces are plotted as a function of bulk AOT concentration, as shown in Fig. S1A. The Gibbs adsorption isotherm equation can be used to correlate the interfacial pressure with the bulk surfactant concentration to determine the maximum surface excess (Γ) and the interfacial area of the surfactant head group at equilibrium (34). The maximum surface excess can be determined from Eq. S1 using the slope of the linear fit of the plot of the interfacial pressure vs. natural logarithm of bulk concentration shown in Fig. S1B.

$$\mathrm{\Gamma }=\frac{-1}{n_{i}RT}{\left(\frac{\partial \mathrm{\Pi }}{\partial \log \left[C_i\right]}\right)}_T.$$ [S1]

For our experiments, n = 2 to account for the counterion species, and room temperature was measured at 295 K. The maximum surface excess, Γ, was found to be 1.3 × 10⁻¹⁰ (±0.1 × 10⁻¹⁰) and 1.1 × 10⁻¹⁰ (±0.1 × 10⁻¹⁰) mol/cm² for the CCl₄–H₂O and hexadecane–H₂O interfaces, respectively. The inverse of Γ was used to calculate the head group area per surfactant molecule, a_s, using Eq. S2, where Γ is in units of mol/cm².

$$a_s=\frac{{10}^{16}}{N_A\mathrm{\Gamma }}.$$ [S2]

We determined the head group area per AOT molecule to be 131 (±20) and 151 (±23) Ų per molecule for the CCl₄–H₂O and hexadecane–H₂O interfaces, respectively.

Similar experiments were run for K:AOT and Mg:AOT at the CCl₄–D₂O interface. Maximum surface excess was determined to be 1.3 × 10⁻¹⁰ (±0.1 × 10⁻¹⁰) and 1.5 × 10⁻¹⁰ (±0.1 × 10⁻¹⁰) mol/cm².

To ensure that our reverse and regular nanoemulsion systems were under similar conditions, we performed our VSFSS experiments at bulk solution concentrations above that which gives full surface coverage. To calculate the bulk concentration necessary, Eq. S3 was used (6),

$$C_{\text{surf}}=\frac{3\rho \varphi }{r{N}_A},$$ [S3]

where ρ is the surfactant density on the particle (1/ a_S), ϕ is the volume fraction of our nanoemulsions, r is the radius of the nanoemulsion, and N_A is Avogadro’s number. From our interfacial tension and dynamic light scattering (DLS) measurements we determine ρ and r, respectively, with all nanoemulsion samples having a volume fraction of 0.01 for the dispersed phase. For nanoemulsions in this work, full surface coverage occurs at bulk AOT concentrations of 0.4 and 0.3 mM for Na:AOT reverse and regular nanoemulsions, respectively.

VSFS Laser System

Vibrational sum-frequency spectroscopy (VSFS) experiments at the planar oil–water interface have been conducted extensively with experimental details described previously (18–21). VSFS experiments were done with a fixed 532-nm visible (VIS) beam and a tunable infrared (IR) beam (2,300–10,000 nm). The incoming beams were incident on the sample cell and approached the interface from a bottom-up configuration in a total internal reflection (TIR) geometry with incoming angles set to 66° and 75° (with respect to surface normal) for the VIS and IR beams, respectively. The laser system (Nd:YAG; Ekspla) outputs a fundamental frequency (1,064 nm light, 30 ps) that passes through a beam splitter with one portion frequency doubled (532 nm). A portion of the 532-nm beam is sent to the interface, whereas the remaining 532-nm beam is combined with the 1,064-nm fundamental beam to generate a tunable IR in an optical parametric generation (OPG)/optical parametric amplifier (OPA)/difference frequency generation (DFG) setup. The VSFS signal is detected with a monochromator and photo multiplier tube. The spectral resolution of the laser experiment is 2 cm⁻¹ and is determined by the laser pulse width. The planar data presented is an average of at least 300 laser shots per data point and normalized to gold.

VSFSS Laser System

The VSFSS experimental setup and theoretical background has been described previously by Roke et al. (23, 24, 26, 52). The laser (Libra Ti:sapphire regenerative amplifier; Coherent) outputs a fundamental 800-nm beam at 1 kHz frequency and sub-100 femtosecond pulse widths. Using a beam splitter, a portion of the beam is used for the VIS line of the experiment, and the other portion is used to generate a broadband IR pulse by DFG in an OPA (Light conversion OPERA-SOLO 2). The sample cell was composed of a CaF₂ entrance window and a quartz cuvette backing (Helma QS) with an optical path length of 200 μm. The IR beam was focused down with a 90° parabolic Au mirror [focal length (FL) ∼50 mm] to a spot size of ∼80 μm and the VIS beam’s focus was located after the sample cell with a spot size of ∼500 μm in the sample. The signal was collected at a scattering angle of ∼60° (with respect to the forward direction, ${\stackrel{\rightharpoonup }{k}}_{12}$) and collimated with a plano-convex lens (FL ∼20 mm) and then directed to a focusing lens (FL ∼100 mm) before a spectrometer (Isoplane; Princeton Instruments) and an intensified CCD (PIMAX 4; Princeton Instruments). The forward scattering direction (${\stackrel{\rightharpoonup }{k}}_{12})$ was determined by viewing the sum frequency generation of a MgO:LN crystal (P/N MLN5100-SFG(I)-UC) transmitted through the crystal. An incoming etalon-shaped VIS (800 nm, 25 μJ) beam is overlapped in time and space with a broadband IR beam (7–10 μJ) in a sample cell containing AOT emulsions, with the two beams separated by a 25° angle. The spectra were averaged over three 20-min exposures and normalized with a GaAs wafer.

Sum-Frequency Theory

The minimum necessary VSF theory will be discussed below, but a much more extensive theoretical background has been described elsewhere (16, 30, 52–55). The intensity of the VSF signal is proportional to the intensity of the VIS and IR beams and the absolute square of the second order susceptibility [χ⁽²⁾], which has both nonresonant [${\chi }_{NR}^{\left(2\right)}$] and resonant [${\chi }_R^{\left(2\right)}$] components.

$$I\left({\omega }_{SF}\right)\mathrm{\propto }{\left|{\mathit{\chi }}_{NR}^{\left(2\right)}+{\displaystyle \sum _i{\mathit{\chi }}_{R,i}^{\left(\mathrm{2}\right)}}\right|}^{2}I\left({\omega }_{\text{IR}}\right)I\left({\omega }_{\text{vis}}\right).$$ [S4]

The resonant component contains the molecular specificity, which is dependent on the number of interfacial molecular species, N, and their net average orientation, β.

$${\chi }_R^{\left(2\right)}\propto \frac{N}{{\mathit{ϵ}}_O}<\beta >.$$ [S5]

The vibrational sum frequency spectrum is fit to a convolution of a Gaussian and a Lorentzian summed over all sum frequency vibrational modes and a nonresonant contribution to obtain peak frequencies (ω_ν), linewidths (Γ_ν), and vibrational transition strengths (A_ν). The following equation describes the fitting routine used for all spectra in this paper:

$${\chi }_v^{\left(2\right)}\propto A_{NR}{e}^{i\psi }+{\displaystyle \sum _v}{{\displaystyle \int }}^{}\frac{A_v{e}^{i{\phi }_v}{e}^{-{\left[\left({\omega }_L-{\omega }_v\right)/{\mathrm{\Gamma }}_v^2\right]}^2}}{{\omega }_L-{\omega }_{\text{IR}}+i{\mathrm{\Gamma }}_L}d{\omega }_L.$$ [S6]

The first term represents the nonresonant susceptibility with an associated amplitude (A_NR) and phase (ψ). The second term contains frequency terms (ω_IR and ω_L) from the laser and the Lorentzian, respectively, and the homogenous and inhomogenous broadening (Γ_L and Γ_ν).

VSFSS theory has been formulated for spherical particles (22, 26, 52), and we only discuss the minimum theory below. The VSFSS spectrum detected at an angle (θ) can be described by the following equation, which is analogous to Eq. S4:

$$I_{\text{VSFSS}}\left(\theta ,R,\omega \right)\propto \frac{k_0^4}{r_0^2}{\left|{\mathrm{\Gamma }}^{\left(2\right)}\left(\theta ,R,\omega \right)\right|}^{2}I\left({\omega }_{\text{IR}}\right)I\left({\omega }_{\text{vis}}\right).$$ [S7]

The intensity is dependent on the scattering wave vector ($k_0$), the distance between the particle and the detector ($r_0$), the IR and VIS local laser intensities [$I\left({\omega }_{\text{IR}}\right)\hspace{0.17em}\text{and}\hspace{0.17em}I\left({\omega }_{\text{VIS}}\right)$], and the particle susceptibility [${\mathrm{\Gamma }}^{\left(2\right)}\left(\theta ,R,\omega \right)$]. A complete description of the second-order particle susceptibility will not be discussed here, but given its dependence on the second-order molecular susceptibility of surface species it is described in Eq. S8, which is analogous to Eq. S5:

$${\mathrm{\Gamma }}^{\left(2\right)}={\mathrm{\Gamma }}_{NR}^{\left(2\right)}+{\displaystyle \sum _{\upsilon }}\frac{A_{\upsilon }\left(\theta \right)}{{\omega }_{\text{IR}}-{\omega }_{\upsilon }+i{\gamma }_{\upsilon }},$$ [S8]

where it can be shown to be dependent on a nonresonant [${\mathrm{\Gamma }}_{NR}^{\left(2\right)}$] and resonant [${\mathrm{\Gamma }}_{\upsilon }^{\left(2\right)}$] contribution. Both the nonresonant and resonant amplitudes are dependent on the scattering angle (23).

Growth of Reverse Nanoemulsions

Reverse nanoemulsions were created on day 1 by ultrasonicating 1.0 mM Na:AOT with 1% D₂O. DLS measurements on the reverse nanoemulsions give average diameters of 200, 584, 595, and 643 nm, from day 1 through day 4, respectively. VSFSS measurements on these nanoemulsions in the C–H stretching region (Fig. S2) were fit to four peaks with known vibrational frequencies. Over all 4 days, contributions from the CH₂–SS (2,861 cm⁻¹), CH₃–SS (2,871 cm⁻¹), and methine (C–H) (2,905 cm⁻¹) vibrational modes and Fermi resonance splitting (2,937 cm⁻¹) of the CH₃–SS and bending overtone modes were measured. Changes to the relative intensities of the methylene and methyl modes were found to be negligible from day 1 through day 4. Solutions of reverse nanoemulsions were stored in capped vials kept on laboratory bench tops over the course of these measurements, with samples taken from these each day.

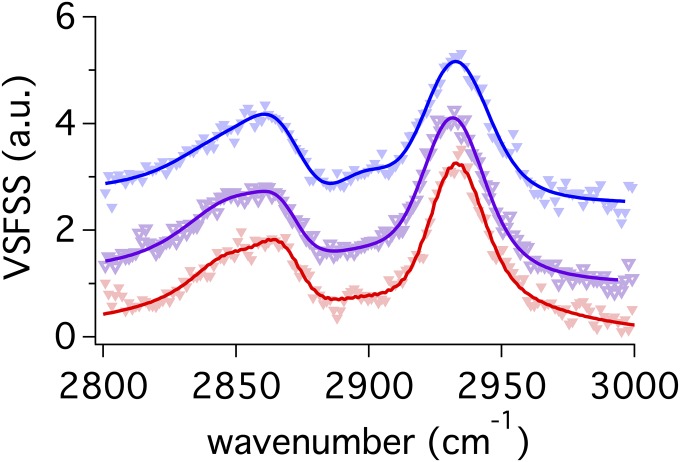
C–H Stretching Spectra for M:AOT at the Reverse Nanoemulsion Interface

VSFSS measurements of Na:AOT, K:AOT, and Mg:AOT stabilized reverse nanoemulsions were taken in the C–H stretching region (Fig. S3). These spectra were fit to peaks assigned to the CH₂–SS, CH₃–SS, and methine vibrational modes and Fermi resonance splitting of the CH₃–SS and bending overtone modes just as all other spectra in the reported work. Changes to the I_d+/I_r ratio between different counterion samples are negligible.