Relationship between season of birth, temperature exposure, and later life wellbeing

Significance

Recent work has demonstrated how exposure to extreme temperatures influences contemporaneous health outcomes, such as infant mortality and morbidity. Additional research has explored how shocks to the early-life environment affect long-run human capital outcomes. However, there is little evidence on the possible long-term consequences of exposure to extreme temperatures in utero or in early childhood. This paper begins to fill this gap by studying long-run effects of temperature on measures of individuals’ economic wellbeing around age 30 y. We find that adult economic outcomes are negatively correlated with prenatal exposure to days with mean temperatures exceeding 32 °C. This relationship is completely mitigated among individuals born in counties with high rates of access to air conditioning.

Abstract

We study how exposure to extreme temperatures in early periods of child development is related to adult economic outcomes measured 30 y later. Our analysis uses administrative earnings records for over 12 million individuals born in the United States between 1969 and 1977, linked to fine-scale, daily weather data and location and date of birth. We calculate the length of time each individual is exposed to different temperatures in utero and in early childhood, and we estimate flexible regression models that allow for nonlinearities in the relationship between temperature and long-run outcomes. We find that an extra day with mean temperatures above 32 °C in utero and in the first year after birth is associated with a 0.1% reduction in adult annual earnings at age 30. Temperature sensitivity is evident in multiple periods of early development, ranging from the first trimester of gestation to age 6–12 mo. We observe that household air-conditioning adoption, which increased dramatically over the time period studied, mitigates nearly all of the estimated temperature sensitivity.

Exposure to extreme temperatures has harmful contemporaneous effects on human health due to an overload on the body’s capacity to self-regulate (e.g., refs. 1–6). Fetuses and infants are especially sensitive to hot temperatures because their thermoregulatory and sympathetic nervous systems are not fully developed (7, 8), with prior research showing that extreme heat during the prenatal period and shortly after birth has adverse effects on birth weight and infant mortality (9, 10).

Yet much less is known about the long-run persistence of the effects of temperature or whether they influence other measures of human capital, such as adult labor market outcomes. This study attempts to fill this gap by providing evidence on the long-term consequences of early-life exposure to extreme temperatures, using data on over 12 million individuals born in the United States between 1969 and 1977 and observed 30 y later.

The possibility that temperature can have lasting effects on human development may be particularly consequential in light of the growing consensus among scientists that climate change is contributing to a gradual warming of the earth. Researchers predict an increase in global mean temperatures, largely driven by a rightward shift in the upper tail of the temperature distribution. For example, the number of days with mean temperature above 32 °C in the average county in the United States is forecasted to increase from about 1/y to about 43/y by 2070–2099 (1). As such, estimates of the long-term consequences of exposure to extreme heat on individuals’ wellbeing may serve as important inputs into calculations of the social cost of carbon (11). These estimates may also help explain whether the persistent correlation between income and temperature around the world in part operates through a causal link between early-life exposure and adult productivity (see refs. 12–19 for a broader literature on the relationship between the environment and economic development).

We also examine whether observed forms of adaptation have the ability to mitigate some of the direct biological effects of temperature on long-term economic outcomes. Adaptation to extreme temperatures could occur through physiological acclimatization (i.e., changes in skin blood flow, metabolic rate, oxygen consumption, and core temperatures) (21), short-run temporal substitution between activities (i.e., limiting time spent outside), or the adoption of more permanent measures of temperature control such as air conditioning (AC), which we study here.

Our analysis uses newly available data from the US Census Bureau’s Longitudinal Employer Household Dynamic (LEHD) Files, which contain information on adult labor market outcomes linked to county and exact date of birth. We combine these longitudinal earnings records with fine-scale daily weather data that spans the United States on a 2.5-km $\times$ 2.5-km grid. We use these data to construct the length of time an individual is exposed to different temperatures in several focal windows of early childhood development. We then estimate flexible statistical models, designed to identify nonlinearities in the long-run effect of early-life temperature exposure on adult labor market outcomes.

Early-life exposure to temperature is potentially correlated with other determinants of human capital development. For example, children born in different seasons within the year differ in their socio-economic backgrounds (22), and families nonrandomly choose to live in geographic locations with distinct climates. The empirical challenge of this paper is to isolate the causal relationship between early-life temperature exposure and adult outcomes from the possible confluence of these other factors. We address this challenge by focusing on the following thought experiment that we observe in our data many thousands of times: Consider two children of the same gender and race, born in the same county on the same day of the year but in different years. Now, suppose that one child experiences an extreme heat wave in his or her second trimester of gestation, while the other does not. Our goal is to quantify any differences in these individuals’ outcomes measured 30 y after birth.

The evidence on the pathways through which temperature influences human health suggests that our statistical models must be flexible enough to account for nonlinearities. We follow recent work, allowing the marginal effect of temperature to differ over both the temperature distribution and different periods of child development (3, 5, 9, 17, 23, 24). Our models also control for county $\times$ day of year $\times$ race $\times$ sex fixed effects (e.g., African-American males born in Harris County, TX on November 18) and year fixed effects. Thus, estimates are purged of time-invariant observed and unobserved determinants of long-run human capital formation in a given county, any seasonal determinants of fertility that may also be correlated with later-life outcomes such as compulsory schooling laws (25) and socio-economic status (22), and aggregate cohort trends.

Finally, we take advantage of the rapid increase in household AC adoption over the course of our sample period to analyze the role of adaptation. We examine whether individuals born in counties with higher levels of household AC penetration exhibit different long-term responses to extreme temperatures relative to individuals born in counties with lower rates of AC adoption. These results are useful for understanding the extent to which adaptation vis-a-vis AC adoption could mitigate the adverse effects of future climate change.

Our study relies on the identifying assumption that, holding constant the county of birth, birth day of year, race, and gender of an individual, there are no unobserved variables that are systematically correlated with both temperature exposure in early life and adult labor market outcomes. While this assumption is inherently untestable, we conduct several indirect tests. First, we check whether temperature episodes occurring before conception are correlated with later-life outcomes. Second, we analyze whether observable population characteristics such as sex and race are correlated with temperature exposure across birth county $\times$ birth day of year cells.

Results

SI Appendix, Table S1 reports some basic statistics from our analysis sample. Areas in the Northeast experience far fewer days above 32 °C than areas in the Southwest. These translate to differences in the average number of days during various critical periods of a child’s development spent in different temperature bins (SI Appendix, Table S1B). In addition, the Western states in our sample experienced some of the smallest changes in AC penetration relative to the states with hotter climates in the South.

To get a sense of the possible scale and scope of the influence of extreme temperature on human capital formation, we first examine the relationship between the conditional mean earnings at age 30 and the conditional mean temperature for a given month of birth. The conditional earnings and temperature measures come from auxiliary regressions, where the dependent variable is either earnings or temperature, and we include a set of fixed effects for birth month, a set of fixed effects for county of birth $\times$ race $\times$ sex, and a set of year fixed effects. The coefficients from the birth month fixed effects in each regression model correspond to the conditional means and are plotted in SI Appendix, Fig. S1 A and B. The R² from a regression of these conditional monthly earnings on the conditional monthly temperature is 0.25, suggesting that 25% of the conditional variation in age 30-y earnings by month of birth is explained by exposure to extreme temperatures during gestation. Of course, there may be other unobserved determinants of long-run human capital formation that covary with month of birth. We next turn to results from statistical models that attempt to address these issues while also flexibly modeling the temperature–human capital relationship.

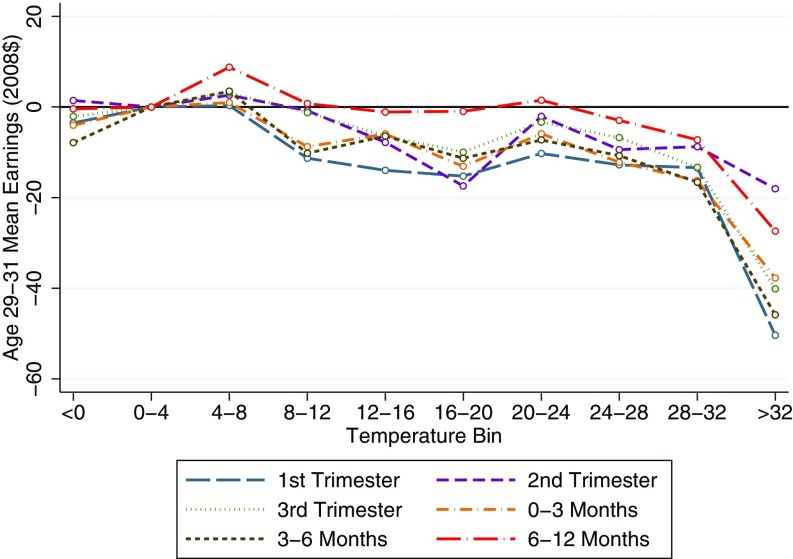
Fig. 1 plots the baseline estimates from a single regression model, relating adult earnings in dollars to temperature at different critical periods of childhood development and at different points of the temperature distribution. Each dashed line in the graph plots the coefficients corresponding to an additional day with mean temperature falling in a temperature bin during the critical period indicated in the key. For example, the dashed blue line in Fig. 1 shows the estimated effect of an extra day in the first trimester of gestation (estimated from the date of birth, as in the case of all critical periods), holding other critical periods fixed and where the coefficient on the effect of a 0 °C to 4 °C day has been normalized to 0. This regression model also controls for race $\times$ sex $\times$ birth county $\times$ birth day of year fixed effects and year fixed effects.

Fig. 1.

Heterogeneous effect of temperature on annual earnings by focal period. The regression estimates are plotted from a single version of Eq. 1. Each circle corresponds to the predicted marginal effect of a 1-d increase in average temperatures in the associated temperature bin (indicated on the x axis) on adult earnings in the critical period indicated in the key. The regression controls for birth county $\times$ day of year $\times$ race $\times$ sex fixed effects, year fixed effects, and a cubic polynomial in precipitation.

There are two key takeaways from Fig. 1. First, the effect of exposure to temperature during gestation and in the first year of life is highly nonlinear—exposure to hot days with average temperatures above 28 °C and, more strongly, above 32 °C has disproportionately large negative effects on adult earnings. Second, the effect across different critical periods between conception and age 1 y is fairly homogeneous, and the negative effect of exposure to temperature above 32 °C on earnings exists in nearly all of the early-life stages we consider. We cannot reject the null hypothesis that the effect of a day with mean temperatures above 32 °C in the first trimester is significantly different from the effect of a day with mean temperatures above 32 °C in the third trimester. (In SI Appendix, Table S5, we find that the effect of exposure to hot temperatures dissipates after around age 1 y.)

Fig. 1 suggests the marginal effect of temperature is constant across the temperature range 0–24 °C. Thus, we estimate more parsimonious models that impose a constant effect over this range to reduce the number of coefficients to be estimated. Table 1 presents results from a specification that aggregates exposure into five temperature bins ($<0°$C, 0–24 °C, 24–28 °C, 28–32 °C, 32$+$ °C), with the 0–24 °C temperature bin normalized to be equal to zero in each critical period. The estimates of the coefficients on exposure to high daily temperatures (i.e., 28–32 °C and 32+ °C) in Table 1 are very similar to those in the baseline nine-bin model.

Table 1.

Effects of temperature over different critical periods on ages 29–31 y annual earnings

Period of exposure	No. days $<$0 °C	No. days 24–28 °C	No. days 28–32 °C	No. days 32+ °C
1st trimester	−6.890	2.772	−8.329*	−55.735***
	(5.112)	(2.948)	(4.668)	(15.425)
2nd trimester	−8.063	−2.220	−4.153	−16.477
	(5.002)	(2.560)	(5.600)	(23.485)
3rd trimester	−10.997*	−4.627	−6.513	−41.789**
	(5.839)	(3.260)	(7.083)	(16.420)
0–3 mo	−10.857**	−6.188**	−4.059	−38.526***
	(4.991)	(2.968)	(6.483)	(12.875)
3–6 mo	−11.097***	−4.169	−6.599	−51.553***
	(4.152)	(2.964)	(6.672)	(12.993)
6–12 mo	−9.332***	−4.379*	3.550	3.279
	(3.041)	(2.553)	(4.329)	(15.844)

Shown are regression coefficients from a version of Eq. 1. Robust standard errors, clustered by state, are in parentheses. All regressions control for birth county × day of year × race × sex fixed effects, year fixed effects, and a cubic polynomial in precipitation. ***P < 0:01, **P < 0:05, *P < 0:1.

The average estimate across all critical periods suggests than an extra day of exposure to temperatures above 32 °C in utero or in the first year of life is associated with around $30 (in 2008 dollars) lower average annual earnings at ages 29–31 y, which translates to a 0.1% effect size when evaluated at the sample mean. This effect size is larger than what would be implied from a back-of-the-envelope calculation that combines prior estimates on the impacts of in utero exposure to temperature on birth weight (9) and the relationship between birth weight and adult earnings from studies of twins (26). There are at least three reasons for this discrepancy. First, our estimates are consistent with the idea that the impacts of early-life shocks operate through channels other than birth weight, which is an imperfect proxy for fetal health (see a recent overview by ref. 27). Second, prior estimates of the effects of temperature on birth weight may be significantly understated, as they come from studies that consider more recent cohorts relative to the ones considered here. Since AC adoption has increased over time, and we show below that AC adoption offsets nearly all of the effects of hot temperatures, it is likely that the relationship between temperature and birth weight is substantially larger for the older cohorts that we study. Third, twin studies of the relationship between birth weight and adult outcomes may generate estimates that are downward biased because of possible compensatory investments by parents (28).

To interpret the magnitude of this effect, we calculate the lifetime earnings impact implied by our estimates. We assume that the percentage loss in earnings remains constant at 0.1% over the life cycle and that earnings are discounted at a 3% real rate (i.e., a 5% discount rate with 2% wage growth) back to age zero, following similar assumptions in other studies of long-run effects (e.g., refs. 29 and 30). Under these assumptions, the mean present value of lifetime earnings at age zero in the US population is ∼$434,000. We calculate this number using the mean wage earnings from the March 2008 Current Population Survey to obtain an earnings profile over the life cycle. Thus, the financial loss associated with being exposed to an additional day with temperature above 32 °C during gestation or in the first year of life is 0.1% of $434,000 or $430 per person. While today, the average person is exposed to about one such hot day per year, this number is expected to increase substantially in the next several decades (1).

We next examine the potential for adaptation to mitigate these negative effects. During the time period that we study, the United States underwent a rapid expansion in the prevalence of in-home AC. In 1960, only about 10% of households had AC in their homes. By 1980, 50% did. AC adoption also varied significantly across counties. We use county-level data on household AC adoption from the 1960, 1970, and 1980 decennial censuses to examine the extent to which AC mitigates the observed effects of extreme temperature. Formally, we augment our main regression model to include an interaction between each of the 24 temperature bins of interest (i.e., 6 critical periods and 4 temperature bins) and the share of households in a county that have AC.

Table 2 presents results from a single regression where each column indexes a particular temperature bin and each row indexes a particular focal period. Focusing on the estimates in Table 2, No. days 32+ °C, the baseline coefficients in column 2 of the table deliver the estimated effect of an extra day of mean temperatures above 32 °C for a county with 0% of households having AC. These estimates are larger than the corresponding estimates in Table 1, consistent with AC adoption being a critical determinant of treatment effect heterogeneity. The corresponding interaction terms in column 4 of Table 2 deliver estimates for a hypothetical county with 100% household AC penetration. Our results suggest that moving from 0% to 100% household AC adoption would completely mitigate any adverse effects of exposure to extreme heat. Taken literally, the magnitudes of the coefficients on the interaction terms in Table 2 suggest that exposure to extremely hot days in a hypothetical county with 100% AC adoption would have a net positive impact on adult earnings. However, confidence intervals imply that we cannot reject the net effect of temperature in a county with 100% AC adoption is zero.

Table 2.

Does the marginal effect of temperature on ages 29–31 y earnings vary with household AC adoption?

Period of exposure	No. days 28–32 °C	No. days 32+ °C	No. days 28–32 °C $\times$ AC	No. days 32+ °C $\times$ AC
1st trimester	−16.068	−12.487	31.943	−32.310
	(14.394)	(26.158)	(19.755)	(44.021)
2nd trimester	−20.692	−4.327	40.700	38.610
	(19.206)	(31.092)	(28.876)	(43.899)
3rd trimester	−25.498*	−79.162**	44.099*	125.243***
	(14.997)	(33.335)	(22.986)	(45.819)
0–3 mo	−44.819***	−56.221	68.943***	83.872
	(10.977)	(66.257)	(14.784)	(97.185)
3–6 mo	−37.815**	−78.937***	63.751***	121.596***
	(17.986)	(29.924)	(23.928)	(43.462)
6–12 mo	−32.894***	−132.973*	49.441***	181.783**
	(9.655)	(77.951)	(12.874)	(89.822)

Shown are regression coefficients from a version of Eq. 2. The regression augments Eq. 1 by including an additional set of temperature response coefficients, now interacted with the fraction of households in a county that have household AC. Robust standard errors, clustered by state, are in parentheses. All regressions control for birth county × day of year × race × sex fixed effects, year fixed effects, and a cubic polynomial in precipitation. ***P < 0:01, **P < 0:05, *P < 0:1.

Discussion

Our results point to a strong nonlinear relationship between temperature exposure during the fetal period and in the first year of life and adult outcomes measured 30 y later. Exposure to extreme heat in these critical periods of human development has lasting adverse effects on adult earnings, and this relationship is very responsive to adaptive behavior (i.e., AC).

Our results are robust to different control variables (including air pollution) and model specifications (SI Appendix, Tables S3 and S9). We have also explored the effects of temperature exposure throughout the earnings distribution (SI Appendix, Table S4). The estimates suggest that the number of days with average temperatures exceeding 32 °C during gestation is correlated with an increase in the likelihood of being in the bottom half of the earnings distribution and a decrease in the likelihood of being in the top half of the earnings distribution.

Further, we explore the sensitivity of our results to measuring exposure at older ages (through age 3 y) as well as measuring earnings at different follow-up ages (ages 28–32 y) (SI Appendix, Tables S5 and S6). With regard to differences in effects across ages at exposure, we find that the effect of hot temperatures dissipates after around age 1 y. With regard to differences across ages at follow-up, we find that, at each age, the results are qualitatively consistent with the baseline results from before; a day with mean temperature exceeding 32 °C predicts reductions in earnings at all of the ages we consider. While there is some heterogeneity across age categories, the confidence intervals overlap. These results reflect the fact that earnings are highly correlated across ages, but they also provide evidence that (i) earnings responses are found at more than one (somewhat arbitrary) age category, and (ii) our results are not confounded by some contemporaneous change in earnings determinants in later years. As evidence of the latter point, consider that columns 1–5 in SI Appendix, Table S6 are estimated using the same individuals, but the earnings are collected at different years [i.e., cohorts born in 1970 show up between 1998 (column 1) and 2002 (column 5)]. Our preferred earnings measure in SI Appendix, Table S6, column 6 serves as a type of “summary index” over the various age categories while also reducing the residual variance in annual earnings. The constant effects over different ages are similar to the findings in ref. 31, which show that early-life exposure to air pollution has a constant and lasting effect on labor market outcomes between the ages of 28 y and 32 y.

There is growing evidence suggesting that seasonal variation in birth outcomes may be correlated with demographic characteristics (22, 32–35). If certain populations give birth in periods of very warm temperatures, and those groups are more economically disadvantaged for reasons unrelated to temperature, then we could falsely attribute temperature variation to this omitted variable. We have attempted to control for this differential seasonality by including race $\times$ sex $\times$ birth county $\times$ birth day of year fixed effects. Nevertheless, SI Appendix, Table S8 explores how differential fertility that is correlated with extreme temperatures may lead to biases in models with a less restrictive set of controls. The outcome measure is an index of observable population characteristics (SI Appendix, Table S8, table notes), and the model controls for birth county$\times$ birth day of year fixed effects (as opposed to our baseline race $\times$ sex$\times$ birth county $\times$ birth day of year fixed effects) to ask whether there is a relationship between observable characteristics of the population and the temperature variation in our data. The results provide little evidence that more disadvantaged populations (indicated by a lower index measure) disproportionately experience high temperature anomalies during gestation. Nonetheless, following prior literature and because differential fertility that covaries with the observed, conditional temperature variation may still be an important source of bias, we control for race $\times$ sex $\times$ birth county $\times$ birth day of year fixed effects in all of our other regression models.

One additional concern for our statistical model is that our temperature variation is picking up some unobserved, differential, time-varying shocks across counties. To investigate this concern, we estimate models in which we include leads in temperature data for the same county–day 2 y before birth (SI Appendix, Table S7). In other words, for each individual, we calculate the hypothetical exposure to temperature in each critical period had he or she been born 2 y before his or her actual date of birth. We choose a 2-y lead to avoid confounding our estimates with any possible conception/fertility effects of temperature (10, 33, 35). Our leads should thus be uncorrelated with the actual treatment effect of exposure during gestation or in the first year of life. SI Appendix, Table S7 presents results from a single regression, where column 1a shows the lead coefficients, while column 1b shows the coefficients on exposure by trimester and through age 12 mo. For parsimony, we report only coefficients on the 32 °C temperature bin. We are not able to reject the null hypothesis from an F test that the temperature coefficients other than 32 °C are equal to zero. We find that exposure to extreme heat 2 y before birth is uncorrelated with age 30 y earnings, while the coefficients on actual early-life exposure to hot temperature remain negative, larger in absolute magnitude, and mostly statistically significant.

Finally, the results in Table 2 suggest that county-level household AC penetration mitigates nearly all of the observed long-run effect of extremely hot temperature. One concern when interpreting these results is that household AC adoption may be correlated with other unobservable determinants of later-life wellbeing, such as income. We investigate this hypothesis in two ways. First, we estimate whether county-level changes in household AC adoption are correlated with other observed changes in that county that may predict later-life outcomes (e.g., per-capita income and population size), using data from the Bureau of Economic Analysis local area employment statistics file (SI Appendix, Table S10). In SI Appendix, Table S10, column 1, we regress the change in the fraction of households in a county that have AC between 1970 and 1980 on the log change in per-capita income over the same time period. We repeat this exercise using instead the log difference in population growth between 1970 and 1980 as the explanatory variable in SI Appendix, Table S10, column 2. Finally, SI Appendix, Table S10, column 3 includes both the log change in population and the log change in per-capita income jointly in the regression model. In all three specifications, we observe little relationship between within-county changes in per-capita income, changes in population, and changes in household AC adoption.

The second way in which we test the robustness of our AC analysis is by using state-level AC penetration, which is likely to be more exogenous (conditional on our baseline controls) than county-level AC adoption (SI Appendix, Table S11). Results remain very similar to those before.

Materials and Methods

We use a newly available data resource that allows us to observe both the county and exact date of birth for 12 million individuals as well as their longitudinal earnings history 30 y later. We combine these data with fine-scaled, daily weather measures on a 2.5 $\times$ 2.5-mile grid for the entire United States.

LEHD Files.

The main data source for this analysis comes from the US Census Bureau’s LEHD Files. (These are restricted-use data that are available to researchers with approved projects through the Federal Statistical Census Research Data Centers. Interested researchers may apply for these data by following the instructions provided by the US Census Bureau at https://www.census.gov/ces/rdcresearch/howtoapply.html.) These files consist of quarterly administrative earnings records for approximately 98% of the US workforce (36, 37). For each worker, these data contain information on race, sex, place of birth, and date of birth, as well as a detailed longitudinal earnings history. (Race and place of birth information comes from the Social Security Administration’s numident file which the Census Bureau has merged to their own internal LEHD files. We aggregate the race codes in the numident file to three different race codes corresponding to White/Caucasian, African-American, and Other.) The place of birth variable in the LEHD is a string variable detailing in most cases the city and state of birth (e.g., “Los Angeles, California”). We developed a matching algorithm to create a crosswalk between this variable and county Federal Information Processing Standards codes (see ref. 31 for more details on the matching algorithm).

As the main outcomes in our analysis, we study mean earnings and the mean number of quarters used between the ages of 29 y and 31 y. We focus on these ages since the correlation between annual earnings and lifetime income rises rapidly as individuals enter the labor market and begins to stabilize only in their late 20s (38, 39). To calculate the average annual number of quarters used and the average annual earnings of an individual between the ages of 29 y and 31 y, we use the following procedure: For each individual in our sample, we calculate the years when he or she turns 29 y, 30 y, and 31 y, and we search for his or her earnings record in the employment history file. We take the combined earnings for a worker in a given year, adding over both employers and states (in the event of multiple job spells within a year). We also calculate the number of quarters the worker has positive earnings in a given year (i.e., $\in [0,\mathrm{\hspace{0.17em}4}]$). If the earnings record is missing for a particular age category (i.e., because the worker is unemployed or has attritted from the data), we estimate specifications where we either keep this earnings record as missing or we replace it with a zero.

We study labor market outcomes averaged for each individual over a set of ages rather than outcomes measured at a particular age (e.g., age 30 y) to (i) minimize the residual variance in the observed employment and earnings distributions and (ii) ameliorate concerns that any effects we see are driven by a contemporaneous economic shock in one particular earnings year. We express all monetary variables in real 2008 dollars, using the Consumer Price Index. For each cohort, we cap earnings at age 28 y equivalent to $100,000, allowing for 2% annual growth in earnings to limit the influence of outliers. (Specifically, we cap earnings at $100,000 for 28-y olds, $102,000 for 29-y olds, $104,040 for 30-y olds, $106,121 for 31-y olds, and $108,243 for 32-y olds.) Our baseline sample consists of earnings records between the years 1998 and 2007 for 12 million individuals born between 1969 and 1976. The mean annual earnings between the ages of 29 y and 31 y are $24,117 in our sample (in 2008 dollars). Additional detail on LEHD data and construction can be found in SI Appendix.

Fine-Scaled Weather Data.

We combine our longitudinal earnings records with fine-scaled, daily weather measures, using information on county and exact date of birth. We begin by constructing the number of days for which the daily mean temperature fell into one of 10 temperature bins ($<$0 °C, 0–4 °C, 4–8 °C, 8–12 °C, 12–16 °C, 16–20 °C, 20–24 °C, 24–28 °C, 28–32 °C, and 32+ °C) over the course of a particular focal period. We examine exposure in the following focal periods: the first, second, and third trimesters of gestation and 0–3 mo, 3–6 mo, and 6–12 mo postbirth. Additional detail on weather data and construction can be found in SI Appendix.

Additional Datasets.

We supplement our data with a variety of other population and demographic data from the Bureau of Economic Analysis Local Area Personal Income files. We also use county-level data on household AC penetration rates in the United States between 1960 and 1980 from the US Census of Population.

Methods.

Eq. 1 describes the primary estimation equation of interest:

$$y_{irgcdt}=\sum _k\sum _j({\theta }_j^{k}Tem{p}_{cdtj}^k)+Pre{c}_{cdt}^k\mathrm{\Phi }+{\gamma }_{rgcd}+{\lambda }_t+{ϵ}_{irgcdt}.$$ [1]

We regress a labor market outcome $y_{irgcdt}$ measured between the ages of 29 y and 31 y for person $i$ of race $r$ and sex $g$ born into county $c$ on day of year $d$ in year $t$ on a series of temperature bins $j$ that describe the total number of days the average daily temperature in a county fell within bin $j$ during critical period $k$. (To calculate the number of days falling into each temperature bin during pregnancy, we assume a 40-wk gestation period.)

Temperature bins are defined in 4 °C intervals (i.e., $j\in [<0$ °C, 0–4 °C, 4–12 °C, 12–16 °C, 16–20 °C, 20–24 °C, 24–28 °C, 28–32 °C, 32+ °C]), and critical periods $k$ are defined as $k\in$ [first, second, or third trimester; 0–3 mo, 3–6 mo, and 6–12 mo]. The 10 temperature bins $j$ are meant to model the effect of temperature in a nonlinear, semiparametric fashion. Similar estimators have been used in recent work by refs. 3, 5, 9, 17, 23, and 24, albeit in the context of different outcomes. This estimation strategy is fairly flexible, except that we restrict the marginal effect of temperature to be the same within 4 °C ranges.

For each critical period $k$, we also include a flexible polynomial (up to a cubic) in mean precipitation $Pre{c}_{cdt}^k$ for the county over that time period. The model also includes race $\times$ sex $\times$ birth county $\times$ birth day of year fixed effects, ${\gamma }_{rgcd}$, to control for time-invariant observed and unobserved determinants of long-run outcomes that vary across space, separately by race and sex. At the same time, race $\times$ sex $\times$ birth county $\times$ birth day of year fixed effects are designed to control for location-specific seasonal patterns in fertility that may also be correlated with later-life earnings (e.g., through compulsory schooling laws). To capture overall trends across cohorts, we include birth-year fixed effects ${\lambda }_t$. The parameter ${ϵ}_{irgcdt}$ is the error term.

Since our temperature bins span the full range of possible temperature outcomes, they are not all separately identified, and we are forced to make a normalization. We normalize the coefficients on $j\in$ [0–4 °C] to be equal to zero for each critical period $k$. One virtue of Eq. 1 is that we can examine the independent relationship between extreme temperatures and later-life outcomes at various critical periods while holding other critical periods constant. The large amount of conditionally random temperature variation provides us with the unique opportunity to examine which periods of child development are most critical for predicting long-run outcomes.

We present several auxiliary specifications that include results in which we estimate Eq. 1 separately for each critical period $k$, results in which we aggregate over temperature bins $j$ to examine more parsimonious forms of temperature heterogeneity $j\in [<\mathrm{\hspace{0.17em}0}$ °C, 0–24 °C, 24–28 °C, 28–32 °C, 32+ °C], results for outcomes at different follow-up ages, and results using different sets of outcome variables. Finally, we estimate regressions that include additional interaction terms between $Tem{p}_{cdtj}^k$ and our county $\times$ year measure of AC adoption, while also including the main effects of county AC exposure,

$$y_{irgcdt}=\sum _k\sum _j\left[\left({\mathrm{\Theta }}_j^k{T}_{cdtj}^k\right)+{\beta }_j^k\left(T_{cdtj}^k\times A{C}_{ct}\right)+P_{cdt}^k\varphi \right]+\delta A{C}_{ct}+{\mathrm{\Gamma }}_{rgcd}+{\mathrm{\Lambda }}_t+{\iota }_{irgcdt},$$ [2]

where the new set of coefficients ${\beta }_j^k$ provides an estimate of the dose–response relationship of earnings at ages 29–31 y to early childhood temperature exposure in various critical periods and in hypothetical counties that have 100% of households with AC in the county $\times$ year (i.e., where $A{C}_{ct}=\mathrm{\hspace{0.17em}1}$). This specification tests the extent to which AC can mitigate the effects of extremely hot temperature days on long-run outcomes.

The baseline model delivers 54 regression coefficients (9 temperature bins $j$ and 6 critical periods $k$). We summarize our results graphically to better interpret the large number of coefficients. Our table-form results rely on more parsimonious specifications with fewer temperature bins $j\in [<0$ °C, 0–24 °C, 24–28 °C, 28–32 °C, 32+ °C], with $j\in$ [0–24 °C] as the omitted category. We conduct inference using standard errors clustered at the state level to account for various forms of both spatial and temporal dependence in the data. Clustering at the state level gives comparable standard errors to approaches that more specifically model the covariance of error terms between counties as a function of distance (40), while also remaining computationally easier to implement (41).

The research described has been approved by the University of California at Berkeley Institutional Review Board and the University of California at Santa Barbara Office of Research Human Subjects Committee.