Mapping local and global variability in plant trait distributions

Significance

Currently, Earth system models (ESMs) represent variation in plant life through the presence of a small set of plant functional types (PFTs), each of which accounts for hundreds or thousands of species across thousands of vegetated grid cells on land. By expanding plant traits from a single mean value per PFT to a full distribution per PFT that varies among grid cells, the trait variation present in nature is restored and may be propagated to estimates of ecosystem processes. Indeed, critical ecosystem processes tend to depend on the full trait distribution, which therefore needs to be represented accurately. These maps reintroduce substantial local variation and will allow for a more accurate representation of the land surface in ESMs.

Abstract

Our ability to understand and predict the response of ecosystems to a changing environment depends on quantifying vegetation functional diversity. However, representing this diversity at the global scale is challenging. Typically, in Earth system models, characterization of plant diversity has been limited to grouping related species into plant functional types (PFTs), with all trait variation in a PFT collapsed into a single mean value that is applied globally. Using the largest global plant trait database and state of the art Bayesian modeling, we created fine-grained global maps of plant trait distributions that can be applied to Earth system models. Focusing on a set of plant traits closely coupled to photosynthesis and foliar respiration—specific leaf area (SLA) and dry mass-based concentrations of leaf nitrogen (${\mathrm{N}}_m$) and phosphorus (${\mathrm{P}}_m$), we characterize how traits vary within and among over 50,000 $\sim 50\times 50$-km cells across the entire vegetated land surface. We do this in several ways—without defining the PFT of each grid cell and using 4 or 14 PFTs; each model’s predictions are evaluated against out-of-sample data. This endeavor advances prior trait mapping by generating global maps that preserve variability across scales by using modern Bayesian spatial statistical modeling in combination with a database over three times larger than that in previous analyses. Our maps reveal that the most diverse grid cells possess trait variability close to the range of global PFT means.

Modeling global climate and the carbon cycle with Earth system models (ESMs) requires maps of plant traits that play key roles in leaf- and ecosystem-level metabolic processes (1–4). Multiple traits are critical to both photosynthesis and respiration, foremost leaf nitrogen concentration (${\mathrm{N}}_m$) and specific leaf area (SLA) (5–7). More recently, variation in leaf phosphorus concentration (${\mathrm{P}}_m$) has also been linked to variation in photosynthesis and foliar respiration (7–12). Estimating detailed global geographic patterns of these traits and corresponding trait–environment relationships has been hampered by limited measurements (13), but recent improvements in data coverage (14) allow for greater detail in spatial estimates of these key traits.

Previous work has extrapolated trait measurements across continental or larger regions through three methodologies: (i) grouping measurements of individuals into larger categories that share a set of properties [a working definition of plant functional types (PFTs)] (4, 15), (ii) exploiting trait–environment relationships (e.g., leaf ${\mathrm{N}}_m$ and mean annual temperature) (1, 16–20), or (iii) restricting the analysis to species whose presence has been widely estimated on the ground (21–24). Each of these methods has limitations—for example, trait–environment relationships do not well explain observed trait spatial patterns (1, 25), while species-based approaches limit the scope of extrapolation to only areas with well-measured species abundance. More critically, the first two global methodologies emphasized estimating a single trait value per PFT at every location, whereas both ground-based (5, 14) and remotely sensed (26) observations suggest that at ecosystem or landscape scales traits would be better represented by distributions. Here, we use an updated version of the largest global database of plant traits (14) coupled with modern Bayesian spatial statistical modeling techniques (27) to capture local and global variability in plant traits. This combination allows the representation of trait variation both within pixels on a gridded land surface and across global environmental gradients.

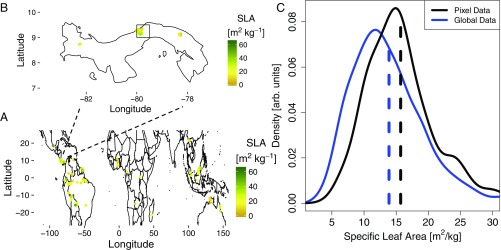
Information is lost when the range of measured trait values is compressed into a single PFT (Fig. 1). We observe that the global range of site-level SLA values for a single PFT such as broadleaf evergreen tropical trees (Fig. 1 A and C) is quite large (2.7–65.2 m²⋅kg⁻¹). Even after limiting the scope to a single well-measured 0.5° × 0.5° pixel within Panama (Fig. 1 B and C), there is still a wide range of SLA values (4.7–37.7 m²⋅kg⁻¹) with a local mean of 15.7 m²⋅kg⁻¹ and a local standard deviation of 5.4 m²⋅kg⁻¹—over one-third of the local mean. By contrast, the mean SLA value of all species associated with broadleaf evergreen tropical trees is 13.9 m²⋅kg⁻¹, over 10% lower than the local average (Fig. 1C). Thus, single trait values per PFT fail to capture variability in trait values within or among grid cells, i.e., over a wide range of spatial scales.

Fig. 1.

Trait data. (A) Global locations and values of specific leaf area measurements for the PFT tropical broadleaf evergreen trees. (B) Locations and values of specific leaf area measurements for the tropical broadleaf evergreen trees in Panama. The square in the center indicates a $0.5°\times 0.5°$ pixel containing the Barro Colorado Island sites (see Fig. 5). These points have been jittered up to 0.05° to highlight the density of measurements. (C) The full distribution of specific leaf area values for all species classified as evergreen broadleaf tropical trees. The blue line is the global data while black is the local pixel, and the dashed vertical lines are the respective means.

Transitioning from a single trait value per PFT (within or among grid cells) to a distribution may lead to significantly different modeling results (20) as critical plant processes, such as photosynthesis, are nonlinear with respect to these traits (28). This is reinforced by recent modeling studies that have begun to incorporate distributions of traits at regional (29, 30) and global (31) scales. It has been shown that using trait distributions leads to different estimates of carbon dynamics (32) and that higher-order moments of trait distributions contribute to sustaining multiple ecosystem functions (33). While species-level mapping (21, 23, 24) does capture trait distributions, it has been limited geographically and restricted to subsets of functional groups.

Even the largest plant trait database offers only partial coverage across the globe in terms of site-level measurements. Hence, gap-filling approaches need to be adopted to extrapolate trait values at regions with no data coverage. Here, we overcome data limitations through PFT classification, trait–environment relationships, and additional location information to develop a suite of models capable of estimating trait distributions across the entire vegetated globe. The simplest one is a categorical model, which assigns traits to maps of remotely sensed PFTs. Every species, with its corresponding trait values, is associated with a PFT and these trait distributions are extrapolated to the satellite-estimated range of the PFT (SI Appendix, Figs. S1 and S2). The second one is a Bayesian linear model that complements the PFT information with trait–environment relationships. The third one is a Bayesian spatial model that, in addition to PFTs and the trait–environment relationships, leverages additional location information via Gaussian processes (Materials and Methods). The use of a spatial Gaussian process in this context is unique and model evaluation reveals the superior predictive performance of this model.

Each of these methods interpolates (and extrapolates) both mean trait values and entire trait distributions across space (i.e., across grid cells on a global map). These models are further stratified by three different levels of PFT categorization: (i) PFT-free, all plants in a single group (i.e., no PFTs); (ii) broad, 4 groups based on growth form and leaf type; and (iii) narrow, 14 groups based on further environmental, phenological, and photosynthetic categories (Materials and Methods). The PFT-free categorization groups all plants into a single class, while the broad grouping (4-PFT) is similar to the vegetation classification used in the Joint UK Land Environment Simulator land surface (34), and the narrow (14-PFT) category is equivalent to the classification used in the Community Land Model (CLM) (4, 15, 35).

The abovementioned methods allow for a representation of global vegetation that enables a more accurate formulation of functional diversity than the single-trait value per PFT paradigm that is widely used (4). The traits studied here—SLA, ${\mathrm{N}}_m$, and ${\mathrm{P}}_m$—are central to predicting variation in rates of plant photosynthesis (5, 6, 9, 11) and foliar respiration (10, 36). The importance of these traits and the more advanced representation of functional diversity developed here may be used to better capture the response of the land surface component of the Earth system to environmental change.

Results and Discussion

Model Evaluation.

Given the full suite of nine models proposed, we conducted extensive model evaluation (Table 1) to determine the trade-offs associated with each methodology and resolution of PFT. We assessed the predictive capability of the models, using the root-mean-square predictive error (RMSPE) based on out-of-sample data (SI Appendix, section S6). Among the nine models, the spatial narrow 14-PFT model emerged as the best predictor of mean trait values for SLA and ${\mathrm{N}}_m$ and the second best for ${\mathrm{P}}_m$ (Table 1). However, the spatial broad 4-PFT model performed nearly as well (Table 1). The models’ abilities to correctly estimate the spread of the trait distributions were assessed using the out-of-sample coverage probabilities (CPs)—the proportion of instances the model-predicted 95% confidence intervals contained the observed trait values. Most of the models provided adequate coverage (CP of around 90% or more). See SI Appendix, section S4, for more detailed definitions of the model comparison metrics.

Table 1.

Model evaluation

Model	ps-R2, %	RMSPE	CP, %
SLA
Cf	NA	8.13	91.2
Cb	16.9	7.13	94.7
Cn	26.0	6.66	95.8
Lf	4.6	7.99	91.3
Lb	23.4	6.93	94.0
Ln	30.7	6.53	95.2
Sf	45.5	7.54	93.6
Sb	58.5	6.31	97.7
Sn	60.2	6.13	97.7
${\mathrm{N}}_m$
Cf	NA	7.16	93.3
Cb	12.5	6.95	93.2
Cn	19.4	6.47	92.7
Lf	5.2	7.28	93.2
Lb	16.7	6.71	94.3
Ln	24.1	6.42	94.6
Sf	44.2	7.19	93.6
Sb	53.7	6.36	96.1
Sn	54.8	6.18	96.1
${\mathrm{P}}_m$
Cf	NA	0.86	90.5
Cb	5.3	0.86	90.5
Cn	28.1	0.78	91.1
Lf	25.6	0.84	87.2
Lb	32.8	0.85	85.3
Ln	35.4	0.82	87.0
Sf	62.0	0.83	90.7
Sb	66.7	0.81	92.0
Sn	67.6	0.80	91.3

Shown are the pseudo-R² (ps-R²), RMSPE, and CP statistics for all nine models, for each of the three traits. The entries in boldface type correspond to the model producing highest ps-R², lowest RMSPE, or CP closest to 0.95. The categorical PFT-free model (Cf) produces a constant estimate and hence ps-R² is not defined. Each model is indicated by a two-letter abbreviation: C, categorical (no regression); L, linear (linear regression); and S, spatial (linear regression with spatial term) and the accompanying PFT resolution: f, PFT-free (no PFT information); b, broad (4-PFT); and n, narrow (14-PFT).

The improvement in prediction afforded by the inclusion of (i) a spatial term and (ii) PFT information (Table 1) invites further examination. First, the spatial term in our model likely incorporates some of the finer-scale variation that is unavailable given the relatively large grid cell size of the environmental covariates used in global studies. Thus, the spatial term allows for adjustment of trait values among neighboring or regional grid cells that the relatively coarse environmental metrics are not able to capture. Finer-scale studies that can evaluate local variations in climate, soil, or other relevant abiotic or biotic covariates may see less improvement from the inclusion of a spatial term, as they may directly measure local sources of variation. Second, the use of PFTs greatly improves the models, perhaps for similar reasons involving the degree of variation the raw data fail to incorporate. The greatest decrease in RMSPE occurs between the PFT-free grouping (a single category for all plants) and the broad (4-PFT) grouping across each of the models tested. If our trait data were perfectly predicted by environment, there would be no usefulness to including PFTs in mapping traits. That this is not so implies that the broad PFTs, based primarily on growth form and leaf type, offer superior predictive skill than environmental covariates on their own (19). However, the extra information in the narrow (14-PFT) grouping does further improve the fit and produces the most accurate predicted trait surface.

Global Maps.

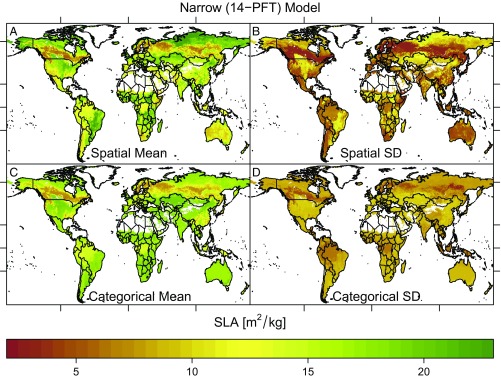
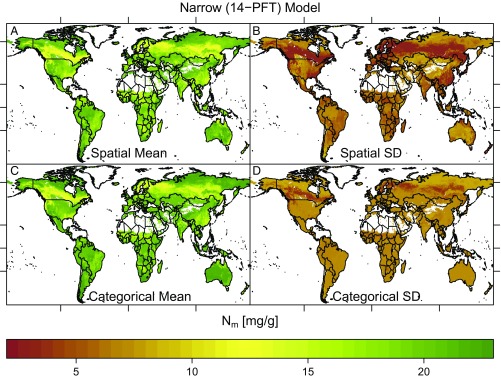
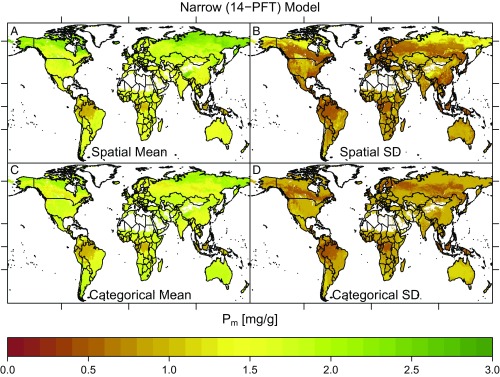
We selected two sets of maps to describe, in broad strokes, how trait distributions vary across the land surface: the narrow 14-PFT spatial model and its categorical counterpart. The narrow 14-PFT spatial model is the best predictor of mean trait values and provided adequate coverage probability (Figs. 2 A and B, 3 A and B, and 4 A and B). For comparison, we also include the 14-PFT categorical model, which is most similar to maps currently used in ESMs (Figs. 2 C and D, 3 C and D, and 4 C and D). Maps for the other models can be found in SI Appendix, Figs. S8–S16. The mean and SD are presented as a summary of the full log-normal distribution within each pixel, but there are full distributions estimated in each pixel (Case Studies).

Fig. 2.

SLA maps. (A and B) Narrow (14-PFT) Bayesian spatial model pixel mean and SD estimates, respectively. (C and D) Narrow (14-PFT) categorical model pixel mean estimates and SD estimates, respectively. For clarity, the color bars have been truncated at the compound 5th and 95th percentiles of both models. Latitude tick marks indicate the equator, tropics, and Arctic Circle and longitude is marked at 100°W, 0°, and 100°E.

Fig. 3.

Nitrogen (mass) maps. (A and B) Narrow (14-PFT) Bayesian spatial model pixel mean and SD estimates, respectively. (C and D) Narrow (14-PFT) categorical model pixel mean estimates and SD estimates, respectively. For clarity, the color bars have been truncated at the compound 5th and 95th percentiles of both models. Latitude tick marks indicate the equator, tropics, and Arctic Circle and longitude is marked at 100°W, 0°, and 100°E.

Fig. 4.

Phosphorus (mass) maps. (A and B) Narrow (14-PFT) Bayesian spatial model pixel mean and SD estimates, respectively. (C and D) Narrow (14-PFT) categorical model pixel mean estimates and SD estimates, respectively. For clarity, the color bars have been truncated at the compound 5th and 95th percentiles of both models. Latitude tick marks indicate the equator, tropics, and Arctic Circle and longitude is marked at 100°W, 0°, and 100°E.

The SD maps (Figs. 2 B and D, 3 B and D, and 4 B and D) compared with the mean maps (Figs. 2 A and C, 3 A and C, and 4 A and C) highlight one of the central results of this analysis—the local SDs of trait values are of similar magnitudes to their respective means. Generally, we observed that the local SD is close to half the local mean value but can approach the global range of the trait mean values; e.g., ${\mathrm{N}}_m$ (Fig. 3) has a maximum local SD of 9 mg N/g, and the global mean range is only ∼10 mg N/g. The maps of the trait SDs follow similar patterns to the means, although there are several regions where the mean varies more markedly than the SD, such as SLA in the southeast United States and China in the categorical model (Fig. 2 C and D) and similarly for ${\mathrm{N}}_m$ in the spatial model across the Sahel in sub-Saharan Africa (Fig. 3 A and C). The lack of variation in the SD is most clear in the categorical model for ${\mathrm{N}}_m$ while both models show relatively modest variation in ${\mathrm{P}}_m$.

For each of the three traits, the broad features of both the categorical and spatial models are similar, but there are numerous marked differences across regional and fine spatial scales (Figs. 2–4). The shared broad features of the maps from both models include SLA (Fig. 2) and ${\mathrm{P}}_m$ (Fig. 4) increasing from the tropics to the poles, while ${\mathrm{N}}_m$ (Fig. 3) has more modest variation, except that it tends to be lower in regions dominated by needle-leaved trees. Some of the notable differences between the models include the spatial model’s greater range and more marked variability of SLA within equatorial regimes (e.g., Brazil or central Africa); it also captures the low SLA of most of arid Australia better than the categorical model (Fig. 2A) and more strongly highlights the gradient of ${\mathrm{P}}_m$ from the tropics to the Arctic (16) (Fig. 4A).

The most consistent estimates between the categorical and spatial models are in the boreal regions dominated by needle-leaved trees; the measurements in this region are relatively sparse, which may have limited the ability of the spatial model to capture differences. On the other hand, broad-leaved trees span a wide range of environments, but a large portion of the measurements come from the tropics (66%), where there is a limited range of values among the climate covariates and therefore little variation with which to estimate a correlation. The grasses and shrubs have the largest SDs of the four broad PFTs (SI Appendix, Table S4) and dominate wide swaths of the land surface, but have fewer measurements—shrubs are the least measured of the broad PFTs in the database, and this appears to reduce the accuracy of the categorical model more than that of the spatial model (Table 1). The fact that shrubs are assumed to dominate in arid and boreal environments, which also tend to be undersampled, also likely contributes to these differences.

Our results also suggest that the breadth of functional niche space is reduced in both boreal and tropical biogeographic regions. The low variation across all three traits within the boreal forest implies that there is strong filtering and smaller niche space available in this relatively harsh environment. Surprisingly, despite the high species diversity in tropical forests, we also find that SLA and ${\mathrm{P}}_m$ have relatively low variation in these forests—suggesting that in this environment the trait space is reduced. This could be, in part, an artifact of the Earth system model PFT classification omitting herbaceous species. Conversely, grasslands and savannahs exhibit large variation in total trait space, suggesting these environments permit a wider range of strategies than in both the boreal and tropical regions. Most broadly, both the data and the spatial model suggest (SI Appendix, Figs. S24 and S25) lowest leaf nitrogen values in temperate climates that increase in both cooler and warmer regions; this may indicate a more complicated leaf biochemistry–temperature relationship than has previously been suggested (16).

Case Studies.

We conducted two regional case studies to provide a more in-depth analysis of the true and predicted shapes of trait distributions than can be provided by the SD maps and coverage probability. In these case studies trait data were pooled over an area to construct full trait distributions and then formally compared with the model predicted distributions.

We considered two areas with substantially different environmental conditions to evaluate the trait distributions obtained from the spatial and categorical models. We chose a single pixel that contained a highly studied site with numerous measurements of tropical trees, Barro Colorado Island (BCI), Panama; and a collection of pixels in an arid environment in which the mean estimates for SLA of the spatial and categorical models substantially disagreed, the southwestern United States. These areas were in the training data, and this analysis constituted a more detailed analysis of the models’ fit to the observed distribution of these locations. Here, the focus was on the structure of the full distribution of traits predicted at these sites; SI Appendix, Fig. S17 is a map of the measurements that comprised these locations and other sites included in this analysis. Both areas offer further insight into the structure of the distributions estimated by the categorical and spatial models.

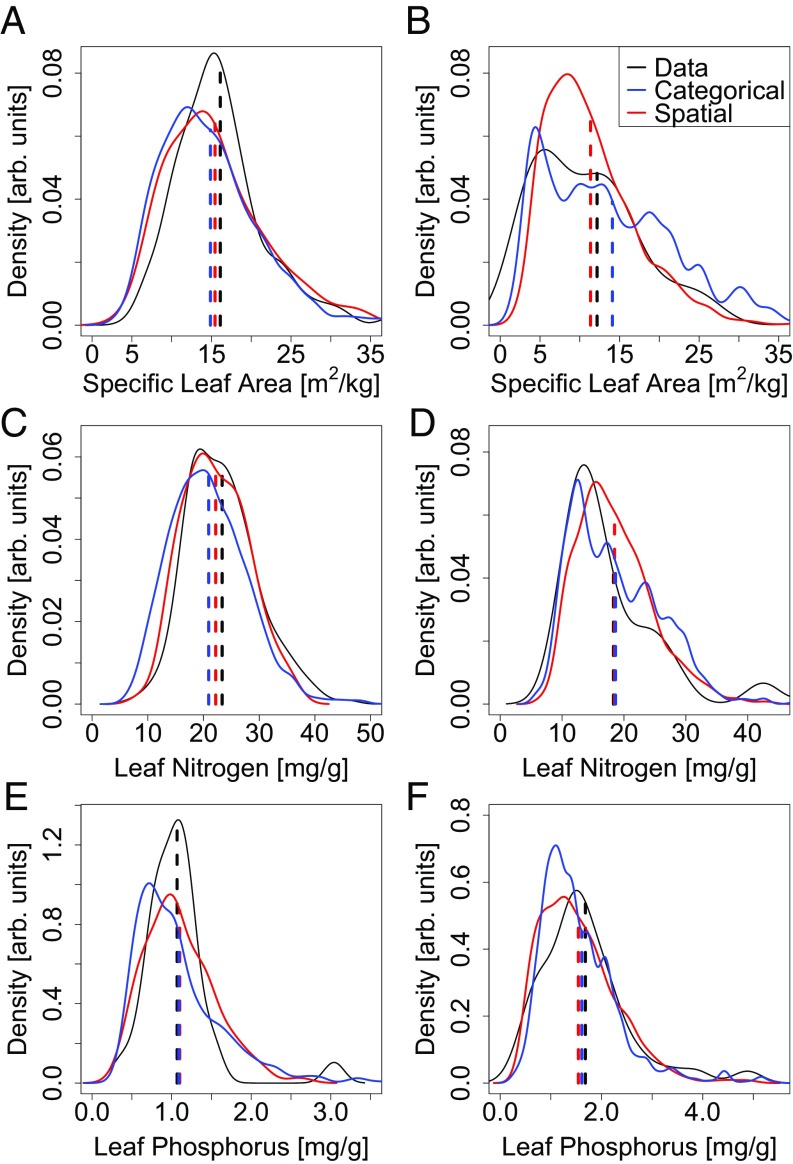
In the pixel containing BCI, the categorical and spatial models broadly agreed for all three traits (Fig. 5 A, C, and E), although the spatial model means were only half as distant from the observed means for SLA and ${\mathrm{N}}_m$ (4% vs. 8% and 5% vs. 10%, respectively). There were only two PFTs present in this pixel: tropical broadleaf evergreen and deciduous trees. Despite the general similarity of the shapes of the distribution, the spatial model appears capable of capturing some subtle features. This is clearest for leaf nitrogen, where the peak of the distribution was quite broad. This is neatly captured in the narrow PFT model, and the pattern was detectable through the Kolmogorov–Smirnov (K-S) statistic, which evaluates the similarity of two full distributions. Indeed, the superiority of the spatial model was reinforced by a closer match for the Bayesian spatial model across all traits at BCI, although for ${\mathrm{P}}_m$ it was the PFT-free spatial model that fitted best (SI Appendix, Table S6).

Fig. 5.

Empirical trait distributions. Barro Colorado Island (A, C, and E) and the US Southwest (B, D, and F). A and B show SLA, C and D show leaf nitrogen, and E and F show leaf phosphorus. Each panel depicts the distribution of the data in solid black, the categorical model in blue, and the Bayesian spatial model in red. The dashed vertical lines indicate mean values.

The differences between the trait distributions of the categorical and Bayesian spatial models were stark in the southwestern United States, although the mean estimates for ${\mathrm{N}}_m$ and ${\mathrm{P}}_m$ were close (Fig. 5 B, D, and F). This may be a result of the topographic complexity of this region and the resulting difficulty of aggregating climate and soil covariates at the 0.5° pixel scale and the sparser sampling than at BCI. To get enough data to approximate a distribution, we aggregated 18 pixels with nine PFTs including every temperate category, although many of them are only marginally present. The inclusion of so many PFTs produced a noisier distribution in the categorical model than suggested by the data and estimated by the spatial model. Neither of the models produced distributions that matched as well with the observations; however, it is notable how close the mean values for both models matched the observations for ${\mathrm{N}}_m$ and ${\mathrm{P}}_m$, and the spatial model did well for the mean SLA.

Environmental Covariates and the Spatial Term.

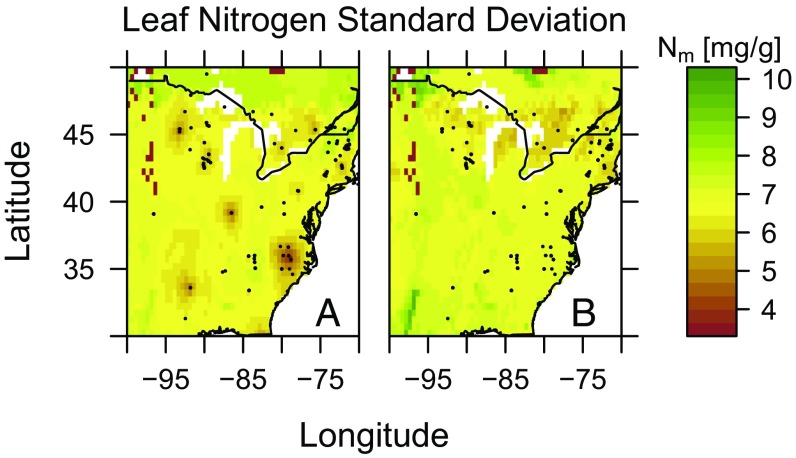
The improvement in prediction from the linear model to the spatial model is partially explained by weak trait–environment relationships (SI Appendix, Tables S1–S3). The magnitude of spatial variation explained by the Gaussian process model is comparable to that of the unexplained trait variation. For most of the spatial models, the estimated spatial range was around 300 km; this suggests a strong spatial effect and implies that the spatial model can provide more precise information about the trait distribution near the locations where we have data. This was largely borne out in the case studies and is illustrated more explicitly in Fig. 6 where the predicted trait SD for the spatial model was up to 50% lower than for the linear nonspatial model near locations with trait measurements. The spatial model leverages local information to reduce the uncertainty of trait estimation near data locations and may provide guidance for future data collection by identifying high-uncertainty regions.

Fig. 6.

Spatial learning. (A) The spatial model SD of ${\mathrm{N}}_m$. The predicted variation near the data locations (black dots) is much lower than variation at locations away from any data point. (B) The linear model SD, which does not account for local spatial information, has no such pattern.

Applications for Trait Distributions.

Plant traits vary across a range of spatial scales, and the spatial model best captures changes across large spatial gradients (such as in Amazonia and Australia) as well as the subtleties within pixels. Maps for all of the models highlight how much information about local variability is lost when representing plant traits with a single value and suggest that a first application of these maps will be for ESMs to incorporate these scales of variability. For process-based ESMs, the simplest model to incorporate will likely be the categorical model as it is closest to the current PFT approach, but this model is also the least flexible. The more sophisticated models developed here provide more accurate large-scale variation and may be used to infer new trait values in a novel climate by perturbing the climatic covariates (37). However, given the likelihood of nonlinear trait–environment relationships, the spatial sparsity of the data, and the possibility of alternate strategies within a PFT that may alter the trait–environment relationship in a future climate some caution is called for when using these models for extrapolation. Future ecosystem models could also integrate the leaf-level variation in these maps with canopy-scale changes in leaf display traits—leaf angle, azimuth, and total area.

We have emphasized the quality of the Bayesian spatial model with narrow PFTs, but there is an intriguing possibility opened by the PFT-free model (SI Appendix, Figs. S8, S11, and S14)—that being the representation of vegetation without reference to PFTs (1). In this case the representation of vegetation would rely entirely on the structure of trait distributions at various landscape scales (1). Such a representation eliminates the need to separately model the future locations of PFTs (or species) when inferring the future distribution of traits; hence, the output of a model like that developed here could be updated with future environmental covariates, with the caveats that “out of sample prediction” may entail. At the same time, this method would allow for greater functional diversity than multiple PFTs with single-trait values, as is currently used in most ESMs. Adopting this approach does, however, raise the issue of how to deal with the paucity of surface observations in some regions, as evidenced by the greater errors associated with estimating out of sample values with this model (Table 1). Complementary work has retrieved leaf trait maps from a global carbon cycle model fused with Earth observations (38), providing another method that could be used for direct comparison against the trait maps produced here. While the methodology outlined in our analysis brings the possibility of a PFT-free land surface closer, we remain several steps away from being able to make such maps as accurately as we do using PFT characterizations for trait prediction. Several actions can bring us closer to that goal. First, incorporation of additional information (such as phylogenetic relatedness and trait–trait covariance) will likely improve trait maps, even using existing observations. Second, as the current level of observations is extremely sparse in some regions and sparse in most regions, expanded trait databases will also aid in development of PFT-free trait maps.

Conclusions

SLA and ${\mathrm{N}}_m$ are essential inputs into the land surface components of Earth system models, and while phosphorus has not yet been as widely incorporated into ESMs, it has been shown—particularly across the tropics—to be important to photosynthesis (9, 11, 39–42) and respiration (11, 12, 36). The maps and trait–environment relationships presented here may be used by existing land surface models that use similar categories to classify vegetation. However, it should be noted that PFT-dependent models often have many other parameters that have been calibrated to historical estimates of particular trait values (4). Thus, the values developed here, while likely drawing from a larger pool of measurements than has been done previously, cannot necessarily be adopted without further modification of other model elements (37, 43). Nonetheless, these results can be incorporated into a wide class of models with relative ease. We can now provide global trait distributions at the pixel scale.

The global land surface is perhaps the most heterogeneous component of the Earth system. Reducing vegetation to a collection of PFTs with fixed trait values has been the preferred method to constrain this heterogeneity and group similar biochemical and biophysical properties; however, this has been at the expense of functional diversity. This analysis quantifies the substantial magnitude of this ignored trait variation. The approach and methods presented here retain the simplicity of the PFT representation, but capture a wider range of functional diversity.

Materials and Methods

Data.

The TRY database (www.try-db.org) (14) provided all data for leaf traits and the categorical traits to aggregate PFTs (TRY–Categorical Traits Dataset, https://www.try-db.org/TryWeb/Data.php#3, January 2016) used in the analysis. The TRY data may be requested from the TRY database custodians. See SI Appendix, section S10 for a complete list of the original publications associated with this subset of TRY. The extract from TRY used here has just under 45,000 measurements of individuals from 3,680 species with measurements of at least one of SLA, leaf nitrogen per dry leaf mass (${\mathrm{N}}_m$), and/or leaf phosphorus per leaf dry mass (${\mathrm{P}}_m$). The number of individual measurements varies from 32,315 for SLA on 2,953 species to 19,282 for ${\mathrm{N}}_m$ on 3,053 species down to 8,052 for ${\mathrm{P}}_m$ on 1,810 species; see SI Appendix, Table S4 for the number of unique measurements and species found in all categorizations used in the analysis. The species taxonomy was standardized using The Plant List (www.theplantlist.org/). Measurements were associated with environmental categories through Köppen–Geiger climate zones (44). All environmental variables are on a $0.5°\times 0.5°$ grid. Climate variables use 30-y climatologies from 1961 to 1990 as estimated by the Climate Research Unit (45, 46). Soil variables are from the International Soil Reference and Information Center–World Inventory of Soil Emission Potentials (ISRIC-WISE) (47). The spatial extent of PFTs has been previously estimated through satellite estimates of land cover around the year 2005 (48), and these estimates have been refined into climatic categories (15, 35). While TRY, and thus the data used here, represents the largest collection of plant traits in the world, most of the measurements come from a subset of global regions: North America, Europe, Australia, China, Japan, and Brazil. There are still large sections of the planet with extremely sparse measurements, notably much of the tropics outside of the Americas, large swaths of Central Asia, the Russian Federation, South Asia, and much of the Arctic (SI Appendix, Fig. S17). Improving data collection in these regions will greatly improve future modeling efforts. Until observations are more complete there remains the possibility of spurious patterns, although we have found little evidence to suggest their presence in this analysis, even in comparison with detailed regional studies (SI Appendix, Fig. S26) (49).

Classification of PFTs and Categorical Model.

We used three nested levels of PFT classification. In the first level, all plants are categorized into a single group (“PFT-free”). In the second level (“broad”), all plants are categorized into PFTs based on categorical traits associated with growth form (grass, shrub, tree) and leaf type (broad and needle-leaved), leading to the following four PFTs: grasses, shrubs, broad-leaved trees, and needle-leaved trees (SI Appendix, Fig. S1). In the third level (“narrow”), the broad PFTs are further refined by their climatic region—tropical, temperate, boreal—as well as leaf phenology and, for the grasses, photosynthetic pathway (${\mathrm{C}}_3$ or ${\mathrm{C}}_4$). This produces 14 PFTs (SI Appendix, Fig. S2), which correspond exactly to those found in the CLM (4). Note that these PFT classifications exclude nonwoody eudicots (“herbs”), which were excluded from the analysis, on account of their lack of dominance within these PFT categories (50) and therefore, on account of being widely measured could overly influence the structure of the trait distributions if they were included. Satellite estimates of the PFT abundance that correspond to the narrow PFT categories defined above have already been calculated (15, 48) and we used these to assign a percentage of each $0.5°\times 0.5°$ pixel to each PFT present according to the fraction of the land surface within that pixel occupied by the PFT. The broad PFT fractions are calculated by summing the narrow PFT categories within each broad classification.

The categorical model uses the PFT categories and averages trait values for each species across individual measurements at each measured location. This defines the PFT as the interspecies range of trait values and ignores all local environmental factors. The results of the categorical model are summarized by the mean and SD of each PFT’s trait values (SI Appendix, Table S4) for all three resolutions of the model. Note that in the PFT-free case where no PFT information is used, the categorical model produces a constant trait distribution across the entire vegetated world. The categorical model and the Bayesian models described in the following section all use location-specific species mean values to estimate trait distributions. We assume no intraspecific variation in trait values. However, in regions dominated by a small number of species this may lead to biased predictions. The hyperdominance of a small group of species in the Amazon has recently been demonstrated (51) and thus serves as a case study to evaluate our assumption of equal species weighting (SI Appendix, section S8, Fig. S23). We found that equal weights (species means) produced trait distribution estimates closest to those of the hyperdominant trait abundances and this reinforces the use of this assumption globally. Further, as noted above, the omission of herbaceous species from tropical regions in this analysis (and ref. 51) may unduly limit trait diversity and calls for further research.

Bayesian Models.

A more fine-tuned depiction of geographical or spatial variation of plant trait values within each PFT can be achieved by leveraging environmental and location information, which allows trait values to adjust based on local conditions. Data for 17 climate- (45, 46) and soil-based (47) environmental predictors were available at the $0.5°\times 0.5°$-pixel resolution used to create the trait maps. To avoid overfitting and collinearity issues, these 17 predictors were screened (SI Appendix, section S7) based on correlations among predictors, based on their individual correlation with the traits, and to include climate covariates along different axes of environmental stress and both chemical and physical soil covariates. We finally selected 5 predictors—mean annual temperature (MAT), total annual radiation (RAD), moisture index (precipitation/evapotranspiration) (MI), percentage of hydrogen (aqueous) (pH), and percentage of clay content (CLY). Remote-sensing data products, such as Normalized Difference Vegetation Index (52), are not used as covariates, to allow for inference outside of the historical observation period through perturbations of environmental covariates.

We used environment–trait relationships to obtain predictions of trait values (1, 16–18, 37, 43) in a linear regression setup. The formal details of the initial model are as follows. We denote log-transformed trait values at a geographical location $s$ as $y_{\mathit{trait}}(s)$. This set of five predictors at a location $s$ is denoted by the vector $x(s)={(x_1(s),x_2(s),\dots ,x_5(s))}^{\prime }$. A linear regression model relating the trait to the environmental predictors is specified as

$$y_{\mathit{trait}}(s)=b_0+b_1{x}_1(s)+b_2{x}_2(s)+\dots +b_5{x}_5(s)+ϵ(s),$$ [1]

where $b_i$ are the regression coefficients and $ϵ(s)$ is the error term explaining residual variation. Estimation of model parameters and prediction were achieved with a fully Bayesian hierarchical model. This enables inclusion of prior information and prediction of full trait distributions instead of representative values (like mean or median), thereby ensuring that the uncertainty associated with the estimation of model parameters is fully propagated into the predictive trait distributions.

We then generalized the above model into a Bayesian spatial linear regression model that borrows information from geographically proximal regions to capture residual spatial patterns beyond what is explained by environmental predictors. A customary specification of a spatial regression model is obtained by splitting up the error term $ϵ(s)$ in Eq. 1 into the sum of a spatial process $w(s)$ and an error term $\eta (s)$ that accounts for the residual variation after adjusting for the spatial effects $w(s)$. The underlying latent process $w(s)$ accounts for local nuances beyond what is captured by the environmental predictors and is often interpreted as the net contribution from unobserved or unusable predictors. Gaussian processes (GPs) are widely used for modeling unknown spatial surfaces such as $w(s)$, due to their convenient formulation as a multivariate Gaussian prior for the spatial random effect, unparalleled predictive performance (53), and ease of generating uncertainty-quantified predictions at unobserved locations. We use the computationally effective nearest-neighbor GP (27), which nicely embeds into the Bayesian hierarchical setup as a prior for $w(s)$ in the second stage of the model specification. All technical specifications of the Bayesian spatial model are provided in SI Appendix, section S1.

The linear regression models used in previous studies (1, 16–18) and both the spatial and nonspatial Bayesian models described above assume a global relationship between the traits and environment. Given the goal of predicting trait values for the entire land surface, the assumption of a universal trait–environment relationship may be an oversimplification (54). Moreover, if there is significant variation in plant trait values among different PFTs, the estimated parameters will be skewed toward values from abundantly sampled PFTs, such as broad-leaved trees. Additional information about plant characteristics at a specific location, if available, can potentially be used to improve predictions. As mentioned earlier, we have PFT classifications for each observation of the dataset used here and satellite estimates of PFT abundance at all pixels. The global regression approaches described above ignore this information and can yield biased predictions at locations dominated by PFTs poorly represented in the data, such as shrubs. Hence, we also incorporate the PFT information in these regression models by allowing the trait–environment relationship to vary between different PFTs. Finally, the PFT-specific distributions from the Bayesian models were weighted by the satellite-based PFT abundances to create a landscape-scale trait distribution, thereby enabling straightforward comparison between all three categorizations of PFT. Details of the PFT-based Bayesian models are provided in SI Appendix, section S2. The use of a GP-based spatial model as well as the Bayesian implementation of the regression models was unique to this application of plant trait mapping and, as results indicated, were critical to improving model predictions as well as properly quantifying trait distributions.