Significance
Molecular chaperones have evolved to assist the folding of proteins and RNA, thus avoiding the deleterious consequences of misfolding. Thus, it is expected that increasing chaperone concentrations should enhance the yield of native states. While this has been observed in GroEL-mediated protein folding, experiments on Tetrahymena ribozyme folding assisted by CYT-19 surprisingly show the opposite trend. Here, we reconcile these divergent experimental observations by developing a unified theory of chaperone-assisted protein and RNA folding. We show that these ATP-fueled machines drive their substrates out of equilibrium, maximizing the nonequilibrium native yield in a given time rather than the absolute yield or folding rate. The theory predicts that in vivo the number of chaperones is regulated to optimize their functions.
Keywords: molecular chaperones, protein folding, RNA folding, optimizing short-term yield, nonequilibrium steady state
Abstract
Molecular chaperones facilitate the folding of proteins and RNA in vivo. Under physiological conditions, the in vitro folding of Tetrahymena ribozyme by the RNA chaperone CYT-19 behaves paradoxically; increasing the chaperone concentration reduces the yield of native ribozymes. In contrast, the protein chaperone GroEL works as expected; the yield of the native substrate increases with chaperone concentration. The discrepant chaperone-assisted ribozyme folding thus contradicts the expectation that it operates as an efficient annealing machine. To resolve this paradox, we propose a minimal stochastic model based on the Iterative Annealing Mechanism (IAM) that offers a unified description of chaperone-mediated folding of both proteins and RNA. Our theory provides a general relation that quantitatively predicts how the yield of native states depends on chaperone concentration. Although the absolute yield of native states decreases in the Tetrahymena ribozyme, the product of the folding rate and the steady-state native yield increases in both cases. By using energy from ATP hydrolysis, both CYT-19 and GroEL drive their substrate concentrations far out of equilibrium, thus maximizing the native yield in a short time. This also holds when the substrate concentration exceeds that of GroEL. Our findings satisfy the expectation that proteins and RNA be folded by chaperones on biologically relevant time scales, even if the final yield is lower than what equilibrium thermodynamics would dictate. The theory predicts that the quantity of chaperones in vivo has evolved to optimize native state production of the folded states of RNA and proteins in a given time.
Small single-domain proteins fold rapidly with sufficient yield as envisioned by Anfinsen (1–3). However, larger proteins, especially those with complex native (N) state topologies, are often kinetically trapped in metastable states for sufficiently long times that protein aggregation becomes a major problem (4–6). In such nonpermissive conditions, the N state yield is extremely low. To remedy this deleterious situation, molecular chaperones have evolved to rescue those substrate proteins (SPs) that are prone to aggregate and hence do not fold spontaneously with enough yield on cellular time scales (7, 8). The best studied example is the bacterial chaperonin GroEL (8, 9), a promiscuous stochastic ATP-consuming machine that mediates folding of a variety of SPs regardless of the topology they adopt in the N state. Indeed, nearly 30 years ago, it was shown that GroEL recognizes SPs as long as they are in the misfolded (M) state, thus exposing hydrophobic residues that are usually buried in the N state (10). In contrast to protein chaperones, much less is known about RNA chaperones and their functions. Under typical in vitro conditions, ribozymes readily misfold into a manifold of metastable states (11–13). The barriers between these states and the N state are much larger than the thermal energy, thus making the time scales for transition between the metastable states and the N state longer than the cell doubling time.
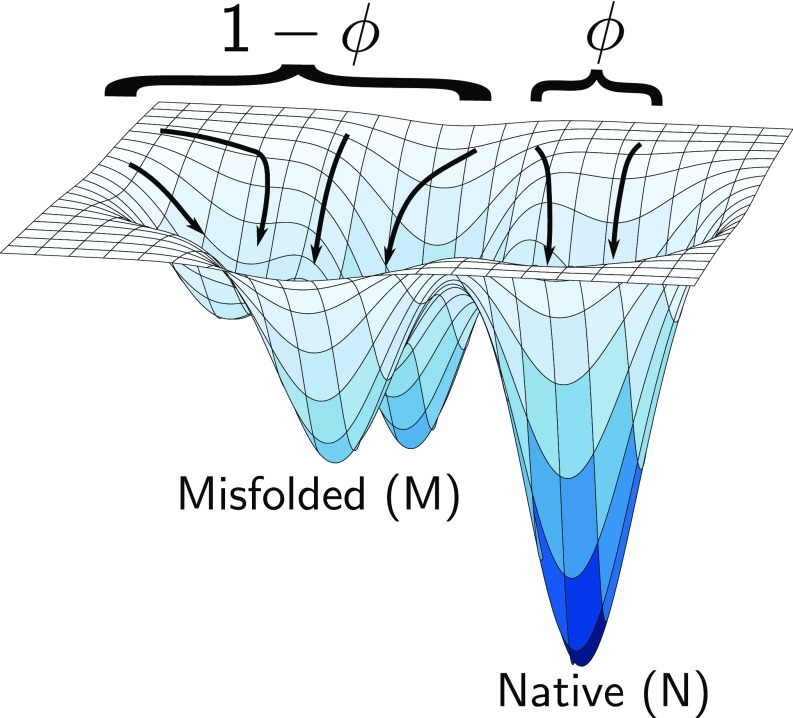
The need for chaperones is best understood by considering spontaneous folding of proteins and RNA under nonpermissible conditions. The kinetic partitioning mechanism (KPM) (14) provides a common unifying description of chaperone-free folding of SPs as well as ribozymes in rugged energy landscapes (11, 15, 16). According to the KPM (illustrated in Fig. 1), a fraction of the initial population of molecules, referred to as the partition factor , folds rapidly to the N state while the remaining fraction, , is kinetically trapped in M states for times exceeding viable biological times. Proteins and ribozymes, which reach the folded state with sufficient yield (), do not require chaperones. In contrast, the protein Rubisco with (17) and the Tetrahymena ribozyme () (11–13) require assistance from chaperones.
Fig. 1.
Illustrating the KPM of spontaneous folding of proteins and RNA in a rugged folding free energy landscape. Under nonpermissive conditions, only a fraction of the unfolded molecules fold rapidly to the N state. The rest misfold and remain kinetically trapped in a manifold of long-lived metastable states. If is small, as is the case in the folding of ribozymes and proteins under nonpermissible conditions, its folding requires the chaperone machinery.
The mechanism of GroEL action has remained unnecessarily controversial. Two diametrically opposite models have been proposed—the Anfinsen cage mechanism (passive or active) and the Iterative Annealing Mechanism (IAM). The former posits that the GroEL encapsulates the misfolded SP and provides an environment that avoids SP–SP interaction, thereby preventing aggregation and promoting folding (18, 19). It should be noted that the folding rate could be enhanced due to confinement in a noncycling artificial GroEL mutant (20), as predicted theoretically (21–23). On the other hand, the IAM proposes that GroEL uses the energy from ATP binding and hydrolysis, leading to large conformational changes in GroEL (17, 24–26). The allosteric changes lead to partial unfolding and encapsulation of the misfolded SP, thus giving the SP another chance to fold to the correct N state. Iterating the cycles of encapsulation and unfolding eventually leads to a high yield of the native SPs (17). Unlike the cage model, the IAM quantitatively explains all of the available experimental data, including the effect of GroEL variants in the rescue of mitochodrial Malate Dehydrogenase (mtMDH) and Citrate Synthase (27). Relative to the wild-type (WT) GroEL, the ability to rescue these substrates is greatly compromised (28) in GroEL variants, generated by mutating specific residues. The Anfinsen cage model would predict no change in assisted folding in going from the WT to the mutants, a conclusion that contradicts the experimental findings (28).
In the context of chaperone-mediated RNA folding, a large number of studies unequivocally suggest that the IAM is the dominant mechanism of RNA folding (29–32) without the benefit of quantitative analyses. This has been attributed to the ubiquitous role of superfamily-2 (SF2) helicases performing RNA remodeling and chaperone activities, many of which are known to unwind nucleic acids either processively or in a local manner (33, 34). The suspected helicase activity of RNA chaperones suggests that kinetic traps are resolved by first partially unwinding (thereby unfolding) M states of the substrate.
The proposal that assisted folding by GroEL and RNA chaperones involves unfolding of the substrates suggests that there ought to be a universal mechanism of chaperon-assisted protein and RNA folding, referred to as the generalized IAM (35). The generalization is required since it was shown that unlike the case of proteins where chaperones recognize only the misfolded SPs, the RNA chaperones also bind and unwind native RNA folds (30, 31). Therefore, while the basic principle of repeated rounds of misfolded substrate recognition and partial unfolding remains identical between proteins and RNA chaperones, there is an additional element of N state recognition by the chaperone in the case of RNA. However, this additional aspect of N state recognition leads to an immediate conundrum, which was observed in experiments of CYT-19–mediated folding of Tetrahymena ribozymes—as the chaperone (in this case CYT-19) concentration is increased, the final yield of the N state is reduced (30). This finding is qualitatively different from the observations on GroEL-mediated folding of proteins, where increasing the chaperone concentration increased the final yield of the native protein (17).
Here, we create a stochastic model based on the generalized IAM, which quantitatively explains the apparently paradoxical results in the chaperone-dependent folding of RNA and protein within a unified theory. We analyze a host of experimental data on CYT-19–mediated folding of the Tetrahymena ribozyme (and its mutants) as well as Rubisco and recent data on mtMDH (36). In both proteins and RNA, it is neither the absolute steady-state native yield [] nor the folding rate () that is maximized but rather the product that represents a balance between the two quantities. We further show that the chaperones achieve optimal performance by hydrolyzing ATP and driving their substrates into steady-state concentrations that are far from equilibrium. While equilibrium thermodynamics would predict far higher long-term native yields in assisted folding of RNA, cellular time scales are much shorter than the times needed to reach equilibrium. Our work, therefore, suggests that cells settle for less native substrate than is theoretically possible but that is obtained over much faster time scales by allowing chaperones to use nonequilibrium processes.
Unified Model for Protein and RNA Folding by Chaperones
The crucial prediction of the IAM for proteins (17) is that GroEL binds to misfolded SPs and unfolds it fully or partially, giving the SP another chance to fold correctly. RNA chaperones (CYT-19 for example) are more indiscriminate in that they also unfold the native substrate (30). We subsume these scenarios using a three-state model, which we demonstrate not only fits all of the data but leads to general principles of chaperone function and the associated optimization problem that nature has solved to prevent aggregation. Both GroEL and dead-box proteins that act as RNA chaperones have been shown to efficiently release their substrates and engage in multiple rounds of substrate binding/release (37–39). These findings are in accord with the basic tenets of the IAM.
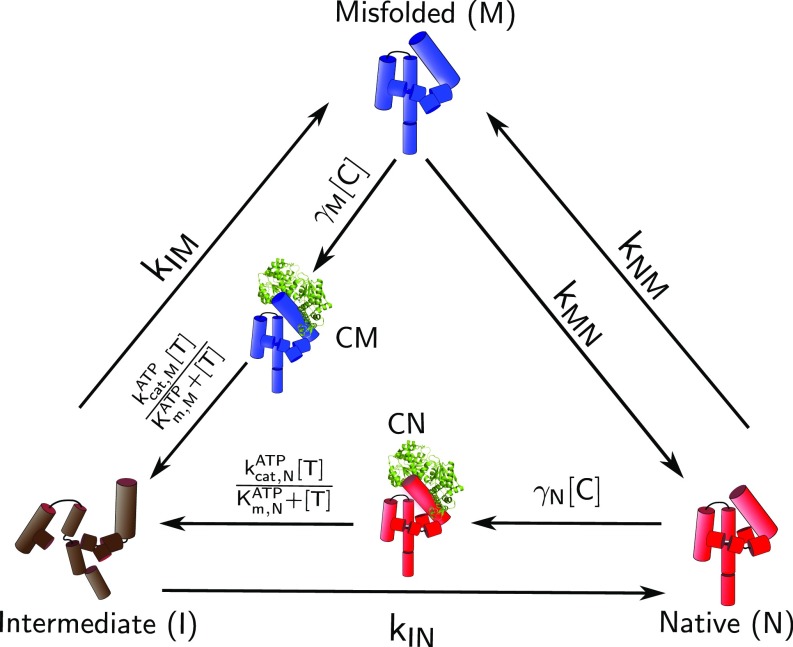
We define the three main states—I, N, and M, corresponding to intermediate, native, and misfolded, respectively (Fig. 2). The substrate may be fully or partially unfolded by the chaperone (8, 30). Hence, the free substrates, before folding, belong to the I state in our model. We assume that the chaperones do not bind to the unstructured I state because doing so would result in an unstable complex. In addition, to describe dependence of the folding rates on the chaperone concentration dependence, we define two additional states, CM and CN, corresponding to chaperone bound to M and N states, respectively (Fig. 2).
Fig. 2.
Schematic illustration of the model for a unified description of chaperone-assisted folding. We use Tetrahymena ribozyme for illustration purposes. The ribozyme in the I (brown), N (red), and M (blue) states and Ribonucleoprotein (RNP) complexes are illustrated in the scheme. The CYT-19 is represented in green. The same model is applicable to describe GroEL-associated folding, except CYT-19 is replaced by the chaperonin machinery.
The rates correspond to transitions from state to , where . Starting from an ensemble of SPs in the unfolded state, the ribozyme population (or SPs) rapidly collapses to the I (11). From the I state, a fraction of molecules () fold rapidly to the N state, while the rest of them () are trapped in long-lived metastable misfolded intermediates M, which slowly fold to the N state, as predicted by the KPM (11, 29, 40). The kinetic partition factor is related to and by:
| [1] |
Although there are a multitude of states in the I and M ensembles in a rugged folding landscape (29), we subsume all such possible states into I and M for simplicity. In vitro experiments, in the absence of chaperone, suggest a rapid equilibration between the multitude of states in the misfolded ensemble, and hence, the M to N state transition can be described by a single rate (11, 15, 40, 41). The effective rates and are assigned to the transitions to the N and M states, respectively.
To model the function of the GroEL and CYT-19, we allow the chaperone to recognize both M and N, taking the M and N states back to the I state with rates and , respectively. The chaperone–ribozyme or chaperone–protein complexes formed with M and N states, denoted as CM and CN, respectively, use energy obtained from ATP hydrolysis to revert to the partially unfolded I.
The chaperone binds to M and N with second order rate constants and , respectively. Note that and can be interpreted as the effective rate of protein/ribozyme recognition and processing by the chaperone, which reduces to at low chaperone concentration, provided that GroEL/CYT-19 binding to M or N follows Michaelis–Menten kinetics (31). It has been shown that the CYT-19–dependent rate of unfolding of the ribozyme is linear up to 500 nM, indicating that the lower bound of the effective Michaelis–Menten constant is 500 nM. We assume that the transitions from CN or CM to I follow Michaelis–Menten kinetics with the ATP concentration [], with distinct turnover rates (, ), and Michaelis constants (, ) (Fig. 2). The transition rates involving the states CM and CN, shown in Fig. 2, can be subsumed into one by observing that each of the transition times for M I and N I is a sum of two time scales—that is, binding of chaperone to substrate and ATP-dependent partial unfolding. Therefore, the overall rates of chaperone and ATP-mediated unfolding rates can approximately be written as and . We are thus left with only the three states—I, M, and N—which greatly simplifies the analyses of the experimental data. Finally, the transition rate from M to N is , while the reverse rate is , such that the free energy difference between the two states is given by .
Note that in our model we have disallowed the M I and N I conversions in the absence of chaperone or ATP (Fig. 2). While spontaneous conversion from M and N to I will undoubtedly occur to some extent, the key element that allows us to make the simplifying assumptions in our model is a comparison of time scales. The barriers between M and N states and I are large enough that spontaneous transitions to I occur on much longer time scales than any other time scale in the problem. For instance, Tetrahymena ribozyme is kinetically trapped in the M state over time scales of days in vitro (11), whereas the introduction of CYT-19 and ATP accelerates the folding process to a matter of minutes (30). Therefore, the wide separation of time scales allows us to neglect the spontaneous M I and N I conversions, which we do for the sake of simplicity and to keep the number of free parameters in the model to the minimum possible.
Results and Discussion
Assisted Kinetics and the Time Evolution of Native Substrate.
The time evolution of the probability of the system being in the state at time is given by the master equation:
| [2] |
with . This equation allows for exact solutions of the probability of observing each state (N, M, or I) as functions of time (details in Eq. S2). These solutions are complete in the sense that they govern all time scales, giving a full description of the time evolution of the system from to . At large times (), these solutions represent steady-state behavior. The nonequilibrium steady-state population of the N state is reached from any initial condition and is given by (see Supporting Information for details):
| [3] |
where . Note that this steady-state value of the native yield depends on both the concentration of the chaperone [C] as well as the ATP concentration [T]. If , which happens when either [C] = 0 and/or [T] = 0, the native population becomes:
| [4] |
which is the expected result at thermodynamic equilibrium () between the two states, N and M.
Remarkably, the behavior of the steady-state native substrate yield under the action of RNA chaperone CYT-19 is strikingly different compared with that of GroEL. While the steady-state yield of the folded protein increases on increasing the GroEL concentration, the steady-state yield of native ribozyme decreases on increasing CYT-19 concentration. The contrasting behavior is fully explained by our model. Our theory predicts that is a monotonically increasing function of [C] if the inequality:
| [5] |
is satisfied. On the other hand, if:
| [6] |
then will be a monotonically decreasing function of [C] (see Supporting Information for details).
Substituting the parameters from Table S1 (see CYT-19–Mediated Folding of Tetrahymena Ribozymes and GroEL-Mediated Folding of Rubisco and MDH), we see that the inequality in Eq. 6 is indeed satisfied by Tetrahymena ribozyme. Similarly, the best fit parameters from Table S2 show that Rubisco satisfies the inequality in Eq. 5, thus explaining the increase in native yield of Rubisco as GroEL concentration is increased.
Generalized IAM and the N State Recognition Factor.
Without chaperones, only a small fraction of the original unfolded ensemble reach the N state spontaneously. The rest, , remain trapped in long-lived metastable states. To rescue these kinetically trapped proteins to the N state, the chaperone molecules recognize and bind to the exposed hydrophobic regions of the misfolded protein. The remaining fraction, , is assisted by GroEL, in all likelihood reverting it to the more expanded form, and the whole process is repeated over and over again. The yield of the N state as a function of such reaction cycles is given by . As becomes large, the native yield can theoretically reach .
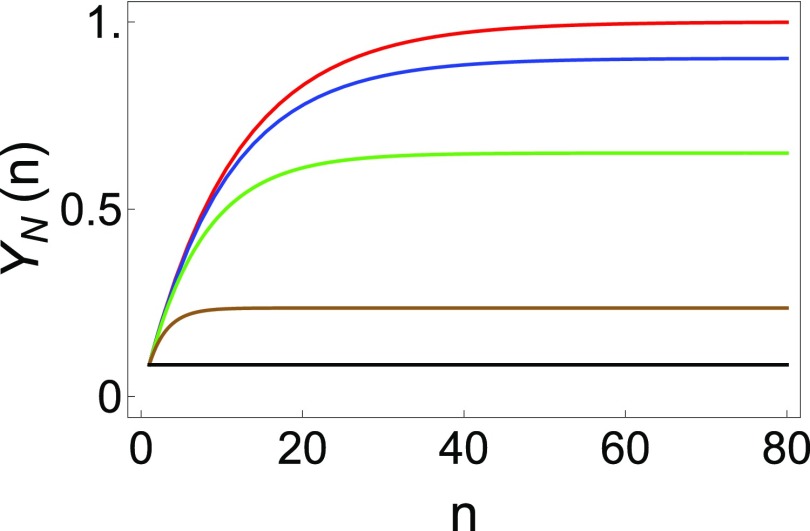
The generalized IAM (35) allows for the possibility of N state recognition by the RNA chaperone, CYT-19, which was not considered previously (42). The chaperone is allowed to act on the N state in addition to the M states of protein or RNA and redistributes again into N states and M states, where is the degree of discrimination by the chaperone between the N and M states. A fraction of the original native population remains unperturbed in the same N state. It is easy to show that the net gain in the fraction of N state after iterations is given by (where ). The total yield of the N state after iterations (Fig. 3) is therefore , and the conditions of and lead to:
| [7] |
The physical meaning of the discrimination factor, , is evident by making an approximate mapping of the long-time yield to the equivalent expression in our master-equation framework, . By substituting into Eq. 7 and taking the limit , we obtain , while with , , and reduces to . Therefore, is approximately the ratio of two rate constants associated with chaperonin-induced unfolding:
| [8] |
which is in accord with the intuitive definition of given in Eq. 7. It is worth noting that depends on the chaperone () and ATP () concentrations, which suggests that it is possible to reduce by increasing or . Evidently, for GroEL, because is negligible.
Fig. 3.
Generalized IAM for proteins and RNA, showing the effect of varying on the yield of the N state. Shown is the plot of the yield, (see Eq. 7), as a function of number of cycles . The native fraction in the limit of large therefore depends on , the efficiency of chaperone recognition of the N state: (red), (blue), (green), (brown), and (black).
CYT-19–Mediated Folding of Tetrahymena Ribozymes.
Since the discovery of self-splicing enzymatic activity in the group I intron Tetrahymena thermophila ribozyme (43–45), the Tetrahymena ribozyme has been the workhorse used to reveal the general principles of RNA folding. In accord with the KPM (Fig. 1), the value of of the WT Tetrahymena ribozyme that attains catalytic activity in the absence of CYT-19 is only 6% to 10% (at 25 ∘C), while the majority of ribozymes remain inactive (11, 13). In the case of the Tetrahymena ribozyme, it is suspected that the formation of incorrect base pairs stabilizes the misfolded conformations (46). For example, to disrupt a six base-paired helix, a secondary structure motif ubiquitous in RNA, the free energy barrier is 10 to 15 kcal/mol (=5 stacks 2 to 3 kcal/mol per stack). The timescale with s (47) for a spontaneous disruption of base stacks is estimated to be s. Thus, once trapped into a mispaired conformation, it is highly unlikely to autonomously resolve the kinetic trap on a biologically viable time scale (46).
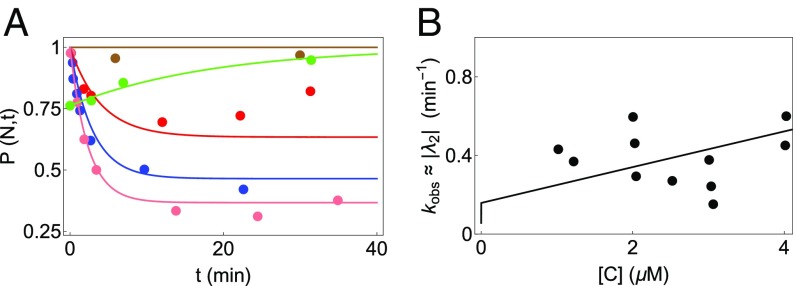
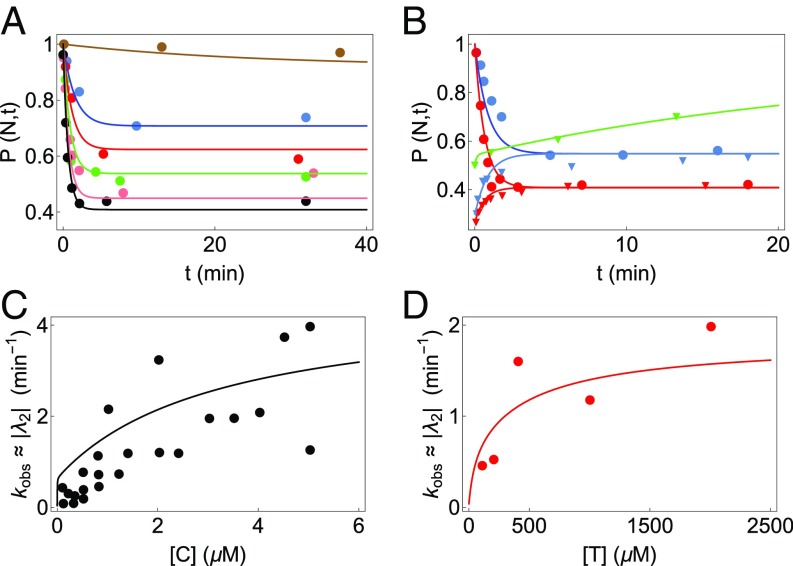
We first analyze the ability of CYT-19 to facilitate the folding of Tetrahymena ribozyme. Time-resolved kinetics of two variants [P5a mutant and P5abc-deleted (P5abc) ribozyme] as well as the WT of the ribozyme were probed by varying CYT-19 and ATP concentrations (30). We establish the validity of our theory by using Eq. S2 to quantitatively fit an array of experimental data on the WT and P5a mutant (Figs. 4A and 5 A and B, respectively). In the experiments, the fraction of native ribozyme was probed as a function of time, under different initial conditions: (i) starting from completely folded (N) ribozymes, (ii) starting from primarily misfolded (M) ribozymes, and (iii) CYT-19 chaperone inactivated by addition of proteinase K. To probe the effects of CYT-19 and ATP on the production of active (N) state, CYT-19 was varied for cases i and ii, and ATP concentration was varied for case i. In total, we used our theory to fit five sets of data for the WT (Fig. 4A) and 11 sets of data for the P5a variant (Fig. 5 A and B) ribozyme. By accounting quantitatively for the dataset, we extracted the best fit parameters, given in Table S1.
Fig. 4.
Analysis of CYT-19–mediated folding of the WT Tetrahymena ribozyme. Circles represent experimental data, while the curves are plots of Eq. S2. The five sets of data in A have been fit simultaneously to determine the best parameters for the WT (given in Table S1). (A) Kinetics of WT ribozyme in 2 mM ATP concentration for various concentrations of CYT-19: no CYT-19 (brown), 1 M CYT-19 (red), 2 M CYT-19 (blue), and 3 M CYT-19 (pink). The curve in green is obtained for a mixture of native and misfolded WT ribozymes when proteinase K is introduced to inactivate CYT-19. (B) Dependence of of WT ribozyme on CYT-19 (data from figure 1d of ref. 30). The curve is the CYT-19 dependence of the second eigenvalue obtained from our model (see Supporting Information), with parameters obtained from the fits in A. Given the large experimental uncertainty, only the trend “ increases as [C] increases” is meaningful.
Fig. 5.
Analysis of CYT-19–mediated folding of the P5a variant of Tetrahymena ribozyme. The circles and inverted triangles represent experimental data, while the curves are plots of Eq. S2. The 11 sets of data in A and B were fit simultaneously to determine best fit parameters (given in Table S1). (A) CYT-19 (1 M)-induced kinetics starting from the native P5a variant ribozyme in 5 mM at various ATP concentrations: no ATP (brown), 100 M ATP (blue), 200 M ATP (red), 400 M ATP (green), 1 mM ATP (pink), and 2 mM ATP (black). (B) Kinetics of P5a variant folding for different CYT-19 concentrations. Starting conditions were primarily native (circles) or primarily misfolded (triangles) P5a variants. Cyt-19 concentrations are 0.5 M (blue) and 1 M (red). The curve in green is obtained for a mixture of native and misfolded P5a variant ribozymes when proteinase K is introduced to inactivate CYT-19. (C and D) Dependence of of the P5a variant on CYT-19 (data from figure S3 of ref. 30) and ATP concentration (data from figure S4c of ref. 30), respectively. The lines are CYT-19 or ATP dependence of the second eigenvalue obtained from our model, with parameters obtained from the fits in A and B.
The overall trends in the parameters, extracted by simultaneous fit of the available data, are consistent with the direct experimental measurements and estimates (see Table S1). Note that some of the experimental results cited in Table S1 were performed under different conditions (temperature, ion concentration, or absence of CYT-19) than the experiments analyzed using our theory. These differences could affect the various rates and are pointed out in Table S1. For the P5a mutant, the fraction of ribozymes that fold directly to the N state was estimated to be (30), while (Eq. 1) calculated from our fitted values of and is . The free energy difference, , calculated from and gives 2.6 . This value is in rough accord with experimental results showing that the N state of P5a is less stable compared with the WT with (11, 48).
For all three variants of the ribozyme, one dominant eigenvalue () of the master equation formulation describes the overall kinetic behavior of the three-state model (see Supporting Information). Thus, the time evolution of the fraction of N state is primarily governed by the exponential term , making comparable to the experimentally observed rate . To assess the effect of varying ATP and CYT-19 concentrations on the chaperone-induced unfolding kinetics of the native ribozyme, we compared (computed from the parameters in Table S1) with data on as a function of CYT-19 (Fig. 4B for WT and Fig. 5C for P5a) and ATP concentration (Fig. 5D for P5a). The reasonable agreement of these curves with the experimental data and the best fit parameters with their corresponding experimentally measured values indicate that our kinetic model faithfully describes CYT-19–mediated folding/unfolding of Tetrahymena ribozyme. The agreement is especially satisfactory given the large scatter in the experimental data.
The ratio , which quantifies how indiscriminately the chaperone unwinds both the N and M states, is roughly 40 to 80 in the ribozyme M concentration range of CYT-19 and at 1 mM ATP using the parameters for the P5a variant in Table S1. We obtained qualitatively similar results if parameters from the WT are used. Since more of the P5a parameters could be robustly fit, we report for only the P5a variant.
Finally, to test the importance of the N state recognition by CYT-19, we analyzed how the long-term N state yield (Eq. 3) changes due to perturbations of the parameter around the best fit values of the WT ribozyme (Fig. S2). We also perturbed some of the other parameters that could conceivably be changed by making mutations in the chaperone domains—for example, the ATP hydrolysis rates and the binding constant (Fig. S2). Interestingly, is most sensitive to changes in compared with the other parameters (Fig. S2), thereby indicating that changes in recognition and binding of CYT-19 to native RNA can result in significant shifts in the final N state yield.
Additional Remarks for RNA Chaperones.
Besides ATP-driven rearrangements, certain DEAD-box proteins drive ATP-independent conversions between RNA structures as well (49, 50). However, the ATP independent process is highly inefficient and occurs at much lower rates than the ATP-driven structural rearrangements only when [protein] [substrate] (49, 50). In addition, Yang et al. (49) demonstrate that only the ATP-dependent rearrangements lead to substrate concentrations that are out of equilibrium. The ATP-independent pathways lead to equilibrium concentrations, exactly as our model predicts. Therefore, while the ATP-independent pathways are no doubt present, they are much slower, and hence the ATP-dependent pathways dominate.
Finally, although the Tetrahymena ribozyme is not a natural substrate for CYT-19 and therefore may not refold with maximal efficiency, our focus has been on explaining the differences in refolding driven by different concentrations of CYT-19. This analysis allowed us to show that regardless of the detailed mechanisms, the action of the chaperone is nonequilibrium in nature, with the thermodynamic driving force being ATP hydrolysis. In the presence of CYT-18, the molecular details of the RNA chaperone acting on Tetrahymena ribozyme will most likely be altered, but the nonequilibrium nature of the chaperone action captured by the three-state model will still be maintained.
GroEL-Mediated Folding of Rubisco and MDH.
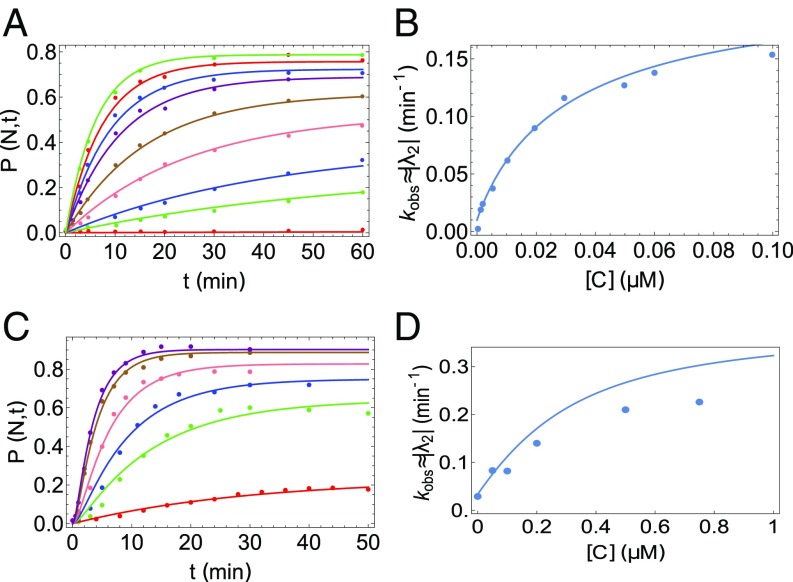
Rubisco is a stringent substrate for GroEL in the sense that the full machinery including ATP and GroES is required to ensure folding. In a previous study, the GroEL-assisted folding of Rubisco as a function of GroEL concentration was reported (17). Starting from acid-denatured Rubisco (in kinetically trapped M states), the yield of the N state increased with time upon addition of the chaperonin system (GroEL and GroES). Using our theory, we simultaneously fit the nine time-evolution curves, corresponding to nine different concentrations of GroEL using Eq. S2. From the results in Fig. 6, we draw the following general conclusions: (i) The excellent fit in Fig. 6A shows that the model quantitatively captures the kinetics of GroEL-assisted folding of Rubisco; (ii) the folding rate increases nonlinearly with GroEL concentration; and (iii) most importantly, the dependence of on chaperonin concentration shows that equilibrium is not reached at long times, despite GroEL being in far excess of the concentration of Rubisco. This crucial point, which also holds for CYT-19–assisted folding of Tetrahymena ribozyme, is further discussed below.
Fig. 6.
Using the kinetic model to analyze GroEL-assisted folding of Rubisco and MDH. (A) Quantitative fits of a time-dependent increase of folded Rubisco at various GroEL concentrations and 1 mM ATP using our kinetic model (data taken from ref. 17). Note that the y axis was converted to a fraction between 0 and 1 by dividing Rubisco concentrations by 50 nM, which was the starting concentration of acid-denatured protein in ref. 17. The concentrations of GroEL are (from bottom to top) 0, 1, 2, 5, 10, 20, 30, 50, and 100 nM. A single set of parameters, listed in Table S2, fits all of the curves. The dependence in the steady-state values of (60 min) is an indication of the departure from equilibrium. In all cases, (60 min) is less than the equilibrium value. (B) Dependence of the rate as a function of GroEL concentration for folding of Rubisco. (C) Fits of time-dependent increase of native MDH at various GroEL concentrations and ATP. Initial concentration of denatured MDH (dMDH) was 0.5 M. Concentrations of GroEL are (from bottom to top) 0, 0.05, 0.1, 0.2, 0.5, and 0.75 . (D) Dependence of the rate as a function of GroEL concentration for folding of MDH. In all panels the dots represent data from experiments, while the curves represent theoretical predictions.
The fitted parameters for GroEL-mediated folding of Rubisco (shown in Table S2) are consistent with previous experimental and theoretical results. From our fits, we obtain the partition factor remarkably close to the expected value from experiments and a previous theory (17). The binding rate of GroEL was measured to be (51), while we obtain . We compare the parameter values predicted using an entirely different kinetic model, describing the coupling between GroEL allosteric transitions during the folding of Rubisco (27). Though the details of the model are completely different from the present work, we can compare some results of both the models. Our estimate of the GroEL binding rate is consistent with the value of , and , extracted from their fits, was 0.02. The consistently small value of the partition factor implies that in a cycling system, which is most relevant for in vivo function of GroEL, only about 1% to 2% of Rubisco reaches the folded state in the absence of a chaperone.
We should point out that unlike the ribozyme analysis, there is not enough data in the GroEL–Rubisco experiment to extract and (and hence ) accurately. However, this does not affect any of the general results of this paper, as both and are small compared with all other rates and do not affect the values of the other parameters. Consistent with the idea that GroEL is much more selective in unfolding only the M states compared with CYT-19, we find using Eq. 8 and the parameters in Table S2 that for GroEL in the concentration range between M and 1 mM ATP concentration. Compared with the values of that we found for the ribozyme system, this result shows that GroEL is indeed much more effective in discriminating between the M and N states. The steady-state yield of the N state as a function of (Fig. 3), which can be altered by mutations (28), is a highly sensitive function of . Finally, we also use our model to analyze refolding data on the protein MDH. The excellent fit of data to our theory (Fig. 6C, parameters in Table S3) further validates the use of the stochastic three-state model to describe chaperone-assisted refolding of proteins. It is worth noting that even at substoichiometric quantities of GroEL, substantial yield of the N state is obtained (Fig. 6 A and C), albeit at lower rates (52). This is in contrast to what is expected in the folding assisted by the single ring GroEL mutant (SR1) from which GroES disassociates in 300 min. In this case, the maximum native yield is set by the concentration of SR1. In other words, each SR1 can at best process only one substrate molecule on time scales less than 300 min, which is far in excess of the typical bacterial cell doubling time. Similar to Tetrahymena ribozyme and Rubisco, the long-time native yield of MDH changes as the GroEL concentration changes, indicating that the steady state reached is far from equilibrium. Despite the fundamentally different mechanistic functions, our model provides a unified description of the action of both GroEL and CYT-19.
Protein and RNA Chaperones Function Far from Equilibrium.
The quality of our fits in Figs. 4–6 and the consistency of the fitted parameters with previous experimental results prove the validity of the theory to describe the general behavior of both protein and RNA chaperones. An important conclusion of our work is that the steady-state yield of N states does not approach a Boltzmann distribution dictated by equilibrium thermodynamics (see Supporting Information for more details). The value of is a function of both the chaperone concentration [C] as well as the ATP concentration [T], as is evident both from Eq. 3 and from the experimental data (Figs. 3–5). This is evidence of departure from equilibrium. For example, the experimentally measured stability of the WT ribozyme (11, 48) indicates that the equilibrium fraction of N state should be . The steady-state fractions of WT ribozyme in the presence of CYT-19 are, however, much less (Fig. 4A). Similarly, since we calculated the stability of the P5a variant of Tetrahymena ribozyme to be , equilibrium thermodynamics would predict a yield . Clearly, this yield is not reached for most concentrations of the chaperone (Fig. 5 A and B). The steady-state yields depend on both ATP and CYT-19, an indication that equilibrium is not reached. Since for Rubisco or MDH is not known to the best of our knowledge, we could not do the same analysis on Rubisco or MDH to estimate the native yield predicted by equilibrium thermodynamics. However, the observation that the steady-state yield of the N state changes with GroEL concentration (Fig. 6 A and C) shows that equilibrium is not attained in the Rubisco–GroEL/MDH systems either. In addition, it is clear from the rate parameters determined in our model that the local detailed balance condition is broken and that a nonzero probability current is established between any two states in the three-state model, further demonstrating that the steady state reached by the chaperone and the system is far from equilibrium (see Supporting Information for details).
Effect of Aggregation.
Note that our three-state model neglects any possibility of aggregation, which introduces at least one and likely many additional parameters. Could the different steady-state yields of substrate at different concentrations of chaperone (especially substoichiometric values; see Fig. 6 A and C) be a consequence of substrate aggregation? From the results in Table S2, we calculated the chaperone-driven rate that primarily brings misfolded Rubisco back into circulation ( is much smaller and can be neglected for this analysis). For the experiments shown in Fig. 6A, 50 nM denatured Rubisco was used, so GroEL concentrations of 1, 2, 5, 10, 20, and 30 nM are substoichiometric. The corresponding values of for these GroEL concentrations as predicted by our theory are 0.39, 0.77, 1.86, 3.58, 6.64, and 9.29 , respectively. On the other hand, using the estimate of for the second-order rate constant for Rubisco aggregation obtained by an elaborate framework (27) and using 50 nM for the misfolded Rubisco concentration (setting an upper limit for the aggregation rate), we find that the aggregation rate is . Note once again that this is an upper limit, and the true aggregation rate will be smaller since not all of the 50 nM Rubisco will be in the M state. Clearly, the aggregation rate is an order of magnitude smaller than for the smallest GroEL concentration used in Fig. 6A (1 nM), while it is over two orders of magnitude smaller when the GroEL concentration is 30 nM. This clearly demonstrates that even though aggregation could be present, it is much slower than the dynamics within the three states of the substrate. As a result, a steady-state probability current will be set up within the three states of I, M, and N on time scales faster than the cumulative rate of aggregation, resulting in the different steady-state concentrations observed for the different GroEL concentrations. These calculations are also in accord with the experimental observations of Rubisco (17) and MDH (36), where no visible aggregation was observed. Therefore, while aggregation likely plays some role in establishing the final steady-state yields, our calculations show that it makes a very minor contribution compared with the role of nonequilibrium dynamics.
Maximization of the Finite-Time Yield by Iterative Annealing and in Vivo Regulation of Chaperone Concentration.
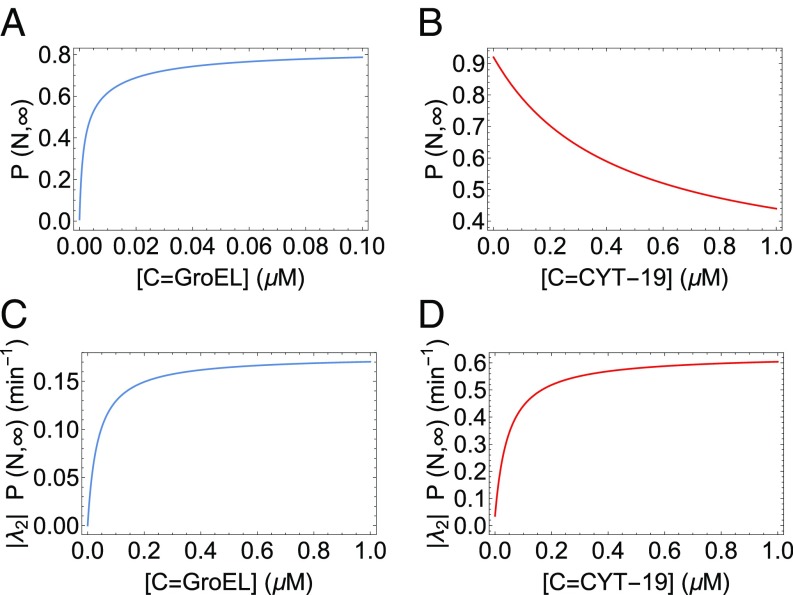
Do chaperones maximize either the absolute yield of the N states or the folding rate? Our theory suggests a general answer to this question in the unified scenario of both RNA and protein chaperones. Using the parameters in Tables S1 and S2, the steady-state native yield is plotted for both Rubisco and Tetrahymena ribozyme in Fig. 7 A and B. The figure highlights that increasing the chaperone concentration results in completely opposite behavior of the native yield for Rubisco and Tetrahymena ribozyme. This immediately suggests that the absolute value of the yield is not maximized, since increasing CYT-19 concentration decreases the native yield of the ribozyme (Fig. 7B). The folding rate () is not maximized either—Fig. 4B for the WT ribozyme and Fig. 5C for the P5a variant both show that the folding rate is an increasing function of CYT-19 concentration, even around . Our theory predicts that the folding rate saturates at much larger CYT-19 concentration (). At such high concentrations, however, the native yield of ribozyme would become very low (Fig. 7B), strongly indicating that neither the folding rate nor the nonequilibrium steady-state yield is maximized. This also suggests that the CYT-19 concentration cannot be arbitrarily large under in vivo conditions and that the chaperone concentrations must be regulated.
Fig. 7.
Maximization of the finite-time yield by iterative annealing. (A and B) Steady-state yield of the N state of Rubisco (A) and ribozyme (B), as functions of chaperone concentration. (C and D) Plots of for protein (C) and ribozyme (D), as functions of chaperone concentration. The curves in A and C were obtained using the best fit parameters for the GroEL–Rubisco system, given in Table S2. The curves in B and D have been produced using the best fit parameters for the mutant P5a ribozyme, given in Table S1. For all of the curves, the ATP concentration [T] was set to 1 mM. The qualitative results do not change for other concentrations of ATP.
Interestingly, the product quantifying the balance between folding rate and amount of steady-state yield reaches saturation at low values of chaperone concentration for both protein and RNA as shown in Fig. 7 C and D. is a monotonically increasing function of the chaperone concentration, reaching saturation values at for both the RNA and the protein. The same plot for MDH is shown in Fig. S1. This intriguing result shows that chaperone concentrations may well be regulated to be in the range of a few M such that is maximized (Fig. 7 C and D), thereby allowing for higher native yields in short biologically relevant times.
Finally, rough estimates of chaperone concentrations in vivo also support our results suggesting the maximization of . There are 10,300 molecules of the yeast RNA chaperone Mss116p (53, 54), which is structurally similar to CYT-19 and catalyzes the efficient splicing of yeast mitochondrial group I and II introns (54). Given an average yeast volume of 37 (55), the concentration of Mss116p is , which is in the saturation region of Fig. 7D. GroEL concentration in vivo is about 5.2 (there are 1,580 14-mer GroEL molecules in a volume of 1 in Escherichia coli, with the functional unit being the 7-mer). As can be seen from Fig. 7C and Fig. S2, a concentration of 5.2 is in the saturation region as well. These two results provide additional support to the idea that by functioning out of equilibrium it is possible to maximize the native yield in biologically relevant time scales under in vivo conditions.
Concluding Remarks
With a doubling time of about 2 hours, Tetrahymena are some of the fastest multiplying free-living eukaryotic cells (56). Therefore, the viable time scale for Tetrahymena ribozyme folding to the N state should be on the order of a few hours. Though a large fraction of the ribozyme ( with ) misfolds and stays kinetically trapped over time scales of days in vitro (11), experiments show that the addition of CYT-19 can accelerate the folding process to a matter of minutes (30). Surprisingly, however, increasing the CYT-19 concentration decreases the final yield of the N states, in stark contrast to GroEL-mediated folding of proteins, where increasing the chaperone concentration increases the native yield at long times.
In this work, we have developed a theoretical model to study the widely contrasting experimental results on protein and RNA chaperones. The representation of assisted folding of protein or RNA using a three-state stochastic model allowed us to explore the concepts of the kinetic partitioning factor (), native population at thermodynamic equilibrium (), and biologically relevant nonequilibrium steady-state yield of the N states []. By using a unified framework to analyze a wide array of data from CYT-19–dependent Tetrahymena ribozyme folding experiments and GroEL-mediated Rubisco and MDH folding studies, we show unequivocally that thermodynamic equilibrium is not attained in these systems. Rather, using energy from ATP hydrolysis. the chaperones drive the substrates out of equilibrium, thereby promoting higher native yields in short, biologically relevant time scales. This purely nonequilibrium effect is a result that is distinct from earlier experimental and theoretical works that have suggested interesting implications for the role of out-of-equilibrium dynamics on the conformational cycles of chaperones (57) and on the affinity of chaperones for their substrates (58).
The time to increase the native yield from to in the absence of chaperones is beyond biologically meaningful time scales. For example, min in the Tetrahymena ribozyme (11), which is far in excess of Tetrhymena cell doubling time. This must imply that the functions of molecular chaperones have evolved to maximize the yield in a given time, rather than the absolute yield. Assisted folding does not maximize the folding rates () either, as erroneously stated in studies based on the efficacy of artificial single mutant (SR1) of GroEL in rescuing SPs. The current work debunks the conclusions of such studies, which have inferred the function of GroEL based on SR1, which is at best a useful model in probing confinement effects on protein folding. Such studies have no relevance to the function of the full chaperonin machinery either in vitro or in vivo.
Just like error-correcting machineries in cellular processes (59, 60), molecular chaperones use energy from ATP hydrolysis to stochastically help fold biomolecules into the functionally active form on biologically meaningful time scales. Our work shows that both the RNA and protein chaperones, which bring systems out of equilibrium, have evolved to promote the finite-time yield of the N state and not simply the absolute yield or folding rate as conventionally surmised. Our results provide a unified framework for the role of chaperones in both protein and RNA folding and may have important implications in our understanding of both protein and RNA homeostasis (61, 62).
Methods
Theory.
The theory is based on the kinetic pathways outlined in Fig. 2, which is translated into the master equation given in Eq. 2. The solution to Eq. 2 and additional analyses presented in the main text can be found in Supporting Information.
MDH Experiments.
MDH was denatured in 6 M freshly prepared urea at a final concentration of 50 M for an hour. The recovery of enzymatic activity from the dMDH refolded in the presence of chaperonins was monitored spectroscopically. We diluted dMDH by 100-fold to a solution containing 50 mM Tris–OAc, pH 7.5, 100 mM KOAc, 10 mM Mg(OAc)2, 0.2 mM PEP, 1 mM DTT, 5 units PK, 12.5 M GroES, plus GroEL of concentration as indicated in the Fig. 6 legend. MDH refolding was carried out at 30 ∘C. The GroEL-assisted MDH refolding was initiated by addition of 1 mM ATP. At various time points, 10 of this refolding reaction was removed and diluted to the 890 L refolding quench solution containing 100 mM TrisOAc, pH 7.5, 50 mM EDTA, 0.15 mM NADH, and 1 M GroEL subunit (to capture free dMDH) and incubated on ice for at least 10 min before being subjected to MDH activity assay. The assay was carried out at 30 ∘C and initiated by addition of 0.5 mM oxaloacetate into the refolding quench solution. The decrease in absorbance at 340 nm was monitored over 4 min. The slopes of the steady-state trace of MDH at different time points were normalized to that of native MDH of the same concentration (5.6 nM) and expressed as percentage of MDH activity recovered. We should add that there was no evidence of aggregation of MDH even in the absence of GroEL, which justifies the neglect of aggregation pathways in the theoretical formulation.
Supplementary Material
Acknowledgments
Much of this work was done while S.C. and D.T. were at the Korea Institute for Advanced Study in 2013. We are grateful to the National Science Foundation (Grant CHE 16-36424) and the Collie-Welch Chair (F-0019) for supporting this work.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1712962114/-/DCSupplemental.
References
- 1.Anfinsen CB. Principles that govern the folding of protein chain. Science. 1973;181:223–230. doi: 10.1126/science.181.4096.223. [DOI] [PubMed] [Google Scholar]
- 2.Anfinsen CB, Scheraga HA. Experimental and theoretical aspects of protein folding. Adv Protein Chem. 1975;29:205–300. doi: 10.1016/s0065-3233(08)60413-1. [DOI] [PubMed] [Google Scholar]
- 3.Schuler B, Eaton WA. Protein folding studied by single-molecule FRET. Curr Opin Struct Biol. 2008;18:16–26. doi: 10.1016/j.sbi.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Thirumalai D, Klimov D, Dima R. Emerging ideas on the molecular basis of protein and peptide aggregation. Curr Opin Struct Biol. 2003;13:146–159. doi: 10.1016/s0959-440x(03)00032-0. [DOI] [PubMed] [Google Scholar]
- 5.Morris AM, Watzky MA, Finke RG. Protein aggregation kinetics, mechanism, and curve-fitting: A review of the literature. Biochim Biophys Acta. 2009;1794:375–397. doi: 10.1016/j.bbapap.2008.10.016. [DOI] [PubMed] [Google Scholar]
- 6.Gershenson A, Gierasch LM, Pastore A, Radford SE. Energy landscapes of functional proteins are inherently risky. Nat Chem Biol. 2014;10:884–891. doi: 10.1038/nchembio.1670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lorimer G. A quantitative assessment of the role of the chaperonin proteins in protein folding in vivo. FASEB J. 1996;10:5–9. doi: 10.1096/fasebj.10.1.8566548. [DOI] [PubMed] [Google Scholar]
- 8.Thirumalai D, Lorimer GH. Chaperonin-mediated protein folding. Ann Rev Biophys Biomol Struct. 2001;30:245–269. doi: 10.1146/annurev.biophys.30.1.245. [DOI] [PubMed] [Google Scholar]
- 9.Gruber R, Horovitz A. Allosteric mechanisms in chaperonin machines. Chem Rev. 2016;116:6588–6606. doi: 10.1021/acs.chemrev.5b00556. [DOI] [PubMed] [Google Scholar]
- 10.Goloubinoff P, Christeller JT, Gatenby AA, Lorimer GH. Reconstitution of active dimeric ribulose bisphosphate carboxylase from an unfolded state depends on two chaperonin proteins and Mg-ATP. Nature. 1989;342:884–889. doi: 10.1038/342884a0. [DOI] [PubMed] [Google Scholar]
- 11.Pan J, Thirumalai D, Woodson SA. Folding of RNA involves parallel pathways. J Mol Biol. 1997;273:7–13. doi: 10.1006/jmbi.1997.1311. [DOI] [PubMed] [Google Scholar]
- 12.Zhuang X, et al. A single-molecule study of RNA catalysis and folding. Science. 2000;288:2048–2051. doi: 10.1126/science.288.5473.2048. [DOI] [PubMed] [Google Scholar]
- 13.Thirumalai D, Lee N, Woodson SA, Klimov DK. Early events in RNA folding. Annu Rev Phys Chem. 2001;52:751–762. doi: 10.1146/annurev.physchem.52.1.751. [DOI] [PubMed] [Google Scholar]
- 14.Guo Z, Thirumalai D. Kinetics of protein folding: Nucleation mechanism, time scales, and pathways. Biopolymers. 1995;36:83–102. [Google Scholar]
- 15.Kiefhaber T. Kinetic traps in lysozyme folding. Proc Natl Acad Sci USA. 1995;92:9029–9033. doi: 10.1073/pnas.92.20.9029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jackson SA, Koduvayur S, Woodson SA. Self-splicing of a group I intron reveals partitioning of native and misfolded RNA populations in yeast. RNA. 2006;12:2149–2159. doi: 10.1261/rna.184206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Todd MJ, Lorimer GH, Thirumalai D. Chaperonin-facilitated protein folding: Optimization of rate and yield by an iterative annealing mechanism. Proc Natl Acad Sci USA. 1996;93:4030–4035. doi: 10.1073/pnas.93.9.4030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Horwich AL, Fenton WA. Chaperonin-mediated protein folding: Using a central cavity to kinetically assist polypeptide chain folding. Q Rev Biophys. 2009;42:83–116. doi: 10.1017/S0033583509004764. [DOI] [PubMed] [Google Scholar]
- 19.Hartl FU, Bracher A, Hayer-Hartl M. Molecular chaperones in protein folding and proteostasis. Nature. 2011;475:324–332. doi: 10.1038/nature10317. [DOI] [PubMed] [Google Scholar]
- 20.Chakraborty K, et al. Chaperonin-catalyzed rescue of kinetically trapped states in protein folding. Cell. 2010;142:112–122. doi: 10.1016/j.cell.2010.05.027. [DOI] [PubMed] [Google Scholar]
- 21.Betancourt MR, Thirumalai D. Exploring the kinetic requirements for enhancement of protein folding rates in the GroEL cavity. J Mol Biol. 1999;287:627–644. doi: 10.1006/jmbi.1999.2591. [DOI] [PubMed] [Google Scholar]
- 22.Klimov D, Newfield D, Thirumalai D. Simulations of -hairpin folding confined to spherical pores using distributed computing. Proc Natl Acad Sci USA. 2002;99:8019–8024. doi: 10.1073/pnas.072220699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Lalng C, Schlick T. Computational approaches to 3D modeling of RNA. J Phys Condens Matter. 2010;22:283101. doi: 10.1088/0953-8984/22/28/283101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lin Z, Madan D, Rye HS. GroEL stimulates protein folding through forced unfolding. Nat Struct Mol Biol. 2008;15:303–311. doi: 10.1038/nsmb.1394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Corsepius NC, Lorimer GH. Measuring how much work the chaperone GroEL can do. Proc Natl Acad Sci USA. 2013;110:E2451–E2459. doi: 10.1073/pnas.1307837110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Lin Z, Puchalla J, Shoup D, Rye HS. Repetitive protein unfolding by the trans ring of the GroEL-GroES chaperonin complex stimulates folding. J Biol Chem. 2013;288:30944–30955. doi: 10.1074/jbc.M113.480178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tehver R, Thirumalai D. Kinetic model for the coupling between allosteric transitions in GroEL and substrate protein folding and aggregation. J Mol Biol. 2008;377:1279–1295. doi: 10.1016/j.jmb.2008.01.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Sun Z, Scott DJ, Lund PA. Isolation and characterisation of mutants of GroEL that are fully functional as single rings. J Mol Biol. 2003;332:715–728. doi: 10.1016/s0022-2836(03)00830-1. [DOI] [PubMed] [Google Scholar]
- 29.Thirumalai D, Hyeon C. RNA and protein folding: Common themes and variations. Biochemistry. 2005;44:4957–4970. doi: 10.1021/bi047314+. [DOI] [PubMed] [Google Scholar]
- 30.Bhaskaran H, Russell R. Kinetic redistribution of native and misfolded RNAs by dead-box chaperone. Nature. 2007;449:1014–1018. doi: 10.1038/nature06235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Tijerina P, Bhaskaran H, Russell R. Nonspecific binding to structured RNA and preferential unwinding of an exposed helix by the CYT-19 protein, a DEAD-box RNA chaperone. Proc Natl Acad Sci USA. 2006;103:16698–16703. doi: 10.1073/pnas.0603127103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Sinan S, Yuan X, Russell R. The Azoarcus group I intron ribozyme misfolds and is accelerated for refolding by ATP-dependent RNA chaperone proteins. J Biol Chem. 2011;286:37304–37312. doi: 10.1074/jbc.M111.287706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Russell R, Jarmoskaite I, Lambowitz AM. Toward a molecular understanding of RNA remodeling by DEAD-box proteins. RNA Biol. 2013;10:44–55. doi: 10.4161/rna.22210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jarmoskaite I, Russell R. RNA helicase proteins as chaperones and remodelers. Annu Rev Biochem. 2014;83:697–725. doi: 10.1146/annurev-biochem-060713-035546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hyeon C, Thirumalai D. Generalized iterative annealing model for the action of RNA chaperones. J Chem Phys. 2013;139:121924. doi: 10.1063/1.4818594. [DOI] [PubMed] [Google Scholar]
- 36.Ye X. 2014. Developing a new model of the GroEL functional cycle and its implications for the GroEL-optimized substrate protein refolding. PhD thesis (University of Maryland, College Park)
- 37.Todd M, Viitanen P, Lorimer G. Dynamics of the chaperonin atpase cycle - Implications for facilitated protein-folding. Science. 1994;265:659–666. doi: 10.1126/science.7913555. [DOI] [PubMed] [Google Scholar]
- 38.Weissman J, et al. Mechanism of GroEL action - Productive release of polypeptide from a sequestered position under GroES. Cell. 1995;83:577–587. doi: 10.1016/0092-8674(95)90098-5. [DOI] [PubMed] [Google Scholar]
- 39.Liu F, Putnam A, Jankowsky E. ATP hydrolysis is required for DEAD-box protein recycling but not for duplex unwinding. Proc Natl Acad Sci USA. 2008;105:20209–20214. doi: 10.1073/pnas.0811115106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Guo Z, Thirumalai D. Kinetics of protein folding: Nucleation mechanism, time scales, and pathways. Biopolymers. 1995;36:83–102. [Google Scholar]
- 41.Russell R, Herschlag D. Probing the folding landscape of the tetrahymena ribozyme: Commitment to form the native conformation is late in the folding pathway. J Mol Biol. 2001;308:839–851. doi: 10.1006/jmbi.2001.4751. [DOI] [PubMed] [Google Scholar]
- 42.Orland H, Thirumalai D. A kinetic model for chaperonin assisted folding of proteins. J Phys France. 1997;7:553–560. [Google Scholar]
- 43.Cech TR, Zaug AJ, Grabowski PJ. In vitro splicing of the ribosomal-RNA precursor of Tetrahymena-involvement of a quianosine nucleotide in the excision of the intervening sequence. Cell. 1981;27:487–496. doi: 10.1016/0092-8674(81)90390-1. [DOI] [PubMed] [Google Scholar]
- 44.Kruger K, et al. Self-splicing RNA - Auto-excision and auto-cyclization of the ribosomal-RNA intervening sequence of Tetrahymena. Cell. 1982;31:147–157. doi: 10.1016/0092-8674(82)90414-7. [DOI] [PubMed] [Google Scholar]
- 45.Guerrier-Takada C, Altman S. Catalytic activity of an RNA molecule prepared by transcription in vitro. Science. 1984;223:285–286. doi: 10.1126/science.6199841. [DOI] [PubMed] [Google Scholar]
- 46.Pan J, Woodson SA. Folding intermediates of a self-splicing RNA: Mispairing of the catalytic core. J Mol Biol. 1998;280:597–609. doi: 10.1006/jmbi.1998.1901. [DOI] [PubMed] [Google Scholar]
- 47.Hyeon C, Thirumalai D. Chain length determines the folding rates of RNA. Biophys J. 2012;102:L11–L13. doi: 10.1016/j.bpj.2012.01.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Johnson TH, Tijerina P, Chadee AB, Herschlag D, Russell R. Structural specificity conferred by a group I RNA peripheral element. Proc Natl Acad Sci USA. 2005;102:10176–10181. doi: 10.1073/pnas.0501498102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Yang Q, Fairman ME, Jankowsky E. DEAD-box-protein-assisted RNA structure conversion towards and against thermodynamic equilibrium values. J Mol Biol. 2007;368:1087–1100. doi: 10.1016/j.jmb.2007.02.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Potratz JP, Campo MD, Wolf RZ, Lambowitz AM, Russell R. ATP-dependent roles of the DEAD-box protein Mss116p in group II intron splicing in vitro and in vivo. J Mol Biol. 2011;411:661–679. doi: 10.1016/j.jmb.2011.05.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Fenton WA, Horwich AL. GroEL-mediated protein folding. Protein Sci. 1997;6:743–760. doi: 10.1002/pro.5560060401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ranson NA, Dunster NJ, Burston SG, Clarke AR. Chaperonins can catalyse the reversal of early aggregation steps when a protein misfolds. J Mol Biol. 1995;250:581–586. doi: 10.1006/jmbi.1995.0399. [DOI] [PubMed] [Google Scholar]
- 53.Ghaemmaghami S, et al. Global analysis of protein expression in yeast. Nature. 2003;425:737–741. doi: 10.1038/nature02046. [DOI] [PubMed] [Google Scholar]
- 54.Huang HR, et al. The splicing of yeast mitochondrial group I and group II introns requires a DEAD-box protein with RNA chaperone function. Proc Natl Acad Sci USA. 2005;102:163–168. doi: 10.1073/pnas.0407896101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Tyson CB, Lord PG, Wheals AE. Dependency of size of Saccharomyces cerevisiae cells on growth rate. J Bacteriol. 1979;138:92–98. doi: 10.1128/jb.138.1.92-98.1979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Asai DJ, Forney JD. ASfCB 2000. Tetrahymena thermophila (Academic Press, San Diego, CA)
- 57.Frank GA, et al. Out-of-equilibrium conformational cycling of GroEL under saturating ATP concentrations. Proc Natl Acad Sci USA. 2010;107:6270–6274. doi: 10.1073/pnas.0910246107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Barducci A, De Los Rios P. Non-equilibrium conformational dynamics in the function of molecular chaperones. Curr Opin Struct Biol. 2015;30:161–169. doi: 10.1016/j.sbi.2015.02.008. [DOI] [PubMed] [Google Scholar]
- 59.Hopfield JJ. Kinetic proofreading: A new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc Natl Acad Sci USA. 1974;71:4135–4139. doi: 10.1073/pnas.71.10.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Hartwell LH, Hopfield JJ, Leibler S, Murray AW. From molecular to modular cell biology. Nature. 1999;402:C47–C52. doi: 10.1038/35011540. [DOI] [PubMed] [Google Scholar]
- 61.Santra M, Farrell DW, Dill KA. Bacterial proteostasis balances energy and chaperone utilization efficiently. Proc Natl Acad Sci USA. 2017;114:E2654–E2661. doi: 10.1073/pnas.1620646114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Huang L, et al. RNA homeostasis governed by cell type-specific and branched feedback loops acting on NMD. Mol Cell. 2011;43:950–961. doi: 10.1016/j.molcel.2011.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.