Abstract
Neurofeedback studies using real-time functional magnetic resonance imaging (rt-fMRI) have recently incorporated the multi-voxel pattern decoding approach, allowing for fMRI to serve as a tool to manipulate fine-grained neural activity embedded in voxel patterns. Because of its tremendous potential for clinical applications, certain questions regarding decoded neurofeedback (DecNef) must be addressed. Specifically, can the same participants learn to induce neural patterns in opposite directions in different sessions? If so, how does previous learning affect subsequent induction effectiveness? These questions are critical because neurofeedback effects can last for months, but the short- to mid-term dynamics of such effects are unknown. Here we employed a within-subjects design, where participants underwent two DecNef training sessions to induce behavioural changes of opposing directionality (up or down regulation of perceptual confidence in a visual discrimination task), with the order of training counterbalanced across participants. Behavioral results indicated that the manipulation was strongly influenced by the order and the directionality of neurofeedback training. We applied nonlinear mathematical modeling to parametrize four main consequences of DecNef: main effect of change in confidence, strength of down-regulation of confidence relative to up-regulation, maintenance of learning effects, and anterograde learning interference. Modeling results revealed that DecNef successfully induced bidirectional confidence changes in different sessions within single participants. Furthermore, the effect of up- compared to down-regulation was more prominent, and confidence changes (regardless of the direction) were largely preserved even after a week-long interval. Lastly, the effect of the second session was markedly diminished as compared to the effect of the first session, indicating strong anterograde learning interference. These results are interpreted in the framework of reinforcement learning and provide important implications for its application to basic neuroscience, to occupational and sports training, and to therapy.
Keywords: fMRI neurofeedback, MVPA, nonlinear modeling, confidence
Introduction
Real-time functional magnetic resonance imaging (rt-fMRI) neurofeedback has enjoyed a considerable rise in interest in recent years, both as a tool for addressing basic neurobiological questions as well as for potential clinical applications (deCharms 2008; Sulzer et al. 2013; Kim & Birbaumer 2014; Sitaram et al. 2016). Whereas most previous studies have mainly focused on participants’ learning to self-regulate a univariate blood-oxygen-dependent-level (BOLD) signal in specific brain areas (Weiskopf et al. 2003; deCharms et al. 2004; Birbaumer et al. 2013; Sulzer et al. 2013), recently rt-fMRI neurofeedback has incorporated connectivity-based approaches (Sulzer et al. 2013; Koush et al. 2013; Koush et al. 2015; Megumi et al. 2015) and multi-voxel pattern analysis (MVPA) [or decoding analysis, (Kamitani & Tong 2005)], opening a new range of possibilities (LaConte et al. 2007; LaConte 2011; Shibata et al. 2011; deBettencourt et al. 2015). Here we investigate some properties of the relatively new procedure called decoded neurofeedback (DecNef), specifically focusing on: bidirectional behavioral changes, the magnitude of each training direction, and the effects of order of training, such as the maintenance of training effects over time and interference between training sessions.
Previously, up-and-down regulation of univariate BOLD signal within a single participant in interleaved block designs of rt-fMRI neurofeedback has been shown to be possible (Weiskopf et al. 2004; deCharms 2008). Subsequently, functional connectivity between regions, as well as univariate activity within specific areas, was shown to be be increased or decreased upon training (Scheinost et al. 2013; Veit et al. 2012). Using a multivariate neurofeedback approach Shibata and colleagues (Shibata et al. 2016) similarly trained participants to activate or deactivate multi-voxel patterns associated with facial attractiveness. In a between-subjects design, different groups of participants learned to activate or deactivate the relevant neural representation, and these led to subsequent increases or decreases in facial-preference ratings (Shibata et al. 2016).
In many of these previous studies participants were given explicit strategies for neural induction (e.g., which neural loci to manipulate) through verbal instructions. In contrast, some other rt-fMRI neurofeedback studies succeeded in training subjects to activate or deactivate (patterns of) neural activity or connectivity covertly without explicit instruction about the target of induction or the purpose of the training (Bray et al. 2007; Megumi et al. 2015; Shibata et al. 2016; Ramot et al. 2016). In these studies participants were simply told to focus somehow on their mental activity in each trial, after which a feedback signal was given that indicated the extent of the reward. Although both approaches have previously been used, there is currently an open debate in the field on which strategy - explicit vs. implicit instruction - is preferable and is most effective (Sulzer et al. 2013; Sitaram et al. 2016).
Nevertheless, since explicit instructions do not seem to be necessary, fMRI neurofeedback can be treated as a neural operant conditioning or reinforcement learning process (Birbaumer et al. 2013; Koralek et al. 2012). From this perspective it is worth noting that so far, to the best of our knowledge, no study has successfully demonstrated opposing behavioral changes for different neurofeedback manipulations within single participants. This open question is important for both practical as well as scientific reasons. Scientifically, as in optogenetics studies in rodents (Deisseroth 2010; Deisseroth 2015) and brain stimulation approaches in humans (Wagner et al. 2007), to rigorously prove the causal relationships between brain activity and behaviors it is desirable to be able to induce and suppress the same pattern of brain activities. Importantly, it is necessary to confirm that these indeed lead to opposite behavioral effects within the same participants. Practically, these considerations are also very important for future studies in basic neuroscience, for therapy and clinical applications of DecNef, as well as if this is to be used for occupational and sport training.
Considering neurofeedback from the perspective of reinforcement learning highlights why manipulating activity in both directions within the same participants may pose specific challenges. Interference of learning across training sessions is expected when we attempt opposite behavioral manipulations in succession. These effects of interference have been studied extensively in motor and visuomotor learning, with various elegant studies showing that previous learning can hinder or interfere with the subsequent practice of a second task (Brashers-Krug et al. 1996; Krakauer et al. 1999; Osu et al. 2004). Interference can be retrograde or anterograde depending on the direction in time of the learning/memory effects. In a classic A1BA2 paradigm, participants are instructed to sequentially learn Task A, Task B, and then Task A again. Retrograde effects reflect how learning of Task B affects the memory maintenance of Task A1, while anterograde effects reflect how the memory of Task A1 affects the learning of Task B (Sing & Smith 2010). Anterograde interference has received less attention in the literature (Sing & Smith 2010). Interference effects have also been shown to be present in perceptual learning (Seitz et al. 2005; Yotsumoto et al. 2009). Hence, anterograde interference of learning resulting from the bidirectional use of DecNef manipulations within participants may prove two aspects: (1) behavioral changes are the result of a true learning process and, (2) behavioral effects should be long lasting.
We therefore aimed to address the following three questions in this research. First, if some behavioral change is induced by a neurofeedback manipulation, is it possible to develop another neurofeedback manipulation to cancel out the first behavioral change? Second, how long is the behavioral change maintained after neurofeedback manipulation? Third, how much interference occurs when two different neurofeedback manipulations are conducted in single participants? The first question is important because it is desirable to have the ability to cancel out negative side effects, should these occur. The second question is related to the efficiency of neurofeedback as a therapeutic method. Megumi et al. showed that 4 days of functional connectivity neurofeedback (FCNef) changed resting-state functional connectivity, and these effects lasted more than two months (Megumi et al. 2015). Amano et al. showed that 3 days of DecNef induced associative learning between color and orientation lasting for 3 to 5 months (Amano et al. 2016). However, there is no quantitative study examining mid-term effects; for example, to what extent are neurofeedback effects maintained one week after manipulation? The third point is ethically important in considering cross-over designs as candidate paradigms for randomized control trials to show statistical effectiveness of neurofeedback therapy. If two different neurofeedback manipulations interfere severely within single patients, a cross-over design is not a suitable option.
To address these questions, here we used DecNef to manipulate a specific cognitive representation - perceptual confidence - bidirectionally, i.e., up (increase confidence), and down (decrease confidence).
Perceptual confidence can be best interpreted as the degree of certainty in one’s own perceptual decisions. Several studies have linked frontoparietal areas with the computation of perceptual confidence, in humans (Huettel et al. 2005; Fleming et al. 2010; Rounis et al. 2010; Simons et al. 2010; De Martino et al. 2012; Zizlsperger et al. 2014; Rahnev et al. 2016) as well as in primates (Kiani & Shadlen 2009; Fetsch et al. 2014) and rats (Kepecs et al. 2008; Lak et al. 2014). Specifically, dorsolateral prefrontal cortex (dlPFC) as well as inferior parietal cortex seem to play a crucial role. For example, gray matter thickness in the dlPFC correlated with metacognitive abilities of participants (Fleming et al. 2010), and transcranial magnetic stimulations (TMS) applied over loci within the dlPFC have been shown to selectively disrupt confidence judgements (Rounis et al. 2010). A recent study has highlighted the temporal structure of confidence processing in cortical areas, demonstrating that electrophysiological correlates of decision confidence can be detected in the left parietal cortex (Zizlsperger et al. 2014).
We first constructed a classifier for high versus low confidence by utilizing MVPA in four bilateral, anatomically defined regions of interest (ROIs): the inferior parietal lobule (IPL), and three subregions of the dlPFC - the inferior frontal sulcus (IFS), middle frontal sulcus (MFS) and middle frontal gyrus (MFG). Next, with a within-subjects design, participants learned to implicitly induce multi-voxel activation patterns reflecting high and low confidence (Up- and Down-DecNef, respectively) over two weeks. In both weeks, induction sessions took place across two consecutive days, and confidence changes were measured with a Pre- and Post-Test, immediately before and after the fMRI induction session. Participants were randomly assigned to one of two groups, defining the order of induction (Up- then Down-DecNef or vice versa). The second DecNef session was carried out one week after the first, in order to measure whether effects would survive after a one-week interval. To best capture the differential effects of DecNef on confidence judgements, we utilized nonlinear equation modeling.
Materials and methods
1. Participants and Experimental Design
All experiments and data analyses were conducted at the Advanced Telecommunications Research Institute International (ATR). The study was approved by the Institutional Review Board of ATR. All participants gave prior written informed consent. A companion paper (Cortese et al. 2016) was published elsewhere, which discussed implications of the results for neural mechanisms of metacognitive functions, especially perceptual confidence and conscious awareness. The experimental data used here is exactly the same, but the research objectives of the two manuscripts are different.
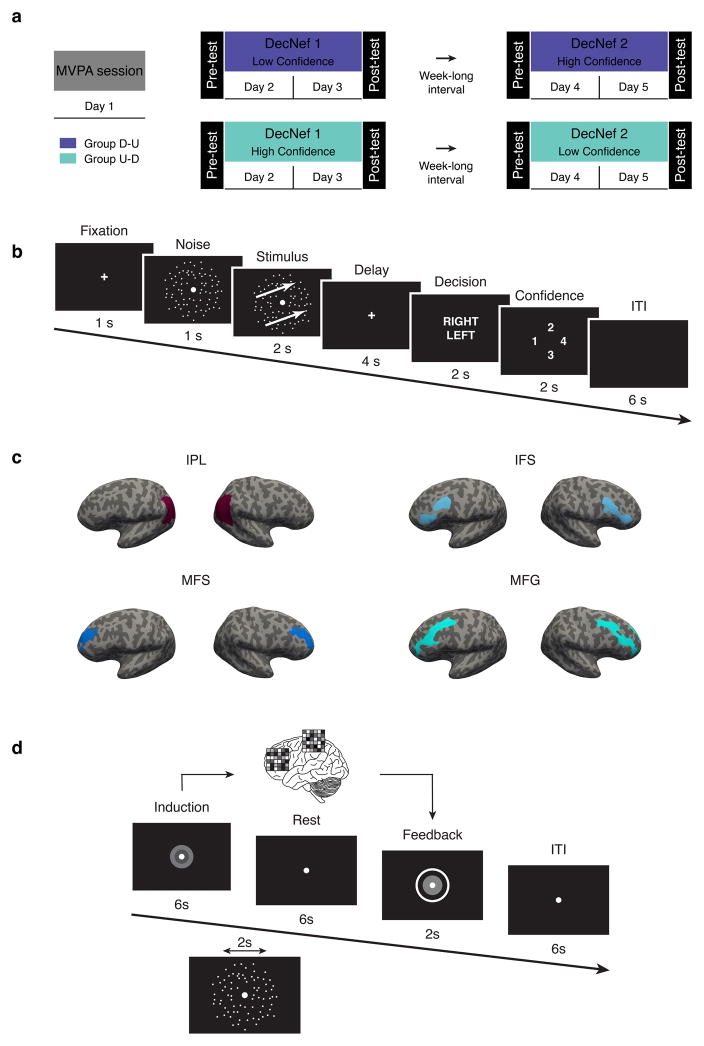
The entire experiment was subdivided into 4 fMRI sessions, spanning over 6 scanning days. In the first session, participants took part in a retinotopy scan, followed by an MVPA session, on separate days (Fig. 1A, the retinotopy data was used to functionally define visual areas but was not used for any of the analyses pertaining to this manuscript, and thus not shown in the figure). During the MVPA session participants performed a 2-alternative forced choice discrimination task with confidence judgements while in the fMRI scanner. This allowed us to decode the activation patterns corresponding to certain levels of perceptual confidence, which were to be manipulated with DecNef. After MVPA, participants undergoing DecNef training were randomly assigned to one of two groups, with different orders of training: Down-Up group (aiming to induce Low confidence, then High confidence, D-U throughout the manuscript) or Up-Down group (aiming to induce High confidence, then Low confidence; U-D throughout the manuscript). The experimenter was not blinded to group assignment, while participant were unaware of the aims of training nor of group assignment. The confidence change between before vs. after DecNef, defined as changes in confidence in the psychophysical tasks, is our primary dependent variable of interest.
Fig. 1.
Experiment timeline and design. (a) The entire experiment consisted of 6 fMRI scanning days grouped into 4 ‘sessions’. The first two days were identical for all participants: a retinotopy session to functionally define visual areas, followed by an MVPA session, during which participants of both groups performed in a 2-forced choice discrimination task with confidence rating. Participants were then randomly assigned to either group D-U or group U-D. For the subsequent DecNef sessions (day 3–4 and 5–6), group U-D first underwent High Confidence followed by Low Confidence DecNef, while group D-U did the reverse sequence. In order to examine the change in confidence due to DecNef, each DecNef session was preceded and followed by a Pre- and Post-test (on the same days), a psychophysical assessment using the same behavioral task employed in the MVPA session. (b) In the MVPA session, and in Pre- and Post-Tests, each trial started with a fixation cross, followed by a noise random dot motion (RDM). The stimulus was then presented, consisting of a coherent RDM with either rightward or leftward motion. After a 4 secs delay, participants were required to report the direction of motion (left or right) and their confidence in their decision of direction during a fixed time window. A trial ended with a 6 secs ITI. Three TRs, starting at stimulus presentation onset, were averaged and used for the actual MVPA. (c) Bilateral frontoparietal ROIs used for MVPA and DecNef, from a representative participant. Each ROI is depicted on an inflated cortical surface for both the right and left hemispheres. IPL: inferior parietal lobule, IFS: inferior frontal sulcus, MFS: middle frontal sulcus, MFG: middle frontal gyrus. (d) A neurofeedback trial commenced with a visual cue indicating the induction period, during which participants were asked to “manipulate, change their brain activity in order to maximize the size of the feedback disc and the reward.” Importantly, the disc for feedback after the induction period equally needed to be maximized both for up- and down- regulation. Induction was followed by a rest period, then the feedback disc was presented for 2 secs and a trial ended with a 6 secs ITI. Group D-U: Down- then Up-DecNef, group U-D: Up- then Down-DecNef; ITI: intertrial interval.
Eighteen participants (23.7 ± 2.5 years old; 4 female) with normal or corrected-to-normal vision were enrolled in the first part of the study (MVPA session). One participant was removed due to corrupted data. Participants were screened out either if they could not or declined to come back for the DecNef sessions, or due to low decoding accuracy (< 55% in more than two ROIs, based on previous work (Amano et al. 2016)). Ten participants performed the full DecNef experiments (24.2 ± 3.2 years old, 3 female). For transparency, Table 1 reports the decoding results of the 17 subjects for which the decoding analysis was run.
Table 1.
Classification of confidence (high vs. low) with permutation testing (n = 1000) for statistical significance evaluation. Columns (4) represent the four ROIs of interest, chosen a priori based on previous studies highlighting their importance in the computation of confidence judgements. Rows represent individual participant’s data, with the first 10 having participated in the full DecNef training program.
| IPL | IFS | MFS | MFG |
|---|---|---|---|
| 69.5 ± 8.3, P = 0.0010 | 80.0 ± 8.2, P = 0.0010 | 61.5 ± 8.4, P = 0.0020 | 66.0 ± 6.5, P = 0.0010 |
| 56.4 ± 7.3, P = 0.0270 | 58.9 ± 5.3, P = 0.0020 | 53.2 ± 7.9, P = 0.2038 | 58.9 ± 7.5, P = 0.0110 |
| 65.0 ± 3.1, P = 0.0010 | 68.9 ± 5.6, P = 0.0010 | 72.3 ± 3.6, P = 0.0010 | 71.4 ± 4.9, P = 0.0010 |
| 53.2 ± 6.3, P = 0.1968 | 58.5 ± 5.5, P = 0.0110 | 55.0 ± 7.0, P = 0.0989 | 64.2 ± 5.7, P = 0.0010 |
| 64.4 ± 6.7, P = 0.0010 | 61.3 ± 2.9, P = 0.0020 | 69.4 ± 4.6, P = 0.0010 | 61.9 ± 6.3, P = 0.0010 |
| 55.0 ± 7.5, P = 0.0649 | 53.3 ± 6.5, P = 0.1738 | 59.4 ± 7.5, P = 0.0010 | 61.1 ± 5.0, P = 0.0020 |
| 72.6 ± 7.0, P = 0.0010 | 75.5 ± 4.4, P = 0.0010 | 63.1 ± 6.5, P = 0.0010 | 85.5 ± 4.4, P = 0.0010 |
| 66.0 ± 6.1, P = 0.0010 | 69.3 ± 4.9, P = 0.0010 | 69.7 ± 4.8, P = 0.0010 | 64.7 ± 5.1, P = 0.0010 |
| 69.3 ± 5.8, P = 0.0010 | 63.8 ± 3.4, P = 0.0010 | 61.0 ± 3.0, P = 0.0010 | 69.0 ± 6.1, P = 0.0010 |
| 65.0 ± 6.4, P = 0.0010 | 63.7 ± 5.4, P = 0.0010 | 67.5 ± 3.3, P = 0.0010 | 75.0 ± 3.7, P = 0.0010 |
| 67.9 ± 6.5, P = 0.0010 | 68.5 ± 2.7, P = 0.0010 | 68.5 ± 4.6, P = 0.0010 | 74.0 ± 4.0, P = 0.0010 |
| 57.5 ± 5.0, P = 0.0270 | 62.5 ± 4.9, P = 0.0010 | 75.0 ± 6.7, P = 0.0010 | 67.5 ± 5.3, P = 0.0010 |
| 71.4 ± 5.0, P = 0.0010 | 59.5 ± 7.2, P = 0.0050 | 67.6 ± 5.3, P = 0.0010 | 68.6 ± 7.1, P = 0.0010 |
| 60.2 ± 5.5, P = 0.0010 | 51.0 ± 4.0, P = 0.3866 | 83.8 ± 4.2, P = 0.0010 | 68.8 ± 5.4, P = 0.0010 |
| 74.8 ± 5.2, P = 0.0010 | 56.4 ± 3.6, P = 0.0350 | 64.0 ± 6.4, P = 0.0010 | 62.1 ± 5.1, P = 0.0020 |
| 71.7 ± 5.6, P = 0.0010 | 67.9 ± 6.3, P = 0.0010 | 62.9 ± 4.1, P = 0.0010 | 77.5 ± 3.5, P = 0.0010 |
| 70.0 ± 9.7, P = 0.0010 | 65.8 ± 6.5, P = 0.0010 | 65.0 ± 7.6, P = 0.0010 | 57.5 ± 5.3, P = 0.0320 |
2. Stimuli, Behavioral Task and DecNef Designs
2.1 Behavioral task
The behavioral task was the same for both MVPA, and Pre-/Post-Tests. In behavioral Pre- and Post-Tests, participants performed the task on a standard computer and gave responses with a standard keyboard outside of the fMRI scanner. In the MVPA session, participants gave their responses via a 4-buttons pad while in the scanner.
The behavioral task was a motion discrimination task with two-alternative forced choice of motion direction and confidence rating using random dot motion (RDM, Fig. 1B). Participants were instructed to indicate the perceived direction of motion (left or right) after a short delay following stimulus presentation, and rate the level of confidence about their perceptual decision (4-point scale). This kind of scale is commonly used in confidence studies as it allows greater sensitivity for participants’ trial-by-trial confidence judgements in ambiguous perceptual decisions compared with a simpler two-options rating (such as high or low) (Fleming et al. 2015). The majority of trials (62.5% of the total number) had threshold coherence of motion, that is, motion coherence that lead to the targeted psychological threshold, midway between floor and ceiling performance. The rest of the trials were divided between catch trials (no coherence, 25% of the total number of trials) and high coherence trials (80% coherence, 12.5% of the total number of trials). The order was randomized within and across runs. This configuration of motion coherences was selected in order to prevent slow drifts in bias (individual criterion in responding) across runs. For all analyses (both behavioral and with fMRI data), only trials at threshold motion coherence were utilized. Thus, for these trials the motion direction was ambiguous, and performance - i.e., task accuracy - in judging the motion direction was not significantly different from the targeted psychological threshold level of 75% correct (76.6% ± 1.5%, t(16) = 1.475, P = 0.16) during the MVPA scanning session.
2.2 Visual stimuli
All stimuli were created and presented with Matlab (Mathworks) using the Psychophysics Toolbox extensions Psychtoolbox 3 (Brainard 1997). Visual stimuli were presented on an LCD display (1024 × 768 resolution, 60Hz refresh rate) during titration and the Pre- and Post-Test stages, and via an LCD projector (800 × 600 resolution, 60Hz refresh rate) during fMRI measurements in a dim room. Stimuli were shown on a black background and consisted of RDM. We used the Movshon-Newsome (MN) RDM algorithm (Shadlen & Newsome 2001). The stimulus was created in a square region of 20×20 deg, but only the region within a circular annulus was visible (outer radius: 10 deg, inner radius: 0.85 deg). Dot density was 0.5 deg−2 (contrast 100%), with a speed of 9 deg/sec and size of 0.12 deg. Signal dots all moved in the same direction (left or right, non-cardinal directions of 20 deg and 200 deg) whereas noise dots were randomly replotted. Dots leaving the square region were replaced with a dot along one of the edges opposite to the direction of motion, and dots leaving the annulus were faded out to minimize edge effects.
2.3 fMRI scans for MVPA
The purpose of the fMRI scans in the MVPA session was to obtain the fMRI signals corresponding to high and low confidence levels. These confidence measures would then be used as labels to compute the parameters for the decoders used in the MVPA and DecNef sessions (Shibata et al. 2011).
During the MVPA session, participants performed a perceptual discrimination task with a confidence rating in the fMRI scanner (see above, subsection “Behavioral task” and Fig. 1B). Throughout the fMRI runs, participants were asked to fixate on a white cross (size 0.5 deg) presented at the center of the display. A brief break period was provided after each run upon participant’s request. Each fMRI run consisted of 16 task trials (1 trial = 18 secs; Fig. 1B), with a 20 secs fixation period before the first trial (1 run = 308 secs). The entire session consisted of 12 runs. The fMRI data for the initial 20 secs of each run were discarded due to possible unsaturated T1 effects. During the response period, participants were instructed to use their dominant hand to press the button on a response pad. Concordance between responses and buttons was indicated on the screen and, importantly, randomly changed across trials to avoid motor preparation confounds (i.e., associating a given response with a specific button press).
2.4 fMRI scans preprocessing
The fMRI signals in native space were preprocessed using custom software (mrVista software package for MATLAB, freely available at http://vistalab.stanford.edu/software/). The mrVista package uses functions and algorithms from the SPM suite (freely available at http://www.fil.ion.ucl.ac.uk/spm/). All functional images underwent 3D motion correction. Hemi-lateral ROIs were anatomically defined through cortical reconstruction and volumetric segmentation using the Freesurfer image analysis suite, which is documented and freely available for download online (http://surfer.nmr.mgh.harvard.edu/). We used the standard ‘Destrieux’ cortical atlas, based on a parcellation scheme that divides the cortex into gyral and sulcal regions (Destrieux et al. 2010) in each hemisphere. Bilateral ROIs were then created by merging the corresponding single left and right hemi-lateral ROIs. Once the ROIs were identified (see Fig. 1C), time-courses of BOLD signal intensities were extracted from each voxel in each ROI and shifted by 6 secs to account for the hemodynamic delay using the Matlab software. A linear trend was removed from the time-course, and the time-course was z-score normalized for each voxel in each run to minimize baseline differences across runs. The data samples for computing the MVPA were created by averaging the BOLD signal intensities of each voxel for 3 volumes, corresponding to the 6 secs from stimulus onset to response onset.
2.5 MVP Analyses
2.5.1 Algorithm
We used sparse logistic regression (SLR) (Yamashita et al. 2008), which automatically selects the relevant voxels in the ROIs for MVPA, to construct individual binary classifiers based on the main behavioral variable of interest: confidence (high vs. low, correct trials only to increase the S/N ratio). Although confidence was rated with a 4-point scale, we used SLR to classify confidence, as opposed to sparse linear regression (SLiR), because the aim was to investigate the bidirectionality of a neurofeedback manipulation within single participants. As such, it was desirable to have a binary classifier, leading to two experimental training sessions, such as induction of High- and Low-Confidence.
2.5.2 Datasets and cross-validation
For each participant’s MVPA we performed a k-fold cross-validation, where the entire data set is repeatedly subdivided into a “training set” and a “test set”. The two data sets can be seen as independent since they were used to fit the parameters of a model (decoder) and evaluate the predictive power of the trained (fitted) model, respectively. For each participant, the number of folds was automatically adjusted between k = 9 and k = 11 in order to approximately equate the number of samples between the data sets. Thus, the number of folds in each cross-validation procedure was ~10, a typical value for k-fold cross-validation procedures (Tong & Pratte 2012). Furthermore, the classification by SLR was optimized with an iterative approach (i-SLR of Hirose et al. 2015). That is, in each fold of the cross-validation, the process was repeated 10 times. On each iteration, the selected features were removed from the pattern vectors, and only the features with unassigned weights were used for the next iteration. At the end of the k-fold cross-validation, the test accuracy was averaged for each iteration across folds, in order to evaluate the accuracy at each iteration. The optimal number of SLRs (number of iterations) was then chosen and used for the final computation of the decoder used in the neurofeedback training procedure (Supplementary Note 1). Because confidence was rated on a 4-point scale, we assigned the intermediate ratings (2, 3) to the low- and high-confidence classes, respectively, in order to collapse the 4 initial confidence levels to 2, and equate the number of trials in each class. For each participant, first we merged one intermediate level with the high- (level 4) or low-confidence (level 1) class depending on the total number of trials. Then, to equate the number of trials, we randomly sampled trials from the left-out intermediate confidence level to the class now having a lower total number of trials. This re-balancing was based on the confidence rating response distribution, and on the final number of trials, and was repeated n times (n = 10, due to the low number of resampled trials). In order to directly compare the information contained in multivoxel patterns pertaining to the confidence dimension across the four ROIs, the best sample set was voted by k-fold cross-validation mean accuracy, given the a priori assumption that these areas are critical for generating confidence. Therefore, once a sample set was selected, the cross-validation mean accuracy for that particular set was used for each ROI, thus ensuring that exactly the same information was used. Importantly, the calculation of weights used for DecNef was done by using the entire data set of correct trials (without cross-validation) and the optimal number of iterations (as described above).
To evaluate the statistical significance of decoding accuracies we used permutation testing. For each subject and each ROI, we performed n = 1000 random permutations, where the labels of low vs. high confidence in the previously selected sample set were each time randomly shuffled. For each permutation the accuracy was averaged across CV runs and SLR iterations, and we thus obtained a distribution of n = 1000 accuracies. Statistical significance was computed as P = sum(Dperm > Dobs + 1)/(nperm + 1), or simply the sum of the permuted accuracies greater than the observed accuracy divided by the number of permutations.
2.5.3 ROIs and voxels for classification
We constructed four decoders in frontoparietal areas, corresponding to the following bilateral anatomical ROIs: inferior parietal lobule (IPL), and three subregions generally regarded as being part of the dorsolateral prefrontal cortex (dlPFC), namely the inferior frontal sulcus (IFS), middle frontal sulcus (MFS), and the middle frontal gyrus (MFG) (Fig. 1C). These areas have been previously linked to confidence judgements in perceptual decisions (Kiani & Shadlen 2009; Fleming et al. 2010; Rounis et al. 2010; Simons et al. 2010; Rahnev et al. 2016). Additionally, we also examined four ROIs in the visual processing stream (V12, V3A, hMT and the fusiform gyrus), because we were evaluating perceptual confidence with visual stimuli in a different study. As reported in Cortese et al. (Cortese et al. 2016), confidence classification was at chance for these ROIs in the visual areas. Thus, for the DecNef training, we selected only the four frontoparietal ROIs that showed higher decoding accuracy, and the decoding results of these four ROIs are presented in the Results section. Each binary decoder was trained to classify a pattern of BOLD signals into either low or high confidence, using data samples obtained from up to 120 trials collected in up to twelve fMRI runs. As a result, the inputs to the decoders were the participants’ moment-to-moment brain activations, while the outputs of the decoders represented the calculated likelihood of each confidence measure. The mean (± s.e.m) number of voxels for decoding was 1802 ± 63 for IPL, 490 ± 19 for IFS, 412 ± 16 for MFS, and 1350 ± 42 for MFG. The mean (± s.e.m) number of voxels selected by i-SLR for each ROI was 62 ± 9 for IPL, 66 ± 10 for IFS, 64 ± 8 for MFS, and 91 ± 13 for MFG. The selected voxels were then used for the DecNef training. We opted for four separate classifiers instead of one large ROI to account for possible individual differences in confidence representation loci at the regional level (Rahnev et al. 2016).
2.6 DecNef training and testing
Once individual confidence classifiers were constructed, ten selected participants completed a two-day DecNef training in each session (aiming to up- or down-regulate confidence level), and each session was separated by at least one week (see Fig. 1A). Each participant went through both Up- and Down DecNef training, and the order was counterbalanced across participants (i.e., Up then Down vs. Down then Up). The neurofeedback task itself is illustrated in Fig. 1D: participants were asked to “manipulate, modulate or change their brain activity in order to make the feedback disc presented at the end of each trial as large as possible”. The experimenters provided no further instructions nor strategies. Importantly, the disc for feedback after the induction period was maximized both for inducing the activation patterns for high confidence and for low confidence, in the up- and down- regulation sessions, respectively. Participants received monetary reward proportional to their induction success (ability to induce the selected activation pattern). Only the experimenter knew which session took place on a certain day, while participants were unaware. After each training day, participants were asked to describe their strategies in making the disc size larger. Answers varied from “I was counting” to “I was focusing on the disc itself” to “I was thinking about food”. When participants were asked to report which group they thought they were assigned to at the end of the experiments (n = 5, 2 months later, and n = 4, 5 months later - 1 participant could not be reached), their answers were at chance at the group level (57% correct, Chi-square test, χ2 = 0.225, P = 0.64).
On each day of a given DecNef session, participants were trained in up to 11 fMRI runs. The mean (± s.e.m) number of runs per day was 10 ± 0.1 across days and participants. Each fMRI run consisted of 16 trials (1 trial = 20 secs) preceded by a 30-secs fixation period (1 run = 350 secs). The fMRI data for the initial 10 secs were discarded to avoid unsaturated T1 effects.
Each trial started with a visual cue (three concentric disks, white, gray and green) signaling the induction period (Fig. 1D). The induction period lasted for 6 secs, and was followed by a 6 secs rest period. The rest period was followed by the neurofeedback disk (a white ring) presented on the gray screen for up to 2 secs. Finally, a trial ended with a 6 secs intertrial interval (ITI). Either during the induction period, or at the beginning of the rest period (pseudo-random onsets: 2, 4, 6, or 8 secs from trial start) a 2 secs noise RDM was also presented. Pseudo-random onsets were designed in order to minimize potential interference of the RDM onset on the induction of brain activity.
During the rest period, participants were asked to simply fixate on the central point and rest. This period was inserted between the induction and the feedback periods to account for the hemodynamic delay, assumed to last 6 secs. The size of the disc represented how much the BOLD signal patterns obtained from the induction period corresponded to activation patterns of the target confidence level (high or low). The white disc was always enclosed in a larger white concentric circle (5 deg radius), which indicated the disc’s maximum possible size.
The size of the disc presented during the feedback period was computed at the end of the rest period according to the following steps. First, measured functional images during the induction period underwent 3D motion correction using Turbo BrainVoyager (Brain Innovation). The subsequent steps were performed using the Matlab software. Second, time-courses of BOLD signal intensities were extracted from each of the voxels identified in the MVPA session, for each of the four frontoparietal ROIs used (IPL, IFS, MFS, and MFG), and were shifted by 6 secs to account for the hemodynamic delay. Third, a linear trend was removed from the time-course, and the BOLD signal time-course was z-score normalized for each voxel using BOLD signal intensities measured for 20 secs starting from 10 secs after the onset of each fMRI run. Fourth, the data sample to calculate the size of the disc was created by averaging the BOLD signal intensities of each voxel for 6 secs in the induction period. Finally, the likelihood of each confidence state was calculated from the data sample using the confidence decoder computed in the MVPA session. The size of the disc was proportional to the averaged likelihood from the four different frontoparietal ROIs (ranging from 0 to 100%) of the target confidence assigned to each participant on a given DecNef block. Importantly, participants were unaware of the relationship between their activation patterns induction and the size of the disk itself. The target confidence was the same throughout a DecNef block. In addition to a fixed compensation for participation in the experiment, a bonus of up to 3000 JPY was paid to the participants based on the mean size of the disc on each day.
3. Mathematical modeling and model comparison
3.1 Nonlinear global model
We constructed a mathematical model to objectively examine the effects of Up and Down DecNef, a decay of learning (of DecNef effect) due to one-weak lapse, and an anterograde interference of learning from the first to second week. The model was fit to 4 confidence measurements at the 4 time points for each participant and possesses 4 model parameters. are the experimentally measured confidence values, while are the estimated confidence values for each participant (with i = 1:10) (i.e., confidence outcome of DecNef effects), at each time point (with j = 1:4; we derived n = 30:3 points of measurement at n = 10 subjects, as the first time point was assumed to be fixed for the global model). The main 4-parameter nonlinear model to describe DecNef effects is formally outlined as follows.
| (1) |
for i = 1:5, group D-U
| (2) |
| (3) |
| (4) |
for i = 6:10, group U-D
| (5) |
| (6) |
| (7) |
| (8) |
Where B is the initial baseline on the first day of the DecNef procedure in the first week (0 - after realignment to a common level for each group). Δ, the confidence change by Up-DecNef in the first week which putatively is the only true result. A Δ value of 0 would indicate no DecNef effects on confidence, while a Δ value of 1 would indicate a 100% confidence increase. ε, the ratio of Down-DecNef effect normalized by Up-DecNef effect, explained as the fact that Down-DecNef effect is of reduced magnitude compared to Up-DecNef in both instances - week 1 for group D-U and week 2 for group U-D. A ε value of 0 would indicate no down effects, while a ε value of -1 would indicate maximum effects (identical magnitude to Up-DecNef effects). γ, the anterograde learning interference resulting in a reduced second week DecNef effect, namely the fact that in the second week there is only limited DecNef effect. A γ value of 0 would indicate that there was full anterograde learning interference thus there existed no learning effect in the second week, while a γ value of 1 would indicate absence of anterograde learning interference. Last, α, the learning persistence (1 − [decay of learning]) across the one-week interval, the remarkable result that the confidence level attained at the end of the first week is preserved at least until the beginning of the next session. An α value of 0 would indicate no learning persistence, while an α value of 1 would indicate perfect memory maintenance, i.e. no memory loss.
3.2 Submodels and alternative simpler models
Submodels are defined by setting different parameters to zero or one, one at a time or concomitantly, following the rationale of prioritizing against model complexity. This gives rise to a hierarchical group of models, from simpler to most complex (capturing single or increasingly more aspects of DecNef effects on the confidence measure). The first model is the simplest and only estimates Δ, with the other parameters setting as ε = 0, γ = 1, α = 1. The second model, by complexity order, assumes Up and Down-DecNef effects, estimates Δ and ε, while γ = 1, α = 1. The third model estimates Δ, ε and γ, with α = 1. Further DecNef-based models estimate Δ, ε and α, with γ = 1; or estimate Δ, ε and α, with γ = 0; or estimate Δ, ε and γ, with α = 0; or finally, estimate Δ, γ, and α, with ε = 0.
We considered alternative models that do not take into account DecNef direction assumptions or a priori conceptions. These are a 1-parameter constant confidence model (the confidence measure does not change, is constant throughout the experiment), with two versions: , or . Other free models are a within-week constant confidence, and within-week fit by first and second degree polynomial.
3.3 Model comparison
For model comparison, we used the second-order or corrected Akaike Information Criterion (AICc) (Burnham & Anderson 2002), which is a corrected version of the Akaike Information Criterion (AIC) (Akaike 1974).
Raw AIC is computed according to the following equation:
| (9) |
where , n is the sample size and k the number of parameters in the model. In our set of global models, n = 30, and k varied from 1 to 4. In the modeling reported for small sample sizes (i.e., n/k ≲ 40), the second-order or corrected Akaike Information Criterion (AICc) should be used instead. Although the AICc formula assumes a fixed-effects linear model with normal errors and constant residual variances, while our model is nonlinear, the standard AICc formulation is recommended unless a more exact small-sample correction to AIC is known (Burnham & Anderson 2002):
| (10) |
For model comparison, two useful metrics are ΔAICc and Akaike weights (wi). is a measure of the distance of each model relative to the best model (the model with the most negative, or lowest, AIC value), and is calculated as:
| (11) |
As indicated in Burnham and Anderson (Burnham & Anderson 2002), suggests substantial evidence for the ith model, while indicates that the model is very unlikely (implausible).
Akaike weights (wi) provide a second measure of the strength of evidence for each model, is directly related to , and is computed as:
| (12) |
AICc, ΔAICc, and wi are reported in Table 2.
Table 2.
AICc analysis. The most negative AICc value indicates the best model fit. ΔAICc < 2 indicate that the current model has a high likelihood of being the best model under different circumstances, i.e., a new dataset.
| Model (est. parms) | Fixed parms | AICc | Δi | wi | |
|---|---|---|---|---|---|
|
|
k | −70.6447 | 24.3397 | 0 | |
|
| |||||
|
|
k | −72.1602 | 22.8242 | 0 | |
|
| |||||
| Within-week const. confidence | k1 k2 | −71.7531 | 23.2313 | 0 | |
| Polynomial 1st deg. (α1, α2) | k | −70.5479 | 24.4365 | 0 | |
| Polynomial 2nd deg. (α1, β1, α2, β2) | k1 k2 | −61.8877 | 33.0967 | 0 | |
|
| |||||
| Sub-model (Δ) | α=1 ε=0 γ=1 | −81.6244 | 13.3600 | 0.0005 | |
| Sub-model (Δ, ε) | α=1 γ=1 | −91.5062 | 3.4782 | 0.0637 | |
| Sub-model (Δ, ε, α) | γ=1 | −89.0275 | 5.9569 | 0.0185 | |
| Sub-model (Δ, ε, γ) | α=0 | −77.3589 | 17.6255 | 0.0001 | |
| Sub-model (Δ, γ, α) | ε=0 | −91.4285 | 3.5559 | 0.0613 | |
|
| |||||
| Sub-model (Δ, ε, γ) | α=1 | −94.9402 | 0.0442 | 0.3549 | |
| Sub-model (Δ, ε, γ, α) | −93.0529 | 1.9315 | 0.1381 | ||
| Sub-model (Δ, ε, α) | γ=0 | −94.9844 | 0 | 0.3629 | |
3.4 Model averaging and cross-validation
In cases such as ours, where a high degree of model selection uncertainty exists (the best AIC model is not strongly weighted), a formal solution is to compute parameter estimates through model-averaging. For this approach, two procedures may be used, depending on the results. The first approach makes use of only a limited subset of models that are closest to the current best model (ΔAICc < 2), while the second approach will consider all models (in fact, this accounts to consider all models with wi ≠ 0). We adopted the first approach, selecting only models with high likelihood to keep the parameter estimates within the same scale as the original single models. Parameters are estimated according to the equation:
| (13) |
Where β̂i is the estimate for the predictor in a given model i, and wi is the Akaike weight of that model.
Unconditional error, necessary to compute the unconditional confidence interval for a model-averaged estimate, can be calculated according to the following equation:
| (14) |
Where is the variance of the parameter estimate in model i, and β̂i and are as defined above. The confidence interval is then simply given by the end points:
| (15) |
For a 95% confidence interval (CI), z1−α/2= 1.96.
Note that the unconditional variance comprises two terms, the first one local (internal variance of model i), while the second one global, in that it represents the variance between the common estimated parameter and the true value in model i.
In order to assess the internal variance of the models, as well as the generalizability and to prevent overfitting, we run a leave-two-out (one for each group, D-U and U-D) cross-validation (CV) model averaging procedure. The procedure was repeated for each CV test-pair: with 10 participants, divided into 2 groups, we thus obtained 25 CV runs (all possible combinations of test pairs). For each CV run, the left-out participant data acted as test set, while the training data set was hence composed of the remaining participants (four in each group). In each CV run, the three best models previously selected by AICc (indicated in bold in Table 2) were fitted on the training data, Akaike weights were calculated, and finally model averaging was performed. After model-averaging, as a measure of the goodness of fit, the predicted confidences were correlated with the observed confidences from the current CV test run. In the main text we report the mean ± std value of correlation values. Furthermore, we also run a correlation of estimated vs. observed confidence changes by pooling all test sets together, to assess significance at the group level. To do so, for each participant we averaged the estimated values from the CV runs (5) in which that specific participant acted as test data. Lastly, the final parameter estimates were computed as follows. First, for each parameter we took the average across the 25 CV runs. As mentioned above, the unconditional error is composed of two terms. The variance of the parameter estimate in model i was taken as the variance in the 25 CV runs model estimation processes. The global variance is computed between the mean final estimate and the mean estimate in each single model. Given the two sources of variance we then evaluated the 95% CI. See Supplementary Fig. 1 for a graphical account of the entire process.
3.5 Nonlinear mixed (global - local) model
In the second part of the modeling approach, we consider all data points, and model population’s individual fits with nonlinear equations with global and local parameters (we thus fit the model to all n = 40:4 points of measurement at n = 10 subjects, as all time points were considered for the mixture model). The equations determining the model are thus very similar to those given above:
| (16) |
for i = 1:5, group D-U
| (17) |
| (18) |
| (19) |
for i = 6:10, group U-D
| (20) |
| (21) |
| (22) |
| (23) |
Compared with the global-parameter model (Eq. 1–8), in this individualized model B (the initial starting point) is now optimized individually, as well as Δ, the confidence change induced by DecNef. For this model, n = 40 (data points), and k = 23 (parameters).
To avoid overfitting and evaluate the internal variance of the model, this final model was estimated with a leave-two-out CV, with a similar approach as for the global model. For each CV run, the model parameters were estimated with the training set, and then evaluated on the left-out test set by correlating observed confidences (two participants’ data in the test data) and predicted confidences. The final parameter estimates are reported as the cross-validated mean ± 95% CI. Results at the group level are reported by correlating all observed confidences with individual predicted confidences. Importantly, because each participant on a given group was tested in 5 different CV runs (due to it being paired once with all other participants in the opposing group), its final estimated change was computed as the mean of the 5 CV runs. See Supplementary fig. 2 for a graphical account of the process.
4. Analysis, statistics and model-solving routines
All analyses were performed with Matlab (Mathworks) versions 2011b and 2014a with custom made scripts. Additional statistical analysis such as ANOVA were performed with SPSS 22 (IBM statistics). We employed Matlab optimization routines to solve the systems of nonlinear equations with a nonlinear programming solver, under least-square minimization. The Matlab solver was fmincon, with the following optimization options. A sequential quadratic problem (SQP) method was used; specifically, the ‘SQP’ algorithm. This algorithm is a medium-scale method, which internally creates full matrices and uses dense linear algebra, thus allowing additional constraint types and better performance for the nonlinear problems outlined in the previous section. As compared with the default fmincon ‘interior-point’ algorithm, the ‘SQP’ algorithm also has the advantage of taking every iterative step in the region constrained by bounds, which are not strict (a step can exist exactly on a boundary). Furthermore, the ‘SQP’ algorithm can attempt to take steps that fail, in which case it will take a smaller step in the next iteration, allowing greater flexibility. We set bounded constraints to allow only certain values in the parameter space to be taken by the estimates, reflecting the biological dimension they were explaining. As such, boundaries were set as: Δ ∈ [0 1], ε ∈ [−1 0], γ ∈ [0 1], and α ∈ [0 1], and for the mixed model B ∈ [1 4]. The function tolerance was set at 10−20, the maximum number of iterations at 106 and the maximum number of function evaluations at 105.
Statistical results involving multiple comparisons are reported in both the corrected and uncorrected forms. The rationale behind this decision is that these comparisons can be interpreted as multiple comparisons of one hypothesis across different mediums, or simply as different hypothesis, in which case no multiple comparisons should be considered. For multiple comparisons, we used the Holm-Bonferroni procedure, where the P-values of interest are ranked from the smallest to the largest, and the significance level α is sequentially adjusted based on the formula for the ith smallest P-values.
5. MRI Parameters
The participants were scanned in a 3T MR scanner (Siemens, Trio) with a head coil in the ATR Brain Activation Imaging Center. Functional MR images for retinotopy, the MVPA session, and DecNef stages were acquired using gradient EPI sequences for measurement of BOLD signals. In all fMRI experiments, 33 contiguous slices (TR = 2 sec, TE = 26 ms, flip angle = 80 deg, voxel size = 3×3×3.5 mm3, 0 mm slice gap) oriented parallel to the AC-PC plane were acquired, covering the entire brain. For an inflated format of the cortex used for retinotopic mapping and an automated parcellation method (Freesurfer), T1-weighted MR images (MP-RAGE; 256 slices, TR = 2 s, TE = 26 ms, flip angle = 80 deg, voxel size = 1×1×1 mm3, 0 mm slice gap) were also acquired during the fMRI scans for the MVPA.
Results
MVPA for confidence was performed with the data from all initial 17 subjects, as reported in Table 1. Significance was assessed through permutation testing (randomly shuffling the labels of high and low confidence). Results were consistent with our a priori hypothesis and previous work that confidence representations are found in frontoparietal cortices (Kiani & Shadlen 2009; Fleming et al. 2010; Rounis et al. 2010; Simons et al. 2010; Rahnev et al. 2016). Furthermore, as reported here, individual differences in confidence decodability were also apparent. Indeed, for many participants one ROI (different across participants) had much lower decoding ability. This outcome illustrates our rationale for using 4 separate ROIs for the DecNef training, instead of selecting a single best one (which would have been different across participants) or a single large unified one.
DecNef can be essentially assumed as a neural operant conditioning and/or reinforcement learning paradigm, with which a multi-voxel pattern corresponding to a specific piece of brain information can be induced without explicit knowledge from the participants. Throughout the manuscript we refer to Up-DecNef for High-Confidence DecNef and Down-DecNef for Low-Confidence DecNef. Since there were two groups (for DecNef order counterbalancing), we will often refer to these as D-U (first session is Down-DecNef while the second is Up-DecNef) and U-D (the reverse, Up-DecNef first, Down-DecNef then) throughout the results section.
The ROIs selected for this study, aside from being important for metacognition, are also part of large-scale functional brain networks associated, for example, with attention and especially top-down modulation of visual attention (Fox et al. 2005; Bressler & Menon 2010; Rosenberg et al. 2016). Previous work showed that rTMS to the DLPFC resulted in lower levels of visibility for stimuli which was pronounced for correct trials (Rounis et al. 2010). We have addressed these crucial concerns in a companion manuscript, which aimed at elucidating the relationship between confidence and perceptual evidence (Cortese et al. 2016). We reported that DecNef effects on confidence were specific and unlikely to result from criterion shifts, mood changes or an attentional modulation (Cortese et al. 2016), thus supporting the view that confidence alone was manipulated. Indeed, task accuracy did not change between Pre- and Post-Tests: two-way repeated measures ANOVA, factors of neurofeedback (Down - Up) and time (Pre - Post), showed non-significant interaction (F1,9 = 0.030, P = 0.867) as well as non-significant main effects of time (F1,9 = 0, P = 0.994) and neurofeedback (F1,9 = 1.854, P = 0.206). Furthermore, similarly as in Scharnowski et al. (2015), any unspecific effects that are related to task demands should only allow to either increase or decrease the confidence level, but it would be difficult to allow bidirectional control (Scharnowski et al. 2015). The current paper aims at exploring and explaining the dynamics of DecNef neurofeedback training on confidence, therefore we will focus on these dynamical aspects.
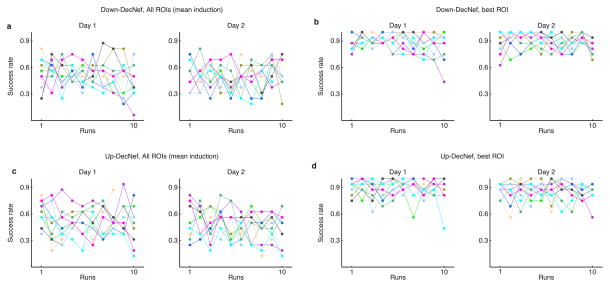
Before exploring the DecNef effects on confidence, it is also important to analyze the ability of participants to induce the target activation patterns in the selected brain regions. The overall induction performance, measured as the ratio of successful trials (trials with induction likelihood > .5 over total trials), for all ROIs averaged did not show a marked learning curve over runs or days of training (Fig. 2A, C). During the DecNef training itself, the feedback signal was also given as the average across all four ROIs. Given the complicated nature of such induction, it is perhaps unsurprising that, overall, there was a mixed success rate in the induction likelihood at the group level (although individual variability seemed to be sizeable). Nevertheless, when looking at the best performing ROI (that is, the single best performing ROI in each trial, that also had induction likelihood > .5), all subjects showed very high success rates (Fig. 2B, D). This in turn indicates that on any given trial, at least one ROI was successfully inducing the target pattern. Although the monetary signal fed back to participants was based on the average of the four ROIs, because the underlying pattern activation was very successful in at least one of the ROIs, probably this had a much larger effect in the learning and therefore on the final measurable confidence changes.
Fig. 2.
Individual participant’s success rates for each DecNef session (total, 4). (a–b) Success rate for Down-DecNef, with (a) representing the overall induction performance (all 4 ROIs averaged), as in the experimental session, while (b) is selective for the best ROI (single ROI with highest induction likelihood on a given trial). (c–d) Success rate for Up-DecNef, description same as above for Down-DecNef. Individual colors represent single participants. Dots represent the ratio of successful trials/total trials in each run.
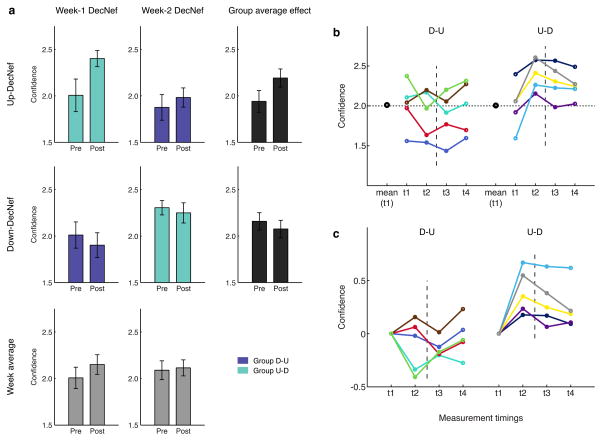
Behavioral data from the Pre- and Post-Tests show that confidence was differentially manipulated by DecNef (Fig. 3). Importantly, the resulting changes in confidence could not be attributed to a simple week order effect (two-way ANOVA with repeated measures, non-significant effects of neurofeedback, F1,9 = 0.370, P = 0.558, and time, F1,9 = 2.834, P = 0.127, and non-significant interaction, F1,9 = 0.844, P = 0.382, Fig. 4A bottom part - week average).
Fig. 3.
Confidence ratings in psychophysical Pre- and Post-Tests. (a) Each group induced both High and Low Confidence, in two separate sessions: group D-U with the order Low- then High-Confidence (Down then Up), and group U-D High- then Low Confidence. Results are color-coded: purple for single group results of group D-U and green for group U-D. Average across groups, representing mere order effect, is depicted in gray, at the bottom, while the grand average per condition (High and Low Confidence), is in black, on the right side. It is apparent that the confidence changes in the first week strongly influence the confidence level in the second week. The Pre- level in the second week remains indeed very close to the previous Post- level attained in the first week. Furthermore, neurofeedback in the first week seems to have a stronger impact than in the second week, and this holds when comparing both High with Low Confidence DecNef. For each bar, n = 5. Error bars represent s.e.m. (b–c) participants’ individual confidence data with the four measurement timings, organized in groups (D-U and U-D), both raw (b) and 0-aligned (c) confidence. In (b) the large black dots represent the group mean confidence level at t1. The horizontal dotted line the confidence level of 2.0. It is apparent that the two independent groups have almost equal starting points. Timings 1 and 2 correspond to Pre- and Post-Test in the first week, respectively; while timings 3 and 4 to Pre- and Post-Test in the second week DecNef. The dotted line represents the week-long interval between the two sessions (DecNef in week 1 and DecNef in week 2). Each colored line represents day-averaged data from one participant (total, n = 10).
Fig. 4.
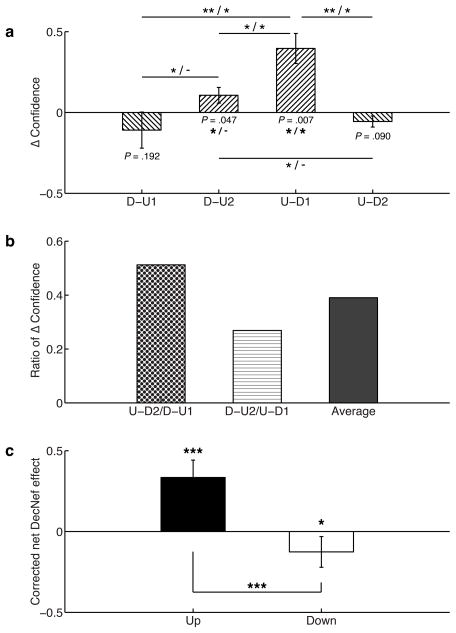
Summary statistics for DecNef effects on confidence. (a) Δ confidence is given by the difference [Post-Test - Pre-Test] of confidence average. D-U1 is the confidence difference in group D-U, DecNef session 1, D-U2 the confidence distance in group D-U, DecNef session 2, U-D1 group U-D, DecNef session 1, and U-D2 group U-D, DecNef session 2. Asterisks to the left of the slashes represent uncorrected significant differences, while asterisks to the right, significant differences after correction for multiple comparisons (* P < 0.05, ** P < 0.01, *** P < 0.005). (b) Ratios of Δ confidence measured as confidence change in the second week divided by the confidence change in the first week, for both Up- and Down-DecNef. The right column indicates the average of the two ratios, used in the analysis displayed in the next panel. (c) Corrected net DecNef effect: the correction is computed by dividing the second week effect by the averaged ratios of Δ confidence. This term accounts for the anterograde learning interference, decreasing the DecNef effect in the second week. Both Up- and Down-DecNef are thus significantly different from zero.
As displayed in Fig. 3A, the confidence change was larger for Up-DecNef than Down-DecNef, but importantly, the level attained at the end of the first week was almost entirely preserved until the beginning of the second week, in the second session. Lastly, the second week effect seemed present but reduced as compared to the first week effect. Thus, order of DecNef (Up then Down, or Down then Up) had a large influence on how confidence was manipulated. A mixed-effects ANOVA with repeated measures, with within-subjects factor time, and between-subjects factors neurofeedback and order, clarified this finding, as it resulted in a significant interaction between the three factors (F1,16 = 4.769, P = 0.044). Furthermore, the factor time (F1,16 = 4.623, P = 0.047) and the interaction between time and neurofeedback (F1,16 = 18.050, P = 0.001) both had significant effect on the dependent variable, confidence.
The results at the group level (Fig. 3A) were mirrored at the individual level (Fig. 3B, C). Fig. 3B shows that the initial confidence level (t1) varied across participants, but also that the group average was the same for both D-U and U-D groups (group D-U, confidence at t1: C̄ = 2.011 ± 0.132; group U-D, confidence at t1: C̄ = 2.006 ± 0.130; paired t-test t4 = 0.023, P = 0.98). Moreover, changes had a clear common trend across participants. Thus, in Fig. 3C, data were realigned to the same starting point, centered on zero. In more detail, Fig. 3C suggests that 7/10 cases in the Down-DecNef and 9/10 cases in the Up-DecNef showed confidence changes in the expected directions. Supposing, as a null hypothesis, that the direction of each confidence change occurs at random, the associated probability is then 1/2. Assuming that each DecNef session is independent, the cumulative binomial probability to obtain 16/20 matches is P(X≥16) = 0.0059. The null hypothesis that increase or decrease in confidence after DecNef training occurred at random is thus statistically implausible; confidence increased in Up-DecNef weeks, and decreased in Down-DecNef weeks. A mixed-effects ANOVA with repeated measures (between-subjects factor of group [D-U and U-D] and within-subjects factor of timing [Fig. 3B, t1, t2, t3, and t4]) resulted in a strongly significant interaction, F3,24 = 8.650, P < 0.001 (univariate effect). Main effects of factors timing, F3,24 = 2.555, P = 0.079, and group, F1,8 = 3.674, P = 0.092, were close to significance.
A concept that has been extensively studied in motor learning and, to a lesser extent, in perceptual learning, is learning interference. In a classic motor learning interference paradigm, Krakauer et al. (Krakauer et al. 1999) showed that learning of another kinematic or dynamic model with conflicting sensorimotor mappings interfered with the consolidation of previously learned models of the same type. Similarly, in this study, we propose that DecNef training also induced an anterograde interference effect, where learning of task B is partly prevented by the previous learning of task A. This effect will be more rigorously examined later.
To effectively analyze the confidence changes, the two DecNef sessions for the two groups, D-U1, D-U2, and U-D1, U-D2, respectively, are presented as differences (Δconfidence, Fig. 4A). For clarity, D-U1 and D-U2 are the same group (resp. U-D1 and U-D2), and the number indicates if the session was D or U (first or second session). As expected, average changes were positive for Up- and negative for Down-DecNef: U-D1 data was significantly different from zero (one-tailed t-test, t4 = 4.253, P = 0.0067 uncorrected; P = 0.026 corrected for multiple comparisons), as well as D-U2 (before multiple comparisons correction, see Supplementary Note 1). Both D-U1 and U-D2 were not statistically different from zero (see Supplementary Note 1). The contrast between D-U1 and U-D1 yielded a statistically significant difference (one-tailed t-test, t4 = −3.822, P = 0.0094 uncorrected; P = 0.0468 corrected). This result is of great importance, because in the two instances only the neurofeedback sign was different, while all other behavioral schemes were the same, and yet different results were obtained. Thus, DecNef purely induced bidirectional confidence changes, and these changes were not caused by general effects of monetary rewards or repeated exposure to random dot stimuli, which are common experimental components of both up and down DecNef. Furthermore, mean differences between U-D1 and U-D2 (one-tailed t-test, t4 = 4.228, P = 0.0067 uncorrected; P = 0.0402 corrected), D-U2 and U-D1 (one-tailed t-test, t4 = −3.661, P = 0.0108 uncorrected; P = 0.0431 corrected) yielded statistically significant results before and after multiple comparisons correction. It should be noted that, although they did not survive a multiple comparisons correction, even the differences between D-U1 and D-U2, and D-U2 and U-D2 were initially significant (see Supplementary Note 1). Since one could argue that the conditions between each comparison are different, because they entail different DecNef directions and therefore assumptions, it is noteworthy to see that most of the confidence differences were significantly distinct.
Fig. 4B plots the ratios of the above differences U-D2/D-U1, D-U2/U-D1 and the average of the two. Because these values are positive and less than 1, the second week effect was in the same direction but smaller in magnitude than the first week effect, an outcome that is likely due to anterograde learning interference. The first two values being relatively similar, the interference effect did not seem to be dependent upon Up-Down or Down-Up sequence.
Therefore, considering that differences in the first and second week of DecNef are quantifiable and can be ascribed to a specific hypothesis, the true Up and Down effects can be computed by applying a simple correction. Reduced Up and Down-DecNef effects in the second week can be corrected for the first week effect by dividing them by the average ratio (Fig. 4C). Both Up and Down effects were statistically significantly different from zero (one-tailed t-test, Up-DecNef t9 = 4.390, P = 0.0009; Down-DecNef t9 = −1.876, P = 0.0467), and they were different from each other (one-tailed t-test, t9 = 4.315, P = 0.001), suggesting a specific DecNef effect to neurofeedback signs.
In order to best capture the different components of DecNef effects while accounting for both Up- and Down neurofeedback, we fitted a system of nonlinear parametric equations with four global parameters (explained in greater detail in the mathematical modeling part of the Materials and methods section). The four global parameters were selected in light of the summary statistics results displayed in Fig. 5. Global parameters hence were the initial (first week) absolute confidence change by Up-DecNef effect (Δ), the ratio of the weaker Down-DecNef effect compared with that of stronger Up-DecNef effect (ε), anterograde learning interference (γ), and the learning persistence between DecNef sessions (α). Importantly, we fitted various alternative models, where some of the parameters had fixed values (such as = 1 or = 0) to account for full effects, or the lack of effects, in order to compare and infer which aspects of DecNef were likely to play a significant role in determining the resulting confidence changes. Simpler models, that did not assume directionality in confidence changes, or other interpretations, included a constant-confidence model, constant-within-week model, and first-grade polynomial models. In order to compare the various models, we used the corrected (second-order) Akaike Information Criterion (AICc), which allocates more importance to the principle of parsimony, and gives higher penalty to more complex models (i.e., with larger number of parameters). Indeed, since the dataset is finite, and the ratio n/k (number of samples/number of parameters) < 40, AICc is strongly recommended to avoid model selection bias (Burnham & Anderson 2002)).
Fig. 5.
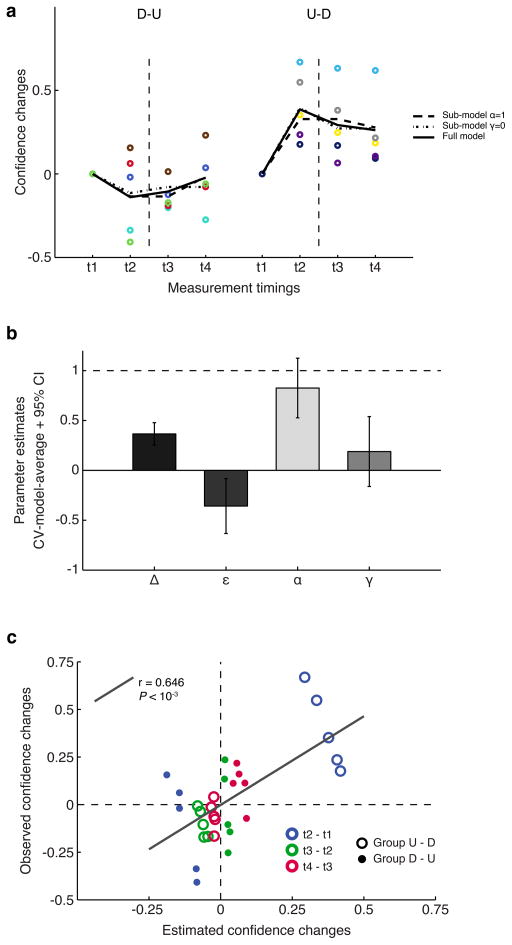
Confidence changes modeled with nonlinear functions with global parameters. (a) Individual and group-modeled data are presented, 0-aligned, with the same color-codes and presentation rules as in Fig. 4. Thick black lines represent the three best model fits as selected by AICc model comparison. These are, respectively, the model with the most negative AICc value, and models having a ΔAICc < 2 from the best model. Empirical data from each participant is shown as colored dots. (b) Global parameters estimates resulting from model averaging. For each model, based on the ΔAICc, Akaike weights were computed (the likelihood of the ith model being the best model). Each parameter was then evaluated as the weighted average of single models estimates. Error bars represent the 95% confidence intervals, computed from the unconditional standard error. (c) Plot of observed confidence changes vs. global model based estimated confidence changes for the test sets in a leave-two-out cross-validation (CV) process. Each CV run sees two participants (one for each group), left out as test set. The process is repeated in order for each pair of participants to be tested (tot. 25 CV runs). In total, there are 30 time points (change between t2 and t1, t3 and t2, t4 and t3), 3 for each of the 10 participants, divided between order groups D-U and U-D. The correlation between the two measures was significant, supporting the validity of the estimated parameters. D-U: Down-Up DecNef order, U-D: Up-Down DecNef order.
When using AIC (and, by extension, AICc), the best model has the most negative (or lowest) score. Absolute values of AICs are not really informative per se, and to effectively compare models we use the distance from the best model (ΔAICc), and the likelihood of each model being the best model, computed as Akaike weights. Normally, a means the ith model cannot be ruled out and has a conspicuous likelihood of being the best model with a different dataset. Accordingly, we computed AICc scores, , and wi (reported in Table 2). As shown in the table, there are three models that can be considered essentially as good as the best model, since the distance between two of them and the most negative AICc is < 2. Furthermore, three more models had ΔAICc < 6, indicating these had a very low likelihood, but nevertheless marginal validity. All other models had distances greater than 10 from the best model, and importantly, among them simpler models such as constant-confidence, within-week constant confidence, and first-grade polynomial models all performed very poorly in fitting the data. These models with ΔAICc > 10 are sufficiently poorer than the best AIC model as to be considered implausible (Burnham & Anderson 2002).
Since model selection uncertainty exists, with very similar AICc values (ΔAICc < 2 compared to the most negative AICc), a formal solution is to apply model-averaging, where each parameter present in the selected models is estimated according to a weighted average based on their corresponding Akaike weights. For model averaging, we used all models for which ΔAICc < 2, keeping the estimated parameters in the same initial scale and focusing the averaging process on the subset of highly likely models.
Fig. 5A reports individual data, as well as fits of the three best models (ΔAICc < 2, full model with 4 global parameters - α, ε, γ, Δ; submodel with γ=0, submodel with α=1), and the simplest model, where confidence does not change and is akin to a 1−k model, with the only parameter being the confidence group average. As can be deduced from the figure, each model provides a good fit, and therefore a high likelihood of being the best one at describing the empirical data. Conversely, a simpler model, where confidence is assumed to be constant, provides a very poor fit to the data, showing that DecNef was indeed successful in inducing confidence changes, and that the no-change model is implausible.
Model-averaged estimates of the 4 parameters, obtained through a cross-validation procedure, suggest that all of them are different from zero or one (Fig. 5B), and thus impact the effects of DecNef. The delta parameter was 0.37 ([0.25 0.48], 95% confidence interval [CI]); thus Up-DecNef on the first week increased confidence by 0.37, or a ~20% absolute change in confidence. Because the standard deviation of confidence ratings in the first day of DecNef (day 1, Pre-Test) was 0.89, a change in confidence of 0.37 would mean a change of ~40% in relative terms. Epsilon was −0.36 ([−0.63 −0.08], 95% CI), thus the Down-DecNef effect was opposite in its sign and close to 40% of the magnitude of Up-DecNef. Furthermore, it is important to note that the CI for ε did not include 0 and that all three best models allowed non-zero ε, meaning that nonlinear modeling formally proved the existence of non-zero down effects. Alpha was 0.83 ([0.53 1.13], 95% CI), hence on average less than 20% of the first week effect was lost during the one-week interval due to memory decay. More importantly, CI for α did not include 0 but included 1, indicating that the preservation of effects was almost perfect after a one-week delay. Gamma was 0.19 ([−0.16 0.54], 95% CI), and thus, due to anterograde learning interference, the second week effect was only ~20% of that of the first week. CI for γ did not include 1, meaning degraded effects were present in the second week, but included 0, indicating the possibility that due to very strong learning interference, no learning occurred in the second week. Our nonlinear modeling robustly indicates that there exist both Up- and Down-DecNef effects, almost perfect preservation of learning effects between sessions one-week apart, and strong anterograde learning interference. This was further supported by plotting observed confidence changes and model-based estimated changes (Fig. 5C). The two data sets were obtained by computing the confidence changes between time points (t2 - t1, t3 - t2, t4 - t3), for each participant (10 participants with 3 confidence changes each, 30 data points in total). The estimated changes were computed with a leave-two-out cross-validation process (one participant per group). The observed and estimated confidence measures indeed correlated well (n = 30, Pearson’s r = 0.646, P < 10−3, [0.372 0.816] 95% CI), which supports the validity of the parameter estimates. The cross-validated average of the correlation coefficients (Rho) ± std in the test runs was 0.705 ± 0.172.
In the second part of the modeling analysis, we considered all data points, and modeled individual fits with nonlinear equations with global and local parameters (mixture model). This approach is warranted by the results from the global model-averaging, where all four parameters have high likelihood of being different from zero or one. This aspect, albeit not entirely backed by the confidence intervals (CIs for γ include 0 and CI for α included 1), is nevertheless supported by the internal variance of the models: these variances are low, indicating high stability within a model’s parameter space. Furthermore, if the models are robust and explain the same phenomena in DecNef, parameter estimates should converge to similar solutions.
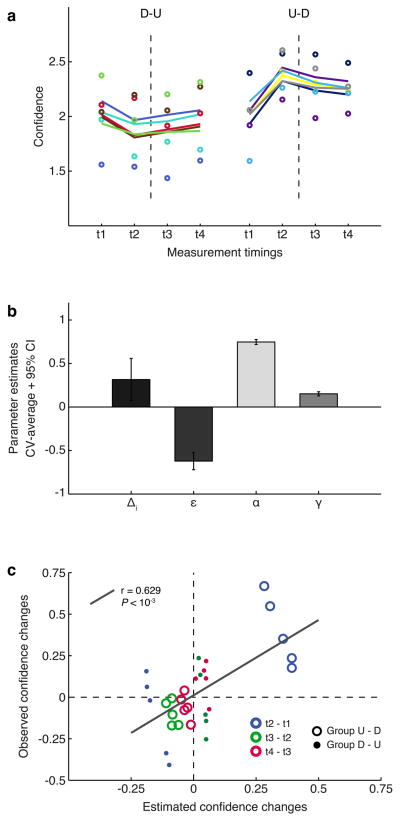
In the mixture model, global parameters were the weaker Down-DecNef effect (ε), the learning persistence between DecNef sessions (α), and anterograde learning interference (γ), while local parameters were the individual initial absolute confidence change for Up-DecNef effect (Δi), and the individual initial point of confidence (bi). The model was estimated through a cross-validated approach, where each test run was evaluated separately. Final estimates are cross-validation averages. Fig. 6A shows the 23 parameter model fit to the raw data, and provides further support for Fig. 4 conclusions. Parameter estimate values (Fig. 6B) are in good agreement in both modeling instances (Fig. 5B and 6B), underscoring the presence and generality of the effects they represent, as well as supporting the robustness of the model analyses. As expected, the linear relationship between observed and estimated confidence changes was also significant (Fig. 6C, same approach as in Fig. 4C; n = 30, Pearson’s r = 0.629, P < 10−3, [0.347 0.806] 95% CI). The average correlation value (Rho) ± std across all cross-validation test runs was 0.595 ± 0.388. It is important to notice that both modeling approaches yielded almost identical correlation coefficients. This result corroborates the idea that DecNef had bidirectional effects, and that the mixed-modelling (global - local parameters) approach could also well describe the various DecNef dynamic effects, building upon the results introduced in the previous figure related to the global parameters model.
Fig. 6.
Mixture global and local parameters modeling. The model is based on the parameters obtained from the previous model-averaging step using global models. This full model accounts for all four major effects of DecNef: Δi, individual differences in Up-DecNef confidence change; ε, reduced Down-DecNef effect; α, learning persistence ([1 − memory decay] in the week-long interval); γ, anterograde learning interference resulting in reduced second week DecNef effect. (a) Thick lines are individual fits, while dots are empirical data. Color-codes and presentation rules are the same as in Figs 2 and 4. (b) Model estimates. Error bars are standard deviation for Δi, and 95% CI for ε, α, and γ. (c) Plot of observed confidence changes vs. mixture model based estimated confidence changes for the test sets in a leave-two-out cross-validation (CV) process. Each CV run sees two participants (one for each group), left out as test set. The process is repeated in order for each pair of participants to be tested (tot. 25 CV runs). There are 30 time points (change between t2 and t1, t3 and t2, t4 and t3), 3 for each of the 10 participants, divided between order groups. The correlation between the two variables was significant, supporting the high fidelity of the estimated parameters in the model with global and local parameters. D-U: Down-Up DecNef order, U-D: Up-Down DecNef order.
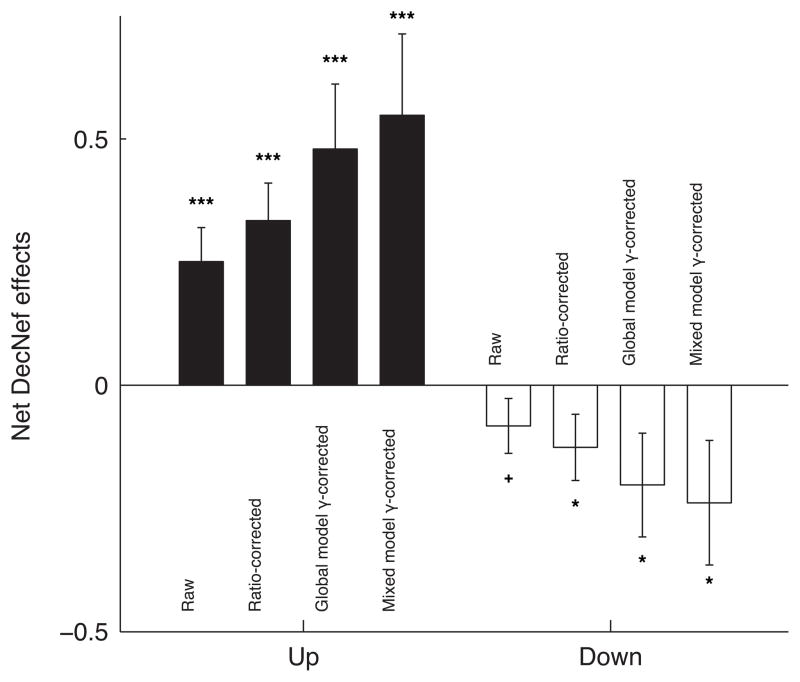
To conclude on the behavioral effects, we present the net DecNef effects, computed by averaging, for each manipulation Up- and Down-DecNef separately, the overall mean change in confidence as measured in Pre- and Post-test in week-1 and week-2. By utilizing the gamma parameter, representing anterograde learning interference, and computed with increasingly stringent methods (ratio of week-2/week-1, global model parameter, and mixed model parameter estimate), we show that DecNef was effective in both directions (Fig. 7). That is, simply discounting the weaker second week effect by correcting (dividing) the individual pre- post- confidence change from the second week by the gamma parameter indeed leads to a significance level that is statistically relevant for both increase and decrease of confidence. Furthermore, the direct relationship between raw data, the method used to estimate gamma, and the final estimate of the net DecNef effects can be directly appreciated in Fig. 7.
Fig. 7.
Net effects of Up- and Down-DecNef trainings. The first bar, labeled “raw”, represents the net change in confidence without any correction being applied. The following bars show the net change in confidence, with the second week difference between Pre- and Post-tests individually corrected by multiplying the difference by 1/γ, the parameter computed in the various modeling approaches described in the main text. One-tailed t-test results: + P = 0.087, * P < 0.05, *** P < 0.005.
Discussion
We hypothesized that DecNef could be successfully used to induce changes in a meta-cognitive state (confidence) for two opposing directions and within the same participants. Furthermore, if DecNef were based on a learning process in the behavioral dimension probed, we expected anterograde learning interference. To directly examine these hypotheses, we constructed individual decoders based on multi-voxel pattern activity associated with confidence judgements in a visual discrimination task, and participants then induced via neurofeedback such multi-voxel activation patterns in two DecNef sessions, i.e., one for High Confidence and one for Low Confidence induction. Importantly, each session was separated by at least one week, which maximized our chance to capture possible learning-maintenance effects relevant for the time-scale in the context of studies about this type of training.
Our analyses and modeling results support the idea that confidence changed due to DecNef according to the following specific pattern. (1) DecNef was successful bidirectionally, and the Up-DecNef effect was more pronounced than Down-DecNef, (2) the acquired confidence level at the end of the first week was subjected to only small degradation, (3) there existed a strong anterograde interference onto the second week DecNef session by the first week DecNef. The consequence was a stronger effect of neurofeedback in the first week as compared to the second week.
The anterograde interference in learning that emerges when training participants to induce activation patterns that correspond to different (opposite) behavioral variables sequentially is important. This effect is remarkable, because it implies that any manipulation through DecNef is likely relying on long term changes akin to sensorimotor learning or perceptual learning, thus providing additional support to previously reported empirical findings in rt-fMRI (Shibata et al. 2011; Megumi et al. 2015; Amano et al. 2016). Specifically, these behavioral changes may be deeply ingrained due to the neural operant conditioning that is subtending such learning processes.
In sensorimotor and visuomotor learning, a conspicuous literature has explored the effect of opposing tasks on the dynamics and modalities of the learning processes (Brashers-Krug et al. 1996; Krakauer et al. 1999; Tong et al. 2002; Osu et al. 2004). Both retrograde and anterograde mechanisms have been suggested to mediate interference in visuomotor learning (Tong et al. 2002; Miall et al. 2004; Krakauer et al. 2005). The vast majority of previous studies have addressed interference in learning within short delays (typically, between a few minutes and up to 24h–48h), but consistent with our results several studies have reported interference effects even after 1 week (Caithness et al. 2004; Krakauer et al. 2005). Furthermore, anterograde interference is thought to have substantially larger effects as compared to retrograde interference (Sing & Smith 2010). It is therefore not surprising that the interference found in this study resulted in a second week effect of only ~20% of the size of the first week, a very significant decrease.
An important point to be considered regards how implicit vs. explicit strategies allow participants to modulate activation patterns in a specific brain region and in specific directions. To the layman, it would seem crucial that knowledge of the manipulation by the participant is necessary. Yet, this does not seem to be the case, as reported by recent relevant rt-fMRI neurofeedback studies (Shibata et al. 2011; Yoo et al. 2012; Ramot et al. 2016). Indeed, because successful induction would always lead to monetary reward, implicit strategies may be building upon simpler but deeper mechanisms of reinforcement learning, akin to subliminal instrumental conditioning for which awareness does not seem to be necessary (Pessiglione et al. 2008) (see also discussion in (Bray et al. 2007)). In a recent study, Scharnowski and colleagues (Scharnowski et al. 2015) showed that learned voluntary control over brain activation levels in two distinct areas caused characteristic behavioral effects that were related to the specific function of each brain region. Although bidirectional brain activation manipulation was performed, behavioral changes were reported only in one dimension, rather than the bidirectional change reported here. Furthermore, strategies were explicitly suggested while successful changes in activation were not rewarded. Thus, these aspects indicate that the mechanism in place may be substantially different. It may be possible that explicit strategies initially facilitate learning but only lead to behavioral effects with a shorter life-time; conversely, reinforcement learning type of approaches, such as ours, may be initially more difficult - perhaps due to less resources being allocated. However, as a result of the conditioning and available neural resources this type of approach may prove more ingrained in the long term memory circuitry and thus show long-term effects (with long-term effects in the scale of months reported in (Megumi et al. 2015; Amano et al. 2016)).
Lastly, the possibility that the effects reported, analyzed and discussed may be accounted for by alternative explanations may never be fully discounted. Given the initial generally low decoding accuracy, the ability of the reward signal to accurately reflect the likelihood of inducing a given activation pattern may be partly impaired. This, together with overlapping functions in the selected ROIs (confidence, but also attention, memory), means that the results could be simply interpreted as, for example, a result of increased attention. However, this explanation does not seem compatible with the behavioral results that nothing except confidence changed. Furthermore, it can be partly refuted by the results of a recent study that showed that increased attention counterintuitively led to more conservative biases of confidence judgements in visual perception (Rahnev et al. 2011). If attention were responsible for the effects on confidence, the pattern of changes would have likely been opposite: larger decrease than increase in confidence following Up-DecNef training.
Because it is now known that neurofeedback training goes beyond the simple ROI level and affects the connectivity between distant regions (Scheinost et al. 2013; Scharnowski et al. 2014; Yuan et al. 2014; Ramot et al. 2016), in the future we plan to run further analyses of the current dataset. For example, it would be of great interest to investigate the temporal changes in connectivity between various brain regions including those involved in the training as well as visual areas and reward centers. Considering the confidence dimension, exploring what was driving the multivoxel patterns or what was different in terms of connectivity and information transmission across areas between Up- and Down-DecNef could advance our understanding of these brain processes.
To conclude, we established the causal nature of DecNef. Because bidirectional brain manipulation led to bidirectional behavioral change, our results showed that DecNef was effective in both increasing and decreasing perceptual confidence. Up and down modulations were asymmetrical, suggesting some differential basic neural mechanisms for confidence encoding. Once acquired, cancelling out DecNef effects was difficult (only 20% cancellation); this possibly requires more days of induction. With such strong anterograde interference in the behavioral results, the effects of DecNef may be best understood in terms of reinforcement learning, likely akin to sensorimotor learning and perceptual learning. These considerations may be particularly relevant from a translational viewpoint and indicate that DecNef has great potential for clinical applications, considering only two days of training were sufficient for more than 80% of the learned change to be maintained after a delay of one week.
Supplementary Material
Acknowledgments
The study was conducted under the “Development of brain machine Interface technologies for clinical application” of the Strategic Research Program for Brain Sciences by Japan Agency for Medical Research and Development (AMED) (http://www.nips.ac.jp/srpbs/). A.C. was supported by a Japanese Government Monbukagakusho MEXT grant. This work is supported partially by a grant from the National Institute of Neurological Disorders and Stroke of the National Institutes of Health (Grant No. R01NS088628) to H.L. The funders had no role in study design, data collection and analysis, decision to publish or preparation of the manuscript. We would like to thank Drs. Giuseppe Lisi and Okito Yamashita for helpful discussions on the modeling implementation.
Footnotes
Competing Interests.
There is a potential financial conflict of interest; one of the authors is the inventor of patents related to the neurofeedback method used in this study, and the original assignee of the patents is ATR, with which M.K. is affiliated.
References
- Akaike H. A new look at the statistical model identification. IEEE transactions on automatic control. 1974;19(6):716–723. [Google Scholar]
- Amano K, et al. Learning to associate orientation with color in early visual areas by associative decoded fMRI neurofeedback. Current biology: CB. 2016;16:1–6. doi: 10.1016/j.cub.2016.05.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Birbaumer N, Ruiz S, Sitaram R. Learned regulation of brain metabolism. Trends in cognitive sciences. 2013;17(6):295–302. doi: 10.1016/j.tics.2013.04.009. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spatial vision. 1997;10(4):433–436. [PubMed] [Google Scholar]
- Brashers-Krug T, Shadmehr R, Bizzi E. Consolidation in human motor memory. Nature. 1996;382(6588):252–255. doi: 10.1038/382252a0. [DOI] [PubMed] [Google Scholar]
- Bray S, Shimojo S, O’Doherty JP. Direct Instrumental Conditioning of Neural Activity Using Functional Magnetic Resonance Imaging-Derived Reward Feedback. Journal of Neuroscience. 2007;27(28):7498–7507. doi: 10.1523/JNEUROSCI.2118-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bressler SL, Menon V. Large-scale brain networks in cognition: emerging methods and principles. Trends in cognitive sciences. 2010;14(6):277–290. doi: 10.1016/j.tics.2010.04.004. [DOI] [PubMed] [Google Scholar]
- Burnham KP, Anderson DR. Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. Springer Science & Business Media; 2002. [Google Scholar]
- Caithness G, et al. Failure to consolidate the consolidation theory of learning for sensorimotor adaptation tasks. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2004;24(40):8662–8671. doi: 10.1523/JNEUROSCI.2214-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortese A, et al. Multivoxel neurofeedback selectively modulates confidence without changing perceptual performance. Nature communications. 2016;7:13669. doi: 10.1038/ncomms13669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Bettencourt MT, et al. Closed-loop training of attention with real-time brain imaging. Nature neuroscience. 2015;18(3):470–475. doi: 10.1038/nn.3940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Charms RC. Applications of real-time fMRI. Nature reviews. Neuroscience. 2008;9(9):720–729. doi: 10.1038/nrn2414. [DOI] [PubMed] [Google Scholar]
- de Charms RC, et al. Learned regulation of spatially localized brain activation using real-time fMRI. Neuro Image. 2004;21(1):436–443. doi: 10.1016/j.neuroimage.2003.08.041. [DOI] [PubMed] [Google Scholar]
- Deisseroth K. Optogenetics. Nature methods. 2010;8(1):26–29. doi: 10.1038/nmeth.f.324. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deisseroth K. Optogenetics: 10 years of microbial opsins in neuroscience. Nature neuroscience. 2015;18(9):1213–1225. doi: 10.1038/nn.4091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Martino B, et al. Confidence in value-based choice. Nature neuroscience. 2012;16(1):105–110. doi: 10.1038/nn.3279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Destrieux C, et al. Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. NeuroImage. 2010;53(1):1–15. doi: 10.1016/j.neuroimage.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fetsch CR, et al. Effects of cortical microstimulation on confidence in a perceptual decision. Neuron. 2014;83(4):797–804. doi: 10.1016/j.neuron.2014.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming SM, et al. Action-specific disruption of perceptual confidence. Psychological science. 2015;26(1):89–98. doi: 10.1177/0956797614557697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fleming SM, et al. Relating introspective accuracy to individual differences in brain structure. Science. 2010;329(5998):1541–1543. doi: 10.1126/science.1191883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, et al. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(27):9673–9678. doi: 10.1073/pnas.0504136102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirose S, Nambu I, Naito E. An empirical solution for over-pruning with a novel ensemble-learning method for fMRI decoding. Journal of neuroscience methods. 2015;239:238–245. doi: 10.1016/j.jneumeth.2014.10.023. [DOI] [PubMed] [Google Scholar]
- Huettel SA, Song AW, McCarthy G. Decisions under uncertainty: probabilistic context influences activation of prefrontal and parietal cortices. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2005;25(13):3304–3311. doi: 10.1523/JNEUROSCI.5070-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamitani Y, Tong F. Decoding the visual and subjective contents of the human brain. Nature neuroscience. 2005;8(5):679–685. doi: 10.1038/nn1444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepecs A, et al. Neural correlates, computation and behavioural impact of decision confidence. Nature. 2008;455(7210):227–231. doi: 10.1038/nature07200. [DOI] [PubMed] [Google Scholar]
- Kiani R, Shadlen MN. Representation of confidence associated with a decision by neurons in the parietal cortex. Science. 2009;324(5928):759–764. doi: 10.1126/science.1169405. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim S, Birbaumer N. Real-time functional MRI neurofeedback: a tool for psychiatry. Current opinion in psychiatry. 2014;27(5):332–336. doi: 10.1097/YCO.0000000000000087. [DOI] [PubMed] [Google Scholar]
- Koralek AC, et al. Corticostriatal plasticity is necessary for learning intentional neuroprosthetic skills. Nature. 2012;483(7389):331–335. doi: 10.1038/nature10845. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koush Y, et al. Connectivity-based neurofeedback: dynamic causal modeling for real-time fMRI. NeuroImage. 2013;81:422–430. doi: 10.1016/j.neuroimage.2013.05.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koush Y, et al. Learning Control Over Emotion Networks Through Connectivity-Based Neurofeedback. Cerebral cortex. 2015:1–10. doi: 10.1093/cercor/bhv311. [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Ghez C, Ghilardi MF. Adaptation to visuomotor transformations: consolidation, interference, and forgetting. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2005;25(2):473–478. doi: 10.1523/JNEUROSCI.4218-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krakauer JW, Ghilardi MF, Ghez C. Independent learning of internal models for kinematic and dynamic control of reaching. Nature neuroscience. 1999;2(11):1026–1031. doi: 10.1038/14826. [DOI] [PubMed] [Google Scholar]
- LaConte SM. Decoding fMRI brain states in real-time. NeuroImage. 2011;56(2):440–454. doi: 10.1016/j.neuroimage.2010.06.052. [DOI] [PubMed] [Google Scholar]
- LaConte SM, Peltier SJ, Hu XP. Real-time fMRI using brain-state classification. Human brain mapping. 2007;28(10):1033–1044. doi: 10.1002/hbm.20326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lak A, et al. Orbitofrontal cortex is required for optimal waiting based on decision confidence. Neuron. 2014;84(1):190–201. doi: 10.1016/j.neuron.2014.08.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Megumi F, et al. Functional MRI neurofeedback training on connectivity between two regions induces long-lasting changes in intrinsic functional network. Frontiers in human neuroscience. 2015:9. doi: 10.3389/fnhum.2015.00160. Available at: http://dx.doi.org/10.3389/fnhum.2015.00160. [DOI] [PMC free article] [PubMed]
- Miall RC, Jenkinson N, Kulkarni K. Adaptation to rotated visual feedback: a re-examination of motor interference. Experimental brain research. Experimentelle Hirnforschung. Experimentation cerebrale. 2004;154(2):201–210. doi: 10.1007/s00221-003-1630-2. [DOI] [PubMed] [Google Scholar]
- Osu R, et al. Random presentation enables subjects to adapt to two opposing forces on the hand. Nature neuroscience. 2004;7(2):111–112. doi: 10.1038/nn1184. [DOI] [PubMed] [Google Scholar]
- Pessiglione M, et al. Subliminal instrumental conditioning demonstrated in the human brain. Neuron. 2008;59(4):561–567. doi: 10.1016/j.neuron.2008.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rahnev D, et al. Attention induces conservative subjective biases in visual perception. Nature neuroscience. 2011;14(12):1513–1515. doi: 10.1038/nn.2948. [DOI] [PubMed] [Google Scholar]
- Rahnev D, et al. Causal evidence for frontal cortex organization for perceptual decision making. Proceedings of the National Academy of Sciences of the United States of America. 2016;113(21):6059–6064. doi: 10.1073/pnas.1522551113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ramot M, et al. Covert neurofeedback without awareness shapes cortical network spontaneous connectivity. Proceedings of the National Academy of Sciences of the United States of America. 2016;113(17):E2413–20. doi: 10.1073/pnas.1516857113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenberg MD, et al. A neuromarker of sustained attention from whole-brain functional connectivity. Nature neuroscience. 2016;19(1):165–171. doi: 10.1038/nn.4179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rounis E, et al. Theta-burst transcranial magnetic stimulation to the prefrontal cortex impairs metacognitive visual awareness. Cognitive neuroscience. 2010;1(3):165–175. doi: 10.1080/17588921003632529. [DOI] [PubMed] [Google Scholar]
- Scharnowski F, et al. Connectivity changes underlying neurofeedback training of visual cortex activity. PloS one. 2014;9(3):e91090. doi: 10.1371/journal.pone.0091090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scharnowski F, et al. Manipulating motor performance and memory through real-time fMRI neurofeedback. Biological psychology. 2015;108:85–97. doi: 10.1016/j.biopsycho.2015.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheinost D, et al. Orbitofrontal cortex neurofeedback produces lasting changes in contamination anxiety and resting-state connectivity. Translational psychiatry. 2013;3:e250. doi: 10.1038/tp.2013.24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seitz AR, et al. Task-specific disruption of perceptual learning. Proceedings of the National Academy of Sciences of the United States of America. 2005;102(41):14895–14900. doi: 10.1073/pnas.0505765102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shadlen MN, Newsome WT. Neural basis of a perceptual decision in the parietal cortex (area LIP) of the rhesus monkey. Journal of neurophysiology. 2001;86(4):1916–1936. doi: 10.1152/jn.2001.86.4.1916. [DOI] [PubMed] [Google Scholar]
- Shibata K, et al. Differential activation patterns in the same brain region led to opposite emotional states. PLoS Biology. 2016;24(9):e1002546. doi: 10.1371/journal.pbio.1002546. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shibata K, et al. Perceptual learning incepted by decoded fMRI neurofeedback without stimulus presentation. Science. 2011;334(6061):1413–1415. doi: 10.1126/science.1212003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons JS, et al. Dissociation between memory accuracy and memory confidence following bilateral parietal lesions. Cerebral cortex. 2010;20(2):479–485. doi: 10.1093/cercor/bhp116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sing GC, Smith MA. Reduction in learning rates associated with anterograde interference results from interactions between different timescales in motor adaptation. PLoS computational biology. 2010;6(8) doi: 10.1371/journal.pcbi.1000893. Available at: https://www.ncbi.nlm.nih.gov/pubmed/20808880. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sitaram R, et al. Closed-loop brain training: the science of neurofeedback. Nature reviews. Neuroscience. 2016 doi: 10.1038/nrn.2016.164. Available at: http://dx.doi.org/10.1038/nrn.2016.164. [DOI] [PubMed]
- Sulzer J, et al. Real-time fMRI neurofeedback: progress and challenges. NeuroImage. 2013;76:386–399. doi: 10.1016/j.neuroimage.2013.03.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong C, Wolpert DM, Flanagan JR. Kinematics and dynamics are not represented independently in motor working memory: evidence from an interference study. The Journal of neuroscience: the official journal of the Society for Neuroscience. 2002;22(3):1108–1113. doi: 10.1523/JNEUROSCI.22-03-01108.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong F, Pratte MS. Decoding patterns of human brain activity. Annual review of psychology. 2012;63:483–509. doi: 10.1146/annurev-psych-120710-100412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veit R, et al. Using real-time fMRI to learn voluntary regulation of the anterior insula in the presence of threat-related stimuli. Social cognitive and affective neuroscience. 2012;7(6):623–634. doi: 10.1093/scan/nsr061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner T, Valero-Cabre A, Pascual-Leone A. Noninvasive Human Brain Stimulation. Annual review of biomedical engineering. 2007;9(1):527–565. doi: 10.1146/annurev.bioeng.9.061206.133100. [DOI] [PubMed] [Google Scholar]
- Weiskopf N, et al. Physiological self-regulation of regional brain activity using real-time functional magnetic resonance imaging (fMRI): methodology and exemplary data. NeuroImage. 2003;19(3):577–586. doi: 10.1016/s1053-8119(03)00145-9. [DOI] [PubMed] [Google Scholar]
- Weiskopf N, et al. Principles of a brain-computer interface (BCI) based on real-time functional magnetic resonance imaging (fMRI) IEEE transactions on bio-medical engineering. 2004;51(6):966–970. doi: 10.1109/TBME.2004.827063. [DOI] [PubMed] [Google Scholar]
- Yamashita O, et al. Sparse estimation automatically selects voxels relevant for the decoding of fMRI activity patterns. NeuroImage. 2008;42(4):1414–1429. doi: 10.1016/j.neuroimage.2008.05.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoo JJ, et al. When the brain is prepared to learn: Enhancing human learning using real-time fMRI. NeuroImage. 2012;59(1):846–852. doi: 10.1016/j.neuroimage.2011.07.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yotsumoto Y, et al. Interference and feature specificity in visual perceptual learning. Vision research. 2009;49(21):2611–2623. doi: 10.1016/j.visres.2009.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuan H, et al. Resting-state functional connectivity modulation and sustained changes after real-time functional magnetic resonance imaging neurofeedback training in depression. Brain connectivity. 2014;4(9):690–701. doi: 10.1089/brain.2014.0262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zizlsperger L, et al. Cortical representations of confidence in a visual perceptual decision. Nature communications. 2014:5. doi: 10.1038/ncomms4940. Available at: http://dx.doi.org/10.1038/ncomms4940. [DOI] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.