Multi-Stage 3D-2D Registration for Correction of Anatomical Deformation in Image-Guided Spine Surgery

Abstract

Purpose

A multi-stage image-based 3D-2D registration method is presented that maps annotations in a 3D image (e.g., point labels annotating individual vertebrae in preoperative CT) to an intraoperative radiograph in which the patient has undergone non-rigid anatomical deformation due to changes in patient positioning or due to the intervention itself.

Methods

The proposed method (termed msLevelCheck) extends a previous rigid registration solution (LevelCheck) to provide an accurate mapping of vertebral labels in the presence of spinal deformation. The method employs a multi-stage series of rigid 3D-2D registrations performed on sets of automatically determined and increasingly localized sub-images, with the final stage achieving a rigid mapping for each label to yield a locally rigid yet globally deformable solution. The method was evaluated first in a phantom study in which a CT image of the spine was acquired followed by a series of 7 mobile radiographs with increasing degree of deformation applied. Second, the method was validated using a clinical data set of patients exhibiting strong spinal deformation during thoracolumbar spine surgery. Registration accuracy was assessed using projection distance error (PDE) and failure rate (PDE > 20 mm – i.e., label registered outside vertebra).

Results

The msLevelCheck method was able to register all vertebrae accurately for all cases of deformation in the phantom study, improving the maximum PDE of the rigid method from 22.4 mm to 3.9 mm. The clinical study demonstrated the feasibility of the approach in real patient data by accurately registering all vertebral labels in each case, eliminating all instances of failure encountered in the conventional rigid method.

Conclusion

The multi-stage approach demonstrated accurate mapping of vertebral labels in the presence of strong spinal deformation. The msLevelCheck method maintains other advantageous aspects of the original LevelCheck method (e.g., compatibility with standard clinical workflow, large capture range, and robustness against mismatch in image content) and extends capability to cases exhibiting strong changes in spinal curvature.

1. Introduction

In image-guided spine surgery, target localization using 2D intraoperative radiographs is an essential step in effective treatment. However, accurate interpretation of anatomy in radiographs during surgery can be a challenging, time-consuming, and error-prone task that can confound even experienced surgeons. In the case of vertebral level identification, surgeons typically acquire multiple radiographic images at shifted fields of view to “count” to the correct level – a process involving considerable time and stress in the OR to ensure accurate localization. Some institutions may implement an additional preoperative procedure for tagging (injection) of radio-opaque cement into the target vertebra under CT guidance to allow fast, unequivocal identification in the OR. Even so, wrong-level spine surgery is reported to occur in approximately 1 in 3110 spine surgeries (and up to 1 in 700 for lumbar disc procedures), and it is estimated that up to half of spine surgeons will encounter this error at some point in their career. A wrong-level error can lead to suboptimal (or failed) surgical product and potentially costly litigation (Mody et al 2008). To prevent such occurrences and potentially improve workflow and confidence in target localization, a 3D-2D registration framework (called LevelCheck) has been shown to automatically overlay relevant target anatomy such as vertebral labels from 3D preoperative imaging (CT or MR) to the intraoperative 2D image as a means of decision support (Otake et al 2012, 2013, 2015, De Silva et al 2016a, b). LevelCheck has been shown to provide robust registration under many challenging scenarios that are commonly encountered in clinical images, including poor image quality and content mismatch (e.g., surgical instrumentation appearing in the radiograph that is not in the 3D image); however, the accuracy of rigid 3D-2D registration may be compromised in the presence of deformation. Spine deformation is particularly common due to the differences in preoperative and intraoperative patient positioning, where 3D preoperative images are typically acquired with the patient lying supine on the scanning bed, whereas intraoperative images are often acquired with the patient prone on an arched surgical table (e.g., Jackson table or Wilson frame). The effect of such deformation on rigid 3D-2D registration is illustrated in figure 1 (right), showing accurate alignment in the central region of the image that diminishes in the superior and inferior regions due to changes in spinal curvature between the preoperative and intraoperative images.

Figure 1.

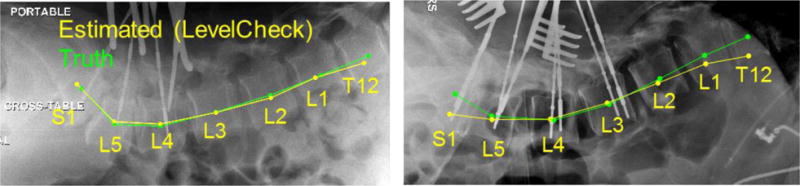
Examples of the LevelCheck output (yellow) compared with the truth definitions (green). On the left is a typical case showing good registration. On the right is a case with a strong change in spinal curvature for which the conventional rigid approach shows a degradation in registration accuracy at the superior and inferior extent of the radiograph.

While 3D-3D deformable registration is a topic of widespread research, the topic of deformable 3D-2D image registration presents a challenge that remains to be fully addressed. Previous work has illustrated that deformable 3D-2D registration is a challenging and often ill-posed problem; for example, in the case of a single 2D view there is degenerate geometric relationship between projection magnification and changes in object size. Several advances in deformable 3D-2D image registration have been reported for scenarios in which multiple 2D images are acquired (Benameur et al 2003, Prummer et al 2006, Rivest-Henault et al 2012, Guyot et al 2013, Uneri et al 2016), in applications such as radiographic vertebrae segmentation and surgical guidance using digital subtraction angiography. For single-view 3D-2D registration, at least two general methods to mitigate the effects of deformation have been proposed: (i) apply a deformable method with constraints imposed by 3D segmentations and deformation models (Groher 2007, Penney et al 2002); and (ii) perform piece-wise rigid registrations, often involving shape models (Schmid and Chênes 2014) or segmentations of rigid bodies. In the context of spine registration, the segmentation methods often utilize 3D vertebral segmentations and perform registration for each vertebra individually (Penney 2000, Weese et al 1997). Our previous work showed that (rigid) LevelCheck provides reasonable registration accuracy overall, even in the presence of deformation (Otake et al 2013); however, recent clinical studies (De Silva et al 2016b) found a reduction in surgical confidence arising even from fairly small errors for which the label was still within cortical boundaries but not near the vertebral centroid.

To provide improved accuracy under conditions of spinal deformation, we propose a method that is analogous to a combination of two common forms of image registration: (i) piecewise rigid registration (as posed in Penney [2000], for example), although our method does not rely on an explicit segmentation of “pieces”; and (ii) block matching (as in Ourselin et al [2000] and Zhu and Ma [2000], for example), where the block definitions are based on relevant anatomical structures using the label annotations specified in the preoperative 3D image, rather than arbitrarily dividing the image into sub-images. Furthermore, our method reflects and extends that of Varnavas et al (2015), in using information from multiple single vertebra registrations; however, we define sub-image masks that incorporate subsets of adjacent vertebrae, rather than single vertebra masking. Moreover, the method is automatic (the same level of automation as with LevelCheck), and beyond the definition of labels in the preoperative image (which can be done manually or automatically [Scholtz et al 2015]), it requires only an initialization in the superior-inferior direction of the CT.

In this paper we present a single-view, multi-stage, 3D-2D registration method that robustly accounts for spinal deformation by rigidly registering sub-images of decreasing size at each subsequent stage. The multi-stage method is referred to as msLevelCheck. The method yields a 3D-2D registration that is locally rigid (with respect to the registration of any particular sub-image and label annotation therein) yet globally deformable (with respect to the overall motion of all label annotations) and results in accurate target localization over the entire field of view. The method is detailed below, focusing on two main aspects of the algorithm: the generation of sub-image masks from the (pre-existing / automatically computed) annotation locations in 3D without segmentation of the vertebrae; and the multi-scale framework for registration of increasingly local rigid regions. The method is evaluated in phantom experiments as well as a clinical study of patients undergoing thoracolumbar spine surgery.

2. Methods

2.1 Rigid 3D-2D registration framework

As in previous work, the method intends to aid target localization by mapping vertebral labels defined in the preoperative CT image (or MR image [De Silva et al 2016c]) to the intraoperative radiograph via image-based 3D-2D registration. Rigid registration is performed by determining a rigid 6 degree-of-freedom (6DOF) transformation of the CT image that optimizes the similarity between the digitally reconstructed radiograph (DRR) and the intraoperative radiograph (p). The resulting transformation enables the vertebral labels in the CT image to be accurately projected and overlaid in p. The overall framework illustrated in figure 2 is consistent with that in Otake et al (2012, 2013, 2015) and De Silva et al (2016a).

Figure 2.

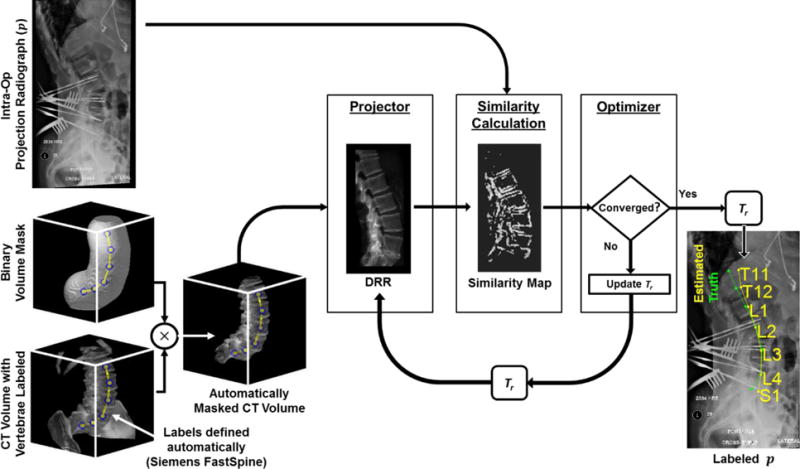
Flowchart for LevelCheck 3D-2D rigid registration.

2.1.1 Binary volume masking

Mismatch of anatomy distal to the spine, such as the ribs, pelvis, and skin line, can challenge robust 3D-2D registration. To mitigate the effect of such surrounding anatomy and to focus the registration on the spine, we introduced a method for automatically masking the CT volume using already defined 3D vertebral label positions as shown in figure 2. In this approach, a 3D linear interpolation of the label positions is computed, and a binary volume mask (scale factor of 0 or 1) is defined to include voxels within a distance r of the interpolated line. Previous work (Ketcha et al, 2016) identified a nominal distance of r = 50 mm, which was used in the studies reported below.

2.1.2. Projection geometry and DRR formation

Forward projections were computed within a fixed camera geometry with a virtual detector centered at the origin and an x-ray point source positioned at (x_s, y_s, z_s) with z_s defined to be perpendicular to the detector plane, as described in Otake et al (2013). A geometry with the piercing point at the center of the detector and a source-to-detector distance (SDD) of 100 cm was assumed. A rigid 6DOF transformation, T_r, consisting of 3 translations (x_r, y_r, z_r) and 3 rotations (η_r, θ_r ϕ_r) defined the pose of the CT volume within this camera geometry. Given the geometry and CT position, a projective transformation matrix, T_3×4, was defined to map a location in the CT coordinate system (x, y, z) to its projected location in the DRR (u, v) according to equation 1:

$$c\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]=T_{3\times 4}\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]=\left[\begin{array}{cccc}{z}_s& 0& x_s& 0\\ 0& z_s& y_s& 0\\ 0& 0& 1& 0\end{array}\right]\left[\begin{array}{cccc}& & & x_r-x_s\\ & R_{3\times 3}({\eta }_r,{\theta }_r,{\varphi }_r)& & y_r-y_s\\ & & & z_r-z_s\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]$$ (1)

where c is a constant that normalizes the third element of the 2D position vector. The DRR was generated via ray-tracing (Cabral et al 1994) with line integrals computed using trilinear interpolation. To achieve pixel-wise correspondence, the virtual detector was defined to have dimensions and pixel size identical to the projection image, which has been resampled to a specified isotropic pixel size (a_pix) and rectangularly cropped to exclude collimator edges and burnt-in text annotations. Assuming a nominal magnification factor of 2, the volume was downsampled isotropically to a_pix/2. The step length for ray casting was chosen to be 2 voxels (equivalently, a_pix) based on a sensitivity study reported in Otake et al (2012). Consistent with Ketcha et al (2016), a soft tissue threshold of 150 HU (shown previously to be insensitive to the particular threshold choice in the range 50 to 300 HU) was applied to the CT image (setting the value to 0 if below) to remove low attenuation regions in the forward projection, and basic overlap of the DRR with the projection image was ensured by translating the CT volume along the longitudinal direction of the patient, thereby determining an initial value for y_r, and resulting in an initial registration error of ~20 – 200 mm. To improve computation time, DRRs were computed using a parallelized implementation in CUDA on GPU (nVidia, Santa Clara, CA).

2.1.3. Similarity metric

Similarity between the DRR and the intraoperative radiograph was evaluated using Gradient Orientation (GO), which was shown in (De Silva et al 2016a) to provide a high degree of robustness against image content mismatch (e.g., presence of surgical tools in the radiograph but not the CT) as well as poor radiographic image quality. The GO similarity was defined as:

$$GO=\frac{1}{max(N,N_{LB})}{\displaystyle \sum _{\left\{i:\nabla DR{R}_i>t\cap \nabla p_i>t\right\}}{w}^{\prime }(i)}$$

$$\text{where}{w}^{\prime }(i)=\frac{2-\ln (|{\theta }_i|+1)}{2}$$ (2)

and reflects the pixel-wise similarity in gradient direction, w′, among pixels whose gradient magnitude passes a threshold t in both images, defined as the median gradient intensity. Here, θ_i is the angle difference (radians) in gradient direction between the DRR and p at pixel i. The normalization constant N is the number of pixel locations for which the metric is evaluated, and N_LB is a lower bound cutoff set to 30% of the total number of pixels to penalize low counts associated with poor overlap (shown in previous studies to be a stable, nominal parameter setting for this application in De Silva et al [2016a]).

2.1.4. Optimization

The GO metric was optimized over the six-dimensional search space to find the transformation T_r. Due to the highly non-convex nature of the objective space, a multi-start covariance matrix adaptation – evolution strategy (CMA-ES) optimization was employed (Hansen 2006). CMA-ES is a stochastic, derivative-free optimization method where, to provide robustness against local minima, the update (which includes both the parameter estimate and covariance matrix) at each iteration is determined by sampling a total of λ points in the parameter space. Sampling is performed according to a Gaussian distribution defined by the covariance matrix and the current parameter estimate. Assuming poor initialization, we incorporated multi-starts in which parallel optimizations were performed with initializations distributed over the entire optimization search range. To distribute these initializations, a plane-splitting kD tree partitioning of the search space (Bentley, 1975) was implemented where the search space was divided by iteratively splitting the largest current subspace in half. The number of multi-starts (MS = 50), the population sampling size (λ = 125), and the search range (SR) along each 6DOF dimension (± [ 100 mm, 200 mm, 75 mm, 15°, 10°, 10°]) were selected based on a sensitivity study using a clinical image dataset, considering trade-offs in computation time, robustness, and initialization error. The chosen SR values reflect the assumption of a coarse estimate longitudinal initialization but fairly accurate rotational initialization that comes from knowledge of patient positioning (e.g., knowing that the image is a lateral radiograph). As detailed in Otake et al (2012, 2013), a rigorous parameter sweep was performed to determine values for MS and lambda that yielded robust performance while minimizing GPU memory and computation time.

Convergence was defined with respect to the covariance matrix, where tolerance cut-off (TolX) was set for the maximum value of the diagonal terms of the covariance matrix, implying that convergence is met when population sampling is contained to a small subspace around the current estimate. Due to the wide distribution of the multi-start initializations, it is expected that a large portion of the optimizations may converge to a false optimum; thus, it is computationally inefficient to set a strong convergence criteria. Therefore, a weak tolerance (TolX = 1) was initially set for all the multi-start optimizations, and following convergence for each of these MS optimizations, a single-start optimization restart was performed using the highest GO solution as an initialization and a stronger convergence criteria (TolX = 0.1).

2.2 Multi-stage LevelCheck framework

To account for anatomical deformation between the CT and radiographic image, we developed a multistage registration framework, henceforth referred to as msLevelCheck. The core feature of this method is that the volume is divided into sub-images at each stage to locally refine T_r and correct for any deformation of the spine. Note that the method maintains the advantageous characteristics of the original rigid LevelCheck algorithm, is primarily automatic (i.e., the progression to smaller local regions at each stage does not require additional user input), and is distinct from strictly piece-wise registration (that typically rely on segmentation). The basic parameters in the (single-stage) LevelCheck method were taken from previous studies of the sensitivity of registration performance to parameter values, identifying the nominal values presented above. The key parameters for the msLevelCheck performance are investigated with respect to accuracy / sensitivity and detailed below.

2.2.1 Multi-stage progression

The key feature of msLevelCheck is that at each subsequent stage, k, the 3D image is divided into multiple 3D sub-images, each focusing on (possibly overlapping) local regions and are independently registered to the p [2D image] using the outputs from the previous stage (T_r;k−1) to determine the initialization. As illustrated in figure 3, the first stage of this framework is equivalent to the rigid LevelCheck algorithm, which provides an accurate registration in some portion of the image. At stage 2, independent registrations are performed on sub-images of the 3D CT defined from masked regions about subgroups of vertebral labels (described in 2.2.2). In subsequent stages, the sub-images are further divided to focus on smaller, increasingly local 3D regions until the final stage at which the output registration transforms are used to compute annotation locations on the 2D image. Note that each level of the multi-stage process (i.e., in progressively smaller sub-image regions), a typical coarse-to-fine morphological pyramid was employed as detailed below, but that morphological pyramid should not be confused with the multi-stage process that achieves a globally deformable transformation based on multiple rigid registrations in successively smaller regions of interest. Thus, the multi-stage framework yields a transformation of the annotations from the 3D CT to the 2D radiograph that is globally deformable yet locally rigid to improve the registration accuracy at each annotation.

Figure 3.

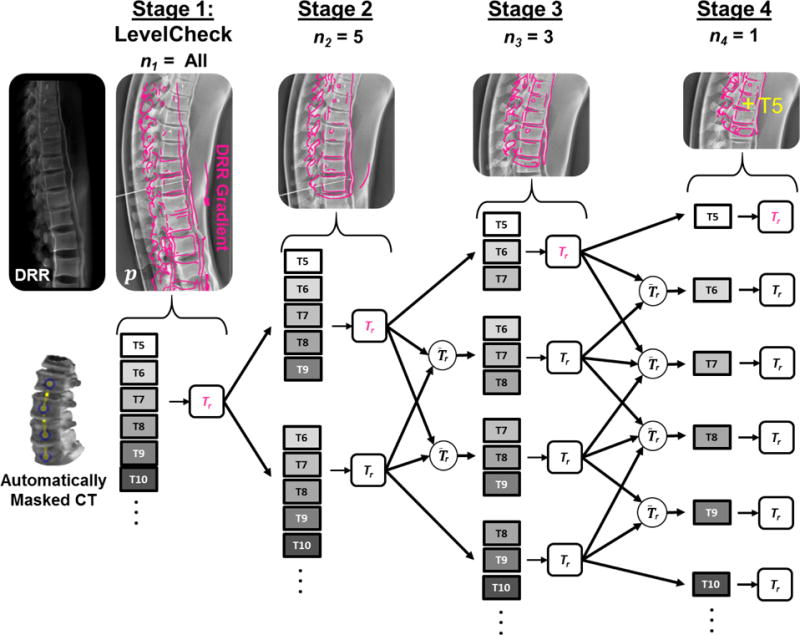
Illustration of msLevelCheck using 4 stages with the sub-image size, n_k, for the stages set to {All, 5, 3, 1}. Images along the top show the projection image p with a DRR gradient overlay in magenta, depicting the progression of msLevelCheck along the upper arm of the registration framework for each stage in the multi-stage method.

2.2.2 Definition of sub-images

To divide the CT into sub-images at each stage, subsets of the 3D preoperative vertebral labels are used to generate 3D binary masks around local regions using the same principle of binary volumetric masking as described in section 2.1.1. The size of the sub-images at each stage k is set by n_k, the number of labels chosen to generate each mask (represented as the number of dots in the binary volume mask of figure 5). Therefore, binary masking provides a segmentation-free region of interest for various locations along the spinal column [e.g., T5–T6 (n_k = 2), T5–T7 (n_k = 3), etc.] and, owing to the distance-based mask, may even include spinal levels outside the specified labels. The number of stages (S) and the method for choosing which subsets of the annotations are used to generate each sub-image is customizable to a particular case or application scenario and must be investigated to accommodate the expected degree and type of deformation; however, the method employed below generally follows that of figure 3. In this method, for each of the S stages, the 3D image is divided into sub-images based on masks that are generated from all adjacent permutations of n_k vertebral labels (i.e., for n_k = 3 we have {T5–T7, T6–T8, T7–T9,…} rather than {T5–T7, T8–T10,…}, for example). At the first stage, n₁ is set as the total number of annotated vertebrae (“All”) and is identical to the rigid LevelCheck method; at each subsequent stage the value is reduced to perform registration using smaller sub-images.

Figure 5.

Sensitivity to the number of vertebrae included in single-stage registration evaluated in 61 clinical radiographs. (a) Examples show n₁ = 1, 3, and 5 vertebrae, each with a 50 mm binary volume mask. (b) Failure rate and maximum PDE measured as a function of n₁. The observation that smaller mask size reduced the max PDE motivated development of the msLevelCheck method to provide both robust global registration (via the initial stages) and more accurate registration local to each vertebra (via the end stages).

2.2.3 Propagation of transforms at each stage

3D-2D registration is performed independently for each sub-image in the multi-stage framework. Initialization for each sub-image is determined by the T_r;k−1 outputs of the previous stage from registrations containing the entire region of the current sub-image (as depicted by the arrows in figure 3). In the scenario where multiple outputs fall into this set, an average over these N_I initialization transformations is used to determine an appropriate initialization. Such an average transformation can be computed by separating the problem into translation and rotation components. For translation, the mean is computed over the input translation components:

$${\overline{T}}_{\mathit{xyz}}=\frac{1}{N_I}{\displaystyle \sum _{j=1}^{N_I}{T}_{\mathit{xyz}}^{(j)}}$$ (3)

Where $T_{\mathit{xyz}}^{(j)}$ is the 3×1 translation vector of the jth T_R. For the average rotation, a quaternion average is computed over rotational components to handle the non-linearity of Euler angles. By representing each of the 3×1 rotation vectors as equivalent 4×1 quaternion rotations, $T_{\eta \theta \varphi }^{(j)}\to q_j$, Markley et al (2007) describes the average of these rotations to be the eigenvector of the matrix M that corresponds to the largest eigenvalue (i.e., U₁ the first column of U when S is a decreasing diagonal matrix and USU^t is the eigen-decomposition of M):

$$M={\displaystyle \sum _{j=1}^{N_I}{q}_j{q}_j^t}=US{U}^t$$ (4)

Following this decomposition, the average quaternion rotation is transformed back into Euler angles, $(U_1\to {\overline{T}}_{\eta \theta \varphi })$, and ${\overline{T}}_r={[{\overline{T}}_{\mathit{xyz}}^t,{\overline{T}}_{\eta \theta \varphi }^t]}^t$ is used to initialize the subsequent registration.

2.2.4 Scaling optimization parameters

The accuracy is expected to gradually improve as the multi-stage registration progresses, and registration parameters are accordingly adjusted to a finer range and scale. As the transformation estimate approaches the solution at each stage, parameters governing the search range (SR, as outlined in section 2.1.4) are scaled to better suit the smaller region of interest and improve registration runtime. In terms of decreasing SR, the parameters of T_r governing the translation direction z_r (corresponding to magnification) and the three rotations were reduced to relatively small empirically-determined fixed values at each stage to cater to the maximum amount of expected deformation. On the other hand, the remaining two translation parameters x_r and y_r (most directly corresponding to [u, v] on the detector) demonstrated greater variability across stages, and thus were reduced in an adaptive manner according to the variation of output poses from the previous stage. The search range, SR_x,y, for these parameters consisted of the addition of two components: (i) a fraction, f_k, of the intervertebral distance (IVD, i.e., the computed mean distance between adjacent vertebral labels on the detector computed from the estimated projected labels of the previous stage); and (ii) an adaptive term,D_a, that extends the SR by the standard deviation among label positions computed from the multiple T_r poses used for the initialization. We selected IVD as a reference based on the finding that registration following stage 1 tends to be accurate within the range of one vertebra; therefore, choosing a search range based on IVD provides a consistent method to constrict the search range (via reducing f_k) in a manner that normalizes effects of patient size and vertebra type (i.e. cervical/thoracic/lumbar).

$$S{R}_{x,y}(f_k)=\frac{z_r}{\mathit{SDD}}(f_k\times \mathit{IVD}+D_a)$$

$$\text{where}{D}_a=\sqrt{\frac{1}{n_k{N}_I}{\sum }_{i=1}^{n_k}{\sum }_{j=1}^{N_I}\Vert d_{ij}-{\overline{d}}_i{\Vert }^2},$$ (5)

$$\text{and}\mathit{IVD}=\frac{1}{(n_k-1)N_I}{\sum }_{j=1}^{N_I}{\sum }_{i=1}^{n_k-1}\Vert d_{ij}-d_{i+1,j}\Vert$$

The term D_a is the standard deviation of the projected label positions on the detector, d_ij(u, v). To compute D_a, the N_I initialization poses $[T_r^{(j)}]$ are used to project each of the n_k labels included in the mask for current registration to achieve d_ij (the projection of label i onto the detector using $T_r^{(j)}$). The standard deviation is then computed by calculating the distance of each d_ij to the centroid location for its associated vertebra, ${\overline{d}}_i$ (mean across j of d_ij). This term is added to the fraction of the IVD (i.e.,f_k × IVD) and scaled by the inverse of the current magnification estimate (z_r/SDD) to approximate this distance in the CT world coordinates. The search range SR_x,y(f_k) therefore provides an increasingly smaller search range (by reducing f_k at each stage) that is extended adaptively based on the agreement among the poses in the previous stage. With this smaller SR and an improved initialization estimate, optimization parameters MS and λ can be relaxed without diminishing performance. Therefore, following stage 1, to improve computation time and reduce GPU memory, MS and λ were reduced to 25 and 100, respectively, before noticeable stochastic effects were observed in the CMA-ES optimizer.

2.2.5 Enhancing structural image features

Each stage in the method facilitates finer registration accuracy and exploits increasingly fine detail of anatomical structures in the underlying images. To achieve a finer level of detail, the downsampling of p is reduced (by decreasing a_pix) along with the kernel width σ (characteristic width of the Gaussian smoothing kernel) for the image gradient calculation when computing the metric GO. A parameter sensitivity study that tested 100 variations of a_pix and σ for stage 1 registration indicated stable performance near 2 mm for both parameters. Following stage 1, the choices for a_pix and σ were incrementally reduced to the final stage value of 1.5 mm and 1.25 mm, respectively, based on empirical tests in a small number of samples and recognizing limitations in GPU memory (noting that a_pix reduction yields a quadratic factor increase in GPU memory use). As a further step to improve memory efficiency, the p image is cropped to contain only the region that is defined by the search range and sub-image extent of the current registration. Following the first stage, adaptive histogram equalization is applied to the radiograph to locally enhance the contrast and thereby accentuate structures that may otherwise fall beneath the gradient threshold applied during GO calculation, an effect that becomes increasingly likely as the impact of noise rises due to the reduction in down-sampling and gradient kernel width.

2.3 Experiments

2.3.1 Single-stage registration with sub-image extent n₁

A sensitivity study was performed to investigate robustness under the scenario of using only one stage in which the 3D CT image is immediately divided into sub-images of size n₁. For example, in scenarios for which the structure of interest is just a single vertebral target level, it may be of interest to register a small sub-image of size n₁ about that level. We therefore investigated the question of how many vertebrae are necessary for a successful registration, particularly in cases of poor initialization.

The robustness of single-stage registration for such small sub-images was evaluated in an IRB-approved retrospective clinical data set of 24 patients undergoing thoracolumbar spine surgery, consisting of 24 CT images and 61 intraoperative radiographs. Preoperative CT included data from three scanner manufacturers (Siemens Healthcare, Erlangen, Germany; Toshiba Corporation, Tokyo, Japan; and GE Healthcare, Little Chalfont, UK) with scan techniques ranging from 120–140 kVp, 80–660 mAs, and 0.24–3.00 mm slice thickness. Intraoperative radiographs were all acquired with a mobile radiography system (DRX-1, Carestream Health, Rochester, NY, USA) with pixel dimensions 0.14 × 0.14 mm². Binary Volumetric masks were automatically generated with the number of adjacent vertebrae (n₁) ranging from 7 down to 5, 3, and 1, centered on a central vertebra in the radiograph. Registration was performed using the rigid LevelCheck algorithm (full search range) with the (stage 1) parameters in table 2, as described in section 2.1.

Table 2.

Summary of nominal parameters in the msLevelCheck algorithm, framework 6.

	nk	apix (mm)	σ (mm)	SR: ± [x, y, z, η, θ, ϕ] (mm, mm, mm, °, °, °)	MS	λ
Stage 1 (rigid)	All	2.00	2.00	[100, 200, 75, 15, 10, 10]	50	125
Stage 2	5	1.75	1.50	[SRx,y (0.4), SRx,y (0.4), 20, 10, 5, 5]	25	100
Stage 3	3	1.75	1.50	[SRx,y (0.2), SRx,y (0.2), 10, 5, 5, 5]	25	100
Stage 4	1	1.50	1.25	[SRx,y (0.15), SRx,y (0.15), 10, 5, 5, 5]	25	100

Registration accuracy was evaluated in terms of the projection distance error (PDE) for each label at the detector, defined for the i^th label as:

$$PD{E}_i=\left|\right|t_i(u,v)-d_i(u,v)|{|}_2$$ (6)

which is the distance between the projected CT label [d (u, v)] to the ground truth label [t (u, v)]. The ground truth position (approximately located at the vertebral body centroid) was manually defined in the radiograph by an expert neuroradiologist. Successful localization involves registration of a label within the bounds of the vertebral body – approximately 15 mm radius for a thoracolumbar level - corresponding to 22.5 mm at the detector for magnification M = 1.5. Therefore, registration failure was conservatively defined as cases for which the mean PDE among projected labels was greater than 20 mm. Intra-user variability in centroid identification was analyzed (and as shown below, found to be the main source of variability in the resulting PDE). Taking again M = 15, and the intra-user variability in centroid definition σ_CT = 2 mm in the CT image, and σ_rad = 2 mm in the radiograph, the resulting error is σ_def = sqrt[(1.5²)(2²) + (2²)] = 3.6 mm. This level of intra-user variability is sufficient for purposes of level definition (i.e., <~20 mm failure criterion). Further, we investigated the influence of anatomical deformation (changes in spinal curvature) when the region being registered is large (for example, n₁ ≥ 7), noting that even in cases of successful registration (mean PDE < 20 mm), there may be individual labels exhibiting large PDE, as illustrated in figure 1; therefore, the maximum PDE was also examined.

2.3.2 Multi-stage framework determination

The msLevelCheck method does not impose explicit constraints on the projected labels, only a ${\overline{T}}_r$ calculation that, coupled with a reduced search range at each stage, acts as an implicit regularization on adjacent vertebral motion. To investigate the degree of regularization that is necessary (in terms of both the number of stages and the sub-image size at each stage), seven potential frameworks for msLevelCheck were tested on a challenging case from the clinical data set. Thus, the goal of this study was to determine a sufficient framework that minimized the number of stages necessary while still being able to accurately correct for the magnitude of deformation that can be expected in spinal procedures. The frameworks presented in table 1 represent a variety in both the depth and structure of possible multi-stage registration trees: from short trees (e.g., {All, 1}) for which the sub-images are immediately divided into small segments to deep trees (e.g., {All, 5, 4, 3, 2, 1}) for which the sub-image division is incremental.

Table 1.

Registration frameworks considered for msLevelCheck. Framework notation for n_k over a number of stages (S) is denoted in { } brackets, with ‘All’ denoting all vertebrae within the radiographic field of view. For example, {All, 5, 3, 1} denotes a four-stage framework in which the registration is computed for all vertebrae (as in the basic LevelCheck algorithm), followed by 5, 3, and finally each (1) single vertebrae. Performance of each framework is shown in figure 6.

Framework	1	2	3	4	5	6	7
S	2	2	2	3	3	4	6
nk	{All, 1}	{All, 2}	{All, 3}	{All, 3, 1}	{All, 4, 1}	{All, 5, 3, 1}	{All, 5, 4, 3, 2, 1}

Following these choices for S and n_k, the remaining parameters to be selected include, f_k, a_pix and σ. By analyzing the clinical dataset, it was seen that (within the region spanned by the radiograph) deformation of the spine tended not to exceed a distance proportional to approximately half of a vertebral body length. Since IVD includes the distance of a full vertebral body plus the intervertebral disk space, to account for the expected level of max deformation, f₂ was set to be 0.4 for each tested framework. For the following stages, it is expected that the initialization is increasingly nearer to the solution; thus, f_k was reduced incrementally, roughly in proportion to the decrease in the sub-image size. As described in 2.5.3, a_pix and sigma were similarly decreased based on n_k from 2 mm (at stage 1) to 1.5 mm (at n_k = 1) for a_pix and 2 mm to 1.25 mm for σ. A table of parameter values for framework 6 is provided in table 2.

The registration of CT labels to the radiograph was repeated 5 times for each framework, and the PDE was analyzed to determine a suitable framework for subsequent studies.

2.3.3 Multi-stage registration in phantom

Evaluation of msLevelCheck in the presence of deformation was performed using a Sawbones® spine phantom (Pacific Research Laboratories, Inc., Vashon Island, WA, USA) within a flexible bulk holder simulating adjacent soft tissue as shown in figure 4. A CT scan emulating the preoperative pose was acquired with the phantom lying flat (as in figure 4(a)–(b), scanned on Toshiba Aquilion One, 120 kVp, 400 mA, Bone standard reconstruction, 0.625 × 0.625 × 0.5 mm³ voxel size). Spinal deformation analogous to that of an arched Wilson operating table was simulated using foam core inserted below (anterior to) the spine as in figure 4(c). Six inserts varying in thickness from 4.9 to 10.1 cm gave a total of 7 curvatures, ranging from flat to strongly kyphotic. For each of the 7 levels of deformation, lateral projection images were acquired using a mobile radiography system (DRX-1, Carestream Health, Rochester, NY, USA) analogous to the images acquired in intraoperative spine level localization, spanning a region of the thoracolumbar spine from roughly T5 to L2. The true location of each vertebral level was manually defined in the CT and each projection image by a single observer (an engineer familiar with the relatively simple anatomy in this phantom).

Figure 4.

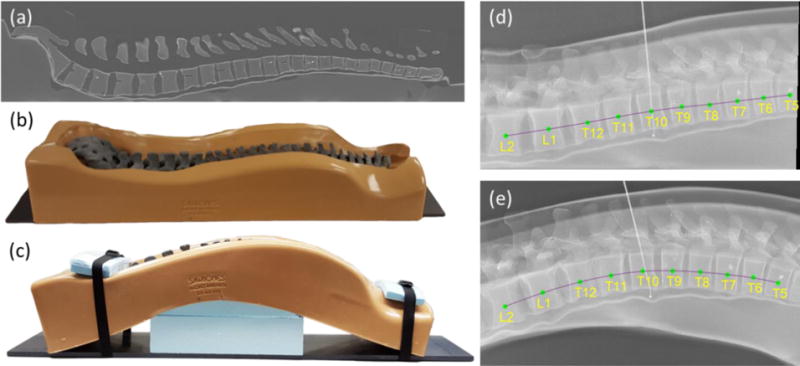
Investigation of spinal deformation in phantom. (a) Sagittal CT slice of the (b) spine phantom lying flat. (c) Photograph of the spine phantom with maximally induced curvature. (d) Lateral radiograph with vertebral levels overlaid of the phantom lying flat (as in (b)). (e) Lateral radiograph of the phantom with maximal deformation (as in (c)), overlaid with level labels.

For this study, the four-stage msLevelCheck framework illustrated in figure 3 was used, with the number of vertebrae in each mask at each stage set to n_k = {All, 5, 3, 1} (i.e., framework 6 in the previous study). This hierarchy was chosen for this setting following the experiment of section 2.3.2 where it proved robust in balancing the tradeoff between solving large deformations and avoiding local optima. The parameters for this framework are detailed in table 2, with parameter choice as described in section 2.2 and 2.3.2.

The msLevelCheck registration of “flat” CT to “deformed” radiograph was repeated 5 times for each of the 7 deformation cases to test the robustness due to the stochasticity of the CMA-ES optimizer. Analysis of registration accuracy was performed by examining the distribution of PDE values for the 7 deformation cases and comparing the performance to the rigid (conventional single-stage LevelCheck) registration. Statistical significance in the difference between rigid and msLevelCheck results was analyzed using a Wilcoxon signed-rank test.

2.3.4 Multi-stage registration in clinical data

The msLevelCheck method was further tested using a subset of the clinical data described in section 2.3.1. The most severe deformation cases among the 61 radiographs were selected by analyzing the rigid registration result (for which the vertebrae in the center of the radiograph was typically well registered) and computing the increasing trend in PDE for vertebrae superior and inferior to the central vertebra (i.e., cases exhibiting greater PDE at superior and inferior extrema). From these data, 7 radiographs from 5 patients were selected as exhibiting the most severe deformation. Using the same four-stage method detailed in figure 3 and table 2, the rigid and msLevelCheck methods were evaluated by examining the mean and maximum PDE.

2.3.5 Comparison to piecewise rigid registration

To test the performance of msLevelCheck to alternative methods, we performed a comparative study to a piecewise rigid approach. Note that the msLevelCheck method is segmentation-free, whereas the piecewise rigid method assumes a reliable segmentation. The piecewise rigid registration was performed by first segmenting individual vertebral bodies in the CT of the spine phantom. Segmentation was accomplished using the active contour method implemented in ITK Snap (Yushkevich et al 2006). A central segmented vertebra was initialized near solution (error to within half of a vertebral body length) for the maximum deformation radiograph case, and 3D-2D registration was performed for the individual segmented vertebrae. Adjacent vertebrae were recursively registered using the output transformation from a previously registered adjacent vertebra as an initialization. Search range constraints were imposed to prevent one-level vertebral “jumps” in registration. Registrations using msLevelCheck and the piecewise rigid method were repeated 5 times each on this maximum deformation spine phantom case. Performance was evaluated in terms of PDE (mean and standard deviation), hypothesizing comparable performance between msLevelCheck and piecewise rigid, but recognizing the advantage of the former operating without segmentation.

3. Results

3.1 Single-stage registration with sub-image extent n₁

Figure 5 shows the performance of single-stage rigid registration as a function of sub-image size, n₁. This single-stage algorithm is equivalent to the previously described LevelCheck algorithm for various choices of n₁ and thus examines performance as the region of support decreases. Figure 5(a) shows examples of the volumetric mask size, DRR, and labeled projection for variable n₁. As shown in figure 5(b), the failure rate increases sharply for fewer vertebrae within the mask, indicating that reliable registration benefits from including longer extent (more vertebrae) in the binary volume mask definition, providing a larger field of view for the registration and improved robustness against local minima. As shown on the second vertical axis of figure 5(b), however, spinal deformation causes some regions within the larger field of view to align poorly (typically at the superior / inferior ends of the image) and exhibits an increase in maximum PDE. Therefore, the LevelCheck algorithm benefits from a larger field of view (increased n₁) but can suffer from anatomical deformation, motivating the multi-stage registration framework analyzed below.

3.2 Multi-stage framework determination

Figure 6 compares the performance of the various multi-stage frameworks shown in Table 1. Two types of error mode are evident. For the shorter (S=2) trees, a broader, more uniform distribution of error is seen, with errors widely distributed over a range of ~15 mm PDE. In the deeper trees, we observed PDE concentrated near ~2.5 mm; however, a fairly large number of failures (PDE >20 mm) were evident for the 3-stage frameworks. The 4-stage framework {All, 5, 3, 1} provided low PDE with the fewest outliers, and the deeper 6-stage framework did not provide further significant improvement. Therefore, the {All, 5, 3, 1} tree was selected as the nominal framework for msLevelCheck in subsequent studies.

Figure 6.

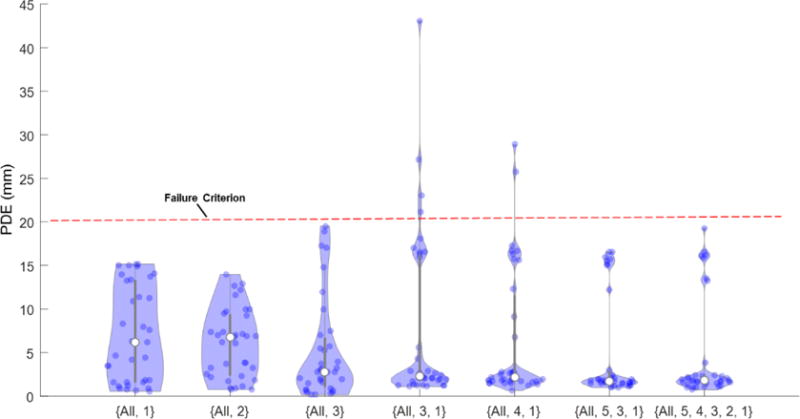
Comparison of various multi-stage frameworks listed in Table 1. Violin plots indicate the distribution of PDE for the registered labels in each framework.

3.3 Multi-stage registration in phantom

Figure 7 summarizes the msLevelCheck performance measured for different degrees of spinal deformation. Figure 7(a) shows an example for the strongest deformation (case 7), where the rigid approach (stage 1) tended to align well in the central region of the radiograph but decreased in accuracy at the inferior and superior ends of the image. The msLevelCheck method, however, was able to accurately map all vertebral labels by incrementally focusing alignment on sub-image regions, improving alignment locally at each stage.

Figure 7.

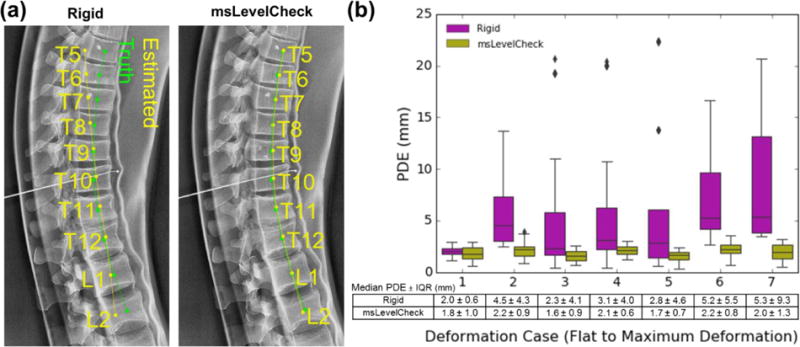
Registration accuracy for the msLevelCheck method under various degrees of deformation (spinal curvature). (a) Illustration of registration for the single-level rigid and msLevelCheck methods for the case of strongest deformation (case 7). (b) Boxplots depicting the distribution of PDE for both registration methods for the 7 deformation cases (cases 1–7, indicating increasing degree of deformation) along with the tabulated numerical values for median PDE and IQR.

Figure 7(b) quantifies the performance improvement in terms of PDE for the seven cases of increasingly strong deformation. For the rigid method, although the median PDE is ≤ 6 mm for all cases, the interquartile range (IQR) and frequency of outliers increased steadily with stronger deformation. Despite such challenge, the msLevelCheck method was unaffected, maintaining median and IQR in PDE across the full range of deformation examined in this study. The distribution in PDE for msLevelCheck showed a statistically significant improvement (p < 0.001) for each case, except for case 1 (no deformation, where both methods performed well). With respect to outliers and maximum PDE, the rigid method showed maximum PDE = 22.4 mm (in case 5), whereas msLevelCheck gave a maximum PDE of 3.9 mm (in case 2), which is below the value indicative of failure (~20 mm).

3.4 Multi-stage registration in clinical data

Figure 8 compares the performance of the rigid and msLevelCheck methods applied to clinical data. Figure 8(a) shows an example case in which the spine was more lordotic in the intraoperative radiograph than the preoperative CT, consistent with typical patient positioning on a Jackson table. The rigid method is seen again to provide good registration at the center of the image, but to lose accuracy at superior / inferior extrema. Figure 8(b) depicts the distribution in mean PDE (and figure 8(c) the maximum PDE) aggregated over all cases in the clinical data set, demonstrating a statistically significant improvement (p <0.001) in both mean and maximum PDE for msLevelCheck. Overall, the average PDE improved from 8.1 mm with the single-stage rigid method to 4.6 mm with msLevelCheck. More importantly, the maximum PDE was reduced from 32.0 mm for the single-stage rigid method to 18.6 mm for msLevelCheck. It bears reiteration that cases selected in the clinical study were those exhibiting the most severe deformation, and while the single-level rigid approach resulted in 6.5% of labels falling outside the 20 mm failure criterion (i.e., outside or near the boundary of a given vertebra) in a manner that may diminish utility of the algorithm, the msLevelCheck method registered all vertebrae within the acceptable range. Note also that the algorithm maintained other desirable aspects of the original LevelCheck method, such as robustness against the presence of interventional tools (as illustrated in figure 8(a)).

Figure 8.

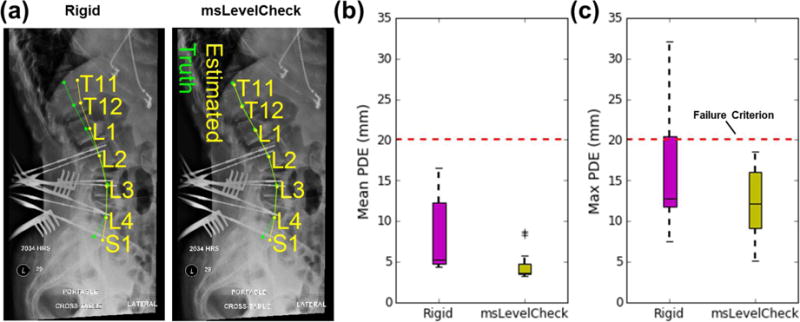
Registration accuracy for msLevelCheck in clinical data. (a) Example case showing single-level rigid registration and msLevelCheck output for a case exhibiting an increase in spinal lordosis in the radiograph compared to preoperative CT. Distribution the mean (b) and maximum (c) PDE pooled over cases in the clinical dataset, showing msLevelCheck to improve registration accuracy and recover from cases that might be considered a registration failure.

3.5 Comparison to piecewise rigid registration

Figure 9b examines the distribution in PDE for the piecewise rigid method in comparison to msLevelCheck (for the the {All, 5, 3, 1} framework), yielding PDE = (2.5 ± 1.9) mm and (2.0 ± 1.4) mm, respectively (median PDE ± IQR). Both methods performed successfully (PDE < 20 mm), and there was no statistically significant difference between the two distributions (paired t-test p-value >0.05). This indicates that msLevelCheck performed at least as well as the piecewise rigid solution but with the benefit of not requiring explicit segmentation involved in the piecewise rigid method.

Figure 9.

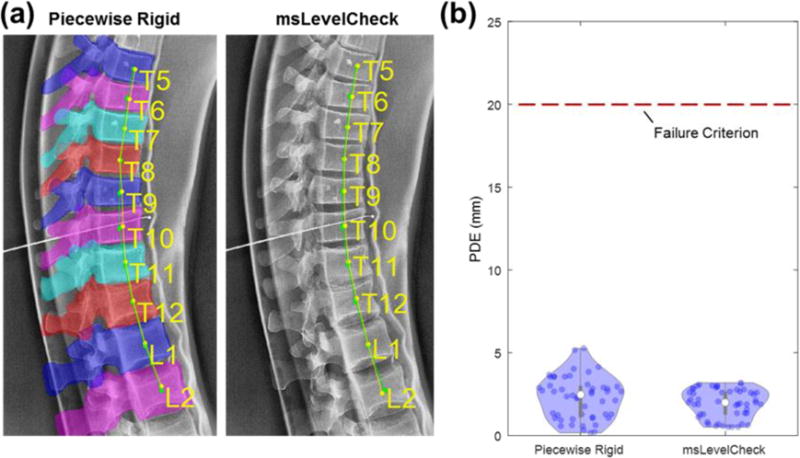
Comparison of performance for piecewise rigid and msLevelCheck. Results are shown for the case of maximum deformation in the spine phantom. (a) Illustration of registration for the piecewise rigid (overlaid with the projections of the requisite vertebrae segmentations) and msLevelCheck methods. (b) Violin plots show the distribution of PDE for the registered labels in each method, with median PDE shown as a solid white circle, upper and lower bounds given by the max and min PDE, and 50 individual sample points shown therein.

4. Discussion and Conclusions

In this paper, we have reported a multi-stage 3D-2D registration algorithm (msLevelCheck) for mapping label annotations (e.g., vertebral labels or other point features demarked in preoperative 3D images as part of existing clinical workflow) to intraoperative radiographs under conditions of strong anatomical deformation. The multi-stage approach amounts to 3D-2D registration that is locally rigid (at progressively finer scales) and yet globally deformable (with respect to mapping of label annotations from the 3D image to the radiograph). The latter point bears reiteration: the method does not constitute a deformable registration of the image; rather, it produces a series of rigid transformations by which point annotation landmarks are transformed independently, and thus deformably with respect to the underlying image. The progressive multi-stage registration framework is shown to be necessary in section 3.1 where we see a high registration failure rate when the sub-images are immediately broken up into small sub-images. Further, section 3.2 indicates that a 4 stage {All, 5, 3, 1} framework provides a sufficient rate of sub-image reduction for this application.

A recent study evaluated the clinical utility of LevelCheck (De Silva et al 2016b) and showed that a clinician’s confidence in target localization could be diminished when some labels (even if far from the target level) were placed near or outside the periphery of a vertebral body. The msLevelCheck method addresses this concern, showing accurate registration of all vertebral levels (2.9 mm median PDE, 3.8 mm IQR, and 0% failures) over a broad range of deformation in clinical data.

The registration runtime is necessarily increased for the multi-stage framework. Previous work showed the original LevelCheck method to run in ~20 s (Otake et al 2013), and runtime as long ~60 s was said to be acceptable within clinical workflow for purposes of decision support in level counting (De Silva et al 2016b). In the current work, the framework was implemented in a simple serial form in which the runtime increases in proportion to S (the number of stages) and V (the number of vertebral labels), implying an increase in runtime by a factor of ~4V for the 4-stage {All, 5, 3, 1} framework of figure 3. However, because each stage contains multiple independent registrations, these registrations within each stage can be parallelized; therefore, in a parallel implementation the increase in runtime is instead proportional to S. Moreover, since SR, MS, and λ are reduced following stage 1, the runtime associated with each registration in these later stages is faster than the first stage (original LevelCheck method). In terms of the number of function evaluations that must be completed along each parallel string (i.e., each sub-image registration), ~250,000 function evaluations were typically required in the first stage, whereas ~110,000 function evaluations were typical for the following stages. A more optimal implementation of the 4 stage method to be developed in future work would therefore scale the runtime by a factor of ~2.3 compared to the original LevelCheck algorithm, amounting to ~50 s.

Apart from anatomical deformation, factors that are known to challenge the original LevelCheck method (delineated in Lo et al [2015]) may similarly challenge msLevelCheck. These include poor radiographic image quality (e.g., large patients and/or poor radiographic technique), poor CT image quality (e.g., thick slices), high density of surgical instrumentation, and gross anatomical mismatch (e.g. corpectomy). To better address these challenges, the msLevelCheck method could be extended to take better advantage in regularizing the entire series of local registration outputs accrued across each stage. By analyzing the trend in output pose across stages and among neighboring registrations, outliers in individual registrations could be detected and trapped, either by retreating to the output of a previous stage, or interpolating across the pose estimates for adjacent regions.

While the multi-stage method presented above focuses on the application of the vertebral labeling as a means of decision support in spine level counting, it is important to note that the framework can be extended to other applications of annotation mapping in which deformation may occur, particularly those incorporating articulated rigid bodies. Potential applications to be considered in future work include registration of other joint spaces (e.g., the knee, sacroiliac, and acetabulum) and comminuted fractures.