A Tutorial on Multilevel Survival Analysis: Methods, Models and Applications

Summary

Data that have a multilevel structure occur frequently across a range of disciplines, including epidemiology, health services research, public health, education and sociology. We describe three families of regression models for the analysis of multilevel survival data. First, Cox proportional hazards models with mixed effects incorporate cluster-specific random effects that modify the baseline hazard function. Second, piecewise exponential survival models partition the duration of follow-up into mutually exclusive intervals and fit a model that assumes that the hazard function is constant within each interval. This is equivalent to a Poisson regression model that incorporates the duration of exposure within each interval. By incorporating cluster-specific random effects, generalised linear mixed models can be used to analyse these data. Third, after partitioning the duration of follow-up into mutually exclusive intervals, one can use discrete time survival models that use a complementary log–log generalised linear model to model the occurrence of the outcome of interest within each interval. Random effects can be incorporated to account for within-cluster homogeneity in outcomes. We illustrate the application of these methods using data consisting of patients hospitalised with a heart attack. We illustrate the application of these methods using three statistical programming languages (R, SAS and Stata).

1 Introduction

Data with a multilevel or hierarchical structure occur frequently in a wide range of research disciplines. For instance, in a study of mortality in patients hospitalised with a heart attack, subjects are clustered within hospitals, which in turn may be clustered within regions. An investigator may be interested in determining the characteristics of patients, hospitals and regions that are associated with an increased risk of death following a heart attack. In conventional multilevel data, each level one unit (e.g. patients) is nested in one and only one level two unit (e.g. hospitals). The level two units may subsequently be nested in one and only one level three unit (e.g. regions). Further levels of clustering or nesting are possible. In the current tutorial, we restrict our attention to multilevel data with two levels. However, the methods described generalise to settings with more than two levels to the data hierarchy. The outcome or response variable is measured at the lowest level of the hierarchy–on the level one units, whereas explanatory or predictor variables can be measured on units at any of the levels of the hierarchy.

Conventional regression models assume that subjects are independent of one another. However, subjects who are nested within the same higher level unit are likely to have outcomes that are correlated with one another, thus violating the assumption of independent observations. This within-cluster homogeneity may be induced by unmeasured cluster characteristics (e.g. hospital culture) that affect the outcome or by unmeasured covariates at the subject level (e.g. genetics or dietary practices when subjects are clustered within families) that take a similar value for all subjects within the cluster. Multilevel regression models allow one to analyse data that have a multilevel structure while accounting for the clustering of lower level units within higher level units. In the past two decades, multilevel models have moved from being a niche specialty (often requiring specialised stand-alone statistical software) to being part of the statistical mainstream (and being able to fit using general purpose statistical software programmes).

Survival analysis refers to methods for the analysis of data in which the outcome denotes the time to the occurrence of an event of interest. A key feature of survival analysis is that of censoring: the event may not have occurred for all subjects prior to the completion of the study. Subjects who are event-free at the end of the study are said to be censored. We refer the interested reader to several of the classic reference books on survival analysis (Cox and Oakes 1984; Kalbfleisch and Prentice 2002; Lawless 1982; Aalen, Borgan and Gjessing 2008; Mills 2011; Klein and Moeschberger 1997; Therneau and Grambsch 2000; Singer and Willett 2003). Of these, only one explicitly describes methods for the analysis of multilevel survival data (Singer & Willett, 2003), while three introduce frailty models for the analysis of clustered survival data (Therneau & Grambsch, 2000; Mills, 2011; Aalen et al., 2008).

There are a large number of books devoted to issues in the analysis of multilevel data (Goldstein, 2011; Raudenbush & Bryk, 2002; Snijders & Bosker, 1999; Hox & Roberts, 2011; Rabe-Hesketh & Skrondal, 2012a; 2012b). These books describe the concept of multilevel data and introduce regression models appropriate for the analysis of such data. The primary focus of many of these books is on the analysis of data in which the outcome is continuous. The hierarchical linear model (HLM) is introduced as the primary method of analysis for multilevel data with continuous outcomes. A secondary focus of a subset of these books is on settings with discrete outcomes. The hierarchical generalised linear model (HGLM) is introduced for the analysis of multilevel data with discrete outcomes. In applied research, time-to-event outcomes occur frequently (Austin et al., 2010). Despite the frequency with which survival outcomes occur, many of the comprehensive reference books listed earlier omit methods for the analysis of multilevel survival data, while others provide a cursory discussion of multilevel survival analysis. Only one, with an emphasis on applications using Stata, provides a more detailed discussion of multilevel survival analysis (Rabe-Hesketh & Skrondal, 2012b).

The objective of this article is to describe statistical models for the analysis of multilevel survival data. The paper is structured as follows: First, we provide a brief review of HGLMs, as these models form the basis for some statistical models for the analysis of multilevel survival data. Second, we describe three different methods for the analysis of multilevel survival data. Third, we provide a case study illustrating the application of these methods. The case study consists of a large cohort of patients hospitalised with acute myocardial infarction (AMI or heart attack), who are nested within the hospitals in which they were treated.

2 Multilevel Logistic and Poisson Regression Models

In this section, we provide a brief overview of HGLMs for the analysis of multilevel data when the outcome is binary or an integer count. The motivation for this review is that two of the methods for the analysis of multilevel survival data make use of these models.

We assume that the data have two levels. Let Y_ij denote the binary or count response variable for the i-th subject nested within the j-th cluster. Let X_1ij, …, X_pij denote p explanatory variables that are measured on this individual (e.g. patient characteristics), while Z_1j, …, Z_qj denote q explanatory variables measured on the j-th cluster (e.g. hospital characteristics).

A random intercept logistic regression model incorporates a single random effect, allowing the intercept to vary randomly across clusters: logit(Pr(Y_ij = 1) = α_0j + α₁ X_1ij + · · · + α_pX_pij + β₁Z_1j + · · ·+β_qZ_qj, where the assumption is made that the random effects follow a normal distribution: α_0j ~ N(α₀, τ²). The random intercept logistic regression model allows the probability of the occurrence of the outcome for a reference subject to vary across clusters. However, the effects of the individual explanatory variables are constrained to be equal across clusters. In a random intercept Poisson regression model for count outcomes, the logit of the probability of the occurrence of the event is replaced by log(μ_ij ), where the distribution of outcomes for the i-th subject in the j-th cluster is assumed to follow a Poisson distribution with mean μ_ij.

The next level of complexity is a random coefficients model, in which the regression coefficients for the subject-level covariates are allowed to vary across clusters: logit(Pr(Y_ij = 1) = α_0j + α_1jX_1ij + · · · + α_pjX_pij + β₁Z_1j + · · · + β_qZ_qj, where it is assumed that $\left(\begin{array}{l}{\alpha }_{0j}\hfill \\ {\alpha }_{1j}\hfill \\ ⋮\hfill \\ {\alpha }_{pj}\hfill \end{array}\right)~\mathit{MVN}\left(\left(\begin{array}{c}{\mu }_0\\ {\mu }_1\\ ⋮\\ {\mu }_p\end{array}\right),\left(\begin{array}{cccc}{\sigma }_0^2& {\sigma }_{01}& \cdots & {\sigma }_{0p}\\ {\sigma }_{01}& {\sigma }_1^2& \cdots & {\sigma }_{1p}\\ ⋮& ⋮& \ddots & ⋮\\ {\sigma }_{p0}& {\sigma }_{p1}& \cdots & {\sigma }_p^2\end{array}\right)\right)$. Not all of the regression coefficients for the subject-level covariates are required to vary across clusters. One can have a random coefficients model in which a subset of the regression coefficients for the subject-level covariates are constrained to be fixed across clusters, while the rest are allowed to vary across clusters.

The reader is referred elsewhere for a more detailed review of multilevel models for use with continuous or discrete outcomes (Snijders & Bosker, 1999; Goldstein, 2011).

3 Statistical Models for Multilevel Survival Analysis

We describe three methods for analysing multilevel survival data: frailty models, which are Cox proportional hazard models with mixed effects, piecewise exponential (PWE) survival models with mixed effects and discrete time survival models with mixed effects. We consider each of these methods in turn in the following subsections.

3.1 Frailty Models: Cox Regression Models with Mixed Effects

The Cox proportional hazards regression model is frequently used for the analysis of survival data. A brief review of this model is provided in Section 1 of Appendix A in the Supporting Information. The inclusion of random effects into a Cox proportional hazards model shares many similarities with methods for the analysis for multilevel data with continuous, binary or count outcomes. A conventional regression model (in this case the Cox proportional hazards model) is enhanced through the incorporation of random effect terms to account for within-cluster homogeneity in outcomes.

The term frailty model is used to denote a survival regression model (typically either a Cox proportional hazards regression model or a parametric survival model) that incorporates random effects. Crowther et al. suggested a differentiation in terminology by using the term ‘frailty model’ to refer to a survival model with only a random intercept while using the term ‘mixed effects model’ to refer to a model that can have multiple random effects (Crowther, Look and Riley 2014). Thus, a frailty model is a special case of the mixed effects survival models. Early frailty models incorporated subject-specific random effects to account for unmeasured subject characteristics that influenced the hazard of the occurrence of the outcome. These models were then extended to models that incorporate cluster-specific random effects to account for within-cluster homogeneity in outcomes. These models have been described as shared frailty models, because the same random effect is shared by all subjects within the same cluster. In this tutorial article, we focus on the inclusion of random effects into the Cox proportional hazard regression model, due to the relative frequency with which this model is used. When random effects are incorporated in the Cox model, these random effects denote increased or decreased hazard for distinct classes (e.g. clusters such as hospitals, schools or workplaces).

Assume that subjects are nested in one of M classes or clusters (e.g. hospitals). A Cox model with mixed effects can be formulated as h_i (t ) = h₀(t ) exp(X_iβ + α_j ), where α_j denotes the random effect associated with the j-th cluster. Rabe-Hesketh and Skrondal use the term ‘shared frailty’ to denote the exponential of the random effect: exp(α_j ) (Rabe-Hesketh & Skrondal, 2012b). The random effect can be thought of as a random intercept that modifies the linear predictor, while the shared frailty term has a multiplicative effect on the baseline hazard function: h_i (t ) = h₀(t ) exp(α_j ) exp(X_j β).

Cox regression models with mixed effects are characterised by the distribution of the shared frailty terms. Different distributions have been proposed for the distribution of the shared frailty terms, including the gamma distribution, the log-normal distribution (the frailty terms will have a log-normal distribution while the random effects will have a normal distribution), positive stable frailty distributions and power variance function distributions (Hougaard, 2000; Wienke, 2011; Duchateau & Janssen, 2008). The first two appear to be the most commonly-used. In the gamma frailty model, the cluster-specific random effects are distributed as the logarithms of independent, identically distributed gamma random variables, having variance θ. The within-cluster correlation of subjects is $\frac{\theta }{\theta +2}$. We refer the interested reader to comprehensive discussions of frailty models (Wienke, 2011; Hougaard, 2000; Duchateau & Janssen, 2008).

In conventional HLMs or HGLMs, it is almost always assumed that the random effects follow a normal distribution. However, researchers using survival models with frailty terms have several distributions from which to select for the distribution of the shared frailty terms. There is a paucity of guidance as to how to select between different frailty families. Methods for choosing between frailty distributions are reviewed in Section 2 of Appendix A in the Supporting Information.

Mixed effect Cox regression models resemble the HGLMs described previously. The cluster-specific random effect terms have a relative effect on the baseline hazard function. Consequently, the relative effect of a given covariate pattern on the baseline hazard function varies across clusters. Because of this similarity between HLMs/HGLMs and Cox shared frailty models, these models are an attractive approach to fitting survival models to multilevel data. As with HLMs/HGLMs, Cox models with mixed effects are not restricted to use with data with only one level of clustering. Rondeau et al. use the term ‘nested frailty model’ to refer to survival models with random effects in which there are two or more levels of clustering (Rondeau, Mazroui & Gonzalez 2012). However, there are some limitations to the use of Cox models with mixed effects. First, Cox shared frailty models require the assumption that each subject is the member of only one level two unit, thus one cannot account for more complex multilevel structures such as multi-membership multilevel data, in which some subjects are clustered within more than one level two unit (Therneau & Grambsch, 2000). Second, while Cox models with mixed effects can be extended to account for multilevel data with more than two levels (e.g. data in which level one units are clustered within level two units, which in turn are clustered within level three units), such extensions have not been incorporated into many popular statistical software packages.

3.2 Piecewise Exponential Survival Models with Mixed Effects

When using a Cox proportional hazards model, one is freed from the necessity of specifying the distribution of the hazard function (or equivalently, from the specifying the distribution of event times). In parametric survival models, the analyst is required to make specific assumptions about the form of the hazard function. Commonly used parametric survival models include the exponential survival model (in which the hazard function is assumed to be constant over time: h(t) = λ) and the Weibull survival model (in which the hazard function is of the form h(t) = λγt^γ−1, with λ and γ denoting the scale and shape parameters, respectively).

The PWE model is a survival model in which the time scale is divided into intervals and the hazard function is assumed to be constant within each interval (Allison, 2010). Thus, one can define a set of K intervals, defined by K+1 cut points: τ₀, τ₁, …, τ_K, (where τ₀ = 0 and τ_K = ∞). In interval k, given by [τ_k−1, τ_k), the hazard function for a given subject is assumed to be constant and is related to the baseline hazard function by the function h(t) = λ_k exp(βX), where λ_k is the baseline hazard function in the k-th interval. In constructing the intervals, Allison suggests that there is some benefit to having approximately equal number of events occur in each interval (Allison, 2010). Accordingly, the intervals do not need to be of the same length. Alternatively, one can select the intervals using subject matter knowledge in such a way that it is reasonable to believe that the hazard is constant within each interval. Examples of applications of the PWE model are provided by Breslow (1974), Whitehead (1980) and Aitkin et al. (1983). Under certain assumptions, regression coefficients equivalent to those obtained from a Cox proportional hazards model can be obtained from a survival model in which one assumes that the hazard function is constant between successive event times (Breslow, 1974; Laird & Olivier, 1981). Thus, the Cox proportional hazards model can be seen as the limiting case of the PWE model.

If the hazard function is constant as a function of time (i.e. λ(t) = λ), then the exponential survival model and the Poisson regression model can be used interchangeably (Laird & Olivier, 1981). Consequently, the PWE model is equivalent to a Poisson regression model (Rodriguez, 2008; Goldstein, 2011). Given survival data consisting of a (possibly censored) observed survival time t_i for the i-th subject and an event indicator d_i denoting whether the event was observed to occur for the i-th subject (d_i =1 denoting the event occurred, 0 otherwise), one can define analogous measures for each duration interval (Rodriguez, 2008). Thus t_ij denotes the survival time for the i-th subject in the j-th interval, and d_ij is an event indicator that takes the value 1 if the i-th subject experienced the event in interval j, and takes the value 0 otherwise. A PWE model can fit by treating the event indicators as if they were Poisson observations with means μ_ij = λ_ij t_ij, where λ_ij is the hazard for the i-th individual in the j-th interval. In doing so, one would need to incorporate an offset variable denoting the logarithm of the time-at-risk during each of the intervals (Crowther et al., 2012).

As noted earlier, both the theoretical framework and the statistical software are more mature for formulating and fitting HLMs and HGLMs. The fact that one can fit a PWE survival model using a generalised linear model (i.e. a Poisson regression model) has important consequences for fitting multilevel survival models. First, one can incorporate cluster-specific random intercepts to incorporate within-cluster homogeneity in outcomes. As with HLMs and HGLMs, one is not restricted to a two-level data hierarchy, with only one source of clustering. Rather, one can develop multilevel models with more than two levels of clustering. Second, while the use of Cox models with random effects allows the baseline hazard function to vary across clusters, the use of a random coefficients Poisson regression model allows the effect of a given covariate to vary across clusters. Random coefficients are more easily incorporated using this approach than with the Cox model with mixed effects. Third, by using the PWE model, and incorporating random effects, one can use statistical procedures that are available in many popular statistical software packages (e.g. R, SAS and Stata).

3.3 Discrete Time Survival Models with Mixed Effects

Discrete time survival models can be used when survival time is measured in discrete values (e.g. years to disease incidence). These models use a discrete version of the hazard function. Binomial regression models, with a logit, probit or complementary log–log link function can be used to model the probability that the event occurred at a specified discrete time point, conditional on the fact that it had not yet occurred (Rabe-Hesketh & Skrondal, 2012b). Even when survival time is (approximately) continuous, the discrete time survival model can be used by dividing survival time into a finite number of discrete intervals. The PWE survival model described earlier divided the time scale into a sequence of intervals, under the assumption that the hazard function was constant within each of these intervals. In fitting the PWE survival model, each subject’s duration of exposure (or at-risk time) during the interval is taken into account (as an offset variable). Discrete time survival models use a similar approach; however, one simply notes whether or not an event occurred within the given interval and disregards each subject’s duration of exposure within the given interval. A regression model for binary outcomes can then be used to model the probability of the occurrence of an event within each interval. Possible link functions for the generalised linear model are the logit link function, the probit link function and complementary log–log link function (Rodriguez, 2008; Allison, 2010; Goldstein, 2011). An advantage to the latter is that the resultant regression coefficients are identical to those of an underlying proportional hazards regression model (Allison, 2010; Rabe-Hesketh & Skrondal, 2012b). Thus, the estimated coefficients can be interpreted as having a relative effect on the hazard of the occurrence of the event. An advantage to discrete time survival models compared with the PWE survival model is that one does not need to make the assumption that the hazard function is constant within each interval.

Discrete time survival models can easily incorporate the multilevel structure of the data. Because one is fitting an HGLM (a binomial model with either a logit link function or a complementary log–log link function), standard statistical methods and software for HGLMs can be employed. Detailed discussions of multilevel discrete time models are provided by Steele (2011), by Barber et al. (2000) and by Rabe-Hesketh & Skrondal (2012b). As with the PWE mixed effects survival model, random coefficients can be readily incorporated by including random coefficients in the HGLM that is being fit.

4 Case Study

4.1 Research Question

There were two primary research questions that we sought to address. The first question was more general: which patient and hospital characteristics increase the risk of death subsequent to hospitalisation for AMI. The second question focused on a specific patient characteristic: the presence of cardiogenic shock at hospital arrival (a condition in which the heart fails to pump properly, with an ensuing drop in blood pressure, which may lead to a loss of patient consciousness). We sought to answer two specific questions related to cardiogenic shock: (i) To what extent does the presence of cardiogenic shock increase the risk of death in patients hospitalised with an AMI? (ii) Does the magnitude of the effect of cardiogenic shock on the hazard of death vary across hospitals?

4.2 Data

We illustrate the analysis of multilevel survival data using data from the Ontario Myocardial Infarction Database, which contains information on patients hospitalised with a diagnosis of AMI at Ontario hospitals between 1992 and 2013. Details on its construction by linking different healthcare administrative databases provided elsewhere (Tu, Austin & Naylor 1999) (the database is updated annually, thus it contains data for years beyond those described in the initial description). For our analyses, we used hospital separations (separations that occurred either because of patient discharge or of in-hospital death) that occurred in the 12-month period between 1 April 2005 and 31 March 2006. For each patient, we noted the identity of the hospital to which the patient was admitted. The data have a hierarchical structure, with patients nested within hospitals. The study sample consisted of 16 985 patients treated at 164 hospitals. The sample consisted of unique patients: Due to the study inclusion and exclusion criteria, no patient had more than one hospital discharge during the 1-year time frame of the study.

Variables were measured on both levels of the hierarchy. Patient-level variables consisted of the eleven variables in the Ontario AMI Mortality Prediction model (age, sex, congestive heart failure, cardiogenic shock, arrhythmia, pulmonary edema, diabetes mellitus with complications, stroke, acute renal disease, chronic renal disease and malignancy) (Tu et al., 2001). Hospital-level variables consisted of academic teaching hospital (vs non-academic hospital), hospital AMI volume in the year prior to the study, and hospital capacity for invasive cardiac procedures (categorised as revascularization (percutaneous coronary intervention or coronary artery bypass graft surgery) capacity versus cardiac catheterisation (coronary angiography) capacity versus no capacity for invasive procedures). The two continuous explanatory variables (age and hospital AMI volume) were each centred around the sample average for that variable. The variable names reported in the statistical software output are described in Section 3 of Appendix A in the Supporting Information.

The patient-level outcome for the case study was the time from hospital admission to the occurrence of death due to any cause. Patients were followed for up to 30 days from the time of hospital admission and were censored after 30 days of follow-up if they were still alive. Death within 30 days of hospital admission occurred for 2 107 (12.4%) patients in the study sample.

4.3 Statistical Software

Analyses in our case study used three different statistical software programmes: R (version 3.0.2), SAS (version 9.3) and Stata (version 13.1). The following R packages were used: survival (version 2.38-2), lme4 (version 1.1-7) and coxme (version 2.2-3). Two Stata functions, mepoisson and mecloglog, were used that were not available in earlier versions of Stata. Statistical software code in R, SAS and Stata is provided in Appendix B in the Supporting Information for all of the analyses. Output from some of the analyses is reported in the text; however, to reduce redundancies, some output is reported in Appendix C in the Supporting Information.

4.4 Statistical Models for Multilevel Survival Data

4.4.1 Cox models with mixed effects

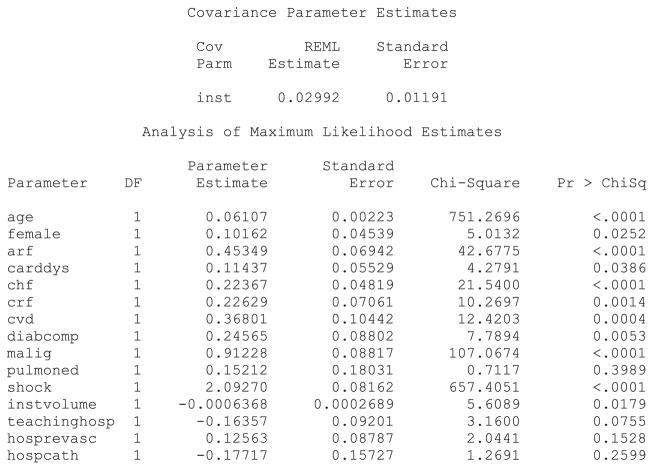
Both R and SAS allow one to choose between two distributions of the shared frailty terms (gamma or log-normal), whereas Stata restricts the user to assuming a gamma distribution. Statistical software code for fitting a Cox proportional hazards models with mixed effects are described in Statistical software code 1 through Statistical software code 5 in Appendix B in the Supporting Information. The SAS output for a Cox model with mixed effects in which the shared frailty terms follow a log-normal distribution is reported in Statistical software output 1.

Statistical software output 1.

SAS output for Cox frailty survival model (log-normal frailty distribution)

The parameter estimates reported in Statistical software output 1 are log-hazard ratios. Exponeniating them produces hazard ratios. Thus, the hazard ratio for cardiogenic shock is exp(2.09270) = 8.11. Therefore, the presence of cardiogenic shock increases the hazard of death by a factor of eight compared with subjects without cardiogenic shock. In examining the output, one observes that, with the exception of pulmonary edema, all patient-level characteristics are associated with the hazard of mortality (P < 0.039). This provides an answer to the first component of our specific research question.

Increasing patient age, female sex, and the presence of eight of the nine risk factors increased the hazard of post-AMI mortality. Increasing hospital volume is associated with a decreasing hazard of mortality (P = 0.018). The hazard ratio for an increase of hospital volume by 100 patients is equal to exp(100 ×−0.0006368) = 0.94. Thus, an increase in hospital volume by 100 patients is associated with a 6% decrease in the rate of patient mortality. The effect of the hospital’s academic affiliation and the presence of the capacities for invasive procedures are not statistically significantly different from zero (P >0.075). These observations provide answers to our first general research question.

The SAS output for the gamma frailty model is reported in Appendix C in the Supporting Information, in Statistical software output C1. The estimate of θ, the variance of the frailty distribution, was 0.02443. As described earlier, $\frac{\theta }{\theta +2}=0.012$ is an estimate of the within-cluster correlation of outcomes. Thus, the within-cluster correlation of survival times is marginally greater than 0.01. The parameter estimates and levels of statistical significance were very similar between the gamma shared frailty model and the log-normal shared frailty model estimated using SAS. Output for the log-normal shared frailty model estimated using R, the gamma shared frailty model estimated using R and the gamma shared frailty model estimated using Stata are reported in Statistical software output C2, C3 and C4, respectively, in Appendix C in the Supporting Information. The models fitted using R and SAS were very similar to one another. In general, the regression coefficients for the gamma frailty model estimated using Stata was very similar to those from the gamma frailty models estimated using R or SAS; however, there were a few exceptions where there were meaningful differences in the estimated hazard ratios. For instance, in the gamma frailty model estimated using SAS, the hazard ratio for shock was 8.12 (= exp(2.09449)), whereas the corresponding hazard ratio for the gamma frailty model estimated using Stata was 6.0303. Similarly, there was one variable with a qualitatively different level of statistical significance between software packages. The effect of patient sex was statistically significantly different from null in the gamma frailty model estimated using both SAS and R (P = 0.025 in both packages), whereas the estimated hazard ratio was not statistically significantly different from null in the gamma frailty model estimated using Stata (P = 0.160). Apart from this one inconsistency, qualitatively similar conclusions about statistical significance were obtained from the different statistical software packages.

In R, an alternative to the use of the coxph function is the use of the coxme function from the coxme package or the frailty Penal function from the frailtypack package. These alternative functions can be used in fitting Cox models with two different sets of random effects.

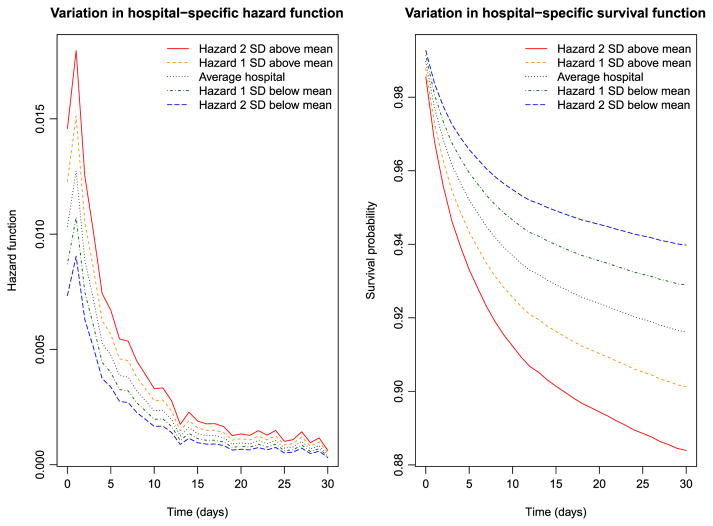
The variation in the hazard and survival functions for a reference subject across hospitals is described in Figure 1. A reference patient was a subject all of whose covariates were equal to zero (i.e. a male patient of average age, with no comorbidities, admitted to a non-teaching hospital with average AMI volume and that had no capacity for invasive cardiac procedures). These figures were derived from the frailty model fitted in R that assumed a log-normal distribution for the shared frailty distribution. The left panel depicts variation in the hazard function for this reference patient across hospitals. The upper two lines represent hospitals whose random effects were one and two standard deviations higher than average, the lower two lines represent hospitals whose frailties were one and two standard deviations lower than average, and the middle one represents an average hospital (with a frailty of zero). The right panel depicts the survival curves for a reference patient at these five hospitals. Note that the ordering of the curves is reversed in this figure: a hospital with a relatively lower hazard of death will have a relatively higher survival function. We observe that the hazard of death is greatest in the period immediately after admission and then declines over time. In the right panel, we observe meaningful differences in survival between these hospitals. The difference in the 30-day survival probabilities between a hospital whose random effect was one standard deviation higher than average and a hospital whose random effect was one standard deviation lower than average was 0.028. The reciprocal of this difference is equal to 35.7, which is equal to the number needed to treat; one would need to move 36 patients from a hospital whose random effect was one standard deviation higher to a hospital whose random effect was one standard deviation lower to avoid one death within 30 days of hospital admission (Altman & Andersen, 1999).

Figure 1.

Variation in hospital-specific hazards and survival ( frailty model). SD, standard deviation. [Colour figure can be viewed at wileyonlinelibrary.com]

4.4.2 Piecewise exponential model with mixed effects

In consultation with a cardiovascular expert, we divided the maximum duration of follow-up into five strata such that it would be reasonable to assume that the hazard of death post-AMI was approximately constant within each interval. The intervals were as follows: [0,2), [2,5), [5,10), [10,20) and [20,30]. For the purposes of the subsequent analyses, we assumed that the hazard of death post-AMI was constant within each of these time intervals.

Fitting the PWE model required that the dataset be restructured. The dataset was modified so that there was one record corresponding to each of the aforementioned time intervals in which the patient was alive. Thus, if a patient died on day 24, the rows of data for this subject would be as follows (note: the following data are purely hypothetical and are used for illustrative purposes only):

Id	interval	start_time	end_time	at_risk_time	event	age
1	1	0	2	2	0	65
1	2	2	5	3	0	65
1	3	5	10	5	0	65
1	4	10	20	10	0	65
1	5	20	24	4	1	65

Fitting the PWE model requires creating an offset variable that is equal to the logarithm of the duration of exposure within each window. Because survival time was measured in integer values of days, there was a non-zero probability that a patient would die at the beginning of the interval, resulting in an exposure time of zero and an offset variable that is undefined. When this occurred, subjects were defined to have an exposure duration of 0.5 days (i.e. assuming that they died in the middle of the day) and an offset variable of log(0.5). In R, the survSplit function in the survival package can be used to structure the dataset appropriately, while in Stata, the stsplit function can be used. In SAS, to the best of our knowledge, programming using data steps must be used to create the necessary dataset.

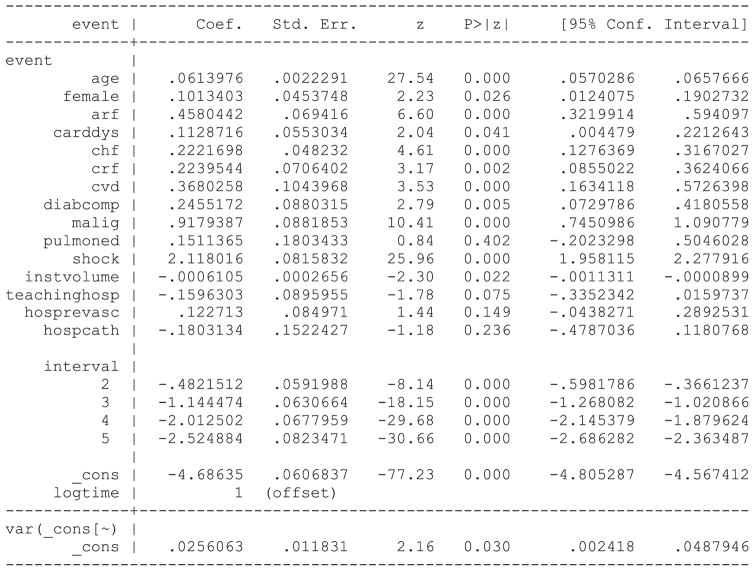
Statistical software code for fitting a PWE mixed effects survival model are described in Statistical software code 6 through Statistical software code 8 in Appendix B in the Supporting Information. Each software function or procedure has a different default estimation method. We specified each function or procedure so that the same estimation method was used in each of the three software packages. In Stata, the function xtpoisson could have been used in place of the function mepoisson. The former function is restricted to settings with two-level multilevel data, while the latter can accommodate data structures with more than one level of clustering. Due to the greater flexibility of the mepoisson function, we have described its use here. The output from the PWE survival model fit using Stata is provided in Statistical software output 2.

Statistical software output 2.

Stata output for PWE survival model

Output for the PWE survival model estimated using R and SAS is reported in Statistical software output C5 and C6, respectively, in Appendix C in the Supporting Information. Estimated regression coefficients and levels of statistical significance are similar across the three statistical software packages. In Stata, the estimate of the variance of the random effect distribution is 0.0256063, while in SAS and R, the estimated variance of the random effects were 0.02578 and 0.02563, respectively. Note that when treating the time interval as a categorical variable, SAS chooses the last interval as the reference level for the categorical variable, while R and Stata choose the first interval as the reference level for the categorical variable. Thus, the estimated intercept and regression coefficients for the non-reference levels of the time interval variable differ between the model estimated using SAS and the models estimated using R and Stata.

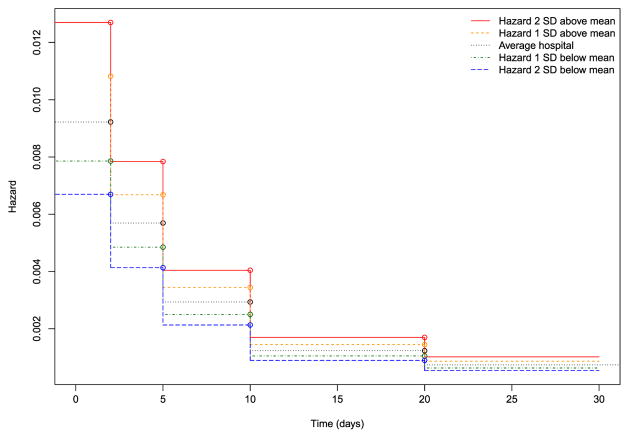
Hazard functions for a reference patient (similar to the one described earlier) for an average hospital and for hospitals whose random effect was one or two standard deviations above or below the average are depicted in Figure 2. These figures were based on the results of the PWE model fit in R. If the PWE model is fit without an intercept and if indicator variables for each of the time intervals are included, then the exponentiated regression coefficient for each time interval is the constant hazard within that interval (Rabe-Hesketh & Skrondal, 2012b). The model described earlier was refitted using this specification to estimate the hazard function (results not shown). One notes that the absolute differences in the hazard of death between different hospitals decrease as time progresses: the greatest differences in the hazard of death between hospitals occurs in the period immediately after hospital admission.

Figure 2.

Variation in hazard functions across hospitals (piecewise exponential model). SD, standard deviation. [Colour figure can be viewed at wileyonlinelibrary.com]

4.4.3 Discrete time mixed effects model

In the discrete time model, we use the complementary log–log model to model the occurrence of an event during each time interval. The same time intervals were used as in the PWE mixed effect model. A dataset appropriate for fitting a conventional survival model would require restructuring in a fashion similar to that used for the PWE survival model. Statistical software code for fitting a discrete time multilevel survival model are described in Statistical software code 9 through Statistical software code 11 in Appendix B in the Supporting Information. As with the PWE models earlier, we specified each function or procedure so that the same estimation method was used in each of the three software packages. In Stata, the function xtcloglog could have been used in place of the function mecloglog. The former function is restricted to incorporating one source of clustering (i.e. two level data structures). The output from the R analysis is described in Statistical software output 3.

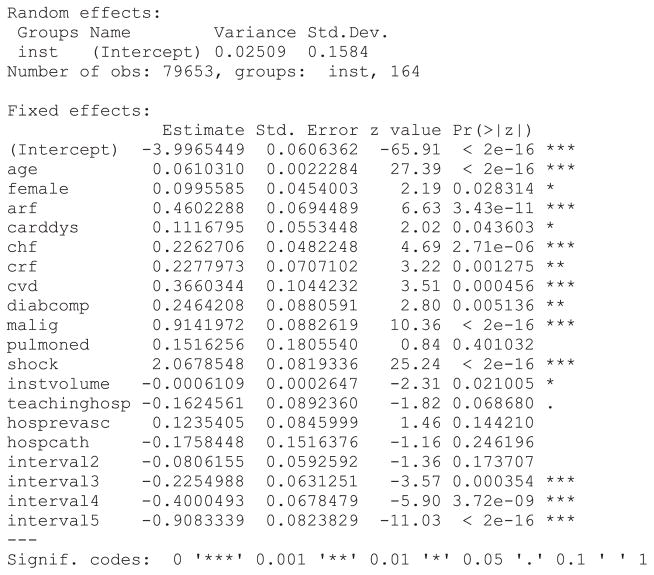
Statistical software output 3.

R output for discrete time mixed effects survival model

The output for the discrete time mixed effects survival model fit using SAS and Stata is reported in Statistical software output C7 and Statistical software output C8, respectively, in Appendix C in the Supporting Information. Estimated regression coefficients and level of statistical significance for the discrete time survival model were similar between the three statistical software packages. The estimated variance of the random effect distribution was 0.02509, 0.02258 and 0.0250974 when using R, SAS, and Stata, respectively.

Increasing patient age, female sex and the presence of seven of the nine risk factors increased the hazard of post-AMI mortality. In all three models, pulmonary edema was not associated with the hazard of post-AMI mortality. When the model was fit using SAS, the presence of cardiac dysrhythmia was not associated with the hazard of death (P = 0.060 ), while it had a statistically significant association in the models estimated in R (P =0.044 ) and Stata (P =0.044 ). Of the measured hospital characteristics, only hospital volume of AMI patients was associated with a decreased hazard of mortality, while the other hospital characteristics did not have a statistically significant association with the hazard of mortality.

4.4.4 Random coefficients models

In the models considered earlier, the effect of each individual patient characteristic was constant across hospitals. In random coefficients models, the effect of individual covariates is allowed to vary randomly across clusters. We illustrated the inclusion of random coefficients by examining whether the effect of cardiogenic shock on the rate of subsequent death varied across hospitals. SAS code for fitting a random coefficients model when using a discrete time mixed effects survival model is described in Statistical software code 12 in Appendix B in the Supporting Information. The resultant output from the SAS analysis is described in Statistical software output 4. R code using the coxme function for fitting a Cox model with mixed effects is described in Statistical software code 13 in Appendix B in the Supporting Information.

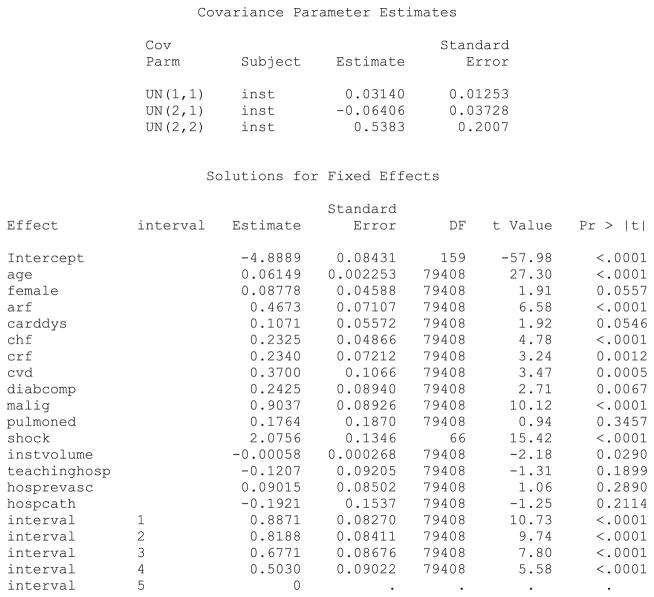
Statistical software output 4.

SAS output for discrete time mixed effects survival model with random intercept and random effect for cardiogenic shock

In the above output, more than one random effect covariance parameter is reported. For the above model, three variance–covariance terms are reported: 0.03140, −0.06406 and 0.5383. The first (0.0314) denotes the variance of the random intercepts across hospitals. The last (0.5383) denotes the variance of the random slope for cardiogenic shock across hospitals. The second term (−0.06406) denotes the covariance between these two random effects. The covariance term is negative, denoting a negative correlation between the hospital-specific random intercepts and the hospital-specific random slopes for cardiogenic shock. The correlation between random intercepts and slopes is equal to $\frac{-0.06406}{\sqrt{0.03140}\sqrt{0.5383}}=-0.49$. Thus, hospitals that have a higher intercept (increased hazard of death for a reference patient) will tend to have a diminished effect of cardiogenic shock on death.

The hazard ratio for cardiogenic shock at an average hospital is exp(2.0756) = 7.97. Thus, at an average hospital, the presence of cardiogenic shock increases the rate of death by a factor of almost eight. Ninety-five percent of hospitals have a log-hazard ratio for cardiogenic shock that lies within the interval $2.0756\pm 1.96\sqrt{0.5383}=(0.638,3.514)$. By taking the endpoints of this interval to the power e, one concludes that 95 percent of hospitals have a hazard ratio for cardiogenic shock that lies in the interval (1.89, 33.58). Thus, while the presence of cardiogenic shock increases the risk of death at the large majority of hospitals, there is a small minority of hospitals at which its presence is particularly lethal. This provides an answer to the second component of our specific research question: the magnitude of the effect of cardiogenic shock varies across hospitals.

The output for the Cox model with mixed effects fit using R is reported in Statistical software output C9 in Appendix C in the Supporting Information.

5 Discussion

Time-to-event outcomes occur frequently across a wide range of fields of research. Multilevel data are common in many of these research fields. While HLMs and HGLMs are well known and used frequently for the analysis of multilevel data with continuous or discrete outcomes, methods for the analysis of multilevel survival data are less well known. The objective of this article is to describe statistical methods for analysing multilevel survival data.

We described three different families of models that allow one to fit survival models to multilevel data: Cox regression models with mixed effects, PWE models with mixed effects, and discrete time survival models with mixed effects. The first approach modifies a Cox proportional hazards regression model by incorporating cluster-specific random effects that modify the baseline hazard function. The second approach divides follow-up time into a finite set of mutually exclusive intervals and fits a survival model that assumes that the hazard function is constant within each interval (equivalent to assuming that survival times follow an exponential distribution within each interval). This approach makes use of the fact that an exponential survival model is equivalent to a Poisson regression model. Thus, one can account for the multilevel structure of the data by fitting a Poisson regression model within each time interval and incorporating cluster-specific random effects. The third approach is similar to the second. However, rather than taking into account the duration of exposure time or at-risk time within each interval, one simply notes whether the subject experienced an event within the given interval. Then a complementary log–log generalised linear model can be fit. As with the PWE model, cluster-specific random effects can be incorporated to account for the multilevel structure of the data.

Relative strengths and limitations of each method are summarised in Table 1. We provide some recommendations for applied analysts when choosing between the models. If the data consist of a two-level multilevel structure, and one simply wants to account for clustering (and possibly to describe the magnitude of the effect of clustering), we recommend that the Cox model with random shared frailty terms be used. This method requires weaker assumptions than the PWE model. Furthermore, it does not require restructuring the dataset and dividing follow-up time into discrete intervals. Such a discretisation process can result in a loss of information. Furthermore, when a Cox model with random shared frailty terms is fit, one can use the median hazard ratio as a measure of the magnitude of the effect of clustering on the hazard of the outcome (Austin et al., 2017). However, several popular statistical analysis packages currently appear to be unable to fit a Cox model with random frailty terms to data in which there are more than two levels to the data hierarchy. Furthermore, the Cox shared frailty model requires that each subject be a member of only one level two unit. Thus, one cannot fit this model to multilevel multi-membership data. Users of some statistical software packages whose research question requires them to fit models with random coefficients (e.g. to examine whether the effect of a given covariate varies across clusters) may be required to choose between the PWE and the discrete time model because the Cox model with random coefficients currently cannot be fit in all popular statistical software packages. Of these two models, the PWE requires the stronger assumption that the hazard function is constant within each time interval. However, the PWE model accounts for the duration of at-risk time within each time interval, whereas the discrete time model simply models whether or not an event occurred during each time interval. Thus, an analyst who had data consisting of more than two levels or who wanted to fit a model with random coefficients may be required to consider either the PWE model or the discrete time model. Strengths and limitations of three popular statistical analysis packages (R, SAS and Stata) are described in Section 4 of Appendix A in the Supporting Information.

Table 1.

Strengths and limitation of each statistical model.

Model	Strengths	Limitations
Cox model with mixed effects	Can easily incorporate shared frailty terms using standard software for the Cox model. Allows hazard function to vary continuously. Familiar to researchers in the epidemiological and biomedical literature.	Random coefficients cannot currently be incorporated in some software packages. Limited information on how to choose between different frailty distributions.
PWE model	Can be fit using software for fitting HGLMs. Can easily incorporate random coefficients using standard software for HGLMs. May be more familiar to researchers in the social and behavioural sciences.	Requires dividing follow-up time into discrete intervals with the assumption that the hazard function is constant within each interval. This may not be a realistic assumption in all settings. Little research on sensitivity to choice of time intervals. Dataset must be restructured.
Discrete time model	Can be fit using software for fitting HGLMs. Can easily incorporate random coefficients using standard software for HGLMs. Regression coefficients are identical to those of an underlying proportional hazards regression model. May be more familiar to researchers in the social and behavioural sciences.	Requires dividing follow-up time into discrete intervals. Does not take the duration of time at-risk within each interval. Little research on sensitivity to choice of time intervals. Dataset must be restructured.

PWE, piecewise exponential; HGLM, hierarchal generalised linear model.

We described three different families of models for the analysis of multilevel survival data: Cox proportional hazards regression models with mixed effects, PWE survival models with mixed effects and discrete time survival models with mixed effects. While we have presented these as three distinct families, they are related to one another. The Cox proportional hazards model with gamma frailty is equivalent to the PWE survival model in which intervals are defined so that there is one event per interval and that incorporates cluster-specific random effects (Rabe-Hesketh & Skrondal, 2012b) (Section 15.9, page 843). Similarly, the complementary log–log discrete time survival model is an approximation to the PWE survival model. The approximation improves as the intervals become narrower (Steele, 2011) (page 5). Consequently, a complementary log–log discrete time survival model with random intercepts will be approximately equivalent to a Cox proportional hazards model with log-normal frailty terms.

In the current tutorial, we focused on models that incorporated random effects to account for within-cluster homogeneity of outcomes. These methods explicitly model the between-cluster variability in the hazard of the occurrence of an outcome. We did not discuss methods that did not explicitly incorporate cluster-specific random effects for accounting for within-cluster homogeneity. Accordingly, our focus was on conditional models, rather than on marginal models. When using marginal models with a two-level data structure, one could use a robust or sandwich-type variance estimator to account for the clustering of subjects (Lin & Wei, 1989). However, this approach can lead to loss of information, as one is not explicitly modelling between-cluster variability. An example of a consequence of this is that one cannot describe variation in the conditional hazard function across clusters. It is important to note that the regression coefficients derived from conditional and marginal models have different interpretations. Regression coefficients from the former family have a conditional interpretation: an estimated regression coefficient denotes the effect of a covariate on the hazard of the occurrence of the outcome conditional on both the random effect being fixed or constant and on the other covariates being fixed. For this reason, the coefficients are sometimes described as having a cluster-specific interpretation. Regression coefficients from a marginal model have a population-average interpretation; an estimated regression coefficient denotes the effect of the covariate comparing two random sample of subjects such that the two samples differ in the value of the covariate by one unit (and all other covariates are fixed) (Therneau & Grambsch, 2000). In general, marginal hazard ratios will be closer to the null than conditional hazard ratios (Gail, Wieand & Piantadosi 1984). A limitation to the use of marginal models is that it is more difficult to account for clustering when the data have more than two levels, whereas such data structures can be readily accommodated with conditional survival models.

In the current paper, we have discussed methods for the analysis of multilevel survival data. Our descriptions have been set in the context of a two-level data structure (e.g. patients nested within hospitals). However, all of the methods can be extended to data in which there are more than one level of clustering (e.g. patients nested within physicians who are in turn nested within hospitals). When using the PWE survival model with mixed effects or the discrete time survival model with mixed effects, methods for fitting HGLMs in major statistical software packages permit the inclusion of more than one source of clustering or the inclusion of more than one set of random effects. When fitting a multilevel Cox model with mixed effects, not all major statistical software packages currently permit the inclusion of more than one set of random effects. However, this is possible in R (e.g. when using the coxme or frailtypack packages).

Multilevel data structures abound across a wide range of fields of research. Time-to-event outcomes occur frequently in many of these fields. Conventional survival models do not permit the analyst to account for the loss of independence that arises from the clustering of subjects in higher level units. Multilevel survival models permit researchers to make valid inferences when examining the effect of both subject characteristics and cluster characteristics on the risk of the occurrence of the outcome.