Abstract
We study evoked calcium dynamics in astrocytes, a major cell type in the mammalian brain. Experimental evidence has shown that such dynamics are highly variable between different trials, cells, and cell subcompartments. Here we present a qualitative analysis of a recent mathematical model of astrocyte calcium responses. We show how the major response types are generated in the model as a result of the underlying bifurcation structure. By varying key channel parameters, mimicking blockers used by experimentalists, we manipulate this underlying bifurcation structure and predict how the distributions of responses can change. We find that store-operated calcium channels, plasma membrane bound channels with little activity during calcium transients, have a surprisingly strong effect, underscoring the importance of considering these channels in both experiments and mathematical settings. Variation in the maximum flow in different calcium channels is also shown to determine the range of stable oscillations, as well as set the range of frequencies of the oscillations. Further, by conducting a randomized search through the parameter space and recording the resulting calcium responses, we create a database that can be used by experimentalists to help estimate the underlying channel distribution of their cells.
Keywords: Astrocytes, Calcium response, Hopf Bifurcation, Store operated calcium channels
1 Introduction
Astrocytes make up approximately 50% of human brain volume (Tower and Young, 1973) and are roughly as numerous as neurons in the mammalian brain (Nedergaard et al., 2003). Filling most of the space between neurons, astrocytes are known for their passive roles in the brain, such as regulating neurotransmitter concentrations (Anderson and Swanson, 2000; Zhou and Danbolt, 2013) and buffering ions released during synaptic activity (Wallraf et al., 2006; Larsen et al., 2014). Recently, astrocytes have also been shown to serve a number of active roles in the brain, including the release of neuroactive compounds (e.g. glutamate, D-Serine, ATP), which is commonly known as gliotransmission (Anderson and Swanson, 2000; Wang et al., 2013; Bezzi et al., 1998; Haydon, 2001; Liu et al., 2004), mediation of the blood-brain barrier, and control of the flow of blood to brain regions based on metabolic demand (Verkhratsky et al., 2012b). Calcium is believed to be a crucial second messenger in many of these pathways. Calcium transients are also observed experimentally after astrocytes are activated by the application of neurotransmitters, such as glutamate and ATP (Wang et al., 2012), even though there is little consensus on the exact role of astrocyte calcium signaling in the brain.
Existing mathematical models of astrocytes helped explore some of the possible roles astrocyte calcium signals play in the brain. Specifically, models have shown that through gliotransmission, astrocytes may be able to significantly change the firing patterns of nearby neurons (Di Garbo et al., 2007; Wade et al., 2011), alter the induction of long-term potentiation and long-term depression (De Pittà and Brunel, 2016), and have consequences for the overall network behavior (Amiri et al., 2012; Reato et al., 2012). However, gliotransmission and other communication pathways are under active investigation and debate in the experimental community (Nedergaard and Verkhratsky, 2012; Fujita et al., 2014; Haydon and Nedergaard, 2015). In the present work, we choose to focus on the detailed exploration of the calcium dynamics itself, and leave the investigation of its role in astrocyte-neuronal communication for future work.
Evoked calcium responses in astrocytes have also been the subject of some modeling studies. In most of these, as well as the model we present in this paper, it is assumed that the calcium release is triggered through the signaling molecule inositol (1,4,5)-trisphosphate (IP3). The modeling has shown that astrocytes may be able to convey signal information via frequency or amplitude of calcium oscillations (De Pittà et al., 2009), that IP3 diffusion may mediate the synchronization of calcium oscillations in neighboring astrocytes (Ullah et al., 2006), and that receptor stochasticity may play an important role in calcium response variability (Toivari et al., 2011). It is important to note, however, that the models found in Ullah et al. (2006) and Toivari et al. (2011) were created in reference to experiments with bath application of agonists to cultured astrocytes (a highly idealized experimental condition), while De Pittà et al. (2009) model includes a closed-cell assumption, i.e. assumes that the total calcium level inside an astrocyte is constant.
Recently, we investigated calcium transients generated in response to a brief pulse of ATP applied near the soma and processes of an astrocyte (Taheri et al., submitted). Based on our results and the astrocyte literature, we developed an open-cell model of astrocyte Ca responses and used the model to show that the observed response variability can be explained by differences in calcium channels and IP3 dynamics (Taheri et al., submitted).
In this manuscript we present a more detailed mathematical analysis of this model to reveal key mathematical features underlying the diversity of responses. First, we show the bifurcation structure that allows the model to generate four main experimentally-observed response types (Single-Peak, Multi-Peak, Plateau, and Long-Lasting). We then manipulate the maximal flow through three of our included calcium channels/pumps, specifically store-operated calcium (SOC) channels, sarco/endoplasmic reticulum calcium ATPase (SERCA) pumps, and plasma membrane calcium-ATPase (PMCA) pumps. This manipulation mimics application of non-competitive blockers for these channels in experiments. The results reveal, surprisingly, that blocking store-operated calcium channels, which remain relatively inactive during a calcium transient, can have a large effect on the shapes of calcium transients, eliminating the occurrence of Plateau and Long-Lasting response types entirely. This analysis also explains previous results in Taheri et al. (submitted), where we found that blocking each of the channels changes the observed distribution of calcium response types. This observation results from shortening or lengthening of the oscillatory regime in the bifurcation structure, as well as changing the frequency range of these oscillations. Further, by randomly varying channel parameters and recording the resulting calcium responses, we create a database that can be used by experimentalists to help determine the structure of their cells.
2 The Mathematical Model
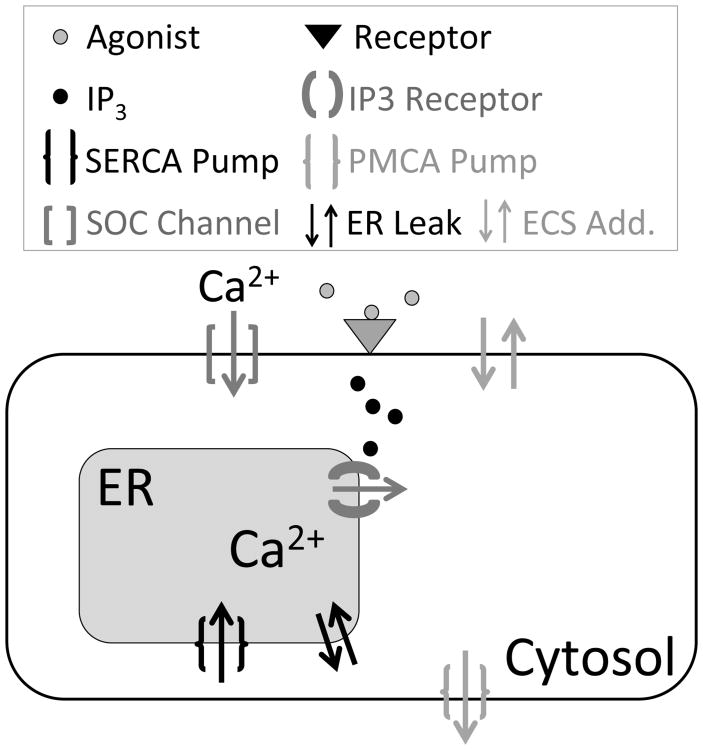
Fig. 1 shows a simplified schematic of the calcium activity components in our model. The corresponding mathematical model is first presented in Taheri et al. (submitted), and the model equations can be found in the Appendix. Briefly, when membrane receptors are activated by their agonist (e.g. ATP, glutamate), it triggers a cascade of reactions, resulting in the production of IP3 and its increased concentration in the cytosol (Agulhon et al., 2012). After peaking within seconds, the IP3 concentration then decays as IP3 diffuses away or degrades (Höfer et al., 2002). In our model we explicitly postulate the time evolution of the amount of IP3 as growing to a maximal level, then exponentially decaying. IP3 is then responsible for activating the calcium pathway via the IP3 receptor (IP3R), which releases calcium from the endoplasmic reticulum (ER), a calcium store in astrocytes, in the cytosol. The other fluxes, JSERCA (pumping calcium back into the ER), JPMCA (pumping calcium out of the cell), JSOC (activated by ER calcium depletion), the leak flux between the ER and cytosol JER_leak, and the additional fluxes on the plasma membrane JECS_add, all play an active role in shaping the calcium transient and returning the system to steady state post-evoked response. Investigating the exact role of these fluxes is a major focus of this paper. Throughout this paper, we denote cytosolic calcium as c, total free calcium in the cell as ctot, calcium in the ER as cER, and IP3 as p.
Fig. 1.
Simplified schematic of an astrocyte and its major calcium components. Arrows show the direction of calcium flux.
2.1 Calcium Response Types
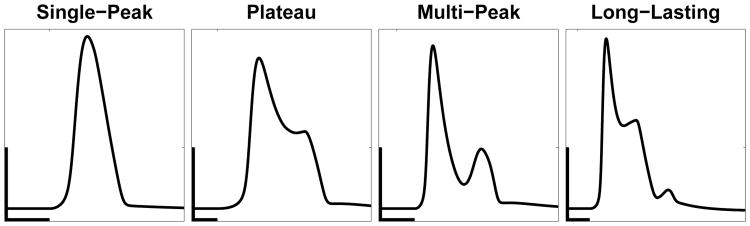
In our recent work, we experimentally observed four distinct types of calcium responses in astrocytes after focally applying a short (<250 ms) pulse of ATP: a Single-Peak (SP) response, a Plateau (PL) response, a Multi-Peak (MP) response, and a Long-Lasting (LL) response (Taheri et al., submitted). By only varying key IP3 parameters (Table 1), the mathematical model is capable of reproducing these four response types (Fig. 2). A detailed classification method is given in Taheri et al. (submitted). Furthermore, the general shape of the IP3 time course and a reasonable range of IP3 parameters (A, drise, rrise, and ddecay; see Table 1) for use in our simulations is based on previous experimental (Pasti et al., 1995; Tanimura et al., 2009; Nezu et al., 2010) and modeling (De Pittà et al., 2009) studies, as described in more detail in Taheri et al. (submitted). For example, the rise duration estimates vary from about 1 to 40 seconds and could vary between different subcompartments (soma vs. processes) of an astrocyte. The full model, as well as this classification algorithm can be found at ModelDB, (Hines et al. (2004); http://senselab.med.yale.edu/modeldb/default.asp; Model no. 189344).
Table 1.
Model parameters. γ is from Ullah et al. (2006), kSERCA and υSERCA are from De Pittà et al. (2009), υin is from Lavrentovich and Hemkin (2008), υSOC is found in Croisier et al. (2013), and d1, d2, d3, and d5 are from the model developed by De Young and Keizer (1992).
| Parameter | Description | Value | Units |
|---|---|---|---|
| γ | (Cyt vol) / (ER vol) | 5.4054 | – |
| υIP3R | Max IP3 Receptor Flux | 0.222 | s-1 |
| υER_leak | Cytosol to ER leak | 0.002 | s-1 |
| υin | Rate of leak into Cytosol from Plasma Membrane | 0.05 | μM s-1 |
| kout | Rate of leak out of Cytosol from Plasma Membrane | 1.2 | s-1 |
| υSERCA | Max SERCA Flux | 0.9 | μM s-1 |
| kSERCA | Half-Saturation for SERCA | 0.1 | μM |
| υPMCA | Max PMCA Flux | 10 | μM s-1 |
| kPMCA | Half-Saturation for PMCA | 2.5 | μM |
| υSOC | Max SOC channels Flux | 1.57 | μM s-1 |
| kSOC | Half-Saturation for SOC channels | 90 | μM |
| δ | Ratio of membrane transport to ER transport | 0.2 | – |
| d1 | Dissociation constant for IP3 | 0.13 | μM |
| d2 | Dissociation constant for Ca2+ inhibition | 1.049 | μM |
| d3 | Receptor dissociation constant for IP3 | 0.9434 | μM |
| d5 | Ca2+ activation constant | 0.08234 | μM |
| a2 | Ca2+ inhibition constant | 0.04 | μM s-1 |
| drise | Rate of Exponential Growth | 0.002-12 | s-1 |
| ddecay | Duration of IP3 decline | 15-220 | s |
| drise | Duration of IP3 increase | 1-41 | s |
| A | Max amplitude of IP3 transient | 0.2-0.9 | μM |
Fig. 2.
Example traces of the four calcium response types produced from the model. From left to right these response types and IP3 parameters are: SP (A=0.2, drise = 10, rrise = 0. 2, and ddecay = 97), PL (A=0.375, drise =34, rrise=0.002, and ddecay= 138), MP (A=0.26, drise=41, rrise=0.12, and ddecay= 200), and LL (A=0.55, drise=39, rrise=0.002, and ddecay=179). Default channel parameters, found in Table 1, were used in all response types. The x- and y-scale bars are 10 seconds and 0.5 μM respectively.
3 Results
Building off our previous work focused on reproducing all four categories of experimentally-observed calcium response types (Taheri et al., submitted), we now investigate in more detail the underlying mathematical dynamics that allow for this diversity of calcium responses. We start with a bifurcation analysis of the system using the default parameters. Then, by systematically weakening or blocking specific calcium-handling mechanisms (i.e. calcium channels and pumps), we examine how this underlying dynamical landscape changes.
3.1 The Default Dynamical Landscape: Role of IP3
3.1.1 Mechanisms Underlying the Four Types of Calcium Responses
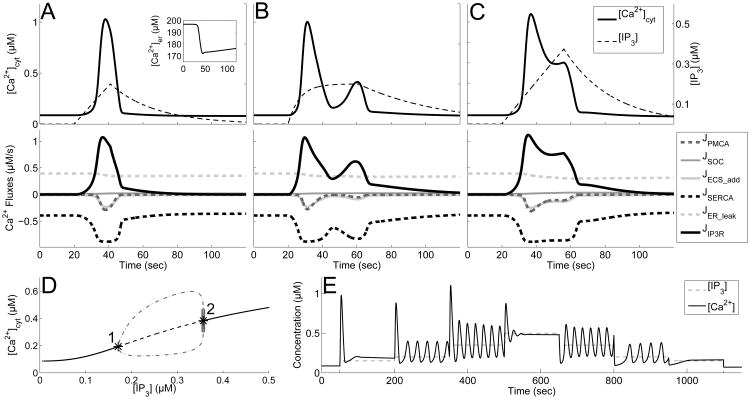
We first consider the SP response and the individual calcium fluxes governing it (Fig. 3A). Before the IP3 (black, dashed curve) input begins, the system is at rest with most of the fluxes being completely inactivated. The steady state of the system is created by a balance between the SERCA pump and calcium leak from the ER (black, dashed and light gray, dashed curves respectively). If this balance is upset, for example by blocking of SERCA pumps, it would result in a prompt emptying of ER stores, as observed experimentally (Jousset et al., 2007).
Fig. 3.
Variability of calcium response types and underlying bifurcation structure. A-C: (top panel) calcium time course (black) and IP3 stimulus (black, dashed) with default channel parameters. (lower panel) Calcium fluxes through channels. Positive value represents flow into the cytosol. A: SP, with A = 0.2 drise = 21, and rrise = 0.002, and ddecay = 97, (inset shows calcium dynamics in the ER). B: MP with A = 0.2, drise = 41, rrise = 0.15, and ddecay = 179. C: PL with A = 0.375, drise = 36, rrise = 0.002, and ddecay = 120. D: Bifurcation diagram using IP3 as the parameter. Shows stable steady states (black, curve), unstable steady states (black, dashed curve), and projection of maximum and minimum values of stable (gray, dot-dashed curve) and unstable (light gray circles) oscillations. Hopf bifurcations occur at labeled points (1 and 2). E: Calcium times course (black curve) in the presence of step increases in IP3 (black, dashed curve).
As IP3 is added into the system, the IP3 receptor (IP3R) is activated, causing this channel to open and release calcium into the cytosol from the ER (JIP3R, black curve). This initial calcium release has a positive feedback onto the IP3R, and the channel opens very quickly. Consequently, the SERCA pump responds by pumping some of the newly released calcium back into the ER (JSERCA, black, dashed curve). Initially, cytosolic calcium concentration continues to rise, because the SERCA pump is unable to completely counteract the flux out of the ER through the IP3R. Eventually, the PMCA (gray, dashed curve) and the additional fluxes on the plasma membrane (light gray curve) begin to release calcium from the cytosol into the extracellular space (JPMCA and JECS_add), and the cytosolic calcium concentration begins to decrease. Meanwhile, the flux through the IP3R is eliminated, as IP3 concentration decreases, along with the negative feedback the receptor feels from the elevated cytosolic calcium levels. The SOC channel flux (JSOC, gray) remains largely inactive during this single calcium response, since the calcium levels in the ER do not approach the half-saturation constant of these channels (kSOC = 90). Nonetheless, this channel plays a significant role in IP3-induced calcium dynamics as described later in Section 3.2.
Overall, this SP calcium response causes a ∼12% decrease in ER calcium concentration (inset of Fig. 3A top). Although the remaining pumps and channels appear to return to steady state levels immediately after the calcium transient, the calcium concentration in the ER remains below steady state well after the calcium transient in the cytosol is completed, and is restored to > 95% after approximately 10 minutes (not shown). During this time, the pumps and channels continue to work at low levels to completely restore the system. However, even during this refilling period, there is a sufficient amount of calcium in the ER to produce another calcium transient if the astrocyte is stimulated again.
Extending our analysis now to all response types, we found that it was only necessary to vary the amplitude (A) of the IP3 trace in order for the model to generate SP, MP and PL responses, and increasing the duration (ddecay) of the IP3 input, results in a LL response (figure not shown). Further, our previous study found that varying all four of the IP3 transient kinetics (amplitude (A), rise duration (drise), decay duration (ddecay), and the rise rate (rrise)) within a biologically plausible range (see Section 2.1) results in similar calcium kinetics and response types (Taheri et al., submitted). Using these results, we now propose specific mechanisms driving the MP, PL and LL calcium responses before taking a closer look at the underlying mathematical structure. The MP example trace in Fig. 3B has an IP3 transient with the same amplitude as the IP3 transient underlying the SP response in Figure 3A; however, the IP3 transient responsible for the MP response remains elevated for a longer period of time (greater drise and ddecay, as well as an increased rrise). With this IP3 transient, after the initial calcium transient is completed and the negative feedback on the IP3R wears off, another response, although a smaller one, is generated due to the ongoing elevation of IP3. The example PL response (Fig. 3C) has an IP3 trace that has a higher amplitude than the SP and MP examples (with the same rrise as the SP response and drise and ddecay values lower than the MP response). The IP3 levels underlying this PL response are high enough to be able to counteract the negative feedback onto the IP3 receptor from cytosolic calcium; therefore, the channel associated with the IP3R remains open for longer, leading to an elevated calcium response. The final experimentally observed response (LL) remained sufficiently elevated for more than 70 s (figure not shown). We found that LL responses are fundamentally similar to those underlying PL responses, but have larger IP3 amplitude and ddecay, allowing for the calcium response, or elevated oscillations, to linger for a longer time. For this reason, the rest of the paper focuses primarily on the SP, MP, and PL response types.
To elucidate the mathematical structures underlying the above-described dynamics, we note that although the concentration of IP3 is a dynamic variable, it is uncoupled from the full system and its time course is set. Therefore, if we consider IP3 transients with a much slower timescale than the other model variables, then key features of the full model can be explained, by examining the three dimensional system consisting of only c, ctot, and h (Appendix: Equations (1)-(3)), while treating IP3 as a bifurcation parameter. The bifurcation diagram of this subsystem can be seen in Fig. 3D. As illustrated in this figure, a supercritical Hopf bifurcation occurs at [IP3]≈0.18 (black asterisk 1) that causes the single stable steady state to transition into a stable limit cycle, shown as the gray, dot-dashed curve in the figure. This stable limit cycle is eliminated by an unstable limit cycle (light gray open circles) originating at a subcritical Hopf bifurcation at [IP3]≈0.35 (black asterisk 2).
With this diagram in mind, one can visualize how a stereotypical SP, MP, and PL response can be generated if the underlying IP3 transient was on a much slower timescale compared to the rest of the system. Due to the excitability of the IP3R, a large enough IP3 transient produces an initial calcium response. If the amplitude of this IP3 transient is small enough (below the supercritical Hopf bifurcation point), the calcium levels simply return to steady state, generating a SP response. On the other hand, if the IP3 transient amplitude goes beyond this first bifurcation point (but under the second bifurcation point), we are placed in the oscillatory regime, and if IP3 remains elevated long enough, a MP response is generated. Lastly, if the IP3 transient amplitude goes past the second bifurcation point, the calcium levels land on the higher steady state before decaying back to baseline; thus, a PL response is generated.
Note that the above analysis is simplified, since the IP3 timescale in our simulations is not always slower than the rest of the system. However, this general framework proved useful in the classification of calcium responses types, and changes in the underlying bifurcation diagram will be used to explain differences between different parameter regimes.
3.1.2 Sustained Calcium Oscillations May Be Attained without IP3 Oscillations
The bifurcation diagram of the system suggests that sustained calcium oscillations can be generated without IP3 oscillations, as long as IP3 is held constant at certain levels (between the supercritical and subcritical Hopf bifurcations at 0.18 - 0.35 μM). This is in agreement with the work done by Li and Rinzel (1996) and Sneyd et al. (2006), which noted that the positive and negative feedback mechanisms in the Li-Rinzel IP3 receptor model are capable of supporting calcium oscillations. Viewing IP3 as a slow changing parameter is realized in experiments where intracellular IP3 concentration is fixed (e.g. uncaging experiments or, possibly, agonist bath applications), further motivating our pursuit of this analysis. Fig. 3E illustrates the calcium dynamics in response to step-wise increases in IP3 concentration. In agreement with the bifurcation diagram, sustained oscillations exists for IP3 concentrations in the range of 0.18 - 0.35 μM. In addition, this figure also illustrates that steps from a lower to higher IP3 concentration are accompanied by a brief, high amplitude transient, either in addition to the sustained oscillations or as a stand alone. We predict that such a transient would be observable experimentally. However, this transient does not occur if we step from a higher IP3 concentration to a lower one. This result can be explained by the dynamics of the IP3R. When rapidly increasing the concentration of IP3, the IP3Rs quickly open, resulting in a sudden initial increase and transient as the system settles into its new steady state. But when the concentration of IP3 is lowered, IP3Rs remain closed and do not contribute to a transient oscillation.
3.2 Contribution of SOC channels to the Dynamical Landscape
3.2.1 Calcium Flux Levels through SOC Channels are Low, but Play a Major Role in Shaping Calcium Responses
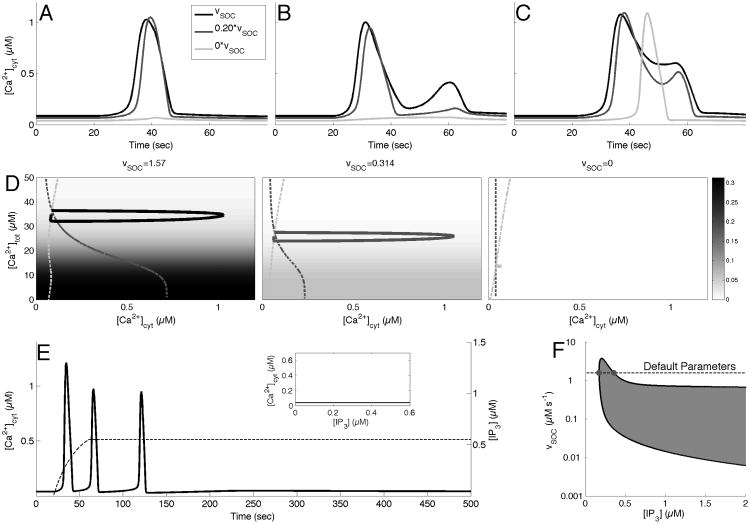
In Taheri et al. (submitted), we showed that completely blocking SOC channels significantly changed the distribution of possible response types across the range of IP3 parameters, entirely eliminating the occurrence of PL and LL response types. We investigate this result more closely by examining the effect of a partial and complete block of SOC channels on the response types. Specifically, Fig. 4A-C show that with a partial SOC block (0.20 * υSOC, gray curves), the SP response becomes shorter, the second peak in the MP response is eliminated, turning it into an SP response, and the PL response develops a second peak to become an MP response. Further, when SOC is completely blocked in these examples (light gray curves), the SP and MP responses disappear, while the PL response is reduced to a SP response.
Fig. 4.
Effect of blocking SOC channels on response times and phase space. A-C: Calcium response types with default parameters (black curve), υSOC = 0.3140 (gray curve) and υSOC = 0 (light gray curve). A: SP, with A = 0.2 drise = 21, and rrise = 0.002, and ddecay = 97. B: MP with A = 0.2, drise = 41, rrise = 0.15, and ddecay = 179. C: PL with A = 0.375, drise = 36, rrise = 0.002, and ddecay = 120. D: The(c, ctot)-phase space with c-nullcline (light gray, dashed) and ctot-nullcline (gray, dashed curve), along with the calcium transients (in black, gray, and light gray curves) corresponding to those in A (left panel). The color scale corresponds to the value of δ · JSOC(cER). E: Calcium response (black curve) to a prolonged IP3 stimulus (black, dashed curve) with υSOC = 0. Inset shows the corresponding bifurcation diagram of the system. F: Two parameter bifurcation diagram tracking the Hopf bifurcation points (black curve). Shaded region corresponds to regions that support stable oscillations. Gray dots represent the Hopf bifurcation points with default parameters. Notice log-scale on the y-axis.
Thus, SOC channels are instrumental in shaping calcium response dynamics, however, in the previous flux traces (Fig. 3A-C), these channels appeared as relatively inactive during all of the calcium transients. However, the influence of SOC channels is misrepresented in these figures. Since the other fluxes work to counteract each other (i.e. JIP3R vs. JSERCA), the following partial sum of fluxes,
has, in fact, a similar magnitude as δ · Jsoc (figure not shown). As a result, eliminating the flux through SOC channels will have a larger impact on calcium transients than one might initially expect.
We can also gain insight into this rather counterintuitive result by investigating the projection of our system onto the (c, ctot) phase space (Fig. 4D). As the figure illustrates, JSOC plays a crucial role in shaping the underlying dynamics, particularly the shape of the ctot-nullcline. The progression of the ctot-nullcline (gray curve) in Fig. 4D from left to right, corresponding to decreasing vSOC from its default value of 1.57, shows that as υSOC is blocked, this nullcline flattens out and becomes completely vertical when υSOC = 0. Examining the equation for this ctot-nullcline, we have
The JSOC term makes this a function of c and cER, as opposed to just c. When the SOC component is eliminated, one obtains a quartic function of c that has an unique solution, and is therefore constant for all levels of IP3 (Fig. 4E, inset). The background color of these figures illustrate that while υSOC has the ability to shift nullclines and reshape the direction field, calcium transients exists in the region where JSOC remains small (white background).
Additional evidence supporting the surprisingly large role SOC channels have in the model can be found by investigating the two-parameter bifurcation diagram presented in Fig. 4F, which uses IP3 and υSOC as parameters (note log scale on y-axis). The shaded region represents the parameter regime that supports stable oscillations, and the dotted line indicates the default vSOC parameter value (vSOC = 1.57), with the gray dots representing the original Hopf bifurcation points (from Fig. 3D). It is clear from this figure that as υSOC goes to zero, the leftmost Hopf bifurcation point increases beyond a realistic value of IP3, and so with zero SOC flux the sustained oscillations are not supported. However, the oscillatory region lies close to the IP3-axis, and, as a result, even small levels of SOC flux can move the solution across the boundary into the oscillatory region, changing the dynamics of the system.
However, the oscillatory regime remain close to the IP3-axis, and as a result, even small values of JSOC can result in large changes in the underlying dynamics of the system.
3.2.2 Sustained Calcium Oscillations are Not Possible without Functional SOC Channels
Even though the system can only sustain stable calcium oscillations for positive values of υSOC, MP responses are still observable when υSOC=0, though they occur through a different mechanism. In fact, Fig. 4E shows that elevating IP3 and holding it elevated can result in such a response. These MP responses with υSOC=0 are created by the system spiraling back to the steady state level for cytosolic calcium. These are not sustainable oscillations in a sense that their amplitude decays to zero even if the IP3 level stays constant. As a result, this is an inherently different type of MP response than those with υSOC at the default value (Fig. 3B and Fig. 3E), where the MP response was created due to the underlying oscillatory regime in the bifurcation diagram. In addition, the bifurcation diagram found in Fig. 4E (inset) demonstrates the fact that PL and LL responses are no longer possible when υSOC = 0, since there exists no elevated steady state. Consistent with this analysis, we have previously shown that blocking SOC channels allows for only SP and MP responses (Taheri et al., submitted).
3.2.3 Partially blocking SOC Channels Increases the Incidence of Calcium Oscillations
The two-parameter bifurcation diagram in Fig. 4F also indicates that there is a drastic difference between completely blocking and partially blocking SOC channels. A complete block will eliminate stable oscillations, whereas a partial block, such as decreasing υSOC by over 85% of its default value (υSOC = 0.2), will result in a significantly larger region of stable oscillations. This is a testable prediction that can be verified experimentally using partial blocking techniques, such as those used by Jousset et al. (2007). This also provides a metric into the effectiveness of an SOC blocker: a more effective, though partial, blocker will have a larger regime of stable calcium oscillations, which could be potentially measured using an IP3 uncaging technique (Kantevari et al., 2011).
3.2.4 Verification of SOC Channel Activation
Despite remaining relatively inactive during calcium transients, the flux through SOC channels in our model can be activated when the ER is sufficiently depleted. In fact, a common method to test for the presence of SOC channels experimentally involves completely depleting the calcium in the ER by blocking the re-uptake of calcium through SERCA blockers (Jousset et al., 2007; Roos et al., 2005; Malarkey et al., 2008). In one such experiment, extracellular calcium is initially removed, driving some amount of calcium out of the cytosol and into the extracellular space. Then, by applying a SERCA pump blocker such as Thapsigargin (a permanent blocker), calcium is prevented from returning to the ER and therefore continues to leave the cell. Once the ER is empty (thus, activating SOC channels), calcium is introduced back into the extracellular space. This results in calcium entry to the cytosol through the SOC channel.
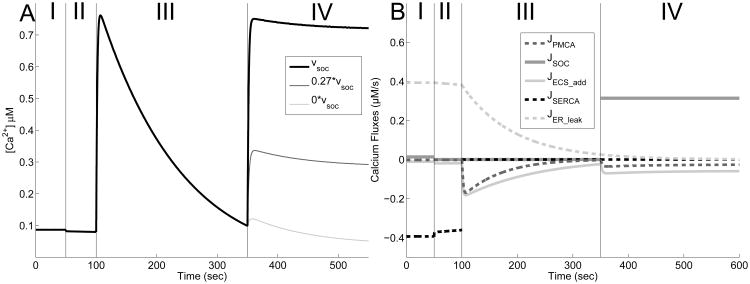
Our model can be used to simulate similar experimental conditions (Fig. 5). Beginning at steady state (Phase I), we simulate the removal of calcium from the extracellular space by setting υin = υSOC = 0 at 50 s. As seen, a slight amount of calcium is observed to leave the cytosol and enter the extracellular space (Phase II). We then block SERCA pumps by setting υSERCA = 0 at 100 s, causing a calcium spike in the cytosol via the leak out of the ER (Phase III). This causes fluxes in both the PMCA pump and ECS leak, and would eventually lead to the majority of intracellular calcium to be removed. Before this occurs, calcium is reintroduced to the extracellular space (υin = 0.05, υSOC = 1.57) and calcium rapidly reenters the cell (Phase IV). In experiments, this increase is believed to be caused primarily by an influx via SOC channels since the response is largely eliminated by knocking down the gene responsible for the creation of STIM1 proteins (Jousset et al., 2007). Indeed, this is true in our model as well.
Fig. 5.
Simulation of dual blocking (SERCA and SOC) experiment. A: The system rests at steady (Phase I), and at t = 50s, calcium is removed from the system by setting υin = υSOC = 0 (Phase II). At t = 100s, υSERCA = 0 in order to simulate the application of the drug thapsigargin, and an increase in cytosolic calcium in observed (Phase III). Finally, at t = 350s, calcium is reintroduced to the system by restoring υin = 0.05, and υSOC to various amounts (Phase IV). υSOC = 1.57 is shown in black, υSOC = 0.4239 in gray, and υSOC = 0 in light gray. B: Figure show the corresponding fluxes for the case υSOC= 1.57. JIP3R is 0 throughout this simulation (not shown).
3.3 Role of SERCA Pumps, PMCA Pumps, and leak terms
3.3.1 Partially Blocked SERCA Pumps Prevents Oscillations
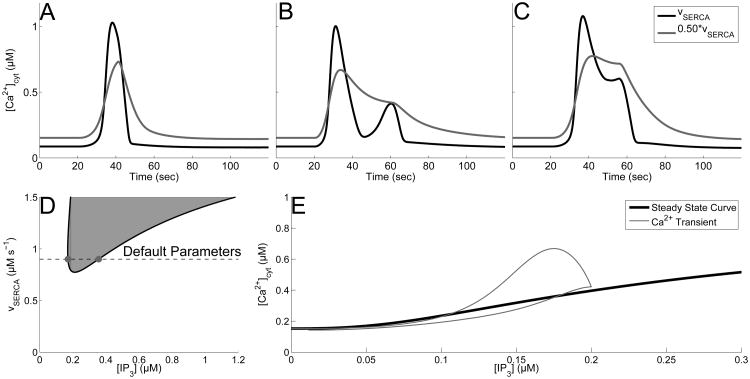
We have previously reported that blocking SERCA pumps by 50% entirely eliminates MP responses, while increasing the number of LL responses, for our given range of IP3 transients (Taheri et al., submitted). Here, Fig. 6A-C demonstrates that blocking SERCA pumps by 50% affects the default response types in the following way: it shortens the amplitude, but increases the duration of the SP response, transforms the MP response into a PL, and flattens out the PL response.
Fig. 6.
Effect of blocking SERCA channels on response times and bifurcation structure. A-C: Calcium response types with default parameters (black), υSERCA = 0.45 (gray). A: SP, with A = 0.2 drise = 21, and rrise = 0.002, and ddecay = 97. B: MP with A = 0.2, drise = 41, rrise = 0.15, and ddecay = 179. C: PL with A = 0.375, drise = 36, rrise = 0.002, and ddecay = 120. D: Two parameter bifurcation diagram tracking the Hopf bifurcation points (black curve). Shaded region corresponds to regions that support stable oscillations. Gray dots represent the Hopf bifurcation points with default parameters. E: Bifurcation diagram with υSERCA = 0.45 (stable steady state shown in black), overlaid with the calcium transient from panel B (gray).
By investigating the two parameter bifurcation diagram (Fig. 6D), now using υSERCA as the second parameter, we see in fact that oscillations are eliminated by decreasing υSERCA. In fact, 0.5 υSERCA rests a sufficient distance away from this oscillatory regime, unlike in the SOC channel case, and the steady state is not a spiral. Furthermore, unlike the bifurcation diagram found in Fig. 4E (inset), the single parameter bifurcation diagram for 0.50 * υSERCA (i.e. when SERCA is 50% blocked) illustrates that decreasing υSERCA does not lead to a constant value for the steady state of cytosolic calcium. Instead, it remains a monotonically increasing function of IP3 concentration, without an oscillatory regime. Without this oscillatory regime and the steady state not being a spiral, MP response types are no longer possible, which explains why we observed a higher distribution of LL responses when SERCA channels are 50% blocked in Taheri et al. (submitted).
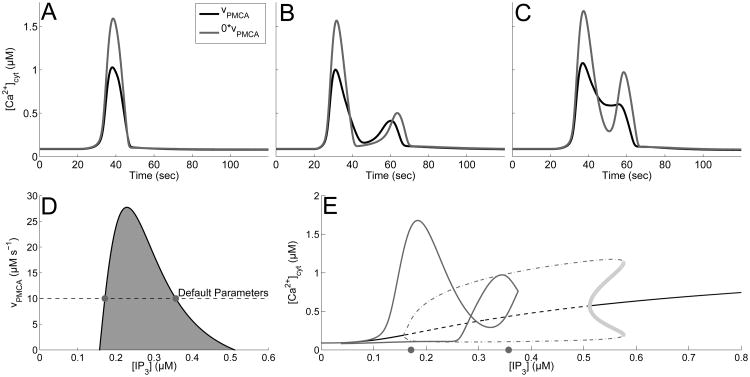
3.3.2 Blocking PMCA Pumps Creates a Larger Oscillatory Regime
We also reported in Taheri et al. (submitted) that blocking PMCA pumps fully almost entirely eliminates PL and LL responses, while the incidence of MP responses increase. Examples in Figure 7A-C also illustrate that while blocking PMCA pumps increases the max amplitude in all three cases, the response type of the first two cases (SP and MP) remain intact. On the other hand, the PL response changes noticeably and becomes a MP response. This can be explained by the two-parameter bifurcation diagram in Figure 7D, using IP3 and υPMCA as parameters. Figure 7D shows that decreasing υPMCA increases the width of the oscillatory regime caused by the Hopf bifurcations. This increased oscillatory region increases the occurrences of MP responses. Figure 7E illustrates this fact by overlaying the MP calcium trace found in Fig. 7C (gray curve) with the elongated bifurcation diagram caused by blocking PMCA pumps (the gray dots on the x-axis mark the location of the Hopf bifurcation points with the default parameters).
Fig. 7.
Effect of blocking PMCA channels on response times and bifurcation structure. A-C: Calcium response types with default parameters (black curve), υPMCA = 0 (gray curve). A: SP, with A = 0.2 drise = 21, and rrise = 0.002, and ddecay = 97. B: MP with A = 0.2, drise = 41, rrise = 0.15, and ddecay = 179. C: PL with A = 0.375, drise = 36, rrise = 0.002, and ddecay = 120. D: Two parameter bifurcation diagram tracking the Hopf bifurcation points (black curve). Shaded region corresponds to regions that support stable oscillations. Gray dots represent the Hopf bifurcation points with default parameters. E: Bifurcation diagram with υPMCA = 0, overlaid with the calcium transient from panel C (gray curve). Shows stable steady states (black, curve), unstable steady states (black, dashed curve), and projection of maximum and minimum values of stable (gray, dot-dashed curve) and unstable (light gray circles) oscillations.
3.3.3 υin and γ Parameters Have Minor Influences on Calcium Responses
Unlike the previous parameters, significantly changing υin (increasing by 300% and decreasing the value to 0), showed very little change in the underlying bifurcation diagram (figure not shown). However, this parameter does play a key role in setting the steady state calcium concentrations in the cytosol and the ER. Specifically, decreasing υin to 0 decreases the cytosolic calcium steady state by approximately 11%. This inward leak term implicitly represents many of the other channels not explicitly included in the model, such as TRPA channels. This channel has been shown experimentally to play a large role in setting the basal concentration of calcium (Shigetomi et al., 2012), which is consistent with our simulations.
We also investigated the effects of changing the γ, the parameter that represents the ratio of cytosolic volume to ER. This parameter helps set the total amount of free calcium in the cell, but does not change the steady state levels of calcium in the ER and cytosol. Decreasing γ from 5.4054 to 1, representing a cell that has an ER equal to volume as the cytosol, marginally increased the range of stable calcium oscillations from 0.1711-0.3569 μM to 0.1693-0.3722 μM. Further, increasing γ to 20 marginally decreased the rang of stable calcium oscillations to 0.1796-0.3041 μM (figure not shown).
3.4 Frequency of Calcium Oscillations
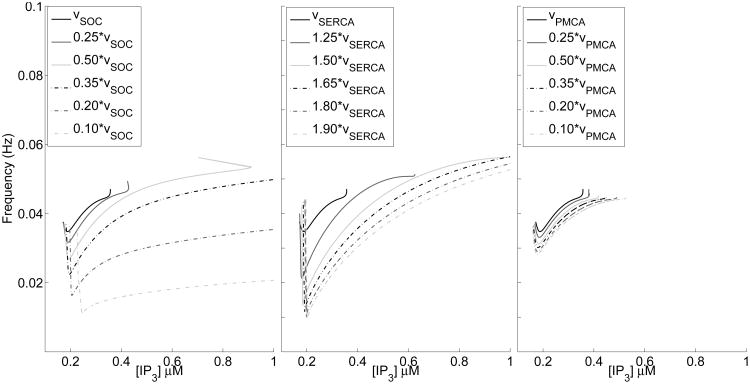
The intrinsic frequency of calcium oscillations are viewed as potentially crucial in regulating mechanisms such as gliotransmission (De Pittà et al., 2009; Croft et al., 2016). As a result, in this section we investigate how the parameters υSOC, υSERCA, and υPMCA affect the range of supported frequency, known as the dynamic range, of these calcium oscillations. Building off of Sections 3.2 and 3.3, where we saw that decreasing υSOC and υPMCA, and increasing υSERCA lead to an increase in the range of stable oscillations, Fig. 8 shows how the frequency of these oscillations change.
Fig. 8.
Frequency curves for the oscillations under different parameters. Left: decreasing υSOC Middle: increasing υSERCA Right: decreasing υPMCA.
In the first panel, decreasing υSOC sharply drops the frequency curve for a wide range of IP3 values, shifting the oscillation to lower frequencies, while having a minor effect on the dynamical range. This further emphasizes that small changes in υSOC will result in large changes in the dynamical system. Increasing υSERCA shows a sharp initial drop in frequency, with quick rise, hence increasing the dynamic range, but leaving it centered in a similar frequency range as the default case. These frequency curves do not show the same separation as was seen with changes in υSOC. Lastly, unlike the other two parameters, decreasing υPMCA has very little effect on the underlying frequency curve.
Overall, this figure suggests that these currents can play very different roles in controlling the frequency of calcium oscillations, with PMCA pumps having no effect, SERCA pumps adjusting the width of the dynamic range, and SOC channels shifting the overall location of the dynamic range. This effect is in addition to determining the type of calcium responses the cell can support, as discussed in previous sections.
3.5 Tuning Model Parameters to Reproduce Specific Experimental Conditions
Experimentally, the expression levels or functional properties of the model components discussed above may be different in different astrocytes or different subcompartments (i.e. soma, large processes, small processes) of one astrocyte. For example, there may be a difference between astrocytes in the densities of their agonist receptors (which would change the resulting IP3 kinetics) or calcium channels/pumps. Moreover, these channels, pumps, and receptors may be up- or down-regulated (or may change in their functional properties) under different conditions, such as when astrocytes become reactive in disease (de Lanerolle et al., 2010; Takahashi et al., 2010).
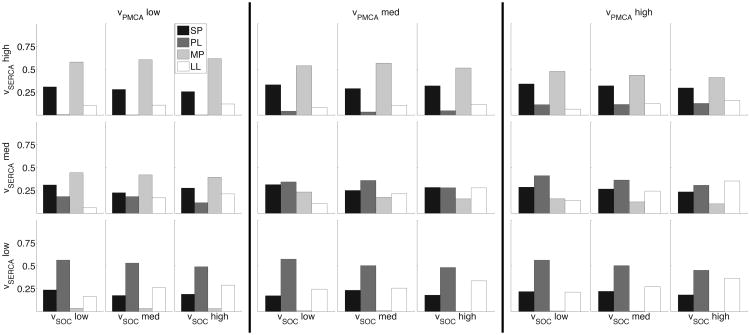
To examine such changes between different astrocytes, we consider how simultaneous changes in relevant model parameters affect the distribution of generated calcium response types. From a theoretical point of view, this addresses the sensitivity of the calcium response distribution to major parameters in the model. For each IP3 transient (with parameter ranges as in Table 1, the total of N = 600 IP3 transients), we randomly chose the parameters υPMCA, υSERCA, υSOC within ±50% interval around the default values, and repeated this process 30 times for each IP3 transient. We then binned the υPMCA, υSERCA, vSOC parameter space into 27 boxes, and reported the distribution of calcium response types within each box, as seen in Fig. 9. For example, the distribution in the upper left-hand corner represents the parameter box (υPMCA, υSERCA, υSOC) ∈ [5.0, 8.33] × [1.05, 1.35] × [0.785, 1.31].
Fig. 9.
Three-dimensional space of parameter variation over entire IP3 distribution showing differences in calcium response type distributions. From left to right, the three panels consider the followings bins for υPMCA: [5.0, 8.33], [8.33, 11.67], and [11.67, 15.0]. The three rows bin υSERCA according to [0.45, 0.75] (bottom), [0.75, 1.05] (middle), and [1.05, 1.35] (top). Within each panel, the columns show variations in υSOC according to [0.785, 1.31] (left), [1.31, 1.83] (center), and [1.83, 2.36] (right). The distributions represent that calcium response types recorded in each subspace (SPs are in black, PLs are in gray, MPs are in light gray, and LLs are in white).
As the figure illustrates, different boxes in the parameter space have different distributions of calcium responses. This allows us to visualize how changes in parameter values effect these response type distributions. For instance, we can quickly investigate the situation where we simultaneously increase the calcium flux through SERCA pumps and SOC channels, while keeping PMCA constant (i.e. moving diagonally within the same panel from bottom left to top right). In all three panels, we see that the number of observed MP responses increases, while PL responses decrease.
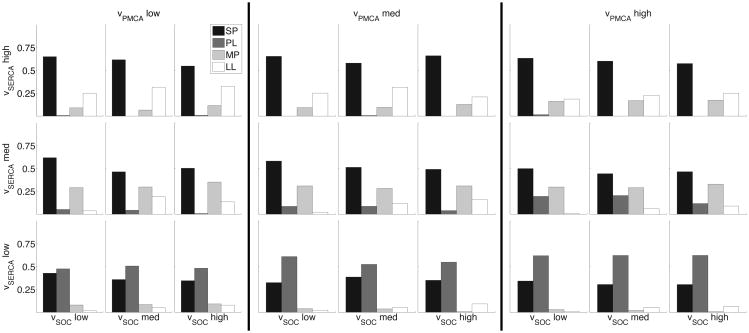
We can also examine how the distributions in each of these subspaces change with different IP3 kinetics. Figure 10 illustrates the same 27 subspaces for low amplitude (A ≤ 0.3) IP3 transients. For the subspaces where calcium flux through PMCA and SERCA pumps is high and SOC is constant (i.e. distributions in the top row in the third panel), decreasing the IP3 amplitude decreases the incidence of MP responses and increases the incidence of SP responses.
Fig. 10.
Three-dimensional space of parameter variation over low amplitude IP3 transients. Organization follows the same as Fig. 9.
Such a parameter map can be used by experimentalists to elucidate differences in calcium handling mechanisms between various astrocyte populations. For instance, the response type distribution profile of reactive astrocytes in disease, such as in epilepsy, can be compared against that of healthy astrocytes and be reproduced in the model. The model parameters that need to be modified to reproduce such calcium distributions could indicate how the expression levels and functional properties of channels, pumps, and membrane bound receptors may change in reactive astrocytes. This approach was used to explain the variability in responses of different astrocyte subcompartments (Taheri et al., submitted).
4 Discussion
Through bifurcation analysis and simulations, we investigated the role SOC channels, SERCA pumps, and PMCA pumps have in shaping the underlying dynamical landscape of our model of evoked calcium responses in astrocytes. Surprisingly, despite the low amount of calcium that flows through SOC channels during a calcium transient, we showed that these channels are necessary for PL and LL response types, as well as for stable oscillations. Partially blocking SERCA also eliminated stable oscillations, but PL and LL response types were observed in the system. Further, blocking PMCA pumps significantly widened the IP3 range that supported oscillations, and thus, increased the occurrences of MP response types. We have also shown that the strength of SOC channels is a critical parameter in determining the location of the dynamical range of calcium oscillations, while the parameter corresponding to the strength of SERCA pumps has the ability to tune the width of supported frequencies. Lastly, we presented a novel method for fitting parameters of the model given experimental data of calcium response type alone. In this section, we discuss the potential physiological role of SOC channels, as well as discuss specific limitations of our model.
4.1 Analysis of Calcium Dynamics
Open-cell calcium dynamics have been the focus of numerous research publications (Sneyd et al., 2004; Ullah et al., 2006; De Pittà et al., 2009; Croisier et al., 2013), and have been reviewed in Falcke (2004), Dupont (2014), and Dupont et al. (2016). Building off this previous work, this paper analyzes the calcium dynamics stemming from a unique and astrocyte-specific combination of calcium fluxes and external stimulation. In addition, the models parameters were chosen in order to capture qualitative and quantitative behavior from astrocyte-specific experiments. Further, while there has been a recent focus of some mathematical models to investigate the role of SOC channels in calcium dynamics, the fields understanding of this channel is still incomplete (Liu et al., 2010; Croisier et al., 2013). In this work, we provide a detailed analysis of this flux and how the underlying dynamical structure is dependent on this quiet, yet influential channel. Our systematic approach to blocking and adjusting the relative strengths of individual fluxes (JPMCA, JSERCA, and JSOC) allowed us to provide an in-depth analysis of the role each of these channels have on the underlying bifurcation structure, the diversity of calcium transients, and the frequency of calcium oscillations.
4.2 Mechanism and Role of SOC Channels
While the expression of SOC channels has been identified in astrocytes, specifically the transient receptor potential channel, the exact mechanism allowing these channels to communicate with the ER and allow for the flow of calcium is still under investigation (Verkhratsky et al., 2012b). Instead of modeling this complex mechanism, we focused on qualitatively capturing the characteristic that SOC channels open after calcium is depleted from the ER. Therefore, as a simplified first step, we used a reverse Hill equation to model the activation of these channels, as in Cao et al. (2014). Store-operated calcium entry is a subject of intense ongoing research, and the model will need to be re-evaluated and updated as more data becomes available. For example, there is evidence presented in Courjaret and Machaca (2014) that in oocytes at least some fraction of calcium entering through SOC channels is transported directly into the ER, and would thus need to be included as part of ER calcium in the model. Similar mechanisms may be present in astrocytes as well, and their experimental and theoretical consequences will need to be explored in future work.
An additional delay (capturing the potential time it takes the ER to communicate with the plasma membrane) was also considered, but did not significantly change the results, primarily because JSOC remained silent during the calcium transients. Experimentally, the presence of SOC channels is confirmed via SERCA blockers that completely empty the ER (Malarkey et al., 2008). The model suggests that this type of confirmation may be necessary, because SOC channels remain mostly silent during calcium transients. Nonetheless, despite little activity during transients, SOC channels shape the background dynamics necessary for prolonged responses.
4.3 IP3 Dynamics
Detailed, mechanistic models of IP3 dynamics exists in the literature (De Pittà et al., 2009), but the necessary kinetic details of such models are unknown in astrocytes. New information is even being revealed in non-astrocytic cells, e.g. Bartlett et al. (2015) recently showed how differential regulation of intermediate steps in IP3 creation can have a significant impact on calcium transients. The range of IP3 transients considered here attempt to indirectly account for the uncertainty caused by the number of membrane-bound receptors that are bound and activated by ATP molecules, the duration of this activation, calcium feedback, and PKC regulation to name a few. However, our explicit function for IP3 (Equation (4)) is potentially missing details that would be found in experimental measurements of IP3 concentration, and can be extended in future work.
4.4 Modeling of Non-competitive Blockers
To mathematically model the presence of channel blockers, we simply reduce the corresponding maximum flux term associated the channel of interest. For example, a 50% block of an unspecified channel is simply
This approach includes the implicit assumption that the blockers are assumed to decrease the overall activity of the channel, while not competing directly with calcium for binding sites. Examples of such non-competitive blockers include thapsigargin and Cyclopiazonic Acid (CPA) for the SERCA pump (Plenge-Tellechea et al., 1997; Singh et al., 2005), and eosin for the PMCA pump (Gatto and Milanick, 1993). Due to the relative novelty of SOC channels, specific non-competitive blockers have not been developed. However, genetic knockdown of the STIM1 protein, has been shown to down-regulate these channels (Jousset et al., 2007), which we assume to have a similar effect as a non-competitive blocker.
4.5 Higher Dimensional Parameter Spaces
This work focused primarily on investigating how the parameters υSOC, υPMCA, and υSERCA influence the underlying dynamics of the model proposed in (Taheri et al., submitted). Further, even though we did not vary υIP3R directly, we considered a range of IP3 amplitudes, a parameter which has a similar effect as varying the maximum flux through the IP3R. However, other parameters of the model also influence the calcium response types. For example, varying the parameter a2, which controls the time constant of the IP3R inactivation variable h(t), can significantly change the type of calcium response types observed. Specifically, decreasing a2 (effectively increasing the time constant of h(t)), prevents the inactivation of IP3Rs, leading most calcium responses to become SPs, while increasing a2 leads to a faster and stronger inactivation of IP3Rs, allowing for MPs to become more prevalent (figure not shown). Though not completed here, the above analysis, specifically the tuning method outlined in Section 3.5, can be extended to account for variations in additional parameters. To account for a higher dimensional space, Latin hypercube sampling may be used as a more effective way to sample the multidimensional parameter distribution (McKay et al., 1979), and an automated least squares method can be used to find the region most closely related to one's experimental calcium response type distributions.
4.6 Healthy and Reactive Astrocytes
While we found that the value of γ played a minor role in determining the dynamics of the model, the ratio of ER volume to cytosol volume is known to vary between healthy and reactive astrocytes. Reactive astrocytes are characterized in part by hypertrophy and up-regulation of glial fibrillary acidic protein (GFAP) (Agulhon et al., 2012). Specifically when the central nervous system is injured, astrocytes extend their processes and increase in volume by producing additional GFAP (Ridet et al., 1997). While experimentally observed calcium transients vary in these two states (Aguado et al., 2002), the model suggests that this volume ratio change is not sufficient to produce the change from one state to the other. Thus, a model of reactive astrocytes would need to account for other parameters that may be affected by this ratio change. These could include the change in density of different channels/pumps, the distance of the plasma membrane from the ER and its effects on SOC channel function, and how quickly the SERCA pump can uptake cytosolic calcium, to name a few.
Acknowledgments
This work was supported by the National Science Foundation (DMS-1022945 to A. Borisyuk; DMS-1148230, to A. Borisyuk and G. Handy) and the National Institutes of Health (R01 NS078331, to J.A. White and K.S. Wilcox).
Appendix: Mathematical Model
The differential equations driving the model are
| (1) |
| (2) |
| (3) |
where we denote the calcium concentration in the ER as cER = (ctot − c)γ, and IP3 concentration as p. The Ji's are the fluxes found in Fig. 1. Specifically, we use the Li-Rinzel IP3 receptor model to capture the calcium dynamics through the IP3R channel (Li and Rinzel, 1996), which is governed by the following equations
where
and
The SERCA and PMCA pumps are both model as Hill functions, the forms found in Cao et al. (2014) and Croisier et al. (2013) respectively, and are given by the equations,
and
Similar to the work in Cao et al. (2014), we model SOC channels as the following reverse Hill function
since it has been shown that they open when calcium is depleted in the ER (Verkhratsky et al., 2012b). The model also includes an IP3R-independent leak between the cytosol and the ER with the following equation
Further, we account for additional fluxes across the plasma membrane with the equation
where υin captures the constant leak from the extracellular space, and −koutc accounts for additional calcium extrusion not explicitly model, such as the sodium-calcium exchanger (Höfer et al., 2002; Ullah et al., 2006; Keener and Sneyd, 2009; Verkhratsky et al., 2012a). Lastly, the explicit equation for IP3 is
| (4) |
where
t* is the time of stimulus, A is the max amplitude, rrise and rdecay are the rate of rise and decay respectively, and drise and ddecay are the duration of the rising and decaying phase. These parameters allow us the flexibility to explore a large distribution of IP3 responses easily and effectively.
The complete range of IP3 parameters, as well as the other parameters mentioned in this section, are included in Table 1. Specific values used in the figures are included in the figure captions and text.
Contributor Information
Gregory Handy, Department of Mathematics, University of Utah, Salt Lake City, UT 84112, USA.
Marsa Taheri, Department of Bioengineering, University of Utah, Salt Lake City, UT 84112, USA.
John A. White, Department of Biomedical Engineering, Boston University, Boston, MA 02215, USA
Alla Borisyuk, Department of Mathematics, University of Utah, Salt Lake City, UT 84112, USA, Phone: (+1-801) 585-1639, Fax: (+1-801) 581-4148 (Attn: Alla).
References
- Aguado F, Espinosa-Parrilla J, Carmona M, Soriano E. Neuronal activity regulates correlated network properties of spontaneous calcium transients in astrocytes in situ. The Journal of Neuroscience. 2002;22(21):9430–9444. doi: 10.1523/JNEUROSCI.22-21-09430.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Agulhon C, Sun M, Murphy T, Myers T, Lauderdale K, Fiacco T. Calcium signaling and gliotransmission in normal vs. reactive astrocytes. Frontiers in Pharmacology. 2012;3(139) doi: 10.3389/fphar.2012.00139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amiri M, Bahrami R, Janahmadi M. Functional contributions of astrocytes in synchronization of a neuronal network model. Journal of Theoretical Biology. 2012;292:60–70. doi: 10.1016/j.jtbi.2011.09.013. [DOI] [PubMed] [Google Scholar]
- Anderson C, Swanson RA. Astrocyte glutamate transport: review of properties, regulation, and physiological functions. Glia. 2000;5:81–94. [PubMed] [Google Scholar]
- Bartlett P, Metzger W, Gaspers L, Thomas A. Differential regulation of multiple steps in inositol 1,4,5-trisphosphate signaling by protein kinase c shapes hormone-stimulated ca2+ oscillations. The Journal of Biological Chemistry. 2015;290(30):18519–18533. doi: 10.1074/jbc.M115.657767. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bezzi P, Carmignoto G, Pasti L, Vesce S, Rossi D, Rizzini Bl, Pozzan T, Volterra A. Prostanglandins stimulate calcium dependent glutamate release from astrocytes. Nature. 1998;391:281–5. doi: 10.1038/34651. [DOI] [PubMed] [Google Scholar]
- Cao P, Tan X, Donovan G, Sanderson M, Sneyd J. A deterministic model predicts the properties of stochastic calcium oscillations in airway smooth muscle cells. PLOS Computational Biology. 2014;10(8) doi: 10.1371/journal.pcbi.1003783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Courjaret R, Machaca K. Mid-range ca2+ signalling mediated by functional coupling between storeoperated ca2+ entry and ip3-dependent ca2+ release. Nat Commun. 2014;5(3916) doi: 10.1038/ncomms4916. [DOI] [PubMed] [Google Scholar]
- Croft W, Reusch K, Tilunaite A, Russell N, Thul R, Bellamy T. Probabilistic encoding of stimulus strength in astrocyte global calcium signals. Glia. 2016;64(4):537–552. doi: 10.1002/glia.22947. [DOI] [PubMed] [Google Scholar]
- Croisier H, Tan X, Perez-Zoghbi J, Sanderson M, Sneyd J, Brook B. Activation of store-operated calcium entry in airway smooth muscle cells: Insight from a mathematical model. PLOS One. 2013;8(7) doi: 10.1371/journal.pone.0069598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Lanerolle N, Lee T, S DD. Astrocytes and epilepsy. Neurotherapeutics. 2010;7(4):424–438. doi: 10.1016/j.nurt.2010.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Pittà M, Brunel N. Modulation of synaptic plasticity by glutamatergic gliotransmission: A modeling study. Neural Plasticity. 2016;2016 doi: 10.1155/2016/7607924. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Pittà M, Goldberg M, Volman V, Berry H, Ben-Jacob E. Glutamate regulation of calcium and ip3 oscillating and pulsating dynamics in astrocytes. Journal of Biological Physics. 2009;35:383–411. doi: 10.1007/s10867-009-9155-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Young G, Keizer J. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in ca2+ concentration. Proc Natl Acad Sci. 1992;89:9895–99. doi: 10.1073/pnas.89.20.9895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Garbo A, Barbi M, Chillemi S, Alloisio S, Nobile M. Calcium signalling in astrocytes and modulation of neural activity. BioSystems. 2007;89(1-3):74–83. doi: 10.1016/j.biosystems.2006.05.013. [DOI] [PubMed] [Google Scholar]
- Dupont G. Modeling the intracellular organization of calcium signaling. WIREs Syst Biol Med. 2014;6:227–237. doi: 10.1002/wsbm.1261. [DOI] [PubMed] [Google Scholar]
- Dupont G, Falcke M, Kirk V, Sneyd J. Models of Calcium Signalling. Springer International Publishing; 2016. [Google Scholar]
- Falcke M. Reading the patterns in living cells-the physics of ca2+ signaling. Advances in Physics. 2004;53:255–440. [Google Scholar]
- Fujita T, Chen MJ, Li B, Smith NA, Peng W, Sun W, Toner MJ, Kress BT, Wang L, Benraiss A, Takano T, Wang S, Nedergaard M. Neuronal transgene expression in dominant-negative snare mice. J Neurosci. 2014;34(50):16594–16604. doi: 10.1523/JNEUROSCI.2585-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gatto C, Milanick MA. Inhibition of the red blood cell calcium pump by eosin and other flurescein analogues. Am J Physiol. 1993;264(6 Pt 1):C1577–86. doi: 10.1152/ajpcell.1993.264.6.C1577. [DOI] [PubMed] [Google Scholar]
- Haydon PG. Glia: Listening and talking to the synapse. Nature Reviews. 2001;2:185–193. doi: 10.1038/35058528. [DOI] [PubMed] [Google Scholar]
- Haydon PG, Nedergaard M. How do astrocytes participate in neural plasticity? Cold Spring Harb Perspect Biol. 2015;7 doi: 10.1101/cshperspect.a020438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hines M, Morse T, Migliore M, Carnevale N, S GM. Modeldb: a database to support computational neuroscience. J Comput Neurosci. 2004;17(50):7–11. doi: 10.1023/B:JCNS.0000023869.22017.2e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Höfer T, V L, Giaume C. Control and plasticity of intercellular calcium waves in astrocytes: a modeling approach. J Neurosci. 2002;22:4850–4859. doi: 10.1523/JNEUROSCI.22-12-04850.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jousset H, Frieden M, Demaurex N. Stim1 knockdown reveals that store-operated ca2+ channels located close to sarco/endoplasmic ca2+ atpases (serca) pumps silently refill the endoplasmic reticulum. Journal of Biological Chemistry. 2007;282(15):11456–11464. doi: 10.1074/jbc.M609551200. [DOI] [PubMed] [Google Scholar]
- Kantevari S, Gordon G, MacVicar B, ED GCR. A practical guide to the synthesis and use of membrane-permeant acetoxymethyl esters of caged inositol polyphosphates. Nature Protocols. 2011;6:327–337. doi: 10.1038/nprot.2010.194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keener J, Sneyd J. Mathematical Physiology. Springer Science+Business Media; 2009. [Google Scholar]
- Larsen BR, Assentoft M, Cotrina ML, Hua S, Nedergaard M, Kaila K, Voipio J, MacAulay N. Contributions of the na+/k+-atpase, nkcc1, and kir4.1 to hippocampal k+ clearance and volume responses. Glia. 2014;62(4):608–622. doi: 10.1002/glia.22629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lavrentovich M, Hemkin S. A mathematical model of spontaneous calcium(ii) oscillations in astrocytes. Journal of Theoretical Biology. 2008;251:553–560. doi: 10.1016/j.jtbi.2007.12.011. [DOI] [PubMed] [Google Scholar]
- Li YX, Rinzel J. Equations for insp3 receptor-mediated ca2+ oscillations derived from a detailed kinetic model: A hodgkin-huxley like formalism. Journal of Theoretical Biology. 1996;166:461–473. doi: 10.1006/jtbi.1994.1041. [DOI] [PubMed] [Google Scholar]
- Liu Q, Xum Q, Kangm J, Nedergaard M. Astrocyte activation of presynaptic metabotropic glutamate receptors modulates hippocampal inhibitory synaptic transmission. Neuron Glia Biol. 2004;1(4):307–316. doi: 10.1017/S1740925X05000190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu W, Tang F, Chen J. Designing dynamical output feedback controllers for store-operated ca2+ entry. Mathematical BioSciences. 2010;228:110–118. doi: 10.1016/j.mbs.2010.08.013. [DOI] [PubMed] [Google Scholar]
- Malarkey E, Ni Y, Parpura V. Ca2+ entry through trpc1 channels contributes to intracellular ca2+ dynamics and consequent glutamate release from rat astrocytes. Glia. 2008;56:821–835. doi: 10.1002/glia.20656. [DOI] [PubMed] [Google Scholar]
- McKay M, Beckman R, Conover W. A comparison of three methods for selecting values of input variables in the analysis of output from a computer code technometrics. Glia. 1979;21(2):239–245. [Google Scholar]
- Nedergaard M, Ransom BR, Goldman SA. New roles for astrocytes: redefining the functional architecture of the brain. Trends Neuroscience. 2003;26:523–530. doi: 10.1016/j.tins.2003.08.008. [DOI] [PubMed] [Google Scholar]
- Nedergaard M, Verkhratsky A. Artifact versus reality–how astrocytes contribute to synaptic events. Glia. 2012;60 doi: 10.1002/glia.22288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nezu A, Tanimura A, Morita T, Tojyo Y. Use of fluorescence resonance energy visualization of ins(1,4,5)p3 dynamics in living cells: two distinct pathways for ins(1,4,5)p3 generation following mechanical stimulation of hsy-ea1 cells. Journal of Cell Science. 2010;123:2292–2298. doi: 10.1242/jcs.064410. [DOI] [PubMed] [Google Scholar]
- Pasti L, Pozzan T, Carmignoto G. Long-lasting changes of calcium oscillations in astrocytes. a new form of glutamate-mediated plasticity. Journal of Cell Science. 1995;270(25):15203–10. doi: 10.1074/jbc.270.25.15203. [DOI] [PubMed] [Google Scholar]
- Plenge-Tellechea F, Soler F, Fernandez-Belda F. On the inhibition mechanism of sarcoplasmic or endoplasmic reticulum ca21-atpases by cyclopiazonic acid. Journal of Biological Chemistry. 1997;272(5):2794–2800. doi: 10.1074/jbc.272.5.2794. [DOI] [PubMed] [Google Scholar]
- Reato D, Cammarota M, Parra L, Carmignoto G. Computational model of neuron-astrocyte interactions during focal seizure generation. Frontiers in Computational Neuroscience. 2012;6(81) doi: 10.3389/fncom.2012.00081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ridet J, Malhotra SK, P A, Gage FH. Reactive astrocytes: cellular and molecular cues to biological function. Trends in Neuroscience. 1997;20(12):570–577. doi: 10.1016/s0166-2236(97)01139-9. [DOI] [PubMed] [Google Scholar]
- Roos J, DiGregorio P, Yeromin A, Ohlsen K, Lioudyno M, Zhang S, Safrina O, Kozak J, Wagner S, Cahalan M, Veliçelebi G, Stauderman K. Stim1, an essential and conserved component of store-operated ca2+ channel function. Journal of Cell Biology. 2005;169(3):435–445. doi: 10.1083/jcb.200502019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shigetomi E, Tong X, Kwan K, Corey D, Khakh B. Trpa1 channels regulate astrocyte resting calcium and inhibitory synapse efficacy through gat-3. Nature Neuroscience. 2012;15(1) doi: 10.1038/nn.3000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Singh P, Mhaka AM, Christensen SB, Gray JJ, Denmeade SR, Isaacs JT. Applying linear interaction energy method for rational design of noncompetitive allosteric inhibitors of the sarco- and endoplasmic reticulum calcium-atpase. J Med Chem. 2005;48:3005–3014. doi: 10.1021/jm049319a. [DOI] [PubMed] [Google Scholar]
- Sneyd J, Tsaneva-Atanasova K, Reznikov V, Bai Y, Sanderson M, Y DI. A method for determining the dependence of calcium oscillations on inositol trisphosphate oscillations. PNAS. 2006;103(6):1675–1680. doi: 10.1073/pnas.0506135103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sneyd J, Tsaneva-Atanasova K, Yule D, Thompson J, Shuttleworth T. Control of calcium oscillations by membrane fluxes. PNAS. 2004;101(5):1392–1396. doi: 10.1073/pnas.0303472101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi D, Vargas J, Wilcox K. Increased coupling and altered glutamate transport currents in astrocytes following kainic-acid-induced status epilepticus. Neurobiology of Disease. 2010;40:573–585. doi: 10.1016/j.nbd.2010.07.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanimura A, Morita A, Nezu A, Shitara A, Hashimoto N, Tojyo Y. Use of fluorescence resonance energy transfer-based biosensors for the quantitative analysis of inositol 1,4,5-trisphosphate dynamics in calcium oscillations. Journal of Biological Chemistry. 2009;284(13):8910–8917. doi: 10.1074/jbc.M805865200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Toivari E, Manninen T, Nahata A, Jalonen T, Linne M. Effects of transmitters and amyloid-beta peptide on calcium signals in rat cortical astrocytes: Fura-2am measurements and stochastic model simulations. PLOS One. 2011;6(3):e17914. doi: 10.1371/journal.pone.0017914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tower D, Young OM. The activities of butyrylcholinesterase and carbonic anhydrase, the rate of anaerobic glycolysis, and the question of a constant density of glial cells in cerebral cortices of various mammalian species from mouse to whale. Journal of Neurochemistry. 1973;20:269–278. doi: 10.1111/j.1471-4159.1973.tb12126.x. [DOI] [PubMed] [Google Scholar]
- Ullah G, Jung P, Cornell-Bell AH. Antiphase calcium oscillations in astrocytes via inositol (1,4,5)-trisphosphate regeneration. Cell Calcium. 2006;39:197–208. doi: 10.1016/j.ceca.2005.10.009. [DOI] [PubMed] [Google Scholar]
- Verkhratsky A, Rodríguez J, Parpura V. Calcium signalling in astroglia. Molecular and Cellular Endocrinology. 2012a;353:45–56. doi: 10.1016/j.mce.2011.08.039. [DOI] [PubMed] [Google Scholar]
- Verkhratsky A, Sofroniew MV, Messing A, deLanerolle NC, Rempe D, Rodríguez JJ, Nedergaard M. Neurological diseases as primary gliopathies: a reassessment of neurocentrism. ASN Neuro. 2012b;4(3):e00082. doi: 10.1042/AN20120010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wade J, McDaid L, Harkin J, Crunelli V, Scott Kelso J. Bidirectional coupling between astrocytes and neurons mediates learning and dynamic coordination in the brain: A multiple modeling approach. PLOS One. 2011;6(12):e29445. doi: 10.1371/journal.pone.0029445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wallraf A, Kohling R, Heinemann U, Theis M, Willecke K, Steinhauser C. The impact of astrocytic gap junctional coupling on potassium buffering in the hippocampus. J Neuroscience. 2006;26:5438–5447. doi: 10.1523/JNEUROSCI.0037-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F, Smith NA, Xu Q, Fujita T, Baba A, Matsuda T, Takano T, Bekar L, Nedergaard M. Astrocytes modulate neural network activity by ca2+ - dependent uptake. Sci Signal. 2012;5(218):ra26. doi: 10.1126/scisignal.2002334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F, Smith NA, Xu Q, Goldman S, Peng W, Huang JH, Takano T, Nedergaard M. Photolysis of caged ca2+ but not receptor-mediated ca2+ signaling triggers astrocytic glutamate release. J Neuroscience. 2013;33(44):17404–17412. doi: 10.1523/JNEUROSCI.2178-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou Y, Danbolt NC. Gaba and glutamate transporters in brain. Front Endocrinol. 2013;4(165) doi: 10.3389/fendo.2013.00165. [DOI] [PMC free article] [PubMed] [Google Scholar]