Nanometer-precision linear sorting with synchronized optofluidic dual barriers

Researchers explore loosely overdamped system with extreme low stiffness for nanoparticle sorting with nanometer precision.

Abstract

The past two decades have witnessed the revolutionary development of optical trapping of nanoparticles, most of which deal with trapping stiffness larger than 10⁻⁸ N/m. In this conventional regime, however, it remains a formidable challenge to sort out sub–50-nm nanoparticles with single-nanometer precision, isolating us from a rich flatland with advanced applications of micromanipulation. With an insightfully established roadmap of damping, the synchronization between optical force and flow drag force can be coordinated to attempt the loosely overdamped realm (stiffness, 10⁻¹⁰ to 10⁻⁸ N/m), which has been challenging. This paper intuitively demonstrates the remarkable functionality to sort out single gold nanoparticles with radii ranging from 30 to 50 nm, as well as 100- and 150-nm polystyrene nanoparticles, with single nanometer precision. The quasi-Bessel optical profile and the loosely overdamped potential wells in the microchannel enable those aforementioned nanoparticles to be separated, positioned, and microscopically oscillated. This work reveals an unprecedentedly meaningful damping scenario that enriches our fundamental understanding of particle kinetics in intriguing optical systems, and offers new opportunities for tumor targeting, intracellular imaging, and sorting small particles such as viruses and DNA.

INTRODUCTION

Optical manipulation of nanoparticles has gained enormous attention during the past two decades owing to its versatile and noninvasive characteristics and significant value in biological and physical applications (1–8), such as virus trapping (9, 10), DNA stretching (11, 12), drug delivery (13, 14), and biochemical reactions (15). Optical trapping, including single-beam, optoelectric, and plasmonic trapping, has advanced this field into manipulation of sub–10-nm particles (16–21), even atoms via optical cooling technology (22, 23). Particles being trapped remains the holy grail of optical micromanipulation because multiple particles tend to aggregate due to the gradient force in the tweezers (24). Nevertheless, biomedical applications are in tremendous need of a setup that could not only trap nanoparticles stably down to a few tens of nanometers but also sort those nanoparticles up to the precision of single-nanometer resolution (25–27). In this connection, optical sorting has shown progress. Most methods including holographic optical tweezers (28), optical switching (29), optical chromatography (30, 31), and interference patterns (32, 33) suffice to sort microsized particles. In the submicrometer and a few hundreds of nanometer scale, dielectric nanoparticles have been sorted using standing waves (34) and acoustofluidics (35, 36), whereas metallic counterparts were separated using size-dependent surface plasmon resonance in an evanescent wave (37), thermal-hydrodynamic forces (38), and fluidic systems (39). Recently, advanced optical tweezers have been exploited to develop micromotors using microparticles such as Janus particles (40–43), colloidal particles (44, 45), and magnetic particles (46). However, those micromotors are incapable of particle sorting and usually limited to microparticles or even special particles. Moreover, the microscopic self-oscillation of nanoparticles in novel systems still remains an enigma.

RESULTS AND DISCUSSION

Optical manipulation roadmap for the sorting of nanoparticles

Efforts aiming at establishing correlations between particle size and material property and the adopted approach seem quite sporadic, and it is intuitively believed that many unexplored treasures may have been neglected. In this regard, we establish, for the very first time, a damping roadmap (diagram; Fig. 1A) taking three primary factors into account: (i) stiffness k, (ii) viscosity η, and (iii) mean square displacement (MSD), which unanimously unfold a complete map for the joint realm of sorting and trapping. A system can be first classified into two possible categories: overdamped (ω₀ ≤ 1/2τ_p) and underdamped (ω₀ > 1/2τ_p), where ${\mathrm{\omega }}_0=\sqrt{\mathit{k}/\mathit{m}}$ is the resonant frequency with trapping stiffness k and τ_p = m/γ_f is the momentum relaxation time of a nanoparticle with mass m, radius R, and Stokes viscous drag coefficient γ_f = 6πηR (47). The overdamped and underdamped systems can be divided by the red dashed line expressed as $\text{lg}(\mathrm{\eta })=\frac{1}{2}\text{lg}(\mathit{k})+\text{lg}\left(\frac{\sqrt{\mathit{m}}}{3\mathrm{\pi }\mathit{R}}\right)$ in the diagram. Optical trapping in the right side of the roadmap relies on the tight focus (k ~ 10⁻⁶ to 10⁻⁴ N/m) to attract nanoparticles to the focal point in either a liquid or gas. When a nanoparticle (for example, R = 40 nm) is trapped in the gas with a viscosity η of 10⁻⁵ Pa·s and drag coefficient γ_f of 7.54 × 10⁻¹² N·s m⁻¹ (48–51), the system is underdamped. Experiments involving optical trapping of nanoparticles are often conducted in liquids with viscosities of approximately 10⁻³ Pa·s, in which 1/2τ_p could easily turn to 7.3 × 10⁷ Hz and the system becomes overdamped (52–54). Conventional optical chromatography builds potential wells with low stiffness (10⁻⁸ to 10⁻⁶ N/m) and has been widely used to sort microparticles and spores (30, 31). This technology so far falls into the region of highly overdamped system in the middle of the diagram shown in Fig. 1A. In addition to the highly overdamped region, we discover a nearly unexplored region with stiffness from 10⁻¹⁰ to 10⁻⁸ N/m in the leftmost side of the diagram, which represents a “loosely overdamped” system (ω₀ << 1/2τ_p). Surprisingly, this long-ignored region empowers single-nanometer precision linear sorting with marked displacement position offset. This established the value of our physical model and damping diagram.

Fig. 1. Damping diagram unfolds the complete map of trapping and sorting particles in optofluidic systems: Classic trapping, microscale sorting, and nanoscale sorting.

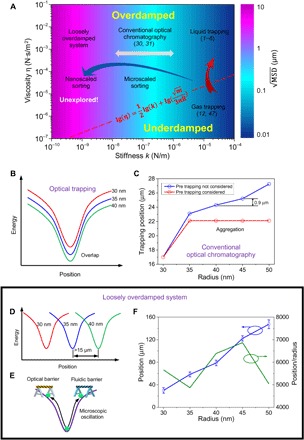
(A) Oscillation diagram with stiffness of optical tweezers (k) and viscosity of the medium (η). Functions of optical manipulation from left to right are loosely overdamped system for nanoscale sorting (k ~ 10⁻¹⁰ to 10⁻⁸ N/m), optical chromatography for microscale sorting (k ~ 10⁻⁸ to 10⁻⁶ N/m), and optical trapping (k ~ 10⁻⁶ to 10⁻⁴ N/m). The optical trapping can be divided into liquid and gas trapping based on different viscosities. Parameters of m and R in the equation (the dividing line of underdamped and overdamped systems) are the mass and radius of particle, respectively. (B to F) Illustration of optical sorting of gold nanoparticles with radii of 30, 35, and 40 nm using technologies in the diagram. (B) Optical trapping is shown to be unable to sort nanoparticles because of the overlap of potential wells of different nanoparticles. (C) Calculation of trapping positions of 30- to 50-nm gold nanoparticles in the optical chromatography. Individual gold nanoparticles with different radii can be trapped in different positions using the Gaussian beam with a numerical aperture (NA) of 0.12. However, the theoretical minimum separation distance between them is only 0.9 μm. When the gold nanoparticles are trapped in the beam, the smaller nanoparticle absorbs light and greatly influences the trapping positions of larger gold nanoparticles. Therefore, 35-, 40-, 45-, and 50-nm gold nanoparticles will eventually aggregate. Detailed proof has been provided in the Supplementary Materials. (D) A loosely overdamped system is an ideal platform for nanoparticle sorting, in which 30-, 35-, and 40-nm gold nanoparticles can be separated with a large distance (>15 μm) away from each other. (E) Nanoparticles oscillate in microscale without escaping the system with stiffness of 10⁻¹⁰ to 10⁻⁸ N/m under the control of synchronized optical and fluidic barriers. (F) The experimentally observed sorting distance increases linearly with the radius, implying that each nanoparticle has a specific trapping position in the system. The separation sensitivity (position/radius) is shown on the right y axis.

The damping roadmap facilitates the probing of the underlying physics behind various manipulation phenomena hosted in different regions of Fig. 1A. It reveals that if 30-, 35-, and 40-nm gold nanoparticles coexist in the optical trapping, their potential wells overlap (55), resulting in the aggregation of particles as shown in Fig. 1B. These circumstances usually refer to the rightmost region of Fig. 1A, that is, liquid and gas trapping with relatively higher stiffness. Conventional optical chromatography, in the middle of the roadmap (k ~ 10⁻⁸ to 10⁻⁶ N/m), is also not an optimal solution to the same batch of nanoparticles, and it shows severe aggregation when the radii of nanoparticle are very close as shown in Fig. 1C. Because of the strong absorption of gold nanoparticles, the smaller gold nanoparticles that are trapped near the focus of the beam block the light beam and prevent the separation of larger nanoparticles. The simulation result in Fig. 1C shows that 35-, 40-, 45-, and 50-nm gold nanoparticles aggregate because of blocking of light by the smaller gold nanoparticles. Even for individual gold nanoparticles, the minimum difference of the trapping distance is only 0.9 μm, which is of the same order as the estimated oscillation range $\sqrt{\text{MSD}}$ in that particular stiffness region, thereby introducing difficulties to separate the particles. Detailed calculation of the trapping positions of nanoparticles in the conventional optical chromatography regime can be found in the Supplementary Materials. The untouched loosely overdamped system offers a paradigm shift in addressing the existing and aforementioned challenges. Evidently, nanoparticles with radii of 30, 35, and 40 nm can be well separated with interval distances above 15 μm, and simultaneously, their trapping distance increases linearly with the size of nanoparticles as shown in Fig. 1D. Note that the potential well now is of extremely low stiffness (10⁻¹⁰ to 10⁻⁸ N/m), making it unable to hold a certain sized nanoparticle at its corresponding position using optical force alone. At this point, our dual-barrier synchronization becomes crucial, that is, optical (extinction force from the synergy of scattering and absorption forces) and fluidic (drag force due to the flow) barriers imposed on both sides of the potential well, which are coordinated judiciously to prevent the nanoparticle from escaping the well, as shown in Fig. 1E. Experimental observation verified the feasibility of separation of 30- to 50-nm gold nanoparticles along the microchannel, as shown in Fig. 1F. The maximum separation range for 30- and 50-nm gold nanoparticles is approximately 100 μm. The separation distance between each nanoparticle with size difference of 5 nm is larger than 15 μm, indicating that the separation sensitivity (position/radius) could be above 4000 to enable unparalleled capability of sorting nanoparticles in a loosely overdamped system.

Microscopic oscillation and linear trapping via synchronized optofluidic barriers

The physics of the synchronized dual barriers associated with the loosely overdamped system is described in Fig. 2A. The optical barrier on the left side is created by the dominant extinction force, whereas the fluidic barrier is actuated via the drag force. Normally, the thermal fluctuations of the nanoparticle (10k_BT) would easily overcome the depth of a potential well (U) with a trapping stiffness smaller than 10⁻⁶ N/m, enabling the nanoparticle to escape the barrier of the well (56–58). On the contrary, in this optofluidic system, even a potential well with trapping stiffness as low as 10⁻¹⁰ N/m can confine the nanoparticle by virtue of the dual barriers. Assuming that the light propagates from left to right and the fluid flows along the opposite direction, the optical/fluidic barrier pushes the nanoparticle toward the equilibrium position when the nanoparticle is on the left/right of the equilibrium position.

Fig. 2. Microscopic oscillation via synchronized dual optofluidic barriers.

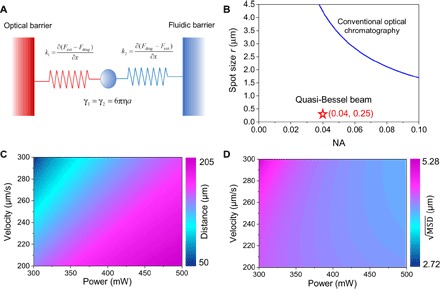
(A) Physical model of the microscopic oscillation of a single nanoparticle. The movement of the nanoparticle is confined by the optical and fluidic barriers. (B) The size of the focal point is inversely proportional to the NA in a conventional beam, whereas the quasi-Bessel beam has a tight focus with a radius of 0.25 μm and a low NA of 0.04 at the same time. Trapping distance (C) and oscillation amplitude (D) of the 40-nm gold nanoparticle can be tuned by synchronizing optical and fluidic barriers.

To exploit the sorting capability of a loosely overdamped system, one needs to design a system with a low NA and small focusing spot size simultaneously, which sounds counterintuitive (59, 60). For a conventional Gaussian beam, the focal spot size of the beam is inversely proportional to NA, as shown in Fig. 2B, and thereby, one always gains on one end and loses on the other. For example, to have a small NA of 0.04, the spot size is approximately 8 μm, which is obviously insufficient to trap nanoparticles efficiently. Fortunately, it is found that a quasi-Bessel beam could be engineered to exhibit a small focal spot size (radius ~ 0.25 μm) and a low NA (0.04) owing to light interference. Thus, it solves the aforementioned dilemma because it meets the requirements of sufficient separation distance and stable trapping. The controllable degrees of freedom in our optofluidic system could also be used to tune the trapping position of the nanoparticles (for example, 40 nm in radius) by altering the laser power and flow velocity, as verified in Fig. 2C. For example, the in situ tunable trapping position can be manipulated from 50 to 205 μm when the laser power increases from 300 to 500 mW and the flow velocity increases from 200 to 300 μm/s. In addition, $\sqrt{\text{MSD}}$ varies with laser power and velocity (see the Supplementary Materials for the tuning of trapping stiffness). Basically, a lower laser power and a higher flow velocity will result in a larger $\sqrt{\text{MSD}}$ because of the smaller stiffness in the shorter trapping distance. $\sqrt{\text{MSD}}$ ranges from 2.72 to 5.28 μm given the same conditions in Fig. 2D. The introduction of $\sqrt{\text{MSD}}$ enables us to control the experimental conditions to ensure that the oscillation range of each nanoparticle does not overlap, mitigating interference from each other, especially the direct contact by the oscillation.

Sorting of nanoparticles and microorganisms

The profile of the quasi-Bessel beam shown in Fig. 3A elucidates the potential of sorting sub–50-nm gold nanoparticles because of tightly focused light and low equivalent NA. Meanwhile, the quasi-Bessel beam also demonstrates the self-healing property (61–63) like conventional Bessel and Airy beams, as shown in Fig. 3B. Even when an absorbing particle (0.5 μm in radius) completely blocks the main lobe of the quasi-Bessel beam (radius ~ 0.25 μm), the beam can reconstruct itself while propagating. This characteristic enables the trapping of multiple gold nanoparticles along the microchannel. Conventional beams do not have this self-healing property, which results in the disturbance of trapping positions of subsequently trapped nanoparticles, and even causes nanoparticle aggregation as shown in Fig. 1C.

Fig. 3. Nanometer-precision sorting of nanoparticles and microorganisms in the loosely overdamped system.

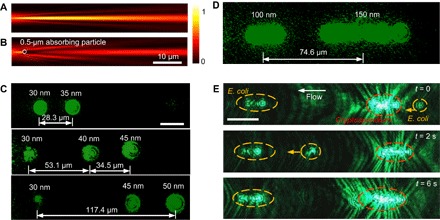
(A) Light intensity profile of the quasi-Bessel beam. (B) Self-healing property of the quasi-Bessel beam. The quasi-Bessel beam reconfigures itself after propagating through an absorbing particle (0.5 μm in radius) that is completely blocking the main lobe of the beam (radius ~ 0.25 μm). (C) Trapped nanoparticles with different diameters in the microchannel. The laser power is 400 mW, and the flow rate is 300 μm/s. Scale bar, 20 μm. (D) Separation of polystyrene nanoparticles with radii of 100 and 150 nm. Two clusters of 100- and 150-nm polystyrene nanoparticles were trapped in isolated locations. (E) Separation of E. coli and Cryptosporidium in the microchannel.

Experimental sorting of nanoparticles with radii of 30, 35, 40, 45, and 50 nm in Fig. 3C perfectly echoes the working principle related to Fig. 1D and verifies the theoretical model in Fig. 2. A single nanoparticle with a radius of 30 nm is trapped at z = 30 μm, and its presence is kept in each frame to serve as a reference for individual positions of larger nanoparticles. In addition, its presence and location could function as a reference to ensure that the trapping condition (for example, laser power and flow rate) remains the same for subsequent sorting experiments. Separated trapping of 100- and 150-nm polystyrene nanoparticles is also demonstrated in Fig. 3D. Two clusters of nanoparticles with different radii are trapped along the microchannel with a separation distance of 75 μm. This dual-barrier system operating in the loosely overdamped region has been used to separate bacteria and protozoa efficiently as shown in Fig. 3E. Escherichia coli (rod-shaped, approximately 0.5 μm in width by 2 μm in length) and Cryptosporidium oocysts (spherical to oval in shape, 2 to 3 μm in radius) are separately trapped, forming the left and right clusters, respectively. The distance between the two groups is approximately 145 μm. It is observed that an additional E. coli initially wandering on the right side of the whole region (t = 0) would walk through the cluster of Cryptosporidium oocysts (t = 2 s) and be eventually trapped in the left cluster (t = 6 s), showing the reliable sorting functionality in practice.

Microscopic oscillation of nanoparticles

When nanoparticles are separately trapped in the microchannel, they will oscillate in different positions based on the stiffness of their trapping locations. When the potential well for the larger particle is positioned at the location with a larger optical extinction force, resulting in a higher trapping stiffness, the oscillation of the nanoparticle is confined to a shorter displacement. For instance, in a conventional single-beam optical tweezer with NA = 1.4 (stiffness k = 10⁻⁶ to 10⁻⁴ N/m) (3, 4), the Brownian motion of the nanoparticles is normally confined to a displacement smaller than 100 nm. For instance, the width of potential energy for a 40-nm gold nanoparticle to reach 10k_BT is only 40 nm, as shown in the inset of Fig. 4A, which indicates the sub–100-nm oscillation range. The loosely overdamped system (k = 10⁻¹⁰ to 10⁻⁸ N/m) generated by the quasi-Bessel beam makes the nanoparticles oscillate at micrometer-scale displacement. The widths of the potential energy are 25.6, 16.8, and 14 μm for thermal fluctuation corresponding to 10k_BT for 30-, 40-, and 50-nm gold nanoparticles, respectively. The ranges for this displacement magnitude are explained by the Langevin equation describing the Brownian motion of particles in a thermal and external force field, that is, ${\mathit{m}}_{\mathrm{e}}\ddot{\mathit{x}}(\mathit{t})+{\mathrm{\gamma }}_{\mathrm{f}}\stackrel{.}{\mathit{x}}(\mathit{t})+\mathit{K}\mathit{x}(\mathit{t})={\mathit{F}}_{\text{th}}(\mathit{t})+{\mathit{F}}_{\text{ext}}$, where F_th and F_ext are the thermal and external forces on the nanoparticle, respectively. The effective mass m_e includes the mass of the nanoparticle and the inertial mass of the fluid, 2/3πr³ρ_f (53). For a trapping system in a stationary environment, the spring constant of the system directly results from the optical gradient force, that is, K(x) = F_grad(x)/δx. However, the harmonic spring constant in the optofluidic system arises from the combination of the optical extinction force and drag force, that is, K(x) = [F_ext(x) − F_drag(x)]/δx = [F_ext(x) − γ_fv_f(x)]/δx. The Basset force resulting from the memory effect in a viscous liquid can be ignored over a long period of time (54). Therefore, MSD of the nanoparticle in an overdamped system can be expressed as (64)

$$\text{MSD}(\mathit{t})=\frac{1}{{\mathit{m}}_{\mathrm{p}}{\mathrm{\omega }}_0^2\mathrm{\gamma }}[1-\frac{1}{2|{\mathrm{\omega }}_1|{\mathrm{\psi }}_{+}^{\prime }}{\mathit{e}}^{-\mathit{t}/{\mathrm{\psi }}_{-}^{\prime }}+\frac{1}{2|{\mathrm{\omega }}_1|{\mathrm{\psi }}_{-}^{\prime }}{\mathit{e}}^{-\mathit{t}/{\mathrm{\psi }}_{+}^{\prime }}]$$ (1)

where ${\mathrm{\omega }}_1=\sqrt{{\mathrm{\omega }}_0^2-{(1/2{\mathrm{\tau }}_{\mathrm{p}})}^2}$is the corner frequency and ${\mathrm{\psi }}_{\pm }^{\prime }=2{\mathrm{\tau }}_{\mathrm{p}}/(1\pm 2{\mathrm{\tau }}_{\mathrm{p}}|{\mathrm{\omega }}_1|)$.

Fig. 4. Characterization of the microscopic oscillations of nanoparticles in the loosely overdamped system.

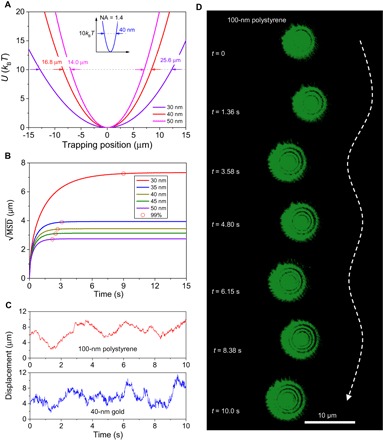
(A) Potential energies of 30-, 40-, and 50-nm gold nanoparticles trapped in the loosely overdamped system. The potential wells have widths of 14, 16.8, and 25.6 μm for 30-, 40-, and 50-nm gold nanoparticles when the energy is 10k_BT, respectively. Inset shows the potential energy of a 40-nm gold nanoparticle trapped in a single-beam optical tweezer, with an NA of 1.4 and laser power of 30 mW. The width for 10k_BT is only 40 nm in this single-beam trapping. (B) Square root of MSD of gold nanoparticles in their trapped positions. The red circles indicate the situations when the individual systems approach 99% of the steady states. (C) Experimentally measured displacements of 100-nm polystyrene nanoparticles and 40-nm gold nanoparticles during oscillation. (D) Experimental observation of local microscopic oscillation of the 100-nm polystyrene nanoparticle in the microchannel. Scale bar, 10 μm.

The absolute value of the trapping stiffness rises linearly from 2.45 × 10⁻¹⁰ to 1.66 × 10⁻⁹ N/m when the radius of the nanoparticles increases from 30 to 50 nm because greater forces are exerted on larger nanoparticles. Figure 4B shows the calculated $\sqrt{\text{MSD}}$ for the studied nanoparticles, which decreases as the particle size increases because of the increasing stiffness. The measured displacements for 40-nm gold and 100-nm polystyrene nanoparticles in the loosely overdamped system are shown in Fig. 4C. The movement of the gold nanoparticle is more chaotic compared to the polystyrene nanoparticle because of the higher local temperature induced on the highly absorbing gold nanoparticles (see the Supplementary Materials for the simulation of temperature). The oscillation range of two nanoparticles is almost identical despite the different sizes. This is caused by the strong enhancement of the optical excitation and the high local temperature of the gold nanoparticles. The oscillation range matches reasonably well with the calculation result shown in Fig. 4B. It is noted that the range of nanoparticle oscillation is smaller than the separation distance between the trapping positions of two gold nanoparticles (for example, 30- and 35-nm nanoparticles). The 5-nm separation precision is still a very conservative value, and this could most likely be further improved once we develop strategies to accurately produce nanoparticles of predefined size (for example, 31, 32, and 33 nm).

Experimental observation of the oscillation of 100-nm polystyrene nanoparticles is presented in Fig. 4D. The oscillation of 100-nm nanoparticles revealed a displacement of 6 μm during an average period of 3 s. The observed oscillation is distinctly different from that in the tightly focused optical trapping regime, in which the oscillation range is usually smaller than 100 nm.

CONCLUSION

The damping roadmap and the coordinated dual-barrier system lead to the discovery of the long overlooked loosely overdamped region, in which optical trapping of nanoparticles was formerly considered impossible due to the low stiffness (10⁻¹⁰ to 10⁻⁸ N/m). We have successfully demonstrated that 30- to 50-nm gold nanoparticles and 100- to 150-nm polystyrene nanoparticles can be effectively trapped separately while oscillating in loosely overdamped potential wells. The trapping position and oscillation range can be controlled by tuning the laser power and flow rate. The physical model describing the microscopic oscillation is also presented. In the experiment, nanoparticles were observed to oscillate at large displacement amplitudes (>3 μm) in the isolated potential wells with a minimum separation distance of more than 15 μm. Moreover, the absolute precision of the trapping position was estimated to fall in the single-nanometer resolution. The wavelength of the quasi-Bessel beam and the beam shape, which have not been considered in this work yet, may provide additional degrees of freedom for advanced separation of viruses and DNA. Our studies offer a deeper understanding of particle kinetics in intriguing systems such as loosely overdamped system. It makes possible single-nanometer precision sorting of nanoparticles, sheds light on promising biomedical applications in screening and separation, and may also inspire the future development of nanosorters and Brownian motors in microfluidic systems.

MATERIALS AND METHODS

Experimental setup

The optofluidic chip was fabricated using polydimethylsiloxane by soft lithography processes. The microchannel had a length of 1000 μm, a width of 70 μm, and a height of 50 μm. A microlens was built between the fiber groove and the microchannel. A solid-state laser (532 nm, mpc 6000, Laser Quantum) was coupled to an optical fiber and inserted into the fiber groove near the microlens. Images were captured using an inverted optical microscope (TS 100 Eclipse, Nikon) through a charge-coupled device camera (Photron FASTCAM SA3). The nanoparticles and cells were dispersed in the deionized water and injected into the microchannel using syringe pumps (Genie, Kent Scientific Corporation).

Simulation of the temperature and permeability of nanoparticles

The absorption of a large number of photons raises the temperature of the nanoparticles. Heat transfer in fluids is expressed as (65)

$$\mathrm{\rho }{\mathit{C}}_{\mathrm{p}}\frac{\partial \mathit{T}}{\partial \mathit{t}}+\mathrm{\rho }{\mathit{C}}_{\mathrm{p}}\mathit{v}\nabla \mathit{T}=\nabla \cdot (\mathit{k}\nabla \mathit{T})+{\mathit{Q}}_{\mathrm{e}}$$ (2)

where ρ, C_p, v, and k are the density, heat capacity, velocity, and thermal conductivity of the fluid, respectively. Q_e is the electromagnetic heat source, which can be expressed as Q_e = J ⋅ E, where J is the current density and E is the electric field strength. The Drude model is used to calculate the permeabilities of the nanoparticles, which can be expressed as (66, 67)

$$\mathrm{\epsilon }(\mathrm{\omega })={\mathrm{\epsilon }}_{\text{bound}-\text{electrons}}(\mathrm{\omega })+{\mathrm{\epsilon }}_{\text{free}-\text{electrons}}(\mathrm{\omega })$$ (3)

where ε_{bound-electrons} and ε_{free-electrons} are the contributions from bound and free electrons, respectively. The equations of permeability were then used to fit the optical scattering spectrum with Rayleigh scattering theory to obtain the parameters for the calculation of the optical forces. Rigorous simulations of energy transfer from the laser to the nanoparticles and further to the flow stream were implemented in COMSOL and shown in the Supplementary Materials. The dimensions of the simulation region were 1 × 1 × 1 μm, and the maximum grid sizes for the surrounding medium and the gold nanoparticles were 10 and 1 nm, respectively.

Calculation of MSD in the underdamped region

The MSD of a nanoparticle in an underdamped system can be expressed as (64)

$$\text{MSD}(\mathit{t})=\frac{2{\mathit{k}}_{\mathrm{B}}\mathit{T}}{{\mathit{m}}_{\mathrm{p}}{\mathrm{\omega }}_0^2}[1-{\mathit{e}}^{-\mathit{t}/2{\mathrm{\tau }}_{\mathrm{p}}}(\text{cos} {\mathrm{\omega }}_1\mathit{t}+\frac{\text{sin} {\mathrm{\omega }}_1\mathit{t}}{2{\mathrm{\omega }}_1{\mathrm{\tau }}_{\mathrm{p}}}\left)\right]$$ (4)

Parameters in Eq. 4 are the same as those in Eq. 1.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/1/eaao0773/DC1

Supplementary Materials and Methods

fig. S1. Sorting of gold nanoparticles using conventional optical chromatography.

fig. S2. Simulation of temperature on gold nanoparticles in the flow stream.

fig. S3. Tuning of trapping stiffness by coordinating laser power and flow velocity.

fig. S4. Determination of the refractive indices by fitting the spectra.

fig. S5. Micrograph of the optofluidic chip.

fig. S6. Calculation of optical extinction forces in water.