Accelerated 3D Multispectral MRI with Robust Principal Component Analysis for Separation of On and Off-resonance Signals

Abstract

Purpose

To enable highly accelerated distortion-free MRI near metal by separating on-and off-resonance to exploit the redundancy of slice-phase encoding for the dominant on-resonance component.

Methods

Multispectral MRI techniques resolve off-resonance distortions by a combination of limited excitation bins and additional encoding. Inspired by robust principal component analysis, a novel compact representation of multispectral images as a sum of rank-one and sparse matrices corresponding to on- and off-resonance respectively is described. This representation is used in a calibration-free and model-free reconstruction for data with an undersampling pattern that varies between bins. Retrospective undersampling was used to compare the proposed reconstruction and bin-by-bin compressed sensing. Hip images were acquired in 8 patients with standard and prospectively undersampled 3D MSI, and image quality was evaluated by two radiologists on a 5-point scale.

Results

Experiments with retrospective undersampling showed that the enhanced sparsity afforded by the separation greatly reduces reconstruction errors and artifacts. Images from prospectively undersampled MSI offered 2.6–3.4-fold (18–24-fold overall) acceleration compared to standard MSI with parallel imaging and partial-Fourier acceleration with equivalence in all qualitative assessments within a tolerance of one point (P < 0.004).

Conclusion

3D MSI can be highly accelerated by varying undersampling between bins and separating on- and off-resonance.

Introduction

3D multispectral imaging (MSI) techniques that use slice phase encoding correct most distortion in MRI near metallic implants. In slice encoding for metal artifact correction (SEMAC) (1), 2D slices are excited and imaged with 3D phase encoding to resolve slice distortion induced by off-resonance, while in-plane distortion is corrected using a view-angle tilting (VAT) technique (2). Although a frequency-selective approach, multi-acquisition variable-resonance image combination (MAVRIC) (3), can also provide distortion-free images near metal, SEMAC and the MAVRIC-SEMAC hybrid (4), use spatially-selective excitation to limit the required amount of phase encoding and reduce scan time (5). In 3D MSI, a bin refers to one of multiple excited volumes (e.g. 2D slices or frequency offsets) that are encoded in 3D and combined to form a volumetric image with reduced distortion. The additional bin dimension required to resolve metal-induced slice distortion results in significantly longer scan times than 2D or 3D fast spin echo techniques not offering metal artifact suppression.

Most existing methods for constrained 3D MSI offer approximately twofold acceleration and are limited as they do not exploit the redundancy between bins (6–9). One approach has been proposed to exploit the redundancy between bins in 3D MSI methods based on slice phase encoding, and it explicitly represents the nonlinear relationship between quantitative parameters (e.g. magnetization, field map, profile width) and undersampled k-space data (10). However, model-based reconstruction can be less robust due to modeling errors that are specific to sequence parameters and faces a challenging non-convex optimization problem. Existing methods also do not exploit the redundancy of slice phase encoding associated with the dominant on-resonance signal. Other work has exploited the spatial distribution of off-resonance in MAVRIC using a calibration procedure across bins but has limited generality (11).

A second challenge is to effectively combine complementary acceleration methods. Signal loss from field-inhomogeneity-related dephasing is reduced in 3D MSI with spin echo sequences (FSE, TSE, RARE), which produce images with slow phase variation and thus are typically accelerated with partial Fourier. Parallel imaging offers additional acceleration, but estimating coil sensitivities in 3D MSI is challenging, and robust data-driven parallel imaging is generally required (12). However, the required calibration for parallel imaging and partial Fourier introduces significant overhead (≈ 6.5% of fully-sampled scan time), as through-plane resolution is often limited (e.g. 24 slices), and to reduce these requirements, methods have been proposed using external calibration (13). Existing acceleration methods have not demonstrated their efficacy in combination with both parallel imaging and partial Fourier reconstruction.

This work first addresses the challenges of partial Fourier and parallel imaging with the use of a novel calibration-free technique and a flexible optimization framework. With these tools, a novel calibration-free and model-free technique to accelerate 3D MSI is proposed to exploit the redundancy of slice-phase encoding for the dominant on-resonance signal. Inspired by robust principal component analysis (14) (RPCA), our technique is based on a compact representation of multispectral images as a sum of rank-one and sparse matrices corresponding to on- and off-resonance signals. The representation is data-dependent, making it independent of many sequence parameters, and it relies only on the sparsity of off-resonance and signal separability of the on-resonance signal. It is also built on an optimization framework that enables integration with other constraints such as parallel imaging and partial Fourier acceleration.

Theory

Image model

We first describe the MRI signal in 3D MSI based on slice phase encoding. We refer to excited slices as “bins.” The excited signal in a voxel x, y, z and bin b can be written

$$s(x,y,z,b)=RF(\mathrm{\Delta }f(x,y,z)+\frac{\gamma }{2\pi }{G}_{z}z-f_b)s_0(x,y,z)$$ (1)

where s₀(x, y, z) is the signal at voxel (x, y, z), and $RF(\frac{\gamma }{2\pi }{G}_{z}z-f_b)$ is the RF profile weighting for bin b with frequency offset f_b, G_z is the slice select gradient strength, and γ is the Larmor frequency.

Consider a decomposition of the RF profile as a linear combination of the bin-profile from on-resonance and a residual from off-resonance terms of the form

$$RF(\mathrm{\Delta }f(x,y,z)+\frac{\gamma }{2\pi }{G}_{z}z-f_b)=\underset{\text{on}-\text{resonance}}{\underbrace{R{F}_0(\frac{\gamma }{2\pi }{G}_{z}z-f_b)}}+\underset{\text{off}-\text{resonance}}{\underbrace{\delta RF(x,y,z,b)}}$$ (2)

For δRF to represent only off-resonance, additional constraints must be specified that make the decomposition unique. Multiple choices such as sparsity constraints on δRF are possible and will be described subsequently. Substituting this into Eq. 1 and defining e(x, y, z, b) = δRF(x, y, z, b)s₀(x, y, z) yields

$$s(x,y,z,b)=\underset{\text{function}\text{of}z,b}{\underbrace{R{F}_0(\frac{\gamma }{2\pi }{G}_{z}z-f_b)}}\underset{\text{function}\text{of}x,y,z}{\underbrace{s_0(x,y,z)}}+\underset{\text{sparse}\text{off}-\text{resonance}}{\underbrace{e(x,y,z,b)}}$$ (3)

At a fixed z, the on-resonance signal can be expressed as the product of a function of b and a function of x, y. On-resonance bin profiles are spanned by RF₀, and in the presence of metal, off-resonance induces a sparse error. Rather than explicitly representing RF₀, our approach will be to model only the separability expressed by the first term in Eq. 3 and effectively derive the on-resonance bin profile from the data.

We now describe Eq. 3 in terms of matrix constructions. For a spatial location z ∈ {1, 2, … , N_z}, define the Casorati matrix

$${\mathbf{C}}_{\mathbf{z}}=\left[\begin{array}{cccc}{s}_{z,1}& s_{z,2}& \dots & s_{z,N_b}\end{array}\right],$$ (4)

where s_z,b denotes a column vector consisting of all elements of the array s extracted at slice z and bin b ∈ {1, 2, … , N_b}. Due to the separability of Eq. 3 at each z, each C_z is a rank 1 matrix in the absence of off-resonance, which corresponds to no out-of-slice excitation. Metal implants only affect a small region of space in the overall imaging volume, and thus only a small subset of the rows of C_z. Under the assumption that C_z is rank 1, on- and off-resonance can be separated by solving the following minimization problem

$$\begin{array}{ll}\underset{{\mathbf{L}}_{\mathbf{z}},{\mathbf{S}}_{\mathbf{z}}}{\text{minimize}}\hfill & J_L({\mathbf{L}}_{\mathbf{z}})+J_S({\mathbf{S}}_{\mathbf{z}})\hfill \\ \text{subject}\text{to}\hfill & {\mathbf{C}}_{\mathbf{z}}={\mathbf{L}}_{\mathbf{z}}+{\mathbf{S}}_{\mathbf{z}},\hfill \end{array}$$ (5)

where J_L and J_S are penalties encoding properties of the on-resonance and off-resonance signals. One choice of J_L is a nonconvex regularizer encoding the z-dependent rank-one constraint:

$$J_L({\mathbf{L}}_{\mathbf{z}})=\{\begin{array}{ll}\infty ,\hfill & \text{rank}({\mathbf{L}}_{\mathbf{z}})>1\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (6)

Alternatively, the rank constraint can be replaced by its convex envelope, the nuclear norm. Another choice of J_S is a sparsity-inducing penalty such as an ℓ₁-norm, which is used in robust principal component analysis (RPCA) (14, 15).

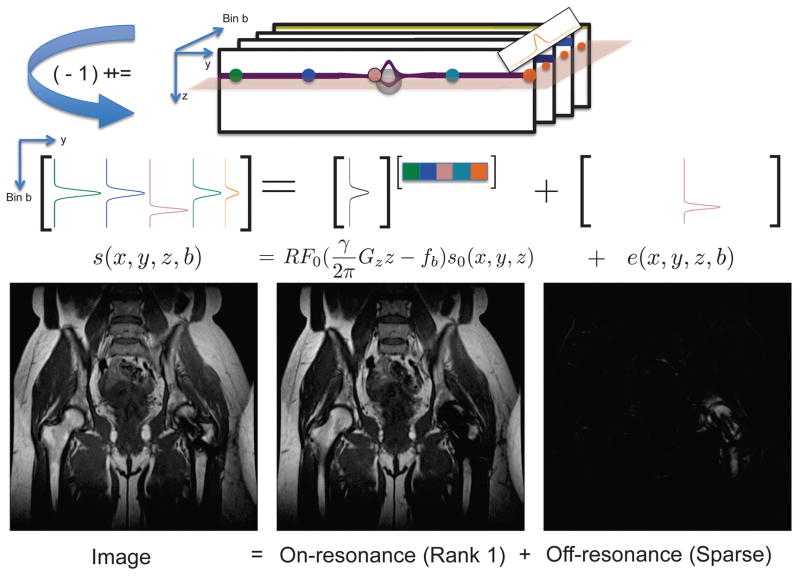
Although computing the decomposition via Eq. 5 necessitates an iterative optimization procedure in general, one exception is the combination of J_L given by Eq. 6 and the choice of $J_S({\mathbf{S}}_{\mathbf{z}})={\Vert {\mathbf{S}}_{\mathbf{z}}\Vert }_F^2$, the Frobenius norm. In this case, classical Principal Component Analysis (PCA) solves Eq. 5 exactly using the singular value decomposition. The result from PCA is shown for an MSI dataset in Figure 1. The first principal component contains 93% of the energy, which appears away from metal, and the residual appears near the metal where the off-resonance is present.

Figure 1.

3D MSI bin images can be analyzed at each z location by constructing matrices with bin profiles mapping to columns. The first principal component corresponds to onresonance signal (93% of the energy) spanned by the bin profile RF₀, and the residual off-resonance signal exhibits sparsity.

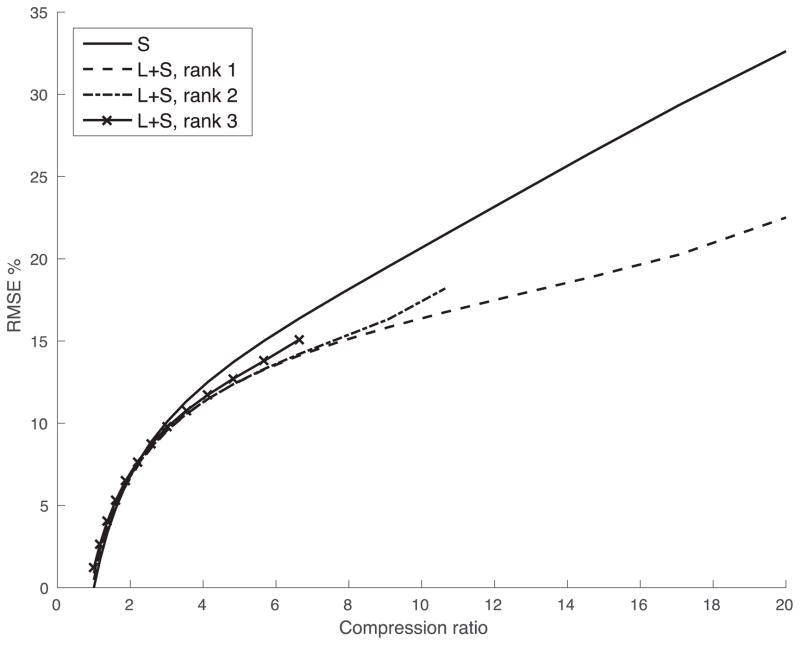
The energy compaction provided by PCA can also be seen from rate-distortions plots showing root-mean-squared-error vs. compression ratio. Plots were generated with the method of (16) to the images in Figure 1. To perform data compression of C_z matrices with L_z + S_z at a compression ratio of C, L_z matrices were obtained by truncating the SVD to rank 1, as in Figure 1, 2, and 3, and S_z were obtained from subtracting L_z from C_z and retaining only the largest n/C−n_L voxels, where n is the number of voxels in the image, n_L = N_zr(N_b+N_y−r) and r is the rank of all C_z matrices. Compression using the sparse model was performed with r = 0 (i.e. thresholding the image). The improved rate-distortion performance of a rank-one-plus-sparse model shown in Figure 2 suggests that it most compactly represents the images and has potential to allow acceleration factors.

Figure 2.

Rate-distortion curves showing RMSE vs compression ratio for a hip implant image using sparsity of the C_z matrices and low rank + sparse components. Low rank + sparse compression ratios were computed with trunction of 1, 2, and 3 singular values of C_z. The highest efficiency was achieved with rank 1, corresponding to a single dominant resonance frequency. This high compressibility is expected to allow higher undersampling factors.

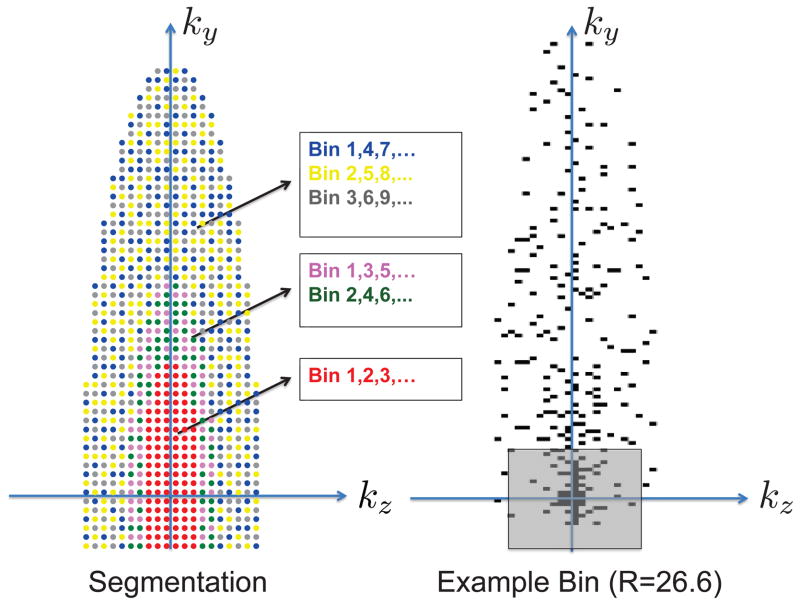
Figure 3.

Variable-density complementary Poisson-disc sampling is used to segment annular regions of the phase encode plane into sample distributions with minimum spacing in k_y-k_z-bins space. a: Colored dots show sample locations acquired within an elliptical region, each color corresponding to a subset of bins in which the sample is acquired. Toward the outer annular regions of k-space, higher undersampling may be used by acquiring each sample in a smaller subset of the bins. b: block dots indicate acquired samples and the sizes of regions were chosen to achieve an overall reduction factor of 26.6. The shaded square indicates what would be a fully-sampled calibration region.

Although classical PCA shows that the sparsity of off-resonance can be observed in images, its extension to reconstruction from undersampled data must make the a priori assumption sparsity of the off-resonance with the use of a sparsity-inducing penalty for J_S. These assumptions must also be coupled with parallel imaging and partial Fourier acceleration, and to provide the necessary framework, a calibration-free approach is first introduced.

Calibration-free Phase-constrained Parallel Imaging

Calibration-free parallel imaging has potential to overcome limitations on the sampling patterns required for highly accelerated 3D MSI and the challenge of accurately estimating coil sensitivity maps from different bins. CLEAR offers computationally inexpensive image-domain-based calibration-free parallel imaging (17).

The partial Fourier acquisitions used in 3D MSI conventionally require low-resolution calibration to demodulate a slowly-varying image phase. Due to the nature of the image-domain approach of CLEAR and lack of calibration data, it is necessary to encourage slow phase variation in the solution while maintaining low computational expense. To achieve this, we modify the matrix construtions in CLEAR as follows.

Let an image at channel c ∈ {1, … , N_C} be represented by the vector X_c and concatenate these vectors in the matrix

$$\mathbf{X}=\left[\begin{array}{cccc}{\mathbf{X}}_{\mathbf{1}}& {\mathbf{X}}_{\mathbf{2}}& \cdots & {\mathbf{X}}_{{\mathbf{N}}_{\mathbf{C}}}\end{array}\right]$$ (7)

Let S_c be the vectorized sensitivity of channel c and S be the concatenation

$$\mathbf{S}=\left[\begin{array}{cccc}{\mathbf{S}}_{\mathbf{1}}& {\mathbf{S}}_{\mathbf{2}}& \cdots & {\mathbf{S}}_{{\mathbf{N}}_{\mathbf{C}}}\end{array}\right].$$ (8)

X can be written as X = S diag |X₀|e^i∠X₀, where |X₀| and ∠X₀ are the magnitude and phase of some underlying magnetization X₀. Let R_b be an operator that extracts a small B × B block from a set that uniformly tile the image. Consider the matrix

$${\mathbf{R}}_{\mathbf{b}}\left[\begin{array}{cc}\Re \mathbf{X}& \Im \mathbf{X}\end{array}\right]=\left[\begin{array}{cc}\Re \text{diag}({\mathbf{R}}_{\mathbf{b}}{\mathbf{X}}_{\mathbf{0}}){\mathbf{R}}_{\mathbf{b}}\mathbf{S}& \Im \text{diag}({\mathbf{R}}_{\mathbf{b}}{\mathbf{X}}_{\mathbf{0}}){\mathbf{R}}_{\mathbf{b}}\mathbf{S}\end{array}\right]$$ (9)

$$=\text{diag}({\mathbf{R}}_{\mathbf{b}}\mid {\mathbf{X}}_{\mathbf{0}}\mid ){\mathbf{R}}_{\mathbf{b}}\left[\begin{array}{cc}\text{diag}(cos(\angle {\mathbf{X}}_{\mathbf{0}}))\mathbf{S}& \text{diag}(sin(\angle {\mathbf{X}}_{\mathbf{0}}))\mathbf{S}\end{array}\right].$$ (10)

Analogous to the original CLEAR method, Eq. 9 is shown to be the product of a fullrank matrix and a low-rank matrix ${\mathbf{R}}_{\mathbf{b}}\left[\begin{array}{cc}\text{diag}(cos(\angle {\mathbf{X}}_{\mathbf{0}}))\mathbf{S}& \text{diag}(sin(\angle {\mathbf{X}}_{\mathbf{0}}))\mathbf{S}\end{array}\right]$, which can be viewed as 2N_C real-valued channel sensitivities. A modifed regularizer is

$$J_C(\mathbf{X})=\lambda \sum _b{\Vert \left[\begin{array}{cc}\Re {\mathbf{R}}_{\mathbf{b}}\mathbf{X}& \Im {\mathbf{R}}_{\mathbf{b}}\mathbf{X}\end{array}\right]\Vert }_{\ast }.$$ (11)

The regularizer is very similar and perhaps equivalent to applying a CLEAR reconstruction to the original and virtual conjugate coils (18), which offers the convenience of working only with complex variables in optimization methods.

To reduce the computation required, a joint coil compression procedure can be used prior to the reconstruction (Supporting Figure S1).

Robust PCA for Accelerated 3D MSI

Taking inspiration from other low-rank-plus-sparse models used in MRI (16, 19), we extend the 3D MSI image model in Eq. 5 to enable reconstruction from undersampled data. Our strategy couples the redundancy associated with on-resonance with calibration-free parallel imaging and partial Fourier with the use of the term given by Eq. 11.

Rank-one and sparse components can be reconstructed from undersampled k-space data Y by solving

$$\underset{\mathbf{L},\mathbf{S}}{\text{argmin}}{\Vert \mathbf{Y}-\mathbf{D}ℱ(\mathbf{L}+\mathbf{S})\Vert }_2^2+\sum _z{J}_L({\mathbf{R}}_{\mathbf{z}}\mathbf{L})+{\lambda }_S{\Vert \mathbf{TS}\Vert }_{2,1}+J_C(\mathbf{L}+\mathbf{S}),$$ (12)

where R_z is the linear operator extracting slice z from the multi-bin image (L_z in Eq. 5), D is a diagonal operator with 1 and 0 on the diagonal at acquired and non-aquired k-space locations respectively, ℱis a Fourier transform, T is a sparsifying transform (e.g. wavelet) applied coil-by-coil, J_L is given by Eq. 6, and the fourth term is the penalty term for phase-constrained parallel imaging described subsequently, and || · ||_2,1 is the mixed ℓ₁ − ℓ₂ norm exploiting joint multicoil sparsity.

Equation 12 couples phase-constrained parallel imaging and the separation into rank-one and sparse components through the use of the fourth term, which requires that L+S satisfy the a priori assumptions of parallel imaging.

If J_L were convex, a globally optimal solution could be obtained with a constrained convex optimization method such as the Alternating Direction Method of Multipliers (ADMM) (20). Here, we take the approach of incorporating the nonconvex regularizer in Eq. 6, which eliminates a regularization parameter for the rank constraint and incorporates knowledge of the rank of C_z. This strategy is described in the Appendix. Although it is closely associated with a convex optimization problem, ADMM can be considered a local optimization method in this case.

Robust PCA for 3D MSI has the advantage of making minimal assumptions. In particular, the separability (rank-one property) of the signal holds independent of the RF slice profiles and value of RF₀. Given that a large number of on-resonance voxels are present at each z-location, exactly knowing RF₀ is not expected to be critical, even in the presence of off-resonance. A simple model is imposed in the spatial and spectral domain for the on-resonance, but not for the off-resonance, which is considerably more challenging to model accurately due to rapid spatial variations of frequency near metal.

Variable density Complementary Poisson-disc sampling

An appropriate sampling strategy should allow partial Fourier acceleration, provide good conditioning for parallel imaging, and ensure that the aliasing pattern varies along bins with noise-like properties. Poisson-disc sampling is one sampling strategy that provides both uniform and random sample distributions and has empirically performed well in joint CS parallel imaging reconstruction. In multispectral imaging, minimum spacing of samples in the bin dimension should be imposed due to overlap in the RF profiles for adjacent bins, similar to dynamic imaging. Here, we use the complementary Poisson-disc (CPD) sampling approach previously proposed for dynamic MRI to segment k-space into sampling patterns that have a minimum distance between samples in k_y − k_z–bin space (21). This approach, illustrated in Figure 3, also allows a flexible choice of sampling density as a function of k-space radius. Other approaches based on minimum inter-sample distance criteria may also be well-suited to 3D MSI (22).

Methods

Initial experiments with retrospective undersampling were used to show the impact of modifying CLEAR for partial-Fourier acquisitions and to compare RPCA-accelerated MSI to a bin-by-bin CS reconstruction. Next, prospectively undersampled 3D MSI was compared to standard MSI in 8 patients, and evaluated by two musculoskeletal radiologists using four image quality criteria.

Calibration-free Parallel Imaging

To demonstrate the impact of extending CLEAR to reconstructing images with slow phase variation, experiments with retrospective undersampling were performed. Images were reconstructed by solving

$$\underset{\mathbf{X}}{\text{minimize}}{\Vert \mathbf{Y}-\mathbf{D}ℱ\mathbf{X}\Vert }_2^2+J(\mathbf{X})$$ (13)

where J(X) was substituted for Eq. 11 and the penalty from CLEAR unmodified for partial Fourier to evaluate the impact of separating real and imaginary parts in a partial Fourier acquisition. The sharpness and spatial frequency content of the two reconstructions were compared to determine if the smooth phase could be demodulated.

Experiments with Retrospective Undersampling

To compare the accuracy of RPCA and bin-by-bin CS and the impact of the additional regularization term used in RPCA to induce the separation, initial experiments with retrospective undersampling were performed with a range of reduction factors. A subject with a hip implant was scanned with standard MSI. Scan parameters were 3T; Coronal; FOV=40×40cm²; TE=14.1ms; TR=4 seconds; radial echo-train ordering; echo-train length (ETL) 20; matrix size = 512×256×24; 2×2 uniform subsampling for autocalibrating parallel imaging; half Fourier; elliptical k-space coverage. Data accelerated with 2 × 2 uniform subsampling was reconstructed with an autocalibrating parallel imaging method (23) to provide a “fully-sampled” set of k-space data, which were retrospectively undersampled using variable density complementary Poisson-disc sampling patterns with partial k_y acceleration. Although “fully-sampled” data had lower SNR due to autocalibrating parallel imaging, this was done to allow clinically feasible scan times.

Data was reconstructed with RPCA Eq. 12 and a bin-by-bin compressed sensing parallel imaging reconstruction performed by solving

$$\underset{\mathbf{X}}{\text{minimize}}{\Vert \mathbf{Y}-\mathbf{D}ℱ\mathbf{X}\Vert }_F^2+{\lambda }_S{\Vert \mathbf{TX}\Vert }_{2,1}+J_C(\mathbf{X}),$$ (14)

which does not include the regularization term used in RPCA to induce the separation.

Non-overlapping 8 × 8 blocks with periodic boundary conditions were used in the penalty term Eq. 11 for both reconstructions. To allow fair comparison with the reference data, the nonacquired half of k-space was cropped after the optimization, and homodyne (24) was applied. Percentage root mean-square-error was used for quantitative image quality comparisons. Typical reconstruction times for bin-by-bin CS and RPCA in CPU-based implementations were 13 minutes and 14 minutes respectively.

Prospectively Undersampled Acquisition

8 patients with total hip replacements were examined using standard and prospectively undersampled MSI acquisitions with slice phase encoding. The same scan parameters were used in experiments with retrospective and prospective undersampling, with the exception of CPD undersampling instead of 2 × 2 autocalibrating parallel imaging for accelerated MSI. Prospectively undersampled MSI used variable density complementary Poisson-disc sampling. Acquisition times were 6–8.8min for standard MSI and 2–3.5 min for accelerated, a 2.6–3.4-fold reduction (18–24-fold overall).

Images from standard and accelerated 3D MSI reconstructed with RPCA and bin-by-bin CS (Eq. 14) were evaluated by two experienced musculoskeletal radiologists using a 5-point scale (1=nondiagnostic, 2=limited, 3=diagnostic, 4=good, 5=excellent) in five categories: 1) overall image quality, 2) sharpness near metal, 3) sharpness away from metal, 4) blockiness/artificial appearance (5=not blocky), 5) signal loss artifacts near metal. A paired Wilcoxon test was used to assess the null hypothesis that accelerated MSI images reconstructed with each method were one point worse than standard MSI images. A P-value of 0.05 used as a criterion of statistical significance. Rejecting the null hypothesis indicates that accelerated images were the same or better than the original within a tolerance of one point.

Interobserver agreement between the readers was analyzed for each criterion using weighted kappa coefficients. Weighted kappa coefficients were interpreted as almost perfect (0.8–1), substantial (0.6–0.8), moderate (0.4–0.6), fair (0.2–0.4), slight (0–0.2), and poor (<0).

Results

Calibration-free reconstruction

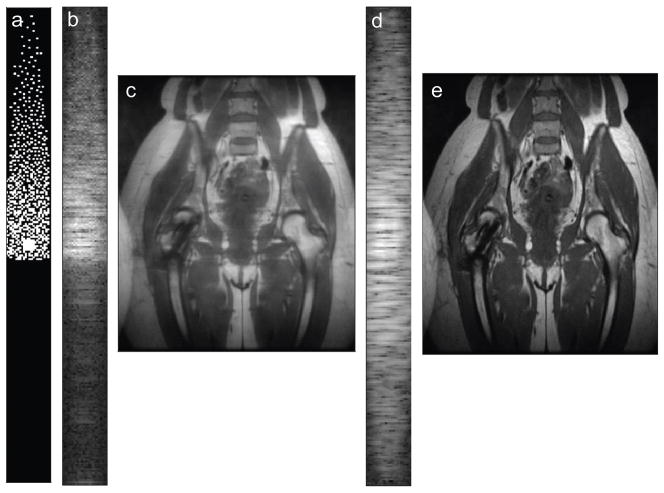
Images reconstructed from undersampled, partial k_y-accelerated data shown in Figure 4 show that CLEAR does not recover both halves of k-space, resulting in blurring. Modifying matrices in the CLEAR penalty to separate real and imaginary parts imposes slow phase variation, resulting in a symmetric recovery.

Figure 4.

Calibration-free parallel imaging reconstruction from partial k-space data does not impose smooth phase variation and does not recover both halves of k-space as seen in the k_y−k_z-plane for the first coil (a), which results in blurring in the image, shown reformatted in the xy-plane (b). Modifying calibration-free parallel imaging to separate real and imaginary parts also imposes smooth phase variation, which allows recovery of both halves of k-space (c), resulting in sharper images (d).

Experiments with Retrospective Undersampling

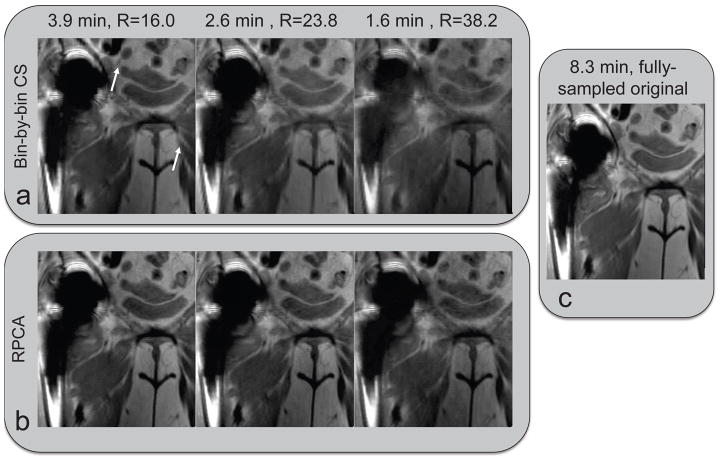
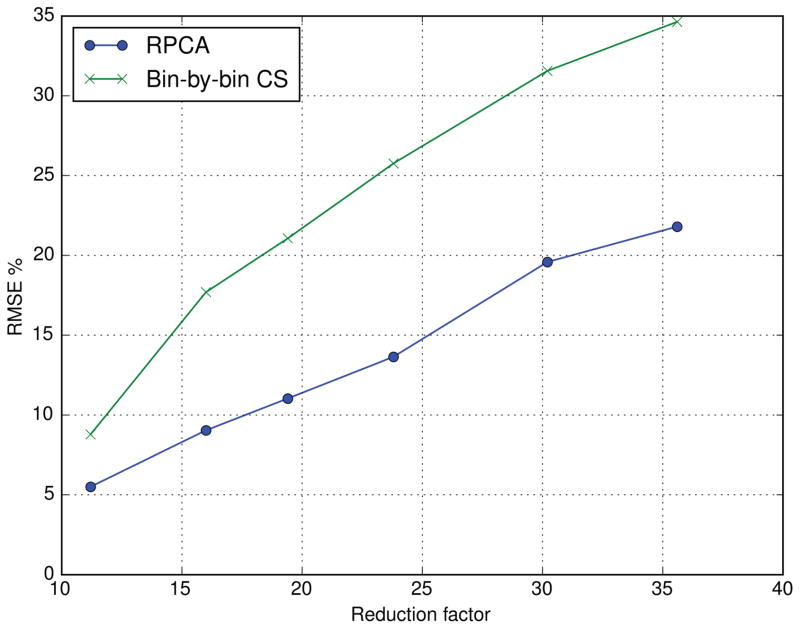
Figure 5 shows coronal images reconstructed with RPCA and bin-by-bin CS from data retrospectively undersampled at reduction factors of 16.0, 23.8, and 38.2. At high acceleration factors, bin-by-bin CS show blurring and an artificial appearance, while RPCA images appear sharper and show SNR loss. Figure 6 quantifies the reconstruction errors, showing that RPCA reconstructions have much lower RMSE over a range of reduction factors, with large differences at high reduction factors.

Figure 5.

In vivo experiment with retrospective undersampling. Data was retrospectively undersampled by factors of 16.0, 23.8, and 38.2 and reconstructed with RPCA and bin-by-bin CS to show the impact of the separation induced by the additional regularization term used in RPCA. RPCA images appear sharp and higher acceleration mostly degrades SNR without other artifacts, while bin-by-bin CS images show blurring and an artificial appearance (white arrows).

Figure 6.

The enhanced sparsity due to the separation of on- and off-resonance in RPCA greatly improves reconstruction accuracy.

Prospectively Undersampled Acquisition

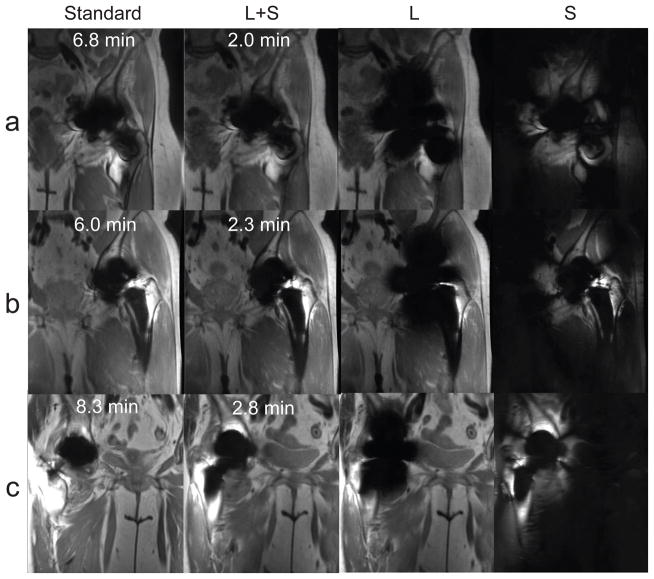
Figure 7 shows images from standard MSI and prospectively undersampled 3D MSI acquisitions reconstructed with RCPA and L and S components. Table 1 shows results of the paired Wilcoxon test. All null hypotheses were rejected, indicating that bin-by-bin CS and RPCA images are both at equivalent to standard MSI images within the tolerance of one point for all qualitative assessments.

Figure 7.

Images reconstructed with RPCA from k-space data with prospective undersampling (R = 18–24).

Table 1.

Image quality scores (average ± standard deviation) from two musculoskeletal radiologists for Standard MSI and accelerated MSI with bin-by-bin compressed sensing and RPCA reconstructions. A one-way paired Wilcoxon test was used to assess the null hypothesis that RPCA and bin-by-bin CS images were at least one point worse than standard MSI images. All null hypotheses were rejected at the 0.05 level.

	Standard MSI	Bin-by-bin CS		RPCA
	Mean ± Std. Dev. (Reader 1/Reader 2)	Mean ± Std. Dev. (Reader 1/Reader 2)	P-value	Mean ± Std. Dev. (Reader 1/Reader 2)	P-value
Image quality	3.5 ± 0.71/3.5 ± 0.50	3.1 ± 0.60/3.1 ± 0.60	0.017	3.2 ± 0.43/3.4 ± 0.48	0.004
Sharpness away from metal	3.6 ± 0.48/3.5 ± 0.50	3.1 ± 0.33/3.0 ± 0.50	0.007	3.5 ± 0.50/3.5 ± 0.50	0.001
Sharpness near metal	3.4 ± 0.48/3.1 ± 0.78	3.0 ± 0.50/3.0 ± 0.71	< 0.001	3.2 ± 0.43/3.0 ± 0.71	0.001
Blockiness/artificial appearance	3.9 ± 0.33/3.8 ± 0.43	3.5 ± 0.71/3.5 ± 0.71	0.009	4.0 ± 0.00/4.0 ± 0.00	< 0.001
Signal loss near metal	3.2 ± 0.66/3.0 ± 0.87	3.4 ± 0.48/3.0 ± 0.71	< 0.001	3.6 ± 0.48/3.4 ± 0.70	< 0.001

Bin-by-bin CS reconstructions had lower mean scores for all qualitative assessments compared to RPCA. Some CS reconstructions showed blocky artifacts that were not seen in RPCA reconstructions (Figure 8). Both RPCA and CS received slightly lower scores for sharpness very close to metal than standard MSI.

Figure 8.

Standard and prospectively accelerated MSI with RPCA and bin-by-bin CS reconstructions are shown. Left (a) and right (b) hips from the same subject are shown. Bin-by-bin CS shows blocky artifacts due to wavelet-sparsity-based regularization of the entire image, while RPCA reconstructions assume only sparsity of the off-resonance.

Table 2 shows the results of interobserver agreement based on weighted kappa coefficients for all evaluation criteria. The two readers had substantial or almost perfect agreement in all categories except for signal loss near metal (fair to moderate agreement). For RPCA, all images received scores of 4 for blockiness/articial appearance, which yields an undefined kappa value.

Table 2.

Interobserver agreement using weighted kappa coefficients between readers 1 and 2 for all five image quality ratings

	Standard MSI	Bin-by-bin CS	RPCA
Image Quality	Substantial	Almost perfect	Substantial
Sharpness Away From Metal	Substantial	Substantial	Almost perfect
Sharpness Near Metal	Substantial	Substantial	Substantial
Blockiness/Artificial Appearance	Substantial	Almost perfect	-
Signal Loss Near Metal	Almost perfect	Moderate	Fair

Discussion

Although 3D MSI methods using slice phase-encoding do not directly encode on and off-resonance separately, this work describes on-resonance in terms of a low-rank property, which can be demonstrated using classical PCA (Figure 1). Off-resonance can be characterized as a sparse error. Effects such as flip angle modulation, T2 decay, and the presence of water and fat may not be represented by a single bin profile shape. However, a rank-one-plus-sparse representation may be accurate enough for acceleration.

The theory of RPCA describes two situations under which it fails to separate the two components: 1) the low rank part is sparse in the basis where the sparse part is represented and 2) the sparsity pattern of the sparse part is contained in one column or not sufficiently spread out (14, 25). In the latter case, it may negate the corresponding column of the low rank part without changing its rank. In 3D MSI, L_z may be approximately sparse in the standard basis when there is little slice overlap. However, the separation still works due to the fact that S_z is not an arbitrary sparse matrix and has columns that are not correlated with RF₀. Off-resonance shifts the bin profile relative to RF₀, causing it to not correlate with RF₀ and be represented in S_z. L_z is expected to accurately recover RF₀ as its singular vector, since it represents the majority of columns, resulting in the most sparse S_z. The second situation does not pose a problem, since for the nonzero columns in S_z corresponding to off-resonance voxels, the corresponding columns in L_z should be negated as a voxel could not be both on- and off-resonance.

The rank-one-plus-sparse representation of RPCA is more compact than the sparse representation used in bin-by-bin CS, and this accounts for the reduction in reconstruction errors (Figure 6). The acceleration factors shown in this work are 18 − 24-fold overall and approximately 3-fold compared to standard MSI, which makes use of parallel imaging, partial Fourier, and elliptical k-space coverage to allow acceleration factors of approximately 7 overall. In the absence of off-resonance, acceleration up to the number of bins should be possible. Hip implants have moderate amounts of off-resonance, limiting the achievable acceleration factors to about 3.

While image quality scores indicate equivalence of standard and both accelerated MSI reconstructions, RPCA reconstructions received higher mean scores than CS reconstructions in all categories by both readers and did not show blocky artifacts of ℓ₁-wavelet regularization (Figure 8). Sharpness scores indicated slight blurring in RPCA and CS reconstructions very close to metal. Moderate acceleration factors with balanced sampling requirements for L and S images may be required with greater amounts of off-resonance. Some patients in the study had conventional hip arthroplasties that contain large amounts of off-resonance, and higher acceleration compared to CS is expected when imaging resurfacing hip arthroplasties, smaller implants, or at lower field strengths, where most energy is represented in the L component.

One advantage of the RPCA formulation is that it makes minimal assumptions. The low-rank-plus-sparse image model is not dependent on the slice profiles or their support. Knowing RF₀ and spatial support would not further reduce the number of degrees of freedom in the representation and thus is not expected to yield an improvement. Since S is sparse and L has limited spatial support, a solution with limited spatial support is guaranteed. No assumptions are made about the spatial smoothness in the L component, and so it does not introduce blocky or cartoon-like artifacts seen in ℓ₁-wavelet-based reconstructions. Even near metal, these artifacts do not appear in the S component due to the enhanced sparsity.

The CPD sampling strategy attempts to achieve sampling requirements for L and S. In the absence of off-resonance, the S component is zero, leaving only one bin profile scaling per spatial location, a reduction in dimensionality equal to the number of bins that could potentially be matched in acceleration. In the absence of on-resonance and with L = 0, the reconstruction of S is equivalent to bin-by-bin CS, which is then a natural approach. The additional acceleration in k_z is roughly limited either by the support of S or the number of bins for L. The overall accelerations allow scan times comparable to those of 2D-FSE, suggesting that accelerated 3D MSI may be a competitive alternative.

The study has several limitations. Experiments used data accelerated with autocalibrating parallel imaging, which has lower SNR than prospectively undersampled data, but this was done to allow clinically feasible scan times. As a small pilot study, only 8 patients were included, and further studies in larger patients cohorts are warranted. Only hip replacements were imaged, and most had similar amounts of off-resonance. A variety of metallic implants would help to identify how limits of acceleration depend on the distribution of energy between L and S images. Performance at higher resolution with equivalent scan time should also be assessed and would require further development to overcome readout effects such as VAT-induced blurring.

Conclusion

This work shows that separation of on-resonance and off-resonance signals in 3D MSI can be achieved with a novel approach inspired by robust principal component analysis, allowing acceleration factors well beyond what were previously achievable. The dominant on-resonance signal at each z location can be compactly represented by a rank-one matrix, and the remaining off-resonance signal are considered to be only a sparse error. These representations are independent of almost all sequence parameters, including slice profiles, and only depend on a separability property. The reconstruction allows the use of additional penalties, and we have introduced a calibration-free approach for parallel imaging and partial Fourier acceleration that enables all accelerations to be used simultaneously.

Appendix: Optimization for RPCA

An Alternating Direction Method of Multipliers (ADMM) algorithm can be used to solve Eq. 12. For brevity of the algebraic manipulations performed in solving ADMM’s subproblems, all variables are complex-valued and it is assumed that virtual conjugate coils may be used instead of the term in Eq. 11.

Equation 12 can be rewritten

$$\begin{array}{ll}\underset{\mathbf{L},\mathbf{S}}{\text{minimize}}\hfill & {\Vert \mathbf{Y}-\mathbf{D}ℱ(\mathbf{L}+\mathbf{S})\Vert }_2^2+J_L({\mathbf{Z}}_{\mathbf{1}})+{\lambda }_S{\Vert {\mathbf{Z}}_{\mathbf{2}}\Vert }_{2,1}+J_{\text{CLEAR},1}({\mathbf{Z}}_{\mathbf{3}})\hfill \\ \text{subject}\text{to}\hfill & {\mathbf{Z}}_{\mathbf{1}}=\mathbf{L},{\mathbf{Z}}_{\mathbf{2}}=\mathbf{TS},{\mathbf{Z}}_{\mathbf{3}}=\mathbf{L}+\mathbf{S}.\hfill \end{array}$$ (15)

The Augmented Lagrangian for Eq. 15 is

$${ℒ}_{\rho }(\mathbf{L},\mathbf{S},{\mathbf{Z}}_{\mathbf{1}},{\mathbf{Z}}_{\mathbf{2}},{\mathbf{Z}}_{\mathbf{3}},{\mathbf{U}}_{\mathbf{1}},{\mathbf{U}}_{\mathbf{2}},{\mathbf{U}}_{\mathbf{3}})={\Vert \mathbf{Y}-\mathbf{D}ℱ(\mathbf{L}+\mathbf{S})\Vert }_2^2+J_L({\mathbf{Z}}_{\mathbf{1}})+{\lambda }_S\Vert {\mathbf{Z}}_{\mathbf{2}}\Vert +J_{\text{CLEAR},1}({\mathbf{Z}}_{\mathbf{3}})$$ (16)

$$+\rho /2({\Vert \mathbf{L}-{\mathbf{Z}}_{\mathbf{1}}+{\mathbf{U}}_{\mathbf{1}}\Vert }_2^2+{\Vert \mathbf{TS}-{\mathbf{Z}}_{\mathbf{2}}+{\mathbf{U}}_{\mathbf{2}}\Vert }_2^2+{\Vert \mathbf{L}+\mathbf{TS}-{\mathbf{Z}}_{\mathbf{3}}+{\mathbf{U}}_{\mathbf{3}}\Vert }_2^2$$ (17)

An ADMM algorithm (Algorithm 1) can be used to minimize Eq. 15.

Algorithm 1.

ADMM-RPCA

while stopping criteria false do

Lk+1, Sk+1 ← argminLS ℒ_(L, S, Z1k, Z2k, Z3k, U1k, U2k, U3k)

Z1k+1 ← argminZ1 ℒ_(Lk+1, Sk+1, Z1, Z2k, Z3k, U1k, U2k, U3k)

Z2k+1 ← argminZ2 ℒ_(Lk+1, Sk+1, Z1k, Z2, Z3k, U1k, U2k, U3k)

Z3k+1 ← argminZ3 ℒ_(Lk+1, Sk+1, Z1k, Z2k, Z3, U1k, U2k, U3k)

U1k+1 ← U1k + Lk+1 − Z1k+1

U2k+1 ← U2k + TSk+1 − Z2k+1

U3k+1 ← U3k + Lk+1 + Sk+1 − Z3k+1

end while

return L, S

The subproblem required to compute the L, S-update can be simplified to

$${\mathbf{L}}^{k+1},{\mathbf{S}}^{k+1}\leftarrow arg\underset{\mathbf{L},\mathbf{S}}{min}{ℒ}_{\rho }(\mathbf{L},\mathbf{S},{{\mathbf{Z}}_{\mathbf{1}}}^k,{{\mathbf{Z}}_{\mathbf{2}}}^k,{{\mathbf{Z}}_{\mathbf{3}}}^k,{{\mathbf{U}}_{\mathbf{1}}}^k,{{\mathbf{U}}_{\mathbf{2}}}^k,{{\mathbf{U}}_{\mathbf{3}}}^k),$$ (18)

$$\leftarrow {\mathbf{H}}^{-\mathbf{1}}\left[\begin{array}{l}{ℱ}^H\mathbf{Y}+\rho ({{\mathbf{Z}}_{\mathbf{1}}}^k+{{\mathbf{Z}}_{\mathbf{3}}}^k+{{\mathbf{U}}_{\mathbf{1}}}^k+{{\mathbf{U}}_{\mathbf{3}}}^k)\hfill \\ {ℱ}^H\mathbf{Y}+\rho ({{\mathbf{Z}}_{\mathbf{2}}}^k+{{\mathbf{Z}}_{\mathbf{3}}}^k+{{\mathbf{U}}_{\mathbf{2}}}^k+{{\mathbf{U}}_{\mathbf{3}}}^k)\hfill \end{array}\right],$$ (19)

where

$$\mathbf{H}=\left[\begin{array}{c}\mathbf{I}\\ \mathbf{I}\end{array}\right]{ℱ}^H\mathbf{D}ℱ\left[\begin{array}{cc}\mathbf{I}& \mathbf{I}\end{array}\right]+\rho \left[\begin{array}{cc}2\mathbf{T}& \mathbf{I}\\ \mathbf{I}& \mathbf{I}+{\mathbf{T}}^H\mathbf{T}\end{array}\right]$$ (20)

$$={\mathbf{I}}_{\mathbf{2}}\otimes {ℱ}^H\left[\begin{array}{c}\mathbf{I}\\ \mathbf{I}\end{array}\right]\mathbf{D}\left[\begin{array}{cc}\mathbf{I}& \mathbf{I}\end{array}\right]{\mathbf{I}}_{\mathbf{2}}\otimes ℱ+\rho \left[\begin{array}{cc}2\mathbf{I}& \mathbf{I}\\ \mathbf{I}& \mathbf{I}+{\mathbf{T}}^H\mathbf{T}\end{array}\right]$$ (21)

When T is unitary,

$${\mathbf{H}}^{-1}={\mathbf{I}}_{\mathbf{2}}\otimes {ℱ}^H{(\left[\begin{array}{c}\mathbf{I}\\ \mathbf{I}\end{array}\right]\mathbf{D}\left[\begin{array}{cc}\mathbf{I}& \mathbf{I}\end{array}\right]+\rho \left[\begin{array}{cc}2\mathbf{I}& \mathbf{I}\\ \mathbf{I}& 2\mathbf{I}\end{array}\right])}^{-1}{\mathbf{I}}_{\mathbf{2}}\otimes ℱ$$ (22)

Expressing the matrix D as a block matrix via the permutation P,

$$\mathbf{D}={\mathbf{P}}^T\left[\begin{array}{cc}\mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]\mathbf{P}$$ (23)

yields

$${\mathbf{H}}^{-1}={\mathbf{I}}_{\mathbf{2}}\otimes {ℱ}^H{(\left[\begin{array}{c}\mathbf{I}\\ \mathbf{I}\end{array}\right]P^T\left[\begin{array}{cc}\mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}\end{array}\right]\mathbf{P}\left[\begin{array}{cc}\mathbf{I}& \mathbf{I}\end{array}\right]+\rho \left[\begin{array}{cc}2\mathbf{I}& \mathbf{I}\\ \mathbf{I}& 2\mathbf{I}\end{array}\right])}^{-1}{\mathbf{I}}_{\mathbf{2}}\otimes ℱ$$ (24)

$$={\mathbf{I}}_{\mathbf{2}}\otimes {ℱ}^H{({\mathbf{I}}_{\mathbf{2}}\otimes {\mathbf{P}}^T\left[\begin{array}{cccc}\mathbf{I}& \mathbf{0}& \mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{I}& \mathbf{0}& \mathbf{I}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}& \mathbf{0}\end{array}\right]{\mathbf{I}}_{\mathbf{2}}\otimes \mathbf{P}+\rho \left[\begin{array}{cc}2\mathbf{I}& \mathbf{I}\\ \mathbf{I}& 2\mathbf{I}\end{array}\right])}^{-1}{\mathbf{I}}_{\mathbf{2}}\otimes ℱ$$ (25)

$$={\mathbf{I}}_{\mathbf{2}}\otimes {ℱ}^H{\mathbf{P}}^T{\left[\begin{array}{cccc}(1+2\rho )\mathbf{I}& \mathbf{0}& (1+\rho )\mathbf{I}& \mathbf{0}\\ \mathbf{0}& 2\rho \mathbf{I}& \mathbf{0}& \rho \mathbf{I}\\ (1+\rho )\mathbf{I}& \mathbf{0}& (1+2\rho )\mathbf{I}& \mathbf{0}\\ \mathbf{0}& \rho \mathbf{I}& \mathbf{0}& 2\rho \mathbf{I}\end{array}\right]}^{-1}{\mathbf{I}}_{\mathbf{2}}\otimes \mathbf{P}ℱ$$ (26)

The block matrix in Eq. 26 can be expressed as a block diagonal matrix via a permutation

$$\mathbf{Q}\left[\begin{array}{cccc}(1+2\rho )\mathbf{I}& \mathbf{0}& (1+\rho )\mathbf{I}& \mathbf{0}\\ \mathbf{0}& 2\rho \mathbf{I}& \mathbf{0}& \rho \mathbf{I}\\ (1+\rho )\mathbf{I}& \mathbf{0}& (1+2\rho )\mathbf{I}& \mathbf{0}\\ \mathbf{0}& \rho \mathbf{I}& \mathbf{0}& 2\rho \mathbf{I}\end{array}\right]={\mathbf{Q}}^T\left[\begin{array}{ll}\mathbf{I}\otimes \left[\begin{array}{cc}1+2\rho & 1+\rho \\ 1+\rho & 1+2\rho \end{array}\right]& \mathbf{0}\\ \mathbf{0}& \mathbf{I}\otimes \left[\begin{array}{cc}2\rho & \rho \\ \rho & 2\rho \end{array}\right]\end{array}\right]\mathbf{Q}$$

Inversion of the block matrix can be expressed in terms of Q as

$${({\mathbf{Q}}^T\left[\begin{array}{ll}\mathbf{I}\otimes \left[\begin{array}{cc}1+2\rho & 1+\rho \\ 1+\rho & 1+2\rho \end{array}\right]& \mathbf{0}\\ \mathbf{0}& \mathbf{I}\otimes \left[\begin{array}{cc}2\rho & \rho \\ \rho & 2\rho \end{array}\right]\end{array}\right]\mathbf{Q})}^{-1}={\mathbf{Q}}^T\left[\begin{array}{ll}\frac{1}{3{\rho }^2+4\rho }\mathbf{I}\otimes \left[\begin{array}{cc}1+2\rho & -1-\rho \\ -1-\rho & 1+2\rho \end{array}\right]& \mathbf{0}\\ \mathbf{0}& \frac{1}{3{\rho }^2}\mathbf{I}\otimes \left[\begin{array}{cc}2\rho & -\rho \\ -\rho & 2\rho \end{array}\right]\end{array}\right]\mathbf{Q}$$ (27)

The update is performed by applying one of the two 2×2 matrix inverses in Eq. 27 depending on whether the phase encode location is acquired.

Updates for Z_i reduce to application of the proximal operators:

$${{\mathbf{Z}}_{\mathbf{1}}}^{k+1}={\text{prox}}_{1/\rho J_L}({\mathbf{L}}^{k+1}+{{\mathbf{U}}_{\mathbf{1}}}^k)$$ (28)

$${{\mathbf{Z}}_{\mathbf{2}}}^{k+1}={\text{prox}}_{{\lambda }_S/\rho {\Vert ·\Vert }_1}(\mathbf{T}{\mathbf{S}}^{k+1}+{{\mathbf{U}}_2}^{k+1})$$ (29)

$${{\mathbf{Z}}_{\mathbf{3}}}^{k+1}={\text{prox}}_{1/\rho J_{\text{CLEAR}}(·)}({\mathbf{L}}^{k+1}+{\mathbf{S}}^{k+1}+{{\mathbf{U}}_{\mathbf{3}}}^{k+1}),$$ (30)

where prox_f(·) denotes the proximal operator for the function f(·), C_z-by-C_z low rank approximation, element-wise soft thresholding and block-wise singular value soft thresholding for Z₁, Z₂, and Z₃ respectively.