Improving Registration Robustness for Image-Guided Liver Surgery in a Novel Human-to-Phantom Data Framework

Abstract

In open image-guided liver surgery (IGLS), a sparse representation of the intraoperative organ surface can be acquired to drive image-to-physical registration. We hypothesize that uncharacterized error induced by variation in the collection patterns of organ surface data limits the accuracy and robustness of an IGLS registration. Clinical validation of such registration methods is challenged due to the difficulty in obtaining data representative of the true state of organ deformation. We propose a novel human-to-phantom validation framework that transforms surface collection patterns from in vivo IGLS procedures (n = 13) onto a well-characterized hepatic deformation phantom for the purpose of validating surface-driven, volumetric nonrigid registration methods. An important feature of the approach is that it centers on combining workflow-realistic data acquisition and surgical deformations that are appropriate in behavior and magnitude. Using the approach, we investigate volumetric target registration error (TRE) with both current rigid IGLS and our improved nonrigid registration methods. Additionally, we introduce a spatial data resampling approach to mitigate the workflow-sensitive sampling problem. Using our human-to-phantom approach, TRE after routine rigid registration was 10.9 ± 0.6 mm with a signed closest point distance associated with residual surface fit in the range of ±10 mm, highly representative of open liver resections. After applying our novel resampling strategy and improved deformation correction method, TRE was reduced by 51%, i.e., a TRE of 5.3 ± 0.5 mm. This paper reported herein realizes a novel tractable approach for the validation of image-to-physical registration methods and demonstrates promising results for our correction method.

I. Introduction

IMAGE-GUIDED liver surgery (IGLS) aims to improve surgical precision by providing intraoperative guidance of instrumentation. True IGLS requires (1) full volumetric preoperative imaging, (2) the ability to localize instrumentation in physical space, (3) a method of image-to-physical space registration, (4) a method to correct for intra-procedural organ changes, and (5) a display of instrumentation position in accordance to preoperative imaging. A problem central to IGLS is the task of registration in the soft-tissue environment; where organ shape changes that occur between preoperative imaging and intraoperative presentation create significant challenges to the guidance environment. The overall utility of IGLS methods fundamentally hinges on the accuracy of the image-to-physical space mapping. In addition and not often discussed, there is a fundamental challenge that consists of acquiring sufficient extent and quality of geometric data such that guidance updates are accurate while not compromising the workflow of procedural care. IGLS embodies this demanding and often vexing problem.

With respect to IGLS workflow (for both open and laparoscopic indications), it is clear that the anterior surface of the organ and some salient features are routinely available (i.e. falciform ligament and inferior ridges [1], [2]). It is also clear that digitization technologies for acquiring these surfaces are still somewhat limited [3]. Tracked ultrasound imaging is commonly used and allows for major vasculature to be digitized during surgery [4]. With respect to commercial IGLS developments, both surface and ultrasound registration approaches are being pursued. When it comes to surface based registration techniques, these typically rely on an iterative approach with an estimated surface correspondence and also assume that surfaces being registered share a high degree of similarity [5]–[8]. With respect to ultrasound based approaches, these typically rely on local alignments between CT-rendered and ultrasound-identified vasculature. With each of these approaches, of course, alignments can be compromised by deformations from pre-to-intraoperative organ shape changes, respiration, liver mobilization, and resection [9]–[11]. In recognition of this, ongoing efforts have been made towards soft-tissue deformation correction in IGLS using these modalities of geometric data. For example, in [12] an elastic registration technique is used in combination with ultrasound vasculature data to nonrigidly correct for deformations. In our work, we have concentrated on approaches that minimize differences between surfaces extracted from the preoperative imaging and those gathered intraoperatively. Our approaches use patient-specific biomechanical models to nonrigidly align the data [1], [6], and [13] (adding very sparse subsurface data, i.e. tumor centroid location in [13], has also been pursued).

With respect to sparse surface data digitization for IGLS, registration has been performed using manual swabbing with a tracked probe [14], laser-range scanning [5], ultrasound [1], [15], [16], time of flight imaging [17], stereoscopic imaging [18], [19], and conoscopic holographic surface scanning [20]. Recently, we did a comprehensive study comparing registration results using swabbing, laser range scanning, and conoscopic holographic scanning in [21]. While results indicated better performance from non-contact digitization methods, challenges of integration into the operating room still persist which is why manual surface swabbing is still the only commercial IGLS surface-based approach in use today.

Regardless of the sparse-data source, data collection is commonly contingent on the surgeon’s ability to acquire data within a surgical procedure. As a result, variability in density, uniformity, extent, and degree of noise (either from the modality of measurement or physician technique) all affect registration but have received limited study. This is largely due to the extreme challenge of needing extensive bystander acquisition capabilities to assess and record data within the operating room. Going further, the resources for validation precipitate an even more excessive clinical burden, i.e. intraoperative volumetric imaging and a series of consenting patients. The encumbrance of intraoperative volumetric validation, either with partial volume methods such as tracked intraoperative ultrasound [1] or full volumetric imaging methods such as computed tomography or magnetic resonance imaging [15], [22], is considerable and adds impetus for a new way to characterize methods rapidly. Therefore, we present a novel human-to-phantom validation framework which aims to bypass the burden of such cumbersome clinical data acquisition.

In the work presented herein, routine intraoperative patient data associated with conventional IGLS were collected to study the influence of variability in organ surface acquisition. This study has been motivated by the observation of a high degree of variation in the spatial pattern and density of surface data in a series of intraoperative procedural acquisitions (Fig. 1). The aim of this study was to characterize the influence that these variations have on IGLS accuracy using both conventional rigid and our improved nonrigid registration methods. While we report on the characterization of our particular approach, the framework described herein has broader impact by demonstrating how clinical workflow data can be combined with a realistic phantom for rapid methodological prototyping.

Fig. 1.

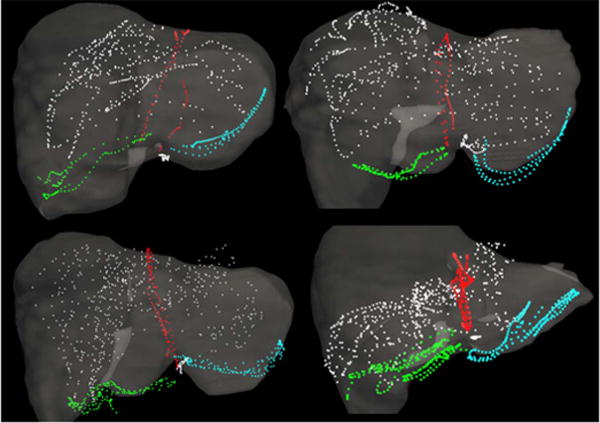
Manual surface swabbing results collected within the Explorer™ Liver navigation system. Digitized surface and feature data are presented for 4 clinical cases following an initial rigid alignment generated by the salient feature registration algorithm of Clements et al. [6]. Data representing the falciform, left inferior ridge, right inferior ridge, and anterior organ surface are presented in red, blue, green, and white respectively.

Briefly described, in the human-to-phantom validation framework, the surface collection patterns of a series of clinical surface data were individually transformed and applied to a well-characterized hepatic deformation phantom designed to have deformations similar to the OR. This allows the replication of multiple independent surface collections while facilitating the measurement of full volumetric shift with CT imaging and distributed CT-visible targets, thus providing ground truth data for accuracy and reproducibility assessment. Such complete and discrete ground-truth data is typically unavailable in clinical data and has become a major obstacle in the quantitative assessment of registration accuracy. In addition, we use the novel framework to assist in designing a spatial data resampling strategy that demonstrates dramatic improvements in both rigid and nonrigid registration results. We conclude by discussing the methods and results of our study in an effort to understand the influence of data collection on registration accuracy in IGLS.

II. Methodology

A. Overview of Experimental Design

The methods of this study are designed to accomplish three goals: first, create a novel human-to-phantom data framework for extensive use in IGLS methodological validation; second, develop a resampling approach which improves the accuracy and variance of IGLS registration methods; third, perform an analysis to systematically study the impact that variations in organ surface data quality have on IGLS registration methods.

B. Patient Data Collection

Patients were consented and enrolled in an ongoing prospective study of deformation correction for IGLS approved by the Memorial Sloan Kettering Cancer Center (MSKCC) Institutional Review Board. Thirteen patients undergoing open liver resection at MSKCC are presented within this study. Prior to surgery, contrast enhanced CT images were acquired of each patient as part of routine clinical management. 3D anatomical models of the liver, tumors, and vasculature were generated using surgical planning software (Scout™ Liver, Analogic Corporation, Peabody, MA). Following this processing, the preoperative 3D model was loaded into a surgical navigation system (Explorer™ Liver, Analogic Corporation, Peabody, MA). During surgery, after organ mobilization, the surgeon manually swabbed anatomical surfaces with an optically tracked stylus. This digitization creates a sparse 3D point cloud representing the organ surface and salient anatomical features. A visualization of intraoperative surface collection is presented in Fig. 1.

C. Phantom Data Collection

Phantom data were acquired consistent with a previously reported study by Rucker et al. [13]. Briefly, a compliant hepatic phantom was created to mimic clinical organ deformation based on our experience in a previously reported 75 patient multi-center clinical trial [23]. The phantom consisted of water, 7% by volume polyvinyl alcohol, and 10% by volume glycerin that was subjected to a 12-hour freeze-thaw cycle to develop stiffness [24]. The phantom incorporated 47 subsurface plastic beads, which served as ground truth target locations. Similarly to clinical cases, a preoperative CT scan of the phantom in an undeformed state was acquired to generate an organ model and to identify target locations. Intra-operative organ deformation was replicated by altering support at the posterior phantom surface (Fig. 2). An intraoperative CT scan of the deformed phantom was captured to acquire the true deformed organ surface, volume, and target locations. Salient anatomical feature regions (falciform ligament and inferior ridges) were designated from the intraoperative CT.

Fig. 2.

The CT segmented preoperative and intraoperative phantom surfaces are presented in red and blue respectively. The differences in surfaces highlights the volumetric deformation undergone in the simulated phantom data.

D. Human-to-Phantom Data Preparation

Thirteen clinically acquired surface datasets (II.B) were applied as collection patterns to the hepatic deformation phantom (II.C) to observe the effect of intraoperative organ surface digitization on registration accuracy. Furthermore, randomized sinusoidal noise was applied to these collection patterns to simulate the natural periodic level of contact that occurs during manual organ swabbing (i.e. compressing into or lifting off the surface) – resulting in easily generated, unique, and realistic digitizations of the intraoperative phantom surface.

The clinical surface data were aligned to the intraoperative phantom data using rigid salient feature weighted registration [6]. This registration aligned the phantom and clinical data according to the salient features, but differences in organ size and extent remained. We should also note that others are also following this approach [25]. Following initial rigid alignment, the finite iterative closest point registration method by Kroon [26] incorporated scale and skew into the optimization of a transformation matrix, providing an affine registration which accounts for differences in data extent and organ size. Following alignment and scaling of the clinical and phantom intraoperative surfaces, the clinical surface data were projected to their closest point on the intraoperative phantom CT, producing thirteen clinically representative surface digitizations of the CT documented deformed phantom surface.

Next, realistic noise was added to the phantom collections along the spatial trajectory associated with the particular clinical swab. To accomplish this, randomized sinusoidal waveforms were generated for each simulated phantom surface and feature designation (Fig. 3). Independent noise was applied in the normal and tangential directions for each data point as follows:

$$\widehat{N}=(\text{sin}(2\pi s{f}_1+{\phi }_1)+a\cdot \mathit{sin}(2\pi s{f}_2+{\phi }_2)+R)\ast \widehat{d}$$ (1)

where $\widehat{N}$ is the vector of applied noise, $\widehat{d}$ defines the normal or tangential directions at each data point, f_i is a randomly assigned low frequency (between 0-10 Hz in qualitative accordance with clinical swabbing), φ_i is a randomly assigned phase shift (between 0–2π), a is a randomly assigned amplitude (between 0–5), and R is uniform pseudorandom noise. Applying smoothly varying noise in the spatial order of clinical collections mimicked the pattern of noise associated with intraoperative data collection. The amplitude of noise was established by curve fitting each clinical data swab and averaging the residual error in the directions normal and tangential to the organ surface. The RMS amplitudes of noise in the normal (0.9 mm) and tangential (1.8 mm) directions were specified by the average noise measured across the whole clinical data set. Each application of random noise to a clinical surface data pattern results in an independent simulated surface digitization of the intraoperative phantom. To ensure adequate characterization, we used this strategy to simulate 50 phantom surface data acquisitions with independent randomized noise added for each of the 13 clinical cases (Fig. 4). With the above process realized, any organ surface data pattern taken intraoperatively could be transformed with noise onto our 3D deformation phantom system, thus allowing for a quantitative assessment of its impact on any proposed registration scheme in the presence of realistic deformations.

Fig. 3.

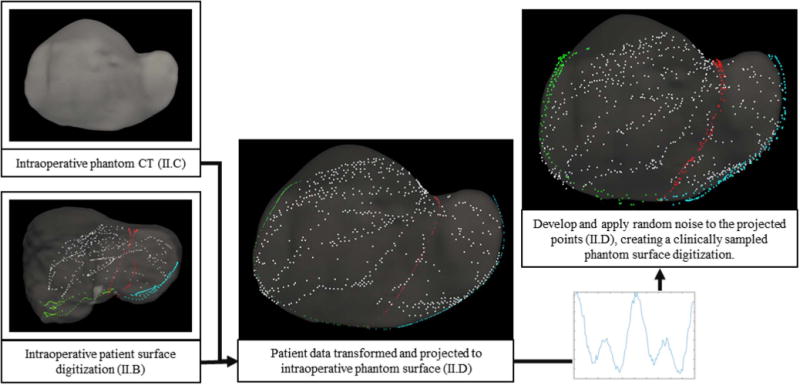
Structure of the proposed human-to-phantom data set presented in flowchart form. Human data is aligned, scaled, and projected onto the intraoperative phantom CT surface. Randomly defined sinusoidal waveforms are generated and applied to the projected data to simulate collection noise. Noise patterns are applied independently to the surface and feature data. The right and center columns serve as examples of surface digitization with and without applied noise.

Fig. 4.

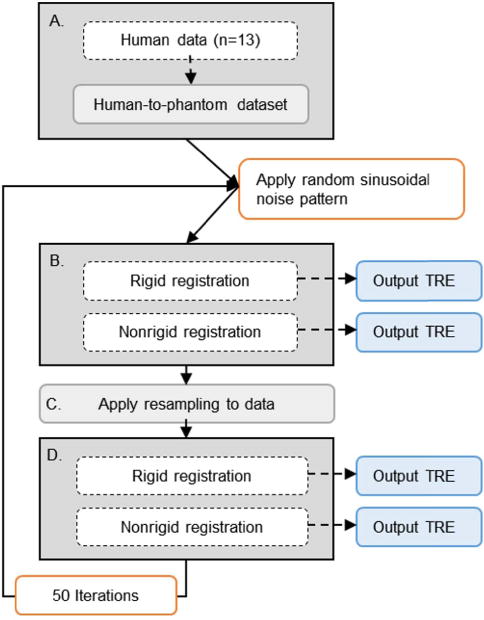
Schematic of the proposed study. For a given clinical case (n = 13), surface data is aligned, scaled, and projected onto the intraoperative phantom CT surface with a randomly determined noise pattern (A). Our rigid and nonrigid registration methods are applied, while quantifying subsurface TRE (B). The simulated surface is then resampled (C) and registrations are recalculated (D). This process is repeated with 50 different applications of noise per clinical case – creating 50 independent surface acquisitions for each of the (n = 13) clinical organ surface digitization patterns.

E. Data Resampling

In our experience with OR-amenable IGLS processes, surface data collection varies with real-world surgeon use. To improve robustness in light of this variability, we propose a resampling approach and test its impact using our novel human-to-phantom framework. To begin, we assume that the anterior organ surface, where the sparse surface data were collected, may be treated as a bounded, continuous, and unique surface of the form:

$$z=f(x,y)$$ (2)

This assumption reduces dimensionality, thus decreasing complexity and computational burden. To improve consistency regardless of initial raw data orientation in Cartesian space, a 3D least squares plane was fit to the raw data and a rigid registration was determined which transforms the least squares plane to the x – y plane by aligning its normal to the z axis. A discrete grid was fit to the transformed raw data using a joint interpolation and approximation method [27]. The approach fits locally to the transformed raw data using barycentric interpolation as follows:

$$f(x,y)={\displaystyle \sum _{i=1}^3{\lambda }_{i}f(x,y_i)}$$ (3)

where the height at a location within the triangular grid, f (x, y), is reconstructed as a linear combination of the heights at the vertices of an encompassing triangle, f (x_i, y_i), weighted by the ratio of area within the triangle, λ_i, where each vertex contributes to the queried location. The approach then regularizes the grid with a discrete approximation of the Laplacian using the finite difference method for a given grid node as follows:

$${\nabla }^{2}f(x,y)=\frac{d^{2}z}{d{x}^2}+\frac{d^{2}z}{d{y}^2}=0$$ (4)

$${\nabla }^{2}f(x,y)\approx \frac{1}{h^2}(f(x-h,y)+f(x+h,y)+f(x,y-h)+f(x,y+h)-4f(x,y))$$ (5)

where f (x, y) is a nodal height value and h is the grid spacing. Next, a weighting scheme was applied which sampled the surface more densely in areas local to the raw surface data. Weighting in this manner increases the influence of well-fit areas of the resampled surface on our nonrigid correction method. The strategy was composed of (1) a sparse set of points set at 5 mm spacing underlying the full extent of the surface and (2) a dense set of points set at 0.25 mm spacing within a specified capture radius, 1 mm, of the raw surface data. Parameter values were established through a parametric sweep. Finally, the fitted surface was trimmed, such that it represents a single region accurately bounded by the outer contour of the raw data, using a dilate-and-fill image processing procedure.

F. Rigid Registration

For the purposes of image-to-physical registration, rigid alignment was determined using a salient feature weighted iterative closest point registration [6], specifically designed for liver anatomy and used in a commercial IGLS system. More specifically, salient feature registration utilizes homologous anatomical features to bias point correspondence estimation at each iteration. The biased weighting scheme preferentially favors alignment of preoperatively designated anatomical features with corresponding intraoperative surface data, producing a robust initial alignment that provides support to successive digitization of the remainder of the organ surface. Correspondence is estimated using a conventional closest point operator. The algorithm provides a coordinate transformation that minimizes residual error between preoperative and intraoperative organ surface data.

G. Nonrigid Registration

With respect to modeling nonrigid behaviors, we employ a linear elastic biomechanical model of the preoperative organ described previously [13]. Large deformations and more sophisticated constitutive models are possible; however, applying a rigid registration followed by smaller nonrigid deformations is a first order deformation correction approach which, when considering localization errors and tracking accuracy, is appropriate. The benefit of a nonlinear corotational finite element formulation (one nonlinear approach for accounting for large deformations) yielded no statistical difference in our previous work [13]. It is likely that geometric and material nonlinearities will be needed in the future as instrumentation integration matures but our present framework does represent a step forward in providing significant localization improvement over rigid registration. In addition, the use of a linear model allows for pre-computation strategies for providing fast intra-operative nonrigid registration for real time use. The patient-specific geometric model assumes that the liver is an isotropic solid described by the 3D Navier-Cauchy equation:

$$\nabla \left(\frac{E}{1(1+v)(1-2v)}\nabla \cdot u\right)+\nabla \cdot \left(\frac{E}{2(1+v)}\nabla u\right)=0$$ (6)

E is Young’s modulus, v is Poisson’s ratio, and u is the displacement vector. We solve the system of partial differential equations (PDE) by applying the Galerkin weighted residual method using linear Lagrange basis functions on tetrahedral finite elements. Displacement boundary conditions are employed on the posterior liver surface to simulate the impact of liver mobilization and packing. On remaining surfaces, the natural stress free boundary condition is employed. Potential posterior displacement surfaces can be designated a priori and allow for pre-computation strategies for fast model correction. We embed this model within a novel nonrigid registration framework. In the surgical setting, the organ is first mobilized from abdominal connective tissue and packed with supportive material for presentation. These changes in support manifest as deformations, i.e. global shape changes, in comparison to the preoperative organ configuration. The algorithm we employ to correct for these deformations is an improved form of the nonrigid registration method introduced by Rucker et al. [13]. The method assumes a predetermined support surface based on operative approach, in this case the posterior surface of the liver. A parameterized posterior displacement field is iteratively computed to minimize residual error between the intraoperatively collected anterior surface data and the deformed model surface. The result is a reconstructed volumetric prediction of the deformed organ based on the preoperative biomechanical model and sparse intraoperative surface data. With respect to modifications to the method presented in Rucker et al. [13], posterior support surfaces were allowed to move only in the direction of the posterior surface normal. In this paper, we employ an improved extension to the posterior surface parameterization to include tangential displacements as well. Thus, the set of parameters used to generate our nonrigid fitting is:

$$P=\{{\overline{c}}_n,{\overline{c}}_{t1},{\overline{c}}_{t2},t_x,t_y,t_z,{\theta }_x,{\theta }_y,{\theta }_z\}$$ (7)

where t_x, t_y, t_z, θ_x, θ_y, θ_z are the traditional translational and rotational components associated with rigid body registration, and ${\overline{c}}_n$, ${\overline{c}}_{t1}$, ${\overline{c}}_{t2}$ are the control parameters for the posterior surface conditions for the normal and the newly added two tangential components. The control parameters are associated with a bivariate polynomial that systematically deploys boundary conditions to the entire support surface in a given iteration. The methodology has incorporated the salient feature weighting throughout and traditional elastic energy constraints for controlled deformations. Following Rucker et al., the Levenberg-Marquardt algorithm was employed to reconstruct the optimal parameter set to fit acquired surface data.

H. Experimental Design

To evaluate the accuracy and robustness of surface based IGLS registration methods as a function of surface collection pattern, density, and noise level, we conducted an extensive study with our novel human-to-phantom IGLS validation framework. An overview of the simulation design is presented in Fig. 4. In this simulation, for each clinical surface collection pattern (i.e. one of the n = 13 cases reported herein), surface data were aligned, scaled, and projected onto the intraoperative phantom CT surface (as described in II.D). For each clinical pattern, 50 distinct surface digitizations were created by temporally applying distinct random sinusoidal noise patterns, resulting in a total of 650 independent, clinically representative digitizations of the intraoperative phantom surface. Our rigid (II.F) and nonrigid (II.G) registration methods were used to determine predictions of the intraoperative subsurface target locations. Our resampling approach (II.E) was applied to the simulated surface collections. Similarly, the resampled data were used to drive rigid and nonrigid registration to form predictions of the intraoperative subsurface target locations. This analysis was repeated with increasing levels of noise (base, 2×, 4×, and 8×). Notably, any surface based registration, rigid or nonrigid, can be evaluated using this novel validation approach while requiring no additional clinical effort.

It is important to emphasize that all simulated surface digitizations of the human-to-phantom data set exist on the same phantom which underwent mock OR deformation documented within a CT imaging unit. Furthermore, subsurface beads embedded within the hepatic phantom and tracked throughout deformation provided true positions of targets for the evaluation of registration accuracy. For this study, target registration error (TRE) serves as the primary measurement of accuracy. Deformed target locations extracted from the mock intraoperative CT serve as the observed, true locations of targets. TRE is calculated as the Euclidean distance between the model predicted and true observed target locations.

The Wilcoxon rank-sum test was used to determine significance in differences between registration results between the 4 categories of results: raw data rigid registration, raw data nonrigid registration, resampled data rigid registration, and resampled data nonrigid registration. The Wilcoxon rank-sum test tested the null hypothesis that the distributions of average TRE for given methods were equivalent with a significance level of α = 0.05.

III. Results

A. Phantom and Resampling Suitability

Clinically acquired organ surface digitizations (i.e. FIG. 5.A) were applied to the hepatic deformation phantom (i.e. FIG 5.B) in an effort to observe the impact that clinically-relevant variation in organ surface digitization has on IGLS registration accuracy and variance. As Fig. 5.B demonstrates, the ability of the proposed method to transform clinically collected surface data as a template for surface acquisition on the hepatic phantom is quite appropriate. In each set shown (left, and right column of Fig. 5.A–B), regional point density and acquisition pattern are preserved from clinical to phantom surface. The base amount of applied noise resulted in measured noise within the simulated surfaces of approximately 1.0 ± 0.7 mm. Fig 5.C shows the resampling treatment of the data from each case using methods described in II.E. The overall fit of the resampled surface to the raw input data had a residual closest point error of 1.5 ± 1.3 mm.

Fig. 5.

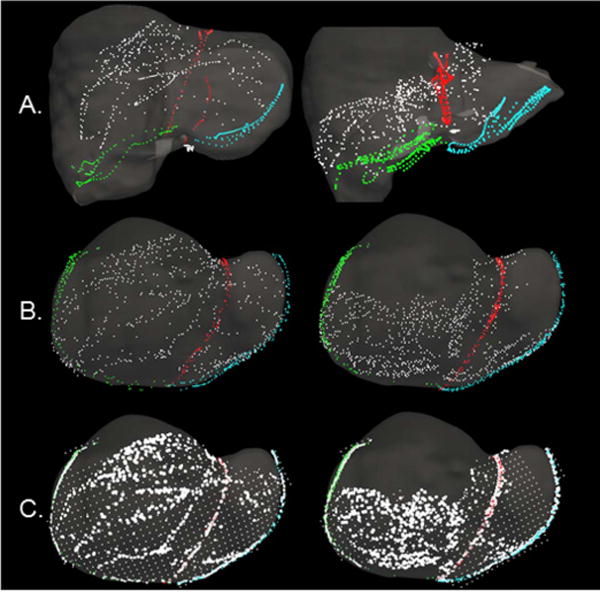
Surface digitizations from two cases are presented. Anterior organ surface, falciform, left inferior ridge, and right inferior ridge data are presented in white, red, blue, and green respectively. (A) Surface data from clinical studies collected with an optically tracked stylus. Surface data are overlaid on the preoperative organ model following rigid registration. (B) Examples of the human-to-phantom data set following translation of the clinical surface data from (A) onto the hepatic deformation phantom – used to simulate clinical collection patterns and sampling. (C) A representation of the spatial data resampling approach applied to the human-to-phantom data in (B). Areas of high density and sparse surface points present as the bright white and gridded white points respectively. For (B) and (C), surface data are overlaid on the intraoperative phantom CT model.

A qualitative analysis of the degree and pattern of deformation within the phantom is presented in Fig. 6. Rigid registration results are displayed for a representative clinical data registration in Fig. 6.A and its hepatic phantom counterpart data in Fig. 6.B. In both, the preoperative derived model surface is color-coded by the signed closest point distance of the rigidly registered intraoperative surface data (note that as phantom data is acquired from CT images, we have access to the entire surface extent). The phantom presents a similar pattern and magnitude of deformation to the clinical case.

Fig. 6.

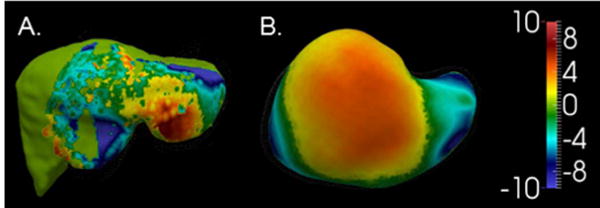
Deformed surfaces from (A) a clinical/human data case and (B) the phantom case are shown. The color map illustrates the observed deformation in each case as the Euclidean distance between the preoperative and intraoperative organ anterior surfaces (in mm) following rigid registration.

B. Registration Error

The objective of this investigation was to characterize the impact that variations in collected organ surface data have on surface based IGLS registration techniques in a clinically-relevant manner. TRE results using both raw and resampled surface acquisitions were compiled following rigid and nonrigid registration. Fig. 7 presents a histogram of the average values of TRE measured from subsurface targets for each case of surface data in our human-to-phantom data set. The (∗) represents the difference between procedural standard and the approach we are proposing. Fig. 8 presents a scatterplot which contrasts the raw data TRE and resampled data TRE for both rigid (blue) and nonrigid (gold) registration methods. With both clusters, we see a shift to the right side of the unity line indicating that the process of resampling serves to reduce target error. Fig. 8 also indicates that nonrigid registration consistently produces lower TRE than rigid registration. For reference, if the resampling method had no effect on the surface data, all points would align along the line of unity. Table I represents the average value of TRE in a case-by-case manner. In the case of both raw and resampled data, nonrigid registration produced significantly lower TRE (p < .001). Rigid registration with resampled data (8.4 ± 0.5 mm) produced significantly lower TRE (p < .001) than rigid registration with raw data (10.9 ± 0.6). Nonrigid registration with resampled data (5.3 ± 0.5 mm) also produced significantly lower TRE (p < .001) than nonrigid registration with raw data (6.7 ± 0.9 mm). It is particularly noteworthy to point out that nonrigid registration using the proposed resampling method resulted in significantly lower TRE (p < .001) than the current commercially available procedural standard method with unprocessed, raw data. For reference, rigid, and nonrigid registration results using the dense, full anterior surface from the intraoperative phantom CT also are presented in Table I as a gold standard comparison.

Fig. 7.

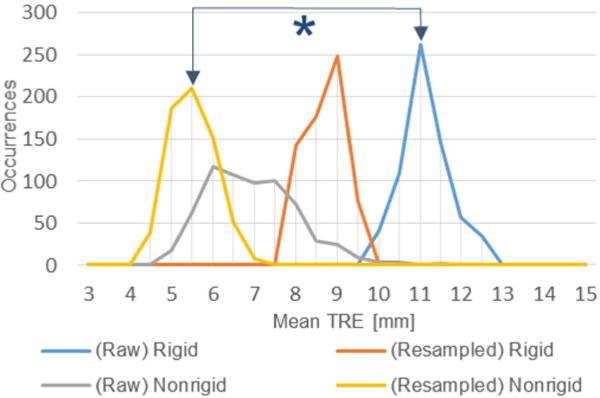
Histogram of average TRE over the 650 simulated cases using raw and resampled data to drive rigid and nonrigid registration. The asterisk denotes significant reduction in error between the current commercial IGLS rigid registration method (blue) and proposed nonrigid registration with resampled data (gold).

Fig. 8.

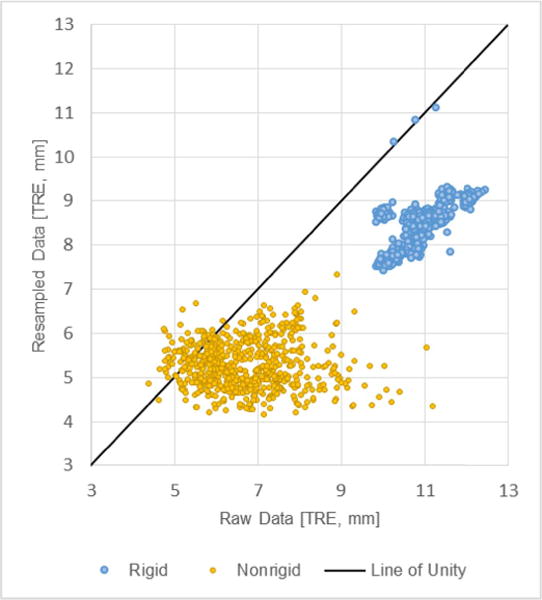
A scatterplot of average TRE over the 650 simulated cases. The x-axis represents average case TRE using a simulated raw surface data scenario while the y-axis represents that simulated surface data after undergoing resampling. Rigid and nonrigid registration results are presented in blue and gold respectively.

TABLE I.

Average Case TRE (mm) at Base Noise Level

Case #	Raw Data		Resampled Data
	Rigid	Nonrigid	Rigid	Nonrigid
1	10.8 ± 0.1	7.0 ± 0.6	7.9 ± 0.1	5.8 ± 0.3
2	10.3 ± 0.1	7.4 ± 0.3	7.9 ± 0.4	5.2 ± 0.3
3	10.2 ± 0.2	7.8 ± 0.5	7.7 ± 0.1	6.2 ± 0.4
4	11.0± 0.1	5.5 ± 0.4	8.3 ± 0.1	5.4 ± 0.2
5	10.7 ± 0.1	5.9 ± 0.8	8.6 ± 0.1	5.6 ± 0.4
6	10.9 ± 0.1	8.3 ± 0.9	8.6 ± 0.1	5.1 ± 0.4
7	11.2 ± 0.1	6.9 ± 0.4	8.7 ± 0.4	4.8 ± 0.2
8	10.8 ± 0.1	7.7 ± 1.3	8.2 ± 0.1	4.6 ± 0.3
9	11.4 ± 0.1	5.6 ± 0.3	8.6 ± 0.1	5.2 ± 0.3
10	11.5 ± 0.1	6.9 ± 0.9	9.1 ± 0.1	4.9 ± 0.2
11	10.7 ± 0.1	6.0 ± 0.5	8.4 ± 0.4	4.9 ± 0.3
12	10.0 ± 0.1	6.2 ± 0.8	8.7 ± 0.1	5.7 ± 0.3
13	12.1 ± 0.1	6.2 ± 0.4	9.0 ± 0.1	5.3 ± 0.3
AVG	10.9 ± 0.6	6.7 ± 0.9	8.4 ± 0.5	5.3 ± 0.5
Ideal Data (CT)	Rigid, 6.4 & Nonrigid, 4.7

Table II presents average TRE results for increasing amounts of noise. The evaluation was implemented for the base level of noise (1.0 mm) and amplifications of 2 (1.9 mm), 4 (3.8 mm), and 8 (7.6 mm) times the base level. For all scenarios of registration method and surface data, TRE results were observed to increase as the noise level was increased. Improvement in rigid registration TRE provided by resampling was observed to remain at all levels of noise. At an amplification of 8 times clinically observed noise the improvement to nonrigid registration provided by resampling was absent.

TABLE II.

Average TRE (mm) at Varying Noise Levels

Noise Level	Raw Data		Resampled Data
	Rigid	Nonrigid	Rigid	Nonrigid
Base	10.9 ± 0.6	6.7 ± 0.9	8.4 ± 0.5	5.3 ± 0.5
2x	10.9 ± 0.5	6.7 ± 0.8	8.5 ± 0.4	5.5 ± 0.3
4x	11.0 ± 0.6	6.9 ± 0.9	8.7 ± 0.5	6.4 ± 0.3
8x	11.3 ± 0.6	7.5 ± 0.9	9.1 ± 0.5	8.5 ± 0.7

IV. Discussion

The results presented illustrate the first study designed to characterize the impact of varying IGLS modus operandi on rigid registration and model-based deformation correction methods. While prior work in the field has investigated varying methods of image-to-physical registration and varying methods of sparse data collection, this study is novel in that it examines the extent to which operational differences in data collection may influence registration results. More explicitly, this study is novel in that it approaches the problem of surface based registration by considering the registration itself as a black box and solely investigates how the quality of input data influences the registration output. In addition, it proposes to investigate this within the context of a novel data-driven approach whereby applied clinically acquired surface digitization patterns are transformed to a hepatic deformation phantom surface for the purpose of rapid and robust systematic methodological validation. This validation framework affords the study of large data sets, with true subsurface validation targets, that would require enormous resources to acquire clinically. Lastly, this novel framework provides the ability to propose and validate a resampling procedure which we show to improve registration robustness. Further, we discuss how the results of this study demonstrate that the nature and quality of the data driving registration is equally as important as the registration method itself and suggest the efficacy of our human-to-phantom data framework.

The representations (shown in Fig. 7, 8 and Tables I, II) of the impact that variation in acquired surface pattern, density, and noise has on sparse surface based registration methods in IGLS indicate that IGLS methods based on raw manually swabbed sparse surface data are not optimal with respect to robustness. This is of note considering our experience in observing that surface data collection extent and density varies across patient presentations and physician utilization of the IGLS system. Fig. 7 and Tables I, II demonstrate the higher variance that is seen in the current nonrigid approach (Raw Nonrigid) in comparison to the commercial rigid registration method (Raw Rigid), i.e. we see a marked spread in the distribution of occurrences of the gray line as compared to the blue. This behavior makes it quite apparent that the nonrigid registration method is sensitive to variations in surface data collection via swabbing. That being said, the evaluated nonrigid registration method consistently outperformed rigid registration in terms of accuracy when using raw data (with ∼39% improvement). The results from our surface resampling technique show our ability to systematically improve the accuracy and reproducibility of both rigid and nonrigid registration methods in IGLS. More specifically, when data are synthesized in a clinically-relevant fashion, surface resampling significantly improved registration results regardless of data pattern and density at reasonable levels of noise. This is dramatically shown in Fig. 7, 8 and Tables I, II. The resampling strategy improved rigid and nonrigid registration TRE by 22.5% and 21.3% respectively. Equally striking, resampling combined with nonrigid registration produced a 51.5% improvement in TRE when compared to the current commercial rigid registration method (take note of the ∗ in Fig. 7).

Central to the proposed framework was that the deformations induced in our phantom scenario have similar characteristics with the intraoperative counterpart. In Fig. 6 we see a direct comparison between clinical signed closest point data in Fig. 6.A and the equivalent (although larger extent) for our phantom setup in Fig. 6.B. To assist interpretation, both surfaces experience similar magnitudes in surface-to-surface misfit. While the phantom surface appears somewhat different than the clinical surface, the distribution demonstrates a general pattern that we often see within image-to-physical rigid registration in IGLS data. More specifically, it is observed that the anterior surface of the organ becomes more planar after mobilization and packing, which produces an observable elevation of the lateral segments while the more medial regions of the organ remain relatively static. In a separate extensive study looking at patterns of intraoperative model-to-OR-data fit, [11] also observed this behavior. Additionally, these phantom results are in accordance with our previous phantom studies which entailed multiple novel deformations as reported in [13] and a different liver phantom as in [28]. We acknowledge that the human-to-phantom validation framework could be further strengthened with additional phantom work (derived from varying clinically acquired anatomy), more deformations, and more clinical sparse surface data patterns; and while demonstrated in past work [13], [28], all of these areas are an important continued direction for the future. However, we should note that this work does add significantly to past contributions. For example, in Fig. 6 it is demonstrated that the current phantom experiences a similar magnitude and a realistic pattern of deformation to routine IGLS data. In Fig. 5, the quality of sparse surface data is maintained between clinical acquisition (Fig. 5.A) and application to the phantom (Fig. 5.B). While further additions as suggested above will undoubtedly improve the utility and clinical accuracy of our human-to-phantom validation framework, the environment we have developed has provided meaningful results and a potentially powerful pathway forward for validation of image-to-physical registration in the future.

V. Conclusions

This investigation represents a significant advancement in the understanding of the degree that acquired intraoperative surface data variation influences the outcome of IGLS sparse-data image-to-physical registration. The work demonstrated that surface data resampling shows significant promise for improving the accuracy and reproducibility of IGLS rigid and nonrigid registration. While further investigation is required to fully characterize the optimal workflow-friendly strategy for IGLS surface data collection, the surface resampling presented here is an advancement toward minimizing the impact of data collection strategy on model-updated surgical navigation systems for the hepatic environment.

While these results are important, it is also important to recognize the novelty and utility of the human-to-phantom framework proposed in this work. As the field of soft-tissue image guidance moves forward, the intraoperative validation of these approaches requires enormous effort either using workflow-cumbersome infrastructure such as intraoperative MRI [22] or lower cost but challenging measurement methods such as spatially localized intraoperative ultrasound [1]. The framework proposed herein creates controlled phantom deformation events comparable to those documented in the OR. The evaluated registrations are driven based on intraoperative data compatible with the IGLS modus operandi, transformed to the mock organ surface. This approach is unique in that it has the advantage of full volumetric deformation measurements in a controlled environment but also uses data acquired from a realistic workflow to drive alignment strategies. We believe this is a significant step forward in validation design for this challenging environment. When comparing the study presented here with our more burdensome ultrasound counterpart study in [1], the compatibility of results suggests that this may indeed be an exciting step forward for more tractable investigations in the future.