Breast tissue stiffness estimation for surgical guidance using gravity-induced excitation

Abstract

Tissue stiffness interrogation is fundamental in breast cancer diagnosis and treatment. Furthermore, biomechanical models for predicting breast deformations have been created for several breast cancer applications. Within these applications, constitutive mechanical properties must be defined and the accuracy of this estimation directly impacts the overall performance of the model. In this study, we present an image-derived computational framework to obtain quantitative, patient specific stiffness properties for application in image-guided breast cancer surgery and interventions. The method uses two MR acquisitions of the breast in different supine gravity-loaded configurations to fit mechanical properties to a biomechanical breast model. A reproducibility assessment of the method was performed in a test–retest study using healthy volunteers and was further characterized in simulation. In five human data sets, the within subject coefficient of variation ranged from 10.7% to 27% and the intraclass correlation coefficient ranged from 0.91–0.944 for assessment of fibroglandular and adipose tissue stiffness. In simulation, fibroglandular content and deformation magnitude were shown to have significant effects on the shape and convexity of the objective function defined by image similarity. These observations provide an important step forward in characterizing the use of nonrigid image registration methodologies in conjunction with biomechanical models to estimate tissue stiffness. In addition, the results suggest that stiffness estimation methods using gravity-induced excitation can reliably and feasibly be implemented in breast cancer surgery/intervention workflows.

1. Introduction

Tissue stiffness interrogation plays a critical role in breast cancer from self-examinations and tumor staging to palpation guided biopsies and surgery. Unfortunately, not all clinically relevant breast lesions are palpable. For example, ductal carcinoma in situs are rarely palpable and are usually diagnosed by microcalcifications seen in x-ray mammography (Hofvind et al 2011). These early stage cancers and other clinically occult breast lesions make tumor localization difficult for biopsies and surgical tumor removal (Pleijhuis et al 2009). These localization complications directly contribute to unacceptably high reoperation rates for breast conserving surgery (20–40% (Landercasper et al 2014)). For this reason, enhanced tumor localization strategies have been suggested and include using image guidance systems that rely on patient specific biomechanical breast models to predict tumor locations for biopsies and surgical removal (Carter et al 2005, Conley et al 2015). Image guided breast surgery (IGBS) is performed by registering pre-surgical images to the same 3D coordinate space as the operating room. The fundamental concept of IGBS is to track the position of surgical instruments using optical or electromagnetic sensors and determine their location with respect to the physical position of the tumor as determined by registered preoperative imaging data, i.e. an image-to-physical registration. For procedures involving soft tissue, such as the breast, deformation between the preoperative image and the operating room position is inevitable; the preoperative images no longer match the surgical reality. For this reason, IGBS relies on a nonrigid alignment between image and patient. One such methodology relies on patient specific biomechanical models to deform the preoperative data to match the geometric configuration of the breast in the operating room. The term patient-specific often implies that highly resolved geometric models are created from individual patient anatomy. In an extension to this broad definition, we have developed a method to further incorporate patient specific mechanical property parameters by estimating the stiffness of the underlying breast tissue to improve the accuracy of these models.

Mechanical models for breast deformation have also been created for needle path and biopsy planning (Misra et al 2008, Vancamberg et al 2010), breast augmentation planning and simulation (Roose et al 2005, del Palomar et al 2008, de Heras Ciechomski et al 2012), and radiation therapy targeting (Eiben et al 2016). Within these applications, various material constitutive models have been employed. For example, breast tissue has been modeled as nonlinear or linear elastic, isotropic or anisotropic, and homogenous or heterogeneous depending on the application, deformation magnitude, and desired accuracy.

With respect to applications, many biomechanical models have been used for predicting breast deformation in biopsy and simulating mammographic compressions. These applications are usually driven by displacement boundary conditions that compress the breast into biopsy and/or mammogram geometries (Azar et al 2002). An estimate of relative stiffness for different breast tissue types is usually sufficient for these applications due to the indeterminate nature of displacement boundary conditions. However, when contact forces or gravitational loading conditions are applied, absolute material property values are required. There are several models that incorporate gravitational loading and/or contact forces for applications in aligning prone and supine images (Eiben et al 2016), modeling mammographic compressions (Chung et al 2008b), and performing image-to-physical space registration of preoperative breast image volumes for use in guiding surgery (Conley et al 2015). In many of these studies, the material properties are estimated using literature values and are not patient specific. In addition, a recent review of the biomechanical properties of breast tissue (Ramião et al 2016) reported a large variation in stiffness properties for fibroglandular, adipose, ductal carcinoma in situ, and invasive ductal carcinomas. Variations in reported stiffness properties are mainly due to differences in testing methodologies, continuum assumptions, measurement errors, and natural inter and intra patient differences in tissue elasticity. Breast material properties vary greatly between subjects so generalized applications of mechanical properties in biomechanical models used for clinical guidance is not ideal. For example, variations in material properties among subjects have been attributed to age (more adipose, less fibroglandular tissue (Lee et al 1997) and breakdown of connective tissue), genetic factors, and hormonal changes (Lorenzen et al 2003). Therefore, for procedure planning and guidance purposes, patient specific in vivo mechanical property estimation is likely to result in improved accuracy.

In most conventional techniques to estimate absolute stiffness properties, a known force or pressure must be applied followed by an observed measurement of tissue deformation. In the methodology described in this study, changes in the direction of gravitational loading are used as the known excitation force and magnetic resonance imaging (MRI) is used to quantify tissue deformation. One advantage to the methodology is that breast mechanical properties are being determined in a testing configuration that is extremely close to its surgical counterpart. Others have also made similar investigations. In Chung et al (2008a), a method is reported that estimates material properties using gravity induced deformations within the context of modeling mammographic compression. With that work, a gel phantom with a simplistic breast shape was imaged in two gravity loaded configurations (0° and 10.5° inclines off the superior–inferior axis). A single optimal material parameter was found by minimizing the root mean square (RMS) distance error between model predicted and experientially acquired surface points. In similar work, the concept of using multiple gravity-loaded configurations to estimate mechanical properties was further reported in Gamage et al (2011) using a two-layered gel cantilever beam. In vivo realizations of generating stiffness estimates by fitting model parameters to observed deformations due to changes in gravitational loading have been performed (del Palomar et al 2008, Rajagopal et al 2008, Carter et al 2009). In del Palomar et al (2008), a single material constant was iteratively adjusted to minimize residual errors of 7 surface landmarks between supine and standing breast configurations. In Rajagopal et al (2008), MR image volumes of the prone breast submerged in water were used to represent a gravity-free mechanical reference state. In this configuration, buoyancy forces were estimated to counteract the effects of gravity. Neutral buoyancy images (gravity-free) and prone images (gravity-loaded) were used to estimate a single material property. A similar study using submerged and unsubmerged prone breast images reproduced this technique (Carter et al 2009), except individual stiffness properties for fibroglandular and adipose tissue were used as opposed to a single material definition for the whole breast. In Rajagopal et al (2008), the purpose was to validate a computational approach for estimating the gravity-free reference state of the breast for applications in prone to supine registration. In both studies, the authors concede that submerging the breast in water during the MRI exam is not clinically practical for routine study.

While mechanical property estimations using gravity induced deformations have been performed in gel phantoms, there is a lack of data showing feasibility of this concept in human subjects in terms of reliable tissue stiffness identification with techniques amenable to clinical settings. In (Rajagopal et al 2008, Carter et al 2009), the gravity-induced excitation (submerged/unsubmerged prone breasts) is not clinically feasible. In (del Palomar et al 2008), errors induced by nonlinearity and gravitational pre-stress may have been compounded by very large deformations between supine and standing breast configurations. Overall, while estimates of mechanical properties in vivo have been produced using gravitational excitation, they represent only a feasibility sampling of one to two subjects with no sense of methodological repeatability and reproducibility (del Palomar et al 2008, Rajagopal et al 2008, Carter et al 2009). We address these limitations and challenges in this paper by developing a stiffness estimation framework that is based on two supine gravity loaded configurations of the breast. Our method takes advantage of image registration principles to capture the driving deformation source (i.e. a change in the direction of gravitational loading). We use rich image similarity data rather than spare point displacement errors used in all previously reported gravity-based stiffness estimation methods. Validation work has been performed in phantoms using image similarity to drive mechanical property estimation (Weis et al 2013, 2014, 2015a). In (Weis et al 2015a), stiffness ratios as determined by mechanical testing of the phantom material were compared with stiffness ratios as determined by an in vivo stiffness estimation that relies on the same image similarity parameters used in this current study. The percent errors between the mechanical testing ratios and image-derived stiffness estimations were 8–12%. In this study, we demonstrate feasibility of this approach in humans using ten unique stiffness estimates of fibroglandular and adipose tissue in healthy volunteers and measure reproducibility in five test–retest datasets. To our knowledge, we are the first to perform in vivo reproducibility studies of a gravity-based stiffness estimation method.

2. Methods

2.1. Theory

Before describing each component of our novel stiffness estimation algorithm, an overview is outlined in figure 1, beginning with the acquisition of two supine volumetric images. The first image is acquired with the subject in the supine position. The subject is then slightly rotated along the longitudinal axis of the body by placing a support wedge posterior to the breast and imaged again. Gravity-induced deformations occur due to a change in tissue weight distribution. A biomechanical model is used to simulate breast deformations that occur between the two image acquisitions. The forward model is solved with a range of stiffness properties for each tissue type. An image similarity metric is used to calculate the residual error between the model deformed and experimentally acquired image. Patient specific stiffness property values are selected by optimizing the image similarity metric.

Figure 1.

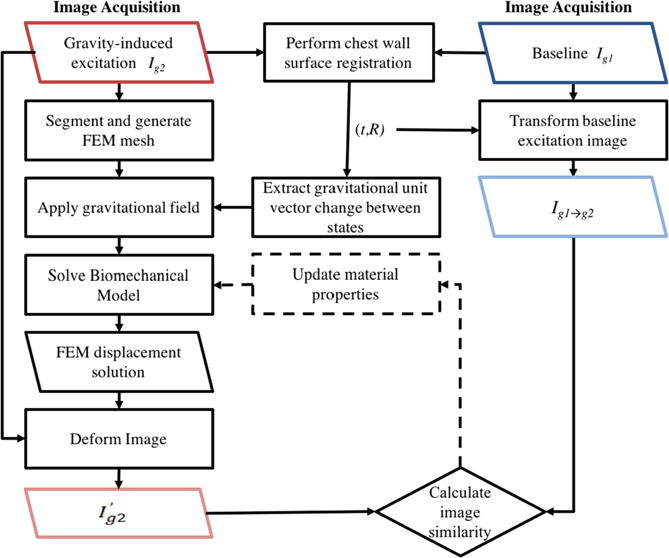
The stiffness estimation framework begins with the acquisition of two gravity loaded image volumes (see figure 2). A rigid alignment between the two configurations is performed using only chest wall intensity information. The rigid registration procedure results in a translation, t, and rotation, R, that is used to transform I_g1 to be rigidly aligned with the chest wall in I_g2 (see figure 4). Also from R, a change in gravitational loading is quantified. A FEM mesh and biomechanical model is built from I_g2. A displacement field is generated from solving the biomechanical model and is used to deform I_g2. An image similarity metric is calculated between the model deformed image $(I_{g2}^{\prime })$ and the rigidly aligned baseline image (I_g1→g2). Stiffness properties are extracted when the calculated image similarity is optimized. An optimization procedure can be employed to iteratively update the material properties until the image similarity metric is minimized.

2.2. Image acquisition and processing

Magnetic resonance (MR) images of the breast are typically acquired using a dedicated breast coil with the patient lying in the prone position with freely hanging breasts. However, supine MR images are desirable within the context of surgical navigation because they more closely represent the surgical position. This position also readily allows for gravity induced deformations amenable to the proposed stiffness estimation method. After informed written consent in an IRB approved study, the study volunteer was positioned in a 3T Achieva MR scanner (Philips Healthcare, Best, The Netherlands). A 16-channel sensitivity encoding torso coil (SENSE XL Torso Coil, Philips Healthcare) was situated carefully as to not induce unnatural deformations to the breast. The ipsilateral arm was placed above the volunteer’s head as to not deform or provide external support to the breast (somewhat similar to the lateral arm extension that occurs during lumpectomy procedures). The healthy subject image data was acquired with: TR = 7.422 ms, TE = 3.91 ms, and flip angle = 10 degrees using SENSE parallel imaging (acceleration factor = 2). High resolution anatomical images were acquired with a T₁-weighted, 3D turbo field echo sequence with fat suppression, a field of view of 200 mm × 200 mm × 160 mm, and a reconstructed voxel size of 0.391 mm × 0.391 mm × 1 mm. The duration of each image volume acquisition was 120.6s.

Image volumes were acquired before and after a gravity-induced excitation for each volunteer. The mechanical excitation for this method involves slightly rotating the subject along the longitudinal axis of the body by placing a 15° foam support wedge posterior to the torso side with the breast being imaged. The torso rotation causes a change in the baseline patient configuration with respect to the acting direction of gravity. Gravity induced deformations occur as a result of changes in tissue weight distributions with the rotating torso. Central axial image slices of the baseline and gravity-induced excitation configurations are shown for a representative subject in figure 2.

Figure 2.

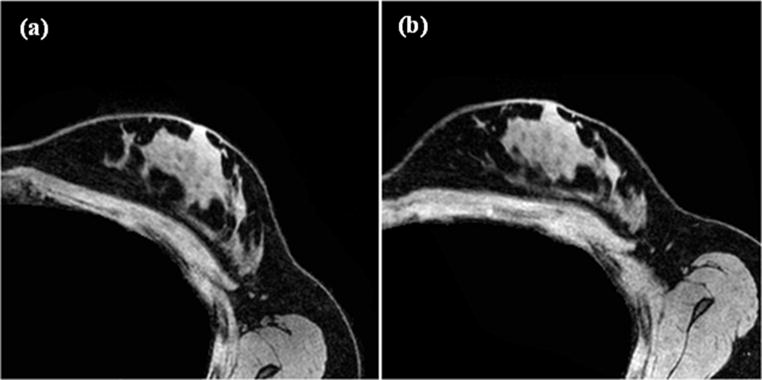
Two representative gravity loaded configurations used as input images in the stiffness estimation method. (a) Represents the baseline configuration (I_g1) while (b) represents the breast after a gravity induced excitation (I_g2).

For computational efficiency, image volumes were downsampled to 256 × 256 × 160 with voxel sizes of 0.78 mm × 0.78 mm × 1 mm. The breast (excluding chest wall muscles) was segmented from the gravity-induced configuration (I_g2) using ITK-SNAP (Yushkevich et al 2006). A region based segmentation method was used to automatically classify breast tissue into two types: adipose and fibroglandular. The Markov random field (MRF)-based algorithm, implemented using the insight toolkit (ITK) (Yoo et al 2002), assumes that adjacent pixels likely belong to the same tissue type or class and performs segmentation using intensity similarity between adjacent pixels. Following segmentation, a binary mask of the whole breast was used to generate a boundary surface using a marching cubes algorithm (Lorensen and Cline 1987), implemented with the visualization toolkit (VTK) (Scheroeder and Auilals 2006). Following surface generation, radial basis function smoothing was applied using the FastRBFToolbox (Farfield Technologies, Christchurch, New Zealand). A volumetric tetrahedral finite element mesh with a nominal edge length of 3 mm was created from this surface using a custom mesh generator (Sullivan et al 1997). Figure 3(a) shows two orthogonal slices of a segmented supine breast classified into adipose (white) and fibroglandular tissue (red) with the FE mesh overlaid in black.

Figure 3.

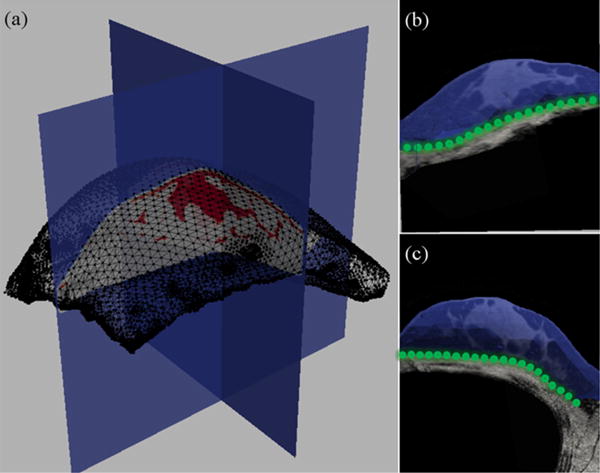
(a) Tetrahedral mesh built from a representative gravity-induced configuration image (I_g2). The black wire outline shows surface elements of the mesh. Two orthogonal cuts of the segmented image volume along the axial and sagittal planes are shown with adipose represented in white and fibroglandular in red. Sagittal (b) and axial (c) slices of the I_g2 image volume are shown with the mesh overlaid in blue. The green nodal spheres in (b) and (c) correspond to fixed boundary conditions along the chest wall. The rest of the mesh moves freely according to the applied body forces.

2.3. Biomechanical model

In this study, we use a mechanics based computational model to simulate breast deformation. The partial differential equation that expresses a static stress distribution in a material in response to a known body force is shown in (1).

$$\nabla \cdot \sigma =\beta$$ (1)

where σ is the stress tensor and where β represents a body force. The stress–strain relationship according to Hooke’s law is

$$\sigma =C\epsilon$$ (2)

where C represents the stiffness tensor of a material and ε is a strain tensor. Biological tissue is often represented using linear strain elements depending upon the application, desired accuracy, and computational requirements. The full nonlinear formulation, known as Green’s strain tensor, results in a nonlinear algebraic system that is computationally expensive while the linear approximation to Green’s tensor (Cauchy tensor) is violated under larger rotations and deformations. In this study, we employ a nonlinear corotational FEM formulation (Georgii and Westermann 2008), which represents a compromise in terms of computational burden and accuracy between the full nonlinear strain tensor and the linear approximation (i.e. neglecting quadratic terms in Green’s tensor). In the corotational formulation, large local rigid body rotational movements are accounted for and the remaining deformation is modeled using linear elastic mechanics. While not a nonlinear constitutive relationship per se, accounting for large local tissue rigid motion does not require an iterative nonlinear approach. Corotational FEM models have been widely used within the soft-tissue large deformation mechanics literature (Georgii and Westermann 2008, Dick et al 2011, Georgii et al 2014). With respect to constitutive behavior, the conventional stress–strain relationship, Hooke’s Law, requires two material property constants to describe any given tissue, namely, ν (Poisson’s ratio) and E (Young’s modulus). Young’s modulus represents the stiffness of a material and is optimized during the stiffness estimation process. Poisson’s ratio is the negative ratio of lateral to longitudinal strain in an axially loaded material and represents a characterization of compressibility. Since biological soft tissue is generally quite hydrated, we assume breast tissue to be slightly to nearly incompressible. Largely due to the challenge in soft-tissue material testing, there is sparse data on ν for breast tissue. As a result, ν was added as another degree of freedom in the model varying over the range of ν = 0.40–0.47. Equation (3) shows the stress–strain relationship for a linear elastic, isotropic material.

$$\left[\begin{array}{c}{\sigma }_1\\ {\sigma }_2\\ {\sigma }_3\\ {\sigma }_{23}\\ {\sigma }_{12}\\ {\sigma }_{13}\end{array}\right]=\frac{E}{(1+\nu )(1-2\nu )}\left[\begin{array}{cccccc}1-\nu & \nu & \nu & 0& 0& 0\\ \nu & 1-\nu & \nu & 0& 0& 0\\ \nu & \nu & 1-\nu & 0& 0& 0\\ 0& 0& 0& \frac{1-2\nu }{2}& 0& 0\\ 0& 0& 0& 0& \frac{1-2\nu }{2}& 0\\ 0& 0& 0& 0& 0& \frac{1-2\nu }{2}\end{array}\right]\left[\begin{array}{c}{\epsilon }_1\\ {\epsilon }_2\\ {\epsilon }_3\\ 2{\epsilon }_{23}\\ 2{\epsilon }_{12}\\ 2{\epsilon }_{13}\end{array}\right]$$ (3)

Furthermore, the relationship between strain and displacement is ε_i,j = 1/2(u_i,j + u_j,i) where u defines a 3D displacement field. Using linear basis functions defined on tetrahedral finite elements, we performed the Galerkin Method of Weighted Residuals to obtain a system of equations to resolve the unknown displacement coefficients. Ultimately, we are interested in finding the mechanical properties of breast tissue that produce a displacement field that when used to deform the gravity excited image (I_g2) matches the baseline configuration image (I_g1→g2).

2.4. Boundary conditions

In our model, the chest wall is assumed to be a reliably rigid structure in relation to breast tissue. Therefore, rigid alignment using chest wall intensity information was performed to extract the relative rotation that occurred between the baseline configuration and the torso rotated image configuration. The following image processing steps were performed to extract the geometric change of the breast relative to the direction of gravity:

1. Segment the chest wall muscles in each image:

   • The chest wall was semi-automatically segmented in each image using ITK-SNAP’s implementation of the Snake’s algorithm (Kass et al 1988).
2. Rigidly register the baseline and gravity-induced images:

   • A standard rigid registration (Viola and Wells 1997) was performed using image contrast patterns of the chest walls in the two image volumes to transform the baseline image (I_g1) into the gravity-induced configuration space (I_g2). Figure 4 displays a representative result of such a registration. I_g1 and I_g2 chest wall image masks are highlighted to show the driving components of the registration (figures 4(a) and (b)). The transformation matrix (containing translation, t and rotation, R) is used to rigidly align the baseline image to the gravity-induced configuration image (figure 4(c)). An overlay of the gravity-induced image (I_g2) and registered baseline image (I_g1→g2) is shown in figure 4(d) and visually confirms that the chest wall muscle beneath the breast rigidly aligns compared to the breast tissue above that has deformed due to the difference in gravitational loading. Once aligned, rigid translational components are accounted for and the remaining tissue dissimilarity is due to rotational components that arise from gravity-induced deformations.
3. Extract gravity differential vector:

   • The gravity differential vector was extracted from the rotation matrix using (4):

     $$\mathrm{\Delta }\widehat{g}={\widehat{g}}_1-R\ast {\widehat{g}}_1$$ (4)

     $$\beta =9.8\frac{m}{s^2}\rho \mathrm{\Delta }\widehat{g}$$ (5)

     where ${\widehat{g}}_1$ is assumed to be unit vector normal to the MR table. In (5), β is subsequently applied as a body force of tissue weight in the biomechanical model (1). The tissue density, ρ, is assumed to be uniform and approximately equal to water, 1000 kg m⁻³. The model nodes associated with the chest wall are fixed in the x, y, and z directions, i.e. applied Dirichlet boundary conditions set to zero. Figures 3(b) and (c) show central sagittal and axial image slices with the volumetric mesh overlaid in blue. The green spherical nodes represent the fixed posterior surface along the chest wall.

Figure 4.

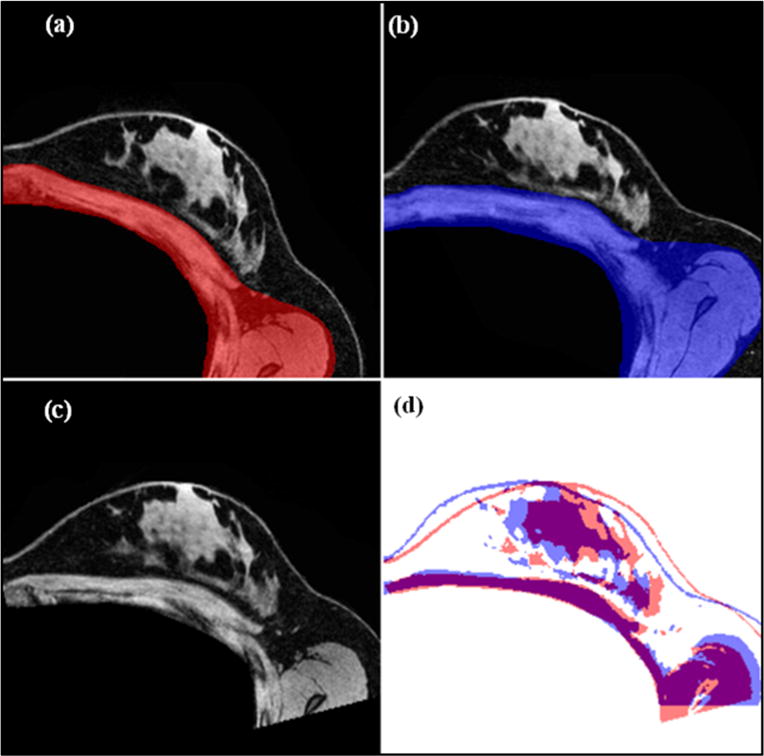
Representation of the rigid alignment procedure described in section 2.3. Central axial slices are shown of the (a) baseline configuration image, and (b) gravity-deformed configuration with overlays of chest wall regions used in initial alignment. The transformation matrix extracted from the rigid registration is used to align the chest walls in the baseline configuration and the gravity-deformed configuration so that the resulting misalignment of breast tissue is due to deformations caused by the change in gravitational loading. In (c), we see the aligned baseline to the gravity-induced reference frame, and (d) contains image masks of the rigidly aligned baseline image (I_g1→g2) (red) and gravity deformed image (I_g2) (blue). It is clear that the chest wall is relatively rigid compared to the mismatch in breast tissue structures due to gravity induced nonrigid deformation.

2.5. Stiffness estimation

The stiffness estimation process first begins with generating an eroded binary mask of the torso-rotated image volume for the purpose of designating a zone in which to compute an image similarity metric between the model deformed image and the chest wall aligned baseline image. The Young’s modulus values for adipose and fibroglandular tissue were then estimated by performing an exhaustive search of the parameter space and selecting the set of properties that optimized the image similarity metric defined by (6).

$$S=(1-\text{CC})$$ (6)

where S is the similarity metric to be minimized and CC is the image correlation coefficient defined by (7).

$$\text{CC}=\frac{{\displaystyle \sum _i(I_{\left|g2\right|i}^{\prime }-{\overline{I}}_{\left|g2\right|}^{\prime })(I_{\left|g1\to g2\right|i}-I_{\left|g1\to g2\right|})}}{\sqrt{{\displaystyle \sum _i(I_{\left|g2\right|i}^{\prime }-{\overline{I}}_{\left|g2\right|}^{\prime })\sqrt{{\displaystyle \sum _i(I_{\left|g1\to g2\right|i}-I_{\left|g1\to g2\right|})}}}}}$$ (7)

where $I_{\left|g2\right|i}^{\prime }$ and I_|g1→g2|i are the intensity values at pixel i for the model deformed and chest wall aligned baseline images, respectively. ${\overline{I}}_{\left|g2\right|}^{\prime }$ and I_|g1→g2| are the mean intensity values of the model deformed and chest wall aligned baseline images. CC has a value of 1 if two images are identical and a value of zero if completely uncorrelated.

2.6. Experiments

2.6.1. Test–retest reproducibility in human subjects

In an IRB approved study with informed written consent, healthy female volunteers over the age of 18 without evidence of pregnancy were recruited for a test–retest study to measure the reproducibility of this stiffness estimation technique. The five test–retest datasets are comprised of three healthy volunteers ages 21–36, with the left and right breasts of two volunteers and the left breast of a third volunteer. Due to differences in right/left breast volumes, fibroglandular content (Zheng et al 2012), tissue hydration levels (Hennessey et al 2014), and a lack of data to suggest symmetry in material properties (Boyd et al 2014), we consider each breast to be an individual dataset. Therefore, this work presents a total of ten stiffness estimates and five test–retest datasets to determine method reproducibility.

A reproducibility assessment was performed using a test–retest approach in which volunteers were scanned in a baseline position and re-set between the two-consecutive gravity-loaded configuration scans. Independent stiffness estimations were then performed for each baseline-gravity-deformed dataset using the methodology described above. The parameter search space used in human subjects is summarized in table 1. The lower and upper bounds of the parameter search space for each tissue type was determined by encompassing the range of previously reported tissue stiffness values in quasi-static/low frequency shear wave MRE studies (Sinkus et al 2000, Lorenzen et al 2002, Chen et al 2013, Ramião et al 2016).

Table 1.

Parameter space used in human subjects study.

Tissue type	Lower bound	Upper bound	Step size
Adipose	0.05 kPa	2.5 kPa	0.05 kPa
Fibroglandular	0.05 kPa	12 kPa	0.05 kPa
Poisson’s ratio	0.40	0.47	0.01

The test–retest variability was calculated as the absolute value of the difference between test–retest stiffness values expressed as a percentage of the mean of both stiffness values:

$$\mathrm{\Delta }E(\%)=\frac{\left|E_1-E_2\right|}{(E_1+E_2)/2}\times 100$$ (8)

Where E₁ and E₂ are the test and retest stiffness estimations, respectively. Test–retest variability was calculated for each tissue type and is commonly reported in quantitative imaging studies (Parsey et al 2000, Abi-Dargham et al 2000) as a measure of standardized variability in measurement errors across subjects. The mean test–retest variability across all datasets is reported as mΔE. The between subject standard deviation (SD) and within subject standard deviation (wSD) was reported to further assess variability and reproducibility. The wSD was calculated according to (Bland and Altman 1999) as follows:

$$\text{wSD}=\frac{\sqrt{\frac{{\displaystyle \sum _{i=1}^n{(E_{1i}-E_{2i})}^2}}{n}}}{\sqrt{2}}$$ (9)

where n represents the number of test–retest datasets. The coefficient of variation (CV) and within subject coefficient of variation (wCV) was calculated by dividing SD and wSD by the overall parameter mean for each tissue type. We calculated the intraclass correlation coefficient (ICC) (Bartlett and Frost 2008), which relates the magnitude of measurement error to the inherent variability between subjects using equation (10). High ICC values indicate that the measurement errors are low in comparison to the true difference between subjects and takes a value between 0 and 1.

$$\text{ICC}=\frac{{(\text{SD})}^2}{{(\text{SD})}^2+{(\text{wSD})}^2}$$ (10)

2.6.2. Simulation

Simulations were performed to investigate the sensitivity of the objective function to two aspects of the testing framework, (1) adipose-to-fibroglandular tissue volume content, and (2) torso rotation extent. In the simulation framework, a model with known material properties, boundary conditions, and gravity-induced excitation was used to create model-deformed images from baseline image volumes. Material properties for adipose and fibroglandular tissue were selected using the approximate average stiffness values from the human subjects study (adipose and fibroglandular stiffness of 0.25 kPa and 2 kPa, respectively were used as ground truth). For each subsequent simulation set, stiffness property values were incrementally assigned based on the parameter search space with bounds described in table 2, a forward corotational linear elastic model was solved to obtain the displacement field, and the field was interpolated onto the baseline image to create a simulated gravity-deformed image. The image-intensity similarity metric described by equation (7) was then calculated between the baseline and model-deformed image volumes. In addition to similarity, a displacement error metric (equation (11)), was also calculated as a measure of difference.

$$\text{RMS}\text{Displacement}\text{Error}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{\left|d_{\text{true},i}-d_{\text{model},i}\right|}^2}$$ (11)

where N is the number of nodes in the FEM mesh, d_true,i are the true nodal displacements provided by the FEM simulation in this case, and d_model,i are the FEM nodal displacements generated by the current mechanical property model parameters.

Table 2.

Parameter space used in simulation study. Ground truth is 0.25 kPa and 2 kPa for adipose and fibroglandular tissue, respectively.

Tissue type	Lower bound (kPa)	Upper bound (kPa)	Step size (kPa)
Adipose	0.1	0.5	0.05
Fibroglandular	1	4	0.05

To study the effect of adipose-to-fibroglandular tissue volume, baseline image volumes from four healthy volunteers were chosen to represent breasts with low (12%), moderate (24%), and high (33 & 39%) fibroglandular contents. A parameter sweep was performed for each simulation set with an applied body force generated from an approximate 30° rotation about the longitudinal axis of the body.

Investigations on the extent of torso-rotation were performed using the moderate level fibroglandular content image volume. The effect of gravity induced deformation magnitude was explored by performing simulation parameter estimations using three angles of rotation corresponding to approximately 15°, 30°. and 45° rotations along the longitudinal axis.

3. Results

3.1. Healthy volunteers

A representative summary of the parameter sweep search results are shown in figure 5 for two test–retest datasets. A central axial slice of the baseline image is shown in figure 5(a) for each stiffness estimation procedure. Masked overlays of the baseline image (gray), gravity-induced configuration image (blue), and model-optimized image (red) are shown to the right of the anatomical baseline image. While single axial image slices are shown for display purposes, property estimations and error calculations were volumetric. Qualitative assessment of these images show a significant improvement in image alignment when stiffness properties are optimized. Below each image set are the image similarity error maps (d). The contour plots show the value of the image similarity metric for each adipose (x-axis)—fibroglandular (y-axis) combination sampled. Each has an elongated minimum region suggesting greater sensitivity to adipose value contrast.

Figure 5.

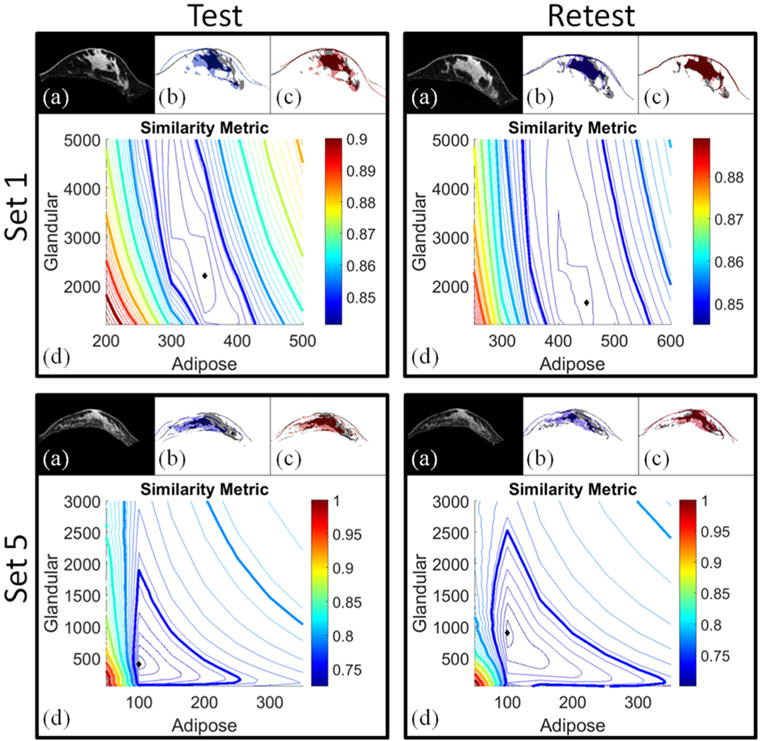
Summary of the stiffness estimation results for Set 1 and Set 5. Image alignment comparisons are displayed in panels (a)–(c) for each test–retest set. In (a), axial anatomical image slices are shown for the baseline configurations. (b) Contains masked versions of the baseline configuration image (gray) and gravity-induced configuration image (blue). In (c), masked image slices of the model-deformed configuration with optimized stiffness values are shown in red overlaid with the baseline configuration (gray). Qualitatively, there is significant improvement in the baseline image alignment when model-optimized stiffness parameters are used. Similarity metric maps are shown in (d) where the diamond in each map represents the minimum value of the contour plot (i.e. the optimal stiffness parameters). Contours represent the error in image similarity for each adipose-glandular value sampled.

Quantitatively, the method provides reliable stiffness values for both adipose and fibroglandular tissue. The demographic information and test–retest stiffness estimations are summarized in table 3. The optimal Young’s modulus values for adipose and fibroglandular tissue were determined by selecting the parameters responsible for producing the best image similarity metric. Among the five test–retest datasets, the highest stiffness properties came from the youngest volunteer (Sets 1 and 2). The ratio of adipose tissue between the left (Set 1) and right (Set 2) breasts ranged from 1.16 to 1.8. The ratio of fibroglandular tissue between the left (Set 1) and right (Set 2) breasts ranged from 4.5–6.2. Set 3 and Set 4 also represent the left and right breasts from the same subject with adipose ratios ranging from 2 to 2.5 and fibroglandular ratios ranging from 1.4–4.2.

Table 3.

Stiffness estimation results for each test–retest dataset.

(a) Demographics for each set:
	Age	Breast volume (cm3)	Fibroglandular content (%)
Set 1	21	85	12
Set 2	21	84	16
Set 3	35	69	27
Set 4	35	61	22
Set 5	36	42	21
(b) Test/retest results: optimal Young’s modulus values (kPa) for adipose and fibroglandular tissue are reported for all 5 test–retest datasets. θ is the angle of rotational about the longitudinal axis of the body calculated from $\mathrm{\Delta }\widehat{g}$.
	θ (°)	Optimal adipose (kPa)	Optimal fibroglandular (kPa)
Set 1
Test	15.5	0.35	2.25
Retest	6.9	0.45	1.65
Set 2
Test	9.2	0.30	10.30
Retest	8.6	0.25	10.15
Set 3
Test	14.3	0.20	0.55
Retest	8.0	0.25	1.05
Set 4
Test	18.9	0.10	0.25
Retest	13.2	0.10	0.35
Set 5
Test	18.3	0.10	0.40
Retest	17.2	0.10	0.90

Reproducibility and variability statistics for the five test–retest datasets are summarized in table 4. Test–retest statistics were calculated for the optimal stiffness parameters. The wCV for fibroglandular tissue was 10.7% with respect to optimal parameter selection. The wCV for adipose tissue was 17.6%. A high reliability parameter (ICC) was observed for fibroglandular tissue at 0.994 and adipose at 0.91 using optimal properties. Overall, the wCV and ICC values combine to show reliable parameter estimates and indicate that the measurement error was substantially low compared to the true difference between subject breast tissue stiffness properties. We note that the Poisson’s ratio selected for optimal stiffness property determination used the full range (shown in table 1) in the best fit process. Given that we did not explicitly fit υ within each tissue type, allowing υ to float among a limited range of possible values tended to regularize the inverse problem.

Table 4.

Reproducibility and variability statistics for adipose and fibroglandular tissue: the mean stiffness values are reported in kPa. SD and CV are the between subject standard deviation and coefficient of variation. wSD and wCV are the within subject standard deviation and coefficient of variation. mΔE is reported as the percent mean ΔE across all test–retest datasets and ICC is the intraclass correlation coefficient. n = 5 test–retest datasets.

Tissue type	Mean (kPa)	SD (CV)	wSD (wCV)	mΔE (%)	ICC
Adipose	0.22	0.123(0.559)	0.0387 (0.176)	13.08	0.91
Fibroglandular	2.79	3.97 (1.426)	0.2987 (0.107)	41	0.994

3.2. Simulations

3.2.1. Effect of fibroglandular tissue

Fibroglandular content affects the shape of the similarity metric map. As shown in figure 6, low fibroglandular content results in poor contrast in resolving fibroglandular tissue as evidenced by a lack of objective function gradient across varying values of fibroglandular stiffness. In contrast, the dramatic objective function gradients across varying adipose tissue values speak to considerable contrast. To some degree expected, we see a shift in convexity of the objective function with better contrast in the fibroglandular tissue with increased fibroglandular content along with a more dramatic gradient.

Figure 6.

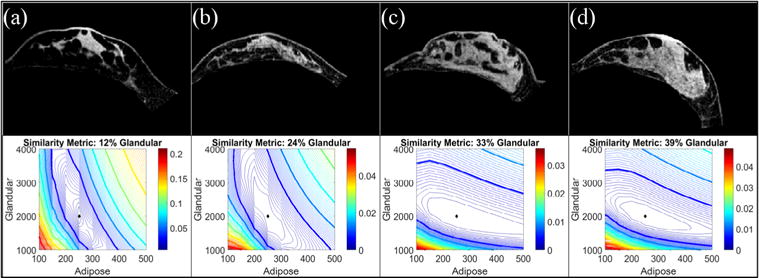
Simulation results investigating the effect of fibroglandular content on the form of the similarity metric. Baseline images are shown from subjects with fibroglandular tissue volume contents of (a) 12%, (b) 24%, (c) 33%, (d) 39%. Using a 30° change in the gravitational unit vector and Young’s modulus values of 0.25 kPa (adipose) and 2 kPa (fibroglandular), simulated gravity-deformed images were created for each baseline image shown in the top panel. The bottom panel shows the resulting similarity error contour maps. The diamond represents the error map minimum.

3.3.2. Effect of gravity-induced deformation magnitude

Amplification of the gravity induced deformation via increased torso rotation directly impacts the convexity of the similarity metric as well as the shape of the RMS displacement error. In figure 7, the three panels show an increase in deformation magnitude from left to right. Gray masks of a central axial slice of the baseline image are overlaid with magenta masks of the (a) 15°, (b) 30°, and (c) 45° rotated simulation images. Below each masked overlay are the image similarity metric and displacement error maps for each rotation. The displacement error maps are marked to indicate the contour levels that approximate the full (0.8 mm) and half (0.4 mm) in-plane voxel sizes.

Figure 7.

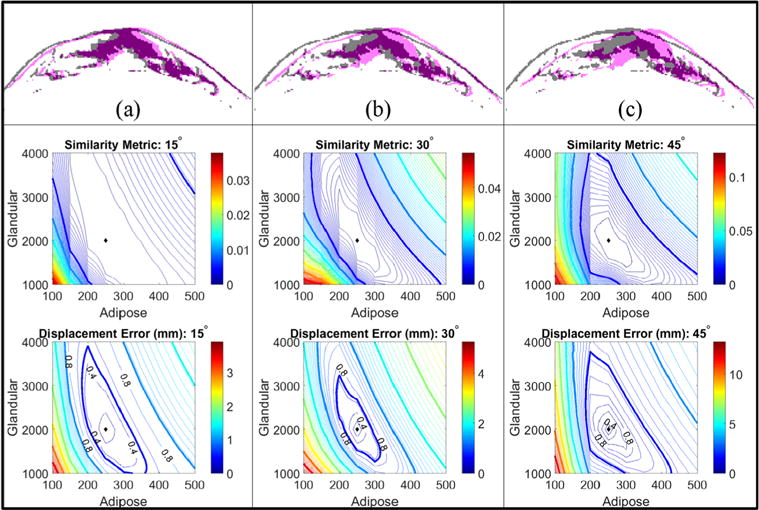
Simulation results investigating the effect of deformation magnitude on the form of the error metrics. 15 (a), 30 (b), and 45 (c) degree changes in gravitational loading conditions with Young’s modulus values of 0.25 kPa (adipose) and 2 kPa (fibroglandular) were used to simulate gravity-deformed images with increasing (from left to right) deformation magnitudes. Contour plots of the image-based similarity metric are shown above the nodal displacement error contour maps for each rotation level. The displacement error maps are marked to indicate the contour levels that approximate the full (0.8 mm) and half (0.4) in-plane voxel sizes. The diamonds indicate the minimum value in each contour plot.

As the deformation magnitude increases, the convexity of the error metrics increases. The average and maximum deformation magnitude caused by the simulated excitation was 2.8 (max = 6.3) mm, 5.7 (max = 12.9) mm, and 8.1 (max = 18.6) mm for the 15°, 30°, and 45° rotation levels, respectively. Contour levels far below the voxel size indicate a limit in stiffness property resolution as changes in the image similarity cannot be detected below these levels. Elongation of the image similarity objective function maps is observed when compared to the RMS displacement error maps (which is a representation of true error). This observation may be attributed to the non-exact nature of feature comparison when using image similarity, image downsampling, partial volume effects, smoothing, and edge effects.

4. Discussion

In this study, we established a comprehensive stiffness estimation procedure using deformations representative of supine breast cancer interventions. Using our unique tissue excitation technique and novel calculation of the driving gravity induced body forces, we produced absolute stiffness parameter estimates for 10 unique image volumes which to our knowledge has never been studied as extensively. In addition, the methodology we have investigated is completely compatible with a supine breast image-guided surgery methodology previously reported (Conley et al 2015). This clinically amenable workflow requires no complicated motion-sensitive imaging sequences or highly specialized equipment to induce and measure tissue deformations. This study reports important observations regarding the resolution of mechanical properties with respect to displacement extent and image intensity feature volumes. Overall, the results are very encouraging, demonstrating that absolute and reproducible measures are possible and an investigation towards optimal imaging sequences to ensure satisfactory resolution of the objective function are suggested for future work.

While MR images were used in this work, the method has been shown to be somewhat modality independent (Miga 2003), as its estimates mechanical properties using image similarity metrics rather than relying on displacement measurement techniques inherent to a specific imaging modality (the method has been used previously with CT images and optical images (Miga et al 2005, Ou et al 2007)). However, this work goes further than the closely-related investigations of the elastography method called modality independent elastography (MIE) (Miga 2003, Miga et al 2005, Ou et al 2007, Pheiffer et al 2011, Weis et al 2013, 2015a). More specifically, previous MIE investigations were only successful in predicting soft-tissue stiffness ratios between adipose, fibroglandular, and tumor due to the use of indeterminate displacement boundary conditions. In this study, we deploy an adaptation that uses gravitational body forces for excitation, which as equation (1) shows, transforms the approach to generating absolute quantitative stiffness tissue values.

To our knowledge, this study reports the first test–retest reproducibility assessment of an MRI-derived, absolute quantitative breast tissue stiffness estimation method using gravity-induced excitations. Our test–retest wCV (wCV-10.7% and 17.6% for fibroglandular and adipose, respectively) and ICC (ICC-0.994 and 0.91 fibroglandular and adipose, respectively) values are comparable to other quantitative imaging reproducibility studies. In Weis et al (2015a), the reproducibility of the MIE method in murine breast cancer models was studied. The wCV ranged from 13% at the bulk level to 32% at the voxel level. The ICC values reported in Weis et al (2015a) ranged from 0.70–0.99. Due to our modest sample size, robust statistical analysis for true significance is limited; however, this work is suggestive and quite encouraging.

From the perspective of clinical workflow, this work suggests various improvements to the image acquisition and mechanical excitation procedure that can be adapted to improve the performance of the method. The shifts in convexity of the similarity objective function maps shown in figures 6 and 7 was a significant finding in the simulation studies. These results indicate that a lack of signal (or decreased image volume texture) in either tissue type will cause the objective function to provide less contrasting gradients with respect to the tissue-type of decreasing signal content. In future studies, weighting schemes and adjustment of image acquisition sequences will need to be studied to further investigate this observation and perhaps develop novel image acquisition frameworks to maximize contrast performance. For example, in previous MIE studies, simultaneous MRI acquisitions of fat-only and water-only images were performed using a commercially available Dixon sequence (Weis et al 2015b). We can utilize these image sequences to improve objective function sensitivity depending on tissue-type content. Similarly, we also observed in this study that amplifying the deformation magnitude by increased torso rotation will better condition the objective function for future inverse property reconstruction methods. The degree of rotation in the volunteer study overall best corresponds to the 15° rotation in the simulation study. We experimentally observed that increased torso rotations are particularly important for small and/or stiff breast volumes. Therefore, we can customize our image acquisition protocol to accommodate breast density. Lastly, all of these observations will be particularly important as we use this information to advance the performance of inverse reconstruction procedures based on similarity (e.g. MIE).

With respect to limitations of this work, in addition to our modest sample sizes, the average volunteer age was 30, which is relatively young compared to the average breast cancer patient. It is likely that additional work would be needed to resolve aspects that vary with age. Across all subject types, it is likely that more advanced nonlinear constitutive relationships will be needed in the future to further improve accuracy of such methods. Similarly, quasi-static excitation neglects a potentially rich source of time-varying viscoelastic effects that may be important for interactive IGBS systems. Additionally, we also need to consider the accuracy of boundary conditions. While the model accounts for gravity induced deformations, it ignores contributions from Cooper’s ligaments, pectoral muscle forces, and rigid registration errors during the initial alignment procedure. Understanding the impact of these missing factors and sources of error is an important direction for improving performance. Clearly, another limitation is that we prescribe the tissue types as isotropic and homogeneous. In future work, spatially discretized region-based mechanical property reconstructions, similar to that of the MIE methodology, may be needed to create better geometric maps of tissue stiffness. With this last item, these capabilities tend to be goals within diagnostic elastography applications. In terms of image acquisition protocols, there are areas to be improved. The image acquisition methods performed in this study were adapted from an existing prone imaging protocol (Li et al 2015). For a healthy volunteer, the signal to noise ratio (SNR) calculated according to (Janssen et al 2017) was measured in a prone and supine setup using the image parameters defined in section 2.2. In the prone acquisition, a dedicated breast coil (16-channel receive double-breast coil, Philips Healthcare, Best, The Netherlands) was used. The SNR in the prone images was 55.8 while the supine image SNR was 27.2. The reduced SNR in the supine images is due to respiratory and motion artifacts while also compounded by the fact that the torso coil used in the study is not optimized for breast imaging. An avenue worth pursuing in the future is to use respiratory-triggered MR acquisitions, which have been shown to improve the SNR of supine breast images (Janssen et al 2017).

As the work moves forward, we must establish which features are most important for the accurate execution of IGBS. Nevertheless, it is encouraging that our preliminary stiffness values are within range of low frequency, minimal pre-compression elastography methods. For example, in Chen et al (2013), a non-compressive elastography system with relatively low frequency shear waves (40 Hz) was tested in 7 healthy subjects. The stiffness range for adipose tissue was 0.25–0.41 kPa and 0.46–0.9 kPa for fibroglandular tissue. In (Lorenzen et al 2002), MR elastography values for 20 patients and 15 healthy volunteers were reported with 0.5–4 kPa (median = 1.7 kPa) for adipose tissue and 1–15 kPa (median = 2.5 kPa) for fibroglandular tissue. Traditionally, magnetic resonance elastography studies report stiffness values in terms of shear modulus (G), which can be approximated to Young’s modulus by E = 3G. With our quasi-static study herein, we report mean Young’s modulus values of adipose tissue to be 0.2 ± 0.1 kPa and 2.8 ± 4.0 kPa for fibroglandular tissue. As breast tissue properties have been shown to be frequency dependent (increased reported stiffness values with increased frequency and precompression (Barr and Zhang 2012, Liu et al 2016, Ramião et al 2016)), we report lower stiffness values in this study than measured by dynamic based excitation methods.

5. Conclusion

In summary, we have established a novel quantitative breast tissue stiffness estimation framework amenable to clinical workflows associated with interventional/surgical image-guided environments. We characterized the performance of the method in simulation and established the test–retest reproducibility of the resulting stiffness values in vivo in healthy volunteers. The feasibility and reproducibility of the stiffness estimation method presented here is encouraging and several future opportunities for improvement and implementation into other applications exist. The framework suggested in this work can be seamlessly integrated and adds only a single additional 2 min scan to a supine imaging procedure. With this single additional scan, we realize an ability to develop patient-specific breast geometric models with appropriate quantitative stiffness estimates for use within novel image guided-breast surgery systems with no specialized equipment and using standard imaging sequences available on traditional clinical MR scanners.