Statistical power to detect violation of the proportional hazards assumption when using the Cox regression model

Abstract

The use of the Cox proportional hazards regression model is widespread. A key assumption of the model is that of proportional hazards. Analysts frequently test the validity of this assumption using statistical significance testing. However, the statistical power of such assessments is frequently unknown. We used Monte Carlo simulations to estimate the statistical power of two different methods for detecting violations of this assumption. When the covariate was binary, we found that a model-based method had greater power than a method based on cumulative sums of martingale residuals. Furthermore, the parametric nature of the distribution of event times had an impact on power when the covariate was binary. Statistical power to detect a strong violation of the proportional hazards assumption was low to moderate even when the number of observed events was high. In many data sets, power to detect a violation of this assumption is likely to be low to modest.

1. Introduction

Survival or time-to-event outcomes occur frequently in the medical literature [1]. In the medical and epidemiological literature, the Cox proportional hazards regression model is the most common regression model for examining the effect of covariates on survival outcomes. This model allows one to model the effect of explanatory variables on the hazard of the outcome [2]. A key assumption of this model is that of proportional hazards: the relative effect of a covariate on the hazard function does not change over time.

Applied analysts often assess the validity of the proportional hazards assumption when fitting hazard models. However, the statistical power of such assessments has received little attention. The objective of this paper was to examine the statistical power to detect violations of the proportional hazards assumption when fitting a Cox proportional hazards model. In order to conduct simulations to assess the statistical power of different statistical methods for detecting violations of the proportional hazards assumption, there is a need to describe a data-generating process for the Cox proportional hazard model in the presence of time-varying covariate effects. The paper is structured as follows. In Section 2, we describe a data-generating process for settings in which there is a time-varying covariate effect (i.e. for settings in which the proportional hazards assumption is violated). We consider scenarios in which the distribution of event times follows one of three distributions: exponential, Weibull, and Gompertz. In Section 3, we conduct a series of Monte Carlo simulations to investigate the statistical power of different methods to detect violation of the proportional hazards assumption when fitting a Cox regression model. Finally, in Section 4 we summarize our findings and place them in the context of the existing literature.

2. Data-generating processes for models with time-variant covariate effects or non-proportional hazards

In this section we describe data-generating processes for models with time-varying covariate effects. For simplicity, we assume that there is a single covariate whose effect on the hazard function varies over time, while the remaining covariates have time-invariant effects on the hazard function. Our results easily generalize to more complex settings with multiple covariates with time-varying covariate effects. We consider the setting in which the regression coefficient changes as a linear function of time. In Section 2.1, we provide relevant background information. In Section 2.2, we summarize previous work on generating time-to-event data for a Cox model with time-invariant covariate effects. Data-generating processes for models with time-varying covariate effects, which are extension of these methods, are described in Section 2.3.

2.1. Background and notation

Let h(t|x) = h₀(t) exp (β′x) denote the conventional Cox proportional model with time-invariant covariate effects, where t denotes time, x is the vector of time-invariant covariates, β is the vector of time-invariant regression coefficients, and h₀(t) denotes the baseline hazard function. The model can also be written in additive form: log(h(t|x)) = log(h₀(t)) + β′x. The model can be modified to incorporate time-varying covariate effects as follows: h(t|x) = h₀(t) exp (β(t)′x).

The survival function of the model with time-invariant covariate effects is S(t|x) = exp(−H₀(t) exp (β′x)), where H₀(t) is the cumulative baseline hazard function, which is defined as $H_0(t)={\int }_0^t{h}_0(u)\mathrm{d}u$. The distribution function of event times under the Cox proportional hazards model is F(t|x) = 1 − exp(−H₀(t) exp (β′x)).

2.2. Generating data with time-invariant covariate effects

In the setting with time-invariant covariates and time-invariant covariate effects, both Leemis and Bender et al. showed that an event time, T, can be generated by $T=H_0^{-1}[-log(u)\text{exp}(-{\mathbf{\beta }}^{\prime }\mathbf{x})]$, where u ~ U(0,1) (where U (0,1) denotes the standard uniform distribution) [3,4]. Both sets of authors had the key insight that simulating event times from a Cox model with time-invariant covariates requires inverting the survival function.

Bender et al. note that among the commonly-used distributions for survival times, only the exponential, the Weibull, and the Gompertz distributions also share the assumption of proportional hazards with the Cox model. The parameters required for each distribution, the hazard function, the cumulative hazard function, the inverse of the cumulative hazard function, and the formula for simulating survival times from each distribution in the setting of time-invariant covariates are described in Table 1 (see Bender et al. [4] for further details). While there are different parameterizations of the Weibull distribution, we use the parameterization of Bender et al.

Table 1.

Characterization of the exponential, Weibull, and Gompertz distributions.

Characteristic	Exponential distribution	Weibull distribution	Gompertz distribution
Parameter	Scale parameter λ > 0	Scale parameter λ > 0 Shape parameter ν > 0	Scale parameter λ > 0 Shape parameter −∞ < α < ∞
Hazard function	h0(t) = λ	h0(t) = λνtν−1	h0(t) = λ exp(αt)
Cumulative hazard function	H0(t) = λt	H0(t) = λtν	$H_0(t)=\frac{\lambda }{\alpha }(exp(\alpha t)-1)$
Inverse cumulative hazard function	$H_0^{-1}(t)={\lambda }^{-1}t$	$H_0^{-1}(t)={({\lambda }^{-1}t)}^{1/\nu }$	$H_0^{-1}(t)=\frac{1}{\alpha }log\left(\frac{\alpha }{\lambda }t+1\right)$
Simulating survival times with time-invariant covariates and time-invariant covariate effects (u ~ U(0, 1))	$T=-\frac{log(u)}{\lambda exp({\beta }^{\prime }x)}$	$T={\left(-\frac{log(u)}{\lambda exp({\beta }^{\prime }x)}\right)}^{1/\nu }$	$T=\frac{1}{\alpha }log\left(1-\frac{\alpha log(u)}{\lambda exp({\beta }^{\prime }x)}\right)$

2.3. Generating data with time-varying covariate effects

We let the vector of covariates be decomposed as follows: (x, z), where x denotes the vector of covariates whose effects on the hazard function are constant or time-invariant, while z denotes the single covariate whose effect on the hazard function varies over time. In each scenario we consider three distributions of event times: exponential, Weibull, and Gompertz. While the data-generating function is described in the text, complete derivations for all distributions are reported in Appendices A1.1–A1.3.

We used the framework described by Leemis and by Bender et al. [3,4], whose key observation was that survival times could be generated by inverting the survival function. This approach has been modified elsewhere for simulating time-to-event data from a model with time-varying covariates [5]. Each of our derivations follows the same pattern. First, we integrate the hazard function to determine the cumulative hazard function. Second, we compute the survival function as the exponential function evaluated at the negative of the survival function. Third, we invert the survival function. This method for simulating event times with time-dependent effects has been described previously by Crowther and Lambert [6].

Throughout this section we assume that the regression coefficient associated with z is a linear function of time: β(t)z = (β₀ + β₁t)z.

2.3.1. Exponential distribution of event times

If event times follow an exponential distribution, an event time can be simulated by evaluating

$$T=\{\begin{array}{l}\frac{1}{{\beta }_{1}z}log\left(1-\frac{{\beta }_{1}zlog(u)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}\right),\text{provided}\text{that}{\beta }_{1}z\ne 0,\hfill \\ \frac{-log(u)}{\lambda e^{\gamma x}{e}^{{\beta }_{0}z}},\text{if}{\beta }_{1}z=0,\hfill \end{array}$$

where u ~U(0,1) (see Appendix A1.1 for derivation).

R and SAS code for simulating data from this distribution is described in Appendix A2.1.

2.3.2. Weibull distribution of event times

If event times follow an exponential distribution, then generation of event times requires determining the inverse of the survival function: exp[−λυe^γxe^β₀z(t^υ (−β₁tz)^−υ (Γ(υ) − Γ(υ,−β₁tz)))] (where Γ(x) and Γ(x, a) denote the Gamma and Incomplete Gamma functions, respectively), and evaluating it at u ~ U(0, 1) (see Appendix A1.2 for derivation).

A closed-form expression for the inverse of the survival function does not exist. Instead, numerical methods would need to be used to approximate the inverse of this function. For a given value of u, one can define a new function: S(t) – u and then find the roots of this function. Two options for finding roots are the Brent method and the Newton–Raphson method for root finding. Crowther and Lambert found that the former tended to have superior performance to the latter [6]. R code for simulating data from this distribution is described in Appendix A2.2 (SAS code is not provided due to limitations to implementing Brent’s root finder in SAS).

2.3.3. Gompertz distribution of event times

If event times follow a Gompertz distribution, then event times can be simulated by evaluating

$$T=\{\begin{array}{ll}\frac{1}{\alpha +{\beta }_{1}z}log\left(1-\frac{(\alpha +{\beta }_{1}z)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}log(u)\right),\hfill & \text{if}\alpha +{\beta }_{1}z\ne 0,\hfill \\ \frac{-log(u)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}\hfill & \text{if}\alpha +{\beta }_{1}z=0,\hfill \end{array}$$

where u ~ U(0, 1) (see Appendix A1.3 for derivation).

R and SAS code for simulating data from this distribution is described in Appendix A2.3.

3. Monte Carlo simulations to assess statistical power to detect violation of the proportional hazards assumption

We used Monte Carlo simulations to estimate the statistical power to detect violation of the proportional hazards assumption when fitting a Cox proportional hazards regression model. We allowed the covariate for which the proportional hazards assumption was violated to be either binary or continuous. We examined the effect of the following three factors on statistical power to detect this violation: (i) number of observed events; (ii) the magnitude of deviation from proportionality; (iii) the prevalence of the binary covariate.

3.1. Methods

3.1.1. The proportional hazards assumption was violated for a binary covariate

We assumed that there was a binary covariate with a time-varying covariate effect, such that its regression coefficient varied as a linear function of time after adjusting for a continuous covariate. The single continuous covariate can be thought of either as a single covariate (e.g. age) or as a risk score summarizing the contribution of a vector of covariates. Furthermore, conditional on the covariates, we assumed that event times followed a Gompertz distribution with parameters α = 0.025 and λ = 0.001.

For each of N subjects, a continuous covariate was simulated from a standard normal distribution: x ~ N(0, 1) and a binary covariate was simulated from a Bernoulli distribution with parameter p_binary: z ~ Be(p_binary). Time-to-event outcomes were simulated from the following model using methods described in the previous section: log (h(t|x, z)) = log(h₀(t)) + log(1.5)x + (log(1.1) + t log(hr_interaction))z, where the baseline hazard function h₀(t) = λ exp (αt). Thus, a one-standard deviation increase in the continuous covariate is associated with a 50% increase in the hazard of the outcome. The effect of the binary covariate varies with time. At t = 0, the presence of the condition indicated by z is associated with a 10% increase in the hazard of the outcome, while at t = 365, the presence of the condition is associated with an exp(log(1.1) + 365 log (hr_interaction)) increase in the hazard.

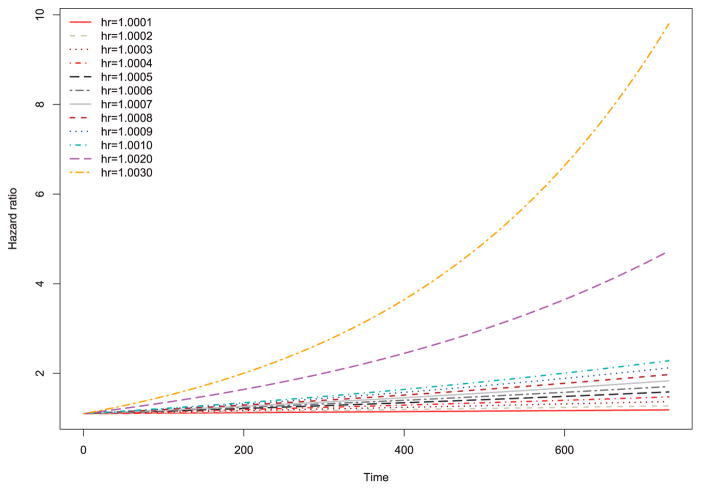
The values of the time-specific hazard ratios are described in Figure 1 for 12 values of hr_interaction: 1.0001 to 1.0010 in increments of 0.0001, and 1.002 and 1.003. Each of the 12 lines shows the value of the time-specific hazard ratio as time ranges from 0 to 730 (i.e. two years). For all values of hr_interaction, the value of the hazard ratio was 1.1 at t = 0. When hr_interaction = 1.003, the value of the hazard ratio for the binary exposure variable was 9.8 at two years (t = 730). When hr_interaction = 1.002, the value of the hazard ratio was 4.7 at two years. In the simulations that follow, we made the subjective decision to use hr_interaction = 1.003 to denote a very strong violation of the proportional hazards assumption and hr_interaction = 1.002 to denote a strong violation of the proportional hazards assumptions.

Figure 1.

Hazard ratio as a function of time.

In each simulated data set, we fit the following hazard regression model: log(h(t|x, z)) = log(h₀(t)) + γx + (β₀ + β₁t)z. We tested the statistical significance of the time-varying effect of z: H_0: β₁ = 0. The proportional hazards assumption was rejected if the significance of this component was less than or equal to 0.05. This process was repeated 1000 times for each of the scenarios. The estimated statistical power was the proportion of the simulated data sets in which the proportional hazards assumption was rejected.

The methods described above permit an assessment of the statistical power of a model-based approach to assessing the validity of the proportional hazards assumption. We also examined the statistical power of an alternative approach based on cumulative sums of martingale residuals over time that was described by Lin et al. [7]. We used a Kolmogorov-type supremum test that was computed on 1000 simulated patterns. When using this method, the following model was fit in each simulated data set: log(h(t|x, z)) = log(h₀(t)) + β₁x + β₂z. For this method, 500 iterations were conducted for each of the scenarios due to the increased computational complexity of each individual analysis.

We then repeated the above analyses simulating data such that the distribution of event times was exponential with parameter λ = 0.01.

We conducted three separate sets of simulations. In the first set of simulations, we examined the effect of the observed number of events on statistical power to detect violation of the proportional hazards assumption. We fixed hr_interaction in the above data-generating process at 1.002 (to denote a strong violation of the proportional hazards assumption) and the prevalence of the binary covariate at 0.25. We then allowed the sample size to range from 100 to 1000 in increments of 100. We did not induce censoring in the simulated data set, so that the number of events would equal the sample size. In the second set of simulations, we examined the effect of the magnitude of the change in the hazard ratio over time on statistical power to detect violation of the proportional hazards assumption. We fixed the sample size at 1000 subjects (and did not induce censoring, so that the number of observed events would equal 1000) and the prevalence of the binary covariate at 0.25. When then allowed hr_interaction to take 12 values: 1.0001 to 1.0010 in increments of 0.0001, and 1.002 and 1.003 (see text above and Figure 1 for illustration of the magnitude of the violation of the proportional hazards assumption). In the third set of simulations, we examined the effect of the prevalence of the binary covariate on statistical power to detect violation of the proportional hazards assumption. We fixed the sample size at 1000 subjects (and did not induce censoring, so that the number of observed events would equal 1000) and hr_interaction at 1.002 (to denote a strong violation of the proportional hazards assumption). We then allowed the prevalence of the binary covariate to range from 0.05 to 0.50 in increments of 0.05.

3.1.2. The proportional hazards assumption was violated for a continuous covariate

We modified the simulations described above in order to examine scenarios in which there was a continuous covariate with a time-varying covariate effect, such that its regression coefficient varied as a linear function of time after adjusting for a second continuous covariate. The following minor modification was made to the simulations described above: for each subjects a continuous covariate was simulated from a standard normal distribution: x ~ N(0, 1) and a second continuous covariate was simulated from a standard normal distribution: z ~ N(0, 1). The two normal distributions were assumed to be independent of one another. Apart from this modification, the simulations and analyses were identical to those described above (with the obvious exception that we only examined the effect of the number of events and the magnitude of the interaction with time on statistical power and did not consider prevalence). The values of the time-specific hazard ratios for the continuous covariate are described in Figure 1 for 12 values of hr_interaction. For this set of simulations, the hazard ratios can be interpreted as the relative change in the instantaneous hazard of the event associated with a one standard deviation increase in the continuous covariate.

3.2. Results

3.2.1. Results – binary covariate with a time-varying effect

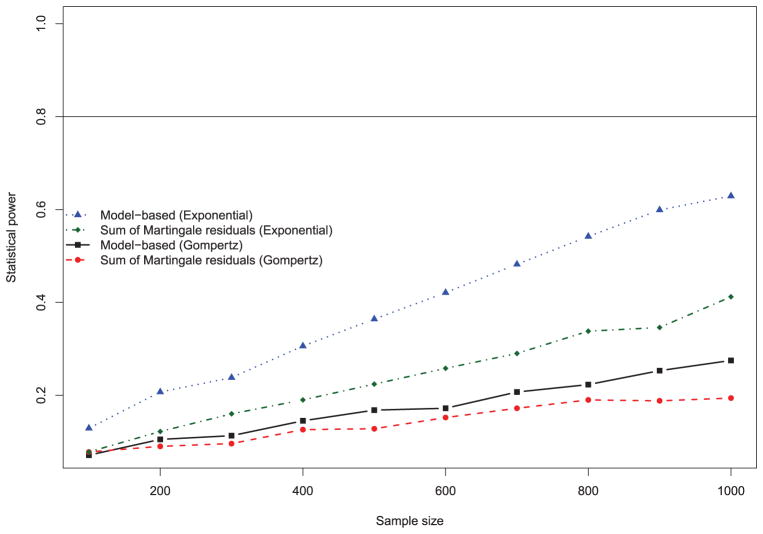
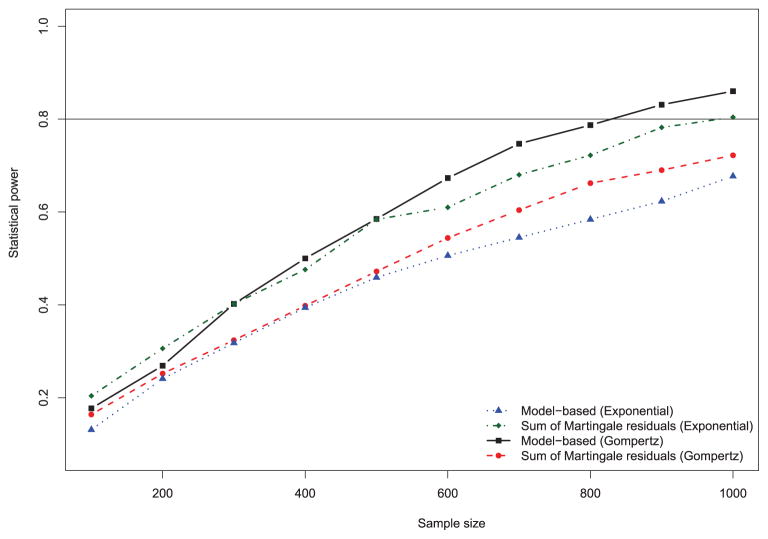
The effect of the number of observed events on the statistical power of each of the two methods for assessing the validity of the proportional hazards is described in Figure 2 for each of the two distributions of event times. We have superimposed on the figure a horizontal line denoting statistical power of 0.8 (or 80%). As would be expected, statistical power increased with increasing number of events. For a given distribution of event times, the model-based test of the proportional hazards assumption had greater power to detect violation of this assumption than did the method based on sums of cumulative martingale residuals. Differences in statistical power between the two methods were greater when event times followed an exponential distribution than when event times followed a Gompertz distribution. Interestingly, for a given method of assessing non-proportionality, there was greater statistical power to detect a violation of the proportional hazards assumption when event times followed an exponential distribution than when the distribution was Gompertz. Despite the fact that the effect of the covariates on the hazard function was the same between the two models, the underlying distribution of event times had a substantial impact on the statistical power to detect a violation of the proportional hazards assumption. For both distributions, statistical power to detect a strong violation of the proportional hazards assumption (hr_interaction = 1.002) was low to moderate. When the distribution of event times was exponential and the number of events was equal to 1000, statistical power was 0.63 when using a parametric test. When the distribution of event times was Gompertz and the number of events was 1000, statistical power was 0.28when using a parametric test. In no scenarios was the empirical estimate of statistical power close to 0.80, which is often used as the minimally acceptable power when designing studies.

Figure 2.

Effect of number of events on power to detect violation of the proportional hazards assumption (binary covariate).

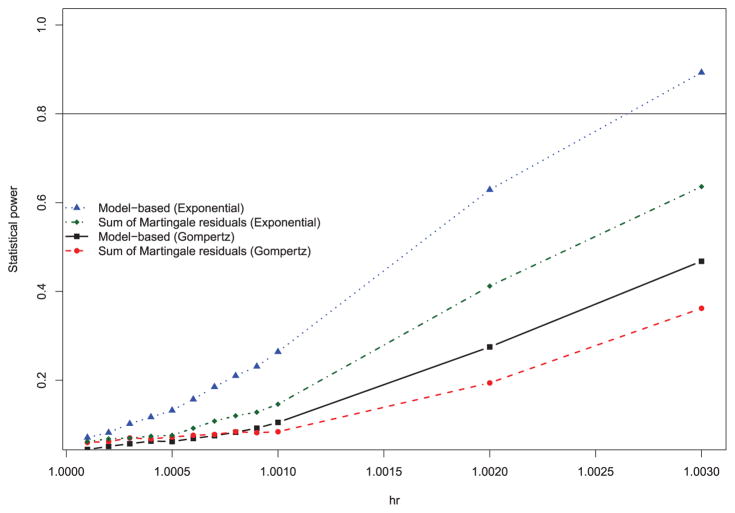
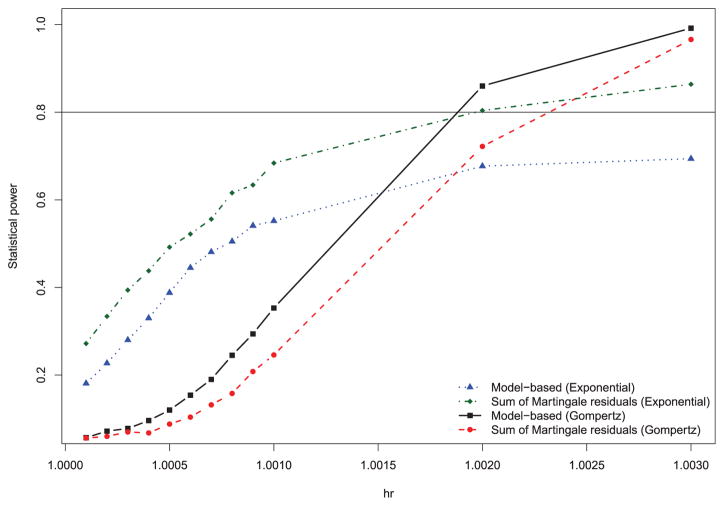
The effect of the magnitude of the time-covariate interaction (i.e. hr_interaction) on the statistical power of each of the two methods for assessing the validity of the proportional hazards is described in Figure 3 when the number of observed events was 1000 and the prevalence of the binary covariate was 0.25. As would be expected, for a given statistical method and distribution of event times, statistical power increased as the magnitude of the deviation from proportionality (hr_interaction) increased. As above, for a given distribution of event times, the model-based test of the proportional hazards assumption tended to have greater power than did the method based on sums of cumulative martingale residuals (when the interaction was weak and the distribution of event times was Gompertz, then the method based on sums of cumulative martingale residuals had slightly greater power; however, the power of both methods was very low in these settings). As above, there was greater statistical power to detect a violation of the proportional hazards assumption when event times followed an exponential distribution than when the distribution was Gompertz. When the distribution of event times was exponential, statistical power to detect non-proportionality exceeded 80% only once the value of hr_interaction was 1.003, which, as illustrated above, is a very strong violation of the proportional hazards assumption (Figure 1). When the distribution of event times was Gompertz, then neither method had statistical power that exceeded 80% even when there was a very strong violation of the proportional hazards assumption. When the magnitude of the violation of the proportional hazards assumption was weak to moderate, statistical power to detect this violation was low.

Figure 3.

Effect of magnitude of interaction with time on power to detect violation of the proportional hazards assumption (binary covariate).

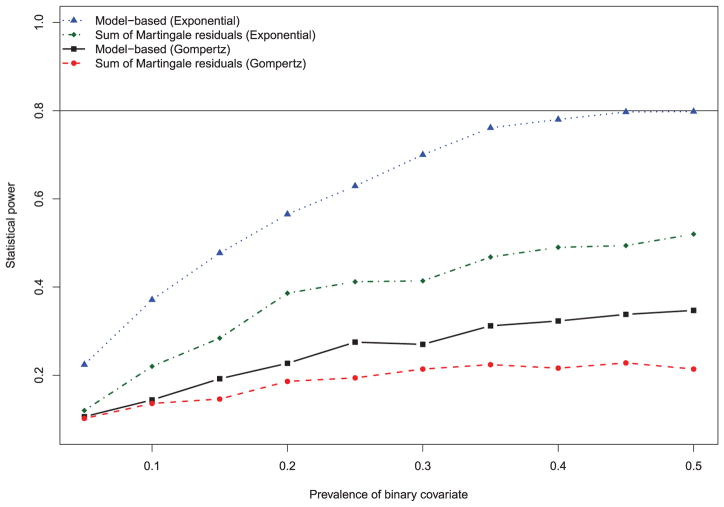
The effect of the magnitude of the prevalence of the binary covariate on the statistical power of each of the two methods for assessing the validity of the proportional hazards is described in Figure 4 when the number of observed events was 1000 and the value of hr_interaction was 1.002 (which, as described above, is a strong violation of proportionality). Statistical power to detect violation of proportionality increased as the prevalence of the binary covariate increased from 0.05 to 0.50. As above, for a given parametric distribution of event times, the model-based test of the proportional hazards assumption had greater power than did the method based on sums of cumulative martingale residuals. Similar to above, there was greater statistical power to detect a violation of the proportional hazards assumption when event times followed an exponential distribution than when the distribution was Gompertz. Even with a large number of observed events (N = 1000) and a strongly non-proportional effect (hr_interaction = 1.002), statistical power was still below 80% regardless of the prevalence of the binary covariate and the distribution of event times. Statistical power approached 80% when the prevalence of the binary covariate was 0.50 and the distribution of event times was exponential.

Figure 4.

Effect of prevalence on power to detect violation of the proportional hazards assumption (binary covariate).

3.2.2. Results – continuous covariate with a time-varying effect

In this section we present the results for the simulations in which the variable that had a non-proportional effect was continuous. The effect of the number of events on statistical power is described in Figure 5. As one would expect, statistical power increased as the number of events increased. Apart from this unsurprising observation, some of the observations differed from the setting in which a binary covariate had a time-varying effect. First, statistical power tended to be modestly higher when the covariate was continuous compared to when the covariate was binary. When the number of events was large (≥900) then the statistical power to detect a non-proportional covariate effect exceeded 80% for some distributions of event times and some methods of testing non-proportionality. Second, for a given testing method (model-based or sums of cumulative of Martingale residuals), statistical power was not always higher when event times followed an exponential distribution compared to a Gompertz distribution. Indeed, the distribution that resulted in the greatest statistical power depended on the method used to test for non-proportionality. Third, when the distribution of events was exponential, the method based on the sums of cumulative of Martingale residuals resulted in greater statistical power than did the model-based method of testing (whereas the converse was true when the distribution of events was Gompertz).

Figure 5.

Effect of number of events on power to detect violation of the proportional hazards assumption (continuous covariate).

The effect of the magnitude of the time-covariate interaction (i.e. hr_interaction) on the statistical power of each of the two methods for assessing the validity of the proportional hazards is described in Figure 6 when the number of observed events was 1000. As would be expected, statistical power increased as the magnitude of the deviation from proportionality (hr_interaction) increased. However, some differences were observed from the scenario with a binary covariate. First, when event times followed an exponential distribution, the use of the method based on the sums of cumulative of Martingale residuals had greater statistical power to detect non-proportionality compared to the model-based method. Second, for a given statistical method of assessing non-proportionality, statistical power was not consistently greater under the exponential distribution than under the Gompertz distribution. When the deviation from proportionality was weaker, greater statistical power was observed under the exponential distribution than under the Gompertz distribution. However, the reverse was true when the deviation from proportionality was stronger.

Figure 6.

Effect of magnitude of interaction with time on power to detect violation of the proportional hazards assumption (continuous covariate).

4. Discussion

The analysis of survival data is pervasive in modern biomedical and epidemiological research and the use of the Cox proportional hazards regression model is ubiquitous in modern biostatistical applications. One of the assumptions of the Cox proportional hazards models is that the effect of a given covariate on the hazard function is proportional over time. Applied biomedical investigators often assess the validity of this assumption in their analyses. While this assumption is often tested (either at the analyst’s initiative or at the request of a reviewer after submission of a manuscript for peer-review), the statistical power of such assessments have not been well described. We used MonteCarlo simulations to assess the statistical power to detect violation of the proportional hazards assumption.

We found that even when the number of events that were observed was large (e.g. 1000) statistical power was low to modest to detect a strong violation of the proportional hazards assumption when the covariate in question was binary. Statistical power tended to be higher when the covariate was continuous. Statistical power was very low to moderate (<80%) to detect a weak to modest violation of the proportional hazards assumption. We suspect that in many clinical data sets, statistical power to detect violations of the proportional hazards assumption would be poor. However, in studies conducted using large electronic health care administrative databases, which typically have much larger sample sizes, statistical power to detect such a violation is likely substantially higher. However, when studying rare outcomes, even large electronic administrative databases may result in sub-optimal power to detect violation of the proportional hazards assumption. From our simulations it would appear that three conditions need to be met simultaneously in order for statistical power to exceed 80%: (i) a large number of events, (ii) a strong deviation from proportionality, and (iii) a binary covariate that has a prevalence close to 0.50. When the covariate is continuous then one requires both a large number of events and a strong deviation from proportionality.

We explicitly described data-generating processes for simulating data with a non-proportional effect of a given covariate on the hazard of the outcome. We have provided R and SAS code for implementing these data-generating processes in the Appendices. This will allow analysts to estimate the statistical power in scenarios that are representative of their research setting. The simulations described in this paper can be customized to specific settings to permit an investigation of statistical power in diverse settings.

We compared the empirical estimates of statistical power of two different approaches to detect violation of the proportional hazards assumption. The first approach was model-based and was based on testing the statistical significance of the interaction between time and the regression coefficient for the variable of interest. The second approach was the method proposed by Lin et al. that used cumulative sums of martingale residuals over time [7]. When the covariate that a non-proportional effect was binary, we found that the model-based approach had higher statistical power to detect violation of the proportional hazards assumption. However, when the covariate that had a non-proportional effect was continuous, the statistical method for assessing non-proportionality that had the highest statistical power depended on the distribution of event times. When the covariate was binary the distribution of event times had a moderate impact on statistical power. Statistical power was moderately greater when event times followed an exponential distribution compared to when event times followed a Gompertz distribution. However, this was not the case when the covariate was continuous.

A Cox regression model with a time-invariant hazard ratio (i.e. a model in which the proportional hazards assumption is satisfied) provides a simple interpretation of the effect of the covariate: the relative effect of the covariate on the instantaneous hazard of the outcome is constant across time. Such an interpretation is relatively simple to communicate to non-statistical audiences. However, if this assumption is violated, then the relative effect of the covariate on the instantaneous hazard of the outcome varies over time. Authors can report time-specific hazard ratios (e.g. the hazard ratio at one year, two years, etc.) [8]. A relevant question is what are the consequences of ignoring a time-varying covariate effect and fitting a model with a time-invariant covariate effect. Beyersmann et al. suggest that fitting a model that assumes a time-invariant covariate effect produces a coefficient that can be interpreted as a time-averaged effect [9] (page 144). Thus, a model that ignores the time-varying effect of a covariate can be thought of as estimating the average instantaneous effect of the covariate over the duration of follow-up. In settings that are likely to have sub-optimal statistical power to detect violations of the proportional hazards assumption, the analyst may have to be satisfied with reporting time-averaged effects of the model covariates.

In summary, statistical power was modest to detect a strong violation of the proportional hazards assumption even when the number of observed events was large. Detecting a weak to moderate violation of the assumption would require a very large number of observed events. Many clinical data sets may have insufficient sample size to detect meaningful departures from the proportional hazards assumption.

Appendix 1

A1.1. Exponential distribution of event times (covariate effect is a linear effect of time)

If event times follow an exponential distribution, the baseline hazard function is equal to λ₀(t) = λ. Then the cumulative hazard function is equal to

$$\begin{gathered} H(t\mid \mathbf{x},z)={\int }_0^t{\lambda }_0(s)e^{\gamma \mathbf{x}+\beta (s)z}\mathrm{d}s={\int }_0^t\lambda e^{\gamma \mathbf{x}}{e}^{\beta (s)z}\mathrm{d}s=\lambda e^{\gamma \mathbf{x}}{\int }_0^t{e}^{\beta (s)z}ds \\ =\lambda e^{\gamma \mathbf{x}}{\int }_0^t{e}^{({\beta }_0+{\beta }_{1}s)z}\mathrm{d}s=\lambda e^{\gamma \mathbf{x}}{\int }_0^t{e}^{{\beta }_{0}z}{e}^{{\beta }_{1}sz}ds=\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}{\int }_0^t{e}^{{\beta }_{1}sz}ds \\ =\frac{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}{{\beta }_{1}z}{[e^{{\beta }_{1}sz}]}_0^t=\frac{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}{{\beta }_{1}z}[e^{{\beta }_{1}tz}-1](\text{provided}{\beta }_{1}z\ne 0). \end{gathered}$$

The distribution function of the event times is equal to

$$F(t\mid \mathbf{x},z)=1-exp(-H(t\mid \mathbf{x},z)=1-exp\left(-\frac{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}{{\beta }_{1}z}[e^{{\beta }_{1}tz}-1]\right).$$

Therefore,

$$u=exp\left(-\frac{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}{{\beta }_{1}z}[e^{{\beta }_{1}tz}-1]\right)~U[0,1].$$

Solving for t gives:

$$log(u)=-\frac{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}{{\beta }_{1}z}(e^{{\beta }_{1}tz}-1),$$

thus

$$\frac{-{\beta }_{1}zlog(u)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}=e^{{\beta }_{1}tz}-1,$$

thus

$$1-\frac{{\beta }_{1}zlog(u)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}=e^{{\beta }_{1}tz},$$

thus

$$log\left(1-\frac{{\beta }_{1}zlog(u)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}\right)={\beta }_{1}zt,$$

resulting in

$$t=\frac{1}{{\beta }_{1}z}log\left(1-\frac{{\beta }_{1}zlog(u)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}\right),\text{provided}\text{that}{\beta }_{1}z\ne 0.$$

If β₁z = 0, then the effect of the covariate is time-invariant and methods based on those described by Bender et al. can be used to generate an event time.

A1.2. Weibull distribution of event times (covariate effect is a linear effect of time)

The baseline hazard function is equal to λ₀(t) = λυt^υ−1. Then the cumulative hazard function is

$$\begin{gathered} H(t\mid \mathbf{x},z)={\int }_0^t{\lambda }_0(s)e^{\gamma \mathbf{x}+\beta (s)z}\mathrm{d}s={\int }_0^t\lambda v{s}^{v-1}{e}^{\gamma \mathbf{x}}{e}^{\beta (s)z}\mathrm{d}s=\lambda v{e}^{\gamma \mathbf{x}}{\int }_0^t{s}^{v-1}{e}^{({\beta }_0+{\beta }_{1}s)z}\mathrm{d}s \\ =\lambda v{e}^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}{\int }_0^t{s}^{v-1}{e}^{{\beta }_{1}sz}\mathrm{d}s=\lambda v{e}^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}[t^v{(-{\beta }_{1}tz)}^{-v}(\mathrm{\Gamma }(v)-\mathrm{\Gamma }(v,-{\beta }_{1}tz))]. \end{gathered}$$

The cumulative hazard function involves a difference of a Gamma function and an Incomplete Gamma function. Then, the cumulative distribution of event times is

$$F(t\mid \mathbf{x},z)=1-exp[-H(t\mid \mathbf{x},z),$$

and

$$u=exp[-\lambda v{e}^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}(t^v{(-{\beta }_{1}tz)}^{-v}(\mathrm{\Gamma }(v)-\mathrm{\Gamma }(v,-{\beta }_{1}tz)))]~U(0,1).$$

An event time can be generated by solving the above expression for t and evaluating the expression at u ~ U(0, 1). However, a closed-form expression for the inverse of the above expression cannot be obtained. As an alternative approach, one could use numerical methods to find an approximate inverse to the above expression for a given value of u.

A1.3. Gompertz distribution of event times (covariate effect is a linear effect of time)

The baseline hazard function is equal to λ₀(t) = λe^αt. Then the cumulative hazard function is

$$\begin{gathered} H(t\mid \mathbf{x},z)={\int }_0^t{\lambda }_0(s)e^{\gamma \mathbf{x}+\beta (s)z}\mathrm{d}s={\int }_0^t\lambda e^{\alpha s}{e}^{\gamma \mathbf{x}}{e^{({\beta }_0+{\beta }_{1}s)}}^z\mathrm{d}s=\lambda e^{\gamma \mathbf{x}}{\int }_0^t{e}^{\alpha s}{e}^{{\beta }_{0}z}{e}^{{\beta }_{1}zs}\mathrm{d}s \\ =\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}{\int }_0^t{e}^{\alpha s}{e}^{{\beta }_{1}zs}\mathrm{d}s=\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}{\int }_0^t{e}^{(\alpha +{\beta }_{1}z)s}\mathrm{d}s \\ =\frac{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}{\alpha +{\beta }_{1}z}{[e^{(\alpha +{\beta }_{1}z)s}]}_0^t=\frac{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}{\alpha +{\beta }_{1}z}[e^{(\alpha +{\beta }_{1}z)t}-1]\text{provided}\text{that}\alpha +{\beta }_{1}z\ne 0. \end{gathered}$$

Then the cumulative distribution of event times is

$$F(t\mid \mathbf{x},z)=1-exp(-H(t\mid \mathbf{x},z))$$

and

$$u=exp(-H(t\mid \mathbf{x},z))~U(0,1).$$

To invert this function, we have that

$$u=exp\left(-\frac{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}{\alpha +{\beta }_{1}z}[e^{(\alpha +{\beta }_{1}z)t}-1]\right),$$

thus

$$\begin{gathered} log(u)=-\frac{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}{\alpha +{\beta }_{1}z}[e^{(\alpha +{\beta }_{1}z)t}-1], \\ \frac{-(\alpha +{\beta }_{1}z)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}log(u)=e^{(\alpha +{\beta }_{1}z)t}-1, \\ 1-\frac{(\alpha +{\beta }_{1}z)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}log(u)=e^{(\alpha +{\beta }_{1}z)t}, \end{gathered}$$

so that

$$log\left(1-\frac{(\alpha +{\beta }_{1}z)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}log(u)\right)=(\alpha +{\beta }_{1}z)t,$$

so that

$$t=\frac{1}{\alpha +{\beta }_{1}z}log\left(1-\frac{(\alpha +{\beta }_{1}z)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}log(u)\right),\text{provided}\text{that}\alpha +{\beta }_{1}z\ne 0.$$

If α + β₁z = 0 then the calculation of the cumulative hazard function must be modified as follows:

$$H(t\mid \mathbf{x},z)=\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}{\int }_0^t{e}^0\mathrm{d}s=\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}{\int }_0^t\mathrm{d}s=\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}t.$$

Then, we have that u = exp(−H(t|x, z)) = exp(−λe^γxe^β₀zt). To invert this expression, we have that log(u) = −λe^γxe^β₀zt and hence that

$$t=\frac{-log(u)}{\lambda e^{\gamma \mathbf{x}}{e}^{{\beta }_{0}z}}.$$

Appendix 2

A2.1. R and SAS code for simulating event time data with an exponential distribution when the log-hazard ratio of the binary variable changes linear with time

# The following software code is provided for illustrative purposes
only and comes with absolutely no warranty.
# Simulate data from a Cox-exponential model when the effect of
# treatment
# varies as a linear function of time.
N <- 10000
# Number of subjects in each simulated dataset.
# Parameter of the exponential distribution.
lambda <- 0.01
g1 <- log(1.5)
# Log-hazard ratio for the continuous covariate.
b0 <- log(1.1)
# Log-hazard ratio for the binary covariate at t = 0.
hr <- 1.005
b1 <- log(hr)
# Effect of time on the log-hazard ratio for the binary covariate.
prev <- 0.25
# Prevalence of the binary covariate.
set.seed(1)
# Set random number seed for reproducibility.
x <- rnorm(N)
z <- rbinom(N,size=1,prob=prev)
u <- runif(N,0,1)
event.time <- ifelse(b1*z= =0,
        −log(u)/(lambda*exp(g1*x)),
     (1/b1*z) * log(1−b1*z*log(u)/(lambda*exp(g1*x + b0*z))))
simdata <- cbind(x,z,event.time)
write(t(simdata),ncol=3,file=”exp.dat”,append=T)
%macro dgp_exp(N=,lambda=,hr_cont=,b0=,b1=,prev=0,ranseed=);
*** N is the size of the simulated dataset;
*** lambda is the parameter for the exponential distribution of
       event times;
*** hr_cont is the hazard ratio for the continuous covariate;
*** b0 is the hazard ratio for the binary variable at time t = 0;
*** b1 is the relative change in the effect of binary covariate
       as a function;
**        of time;
*** prev is the prevalence of the binary covariate;
*** ranseed is a seed for random number generation to ensure ;
***       reproducibility of the results.;
data randata;
   call streaminit(&ranseed);
   do i = 1 to &N;
       /* Random uniform variable for generating event times */
       u = rand(“Uniform”);
       /* The binary covariate with a time-varying covariate effect */
       z = rand(“binomial”,&prev,1);
       /* The continuous covariate for which we are adjusting */
       x = rand(“normal”,0,1);
       /* Parameter for the exponential distribution */
       lambda = λ
       gamma = log(&hr_cont);
       /* A one-standard deviation increase in x increases the hazard
           of the outcome by this amount */
       b0 = log(&b0);
       b1 = log(&b1);
       if (b1*z=0) then
         event_time = −log(u)/(lambda*exp(gamma*x));
       else
         event_time = (1/b1*z) * log(1 − b1*z*log(u)/(lambda*
            exp(gamma*x + b0*z)));
       event = 1;
       output;
   end;
run;
%mend dgp_exp;
%dgp_exp(N=10000,lambda=0.01,hr_cont=1.5,b0=1.1,b1=1.005,
     ranseed=1,prev=0.25);

A2.2. R code for simulating event time data with a Weibull distribution when the log-hazard ratio of the binary variable changes linear with time

# The following software code is provided for illustrative purposes
only and comes with absolutely no warranty.
# Simulate data from a Cox-Weibull model when the effect of
# treatment varies as a linear function of time.
# There is not a closed-form expression for the inverse of the
# survival function (S).
# Numerical methods are used to invert the survival function.
# We use Brent’s method for root finding to invert the function.
library(pracma)
# pracma package has a function for Brent’s method for finding
# roots and a function for the incomplete Gamma function.
N <- 10000
# Number of subjects in each simulated dataset.
# Parameters of the Weibull distribution.
lambda <- 0.001
nu <- 1
g1 <- log(1.5)
# Log-hazard ratio for the continuous covariate.
b0 <- log(1.1)
# Log-hazard ratio for the binary covariate at t=0.
hr <- 1.001
b1 <- log(hr)
# Effect of time on the log-hazard ratio for the binary covariate.
set.seed(1)
# Set random number seed for reproducibility.
simdata.matrix <- NULL
# Define the survival function
S2 <- function(t){
    exp(−lambda*nu*exp(g1*x + b0*z) * ((tˆnu) * (−b1*t*z)ˆ( − nu) *
        (gamma(nu) − gammainc(−b1*t*z,nu)[2]) ) ) − u
}
for (i in 1:N){ u <- runif(1,0,1)
   x <- rnorm(1)
   z <- rbinom(1,size=1,prob=0.25)
   if (z= =0){
     event.time <- (−log(u)/(lambda*exp(g1*x)))ˆ(1/nu)
   } else {
     brent.sol <- brent(S2,0.001,250000)
     event.time <- brent.sol$root
   }
   simdata <- c(x,z,event.time)
   simdata.matrix <- rbind(simdata.matrix,simdata)
}
   write(t(simdata.matrix),ncol=3,file=”weibull.dat”,append=T)

A2.3. R and SAS code for simulating event time data with a Gompertz distribution when the log-hazard ratio of the binary variable changes linear with time

# The following software code is provided for illustrative purposes
only and comes with absolutely no warranty.
# Simulate data from a Cox-Gompertz model when the effect of
# treatment varies as a linear function of time.
N <- 10000
# Number of subjects in each simulated dataset.
# Parameters of the Gompertz distribution.
lambda <- 0.0001
alpha <- 0.025
g1 <- log(1.5)
# Log-hazard ratio for the continuous covariate.
b0 <- log(1.1)
# Log-hazard ratio for the binary covariate at t=0.
hr <- 1.005
b1 <- log(hr)
# Effect of time on the log-hazard ratio for the binary covariate.
prev <- 0.25
# Prevalence of the binary covariate.
set.seed(1)
# Set random number seed for reproducibility.
x <- rnorm(N)
z <- rbinom(N,size=1,prob=prev)
u <- runif(N,0,1)
event.time <- ifelse(alpha+b1*z= =0,
   −log(u)/(lambda*exp(g1*x + b0*z)),
    (1/(alpha + b1*z)) * log(1 − (alpha + b1*z)*log(u)
   /(lambda*exp(g1*x + b0*z))))
simdata <- cbind(x,z,event.time)
write(t(simdata),ncol=3,file=”gompertz.dat”,append=T)
%macro dgp_gompertz(N=,lambda=,alpha=,hr_cont=,b0=,b1=,
      prev=0,ranseed=);
*** N is the size of the simulated dataset;
*** lambda and alpha are the parameters of the Gompertz
       distribution;
*** hr_cont is the hazard ratio for the continuous covariate;
*** b0 is the hazard ratio for the binary variable at time t = 0;
*** b1 is the relative change in the effect of binary covariate
       as a function;
**        of time;
*** prev is the prevalence of the binary covariate;
*** ranseed is a seed for random number generation to ensure;
***       reproducibility of the results.;
data randata;
    call streaminit(&ranseed);
do i = 1 to &N;
    /* Random uniform variable for generating event times */
    u = rand(“Uniform”);
    /* The binary covariate with a time-varying covariate effect */
    z = rand(“binomial”,&prev,1);
    /* The continuous covariate for which we are adjusting */
    x = rand(“normal”,0,1);
/* Parameters for the Gompertz distribution */
    lambda = λ
    alpha = α
    gamma = log(&hr_cont);
    b0 = log(&b0);
    b1 = log(&b1);
    if alpha + b1*z = 0 then
       event_time = −log(u)/(lambda * exp(gamma*x + b0*z));
    else
       event_time = (1/(alpha + b1*z)) * log(1 − (alpha + b1*z)
       *log(u)/(lambda*exp(gamma*x + b0*z)));
    event = 1;
    output;
    end;
run;
%mend dgp_gompertz;
%dgp_gompertz(N=10000,lambda=0.0001,alpha=0.025,hr_cont=1.5,
     b0=1.1,b1=1.005,prev=0.25,ranseed=1);