Abstract
Trabecular bone structure is crucial to normal mechanical behavior of bones. Studies have shown that osteoporosis negatively affects trabecular bone structure, mainly by reducing bone volume fraction (BV/TV) and thus increasing fracture risk. One major limitation in assessing and quantifying the effect of this structural deterioration is that no two trabecular structures are identical. Thus, when we compare a group of healthy bones against a different group of bones that experienced resorption (i.e. decreased BV/TV) we only discover an “average” mechanical effect. It is impossible to quantify the mechanical effect of individual structural deterioration for each sample, simply because we never have the same sample in both states (intact and deteriorated structure). 3D printing is a new technology that can assist in overcoming this issue. Here we report a preliminary study that compares a healthy 3D printed trabecular bone model with the same model after bone resorption was simulated. Since the deteriorated structural bone model is derived from the healthy one, it is possible to directly estimate (percentage wise) the decrease of tissue stiffness and strength as a result of bone resorption for this specific structure. Our results demonstrate that a relatively small decrease in BV/TV (about 8%) leads to a dramatic decrease in structural strength (24%) and structural stiffness (17%), (P<0.01). Structural strength decreased from an average of 9.14±2.85 MPa to 6.97±2.44 MPa, while structural stiffness decreased from an average of 282.5±63.4 N/mm to 233.8±51.2 N/mm. This study demonstrates that 3D printing is a novel and valuable tool for quantifying the effect of structural deterioration on the mechanical properties of trabecular bone. In the future, this approach may help us attain better personal fracture risk assessments by CT scanning, 3D printing and mechanically testing individual bone replicas from patients suffering excessive bone resorption.
Keywords: Bone histomorphometry, Biomechanics, Osteoporosis, Trabecular bone, 3D printing
1. Introduction
Osteoporosis is a systemic skeletal disease characterized by progressive decline of bone mass and microstructural deterioration that leads to reduced bone strength and an increase in the risk for bone fracture (NIH Consensus Statement 2000; WHO 2003). It is triggered by an imbalance in the natural process of bone remodeling, where bone resorption by osteoclasts exceeds bone formation by osteoblast (McDonnell et al., 2007; Parfitt, 1982). This imbalance affects mostly trabecular bone due to its large surface-to-volume ratio, which results in higher remodeling activity (Chappard et al., 2008; Parfitt, 2002; Wark, 1996). As life expectancy is constantly rising - the prevalence of osteoporosis increases and this in turn leads to more people suffering from skeletal fractures and a surge in economic burden (Boonen and Singer, 2008). Seeing that osteoporosis demonstrates a clear cause-and-effect relationship between the deterioration of bone structure and the decrease in mechanical functionality, it would be valuable to find whether this relationship is not only detectable in a large sample size but also could be accurately quantified in individual samples. With the advancement of improved diagnostic tools that can detect the 3D structure of trabecular bone tissue in-vivo (e.g. HR-pQCT) it may be possible in the future to quantify this structure-function relationship in susceptible individuals (e.g. suffering from osteopenia) and by that help predict the risk for fracture in specific bones and personalize a preventative treatment.
Trabecular bone tissue is a spongy internal bone architecture comprised of seemingly stochastic assembly of rods and plate. Yet strong evidence supports the hypothesis that trabecular bone optimizes its structure to support and transfer loads within bones and across joints (Barak et al., 2011, 2013b; Barak and Black, 2017; Pontzer et al., 2006). In humans, trabecular bone fills the entire marrow cavity of short bones (e.g. vertebrae) and the marrow cavity of long bones epiphysis and metaphysis (e.g. proximal and distal femora and humeri) (Buckwalter et al., 1995; Currey, 2002). Previous findings demonstrate that as we grow older - our trabecular bone tissue decreases in mass mainly by thinning of plate-shaped trabeculae into rod-shaped trabeculae (Laib et al., 2000; J C van der Linden et al., 2001). Furthermore, there is also evidence that trabecular bone anisotropy increases with age. This is derived from a preferential resorption of horizontal trabeculae, which leads to a decrease in trabecular bone mechanical properties, such as stiffness and strength, when the bone is loaded off-axis (e.g. fall) (Mosekilde, 1988).
Many studies investigated which trabecular bone parameters predict most accurately the mechanical properties of trabecular bone tissue (Goulet et al., 1994; Hou et al., 1998; Keaveny et al., 1994; Maquer et al., 2015). The vast majority of them point to bone volume fraction (BV/TV, a measure of bone quantity) and fabric anisotropy (DA) as the two main parameters that explain together more than 90% of the variation in trabecular bone tissue elastic properties (Maquer et al., 2015; Van Rietbergen et al., 1998). Yet all of these studies suffer from an inherent limitation – when they compare trabecular bone samples with various BV/TV, they cannot control for the varying 3D architecture of each individual sample. Kleerkoper et al. (1985) and Parfitt (1992) demonstrated that while low bone volume is a major factor of fracture risk, trabecular bone architecture significantly contributes to the biomechanical integrity of the bone tissue. Seeing that no two trabecular bone structures are the same, this introduces an uncontrolled variable into our attempts to correlate trabecular structure to its function (i.e. we are dealing with more than just one independent variable). While this may not always be immediately apparent from the big picture (i.e. running a trend line through all measurements yields a high correlation coefficient R-value), a closer look at individual data points will reveal many times a more complex story where samples with similar BV/TV will yield significantly different mechanical properties. This is especially true when the study compares a cohort of healthy and osteoporotic trabecular bone samples (McCalden et al., 1997; Sprecher et al., 2015). A similar phenomenon was observed by Siffert et al. (1996) where various computer simulations of trabecular bone with the same BV/TV value but different architecture yielded distinct mechanical properties.
One way to overcome this problem is to use finite element modeling (FEM) to simulate the same bone structure in its healthy and osteoporotic states. FEM is a computer-based simulation that predicts how an object will behave in the real world under a specific assigned stress. This is achieved by dividing the object into discrete elements, each with its own mathematical equation that describes its mechanical behavior. FEM has been used extensively to study the mechanical behavior of trabecular bone under different loading conditions and to look inside the bone structure to see where stresses are concentrating and may cause fracture (Liu et al., 2012; Podshivalov et al., 2011; Wang et al., 2012; Webster et al., 2012). Yet, every FEM simulation must be validated with an in vitro mechanical testing, to confirm that the accurate mechanical properties are predicted (Barak et al., 2009; Dobson et al., 2006). This requirement is impossible to attain in FEM simulations that manipulates an existing trabecular structure such as bone remodeling or osteoporosis (e.g. thinning of trabeculae, fenestration of trabeculae) as the derived trabecular structures do not physically exist. Further limitations of the FEM approach are relatively high costs of software and hardware (a finite element simulation can easily result in massive models with tens, and even hundred millions of FE elements, which requires a strong computer) and a steep learning curve (the output can only be as good as the input).
A relatively novel approach that can address the limitation of comparing different trabecular bone samples and the shortcoming of FEM validation is the use of 3D printing (3DP). 3DP is a type of Solid-freeform fabrication (SFF), a process that enables the build of three-dimensional shapes from computer aided design (CAD) representations, by incremental deposition of printing material (a bottom-up approach). This process creates a solid object from sequential two-dimensional layers (Cima et al., 1994; Sachs et al., 1990). By use of non-invasive image acquisition such as micro computed tomography (micro-CT), computer segmentation and three-dimensional reconstruction, and then 3DP, it is possible to reproduce the same trabecular architecture as many times as is required. In addition, by manipulating the segmentation threshold, the same general trabecular architecture can be created with thinner/thicker trabeculae, which functions to control for different values of trabecular bone mass. Thus, 3D printing can be used to validate FEM predictions for manipulated trabecular bone structures that do not physically exist.
3DP technology was developed in the 1980s and 1990s, and while this technology was originally focused on rapid tooling in industry (Sachs et al., 1990), it was recognized very early as a promising technique for the biomedical field. Various biomedical uses and applications were previously reported, ranging from customized drug delivery devices (Leong et al., 2001) to the creation of bone models and replications (D’Urso et al., 2000; Levy et al., 1992), tissue engineering of bone and cartilage from a polymeric scaffold (Chen et al., 2006; Cooke et al., 2003; Hutmacher, 2000), and regeneration of trabecular bone architecture using porous ceramics (Jones and Hench, 2003). Hitherto, only a limited number of preliminary studies investigated the possibilities of 3DP trabecular bone samples and then mechanically tested them (Dobson et al., 2006; kuhn et al., 2014; Langton et al., 1997; Tellis et al., 2009; Yoon et al., 2014).
The goal of this proof-of-concept study is to introduce and validate trabecular bone 3D printed replicas as a useful tool to assess and compare mechanical properties between trabecular bone samples sharing the same underlining architecture but with different BV/TV (simulating bone loss). A cubical volume of interest (4.5×4.5×4.5 mm) was cropped and segmented from a micro-CT scan of a healthy chimpanzee’s third metacarpal head. To simulate excessive bone resorption (reduction of about 10% in BV/TV), a second model was created by raising the grayscale threshold during segmentation; this generated a second model with the same architecture but thinner trabeculae. Next, the original (healthy) and thinned (resorbed structure) models were printed in scale (1:1 to life size) 30 times each, using a 3D-printer (ProJet 1200). Finally, all samples were tested in compression until failure (Instron 5942) and trabecular bone strength and stiffness were calculated. The following working hypotheses were tested:
Printing different sizes of the same trabecular cube model with constant BV/TV and printing the same size of trabecular cube model with different BV/TV values, will both demonstrate a strong linear correlation between volume (derived from the computer model) and weight (derived from the actual 3D printing). Supporting this hypothesis will demonstrate that the 3D printed trabecular cube (3DP-TC) represents accurately and precisely the blueprint segmentation model. This hypothesis will be tested by (1) printing trabecular bone replicas with different volume fractions (within the natural range of trabecular bone tissue) and solid cubes (100% volume fraction, representing cortical bone) and plotting them against their volume fraction to find whether they highly correlate to each other, and (2) printing identical trabecular bone replicas at various size-scales, starting at the original trabecular life size, and finding if the different size replicas correlate linearly with their weight.
As the two trabecular models are printed using the same printing material (VisiJet FTX Green resin), the models’ material stiffness values (Young’s modulus) would be non-significantly different. This hypothesis will be tested by loading the two 3DP-TC models (original and thinned), plotting their stress-strain curves, and calculating material stiffness from the linear segment.
Strength and stiffness of thinned trabecular models will be significantly lower compared to the original model. Supporting this hypothesis will demonstrate that, similar to real-life cases of excessive bone resorption (decrease in bone quantity), the thinned 3DP-TC model has decreased mechanical properties compared to the original 3DP-TC model. This hypothesis will be tested by loading the two 3DP-TC models (original and thinned), plotting their load-deformation and stress-strain curves, and calculating the structural stiffness and strength.
2. Materials and methods
2.1 Micro-CT scanning
The third metacarpal bone from an adult Chimpanzee (Pan troglodytes) was obtained from the Museum of Comparative Zoology, Harvard University, Cambridge MA, USA (bone ID #10736, wild-shot individual from West Africa). The bone had no traces of external bone pathology (Figure 1A). Previous studies have demonstrated that similar to humans, chimpanzees’ bones may suffer structural deterioration and bone loss related to aging (Gunji et al., 2003; Lowenstine et al., 2016; Morbeck et al., 2002; Sumner et al., 1989). The reason we choose a chimpanzee bone (rather than human) was that chimpanzees have thicker trabeculae compared to humans (Barak et al., 2013a). While average trabecular thickness (Tb.Th) in humans’ MC head is about 180–200 µm, the average Tb.Th in chimpanzees’ MC head is about 200–250 µm (Barak et al., 2016; Lazenby et al., 2011b). The latter value is about 4–5 times greater than the minimal layer thickness and resolution of our 3D printer (56 µm spatial resolution and 30 µm layer thickness). Furthermore, several studies have shown that the average resorption lacuna of an osteoclast, ranges in depth between 30 and 50 µm regardless of body size (Eriksen et al., 1985; McNamara et al., 2006; Mulvihill et al., 2008). Hence, the vast majority of trabeculae (if not all) are thicker than 30–50 µm, otherwise every time these trabeculae would be remodeled they would be severed and become non-functional. As the accuracy and reproducibility of the 3D printouts were a crucial aspect of this proof-of-concept study, a larger average Tb.Th was preferred.
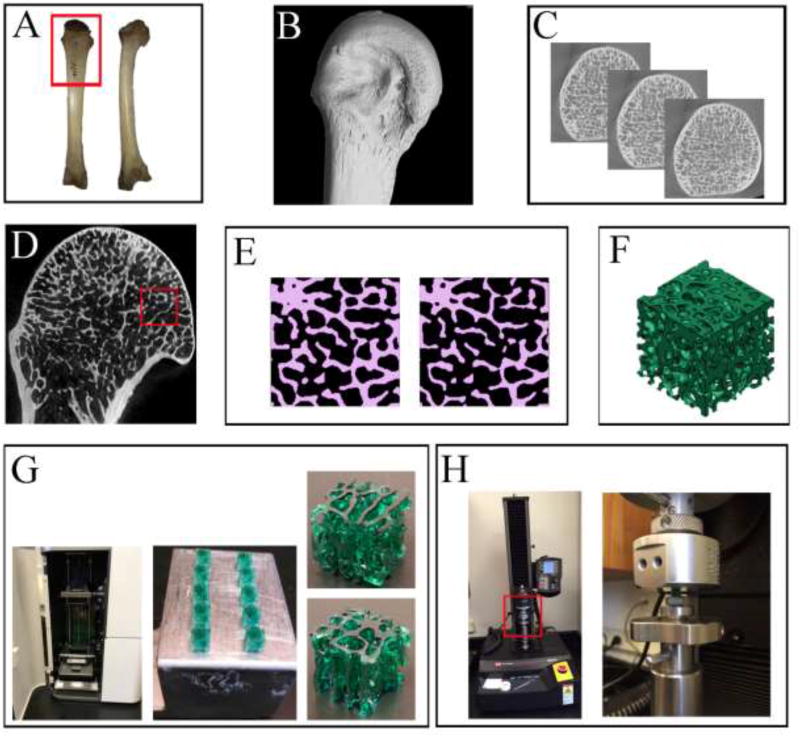
Figure 1.
An overview of the main experimental steps as described in the text. (A) A dorsal (left) and medial (right) view of the chimpanzee’s 3rd MC which was used for this project. The red frame represents the area which was micro-CT scanned. (B) A lateral view of the distal 3rd MC micro-CT reconstruction. (C) Several 2D slices in the transverse plane, displaying the internal trabecular bone structure in the MC head. (D) A close-up view of the 3rd MC head, showing (inside the red frame) where the 4.5 × 4.5mm region was selected and cropped. (E) A representative 2D slice from the cropped cube region demonstrating the binarization process (Amira 6.0). On the left the original threshold (135) and on the right the increased threshold (145) resulting in thinner, more fenestrated and sometimes severed trabeculae. (F) A 3D view of a reconstructed cube (*.stl file type) visualized with the 3D printer profiler software (3D systems). (G) The ProJet 1200 3D printer (3D systems) is shown with its printing chamber open in the left picture. Note that the printing cartridge is located at the bottom and the dynamic printing stage is suspending at the top half of the chamber. The 3DP-TCs are shown on the right. Ten printed cubes are shown still attached to the printing stage (ceneter image), and a single cube (4.5mm3) is displayed in close-up from two different orientations (left images). (H) Left: a view of the Instron 5942 universal testing machine used to load the 3DP-TCs in compression. The red frame represents the area enlarged on the right. Right: A close-up, showing the lower stationary sample-mounting stage and the upper mobile loading stage. In between them is one of the 3DP-TCs.
The distal diaphysis and MC head were micro-CT scanned at the Center for Nanoscale Systems, Harvard University using a Metris X-Tek HMX ST 225 scanner (Nikon Metrology Inc.) at 70 kV and 130 µA with no filter. Scan isotropic voxel size was 30 µm, which is well below average chimpanzee trabecular thickness, given in previous publications (Barak et al., 2013a; Cotter et al., 2009; Lazenby et al., 2011b, 2011a; Maga et al., 2006; Ryan and Walker, 2010). The output raw data (3142 projections, no frame averaging, and detector size 2000×2000 pixels) were imported into CT-Pro software (Nikon Metrology Inc.) and reconstructed into a 3D volume (Figure 1B). Next, the reconstructed 3D volume was imported into a visualization software, VGStudio Max 2.1 (Volume Graphics GmbH, Heidelberg Germany), and was reoriented along the long axis of the bone using the distal MC body, the MC head and its transverse ridges. The reconstructed scan was then cropped and saved as 16-bit TIFF image stack along the transverse plane (proximodistal; Figure 1C). Finally, the image stack was converted into 8-bit TIFF images using ImageJ software version 1.50i (Schneider et al., 2012), decreasing gray levels from 65,536 to 256 (black pixels equal to “0” and white pixels equal to “255”) without affecting spatial resolution.
2.2 Segmentation
The 8-bit TIFF image stack was imported to Amira 6.0 (FEI Visualization Sciences Group Inc.) for segmentation and reconstruction. A cubical volume of interest (VOI) of 4.5 mm3 was cropped from the palmar region of the 3rd MC head, just below the cortex (Figure 1D). After cropping, the image stack was manually segmented (binarized) to differentiate bone from non-bone pixels (Figure 1E - left panel, and Figure 2). A global gray-scale threshold of 135 was selected by two individual observers to best separate bone from non-bone pixels. Next, to correct possible local inaccuracies, each slide of the original micro CT scan was manually inspected and segmentation was corrected (if necessary) in each of the 3 primary axes (axial, radial, and transverse orientations). Once this was completed, Amira reconstructed a 3D surface model (Figure 2).
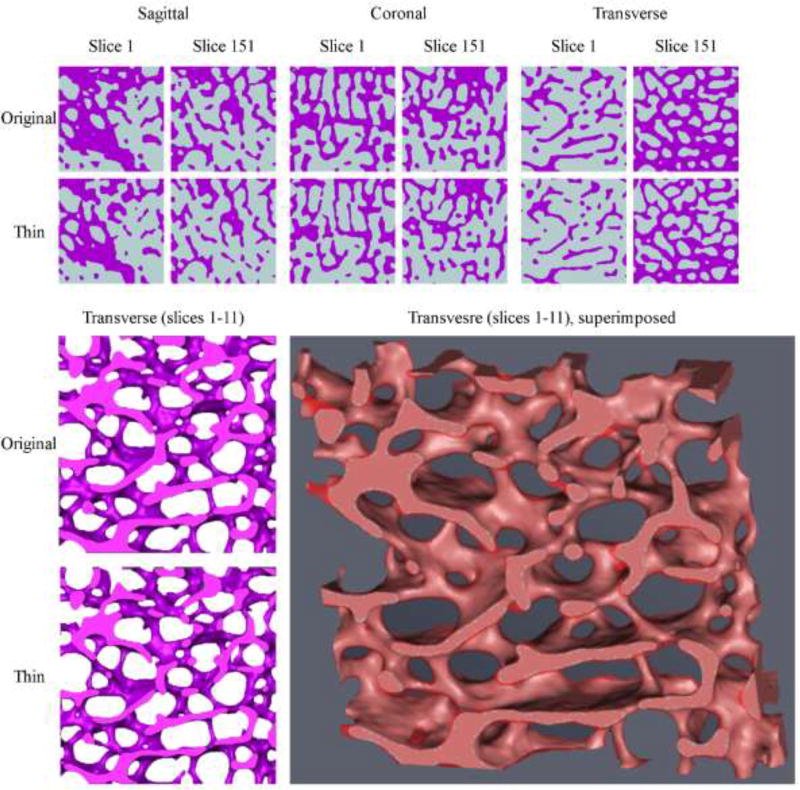
Figure 2.
The upper panel shows the first (#1) and last (#151) 2D slices of the original and thinned binarized cubical VOIs in the sagittal, coronal and transverse orientations. The left lower panel demonstrates a section of the 3D reconstructed cubes (original and thinned; slices #1–11) in the transverse direction. Comparing the two images reveals a significant decrease is trabecular thickness (and consequently an increase in trabecular spacing) throughout the sample. At the center bottom part of the images an originally intact trabecula (upper image) became severed (lower image). The right lower panel reveals the same section when the original and thinned reconstructions are superimposed. The light red areas are where both reconstructions represent ‘bone’. The semitransparent darker red represents areas which are ‘bone’ only in the original reconstruction (for a color version of this figure, please see the online version).
To simulate excessive bone loss, a second model was created from the same cropped VOI by raising the global gray-scale threshold from 135 to 145 (Figure 1E - right panel, and Figure 2). This led to higher numerical values of gray-scale to be assigned as non-bone pixels (i.e. when the threshold was 135, a pixel with a gray-scale value of 137 would be considered bone but when the threshold is 145, the same value of 137 would be considered non-bone and thus the trabeculae will become thinner). Once this step was completed, Amira reconstructed a second “deteriorated” 3D surface model (Figure 2).
Next, both 3D surface models were exported to Drishti v2.5.1 (Limaye, 2012) for meshing and then imported back to Amira and saved in “stl” file format (STereoLithography files, readable by 3D printers).
2.3 Bone histomorphometry
To evaluate and quantify trabecular bone volume fraction (BV/TV), degree of anisotropy (DA) and trabecular thickness (Tb.Th) of both models - measurements were performed on the segmented volumes using ImageJ version 1.50i (Schneider et al., 2012) and its plugin BoneJ version v1.4.1 (Doube et al., 2010). Bone volume fractions (BV/TV) for the original and thinned models were 39.8% and 32.1% respectively. Degree of anisotropy was found to be almost unchanged between the two models with a value of 0.55 for the original model and 0.57 for the thinned model (DA values ranging 0 to 1). Trabecular thickness (Tb.Th) for the original and thinned models were 273 (±77) and 234 (±67) µm respectively. Thus, by changing the global gray-scale threshold we decreased trabecular thickness which reduced bone volume by about 8%, simulating bone resorption. Furthermore, these Tb.Th values verified that both models are within our 3D printer printing capabilities (56 µm spatial resolution and 30 µm layer thickness).
2.4 3D printing (3DP)
Both models’ stl files were exported to our 3D printer software (3DPrint Client V1.1.128, 3DSystems Inc.; Figure 1F) and each model was printed 30 times (4.5×4.5×4.5mm, n=30) using a ProJet 1200 3D printer (3DSystems Inc.; Figure 1G) and VisiJet FTX Green printing resin. This 3D printer uses a technique called micro Stereolithography (µSLA). Briefly, this technique uses a UV laser that projects light via a mirror through a build cartridge of photopolymer liquid to create a part suspended from the build platform. As polymerization starts, the UV laser beam generates the first solid layer (polymer solidifying at focal point, non-exposed polymer remains liquid). Subsequently, as the platform is elevated, the polymerization process is repeated layer-by-layer by tracking the laser beam along the design dictated by the uploaded stl file. After the model is completed, the platform is raised and any excess resin is removed using isopropyl alcohol and air pressure. Finally, the model is cured in a UV chamber (an integral part of the ProJet 1200 3D printer).
2.5 3D printing precision and accuracy validation
To test the accuracy of our printer (the ability to print correctly the segmented model), three additional 4.5×4.5×4.5 mm solid cubes were printed using the same printer. Next, all 3DP-TCs (three solid, 30 original and 30 thinned) were weighed using a Vibra HT analytical balance with an accuracy up to ± 0.0001 gr (Vibra, Shinko Denshi Co. LTD.). Finally, the average weight of the cubes was plotted against their volume fraction (32.1%, 39.8% and 100% for the thinned, original and solid 3DP-TCs respectively, using the origin (0,0) as the fourth definite data point) and a least squares linear regression was calculated.
To test the precision of our printer (the ability to repeatedly print the same segmented model), all 3DP-TCs were weighed (Vibra, Shinko Denshi Co. LTD.) and average ±SD were calculated. In addition, the original model was reprinted again, starting at an initial size of 4.5×4.5×4.5 mm and then increasing all the way to 21×21×21 mm in increments of 1.5mm (i.e. 4.5, 6, 7.5…21; a total of 12 cube sizes). Each cube size was printed three times and all cubes were weighed (Vibra, Shinko Denshi Co. LTD.). The max weight difference between the three cubes of each group size was less than 3% (in most cases closer to 1%). Finally, the average weight of the 3D printed trabecular cubes was plotted against their volume and a least squares linear regression was calculated.
2.6 Mechanical testing – stiffness and strength
Thirty original and thirty thinned 3DP-TCs were loaded in compression until failure using an Instron 5942 Single Column Table frame (Instron Inc., USA; Figure 1H). As our samples were made of 3D printing resin (and not real viscoelastic bone material that contains water), no preconditioning of the samples were executed before the actual experiment. A small compression preload of about 5 N was applied at the beginning of each experiment, after which load and deformation data collection began (measurements were taken every 100 millisecond). Each 3DP-TC was loaded at a rate of 50 µm/min until a load of about 130 N was reached. For each cube the stiffness and strength was calculated from the stress-strain curve (for more details see below).
Contrary to cortical bone, where strength is measured as the highest load (stress) a structure can sustain before failure (i.e. there is a point of peak force), strength measurement in trabecular bone (due to its porous nature) is less straight forward. Trabecular bone tissue failure progresses in two steps: first damage and only later a full fracture (separation in the structure). Damage is the loss of mechanical integrity (e.g. strength) due to microcracks, with the material remaining intact (i.e. no new surfaces are created). Fracture, on the other hand, is the separation of previously damaged material, producing new surfaces. Fyhrie and Schaffler (1994) have investigated the characteristic stress-strain curve of trabecular bone. They showed that when the first trabecula (or trabeculae) buckle and crack (i.e. damage) there is a drop in the stress-strain curve. Yet as more and more trabeculae fail, the specimen starts to collapse and the bone becomes compacted. At that stage, load (stress) may not change (or even increase again) with the increase of deformation (denoted the “plateau region”). Thus, we have determined strength as the first point where the tissue was damaged and load dropped more than 1N between 2 successive measurements. As measurements were recorded every 100 milliseconds and the anvil moved down at a speed of 0.83 µm/second, a drop of 1N in 0.1 second indicated a structural failure in our sample (i.e. buckling trabeculae).
2.7 Data analysis and Statistics
In this experiment we measured both the stiffness of the structure (i.e. load- deformation curve, N/mm) and the stiffness of the material at the apparent level (i.e. stress-strain curve, Young’s modulus, MPa). Stress values were calculated as the ratio between the force measurements and the cross-sectional area of the sample. Since we were testing porous cubes, the cross-sectional area of each cube model (4.5×4.5 mm, equal to 20.250 mm2) was corrected to its actual volume fraction (39.8% and 32.1% for the original and thinned 3DP-TCs respectively). Therefore, instead of using a cross-section of 20.250 mm2 we used 8.056 mm2 and 6.500 mm2 for the original and thinned 3DP-TCs respectively. Strain values were calculated as the ratio between the corrected movement of the anvil (corrected for machine compliance) and the original gap between the two anvils (specimen height, 4.5 mm). A load-deformation and stress vs. strain curves was created for each test and the structural stiffness and material stiffness at the apparent level (Young’s modulus) were determined from the 15–40 N linear region of the curve. It is important to stress the point that since we are using polymer rather than bone material, the actual strength and stiffness values are less informative. However, the ratio between the two models (% difference of structural stiffness and strength) will demonstrate the effect of trabecular structure deterioration on its mechanical behavior.
In order to eliminate any incognizant bias, all raw data files were marked randomly and only after all stiffness, Young’s modulus and strength values were calculated, the files were reassigned to their original group and data was grouped and evaluated.
Statistical analyses were performed using R, version 3.2.0 (R Foundation for Statistical Computing, Vienna, Austria; www.rproject.org). Data (cubes weights, stiffness, Young’s modulus and strength) were found to be distributed normally using the Shapiro test (P > 0.05). Population variances (comparing values for original and thinned 3DP-TCs) were found to be equal using the Bartllet test (P > 0.05). Differences between groups were tested with a one-tailed t-test with equal variance. A one-tailed t-test was used as the decrease in BV/TV was expected to negatively affect the sample’s mechanical properties. Values smaller than 0.05 (P < 0.05) were considered to be statistically significant.
3. Results
3.1 3D printing precision and accuracy validation
The weight of the 3DP-TCs (32.1%, 39.8% and 100% for the thinned, original and solid cubes respectively) was found to significantly correlate with their volume fraction (P<0.01; R2=0.9917).
The average weights for the original and thinned 3DP-TCs (n=30 per group) were 0.066±0.003 gr and 0.060±0.003 gr respectively.
The measured weight of the various cubes sizes was found to significantly correlate with their volume (P<0.01; R2=0.9997).
3.2 Young’s moduli (material stiffness)
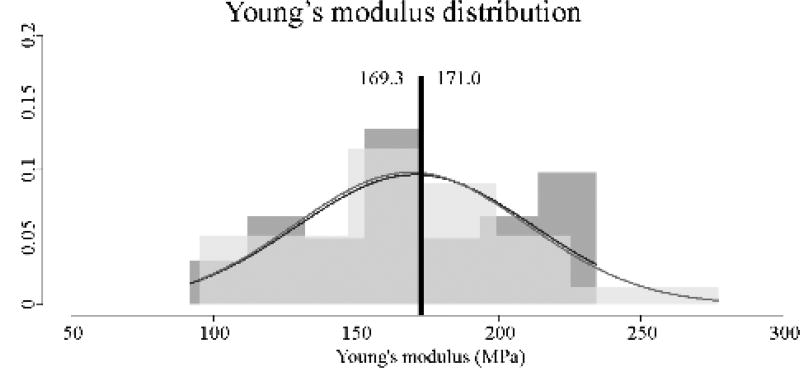
Both the original (healthy) and thinned 3DP-TCs revealed similar, non-significantly different Young’s moduli values (Figure 3). Average Young’s modulus for the original 3DP-TC was 171.0±41.1 MPa and the average Young’s modulus for the thinned 3DP-TC was 169.3±40.6 MPa (P>0.05).
Figure 3.
Material stiffness (Young’s modulus) values for the original (n=30) and thinned (n=30) 3DP-TCs. Results revealed a non-significant difference between the two populations (P>0.05). A histogram view of the 30 material stiffness values for the original (dark grey) and thinned (light grey) 3DP-TCs. Overlapping histogram areas are represented by a medium shade of grey. Superimposed on the histograms are the corresponding normal distributions of each population. Black vertical lines denote the average. Numbers to the left and right of the black line give the average values for the thinned and original 3DP-TCs respectively.
3.3 Structural stiffness and strength
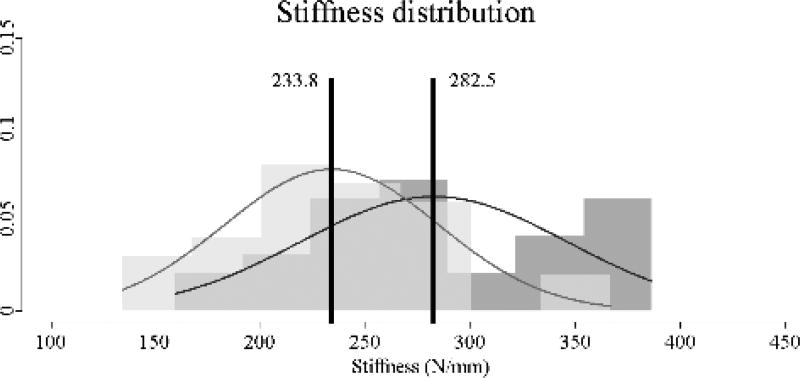
Contrary to material stiffness, the original 3DP-TC revealed significantly higher structural stiffness values compared to the thinned model (Figure 4). Average stiffness for the original 3DP-TC was 282.5±63.4 N/mm and the average stiffness for the thinned 3DP-TC was 233.8±51.2 N/mm (P<0.05). This indicated a 17% decrease in structural stiffness of the thinned model compared to the original one.
Figure 4.
Stiffness values for the original (n=30) and thinned (n=30) 3DP-TCs. Results revealed a significant difference between the two populations (P<0.05). A histogram view of the 30 stiffness values for the original (dark grey) and thinned (light grey) 3DP-TCs. Overlapping histogram areas are represented by a medium shade of grey. Superimposed on the histograms are the corresponding normal distributions of each population. Black vertical lines denote the average. Numbers to the left and right of the black line give the average values for the thinned and original 3DP-TCs respectively.
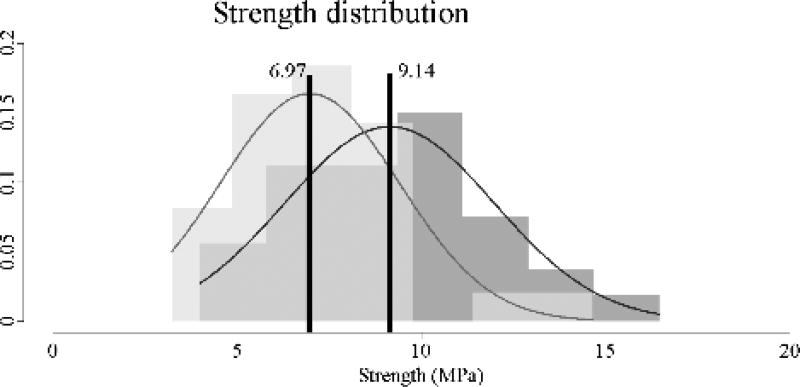
The original 3DP-TC model demonstrated significantly higher strength values compared to the thinned model (Figure 5). Average strength for the original 3DP-TCs was 9.14±2.85 MPa while the average strength for the thinned 3DP-TCs was only 6.97±2.44 MPa (P<0.01). This indicated a 24% decrease in strength of the thinned model compared to the original one.
Figure 5.
Strength values for the original (n=30) and thinned (n=30) 3DP-TCs. Results revealed a significant difference between the two populations (P<0.01). A histogram view of the 30 strength values for the original (dark grey) and thinned (light grey) 3DP-TCs. Overlapping histogram areas are represented by a medium shade of grey. Superimposed on the histograms are the corresponding normal distributions of each population. Black vertical lines denote the average. Numbers to the left and right of the black line give the average values for the thinned and original 3DP-TCs respectively.
4. Discussion
The first key objective of our study was to demonstrate that our 3D printer (ProJet 1200, 3D Systems Inc.) is capable of reproducing accurately and precisely life-size trabecular samples. The weight of the 3DP-TCs (BV/TV of 32.1%, 39.8% and 100%) was found to significantly correlate with their volume fraction (P<0.01; R2=0.9917), indicating that our printer was accurately printing the two trabecular bone models according to their expected volume fraction. In addition, the weight of different size 3DP-TCs (4.5 mm3 to 21 mm3 in increments of 1.5 mm) was found to significantly correlate with their expected volume (P<0.01; R2=0.9997), demonstrating that our printer was precisely and repeatedly printing the 3DP-TC, even in our smallest (life-size) model. These results supported our first hypothesis.
The second objective of our study was to confirm that the 3D printed material stiffness (Young’s modulus) is non-significantly different across different models. Verifying that material quality is a controlled variable in our experiment is a crucial step before we can address the results of different models. Our results showed that the printing material Young’s modulus values for the original and thinned 3DP-TC models were not significantly different from each other (171.0±41.1 MPa and 169.3±40.6 MPa for the original and thinned 3DP-TC models respectively; P>0.05). These results supported our second hypothesis. Nevertheless, it should be noted that while the average Young’s modulus of the printing material was not significantly different between models, the standard deviation (which represent the distribution of individual results) was noticeable. This considerable distribution may indicate that in the current setup, a large sample size (in our case n=60) is required to accurately identify mechanical properties values and trends.
Finally, our third objective was to demonstrate that the strength and stiffness of a 3DP-TC thinned model (with 8% lower BV/TV) is significantly lower compared to the original model. So far, studies that explored the effect of osteopenia and osteoporosis on trabecular bone mechanical properties compared multiple trabecular bone samples, each from a different individual, grouped into “healthy” and “osteoporotic” cohorts (McCalden et al., 1997; Sprecher et al., 2015). While these studies can clearly show trends and tendencies, such as a decreased structural stiffness and strength in response to bone resorption and decreased BV/TV, they cannot directly quantify the effects of specific structural deterioration with their mechanical outcome. This constraint is derived from the simple fact that each sample has its own unique structure and that it is practically impossible to obtain the same sample twice – once in its healthy state and then again after excessive bone resorption. In contrast, our preliminary study uses the same structure twice (healthy and deteriorated states) and thus it is able to reveal a direct relationship between a specific and quantifiable structural damage and its mechanical consequences. Our results showed that a decrease of about 8% in BV/TV will yield a significant decrease in structural stiffness (17%, 282.5±63.4 vs. 233.8±51.2 N/mm for healthy and deteriorated models respectively) and a significant decrease in structural strength (24%, 9.14±2.85 vs. 6.97±2.44 MPa for healthy and deteriorated models respectively). These results supported our third hypothesis. It is important to note here that since we are studying the structural effects of trabecular architecture deterioration, the actual stiffness and strength values are less informative (as the material tested is not bone) but the percentage (%) of reduced stiffness and strength (and their similarity to previously reported findings) is the focus of our discussion.
One of the main advantages of our approach is that we are comparing practically the same trabecular architecture with different BV/TV. This was achieved by changing the global threshold during segmentation and thinning trabecular thickness by about 14% (resulting in BV/TV decrease of about 8%) while maintaining an almost constant degree of anisotropy of 0.55–0.57 (DA values range 0 to 1). Previous studies have demonstrated that BV/TV and DA alone can explain more than 90% of the variance in trabecular bone mechanical properties (Goulet et al., 1994; Homminga et al., 2003; Hou et al., 1998; Keaveny et al., 1994; Maquer et al., 2015). Thus, our approach singled out BV/TV as the only significant independent variable that may affect trabecular bone stiffness and strength. So far, excluding computer simulations, studies were unable to achieve this goal simply because one cannot obtain and test the same trabecular bone twice. McCalden et al. (1997) studied 255 trabecular bone samples harvested from 44 human femora ranging in age between 20 and 102 years old. All bone samples were tested in compression along their axial orientation (load-bearing direction) until failure. Their results demonstrated a clear negative relation between individuals’ age and their bone mass and strength (R2 value of 0.51 for both relations). Yet when looking at the individual data points, one can find cases where young and old people share similar values of bone mass but distinctly different strength values. Sprecher et al. (2015) assessed trabecular bone distribution (BV/TV) in various regions of the proximal femur of osteoporotic and normal individuals. While almost all regions (head, metaphysical, subchondral etc.) demonstrated significantly lower BV/TV values in the osteoporotic patients, in many of the regions there was substantial overlap between BV/TV values (i.e. osteoporotic and normal individuals with similar BV/TV values). These two examples imply that when multiple trabecular variables are differing between samples (BV/TV, DA and the general architecture), BV/TV is not sufficient to predict the severity of osteoporosis and the risk for fracture.
In our study, we have simulated excessive bone resorption by removing about 8% of BV/TV evenly throughout the trabecular bone model. Previous studies that compared normal and osteoporotic trabecular bone samples from various bones found BV/TV to decrease in osteoporotic individuals by 6.6% to 45% depending on the examined bone (iliac bone, distal radius, femoral head, distal femur, vertebra), sex and age (Green et al., 2011; Homminga et al., 2004; Kimmel et al., 1990; Li and Aspden, 1997; Müller and Rüegsegger, 1996; Nikodem, 2012; Parisien et al., 1995; Van Rietbergen et al., 2003). This range places our 8% decrease in BV/TV at the lower end of the osteoporotic scale, corresponding to marked osteopenia or the onset of the osteoporotic cascade. Li and Aspden (1997) tested in compression trabecular bone samples from human femoral heads harvested from normal (n=7) and osteoporotic (n=17) individuals. Trabecular BV/TV ranged between 13% – 41% and 11 – 33% for the normal and osteoporotic individuals respectively (values were calculated from the material and apparent density values given in the paper). Similar to our results they have found a decrease of about 20% in structural stiffness (from 310 MPa to 247 MPa for the normal and osteoporotic individuals respectively) and a decrease of about 24% in structural strength (from 3.3 MPa to 2.5 MPa for the normal and osteoporotic individuals respectively). Muller and Ruegsegger (1996) created a Finite Element model from a peripheral quantitative computed tomography (pQCT) scan of a 55 year old healthy male distal radius. Similar to our study they have simulated bone resorption by changing the global threshold of their segmentation. Their atrophied model had a decrease of 10.4% in BV/TV, which they characterized as “moderate atrophy”. Interestingly, their atrophied model demonstrated a 13.0% decrease in stiffness in the axial direction, which is comparable to the 17% decrease in stiffness we observed. In another FE study, van der Linden et al. (2001) simulated bone loss by either randomly thinning trabeculae or simulating resorption cavities in samples that were micro-CT scanned from the center of human cadavers’ vertebral bodies. When the thinned trabeculae FE models were tested in-silico in compression along the axial direction, a reduction of 8–10% in BV/TV corresponded to a decrease of about 17% in structural stiffness (van der Linden et al. 2001, Figure 3A). These studies present similar results to what we have found and thus they support the validity of our 3D printed model as a tool to investigate the effect of trabecular bone loss on the tissue’s mechanical properties.
Our 3DP-TCs did not include a bone marrow component as part of the model. Previous studies have demonstrated that adding a bone marrow component to an unconfined trabecular bone model will not affect the sample’s mechanical properties (Carter and Hayes, 1977; Pugh et al., 1973; Swanson and Freeman, 1966; Yoon et al., 2014). Carter and Hayes (1977) found that unconfined specimens which included a bone marrow component and were tested at physiological strain rates between 0001 and 1.0 per second showed no enhancement of strength, stiffness, or energy absorption compared to specimen without a bone marrow component. Pugh et al. (1973) showed that the presence of bone marrow in unconfined specimens of trabecular bone, did not influence their viscoelastic behavior. Finally, Yoon et al. (2014) reported that 3D printed trabecular structures (without and with unconstrained bone marrow component) maintained the same elastic properties. A few studies did show an increase in stiffness and strength when a bone marrow component was added to a confined trabecular bone sample (trabecular samples were wrapped in microwavable plastic wrap or a thin cortical shell was added to the sides of the 3D printed model). Yet, as the key strength of our approach is the reproduction of multiple identical replicas and test them in various modes, adding an ‘artificial’ cortical shell to our model would introduce an uncontrolled variable (e.g. should the cortical shell also vary in thickness between models), that would affect our results in an unpredictable and unaccountable way.
To the best of our knowledge, only few previous studies attempted to investigate the application of 3DP to reproduce and test replicas of trabecular bone, yet none of them applied the same approach that was implemented in our study. Most of these studies used older generation of 3D printers with low printing resolution (above 0.1 mm), and they either just used structures that mimic actual trabecular bone (i.e. CAD models), or they never mechanically tested their 3D printed models. Langton et al. (1997) created a 20 mm3 CAD model of cancellous bone modified from the calcaneus of an 80-year-old female cadaver. Modification included smoothing, skeletonization, the addition of elements to connect the structure and finally dilation. In addition, the model was mirrored about both axes to form a larger solid model. Thus, the final CAD model was greatly modified from the actual trabecular structure. Outer surfaces, 0.5 mm in thickness, were added around the four sides to strengthen the structure and to mimic a cortical shell. Next, the CAD model was 3D printed ten times using the SLA method and castor oil was inserted into the bone voids to mimic marrow material. Finally, the printed samples were assessed using ultrasound. The authors reported that their results fell within the range of human calcaneal data and thus they have concluded that 3D printed models of cancellous bone have a potential to assess the dependence between trabecular structure and its mechanical properties. They have further suggested that 3D printed models may help us evaluate the effect of trabecular thinning or trabecular perforation (a phenomenon observed in osteoporosis) on the mechanical behavior of bones. Dobson et al. (2006) used SLA 3D printed models to validate FE predictions for cancellous bone structures. Samples (4 mm3 in size) were 3D printed based on micro-CT scans from human iliac crest, femoral head, calcaneus and lumbar vertebrae. The 3D printed models were tested in compression and their stiffness values demonstrated a strong correlation with the predictions by the FE analysis. The authors concluded that 3D printed models are an important technique to complement the use of FE models, for the assessment of the mechanical properties of complex cancellous bone structures. Furthermore, the authors stated that 3D printed models are the only way to validate FE models of trabecular bone remodeling, as the derived structures do not physically exist. Tellis et al. (2009) used canine femur micro-CT scans of trabecular bone and various porous scaffolds created using a CAD program, to create 3D printed models, which were then mechanically tested to find their stiffness. Next, they micro-CT scanned their 3D printed trabecular models and compared the scans to the scans of their original bone samples to determine printing accuracy. The authors reported that the 3D printed trabecular models matched the original bone samples in porosity but not in connectivity density (only about 10% of the original value) and trabecular separation (around 2.3 times greater than that of the original bone sample). They have attributed these differences to the low resolution of their 3D printer (around 0.25 mm, about 5–6 times lower than our 3D printer) in comparison to the micro-CT. Similarly to Tellis et al. (2009), Kuhn et al. (2014) also used micro-CT scanning to validate the ability of 3D printing to reproduce accurate and precise replicas of actual trabecular bone samples. Several different trabecular bone structures were 3D printed based on micro-CT scans data. Next, the 3D printed samples were scanned using the same micro-CT and the structures were compared by image registration. The authors report high conformity between the actual and reproduced structures. However, contrary to our study, they did not mechanically test their samples to find if their stiffness and strength correlated to the actual trabecular bone samples. Finally, Yoon et al. (2014) tested two 3D printed cubical samples with 50% BV/TV, one sample was a honeycomb structure while the other mimicked a trabecular structure (i.e. the structure was created with a CAD software, not from an actual trabecular structure micro-CT scan). Each sample was mechanically tested in three different conditions – compression of the structure as is, compression of the structure with “bone marrow” (milk with 0.5% fat content) in a confined environment (cubes wrapped within plastic wrap), and compression of the structure with “bone marrow” in an unconfined environment. Their results showed that the honeycomb structure had superior mechanical properties compared to the “trabecular” structure. In addition, the “trabecular” structure demonstrated higher elasticity and toughness when it was tested with “bone marrow” in a confined environment compared to when it was tested as is. This type of study, as indicated by the authors themselves, is impossible to execute with real trabecular bone structures due to the innate differences in the physical structure of the various samples. The authors concluded that their study demonstrates how the use of 3DP is beneficial for comparative study of biomimetic structures.
Our preliminary study has several potential limitations. First, our study includes only one bone sample. While we have reconstructed, 3D printed and mechanically tested several other bones (e.g. sheep tali and human metacarpal bones) these were part of different projects yet to be published, and thus they were not included in the current study. In addition, as our study focused primarily on the proof-of-concept of our system to being able to 3D reproduce trabecular bone samples, we used just one sample but reproduced it many times (thirty replicas per model to a total of sixty replicas). Similarly, several previous studies which used computer models to test the mechanical properties of trabecular bone samples (e.g. FEA) used just one bone sample as the source for their model (Hamed et al., 2012; Hosokawa, 2011; Soons et al., 2012). Second, while bone material is hierarchical and anisotropic (collagen fibers and hydroxyapatite crystals c-axis are aligned in specific orientations), the 3DP resin (VisiJet FTX Green) is isotropic. This has the potential to reduce the biological significance of our results. Nevertheless, as we demonstrated above, our results are supported by several previous studies that have used actual bone samples. Thus, the effect of sub-trabecular structures on the measurement of tissue stiffness and strength appears to be negligible. Furthermore, Kabel et al. (1999) found that the anisotropic and inhomogeneous properties of the bone material have a negligible and insignificant effect on the apparent elastic properties. Finally, bone material anisotropy will have limited effect in our study as the samples were all loaded along their principle loading direction. Third, although the 3DP resin (VisiJet FTX Green) is mechanically isotropic, a printed model may potentially exhibit anisotropy due to the inherently layered construction. Nevertheless, since all of our printed samples were tested orthogonally to the direction of printing, this possible caveat should not affect our results. Fourth, our study only accounts for bone structural changes (trabecular thinning and reduced bone volume fraction) but it does not incorporate any aspect of bone material deterioration (i.e. changes in the Young’s modulus of bone material). Nonetheless, previous studies have shown that either these material effects are either non-existing (Homminga et al., 2002; Li and Aspden, 1997) or at least negligible (Jaasma et al., 2002; Panyasantisuk et al., 2015). Finally, we have reduced bone volume by applying a global threshold that affected all trabeculae evenly. Several previous studies have supported the overall phenomenon of age-related trabecular thinning (Bergot et al., 1988; Laib et al., 2000; Snyder et al., 1993). Bergot et al. (1988) had postulated that trabecular bone loss with age consists of two mechanisms: overall decrease in Tb.Th and the fragmentation and severing of some trabeculae. Thus, areas with plate-like trabeculae will lose thickness and will become rod-like (decrease in Tb.Th), and areas that were rod-like to begin with will demonstrate a significant decrease in Tb.N (Rupprecht et al., 2006). Nevertheless, other studies indicated that in some scenarios bone resorption is selective and it may affect specific elements (e.g. horizontal trabeculae) more than others (Homminga et al., 2004, 2002, Mosekilde, 1989, 1988; Nikodem, 2012). Mosekilde (1988, 1989) revealed an age-related reduction in horizontal, but not vertical, trabeculae and that the distance between adjacent horizontal trabeculae increase with age in human lumbar vertebrae samples. Similarly, Homminga et al. (2002, 2004) showed that in osteoporotic individuals lumbar vertebrae trabeculae were more oriented in the longitudinal direction and that there is a significant decrease in femoral head transverse stiffness due to over-adaptation of the trabecular structure to vertical loading. While general BV/TV and DA explains more than 90% of the mechanical properties of trabecular bone loaded along its principle loading direction (and thus, the specific areas where bone is resorbed is of less importance in this type of loading), it is still a limitation of the current study. We plan to run similar simulations that will repeat the same scenario of bone resorption but this time - bone loss will be secluded to specific locations in the tissue (e.g. horizontal trabeculae) or to fenestrations in trabeculae while holding Th.Th constant. Additional simulations will hold BV/TV constant while changing the ratio between trabeculae rods and plates or changing connectivity density (Conn.D). This will enable us to compare and evaluate the mechanical outcomes of the different situations. Yet another alternative approach would be to implement a computer simulation of stochastic trabecular bone remodeling (resorption and formation) for a given trabecular framework as described in Langton et al. (2000).
In conclusion, this preliminary study aimed to validate the use of 3DP as a valuable new tool to investigate the mechanical properties of various trabecular bone structures. Contrary to current approaches, 3DP enables us to reproduce and test the exact same structure multiple times in different conditions. Our results show that 3DP is capable of accurately and precisely reproducing the trabecular structure with consistent material quality. We further demonstrate that a decrease of about 8% in volume fraction will yield a corresponding reduction of structural stiffness (17%) and strength (24%). These results agree with previous in-vitro studies that were performed using actual bone samples. The use of trabecular bone 3DP may prove beneficial in cases where multiple scenarios are expected to be tested on the same sample (e.g. the effect of aging, the effect of inserting an implant, etc.) or when the use of actual bone samples is impossible (e.g. comparing the mechanical properties of fossil trabecular samples from various extinct hominin). Finally, 3DP of trabecular bone may help in the future to predict the risk for fracture in specific bones and personalize the treatment for osteoporosis and other trabecular bone pathologies.
Highlights.
3D printing enables quantifying the effect of trabecular structural deterioration (excessive bone resorption) on the strength and stiffness of bones.
A healthy 3D printed trabecular bone model was compared with the same model after excessive bone resorption was simulated.
Since both models share the same underlining structure, it is possible to quantify stiffness and strength decrease due to structural deterioration.
A decrease of 8% in volume fraction incited a significant decrease in structural strength (24%) and structural stiffness (17%).
Acknowledgments
This project was supported by SC INBRE grants from the National Institute of General Medical Sciences (8 P20 GM103499) of the National Institutes of Health. Authors’ roles: Study design: MMB. Study conduct: MAB. Data collection: MAB. Data analysis: MMB and MAB. Data interpretation: MMB and MAB. Drafting manuscript: MMB and MAB.
Abbreviations
- 3DP
3D printing
- 3DP-TC
3D Printed Trabecular Cube
- FEM
Finite Element Modeling
- STL
STereoLithography
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Barak MM, Black AM. Using 3D-Printing to Evaluate Trabecular Bone Mechanical Properties. FASEB J. 2017;31:902.23–902.23. [Google Scholar]
- Barak MM, Geiger S, Chattah NL-T, Shahar R, Weiner S. Enamel dictates whole tooth deformation: a finite element model study validated by a metrology method. J. Struct. Biol. 2009;168:511–520. doi: 10.1016/j.jsb.2009.07.019. [DOI] [PubMed] [Google Scholar]
- Barak MM, Lieberman DE, Hublin J-J. Of mice, rats and men: trabecular bone architecture in mammals scales to body mass with negative allometry. J. Struct. Biol. 2013a;183:123–131. doi: 10.1016/j.jsb.2013.04.009. [DOI] [PubMed] [Google Scholar]
- Barak MM, Lieberman DE, Hublin J-J. A Wolff in sheep’s clothing: trabecular bone adaptation in response to changes in joint loading orientation. Bone. 2011;49:1141–1151. doi: 10.1016/j.bone.2011.08.020. [DOI] [PubMed] [Google Scholar]
- Barak MM, Lieberman DE, Raichlen D, Pontzer H, Warrener AG, Hublin J-J. Trabecular evidence for a human-like gait in Australopithecus africanus. PloS One. 2013b;8:e77687. doi: 10.1371/journal.pone.0077687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barak MM, Sherratt E, Lieberman DE. Trabecular orientation in the 3rd metacarpal head of humans and chimps reveals their difference in locomotion behavior. Am. J. Phys. Anthropol. 2016;159:86. [Google Scholar]
- Bergot C, Laval-Jeantet AM, Prêteux F, Meunier A. Measurement of anisotropic vertebral trabecular bone loss during aging by quantitative image analysis. Calcif. Tissue Int. 1988;43:143–149. doi: 10.1007/BF02571311. [DOI] [PubMed] [Google Scholar]
- Boonen S, Singer AJ. Osteoporosis management: impact of fracture type on cost and quality of life in patients at risk for fracture I. Curr. Med. Res. Opin. 2008;24:1781–1788. doi: 10.1185/03007990802115796. [DOI] [PubMed] [Google Scholar]
- Buckwalter JA, Glimcher MJ, Cooper RR, Recker R. Bone biology. I: Structure, blood supply, cells, matrix, and mineralization. J. Bone Jt. Surg. - Ser. A. 1995;77:1256–1275. [PubMed] [Google Scholar]
- Carter DR, Hayes WC. The compressive behavior of bone as a two-phase porous structure. J. Bone Joint Surg. Am. 1977;59:954–962. [PubMed] [Google Scholar]
- Chappard D, Baslé M-F, Legrand E, Audran M. Trabecular bone microarchitecture: a review. Morphol. Bull. Assoc. Anat. 2008;92:162–170. doi: 10.1016/j.morpho.2008.10.003. [DOI] [PubMed] [Google Scholar]
- Chen VJ, Smith LA, Ma PX. Bone regeneration on computer-designed nano-fibrous scaffolds. Biomaterials. 2006;27:3973–3979. doi: 10.1016/j.biomaterials.2006.02.043. [DOI] [PubMed] [Google Scholar]
- Cima M, Sachs E, Cima L, Yoo J, Khanuja S, Borland S, Wu B, Giordano R. Computer-derived micro-structures by 3D printing: bio- and structural materials. Proc. SFF Symp. 1994:181–190. [Google Scholar]
- Cooke MN, Fisher JP, Dean D, Rimnac C, Mikos AG. Use of stereolithography to manufacture critical-sized 3D biodegradable scaffolds for bone ingrowth. J. Biomed. Mater. Res. B Appl. Biomater. 2003;64:65–69. doi: 10.1002/jbm.b.10485. [DOI] [PubMed] [Google Scholar]
- Cotter MM, Simpson SW, Latimer BM, Hernandez CJ. Trabecular microarchitecture of hominoid thoracic vertebrae. Anat. Rec. 2009;292:1098–1106. doi: 10.1002/ar.20932. [DOI] [PubMed] [Google Scholar]
- Currey JD. Bones: structure and mechanics. 2. Princeton University press; Oxford: 2002. [Google Scholar]
- Dobson CA, Sisias G, Phillips R, Fagan MJ, Langton CM. Three Dimensional Stereolithography Models of Cancellous Bone Structures From µCT Data: Testing and Validation of Finite Element Results. Proc. Inst. Mech. Eng. [H] 2006;220:481–484. doi: 10.1243/09544119H00405. [DOI] [PubMed] [Google Scholar]
- Doube M, Kłosowski MM, Arganda-Carreras I, Cordelières FP, Dougherty RP, Jackson JS, Schmid B, Hutchinson JR, Shefelbine SJ. BoneJ: Free and extensible bone image analysis in ImageJ. Bone. 2010;47:1076–1079. doi: 10.1016/j.bone.2010.08.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- D’Urso PS, Earwaker WJ, Barker TM, Redmond MJ, Thompson RG, Effeney DJ, Tomlinson FH. Custom cranioplasty using stereolithography and acrylic. Br. J. Plast. Surg. 2000;53:200–204. doi: 10.1054/bjps.1999.3268. [DOI] [PubMed] [Google Scholar]
- Eriksen EF, Mosekilde L, Melsen F. Trabecular bone resorption depth decreases with age: differences between normal males and females. Bone. 1985;6:141–146. doi: 10.1016/8756-3282(85)90046-8. [DOI] [PubMed] [Google Scholar]
- Fyhrie DP, Schaffler MB. Failure mechanisms in human vertebral cancellous bone. Bone. 1994;15:105–109. doi: 10.1016/8756-3282(94)90900-8. [DOI] [PubMed] [Google Scholar]
- Goulet RW, Goldstein SA, Ciarelli MJ, Kuhn JL, Brown MB, Feldkamp LA. The relationship between the structural and orthogonal compressive properties of trabecular bone. J. Biomech. 1994;27:375–389. doi: 10.1016/0021-9290(94)90014-0. [DOI] [PubMed] [Google Scholar]
- Green JO, Nagaraja S, Diab T, Vidakovic B, Guldberg RE. Age-related changes in human trabecular bone: Relationship between microstructural stress and strain and damage morphology. J. Biomech. 2011;44:2279–2285. doi: 10.1016/j.jbiomech.2011.05.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gunji H, Hosaka K, Huffman MA, Kawanaka K, Matsumoto-Oda A, Hamada Y, Nishida T. Extraordinarily low bone mineral density in an old female chimpanzee (Pan troglodytes schweinfurthii) from the Mahale Mountains National Park. Primates J. Primatol. 2003;44:145–149. doi: 10.1007/s10329-002-0030-8. [DOI] [PubMed] [Google Scholar]
- Hamed E, Jasiuk I, Yoo A, Lee Y, Liszka T. Multi-scale modelling of elastic moduli of trabecular bone. J. R. Soc. Interface. 2012;9:1654–1673. doi: 10.1098/rsif.2011.0814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Homminga J, McCreadie BR, Ciarelli TE, Weinans H, Goldstein SA, Huiskes R. Cancellous bone mechanical properties from normals and patients with hip fractures differ on the structure level, not on the bone hard tissue level. Bone. 2002;30:759–764. doi: 10.1016/s8756-3282(02)00693-2. [DOI] [PubMed] [Google Scholar]
- Homminga J, Mccreadie BR, Weinans H, Huiskes R. The dependence of the elastic properties of osteoporotic cancellous bone on volume fraction and fabric. J. Biomech. 2003;36:1461–1467. doi: 10.1016/s0021-9290(03)00125-8. [DOI] [PubMed] [Google Scholar]
- Homminga J, Van-Rietbergen B, Lochmüller EM, Weinans H, Eckstein F, Huiskes R. The osteoporotic vertebral structure is well adapted to the loads of daily life, but not to infrequent “error” loads. Bone. 2004;34:510–516. doi: 10.1016/j.bone.2003.12.001. [DOI] [PubMed] [Google Scholar]
- Hosokawa A. Numerical investigation of ultrasound refraction caused by oblique orientation of trabecular network in cancellous bone. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2011;58:1389–1396. doi: 10.1109/TUFFC.2011.1958. [DOI] [PubMed] [Google Scholar]
- Hou FJ, Lang SM, Hoshaw SJ, Reimann DA, Fyhrie DP. Human vertebral body apparent and hard tissue stiffness. J. Biomech. 1998;31:1009–1015. doi: 10.1016/s0021-9290(98)00110-9. [DOI] [PubMed] [Google Scholar]
- Hutmacher DW. Scaffolds in tissue engineering bone and cartilage. Biomaterials. 2000;21:2529–2543. doi: 10.1016/s0142-9612(00)00121-6. [DOI] [PubMed] [Google Scholar]
- Jaasma MJ, Bayraktar HH, Niebur GL, Keaveny TM. Biomechanical effects of intraspecimen variations in tissue modulus for trabecular bone. J. Biomech. 2002;35:237–246. doi: 10.1016/s0021-9290(01)00193-2. [DOI] [PubMed] [Google Scholar]
- Jones JR, Hench LL. Regeneration of trabecular bone using porous ceramics. Curr. Opin. Solid State Mater. Sci. 2003;7:301–307. [Google Scholar]
- Kabel J, van Rietbergen B, Dalstra M, Odgaard A, Huiskes R. The role of an effective isotropic tissue modulus in the elastic properties of cancellous bone. J. Biomech. 1999;32:673–680. doi: 10.1016/s0021-9290(99)00045-7. [DOI] [PubMed] [Google Scholar]
- Keaveny TM, Wachtel EF, Ford CM, Hayes WC. Differences between the tensile and compressive strengths of bovine tibial trabecular bone depend on modulus. J. Biomech. 1994;27:1137–1146. doi: 10.1016/0021-9290(94)90054-x. [DOI] [PubMed] [Google Scholar]
- Kimmel DB, Recker RR, Gallagher JC, Vaswani AS, Aloia JF. A comparison of iliac bone histomorphometric data in post-menopausal osteoporotic and normal subjects. Bone Miner. 1990;11:217–235. doi: 10.1016/0169-6009(90)90061-j. [DOI] [PubMed] [Google Scholar]
- Kleerekoper M, Villanueva AR, Stanciu J, Rao DS, Parfitt AM. The role of three-dimensional trabecular microstructure in the pathogenesis of vertebral compression fractures. Calcif. Tissue Int. 1985;37:594–597. doi: 10.1007/BF02554913. [DOI] [PubMed] [Google Scholar]
- kuhn V, Ivanovic N, Recheis W. High resolution 3D-printing of trabecular bone based on micro-CT data. J. Orthop. Transl. 2014;2:238. [Google Scholar]
- Laib A, Barou O, Vico L, Lafage-Proust MH, Alexandre C, Rügsegger P. 3D micro-computed tomography of trabecular and cortical bone architecture with application to a rat model of immobilisation osteoporosis. Med. Biol. Eng. Comput. 2000;38:326–332. doi: 10.1007/BF02347054. [DOI] [PubMed] [Google Scholar]
- Langton CM, Haire TJ, Ganney PS, Dobson CA, Fagan MJ, Sisias G, Phillips R. Stochastically simulated assessment of anabolic treatment following varying degrees of cancellous bone resorption. Bone. 2000;27:111–118. doi: 10.1016/s8756-3282(00)00290-8. [DOI] [PubMed] [Google Scholar]
- Langton CM, Whitehead MA, Langton DK, Langley G. Development of a cancellous bone structural model by stereolithography for ultrasound characterisation of the calcaneus. Med. Eng. Phys. 1997;19:599–604. doi: 10.1016/s1350-4533(97)00027-1. [DOI] [PubMed] [Google Scholar]
- Lazenby RA, Skinner MM, Hublin J-J, Boesch C. Metacarpal trabecular architecture variation in the chimpanzee (Pan troglodytes): Evidence for locomotion and tool-use? Am. J. Phys. Anthropol. 2011a;144:215–225. doi: 10.1002/ajpa.21390. [DOI] [PubMed] [Google Scholar]
- Lazenby RA, Skinner MM, Kivell TL, Hublin J-J. Scaling VOI size in 3D µCT studies of trabecular bone: a test of the over-sampling hypothesis. Am. J. Phys. Anthropol. 2011b;144:196–203. doi: 10.1002/ajpa.21385. [DOI] [PubMed] [Google Scholar]
- Leong KF, Phua KK, Chua CK, Du ZH, Teo KO. Fabrication of porous polymeric matrix drug delivery devices using the selective laser sintering technique. Proc. Inst. Mech. Eng. [H] 2001;215:191–201. doi: 10.1243/0954411011533751. [DOI] [PubMed] [Google Scholar]
- Levy R, Guduri S, Crawford R. Preliminary experience with selective laser sintigraphic (SLS) models of the human temporal bone. Proc. SFF Symp. 1992:161–173. [PMC free article] [PubMed] [Google Scholar]
- Li B, Aspden RM. Composition and mechanical properties of cancellous bone from the femoral head of patients with osteoporosis or osteoarthritis. J. Bone Miner. Res. 1997;12:641–651. doi: 10.1359/jbmr.1997.12.4.641. [DOI] [PubMed] [Google Scholar]
- Limaye A. Drishti: a volume exploration and presentation tool. Proceeding SPIE Dev. X-Ray Tomogr. 2012;VIII 8506:85060X. [Google Scholar]
- Liu XS, Ardeshirpour L, Vanhouten JN, Shane E, Wysolmerski JJ. Site-specific changes in bone microarchitecture, mineralization, and stiffness during lactation and after weaning in mice. J. Bone Miner. Res. 2012;27:865–875. doi: 10.1002/jbmr.1503. [DOI] [PubMed] [Google Scholar]
- Lowenstine LJ, McManamon R, Terio KA. Comparative Pathology of Aging Great Apes: Bonobos, Chimpanzees, Gorillas, and Orangutans. Vet. Pathol. 2016;53:250–276. doi: 10.1177/0300985815612154. [DOI] [PubMed] [Google Scholar]
- Maga M, Kappelman J, Ryan TM, Ketcham RA. Preliminary observations on the calcaneal trabecular microarchitecture of extant large-bodied hominoids. Am. J. Phys. Anthropol. 2006;129:410–417. doi: 10.1002/ajpa.20276. [DOI] [PubMed] [Google Scholar]
- Maquer G, Musy SN, Wandel J, Gross T, Zysset PK. Bone volume fraction and fabric anisotropy are better determinants of trabecular bone stiffness than other morphological variables. J. Bone Miner. Res. 2015;30:1000–1008. doi: 10.1002/jbmr.2437. [DOI] [PubMed] [Google Scholar]
- McCalden RW, McGeough JA, Court-Brown CM. Age-related changes in the compressive strength of cancellous bone. The relative importance of changes in density and trabecular architecture. J. Bone Joint Surg. Am. 1997;79:421–427. doi: 10.2106/00004623-199703000-00016. [DOI] [PubMed] [Google Scholar]
- McDonnell P, McHugh PE, O’Mahoney D. Vertebral osteoporosis and trabecular bone quality. Ann. Biomed. Eng. 2007;35:170–189. doi: 10.1007/s10439-006-9239-9. [DOI] [PubMed] [Google Scholar]
- McNamara LM, Van der Linden JC, Weinans H, Prendergast PJ. Stress-concentrating effect of resorption lacunae in trabecular bone. J. Biomech. 2006;39:734–741. doi: 10.1016/j.jbiomech.2004.12.027. [DOI] [PubMed] [Google Scholar]
- Morbeck ME, Galloway A, Sumner DR. Aging in Nonhuman Primates, Interdisciplinary Topics in Gerontology. Karger; Basel: 2002. Getting Old at Gombe: Skeletal Aging in Wild-Ranging Chimpanzees; pp. 48–62. [Google Scholar]
- Mosekilde L. Sex differences in age-related loss of vertebral trabecular bone mass and structure--biomechanical consequences. Bone. 1989;10:425–432. doi: 10.1016/8756-3282(89)90074-4. [DOI] [PubMed] [Google Scholar]
- Mosekilde L. Age-related changes in vertebral trabecular bone architecture--assessed by a new method. Bone. 1988;9:247–250. doi: 10.1016/8756-3282(88)90038-5. [DOI] [PubMed] [Google Scholar]
- Müller R, Rüegsegger P. Analysis of mechanical properties of cancellous bone under conditions of simulated bone atrophy. J. Biomech. 1996;29:1053–1060. doi: 10.1016/0021-9290(96)00006-1. [DOI] [PubMed] [Google Scholar]
- Mulvihill BM, McNamara LM, Prendergast PJ. Loss of trabeculae by mechano-biological means may explain rapid bone loss in osteoporosis. J. R. Soc. Interface. 2008;5:1243–1253. doi: 10.1098/rsif.2007.1341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nikodem A. Correlations between structural and mechanical properties of human trabecular femur bone. Acta Bioeng. Biomech. 2012;14:37–46. [PubMed] [Google Scholar]
- Osteoporosis prevention, diagnosis, and therapy, 2000. NIH Consens. Statement. 17:1–45. [PubMed] [Google Scholar]
- Panyasantisuk J, Pahr DH, Gross T, Zysset PK. Comparison of mixed and kinematic uniform boundary conditions in homogenized elasticity of femoral trabecular bone using microfinite element analyses. J. Biomech. Eng. 2015;137 doi: 10.1115/1.4028968. [DOI] [PubMed] [Google Scholar]
- Parfitt AM. Misconceptions (2): turnover is always higher in cancellous than in cortical bone. Bone. 2002;30:807–809. doi: 10.1016/s8756-3282(02)00735-4. [DOI] [PubMed] [Google Scholar]
- Parfitt AM. Implications of architecture for the pathogenesis and prevention of vertebral fracture. Bone. 1992;13(Suppl 2):S41–47. doi: 10.1016/8756-3282(92)90196-4. [DOI] [PubMed] [Google Scholar]
- Parfitt AM. The coupling of bone formation to bone resorption: a critical analysis of the concept and of its relevance to the pathogenesis of osteoporosis. Metab. Bone Dis. Relat. Res. 1982;4:1–6. doi: 10.1016/0221-8747(82)90002-9. [DOI] [PubMed] [Google Scholar]
- Parisien M, Cosman F, Mellish RW, Schnitzer M, Nieves J, Silverberg SJ, Shane E, Kimmel D, Recker RR, Bilezikian JP. Bone structure in postmenopausal hyperparathyroid, osteoporotic, and normal women. J. Bone Miner. Res. 1995;10:1393–1399. doi: 10.1002/jbmr.5650100917. [DOI] [PubMed] [Google Scholar]
- Podshivalov L, Fischer A, Bar-Yoseph PZ. 3D hierarchical geometric modeling and multiscale FE analysis as a base for individualized medical diagnosis of bone structure. Bone. 2011;48:693–703. doi: 10.1016/j.bone.2010.12.022. [DOI] [PubMed] [Google Scholar]
- Pontzer H, Lieberman DE, Momin E, Devlin MJ, Polk JD, Hallgrímsson B, Cooper DML. Trabecular bone in the bird knee responds with high sensitivity to changes in load orientation. J. Exp. Biol. 2006;209:57–65. doi: 10.1242/jeb.01971. [DOI] [PubMed] [Google Scholar]
- Prevention and management of osteoporosis, 2003. World Health Organ. Tech. Rep. Ser. 921:1–164. [PubMed] [Google Scholar]
- Pugh JW, Rose RM, Radin EL. A structural model for the mechanical behavior of trabecular bone. J. Biomech. 1973;6:657–670. doi: 10.1016/0021-9290(73)90022-5. [DOI] [PubMed] [Google Scholar]
- Rupprecht M, Pogoda P, Mumme M, Rueger JM, Püschel K, Amling M. Bone microarchitecture of the calcaneus and its changes in aging: a histomorphometric analysis of 60 human specimens. J. Orthop. Res. Off. Publ. Orthop. Res. Soc. 2006;24:664–674. doi: 10.1002/jor.20099. [DOI] [PubMed] [Google Scholar]
- Ryan TM, Walker A. Trabecular bone structure in the humeral and femoral heads of anthropoid primates. Anat. Rec. Adv. Integr. Anat. Evol. Biol. 2010;293:719–729. doi: 10.1002/ar.21139. [DOI] [PubMed] [Google Scholar]
- Sachs E, Cima M, Cornie J. Three-Dimensional Printing: Rapid Tooling and Prototypes Directly from a CAD Model. CIRP Ann. - Manuf. Technol. 1990;39:201–204. [Google Scholar]
- Schneider CA, Rasband WS, Eliceiri KW. NIH Image to ImageJ: 25 years of image analysis. Nat. Methods. 2012;9:671–675. doi: 10.1038/nmeth.2089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siffert RS, Luo GM, Cowin SC, Kaufman JJ. Dynamic relationships of trabecular bone density, architecture, and strength in a computational model of osteopenia. Bone. 1996;18:197–206. doi: 10.1016/8756-3282(95)00446-7. [DOI] [PubMed] [Google Scholar]
- Snyder BD, Piazza S, Edwards WT, Hayes WC. Role of trabecular morphology in the etiology of age-related vertebral fractures. Calcif. Tissue Int. 1993;53(Suppl 1):S14–22. doi: 10.1007/BF01673396. [DOI] [PubMed] [Google Scholar]
- Soons J, Herrel A, Genbrugge A, Adriaens D, Aerts P, Dirckx J. Multi-layered bird beaks: a finite-element approach towards the role of keratin in stress dissipation. J. R. Soc. Interface. 2012;9:1787–1796. doi: 10.1098/rsif.2011.0910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sprecher CM, Schmidutz F, Helfen T, Richards RG, Blauth M, Milz S. Histomorphometric Assessment of Cancellous and Cortical Bone Material Distribution in the Proximal Humerus of Normal and Osteoporotic Individuals: Significantly Reduced Bone Stock in the Metaphyseal and Subcapital Regions of Osteoporotic Individuals. Medicine (Baltimore) 2015;94:e2043. doi: 10.1097/MD.0000000000002043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumner DR, Morbeck ME, Lobick JJ. Apparent age-related bone loss among adult female Gombe chimpanzees. Am. J. Phys. Anthropol. 1989;79:225–234. doi: 10.1002/ajpa.1330790210. [DOI] [PubMed] [Google Scholar]
- Swanson SaV, Freeman MaR. Is bone hydraulically strengthened? Med. Biol. Eng. 1966;4:433–438. doi: 10.1007/BF02476165. [DOI] [PubMed] [Google Scholar]
- Tellis BC, Szivek JA, Bliss CL, Margolis DS, Vaidyanathan RK, Calvert P. Trabecular scaffolds created using micro CT guided fused deposition modeling. Mater. Sci. Eng. C Mater. Biol. Appl. 2009;28:171–178. doi: 10.1016/j.msec.2006.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Linden JC, Birkenhäger-Frenkel DH, Verhaar JAN, Weinans H. Trabecular bone’s mechanical properties are affected by its non-uniform mineral distribution. J. Biomech. 2001;34:1573–1580. doi: 10.1016/s0021-9290(01)00146-4. [DOI] [PubMed] [Google Scholar]
- van der Linden JC, Homminga J, Verhaar JA, Weinans H. Mechanical consequences of bone loss in cancellous bone. J. Bone Miner. Res. 2001;16:457–465. doi: 10.1359/jbmr.2001.16.3.457. [DOI] [PubMed] [Google Scholar]
- Van Rietbergen B, Huiskes R, Eckstein F, Rüegsegger P. Trabecular bone tissue strains in the healthy and osteoporotic human femur. J. Bone Miner. Res. 2003;18:1781–1788. doi: 10.1359/jbmr.2003.18.10.1781. [DOI] [PubMed] [Google Scholar]
- Van Rietbergen B, Odgaard A, Kabel J, Huiskes R. Relationships between bone morphology and bone elastic properties can be accurately quantified using high-resolution computer reconstructions. J. Orthop. Res. 1998;16:23–28. doi: 10.1002/jor.1100160105. [DOI] [PubMed] [Google Scholar]
- Wang H, Ji B, Liu XS, Guo XE, Huang Y, Hwang K-C. Analysis of microstructural and mechanical alterations of trabecular bone in a simulated three-dimensional remodeling process. J. Biomech. 2012;45:2417–2425. doi: 10.1016/j.jbiomech.2012.06.024. [DOI] [PubMed] [Google Scholar]
- Wark JD. Osteoporotic fractures: background and prevention strategies. Maturitas. 1996;23:193–207. doi: 10.1016/0378-5122(95)00974-4. [DOI] [PubMed] [Google Scholar]
- Webster D, Wirth A, van Lenthe GH, Müller R. Experimental and finite element analysis of the mouse caudal vertebrae loading model: prediction of cortical and trabecular bone adaptation. Biomech. Model. Mechanobiol. 2012;11:221–230. doi: 10.1007/s10237-011-0305-3. [DOI] [PubMed] [Google Scholar]
- Yoon Y-J, Moon SK, Hwang J. 3D printing as an efficient way for comparative study of biomimetic structures — trabecular bone and honeycomb. J. Mech. Sci. Technol. 2014;28:4635–4640. [Google Scholar]