Linking temporal medical records using non-protected health information data

Abstract

Modern medical research relies on multi-institutional collaborations which enhance the knowledge discovery and data reuse. While these collaborations allow researchers to perform analytics otherwise impossible on individual datasets, they often pose significant challenges in the data integration process. Due to the lack of a unique identifier, data integration solutions often have to rely on patient’s protected health information (PHI). In many situations, such information cannot leave the institutions or must be strictly protected. Furthermore, the presence of noisy values for these attributes may result in poor overall utility. While much research has been done to address these challenges, most of the current solutions are designed for a static setting without considering the temporal information of the data (e.g. EHR). In this work, we propose a novel approach that uses non-PHI for linking patient longitudinal data. Specifically, our technique captures the diagnosis dependencies using patterns which are shown to provide important indications for linking patient records. Our solution can be used as a standalone technique to perform temporal record linkage using non-protected health information data or it can be combined with Privacy Preserving Record Linkage solutions (PPRL) when protected health information is available. In this case, our approach can solve ambiguities in results. Experimental evaluations on real datasets demonstrate the effectiveness of our technique.

1 Introduction

In the last decade, a lot of efforts have been made to improve the medical information systems enabling the collection and processing of huge amount of data to work toward a multi-institutional collaborative setting.^1–3 However, due to the decentralized nature of medical infrastructures, data are often fragmented, noisy and redundant, resulting in poor usability. To overcome these problems, several solutions for data management and integration have been proposed.^{4, 5} Among them, the record linkage process, which refers to the task of identifying records that belong to the same real-world entity, received much attention over the past years.^6–9 This process can be either applied to remove duplicate data within the same database or to link records across two or more data sources.^10,11

The original record linkage model dates back to the work of Fellegi and Sunter.¹² Over the past years, many techniques have been proposed to improve the utility, scalability, and privacy of the record linkage process.^13,14 Despite the importance of these results, most existing solutions are limited to static settings where attribute values do not change over time. However, in real medical applications, data are often associated with a temporal dimension which reflects the time in which medical events are observed or recorded. For example, in longitudinal medical data (e.g. EHR), the patient’s information (e.g. diagnosis codes, lab test results) is recorded together with the time of the patient’s visit. In this setting, attribute values (e.g. diagnoses) may change over time and therefore it is crucial to take the temporal information into account during the integration process. Standard linkage solutions lack of the ability of incorporating this temporal information into the linkage process. Therefore, they result to be ineffective in this setting.

In this paper, we improve current data integration systems by incorporating the temporal information in the linkage process. This enables patient longitudinal data linkage and provides additional information during the linkage process compared to standard solutions. Our proposed approach takes advantage of the temporal evolution of patient non-protected health information (PHI) data to determine the records that refer to the same patient across multiple institutions. In real settings, patients may visit multiple hospitals, leaving fragments of their medical “pathway” in each local database. While each of these traces may have different data values (i.e. diagnoses, biometric values), if considered in a temporal order, they describe the patient’s evolving medical conditions. In our approach, we reconstruct these fragmented traces by using common diagnosis evolutions represented as “patterns”. These patterns allow us to capture the correlation between diagnoses and they provide important information in linking these fragments. Consider the case of a doctor who wants to reconstruct the diagnostic pathway of a patient with diabetes from fragmented records. Intuitively, only those fragments containing diagnosis codes related to diabetes (e.g. cardiovascular diseases) are likely to be relevant for that patient. In fact, the temporal evolution of the diseases together with their correlation can help combine the fragments and reconstruct the patient’s pathway.

Our linkage technique has significant advantages compared to traditional machine learning-based approaches. First, the diagnostic patterns provide a simple representation of the dependency between diagnoses which can be easily understood. This allows medical doctors, who may not have expertise in machine learning, to acquire a clear and meaningful picture of the important relationships between diagnoses used in our model. Second, the use of these patterns enables our solution to efficiently identify the important features in linking patients without the need to handle the sparsity and high dimensionality of the longitudinal medical data.

Our approach enables the linkage of patient longitudinal records using the temporal evolution of the non-PHI data. In this way, our approach can be used as a stand-alone solution for linking the temporal records or in combination with traditional privacy preserving record linkage techniques to solve ambiguity among records when sensitive information is used in the overall linkage process. Our approach can be used in many real applications. For example, in an emergency/urgent-care situation or when the patient is unable to provide his/her identifying information (e.g. patient is unconscious). In these situations, our approach would enable medical personnel to reconstruct the patient’s medical history by knowing the patient’s current medical conditions. Another possible application is in finding similar patients, whereby exploiting the similarity between their longitudinal non-PHI data to replace certain patients who opt out from a clinical trial. We believe that our solution can improve modern information systems by facilitating data sharing and integration. As we demonstrate on real-world data, the diagnoses present patterns that carry important temporal information that can be effectively used in data integration process across institutions.

1.1 Contributions

The main contributions of this paper are summarized below.

• We model the temporal diagnoses evolution of patients as multidimensional sequential data, named diagnostic pathways. In this representation, we capture the diagnosis dependencies using patterns.

• We propose a linkage score for matching pathways which combines two components: the patterns score and the temporal coherency. These components capture both the dependency and the temporal evolution of diagnoses in the pathways.

• We retrieve a set of possible matching pathways that are ranked according to a linkage score, where higher scores indicate higher chances for the pathways to refer to the same patient. Medical personnel can select the size of the returned set allowing a tradeoff between accuracy and efficiency.

• Extensive experimental evaluations on two real medical datasets demonstrate the effectiveness of our approach.

2 Related work

In this section, we report the works most related to the problem presented in this paper.

Modern healthcare systems enable the collections of a large amount of temporal and heterogeneous data from patients (e.g. biological signals, genomic data, and diagnosis codes). While the extraction of knowledge from these data is extremely useful in many real applications,^15–17 the overall process is very challenging due to the high dimensionality, sparsity, and fragmented nature of the data.

To address the high dimensionality and sparsity of the temporal data, several solutions have been proposed both in the continuous and discrete time domain. For continuous time series data, a general approach consists in transforming the original temporal data (e.g. blood pressure, heart rate) into a discrete representation where numeric data values are encoded into symbols. To perform this transformation, many techniques have been proposed over the past years.^18–21 The knowledge discovery from discrete time series data is typically performed in different ways, for example, by inferring the dependency between time events and employing convolution based techniques.^22–24 Recently, Liu et al. proposed a temporal graph representation of the discrete time data where nodes capture single events and edges capture the temporal relationship between events.²⁵ Despite the effectiveness of these approaches, the fragmented nature of the data and the presence of noise make it difficult to adapt these solutions to our setting.

In this paper, we address both the fragmented nature and the high dimensionality of the data by proposing a record linkage solution. While the classic record linkage problem has been extensively investigated over the past years, the majority of record linkage research focus on static scenarios where the temporal dependency between records is not taken into consideration. Only a few recent works studied the problem of linking temporal records.^26–28 In these techniques, a two-phase approach is employed to handle the temporality of the data. First, a statistical model is defined to describe the evolution of the entities over time. Second, a clustering approach is employed to match only the records that are temporally similar. While these solutions are effective for classic databases, they have limited applicability in our problem setting. In fact, medical data are typically very sparse compared to classic temporal databases (e.g. authors and their publications in DBLP repository) leading to poor-quality statistical models (e.g. overfitting problems). In our setting, a patient may have only a few hospitalizations over years where his/her medical condition may be significantly different across visits. On the other hand, in the DBLP database, a researcher generally produces many temporal records each year (i.e. conference publications and journals). Furthermore, these records preserve partial information about the real entity such as affiliation, research topic and co-authors. Clearly, such rich information is not available in our setting, or in some cases is sensitive information which cannot be made easily available (e.g. SSN, first name, and last name). As a result, the overall linkage task in our setting exhibits novel challenges that cannot be addressed with traditional temporal linkage solutions.

3 Problem definition

At the moment of hospitalization, patients are typically subject to general controls and medications, and a set of diagnosis codes is assigned to denote their medical condition. In this work, we represent the temporal evolution of the patient’s medical condition as a sequence of diagnosis codes (ICD9) assigned by the healthcare institution at each visit. We model this sequence of observed diagnoses as a diagnostic pathway.

Definition 1

A patient diagnostic pathway 𝒳 of length n is an ordered sequence of n pairs $𝒳={\{(X_i,t_i)\}}_{i=1}^n$ representing the set of diseases X_i observed at each time t_i (e.g. admission time at the hospital), where t_i < t_i+1.

Typically in a medical setting, additional features (e.g. lab tests, medications) are recorded at each visit that we could use in modeling the medical condition of the patient over time. However, in this paper we will focus on linking patient temporal data by using only the diagnosis codes.

To link patient diagnostic pathways, two (or more) fragments $𝒳={\{(X_i,t_i)\}}_{i=1}^n$ and $𝒴={\{(Y_j,t_j)\}}_{j=1}^m$ representing data within each local institution are merged to form a unique pathway $𝒵={\{(Z_i,t_i)\}}_{i=1}^{m+n}$. In this process, the diagnostic pathways 𝒳 and 𝒴 are aligned considering their temporal order to preserve the evolution of the patient’s longitudinal data.

Definition 2

Let $𝒳={\{(X_i,t_i)\}}_{i=1}^n$ and $𝒴={\{(Y_j,t_j)\}}_{j=1}^m$ be two diagnostic pathways of length n and m, respectively. Then $𝒵={\{(Z_i,t_i)\}}_{i=1}^{m+n}$ obtained by temporally aligning 𝒳 and 𝒴, denoted as 𝒵 = 𝒳 ⊙ 𝒴, represents the diagnostic pathway obtained by temporally sorting the individual pairs (X_i, t_i) and (Y_j, t_j) from 𝒳 and 𝒴.

In a distributed setting, the same patient’s records are typically associated with the same ID within each local database; however, across institutions the same patient’s records may refer to different IDs. Hence, in linking the same patient’s pathway, we may align fragments across databases that refer to different IDs. To illustrate this concept, consider the following example from the situation in Table 1 which represents the patients’ records of two medical institutions.

Table 1.

Two database tables D₁ (above) and D₂ (below) containing patient records across two institutions.

ID	ICD9	Time
(a) Dataset D1 at institution A
1	250.13, 790.29, 425.4	10
1	250.61, 425.4	15
1	428.23, 786.30	25
2	434.91	12
2	813.41, 808.2	15
3	410.71, 428.33	22
3	410.7, 414.01	25
4	682.3, 486	5
(b) Dataset D2 at institution B
1	969.4	10
1	969.4, 349.82	15
2	250.13, 518.81	8
2	250.63, 429.9	20
3	198.3	20
3	415.19, 995.92	40
4	996.61, 507.0	25
5	423.0, 518.81	7

Note: Each record has a unique identifier within each dataset and it contains the set of diagnosis codes recorded at each visit and the time of the visit. The same patient’s records across the databases may be associated with different IDs.

Example 1

Consider the following pathways 𝒳 = ({250.13, 790.29, 425.4}, 10), ({250.61, 425.4}, 15), ({428.23, 786.30}, 25) and 𝒴 = ({250.13, 518.81}, 8), ({250.63, 429.9}, 20) associated with the patient of ID = 1 in D₁ and the patient of ID = 2 in D₂ respectively. In order to test whether these two fragments belong to the same patient across these institutions, we proceed by considering their alignment 𝒵 = 𝒳 ⊙ 𝒴 = ({250.13, 518.81}, 8), ({250.13, 790.29, 425.4}, 10), ({250.61, 425.4}, 15), ({250.63, 429.9}, 20), ({428.23, 786.30}, 25), where the individual observations are temporally sorted.

In some steps of our linkage solution, we will explicitly use the sequence of visits in the pathway without considering the absolute time values in which each set of diagnoses has been recorded. In such a representation, namely sequential representation of a pathway, we encode each diagnosis into a positive integer number. Each set of diagnoses is sorted, while across all the sets of the pathway, we preserve the order of the observations. Consider for example the pathway 𝒳 = ({250.13, 790.29, 425.4}, 10), ({250.61, 425.4,}, 15), ({428.23, 786.30}, 25). We denote with X = 〈{1, 2, 3}, {3, 4}, {5, 6}〉, the sequential representation of 𝒳, where each single diagnosis code is mapped into an unique integer (e.g. 425.4 maps to 3). While in the sequential representation we lose the information about the time difference between sets of observed diagnosis codes, we still preserve their order. Later in the paper, we will use this representation to develop a robust similarity measure between pathways.

3.1 Overview of our approach

In this work, we link patient records by exploiting the temporal correlation within the patient’s longitudinal data. Specifically, we observe that the temporal evolution of patient conditions contain certain patterns. These patterns may represent how a diagnosis evolves during different stages or how multiple diagnoses are correlated. For example, a patient diagnosed with diabetes is more likely to have in his/her diagnostic pathway codes indicating later stages of diabetes or codes for vascular diseases. In our solution, we aim to use these patterns to exploit the similarity between diagnostic pathways.

Example 2

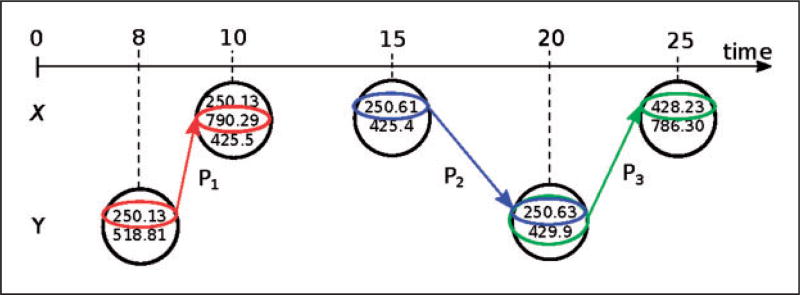
Continuing from Example 1, consider 𝒵 = 𝒳 ⊙ 𝒴 = ({250.13, 518.81}, 8), ({250.13, 790.29, 425.4}, 10), ({250.61, 425.4}, 15), ({250.63, 429.9}, 20), ({428.23, 786.30}, 25). By comparing this pathway with pathways from known patients, we can find some patterns spanning across 𝒳 and 𝒴 that are commonly present in single patient’s pathways. Specifically, as illustrated in Figure 1, the patterns P₁ = ({250.13},8),({790.29},10), P₂ = ({250.61},15),({250.63},20) and P₃ = ({250.63, 429.9},20),({428.23,},25) are specific patterns that represent, respectively, the correlation of diabetes mellitus with hyperglycemia, and complications of diabetes such as cardiac dysfunction and heart failure. These patterns are common factors across patients with diabetes who experience heart failure.²⁹ Therefore, across all the possible alignments that we could obtain from Table 1, 𝒵 contains patterns that are most likely to describe the same patient’s condition (i.e. diabetes). Hence, these patterns provide strong evidences that the pathways 𝒳 and 𝒴 may belong to the same patient.

Figure 1.

Temporal alignment between the pathways 𝒳 = ({250.13, 790.29, 425.4}, 10), ({250.61, 425.4}, 15), ({428.23, 786.30}, 25) (above) and 𝒴 = ({250.13, 518.81}, 8), ({250.63, 429.9}, 20) (below). Across these pathways, we identify three specific patterns P₁, P₂ and P₃ which indicate complications related to diabetes. Therefore, these patterns provide significant evidences that these fragments are likely to be from the same patient.

In our approach, we develop a robust similarity measure that uses these patterns for matching the fragments of pathways and to finally determine if the alignment refers to the same patient.

3.1.1 Framework

Our overall linkage solution follows three majors steps: preprocessing, indexing, and matching as illustrated in Figure 2.

• Preprocessing. In this phase, we construct a training set T which contains a set of diagnostic pathways, each associated with a known patient. We will use this set to determine the similarity between the temporal records and learn weights for matching the pathways. Specifically, this set will help us identify patterns that typically appear within individual pathways. Then, the presence of these patterns in a temporal alignment may indicate if the alignment resembles a real patient pathway. We note that the training set can be obtained from de-identified EHR data or from publicly available labeled longitudinal data.

• Indexing. We apply an indexing phase where we partition the original records into blocks using non-PHI attribute values (e.g. perturbed date of birth, gender, and ethnicity). As a result, the original records in the input datasets D₁ and D₂ are partitioned into n disjoint blocks $B_1^1,B_2^1,\dots ,B_n^1$ and $B_1^2,B_2^2,\dots ,B_n^2$, respectively. This process is performed by grouping records with the same blocking attribute values in the same block. Therefore, to determine the matching pathways, it is sufficient to focus on the record pairs within blocks associated to the same blocking value (i.e. records in $B_i^1$ compared with those in $B_i^2$). The use of indexing reduces the number of candidate pairs evaluated in the matching phase, hence improving the overall scalability.

• Matching. In the matching phase, we consider all the possible candidate alignments generated by the pathways in each pair of blocks referring to the same blocking attribute value. For each alignment, we propose a linkage score which determines the likelihood of a temporally aligned pathway belonging to a single patient. This score combines two measures: patterns score and temporal coherency. The first component uses the patterns from the training set to evaluate the feasibility of the diagnosis evolution in the alignment. The second component measures the temporal coherency within the alignment by considering the changes in the diagnosis codes across observations close in time. These components are combined into a final score using the weights determined in the preprocessing phase.

Figure 2.

Overview of our linkage framework for two data holders D₁ and D₂ aiming to link their temporal data records. (1) Preprocessing: Our linkage model is trained on a training set T. (2) Indexing: The original records are indexed into disjoint blocks. (3) Matching: The temporal records within each corresponding block are linked using our linkage model and the training set T.

Finally, the pathways with the highest linkage score (i.e. top-k) are returned as results.

4 Pathway similarity

Our patterns score, in matching/linking the pathways, aims to measure how likely a candidate pair of pathways 𝒳 and 𝒴 refers to the same patient, by evaluating the similarity of 𝒵 = 𝒳 ⊙ 𝒴 with the pathways in the training set T on their common patterns. Our intuition is that if by aligning 𝒳 and 𝒴 we obtain a sequence Z that shares a large number of patterns with some of the sequences in T, then these patterns are evidences of possible diagnosis evolutions that span between 𝒳 and 𝒴. Hence, these two pathways might have high chance of referring to the same patient.

In the rest of this section, we develop the foundations of this idea by proposing a similarity notion between pair of pathways based on their common subsequences.

4.1 All common subsequence similarity

In our similarity definition, we model patterns as subsequences (i.e. they may have gaps) that are extracted from the sequence representation of the pathways. Our goal is to measure the similarity between pathways by looking at their common subsequences. Despite the rich research on sequence similarity, we observe that sequences obtained from pathways may contain sets of symbols on each observation; therefore, traditional sequence similarity measures are often ineffective in this setting. To illustrate this concept, we consider the following example.

Example 3

Let X = 〈{1, 2}, {3}, {4}〉, Y = 〈{1}, {3}〉, and Z = 〈{1}, {2}, {4}〉 be the sequence representations of three pathways. Consider the task of determining which sequence among Y and Z is closer to X. Using a standard sequence similarity measure such as the Longest Common Subsequence (LCS),³⁰ we obtain that for both Y and Z their longest common subsequence with X has length 2. Specifically, LCS(X, Y) = 〈{1}, {3}〉 and LCS(X, Z) = 〈{1}, {4}〉. Hence, it is not possible to determine which of these two sequences is closer to X by just looking at their longest common subsequence. On the other hand, by taking into consideration all their common subsequences, we can observe that Y shares three sequences (i.e. 〈{1}〉, 〈{3}〉, 〈{1}, {3}〉) with X, while Z shares five sequences (i.e. 〈{1}〉, 〈{2}〉, 〈{4}〉, 〈{1}, {4}〉, 〈{2}, {4}〉). These sets of subsequences suggest that the pathway associated with Z is more similar to X than Y.

The previous example shows that considering all common subsequences is more informative than just using the longest common subsequence in evaluating the sequence similarity. Furthermore, these shared subsequences capture the common data evolution across the pathways, allowing to preserve the correlation between diagnoses. We can also observe that the similarity is completely based on the sequence representation and it does not rely on the specific time value in which the diagnoses are observed. As a result, the similarity is robust against noise/errors in the pathways (e.g. inaccurate admission time or missing data).

4.2 Sequence similarity computation

To compute the patterns’ similarity between two pathways 𝒳 and 𝒴, we proceed to enumerate all the common subsequences of different length. Specifically, from the sequence representations X and Y of the original pathways, we define a vector ACV(X, Y) = [ν₁, ν₂, …, ν_k], namely all common subsequences vector, where the i-th component, ν_i, stores the number of common subsequences (with their multiplicity) of length exactly i. To efficiently compute the common subsequences and fill each component of ACV(X, Y), we use the procedure illustrated in the following theorem.

Theorem 1

Consider two sequences X = {X₁, X₂, …, X_n}, Y = {Y₁, Y₂, …, Y_m} containing n and m observations, respectively. Let N[i, j, l] be the number of common subsequences of length l across X₁, X₂, …, X_i and Y₁, Y₂, …, Y_j (i.e. the prefixes of length i and j for the sequences X and Y). Then, N[i, j, l] can be computed with the following recurrence relationship

$$N[i,j,l]=\{\begin{array}{cc}0\hfill & \hfill \text{if }l>\text{min}\{i,j\}\hfill \\ N[i-1,j,l]+N[i,j-1,l]++N[i-1,j-1,l-1]\times 2^{|X_i\cap Y_j|-1}--N[i-1,j-1,l]\hfill & \hfill \text{otherwise}\hfill \end{array}$$ (1)

Given a pair of diagnostic pathways $𝒳={\{(X_i,t_i)\}}_{i=1}^n$ and $𝒴={\{(Y_j,t_j)\}}_{j=1}^m$, using the procedure in Theorem 1, we have that N[n, m, l] represents the number of common subsequences of length l between X and Y. Therefore, each component ν_l of ACV(X, Y) = [ν₁, ν₂, …, ν_k], can be computed as ν_l = N[n, m, l] for l = 1, 2, …, k, where k = min{n, m}. Assuming the size of the alphabet on which the sequences are defined to be a constant, the overall running time to compute the vector ACV(X, Y) is O(n × m).

Example 4

Continuing from the Example 3, we have that ACV(X, Y) = [2, 1] because X and Y share two patterns of length 1 and one pattern of length 2, while ACV(X, Z) = [3, 2] since three patterns of length 1 and two patterns of length 2 are shared between X and Z.

Using the all common subsequences vector, we can now present the similarity notion between pathways as follows.

Definition 3

Let 𝒳 and 𝒴 be two diagnostic pathways. Then their similarity, denoted as sim(𝒳, 𝒴), is defined as

$$\mathit{\text{sim}}(𝒳,𝒴)=\frac{{\Vert \mathit{\text{ACV}}(X,Y)\Vert }_p}{\text{max}\{{\Vert \mathit{\text{ACV}}(X,X)\Vert }_p,{\Vert \mathit{\text{ACV}}(Y,Y)\Vert }_p\}}$$ (2)

where ‖ · ‖_p denotes a weighted norm of parameter p which allows to assign different weights to the common subsequences with respect to their length.

Specifically, in our approach, we consider ${\Vert \mathit{\text{ACV}}(X,Y)\Vert }_p={\sum }_{i=1}^k{v}_i\times f(p,i)$, where f (p, i) is a weight function of p. We use this function to tune the importance of the common subsequences in the final similarity. In our evaluation, we use f (p, i) = e^i×p, where p = 1 so that an exponentially larger weight is assigned to longer subsequences.

Example 5

From Example 4, we have that $\mathit{\text{sim}}(𝒳,𝒴)=\frac{e\times (2+e)}{e(5+7\times e+3\times e^2)}=0.10$ and $\mathit{\text{sim}}(𝒳,𝒵)=\frac{e\times (3+2\times e)}{e(5+7\times e+3\times e^2)}=0.18$. Since sim(𝒳, 𝒵) > sim(𝒳, 𝒴), the pathway 𝒵 is more similar to 𝒳 than 𝒴.

The proof for Theorem 1 and additional properties of our similarity notion are reported in Appendix 1.

5 Matching diagnostic pathways

In linking patient longitudinal data, we compute a linkage score for each candidate alignment 𝒵 = 𝒳 ⊙ 𝒴, where higher linkage scores imply higher probability for 𝒵 to represent the diagnosis evolution of a single patient. We express the linkage score using two different components, namely patterns score and temporal coherency.

The patterns score aims to measure how well 𝒵 = 𝒳 ⊙ 𝒴 resembles single patient diagnosis evolutions by comparing the alignment with known single pathways in the training set T. The temporal coherency instead measures the coherency among the diagnoses within 𝒵 by considering the variation in the codes across the observations in 𝒳 and 𝒴 over time.

5.1 Patterns score

In computing the patterns score, we take into considerations two aspects. First, we use a component that measures how similar the alignment 𝒵 is to the pathways in the training set T using the notion of sim(·, ·), as defined in the previous section. Intuitively, finding single pathways in T that have common patterns with 𝒵 provides evidence that 𝒵 may be a good candidate to represent a single patient’s pathway. Second, we introduce a component that computes the relative increment of shared patterns in Z compared to just considering X and Y individually. We denote this component as bf (𝒳 ⊙ 𝒴, 𝒜), that expresses the benefit of aligning 𝒳 and 𝒴 with respect to a single patient pathway 𝒜 in the training set T. Its formal definition is reported below.

$$\mathit{\text{bf}}(𝒳\odot 𝒴,𝒜)=1-\frac{\text{max}\{\mathit{\text{sim}}(𝒳,𝒜),\mathit{\text{sim}}(𝒴,𝒜)\}}{\mathit{\text{sim}}(𝒳\odot 𝒴,𝒜)}$$ (3)

Given these components, the overall patterns score for the candidate alignment 𝒵 = 𝒳 ⊙ 𝒴 is defined as follows

$$\mathit{\text{pScore}}(𝒳\odot 𝒴)=\underset{𝒜\in T}{\text{max}}\{\alpha \prime \times \mathit{\text{sim}}(𝒳\odot 𝒴,𝒜)+(1-\alpha \prime )\times \mathit{\text{bf}}(𝒳\odot 𝒴,𝒜)\}$$ (4)

where the optimal value for α′ ∈ [0, 1] can be estimated from the training set T.

To illustrate the intuitions behind these notions, we consider the following example.

Example 6

Continuing from Example 2, to compute the patterns score of 𝒵, we can observe that a pathway 𝒜 ∈ T sharing all the three patterns (P₁, P₂, and P₃) yields a higher score compared to a pathway ℬ ∈ T that shares only one of them. In fact, the presence of all the three patterns leads to sim(𝒵, 𝒜) > sim(𝒵, ℬ) and bf (𝒵, 𝒜) > bf (𝒵, ℬ). Hence, the sequences in the training set that contain more common patterns with the alignment tend to be more informative for determining the patterns score.

5.2 Temporal coherency

This component measures the temporal coherency across sets of diagnoses in the candidate alignment 𝒵 = 𝒳 ⊙ 𝒴. In fact, due to the temporal nature of medical data, the pathways 𝒳 and 𝒴 may have differences across their sets of codes (e.g. different stages of the same disease). For example, a patient may first visit a general hospital where a diagnostic pathway 𝒳 is generated; successively, he may be treated in a specialized clinic where his records form the pathway 𝒴. While both pathways refer to the same patient, due to different time frames of the patient’s hospitalization, they may present different levels of coherency in the diagnoses. To measure the temporal coherency of the alignment, we introduce a function that combines both the temporal and set-based similarity measures between pairs of diagnosis codes in the observations.

For each pair of observations (X_i, t_i) and (Y_j, t_j) from 𝒳 and 𝒴, we first compute the Jaccard similarity between the sets of diagnosis codes X_i and Y_j, denoted as J(X_i, Y_j). This similarity is defined as follows

$$J(X_i,Y_j)=\frac{|X_i\cap Y_j|}{|X_i\cup Y_j|}$$ (5)

and it measures the number of common diagnosis codes between X_i and Y_j. Then, the distance between (X_i, t_i) and (Y_j, t_j) is weighted using a decay function which depends on the temporal gap Δ(i, j) = |t_i − t_j| between the observations. Specifically, our decay function is defined as follows.

$$\mathit{\text{decay}}(t)=\{\begin{array}{cc}0\hfill & \text{if }t>{\delta }_1\hfill \\ e^{-t/{\delta }_2}\hfill & \text{otherwise}\hfill \end{array}$$ (6)

In other words, we compute a smaller weight using a predefined parameter δ₂ for a larger time interval t, when t ≤ δ₁. Otherwise, we ignore the observation pairs with a time interval larger than the threshold δ₁.

Given two pathways $𝒳={\{(X_i,t_i)\}}_{i=1}^n$ and $𝒴={\{(Y_j,t_j)\}}_{j=1}^m$ of length n and m, respectively, the temporal coherency score for their alignment 𝒵 = 𝒳 ⊙ 𝒴 is defined as follows.

$$\mathit{\text{tScore}}(𝒳\odot 𝒴)=\frac{1}{n+m}\sum _{i=1j=1}^{n,m}J(X_i,Y_j)\mathit{\text{decay}}(\mathrm{\Delta }(i,j))$$ (7)

This measure is motivated by the concept of temporal locality, that is, if in a time point a diagnosis is observed, then it is likely that the same diagnosis is observed in a near visit. Therefore, we assign a heavy weight to the coherency score for diagnoses that occur within a small temporal gap, and vice versa.

5.2.1 Linkage score

The final linkage score (lScore) for an alignment 𝒵 = 𝒳 ⊙ 𝒴 is obtained as a linear combination between the patterns score and the temporal coherency, as follows

$$\mathit{\text{lScore}}(𝒳\odot 𝒴)=\alpha \times \mathit{\text{pScore}}(𝒳\odot 𝒴)+\beta \times \mathit{\text{tScore}}(𝒳\odot 𝒴)$$ (8)

where α and β are weights determined using cross validation in the training phase.

6 Results

We conduct our experiments on two real-world datasets: UCSD and MIMIC-III.³¹ The former contains multiple admission records in the hospital at UCSD for a total of 41,730 patients, which are obtained with institutional review board approval. The latter is a de-identified dataset which comprises over 58,000 hospital admissions for 38,645 adults and 7875 neonates.^a

We perform a 10-fold cross validation, where for each patient’s pathway 𝒵 in the test set, a pair of partial pathways 𝒳 and 𝒴 is generated. These pathways are formed by randomly selecting the observations in 𝒵 to simulate how the original patient pathways may be fragmented across two institutions. For those patients that have pathways with a number of observations in the range [l_min, l_max] their fragments 𝒳 and 𝒴 are distributed across D₁ and D₂, while for the other patients their fragments are placed in D₂. Then, our goal is to reconstruct the original pathway 𝒵 from the partial pathways in D₁ by linking them with the fragments in D₂. In our evaluations, we consider pathways of length in the range of [4, 16] observations.

6.1 Utility measure

To evaluate the ability of our approach in reconstructing the original pathways we consider the following notion of accuracy. For each original patient with fragment 𝒳_i in D₁, we return k alignments {𝒵₁ = 𝒳_i ⊙ 𝒴₁, …, 𝒵_k = 𝒳_i ⊙ 𝒴_k}, where 𝒴₁, …, 𝒴_k ∈ D₂, with the top-k highest linkage scores. For each user, the accuracy of our approach is 1 if the original complete pathway is reported in the top-k results; 0 otherwise. In our evaluation, we report the average accuracy which is obtained by averaging the accuracy for each patient.

The detailed statistics of the datasets, the main parameters for our algorithm, and additional experiments on the scalability and impact of the noise in the data are reported in Appendix 2. Below, we present the main evaluation of our technique.

6.2 Evaluation

6.2.1 Impact of the number of returned pathways k

The parameter k determines the number of pathways reported for each patient in input. In our evaluation, k assumes values in the range [1, 50], where for k = 1 only the pathway with the highest linkage score is returned as a match. The results are reported in Figure 3(a) and (b) for the UCSD and MIMIC-III datasets, respectively.

Figure 3.

Accuracy vs. number of returned pathways (k). Two cases of training set are considered: training set and test set overlap (w), and training set and test set disjoint (w/o). (a) UCSD. (b) MIMIC-III.

For this evaluation, we perform a 10-fold cross validation where we consider two configurations of the training set. In the first configuration, labeled with w, for each patient a copy of his/her original pathway is injected in the training set. Instead, in the second configuration, labeled with w/o, test and training set are completely disjointed. The use of the w configuration allows us to validate the results obtained by our solution. In fact, in this case the real pathways are contained in the training set. Therefore, when computing the patterns score, our solution can take advantage of this information and provide nearly optimal accuracy for all values of k. When the test and training set are disjointed, configuration labeled with w/o, the accuracy is generally lower than the previous case and it tends to increase as k increases in both datasets. For k ≥ 10, our approach yields accuracy higher than 0.8, which indicates that more than 80% of the times, the original pathways are correctly returned by our solution among the top 10 results. For larger values of k, the accuracy approaches to 1. For the rest of the experiments, we consider a training set generated with the configuration w/o, where there is no overlap between training and test set.

We observe that these two configurations of the training set are extreme, providing full or no knowledge about the records required to be linked in the training set. In real scenarios, the training set would contain partial information about the records required to be linked (e.g. past records); hence, we would expect accuracy in between the values obtained with these two settings.

6.2.2 Impact of the training set

We measure the accuracy with different number of folds in the cross validation process. Specifically, we increase the number of folds from 2 to 10 and the results with the top five pathways are reported in Figure 4(a) and (b) for the UCSD and MIMIC-III datasets. We observe that as the number of folds increases, a larger training set is constructed. Adding more pathways in the training set helps improve the knowledge of patterns for computing the linkage score. In fact, we observe a stable increment of accuracy in both datasets as the number of folds increases. For 10-fold cross validation, we obtain accuracy as high as 0.8 for UCSD and 0.75 for MIMIC-III datasets. We believe that in a healthcare environment, historical longitudinal data from past patients can be used to construct a large and rich training set. Therefore, our solution can take advantage of this information to link new coming patients.

Figure 4.

Accuracy vs. number of folds. As the number of folds increases, a larger training set is constructed which helps our approach compute a more accurate patterns score. (a) UCSD, (b) MIMIC-III.

In the rest of the evaluations, we report only the average accuracy omitting the quantile box plot. In fact, for our default setting which considers 10-fold cross validation, the accuracy values have small variance; hence, their average provides good indication of the overall performance of our solution.

6.2.3 Significance of our linkage score

In this experiment, we consider the difference in linkage score between the true positive and true negative pathways. Our goal is to understand if our linkage score provides a significant separation between real matching (i.e. original pathways) and non-matching pathways. To assess the significance, we use a t-test between the populations of real matching and non-matching records. Specifically, for each pair of pathways 𝒳 and 𝒴 that either refer to the same patient (i.e. real matching TP) or to different patients (i.e. real non-matching TN), we compute their linkage score. Their scores are reported in Figures 5 and 6 for the UCSD and MIMIC-III dataset, respectively. Table 2 summarizes the statistics of these two populations. The results of the t-test to determine the statistical difference between the means of the TP and TN populations yield p-value < 10⁻⁶. This indicates high statistical difference between the scores for the pathways in TP and TN. Hence, our similarity notion provides a good separation between real matching and non-matching pathways.

Figure 5.

Box plot of the linkage score for true positive (TP) and true negative (TN) in UCSD.

Figure 6.

Box plot of the linkage score for true positive (TP) and true negative (TN) in MIMIC-III.

Table 2.

Sample size, mean and standard deviation for the populations of pathways in TP and TN from UCSD and MIMIC-III dataset.

	UCSD		MIMIC-III
	TP	TN	TP	TN
Sample Size	845	12414	896	6580
Mean	0.49	0.42	0.50	0.48
Stand. Deviation.	0.03	0.1	0.002	0.04

6.2.4 Resolving ambiguities

In this setting, we demonstrate how our linkage score can be used to solve ambiguities in linkage/blocking results that otherwise would require human intervention. Consider a simple blocking approach that uses the date of birth of patients to identify the possible matching pathways. For example, a pair of pathways 𝒳 ∈ D₁ and 𝒴 ∈ D₂ is considered a potential match if the patients associated with these pathways have the same year of birth. Even though this indexing strategy greatly reduces the candidate alignment 𝒵 = 𝒳 ⊙ 𝒴, only a small fraction of these alignments generated within each block are typically real matches (e.g. see blocking results in Appendix 2). As a consequence, to resolve these ambiguities and identify the real matches, human intervention is typically required. However, using our approach, the human intervention cost can be considerably reduced. In fact, our linkage score allows us to rank the candidate alignments and to focus on evaluating only those that are most promising.

For each set B_i of possible matching alignments, we apply our linkage scoring procedure and we select the top-k_i pathways with the highest linkage score, where k_i = γ × |B_i|. The parameter γ determines the fraction of the overall candidate alignments that are returned by our solution. The accuracy obtained by our solution with respect to different values of γ is reported in Figure 7(a) for the UCSD data and Figure 7(b) for MIMIC-III. We observe that with our technique, it is sufficient to examine only 10% of the alignments generated by the indexing technique to achieve accuracy as high as 0.9 for UCSD. For the MIMIC-III data, the same accuracy is achieved by just examining only 1% of the alignments generated by the indexing procedure. For larger γ values, the accuracy approaches to 1. Overall, we observe that our linkage score helps greatly reduce the number of alignments that require human review. Furthermore, we are able to score the candidate alignments and thus resolve ambiguities in the results obtained with the indexing step. By selecting the highest scoring alignments, which are a small fraction of the overall alignments, the final accuracy is well preserved.

Figure 7.

Accuracy vs. γ (percentage of alignments returned). By ranking the alignments within each block in the index step, it is sufficient to examine only a small fraction of the overall candidates to obtain high accuracy.

6.3 Understanding the linkage results

In this setting, we run our linkage approach using k = 10. From the results, we are interested in looking into the differences among two classes of patients: those that are correctly linked (i.e. real match in the top 10), named matched patients, and those that are mismatched (i.e. real match outside the top 10) named mismatched patients. For these patients, we provide a summary across a few dimensions that consider diagnosis, gender information, and presence of cancer. We aim to understand if there are specific features across these sets of patients.

6.3.1 Diagnosis code

To study the influence of diagnosis codes on these sets of patients, we compute for each ICD9 diagnosis code a discriminant score based on the notion of TF/IDF (Term Frequency–Inverse Document Frequency). This score provides an indication about the relevance of each diagnosis code among the sets of patients. The top five diagnoses with the highest scores are reported in Tables 3 and 4 for the UCSD and MIMIC-III dataset, respectively.

Table 3.

Top five most discriminative diagnoses across the sets of matched and mismatched patients in the UCSD dataset.

Matched patients				Mismatched patients
Discr. Score	Code	Description	Freq.	Discr. Score	Code	Description	Freq.
0.0014	572.2	Hepatic encephalopathy	0.038	0.0015	607.3	Priapism	8.48 × 10−4
0.0011	202.80	Oth. lymp. unsp. xtrndl. org.	0.025	0.0015	170.4	Mal. neo. long bones arm.	5.31 × 10−4
8.65 × 10−4	V42.7	Liver transplant status.	0.026	8.94 × 10−4	250.91	DMI unspf. nt. st. uncntrld.	9.55 × 10−4
6.67 × 10−4	585.3	Chr. kidney dis. stage III.	0.026	7.45 × 10−4	151.6	Mal. neo. stom. great curv.	2.65 × 10−4
6.55 × 10−4	V22.1	Supervis. oth. normal. preg.	0.077	7.45 × 10−4	E924.1	Accid-caustic substance.	0.002

Table 4.

Top five most discriminative diagnoses across the sets of matched and mismatched patients in the MIMIC-III dataset.

Matched patients				Mismatched patients
Discr. Score	Code	Description	Freq.	Discr. Score	Code	Description	Freq.
3.29 × 10−4	332.0	Paralysis agitans.	0.031	2.97 × 10−4	V10.85	Hx. of brain malignancy.	0.003
3.29 × 10−4	V10.11	Hx-bronchogenic malignan.	0.037	2.38 × 10−4	714.2	Syst. rheum arthritis NEC.	0.001
1.97 × 10−4	V08	Asymp. HIV infectn. status.	0.024	2.38 × 10−4	054.10	Genital herpes NOS.	0.003
1.82 × 10−4	278.03	Obesity hypovent synd.	0.011	2.08 × 10−4	740.90	Spina bifida.	0.002
1.82 × 10−4	V10.06	Hx-rectal & anal malign.	0.013	1.78 × 10−4	756.89	Soft tissue anomaly NEC.	9.11 × 10−4

We observe that the discriminating codes for patients correctly linked are more likely to relate to chronic diseases while for mismatched patients, the top codes are related to very specific diagnoses. In fact, across the matched patients in the UCSD dataset, chronic diseases related to liver are more discriminative, while Parkinson’s disease and obesity are among the most discriminative in the MIMIC-III dataset. Furthermore, the absolute frequencies of the top-5 most discriminating codes tend to be higher for the patients correctly linked than those mismatched. These results indicate that the diagnostic pathways for the matched patients are better represented in the training set when compared to those mismatched. In other words, patients with rare diseases are harder to link.

6.3.2 Gender and cancer distribution

Here, we study the distribution of the patients in both datasets according to their gender and if they have been diagnosed with cancer^b. The overall results for both datasets are reported in Table 5, while the stratification across matched and mismatched patients is reported in Table 6. In the UCSD data, the gender distribution is roughly the same across the matched and mismatched patients. In the MIMIC-III dataset, among the mismatched patients, there is an increment of the male percentage over the female. This might suggest that the diagnostic pathways of these male patients are hard to link.

Table 5.

Overall statistics for the gender and cancer across UCSD and MIMIC-III datasets.

	UCSD	MIMIC-III
Male	48.9%	55.5%
Female	51.1%	44.5%
Cancer	5%	4%

Table 6.

Stratification for the matched and mismatched patients with respect to gender and presence of cancer.

	UCSD		MIMIC-III
	Matched	Mismatched	Matched	Mismatched
Male	49%	48%	54%	59%
Female	51%	52%	46%	41%
Cancer	5%	4%	3%	5%

In the UCSD data, the distribution of patients with cancers is roughly the same among the matched and mismatched pathways. For the MIMIC-III data, we have a slight increment in percentage of cancer patients in the mismatched cases. This result is in line with the most discriminative diagnosis codes for the mismatched patients in MIMIC-III. In fact, as we can see from Table 4, the most discriminative diagnosis code for mismatched patients is V10.85 which is typically associated with history of cancer of the brain.

7 Discussion and limitations

The proposed approach demonstrates that temporal data evolution can be effectively used to link patient longitudinal records. The temporal non-PHI information allows institutions to perform the linkage with mitigated privacy risks. This is useful in situations where the patients’ identifiable information cannot leave the institutions or when cryptographic solutions are not feasible due to efficiency reasons. We expect that the use of patient temporal data, as illustrated with our approach, can significantly help integrate the fragmented data and potentially accelerate research in the biomedical domain.

While in this work, we developed the foundations for linking patient temporal data, the current solution presents some limitations that provide useful insights for future research. Here, we discuss the following main points.

7.1 Utility

In our current solution, the similarity evaluation between diagnostic pathways is performed solely using diagnosis codes. However, in practice additional temporal information is available at the healthcare institutions (e.g. medications, lab tests). Intuitively, developing a similarity measure that takes into consideration this heterogeneous data would be beneficial for approximate patient linkage or search, and further improve the robustness of our linkage method. Furthermore, medical data are particularly noisy and data values may be affected by medical personal judgment. For example, different doctors may have different prognosis for the same patient across multiple visits raising possible inconsistency in the data. To extend our solution in this setting, a possible future research direction consists in developing statistical data models at diagnosis code level to represent the uncertainty in the prognosis of the patients. Statistical models for sequential data have been extensively investigated over recent years demonstrating promising results in many applications.^33,34 These models could be used in our patterns-based similarity measure to overcome the uncertainty of the diagnosis codes.

7.2 Scalability

The rapid growth of today’s medical information systems casts important challenges on modern linkage solutions. As the number of patients increases, a considerable large amount of candidate pairs of records have to be considered in the matching phase, becoming the bottleneck of the entire record linkage process. To overcome this challenge, our solution can benefit from modern indexing techniques, removing obvious non-matching pairs, while at the same time maintaining high matching quality.¹⁴ Currently, our approach uses standard blocking techniques which can be improved using more sophisticated approaches such as sorted neighborhood, mapping and clustering.¹⁰ Furthermore, in our technique when the training set is large, the computation of the linkage score can be accelerated using sequence-based filtering approaches.^35,36 In this way, the most useful sequences for determining the pathways similarity in the training set T can be efficiently retrieved and used in computing the linkage score for the candidate alignments.

7.3 System deployment

Modern medical information systems enable individual institutions to efficiently store and manage patient information. However, the lack of a common data model poses critical challenges during the data integration process.³⁷ To allow multi-institutional analysis, a promising research direction consists in the developing of a common data model (CMD). Among recent models, PCORnet Common Data Model and Observational Medical Outcomes Partnership (OMOP) CMD show promising results.³⁸ For the future, we aim to employ OMOP CMD and study the benefits and drawbacks of this model in our record linkage application.

8 Conclusion

In this work, we proposed a novel linkage approach that takes advantage of the temporal evolution of non-PHI data to link fragmented patient longitudinal data across institutions. Specifically, our technique combines both the dependency between diagnosis codes and their temporal coherency in a linkage score to identify the fragments related to the same patient. The experiment evaluations on real datasets demonstrate the effectiveness of our solution.

Appendix 1

Pathways similarity

Theorem 1

Consider two sequences X = {X₁, X₂, …, X_n}, Y = {Y₁, Y₂, …, Y_m} containing n and m observations, respectively. Let N[i, j, l] be the number of common subsequences of length l across X₁, X₂, …, X_i and Y₁, Y₂, …, Y_j (i.e. the prefixes of length i and j for the sequences X and Y). Then, N[i, j, l] can be computed with the following recurrence relationship

$$N[i,j,l]=\{\begin{array}{cc}0\hfill & \hfill \text{if }l>\text{min}\{i,j\}\hfill \\ N[i-1,j,l]+N[i,j-1,l]++N[i-1,j-1,l-1]2^{|X_i\cap Y_j|-1}--N[i-1,j-1,l]\hfill & \hfill \text{otherwise}\hfill \end{array}$$ (9)

Proof

The formal proof proceeds by induction on l and on the length of the prefixes. Here, we present a sketch of the proof where we show that we can determine N[i, j, l] by knowing N[i − 1, j, l], N[i, j − 1, l], N[i − 1, j − 1, l − 1] and N[i − 1, j − 1, l]. When a new pair X_i and Y_j is considered in extending the prefixes of X and Y, there are 2^{|X_i∩Y_j|−1} possible ways to extend the already computed common subsequences N[i − 1, j − 1, l − 1] to obtain subsequences of length l. Furthermore, these subsequences are added on top of the sequences of length l computed in N[i − 1, j − 1, l] together with the already computed common subsequences between the prefixes of X and Y ending at position i − 1 and j − 1, respectively.

Properties

It can be shown that our similarity based on all common subsequences sim(𝒳, 𝒴) satisfies the following properties for any 𝒳 and 𝒴.

• (3)Non-negativity: sim(𝒳, 𝒴) ≥ 0
• (4)Identity: sim(𝒳, 𝒴) = 1 if and only if 𝒳 = 𝒴 (i.e. exactly same pathway)
• (5)Symmetry: sim(𝒳, 𝒴) = sim(𝒴, 𝒳)

Furthermore, we can observe that 0 ≤ sim(𝒳, 𝒴) ≤ 1.

Considerations on the similarity measure

Recent works have been proposed to improve similarity measures over sequential data.^39–41 Among them, the work by Egho et al. is the most related to our similarity notion.³⁹ In that work, the authors used all common subsequences to define a robust similarity measure between sequences and applied such a measure to cluster patient longitudinal records. Despite the common theme with our work, we point out that our vector representation differs from their technique in several perspectives. First of all, in our ACV vector representation, an entry ν_i does not only count the number of distinct subsequences of length i shared between the pathways but it also takes into account their multiplicity. In this way, we can identify those subsequences that appear multiple times within the original pathways and may indicate stronger similarity. On the other hand, in Egho et al., only the distinct subsequences are used in defining the similarity measure.³⁹ As a result, the information about the multiplicity of each subsequence is lost. Second, enumerating all the distinct subsequences commonly shared across two sequences is computationally intense. Hence, in applications that consider sequences defined over a large alphabet (e.g. ICD9 diagnosis codes), this counting process may not scale well. Lastly, we point out that our vector representation allows us to distinguish the common subsequences by their length. In this way, we have the flexibility to weight differently each length of the common subsequences to best fit the specific applications.

Table 7.

Properties of the datasets.

	UCSD	MIMIC-III
Tot. number of pathways	18,850	6,588
Min. pathways length	2	2
Max. pathways length	67	42
Avg. pathways length	3.27	2.66

Figure 8.

Distribution of the diagnostic pathways with respect to their length in both datasets. The number of pathways exponentially decreases as their length increases. (a) UCSD. (b) MIMIC-III.

Table 8.

Default parameters value for our solution.

Parameter	Description	Value
k	Number of recommended pathways	5
α′	Weight for computing the pattern score	0.5
δ1	Time threshold	356 days
δ2	Decay weight	7 days
p	Weight of the norm for the ACV vector	1

Appendix 2

Evaluations

2.1 Settings

2.1.1 Data properties

The overall statistics for the datasets considered in our evaluations are reported in Table 7. Figure 8 illustrates the length distribution of the pathways in the input datasets. Since in our evaluation we measure the ability of our solution in reconstructing the original patient’s pathways from their fragments, we only consider pathways that comprise at least two observations. As we observe from Figure 8, the diagnostic pathways length distribution follows a power law distribution, where the majority of the sequences fall in the first quarter of the maximum length. In our evaluation, we focus our linkage task on pathways with a number of observations (i.e. visits) in the range [8, 16] for UCSD and [4, 12] for MIMIC-III.

2.1.2 Parameters

The default values for the parameters used in our evaluation are reported in Table 8. In our experimental evaluation, by setting α′ = 0.5 we assign an equal weight to the pathway similarity and benefit score for computing the patterns score. Regarding the temporal coherency, we consider a time threshold δ₁ = 356 days to consider the coherency between diagnose codes in observations occurring up to one year of distance. Furthermore, by fixing δ₂ = 7 days, we smooth the similarity between sets of diagnosis codes with a decay function that considers interval windows of seven days. In this way, we can provide more relevance to medical events that are relatively close in time. Finally, the weights α and β used in computing the linkage score are data dependent, and in our case we learned them from the training set T.

Table 9.

Blocking results in terms of reduction rate, pair completeness, and pair quality for both datasets.

	UCSD	MIMIC-III
RR	0.998	0.987
PC	1	1
PQ	0.019	0.0097

RR: reduction rate; PC: pair completeness; PQ: pair quality.

2.2 Blocking results

In our approach, we use an indexing technique that partitions the pathways based on the date of birth of the patients. In general, we could use more sophisticated blocking techniques; however, we noticed that in practice this simple solution greatly reduces the number of unnecessary pair comparisons. To measure the benefit of this indexing technique on the overall linkage process, we use the notions of reduction rate (RR), pair completeness (PC), and pair quality (PQ) that have been recently introduced by Christen to assess the quality of indexing techniques in the traditional record linkage setting.⁴² These quantities are positive real values in the range [0, 1]. Specifically, the reduction rate (RR) measures the reduction of the comparisons due to the indexing technique. Intuitively, higher RR values imply that less candidate pairs are generated. Hence, a faster matching step. The pairs completeness (PC) measures how effective the indexing solution is in preserving the real matching pairs (e.g. recall in information retrieval). Typically, record linkage solutions aim to achieve PC = 1, where all the real matching pairs are preserved in the blocking step. Finally, the pair quality (PQ) represents the fraction of true matching pairs generated by the indexing technique over the total number of candidate pairs generated. Therefore, high values of PQ indicate that the indexing technique generates mostly true matches.

Using the metrics described above, we evaluate our indexing technique and the results are reported in Table 9. First of all, we observe that the indexing technique based on date of birth achieves high RR. The number of possible candidate alignments in the linkage score computation is reduced by more than 99.8%. In fact, by blocking the pathways, the candidate alignments are generated across the records within each block rather than on the entire dataset. As a result, we have a substantial reduction of the overall number of total alignments between pathways that require to be considered in the matching step. Second, the pair completeness (PC) of the indexing approach in our datasets achieves perfect value. This is because in our evaluations, the pathways required to be matched are obtained from the same original patient pathways, and therefore they have the same blocking value. In practice, data may be noisy and the date of birth for the same patient may differ in records across multiple institutions resulting in PC < 1. Hence, some real matching records might be placed in different blocks leading to missing real matches. To overcome such a problem, more sophisticated blocking solutions have been recently proposed showing promising results in many record linkage applications.⁴² Therefore, using some of these techniques, we are able to handle noise in the blocking attribute values. Lastly, we notice that the blocking approach yields to low values of PQ. This result is due to the nature of the linkage process that tends to be unbalanced since the records in D₁ are substantially fewer than those in D₂. As a consequence, we have that a large fraction of records in each block are non-matches. In fact, it turns out that only 1.9% of the candidate pairs generated by the indexing approach are real matches in UCSD. This percentage goes down to 0.97% for the MIMIC-III data.

Figure 9.

Accuracy vs. ε (percentage of codes removed in the original pathways). By increasing the perturbation level, the number of possible shared patterns with the pathways in the training set tends to decrease leading to a decrement of accuracy. (a) UCSD. (b) MIMIC-III.

2.3 Impact of the missing data

In this set of experiments, we evaluate the robustness of our linkage solution against perturbation noise present in the data. Specifically, we consider the case of missing data, where a percentage ε of the codes in each observation in the original pathways are randomly removed. In this setting, we evaluate the accuracy of our solution for ε in the interval [0, 0.6]. For ε = 0, the original pathways are fully preserved (i.e. no missing value), while for ε = 0.6, in each observations at most 60% of the original diagnosis codes are randomly removed. From the results in Figure 9, we observe that the accuracy of our approach tends to decrease as the perturbation increases. This decrement in the performance is more evident in the MIMIC-III dataset. Nevertheless, even for ε = 0.6, the overall accuracy is still above 80% for the UCSD data, while is above 65% for MIMIC-III. This demonstrates the robustness of our similarity measure against noise, making our solution suitable in real settings. In fact, the use of all the common subsequences allows us to capture a variety of patterns of different length and with gaps between observations. Therefore, these patterns are more likely to be preserved and this helps the scoring process even in the case of missing diagnosis codes.