Imaging at ultrahigh magnetic fields: History, challenges, and solutions

Abstract

Following early efforts in applying nuclear magnetic resonance (NMR) spectroscopy to study biological processes in intact systems, and particularly since the introduction of 4 T human scanners circa 1990, rapid progress was made in imaging and spectroscopy studies of humans at 4 T and animal models at 9.4 T, leading to the introduction of 7 T and higher magnetic fields for human investigation at about the turn of the century. Work conducted on these platforms has provided numerous technological solutions to challenges posed at these ultrahigh fields, and demonstrated the existence of significant advantages in signal-to-noise ratio and biological information content. Primary difference from lower fields is the deviation from the near field regime at the radiofrequencies (RF) corresponding to hydrogen resonance conditions. At such ultrahigh fields, the RF is characterized by attenuated traveling waves in the human body, which leads to image non-uniformities for a given sample-coil configuration because of destructive and constructive interferences. These non-uniformities were initially considered detrimental to progress of imaging at high field strengths. However, they are advantageous for parallel imaging in signal reception and transmission, two critical technologies that account, to a large extend, for the success of ultrahigh fields. With these technologies and improvements in instrumentation and imaging methods, today ultrahigh fields have provided unprecedented gains in imaging of brain function and anatomy, and started to make inroads into investigation of the human torso and extremities. As extensive as they are, these gains still constitute a prelude to what is to come given the increasingly larger effort committed to ultrahigh field research and development of ever better instrumentation and techniques.

1. Introduction

This article is a scientific review where the science is framed in a historical context so as to recount problems and potential solutions that preoccupied us in the Center for Magnetic Resonance (CMRR), as we launched into the development of high and ultrahigh magnetic fields. As such, it presents a CMRR centric perspective, though relevant contributions of other laboratories have been extensively referenced as well. A purely scientific review does not necessarily reflect the milieu, the context, and the controversies out of which many commonly accepted ideas emerge. For example, it is virtually impossible today to encounter a presentation on ultrahigh field imaging and/or spectroscopy application in humans or animal model systems that would not enthusiastically list as a foregone conclusion that signal-to-noise ratio (SNR) increases with magnetic field strength. However, this was not a concept taken for granted starting from the very beginning of magnetic resonance imaging (MRI), and not even at the time 7 and 8 T efforts for human imaging came into existence.

The nuclear magnetic resonance (NMR) phenomenon was a well-established tool of chemists and biochemists in the early to mid nineteen seventies when it started receiving attention as a potential tool for the study of intact biological systems, including humans. This effort led to the emergence of transformative technologies of MRI (Lauterbur, 1973, 1974) and in vivo magnetic resonance spectroscopy (MRS) (e.g., reviews (Radda and Seeley, 1979; Shulman et al., 1979; Ugurbil et al., 1979; Ackerman et al., 1980a)). Early MR images of humans were obtained at magnetic fields of ∼0.05–0.35 T (∼2–∼15 MHz resonance frequency for the hydrogen (¹H) nuclei of water molecules) (e.g., (Smith et al., 1981; Crooks et al., 1982)). Presumably, this was dictated by the difficulty and the expense of building magnets large enough to accommodate the human body at higher magnetic fields as well as early theoretical considerations suggesting that, in the electrically lossy and conductive human body, the “frequency of operation of the spectrometer with human samples should be less than about 10 MHz [∼0.24 T]” (Hoult and Lauterbur, 1979) because of sensitivity and penetration problems predicted in the modeling. However, in 1983, the feasibility of MRI of the human head at 1.5 T (64 MHz ¹H frequency) was demonstrated (Bottomley et al., 1983; Hart et al., 1983) and, rapidly, the use of 1.5 T (1.5 T) became pervasive as a clinical diagnostic instrument. This development established 1.5 T as the “high field” in MRI at the time. Theoretical calculations also moved to higher fields and frequencies consistent with the experimental data, but still a medium field strength (0.5–1.0 T) was recommended as the “best current compromise [for imaging the human torso and head] when imaging time is of major importance” (Hoult et al., 1986), although the authors qualified their recommendation with the caveat that “new techniques may always invalidate this conclusion”.

In contrast to MRI, in vivo MRS started at very high magnetic fields, 7 to 8.5 T (300–360 MHz ¹H frequency), using vertical bore magnets typically employed by chemists and biochemists of the time. Initially, the experiments utilized magnetic nuclei other than hydrogen, namely ³¹P and ¹³C. Samples used were typically cells in suspension stuffed into ∼8–10 mm diameter NMR tubes at high cell densities, and supplied a carbon source suitable for either aerobic and/or anaerobic metabolism; in the former case, the sample had to be aerated as well which was not a trivial problem for the very high cell density slurries that were necessary to achieve sufficient SNR (e.g., (Ugurbil et al., 1978a, 1978b, 1981; den Hollander et al., 1986)). Alternatively, perfused ex vivo rodent organs were employed (e.g., (Ackerman et al., 1980a)). Fig. 1 illustrates the type of studies that were carried out, in this case with anaerobic E. coli in suspension (Ugurbil et al., 1978b). This particular study and a related one examining aerobic E. coli cells in suspension (Ugurbil et al., 1982) were aimed at investigating Chemiosmotic hypothesis of oxidative phosphor-ylation, which postulated that the coupling between the electron transfer chain and ATP synthesis in mitochondria (in eukaryotic cells) or in bacteria is mediated by a transmembrane gradient of H⁺ ions, as opposed to a chemical intermediate. At the time, this was still a highly debated and controversial topic, and intact cell MR studies such as the one shown in Fig. 1 were really the first in vivo demonstration of this phenomenon, utilizing the chemical shift sensitivity of inorganic phosphate (P_i) to measure pH and hence H⁺ concentration.

Fig. 1.

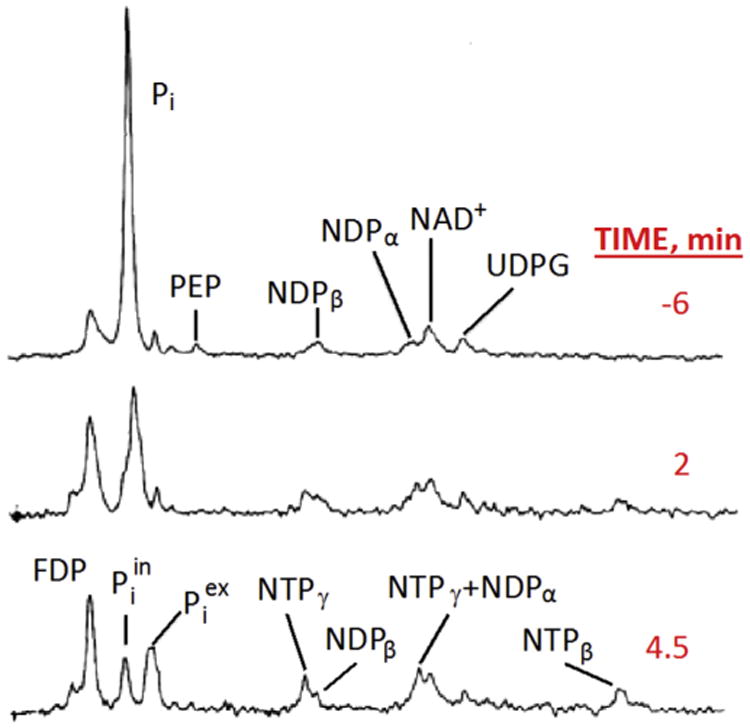
145.7 MHz (8.46 T) ³¹P spectra of anaerobic E. coli cells in suspension, initially without a carbon source. At time 0, glucose was added to the suspension. Each spectrum represents 200 averages collected in 2 min. NDP and NTP, Nucleotide di- and tri-phosphate respectively; PEP, phosphoenolpyruvate; FDP, fructose di-phosphate; P_i inorganic phosphate representing both intracellular and extracellular contributions; ${\mathrm{P}}_{\mathrm{i}}^{\text{ex}}$, ${\mathrm{P}}_{\mathrm{i}}^{\text{in}}$ extra and intracellular inorganic phosphate. Adapted from Ugurbil et al. (1978b).

The tantalizing prospect of probing cellular chemistry in the human body non-invasively was one of the driving forces in the afore-mentioned MRS studies. This led to early explorations of spatially localized MRS methods, (e.g., (Ackerman et al., 1980b; Gordon et al., 1980; Brown et al., 1982; Maudsley et al., 1983; Garwood et al., 1984)) and experiments with whole animals (e.g., (Balaban et al., 1981)) and even humans (e.g., (Ross et al., 1981; Newman et al., 1982; Bottomley et al., 1983; Arnold et al., 1984)) using predominantly the ³¹P nucleus. A push towards higher magnetic fields was a natural tendency in these studies because of the potential gains in chemical shift resolution as well as in SNR. Unlike human MRI, field-dependent SNR gains were not questioned for these spectroscopy studies. With small samples such as cells in suspension or perfused rodent organs, radiofrequency (RF) penetration and sample induced losses in SNR are not a concern; consequently, as in other contemporaneous biological studies such as those aimed at solving macromolecular structure, SNR was expected to increase supralinearly with the magnetic field strength, as much as ${\mathrm{B}}_0^{7/4}$ (Hoult and Richards, 1976) when relaxation effects were ignored. Similarly, intact animal or human studies typically employed a single surface coil and probed only a small sample volume of the entire object. In addition, the ³¹P nuclei used in most of these experiments resonated at a lower frequency compared to ¹H at a given magnetic field, thus not immediately raising alarms about RF penetration effects associated with high frequencies.

Although the MRI world was conflicted in the utility of high magnetic fields, the three major manufacturers of clinical MR instruments, General Electric (GE), Siemens, and Philips, nevertheless launched efforts in the nineteen eighties to explore magnetic fields higher than the 1.5 T “high field” imagers of the time. Each developed a program centered on 4 Tesla (4 T) for human imaging. Initial efforts in the research laboratories of these companies (Barfuss et al., 1988, 1990; Bomsdorf et al., 1988) produced 4 T brain images that were far inferior to the contemporaneous images obtained at 1.5 T and highlighted more problems than advantages at this high field strength (Fig. 2A and B). It was clear that going to 4 T for human imaging would require significant new investment in research and development, and it was not going to be as simple as changing the frequency of the electronics and the RF coils. Likely because of these conclusions, the industry abandoned the 4 T MRI effort at the time, and focused instead only on 1.5 T; I think this was a reasonable decision for the manufacturers. After all, 1.5 T could meet the clinical needs of a vast majority of cases referred for MRI scans, there was already a lucrative and growing market for these instruments, and they were starting to recover the R&D investment they had made to develop these scanners. So why undertake yet another major and potentially difficult R&D effort with questionable gains? Consequently, the systems used by the three manufacturers to explore 4 T were abandoned and ended up in three academic laboratories in the USA. The GE system went to the Intramural Research program at the NIH (effort led by Dr. Robert Balaban); the Philips system went to the University of Alabama (effort led by Dr. Gerald Pohost); and the Siemens system came to my laboratory at the University of Minnesota, which, with the acquisition of the 4 T instrument, became the Center for Magnetic Resonance Research (CMRR). At the time, there were also calls for even higher magnetic fields, namely 10 T, championed by Professor Thomas Budinger from the University of California at Berkeley. His primary motivation was to gain access to the detection of low gyromagnetic ratio elements such as sodium, potassium, chlorine, etc., that are critical in biological function but exist in low concentrations and suffer from inherently low sensitivity as well. Prof. Budinger is now championing a 20 T project, partially justified by the same aims ((Budinger et al., 2016) and see article in this issue).

Fig. 2.

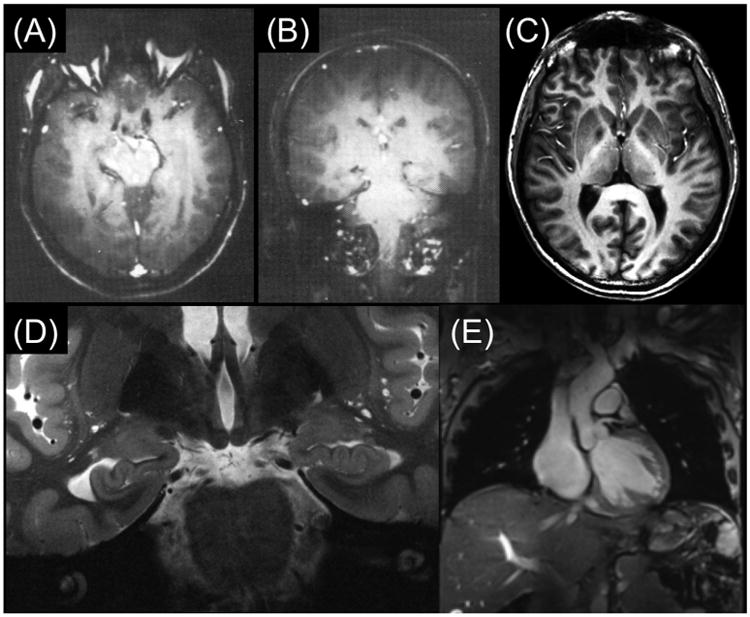
(A) and (B): Early 4 T brain images published from Siemens (Barfuss et al., 1988, 1990); (C) 4 T MDEFT image of human brain obtained at the CMRR (Ugurbil et al., 1993; Lee et al., 1995); (D) Contemporary 7 T brain image in coronal section showing hippocampal formation (Henry et al., 2011); and (E) 7 T image in the human torso displaying a coronal cut through the human heart (Erturk et al., 2017a).

It is interesting to note that, at the time, the three sites that acquired the 4 T human instruments were focused primarily on cardiac research and, in many cases, were conducting spectroscopy studies in whole animal preparations (e.g., (Balaban et al., 1986; Robitaille et al., 1989; Path et al., 1990)); extending such cardiovascular work to humans was the primary motivation for pursuing these high field human instruments. Certainly this was true for us at the CMRR. However, we were not “married” to spectroscopy or cardiac research per se; rather, we were and still are, interested in obtaining unique biological information in vivo using MR techniques. Thus, with the elucidation of the BOLD mechanism (Ogawa et al., 1990a; 1990b, 1990c; Ogawa and Lee, 1990), trying to use this mechanism to obtain maps of human brain activity became our highest priority on the 4 T system even before this magnet arrived in Minnesota circa late 1990 (Ugurbil, 2012).

While GE and Philips each acquired a single (identical) 4 T magnet built by Oxford instruments, Siemens built two 4 T magnets with 100 cm and 125 cm bore sizes. We acquired the 125 cm bore magnet because it promised better immunity to eddy currents at a time when shielded gradients were not extensively developed. This magnet was not designed with shipping in mind. The strategy for shipping had to be carefully thought out. A brand new, specially equipped Mercedes truck was employed. The entire truck was shipped to the USA by sea and the magnet did not leave this truck on its journey from Erlangen, Germany to Minneapolis. Nevertheless, the magnet was damaged. Luckily it was repairable and was repaired; however, we suffered a relatively long delay at the start of the project. During the several years we waited for the 4 T system to arrive and become operational, we were confronted repeatedly with significant skepticism about the high field human effort, probably fueled by the early disappointing work at 4 T from industry, and possibly by the lingering effects of the even earlier dire predictions about high fields for human imaging based on modeling studies (Hoult and Lauterbur, 1979).

We did anticipate that imaging at 4 T magnetic field with the ¹H nucleus would not be easy, but possibly tractable. The first hint of this came from work conducted by Michael Garwood from CMRR. The 4 T system designated for Minneapolis was being developed in California, by SIS Co., a joint venture at the time between Siemens and Varian, using the Siemen 100 cm diameter bore 4 T magnet. They made this system available for us before it was taken apart and the electronics shipped to Minneapolis to be combined with the 125 cm bore 4 T magnet on site in CMRR. Prof. Garwood used this opportunity to work on this 4 T system; he also engaged Prof. Budinger in this effort because of Prof. Budinger's interest in high magnetic fields, and his expertise in MR safety issues. Prof. Garwood was interested at the time in a T₁-weighted imaging sequence that he called MDEFT (Modified Driven Equilibrium Fourier Transform), which relies on detecting the longitudinal magnetization that evolves after a 90°-τ-180-τ-contrast preparation; it can be implemented as a spin-echo or a contrast prepared 2 or 3D gradient echo sequence (Ugurbil et al., 1993; Lee et al., 1995). MDEFT produced 4 T human brain images (Fig. 2C) that looked nothing like what was previously obtained (Fig. 2A and B) and demonstrated for the first time the feasibility of obtaining superior anatomical images of the human brain at 4 T. These images were first presented at a workshop in 1990 (Garwood et al., 1990), and much later in a review article (Ugurbil et al., 1993) and a paper as a 3D version (Lee et al., 1995). Puzzling over and exploring the underlying mechanism of the fantastic improvement in these 4 T MDEFT images, we examined the B₁ sensitivity of this sequence and discovered its relative immunity to B₁ inhomogeneities (Ugurbil et al., 1993); this ameliorated the problems arising from non-uniform B₁'s that increasingly plague imaging at magnetic fields higher than ∼1.5 T and is the cause of the problems seen in the early T₁-weighted 4 T images (Fig. 2A and B). Advances made since these early 4 T images from the manufacturers are further illustrated in Fig. 2D, which displays a contemporary high-resolution 7 T (7 T) image of the human brain, depicting the hippocampal anatomy with exquisite detail and resolution, and even a 7 T image through the human torso (Fig. 2E), a much more difficult target to image at ultrahigh fields.

Immediately after the 4 T system became operational in Minneapolis, one of the two studies (Kwong et al., 1992; Ogawa et al., 1992) that simultaneously and independently introduced functional brain imaging using the BOLD contrast was performed on this system; it was carried out by myself, my post-doctoral fellows Ravi Menon and Jutta Ellermann, and my colleague and friend from Bell Labs Seiji Ogawa, with participation of Seong-Gi Kim at a later stage and Hellmut Merkle building the RF coils (Ogawa et al., 1992). As we waited for the 4 T system to arrive in order to attempt at imaging the activity of the human brain (i.e. fMRI (functional magnetic resonance imaging)), we did not consider conducting these studies at 1.5 T. BOLD contrast arises primarily from magnetic field inhomogeneities induced by magnetic susceptibility differences; this effect scales with the magnetic field magnitude. Initial studies introducing the BOLD effect (Ogawa et al., 1990a; 1990b, 1990c; Ogawa and Lee, 1990) used rather large perturbations in the brain, such as asphyxia, to modulate the deoxyhemoglobin content of blood, and were carried out in rodent models in a 7 T small animal scanner. Detecting changes in the BOLD contrast by smaller perturbations such visual stimuli and detecting this in humans was unknown territory and a much greater challenge. As such, we did not think BOLD would work adequately at low fields like 1.5 T. In principle, we were right, but our understanding of functional signals was incomplete. Today, we know that the fMRI signal is quite complex and can have numerous contributions; such contributions include inflow effects, mostly originating from flow increases in large blood vessels (e.g., (Duyn et al., 1994; Segebarth et al., 1994)), intravascular effects due to changes in blood T2 and T₂* (e.g., (Duong et al., 2003; Silvennoinen et al., 2003)), or relatively large signal changes associated with large veins (Menon et al., 1993; Kim et al., 1994), especially when they occupy a large fraction of the voxel volume (e.g., (Hoogenraad et al., 1999)). We did not fully consider these effects at the time. Rather, we were focused on the extravascular BOLD effect arising from deoxyhemoglobin containing intracortical vessels; this effect is relatively small, hardly, if at all, detectable at 1.5 T (e.g., (Hoogenraad et al., 2001)).

There was a significant difference in the fMRI images presented in the early work introducing fMRI. The 1.5 T data (Bandettini et al., 1992; Kwong et al., 1992) were much courser in resolution than the images we were able to obtain at 4 T (Fig. 3). Unlike the 1.5 T data (Fig. 3A), the higher resolution 4 T images showed quite extensive detail, with the activations displaying attributes of the underlying cortical geometry (Fig. 3B–D). In fact, this 4 T gradient recalled echo (GRE) BOLD fMRI image shows all the features we now understand about the source of fMRI signals: The strongest signals appear to be located in the sulci and cortical surface (associated with pial veins); but there are also functional mapping signals overlaying directly on the cortical gray matter tissue going around a sulcus (which appears dark in the underlying anatomical images) (see arrows in Fig. 3C, which displays only the anatomical image of the slice with the gray matter contours identified in red, and the same arrows and the gray matter contour in Fig. 3D). The nature of these two distinct contributions to functional mapping at 4 T was confirmed in a subsequent study (Menon et al., 1993) where we summarized our findings in the abstract as “two distinct regions (ascribed to be microvasculature and visible venous vessels) identified as giving rise to the signal increase [associated with functional brain images]”. This “draining vein” problem in GRE fMRI was experimentally seen and reported later in other early studies investigating the source of the fMRI mapping signals (e.g., (Lai et al., 1993; Haacke et al., 1994; Kim et al., 1994; Goense and Logothetis, 2006; Polimeni et al., 2010)); the problem was revisited with modeling several years after the first experimental observations, coming to the conclusion that there could be changes in venous blood detectable as apparent “activation” as much as 4 mm beyond the edge of a 100 mm² activated area (Turner, 2002).

Fig. 3.

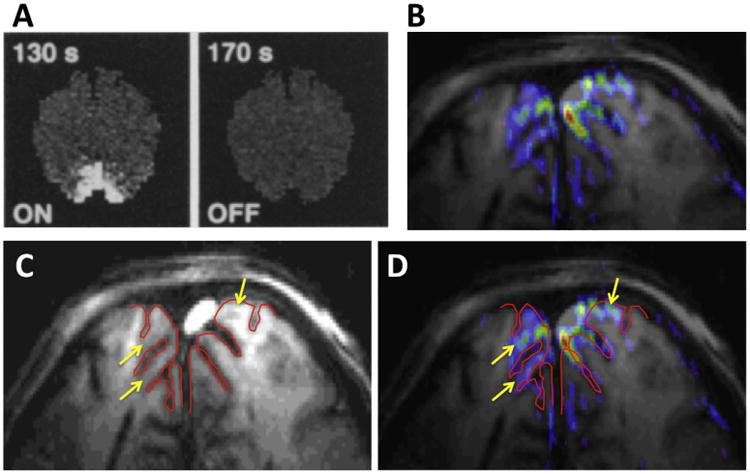
Early functional images produced in the human brain, obtained at (A) 1.5 T (Kwong et al., 1992), and (B) 4 T from CMRR (Ogawa et al., 1992). (C) The anatomical image of slice that was used for the functional imaging in (B), with the cortical surface outlined in red. (D) The same image as (B) but with the same red line outlining the cortical surface superimposed on it.

The realization in 1993 of the large vein contribution was highly disturbing to us. Large veins drain blood from large patches of cortex and their distribution is spatially sparse. Therefore, they cannot provide high spatial fidelity to neuronal activity in functional imaging. Suppressing the draining vein contribution, and/or at least increasing the relative contribution of mapping signals associated with microvasculature (capillaries and small diameter post capillary venules) became a central focus in our research at CMRR. In this goal, we were guided by our early modeling efforts of the BOLD phenomenon (Ogawa et al., 1993), showing the importance of the magnetic field magnitude on BOLD signals, in particular the supralinear gains in extravascular BOLD associated with microvasculature versus a linear dependence of large vessels in GRE fMRI, and the fact that spin-echo (SE) as opposed to GRE fMRI can suppress the large vessel contribution in extravascular BOLD; similar conclusions were subsequently published by many modeling efforts (e.g., (Kennan et al., 1994; Weisskoff et al., 1994; Yablonskiy and Haacke, 1994; Fujita, 2001; Uludag et al., 2009; Gagnon et al., 2015) and references therein), several of which further expanded the modeling to include the intravascular effects (e.g., (Duong et al., 2003; Silvennoinen et al., 2003; Uludag et al., 2009; Ugurbil, 2016) and references therein).

Our first step in exploiting very high magnetic fields for improved fMRI was a 9.4-T/33-cm diameter horizontal bore magnet for animal model studies. We partnered with Magnex Scientific Limited led by David Rayner for this project, at a time when the highest field magnet with such a bore size was 4.7 T. The 9.4-T/33-cm bore magnet, first of its kind to achieve this high magnetic field with such a large bore size, was successfully built and provided a plethora of fMRI as well MR spectroscopy data to warrant the exploration of similar fields for human studies. We also used this magnet to obtain an image of an intact porcine chest, approximating the size of the human head, demonstrating that RF problems can be tackled to achieve human head imaging even at such high fields (Ugurbil, 2012). This 9.4 T work, conducted starting in ∼1993, may represent one of the first uses of multichannel transmit concept since we essentially employed a four loop coil to make a volume coil (arranged as two “quadrature” coils, each of which was made up of two loops coupled through a 90° hybrid); we did not have multiple transmitters but obtained images first with one quadrature pair and then the other, and subsequently combined them. Multichannel transmit is of course quite a bit more complex due to the simultaneity of the transmission; nonetheless, the approach anticipated the multichannel transmit technology developed and implemented many years later for 7 and 9.4 T human imaging (e.g., (Adriany et al., 2005; Vaughan et al., 2006)).

With the initial functional imaging studies conducted on animal models at 9.4 T showing promising results (leading to publications several years later, e.g., (Lee et al., 1999; Duong et al., 2000, 2001; Lee et al., 2002; Harel et al., 2006)), David Rayner and I started discussing the prospect of a high field human system during the ISMAR meeting in Sydney in 1995, where I gave a talk. We looked at many designs, starting conservatively with a small-bore “head-only” human magnet; the first evaluation was completed by August 1995 (Fax, top panel of Fig. 4). Subsequently, we expanded the search up to 7 T/90 cm bore. David reported the results to us on 1 April 1996 (email shown in the lower panel of Fig. 4). In 1996, we decided ultimately on a 7 T/90 cm bore magnet because we did not want to compromise on the bore size; we anticipated that gradients will be a major challenge at this field strength and we did not want the bore size to limit gradient design. This system was installed in 1999 in CMRR. The installation was problematic because of an asymmetric passive shield design that was used (due to financial limitations) to contain the stray field, leading to many months of delays. The complete system was put together by our group from parts we obtained from various manufacturers, with the “console” coming from Varian, gradient amplifiers donated by Siemens, RF amplifiers developed for us by CPC, etc. We built the RF coils and later multichannel receivers and transmitters for this system in house.

Fig. 4.

A Fax (top) and an email (lower) from David Rayner dated 03 August 1995 and 01 April 96, respectively, discussing the 7 T initiative. The approximate pricing supplied is blanked out. The color markings in the 1996 email identify our deliberations in CMRR at the time. Ultimately we decided on the 7.0/900-cm bore magnet; this design was employed on all 7 T systems installed until 2011 when two new, actively shielded 7 T magnets with 830 and 900 cm bore diameters were developed.

This first ever “lego” 7 T human MR system in CMRR was less than ideal but starting with fMRI (Yacoub et al., 2001a), SNR comparisons between 7 T and 4 T (Vaughan et al., 2001), and anatomical imaging of the human brain (Vaughan et al., 2001) showing feasibility and excellent gray-white matter contrast, the data coming from this system started the trend for rapidly increasing number of 7 T systems. The next 7 T human MRI system was a commercial effort, undertaken by Siemens at the Massachusetts General Hospital (MGH) beginning in 2002, leading to first publications in 2005. An 8 T/80 cm bore human system was installed at Ohio State shortly before our 7 T was delivered. Gradient recalled echo images, which are intrinsically not very sensitive to B₁ inhomogeneities as those that require 180° pulses (such as T₁-weighted and/or spin echo based images), were obtained on this system depicting superb anatomical detail (e.g., (Robitaille et al., 2000) and references therein). The early work from 8 T, however, also produced experimental results that were highly controversial, including claims of a disappointingly low SNR at this field strength (Abduljalil et al., 1999), as well as unexpectedly low RF power requirements, decreasing RF heating and lack of B₁ inhomogeneities (e.g., (Leroy-Willig, 1999; Robitaille, 1999)). Regarding the B₁ inhomogeneities, in subsequent work, these investigators were the first in fact to correctly identify their origin (Ibrahim et al., 2001a, 2001b); however, likely because of a lack of appropriate experimental data backing up these early simulation results (e.g., experimental B₁ field maps as opposed to flat looking brain images where the image intensity is a complex function of B₁ and relaxation times), and possibly because of other contentious reports from 8 T at the time, this early simulation work did not end this controversy. These and other issues were reexamined at 7 T, and ultimately it was the 7 T work that defined the path of ultrahigh fields.

It was really the potential impact of ultrahigh magnetic fields on fMRI coupled with the enormous potential impact of fMRI itself on brain sciences that provided us with the motivation for the initial development of the 9.4 T animal system and later the 7 T human instrument. Human fMRI reached new levels of spatial resolution and specificity at 7 T (discussed further on). Although, fMRI provided the primary impetus, we have always been aware of and also motivated by the potential gains in MR spectroscopy as well. Spectroscopy measurements with ¹H and X-nuclei (e.g., ³¹P, ¹⁷O, and ²³Na) obtained at 4 T, 7 T, and subsequently at 9.4 T by several laboratories have provided neurochemical and metabolic information in the human brain with increasing biomedical relevance (e.g., (Chen et al., 2001; Tkac et al., 2001; Lei et al., 2003a; Mangia et al., 2006; Mangia et al., 2007; Avdievich et al., 2009; Tkac et al., 2009; Atkinson and Thulborn, 2010; Deelchand et al., 2010; Oz et al., 2011; Zhu et al., 2012, 2015)). Unique kinetic studies of intracellular enzymatic rates that were previously possible only in cells in suspension or perfused organs, such as the magnetization transfer measurement of ATP turnover rates (e.g., (Kingsley-Hickman et al., 1987, 1990)), originally introduced in 1977 (Brown et al., 1977), were performed two decades later for the first time in the human brain at 7 T (Lei et al., 2003a).

Until recently, all the ultrahigh field studies were in the brain. But feasibility of imaging in the human torso at 7 T, a more challenging goal due to the relative dimensions of the object versus the RF wavelength, was demonstrated in 2008 and 2009 (Metzger et al., 2008; Snyder et al., 2009; Vaughan et al., 2009; Metzger et al., 2010) (and see review (Niendorf et al., 2013)), thus starting a new burgeoning activity in several laboratories.

However, all of these accomplishments faced significant challenges and required either imaging approaches that circumvented the specific problems encountered or generalized technological solutions. Therefore, a substantial part of our early work on 7 T examined experimentally the physics of imaging at this high magnetic field and focused on developing and/or implementing technological solutions. Some of the viable solutions that emerged were discussed in papers based on simulations or theoretical analytical calculations. Such work, even if it is ultimately proven to be wrong, is extremely important in developing a conceptual framework that can motivate experimental studies; but unless experimentally demonstrated, theoretical calculations and modeling cannot necessarily be taken as correct. A good example of this is the work examining the feasibility of human imaging at different magnetic fields, first suggesting human MRI should be conducted at less than ∼0.24 T (10 MHz) (Hoult and Lauterbur, 1979), then between 0.5 and 1 T (Hoult et al., 1986), and ultimately (Hoult, 2000) becoming consistent with the early 7 T and 8 T experimental data appearing at the time.

2. B₁ inhomogeneities, traveling waves and the signal-to-noise ratio

In all MR applications, SNR is critical for image quality, measurement time, and/or spatial resolution. Though taken for granted today, field dependent increases in SNR were a controversial topic at the time for very high magnetic fields like 8 T, as previously discussed, even though there were experimental data demonstrating an approximately linear increase with magnetic field in human imaging up to 4 T (Wen et al., 1994; Gati et al., 1997). Therefore, when the 7 T system became operational, the first task we tackled was to examine the SNR at this ultrahigh magnetic field.

We carefully mapped transmit B₁ fields and measured SNR in the human head images for 4 and 7 T using a TEM (Transverse Electro-Magnetic) “volume” head resonator with identical geometries (Vaughan et al., 2001), taking into account slight differences in coil performance and instrument noise figures. For conditions of full relaxation and same bandwidth, the SNR was found to scale slightly more than linearly with the magnitude of the field (factor 2 vs. 1.75 predicted for linear B0 dependence) in the center of the brain when it was set to experience a 90° pulse; in the periphery however, SNR scaled less than linearly with field magnitude (Fig. 5). When averaged over the entire slice, SNR increased approximately linearly. However, the increase was clearly not spatially uniform. These results were corroborated with electromagnetic simulations as well (Fig. 5C). This non-uniformity in SNR and the field-dependent SNR gain reflect the fact that B₁ is non-uniform in a volume head coil, and that this non-uniformity becomes more pronounced at 7 T relative to 4 T (Vaughan et al., 2001). Fig. 6 displays a more recent and detailed images of transmit B₁ magnitude at 7 T in the entire human head for the same type of TEM volume coil employed for the data shown in Fig. 5. The B₁ is highly non-uniform within each of the transverse slices shown and the extent of this non-uniformity and B₁ magnitude changes in the head-foot direction (i.e., z-direction) as well. Of particular note is the low B₁ magnitude over the temporal lobes (bottom images, Fig. 6) and the cerebellum (not shown).

Fig. 5.

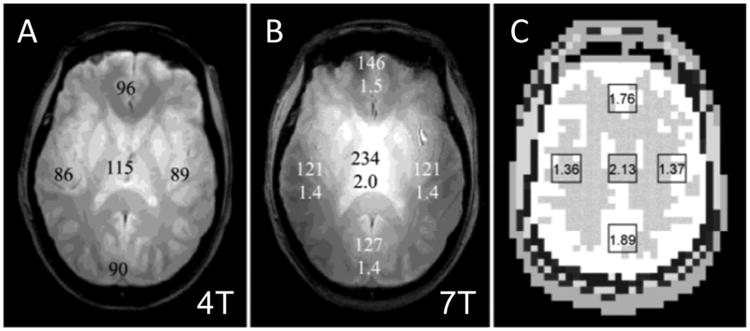
SNR measurements from fully relaxed gradient echo images acquired using the same acquisition parameters and homogeneous TEM volume coils of identical dimensions at 4 T (A), and at 7 T (B). Averaged, regional SNR values are shown on the images. Average 7 T/4 T SNR ratios are listed beneath the SNR data on the 7 T image. (C) shows a figure from Maxwell model with calculated 7 T/4 T SNR ratios, which are consistent with experimental data.

Fig. 6.

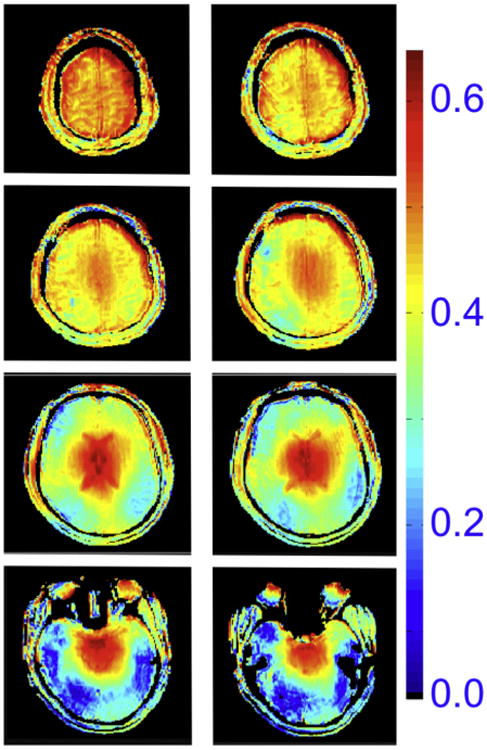
Transmit B1 magnitude in the human head at 7 T, generated by a volume TEM coil. The color code is proportional to μTesla/V.

The mechanism causing this pattern of non-uniformity (Fig. 6) was attributed to a “dielectric resonance” in the early 4 T work (Bomsdorf et al., 1988; Barfuss et al., 1990), and in work performed with electromagnetic simulations of the B₁ field in the human head at 1.5, 3 and 6 T (Jin et al., 1996). The implications of such a mechanism are profoundly negative for human imaging at ultrahigh magnetic fields. Simulations for 8 T (Ibrahim et al., 2001a) and analytical calculations performed for a sphere (Hoult, 2000) argued against this mechanism. Availability of a 7 T instrument provided for the first time the opportunity to reexamine this question experimentally as well as through simulations. Fig. 7 illustrates calculations from Yang et al. (2002) showing gray scale two dimensional (2D) plots of instantaneous transverse |B₁| at 7 T at progressing time points, generated by a surface coil placed on one side of a phantom; the calculations are presented for three different conductivities of the sample. At zero conductivity, a one-wavelength standing wave (i.e., a “resonance”) is established (leftmost column, Fig. 7); under this condition, excitation is simply not possible in certain areas, such as the middle of this standing wave. At higher conductivities approximating human tissue (right most column, Fig. 7), the RF wave is attenuated as it travels away from the coil; consequently, a more familiar surface coil profile emerges. Traveling wave behavior may be difficult to appreciate from these series of static images (Fig. 7) corresponding to snapshots at discrete time points; it is, however, easily seen in a time lapse video generated from these data. These calculations were experimentally verified at 7 T (e.g., see Fig. 3 in Yang et al. (2002)). Thus, we ascribed the spatial non-uniformities in B₁ observed in the human head at 4 and 7 T not to a “dielectric resonance” per se but to “the result of spatial phase distribution and amplitude modulation by the interference of the RF traveling waves determined by a given sample-coil configuration” (quoted from the abstract in Yang et al. (2002)). Essentially, the conclusion is that one is no longer operating in the near-field regime where the wavelengths are large compared to object size. Instead we are moving towards the far-field regime where wavelengths are small compared to object size, leading to the traveling wave behavior.

Fig. 7.

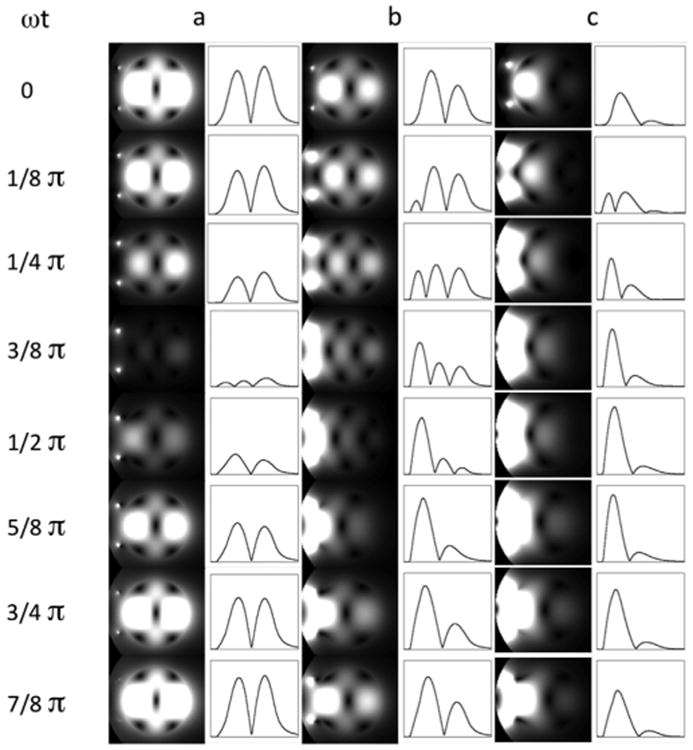
2D plots of instantaneous transverse jB1j for 7 T at progressing points in phantoms with different conductivities: (a) ωt = 0 S/m, (b) ωt = 0.26 S/m, and (c) ωt = 0.67 S/m. The intensity profiles along the horizontal centerlines are also shown on the right of the 2D plots. The surface coil position is indicated by two small dots on the left side of the phantom. Since the temporal B1 strength varies greatly among these three cases, the signal intensities of temporal points are normalized individually for each conductivity condition in order to visualize the temporal change for all the conditions clearly.

The concept of “traveling waves” invoked above (Fig. 7) should not be confused by a later effort that was referred to as “traveling wave MRI”, which used the RF shield within the bore of the MR instrument as a “cavity” to send “traveling waves” within that cavity to excite and detect signals (Brunner et al., 2009). In Yang et al. (2002), we are talking about the fact that when the wavelength of the RF employed is small compared to object dimensions (which is the case in the human head and particularly the human torso relative to the 300 MHz (7 T proton resonance frequency) wavelength of ∼12 cm), the B₁ and accompanying electric fields propagate from the source creating them (the current carrying elements in the RF coil) to and through the object being imaged, getting attenuated and reflected from boundaries during this process, ultimately leading to a complex destructive and constructive interference pattern. An example of this is illustrated in Fig. 8, which shows simulation of the transmit B₁ field for a circumscribing body volume coil. When unloaded, this coil generates a highly uniform B₁ (Fig. 8, upper panel); however, when the human body is inserted into the coil, the B₁ field propagates as a wave and even ends up strongest in the human head although the head is very much outside the RF coil (Fig. 8, lower panel). Similarly, in the approach described in Brunner et al. (2009), even though a uniform B₁ pattern can be generated in the large cavity when unloaded, within the human body, the attenuated traveling wave behavior of the RF and the reflections from the boundaries within the human body leads to a non-uniform excitation and signal detection profile.

Fig. 8.

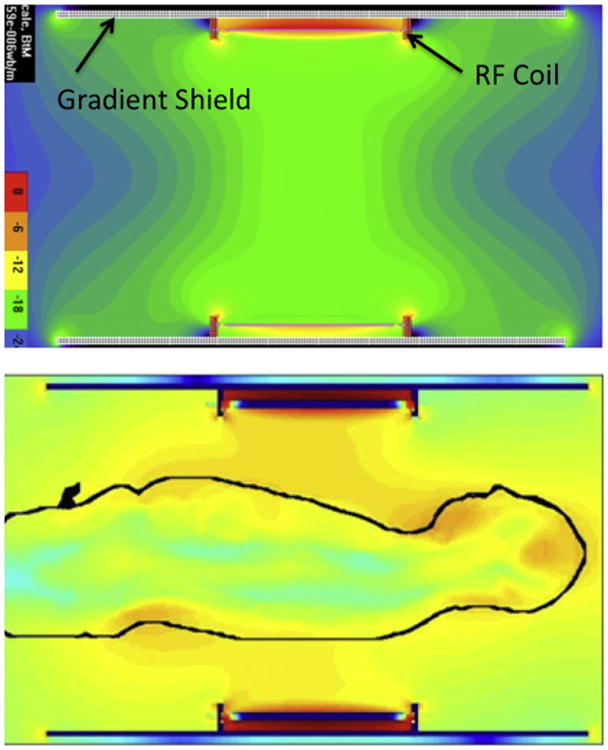
Electromagnetic simulations of the transmit B₁ field in a body RF coil at 7 T. The coil produces a homogenous B₁ when empty (top figure) but not when loaded with the human body (lower figure) (work by Jinfeng Tian and Thomas Vaughan, CMRR).

We experimentally evaluated the implications of these conclusions by breaking a head “volume” coil in effect into decoupled independent elements and controlling each element individually, i.e. a multichannel transmit implementation (Adriany et al., 2005)¹; this is the first published experimental demonstration of multichannel transmit with human imaging. The other early publications reporting on the multichannel transmit were (Zhu, 2004) and (Katscher et al., 2003); these studies were focused on accelerating multidimensional RF pulses and demonstrated this capability experimentally in phantoms as opposed to our effort, which aimed at understanding and correcting transmit B₁ inhomogeneities in the human body at 7 T. Ibrahim et al. (2001b) simulated an approach where a volume TEM coil was driven at multiple ports (up to 24) independently and showed potential improvements in transmit B₁ homogeneity for 8 T in a human model, even though a volume TEM coil is not composed of independent decoupled elements. In our work (Adriany et al., 2005), we took the output of the single RF channel after the amplification stage and split it into different channels using a power splitter and adjusted the phase of each channel by changing the length of the cable connecting to the RF coil element (Adriany et al., 2005). This is commonly referred to today as “RF phase shimming”. An eight channel transmit and receive (Tx/Rx) coil was employed with the same elements being used both for transmission and reception (Fig. 9A). With such a coil, it was possible to transmit with one element and receive with all the elements in the array simultaneously but separately using an 8 channel receiver. Although the concept of multichannel receivers were introduced in 1990 (Roemer et al., 1990), they were relatively new and rare in the early two-thousands. Custom-built solutions were necessary even when working with scanners supplied by major manufacturers, as demonstrated by the effort by Bodurka et al. (2004) and de Zwart et al. (2004) who developed a custom built solution for a 3 T GE scanner. A multichannel receiver certainly was not commercially available for our in-house assembled 7 T system, running on a Varian console. So, we developed our own digital multichannel receiver, which used an Echotek (Huntsville, AL) board to oversample the 20-MHz intermediate frequency (IF) at the rate of 64 MHz and 14-bit resolution (effective resolution becomes significantly higher than 14 bits due to the oversampling), allowing for quadrature detection, band pass filtering, and down conversion to be done digitally, which was programmed in house.

Fig. 9.

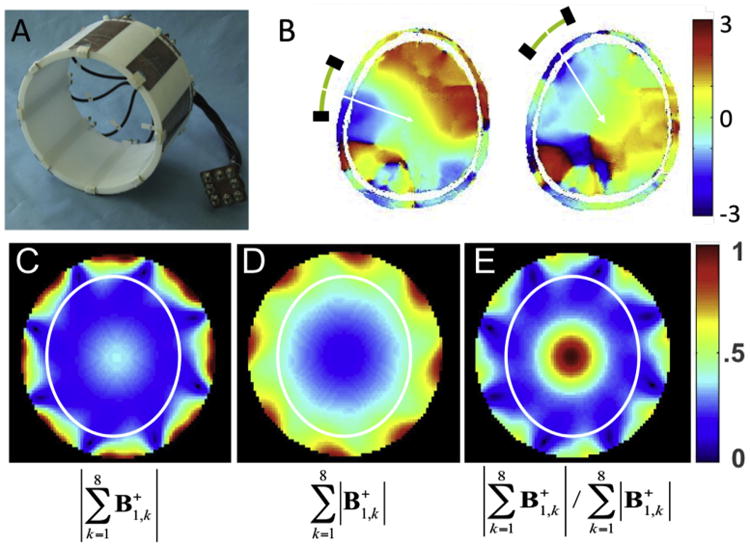
Eight channel transmit/receive RF coil (A) and experimental relative phases measured in the human head from two different individual elements of this coil (B). Lower row shows experimentally measured transmit B₁ magnitude in a cylindrical “phantom” when the individual transmit B₁ vectors from each channel are first experimentally determined, transmitting one channel at a time and receiving with all channels, and subsequently are added according to the constructs shown below each figure (the color code is in arbitrary units) The white ellipse in C, D, and E depicts approximate boundaries of a human head. Adapted from (Van de Moortele et al., 2005).

The afore described multichannel transmit and receive hardware enabled us to experimentally map $B_1^{+}$ phase and amplitude of each individual element and reconstruct $B_1^{+}$ either for the circularly polarized (CP) mode of a volume coil² or using other constructs (Van de Moortele et al., 2005). For the coil shown in Fig. 9A, the $B_1^{+}$ phase pattern in the human head obtained by pulsing only one element and receiving from all elements simultaneously is illustrated for two different individual channels in Fig. 9B; this phase pattern is highly non-uniform spatially (Van de Moortele et al., 2005) as would be expected from the traveling wave nature of the RF at this magnetic field strength. The experimentally measured phase variation is complex and easily covers the range 2π over the human head. When the transmission is in the CP volume coil mode, and the RF power is delivered to all 8 channels simultaneously with the appropriate channel-dependent phases, the vector (ie., complex) addition of $B_1^{+}$ produced by each element is constructive in some places (e.g., the center of the head) or leads to partial cancellation in others, resulting in a “volume coil” transmit B₁ amplitude pattern shown in Fig. 9C (Van de Moortele et al., 2005). If we approximate where the human head boundaries would be and superimpose it on this pattern (white line in Fig. 9C), we would see in the human head the well-known, center bright transmit B₁ profile, as documented previouslsy at 4 and 7 T in Vaughan et al. (2001). If, on the other hand, we transmit with each element individually and form a construct based on $B_1^{+}$ magnitudes alone, analogous to what can be done for multichannel receive operation, then the pattern is no longer center bright (Fig. 9D); on the contrary, it is weak in the center and strong in the periphery (Van de Moortele et al., 2005).

In a CP volume coil, a “vector” addition of $B_1^{+}$ from each current carrying element is accomplished in hardware during the pulse; this produces a pattern like the one shown in Fig. 9C in slices that intersect approximately the middle of the brain (see Fig. 6), with destructive interferences in $B_1^{+}$ leading to relatively lower flip angles in the periphery compared to the center; thus, setting the flip angle to be 90° in the center of the brain leads to relatively lower SNR in the periphery (Fig. 5). There is an additional loss during signal reception since the receive B₁ fields ( $B_1^{-}$), are similarly summed in hardware as a vector in such a coil, and produce a pattern similar to what is shown for $B_1^{+}$ in Fig. 9C (Van de Moortele et al., 2005). Thus, just like $B_1^{+}$, for a single channel volume coil, $B_1^{+}$ magnitude, and hence detection sensitivity, also displays a non-uniform, center high, periphery low profile (Van de Moortele et al., 2005). If, however, these patterns are constructs arising from the specific coil and sample geometry and not intrinsic to 7 T head imaging, as we postulated, it would be still possible to demonstrate an SNR gain from 4 to 7 T in the periphery of the human brain that matched what was observed in the center of the brain (Fig. 5). We were able to do this using a small local surface coil and single voxel spectroscopy executed using small voxels within which transmit B₁ is expected to be relatively uniform and can be set experimentally to 90° at either field strength; with this approach, we reported an SNR increase in the periphery of the human head also by factor 2 in going from 4 to 7 T (Tkac et al., 2009). SNR measurements performed using a 32 channel receive array coil over the human head at 3, 7, and 9.4 T reported that SNR increases as ${\mathrm{B}}_0^{1.65}$ (Pohmann et al., 2016).

Thus, SNR gains are in principle intrinsically spatially inhomogeneous not because of some fundamental physical principles, but arise from a particular set of coil configuration and sample geometry. Therefore, inhomogeneity can be rectified by manipulating the configuration of the current carrying elements and/or their phases and amplitudes, so as to control the interference of RF waves emanating from them; in its most generalized form, this is the concept of multichannel transmit coils with each coil element driven separately, what is now known as parallel transmit or pTx (e.g., (Ibrahim et al., 2001b; Katscher et al., 2003; Vaughan et al., 2004; Zhu, 2004; Adriany et al., 2005; Van de Moortele et al., 2005)). Using various strategies such as B₁-shimming (e.g., (Adriany et al., 2005; Vaughan et al., 2006; Metzger et al., 2008; Snyder et al., 2009; Suttie et al., 2012; Schmitter et al., 2013b)), transmit sense (e.g., (Katscher et al., 2003, 2004; Zhang et al., 2007)), spoke pulses (e.g., (Zelinski et al., 2008; Setsompop et al., 2009; Cloos et al., 2010; Jankiewicz et al., 2010; Ma et al., 2011; Schmitter et al., 2013a; Wu et al., 2013)), k-T pulses (Cloos et al., 2012) etc. pTx technique aims to generate uniform flip angles over a targeted region such as the brain (also see reviews (Grissom et al., 2010; Padormo et al., 2016) and references therein). Even with spatially uniform excitation, the detected signal intensity and sensitivity will still be non-uniform due to the spatially inhomogeneous sensitivity of the receive coil(s). However, “destructive interferences” per se can be avoided or minimized on the receive side if a multichannel receive coil is employed with signals from each channel collected separately but simultaneously and only combined subsequently.

SNR gains with increasing magnetic fields can be substantial and particularly important with low gyromagnetic nuclei such as ¹⁷O, ²³Na, ¹³C, and ³¹P all of which are of great biological interest. Among these nuclei, ¹⁷O and ²³Na resonate at particularly low frequencies. For example, at 9.4 T, ¹⁷O resonates at 54 MHz while the ¹H resonance frequency is 400 MHz. At such low frequencies, SNR can vary with magnetic field according to ${\mathrm{B}}_0^{7/4}$ (Hoult and Richards, 1976; Wen et al., 1994) even in conductive biological samples. Consistent with theory, approximate quadratic dependence of SNR on field strength was experimentally observed between 4.7 and 9.4 T in the rat brain (Zhu et al., 2001) for direct detection of the ¹⁷O nucleus. This sensitivity gain was critical in performing biologically important measurement of oxygen consumption rate in the brain (e.g., (Zhu et al., 2002; Atkinson and Thulborn, 2010)). For these low gyromagnetic nuclei, going to fields higher than 7 T, such as 10.5 T or 11.7 T, will bring much needed additional gains in SNR, hence spatial and/or temporal resolution.

The SNR increases measured for ¹H imaging at 7 T relative to lower field strengths (Vaughan et al., 2001; Pohmann et al., 2016) were for same bandwidth and full relaxation. Such conditions are not universally applicable in image acquisition. With repetitive RF pulsing without full relaxation, SNR will be diminished but more so at higher fields for nuclear spins such as protons, where spin-lattice relaxation times get longer with increasing magnetic fields ((Rooney et al., 2007) and references therein). Other nuclei such as ¹⁷O and ³¹P (Zhu et al., 2001; Lei et al., 2003b) will be unaffected or even gain due to this phenomenon. Similarly, under many conditions, the receiver bandwidth needs to be higher at the higher field strength, leading to an increase in the noise standard deviation as the square root of the bandwidth.

3. Solving the SAR and B₁ inhomogeneity challenges simultaneously

One of the most significant challenges facing ultrahigh fields is SAR (Specific Absorption Rate), i.e., the power deposited into the subject. The general expectation at the time 7 T came into existence was that power requirements (hence also SAR assuming most of the power was deposited in the sample) increases quadratically with the magnetic field. This concept originated from the near-field formulation of the problem (Bottomley and Andrew, 1978; Hoult and Lauterbur, 1979). As previously discussed, already there were hints that we were not operating at the near-field limit even at 4 T. Less than quadratic increase in the power to achieve 90° pulse in the center of the human head was reported for 8 T (Robitaille et al., 1998). Our first experimental and simulation results comparing 4 and 7 T also indicated that power required to achieve a 90° pulse in the center of the human head increased only ∼2 fold for a volume TEM head coil (Vaughan et al., 2001), not ∼3 fold as would be expected from a quadratic dependence. At about this time also, theoretical calculations for a sphere indicated that although at low frequencies (the near-field limit) power increases quadratically, it actually can decrease at higher frequencies and larger samples (Hoult, 2000). Increasingly, experimental evidence is accumulating demonstrating that power requirements and deposition at ultrahigh fields can be considerably less than the quadratic field dependence of the near-field formulation, including when going from 7 T to 10.5 T, as demonstrated with simulations as well as experimentally (Erturk et al., 2016), or even up to 23.5 T (1 GHz proton resonance frequency) as shown with simulations (Winter and Niendorf, 2016).

Nevertheless, the landscape for meeting the requirements for “safe” operation set by regulatory bodies such as the FDA in the United State remains a challenge for ultrahigh fields. FDA sets limits for “global” and “local” SAR. Even though appropriateness of these limits and the science behind them are topics of ongoing debate, they are the guidelines that define safe operating conditions. Global SAR can be experimentally estimated; all MRI scanners are equipped with hardware and software to do so. There are imaging applications, such as GRE based fMRI, that are intrinsically very low in global power deposition and can run without encountering global SAR limits even at 7 T. But many other techniques, such as spin-echo based acquisitions for diffusion weighted imaging, spin echo fMRI, anatomical imaging with Turbo Spin Echoes (TSE), etc. quickly run into limitations.

The greater problem at ultrahigh fields is local SAR. In a clinical scanner with a single channel transmit coil, electromagnetic simulations of the specific coil loaded with different anatomical human models are employed to establish a correlation between global SAR and local SAR for that coil. This correlation, including a safety margin that accounts for possible variations among individuals, is then employed to abide by global and local SAR limits based on the experimental measurement of global SAR alone. However, this approach completely fails for pTx. In a pTx application, amplitudes and phases of the different current carrying elements (i.e., the different transmit channels) no longer have a hardware-fixed relationship as they do in a single transmit coil set up; instead they are now uniquely determined based on the $B_1^{+}$ maps obtained on each individual subject, the targeted region to be imaged, and the pTx RF solution employed.

Therefore, ideally, the pTx approach requires calculation of local SAR for each individual subject and for the pTx RF solution sought. Currently this is far from being feasible within the time dictated by constraints of an MR imaging session. Consequently, one must rely on generic models. Solutions have been proposed based on evaluation of multiple models and techniques for a given coil configuration to set safety margins or employ a library of models to estimate optimal matches (e.g., (Jin et al., 2012; de Greef et al., 2013; Ipek et al., 2013) and references therein).

While pTx technology introduces complications with respect to local SAR, it also provides a solution for the SAR imposed limitations on power demanding imaging methods (e.g., (van den Bergen et al., 2007; Lee et al., 2012; Wu et al., 2013; Guerin et al., 2014, 2015b; Boulant et al., 2016; Erturk et al., 2016; Wu et al., 2016b) and references therein). In one of our first attempts to perform body imaging, where TSE is a commonly used sequence, we were able to achieve a relatively uniform B₁ over the prostate while improving ∼4 fold the transmit efficiency and hence power requirements for a given flip angle in the targeted anatomy; this was done with an 8 channel pTx using B₁ shimming (i.e., 1-spoke pulses) (Metzger et al., 2008). Simulations also indicated that local SAR was reduced as well. Thus, pTx in fact provides the means simultaneously to homogenize the flip angle over the targeted organ of interest as well as increase transmit power efficiency (i.e., flip angle achieved at a given power).

Today, more advanced pulse design strategies than that employed in the early work by Metzger et al. (2008) target a desired spatial pattern of $B_1^{+}$ (e.g., uniform flip angle over a predetermined target) and search for a solution in the presence of a power related penalty term, such as local or global SAR and/or total RF energy contained the pulse etc. This procedure typically generates an “L-curve” that describes the performance of the pulse with respect to the targeted performance (e.g., $B_1^{+}$ uniformity) versus the regularized power parameter. Such an L curve is illustrated in Fig. 10 for a multiband RF pulse design for 7 T brain imaging using a 16 channel parallel transmit coil (Wu et al., 2013). The crossing between the horizontal and vertical dashed lines, labeled “Same fidelity” and “Same energy”, identify the performance of the same coil operated in a circularly polarized (CP) mode. At the same RMSE as the CP mode, the RF energy of the pulse is reduced significantly (∼60% for the same flip angle). The best compromise is where the L shaped curve has an elbow, indicated by the arrow (Fig. 10).

Fig. 10.

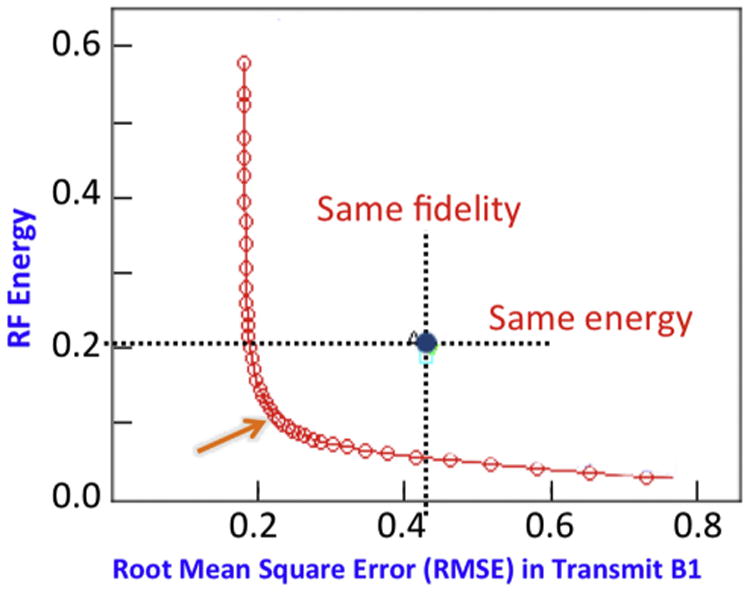
Sixteen channel pTx pulse design for a multiband RF pulse that excites two slices simultaneously in the human brain at 7 T. The L shaped curve quantifies tradeoffs, in this specific case, between total RF energy of the RF pulse and excitation errors (i.e., root mean square error (RMSE)). The crossing between the horizontal and vertical dashed lines, labeled “Same fidelity” and “Same energy”, identify the performance of the same coil operated in a circularly polarized mode. Adapted from Wu et al. (2013).

RF coil design has a significant impact on the gains that can be achieved in reducing local and/or global SAR. For example, design with coil elements distributed not only azimuthally but also along the z-direction (often referred as a z-coil), first introduced by work from our group (Adriany et al., 2006, 2010a, 2010b), and subsequently pursued in other high field efforts (e.g., (Kozlov and Turner, 2011; Shajan et al., 2013)), significantly improve local and/or global SAR reduction with pTx pulses (Guerin et al., 2015a; Wu et al., 2015; Wu et al., 2016b).

When solutions such as the one shown in Fig. 10 are calculated for sequential excitation of slices for slice selective volume coverage (Guerin et al., 2012, 2014) or simultaneous excitation for multiple slices with a multiband pulse (Wu et al., 2014, 2016a, 2016b; Guerin et al., 2015b;), the algorithm can minimize the local SAR by distributing the “hot-spots” to a different location for each excited slice or group of slices respectively, for single or simultaneous multislice excitation. Consequently, hot-spots are not focused and do not add up, thus minimizing local SAR. Solutions have also been proposed to simultaneously constraining more than one power parameter (Guerin et al., 2014). Using these approaches coupled with appropriate coil design, we have demonstrated that it will be possible to perform imaging even in the human torso at 10.5 T without violating local and global SAR guidelines; in fact, whatever one can do at 7 T with single spokes, one can do at 10.5 T with two-spoke pulses with the same or even lower local SAR ((Erturk et al., 2017b) and Fig. 11). This is extremely encouraging since there are a lot of useful imaging studies in the torso one can execute with single spoke pulses at 7 T (e.g., (Schmitter et al., 2013a, 2014)), including with single-spoke simultaneous multi-slice multiband excitation (Schmitter et al., 2017).

Fig. 11.

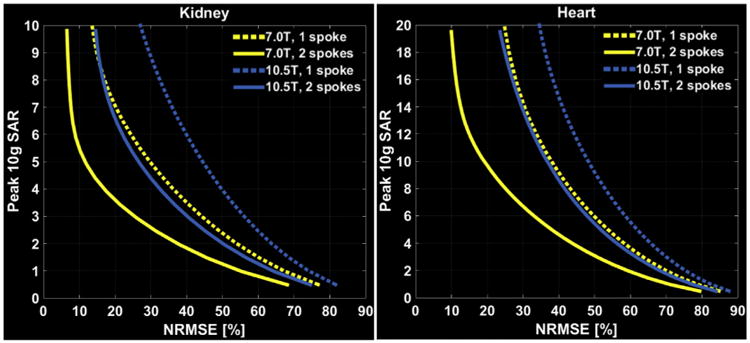
Performance of one-spoke (dashed) and two-spoke (solid) pTx pulses to image the kidneys, and the heart. L-curves display tradeoff between excitation error (NRMSE) and resulting peak local SAR for 7.0 T and 10.5 T arrays when designing the pTx pulses with explicit local SAR constraint. Adapted from Erturk et al. (2017b).

However, all of these elegant pTx solutions to SAR challenges still must be calculated using a human model rather than on an individual subject basis and implemented with a safety margin to account for subject variability. This, of course, sacrifices performance.

4. B₀ inhomogeneities and parallel imaging

As previously stated, the drive to establish a 7 T human scanner came predominantly from our interest in functional brain imaging. This particular application relies on very fast image acquisition strategies such echo planar imaging (EPI), ideally implemented as a single shot, covering the entire k-space after a single excitation, as opposed to segmented k-space coverage. However, such approaches suffer from static magnetic field (B₀) inhomogeneities, which induce phase accrual during the echo train, thus leading to distortions and/or blurring, as well as signal loss due to T₂* decay. Higher in-plane spatial resolution exacerbates the problem, as the echo train gets commensurately longer. In the human head, presence of air cavities in close proximity to the brain and the magnetic susceptibility difference between such cavities and the brain tissue induces large magnetic field inhomogeneities, which become more pronounced with increasing magnetic fields; these inhomogeneities are impossible to eliminate by B₀ profiling from room temperature shims unless very high order shims are present (Pan et al., 2012). Although such methodology and hardware is increasingly developed for ultrahigh field imaging and spectroscopy (e.g. (Hetherington et al., 2006; Juchem et al., 2010; Truong et al., 2014; Stockmann et al., 2016)), current commercially available 7 T scanners only include 2nd and partial 3rd order room temperature shim coils, and early 7 T instruments were equipped with only up to second order terms. The strength of the second order shims were based on our experience at 4 T and worked superbly well, for example, for single voxel spectroscopy even at 7 T (Tkac et al., 2001, 2009). But they are insufficient at any strength for compensating the B₀ non-uniformities inherent in the whole human head, especially at ultrahigh magnetic fields. Thus, together with the afore-discussed B₁ inhomogeneities, these B₀ problems constitute a major challenge in imaging at 7 T, particularly for applications such as fMRI and diffusion imaging that rely on single shot techniques.

The very first cognitive neuroscience application of fMRI at 7 T was mapping of tonotopy in the primary auditory cortex, which we undertook in CMRR in collaboration with colleagues from Maastricht University (Formisano et al., 2003). Multichannel transmit or receive was not yet operational. We started with a volume TEM coil and resolutions typical of studies conducted at 3 and 4 T. We encountered major difficulties. When we mapped the B₀ and B₁ fields, we discovered the problem of getting enough B₁ into the temporal lobe region from a volume TEM head coil (as is evident now from the data shown in Fig. 6), and saw the difficulty of improving the B₀ inhomogeneities with just the first and second order shims. We switched from our fancy TEM whole-head coil to a simple 12 cm diameter loop for transmission and signal reception, placed directly over the region of interest, solving the B₁ problem. We performed localized adjustments of the B₀ field using the FAST(EST)MAP technique, also developed in our lab for localized single voxel spectroscopy studies (Gruetter and Tkac, 2000). Finally, after establishing that 7 T provided the SNR gains needed, we went to higher spatial resolution in order to suppress intravoxel dephasing and consequent signal loss. We were ultimately aiming for high-resolution fMRI at 7 T anyway; synergistically, high resolution significantly ameliorated the problem of signal loss due to highly non-uniform B₀. The advantage of this strategy at ultrahigh fields is demonstrated with a simple example obtained in the very early days of 7 T (Fig. 12). While the benefits of high resolution at 7 T is easy to realize in the slice direction (Fig. 12), higher in-plane resolution creates challenges, as previously mentioned, for fast acquisitions like EPI, especially at high fields due to the diminished T₂*. The solution to this was field of view (FOV) reduction; at the time of the early tonotopy study (Formisano et al., 2003), we achieved this in part by using a single surface coil for transmit and receive, but also by outer volume suppression implemented using a B₁-insensitive outer volume suppression technique we had developed based on adiabatic pulses (Luo et al., 2001; Pfeuffer et al., 2002a).

Fig. 12.

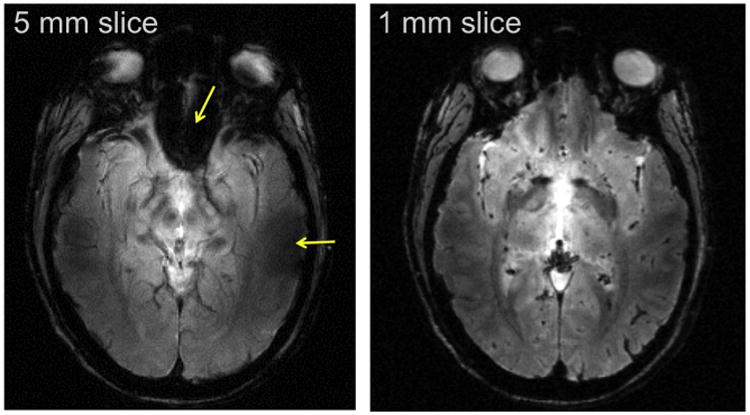
7 T gradient recalled echo (FLASH) image of a single slice in the human head with the same in-plane resolution but with two different slice thickness and hence, different voxel volumes. Arrows in the 5 mm slice point to regions of signal reduction or complete loss due to B₀ inhomogeneities near air filled cavities in the human head. These losses are recovered in the higher resolution, 1 mm thick slice, image.

As a result of the afore described strategies, we were able to obtain excellent and highly reproducible tonotopic maps of the human primary auditory cortex, showing for the first time the existence of a mirror symmetric tonotopic organization (Formisano et al., 2003), as was reported for animal models previously. More or less, the restricted FOV strategy employed in this approach, with or without segmented k-space coverage (depending on the spatial resolution targeted) have been and continue to be employed in our studies of functional organizations that exist in the millimeter to submillimeter scale in the human brain; many of these studies employ a single spin echo (e.g., (Yacoub et al., 2008)) or spin echo/gradient echo based approach (GRASE) (e.g., (Zimmermann et al., 2011; De Martino et al., 2013b)) where the excitation and spin echo pulses are used to select orthogonal slices or slabs, restricting the FOV in two directions by inner volume selection rather than outer volume suppression. However, increasingly high resolution whole brain coverage is possible (discussed further on) and pursued even with power intensive sequences like multiband/simultaneous multislice spin echo acquisitions (Vu et al., 2015). The transformative technology that has made this possible is parallel imaging (Sodickson and Manning, 1997; Pruessmann et al., 1999; Griswold et al., 2002), which in fact allows the acquisition of an image with a FOV smaller than the object to be imaged requires, i.e., a restricted FOV.

Parallel imaging (on the receive side), in its most commonly employed form (which will be referred to as in-plane parallel imaging), accelerates image acquisition by reducing the acquired k-space data in the phase encode direction, and supplementing the missing data with spatial information inherent in an array of receive coils (Sodickson and Manning, 1997; Pruessmann et al., 1999; Griswold et al., 2002). Parallel imaging and ultrahigh fields are synergistic technologies, compensating for the shortcomings of each other. In-plane parallel imaging suffers SNR losses due to undersampling of k-space and image reconstruction. This loss is compensated by the SNR gains inherent at high magnetic fields. The complex B₁ amplitude and particularly phase (Fig. 9B) behavior observed at ultrahigh fields, which was initially seen as a major impediment, is in fact a major advantage for parallel imaging (Ohliger et al., 2003; Wiesinger et al., 2004, 2006), allowing higher acceleration factors and consequent reduction in imaging times. Simulations demonstrating this are reproduced here (Fig. 13) from previous work (Wiesinger et al., 2004, 2006); noise increase due to reconstruction (g-factor) at the center of a spherical object are shown as a function of magnetic field and object size, which, in Fig. 13, is the same as the FOV. The head would correspond approximately to FOV of ∼0.2–0.25 m and the body will be more than 0.4 m for most adults, especially in the left-right and head-to-toe dimension. R is the reduction in FOV and hence k-space coverage, and is equal to the acceleration that can be achieved in image acquisition speed. Thus, significant improvements take place at 7 T (i.e. lower g-factor noise) compared to more commonly available magnetic fields of 3 and 1.5 T, but further improvements are expected at even higher fields.

Fig. 13.

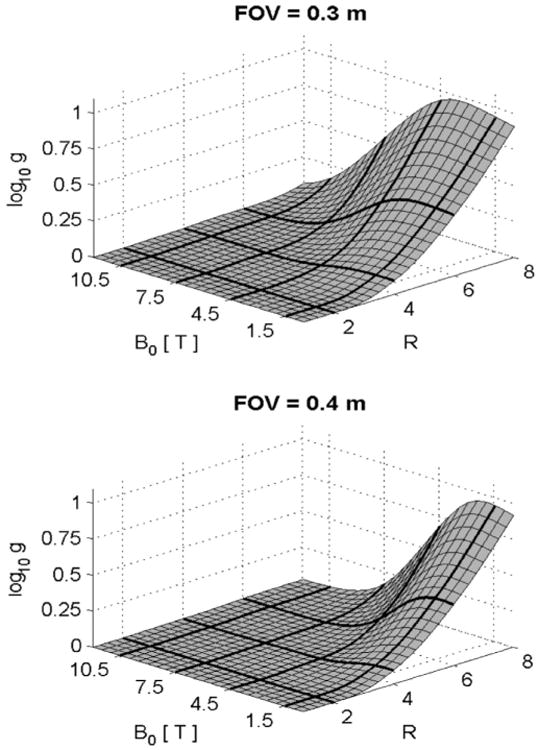
Parallel imaging (SENSE) performance for different object size and field magnitude. Simulation shows the log of g-factor as a function of reduction factor R and magnetic field magnitude. Adapted from Wiesinger et al. (2004, 2006).

In EPI, in-plane parallel imaging reduces echo train length, decreasing phase accrual due to off-resonance effects, and, hence decreasing distortions and reducing signal loss due to T₂* decay during the echo train. We recognized the implications of parallel imaging for single shot sequences like EPI at 7 T and launched into harnessing its potential gains in 7 T fMRI. GRE EPI based fMRI images with diminished distortion artifacts were demonstrated with 2 fold in-plane acceleration at 1.5 and 3 T shortly after the introduction of parallel imaging (e.g., (de Zwart et al., 2002; de Zwart et al., 2006)). We demonstrated for the first time the ability to obtain 1.56 × 1.56 mm² in-plane resolution, GRE EPI fMRI data in the human brain with 4-fold one dimensional acceleration (resulting in 4-fold aliasing in the brain) with low g-factor noise, using a 16 channel coil at 7 T (Moeller et al., 2006).³ The resultant 7 T functional imaging data were robust, in full agreement with expected activation patterns based on prior knowledge, and with full-FOV data acquired with segmented coverage of k-space. In all aspects, the GRE EPI functional maps acquired with parallel imaging outperformed segmented coverage of full k-space. Segmented acquisitions are particularly bad in fMRI due to the presence of physiological contributions to signal amplitude and phase instabilities; hence the improvements in statistical significance of the functional maps with single shot, 4-fold accelerated fMRI data relative to the segmented acquisition were particularly high when “physiological noise” increasingly became dominant relative to thermal noise of the image (Moeller et al., 2006).

In applications like fMRI and diffusion imaging (dMRI) using single-shot image acquisitions like EPI, SNR loss due to the use of parallel imaging does not simply follow the expected factor g√R; there are SNR gains that are also realized by being able to reduce the echo train length and the echo time TE. This is particularly significant at ultrahigh magnetic fields where T₂ and T₂* become shorter. Other considerations come into play also for fMRI. The contrast-to-noise ratio (CNR) of functional maps, in other words functional contrast-to-noise ratio (fCNR), depends on the magnitude of the functional signal changes and on temporal fluctuations of the signals detected in the consecutively acquired images in a fMRI time series, often referred to as temporal SNR (tSNR). In a fMRI time series, tSNR is dominated by thermal noise only when the SNR of any one given image in the time series is low, as in very high-resolution studies of the type we have often pursued with 7 T. When image SNR is high, physiological processes increasingly dominate tSNR (Triantafyllou et al., 2005, 2011). Existence of basal fluctuations in a fMRI time series was first reported in one of the very early fMRI papers coming from our group (Ogawa et al., 1993) followed by solution to suppress respiration and cardiac pulsation related components of these fluctuations (Hu and Kim, 1994). The other contributions come from spontaneous neuronal processes (Bianciardi et al., 2009b) and form the underlying mechanism of resting state fMRI (Biswal et al., 1995). Some of these basal signal fluctuations are proportional to the signal magnitude (Hyde et al., 2001; Kruger and Glover, 2001; Yacoub et al., 2005); as such, they increase with field strength or, at a given field strength, with voxel volume (Triantafyllou et al., 2005, 2011; Yacoub et al., 2005). When tSNR is dominated by these physiological processes, elevating the thermal noise by factor √R does not have a commensurate impact on fCNR (de Zwart et al., 2002; de Zwart et al., 2006; Moeller et al., 2006); it can in fact be beneficial by allowing the use of single-shot versus segmented acquisitions (Moeller et al., 2006), as mentioned above.

Another parameter that impacts the quality of EPI images is the rate at which one can ramp the gradients during the k-space encoding. Fast ramping (or “slew”) rate also decreases the echo train length in an EPI sequence, ameliorating the deleterious consequences of B₀ inhomogeneities and short T₂*. However, whole body gradients of the type used in clinical scanners are restricted in their slew rate because of peripheral nerve stimulation as well as hardware constraints. Head-only gradients, on the other hand, can be ramped significantly (e.g., factor 2 or more) faster. Because of this, from the beginning we opted for head gradients for fMRI.⁴ Head gradients, however, also create problems. Besides negatively impacting subject comfort and tolerance, the limited space within such a gradient constraints RF coil design. Because of this, when we launched the effort for multichannel transmit and receive operations, we initially opted for arrays where the coil elements were used for both transmission and signal reception as opposed to separate transmitter and receiver arrays, which require more space; we developed in-house a 16 channel transmitter, enabling us to do 16 channel transmit and 16 channel receive at 7 T (Adriany et al., 2005). Only when going to 32 channel receive, we deviated from this practice; but we may go back to it since we now have an operational 32 channel transmitter (Auerbach et al., 2017).

When parallel imaging was combined with the use of a head gradient (slew rate of 333 mT/m/ms) thus significantly shortening the echo train length, it became possible to obtain excellent EPI images at 7 T. Fig. 14 shows an example of 7 T whole brain GRE EPI images obtained with a head gradient using 0.75 mm isotropic nominal resolution, 128 slices, 4-fold in-plane acceleration. These images also benefit from the numerous improvements in EPI image reconstruction, including corrections for EPI image intensity variation and spatial shifts due to B₀ off-resonance modulations (Pfeuffer et al., 2002b; Van De Moortele et al., 2002).

Fig. 14.

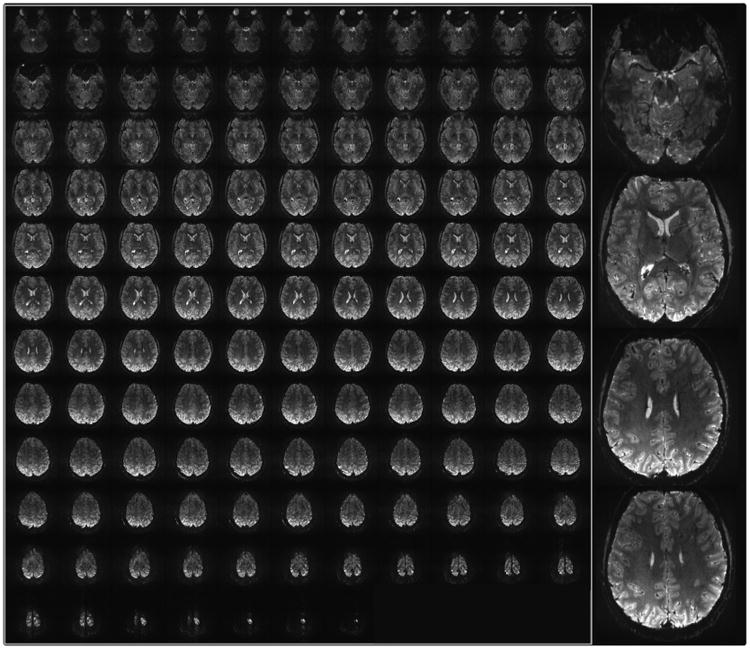
7 T Gradient Recalled Echo EPI images obtained with a head gradient, a 32 channel receive coil, and 4-fold acceleration along the phase encode direction. Nominal resolution = 0.75 mm isotropic; 128 slices; echo spacing = 0.67 ms; 256 × 256 matrix; partial Fourier pf = 6/8; TE = 20 ms; TR = 6 s. Right column displays a blowup of 4 of the slices.

Of course, high resolution whole brain coverage also leads to increased volume acquisition times (TR) necessitating compromises such as large slices, inter-slice gaps or sacrificed temporal resolution (e.g., (Bianciardi et al., 2009a, 2009b, 2009c; Poser and Norris, 2009; van der Zwaag et al., 2009a; van der Zwaag et al., 2009b; Poser et al., 2010)). Motivated by the prospect of acquiring high resolution, whole brain fMRI data at 7 T, but confronted with the long TRs required for whole brain coverage, we turned to parallel imaging again but this time accelerating along the slice direction (Larkman et al., 2001). We demonstrated for the first time functional brain imaging using concurrent accelerations along both the slice and in-plane phase-encode directions (Moeller et al., 2008, 2010). In this approach, referred to as Multiband (MB) and/or Simultaneous Multi-Slice (SMS), several slices are simultaneously excited using multibanded RF pulses and subsequently acquired in a single EPI echo train. We had to develop an unaliasing approach for this two dimensional acceleration with both phase-encode undersampling and multiband excitation. Initially, the separation of aliased slice signals was performed with GRAPPA, but, in contrast to the conventional use of GRAPPA for interpolation of missing k-space, the aliased slice signal was reformulated as being the result of missing Fourier components of an image with a larger FOV. Phase-encode undersampling in k-space corrections were performed with GRAPPA. We reported 16 fold (4×4) two-dimensional acceleration, demonstrating for the first time whole brain functional images for a complex visuo-motor task, acquiring 2×2×2 mm³, 88 slice data in 1.25 sand 1×1×2 mm³, 88 slice data in 1.5 s (Moeller et al., 2008, 2010) and demonstrated that tSNR was not affected by the MB/ SMS approach.

Since each slice is excited and sampled identically, there is no √R SNR loss in MB/SMS acceleration as encountered with parallel imaging with reduced data collection in k-space along the phase encode direction. There are, however, SNR losses associated with the slice unaliasing. A quantitative analysis of this SNR loss is possible using g-factor formulation originally developed for in-plane parallel imaging along the phase encode dimension (Pruessmann et al., 1999). However, g-factors themselves do not inform about residual aliasing among the simultaneously acquired slices. To address this, we introduced a metric named the L-factor (leakage factor) (Moeller et al., 2012; Xu et al., 2013) that quantifies residual aliasing; an alternative approach to evaluating the “leakage” was also introduced subsequently (Cauley et al., 2014).

As with undersampling of k-space, the g- and L-factors achieved for unaliasing of multiple, simultaneously-acquired slices is expected to improve with higher magnetic fields and a larger number of receive channels. Coil geometry and slice orientation also play a significant role. For example, we employed coronal slices and left-right phase encode direction intentionally in Moeller et al. (2008, 2010) since the coil was composed of 16 azimuthally distributed elements that would not have provided much parallel imaging performance in the head-foot direction.

We proposed the MB/SMS fMRI approach for the competitive renewal application of our NIH Biotechnology Research Center (P41) grant in 2007 for high resolution 7 T fMRI, presenting the first results in the site visit that took place for evaluating the grant application the same year⁵ and reported it first at the 2008 ISMRM annual meeting (Moeller et al., 2008), later publishing in 2010 (Moeller et al., 2010).⁶ We were however distracted from following up on this at 7 T fully, with the emergence of the Human Connectome Project (HCP) awarded to Washington University-University of Minnesota-Oxford University consortium (Van Essen et al., 2013). This MB/SMS approach became the corner stone of the HCP in our consortium, both for the large (1200 subject) and smaller (180 subject) data sets generated at 3 T and 7 T, respectively (Ugurbil et al., 2013). A smaller HCP grant was also awarded to the MGH-UCLA consortium, where significant contributions to MB/SMS diffusion imaging were made and the technique was adopted fully for data acquisition for this consortium as well (Setsompop et al., 2012, 2013).

In our HCP consortium, the focus was initially on the 3 T component, which had a very large data collection burden. Only in the later stages of the HCP, we returned to 7 T and developed the approach further specifically for 7 T (Vu et al., 2015, 2017; Glasser et al., 2016). In the HCP, initially we combined the MB/SMS sequence we developed with the SIR approach (Gunther and Feinberg, 2005) for achieving greater acceleration, which we called Multiplexed EPI (Feinberg et al., 2010; Ugurbil et al., 2013); we used this sequence to demonstrate that increasing temporal sampling in a fMRI time series significantly improves the detection of resting state networks at 3 T (Feinberg et al., 2010; Smith et al., 2013).

We noted in our original paper (Moeller et al., 2010) that controlled aliasing (CAIPIRINHA) principles (Breuer et al., 2005) can be applied to slice accelerated multiband EPI to improve the performance of the unaliasing of simultaneously acquired slices. This was accomplished (Setsompop et al., 2012) following the slice-gradient “blipping” strategy (Nunes et al., 2006) while minimizing the detrimental accrual of phase dispersion along the slice thickness leading to a voxel tilt. This was a major development because it allowed significantly higher accelerations in the slice direction. Using this new “blipped-CAIPI” approach (Setsompop et al., 2012), multiplexing with SIR became unnecessary for the HCP project since we could accelerate to a degree where limitation was not noise amplification and/or slice leakage (Ugurbil et al., 2013). In the resulting HCP data, the product of tSNR and the square root of the number of images in the fMRI time series increased going from no acceleration to four fold acceleration (Smith et al., 2013). Accelerating beyond that with MB = 8 did not further increase this product, but resulted in additional benefits due to the higher temporal sampling rate of physiological confounds, the benefit of higher temporal degrees-of-freedom for many analysis techniques (such as high-dimensional ICA), and capturing the resting-state fluctuations with higher fidelity (Smith et al., 2013).

MB/SMS approach is demanding in power. When the number of slices and the volume TR are kept the same, the MB/SMS approach deposits the same power as the conventional single slice excitation. However, accelerating by the MB factor leads to MB-fold increase in power deposition, imposing an SAR limit on performance. In addition, 7 T applications of the technique in fMRI and dMRI, as in the 7 T component of the HCP, are confronted with the flip angle non-uniformity, which impacts particularly the spin-echo based sequences, as employed in dMRI. The problem exists even at 3 T but it is not severe enough to have a disruptive impact on the results (Ugurbil et al., 2013). However, the consequences are much more serious at 7 T and above. We recognized early on the importance of pTx for solving the SAR problem in a unique way for MB/ SMS excitation because different slices can be largely excited by different set of coils in a transmit array (Ugurbil, 2010), thus reducing power deposition. Similar conclusion was also reached in Poser et al. (2014). However, a general formalism for designing pTx MB pulses for improved flip angle over a target while constraining it with some power/energy parameter was first introduced and experimentally demonstrated at 7 T by Wu et al. (2013) and later expanded in several other works, which were previously mentioned (Guerin et al., 2015b; Wu et al., 2016a; Wu et al., 2016b). Peak power can also be a limitation in such pulses. Methods were developed relying on pTx (Sharma et al., 2015) or other strategies (e.g., time shifting (Auerbach et al., 2013) and phase scrambling (Wong, 2012)) to overcome this problem. The latter two were incorporated into the 7 T HCP acquisition sequences (Vu et al., 2015, 2017).

5. High resolution imaging of brain function; mapping activity with cortical layer and column resolution using bold-fMRI and 7T

Detection of functional activity with submillimeter resolution using fMRI in humans has been possible only at 4 T and higher magnetic fields, providing functional maps at the level of cortical columns (Menon et al., 1997; Cheng et al., 2001; Goodyear and Menon, 2001; Fukuda et al., 2006; Yacoub et al., 2007, 2008; Shmuel et al., 2010; Chaimow et al., 2011; Zimmermann et al., 2011; De Martino et al., 2015; Nasr et al., 2016), layers (Polimeni et al., 2010; Koopmans et al., 2011; Olman et al., 2012; De Martino et al., 2013b; De Martino et al., 2015) and other fine scale organizations, such as frequency preference in the human inferior colliculus (De Martino et al., 2013a) and medial geniculate body (Moerel et al., 2015), and digits of the hand (Sanchez-Panchuelo et al., 2010; Stringer et al., 2011). These accomplishments have been possible not only with the introduction of the 7 T systems, but also as a result of extensive theoretical and experimental studies aimed at understanding the complex set of mechanisms underlying the ultimate coupling between neuronal activity and MRI signals. In fact, ultrahigh fields have provided one of the most, if not the most, important tool to study the mechanisms operative in fMRI.

The challenge we faced in targeting activity maps of submillimeter neuronal functional organizations like orientation columns and cortical layers was the “draining vein” problem, which should preclude the detection of such small organizations using GRE fMRI, unless one focused on a small patch of cortex in between such large vessels. We had modeling data suggesting a solution to this challenge through the use of ultrahigh magnetic fields; however, modeling always has many assumptions and approximations, and may have overlooked some of the operative mechanisms or ignored some of the deleterious imperfections inherent in image acquisition methods; as such, modeling alone cannot be counted on unless experimentally tested and verified. Thus, we prioritized experimentally evaluating many aspects of the fMRI signal subsequent to establishing the 9.4 T animal system first and later the 7 T human system.

An idea we pursued, based on our original modeling studies (Ogawa et al., 1993) (later expanded considerably (Uludag et al., 2009) and references therein), was to impose a “vascular filter” in BOLD based fMRI using spin echoes rather than gradient recalled echoes. SE EPI fMRI signal characteristics differ significantly from GRE EPI fMRI (e.g., (Yacoub et al., 2005)) with respect to the diameter of the blood vessels (Fig. 15). As a reference, capillaries have a diameter of ∼5 μm (Pawlik et al., 1981). However, there exist fine but important field dependent mechanistic considerations about SE EPI fMRI that was in fact not considered in our original modeling (though included in the expanded model produced much later (Uludag et al., 2009)); these had to be evaluated experimentally and 7 T provided the opportunity to do so.

Fig. 15.

Extravascular relaxation rate changes for R₂ (solid line) and R₂* (dashed line) (equal to 1/T₂, and 1/T₂*, respectively) induced by simulated blood vessels with a magnetic susceptibility difference between blood vessel interior and exterior (basis of extravascular BOLD effect), shown as a function of blood vessel radius (horizontal axis, log scale) and magnetic susceptibility induced different frequency shifts (in Hz) across the blood vessel. The numbers 32, 48, and 64 Hz correspond to increasing magnetic field strength B₀ at a constant deoxyhemoglobin concentration (∼3, 5, and 7 T at physiological conditions) or increasing deoxyhemoglobin concentration at a constant B₀. GE = Gradient Echo, SE = spin echo. Adapted from Uludag and Ugurbil (2015).

SE fMRI selectivity for small diameter blood vessels (Fig. 15) is true for extravascular BOLD effect; in other words, the BOLD effect associated with magnetic field inhomogeneities induced in tissue outside of a blood vessel containing deoxyhemoglobin (dHb). But, there is also an “intravascular” effect associated with apparent T₂ changes of blood itself caused by neuronal activity alterations through neurovascular coupling (e.g., (Boxerman et al., 1995; Lee et al., 1999; Oja et al., 1999; Duong et al., 2003; Silvennoinen et al., 2003; Uludag et al., 2009) and references therein). The intravascular effect is not subject to vascular selectivity by SE EPI fMRI per se, and appears in all sections of the vascular tree where dHb concentration is altered due to neuronal activity changes, including draining veins, possibly as far away as ∼4 mm (Turner, 2002) from the actual site of neuronal activity changes. Fortuitously, while the T₂ of dHb containing venous blood and the T₂ of tissue both decrease with increasing magnetic fields, the former decreases much more rapidly and dramatically (Duong et al., 2003). Consequently, we expected the MR detectability of dHb containing blood to decrease precipitously with increasing magnetic fields while tissue signals remained highly visible. We were able to demonstrate this by examining fMRI signals at 4 and 7 T and using gradient pulses to suppress blood signals (Duong et al., 2003). Intravascular effects related to neuronal activity changes were minimal at 7 T when TE's employed were approximately equal to brain tissue T₂ or longer (Duong et al., 2003). In contrast, 4 T still contained significant blood contribution in the functional maps unless TE far exceeded tissue T₂ (Duong et al., 2003); however, at that point SNR loss is too severe to make this a viable fMRI approach. Consistent with these results, blood contribution to SE fMRI was shown to be a significant contribution at 3 T (∼50% of the functional mapping signals) (Jochimsen et al., 2004), which implies that, combined with the inherently low sensitivity, SE based fMRI at 3 T is relatively useless.

There is, however, an implementation problem with SE fMRI that can become more severe with increasing magnetic fields unless appropriate steps to counter it are taken. Some GRE BOLD characteristics can leak in because of the imaging sequence, particularly single shot imaging sequences preferred in functional imaging studies. In such sequences, there is only a single point in k-space (i.e., a single time point in the acquired data) that meets the full spin-echo condition. All other points in the data have some gradient echo weighting as well. Thus, in the most commonly used EPI approach, the echo train lengths have to be kept short using approaches such as highly parallel imaging along the phase encoding direction or segmentation, and partial Fourier acquisitions. Otherwise, the spatially nonspecific contributions masquerading as activity maps appear even in SE based functional images (e.g., (Goense and Logothetis, 2006)).

We also pursued other approaches to improve the spatial accuracy of functional maps. Following results from optical imaging of intrinsic signals, we had initiated studies at 4 T that exploiting the time course of the evolution of the neurovascular response; these studies focused on obtaining fMRI data during the early and transient response to a stimulus (i.e., during the “initial dip”) (see review (Hu and Yacoub, 2012), and references therein). We also expected this effect to get larger and more robust at 7 T, and experimentally verified this expectation (Yacoub et al., 2001b) and used it even to calculate an estimate of the oxygen consumption increase induced by increased neuronal activity. However, we ultimately abandoned this approach as a means of reaching the resolution of columns and layers in the human brain, not because it lacks spatial fidelity, but because it is a small effect even at 7 T, and simply does not have the sensitivity as a fMRI method to provide high resolution imaging in the human brain. It will be worth visiting it again at higher magnetic fields.

SE fMRI approach is often criticized because functional mapping signal are small; but this is a price one pays for improved spatial accuracy. This is another very important reason why SE fMRI is an ultrahigh field technique. The SE functional mapping signals increase with magnetic field magnitude initially quadratically, but less so above ∼7 T, and leveling off beyond about 10 T (Uludag et al., 2009; Uludag and Ugurbil, 2015). In fact SE fMRI at 7 T has about the same functional signal change as GRE BOLD fMRI at 3 T. But at a given field strength, GRE BOLD is indeed a significantly larger effect.

The achievable spatial resolution and/or the accuracy of imaging measurements are determined by the CNR. In BOLD fMRI, the contrast-to-noise ratio for functional mapping, i.e., fCNR, is a complex issue because “noise” in the fMRI data is not always equal to the thermal noise of the measurement, as previously discussed. However, in the limit of very high-resolution fMRI studies, as employed to detect layer and columnar functional signals, thermal noise dominates tSNR, and fCNR can be written as

$$\mathit{\text{fCNR}}=\mathrm{\Delta }S/N_{\mathit{\text{thermal}}}=(\mathrm{\Delta }S/S)\cdot \beta ({\mathit{\text{SNR}}}_{\mathit{\text{image}}})$$

where ΔS is the stimulus or task induced signal change, and S is the average signal detected in the fMRI time series. Thus, (ΔS/S) is the fractional signal change in response to a task or a stimulus, usually reported as “percent change” in fMRI experiments; it is also the parameter of choice in fMRI modeling calculations. ΔS/S reflects neuronal activity alterations, neurovascular coupling, and the coupling between these physiological entities and the MR signals. SNR_image is the intrinsic image signal-to-noise ratio, and is a constant for a fMRI time series once the acquisition parameters are set (see Appendix 1). β is dependent on the flip angle, TR, and TE but would also be a constant for a given fMRI experiment (see Appendix 1). This formulation of fCNR demonstrates that fCNR is not just ΔS/S, but rather the product of ΔS/S, reflecting brain function and physics of functional mapping, and the intrinsic SNR of the detection, and both are independently dependent on magnetic field used for the fMRI experiment.

Taking into account what is known about the neurovascular coupling induced physiological changes, the fractional signal changes (ΔS/S) expected in the brain in response to alterations in neuronal activity were calculated (Uludag et al., 2009); independently, SNR_image was reported to scale as ${\mathrm{B}}_0^{1.65}$ based on experimental data obtained over 3 to ∼10 T range with multichannel array coils (Pohmann et al., 2016). Using these data, field dependence of fCNR can be calculated from the equation given above for spin-echo based fMRI (Fig. 16). The ΔS/S calculation was performed with two different assumptions of the microvascular CBV change accompanying neuronal activity alterations, 0% and 16%. The magnitude of the capillary CBV changes due to neurovascular coupling is controversial (e.g., (Hillman et al., 2007; Drew et al., 2011; Hall et al., 2014; Hill et al., 2015)); a recent optical imaging study indicates that capillary diameter changes in the cat visual cortex are small (beyond the detection of the microscopy technique employed or nonexistent) (O'Herron et al., 2016). Hence ΔCBV = 0 curve in Fig. 16 may be the more appropriate one to consider for capillaries. The “macrovascular” contribution shown in Fig. 16 is not universally applicable in all regions of the brain. Unlike microvasculature, large vessels are not always present in each MR voxel; when present, they occupy different fraction of the voxel volume due to their differing sizes and have differing orientations relative to the main magnetic field B₀. In this case (Fig. 16), a single large vessel occupying 5% of the voxel volume was simulated, with the vessel oriented 90° to the main magnetic field (the worst case scenario, i.e., the largest BOLD effect); a large vessel running parallel to the static magnetic field would have no contribution. For the macrovascular effect, vessel diameter would not come into play in the BOLD effect perse (see Fig. 15) but the blood volume occupied by the large blood vessel in the voxel would impact the magnitude of this contribution.

Fig. 16.

Functional Contrast-to-Noise Ratio (fCNR) for SE BOLD fMRI, normalized to the value at 1.5 T. Calculated using Eq. (1) with the parameter β set to 1. These plots are valid only in the limit where the noise in the fMRI time series is dominated by thermal noise of the images, which is the case for example, for high resolution imaging at the level of cortical columns and layers. Plots generated by Uludağ, K. using data from Uludag et al. (2009).

Thus, particularly for BOLD fMRI, increasing magnetic fields provide multiplicative gains: They deliver significant improvements in fCNR that can be utilized for higher spatial resolution, better quantification, and/or detection of weaker effects; in addition, they provide better functional mapping accuracy (Shmuel et al., 2007; Chaimow et al., 2017) because of fCNR gains in microvascular mediated mapping signals and suppression of intravascular effects. These multiplicative gains in turn could allow functional mapping at the level of small functional ensembles such as cortical columns and layers, fine scale organizations that had been accessible at the time only through invasive experiments performed in animal models. Achieving this level of functional sensitivity, resolution and mapping fidelity is the reason why we primarily launched the development of 7 Tesla. Very early in the 7 T fMRI studies, we demonstrated for the first time the detection of negative BOLD (as well negative blood flow) changes occurring in cortex adjacent to regions displaying the positive BOLD and blood flow response to visual stimulation, and ascribed this phenomenon to decreases in neuronal activity (Shmuel et al., 2002); our observations and conclusion was later confirmed with electrophysiology (Shmuel et al., 2006). We measured the spatial point-spread function of the BOLD response at 7T using retinotopic stimuli, and showed that it is significantly smaller than those measured at 1.5 T and 3 T (Shmuel et al., 2007); the increased fCNR at 7T made it possible to demonstrate that the initial phase of the response (up to 4s) is more spatially specific than the subsequent phase (Shmuel et al., 2007). Finally, we used the ocular dominance (Yacoub et al., 2007) and orientations columns (Yacoub et al., 2008) as a test bed, achieving robust maps of orientations columns together with ODC's in the same subjects for the first time in the human brain (Yacoub et al., 2008) (Fig. 17). In the orientation maps, the boundaries of the ODC's are shown as dark lines (Fig. 17). The expanded orientation figure shows many features of the orientation maps that have been known from animal model studies, namely the pinwheel centers (white circles) around which the orientation representation runs either clockwise or counter-clockwise, the pinwheel centers appearing predominantly in the center of the ODCs, and the linear zones of a preferred orientation running approximately orthogonal to the ODC boundaries.

Fig. 17.

Functional maps of orientation and ocular dominance columns in the human brain. Obtained at 7 T using SE fMRI. Adopted from Yacoub et al. (2008).

Although the above data were obtained with SE fMRI, some success can be had in such fine scale mapping with GRE fMRI if one simply avoids regions with the large vessels (Cheng et al., 2001). Fig. 18 shows reproducibility of SE and GRE fMRI maps of ODC on the same subject for two different days (Yacoub et al., 2007). They are both highly reproducible, preserving the pattern of one eye versus the other extremely well except in the transition zones where reproducibility is expected to be poor due to partial volume effects. However, these maps also show that while in the GRE images there are regions where the ODC pattern is observed, in other areas (identified by the dashed white line) the ODC pattern is not present, presumably due to the large vessel confound.

Fig. 18.

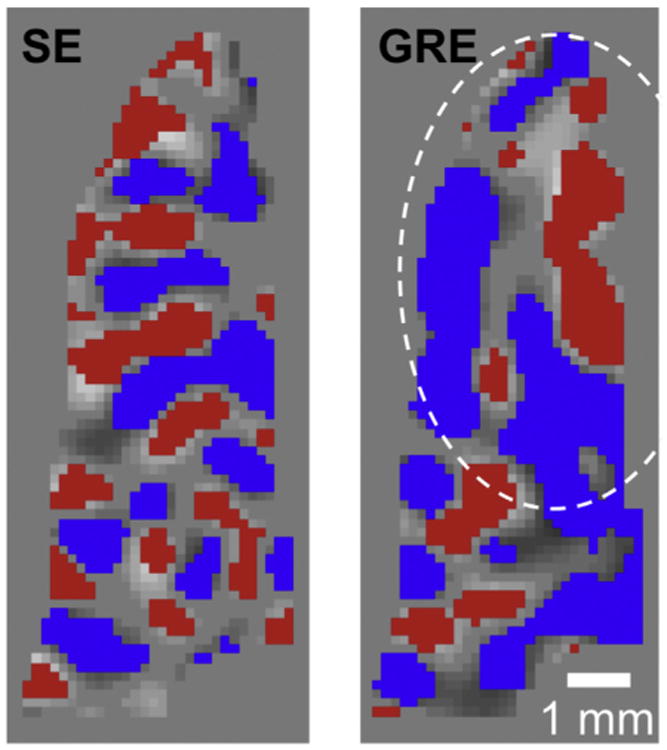
Ocular dominance column functional images obtained either by Spin Echo (SE) or Gradient Echo (GRE) fMRI on two separate occasions on the same individual. Each voxel is labeled with either blue or red color if it is reproducibly assigned to same eye on the two different occasions. Thus the maps shown depict the patterns induced by stimulation of one eye versus the other, as well as their reproducibility in a single subject on the two different occasions. Adapted from Yacoub et al. (2007).

An alternative strategy pursued for high specificity functional mapping with GRE fMRI at 7 T has been to exploit the high resolution nature of the images and strip away some fraction of the outer cortical layers and restrict the analysis to the deeper layers; this eliminates the regions where BOLD effect associated with pial veins reside (Polimeni et al., 2010). This approach was used to map color- and disparity-selective columns within human visual system (Nasr et al., 2016). Note that one cannot just strip off the anatomical space occupied by the blood vessel itself because the extravascular BOLD effect penetrates into the space surrounding the blood vessel. Therefore, one must strip away some of the superficial cortical layers for this analysis. This is also a vascular filter, but imposed based on spatial location of vessels. This approach, of course, also reduces the magnitude of the detected functional mapping signals, but gains in spatial fidelity, just like SE fMRI.

Fig. 19 displays a composite figure that summarizes accomplishments with 7 T in high resolution functional mapping we at CMRR have undertaken in collaboration with colleagues from Maastricht University since 7 T became operational in CMRR. It also illustrates the evolution of ultrahigh field fMRI, and what is now feasible with this technology. As previously mentioned, 7 T showed the first mirror symmetric tonotopic maps in the human primary auditory cortex, and demonstrated extremely high reproducibility of the functional maps as well (Formisano et al., 2003). The functional organization of human auditory subcortical structures were only inferred from animal models until organization of spectral responses were mapped for the first time in the human inferior colliculus (IC), a small ∼7×7×7 mm³ subcortical structure fundamental for sound processing, revealing a tonotopic map and a spatial organization of spectral selectivity (tuning) (De Martino et al., 2013a). In 2015, 7 T was used again to map tonotopy in the Medial Geniculate Body (MGB), a smaller subcortical structure than the IC, with dimensions of ∼4×5×4.5 mm³, showing that two tonotopic maps characterized the MGB, reflecting the two MGB subdivisions (Moerel et al., 2015). More recently, going back to the auditory cortex, high-resolution fMRI experiments at 7 T provided evidence for the columnar organization of the processing of sound frequency and showed that frequency preference is stable through cortical depth in primary auditory cortex (De Martino et al., 2015). Furthermore, in this highly columnar cortex, the high-resolution fMRI data with laminar resolution revealed that task demands sharpen the frequency tuning in superficial cortical layers more than in middle or deep layers (De Martino et al., 2015).

Fig. 19.

Functional mapping frequency selectivity in the auditory pathway at 7 T. Adapted from Formisano et al. (2003), De Martino et al., 2013a,b, Moerell et al., 2015, and De Martino et al., 2015.

The afore-listed auditory studies were conducted using tones as well as natural sounds, the later using encoding methods similar to the approach introduced for the study of the visual cortex (Kay et al., 2008; Naselaris et al., 2011). Some of these studies used both 3 T and 7 T data and different models for the processing of sounds in the human brain. For each model, however, 7 T data outperformed the 3 T data significantly (Santoro et al., 2014). The cause of this is likely not only the increased SNR and fCNR at the higher field strength but also the fact that at these high fields there is higher granularity to the information content detected in fMRI; in other words, distinctly different functional information content that is organized at a much finer spatial scale can be detected and distinguished in adjacent voxels. At lower fields, when the capillary contributions are weak and the fMRI data are dominated by effects originating from large blood vessels, many adjacent voxels are expected to be highly correlated no matter how high the intrinsic resolution of the image is. At 7 T and beyond, however, increasingly each voxel begins to display independent information even at very high resolution. Ultimately, the purpose of such high resolution and high fidelity mapping is that when such granularity of computation exists in the brain, we need to incorporate it in any model of how the brain processes this information. In this respect, the ultrahigh field studies hold major advantages and the auditory cortex work referenced above and similar work conducted on the visual system at 7 T (Naselaris et al., 2015) provide examples of significant improvements.

6. The human brain connectome and ultrahigh fields

In the Human Connectome Project, we proposed the use of both 3 T and 7 T for connectivity mapping. In many ways, the 7 T component represented a major challenge because HCP aimed at high resolution whole brain studies. The challenges that stood in front of this goal, such as B₁ and B₀ inhomogeneities, SAR limitations etc., have already been discussed. Nevertheless, these challenges were largely overcome at the end, though not all of the solutions made it into the 7 T HCP data collection.

6.1. Resting state networks

Resting state functional magnetic resonance imaging (rfMRI) uses correlations in the spontaneous temporal fluctuations in a fMRI time series to deduce ‘functional connectivity’; it serves as an indirect but nonetheless invaluable indicator of gray-matter regions that interact strongly and, in many cases, are connected anatomically (e.g., see (Smith et al., 2013) and references therein).

Prior to the HCP, rfMRI studies conducted at 3 T typically used voxel volumes of approximately 27 mm³ (i.e., 3 mm isotropic voxels) to achieve sufficient minimum SNR and fCNR. Furthermore, typically, these studies employed spatial smoothing with large Gaussian kernels (∼4–6 mm FWHM (full width at half maximum)) to reduce noise, and often also resort to group averaging, which further amplifies spatial blurring and constrain the spatial accuracy of the resulting rfMRI maps. The exception to the very large voxel sizes typically employed at 3 T are the recent data generated within the HCP (Van Essen et al., 2013) where the voxel size for the rfMRI data is 2 mm isotropic (Smith et al., 2013; Ugurbil et al., 2013). This was feasible because of the use of slice accelerated MB/SMS technique resulting in subsecond (0.7 s) whole brain coverage (Smith et al., 2013; Ugurbil et al., 2013) as well as the extensive averaging achieved through one hour of data acquisition.

Given the ultrahigh field advantages in detecting functional mapping signals, it is easy to anticipate significant gains in rfMRI at 7 T even over and above what was achieved for 3 T HCP data. A high resolution examination of resting state networks (RSNs) conducted at 7 T (De Martino et al., 2011) demonstrated the detection of spontaneous fluctuations within functionally connected networks in single subjects without the need for spatial smoothing, at nominal voxel volumes as small as 1 mm³ (isotropic voxel dimension), significantly smaller than the voxel sizes employed at 3 T. In the HCP, slice-accelerated MB/SMS sequences were employed for the first time for rfMRI, collecting rfMRI both at 7 T and at 3 T on the same 180 individuals. These carefully controlled data showed significantly improved CNR in detecting resting state spontaneous fluctuations and yielded larger number of ICA components at 7 T even though the higher resolution 7 T data had factor 2 smaller voxel volumes compared to 3 T (Vu et al., 2017).

6.2. Diffusion weighted MRI (dMRI) for tractography

A critically important goal for the dMRI component of the HCP is to characterize the anatomical white matter connectivity patterns throughout the entire brain with as much spatial precision and accuracy as possible (Van Essen et al., 2013). Paramount to this goal is achieving higher SNR through shorter echo times for diffusion encoding, and accelerating the data acquisition rate without significantly impacting SNR. Higher field strengths provide higher intrinsic SNR for dMRI but fully realizing this potential for whole brain dMRI is challenging due to shorter transverse relaxation times because of which SNR is lost more rapidly during diffusion encoding at higher magnetic fields. This challenge adds to the major challenges of increased B₀ and ${\mathrm{B}}_1^{+}$ inhomogeneity, and SAR faced at the higher field.

High resolution dMRI studies at 7 T prior to the HCP utilized partial-brain coverage (Heidemann et al., 2012a, 2012b; Eichner et al., 2014a; Eichner et al., 2014b; Strotmann et al., 2014) combining in-plane parallel imaging methods with outer-volume suppression (OVS) in order to shorten the EPI echo train length and thus minimize T₂* decay/blurring and distortion artifacts caused by B₀ inhomogeneity. The combination of these two techniques suppresses g-factor based SNR penalties compared to using in-plane parallel imaging alone for the same FOV reduction. However, SNR is also lost with OVS through the magnetization transfer (MT) effect, which has been shown to diminish gray/white matter signal by ∼20–50% at 7 T (Pfeuffer et al., 2002c). Furthermore, the addition of the OVS pulses increases both acquisition time (3 s per TR (Heidemann et al., 2012a)) and SAR, while providing only smaller brain coverage. This latter point is particularly problematic since connectomics information is ideally desired over the entire brain. In these earlier 7 T diffusion studies also, the b-values employed were restricted to 1 K s/ mm². This of course reduces TE, thus significantly lessening SNR loss during diffusion encoding; it also significantly reduces the loss in SNR imposed by diffusion encoding itself compared to images acquired with higher b-values. Thus, such a low b-value raises SNR. However, higher b-values as well as the use of multiple b-values are critical for resolving three-way fiber crossing (see Fig. 3 in Sotiropoulos et al. (2013)).

We undertook two years of intensive efforts to optimize many aspects of 7 T dMRI acquisition for the HCP, which allowed us finally to obtain high resolution (1 mm isotropic), whole brain dMRI data, using higher b-values (1 and 2 K s/mm²) than previously employed at 7 T. The 7 T HCP dMRI data contained fewer q-space samples (128 directions + 15 b = 0 vs. 270 + 18 b = 0 at 3 T), in part because it was acquired for 40 min as opposed 60 min and in part because we could not accelerate as much as in the 3 T HCP dMRI data due to SAR constraints (slice acceleration was 2 (i.e., MB = 2) at 7 T as opposed to 3 in the 3 T HCP data). 7 T dMRI data also lacked the third b = 3 K s/mm² shell of the 3 T HCP acquisition. Despite these shortcomings, 7 T HCP data compared favorably with the 3 T HCP data (obtained on the same subjects), in fact beating the 3 T data in some aspects (Vu et al., 2015; Sotiropoulos et al., 2016), in particular for the gyral bias problem (Sotiropoulos et al., 2016) (Fig. 20).

Fig. 20.

Angle between surface tangent and fiber orientations at the inflated WM/GM boundary surface for the same subject scanned at 3 and 7 T with the respective HCP protocols. For every surface vertex, the maximum dot product between fiber orientations (with volume fraction f > 5%) at this location and the surface normal is computed. This is then converted to the color-code angle shown on the inflated surface. Blue perpendicular, red parallel. From Sotiropoulos et al. (2013).

These 7 T HCP results are indicative of what 7 T can achieve in dMRI, and represent only a prelude in 7 T based tractography. Current 7 T HCP dMRI data and virtually all other 7 T dMRI data use gradients with 70 mT/m maximal gradient strength. The HCP 3 T data employs 100 mT/ m gradients. There is no reason why 100 mT/m gradients or even higher maximal strength gradients cannot be used at 7 T. This would improve SNR substantially. Significant improvements in slice acceleration as well as SNR per unit time will be possible by incorporating multichannel transmit methods to manage SAR limitations (allowing higher acceleration) and increase transmit B₁ uniformity (achieving SNR uniformity over the head) (Wu et al., 2017). These gains will enable higher spatial resolutions and higher b-values. Finally, combined with these, higher number of receive channels that are coming finally to 7 T (Auerbach et al., 2017) will permit the higher accelerations needed for higher resolution imaging.

With the above referenced gains in rfMRI demonstrated, 7 T is now the best Human Connectome Scanner for functional connectivity derived from resting state data! With some of the additional developments possible in dMRI, 7 T or even higher fields can and will become the best overall Human Connectome Scanner!

7. Conclusion

Starting with early spectroscopy studies, but gaining momentum after the introduction of fMRI, a systematic push was initiated for exploiting higher magnetic fields, motivated predominantly, though not exclusively to improve the accuracy and sensitivity of fMRI maps. Steady improvements in high field instrumentation and ever expanding armamentarium of image acquisition and engineering solutions to challenges posed by ultrahigh fields has brought fMRI to submillimeter resolution in the whole brain at 7 T, the scale necessary to reach cortical columns and laminar differentiation. Although not covered in this article, 7 T has also emerged as a platform that provides exquisite anatomical detail in many organ systems of the human body and is rapidly evolving at the present in biomedical research and clinical diagnosis based on this capability. Especially with the introduction of commercial instruments with increasing sophistication, these advances are sure to continue unabated for years to come as the incessant creativity of the MR community produces new capabilities and overcome impediments, impacting not only functional imaging but clinical applications in the entire body. The solutions that emerged in response to the significant technological challenges posed by 7 T have also propagated and continue to propagate to lower field clinical systems, a major advantage of the ultrahigh field effort that is underappreciated. Similarly, many of these solutions will also enable imaging at magnetic fields much higher than 7 T. Further improvements at 7 T are inevitable and are ongoing currently in numerous laboratories. Further translation of these improvements to lower field clinical systems to achieve new capabilities and to magnetic fields significantly higher than 7 T to enable human imaging with increasing biological importance is inescapable.

Appendix 1

$$\mathit{\text{fCNR}}=\mathrm{\Delta }S/N_{\mathit{\text{thermal}}}=(\mathrm{\Delta }S/S)\cdot (S/N_{\mathit{\text{thermal}}})$$ (1)

$$\mathit{\text{fCNR}}=(\mathrm{\Delta }S/S)\cdot ((S_{ss}sin\theta )e^{-\mathit{\text{TE}}/T_2^X})/N_{\mathit{\text{thermal}}}$$ (2)

where S is the temporal average of the signal detected (after taking out slow drifts that occur in these signals (i.e., detrending)) in the absence of the task or stimulus induced signal changes that are captured in the term ΔS. Note that ΔS≪S, and both are dependent on the echo time TE (Menon et al., 1993). N_thermal is thermal noise. For people used to thinking in terms of tSNR in a fMRI time series, Eq. (1) can be arrived at from the expression fCNR = (ΔS/S) (tSNR) for conditions where the noise in tSNR (i.e., standard deviation of signal fluctuations) is dominated by thermal noise. Eq. (2) follows from the fact that during the fMRI time series, the longitudinal magnetization reaches a steady state magnitude (S_ss) which is less than or equal to the thermal equilibrium magnetization S₀. The exponentially decaying term in Eq. (2) comes from the echo time TE that is used to impose functional contrast, during which the signal will be decaying with time constant $T_2^x$, representing $T_2^{\ast }$ or T₂ for gradient or spin echo BOLD fMRI experiments, respectively. The signal detected at TE = 0, immediately after excitation with flip angle θ is equal to (S_ss sin θ). The ratio S_ss/S₀ is determined by the repetition time TR and the excitation flip angle θ and remains virtually constant during the fMRI experiment – there may be small fluctuations coming from, for example, blood flow and/or blood volume changes induced by spntaneous neuronal activity. The former can present itself through inflow effects (if the pulse sequence used permits it), and the latter by altering the voxel composition of blood versus tissue water pools which can have different relaxation properties etc., all of which are small and are being ignored for this relatively simple derivation. Thus, one can recast Eq. (2) as

$$\mathit{\text{fCNR}}=(\mathrm{\Delta }S/S)\cdot ((\sigma S_{0}sin\theta )e^{-\mathit{\text{TE}}/T_2^X})/N_{\mathit{\text{thermal}}}$$ (3)

where σ is a parameter that depends on TR and flip angle θ, and is a constant for a given fMRI time series. Finally, S₀/N_thermal is by definition the intrinsic SNR of the image, i.e. SNR_image. Thus we can define a new parameter β as $(\sigma sin\theta )e^{-\mathit{\text{TE}}/T_2^X}$ which is dependent on the flip angle, TR, and TE but would be a constant for a given fMRI experiment where these parameters are chosen and set before data acquisition begins, arriving at

$$\mathit{\text{fCNR}}=\mathrm{\Delta }S/N_{\mathit{\text{thermal}}}=(\mathrm{\Delta }S/S)\cdot {\beta \mathit{\text{SNR}}}_{\mathit{\text{image}}}$$ (4)

The parameter σ can be easily derived when no coherences are left on the transverse plane (e.g., as in a fMRI study) and is given by

$$\sigma =(1-e^{-\mathit{\text{TR}}/T_1})/(1-(cos\theta )e^{-\mathit{\text{TR}}/T_1})$$ (5)

For a GRE fMRI experiment, β would be typically set at the Ernst angle (θ_ernstangle = cos⁻¹ [e^−TR/T₁]). However, achieving a uniform Ernst angle or a 90° condition is difficult to satisfy for all voxels in the human brain, as discussed, due to B₁ inhomogeneities, unless pTx or adiabatic pulses are employed. Eq. (5) is also applicable for a spin-echo acquisition but only when θ = 90°, which is the typically used flip angle for such an experiment.