Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Dec 8;9(1):25–30. doi: 10.1021/acs.jpclett.7b02767

Unraveling the Electronic Structure of Narrow Atomically Precise Chiral Graphene Nanoribbons

Néstor Merino-Díez †,‡, Jingcheng Li ‡,§, Aran Garcia-Lekue †,∥, Guillaume Vasseur †,§, Manuel Vilas-Varela ⊥, Eduard Carbonell-Sanromà ‡, Martina Corso ‡,§, J Enrique Ortega †,§,#, Diego Peña ⊥, Jose I Pascual ‡,∥, Dimas G de Oteyza †,‡,§,∥,*
PMCID: PMC5759029  PMID: 29220194

Abstract

graphic file with name jz-2017-027672_0005.jpg

Recent advances in graphene-nanoribbon-based research have demonstrated the controlled synthesis of chiral graphene nanoribbons (chGNRs) with atomic precision using strategies of on-surface chemistry. However, their electronic characterization, including typical figures of merit like band gap or frontier band’s effective mass, has not yet been reported. We provide a detailed characterization of (3,1)-chGNRs on Au(111). The structure and epitaxy, as well as the electronic band structure of the ribbons, are analyzed by means of scanning tunneling microscopy and spectroscopy, angle-resolved photoemission, and density functional theory.

The growth and characterization of new atomically precise graphene nanoribbon (GNR) structures is a challenging quest. The research efforts toward that goal are continuously increasing, driven by the promising prospects of GNR-based technologies.1,2 As a result, a relatively large variety of armchair graphene nanoribbons (aGNRs) has already been synthesized on different coinage metal surfaces.3−7 Their subsequent characterization has proved the predicted band-gap dependence on the ribbon width to be true.8−10 Also, zigzag GNRs (zGNRs) have been successfully synthesized from adequate molecular precursors,11 further proving the presence of the highly coveted edge states associated with zigzag edges.11−13 However, graphene nanoribbons with chiral edge orientations, that is, with periodically alternating armchair and zigzag segments, have been hardly characterized to date.14,15 The first report on the synthesis of an atomically precise chiral GNR (chGNR) came from a surprising result in which a precursor designed to render aGNRs resulted in chGNRs when deposited on a Cu(111) surface.16 This unexpected reaction path arises from a very specific molecule–substrate interaction and was studied in detail later on.17,18 However, although some spectroscopic measurements were performed on such Cu(111)-supported ribbons,19 important figures of merit like the band-gap value or the frontier bands’ effective masses remain unknown.

Recently we reported the design of an alternative precursor molecule (2,2′-dibromo-9,9′-bianthracene) that resulted in the formation of (3,1)-chGNRs independently of the substrate used, at least on the explored Au(111), Ag(111), and Cu(111) surfaces.20 Thus, in addition to the advantages in the growth process that lead to longer chGNRs at reduced processing temperatures, it places at our disposal chGNRs on a weaker interacting surface like Au(111). On such a surface, hybridization effects with the substrate are weaker and the ribbon’s properties are easier to probe. In this work we have made use of this advantage, studying the structural and electronic properties of (3,1)-chGNRs on Au(111) and Au(322) by scanning tunneling microscopy and spectroscopy (STM and STS), angle-resolved photoemission spectroscopy (ARPES), and density functional theory (DFT).

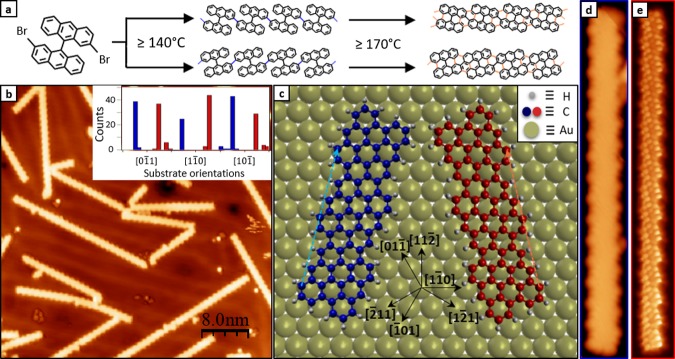
The precursor molecule and the two-step reaction path toward the final chGNR are displayed in Figure 1a.20 In a first step, Ullmann coupling of the surface-supported precursors sets in at temperatures above 140 °C, leading to nonplanar polymeric structures due to the steric hindrance exerted mainly by hydrogen atoms placed within the anthracene units. In a second step, cyclodehydrogenation of the polymeric structures ends up in planar chGNRs (Figure 1d,e), formed entirely by sp2 carbon atoms, saturated with single H atoms along the edges. As previously reported,20 the strained structure of the polymer lowers the cyclodehydrogenation threshold temperature below 200 °C, allowing us to obtain these ribbons at temperatures much lower than most other GNRs published to date.3,4,7,11

Figure 1.

Figure 1

Open in a new tab

Synthesis, structure, and epitaxy of (3,1)-chGNRs on Au (111). (a) Schematic reaction path for the synthesis of (3,1)-chGNRs with threshold temperatures indicated for each synthetic step. (b) Constant current STM image (45 nm × 45 nm; Vs = −0.15 V; It = 0.05 nA) of a representative (3,1)-chGNRs sample on Au(111) after annealing to 350 °C, with the histogram on the azimuthal orientation distribution with respect to the high-symmetry substrate directions (inset) obtained from the analysis of 245 different nanoribbons. (c) Epitaxial relation exemplified with three-monomer-long (3,1)-chGNRs enantiomers on Au(111), where blue/orange dashed arrows depict the commensuration every two unit cells. The translational adsorption site in the model is arbitrary because the particular adsorption position could not be unambiguously extracted from the experimental images. (d) Constant current STM (15.4 nm × 2.5 nm; Vs = −1.1 V; It = 0.11 nA) and (e) constant height STM image (15.4 nm × 2.5 nm; Vs = 2 mV) obtained with a CO-functionalized tip. Red/blue colors are employed to specify the information associated with each enantiomer in panels b (inlet), c, d, and e.

Characterization of the GNR structure and distribution has been performed by STM. Low-temperature STM (LT-STM) using CO-functionalized tips allows achieving high intramolecular resolution when scanning at short tip–sample distances within the Pauli repulsion regime.21−24 As displayed in Figure 1e, we have made use of this effect to resolve the nanoribbon’s internal bonding structure. From larger scale images, it becomes evident that the ribbons display six well-defined preferential orientations (Figure 1b), each with the ribbon’s axis deviated ∼16° from the [10-1] (and equivalent) substrate directions. The distribution of chGNR orientations is plotted in the inset of Figure 1b, including high-symmetry substrate directions on the x-axis as a reference. Given the chiral nature of the ribbons, the six orientations correspond to three substrate-related azimuthally equivalent directions for each of the two enantiomeric structures (marked by blue and red in Figure 1, respectively). The associated epitaxial model extracted from high-resolution images is displayed in Figure 1c, showing commensuration at every second unit cell of the chiral ribbons.

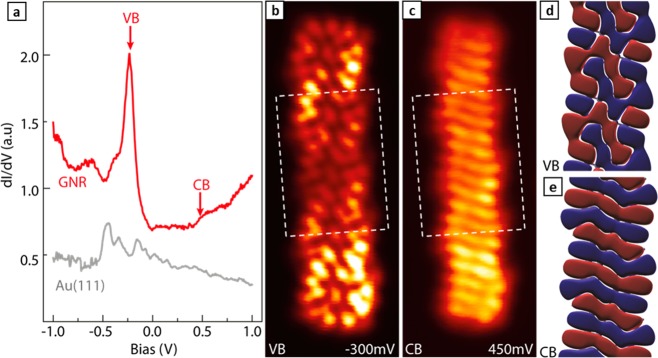
The electronic properties of the ribbons have been first characterized by STS. Figure 2a displays a conductance point spectrum on a ribbon, together with a reference spectrum on the surrounding substrate. Because tunneling conductance is proportional to the local density of states (LDOS) at the probe position, one can clearly distinguish the onset of the ribbon’s valence band (VB) and conduction band (CB). From a statistical analysis of several tens of ribbons, we find the bands’ onsets at −0.22 ± 0.05 V and 0.45 ± 0.02 V, respectively. The resulting band gap of 0.67 ± 0.06 eV is larger than that obtained from DFT calculations (Figure S1; note that the underestimation of band gaps is a well known limitation of DFT). However, the constant-height conductance maps at the onset energies (Figure 2b,c) show excellent agreement with the calculated wave functions (Figure 2d,e) of the frontier states of valence and conduction band at the gamma point (despite being measured with a CO-functionalized tip25), providing further confirmation on the nature of those experimentally measured states. This is also confirmed by constant-current conductance maps with a nonfunctionalized metallic tip (Figure S2), where clear GNR-related density of states appears as the energy reaches either band onset, evidencing similar patterns as those in Figure 2. Those patterns are clearly different for VB and CB, the latter appearing with a characteristic wavefront structure, while the former displays a more complex sequence of lobes (Figure 2).

Figure 2.

Figure 2

Open in a new tab

Spectroscopic characterization of frontier molecular orbitals of (3,1)-chGNRs on Au(111). (a) Representative dI/dV point spectra obtained from (3,1)-chGNRs on Au(111) (in red) with Au(111) signal (in gray) included as background reference (open-feedback parameters: Vs = 1.0 V, It = 0.5 nA, modulation voltage Vrms = 0.1 mV). (b,c) STM constant-height conductance maps (2.0 nm × 5.2 nm; open-feedback parameters: Vs= 0.2 V; It = 0.06 nA; Vrms= 1 mV) near the (b) valence (−300 mV) and (c) conduction (450 mV) band onsets. (d,e) DFT simulations of the wave function for states at the onset of (d) valence and (e) conduction bands (at the Γ point) on an area equivalent to the dashed rectangle in panels b and c, respectively. Red and blue colors represent isosurfaces of positive and negative wave function amplitudes for an isovalue of 0.015 Å–3/2.

Both conduction and valence bands display a dispersive behavior as they deviate from Γ (Figure S1). A fingerprint of it is found in conductance maps over a wider energy range of the VB, revealing an additional energy-dependent LDOS modulation along the ribbon axis (Figure 3a–f). To quantify this effect, we measured equidistant point spectra along the edge of a GNR (Figure 3g), displayed in Figure 3h as a function of its position along the ribbon with a color-coded conductance intensity (z-axis). In addition to the edge periodicity arising from the chGNR structure, another energy-dependent modulation appears. It coincides with that observed in the conductance maps, in which the number of nodes increases as the energy departs from the band onset. It relates to the formation of standing waves from electronic states scattered at the nanoribbon edges, thus holding the band’s dispersion relation information. This can be distinguished best in Figure 3i, which depicts a line-by-line Fourier transform (FT) of Figure 3h and thus the dispersion of the probed bands.

Figure 3.

Figure 3

Open in a new tab

STM constant-height conductance maps (10.3 nm × 2.0 nm; It = 0.03 nA; modulation voltage Vrms = 12 mV) (a) within the band gap at −50 mV, (b) near the valence band onset at −150 mV, (c) at −250 mV, (d) at −350 mV, (e) at −550 mV, and (f) at −650 mV, exhibiting confined standing waves along the ribbon. (g) Constant current STM image of the same ribbon, showing the path (red dashed line) followed by the equidistant dI/dV spectra. (h) Color-coded conductance signal obtained from equidistant dI/dV point spectra (open-feedback parameters: Vs = 1.50 V; It = 0.8 nA; Vrms= 12 mV) on the ribbon and along the red dashed line displayed in panel g. (i) Line-by-line Fourier transform from the stacked spectra in panel h, showing the two-parameter parabolic fit (gray dashed line) used for extracting the effective mass. The additional parabola centered around the Brillouin zone edge is displayed with a green dashed line. Gray horizontal lines corresponding to the voltage biases of maps in panels a–f are superimposed in panels h and i as a guide to the eye.

The VB is observed dispersing down with an effective mass of −0.34 ± 0.05 m0, as obtained from a parabolic fit to the topmost region of the band. In contrast, no dispersion information has been obtained for the CB from the FT-STS analysis. Indeed, the CB is much harder to detect in STS measurements, as can already be guessed from the marked asymmetry in the signal strength of the STS spectrum in Figure 2a for VB and CB. As explained in detail in previous works,7,26 the faster a wave function changes its sign along the ribbon axis, the lesser it extends into the vacuum along the GNR normal. This makes it less accessible to STM/STS measurements, where tip–sample distances remain typically above 5 Å. Our wave function calculations of (3,1)-chGNRs in Figure 2d,e reveal the CB to change sign along the ribbon axis faster than the VB, thus agreeing with its poorer detection in our spectral measurements.

Interestingly, additional features in the FT-spectral map of the VB are observed, not present in previous works performing a similar analysis on aGNRs.7,26 A replica of the dispersive band appears shifted by 3.5 nm–1 (displayed with a green dashed line in Figure 3i), namely, centered at the Brillouin zone edge, which is defined by the GNR periodicity arising from its chiral edges (periodicity a = 8.97 Å = π/(3.5 nm–1)). This band replica and the increased intensity line at the zone edge can be traced back to the additional modulation from the GNR chirality. The imposed periodicity stresses the Bloch wave function character of the electronic states, whose coherent addition resulting from scattering events has been previously shown to lead to exactly those two types of features in FT-STS.27 The periodicity of these features in reciprocal space can be additionally observed in the line-by-line FT spectra plotted over a wider energy and momentum range displayed in Figure S3.

To compare the VB dispersion properties obtained from FT-STS with results from a more standard approach, we have characterized the (3,1)-chGNRs also by angle-resolved photoemission spectroscopy (ARPES). Similar comparisons have been performed previously on the VB dispersion of 7-aGNRs and 9-aGNRs. In the former, the effective mass extracted from FT-STS and ARPES differed by a factor 2,26,28 whereas in the latter both techniques were in agreement within error bars.7 Because ARPES is an ensemble-averaging technique, having uniaxially aligned GNRs is a requirement to measure the dispersion along a well-defined direction. The aligned growth of aGNRs has been successfully achieved by using a Au(788) surface as template,28,29 which features ∼4 nm wide (111) terraces periodically separated by steps running along the compact [10-1] direction. However, because the chiral GNRs studied here display a markedly preferred growth orientation at 16° off from the compact [10-1] (and equivalent) direction (see Figure 1), the Au(788) terraces do not satisfactorily guide an uniaxial growth of the ribbons. Instead, the growth results in low-quality samples with short ribbons oriented partially along the step edges but also along their epitaxially favored directions (Figure S4). The scenario changes when using narrower terraces. The ∼1.2 nm wide terraces of Au(322) are wide enough to host a (3,1)-chGNR but narrow enough to largely inhibit molecular coupling along any other orientation than following the terraces. As a result, uniaxially aligned ribbons could be grown on Au(322), as shown in Figure 4a,b.

Figure 4.

Figure 4

Open in a new tab

(a) Large-scale constant current STM topography image (50 nm × 50 nm; Vs = −0.2 V; It = 0.02 nA) and (b) zoom in (10 nm × 10 nm) for an easier appreciation of details of (3,1)-chGNRs on Au(322). (c) Second derivative of the photoemission intensity reflecting the valence band dispersion (raw photoemission intensity data are displayed in the Supporting Information). Dotted lines mark the center of first, second, and third Brillouin zones.

The subsequent ARPES characterization is displayed in Figure 4c (associated raw data are shown in Figure S5). Whereas no GNR signal is observed in the first Brillouin zone and only a weak shadow in the second, the VB is nicely resolved in the third Brillouin zone. From a parabolic fit to the topmost VB region we extract values of −0.50 ± 0.02 eV and −0.36 ± 0.04 mo for the band’s onset energy and effective mass, respectively. Compared with the results from FT-STS, the effective mass shows agreement within error margins (−0.36 ± 0.04 m0 from ARPES vs −0.34 ± 0.05 m0 from FT-STS), but the band onset is notably lower in energy (i.e., −0.5 ± 0.02 eV from ARPES vs −0.22 ± 0.05 mV from STS). This, however, can be easily explained by the different nature of the probed samples. The large step density of Au(322) lowers its work function with respect to that of Au(111). As extracted from measurements of the cut-off energy of photoemitted electrons from either surface (Figure S6), the work function changes by 0.25 eV, fitting well with the measured difference in VB onsets (∼0.28 eV). A vacuum-level change rigidly shifting down the adsorbate’s band structure in a simple vacuum-level pinning scenario readily explains the offset and provides a fully coherent scenario for the comparison of STS and ARPES data.

At this point it is interesting to compare the electronic properties of (3,1)-chGNRs and of 7-aGNRs. Both ribbons have comparable widths and result from precursors sharing the same carbon backbone, although polymerizing along different directions. However, the change in edge orientation from armchair to a chiral (3,1) direction brings about dramatic changes in the electronic properties. By way of example, the band gap is reduced from 2.37 ± 0.06 eV in the former26 to 0.67 ± 0.06 eV in the latter, although without evident signatures of the spin-polarized edge states predicted to appear around the Fermi level in chiral ribbons.30−33 This is presumably due to a too small GNR width and the associated band-gap opening.30−32 According to calculations, a closing of the band gap and the appearance of edge states are predicted to occur either increasing the GNR width or also maintaining a similar GNR width but with chiralities closer to the zigzag direction (as well as for pure zGNRs).30−32 However, an experimental confirmation of such behavior is still missing.

In the intuitive picture of GNR bands being directly related to the dispersion properties of the parent material graphene (as happens with aGNRs),12 the effective mass is expected to correlate with the band gap.34 Indeed, experimental data revealed that a band-gap drop from 2.4 to 1.4 eV going from 7-aGNRs to 9-aGNRs brings about a substantial effective mass reduction from 0.21 m0 (obtained from ARPES)28 or 0.41 ± 0.08 m0 (obtained from FT-STS)26 to ∼0.1 m0 (obtained from FT-STS and ARPES alike).7 However, that scenario gets much more complicated as GNRs with different edge orientations are compared, whereby the GNR bands are no longer trivially related to those of graphene.12 As a result, our DFT calculations predict only a minor decrease in the effective mass going from 7-aGNRs (0.33 m0(35)) to (3,1)-chGNRs (0.27 m0) despite the greatly diminished band gap from 2.37 to 0.67 eV. Experimentally the effective mass changes from 0.21 m0 (ARPES)28 or 0.41 ± 0.08 m0 (FT-STS)26 in 7-aGNRs to ∼0.35 m0 (FT-STS and ARPES) in (3,1)-chGNRs, confirming the dramatically different behavior of GNRs with different edge orientations.

In conclusion, we have provided a thorough characterization of the structural and electronic properties of (3,1)-chGNRs on Au(111). A strong favoritism for commensurate adsorption directions is observed that can, however, be overcome with the use of adequately stepped surfaces that prevent the ribbon growth along any other direction than following the terraces. Such samples have been used to characterize the band dispersion by ARPES and to compare the results with those obtained from Fourier transform scanning tunneling spectroscopy measurements. We end up with a fully coherent picture of the GNR’s band gap (0.67 ± 0.06 eV), effective mass (∼0.35 m0), and energy level alignment (shifting with the substrate work function as in an ideal vacuum level pinning scenario) that will enable a better understanding of their performance in future electronic devices and allow a rational design of heterostructures with complementary GNRs.

Methods

For the preparation of the different samples, 2,2′-dibromo-9,9′-bianthracene molecular precursor was sublimated at ∼425 K from a Knudsen cell and oriented to metallic substrates for deposition. Atomically cleaned Au(111) and Au(322) surfaces were achieved by standard sputtering and annealing cycles. Measurements on Au(111) were performed on a home-built, low-temperature STM under ultrahigh vacuum (UHV) at pressures below 10–10 mbar and a base temperature of 4.8 K. Measurements on Au(322) were performed in a UHV system combining a commercial Omicron VT-STM connected to a home-built ARPES system equipped with a closed-circuit He-compressor-cooled manipulator, a monochromatized gas discharge lamp, and a SPECS Phoibos 150 electron analyzer. STM and ARPES measurements could thus be performed sequentially on the same sample without breaking the UHV conditions. ARPES measurements were performed at a sample temperature of 90 K using the He I line (21.2 eV). All STM images were processed by WSxM software.36

The structural and electronic properties of free-standing (3,1)-chGNRs were calculated using density functional theory (DFT), as implemented in the SIESTA code.37 We considered a supercell consisting of a (3,1)-chGNR infinite along the x axis, with vacuum gaps of ∼15 Å in y and z directions to avoid interactions between ribbons in adjacent cells. A Monkhorst–Pack k-point grid with 101 × 1 × 1 k-points was used for the Brillouin zone sampling, and the mesh cutoff for real-space integrations was set to 300 Ry. A basis set consisting of split-valence double-ζ plus polarization DZP orbitals was employed, and a variable-cell relaxation of the periodic system was performed until residual forces on all atoms were <0.01 eV/Å. Dispersion interactions were taken into account by the nonlocal optB88-vdW functional.38

Acknowledgments

The project leading to this publication has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement no. 635919), from the Spanish Ministry of Economy, Industry and Competitiveness (MINECO, grant nos. MAT2016-78293-C6, FIS2015-62538-ERC), from the Basque Government (grant nos. IT-621-13, PI-2015-1-42, PI-2016-1-0027), from the European Commission in FP7 FET-ICT “Planar Atomic and Molecular Scale Devices” (PAMS) project (contract no. 610446), from the Xunta de Galicia (Centro singular de investigación de Galicia accreditation 2016–2019, ED431G/09), and from the European Regional Development Fund (ERDF).

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jpclett.7b02767.

  • Constant current conductance maps evidencing the absence of signal at energies within the gap and the clear GNR-related signal at the VB and CB onsets. DFT calculated band structure for (3,1)-chGNRs. Line-by-line FT-STS data displayed in Figure 3i depicting the complete energy and momentum range experimentally measured. Comparative STM images of (3,1)-chGNR growth on Au(788) and Au(322). ARPES measurements displaying the raw photoemission data of the GNR-related dispersive band. Work function measurements of Au(111) and Au(322) surfaces. (PDF)

The authors declare no competing financial interest.

Supplementary Material

jz7b02767_si_001.pdf (577.2KB, pdf)

References

  1. Bonaccorso F.; Colombo L.; Yu G.; Stoller M.; Tozzini V.; Ferrari A. C.; Ruoff R. S.; Pellegrini V. Graphene, Related Two-Dimensional Crystals, and Hybrid Systems for Energy Conversion and Storage. Science 2015, 347, 1246501–1246501. 10.1126/science.1246501. [DOI] [PubMed] [Google Scholar]
  2. Celis A.; Nair M. N.; Taleb-Ibrahimi A.; Conrad E. H.; Berger C.; de Heer W. A.; Tejeda A. Graphene Nanoribbons: Fabrication, Properties and Devices. J. Phys. D: Appl. Phys. 2016, 49, 143001. 10.1088/0022-3727/49/14/143001. [DOI] [Google Scholar]
  3. Cai J.; Ruffieux P.; Jaafar R.; Bieri M.; Braun T.; Blankenburg S.; Muoth M.; Seitsonen A. P.; Saleh M.; Feng X.; et al. Atomically Precise Bottom-up Fabrication of Graphene Nanoribbons. Nature 2010, 466, 470–473. 10.1038/nature09211. [DOI] [PubMed] [Google Scholar]
  4. Chen Y.-C.; de Oteyza D. G.; Pedramrazi Z.; Chen C.; Fischer F. R.; Crommie M. F. Tuning the Band Gap of Graphene Nanoribbons Synthesized from Molecular Precursors. ACS Nano 2013, 7, 6123–6128. 10.1021/nn401948e. [DOI] [PubMed] [Google Scholar]
  5. Abdurakhmanova N.; Amsharov N.; Stepanow S.; Jansen M.; Kern K.; Amsharov K. Synthesis of Wide Atomically Precise Graphene Nanoribbons from Para-Oligophenylene Based Molecular Precursor. Carbon 2014, 77, 1187–1190. 10.1016/j.carbon.2014.06.010. [DOI] [Google Scholar]
  6. Zhang H.; Lin H.; Sun K.; Chen L.; Zagranyarski Y.; Aghdassi N.; Duhm S.; Li Q.; Zhong D.; Li Y.; et al. On-Surface Synthesis of Rylene-Type Graphene Nanoribbons. J. Am. Chem. Soc. 2015, 137, 4022–4025. 10.1021/ja511995r. [DOI] [PubMed] [Google Scholar]
  7. Talirz L.; Söde H.; Dumslaff T.; Wang S.; Sanchez-Valencia J. R.; Liu J.; Shinde P.; Pignedoli C. A.; Liang L.; Meunier V.; et al. On-Surface Synthesis and Characterization of 9-Atom Wide Armchair Graphene Nanoribbons. ACS Nano 2017, 11, 1380–1388. 10.1021/acsnano.6b06405. [DOI] [PubMed] [Google Scholar]
  8. Kharche N.; Meunier V. Width and Crystal Orientation Dependent Band Gap Renormalization in Substrate-Supported Graphene Nanoribbons. J. Phys. Chem. Lett. 2016, 7, 1526–1533. 10.1021/acs.jpclett.6b00422. [DOI] [PubMed] [Google Scholar]
  9. Deniz O.; Sánchez-Sánchez C.; Dumslaff T.; Feng X.; Narita A.; Müllen K.; Kharche N.; Meunier V.; Fasel R.; Ruffieux P. Revealing the Electronic Structure of Silicon Intercalated Armchair Graphene Nanoribbons by Scanning Tunneling Spectroscopy. Nano Lett. 2017, 17, 2197–2203. 10.1021/acs.nanolett.6b04727. [DOI] [PubMed] [Google Scholar]
  10. Merino-Díez N.; Garcia-Lekue A.; Carbonell-Sanromà E.; Li J.; Corso M.; Colazzo L.; Sedona F.; Sánchez-Portal D.; Pascual J. I.; de Oteyza D. G. Width-Dependent Band Gap in Armchair Graphene Nanoribbons Reveals Fermi Level Pinning on Au(111). ACS Nano 2017, 11, 11661–11668. 10.1021/acsnano.7b06765. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Ruffieux P.; Wang S.; Yang B.; Sánchez-Sánchez C.; Liu J.; Dienel T.; Talirz L.; Shinde P.; Pignedoli C. A.; Passerone D.; et al. On-Surface Synthesis of Graphene Nanoribbons with Zigzag Edge Topology. Nature 2016, 531, 489–492. 10.1038/nature17151. [DOI] [PubMed] [Google Scholar]
  12. Wakabayashi K.; Sasaki K.; Nakanishi T.; Enoki T. Electronic States of Graphene Nanoribbons and Analytical Solutions. Sci. Technol. Adv. Mater. 2010, 11, 054504. 10.1088/1468-6996/11/5/054504. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Wang S.; Talirz L.; Pignedoli C. A.; Feng X.; Müllen K.; Fasel R.; Ruffieux P. Giant Edge State Splitting at Atomically Precise Graphene Zigzag Edges. Nat. Commun. 2016, 7, 11507. 10.1038/ncomms11507. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Tao C.; Jiao L.; Yazyev O. V.; Chen Y.-C.; Feng J.; Zhang X.; Capaz R. B.; Tour J. M.; Zettl A.; Louie S. G.; et al. Spatially Resolving Edge States of Chiral Graphene Nanoribbons. Nat. Phys. 2011, 7, 616–620. 10.1038/nphys1991. [DOI] [Google Scholar]
  15. Pan M.; Girão E. C.; Jia X.; Bhaviripudi S.; Li Q.; Kong J.; Meunier V.; Dresselhaus M. S. Topographic and Spectroscopic Characterization of Electronic Edge States in CVD Grown Graphene Nanoribbons. Nano Lett. 2012, 12, 1928–1933. 10.1021/nl204392s. [DOI] [PubMed] [Google Scholar]
  16. Han P.; Akagi K.; Federici Canova F.; Mutoh H.; Shiraki S.; Iwaya K.; Weiss P. S.; Asao N.; Hitosugi T. Bottom-Up Graphene-Nanoribbon Fabrication Reveals Chiral Edges and Enantioselectivity. ACS Nano 2014, 8, 9181–9187. 10.1021/nn5028642. [DOI] [PubMed] [Google Scholar]
  17. Sánchez-Sánchez C.; Dienel T.; Deniz O.; Ruffieux P.; Berger R.; Feng X.; Müllen K.; Fasel R. Purely Armchair or Partially Chiral: Noncontact Atomic Force Microscopy Characterization of Dibromo-Bianthryl-Based Graphene Nanoribbons Grown on Cu(111). ACS Nano 2016, 10, 8006–8011. 10.1021/acsnano.6b04025. [DOI] [PubMed] [Google Scholar]
  18. Schulz F.; Jacobse P. H.; Canova F. F.; van der Lit J.; Gao D. Z.; van den Hoogenband A.; Han P.; Klein Gebbink R. J. M.; Moret M.-E.; Joensuu P. M.; et al. Precursor Geometry Determines the Growth Mechanism in Graphene Nanoribbons. J. Phys. Chem. C 2017, 121, 2896–2904. 10.1021/acs.jpcc.6b12428. [DOI] [Google Scholar]
  19. Han P.; Akagi K.; Federici Canova F.; Shimizu R.; Oguchi H.; Shiraki S.; Weiss P. S.; Asao N.; Hitosugi T. Self-Assembly Strategy for Fabricating Connected Graphene Nanoribbons. ACS Nano 2015, 9, 12035–12044. 10.1021/acsnano.5b04879. [DOI] [PubMed] [Google Scholar]
  20. de Oteyza D. G.; García-Lekue A.; Vilas-Varela M.; Merino-Díez N.; Carbonell-Sanromà E.; Corso M.; Vasseur G.; Rogero C.; Guitián E.; Pascual J. I.; et al. Substrate-Independent Growth of Atomically Precise Chiral Graphene Nanoribbons. ACS Nano 2016, 10, 9000–9008. 10.1021/acsnano.6b05269. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Weiss C.; Wagner C.; Kleimann C.; Rohlfing M.; Tautz F. S.; Temirov R. Imaging Pauli Repulsion in Scanning Tunneling Microscopy. Phys. Rev. Lett. 2010, 105, 086103. 10.1103/PhysRevLett.105.086103. [DOI] [PubMed] [Google Scholar]
  22. Kichin G.; Weiss C.; Wagner C.; Tautz F. S.; Temirov R. Single Molecule and Single Atom Sensors for Atomic Resolution Imaging of Chemically Complex Surfaces. J. Am. Chem. Soc. 2011, 133, 16847–16851. 10.1021/ja204624g. [DOI] [PubMed] [Google Scholar]
  23. Kichin G.; Wagner C.; Tautz F. S.; Temirov R. Calibrating Atomic-Scale Force Sensors Installed at the Tip Apex of a Scanning Tunneling Microscope. Phys. Rev. B: Condens. Matter Mater. Phys. 2013, 87, 081408. 10.1103/PhysRevB.87.081408. [DOI] [Google Scholar]
  24. Krejci O.; Hapala P.; Ondracek M.; Jelinek P. Principles and Simulations of High-Resolution STM Imaging with Flexible Tip Apex. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 95, 045407. 10.1103/PhysRevB.95.045407. [DOI] [Google Scholar]
  25. Gross L.; Moll N.; Mohn F.; Curioni A.; Meyer G.; Hanke F.; Persson M. High-Resolution Molecular Orbital Imaging Using a p-Wave STM Tip. Phys. Rev. Lett. 2011, 107, 086101. 10.1103/PhysRevLett.107.086101. [DOI] [PubMed] [Google Scholar]
  26. Söde H.; Talirz L.; Gröning O.; Pignedoli C. A.; Berger R.; Feng X.; Müllen K.; Fasel R.; Ruffieux P. Electronic Band Dispersion of Graphene Nanoribbons via Fourier-Transformed Scanning Tunneling Spectroscopy. Phys. Rev. B: Condens. Matter Mater. Phys. 2015, 91, 045429. 10.1103/PhysRevB.91.045429. [DOI] [Google Scholar]
  27. Pascual J. I.; Song Z.; Jackiw J. J.; Horn K.; Rust H.-P. Visualization of Surface Electronic Structure: Dispersion of Surface States of Ag(110). Phys. Rev. B: Condens. Matter Mater. Phys. 2001, 63, 241103. 10.1103/PhysRevB.63.241103. [DOI] [Google Scholar]
  28. Ruffieux P.; Cai J.; Plumb N. C.; Patthey L.; Prezzi D.; Ferretti A.; Molinari E.; Feng X.; Müllen K.; Pignedoli C. A.; et al. Electronic Structure of Atomically Precise Graphene Nanoribbons. ACS Nano 2012, 6, 6930–6935. 10.1021/nn3021376. [DOI] [PubMed] [Google Scholar]
  29. Linden S.; Zhong D.; Timmer A.; Aghdassi N.; Franke J. H.; Zhang H.; Feng X.; Müllen K.; Fuchs H.; Chi L.; et al. Electronic Structure of Spatially Aligned Graphene Nanoribbons on Au(788). Phys. Rev. Lett. 2012, 108, 216801. 10.1103/PhysRevLett.108.216801. [DOI] [PubMed] [Google Scholar]
  30. Nakada K.; Fujita M.; Dresselhaus G.; Dresselhaus M. S. Edge State in Graphene Ribbons: Nanometer Size Effect and Edge Shape Dependence. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 17954–17961. 10.1103/PhysRevB.54.17954. [DOI] [PubMed] [Google Scholar]
  31. Jiang Z.; Song Y. Band Gap Oscillation and Novel Transport Property in Ultrathin Chiral Graphene Nanoribbons. Phys. B 2015, 464, 61–67. 10.1016/j.physb.2015.02.003. [DOI] [Google Scholar]
  32. Suda S.; Oshiyama A. Energetics, Electron States, and Magnetization in Nearly Zigzag-Edged Graphene Nano-Ribbons. J. Phys. Soc. Jpn. 2015, 84, 024704. 10.7566/JPSJ.84.024704. [DOI] [Google Scholar]
  33. Carvalho A. R.; Warnes J. H.; Lewenkopf C. H. Edge Magnetization and Local Density of States in Chiral Graphene Nanoribbons. Phys. Rev. B: Condens. Matter Mater. Phys. 2014, 89, 245444. 10.1103/PhysRevB.89.245444. [DOI] [Google Scholar]
  34. Raza H.; Kan E. C. Armchair Graphene Nanoribbons: Electronic Structure and Electric-Field Modulation. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 77, 245434. 10.1103/PhysRevB.77.245434. [DOI] [Google Scholar]
  35. Carbonell-Sanromà E.; Brandimarte P.; Balog R.; Corso M.; Kawai S.; Garcia-Lekue A.; Saito S.; Yamaguchi S.; Meyer E.; Sánchez-Portal D.; et al. Quantum Dots Embedded in Graphene Nanoribbons by Chemical Substitution. Nano Lett. 2017, 17, 50–56. 10.1021/acs.nanolett.6b03148. [DOI] [PubMed] [Google Scholar]
  36. Horcas I.; Fernández R.; Gómez-Rodríguez J. M.; Colchero J.; Gómez-Herrero J.; Baro A. M. WSXM: A Software for Scanning Probe Microscopy and a Tool for Nanotechnology. Rev. Sci. Instrum. 2007, 78, 013705. 10.1063/1.2432410. [DOI] [PubMed] [Google Scholar]
  37. Soler J. M.; Artacho E.; Gale J. D.; García A.; Junquera J.; Ordejón P.; Sánchez-Portal D. Daniel Sánchez-Portal. The SIESTA Method for Ab Initio Order- N Materials Simulation. J. Phys.: Condens. Matter 2002, 14, 2745. 10.1088/0953-8984/14/11/302. [DOI] [Google Scholar]
  38. Klimeš J.; Bowler D. R.; Michaelides A. Chemical Accuracy for the van Der Waals Density Functional. J. Phys.: Condens. Matter 2010, 22, 022201. 10.1088/0953-8984/22/2/022201. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz7b02767_si_001.pdf (577.2KB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES