Groupwise Registration of MR Brain Images with tumors

Abstract

A novel groupwise image registration framework is developed for registering MR brain images with tumors. Our method iteratively estimates a normal-appearance counterpart for each tumor image to be registered and constructs a directed graph (digraph) of normal-appearance images to guide the groupwise image registration. Particularly, our method maps each tumor image to its normal appearance counterpart by identifying and inpainting brain tumor regions with intensity information estimated using a low-rank plus sparse matrix decomposition based image representation technique. The estimated normal-appearance images are groupwisely registered to a group center image guided by a digraph of images so that the total length of “image registration paths” to be the minimum, and then the original tumor images are warped to the group center image using the resulting deformation fields. We have evaluated our method based on both simulated and real MR brain tumor images. The registration results were evaluated with overlap measures of corresponding brain regions and average entropy of image intensity information, and Wilcoxon signed rank tests were adopted to compare different methods with respect to their regional overlap measures. Compared with a groupwise image registration method that is applied to normal-appearance images estimated using the traditional low-rank plus sparse matrix decomposition based image inpainting, our method achieved higher image registration accuracy with statistical significance (p=7.02×10⁻⁹).

Introduction

Deformable registration of brain tumor images of different patients into a common stereotaxic space facilitates atlas based segmentation and atlas construction with statistical pathological information (Cuadra et al., 2004, Shattuck et al., 2008, Zacharaki et al., 2008). Many image registration methods have been proposed to register pathological brain images and most of them could be classified into 3 main categories: mask based methods, pathology simulation methods, and inpainting based methods. The pioneering mask based method is Cost Function Masking (CFM) that excludes pathological brain regions in the image registration processing (Brett et al., 2001). Specifically, pathological brain regions are first segmented and then image information in the pathological regions is excluded in the image registration’s cost function so that the image registration is driven mainly by corresponding healthy parts of the brain. The CFM technique has been widely adopted in studies of pathological image registration (Stefanescu et al., 2004, Crinion et al., 2007, Andersen et al., 2010, Parisot et al., 2012). Different from the CFM method, the pathology simulation methods synthesize pathological regions in a normal atlas image in order to create an atlas image that is similar to the pathological image and therefore a typical image registration algorithm can be adopted for registering these images (Zacharaki et al., 2008, Gooya et al., 2011). Similar to the pathology simulation methods, the inpainting based methods also generate simulated images by replacing abnormal regions of pathological images with normal appearance information in order to make images to be registered comparable (Sdika and Pelletier, 2009, Liu et al., 2014). For example, the inpainting strategy was used to fill white matter lesions with normal white matter information (Sdika and Pelletier, 2009), and low-rank images with normal appearance were derived from pathological brain images for image registration (Liu et al., 2014, Liu et al., 2015). Although all these methods have demonstrated promising performance in pairwise image registration studies, the inpainting strategy might be a better choice for registering multiple pathological brain images to a common space in a groupwise image registration setting.

Many Groupwise Image Registration (GIR) methods have been proposed to achieve registration of a group of images without specific atlas images. To minimize bias introduced by the template image used in the GIR, the template image should be a group center. The average of input images has been widely adopted as a template image in GIR studies (Joshi et al., 2004, Ashburner, 2007). However, the average image based template might degrade the GIR performance (Wu et al., 2011). Instead of generating a template image from input images, several studies have opted for a specific input image that best represents the group center (Park et al., 2005, Hamm et al., 2009). Particularly, the geometric mean of input images, determined according to pairwise registration results of all input images, could be adopted as the template image (Park et al., 2005). The group center image could also be identified using graph theoretic methods that have demonstrated improved GIR performance in a variety of studies (Hamm et al., 2009, Jia et al., 2010, Crum et al., 2013, Tang and Fan, 2016). However, these GIR techniques are not equipped to register pathological images.

Recently, an inpainting based GIR method for pathological images was proposed to build a brain image atlas based on a group of pathological brain images (Liu et al., 2014, Liu et al., 2015). This method maps pathological brain images to their normal-appearance counterparts and uses their average image as the template image for achieving least biased registration of pathological brain images. Particularly, a Low Rank plus Sparse matrix Decomposition (LRSD) technique proposed in (Peng et al., 2012) was adopted to decompose the pathological brain images into low-rank images and sparse components, and then the low-rank images were used to drive the GIR. Although this method achieved promising performance, the low-rank images may have blurred and even distorted appearance, as illustrated by the example low rank image and sparse component image shown in Fig. 1. Moreover, this method adopted average of the low-rank images as the template image and therefore suffers from the same problem as those methods developed for registering images with normal appearance (Wu et al., 2011).

Fig. 1.

A brain image with a tumor (left), its corresponding low-rank image (middle), and its sparse component (right). Arrows indicate blurred and distorted normal brain regions in the low-rank image. The sparse component captures not only the tumor region but also normal brain regions with large intensity variations across different images. The colorbar indicates relative values of the sparse component image.

To achieve a robust GIR of pathological brain images and overcome limitations of the existing techniques, we propose a novel framework for registering MR brain images with tumors. It is worth noting that our framework is also applicable to other pathological brain images which share the same properties of brain tumors (e.g., inconsistent locations across subjects). Particularly, we iteratively estimate a normal-appearance counterpart for each tumor image to be registered, inspired by the success of mask based and inpainting based strategies for pathological image registration, and construct a directed graph (digraph) of normal-appearance images to guide the GIR. We map tumor images to their normal appearance counterparts by replacing tumor regions with intensity information estimated using a LRSD technique (Peng et al., 2012), instead of directly taking the low-rank images as input for the GIR. The estimated normal-appearance images are then groupwisely registered to a group center image guided by a digraph of images so that the total length of “image registration paths” is the minimum (Tang and Fan, 2016). We have evaluated and validated the proposed method using both simulated images and real MR brain images with tumors.

Methods

Our method consists of 2 major components: a mask based LRSD method for image inpainting (denoted as M-LRSD) (Sdika and Pelletier, 2009, Peng et al., 2012) and a Dynamic Digraph based GIR Method (DDGM) (Tang and Fan, 2016), as illustrated by the flowchart shown in Fig. 2. Our algorithm iteratively refines the image inpainting of brain tumors and the GIR results so that all images are registered to a group center image that is adaptively updated with the GIR progression. Finally, the resulting deformation fields are applied to their corresponding original input images to compute the registration results.

Fig. 2.

Flow diagram of the proposed GIR method for brain images with tumors.

The method is generally applicable to brain tumor images of the same imaging modality. In this study, we have focused on T1-weighted MR images of the human brain. All images to be registered are preprocessed using following steps. Non-uniformity correction is applied to individual images using BrainSuite (brainsuite.org), then an affine transformation based image registration is used to spatially normalize the images to a standard template, namely MNI152 (Fonov et al., 2009), and finally image intensities of the images are normalized using histogram matching (Gonzalez and Woods, 2008).

Image inpainting using Mask based LRSD (M-LRSD)

Inspired by the success of mask based and inpainting based strategies for pathological image registration (Brett et al., 2001, Stefanescu et al., 2004, Crinion et al., 2007, Sdika and Pelletier, 2009, Andersen et al., 2010, Parisot et al., 2012, Liu et al., 2014, Liu et al., 2015), we estimate a normal-appearance counterpart for each tumor image to be registered. Since brain tumor regions usually appear in different locations across subjects and with distinct image appearances, we adopt a LRSD method (Peng et al., 2012) to map pathological images to their normal appearance counterparts based on the LRSD’s low-rank part. The low-rank images typically have normal brain appearance since the brain tumor regions are characterized by the sparse components. However, due to inter-subject anatomical variability and the low-rank constraint, the low-rank images typically have blurred appearances in normal brain regions, as illustrated by Fig. 1. Instead of directly using the low-rank images as a normal-appearance counterpart for each brain tumor image (Liu et al., 2014, Liu et al., 2015), we identify tumor regions based on the LRSD’s sparse component using a graph cut technique (Boykov et al., 2001), and combine low-rank image information within the tumor regions and original image information outside of the tumor regions to obtain an inpainted version of the original tumor image.

Given n input images D = [I₁, …, I_n] ∈ R^m×n, each of them having m voxels, coded by a column vector I_j, j = 1, …, n, the LRSD decomposes the input images D into low-rank images B = [B₁, …, B_n] ∈ R^m×n and sparse components S = [S₁, …, S_n] ∈ R^m×n by optimizing (Sdika and Pelletier, 2009, Peng et al., 2012)

$$\underset{B,S}{\mathit{min}}({\Vert \mathit{B}\Vert }_{\ast }+\lambda {\Vert \mathit{S}\Vert }_1),\text{subject}\text{to}\mathit{D}=\mathit{B}+\mathit{S},$$ (1)

where ||B||_* is the nuclear norm, i.e., sum of singular values of B, ||S||₁ is the L1 norm of S, and λ is a trade-off parameter. The low-rank images are representations of the input images in a linear subspace, while the sparse components capture tumor regions that are spatially sparse. However, the sparse component may also capture inter-subject anatomy variability, yielding blurred and distorted normal brain regions in low-rank images.

To identify tumor regions, we adopt a graph cut method to segment sparse components (Boykov et al., 2001). Specifically, given sparse components S = [S₁, …, S_n] = {S_ij} ∈ R^m×n, we identify tumor regions M = [M₁, …, M_n] = {M_ij} ∈ R^m×n by optimizing

$$\underset{M}{\mathit{min}}\sum _{\begin{array}{c}1\le i\le m,\\ 1\le j\le n\end{array}}{(P_{ij}-M_{ij})}^2+\sum _{\begin{array}{c}1\le i,k\le m,\\ 1\le j,l\le n\end{array}}{W}_{ij,kl}|M_{ij}-M_{kl}|,$$ (2)

where M_ij = 1 indicates that the i-th voxel of the j-th column (image) of D belongs to a tumor region while M_ij = 0 indicates the voxel belongs to a normal region; W ∈ R^{(m×n)×(m×n)} is an adjacent matrix and W_ij,kl = 1 indicates that element S_ij is adjacent to element S_kl, otherwise W_ij,kl = 0 (voxels within a 3×3×3 voxel range in the same image are regarded as adjacent voxels); and P = {P_ij} ∈ R^m×n encodes occurrence probability of brain tumor regions estimated based on the sparse component S as

$$P_{ij}=\{\begin{array}{cc}1-\frac{1}{n}\sum _{1\le l\le n}{T}_{{\mu }_l}(S_{il}),& \left|S_{ij}\right|\ge {\mu }_j\\ 0,& \left|S_{ij}\right|<{\mu }_j\end{array},$$ (3)

where S_ij (or S_il) is the element at the i-th row and j-th (or l-th) column of S, T_μl(S_il) = 1 if |S_il| ≥ μ_l or 0 otherwise, and μ_j (or μ_l) is the average of absolute values of all non-zero values of S_i (or S_l), i.e., the sparse component of the j-th (or l-th) image. In particular, P_ij is equal to 0 if S_ij has a relatively small value. When S_ij is larger than μ_j, probability of the i-th voxel of the j-th column (image) of D belonging to a tumor region is inversely proportional to the frequency that the same voxel of other images have larger values in S. Both tumor regions and regions with large inter-subject variability may have larger values in S; however tumors may appear at the same spatial location across different subjects with low frequency and the inter-subject variability in normal brain tissues may have large coincidence to present at the same spatial location. The optimization problem of Eqn. 2 can be solved by graph cut methods (Boykov et al., 2001).

Once the low rank images and tumor masks are available, inpainted images can be obtained straightforwardly by replacing tumor parts of the original images with the corresponding low rank parts. The inpainted images will be input to the GIR algorithm detailed as following.

Groupwise registration of inpainted images using Dynamic Digraph based GIR Method (DDGM)

Given input n images D = [I₁, …, I_n] ∈ R^m×n, their low-rank images B = [B₁, …, B_n] ∈ R^m×n and corresponding sparse component S = D−B = [S₁, …, S_n] ∈ R^m×n are first obtained using LRSD. Based on the sparse components S, the mask information M of brain tumor regions in input images is then computed using the graph cut technique. Finally, inpainted images are obtained: D′ = D · (1−M) + B·M, where 1 ∈ R^m×n, 1_ij = 1. The inpainted images are registered groupwisely using the DDGM algorithm. The image inpainting and the GIR are iterated alternatively until convergence. Fig. 2 shows a flowchart of the algorithm. In each iteration step, the LRSD technique decomposes D^iter into B^iter and S^iter, and then M^iter and inpainted images D^iter′ are obtained for building a digraph of images to guide the GIR (Tang and Fan, 2016). The iterative process stops when all images have been registered to the root image. The algorithm is summarized in Algorithm 1.

Algorithm 1.

Groupwise registration of inpainted images using DDGM

Input: Diter = [I1iter, …, Initer] ∈ Rm×n, iter = 0(original images)
1.	Get Biter and Siter from Diter using $\text{LRSD}:\underset{{\mathit{B}}^{\mathit{iter}},{\mathit{S}}^{\mathit{iter}}}{\mathit{min}}\left({\Vert {\mathit{B}}^{\mathit{iter}}\Vert }_{\ast }+\lambda {\Vert {\mathit{S}}^{\mathit{iter}}\Vert }_1\right)$, Diter = Biter + Siter
2.	Calculate Piter based on ${\mathit{S}}^{\mathit{iter}}:P_{ij}^{\mathit{iter}}=\{\begin{array}{cc}1-\frac{1}{n}{\sum }_{1\le l\le n}{T}_{{\mu }_l}(S_{il}^{\mathit{iter}}),& \left|S_{ij}^{\mathit{iter}}\right|\ge {\mu }_j^{\mathit{iter}}\\ 0,& \left|S_{ij}^{\mathit{iter}}\right|<{\mu }_j^{\mathit{iter}}\end{array}$
3.	Get mask ${\mathit{M}}^{\mathit{iter}}:{\mathit{M}}^{\mathit{iter}}\leftarrow \underset{M}{\mathit{min}}{\sum }_{\begin{array}{c}1\le i\le m,\\ 1\le j\le n\end{array}}{(P_{ij}^{\mathit{iter}}-M_{ij}^{\mathit{iter}})}^2+\alpha ·{\sum }_{\begin{array}{c}1\le i,k\le m,\\ 1\le j,l\le n\end{array}}{W}_{ij,kl}|M_{ij}^{\mathit{iter}}-M_{kl}^{\mathit{iter}}|$
4.	Diter′ = [I1iter′, …, Initer′] ∈ Rm×n ← Diter · (1 − Miter) + Biter · Miter
5.	Apply DDGM to Diter′ for computing displacement fields $d_1^{\mathit{iter}}(x),\dots ,d_n^{\mathit{iter}}(x)$
6.	${\mathit{D}}^{\mathit{iter}}=[{I_1}^{\mathit{iter}}\left(d_1^{\mathit{iter}}(x)\right),\dots {I_n}^{\mathit{iter}}\left(d_n^{\mathit{iter}}(x)\right)$
7.	7iter = iter + 1
8.	8. Do step 1–7 until all non-root images have been registered to the root image.
$\mathbf{Output}:{I_1}^{\mathit{ite}{r}^{\prime }}(d_1^{\mathit{iter}}(x)),\dots ,{I_n}^{\mathit{ite}{r}^{\prime }}\left(d_n^{\mathit{iter}}(x)\right)$

The groupwise registration of inpainted images is implemented by the DDGM that is a graph based GIR method (Tang and Fan, 2016). Particularly, a digraph of images to be registered is constructed to estimate their groupwise similarity. The distance of directed edges connecting two images in the digraph is inversely proportional to their similarity measured by sparse coding (Cheng et al., 2010). According to the digraph of images, a group center is selected as the root of the digraph and each non-root image is registered to the root image following the shortest path connecting the non-root image to the root image.

Validation and Evaluation

We evaluated our method, referred to as DDGM+M-LRSD, based on both simulated and real brain tumor images, and compared it with the GIR method proposed by Liu et al (Liu et al., 2015). The latter method uses low-rank images as input images and a group average image is used as the group template, and therefore is referred to as AVG+LRSD. The low-rank images obtained in AVG+LRSD are referred as inpainted images hereafter. We also applied DDGM to original brain tumor images without inpainting, referred as DDGM+ORI. In all the groupwise image registration methods, diffeomorphic demons algorithm was adopted for registering two images (Vercauteren et al., 2009).

Dataset I: MR brain images with simulated tumors

Dataset I comprises 40 T1-weighted MR brain images obtained from a publicly available database LPBA40 (http://www.loni.usc.edu/atlases) (Shattuck et al., 2008). Particularly, image data of ‘LPBA40 Subjects in Delineation Space’ were used in the present study. The images are T1-weigthed, and have a spatial resolution of 1mm³. Each of the images has a label image of 54 brain regions. For each LPBA40 image, a brain tumor is simulated based on a T1-weighted image with tumors with manually labelled tumor mask. The tumor image was randomly selected from the BRATS2015 dataset (Menze et al., 2015), and different tumor images were selected for the LBPA40 images. Particularly, the tumor image was registered to the LPBA40 image using affine transformation by optimizing their mutual information, and then the LBPA40 image information within the registered tumor mask was replaced with brain tumor information of the tumor image. Fig. 3 shows example images of dataset I.

Fig. 3.

Example images of dataset I.

Dataset II: MR brain images with tumors

Dataset II comprises 28 T1-weighted MR brain images obtained from the BRATS2015 (Menze et al., 2015). These T1-weighted MR brain images were randomly chosen from BRATS2015 training dataset (https://www.smir.ch/BRATS/Start2015). All the images have been aligned to the MNI space and interpolated to 1mm³ voxel resolution. Each of these images has at least one tumor. Fig. 4 shows example images of dataset II.

Fig. 4.

Example images of dataset II.

Image registration evaluation

For dataset I, we have the ground truth of tumor-free images and tumor regions. Therefore, inpainted images obtained by M-LRSD and LRSD were evaluated according to image error ratio. The image error ratio is defined as $e_i=\frac{\sum \left|I_i^{tf}-B_i\right|}{\sum I_i^{tf}}$ for the i-th image, where B_i is the inpainted image, $I_i^{tf}$ is its corresponding tumor-free image, $\sum \left|I_i^{tf}-B_i\right|$ and $\sum I_i^{tf}$ are the sum of image intensity of $\left|I_i^{tf}-B_i\right|$ and $I_i^{tf}$, respectively.

Besides the image error ratio, image registration accuracy was also quantified by calculating the average Jaccard indexes of brain regions based on all possible image pairs. Specifically, the resulting deformation field of each image was applied to its corresponding label image with 54 manually labeled regions. Then the Jaccard indexes of brain regions between each pair of deformed label images were computed as $J_{ij}^l=\frac{|{\mathrm{\Omega }}_i^l\cap {\mathrm{\Omega }}_j^l|}{|{\mathrm{\Omega }}_i^l\cup {\mathrm{\Omega }}_j^l|}$ l = 1, … 54; i,j = 1, …, 40; i>j, where $\left|{\mathrm{\Omega }}_i^l\right|$ and $\left|{\mathrm{\Omega }}_j^l\right|$ are volumes of the l-th brain region in the i-th and j-th label images respectively. Dataset I comprises 40 images, so there were $\left(\begin{array}{c}40\\ 2\end{array}\right)=780$ possible label image pairs. To compare different methods with respect to their regional overlap measures, Wilcoxon signed rank tests were adopted.

Since dataset II does not have ground truth of tumor-free images or brain parcellation label images, so image registration quality was quantified by an average entropy value of all image voxels. In particular, for each voxel entropy of image intensity values across all registered images was computed and an average entropy value of all the voxel was used to quantify the image registration, with an assumption that images registered with higher accuracy have lower entropy.

Tumor segmentation evaluation

The tumor segmentation performance was evaluated based on the Jaccard index and Recall between automatically segmented tumor mask and manually labelled mask. In particularly, $\text{Recall}=\frac{\left|\text{true}\text{positives}\right|}{\left|\text{true}\text{positives}\right|+\left|\text{false}\text{negatives}\right|}$, where the manually labelled brain mask was treated as ground-truth, true positives were the ground-truth tumor voxels that were segmented as tumor voxels by the automatic tumor segmentation method, and false negatives were the ground-truth tumor voxels that were segmented as normal voxels by the automatic tumor segmentation method. To evaluate how the brain tumor segmentation affects the registration results, we also generated inpainted images based on the manually labelled tumor masks and obtained the registration results using the proposed method.

Parameters selection

The weighting factor, λ, used in LRSD may affect the image inpainting and subsequently image registration accuracy. In our experiment, λ was manually set according to the input images. Specifically, we tested different values for λ and chose one with the best performance for recovering tumor-free images.

Results

Fig. 5 shows low-rank images of randomly selected images from each of the image datasets, obtained by applying LRSD to the input images of different datasets with different values of λ. Based on visual inspection of these results, λ was set to 0.003 for both the datasets in our experiments.

Fig. 5.

Low-rank images obtained with different values of λ. The images were randomly selected from dataset I (top) and dataset II (bottom), respectively.

Registration and segmentation results of Dataset I

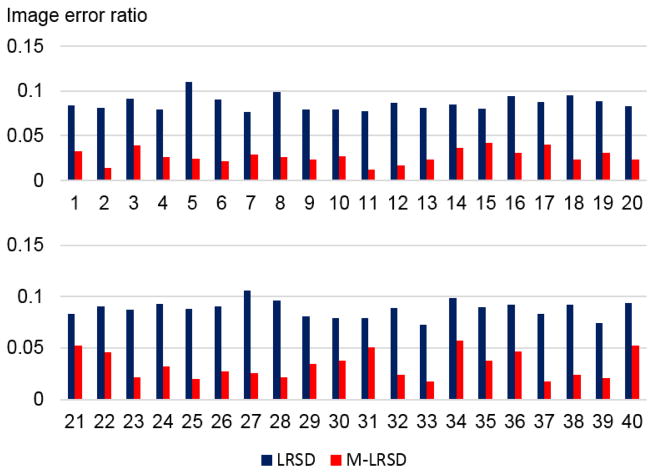
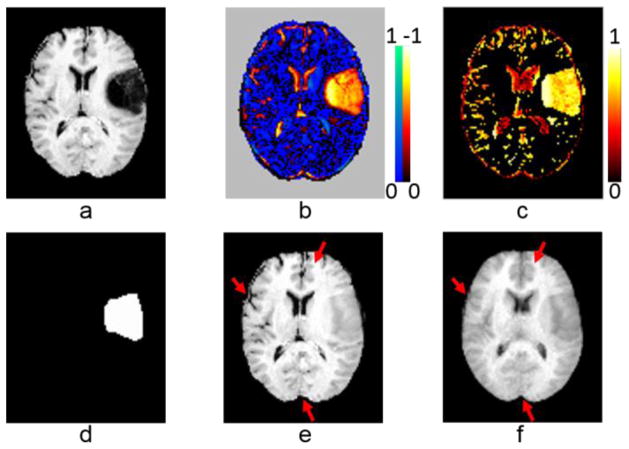
Fig. 6 shows image inpainting and intermediate results of a randomly selected image obtained by applying M-LRSD and LRSD to the input images, including the original image, sparse component, occurrence map, tumor mask, and inpainted images. As shown in Fig. 6 (e) and (f), the inpainted image obtained by M-LRSD better preserved normal regions of the original image than that obtained by LRSD. The image error ratio results shown in Fig. 7 further demonstrated that the images registered by M-LRSD had lower image error ratio than those obtained by LRSD.

Fig. 6.

Image inpainting and intermediate results of a randomly selected image of dataset I: (a) an original image in dataset I, (b) sparse component, (c) tumor occurrence map, (d) tumor mask, (e) inpainted image obtained by M-LRSD, and (f) inpainted image obtained by LRSD. Normal brain regions of the original image were better preserved by M-LRSD than LRSD, as marked by the red arrows. The colorbars indicate relative value of sparse component and tumor occurrence map.

Fig. 7.

Image error ratios of low-rank images of dataset I using LRSD and M-LRSD.

Fig. 8 shows registered images of one randomly selected subject and group average images of all the registered images obtained by applying DDGM+ORI, AVG+LRSD, and DDGM+M-LRSD to the input images of dataset I. In particular, AVG+LRSD converged and obtained the image registration results after 6 iteration steps, while DDGM+ORI and DDGM+M-LRSD converged and obtained their image registration results after 4 iteration steps. As shown in Fig. 8, DDGM+ORI had the worst performance due to the tumors presented in the images to be registered, yielding an average image with blurred and distorted appearance. With the help of image inpainting, the average images obtained by other methods had better contrasts between different brain tissues.

Fig. 8.

Registered images of one randomly selected subject (top row) and average images of registered images (bottom row) obtained by DDGM+ORI, AVG+LRSD and DDGM+M-LRSD.

The image registration results were further evaluated using Jaccard index based on 54 manually labeled regions. For each region, an average value of 780 Jaccard indexes, referred to as regional Jaccard index, was obtained to quantify the image registration accuracy. As shown in Fig. 9, images registered by DDGM+M-LRSD had higher Jaccard indexes at most of the brain regions than those obtained by DDGM+ORI and AVG+LRSD. The average values of regional Jaccard indexes and standard deviations σ for registration results obtained by different methods were 0.543 with σ = 0.022 (DDGM+ORI), 0.555 with σ = 0.034 (AVG+LRSD), and 0.586 with σ = 0.020 (DDGM+M-LRSD), indicating that the proposed achieved better image registration performance than the alternative methods. As summarized in Table 1, p-values of Wilcoxon signed testing of regional Jaccard indexes further indicated that the proposed method achieved better image registration performance with statistical significance.

Fig. 9.

Average Jaccard indexes of 54 brain regions of registered images obtained by DDGM+ORI, AVG+LRSD, and DDGM+M-LRSD. L: left, R: right.

Table 1.

Regional Jaccard indices of image registration results obtained by different methods and Wilcoxon signed rank test results between DDGM+M-LRSD and others.

	Jaccard index (mean± standard deviation)	p value (Wilcoxon signed rank test)
DDGM+ORI	0.543±0.022	1.82 × 10−10
AVG+LRSD	0.555±0.034	7.02 × 10−9
DDGM+M-LRSD	0.586±0.020

Fig. 10 (top row) shows the automatic tumor segmentation performance for dataset I. The relatively high Recall rates indicated that the brain tumors were largely covered by the automatically generated brain tumor masks. However, Jaccard indices of the automatically generated brain tumor masks indicated that there is much room for further improving the automatic segmentation method. Our experimental results demonstrated that inpainted images obtained with the manually labelled tumor masks yielded better registration accuracy than inpainted images obtained with the automatically segmented tumor masks for dataset I. Particularly, the average of Jaccard indices of the registration results obtained with the manually labelled tumor masks was 0.589, larger than that obtained with the automatically segmented tumor masks (0.586, p=9.67×10⁻⁵, Wilcoxon signed rank test).

Fig. 10.

Image segmentation performance for dataset I (top row) and dataset II (bottom row). The high Recall rates indicated that the automatically generated tumor masks largely covered the brain tumors for most of the images.

Registration results of Dataset II

Fig. 11 shows image inpainting and intermediate results of a randomly selected image obtained by applying M-LRSD and LRSD to the images of dataset II, including the original image, sparse component, occurrence map, tumor mask, and inpainted image. Similar to the results of dataset I, normal brain regions were better preserved by M-LRSD than LRSD.

Fig. 11.

Image inpainting and intermediate results of a randomly selected image of dataset II: (a) an original image in dataset II, (b) sparse component, (c) tumor occurrence map, (d) tumor mask, (e) inpainted image obtained by M-LRSD, and (f) inpainted image obtained by LRSD. Normal brain regions of the original image were better preserved by M-LRSD than LRSD, as marked by the red arrows. The colorbars indicate relative value of sparse component and tumor occurrence map.

Registered images of one randomly selected subject and group average images of registration results obtained by applying DDGM+ORI, AVG+LRSD, and DDGM+M-LRSD to the images of dataset II are shown in Fig. 12. In particularly, AVG+LRSD converged and obtained its registration results after 7 iteration steps, while DDGM+ORI, and DDGM+M-LRSD converged and obtained their registration results after 4 iteration steps.

Fig. 12.

Registered images of one randomly selected subject (top row) and group average images of registered images (bottom row) obtained by DDGM+ORI, AVG+LRSD and DDGM+M-LRSD.

To quantitatively evaluate the image registration results, we calculated entropy at every image voxel across the registered images of dataset II obtained by different methods, including the input images (registered to MNI space with affine image registration). The average entropy values were 1.779 (affine image registration), 1.793 (DDGM+ORI), 1.738 (AVG+LRSD), and 1.729 (DDGM+M-LRSD), respectively. Surprisingly, registered images obtained by DDGM+ORI had larger average entropy than images registered with affine transformation, indicating that brain tumors misled the deformable image registration. Since inpainted images obtained using M-LRSD had better image quality, DDGM+M-LRSD achieved the lowest average entropy.

Fig. 10 (bottom row) shows the automatic tumor segmentation performance for dataset II. Similar to the results obtained for dataset I, the relatively high Recall rates indicated that the brain tumors were largely covered by the automatically generated brain tumor masks.

Discussion and Conclusions

We have proposed a new GIR method for registering brain images with tumors by extending our previous proposed GIR method, namely DDGM (Dynamic Digraph based Method). Specifically, the new method is built upon the success of mask based and inpainting based strategies for pathological image registration, takes advantage of a low-rank plus sparse matrix decomposition method to compute inpainted images, and computes deformation fields based on the inpainted images. Instead of directly using the low-rank images as the inpainted results (Liu et al., 2015), we integrate the mask based and inpainting based strategies to obtain better inpainted images. In particular, the low-rank sparse decomposition method is adopted to compute low-rank images and sparse components given a set of tumor images to be registered, then a tumor mask is computed for each individual tumor image by segmenting its sparse component obtained in the low-rank sparse decomposition, and finally an inpainted image is obtained for each individual tumor image by replacing its image information within the tumor mask with its corresponding low-rank image.

In our GIR method, the registration of brain images with tumors is driven by the inpainted images, instead of the original images. Compared with the image registration results obtained by applying the DDGM method to the original images, the registered images obtained by the new method had better spatial correspondence and low entropy across different images. In this study, we adopted two different strategies to evaluate the image registration performance. For the images of dataset I, we adopted Jaccard index to measure spatial correspondence of the registered images based on their manually labeled brain regions. For the images of dataset II, we used average voxelwise entropy of image intensity values across the registered images to evaluate their spatial correspondence. In all the experiments, our method achieved better registration performance than the alternative algorithms.

In our method, the root image is one of the images to be registered, and no image warping is applied to the root image. The graph of images is updated with the image registration progression, and the root image might change from one image to the other to remain as the center of the image manifold. However, once the image registration converges, all the images except the root image are warped to the root image space with the deformation fields obtained in the registration process. The root image can be registered to the group mean image if needed so that all the images to be registered are processed similarly.

The new GIR method for registering brain images with tumors is capable of registering pathological brain images with promising performance, statistically better than the methods under comparison. The registration performance obtained for tumor images is comparable to that obtained by other groupwise image registration for normal brain images. Particularly, a kNN graph based groupwise image registration method obtained an average Jaccard index of 0.575 for LBPA40 images (Tang and Fan, 2016).

In this study, we have focused on brain tumor image data. However, the method is generally applicable to other images of the same modality. Our experimental results have also demonstrated that the image registration performance could be improved with inpainted images obtained with better brain tumor masks, indicating better tumor segmentation might be able to further improve the image registration performance. However, it remains a challenging task to segment brain tumors with diffuse boundaries (Müller et al., 2016, Lok et al., 2017). Our tumor segmentation method may yield under-segmented tumor masks for tumors with diffuse boundaries, which may degrade the subsequent image registration performance. It is also worth noting that for the low-rank sparse decomposition it is difficult to obtain the same trade-off parameter that is optimal for all the images.

Our future work will focus on improving the tumor segmentation (Zhao et al., 2016). The groupwisely registered tumor images may provide a statistical atlas in the tumor segmentation studies to reduce false positive rate. On the other hand, the improved tumor segmentation may facilitate better image inpainting and subsequently improve the groupwise registration of tumor images.