In vivo B₀ field shimming methods for MRI at 7 T

Abstract

Functional MRI (fMRI) at 7 T and above provides improved Signal-to-Noise Ratio and Contrast-to-Noise Ratio compared to 3 T acquisitions. In addition to the beneficial effects on spin polarization and magnetization of deoxyhemoglobin, the increased applied field also further magnetizes air and tissue. While the magnets themselves typically provide a static B₀ field with sufficient spatial homogeneity, the diamagnetism of tissue and the paramagnetism of air causes local field deviations inside the human head. These spatially-varying field offsets (ΔB₀) cause image artifacts, especially in single shot EPI, including geometric distortion, signal dropout, and blurring. These effects are particularly strong near air-tissue interfaces such as the frontal sinus, and ear canals. Furthermore, if the field offsets are dynamically modulated through physiological processes such as respiration or motion, then the effect on the image time-series can be even more problematic.

While post-processing methods have been developed to mitigate these effects, the ideal solution would be to reduce the ΔB₀ variations at their source. Typically 7 T scanners contain 2nd and some 3rd order spherical harmonic shim coil terms to cancel static ΔB₀ variations of low spatial order. In this article, we will motivate the need for improved, higher-order compensation for B₀ inhomogeneity and potentially add dynamic control of these fields. We discuss and compare several promising hardware approaches for static and dynamic B₀ shimming using either higher-order spherical harmonic shim coils or multi-coil shim arrays as well as passive shimming approaches, and active variants such and adaptive current networks.

Introduction

Ultra-high field MRI at 7 T holds several advantages over 3 T MRI for clinical and scientific brain imaging, including the potential for improved characterization of biological function and anatomy in health and disease. The improved Signal to Noise Ratio (SNR) and Contrast to Noise Ratio (CNR) at 7 T are particularly beneficial for susceptibility contrast imaging methods such as Blood Oxygen Level Dependent (BOLD) functional MRI and ultra-high resolution susceptibility weighted imaging (SWI) (Duyn, 2010). These imaging modalities focus on anatomic contrast generated by microscopic susceptibility accompanying de-oxyhemoglobin, iron, or myelin content changes in the tissue.

Unfortunately, the same strong applied field which produces an increased magnetization of the desired microscopic structures also magnetizes macroscopic structures. The resulting perturbations of the background magnetic field ΔB₀ cause unwanted macroscopic phase changes on SWI, as well as uninteresting signal loss in T₂* weighted images and geometric distortion in EPI-based methods (Jezzard and Balaban, 1995) such as fMRI and diffusion. Furthermore, ΔB₀ causes line broadening and reduces the effectiveness of water and lipid suppression (Rosen et al., 1984; de Graaf, 2007) in MR spectroscopy (Juchem and de Graaf, 2016a). ΔB₀ also has undesired effects on RF excitation pulses, including lipid saturation, RF inversion and VERSE pulses (Hargreaves et al., 2004). For 7 T functional brain studies, the most problematic effect from ΔB₀ during excitation is probably the contrast changes in T₁-weighted MPRAGE in poorly shimmed areas which has compelled the use of off-resonance tolerant RF inversion pulses (Wrede et al., 2012) and parallel transmit pulse design optimizations which either utilize the ΔB₀ map during pulse design (Grissom et al., 2006) or trajectory design (Schneider et al., 2014; Davids et al., 2016) or optimize the design over a range of frequencies (Setsompop et al., 2009).

Appropriate control of B₀ shim fields to cancel static macroscopic susceptibility patterns is the first line of mitigation against the adverse macroscopic effects. Since the shim field patterns are of a limited spatial order, they have no harmful effect on the desirable susceptibility effects (which occur on a length scale of the capillary diameter in BOLD or arise from microscopic distributions of iron or myelin in SWI.) In contrast, the undesirable field patterns arise from structures on the centimeter scale, such as the sinuses, ear canals, oral cavity, or bones. Thus an externally applied field with spatial content on this order is needed to cancel it. The shimming process typically involves (1) acquiring low-resolution ΔB₀ field maps over the region/volume of interest, and (2) calculating and applying an optimal linear combination of the basis set of field maps from the available shim coils (subject to constraints on the maximum current in each coil).

Several methods for field mapping and optimal shim field computation have been demonstrated (Kim et al., 2002; Hetherington et al., 2006) and have been recently reviewed (de Graaf and Juchem, 2016) and we do not provide a complete review here. Instead we concentrate on a variety hardware strategies for generating the shim fields. The standard configuration, available on most research scanners, consists of first and second order spherical harmonic field patterns. The 3 first order terms are often generated by adding offset currents to the gradient coils and the 5 second order terms are from separate coils embedded in the gradient coil (de Graaf and Juchem, 2016). This basic configuration of static 1st and 2nd-order spherical harmonic shims has not changed on vendor-provided scanners in 2 decades.

While 1st and 2nd-order spherical harmonic terms are effective at removing the lowest spatial order variations (which are the strongest ones) (Spielman et al., 1998) significantly higher order spherical harmonics are needed to mitigate more localized B₀ offsets (Pan et al., 2012). Fig. 1 shows a typical ΔB₀ field map in the brain after 1st–2nd order shims have been optimized. Severe residual B₀ inhomogeneity in the frontal lobes, temporal lobes, and brainstem remain. Fig. 2 shows how these field patterns effect the phase of a high resolution T₂* weighted image, particularly in the inferior temporal lobe, brainstem and cervical spine.

Fig. 1.

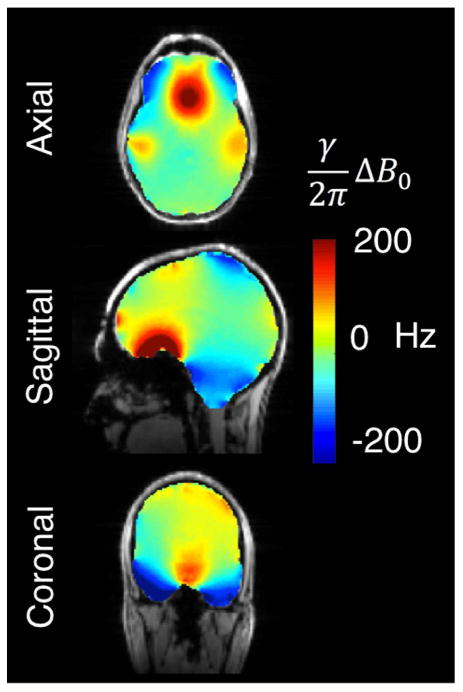
Representative ΔB₀ brain field map acquired at 7 T overlaid on a reference structural image. The FOV has been shimmed with 1st and 2nd order spherical harmonics on a 7 T Siemens scanner. The residual B₀ inhomogeneity is particularly severe in regions bordering the sinuses, ear canals, and oral cavity, especially the orbitofrontal cortex, inferior temporal lobes, and brainstem. The standard deviation of ΔB₀ within the masked region of the ΔB₀ field map, σ_B0^Global, is 51.9 Hz. Field maps are acquired using a two-echo gradient echo sequence with 2.4 × 2.4 mm in-plane resolution, 2 mm slices, and ΔTE = 1.02 ms.

Fig. 2.

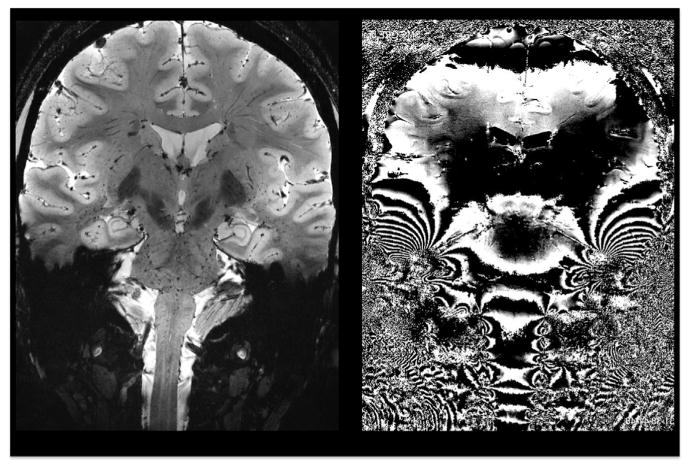
Coronal T₂*-weighted 7 T magnitude (left) and phase gradient echo images showing phase effects of severe spatial B₀ variations. Both static and dynamic B₀ variations in inferior brain areas pose a serious obstacle to structural and functional imaging. Data courtesy of Thomas Witzel, MGH.

In addition to static B₀ offsets, time-varying B₀ fluctuations arising from physiological processes such as respiration pose an even greater challenge. Like the static ΔB₀ sources, these dynamic fields also increase linearly with B₀. Major sources of time-varying ΔB₀ in the brain and spine include the changing volume and oxygenation of air in the lungs, the movement of the chest wall and changes in blood oxygenation over the respiratory cycle. These processes create both global and spatially-varying B₀ field offsets. The problem increases for regions closer to the lungs such as the brainstem and cervical spine (Van de Moortele et al., 2002). The temporal variance added to the signal phase causes issues if the EPI phase corrections or GRAPPA ACS measurements are not performed in the same phase as the respiratory cycle. The result is ghosting and ringing in structural images (Van Gelderen et al., 2007) as well causing time-series instability in EPI data (Hagberg et al.,2012).

To compensate time-varying B₀ fields, shimming hardware must be able to update the shim fields as a function of the respiratory cycle. Ideally it would also allow updates between slice excitations in 2D imaging sequences, providing the ability to optimize the shim fields for each slice rather than accepting a global compromise shim setting. Temporal control of the shim fields is known as dynamic or real-time shimming and is currently not available on standard commercial scanners.

Fortunately, the last half decade has brought significant progress on a variety of flexible, high-spatial order shimming hardware approaches. Based on promising published results, we are optimistic that widespread adoption of these systems will enable neuroimaging users to achieve 7 T B₀ homogeneity comparable to what is seen at lower field (1.5 T and 3 T). This would allow a reduction in negative effects of macroscopic susceptibility to levels comparable to 1.5 T and 3 T imaging while retaining the positive benefits of the increased microscopic susceptibility associated with ultra-high field. We review the performance of two classes of hardware systems that are the furthest developed for 7 T fMRI applications: higher-order spherical harmonic (SH) insert coils (Punchard et al., 2011) and multi-coil (MC) shim arrays of local, independently-driven loops, including both stand-alone MC arrays (Juchem et al., 2011a) and integrated RF-B₀ shim arrays (Truong et al., 2014; Stockmann et al., 2016a). We also assess these two methods in simulated shimming of 7 T B₀ field-map data to assess a broad range of geometries and to allow the two methods to be directly compared. We will consider issues that arise when a shimming system is operated in the scanner environment and integrated with other scanner hardware (magnet, gradients, and RF coils). We then briefly highlight a few less developed strategies for B₀ shimming hardware such as magnetic pebbles and adaptive current networks. Finally, we close with a brief look at the key role that B₀ shimming would likely play in a future, ultra-high field system such as the hypothetical 20 T scanner discussed in this Special Issue.

Unmet needs for improved B₀ shimming in 7T fMRI

Problems caused by static B₀ inhomogeneity

The two classic problems caused by B₀ inhomogeneity in the functional imaging time-series are local T₂* changes and resulting signal drop-out (through voxel dephasing) and image distortion in EPI (or image blurring in spiral acquisitions). The local reductions in T₂* and associated signal drop-out in long TE scans renders the image dark in these regions if the T₂* weighing (TE) is optimized for well-shimmed regions. The dropouts make it difficult to see the BOLD effect. If a shorter TE is chosen, the signal dephasing will be reduced and BOLD detection can be improved, but the acquisition is then no longer optimal for well-shimmed regions of the brain.

The T₂* reduction and dropout comes from phase rolls which accumulate with the voxel. The problem is most acute for a susceptibility gradient in the slice direction, partially because this is often the direction of the largest voxel dimension, but also because phase rolls as a function of space mainly cause a shift of the center of k-space if the gradient is in the phase or frequency encode direction. The reduced T₂* in a voxel also reduces the intensity for the kspace samples at the end of the readout. This can cause a loss of spatial resolution (blurring), especially in spiral-out acquisitions and partial-Fourier EPI.

Fig. 3 shows 7 T brain T₂* maps calculated using a multi-echo gradient-echo scan and co-registered ΔB₀ field maps. The measured T₂* values in areas where B₀ inhomogeneity poses a problem differ from normal values for gray and white matter tissue by up to an order of magnitude. The apparent T₂* value also depends on the acquired voxel size, since large voxels experience more intra-voxel dephasing. Fig. 4 shows signal loss caused by through-slice dephasing as a function of slice thicknesses in 7 T EPI slices acquired with TE = 26 ms. The images demonstrate the recovery of signal lost in susceptibility areas by using thinner slices. Very little drop-out is seen in the 0.75 mm thick slice. Another remedy for through-slice dephasing is the “z-shimming” technique (Constable and Spencer, 1999), which refocuses linear susceptibility gradients with an applied “blip” of the slice-select gradient. Usually, multiple acquisitions with different refocusing blips are used, which unfortunately reduces the temporal resolution of the time series. A single compromise refocusing blip can also be applied (Deichmann et al., 2002) and the slice orientation can be optimized (Deichmann et al., 2003). Finally, we note that the T₂* shortening and signal dropout is mainly a problem of gradient echo imaging. The spin echo refocuses the phase accumulation across the voxel.

Fig. 3.

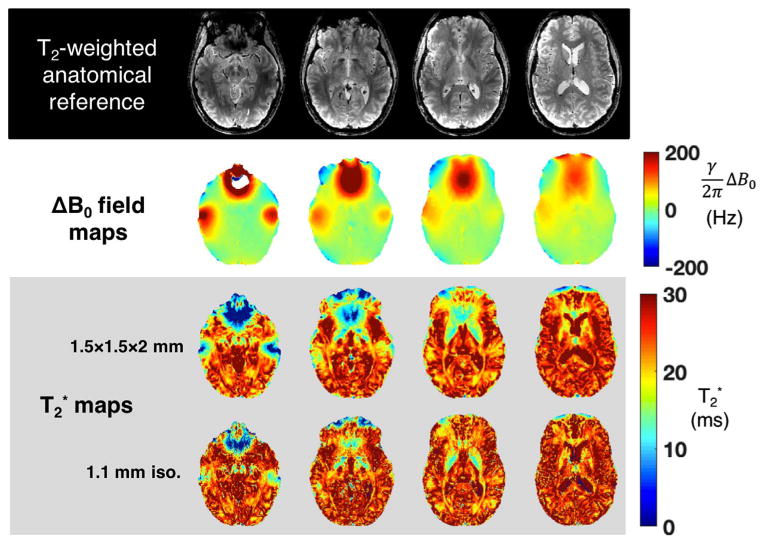
ΔB₀ and T₂* maps from four representative slices of acquired at 7 T on a healthy volunteer. The macroscopic variation in B₀ over each voxel makes it difficult to measure the underlying intrinsic tissue T₂* value. The T₂* maps are acquired at two different resolutions to illustrate the impact of voxel size on this problem. In regions of severe ΔB₀, the mapped T₂* values deviates substantially from the values exhibited by gray and white matter in regions with relatively homogeneous B₀ distributions. T₂* maps are calculated from gradient echo images acquired with the following range of TE values: [3.2, 17.3, 26.1, 32.7, 39.3, 46] ms. FOV = 210 × 183 mm. Resolution of acquired T₂* maps: 1.5 mm in-plane with 2 mm slices; 1.1 mm isotropic.

Fig. 4.

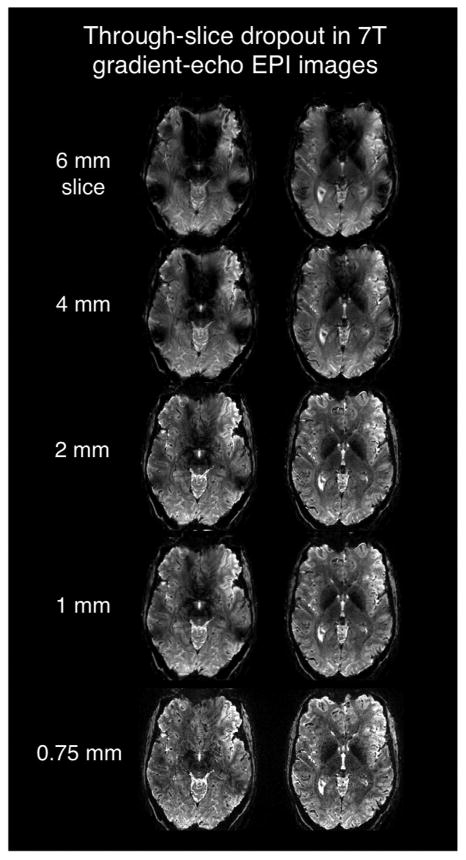
Two slices in the inferior frontal lobes acquired with a T₂* -weighted 7 T gradient echo 2D EPI sequence showing the relationship between slice thickness and signal dropout in regions of high ΔB₀ (above the sinus and ear cavities.) The acquisition used conventional 1st–2nd order global B₀ shimming. EPI parameters: TE/TR = 26/4000 ms, 0.75 × 0.75 mm in-plane, R = 4 GRAPPA acceleration, bandwidth = 1150 Hz, 0.24 effective echo spacing. Images courtesy of Jon Polimeni, MGH.

Perhaps the most well-known and problematic artifact caused by ΔB₀ in EPI scans is geometric distortion, which effects both gradient-echo and spin-echo acquisitions. The B₀ offset in a given voxel applies a k-space phase ramp along the phase encode direction for signals originating in the voxel, leading to a spatial translation in the image domain. The resulting pixel shift depends on the EPI echo spacing (esp) and on the amplitude of ΔB₀. Parallel imaging methods such as GRAPPA (Griswold et al., 2002) skip k-space lines during the echo train and thus reduce the effective echo spacing, esp_eff. Since the phase encode bandwidth is equal to 1/esp_eff, a voxel with a frequency shift of (γ/2π)ΔB₀ = 1/esp_eff will experience a pixel shift equal to the full field-of-view (FOV_y) (Wald, 2012). In units of mm, the pixel shift can be expressed as (Wald, 2012):

$$\mathit{\text{distortion}}\left[\text{mm}\right]=\frac{\gamma }{2\pi }\left[\text{Hz}\right]{\mathit{\text{esp}}}_{\mathit{\text{eff}}}\left[\mathrm{s}\right].\mathit{\text{FOV}}\left[\text{mm}\right]=\frac{\gamma }{2\pi }\frac{\mathit{\text{esp}}.\mathit{\text{FOV}}}{R_y}$$

where γ/2π is the gyromagnetic ratio in Hz and R_y is the acceleration factor.

To take a concrete example for 7 T fMRI, consider signal originating in a voxel where $\frac{\gamma }{2\pi }\Delta B_0=300\text{Hz}$ (∼ 1 ppm), near the most inhomogeneous B₀ area of the prefrontal cortex. Then for an fMRI acquisition with a “typical” echo spacing of 0.5 ms and an in-plane image grid of 100 × 100 pixels (or 20 Hz/pixel in the phase encode direction), the displacement would be (300/2000)*100 = 15 pixels. Using GRAPPA R = 2 or R = 3 acceleration reduces the shift to 10 and 5 pixels, respectively, which is still quite severe.

Fig. 5 compares geometric distortion in gradient-echo EPI slices acquired with the same echo spacing at 3 T and 7 T. The EPI slices are acquired with both phase encode directions (anterior-posterior (A-P) and posterior-anterior (P-A)). This acquisition choice determines the direction the pixel is shifted along the PE axis. Thus comparing the two acquisitions highlights the ΔB₀ induced distortions. As expected, the ΔB₀ frequency offsets and thus EPI pixel shifts are approximately twice as large at 7 T compared to 3 T. The resulting displacement of the ventricles (orange line) and cortical surface in the frontal lobes (blue arrows) is larger at 7 T. Additionally, the through-slice dephasing near the sinus cavities is also more pronounced at 7 T (green arrows).

Fig. 5.

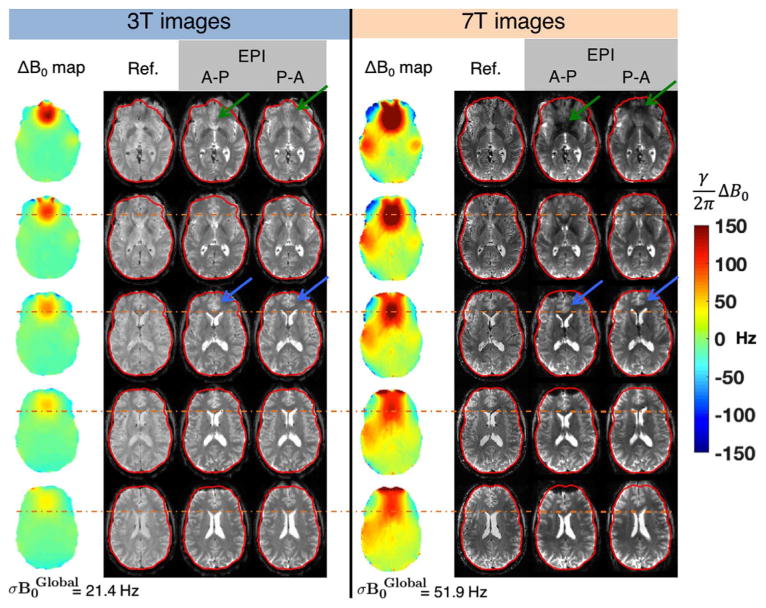
Five slices showing the ΔB₀ field maps, undistorted T2-weighted gradient echo reference images, and co-registered EPI slices acquired on 3 T and 7 T after global 1st–2nd order shims have been applied. The EPI protocols use an identical echo spacing (0.56 ms), resolution (2 mm isotropic), readout bandwidth, and GRAPPA factor (R = 2). The TE was 30 ms at 3 T and 23 ms at 7 T. The EPI images were acquired with phase encoding running both anterior-posterior (A-P) and posterior-anterior (P-A) to more clearly depict the increased geometric distortion present in the 7 T images. For a given echo spacing, voxel shift scales linearly with ΔB₀, resulting in distortion especially in the frontal lobe above the sinuses at 7 T. The outline of the cortical surface from the undistorted reference image is shown in red. The orange dotted line shows the position of the anterior tip of the lateral ventricles in the undistorted image, showing increased displacement in the 7 T EPI. The blue arrows highlight the same effect for anterior cingulate cortex. Signal voids due to through-slice dephasing are also more severe within B₀ hotspots at 7 T, especially in the frontal lobe for slices close to the sinuses (green arrows) and above the ear canals. ΔB₀ field maps are acquired with 2.4 × 2.4 mm in-plane resolution and 2 mm slices.

A variety of post-processing methods exist for unwarping EPI images including ΔB₀ field map-based corrections (Jezzard and Balaban, 1995) and point spread function mapping (Zeng and Constable, 2002). Methods such as TOPUP (Andersson et al., 2003) additionally use spin echo EPI data acquired in both the A-P and P-A directions to estimate the underlying B₀ field map and to correct for pixel shifts. However, all of these methods have limited efficacy in areas with severe ΔB₀ where pixels pile up into singularities that are difficult to unwarp. In these cases, the unwarping procedure may change the intensity of the voxels in the final image, biasing fMRI analysis of the EPI time series. The non-linear warping of the image also incurs some blurring.

On the acquisition side, geometric distortion can be reduced by (a) using parallel imaging with high acceleration factors (R_y) to minimize esp_eff, (b) limiting the phase-encode FOV, (c) using stronger gradients with higher slew rates, and (d) improving the B₀ shimming hardware. Nonetheless, the distortion in high resolution single shot EPI at 7 T remains a problem.

Further improvements beyond global static shimming can be achieved in 2D acquisitions by dynamically updating the shim settings on a slice-by-slice basis during the acquisition (Blamire et al., 1996; Morrell and Spielman, 1997; de Graaf et al., 2003; Koch et al., 2006a). By using the available degrees of freedom to shim a much smaller ROI, dynamic shimming can achieve superior B₀ homogeneity compared to a global optimum. Thus it is desirable that new hardware for high-order B₀ shimming be designed to handle the rapid switching required for dynamic shim updating. This imposes additional requirements on shim current amplifiers, such as high voltage compliance if the coil inductance is large. Also eddy-current pre-emphasis and/or shielding coils might be needed if the shim fields extend to the metallic bore of the scanner.

Time-varying B₀ fields and the need for real-time shimming

In addition to the static ΔB₀ effects described above, artifacts arising from physiology-induced B₀ fluctuations also grow more severe at 7 T, particularly in inferior brain areas (Bianciardi et al., 2013). Recent work suggests that the respiratory cycle explains the largest share of variance (∼ 65%) in the phase of resting-state EPI time-series data (Bianciardi et al., 2014a, 2012). We refer the reader to the article by Sclocco et al. in this Special Issue for further details about the effects of physiological noise on fMRI data.

Some ghosting and ringing artifacts can be removed by using a phase navigator on each shot of a mulit-shot image, sometimes called “phase stabilization”. In this approach, the polarity of the readout gradient is reversed before the end of the TR to acquire an additional navigator readout. However, this approach only corrects for global B₀ fluctuations (though new approaches exist such as “FatNavs” (Gretch et al., 2016)).

The issues associated with the dynamic field changes from respiration have motivated the development of real-time shimming systems using 1st and 2nd order shim fields gated together with a respiratory bellows. This has allowed dynamic cancellation of respiration-induced B₀ fluctuations up to 2nd order (Van Gelderen et al., 2007). While highly effective in reducing artifacts, this approach could be further improved through the addition of higher spatial order shim fields. Recent dynamic shimming simulations based on field maps acquired at different phases of the respiratory cycle have shown significant improvements in time-series stability if 3rd–5th order dynamic shims were available (Bianciardi et al., 2014b). Further work has used field probes (De Zanche et al., 2008) to track respiration induced field offsets rather than depending on predictions from the respiratory bellows (Boer et al., 2012).

Overview of B₀ shim field generation hardware

Passive shimming

In passive B₀ shimming, magnetic materials are placed around or inside the body. When placed in the magnet, they also magnetize in a pattern designed to cancel the ΔB₀ perturbations in the tissue region of interest (e.g. the brain). A similar strategy is also used to shim the empty magnet. Since the main target areas are orbital frontal cortex and the inferior temporal lobes (above the ear canals), a natural target is to place material in the subject's mouth and ears. The Oxford group showed some success with this approach using diamagnetic graphite (Wilson and Jezzard, 2003; Wilson et al., 2002). This approach is typically used in conjunction with the scanner spherical harmonic shims (Juchem et al., 2006).

Although there are advantages of placing the magnetic material in the mouth and ears to be close to the source of the nuisance fields, there are clear disadvantages to this in terms of patient comfort. Passive shims have also been placed outside the body, for example on a cylindrical surface around the head (Koch et al., 2006b). While very high order shim fields can be generated, updating them for patient specific shimming can be time-consuming. Approaches to improving this process have included printing the shims on paper using the magnetic toner found in laser printers (Jesmanowicz et al., 2001) or using ferromagnetic liquids (Shen et al., 2007). Notwithstanding these advances, it remains difficult to implement passive shims on a subject-specific basis and more work is needed to develop a robust workflow. Therefore they are seldom used in research or clinical neuroimaging.

Spherical harmonic shimming

Active shim fields are created from current distributions on wire windings, usually outside the body. This provides convenient control through the current source. Among active shims, coils which generate spherical harmonic (SH) field patterns have, by far, the longest track record of use in MRI (Golay, 1958; Romeo and Hoult, 1984). Commercial scanners now typically have 1st–2nd order coils. Therefore we refer to orders of 3 or more “higher order SH” shims. The SH basis set of order n contains 2n + 1 spatial components. The total number of SH shim coils in a “n-order shim set” is the sum of these components over all the orders present. For example, a SH coil equipped with B₀ shim field terms up to 3rd order will have 1st, 2nd, and 3rd orders present with (2n + 1) = 3, 5, and 7 terms respectively providing a total of 15 shim fields. However, it is common practice to implement only the most important terms in the higher order (n ≥ 3) SH coils.

The fields are orthogonal in the sense that the product of any two different patterns integrated over a spherical surface centered at the origin is zero. This makes their use as a basis set to describe a ΔB₀ pattern very efficient and limits coupling between the coils. We note however that in practice decoupling between coils is not complete, especially between the odd orders and the 1st order gradient fields. The most commonly used SH terms are a subset of the 3rd–4th order terms and occasionally a few of the 5th and 6th order terms (Kim et al., 2016). When high-spatial order SH shim sets have been employed in brain research, the additional coils are typically on an insert coil that is added inside the bore in between the gradient coil and the local RF transmit-receive coil. Fig. 6a shows an example of a commercial SH insert coil with 14 SH added terms (selected SH from 3rd through 5th order). For a discussion of the mathematical properties of the SH fields and the wire patterns used to generate them, we refer the reader to the review chapter by de Graaf and Juchem (2016).

Fig. 6.

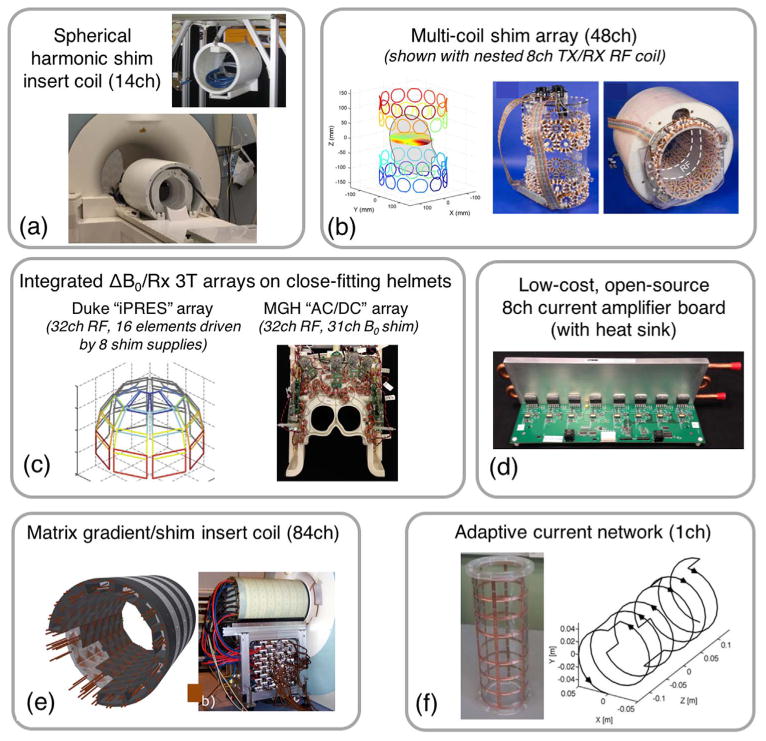
Photographs and diagrams of hardware systems that have been proposed for active, high-spatial order B₀ shimming. (a) High Order Spherical Harmonic shimming system for 7 T MRI with 14 SH channels (up to 5th order) (photos courtesy of Piotr Starewicz of Resonance Research, Inc. and Assaf Tal of the Weizmann Institute). (b) 48ch 7 T multi-coil shim array made with four rings of 100-turn, 4.7 cm diameter shim coils arranged on a elliptic cylinder with a gap to accommodate the RF coils (Juchem et al., 2011a). (c) “iPRES” (Truong et al., 2014) or “AC/DC” (Stockmann et al., 2016a) integrated ΔB₀/Rx coil arrays. These elements use the same conducting loops for RF receive and B₀ shimming on close-fitting helmets (3 T designs shown). (d) Open-source, low-cost current amplifier designed to drive shim coils. (e) 84ch matrix gradient insert coil designed for both spatial encoding and high-order B₀ shimming (Jia et al., 2016). (f) Adaptive current network using 14 MOSFET switches to route current along a grid on a cylindrical surface for tailored B₀ shimming (Harris et al., 2014).

Kim et al. (2016) report 7 T global B₀ shim performance for a state-of-the-art 18-channel SH shim insert coil with 3rd and 4th order terms as well as two 5th order terms. The insert coil improves ΔB₀ in ∼ 40% of voxels over the brain as compared to 1st–2nd order shimming, while degrading ΔB₀ in only ∼ 10% of the voxels. Across 8 healthy volunteers, the authors report an improvement in the standard deviation of ΔB₀ over the whole brain volume (σ_B0^Global) of 25.0 ± 3.3% using the higher-order shim fields (σ_B0^Global decreased from 29.72 Hz to 22.38 Hz). Fig. 7 shows ΔB₀ field maps and EPI slices (esp_eff = 0.75 ms) from this study comparing the performance of 1st–2nd to 1st–4th order shimming. Axial and sagittal ΔB₀ field map slices show improvements in the anterior temporal lobes and inferior frontal lobes. This substantially reduces geometric distortion in the EPI slices, but does not fully mitigate it. The results are likely limited by the limited number of orders used. This constraint arises from practical issues such as available space, efficiency of the coils and coil cooling, and number of available current amplifiers.

Fig. 7.

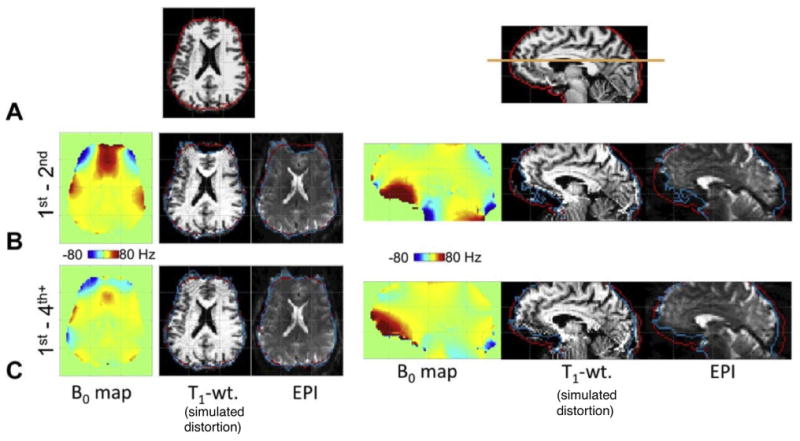
Figure reproduced with permission from Kim et al., (2016). 7 T ΔB₀ field maps, undistorted anatomical T1 images, simulated distortions and EPI acquisitions for global spherical harmonic (SH) shimming. Results for 1st–2nd order terms are compared to 1st–4th order terms achieved using a dedicated high-order SH shim insert coil. Row A: Undistorted reference images for the representative axial and sagittal slices used for the comparison. Row B: results with 1st–2nd order shims applied. Row C: Results with 1st–4th order shims applied. The use of 3rd–4th order shim terms reduces σ_B0^Global by 25% and corrects a significant fraction of the EPI geometric distortion, especially in the prefrontal cortex, bringing the cortical surface into closer alignment with its expected position (the red outline). The EPI acquisition used 2 mm iso. resolution and 0.75 ms echo spacing with no in-plane acceleration.

Dynamic spherical harmonic shimming

Efforts toward further improvement by dynamically switching the SH shims on a slice-by-slice basis have been also been pursued. But dynamic shimming with SH coils requires careful monitoring and compensation of short and long-lived eddy currents induced by the shim coil switching in nearby metallic structures in the bore (especially the gradient coils, 2nd order SH shim coils, and magnet cryostat). The problem is compounded by the fact that unlike imaging gradient coils, shim insert coils do not typically include active shield windings. Depending on the exact geometry and symmetry of the set of coils in the bore, shim coils can induce global B₀ eddy currents as well as linear and higher-order eddy current fields, causing deviations from the desired k-space trajectory. In EPI, this produces image artifacts such as shear distortion and displacement along the phase encode-direction.

The most common method for mitigating the effects of shim coil-induced eddy currents is to add pre-emphasis “overshoot” to the shim and gradient current waveform during shim updating (de Graaf et al., 2003). The pre-emphasized waveform generates additional shim field offsets that counteract the transient fields created by shim coil-induced eddy currents. Global B₀ offsets are handled either with a dedicated 0th order SH coil or by applying a Larmor frequency offset during signal readout or in post-processing. For practical shim coils with multiple channels, the full matrix of cross-coupling terms between the channels must also be considered when designing the pre-emphasis waveform. Koch et al. used pre-emphasis on the 0th–2nd order shim terms to enable dynamic shimming for multi-slice imaging (Koch et al., 2006a) as well as multi-voxel spectroscopy (Koch et al., 2007). Others have noted that slower switching can be used to successfully avoid eddy currents (Hetherington, 2016). Compared to 1st–3rd order static shimming, Sengupta et al. (2011) demonstrate performance gains from combining 1st–2nd order dynamic shimming with static 3rd order shims, achieving reduced distortion and through-slice dephasing in EPI slices. Juchem et al. (2010) report significant gains for 0th–3rd order dynamic shimming as compared with 0th–2nd order dynamic shimming.

Advances in the availability of NMR field probe cameras (Barmet et al., 2008) have enabled accurate measurement of gradient and shim coil impulse response functions (Vannesjo et al., 2013). These functions are used to create a linear time-invariant model of all coil-field dynamics which can then be inverted to obtain pre-emphasis waveforms that null all unwanted dynamics. This approach has been used to achieve 0th–3rd order shim updating with settling times on the order of 1 ms (Vannesjo et al., 2016) or 2 ms (Fillmer et al., 2016). Field camera-monitored dynamic 1st–3rd order SH shimming has been used to acquire fMRI time series EPI slices (Fillmer et al., 2016) that show no visible eddy current artifacts. Notably, limitations on shim amplifier voltage and current headroom prevented the full benefit of the pre-emphasis from being realized in these experiments. This draws attention to the challenges posed by the relatively high inductance of the shim coils; namely, the voltage compliance of the shim amplifier limits the rate at which the shim coils can be switched for dynamic shimming and for playing pre-emphasis waveforms. Furthermore, coupling between the linear gradients and the shim coils (particularly odd-order coils) means that shim amplifiers must have enough bandwidth and voltage headroom to maintain the needed current in the face of a back-EMF induced in the shim coils by the slewing gradient field during the EPI readout.

Overall, the success of the shim hardware setup must be evaluated using the EPI image quality (k-space deviations) as well as temporal stability. In both static and dynamic shimming, temporal stability can be assessed using the tSNR of the EPI time series data. For static shimming, Kim et al. (2016) reports a slight improvement in tSNR for 1st–4th order global SH shims compared to 1st–2nd order shims, with most of the gains occurring in the frontal lobe where the high-order shimming reduces signal loss from geometric distortion and intravoxel dephasing (giving a ∼ 4% increase in activated voxels). This result suggests that the shim currents are relatively stable during the EPI readouts; however, the experiment did not compare tSNR with and without the SH insert coil present in the bore. For the case of dynamic SH shimming, Fillmer et al. (2016) shows resting-state fMRI correlation maps acquired with pre-emphasized higher-order dynamic SH shimming, but the paper does not report the tSNR compared to baseline data acquired with static 1st–2nd order shimming. This is an important figure of merit that would be useful to measure in future work on dynamic SH shimming.

How many spherical harmonic terms are needed?

Pan et al. (2012) simulated B₀ SH shimming up to 15th order on two representative brain slices (one superior and one inferior). The results show that most macroscopic variations are removed with 1st–8th order slice-optimized shimming, leaving only marginal improvements to be gained from even higher order terms. After 1st–8th order simulated shimming, the residual ΔB₀ patterns visibly resemble the contours of the underlying gray matter, white matter, and CSF. However, an analogous simulation has not been shown for whole-brain global shimming. Note that a full set of SH field coils for 1st to 8th order requires 80 bore-sized coils.

Rather than simply adding more SH fields to the basis set, an alternative approach is to find a basis set that represents the particular spatial patterns of ΔB₀ occurring in the brain using fewer basis field terms. Adalsteinsson et al. (1999) applied a singular value decomposition (SVD) to multiple brain ΔB₀ field maps and used the singular vectors as orthogonal shim basis fields. In simulations, using this approach with just the first singular vector field provided better shim performance than 1st through 3rd SH fields. Of course, the orthogonal basis SVD-generated field patterns may be challenging to generate in practice and may not even satisfy Maxwell's equations. Also, the effects of variations across individuals needs to be analyzed. Nonetheless, the analysis in Adalsteinsson et al. (1999) invites the exploration of basis sets other than spherical harmonics for shimming.

Multi-coil shim arrays

In this approach, the orthogonality of the shim field basis set is discarded in exchange for practical benefits such as ease of construction. The matrix shim (aka “multi-coil” shim) approach has a long literature in the NMR spectroscopy community. Motivated by a desire to reduce power consumption, Konzbul et al. used a specially-designed set of coils driven in different linear combinations in order to generate one or more SH fields for B₀ shimming (Konzbul and Svéda, 2000). By contrast, the past decade has seen a surge of effort to evaluate generic arrays of local shim coils independently driven by DC currents to generate non-orthogonal shim fields for B₀ shimming. The goal of the non-orthogonal multi-coil (MC) shim approaches is the same as that of higher order SH shim sets: To obtain the high spatial order field patterns needed to cancel the spatially localized ΔB₀ field variations. Because the MC basis fields are not orthogonal, it is clear that more channels will be needed to achieve a given level of performance. Ideally, the ease of their commoditized construction, improved dynamic control, and high efficiency will overcome the negatives of losing orthogonality.¹

Because the multi-coil (MC) shim coils are typically simple loop geometries placed close to the anatomy, they can be driven and quickly switched using low-cost, low-voltage current amplifiers. The reduced voltage compliance requirements arising from the low inductance of MC shim loops also means that both their own back-EMF (induced in the loops by slewing the current in the coil) is reduced as well as the induced EMF from gradient slewing. Together this means low-voltage amplifiers can be used. Additionally, the low inductance of the MC loops and their physical separation from metallic bore structures (gradient shield and magnet) means that dynamic MC shimming does not create significant eddy currents, although we note that a small SH shim set distanced from the bore will also have improved eddy current performance relative to standard SH coil sets (which are adjacent to the magnet bore). Finally, by placing the coils relatively close to the head, B₀ offsets in the brain large enough for 7 T shimming can be generated using modest current amplitudes on the order of a few amperes.

As mentioned above, the ΔB₀ fields patterns of MC arrays typically form a non-orthogonal basis set. Nonetheless, a simple linear optimization problem can be set up to solve for the currents that optimize the shim in a specific ROI.

Building on early MC shim coils for mice (Juchem et al., 2011b), recent work has specifically targeted 7 T human imaging. Fig. 6b shows a MC array designed for dynamic shimming of the human brain at 7 T (Juchem et al., 2011a). The system uses 48 channels of 100-turn, 4.7 cm diameter coils arranged in four rings on an elliptic cylinder with a gap to accommodate a nested 8ch transmit-receive RF coil. The loops are driven by low-voltage, real-time amplifiers that use current-feedback control to supply stable shim currents of up to ±1 amp per channel (Nixon et al., 2010).

The 48 channel MC shim array outperformed dynamic 1st–3rd order SH shimming in the brain (Juchem et al., 2011a). Fig. 8 compares the efficacy of global 1st–3rd order shimming and 48ch MC dynamic shimming for improving EPI image quality and T₂* maps (Juchem et al., 2015a). Global SH shimming removes smoothly-varying components of B₀, but provides limited improvement in areas with steep B₀ variation such as the frontal lobes. Across 5 subjects, the average σ_B0^Global values achieved with global 1st–3rd order shims and dynamic MC shims were 32.3 Hz and 13.3 Hz, respectively, an impressive 59% improvement. EPI slices also showed substantially improved distortion. The improved shimming is also evident in the T₂* maps although problems remain in orbital frontal cortex. In these experiments, MC shim settings were updated in under 1.5 ms during a 300 ms inter-slice delay without causing any apparent artifacts in the EPI slices (TR was 4.2 s). Simulations of shim performance in Juchem et al. (2015a) show that the 48ch MC shim system can in principle outperform global 1st–5th order and dynamic 1st–4th order SH shimming. Other researchers have simulated the added benefit of using irregular optimized loop shapes (Zivkovic et al., 2016; While and Korvink, 2014).

Fig. 8.

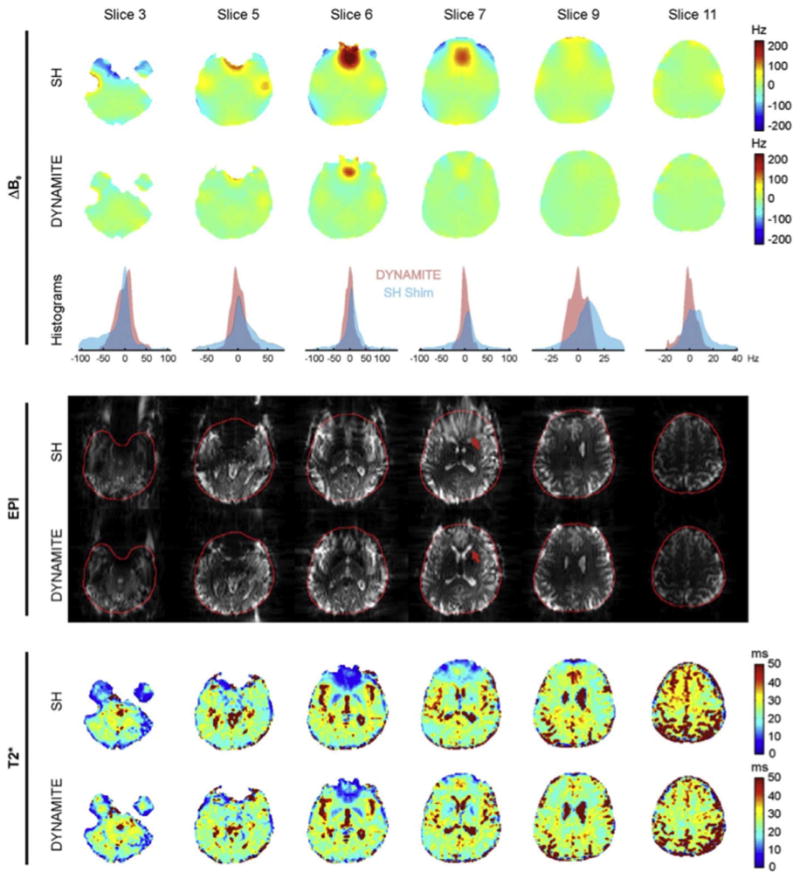
Reproduced with permission from Juchem et al. (2011). Data from 6 brain slices comparing experimental 1st–3rd order global SH shimming with 48ch single slice optimized dynamic MC shimming using the array shown in Fig. 6b. For each of the two shim methods, ΔB₀ field maps, voxel ΔB₀ histograms, multi-shot EPI images, and T₂* maps are shown. Global SH shimming removes smoothly-varying components of B₀, but provides limited improvement in areas with steep B₀ variation such as the frontal lobes. Dynamic MC shimming helps mitigates these areas of peak ΔB₀ and reduces geometric distortion both inside the brain (red arrow) and at the brain surface. Signal voids caused by through-slice dephasing are also mitigated. After MC shimming, the T₂* distributions more closely match the values expected for the underlying tissue types (especially in the frontal lobe region of slice 7). The MC shim currents were updated in 1.5 ms and no artifacts were observed due to eddy currents or other transient effects. Across 5 human subjects, the average reported σ_B0^Global values were 32.3 Hz for the global 1st–3rd order shims and 13.3 Hz for the dynamic MC shims, a 59% difference.

Juchem et al. (2010a) have shown that MC shim arrays can generate SH fields within a target imaging ROI with efficiencies equal to or greater than those of SH coils with conventional wire patterns. Linear combinations of MC shim fields were used to approximate 1st–3rd order SH fields and the resulting efficiency was quantified in units of Hz/A/meter of wire used. According to this metric, the efficiency ratio (MC/SH) within the ROI is approximately 1, 1.6, and 3.5 for 1st, 2nd, and 3rd order SH fields, respectively. This suggests that the efficiency of SH coils decreases relative to MC shim arrays as the spatial order of the fields increases. The fact that MC arrays can generate SH field patterns immediately suggests that they could be used to generate linear encoding fields for slice-selection, readout, and phase encoding (Juchem et al., 2010a, 2015b). Using this approach, simultaneous spatial encoding and B₀ shimming has recently been demonstrated using MC arrays (Rudrapatna et al., 2017). While local MC arrays are unlikely to rival the strength of conventional gradient coils anytime soon, the MC arrays could be used for supplementary spatial encoding or unconventional MR scanner applications (M. Jayatilake et al., 2016). These geometries ultimately come to resemble PatLoc-style coils (Hennig et al., 2008).

Taking this approach to a larger spatial scale, an 84ch matrix insert coil has been constructed to perform flexible PatLoc spatial encoding at 3 T using linear and/or nonlinear spatial encoding fields (Littin et al., 2015; Layton et al., 2016; Jia et al., 2016). Fig. 6e shows a diagram of the coil design and photograph of the completed insert coil. Simulations of 3 T brain shimming show that this coil outperforms 4th order SH shimming even when constrained to 10 amps per channel (Jia et al., 2016; Littin et al., 2017). Even better performance is achieved when the current limit is relaxed. Because the inductance of each element is relatively large, and fast gradient switching is desired, the voltage and current requirements for the amplifiers are high; more resembling gradient amplifiers than shim amplifiers. Such a configuration would be expensive to drive with 84 independent channels. Thus, recent work has explored using a switching network to route a few amplifier's outputs through a optimized subset of the matrix coils (Yu et al., 2015). Progress has also been made on a moderate-cost ( < 1000 Euros/ch), 100 A, 100 V current amplifier for driving this type of coil (Yu et al., 2016).

Multi-coil arrays have also been proposed for generating non-linear encoding fields for imaging in inhomogeneous magnets designed to be lightweight and portable (Vaughan et al., 2016). In a spatiotemporal encoding scheme called STEREO (“steering resonance over the object”), a frequency-swept RF excitation pulse is played while time-varying gradient fields are used to move the excited ROI through the FOV during the pulse, producing sequential excitation and echo formation (Snyder et al., 2014). By suitably modulating the RF pulse and/or gradient waveform, both B₀ and B₁ inhomogeneities can be compensated. A 64 channel multi-coil array of loops arranged on a cylinder has been proposed to generate nonlinear STEREO encoding fields for controlling the shape and location of the excited ROI at each point in time during the RF pulse (Jayatilake et al., 2017).

Outside of the brain, a 24ch MC shim array has recently been demonstrated for high-spatial order static and dynamic shimming of the spine (Topfer et al., 2016), where severe artifacts occur in EPI data both due to susceptibility gradients and respiration-induced field fluctuations. It was previously shown that EPI data acquired to study functional connectivity between the brain and spine benefits from dynamically updating the linear shims in between slice acquisitions, rather than trying to globally shim the large brain-spine volume (Finsterbusch et al., 2013). MC shimming and dynamic shim updating thus appear to be a particularly promising approach for use in the spine.

One approach to the design of new MC arrays is to target specific anatomy with a small number of coils. Hsu and Glover showed in 2005 that three intra-oral active shim coils improve B₀ homogeneity and reduce through-slice dephasing in the frontal lobes at 1.5 T (Hsu and Glover, 2005). Local shim coils placed in the mouth or over the nose have also been used at 3 T to reduce signal dropout in single-shot EPI (Wong and Mazaheri, 2004). Building on this work, Juchem et al. (2010b) used 6 shim coils strategically positioned over the face area to improve frontal lobe B₀ homogeneity at 7 T. The judicious use of even a single local shim coil has been shown to benefit B₀ homogeneity in the cervical spine region (Biber et al., 2012).

Integrating B₀ shim field generation into the RF receive coil

As the MC array elements become close to the body and more numerous, they start to compete with the RF receive array for space. One approach to solving this problem is to unify the B₀ shim field production and RF receive functionality into the same physical coil winding. This is typically achieved by using inductive chokes to bridge DC current into the RF coil loop and across RF tuning capacitors. This approach was introduced in 2013 and is referred to as either an “Integrated parallel reception excitation and shimming” (iPRES) coil (Han et al., 2013a) or an “AC/DC” coil (Stockmann et al., 2013). Initial work was followed by 8 B₀ shim channel (Truong et al., 2014) and 31 B₀ shim channel demonstration systems (Stockmann et al., 2016a) that were integrated into 3 T 32ch RF receive arrays. We refer to the approach here as an integrated ΔB₀/Rx array. We change the name of this approach because the original iPRES acronym includes the presence of Tx functionality which is not present in most of the demonstrations, and our original term, AC/DC, is not immediately associated with RF reception (the “AC” part), nor is the B₀ shim always “DC”.

Table 1 attempts to summarize the design goals and benefits of SH and MC approaches as well as Rx arrays. The field patterns of MC shim array coils and Rx array coils are not generally orthogonal (like SH basis fields), but it is desirable for them to be independent. In general, as many coils/degrees of freedom as possible are needed to improve the nulling of high-spatial order ΔB₀ fields while benefiting the parallel imaging performance of RF arrays. The efficiency of a given coil is determined by the magnitude of the transverse field component (for RF Rx coils) or the longitudinal (z) component (for B₀ shim coils) at the region of interest. The magnitude of the effective component is affected by size, distance, orientation and the number of turns in the coil, although practical considerations typically limit RF Rx coils to a single turn.

Table 1. General guiding principles for designing integrated ΔB₀/Rx arrays in which the RF receive arrays and multi-coil (MC) shim arrays use the same conductor windings.

Design principle	Benefit for RF receive arrays	Benefit for MC shim array
Place and orient loops optimally with respect to the region of interest.	Increased RF coverage, sensitivity and SNR	Generate B0 offsets in the body with high efficiency
Use as many coils/degrees of freedom as possible	Improve parallel imaging performance	Cancel high-spatial order B0 inhomogeneity

A departure of the integrated ΔB₀/Rx approach from the previous MC shim arrays was to utilize the same close-fitting helmets used in RF arrays, rather than cylindrical geometries. Further thought has suggested other methods to integrate the shim current with the RF coil circuit (Winkler et al., 2015) and geometries that split the shim currents to form two or more shim loops per RF loop (Darnell et al., 2017).

Fig. 6c shows prototype 3 T configurations of integrated ΔB₀/Rx brain arrays based on conventional RF coil geometries. Measured RF SNR maps before and after conversion to an integrated ΔB₀/Rx array show only a modest impact, with no change measured in the Duke coil (Han et al., 2013b) and a 13% average SNR decrease measured in the MGH coil (Stockmann et al., 2016a). No significant change was observed in the RF inter-element noise correlation matrix or parallel imaging performance (Stockmann et al., 2016a).

To drive DC currents in the loops, a low-cost, open-source, current-feedback controlled amplifier has been developed that can supply up to 5 amps per channel and operates at 12 V (Fig. 6d) (Arango et al., 2016). The feedback control loop has sufficient bandwidth to maintain stable currents during EPI readout gradient slewing. Digital commands for updating all shim settings can be issued in less than 1 ms. In single-channel tests, the output was ramped from 0 to 2 A starting 500 μs before the beginning of the RF excitation pulse, without introducing any artifacts (TR = 9 s) (Arango et al., 2016). Due to their low inductance (∼ 10 μH), individual ΔB₀/Rx coil elements can be switched very quickly ( < 50 μs). The open-source design and circuit board files have been published online (Arango et al., 2016).

Fig. 9 shows 3 T ΔB₀ field maps and EPI slices acquired by the MGH integrated shim and receive array after static slice-optimized shimming (Stockmann et al., 2016a). Compared to global 1st–2nd shimming alone, the MC shim reduces the standard deviation in each slice, σ_B0^Local, by as much as 55%. This mitigates the majority of the geometric distortion in the EPI slices and brings the A-P and P-A phase encoded images into closer alignment.

Fig. 9.

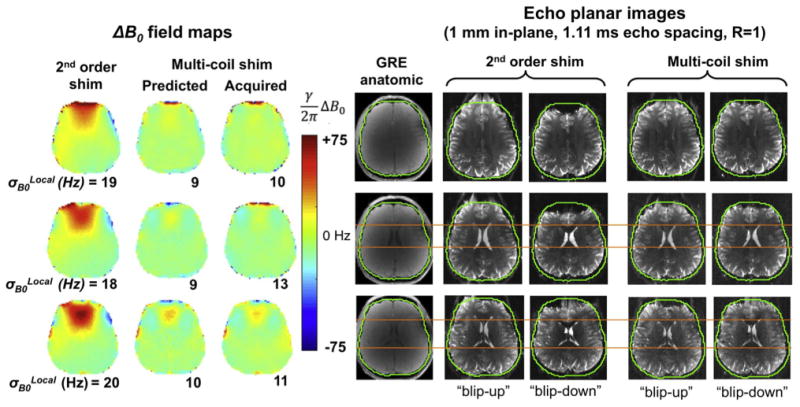
Reproduced with permission from Stockmann et al. (2016a). Demonstration of static slice-optimized B₀ shimming performed at 3 T with the integrated 32ch ΔB₀/Rx array coil described in Stockmann et al. (2016a) and shown in Fig. 6c. Three representative slices are compared for conventional global 2nd order shims and for global 2nd order + slice optimized MC shims. The data shown include ΔB₀ field maps, undistorted anatomic images, and 1 mm EPI acquired with both anterior-posterior and posterior-anterior and anterior-posterior phase encoding directions and with echo spacing = 1.11 ms and no in-plane GRAPPA acceleration to exaggerate the distortion. The predicted and acquired ΔB₀ field maps agree relatively well. MC shimming reduces the standard deviation of ΔB₀ in each slice, σ_B0^Local, by up to 55%. The orange line shows reduced distortion with MC shimming at the anterior aspect of the lateral ventricles. EPI parameters: 1 mm in-plane, 2 mm slice thickness, TE/TR = 65/18,940 ms, 6/8 partial Fourier, readout bandwidth 1190 Hz/pixel.

Stockmann et al. (2016a) show B₀ shimming simulations of array sizes ranging from 8 to 128 channels, constrained by a maximum DC current of 2.5 A per channel. The simulations are performed on an in vivo field map acquired at 3 T. Performance improves with channel count even though the diameter of the loops decreases. Alternatively, following the work of Juchem et al. (2010b), we evaluate a “hybrid” integrated ΔB₀/Rx array design consisting of 32 ΔB₀/Rx coils on the helmet plus 8 additional shim-only coils placed over the face for targeted shimming of the prefrontal cortex (Stockmann et al., 2016b). Another path forward is to reduce the channel count while minimizing loss of shim performance, simplifying the design and making it more attractive for adoption on clinical scanners. Toward this end, we have used a genetic algorithm in simulations of a 40 channel shim array to find optimal sub-arrays that perform nearly as well as the full array while using only half of the channels (Stockmann et al., 2016b).

The integrated ΔB₀/Rx approach has recently been extended to 7 T. Fig. 10a shows early results for a 7 T ΔB₀/Rx prototype with 31 RF Rx channels and 31 ΔB₀ channels, but where 6 of the ΔB₀ shim channels (placed over the face) do not have Rx functionality. Adding the B₀ shim components (wires and chokes) to the coil caused a ∼5–10% average SNR loss in phantom measurements compared to the benchmark before these components were added. This loss is consistent with previous SNR maps acquired on single loops (Stockmann et al., 2013). Similarly, a modest 5% reduction in transmit coil efficiency was observed. Fig. 10b shows measured brain ΔB₀ field maps in the three cardinal planes for one subject acquired with 2nd-order global shimming and with both global and dynamic slice-optimized MC shimming. Marked improvements are seen in the inferior frontal and anterior temporal lobes, especially with dynamic shimming, but a few areas also become worse (especially the anterior edge of the frontal lobes). Compared to the 2nd-order shim baseline, the ΔB₀/Rx coil reduces σ_B0^Global by approximately 37% in global MC shimming and 56% in dynamic MC shimming. With dynamic MC shimming the σ_B0^Global is thus reduced to almost what is expected for a 3 T acquisition. Fig. 10c shows a representative EPI slice acquired with anterior-posterior and posterior-anterior phase encoding directions to highlight the distortion (1.1 mm in-plane, R = 3 GRAPPA undersampling, esp_eff= 0.27 ms). The MC shims reduce geometric distortion over most of the frontal lobes, as demonstrated by the reduced displacement of the anterior aspect of the lateral ventricles. The shims do not fully remove the distortion at the anterior edge of the brain, revealing the performance limits of the 31 channel ΔB₀/Rx array configuration tested.

Fig. 10.

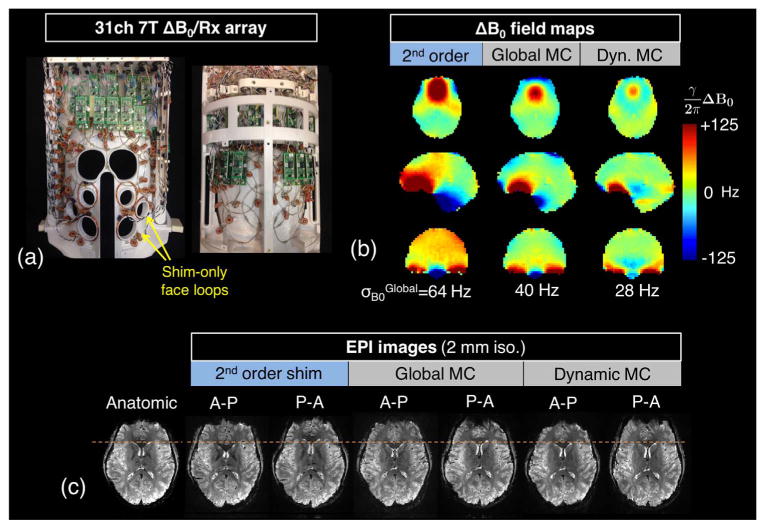
Early B₀ shim results and EPI distortion correction using a prototype 7 T 31ch ΔB₀/Rx array built on a close-fitting helmet. (a) Photograph of the top and bottom halves of the coil showing 6 ΔB₀ shim-only loops added over the face for targeted shimming of the frontal lobes. (b) In vivo ΔB₀ field maps shown in the three cardinal planes acquired with global 2nd-order shimming, global multi-coil (MC) shimming, and dynamic MC shimming. (c) A representative EPI slice acquired for the three shimming cases. Both posterior-anterior and anterior-posterior phase encoding directions are used to emphasize geometric distortion. The slice-optimized MC shims significantly reduce distortion in unaccelerated EPI images, bringing features such as the anterior tip of the lateral ventricles into closer alignment with an undistorted anatomic image (orange dotted lines). Shim currents were constrained to 2.5 A per channel and 20 A total. EPI parameters: 200 × 200 mm in-plane FOV, 1.1 mm in-plane, 2 mm slice, GRAPPA R = 3, echo spacing 0.81 ms (esp_eff = 0.27 ms), 7/8 partial Fourier, BW = 1544 Hz/pix, TE = 26 ms, TR = 2710 ms, flip angle = 90°. The contrast-matched reference image uses a 1 mm in-plane gradient echo acquisition.

Simulations of very high order 7 T B₀ shim arrays

Several simulation studies have been performed to assess the benefit of even higher channel number shim arrays and SH order (Stockmann et al., 2016a; Juchem et al., 2015a; Han et al., 2013b). Fig. 11 shows visualizations of the MC geometries ranging from 8 to 128 channels, including several of the geometries that have already been constructed and tested. The figure compares both global shimming and dynamic slice-optimized shimming. Given the growing use of Simultaneous MultiSlice (SMS) acquisitions (Feinberg and Setsompop, 2013) with MultiBand (MB) factors of at least 2 or 3, we also assess slice-optimized shimming for those case. The slice locations studied are shown in Fig. 12b. Kim et al. (2016) observed that as the MB factor increases, the slice-optimized result will approach the global shimming result.

Fig. 11.

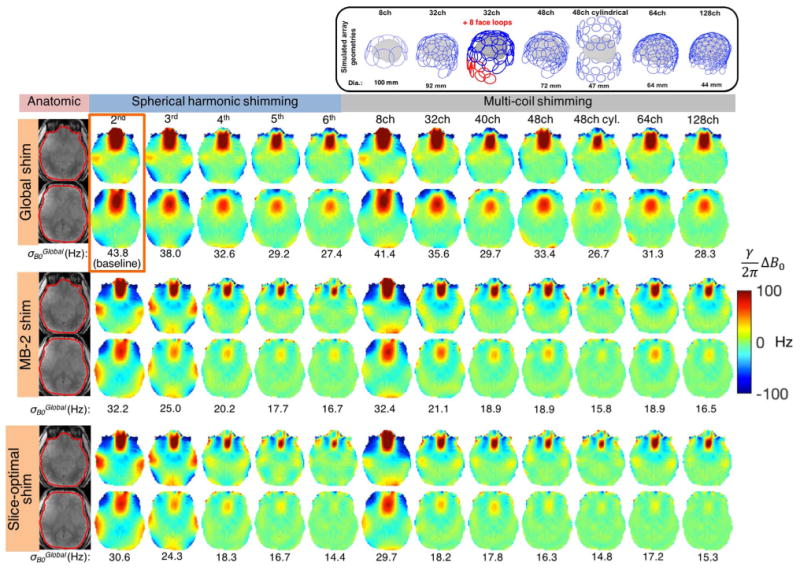
Simulated B₀ shimming for multiple high order shim configurations tested on an acquired 7 T brain ΔB₀ field maps. We assess 2nd through 6th order SH terms along with 7 multi-coil (MC) shim geometries are shown in two representatives slices. Global shimming, slice optimized shimming and optimization of 2 slices for Simultaneous MultiSlice (SMS) acquisitions are compared. The baseline 1st–2nd order SH global shim is shown in the orange box. For both SH and MC shimming, slice-optimized shimming performs better than global shimming, as expected. However, for almost all of the coils, MB-2 shim performance is nearly as good as slice-optimized shimming, demonstrating the flexibility of the high-spatial order shim basis sets to simultaneously shim two slices separated by a gap. The constrained optimization for the MC setups used maximum current amplitudes of 3 A/ch and 50 A/total.

Fig. 12.

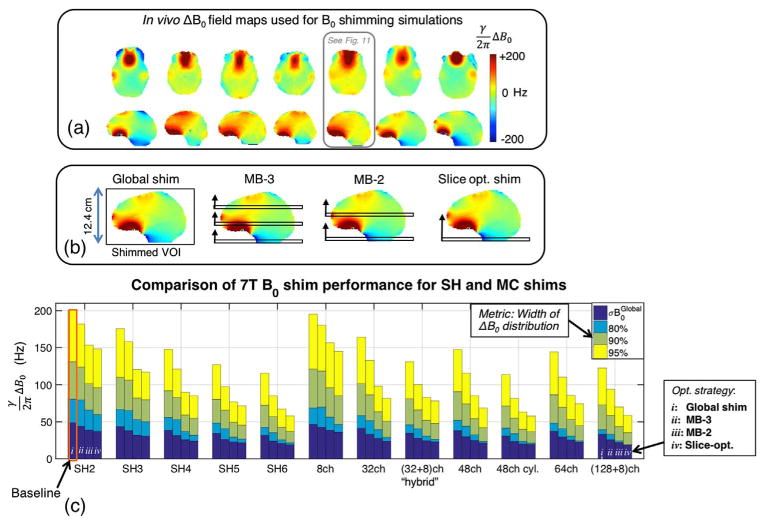
Simulated shim performance for the high order shim hardware configurations shown in Fig. 11. (a) Set of seven brain 7 T ΔB₀ field maps acquired on healthy volunteers that were used in the simulations. Results for the ΔB₀ field map boxed in blue are shown in Fig. 11. (b) Diagram of the four shim strategies simulated: global, MB-2, MB-3, and single slice-optimized. (c) Bar graph showing the 95%, 90%, and 80% residuals as well as σ_B0^Global for simulated shimming over all field maps (error bars reported in Table 2). Global, MB-2, MB-3, and slice-optimized results are reported from left-to-right in the bar cluster for each shimming system. As expected, slice-optimized shimming performs better than global shimming, since it requires fewer degrees of freedom to shim a single slice as compared to a whole brain. For both SH and MC shims, dynamic shim updating significantly improves σ_B0^Global and the residuals for SMS acquisitions as compared to global shimming. While shim performance degrades as the number of SMS slices increases, both MB-2 and MB-3 still substantially outperform global shimming. The biggest improvement over baseline global 2nd order shimming (orange box) was provided by slice-optimized 6th order SH shims and 48ch cyl. MC shims (∼ 60% reduction in σ_B0^Global).

The simulations shown in Figs. 11 and 12 were performed using 7 T ΔB₀ field maps acquired on seven healthy volunteers shimmed globally up to 2nd order (12.4 cm of coverage in the superior-inferior direction). The brain field maps were masked using FSL Brain Extraction Tool (Smith, 2002) and phase unwrapped using FSL PRELUDE (Jenkinson et al., 2012). The ΔB₀ field profiles for each element were calculated using the Biot-Savart law (Lin, 2005). Optimal shim currents were calculated using the “fmincon” Matlab function with the Interior Point Method selected for the solver. The optimization used a root-mean-square objective function on ΔB₀ within the brain mask and a 3 A per channel constraint on the maximum current in an element (50 A total per array). In all MC simulations, 0th–2nd order SH fields are included in the basis set for global shimming. But for the dynamic slice-optimized and SMS simulations for the MC cases, only the 0th–1st order SH shims are updated on a slice-optimized basis, while the 2nd order shims are applied once globally. This choice reflects the fact that the 2nd order SH shims can not be updated dynamically on most conventional scanners.

We have made all of the aforementioned Matlab scripts available online, including scripts for processing brain ΔB₀ field maps, calculating ΔB₀ fields for MC array geometries, and finding optimal MC shim current amplitudes for shimming a target ROI (Stockmann and Wald, 2016).

Fig. 12c and Table 2 display the frequency range containing 95%, 90%, and 80% of the residual ΔB₀ and σ_B0^Global for simulated shimming across all 7 subjects (adopting the metrics used in de Graaf and Juchem (2016) and Juchem et al. (2015a) to better characterize the typically non-gaussian distribution of off-resonance in vivo). Fig. 11 shows three representative ΔB₀ field map slices for one of the subjects for global, slice-optimized, and MB-2 shimming. For global shimming, the simulations show an approximately 25% improvement in σ_B0^Global with the addition of 3rd–4th order spherical harmonics as compared to 1st–2nd order shimming; which agrees with the simulations reported by de Graaf and Juchem (2016) as well as the 1st–4th order experimental shimming data (Kim et al., 2016).

Table 2.

Performance metrics for B₀ shimming simulations of spherical harmonic and multi-coil shim array setups applied to seven in vivo 7 T brain ΔB₀ field maps. Mean values and error bars for three ΔB₀ residuals and σ_B0^Global (both in Hz) over all slices in the brain are reported. The mean values of each metric are also plotted in Fig. 12c. The error bars were difficult to visualize in Fig. 12c and are therefore included in this table for completeness.

B0 shimming simulation performance metrics
Scenario	Metric (Hz)	Spherical harmonic shim basis set					Multi-coil shim array
		2nd order	3rd order	4th order	5th order	6th order	8ch	32ch	32ch + 8ch	48ch helmet	48ch cyl.	64ch	128ch
GLOBAL	95% residual	200.5 ± 31.4	175.6 ± 32.1	147.8 ± 28.9	127.0 ± 24.0	115.5 ± 21.0	195.2 ± 35.2	164.4 ± 31.1	131.0 ± 25.4	147.6 ± 27.6	113.7 ± 23.9	144.2 ± 29.9	122.7 ± 22.5
	90% residual	131.0 ± 17.6	110.0 ± 14.6	92.0 ± 13.4	80.4 ± 11.7	72.4 ± 10.0	121.1 ± 18.0	101.3 ± 12.8	81.0 ± 12.3	90.9 ± 11.2	71.5 ± 12.2	86.6 ± 13.4	72.6 ± 9.8
	80% residual	80.6 ± 7.2	66.5 ± 6.9	55.9 ± 6.5	48.3 ± 6.2	42.4 ± 6.2	68.8 ± 8.7	58.4 ± 6.0	45.9 ± 6.6	52.0 ± 4.0	41.6 ± 6.1	48.0 ± 6.4	39.3 ± 6.1
	σB0,GLOBAL	48.7 ± 6.2	43.5 ± 6.3	38.7 ± 6.3	34.7 ± 6.0	31.7 ± 5.5	46.6 ± 6.6	41.2 ± 6.2	34.8 ± 5.5	38.1 ± 5.9	30.9 ± 6.0	37.3 ± 6.2	33.2 ± 5.4
MB-3	95% residual	182.1 ± 29.1	158.0 ± 28.1	121.3 ± 20.6	97.4 ± 19.2	85.0 ± 16.2	180.3 ± 32.5	133.0 ± 22.1	100.1 ± 19.8	115.5 ± 22.8	81.7 ± 15.1	110.1 ± 23.1	94.0 ± 18.2
	90% residual	124.0 ± 15.5	106.0 ± 14.7	82.9 ± 10.3	65.6 ± 10.3	56.9 ± 8.9	118.5 ± 16.3	86.4 ± 11.4	66.0 ± 10.2	74.0 ± 11.3	55.2 ± 8.6	69.6 ± 11.6	58.7 ± 9.3
	80% residual	79.5 ± 6.1	65.2 ± 7.8	52.9 ± 6.3	40.7 ± 6.1	35.4 ± 5.3	69.8 ± 7.7	51.4 ± 5.7	40.5 ± 5.9	44.3 ± 5.3	34.1 ± 5.4	40.6 ± 5.9	33.0 ± 3.8
	σB0,GLOBAL	44.0 ± 6.5	38.0 ± 6.5	31.5 ± 5.8	26.3 ± 5.8	23.9 ± 5.4	42.8 ± 6.9	33.3 ± 5.7	27.7 ± 5.7	30.0 ± 6.3	23.4 ± 5.3	29.5 ± 6.4	25.8 ± 5.4
MB-2	95% residual	153.6 ± 29.4	120.6 ± 21.3	89.9 ± 15.6	76.8 ± 12.8	67.5 ± 10.6	156.6 ± 30.8	97.9 ± 19.1	78.3 ± 14.0	68.5 ± 16.8	57.9 ± 9.4	74.4 ± 16.8	58.8 ± 12.3
	90% residual	101.4 ± 15.4	82.0 ± 12.9	59.5 ± 8.5	49.3 ± 7.5	42.9 ± 5.7	96.0 ± 14.5	63.6 ± 10.0	52.0 ± 7.2	54.4 ± 8.4	40.0 ± 5.2	53.1 ± 8.1	43.4 ± 6.0
	80% residual	65.7 ± 7.5	53.0 ± 7.5	36.9 ± 4.4	29.4 ± 4.4	25.5 ± 2.9	56.5 ± 7.4	39.4 ± 5.1	30.8 ± 4.1	32.4 ± 4.1	23.5 ± 2.9	30.8 ± 4.3	24.3 ± 2.6
	σB0,GLOBAL	38.9 ± 6.6	32.0 ± 6.0	25.8 ± 5.1	22.8 ± 5.1	21.0 ± 4.8	38.8 ± 6.7	27.6 ± 5.6	24.5 ± 5.0	25.0 ± 5.3	20.3 ± 4.8	25.3 ± 5.3	22.1 ± 4.7
SLICE	95% residual	148.3 ± 29.1	116.9 ± 19.6	85.2 ± 15.0	71.7 ± 12.9	58.0 ± 9.2	145.2 ± 29.5	81.7 ± 15.0	78.3 ± 13.8	68.5 ± 10.3	57.9 ± 8.3	74.4 ± 12.4	58.8 ± 7.7
	90% residual	95.6 ± 15.8	79.9 ± 13.1	54.7 ± 8.8	45.4 ± 7.2	37.0 ± 5.3	85.1 ± 13.0	50.9 ± 8.0	47.7 ± 7.1	41.9 ± 5.0	36.5 ± 4.4	44.6 ± 5.8	35.4 ± 3.6
	80% residual	59.7 ± 7.8	50.0 ± 6.9	32.1 ± 4.7	26.7 ± 4.0	21.6 ± 3.2	46.5 ± 5.4	29.0 ± 3.7	26.6 ± 3.2	23.5 ± 2.6	21.2 ± 2.5	24.3 ± 2.8	19.1 ± 2.4
	σB0,GLOBAL	37.2 ± 6.7	30.7 ± 5.6	23.9 ± 5.2	21.5 ± 5.1	19.0 ± 4.8	36.1 ± 6.3	23.7 ± 5.0	23.0 ± 4.9	21.2 ± 4.7	19.3 ± 4.8	22.7 ± 4.9	20.0 ± 4.3

For all basis fields, slice-optimized shimming performs better than global shimming, as expected. Surprisingly, the MB-2 performance is almost as good as slice-optimized shimming, for all the arrays that have more than one row of elements. For example, for the 32 + 8ch array and the 48ch cylindrical array, the σ_B0^GLOBAL is only 6.7% and 5.6% higher, respectively, when optimized over 2 slices (simulating a MB = 2 acquisition) rather than over a single slice. For MB = 3 the σ_B0^Global for these arrays increases by 17% and 18%. By comparison, σ_B0^GLOBAL would need to increase by 51% and 60% for the two arrays to revert back to the global shim result. Similar performance for the SMS acquisitions is seen for the SH coils. This suggests an important role for dynamic shimming as SMS acquisitions become widely adopted for fMRI.

The simulations in Figs. 11 and 12 show that a very high degree of B₀ field control can be achieved in the head with sufficiently high order coils (either SH or MC arrays). Comparing the MC arrays, it is clear that the cylindrical geometry gives better performance “per channel” than the helmet designs. This was more thoroughly evaluated in de Graaf and Juchem (2016). This is counter to experience with Rx arrays, and likely reflects some differing needs of the B₀ shimming and Rx functions. For example, sensitivity is paramount for Rx coils, while its counterpart for shimming, field generation efficiency, can be approached by using more current or windings. Finally, we note that this simulation compares only shim performance, and ultimately it is a combination of B₀ shim and Rx performance that is of interest when deciding how to best utilize the valuable “real-estate” around the head.

Adaptive current network (ACN)

Here, a grid of MOSFET switches is used to route a DC shim current onto a desired geometric path to generate a target ΔB₀ field in the body. Fig. 6f shows a photograph of a prototype ACN with 14 MOSFET switches to create a single continuous current path on a cylindrical surface (Harris et al., 2014). In this approach, a target-field method is used to calculate the current path on the cylinder that optimally shims the target ΔB₀ field in the body. Advantages of this approach include: (a) high-order shimming can be performed with high efficiency using only a single shim current amplifier (b) the current path and thus the shim field setting can be changed very quickly for dynamic shimming, and (c) the entire current path contributes to the desired field. This last feature avoids the loss of efficiency that can occur in MC shim arrays when neighboring current elements “fight each other” with oppositely directed current vectors. However, the following potential issues remain to be dealt with: (a) dissipation of heat in the MOSFET switches, (b) the complexity of running control wires to each MOSFET switch, (c) interactions with the RF coils, and (d) methodology to field map or otherwise obtain estimates of field basis sets or calibration the many possible current paths. To date, experimental results are limited to generating target ΔB₀ field profiles in phantoms, and the method has not yet been applied for B₀ shimming in vivo.

Other approaches to high-order B₀ shimming

In just the past year, two new B₀ shimming approaches have been proposed that each mark a clear departure from the other methods discussed in this review. First, Brunner et al. (2016) have shown that B₀ shimming can be performed with nickel-copper alloy “magnetic pebbles” whose susceptibility varies with temperature. Thus instead of using a coil winding to convert current to field, the current is used to resistively heat the material, which then alters its magnetic susceptibility and, in turn, its local B₀ field pattern. This immediately begs the question of how quickly the field can be altered; the authors suggest the B₀ field can be altered by 1 μT (43 Hz) per second. The second new proposal, by Boer and Petersen (2016) is to use “plasma coils” in which DC currents are driven through the plasma which is excited inside a gas-filled tube (e.g., a fluorescent light bulb). The conductor of these shim coil is a plasma (which can be switched on/off) rather than a copper wire. The advantage of this approach is that the conductor can be “removed” during the gradient coil switching. Of course, the shim field is needed during signal reception, therefore the plasma conductor must be present during readout (but could be turned off during EPI ramps in non-ramp sampled EPI). While magnetic pebbles and plasma coils are still in the early stages of development, we look forward to following these interesting methods as they mature in the years ahead.

Future directions: toward 20 T imaging

In this Special Issue, Budinger et al. discuss the possibility of building a 20 T MRI scanner. While this proposal invites a host of interesting engineering questions, we take it as an opportunity to illustrate the growing importance that high-order B₀ shimming is expected to play at field strengths above 7 T. Fig. 13 shows an acquired 7 T ΔB₀ brain field map slice (shimmed up to 2nd order) and 1.5 T and 20 T maps generated from this acquired map by scaling linearly with the B₀ field. Fig. 13 also shows simulated geometric distortion for a 2 mm resolution single-shot EPI slice for the three field strengths. The distortions were introduced into an undistorted gradient echo reference image (TE = 23 ms) using the FSL FUGUE tool (Jenkinson et al., 2012), assuming an EPI echo spacing of 0.58 ms with R = 2 acceleration (effective echo spacing of 0.28 ms). As expected, the resulting voxel shifts are mild at 1.5 T but grow linearly with field strength, resulting in severe, cartoonish distortions at 20 T. Fig. 13 also shows the expected effect of slice-optimized shimming with the 64 channel helmet ΔB₀/Rx array shown in Fig. 11. To compensate the larger B₀ field offsets at 20 T, the current limits in the simulation were raised to 5 A/ch and 100 A/total for the 20 T case. In the slice shown, the high-order shim array is capable of reducing the 20 T ΔB₀ distribution to less than what we now expect from 7 T with 2nd-order shimming. This suggests that high-order B₀ shimming will be indispensable for field strengths in this regime.

Fig. 13.

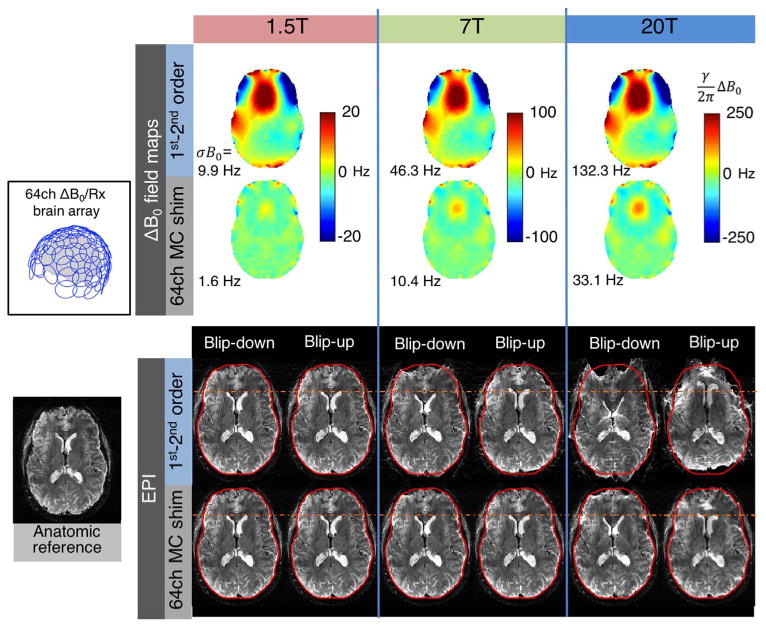
ΔB₀ field maps and simulated EPI distortion for 1.5 T, 7 T, and 20 T brain imaging. The 1.5 T and 20 T ΔB₀ field maps are scaled versions of an acquired 7 T brain field map. Two cases are shown: global 1st–2nd order SH shimming and global 1st–2nd order SH shimming+slice-optimized 64ch MC shimming using the close-fitting ΔB₀/Rx helmet coil configuration shown in Fig. 11. Geometric distortion is applied to a T₂*-weighted anatomic reference image using FSL FUGUE for an echo spacing of 0.56 ms with GRAPPA acceleration of R = 2 (effective echo spacing of 0.28). Both anterior-posterior and posterior-anterior distortions are simulated to emphasize the distortion. ΔB₀ and EPI voxel shifts scale linearly with field strength. While negligible at 1.5 T, the distortion becomes pronounced at 7 T, and at 20 T the images are cartoonishly warped. The voxel shifts are 13 times larger at 20 T than at 1.5 T. The 64ch multi-coil shim array is capable of reducing the distortion to less than what occurs at 7 T with global 2nd order shimming (σ_B0 within the slice is 33.1 Hz for 20 T MC shim versus 46.3 Hz for 7 T 1st–2nd order SH shim). This highlights the need for high-spatial order shimming systems to enable functional MR imaging on envisioned scanners of the future with field strengths well above 7 T.

The prospect of using integrated ΔB₀/Rx coils at field strengths up to 20 T begs the question of how to combine DC shim currents and RF receive functions at such high fields in a practical circuit design.

RF receive loops in “conventional” brain arrays at 7 T typically include ∼3–5 gaps around the loop for discrete tuning in order to distribute the electric field more evenly and reduce electric field coupling to the body (which can cause subject-dependent resonant frequency shifts) (Keil et al., 2010). With this design at 7 T, it is feasible to bridge each gap in the loop with chokes in order to pass DC shim currents. However, as the B₀ field strength increases, a greater number of distributed discrete tuning capacitors are needed to maintain RF receive performance. Thus, a 20 T integrated ΔB₀/Rx array would require an impractical number of chokes. One potential solution to this problem is to use a Transmission Line Resonator (TRL) circuit for the RF receive loops (Frass-Kriegl et al., 2016; Mareyam et al., 2010). In the TRL design, which has been bench-tested for RF receive performance at 11.7 T an 14 T (Mareyam et al., 2010), the tuning capacitance is continuously distributed between two concentric loop traces on a printed circuit board substrate, with few or no gaps in the traces to block the flow of DC. The TRL therefore provides one potential solution for combining DC and RF into the same conducting loops to enable simultaneous Rx and high spatial order B₀ shimming at 20 T. As a step in this direction, proof-of-concept single-channel integrated ΔB₀/Rx TRL coils have recently been demonstrated at 7 T (Stara et al., 2017).

Reproducibility of research

As the number of proposed hardware systems for B₀ shimming has grown, investigators have noted the importance of performing reproducible simulations and experiments across research sites. In a survey of recent publications, Kim et al. identified significant variability in reported values of σ_B0^Global over the brain for the same shim hardware setups (including conventional 2nd order SH shimming). While the underlying cause of these variations has not yet been conclusively determined, we note that there is substantial variation in σ_B0^Global between individual human subjects, and the reported values may further depend on methodological details which differ across sites. For example, in our experience, the calculated value of σ_B0Global is very sensitive to the exact brain mask used.

It is also important that investigators know the field profiles accurately (or at least the wire patterns) for different shim coil setups in order to simulate accurate comparisons. In this vein, a “Public Multi-Coil Information” (PUMCIN) Policy has recently been proposed to establish a common data format for MC wire geometries so that they can be easily shared with other investigators (Juchem and de Graaf, 2016b). The PUMCIN policy also encourages investigators to share performance comparisons of proposed MC designs versus SH shimming (or previously-published MC designs); experimental details such as ROI positioning; software for computing optimal shim settings; and in vivo experimental data when possible. We support this effort. It will facilitate fair comparisons between different MC shim array designs and likely lead to faster, more reproducible progress in B₀ shimming research.

In this spirit, our own ΔB₀/Rx array geometries are available for download, along with Matlab code for MC shimming simulations and a genetic algorithm for selecting optimal MC sub-arrays (Stockmann and Wald, 2016). We are also sharing our open-source, low-cost shim current amplifier circuit (Arango et al., 2016); an early version of the circuit board is already available for download, and an improved, more user-friendly design including a fiber optic interface is expected in 2017.

Conclusion

Recent proposals for high spatial order, dynamic B₀ shimming are reinvigorating the field of B₀ shim research. Simulations and experimental results show clear benefits from increasing the spatial order of shim fields and for dynamic shimming over static. In this article, we review several promising hardware approaches for static and dynamic B₀ shimming at 7 T such as high-order SH coils and several MC designs. It is perhaps too soon to predict which of these systems, if any, will be adopted by commercial scanner manufacturers. Ultimately, whatever choice is made for shim hardware, careful integration with the other scanner sub-systems will be critical.