Nonlinear Joint Latent Variable Models and Integrative Tumor Subtype Discovery

Abstract

Integrative analysis has been used to identify clusters by integrating data of disparate types, such as deoxyribonucleic acid (DNA) copy number alterations and DNA methylation changes for discovering novel subtypes of tumors. Most existing integrative analysis methods are based on joint latent variable models, which are generally divided into two classes: joint factor analysis and joint mixture modeling, with continuous and discrete parameterizations of the latent variables respectively. Despite recent progresses, many issues remain. In particular, existing integration methods based on joint factor analysis may be inadequate to model multiple clusters due to the unimodality of the assumed Gaussian distribution, while those based on joint mixture modeling may not have the ability for dimension reduction and/or feature selection. In this paper, we employ a nonlinear joint latent variable model to allow for flexible modeling that can account for multiple clusters as well as conduct dimension reduction and feature selection. We propose a method, called integrative and regularized generative topographic mapping (irGTM), to perform simultaneous dimension reduction across multiple types of data while achieving feature selection separately for each data type. Simulations are performed to examine the operating characteristics of the methods, in which the proposed method compares favorably against the popular iCluster that is based on a linear joint latent variable model. Finally, a glioblastoma multiforme (GBM) dataset is examined.

1. INTRODUCTION

With the rapid development of microarray technologies, many molecular changes become possible to be monitored at the DNA and RNA levels. In addition to gene expression, genome-wide data, capturing both DNA methylation changes and DNA copy number alterations, are also available for the same biological samples [1–3]. As advocated in [4–6], integrative analysis incorporating multiple data types simultaneously offers a novel characterization of tumor etiology, often based on a joint probability model [7–10].

Commonly used methods for integrative analysis assume a joint probability Model, such as a latent variable model [8–11], representing the joint distribution of the multiple types of data over a common lower-dimensional space defined by latent variables. On this ground, integrative clustering is performed over the lower-dimensional space, where a latent vector can be considered a cluster indicator vector. Generally, there are two main approaches to formulating a latent variable model for integrative analysis: joint factor analysis [8,10] and joint mixture modeling [7]. Joint factor analysis introduces a continuous parameterization of the cluster indicator vector and further assumes that the continuous parameterization follows a Gaussian distribution with a zero mean and an identity covariance matrix [8,10]; in contrast, joint mixture modeling directly defines the cluster indicator vector to be a discrete latent vector [7]. Despite their successes, many issues remain. For joint factor analysis, one issue is that the conventional Gaussian latent variable model may be inadequate to model multiple clusters due to its unimodality. For mixture-based analysis, existing methods, for example, the integrative method in ref. [7], cannot perform feature selection and dimension reduction.

This article introduces a new framework of integrative modeling to account for multiple clusters and conduct dimension reduction and feature selection. This framework involves a nonlinear Gaussian mixture latent model with regularization, called integrative and regularized generative topographic mapping (irGTM). We specifically propose a regularized log-likelihood to integrate multiple types of data, achieving dimension reduction by seeking a common latent vector across all data types while simultaneously performing feature selection on each data type by regularizing the model parameters. As showed by our numerical results, irGTM yields a great improvement over existing methods in terms of clustering accuracy.

The major contributions of irGTM are two-fold: modeling multiple integrative clusters (i.e. clusters defined by multiple types of data) while achieving feature selection, which tends to overcome the difficulty that existing integrative analysis methods are incapable of achieving the two goals simultaneously. Although the nonlinear framework of GTM [12] may describe and distinguish clusters with special shapes, it is greatly inefficient in computation due to overparametrization. Therefore, to be computationally feasible in high-dimensional situations, we modify GTM to model multiple clusters using a smaller number of parameters Based on this, some examples will be studied subsequently to investigate the performance of irGTM with respect to distinguishing multiple integrative clusters or subtypes of cancers.

Note that in addition to clustering analysis as focused here, integrative analysis of multiple types of genomic data has also been developed and applied for other purposes, [13–16]. As these purposes are not our main concern, we will not introduce them in detail in this article.

This article is organized as follows: Section 2 introduces irGTM in detail. Section 3 compares irGTM with iCluster based on some benchmark examples, demonstrating the advantage of the proposed method. In Section 4, we apply irGTM to integrate gene expression, DNA methylation and copy number data for subtype discovery based on a glioblastoma multiforme dataset.

2. METHODS

2.1. Joint probability model

Given multiple types of data expressed as 𝒳 = {𝒳^(s), s ∈ {1, …, S}}, where each s ∈ {1, …, S} indexes one type of data, and ${\mathcal{X}}^{(s)}=\{{\mathit{X}}_1^{(s)},\cdots ,{\mathit{X}}_N^{(s)}\}$ is observed data of type s, with ${\mathit{X}}_n^{(s)}={(X_{n1}^{(s)},\cdots ,X_{n{D}^{(s)}}^{(s)})}^T$ for each n ∈ {1, …, N}. Specifically, { ${\mathit{X}}_n^{(s)}$, n ∈ {1, ···, N}} are independent and identically distributed (i.i.d.) with the same distribution as a length-D^(s) random vector ${\mathit{X}}^{(s)}={(X_1^{(s)},\cdots ,X_{D^{(s)}}^{(s)})}^T$.

In our framework, random vectors {X^(s), s ∈ {1, ···, S}} are linked to a common latent vector Z = (Z₁, ···, Z_D)^T, which has a lower-dimension with D possibly much smaller than D^(s) for each s ∈ {1, ···, S} and is introduced to simultaneously express the distributions of all data types, Based on this, we assume that the latent vector corresponds to the integrative clustering of the pooled multiple types of data 𝒳.

We now introduce the framework of a joint probability model of these multiple types of data. First, assume that {X^(s), s ∈ {1, ···, S}} are conditionally independent given the latent variables Z, that is:

$$p\left({\mathit{X}}^{(1)},\cdots ,{\mathit{X}}^{(S)}\mid \mathit{Z}\right)=\prod _{s=1}^{S}p\left({\mathit{X}}^{(s)}\mid \mathit{Z}\right),$$ (1)

where each conditional distribution p(X^(s)|Z) with s ∈ {1, ···, S} is given through a nonlinear mapping W^(s)ϕ(Z) from the latent variables Z to the observed data variables X^(s):

$${\mathit{X}}^{(s)}={\mathit{W}}^{(s)}\varphi (\mathit{Z})+{\mathit{E}}^{(s)}.$$ (2)

In particular, for each s ∈ {1, ···, S}, W^(s) is a D^(s) × K coefficient matrix; ϕ(Z) = (ϕ₁(Z), ···, ϕ_K(Z))^T is a radially symmetric Gaussian basis function with

$${\varphi }_k(\mathit{Z})=exp\left(-\frac{{\Vert \mathit{Z}-{\mathit{\mu }}_k\Vert }_2^2}{2{\delta }^2}\right)$$ (3)

for each k ∈ {1, ···, K}, and {E^(s), s ∈ {1, ···, S}} are Z-independent noise random vectors following mutually independent isotropic Gaussian distributions with variances {σ^(s)2, s ∈ {1, ···, S}}, respectively, where K denotes the number of integrative clusters of the multiple types of data 𝒳, δ > 0 is the scale of the Gaussian basis function, and {μ_k, k ∈ {1, ···, K}} are the centers corresponding to the K integrative clusters. As the dependent variable of the proposed Gaussian basis functions is the latent vector Z, where all the possible values of Z belong to a sample-independent latent space, we set the radius of the latent space as the scale, which seems to perform well as shown in the simulation results in Section 3.

Generally, in a latent variable model of (integrative) clustering analysis, such as iCluster [8], a length-(K−1) continuous parameterization Z^* following a Gaussian distribution is used to replace the cluster indicator vector (I[{X^(s), s ∈ {1, ···, S}} belongs to cluster 1], ···, I[{X^(s), s ∈ {1, ···, S}} belongs to cluster K])^T for computational reasons, and then, clustering is achieved based on the posterior mean of Z^*. As a Gaussian distribution implies only one mode or center, a continuous parameterization of Z^* by a Gaussian distribution may not be sufficient to represent multiple clusters. As in a K-means algorithm or a Gaussian mixture model, multiple centers are introduced to describe multiple clusters, suggesting that a more flexible parameterization with multiple centers may perform better than that with a single center. Based on this, we propose using the radially symmetrical Gaussian basis functions ϕ(Z) with K centers {μ_k, k ∈ {1, ···, K}} to approximate the cluster indicator vector.

Next, we assume that Z follows a discrete uniform distribution:

$$p(\mathit{Z})=\frac{1}{M}\sum _{m=1}^M\delta (\mathit{Z}-{\mathit{\nu }}_m),$$ (4)

where for each m ∈ {1, ···, M}, δ(Z − ν_m) = 1 if Z = ν_m, otherwise δ(Z − ν_m) = 0. We let the latent space be a unit circle on ℝ², and let the latent-space sample points {ν_m, m ∈ {1, ···, M}} be spread uniformly along the circle, that is, ν_m = (cos(2π(m − 1)/M), sin(2π(m − 1)/M))^T for each m ∈ {1, ···, M}. Accordingly, we let μ_k = (cos(2π(k − 1)/K), sin(2π(k − 1)/K))^T for each k ∈ {1, ···, K}, which are the most mutually exclusive K points on the unit circle. As suggested by ref. [12], the choice of the number M and the locations of the latent-space sample points are not critical. Therefore, hereafter, we set the latent-space sample points and the centers of the basis functions as above and fix M = 100

Combining (1), (2) and (4) leads to the joint probability distribution of {X⁽¹⁾, ···, X^(S)} as follows:

$$p\left({\mathit{X}}^{(1)},\cdots ,{\mathit{X}}^{(S)};{\left\{{\mathit{W}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }^{(s)2}\right\}}_{s=1}^S\right)=\frac{1}{M}\sum _{m=1}^M\prod _{s=1}^{S}p\left({\mathit{X}}^{(s)}\mid {\mathit{\nu }}_m;{\mathit{W}}^{(s)},{\sigma }^{(s)2}\right),$$ (5)

where

$$p\left({\mathit{X}}^{(s)}|{\mathit{\nu }}_m;{\mathit{W}}^{(s)},{\sigma }^{(s)2}\right)=p\left({\mathit{X}}^{(s)}|\mathit{Z}={\mathit{\nu }}_m;{\mathit{W}}^{(s)},{\sigma }^{(s)2}\right)$$

is a Gaussian distribution with a mean vector of W^(s)ϕ(ν_m) and covariance matrix of σ^(s)2I_D(s), and I_D^(s) is an identity matrix of size D^(s). Given the observed multiple types of data 𝒳 = {𝒳^(s), s ∈ {1, …, S}}, we estimate ${\{{\mathit{W}}^{(s)}\}}_{s=1}^S$ and ${\{{\sigma }^{(s)2}\}}_{s=1}^S$ by maximizing the log-likelihood:

$$\mathcal{L}\left({\left\{{\mathit{W}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }^{(s)2}\right\}}_{s=1}^S\right)=\sum _{m=1}^{N}ln\left\{\frac{1}{M}\sum _{m=1}^M\prod _{s=1}^{S}p\left({\mathit{X}}_n^{(s)}\mid {\mathit{\nu }}_m;{\mathit{W}}^{(s)},{\sigma }^{(s)2}\right)\right\}.$$ (6)

Maximization may proceed by using the expectation maximization (EM) algorithm [17] to deal with the latent variables, which we will elaborate next.

2.2. The EM algorithm

To detail our EM algorithm, we first introduce the E-step. Let {Z_n, n ∈ {1, ···, N}} denote the latent vectors of all the samples in 𝒳, which are independent and identically distributed (i. i. d.) with the same distribution as Z. Then, the complete-data log-likelihood is

$${\mathcal{L}}_c({\{{\mathit{W}}^{(s)}\}}_{s=1}^S,{\{{\sigma }^{(s)2}\}}_{s=1}^S)=\sum _{n=1}^N\sum _{s=1}^{S}ln\left\{p\left({\mathit{X}}_n^{(s)}\mid {\mathit{Z}}_n;{\{{\mathit{W}}^{(s)}\}}_{s=1}^S,{\{{\sigma }^{(s)2}\}}_{s=1}^S\right)\times \frac{1}{M}\sum _{m=1}^M\delta ({\mathit{Z}}_n-{\mathit{\nu }}_m)\right\}.$$ (7)

To seek sparse estimates of the coefficient matrices ${\{{\mathit{W}}^{(s)}\}}_{s=1}^S$, we employ an L₁-penalized complete-data log-likelihood as in ref. [8]:

$${\mathcal{L}}_{c,p}\left({\left\{{\mathit{W}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }^{(s)2}\right\}}_{s=1}^S\right)\triangleq {\mathcal{L}}_c\left({\left\{{\mathit{W}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }^{(s)2}\right\}}_{s=1}^S\right)-\sum _{s=1}^S{J}_{\lambda (s)}\left({\mathit{W}}^{(s)},{\sigma }^{(s)2}\right),$$ (8)

where

$$J_{{\lambda }_s}\left({\mathit{W}}^{(s)},{\sigma }^{(s)2}\right)=\frac{{\lambda }^{(s)}}{{\sigma }^{(s)2}}\sum _{d=1}^{D^{(s)}}\sum _{k=1}^K\mid W_{dk}^{(s)}\mid$$ (9)

is the L₁-penalty of the sth data type with a non-negative tuning parameter λ^(s), controlling its model complexity ref. [18].

Given the current coefficient matrices ${\{{\mathit{W}}_{\mathit{old}}^{(s)}\}}_{s=1}^S$ and the current noise variances ${\{{\sigma }_{\mathit{old}}^{(s)2}\}}_{s=1}^S$, the conditional expectation of the penalized complete-data log-likelihood is as follows:

$$\sum _{s=1}^S\sum _{n=1}^N\sum _{m=1}^M{R}_{mn}\left({\left\{{\mathit{W}}_{\mathit{old}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }_{\mathit{old}}^{(s)2}\right\}}_{s=1}^S\right)ln\{p({\mathit{X}}_n^{(s)}\mid {\mathit{\nu }}_m;{\mathit{W}}^{(s)},{\sigma }^{(s)2})\}-\sum _{s=1}^S\frac{{\lambda }^{(s)}}{{\sigma }^{(s)2}}\sum _{d=1}^{D^{(s)}}\sum _{k=1}^K\mid W_{dk}^{(s)}\mid ,$$ (10)

where for each m ∈ {1, ···, M} and each n ∈ {1, ···, N}, the posterior probability

$$\begin{gathered} R_{mn}\left({\left\{{\mathit{W}}_{\mathit{old}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }_{\mathit{old}}^{(s)2}\right\}}_{s=1}^S\right)\triangleq p\left({\mathit{\nu }}_m\mid {\left\{{\mathit{X}}_n^{(s)}\right\}}_{s=1}^S;{\left\{{\mathit{W}}_{\mathit{old}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }_{\mathit{old}}^{(s)2}\right\}}_{s=1}^S\right) \\ =\frac{{\prod }_{s=1}^{S}p\left({\mathit{X}}_n^{(s)}\mid {\mathit{\nu }}_m;{\mathit{W}}_{\mathit{old}}^{(s)},{\sigma }_{\mathit{old}}^{(s)2}\right)}{{\sum }_{m^{\prime }=1}^M{\prod }_{s=1}^{S}p\left({\mathit{X}}_n^{(s)}\mid {\mathit{\nu }}_{m^{\prime }};{\mathit{W}}_{\mathit{old}}^{(s)},{\sigma }_{\mathit{old}}^{(s)2}\right)} \end{gathered}$$ (11)

is evaluated using Bayes’ theorem.

For the M-step, note that maximizing (10) with respect to {W^(s), s ∈ {1, ···, S}} is equivalent to minimizing S L₁-penalized least squares problems separately. As a result, for each s ∈ {1, ···, S}, the solution ${\mathit{W}}_{\mathit{new}}^{(s)}$ can be evaluated using some existing software for a penalized least squares problem, such as glmnet package of R or Matlab. Alternatively, we can simply use the soft-thresholding estimator ${\mathit{W}}_{\mathit{newST}}^{(s)}$ as an approximation:

$${\mathit{W}}_{\mathit{newST}}^{(s)}=\text{sign}\left({\mathit{W}}_{\mathit{new}}^{\ast (s)}\right){\left(\mid {\mathit{W}}_{\mathit{new}}^{\ast (s)}\mid -{\lambda }^{(s)}\right)}_{+},$$ (12)

with

$${\mathit{W}}_{\mathit{new}}^{\ast (s)}={\left({\left({\mathbf{\Phi }}^T{\mathit{G}}_{\mathit{old}}\mathbf{\Phi }\right)}^{-1}{\mathbf{\Phi }}^T{\mathit{R}}_{\mathit{old}}{\mathit{X}}^{(s)}\right)}^T,$$ (13)

where sign(·)(|·| − λ^(s))₊ is applied component-wise; Φ is an M × K matrix with elements Φ_mk = ϕ_k(ν_m), m ∈ {1, ···, M}, k ∈ {1, ···, K}; X^(s) is an N × D^(s) matrix with elements $X_{nd}^{(s)}$, n ∈ {1, ···, N}, d ∈ {1, ···, D^(s)}; R_old is an M × N matrix with elements $R_{mn}\left({\left\{{\mathit{W}}_{\mathit{old}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }_{\mathit{old}}^{(s)2}\right\}}_{s=1}^S\right)$, m ∈ {1, ···, M}, n ∈ {1, ···, N}; and G_old is an M ×M diagonal matrix with elements

$${(G_{\mathit{old}})}_{mm}=\sum _{n=1}^N{R}_{mn}\left({\left\{{\mathit{W}}_{\mathit{old}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }_{\mathit{old}}^{(s)2}\right\}}_{s=1}^S\right),$$ (14)

m ∈ {1, ···, M}. In particular, (13) can be solved using standard matrix inversion methods based on the singular value decomposition to allow for possible ill conditioning. Moreover, maximizing (10) in {σ^(s)2, s ∈ {1, ···, S}} leads to the following updating formula based on ${\{{\mathit{W}}_{\mathit{new}}^{(s)}\}}_{s=1}^S$:

$${\sigma }_{\mathit{new}}^{(s)2}=\frac{1}{N{D}^{(s)}}\{\sum _{n=1}^N\sum _{m=1}^M{R}_{mn}\left({\left\{{\mathit{W}}_{\mathit{old}}^{(s)}\right\}}_{s=1}^S,{\left\{{\sigma }_{\mathit{old}}^{(s)2}\right\}}_{s=1}^S\right)\times {\Vert {\mathit{W}}_{\mathit{new}}^{(s)}\varphi ({\mathit{\nu }}_m)-{\mathit{X}}_n^{(s)}\Vert }_2^2+2{\lambda }^{(s)}\sum _{d=1}^{D^{(s)}}\sum _{m=1}^M\left|{(W_{\mathit{new}}^{(s)})}_{dm}\right|\},$$ (15)

for each s ∈ {1, ···, S}. The EM algorithm iterates between the E-step and M-step until convergence, and we use ${\left\{{\widehat{\mathit{W}}}^{(s)}\right\}}_{s=1}^S$ and ${\left\{{\widehat{\sigma }}^{(s)2}\right\}}_{s=1}^S$ to denote the converged estimates.

In the above EM algorithm, we initialize W⁽¹⁾ so that the GTM model of X⁽¹⁾ initially approximates the corresponding principal component analysis (PCA) following the initialization method in ref. [12]. To be specific, we first evaluate the sample covariance matrix of 𝒳⁽¹⁾, compute its first and second principal eigenvectors, and then determine the initial estimate of W⁽¹⁾ by minimizing the following error function:

$${\mathit{Err}}^{(1)}=\frac{1}{2}\sum _{m=1}^M{\Vert W^{(1)}\varphi ({\mathit{\nu }}_m)-{\mathit{U}}^{(1)}{\mathit{\nu }}_m\Vert }_2^2,$$ (16)

where the columns of U⁽¹⁾ are given by the two eigenvectors. As suggested by ref. [12], this represents the sum-of-squares error between the projections of the latent points into the data space by the GTM model of X⁽¹⁾ and the corresponding projections obtained from PCA. Next, we initialize each W^(s) with s ∈ {2, ···, S} as a D^(s) × K matrix with zero-elements. In addition, for each s ∈ {1, ···, S}, we initialize σ^(s)2 as the third eigenvalue of the sample covariance matrix of 𝒳^(s), representing the variance of 𝒳^(s) away from the corresponding PCA plane of 𝒳^(s). It is worth noting that based on our limited experience, initializing each W^(s) with s ∈ {2, ···, S} using the same method as in (16), irGTM often performs poorly. This is possibly because separate estimates of W^(s) may not contribute to a common latent vector Z across all the data types. As suggested by the following simulation studies, clustering performance of irGTM is quite similar to that based on different orders of data types.

2.3. Tuning parameters

Here, we introduce a resampling-based procedure for selecting the regularization parameters, similar to that of [19]. The procedure partitions the multiple types of data into a training set and a test set iteratively. In each iteration, we first train the irGTM model using the training set and let ${\left\{{\widehat{\mathit{W}}}_{tr}^{(s)}\right\}}_{s=1}^S$ and ${\left\{{\widehat{\sigma }}_{tr}^{(s)2}\right\}}_{s=1}^S$ be the corresponding estimators. Then, for each observation $\left\{{\mathit{X}}_{n_{te}}^{(1)},\cdots ,{\mathit{X}}_{n_{te}}^{(S)}\right\}$ in the test set, we compute the posterior mean of the latent variables

$$\begin{gathered} \langle \mathit{Z}|{\left\{{\mathit{X}}_{n_{te}}^{(s)}\right\}}_{s=1}^S;{\left\{{\widehat{\mathit{W}}}_{tr}^{(s)}\right\}}_{s=1}^S,{\left\{{\widehat{\sigma }}_{tr}^{(s)2}\right\}}_{s=1}^S\rangle =\int p\left(\mathit{z}|{\left\{{\mathit{X}}_{n_{te}}^{(s)}\right\}}_{s=1}^S;{\left\{{\widehat{\mathit{W}}}_{tr}^{(s)}\right\}}_{s=1}^S,{\left\{{\widehat{\sigma }}_{tr}^{(s)2}\right\}}_{s=1}^S\right)\mathit{z}d\mathit{z} \\ =\sum _{m=1}^M{R}_{m{n}_{te}}\left({\left\{{\widehat{\mathit{W}}}_{tr}^{(s)}\right\}}_{s=1}^S,{\left\{{\widehat{\sigma }}_{tr}^{(s)2}\right\}}_{s=1}^S\right){\mathit{\nu }}_m. \end{gathered}$$ (17)

Next, we compute the Euclidean distance d_te|tr of the posterior means. We denote by $n{e}_{te\mid tr}^{N_{ne}}(n_{te})$ the N_ne-nearest neighbors of the posterior mean of the latent variables for each n_te in the index set of the test set, where N_ne is a given number smaller than the sample size of the test set. On the other hand, we train the irGTM model using the test set, compute the corresponding posterior mean of the latent variables for each observation indexed by n_te in the test set, and then compute the corresponding Euclidean distance d_te of the posterior means. Let $n{e}_{te}^{N_{ne}}(n_{te})$ denote the N_ne-nearest neighbors of the posterior mean of the latent variables for each n_te in the index set of the test set.

Then, we define the prediction strength as follows:

$$\frac{1}{N_{te}}\sum _{n_{te}}\frac{\left|{\text{ne}}_{te\mid tr}^{N_{ne}}(n_{te})\cap {\text{ne}}_{te}^{N_{ne}}(n_{te})\right|}{N_{ne}},$$ (18)

where | · | represents the number of elements in a set. For selection of the penalty parameters {λ^(s), s ∈ S}, we choose the ones with the highest average prediction strength.

Note that while the penalty parameters are large enough, the posterior means of the latent variables of the points in the test set will converge to one point. Then, ${\text{ne}}_{te\mid tr}^{N_{ne}}(n_{te})$ and ${\text{ne}}_{te}^{N_{ne}}(n_{te})$ will be the same if they are obtained by choosing N_ne points with the lowest indices in the test set without n_te, which forces the prediction strength to be 1. To avoid such a situation, we add small random Gaussian noise to the posterior mean of the latent variables of each data point in the test set before computing the Euclidean distance d_te|tr and d_te.

This procedure is used to select the regularization parameters in a situation where the number of clusters K is fixed in advance. When K is unknown, we may use a method that is commonly used in determining the number of clusters in clustering analysis, such as the highest Silhouette index [20]. To be specific, for each K >1 in 𝒦 (a candidate set of positive numbers), we obtain the resulting clustering assignment l(K) by fixing the number of clusters as K and then select K̂ ∈ 𝒦 with the highest Silhouette index as the optimal estimate of the number of clusters, based on which, we obtain the final estimate of the clustering assignment, say l(K̂).

2.4. Integrative clustering

The goal of irGTM is for integrative clustering, which is achieved by using Bayes’ theorem, to invert the transformation from the latent space to the data space. To be specific, for each data point ${\{{\mathit{X}}_n^{(s)}\}}_{s=1}^S$ with n ∈ {1, · · ·, N}, we summarize the posterior distribution by the posterior mean:

$$\langle \mathit{Z}|{\left\{{\mathit{X}}_n^{(s)}\right\}}_{s=1}^S;{\left\{{\widehat{\mathit{W}}}^{(s)}\right\}}_{s=1}^S,{\left\{{\widehat{\sigma }}^{(s)2}\right\}}_{s=1}^S\rangle =\sum _{m=1}^M{R}_{mn}\left({\left\{{\widehat{\mathit{W}}}^{(s)}\right\}}_{s=1}^S,{\left\{{\widehat{\sigma }}^{(s)2}\right\}}_{s=1}^S\right){\mathit{\nu }}_m.$$ (19)

These posterior means are used for dimension reduction and then integrative clustering. The cluster memberships will then be specifically figured out by applying a standard K-means clustering algorithm [21] on the posterior means.

Alternatively, we can compute the posterior mean of ϕ(Z) rather than of Z:

$$\langle \varphi (\mathit{Z})|{\left\{{\mathit{X}}_n^{(s)}\right\}}_{s=1}^S;{\left\{{\widehat{\mathit{W}}}^{(s)}\right\}}_{s=1}^S,{\left\{{\widehat{\sigma }}^{(s)2}\right\}}_{s=1}^S\rangle =\sum _{m=1}^M{R}_{mn}\left({\left\{{\widehat{\mathit{W}}}^{(s)}\right\}}_{s=1}^S,{\left\{{\widehat{\sigma }}^{(s)2}\right\}}_{s=1}^S\right)\mathit{\varphi }(v_m),$$ (20)

and assign ${\{{\mathit{X}}_n^{(s)}\}}_{s=1}^S$ to cluster k ∈ {1, · · ·, K} whenever the kth element of

$$\langle \varphi (\mathit{Z})|{\left\{{\mathit{X}}_n^{(s)}\right\}}_{s=1}^S;{\left\{{\widehat{\mathit{W}}}^{(s)}\right\}}_{s=1}^S,{\left\{{\widehat{\sigma }}^{(s)2}\right\}}_{s=1}^S\rangle$$

is the largest element of the vector as ϕ(Z) is an approximation of the cluster indicator vector.

3. SIMULATION STUDIES

This section performs simulations to examine the operating characteristics of the proposed method and compare it against its competitors: iCluster [8], naive integration of PCA (NI) [22], and several methods applicable to two types of data, such as partial least squares regression (PLS) [23], co-inertia analysis (CIA) [24], and canonical correlation analysis (CCA) [25] in terms of clustering accuracy measured by the Rand index and the adjusted Rand index [26]. Note that we exclude comparison with ref. [7] as the latter is not designed for cases involving many non-informative variables.

3.1. Simulation set-ups

Three examples are considered, which are based on benchmark examples in refs. [8,10]. In these examples, for each type of data, the cluster information is associated with a small number of variables that are thought of as clustering features, based on which one cluster is distinguishable from the other two that remain non-separable.

Case 1: A random sample of n = 150 is taken from three clusters with {1, · · · , 50}, {51, · · · , 100}, and {101, · · · , 150} from clusters 1–3, respectively. Let D⁽¹⁾ = D⁽²⁾ = 500 and μ = 1.5. For s = 1, $X_{ij}^{(1)}~\mathcal{N}(\mu ,1)$; i = 1, · · · , 50, j = 1, · · · , 10; $X_{ij}^{(1)}~\mathcal{N}(1,1)$; i = 51, · · ·,100, j = 101, · · · , 110; and $X_{ij}^{(1)}~\mathcal{N}(0,1)$ for the rest. For s = 2, $X_{ij}^{(2)}=0.5X_{ij}^{(1)}+{\epsilon }_{ij}$, where ε_ij ~ 𝒩(0, 1); i = 1, · · · , 50, j=1, · · · , 10; $X_{ij}^{(2)}~\mathcal{N}(\mu ,1)$; i = 101, · · · , 150, j = 101, · · · , 110; and $X_{ij}^{(2)}~\mathcal{N}(0,1)$ for the rest. Interestingly, the two types of data in Case 1 are correlated in the first 10 dimensions. In addition, for each data type, there are two groups of features, {1, · · · , 10} and {101, · · · , 110}, which allow us to discriminate one cluster from the other two.

Cases 2 and 3 are similar to Case 1, except μ = 1.3 and μ = 1.1, respectively. As the value of μ determines the strength of clustering features, these cases are used to investigate the clustering performance of the methods in the presence of weaker clustering features.

To guard against potential confounding due to different choices of the number of integrative clusters K, we fix K at 3 for Cases 1–3. To choose the tuning parameter λ = (λ⁽¹⁾, · · · , λ^(S))^T ∈ Λ ⊆ ℝ^S for irGTM, we use the resampling-based procedure in Section 2.3 with |Λ| = |{λ^(1,1), · · · , λ^(1,8)}×· · ·×{λ^(S,1), · · · , λ^(S,8)}| = 8^S and for iCluster with |Λ| = |{λ₁, · · · , λ₈}| = 8, which is set in default in the R package ‘ iCluster’. Here, | · | denotes the number of elements in a set. All the simulations are performed on a PC with a single processor Intel(R) Core(TM) i7 CPU @ 3.40GHz (16G Memory), except that iCluster was run with four processors for parallel computation. For a fair comparison, reported run times for iCluster were simply four times the original run times.

Note that to investigate clustering performances of irGTM with different orders of data types, let irGTM₁ denote the proposed method of the order of (X⁽¹⁾, X⁽²⁾) and irGTM₂ denote that of the order of (X⁽²⁾, X⁽¹⁾).

3.2. Simulation results

Table 1 summarizes the results of all the methods considered in Cases 1–3 based on 100 repetitions respectively.

Table 1.

Sample means (SD in parentheses) of Rand index (Rand) and adjusted Rand index (aRand) between the clustering assignment by each method and the true assignment as well as the run time (RT) for the three cases based on 100 repetitions. Here, irGTM₁, irGTM₂, iCluster, PCA NI, PLS, CIA, and CCA denote the proposed method with different orders of data types, iCluster of ref. [8], naive integration of PCA, partial least squares regression of ref. [23], co-inertia analysis of ref. [24], and canonical correlation analysis of [25].

Case	n, p, μ	Method	Rand	aRand	RT (min)
1	n = 150	irGTM1	0.987 (0.012)	0.972 (0.028)	12.37 (0.036)
		irGTM2	0.988 (0.011)	0.974 (0.022)	12.32 (0.032)
	p(1) = p(2)	iCluster	0.978 (0.018)	0.952 (0.042)	152.5 (10.44)
	= 500	PCA NI	0.923 (0.024)	0.826 (0.056)	0.004 (0.001)
	μ = 1.5	PLS	0.762 (0.063)	0.464 (0.143)	0.027 (0.008)
		CIA	0.888 (0.030)	0.746 (0.069)	0.008 (0.002)
		CCA	0.954 (0.065)	0.896 (0.147)	0.007 (0.001)
2	n = 150	irGTM1	0.979 (0.011)	0.954 (0.026)	12.26 (0.260)
		irGTM2	0.981 (0.013)	0.957 (0.029)	12.28 (0.281)
	p(1) = p(2)	iCluster	.946 (0.041)	0.877 (0.092)	152.0 (9.992)
	= 500	PCA NI	0.756 (0.047)	0.450 (0.105)	0.006 (0.000)
	μ = 1.3	PLS	0.722 (0.054)	0.373 (0.120)	0.025 (0.000)
		CIA	0.727 (0.050)	0.387 (0.112)	0.008 (0.000)
		CCA	0.901 (0.079)	0.778 (0.178)	0.006 (0.000)
3	n = 150	irGTM1	0.938 (0.019)	0.855 (0.043)	12.28 (0.308)
		irGTM2	0.936 (0.023)	0.856 (0.051)	12.27 (0.320)
	p(1) = p(2)	iCluster	0.843 (0.085)	0.647 (0.191)	84.96 (16.99)
	= 500	PCA NI	0.677 (0.044)	0.272 (0.100)	0.005 (0.000)
	μ = 1.1	PLS	0.657 (0.030)	0.229 (0.067)	0.018 (0.000)
		CIA	0.656 (0.032)	0.227 (0.072)	0.005 (0.000)
		CCA	0.792 (0.101)	0.531 (0.226)	0.005 (0.000)

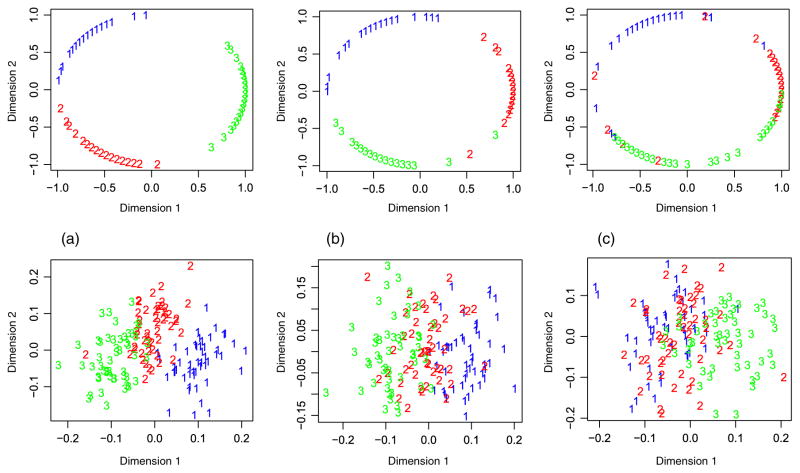
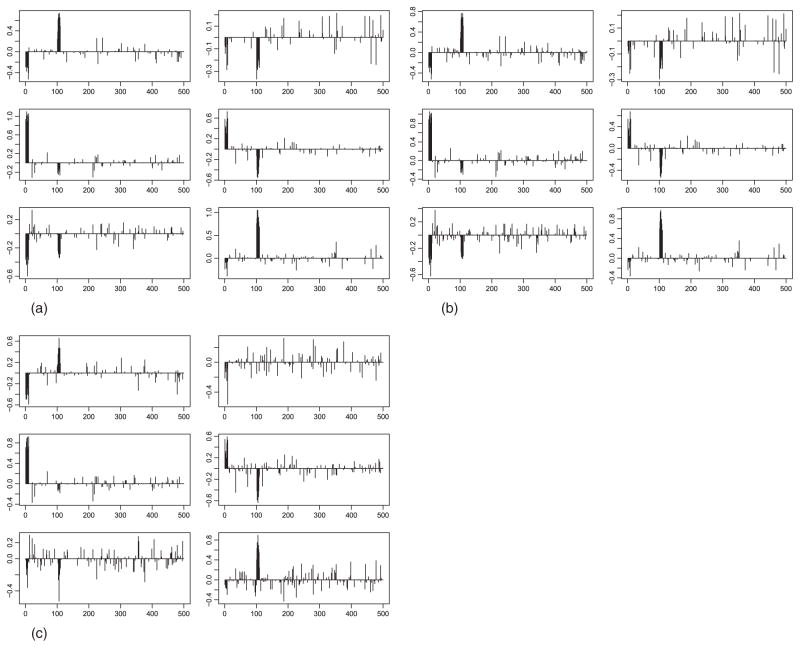
For Case 1, as indicated by Table 1, irGTM and iCluster outperform their competitors in terms of the accuracy of clustering, measured by the Rand index and adjusted Rand index. As suggested by panel (A) of Figure 1, irGTM and iCluster make the three clusters almost separable. Moreover, in view of panel (A) of Figure 2, we note that the informative variables {1, · · · , 10} and {101, · · · , 110} are almost correctly identified by irGTM. Note that this example was ideal for iCluster, which was used in [8] to demonstrate the advantages of iCluster over integration by PCA for each type of data. For Cases 2–3, iCluster and naive fail to capture the clustering structure due to weaker clustering information. Again, as demonstrated in Table 1, irGTM outperforms its competitors in terms of the clustering accuracy.

Fig. 1.

Plots of the first two dimensions after dimension reduction by both methods compared for each case. Panels (a–c) and Panels (d–f) correspond to Cases 1–3, respectively. Here, irGTM, iCluster denote the proposed method (irGTM₁) and iCluster of ref. [8], respectively. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Fig. 2.

Plots of the estimates of parameters in irGTM₁. Panels (a–c) correspond to Cases 1–3. For each panel, the (k, s)-th entry is the plot of ${\mathit{W}}_k^{(s)}$ (the kth column of W^(s)) for k ∈ {1, ···, K = 3} and s ∈ {1, ···, S = 2}.

In summary, irGTM is competitive for high-throughput genomic data and is much more accurate than iCluster in integrative clustering of different types of data, especially in situations where clustering features are relatively weak. Moreover, it is more computationally more efficient than iCluster.

4. APPLICATIONS

We now consider a glioblastoma multiform (GBM) dataset generated by The Cancer Genome Atlas (TCGA) [27], which is available in the R package ‘iCluster’. Based on only 1,740 most variable expression levels [27], four distinct GBM subtypes, Proneural (P), Neural (N), Classical (C), and Mesenchymal (M), were identified.

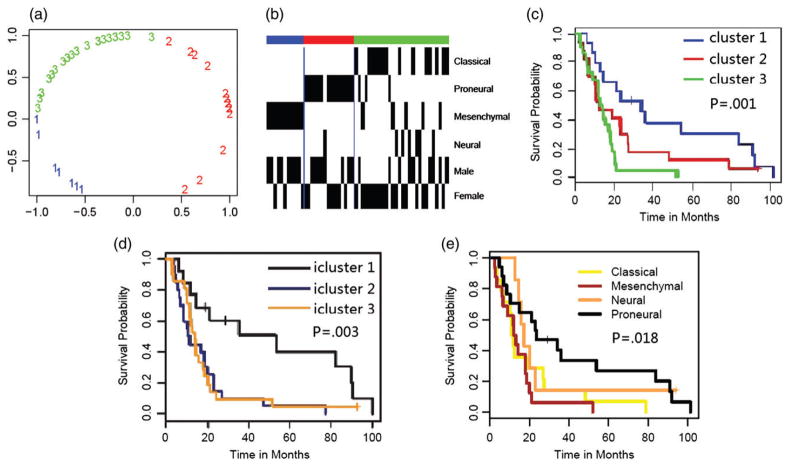
The Kaplan–Meier (K–M) curves [28] are often used to confirm whether some patient groups identified by a clustering analysis have distinct survival outcomes. From the K–M plot of the four GBM subtypes (panel (e) of Figure 4), the survival probability of the Proneural subtype is higher than those of the other three subtypes, while the differences in survival among the latter three subtypes are small. For instance, after 2 years, about 50% patients in the Proneural subgroup survive, but only less than 20% patients in each of the latter three subgroups of GBM survive.

Fig. 4.

Panels (a–e) are based on the DNA copy number data, the mRNA expression data and the methylation data of the 55 GBM patients from TCGA, where P denotes the p-value of the Mantel-Haenszel test. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

For the four subtypes, the overall differences among the four survival curves are only Moderate, with a relatively high p-value 0.018 from the Log-rank test, testing survival differences among the four patient groups [29].

Integrative analysis of gene expression data and other data may help identify novel subtypes with more distinguished survival outcomes. Shen et al. [8] performed an integrative analysis by iCluster, combining the use of DNA copy number, methylation, and mRNA expression in the GBM data. They divided 55 GBM patients into three integrative clusters (iClusters 1, 2, and 3). From panel (d) of Figure 4 (regenerated Figure 6 of ref. [9]), iCluster 1 is associated with a higher survival curve, while both iClusters 2 and 3 are associated with two lower and similar survival curves. Furthermore, the p-value of the Log-rank test is 0.003, much more significant than that of the above four subtypes.

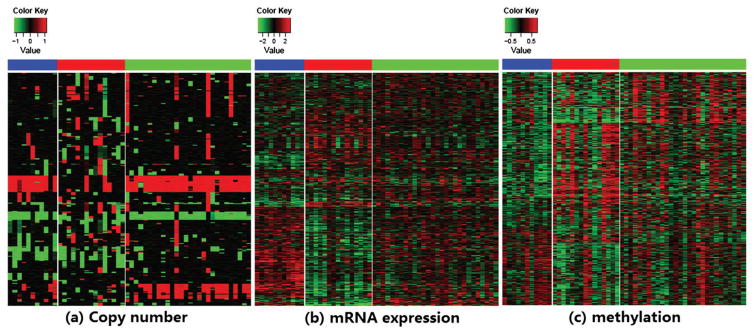
To test the performance of the proposed method and to compare with iCluster, we analyze the same dataset with the same 55 GBM patients and three types of data. Details of the corresponding results are summarized in Figures 3 and 4, including the heat map of each data type, plot of posterior means of the latent vector, and the survival curves (K–M plots) of the subtypes via iCluster and irGTM. From panel (c) of Figure 4, it seems that cluster 1 is associated with the highest survival curve, which mainly includes the Proneural (P) subtype; cluster 3 is associated with the lowest survival, and the survival of cluster 2 is intermediate between those of the other two clusters. In contrast to the three clusters identified by iCluster [9], the three clusters uncovered by the proposed method can be better distinguished from each other with more significant survival differences with a smaller p-value, 0.001, by the Log-rank test. Note that in this application, the results of irGTM with different orders of the three data types are almost the same and thus omitted.

Fig. 3.

Panels (a–c) are heat maps of the DNA copy number data, the mRNA expression data and the methylation data of the 55 GBM patients from The Cancer Genome Atlas (TCGA) respectively, where the columns (tumors) are arranged by clusters identified by irGTM₁.[Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

5. DISCUSSIONS

5.1. Alternative choice of ϕ(Z)

In this subsection, we investigate the performance of irGTM with an alternative choice of ϕ(Z) = (ϕ₁(Z), ···, ϕ_K (Z))^T in (2). In particular, for each k ∈ {1, ···, K}, ϕ_k(Z) is replaced by the angle distance between Z and μ_k,

$${\varphi }_k(\mathit{Z})=arccos(\frac{{\mathit{Z}}^T{\mu }_k}{\Vert \mathit{Z}\Vert \Vert {\mu }_k\Vert }).$$

Now, reconsider all the three set-ups in Section 3 with the above angle distance to obtain quite similar Rand and adjusted Rand index results, measuring the integrative clustering performance, which is summarized in Table 2.

Table 2.

Running time (in minutes), Rand and adjusted Rand index results of Cases 1–3 by using irGTM₁ with ϕ(Z) = arccos $\varphi (\mathit{Z})=arccos\left(\frac{{\mathit{Z}}^T{\mu }_k}{\Vert \mathit{Z}\Vert \Vert {\mu }_k\Vert }\right)$.

	Rand	aRand	RT (min)
Case 1	0.984 (0.012)	0.964 (0.027)	8.780 (0.422)
Case 2	0.969 (0.018)	0.931 (0.042)	8.634 (0.416)
Case 3	0.920 (0.048)	0.819 (0.110)	8.792 (0.425)

5.2. Alternative choice of latent space and centers of clusters

As mentioned in [12], in general, the performance of GTM does not greatly depend on the choice of latent space and its centers. Here, we investigate the performance of irGTM with an alternative choice of latent space and cluster centers. Here, we let the latent space be a three-dimensional unit sphere and choose M = 100 points uniformly from the surface of the unit sphere as the sample points. Then, we choose K mutually exclusive points on the surface of the unit sphere as the corresponding centers of the K clusters. We reconsider all the three set-ups in Section 3 with the above choice of latent space and cluster centers. From Table 3, the Rand and adjusted Rand index results are similar to those of the proposed method in Table 1. However, we see that the computational cost increases as the number of latent variables (or the dimension of the latent space) increases.

Table 3.

Running time (in minutes), Rand and adjusted Rand index results of Cases 1–3 by using irGTM₁ with an alternative choice of latent space (three-dimensional space) and cluster centers.

	Rand	aRand	RT (min)
Case 1	0.988 (0.010)	0.974 (0.023)	24.57 (0.206)
Case 2	0.973 (0.027)	0.939 (0.061)	24.59 (0.170)
Case 3	0.933 (0.061)	0.849 (0.139)	24.56 (0.186)

On the other hand, once the latent space is still a unit circle, and the latent-space sample points as well as its cluster centers perform a rotation on the circle, the clustering performance of the proposed method may be almost unchanged, which is supported by some additional numerical results not exhibited in this article to avoid reduplicate statements.

5.3. Alternative choice of basis functions

In this subsection, we rebuilt irGTM by replacing the basis functions of latent variables with the latent vector itself, that is, the cluster indicator vector. In addition, we let the latent space be composed of all the values of the length-K cluster indicator, that is, {(1, 0, ···, 0)^T, (0, 1, 0, ···, 0)^T, ···, (0, ···, 0, 1)^T}, and just let the sample points be these values of the cluster indicator. We summarize the corresponding results in Table 4, where the computation of the rebuilt irGTM is improved, but the clustering performance becomes a bit worse.

Table 4.

Running time (in minutes), Rand and adjusted Rand index results of Cases 1–3 by using irGTM with an alternative choice of basis functions of latent variables.

	Rand	aRand	RT (min)
Case 1	0.986 (0.023)	0.970 (0.051)	5.873 (0.046)
Case 2	0.967 (0.045)	0.927 (0.101)	5.953 (0.079)
Case 3	0.926 (0.076)	0.833 (0.171)	5.976 (0.078)

5.4. Alternative choices of the scale of the basis function

In this subsection, we investigate the performance of irGTM with other choices of the scale of the basis function. From Table 5, in Cases 1–3, the performance of irGTM with the scale δ belonging to [0.5,1] is similar to that with δ = 1.

Table 5.

Running time (in minutes), Rand and adjusted Rand index results of Cases 1–3 by using irGTM₁ with alternative choices of the scale of the proposed basis function.

	δ	Rand	aRand
Case 1	0.5	0.990 (0.011)	0.978 (0.022)
	0.75	0.990 (0.011)	0.979 (0.026)
	1.5	0.976 (0.016)	0.946 (0.036)
Case 2	0.5	0.981 (0.013)	0.957 (0.031)
	0.75	0.982 (0.045)	0.959 (0.101)
	1.5	0.923 (0.078)	0.828 (0.175)
Case 3	0.5	.956 (0.018)	0.900 (0.042)
	0.75	.958 (0.020)	0.906 (0.045)
	1.5	.849 (0.099)	0.661 (0.223)

Finally, based on all the exhibited numerical results in this section, in general, the clustering performance of the proposed method may not greatly depend on the choice of basis function, latent space and space centers, which implies that the proposed method may mainly benefit from using a discrete distribution of the latent variables, while a nonlinear framework with alternative choices of basis functions, latent space, and space centers may offer a more flexible and general model.

6. CONCLUSION

This paper introduces a novel integrative analysis method based on a nonlinear latent model, called irGTM, which is computationally efficient using an EM algorithm. It has one key feature in defining a novel parameterization to better approximate the latent cluster indicators by introducing a discrete latent space as well as a nonlinear mapping from the latent space to each data space. This permits flexible modeling to account for multiple clusters and to perform dimension reduction and feature selection. As a result, it may improve the performance for integrative clustering.