Differences in adaptive dynamics determine the success of virus variants that propagate together

Abstract

Virus fitness is a complex parameter that results from the interaction of virus-specific characters (e.g. intracellular growth rate, adsorption rate, virion extracellular stability, and tolerance to mutations) with others that depend on the underlying fitness landscape and the internal structure of the whole population. Individual mutants usually have lower fitness values than the complex population from which they come from. When they are propagated and allowed to attain large population sizes for a sufficiently long time, they approach mutation-selection equilibrium with the concomitant fitness gains. The optimization process follows dynamics that vary among viruses, likely due to differences in any of the parameters that determine fitness values. As a consequence, when different mutants spread together, the number of generations experienced by each of them prior to co-propagation may determine its particular fate. In this work we attempt a clarification of the effect of different levels of population diversity in the outcome of competition dynamics. To this end, we analyze the behavior of two mutants of the RNA bacteriophage Qβ that co-propagate with the wild-type virus. When both competitor viruses are clonal, the mutants rapidly outcompete the wild type. However, the outcome in competitions performed with partially optimized virus populations depends on the distance of the competitors to their clonal origin. We also implement a theoretical population dynamics model that describes the evolution of a heterogeneous population of individuals, each characterized by a fitness value, subjected to subsequent cycles of replication and mutation. The experimental results are explained in the framework of our theoretical model under two non-excluding, likely complementary assumptions: (1) The relative advantage of both competitors changes as populations approach mutation-selection equilibrium, as a consequence of differences in their growth rates and (2) one of the competitors is more robust to mutations than the other. The main conclusion is that the nearness of an RNA virus population to mutation-selection equilibrium is a key factor determining the fate of particular mutants arising during replication.

1. Introduction

RNA virus replication is a fast process that takes place at a very high error rate, in the order of 10⁻⁴ to 10⁻⁵ errors per nucleotide copied (Holland et al. 1982; Sanjuán et al. 2010). Under these conditions, individual virus variants have a transient existence and live in a permanent state of diversification and regeneration from related sequences. As a consequence, RNA virus populations are composed of a highly heterogeneous and dynamic ensemble of genomes on which natural selection acts in non-trivial ways to shape their diversity and phenotypic distribution (Domingo, Sheldon, and Perales 2012). Each of the mutants composing a virus population is defined by a fitness value that measures its performance in the particular environment (biotic and abiotic) in which it replicates. This relationship of fitness with the biotic conditions entails that the value for each individual depends on the set of mutants with which it coexists. In addition, environmental variability means that fitness is also determined by the ability to generate variants at a rate that allows adaptation to novel conditions (Aguirre, Lázaro, and Manrubia 2009; Stich, Manrubia, and Lázaro 2010a). The high error rates characteristic of RNA viruses promote adaptation, but also entail a large fraction of mutations with deleterious effects on fitness (Lee et al. 1997; Sanjuán, Moya, and Elena 2004, Carrasco, de la Iglesia, and Elena 2007; Domingo-Calap, Cuevas, and Sanjuán 2009; Sanjuán 2010; Stich, Manrubia, and Lázaro 2010b). Therefore, mechanisms able to increase genetic robustness, understood as the preservation of the phenotype in the face of mutations, might be traits subjected to selection, especially under increases in the error rate (e.g. in the presence of a mutagen) or rises in the negative effect of mutations (e.g. under environmental changes) (de Visser et al. 2003; Wagner 2005; Sanjuán et al. 2007; Domingo-Calap, Pereira-Gómez, and Sanjuán 2010; Elena 2012; Lauring, Frydman, and Andino 2013).

In the long term, for large enough population sizes under constant selection pressures, virus populations approach a mutation-selection equilibrium analogous to the stationary state defined in quasispecies theory for molecular replicators (Biebricher and Eigen 2006). During the transition to equilibrium the population increases its fitness value, which may be accompanied by the fixation of mutations in the consensus sequence or just arise as a consequence of changes in the composition of the mutant spectrum (Bordería et al. 2010; Lorenzo-Redondo, Bordería, and Lopez-Galindez 2011). Individual viruses isolated from the same parental population and propagated under identical conditions can follow different trajectories during this process as a result of the intrinsic stochasticity of mutations and of differences in the parameters that determine their initial fitness values (e.g. growth rate, mutation rate, virion extracellular stability or robustness). Another important factor influencing fitness trajectories is the underlying fitness landscape (Clune et al. 2008; Cervera, Lalić, and Elena 2016a), which determines the most accessible fitness peak for each genome. Populations can be trapped in quasi-mutation-selection balance on these suboptimal fitness peaks for a very long time (Jain and Krug 2007; Cervera, Lalić, and Elena 2016b), such that the global maximum is not always found before a new perturbation affects the population.

Interestingly, most of the resulting progeny after the first replication rounds of a virus has lower fitness than the parental genome (Duarte et al. 1994; Schulte and Andino 2014; Cervera and Elena 2016). This fact is evidenced by the analysis of the subclonal components of virus clones and by the numerous observations showing that propagation of viruses through successive population bottlenecks gives rise to the accumulation of deleterious mutations and to fitness losses until the population becomes extinct (Yuste et al. 1999) or stabilizes in a low-fitness state (Lázaro et al. 2003; Lázaro, Escarmís, and Manrubia 2006), the latter probably due to the acquisition of compensatory mutations. Once population sizes are large enough, there is sufficient availability of beneficial mutations, giving rise to fitness increases (Novella et al. 1995; Elena et al. 1996; Escarmís et al. 1999). All of the above indicates that both the population size and the number of replication rounds experienced by a virus may be strong determinants of the final outcome when it co-propagates with a different strain. For example, it was shown that a vesicular stomatitis virus (VSV) mutant could coexist with the wild-type virus during the generations elapsed for up to about eleven passages, although it was consistently displaced in prolonged competitions (Quer et al. 1996; Quer et al. 2001).

In this work we address the competition dynamics between a wild-type virus and two mutants of the RNA bacteriophage Qβ that were isolated upon evolution at increased temperature (Arribas et al. 2014). Since these mutants, which present an amino acid change in the replicase protein, have never been detected during evolution of the virus at standard temperature, we expected that they would be dominant under restrictive conditions (43 °C) and selected against under permissive conditions (37 °C). However, our results showed that the outcome of the competitions under permissive conditions depended on the previous evolutionary history of both competitors. Thus, we designed a set of experiments and population dynamics models that allow us to analyze which parameters, among those determining virus adaptive dynamics, could better explain the observed behavior.

2. Methods: experiments

2.1 Virus and bacteria: standard procedures for infection

Virus infections were carried out in Escherichia coli, strain Hfr (Hayes) in NB medium (8 g/l Nutrient Broth from Merck and 5 g/l NaCl). Infections in liquid medium were always carried out using fresh log-phase E.coli cultures with an OD₅₅₀ between 0.6 and 0.8, which were infected at the multiplicity of infection (moi) indicated in each experiment. After 2 h of incubation either at 37 °C (optimal temperature) or 43 °C (suboptimal or selective temperature) with good aeration (250 rpm), cultures were treated with 1/20 volume of chloroform for 15 min at 37 °C with shaking (900 rpm). Virus supernatants were harvested upon centrifugation at 13,000 × g. Virus titers were determined by plaque assay and expressed as the number of plaque forming units (pfu) per ml of the phage suspension.

The plasmid pBRT7Qβ, which contains a cDNA of bacteriophage Qβ cloned in the plasmid pBR322 (Taniguchi, Palmieri, and Weissmann 1978; Barrera et al. 1993), was used to transform E.coli DH5-α. The supernatant of an overnight culture obtained from a transformed colony was used to isolate a biological clone (virus Qβ_wt), which had no mutations relative to the sequence of the cloned cDNA.

Biological clones corresponded to lytic plaques obtained in semisolid agar. They were isolated by punching and removing the top and the bottom agar around well-separated lytic plaques. The agar containing each plaque was transferred into a tube with 1 ml of phage buffer (1 g/l gelatin, 0.05 M Tris–HCl, pH 7.5, and 0.01 M MgCl₂) and 50 μl of chloroform, and incubated for 1 h at 25 °C with shaking (900 rpm). After centrifugation at 13,000 × g for 15 min to clarify the supernatant, the latter was stored over 25 μl of chloroform.

2.2 Preparation of Qβ single mutants through site-directed mutagenesis

The plasmid pBRT7Qβ was used to engineer single mutant viruses containing the replicase substitutions U2776C or U3402C (virus Qβ_U2776C and Qβ_U3402C). Mutagenesis was carried out using the QuickChange II Site-Directed Mutagenesis Kit (Stratagene) and the primers 5′GCTAATAGGAGATGCTCCGTCCGTTGAGGG3 ′ and its complementary (for U2776C), and 5′GAGATACTGGACTTAGACCCGTCTGAGGTCACTG3′ and its complementary (for U3402C). The procedures to build and isolate the site-directed mutants have been previously described (Arribas, Cabanillas, and Lázaro 2011; Cabanillas, Arribas, and Lázaro 2013). Several well-separated lytic plaques of each mutant were picked and sequenced, and those in which the introduced mutation was the only one present in the virus genome were used for further analysis.

2.3 Propagation of Qβ virus clones to generate heterogeneous populations

The viruses Qβ_wt, Qβ_U2776C, and Qβ_U3402C were used to infect 10⁸ bacteria in a final volume of 1 ml at an moi of 0.1 pfu/cell either in the absence or in the presence of 40 μg/ml of 5-azacytidine (AZC). After 2 h of incubation at 37 °C, viral supernatants were collected, and approximately 10⁷ pfu of each phage suspension were used to infect a fresh E.coli culture, keeping the moi around 0.1. The process was repeated until reaching a total of ten passages.

2.4 Growth rate determinations

Triplicate liquid cultures containing 10⁸ bacteria growing in exponential phase were inoculated with 10⁴ pfu of the virus assayed in a final volume of 1 ml. After 2 h of incubation at the temperature indicated, the virus supernatants were collected as described above, and titrated to estimate the virus yield. Absolute growth rates were expressed as the log₂[(N_f – N₀)/N₀], where N₀ was the initial input of virus and N_f was the number of pfu recovered in the assay. Relative growth rates corresponded to the absolute growth rate divided by the value obtained for the virus Qβ_wt in a parallel determination. Previous assays showed that the virus Qβ_wt grew exponentially under the experimental conditions described.

2.5 Competition assays

Competitions were carried out by infecting 10⁸ bacteria with equal amounts of the wild type and the mutant viruses (10⁵–10⁶ pfu) in a final volume of 1 ml. After 2 h of incubation at the temperature indicated, viral supernatants were collected, and a fraction was used to initiate a new passage, keeping the moi around 0.01 pfu/cell. All competitions were carried out in duplicate. The consensus sequences of the populations obtained after five passages were determined. Raw chromatograms, non-subjected to any process of filtering and smoothing, were visually inspected to determine qualitatively the relative amount of the wild type and the mutant nucleotide (Fig. 1). While Sanger sequencing is an inadequate means of assessing the frequency of a minor variant, it is good enough for binary distinction between a frequency of around 50 per cent and a frequency of 10 per cent or lower, which is required for the conclusions presented. When the discriminating nucleotide was still polymorphic after five passages, competitions were extended until a maximum of fifteen passages and sequences were analyzed at every fifth passage. Intervals 2, 3, and 4 in Fig. 1 should not be taken as quantitative estimations but as an indicator of the transient state observed at passage number 5, in the situations in which no competitor has become dominant.

Figure 1.

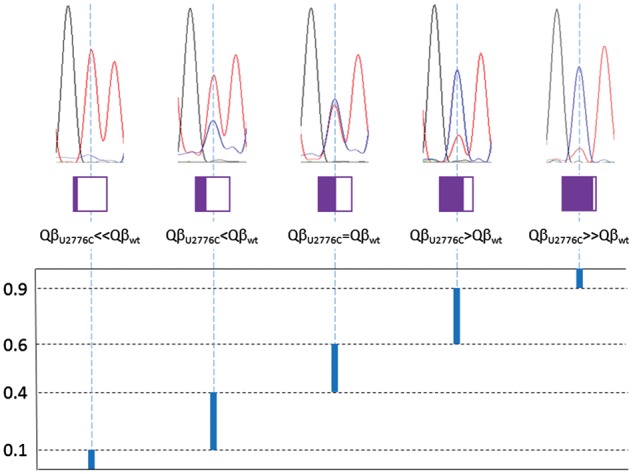
Code used to indicate the relative amount of wild-type and mutant nucleotides at polymorphic positions. Above, we show example chromatograms for each of the five qualitative intervals of abundance for mutant Qβ_U2776C. The area colored in purple inside the different boxes just below the chromatograms qualitatively represents the relative amount of mutant nucleotides, as used in other figures. Below, vertical, thick blue lines indicate the interval within which the maximum height of the mutant nucleotide band (blue line in the chromatogram) is found relative to that of the wild-type nucleotide (red line in the chromatogram). Numbers in the lower panel are just a loose quantitative approximation to the broad intervals defined, which need to be translated to computational results regarding population fractions: from 0 to 0.1 (first interval, only wild type present), from 0.1 to 0.4 (second, mutant present in a low amount), from 0.4 to 0.6 (third, mutant and wild type present in similar amounts), from 0.6 to 0.9 (fourth, wild type present in a low amount), and from 0.9 to 1 (fifth, only mutant present). Numerical values are only used to guide the eye in comparing experiment and model in Fig. 5.

2.6 RNA extraction, cDNA synthesis, PCR amplification, and nucleotide sequencing

Viral RNA was prepared either from virus clones or populations following standard procedures. RNAs were used for cDNA synthesis with the avian myeloblastosis virus reverse transcriptase (Promega), followed by PCR amplification using Expand high-fidelity DNA polymerase (Roche). PCR products were column purified (Qiagen) and subjected to standard Sanger sequencing (Cabanillas, Arribas, and Lázaro 2013). The mutation frequency in the mutant spectrum of particular populations was determined in each case with a sample of fifteen biological clones which were sequenced from nucleotide 1,500 to nucleotide 4,180. Mutation frequencies were expressed as substitutions per nucleotide, this is the number of mutations found (relative to the population consensus sequence) divided by the total number of nucleotides sequenced.

3. Methods: population dynamics model

The computational model describes the evolution of a heterogeneous population of individuals, each characterized by a replicative ability value, subjected to subsequent cycles of replication and mutation. The model works in the large-population limit and is deterministic: dynamics is unambiguously determined by the initial conditions and the values of the parameters. It is also a mean-field model, meaning that the effect of the different variables affects the viral genomes in an average manner. The mean-field approximation is justified in the light of the permanent stirring of the liquid in which the viral populations grow and compete, where all individuals are expected to be well mixed at all times. Initially, all individuals belong to the same replicative ability class and upon subsequent generations where the population replicates and mutates, a diversity distribution progressively builds up. We consider an effective microscopic representation of the mutation process, where a genome incorporates an average number of mutations that is a parameter of the model: it takes its lower value for the basal mutation rate and higher values when it mimics the presence of a mutagen. The main features of the current model of viral evolution are inspired in previous models (Lázaro et al. 2002; Manrubia et al. 2005; Aguirre and Manrubia 2007) that successfully reproduced a number of observations. In the light of the experimental protocol here used, the process is formally implemented as follows.

3.1 Replication

Each individual in a population is characterized by its replicative ability f, that is, the number of copies it produces per generation. At each discrete generation g, the population is described by a vector $\overrightarrow{n}\left(g\right)$ whose components correspond to the number of individuals in each replicative ability class f. The parental population is maintained after each generation, and the new copies can mutate and therefore contribute to a different replicative ability class. Such replicative ability cannot grow beyond a maximal value F, and mutations to f = 0 represent lethal mutations.

3.2 Mutation

The evolution of the population can be formally written as $\overrightarrow{n}\left(g+1\right)=\overrightarrow{n}\left(g\right)\text{+}\mathbf{M}\overrightarrow{n}\left(g\right)$, where M is a transition matrix of size (F + 1) × (F + 1) whose elements M_ff′ denote the fraction of individuals of class f′ that mutate to class f in one generation. Elements of matrix M are calculated as follows. The number of mutations per genome and replication event is denoted by m. We assume an additive landscape without epistatic interactions, such that the total change in replicative ability ΔW is given by the sum of the individual effects of the mutations occurring in the same sequence at each replication event,

$$\Delta W=\sum _{j=1}^m{\left(\delta W\right)}_j.$$

The sum runs over the number of individual mutations m, and the absolute value of each of them |δW| is obtained from an exponential probability distribution,

$$P(|\delta W|)=\frac{1}{m_{\text{ef}}}\text{exp}\{-|\delta W|/m_{\text{ef}}\},$$

where m_ef stands for the average mutational effect in replicative ability of a single mutation. The effect of a single mutation is negative (deleterious) with probability p and positive (beneficial) with probability q. Therefore, δW = –|δW| with probability p and δW = |δW| with probability q. We generate a large number of events (2 × 10⁶ in this work) to obtain an accurate approximation to the distribution of ΔW for each value of p, q, m, and m_ef (Supplementary Fig. S1A). As the replicative ability classes of the population are not continuous in our model, we discretize the distribution of ΔW and obtain the probability D_k of an individual of class f to become of class f + k, where k goes from –F to F (Supplementary Fig. S1A). Note that D_k is the same for all values of f.

Parameter F sets a maximum to the number of copies that a genome can produce in one generation. The individuals that mutate to the non-biological classes f < 0 and f > F are either eliminated (because they are unable to replicate) or included in the limit class f = F, respectively.

3.3 Dynamics

The evolutionary dynamics of the replicative ability classes in the population can be written as

$$n_f\left(g+1\right)=n_f\left(g\right)+\sum _{f^{\mathrm{\text{'}}}=1}^F{M}_{f{f}^{\mathrm{\text{'}}}}{n}_{f^{\mathrm{\text{'}}}}\left(g\right),$$ Eq. (1)

where the elements M_ff′ of the transition matrix M (i.e. the fraction of individuals of class f′ that mutate to class f in one generation) are:

$$M_{ff\mathrm{\text{'}}}=\left\{\begin{array}{l}{f}^{\mathrm{\text{'}}}\sum _{k=-F}^{-f^{\mathrm{\text{'}}}}{D}_k\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{f}\text{ = }0,\hfill \\ f^{\mathrm{\text{'}}}{D}_{f-f^{\mathrm{\text{'}}}} \mathrm{f}\mathrm{o}\mathrm{r}0\text{<}\mathrm{f}\text{<}\mathrm{F}\\ f^{\mathrm{\text{'}}}\sum _{k=F-f^{\mathrm{\text{'}}}}^F{D}_k\mathrm{f}\mathrm{o}\mathrm{r}f=F.\end{array},\right.$$

Given the population size at generation g, $N\left(g\right)={\sum }_{f=1}^F{n}_f\left(g\right)$, and the average replicative ability at that time, $\stackrel{-}{f}\left(g\right)=\frac{{\sum }_{f=1}^{F}f{n}_{f\left(g\right)}}{N\left(g\right)}$, the total population evolves according to $N\left(g+1\right)=\left(1+\stackrel{-}{f}\left(g\right)\right)N\left(g\right)$.

The initial dynamics of the average replicative ability (and therefore of the whole population) is very dependent on the initial distribution of the population in different replicative ability classes while, as g grows, the average replicative ability attains an asymptotic value $\lambda$ that corresponds to the largest eigenvalue of matrix M, $\stackrel{-}{f}\left(g\right)\to \lambda .$ Therefore, for large times (large g) the growth of all individuals in the population becomes independent of the initial conditions. Eventually, the population attains a fixed distribution given by the eigenvector associated to $\lambda$. In Supplementary Fig. S1 we supply further details on the model, including the expected shape of the distribution D_k as a function of k, and the asymptotic dependence of equilibrium population distributions and of D_k on the model parameters p, q, m, and m_ef.

4. Empirical results

4.1 Clonal populations of mutants carrying substitutions U2776C or U3402C are able to outcompete a clonal population of the wild-type virus when seeded at equal frequencies

To evaluate the effects of the replicase substitutions U2776C and U3402C, which were selected during adaptation of Qβ at high temperature (43 °C), we generated the single mutants Qβ_U2776C and Qβ_U3402C through site-directed mutagenesis of an infectious clone of the virus (see Section 2.2). Expression of the non-mutagenized infectious clone allowed us to obtain a clonal wild-type virus (Qβ_wt, see Section 2.1), which was used as reference in this study. Determination of the relative growth rates showed that both mutants had values similar to the wild-type virus at 37 °C (Qβ_U2776C = 1.02 ± 0.01, P = 0.15 and Qβ_U3402C = 0.93 ± 0.15, P = 0.25; Student’s t-test) and significantly higher values at 43 °C (Qβ_U2776C = 1.25 ± 0.05, P < 0.01 and Qβ_U3402C = 1.96 ± 0.15, P < 0.01; Student’s t-test), a result that agrees with the rapid selection and fixation of both substitutions at this temperature.

To further assess the selective value of substitutions U2776C and U3402C, we performed competition experiments between each single mutant and the virus Qβ_wt at both 43 °C and 37 °C using equal amounts of each competitor virus (see Section 2.5). Determination of the consensus sequences of the populations obtained after five passages at 43 °C showed the dominance of the mutants in both cases, which agrees with the values of their growth rates at this temperature, higher than that of Qβ_wt. Unexpectedly, the mutants also dominated in the competitions carried out at 37 °C, a temperature at which they had growth rates similar to that of Qβ_wt. This result is apparently at odds with the fact that none of the mutants had previously been detected in our laboratory during the propagation of Qβ at this temperature—as it would be expected should they have a selective advantage. A possible explanation for this result is that the rise of the mutant to fixation depends on its initial frequency. To test this possibility, we performed new competitions between mutant viruses Qβ_U2776C or Qβ_U3402C and the wild type at 37 °C with an initial ratio 1:100. Subsequent passages were carried out as described in Section 2 for standard competitions. Both mutant viruses were selected against at passage number 5, supporting a dependence of fitness on frequency.

4.2 The number of passages experienced by competitor viruses prior to their co-propagation determines the outcome of the competitions carried out at 37 °C

To investigate whether the outcome of competitions is affected by the number of replication rounds experienced by each virus upon its isolation as a biological clone, we performed new competitions between each of the clonal viruses Qβ_U2776C and Qβ_U3402C and wild-type populations generated upon propagation of the clonal virus Qβ_wt for three, five, and ten passages at 37 °C (Qβ_wtP3, Qβ_wtP5, and Qβ_wtP10) using large population sizes (Fig. 2A). The consensus sequences of the populations obtained after five passages of competition were determined to evaluate the relative amount of each virus. We observed that the higher the number of passages experienced by the wild-type virus previously to the competition, the lower the amount of both mutants at 37°C. To test whether the wild-type virus could become dominant at later passages in the cases in which it still coexisted with the mutants at passage number 5, we extended the competitions carried out with Qβ_wtP5 and Qβ_wtP10. We observed that the mutant virus Qβ_U2776C was totally displaced at passage number 15 (when it competed with Qβ_wtP5) and at passage number 10 (when it competed with Qβ_wtP10). Competitions between Qβ_U3402C and Qβ_wtP5 still showed the co-existence of both viruses after 15 passages, whereas the virus Qβ_U3402C was selected against at passage number 15 when it competed with Qβ_wtP10. Overall, the results confirm that the superiority of the wild type over the mutants increases with the number of passages experienced before their joint propagation. Determination of the consensus sequence of population Qβ_wtP10 did not reveal any new mutation, suggesting that the change in the composition of the mutant spectrum, and especially its enrichment in genetic variation, was responsible for the behavior observed.

Figure 2.

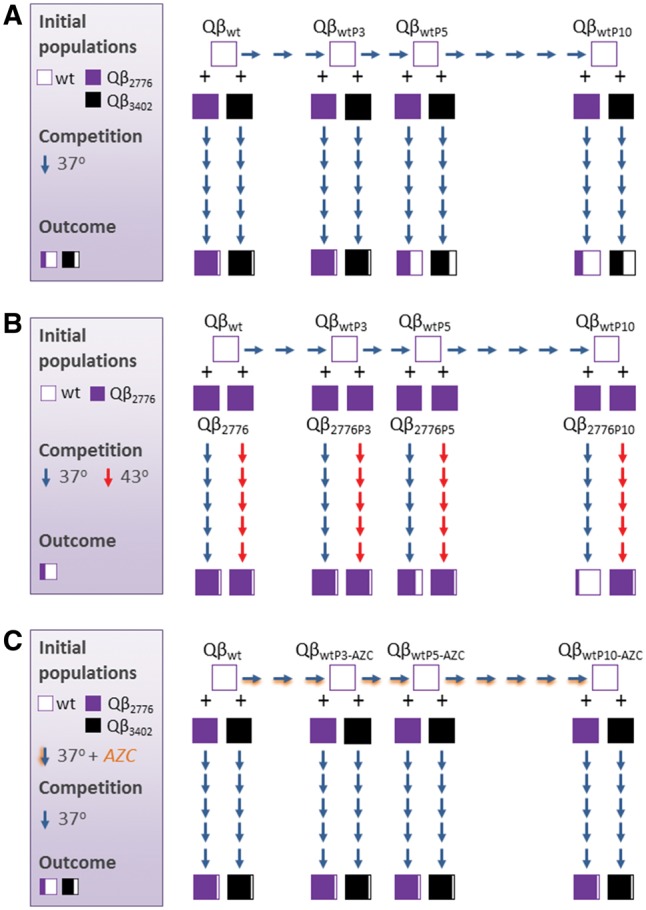
Competition experiments between different viral populations. (A) A wild-type biological clone (Qβ_wt, see Section 2.1) was serially transferred in E.coli for ten passages, keeping the moi around 0.1. The clonal virus Qβ_wt (white squares) and the populations obtained after three, five, and ten passages in E.coli (also represented with white squares) were mixed with equal amounts of a biological clone of either the virus Qβ_U2776C (purple squares) or the virus Qβ_U3402C (black squares), and allowed to compete for five passages in E.coli. The consensus sequence of the new populations obtained was determined. The relative amount of each nucleotide, U or C, in the chromatograms is indicated with squares colored with the corresponding amount of white (wild-type nucleotide) and black/purple (mutant nucleotides), see Fig. 1 for definitions. (B) Both the virus Qβ_wt and the mutant Qβ_U2776C were transferred ten times to obtain heterogeneous populations which competed as in (A). (C) As in (A), but with virus Qβ_wt transferred in the presence of 40 µg/ml of AZC. For each experiment, the box in the left-hand side schematically represents the overall organization. Competitions were carried out in duplicate. In all cases the relative amount of the mutant and the wt nucleotide obtained in the two replicas of the same experiment lye in the same interval (Fig. 1) with minor differences that are non-significant in data obtained through Sanger sequencing.

The findings above prompted the question of whether mutant populations could recover their superiority if prior to the competitions they were propagated under the same conditions as the wild-type virus. Therefore, we subjected the virus Qβ_U2776C to up to ten serial passages at 37 °C using large population sizes. As it happened with the wild-type virus, no additional mutations were fixed in the mutant consensus sequence. Populations obtained at passages three, five, and ten (Qβ_U2776CP3, Qβ_U2776CP5, and Qβ_U2776CP10) were mixed with the analogous wild-type populations and allowed to compete for five passages (Fig. 2B). The outcome of the competitions showed that when both competitor viruses had experienced a short number of passages (three or five passages) prior to the competition, the mutant was still able to displace the wild type. However, when the number of passages increased (ten passages in the experiment), the wild type became the winner, suggesting that the optimization dynamics of the competitor viruses at 37 °C cross at some point. In agreement with the selective advantages of the mutant at 43 °C, similar competitions carried out at this temperature led to its total dominance, regardless the number of passages previously experienced by each competitor. These qualitative results were identical in the two replicas performed for each experiment.

4.3 Propagation of the wild-type virus at artificially increased error rate eliminates its ability to outcompete the mutants carrying substitutions U2776C or U3402C

Another important parameter influencing the fitness values reached by RNA viruses is the replication error rate. Higher-than-standard error rates increase the heterogeneity of populations, augmenting in general the generation of both deleterious and beneficial mutations, and interfering in particular with selection of the latter. Propagation of the virus Qβ_wt in the presence of the mutagenic nucleoside analogue AZC for ten passages (Fig. 2C) led to the generation of a population with no mutations fixed in the consensus sequence but with a mutation frequency in the mutant spectrum of 1.8 × 10⁻³ substitutions per nucleotide. This value was significantly higher (P < 0.001, Student’s t-test) than that obtained for the equivalent population transferred in the absence of AZC (Fig. 2A), which had a mutation frequency of 1.5 × 10⁻⁴ substitutions per nucleotide. Competitions between any of the mutant viruses Qβ_U2776C or Qβ_U3402C and the populations generated after propagation of the virus Qβ_wt for three, five, and ten passages in the presence of AZC always led to the dominance of the mutant, indicating that the increase of the error rate produced lower-fitness populations unable to outcompete mutants (Qβ_U2776C or Qβ_U3402C) that would have been eliminated if diversity had been generated at standard error rate.

4.4 Individual viruses isolated from a heterogeneous wild-type population differ in their ability to outcompete the mutant Qβ_U2776C

To further explore the role of the structure of the mutant spectra in the outcome of the competition experiments, we analyzed the behavior of individual viruses isolated from the population Qβ_wtP10, which outcompetes the clonal mutant Qβ_U2776C when they co-propagate. We isolated five biological clones from the population Qβ_wtP10 and competed each of them against the clonal mutant Qβ_U2776C (Fig. 3). After competition for five passages, only one of the wild-type clones dominated in the competition, another one was outcompeted, and the remaining three were present in similar amounts with the mutant. The result shows that the behavior of a heterogeneous population when it competes with a particular mutant may differ from the behavior of the individual viruses composing it.

Figure 3.

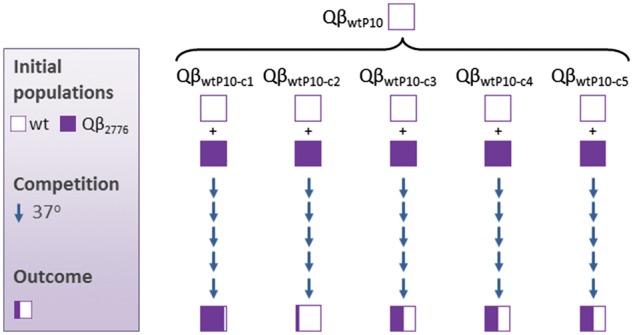
Competition of the virus Qβ_U2776C with different biological clones isolated from a heterogeneous wild-type population. The population Qβ_wtP10 (Fig. 2A) was used to isolate five biological clones (c1 to c5) which were mixed with equal amounts of the virus Qβ_U2776C. After competition for five passages the consensus sequence of the resulting populations was determined. The relative amount of each nucleotide, U or C, in the chromatograms (estimated as shown in Fig. 1) is indicated with squares colored with the corresponding amount of white (wild-type nucleotide) and purple (mutant nucleotide). Competitions were carried out in duplicate. In all cases the relative amount of the mutant and the wt nucleotide obtained in the two replicas of the same experiment lye in the same interval (Fig. 1) with minor differences that are non-significant in data obtained through Sanger sequencing.

5. Numerical results

5.1 Working hypotheses

The contrasting results obtained in the competition experiments carried out between the clonal mutants Qβ_U2776C and Qβ_U3402C and the wild type, and between Qβ_U2776C and clones from the evolved population Qβ_wtP10, show how important the mutant spectrum is to determine dominance in viral competitions. We have shown how the outcome of the experiments depends, in particular, on the distance to the clonal origin and on the mutation rate.

Natural viral populations are heterogeneous regarding their genotypes and their phenotypes, i.e. there is a varying proportion of viral genomes in different fitness classes. Beyond the number of generations experienced, the composition and structure of the mutant spectrum generated upon replication of a clonal virus depends on parameters such as the initial replicative ability, the mutation rate, or the effect of mutations on fitness. To evaluate how differences in these parameters could contribute to the outcome of the competitions carried out between different populations, we designed a theoretical model (as detailed in Section 3) that we now explore in situations analogous to the competition experiments reported.

There are two possible, non-excluding scenarios that may, in principle, explain in a coherent fashion the observations. We present them as separated possibilities to disentangle the effect each scenario might have in the competition experiments; however, the available evidence supports that the actual dynamics includes elements from both scenarios.

Scenario 1: The replicative ability of the initial wild type is lower than the replicative ability of the initial mutant, but the average replicative ability at mutation-selection equilibrium is higher for the wild type. Here, both strains would regenerate mutation-selection equilibrium at a comparable rate (i.e. with the same rate of generation of deleterious, neutral and beneficial mutations), though the progeny of the wild type would have lower average replicative ability at short times after competition is started, and higher average replicative ability after sufficiently long time has elapsed (see Fig. 4A).

Figure 4.

Dynamics of the populations of wild type and mutant with number of passages. (A, B) Average replicative ability of wild type and mutant for the two different scenarios. The initial distribution of the clonal populations and the asymptotic equilibria for the replicative ability f are plotted in the insets. (A) Scenario 1. Parameters are p_wt = p_mut = 0.2, q_wt = q_mut = 0.01, m_{ef, wt} = m_{ef, mut} = 0.5, F_wt = 10, F_mut = 9, f_{0, wt} = 6, f_{0, mut} = 8. (B) Scenario 2. Parameters are: p_wt = p_mut = 0.5, q_wt = q_mut = 0.001, m_{ef, wt} = 0.5, m_{ef, mut} = 0.25, F_wt = 11, F_mut = 9, f_{0, wt} = f_{0, mut} = 8. (C, D) Single realizations of competitions between the wild-type and the mutant populations for Scenario 1 (C) and Scenario 2 (D). The circles represent populations at each viral generation. In the cases shown in (C) and (D), the mutant displaces the wild-type population after four and eleven passages, respectively.

Scenario 2: The replicative abilities of the initial wild type and mutant are comparable, but (1) the mutation-selection equilibrium has higher average replicative ability for the population regenerated from the wild type and (2) the mutant is more robust to mutations, implying that the effective rates of deleterious, neutral, and beneficial mutations are strain-dependent. Here both competitors start with the same replicative ability, so the advantage of the mutant at short times observed in the experiments is ascribed to increased robustness. Again, the wild type is superior in the long run (see Fig. 4B).

The numerical results that we will show in the following have been obtained through an implementation of one or another scenario, with comparable results in appropriate parameter ranges. For simplicity, we describe in detail simulations in Scenario 1 in the main text of this work, and present results for Scenario 2 as figures in the Supplementary data. In the final section we will discuss further empirical support for each scenario.

5.2 Competition between two populations

Competition mimics the experimental procedure. Populations 1 and 2 start at an initial size of N₀/2 individuals and grow unrestrictedly following Eq. (1). Every g_T generations a passage takes place such that populations N_i(g) (i = 1, 2) are normalized, this action mimicking the random selection of N₀ individuals from the population. Therefore, the new populations become

$$N_i^{\mathrm{*}}\left(g\right)=\frac{N_i\left(g\right)}{N_1\left(g\right)+N_2\left(g\right)}{N}_0.$$

The competition ends when one population becomes γ times larger than its opponent, and we term this generation g_c. The equivalent number of passages that have taken place at that time is defined as the competition time t_c (i.e. $t_c=\raisebox{1ex}{$g_c$}\!\left/ \!\raisebox{-1ex}{$g_T$}\right.$). Furthermore, it is important to remark that the evolution of the average replicative ability $\stackrel{-}{f_i}\left(g\right)$ of both species toward their asymptotic growth rate λ_i is independent of their populations and of the passage events.

In Scenario 1 the wild type has lower initial replicative ability (f_{0, wt} < f_{0, mut}) but a fitter asymptotic distribution, a feature implemented through parameter F: F_wt > F_mut—this is a condition that implies λ_wt > λ_mut. In Scenario 2 we maintain F_wt > F_mut, but now the wild type and the mutant have equal replicative ability when the competition begins (f_{0, wt} = f_{0, mut}); also, the mutant is more robust to mutations, a condition implemented through the variable m_ef (m_{ef, wt} > m_{ef, mut}).

Examples of competitions between two populations (wild type and mutant) are shown in Fig. 4C (Scenario 1) and Fig. 4D (Scenario 2). Parameters are chosen so as to reproduce as closely as possible the experimental procedure: competitions start with initial clonal populations of 5 × 10⁴ individuals per competitor (N₀ = 10⁵) and passages are applied after every three generations (g_T = 3, when total populations have grown to about 10⁸ individuals). When a passage occurs both populations are rescaled maintaining their relative proportion such that the new total population is 10⁵. The competition time t_c is the number of passages until one competitor is less than 10 per cent (γ = 10) of the other. This condition has been chosen in agreement with the interval defined experimentally, see Fig. 1. The mutagenicity of the culture medium is tuned by the number of mutations per genome and generation m (m = 1 represents absence of mutagenic AZC and m > 1 presence of AZC).

5.3 Comparison to competition experiments

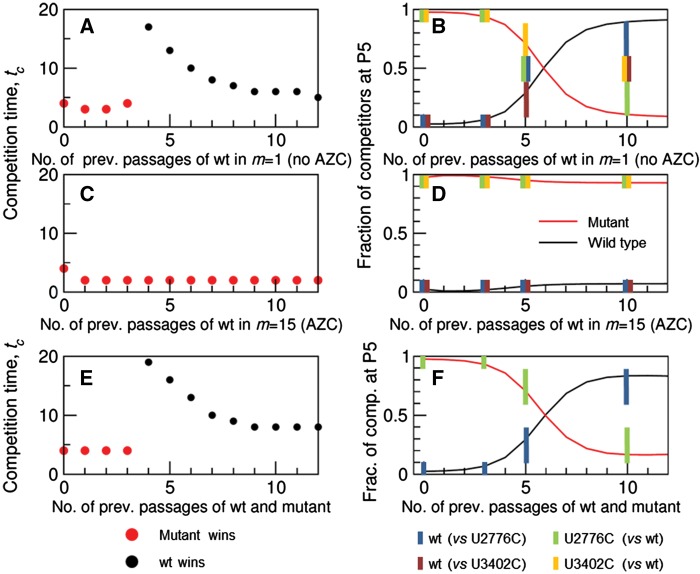
Figure 5 summarizes the relationship between computational and experimental results, illustrating how the observations can be integrated into a unique framework. Consider the experiments represented in Fig. 2A and C, where the wild-type population obtained at different passages competes with clonal populations of either mutant. In the light of our previous discussion, the larger the number of passages, the closer is the wild-type population to mutation-selection equilibrium and, therefore, the larger its advantage. The number of passages undergone by the wild type is represented in the x-axis of Fig. 5A (without AZC) and Fig. 5C (with AZC); the y-axis represents the time until one of the populations displaces the other and the winner of the competition is highlighted. While for short distances to the clonal origin the mutant is the winner, the situation changes when the wild type has sufficiently regenerated its mutant spectrum. Figure 5B and D shows the fraction of individuals in each of the populations at passage five of the competition; numerical results are compared to approximate abundances in experiments, represented as colored bars (outcome of competitions in Fig. 2A and C). Figure 5E and F shows analogous results when both populations are independently passaged (therefore independently regenerate their mutation-selection equilibrium) before competition starts. As in previous cases, the initial advantage of the mutant populations is lost as the wild type approaches its equilibrium distribution. The numerical expectations are compared in Fig. 5F to the results of the experiments illustrated in Fig. 2B. Qualitatively identical results are obtained in Scenario 2, as described in Supplementary Fig. S2. A good qualitative agreement between experimental and computational results is obtained in all cases.

Figure 5.

Effect of heterogeneity in the competition between the wild type population and the mutant population—Scenario 1. The competition procedure and populations parameters are those of Scenario 1 (Sections 5.1, 5.2, and Fig. 4A). The x-axes denote the number of passages applied to initial populations before starting competition. These previous passages take place in the absence (A, B, m = 1) and presence (C, D, m = 15) of the mutagenic AZC for the wild type, although competitions occur in absence of AZC (m = 1). The competition time and the winner of the competition are plotted in (A, C), while (B, D) show the populations after five passages. (E, F) As above, but now both the wild-type and the mutant competitor are generated upon propagation in the absence of AZC (m = 1). The competition time and the winner of the competition are plotted in (E), while (F) shows the populations after five passages. Experimental results for the wild type competing against clonal virus Qβ_U3402C at 37 °C appear in (B) and (D), and experimental results for the wild type competing against clonal virus Qβ_U2776C at 37 °C are plotted in (B), (D), and (F), as indicated in the legend and using the code defined in Fig. 1.

The intrinsic heterogeneity of all populations once the initial clones start replicating entails indeterminacy in the fitness of any sequence randomly drawn from the population, this indeterminacy increasing with the degree of heterogeneity, i.e. with the number of passages. The results of the experiments in Fig. 3 are therefore in agreement with expectations. We have also repeated competitions between randomly selected clones of the wild type after ten passages and the mutant Qβ_U2776C in the framework of our model. In Scenario 1, and after competition going on for ten passages, we obtain that the mutant wins in 6 per cent of cases, both populations coexist in 60 per cent of cases, and the wild type displaces the mutant in 34 per cent of cases (see Supplementary Fig. S3). The results agree with the observations, though additional data would be required to quantitatively assess this agreement. Scenario 2 yields comparable results, see Supplementary Fig. S4.

6. Discussion

The results presented in this work show that the outcome of competitions between two virus populations depend on the number of generations experienced by each virus prior to co-propagation, and on the error rate at which previous replication has occurred. Our results add to previous observations supporting fundamental differences between the fitness conferred by the consensus sequence and that of the whole population, and corroborate that RNA virus populations can only be defined through the properties of the ensemble (Vignuzzi et al. 2006; Domingo, Sheldon, and Perales 2012; Andino and Domingo 2015; Bordería et al. 2015).

Specifically, we have shown that two mutants of the bacteriophage Qβ selected at higher-than-optimal temperature (43 °C) can displace a wild-type virus at standard temperature (37 °C) when both competitors are clonal and seeded at a comparable frequency. The advantage of the mutants is lost when the wild-type virus is allowed to replicate for a certain number of generations prior to competition. The mutants do not reach dominance when seeded at low frequency, which provides an explanation to the fact that substitutions U2776C and U3402C have never been detected in the consensus sequence of Qβ populations evolved at 37 °C. Interestingly, the wild-type virus loses its ability to displace the mutants if allowed to replicate at increased error rate before competition starts, thus suggesting that sufficiently large increases in the error rate reduce the competitive fitness reached by the wild-type population upon its propagation. Consequently, mutants that were never dominant in populations generated at standard error rate could invade analogous populations propagated at increased error rate. This nonetheless, it should be recalled that the effects of increasing the mutation rate are dose-dependent. In fact, too low increases in the mutation rate should very slightly affect the ability of the wild type to become optimized, and could even promote adaptation (Cases-González et al. 2008; Iranzo et al. 2011; Lázaro 2014; Arribas et al. 2016). The qualitative transition from low increases in the mutation rate, with quasi-neutral or beneficial effects, to high increases causing a deleterious impact is clearly described and understood in the framework of our current and related models (Stich, Manrubia, and Lázaro 2010a).

All the experimental results here obtained have been coherently explained in the framework of a computational model for the dynamics of heterogeneous populations where the effect of mutations is implemented in an effective way. The model makes some assumptions worth discussing: (1) it disregards epistatic interactions, since the joint effect of mutations is taken as the sum of their independent effects, (2) it works in the infinite population limit, thus ignoring the role of stochasticity. This fact likely does not play any essential role in competition dynamics since initial populations are of order 10⁵, and empirical mutation rates are above 10⁻⁴, so its product is larger than 1, (3) in our model, the mutation-selection equilibrium would be unique given the values of p, q, F, m, and m_ef provided that regeneration time and population sizes were large enough so as to allow for competition among all the possible mutants, (4) the model works with effective replicative ability classes and disregards specific sequence composition. While this approximation is unavoidable for the model to be computationally tractable when simulating large populations, it forbids an explicit representation of genomic diversity, and (5) a combination of the latter condition and lack of stochasticity permits the model to keep track of all minor phenotypic variants. These approximations should be taken as strengths of the model in that none of those mechanisms (summarized in epistasis, stochasticity, and a microscopic description of genomes) are needed to explain the observations.

The representation of the local, metastable equilibrium reached by the empirical populations as a truly asymptotic mutation-selection equilibrium in the model deserves some discussion. If natural populations were able to explore the whole genomic space, it is highly likely that regions with fitness larger than the one observed and with a different consensus sequence would be reached. However, such regions can only be attained after a time which is much longer than the typical evolutionary time, not only in the laboratory, but also in vivo. Adaptation usually occurs at a local scale, by fixing one or a few mutations that confer an immediate advantage to populations. The typical time subsequently spent in this metastable state (a local fitness maximum) can be so large that, in all likelihood, the global maximum is never observed, and this local maximum works in practice as the asymptotic mutation-selection equilibrium (Catalán et al. 2017).

The former considerations notwithstanding, it has been shown that the minimal rules implemented in the model suffice to reproduce the experimental results and to understand their origin in a unifying context. Scenario 1 is based on the simplest assumptions that, under permissive conditions (i.e. 37 °C), the wild-type virus has lower initial replicative ability than the mutants do, although it can reach a higher value upon replication. This is formally translated as a higher maximum replicative ability class F value, which is the only way to yield a higher growth rate at equilibrium for fixed mutation probabilities p and q. The feasibility of a lower F value for the mutants comes from indirect empirical evidence. Substitutions U2776C and U3402C were selected at higher-than-optimal temperature (Arribas et al. 2014), a condition that favors the selection of stabilizing mutations (Chen and Shakhnovich 2010; Lee et al. 2011), which often have a fitness cost at standard temperature because more stable proteins generally perform their function at a lower rate (Feller 2010; Elias et al. 2014; Xie et al. 2014). In Scenario 2, the condition on the wild-type virus having lower initial replicative ability than the mutants is replaced by equal values for both viruses. We test if an increased robustness of the mutants to mutations (i.e. lower values of the parameter implementing the average effect of mutations on replicative ability, m_ef) could explain their advantage when they are close to their clonal origin. The reason to consider that robustness may be a beneficial character at high temperature comes from the fact that under this condition the deleterious effects of many mutations that induce protein misfolding are exacerbated (Tokuriki and Tawfik 2009; Wylie and Shakhnovich 2011). Under this scenario, substitutions U2776C and U3402C would provide an advantage when the relative amount of deleterious mutations is high, as it happens right after a strong population bottleneck. Further replication at large population sizes increases the frequency of beneficial mutants, eliminating the advantage provided by the mutations. A possible mechanism by which the replicase substitutions U2776C and U3402C could confer increased robustness is a change in the replicase mutational bias that alters the ratio of synonymous and non-synonymous mutations, a phenomenology that has been documented in thermophilic organisms (Lynn, Singer, and Hickey 2002; Singer and Hickey 2003; Lobry and Necşulea 2006). However, further experiments are necessary to test this idea. Scenarios 1 and 2 are not mutually exclusive; on the contrary, they represent limit cases of a continuum of possibilities where the relative initial fitness of wild type and mutants and different robustness to mutations could be present.

As a general conclusion, co-propagation of viruses can give rise to different outcomes, as a consequence of differences in the degree of optimization reached by the populations prior to their joint spreading. These differences may be caused by particular properties of the competitor viral strains that determine the dynamics toward mutation-selection equilibrium, and by the shape of the underlying fitness landscape that quantifies the effect of mutations in fitness and the most accessible local fitness maxima for each virus. Co-propagation of viruses is not only a phenomenon that takes place in the laboratory but it is also frequent during the transmission of viruses in nature, as a result of co-infection with different variants of the same virus or when virus dispersion through biological or physical agents causes the invasion of ecosystems by new competing viruses. This can be a quite complex phenomenon, not only due to the contribution of the evolutionary history of each virus to the final outcome, as described here, but also because natural environments are continuously changing, which have consequences on the relative advantage of different viruses. In summary, a correct understanding of the adaptive dynamics followed by different virus variants is crucial to describe the effect of the coexistence of viral populations on the ecological organization and the species diversity of the Virosphere.

Data availability

All data supporting the conclusions contained in this manuscript are available upon request to the corresponding author.

Supplementary data

Supplementary data are available at Virus Evolution online.

Funding

This work has been supported through Projects FIS2014-57569-P (AEI/FEDER, UE) and SEV-2013-0347.

Conflict of interest: None declared.