Dissociable Decoding of Spatial Attention and Working Memory from EEG Oscillations and Sustained Potentials

Abstract

In human scalp EEG recordings, both sustained potentials and alpha-band oscillations are present during the delay period of working memory tasks and may therefore reflect the representation of information in working memory. However, these signals may instead reflect support mechanisms rather than the actual contents of memory. In particular, alpha-band oscillations have been tightly tied to spatial attention and may not reflect location-independent memory representations per se. To determine how sustained and oscillating EEG signals are related to attention and working memory, we attempted to decode which of 16 orientations was being held in working memory by human observers (both women and men). We found that sustained EEG activity could be used to decode the remembered orientation of a stimulus, even when the orientation of the stimulus varied independently of its location. Alpha-band oscillations also carried clear information about the location of the stimulus, but they provided little or no information about orientation independently of location. Thus, sustained potentials contain information about the object properties being maintained in working memory, consistent with previous evidence of a tight link between these potentials and working memory capacity. In contrast, alpha-band oscillations primarily carry location information, consistent with their link to spatial attention.

SIGNIFICANCE STATEMENT Working memory plays a key role in cognition, and working memory is impaired in several neurological and psychiatric disorders. Previous research has suggested that human scalp EEG recordings contain signals that reflect the neural representation of information in working memory. However, to conclude that a neural signal actually represents the object being remembered, it is necessary to show that the signal contains fine-grained information about that object. Here, we show that sustained voltages in human EEG recordings contain fine-grained information about the orientation of an object being held in memory, consistent with a memory storage signal.

Introduction

Working memory (WM) is fundamentally important in cognitive processing, and substantial effort has been devoted to understanding the neural coding of WM representations. Most research has focused on the persisting neural activity that is present during the delay period of WM tasks (Miller et al., 1991; Todd and Marois, 2004; Fukuda et al., 2015; but see Stokes, 2015; Rose et al., 2016). However, this delay-period activity could reflect support processes rather than the actual memory representations, and showing that the content of the memory can be decoded from a neural signal provides much stronger evidence that the signal represents the memory itself (Postle, 2016).

New EEG-based decoding methods show promise for studying the neural coding of human WM (LaRocque et al., 2013; Foster et al., 2016; Rose et al., 2016; Wolff et al., 2017). These studies used the scalp distribution of EEG signals to decode or track the information being held in WM. However, it is quite plausible that they were actually tracking the direction of spatial attention. For example, the scalp distribution of alpha-band EEG activity during the delay period of a spatial WM task was found to track which of eight locations was being remembered (Foster et al., 2016), but alpha oscillations are closely linked with spatial attention (Worden et al., 2000), and observers often maintain spatial attention on the to-be-remembered location in spatial WM tasks (Awh et al., 1998, 2000). Indeed, Rihs et al. (2007) showed that the scalp distribution of alpha-band activity varies systematically according to which of eight different locations is being attended. Moreover, Foster et al. (2017b) found that alpha-band activity tracks shifts of spatial attention, and van Ede et al. (2017) found that alpha-band activity tracks the location of the item that is currently most relevant in WM. In addition, LaRocque et al. (2013) and Rose et al. (2016) used EEG oscillations to decode the attended stimulus dimension in a WM task, but they did not attempt to decode the specific feature value being maintained in WM. It is possible that sustained attention is actually the mechanism of WM maintenance (Awh and Jonides, 2001), but this is currently an open question (Woodman et al., 2001; Johnson et al., 2008; Chun et al., 2011; Ester et al., 2012; Gazzaley and Nobre, 2012; Tas et al., 2016).

Sustained potentials are also present in averaged ERP waveforms during the delay period of visual WM tasks (Perez and Vogel, 2012). These sustained potentials are strongly tied to individual and group differences in WM storage capacity (Vogel and Machizawa, 2004; Leonard et al., 2013), but no prior research has determined whether these potentials represent the features of the remembered objects.

Both ERPs and fMRI have been used to decode the contents of WM in orientation memory tasks (Harrison and Tong, 2009; Serences et al., 2009; Ester et al., 2013; Wolff et al., 2015, 2017), but these tasks may have encouraged participants to focus attention on the end of the oriented grating (Fig. 1a), and it is possible that the direction of spatial attention was being decoded rather than orientation per se (Fahrenfort et al., 2017). Thus, it is not yet known whether EEG signals contain information about nonspatial features being maintained in WM.

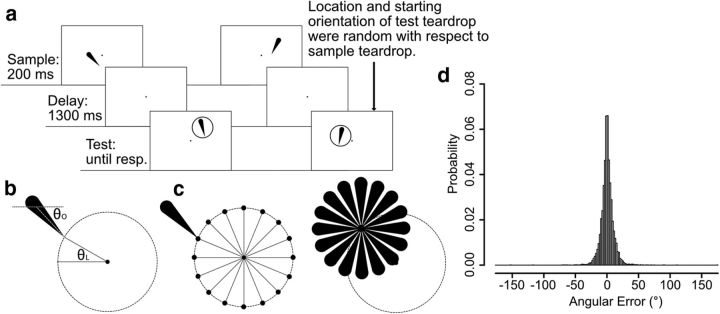
Figure 1.

a, Possible attention-based strategy for remembering an orientation. Maintaining attention on one or both of the extreme ends of the grating over a delay interval could help an observer reproduce the orientation or detect changes in orientation at the end of the interval. Even if this was not the sole mechanism being used for the task, it would likely be useful for performing the task, and neural signals related to spatial attention could potentially be sufficient to produce above-chance decoding of the orientation. b, Delayed estimation task used in Experiment 1. On each trial, participants fixated at the central dot for 500 ms (not shown here) and then saw a 200 ms teardrop. After a 1300 ms delay period, a response ring appeared, followed by a test teardrop as soon as the participant began moving the mouse. Participants used the mouse to adjust the orientation of the test teardrop until it matched the remembered orientation of the sample teardrop. The tip of the test teardrop pointed toward the mouse cursor, and participants clicked the mouse button to finalize their report. c, Probability distribution of response errors in Experiment 1, collapsed across all participants.

In the present study, we conducted two EEG decoding experiments, one using a simple orientation task that could potentially be performed by means of either spatial attention or location-independent orientation representations (or both), and one that can dissociate between orientation and location. Given the close association between sustained ERP responses and WM capacity (Vogel and Machizawa, 2004), we predicted that these responses would reflect the specific feature value being maintained in WM. By contrast, given the close association between alpha-band oscillations and attention (Worden et al., 2000; Rihs et al., 2007), we predicted that these oscillations would reflect the location of the to-be-remembered object rather its features.

Materials and Methods

Participants.

Sixteen college students between the ages of 18 and 30 with normal or corrected-to-normal visual acuity participated in each experiment for monetary compensation (Experiment 1: 10 female, 6 male; Experiment 2: 9 female, 7 male). All participants had experience with at least one prior WM task. The study was approved by the University of California-Davis Institutional Review Board.

Stimuli and apparatus.

Stimuli were generated in MATLAB (MathWorks) using PsychToolbox (Brainard, 1997; Pelli, 1997) and were presented on an LCD monitor (Dell U2412M) with a gray background (31.2 cd/m²) at viewing distance of 100 cm. A black fixation dot was continuously present in the center of the display except during the intertrial interval, and participants were instructed to maintain fixation on this dot except during the response period and intertrial interval.

Experiment 1: behavioral task.

We conducted two experiments using different behavioral tasks. Experiment 1 was designed to establish our ability to decode the feature value being remembered using both alpha-band and sustained ERPs in a simple task that could be performed either by means of spatial attention or orientation memory (or both). Experiment 2 was designed to dissociate spatial attention from orientation.

Experiment 1 used a standard delayed estimation task (Fig. 1b). Each trial started with a 500 ms presentation of the fixation dot followed by a 200 ms presentation of a black, teardrop-shaped sample stimulus (2.17° long, 0.8° maximum width) that was centered on the fixation dot. Sixteen discrete teardrop orientations were used (0°, 22.5°, 45°, 67.5°, 90°, 112.5°, 135°, 157.5°, 180°, 202.5°, 225°, 247.5°, 270°, 292.5°, 315°, and 337.5°), tested in random order with equal probability. Participants were instructed to remember the orientation of this teardrop as precisely as possible over a 1300 ms delay period during which only the fixation dot was visible. A response ring (radius 2.17°) was then presented to indicate that a response should be made; once the participant started moving the mouse to respond, a test teardrop appeared at the center of the response ring. Participants were instructed to adjust the orientation of the test teardrop so that it matched the remembered orientation of the sample teardrop. The test was identical to the sample, except that its initial orientation was determined by the mouse pointer position when the participant began to respond (and was therefore unrelated to the orientation of the sample teardrop). The orientation of the test teardrop was continuously updated while the mouse moved so that the tip of teardrop always pointed toward the current mouse pointer position. This made the tip of the teardrop highly salient. Once participants were satisfied with the orientation, they finalized the report by clicking a mouse button. The display then blanked completely, and the next trial started after a 1000 ms delay. Note that participants could potentially perform this task by focusing spatial attention onto the location of the sample teardrop's tip during the delay period and then adjusting the test teardrop until its tip was at the attended location, without remembering the orientation of the teardrop per se. Even if they did not use this as the sole memory strategy, they may have focused attention on the remembered location of the teardrop during the delay period as they prepared to make their response.

Each participant completed a total of 640 trials (40 trials for each of the 16 orientations, in random order). Each participant received at least 16 practice trials before beginning the task.

Note that the teardrop-shaped stimuli used in this study provide 360° of distinct orientations, whereas other classes of commonly used orientation stimuli (e.g., Gabor patches) can produce only 180° of distinct orientations. In mathematical terms, the present stimuli can be described in terms of the orientation of a ray, whereas stimuli such as Gabor patches can be described in terms of the orientation of a line (of infinite length).

Experiment 2: behavioral task.

The task in Experiment 2 (see Fig. 4) was designed to completely dissociate the orientation of the teardrop from its location, making it possible to determine whether a given neural signal contains information about location or about orientation (or both). It was identical to the delayed estimation task used in Experiment 1, except that the location of the sample and test teardrops varied independently from trial to trial. Thus, the location of the tip of the sample teardrop provided no information about the orientation of the teardrop.

Figure 4.

a, Two example trials of the delayed estimation used in Experiment 2: on each trial, participants fixated the central dot for 500 ms (not shown) and then saw a 200 ms teardrop. After a 1300 ms delay period, a second teardrop was presented at a different random location, and the participant used a mouse to adjust this second teardrop's orientation so that it matched the remembered orientation of the first teardrop. b, Definition of θ_L (the angular location of the teardrop tip) and θ_O (the orientation of the teardrop): θ_L was defined by the location (in polar coordinates) of the tip of the teardrop object relative to an invisible circle with a radius of 2.17°, centered on the fixation dot. θ_O was defined by the orientation of the tip of the teardrop relative to the center of the teardrop. c, Independence of θ_L and θ_O. The tip of a teardrop with a given θ_O could be presented at any of the 16 θ_L values, and a teardrop with a given θ_L could have any of the 16 θ_O values. d, Probability distribution of response errors collapsed across all participants.

We assumed that attention would be directed to the location of the sample teardrop when it was being perceived and encoded, but the stimuli were designed so that maintaining attention on this location would not allow participants to report the teardrop orientation at the time of test. In addition, this procedure allowed us to independently decode both the location and the orientation of the sample teardrop. We predicted that alpha-band activity could be used to decode the location but not the orientation of the teardrop, indicating that this signal primarily reflects spatial attention. By contrast, we predicted that sustained EEG voltages could be used to decode the orientation of the teardrop, indicating that this signal reflects a location-independent WM representation. There are multiple ERP components that track the location being attended (N2pc and sustained posterior contralateral negativity; Jolicoeur et al., 2008; Luck, 2012; Fahrenfort et al., 2017), so we assumed that we would be able to decode the location of the teardrop as well as its orientation from the ERP signals.

The orientation of a given teardrop was defined by the angular position of the tip relative to the center of the object itself (see Fig. 4b, θ_O). As in Experiment 1, 16 discrete orientations were possible (0°, 22.5°, 45°, 67.5°, 90°, 112.5°, 135°, 157.5°, 180°, 202.5°, 225°, 247.5°, 270°, 292.5°, 315°, and 337.5°). The tip of the sample teardrop was always located at one of 16 discrete locations (0°, 22.5°, 45°, 67.5°, 90°, 112.5°, 135°, 157.5°, 180°, 202.5°, 225°, 247.5°, 270°, 292.5°, 315°, and 337.5°) on an invisible circle with a radius of 2.17° that was centered on the fixation dot. Its location was defined by the angular position of the tip relative to the center of this invisible circle (see Fig. 4b, θ_L). The location and orientation of the sample teardrop on a given trial were chosen at random from the 256 possible combinations of the 16 orientations and 16 tip locations so that the orientation and location were completely independent (see Fig. 4c). For example, the tip of a teardrop with a 45° orientation could be placed at any of the 16 locations. Similarly, a teardrop with a tip located at 292.5° could have any of the 16 orientations. The only constraint was that each of the 16 orientations and each of the 16 locations occurred on the same number of trials (but selected independently of each other). Consequently, remembering the location of the teardrop would not help in reporting its orientation. Participants were told nothing about the constraints on the orientation and location of the teardrop; they were simply told that the locations of the sample and test teardrops would differ and that they should adjust the orientation of the test teardrop so that it matched the orientation of the sample.

Orientation cannot be completely dissociated from location because orientation is defined by a pattern of change over space. In the present experiment, teardrop orientation can therefore be defined as the location of the tip of the teardrop relative to the center or thick end of the teardrop. Thus, the contrast between stimulus orientation and stimulus location can be equivalently framed as a difference between an object-centered spatial representation (orientation) and an environment-centered (or retinotopic) spatial representation (which is a fundamental issue in visual coding; Bisiach, 1996). For the sake of simplicity, however, the present paper uses the term orientation to mean an object-centered representation and the terms location and space to refer to an environment-centered or retinotopic representation.

In orthogonalizing the location and orientation of the teardrop, we focused on the teardrop's tip because it was the part of the teardrop that provided the most precise location information and because the tip always pointed toward the location of the mouse pointer while the participant was attempting to reproduce the sample orientation, making it highly salient. In theory, the location of the thick end of the teardrop could provide some information about the teardrop's orientation in this task, but a later section will provide evidence that this could not have influenced our orientation decoding results.

The location of the test teardrop was determined by a new random combination of orientation and location, selected at random on each trial, independently of the orientation and the location of the sample teardrop on that trial. In other words, the test teardrop was selected at random from among the same set of 256 possibilities as the sample teardrop. However, when the observer rotated the teardrop, its tip was no longer constrained to fall on the invisible circle used to define the sample teardrop locations. Consequently, participants could not use the location of the test teardrop to guess the orientation of the sample teardrop. In addition, this task makes it possible to determine whether a decoder that is trained with orientations at one set of locations can decode orientations presented at a different set of locations.

After at least 16 practice trials, each participant completed a total of 640 trials (40 for each of the 16 orientations, collapsed across location, which was also 40 for each of the 16 locations, collapsed across orientation).

EEG recording and preprocessing.

The continuous EEG was recorded using a Brain Products actiCHamp recording system (Brain Products GmbH). Recordings were obtained from a broad set of scalp sites (FP1, FP2, F3, F4, F7, F8, C3, C4, P3, P4, P5, P6, P7, P8, P9, P10, PO3, PO4, PO7, PO8, O1, O₂, Fz, Cz, Pz, POz, and Oz), which was similar to the montage used in the spatial WM study of Foster et al. (2016). Electrodes on the left and right mastoids were recorded for use as reference sites. The horizontal electrooculogram (EOG) was recorded from electrodes placed lateral to the external canthi and was used to detect horizontal eye movements; the vertical EOG was recorded from an electrode placed below the right eye and was used to detect eyeblinks and vertical eye movements. Electrode impedances were maintained <50 KΩ. All signals were recorded single-ended and then referenced offline. The EEG was filtered online with a cascaded integrator-comb antialiasing filter (half-power cutoff at 130 Hz) and digitized at 500 Hz.

Signal processing and analysis was performed in MATLAB using EEGLAB Toolbox (Delorme and Makeig, 2004) and ERPLAB Toolbox (Lopez-Calderon and Luck, 2014). The scalp EEG was referenced off-line to the average of the left and right mastoids. A bipolar horizontal EOG derivation was computed as the difference between the two horizontal EOG electrodes, and a vertical EOG derivation was computed as the difference between Fp2 and the electrode below the right eye. All the signals were bandpass filtered (noncausal Butterworth impulse response function, half-amplitude cutoffs at 0.1 and 80 Hz, 12 dB/oct roll-off) and resampled at 250 Hz. Portions of EEG containing large muscle artifacts or extreme voltage offsets (identified by visual inspection) were removed. Independent component analysis (ICA) was then performed on the scalp EEG for each subject to identify and remove components that were associated with blinks (Jung et al., 2000) and eye movements (Drisdelle et al., 2017). The ICA-corrected EEG data were segmented for each trial from −500 to +1500 ms relative to the onset of the sample teardrop. To verify that eye movements did not impact the decoding results, we also conducted a set of decoding analyses in which trials with eye movements were excluded and ICA-based correction was not applied (see below).

Decoding overview.

We attempted to decode the orientation of the sample stimulus based on the scalp distribution of two different signals, the phase-independent alpha-band EEG power and the phase-locked ERP voltage. To ensure that we were decoding non-overlapping signals in these two analyses, the ERP decoding procedure was limited to frequencies <6 Hz, and the alpha-band decoding procedure was limited to frequencies between 8 and 12 Hz. Thus, we could be certain that the ERP decoding was not contaminated by alpha-band oscillations, which can masquerade as sustained ERPs under some conditions (Mazaheri and Jensen, 2008; van Dijk et al., 2010), and we could also be certain that the alpha-band decoding was not contaminated by low-frequency sustained potentials. Decoding was performed independently at each time point, but the statistical analysis focused on temporally contiguous clusters of above-chance decoding performance.

There are many ways to assess the relationship between a stimulus parameter such as orientation and a neural signal, but the most common approaches are forward encoding models and decoding procedures (Serences et al., 2009; Brouwer and Heeger, 2011; Foster et al., 2016; Fahrenfort et al., 2017). Here, we chose to focus on decoding because the goal was to determine whether the signals contain information about the orientation of the sample stimulus, and above-chance decoding accuracy provides the most straightforward evidence that such information is present. Forward encoding models can be very valuable, but they make assumptions about the nature of the underlying representation that may not be justified for a given feature dimension and are not relevant to the questions being asked in the present study. Although we report only the decoding approach here, we have also applied the forward encoding approach (using the method of Foster et al., 2016), which yielded a comparable pattern of results.

As in other EEG decoding/encoding studies (Foster et al., 2016, 2017b), the data from a given orientation were averaged across multiple trials to improve the signal-to-noise ratio (after extracting the phase-independent alpha power or the low-frequency EEG signals), and decoding was performed on these averages rather than on single-trial data. A separate classifier was trained to discriminate between each orientation (after averaging across trials) and all the other orientations. Decoding accuracy was then computed for the average of a set of trials for each orientation that was left out of the training data. Decoding was considered correct only if the classifier correctly determined which one of the 16 orientations was being held in WM. Chance performance was therefore 6.25% (1/16).

We focused our oscillatory power analyses on the alpha band, which is the frequency that exhibited the most consistent relationship with WM in previous EEG research (Foster et al., 2016). We also conducted exploratory analyses of a broad range of frequencies (4 Hz bands between 4 and 48 Hz). Some weak decoding was observed in the low beta range (12–16 Hz), but no clear decoding was present beyond the initial stimulus encoding period in any other band, so the present paper will focus only on the alpha band.

Experiment: 1 decoding analysis.

The decoding procedure for Experiment 1 was the same for the alpha-band signals and the low-frequency ERP signals, except for the initial steps used to isolate the signal-of-interest. For the alpha-band decoding, the segmented EEG was bandpass filtered at 8–12 Hz using the EEGLAB eegfilt() routine, which implements a two-way least-squares finite impulse response filter with maximally steep roll-offs and an extremely narrow transition band. The bandpass filtered EEG segments were then submitted to a Hilbert transform to compute the magnitude of the complex analytic signal, and this magnitude was then squared to compute total power in the 8–12 Hz band at each time point. For the ERP decoding, the segmented EEG was simply low-pass filtered at 6 Hz, again using the EEGLAB eegfilt() routine. In both cases, the data were then resampled at 50 Hz (1 data point per 20 ms) to increase the efficiency of the analyses. For each of the two signals, this gave us a 4-dimensional data matrix for each participant, with dimensions of time (100 time points), orientation (16 different values), trial (40 individual trials for each orientation), and electrode site (the 27 scalp sites).

We used the combination of a support vector machine (SVM) and error-correcting output codes (ECOC; Dietterich and Bakiri, 1995) to classify the orientation of the sample teardrop on the basis of the spatial distribution of the signal over the 27 scalp electrodes. The ECOC model solves multiclass categorization problems by combining results from multiple binary classifiers. This model was implemented through the Matlab fitcecoc() function. The data were decoded separately for each of the 100 time points from −500 to +1480 ms (relative to sample array onset). However, our statistical analyses focused only on the delay interval (the 1300 ms period beginning at the offset of the sample teardrop and continuing through the last sample before the onset of the test teardrop).

The decoding for a given time point had separate training and test phases. In the training phase, 16 different SVMs were trained, one for each orientation. A one-versus-all approach was taken, in which each SVM was trained to distinguish between one specific orientation and all the other orientations. In the test phase, new data from each of the 16 orientations was fed into all 16 SVMs, and the set of orientation assignments that minimized the average binary loss across the set of 16 SVMs was selected (see below). This procedure was used to classify the test data for each of the 16 orientations.

Separate trials were used for training and testing. Specifically, the decoding for each time point used a threefold cross-validation procedure in which the data from 2/3 of the trials (selected at random) were used to train the classifier, and then the performance of the classifier was assessed with the data from the remaining 1/3 of trials. As a first step, we organized the data with respect to teardrop orientation and then divided the trials into three equal-sized groups of trials (3 groups of 13 trials for each of the 16 orientations). One random trial from each of the 16 orientations was omitted because 40 is not evenly divisible by 3. The trials for a given orientation in each group were averaged together, producing a scalp distribution for the time point being analyzed (a matrix of 3 groups × 16 orientations × 27 electrodes). The data from two of the three groups served as a training dataset, and the remaining group served as a testing dataset. The two training datasets were simultaneously submitted to the ECOC model with known orientation labels to train the 16 SVMs. Each SVM learned to perform a binary classification that separated one of the 16 orientations from the other 15 orientations at the current time point.

Next, the set of 16 trained ECOC models was used to predict which of the 16 orientations was present for each of the unlabeled orientations in the group of data that were reserved for testing. This was done with the MATLAB predict() function. This function assigns a class label for each observation in the testing dataset by minimizing the average binary loss over the 16 SVMs. The output of this function provides one predicted orientation for each of the 16 orientations in the testing dataset. Decoding accuracy was then computed by comparing the true orientation labels with the predicted labels. To be considered correct, we required that the predicted orientation exactly match the true orientation, providing a very stringent assessment of decoding. We have conducted additional analyses examining “near misses”, but those analyses are beyond the scope of this paper.

This procedure was repeated three times, once with each group of data serving as the testing dataset. To minimize idiosyncrasies associated with the assignment of trials to groups, we iterated the entire procedure 10 times with new random assignments of trials to the three groups. After completing all the iterations of the cross-validation procedure, decoding accuracy was collapsed across the 16 orientations, across the three cross-validations, and across the 10 iterations, producing a decoding percentage for a given time point that was based on 480 decoding attempts (16 orientations × 3 cross validations × 10 iterations). After this procedure was applied to each time point, the averaged decoding accuracy values were smoothed across time points to minimize noise using a five-point moving window (equivalent to a time window of ±40 ms).

The temporal precision resulting from the entire EEG processing and decoding pipeline was ∼±50 ms. This was determined by running a 600 ms boxcar function through the portions of the pipeline that produced low-pass filtering (including the final smoothing step), which produced a temporally smeared version of the boxcar function. The point at which this function reached 10% of the maximum voltage was ∼50 ms before the beginning and 50 ms after the end of the original boxcar function. Small ripples extended further in time but were <10% of the original signal size.

Statistical analysis of decoding accuracy.

If the pattern of voltage over the 27 electrodes contains information about the stimulus orientation, then decoding accuracy should be greater than chance, which was 1/16 because we used 16 teardrop orientations. To compare decoding accuracy to chance at each time point while controlling for multiple comparisons, we used a nonparametric cluster-based Monte Carlo simulation technique that is analogous to the cluster-based mass univariate approach that is commonly used in EEG research (Maris and Oostenveld, 2007; Groppe et al., 2011). This method is useful here both because it provides an intelligent correction for multiple comparisons and because decoding accuracy may not be normally distributed. This method involved three main steps.

In Step 1, we tested whether the obtained decoding accuracy at each individual time point during the 1300 ms delay interval was greater than chance using one-sample t tests comparing the mean accuracy across participants to chance (1/16). We used one-tailed tests because the SVM approach could not produce meaningful below-chance decoding. Note that this excluded the first 200 ms following stimulus onset to minimize the contribution of sensory activity to the decoding and focus on signals related to working memory. We then found clusters of contiguous time points for which the single-point t tests were significant (p < 0.05), and the t scores within each such cluster were then summed together to produce a cluster-level t mass. Each cluster-level t mass was then compared against a null distribution for the cluster-level t mass that was determined via Monte Carlo simulations in Step 3. In other words, we asked whether the mass of a cluster of contiguous, individually significant t values was greater than the mass that would be expected by chance. This controls the type I error rate at the cluster level, yielding a probability of 0.05 that one or more clusters would be significant if true decoding accuracy were at chance during the entire delay period (Groppe et al., 2011).

In Step 2, we constructed a Monte Carlo null distribution of cluster-level t mass values. To accomplish this, we first simulated the decoding accuracy that would be obtained if the decoder randomly guessed the orientation of the stimulus with no knowledge of the actual orientation. On each simulated trial, we randomly sampled an integer between 1 and 16 as the response of the decoder for a given target orientation. The response was scored as correct if it was the same as the target value. This was repeated 480 times (16 target orientations × 3 cross-validations × 10 iterations), and the 480 scores were aggregated to compute the mean simulated decoding accuracy at a given time point. This procedure was repeated independently for each of the 100 time points, just as we independently decoded the EEG data at each time point. The resulting series of decoding accuracy values was then smoothed with a five-point running average filter. This is the same procedure that was used to quantify the actual SVM decoding accuracy for a given participant, but using a random decoder instead of the SVM-based decoder. This procedure was then repeated 16 times to represent each of our 16 participants.

We then used these simulated decoding accuracy values to compute the cluster-level t mass using the same procedure described in Step 1 (limited to the time points during the 1300 ms delay period). If there were no significant t values, the cluster mass was zero. If there was more than one cluster of individually significant t values, we took the mass of the largest cluster. This simulated the maximum t mass from a single experiment in which decoding was at chance.

In Step 3, we obtained a null distribution for the cluster mass. This involved simulating a large number of experiments in which the null hypothesis is true (i.e., decoding is at chance) and examining the probability of getting a given maximum cluster mass across these simulated experiments. Specifically, we conducted 10,000 iterations of the procedure from Step 2, making it possible to construct the null distribution of the maximum cluster-level t mass (with a resolution of p = 10⁻⁴). We then computed the p value corresponding to each cluster in the actual dataset by examining where each observed t mass fell within the null distribution. The p value for a given cluster was set based on the nearest percentiles of the null distribution (using linear interpolation). If the obtained cluster-level t mass is larger than the maximum of simulated cluster-level t mass, then we reported p < 10⁻⁴. We rejected the null hypothesis and concluded that the decoding was above chance for any observed cluster-level t mass that was in the top 95% of the null distribution (critical t mass = 12.0717, one-tailed, α = 0.05). Note that this analysis was limited to the 1300 ms delay period because the goal was to test decoding accuracy during working memory maintenance.

Experiment 2: decoding analysis.

The decoding procedure for Experiment 2 was identical to that for Experiment 1, with the following exceptions. First, we independently decoded the orientation of the teardrop and the location of the teardrop's tip. We collapsed across tip locations when we decoded the orientation, and we collapsed across orientations when we decoded the tip location. Because orientation and tip location were completely counterbalanced, the decoding of orientation could not have been influenced by information about tip location, and vice versa.

In addition to the main statistical testing, we also compared decoding accuracy for location versus orientation. We used the same cluster mass approach, but with two differences. First, we used two-tailed t tests because either feature could conceivably produce more accurate decoding. Second, the Monte Carlo null distribution was constructed by randomly swapping labels for the two conditions being compared, matching the procedure used to compare cluster masses for two waveforms in EEG experiments (Groppe et al., 2011). The null distribution constructed by this method represents the probability distribution of the t mass under the assumption that the obtained decoding accuracy for the two conditions are just different instances sampled from the same distribution. We computed the p value corresponding to each cluster in the actual dataset by examining where each observed t mass fell within this null distribution, and we rejected the null hypothesis if the observed t mass fell within the top or bottom 2.5% of values from the null distribution [critical t mass = (−1.88, 2.73), two-tailed, α = 0.05].

As noted earlier, we used the tip of the orientation for the counterbalancing because the tip was the most informative part of the teardrop and was directly controlled by the mouse pointer. However, one might be concerned that participants paid attention to some other part of the teardrop, such as the thick end, causing a small but nonzero association between the orientation of the teardrop and the location of some part of the teardrop. For example, the thick end of the rightward-pointing teardrops was farther to the left, on average, than the thick end of the leftward pointing teardrops (see Fig. 4c). However, both the behavioral task and the decoding algorithm required discriminating between one orientation and all other possible orientations (i.e., not just leftward vs rightward). In addition, almost every location of the thick end of the teardrop was associated with multiple orientations (with all possible combinations of orientations across the possible locations). As a result, attending to the thick end of the teardrop did not provide unique information about the orientation of the teardrop.

For these reasons, it is extremely unlikely that this location information could impact our orientation decoding. To provide support for this assumption, we conducted both an additional analysis and a simulation. In the additional analysis (described in the Cross-Feature Decoding Analyses in Experiment 2 section), we trained the orientation decoder using teardrops presented at one set of locations and then tested the decoder with data from teardrops that were presented at a different set of locations. Above-chance level decoding in this analysis provides evidence that orientation of teardrop can be decoded completely independently of location.

In addition, we conducted a simulation in which we attempted to decode teardrop orientation on the basis of the location of the thick end of each teardrop using the exact x,y coordinates of this location (as if we had two electrodes, one that perfectly represented the x value and one that perfectly represented the y value corresponding to the thick end of the teardrop). Note that the same thick end location can be occupied by multiple orientations and an area of thick end locations of one orientation was occupied by thick end locations of other orientations. As a result, the thick end locations for one orientation were not linearly separable from the thick end locations of the other orientations in the two-dimensional space. Consequently, to provide a stronger test of decodability, we used a nonlinear SVMs with a Gaussian kernel function, which optimizes the effective dimensionality of the input space (Burges, 1998). We found that our one-versus-all decoding algorithm with the kernel function could not decode orientation above chance when provide with this location information, even though it was given perfect, noise-free information. As a check on the validity of this simulation approach, we also attempted to decode the location of the tip of the teardrop (rather than its orientation) from the x,y coordinate of the tip, and we found that decoding accuracy was perfect. These simulations show that our decoding algorithm cannot readily decode orientation on the basis of the location information even with noise-free data (although it can perfectly decode location when given noise-free x, y coordinates). Consequently, any above-chance decoding of teardrop orientation from the actual EEG data was unlikely to have been based on the location of the thick end of the teardrop.

Cross-feature decoding analyses in Experiment 2.

To further demonstrate that orientation can be independently decoded from location, we conducted a cross-feature decoding analysis in which we trained an orientation decoder using trials where the stimulus was presented in the three of the four quadrants of the display and then tested the ability of this decoder to classify orientation in trials were the stimulus was presented in the remaining quadrant (see Fig. 7a). Similarly, we trained a location decoder using trials where the stimulus orientation was in the three of the four quadrants of orientation space and then tested the ability of this decoder to classify location in trials were the stimulus was presented in the remaining set of orientations (see Fig. 7b).

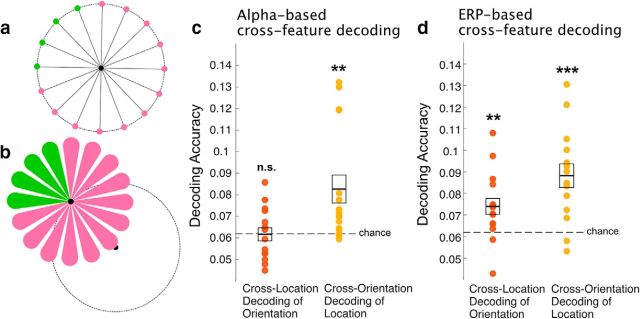
Figure 7.

Cross-feature decoding. a, To completely remove the impact of the tip location on the decoding of orientation, we trained the decoders using data from teardrops presented in three of the four quadrants (indicated by pink locations) and then tested the decoding on trials from the remaining quadrant (indicated by green locations). This was repeated four times, using each quadrant as the test quadrant once. b, The analogous procedure was used for location decoding. The decoders were trained to decode location using ¾ of the orientations (indicated by pink teardrops), and then tested with the other ¼ (indicated by green teardrops). c, Alpha-based cross-feature decoding accuracy for orientation and location, averaged over the entire delay period (d) ERP-based cross-feature decoding accuracy for orientation and location, averaged over the entire delay period for orientation and location. Each participant is represented by a dot, and the mean ± 1 SEM are indicated by the line and box. **p < 0.01, ***p < 0.001.

For both orientation and location, this decoding was repeated four times (4-fold cross-validation), with each quadrant of the irrelevant feature space serving once as the testing data. As in the main decoding procedure, this procedure was applied to each time point independently. Because the quadrants were fixed rather than random, this procedure was not iterated multiple times (as opposed to the cross-validation procedure used in the main decoding analysis, which was based on random subsets of trials). All other aspects of this procedure were identical to the main decoding procedure.

Although the experiment was designed to have equal numbers of trials at each orientation and equal numbers of trials at each tip location, we did not control the number of trials with each orientation-location combination. As a result, the number of trials available for decoding each feature value in the cross-feature decoding procedure varied randomly across iterations, which will tend to reduce the maximum accuracy and reliability of the decoding. Moreover, the cross-feature decoding procedure involved testing the decoder with stimuli that were never used in training, requiring generalization beyond the training set. Thus, if the cross-feature decoding accuracy is above chance, this provides a very stringent test of the ability to decode one dimension with no contribution from the other dimension.

Because this was a more stringent test, we performed a statistical analysis that averaged the decoding over all the points during the 1300 ms delay period. We compared the average accuracy during this window to chance using a one-sample t test. For the sake of completeness, we also report the accuracy for each individual time point using the same cluster-mass Monte Carlo statistical test used for the main decoding analysis.

Decoding after excluding trials with eye movements.

In our main analyses, we used ICA-based artifact correction to remove the voltage fluctuations produced directly by the eye movements, but this procedure may not correct for other differences in neural activity that may result from sustained changes in eye position. To ensure that the decoding was not based on signals related to eye position, we conducted an additional set of decoding analyses using uncorrected data and excluding trials that could potentially involve systematic shifts in eye position during the delay interval.

We first computed the mean HEOG (right EOG − left EOG) and VEOG (lower EOG − upper EOG) voltages over the delay period, and we subtracted the mean prestimulus voltage to correct for the baseline voltage offset. Because systematic eye movements could occur in any direction in this paradigm, it was not sufficient to rely on the individual HEOG and VEOG values. We therefore converted the HEOG and VEOG voltages into a vector (in units of degrees rather than units of μV) representing the angle and amplitude of the eye position relative to the fixation point, using normative scaling values for HEOG (16 μV/°) and VEOG (12 μV/°; Lins et al., 1993). We then excluded trials from decoding analyses if the amplitude of the eye movement was >0.5425° in any direction (because 0.5425° was half the distance from the fixation dot to the tip location). This very conservative procedure excluded ∼55% of the trials in Experiment 1 (but many or most of these trials were likely rejected because of noise in the single-trial HEOG and VEOG data, not because of task-related eye movements). The amplitude of the average eye position for a given orientation in the remaining trials was extremely small (0.08°, SEM = 0.01°), indicating that our rejection procedure was successful.

We used the same procedure to remove trials with eye movements in Experiment 2, but we used a rejection threshold of 1.085° (because this was half of the distance to the invisible circle that defined the possible locations of the teardrop tip). The exclusion procedure removed ∼25% of the trials in Experiment 2. The amplitude of the average eye position for a given orientation or location in the remaining trials was again extremely small (0.13°, SEM = 0.01°).

Excluding trials with eye movements led both to a smaller number of trials and an unequal number of trials for each location and orientation, which would be expected to decrease the reliability of the decoding. Consequently, we focused on average decoding accuracy over the delay period for these analyses.

Code and data availability.

Both the data and the MATLAB analysis scripts are available upon request from G.B.

Results

Experiment 1: behavior

Figure 1c summarizes the behavioral data from Experiment 1. On each trial, accuracy was quantified as the angular difference between the orientation of the sample teardrop and the orientation reproduced by the participant. The mean absolute error was quite small (5.40°, SEM = 0.24). We also fit a standard mixture model to characterize the distribution of response errors in terms of response precision and guess rate (Zhang and Luck, 2008). The vast majority of response errors were clustered ∼0°, and the mean guess rate was extremely low (0.7%, SEM = 0.2). Mean precision was quite high (κ = 77.94, SEM = 5.26).

Experiment 1: scalp distributions

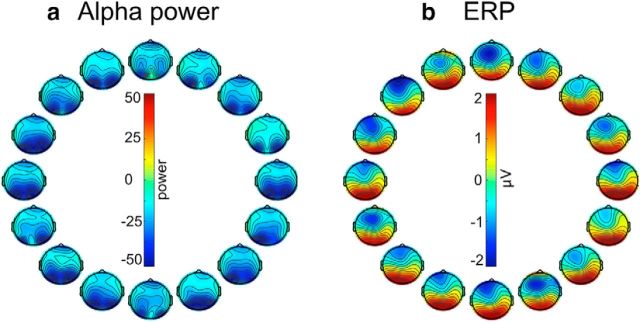
Our decoding methods rely on differences in the scalp distribution of alpha-band power and sustained ERPs across teardrop orientations, and Figure 2 shows the grand average scalp maps (averaged across the entire delay interval) for each orientation. The alpha-band maps indicate that alpha power over occipital scalp sites was suppressed (relative to the prestimulus period), consistent with prior research demonstrating that alpha-band activity is suppressed over visual cortex during the delay period of working memory tasks (Fukuda et al., 2015; Erickson et al., 2017). The ERP maps show a positive voltage over posterior scalp sites and a negative voltage over anterior scalp sites. This may reflect a combination of posterior P3-like activity and the negative slow wave that is often observed in WM tasks (Ruchkin et al., 1990, 1992).

Figure 2.

Topography of (a) instantaneous alpha power and (b) ERP activity for each of 16 sample orientations, averaged across the delay interval and participants in Experiment 1. Both alpha power and ERP amplitude were computed relative to the prestimulus baseline period. The position of each scalp map corresponds to the orientation of the sample teardrop.

For both the alpha-band activity and the sustained ERPs, subtle differences in scalp distribution can be seen across the 16 teardrop orientations. However, there is no simple pattern in the changes. This may reflect the fact that multiple brain regions exhibit orientation-specific delay activity (Harrison and Tong, 2009), which could produce a complex pattern of activity on the scalp. However, the lack of a simple pattern is not problematic for decoding methods, which can discover regularities in the scalp distributions even if they are complex and subtle. Also, the maps shown in Figure 2 were averaged across participants and time points, potentially obscuring information in the single-participant and single-time point scalp distributions that were used by our decoding procedure.

Experiment 1: decoding

Figure 3 shows decoding accuracy for Experiment 1, which used a task that could potentially be performed by means of either spatial attention or orientation memory. Decoding accuracy for alpha-band activity began to rise above chance (0.0625 = 1/16) ∼200 ms after the onset of the sample stimulus, peaked ∼600 ms, and remained high until just before the end of the delay period. The cluster mass test indicated that the decoding was significantly greater than chance (1 cluster, p < 10⁻⁴) for the entire 1300 ms delay period (Fig. 3a, shaded region). When we excluded trials with eye movements (eye-movement rejection) rather than using ICA to subtract the electro-oculogram signals (eye-movement correction), the decoding was still significantly greater than chance when averaged across the delay period (t₍₁₅₎ = 2.8870, p = 0.0113; one-sample t test).

Figure 3.

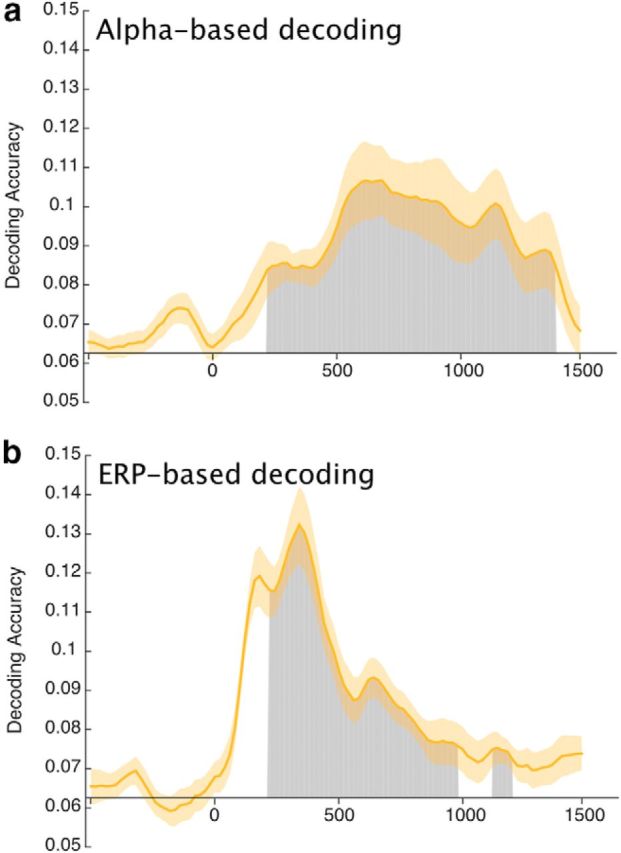
Mean accuracy of (a) alpha-based decoding and (b) ERP-based decoding in Experiment 1. Chance-level performance (0.0625 = 1/16) is indicated by the black horizontal lines. Gray areas indicate clusters of time points in which the decoding was significantly greater than chance after correction for multiple comparisons. Note that the first 200 ms following stimulus onset were excluded from the statistical analysis to minimize any contributions of sensory activity to the decoding. The orange shading indicates ±1 SEM.

ERP-based decoding was also significantly above chance during most of the delay period (2 clusters; p < 10⁻⁴, p = 0.015), even when we used eye-movement rejection instead of correction (t₍₁₅₎ = 3.6601, p = 0.0022; one-sample t test). However, the time course was somewhat different from that for alpha-based decoding. Decoding accuracy was quite high (more than twice the chance level) from ∼150–400 ms after the onset of the sample teardrop, which likely reflects the N2pc component during the initial processing of the teardrop (Fahrenfort et al., 2017). Decoding then fell, but remained significantly above chance until the final 200–300 ms of the retention interval. It should be noted that sustained ERP activity (but not alpha-band activity) becomes less reliable as time progresses away from the prestimulus baseline period because of slow drifts in the EEG offset (Luck, 2014), and this may explain why the decoding accuracy fell to nonsignificant levels by the end of the delay period. Alternatively, if the late ERP activity primarily reflects the content of WM rather than spatial attention, then the decline in ERP-based decoding may reflect reliance on spatial attention rather than true orientation memory to perform the task.

In either case, the present results demonstrate that our methods can be used to both alpha-band oscillations and sustained ERPs to successfully decode the orientation being held in WM for most of the delay interval. However, this decoding could reflect either sustained spatial attention on the location of the teardrop's tip or bona fide representations of the teardrop's orientation (or a combination of both). Experiment 2 will distinguish between these possibilities.

Experiment 2: behavior

In Experiment 2, participants performed the same basic task used in Experiment 1, except that the locations of the sample and test teardrops were independently varied (Fig. 4a). Thus, maintaining attention on the location of the sample teardrop during the delay period could not be used to remember its orientation.

Figure 4d summarizes the behavioral data from Experiment 2. The mean absolute error was again quite low (5.40°, SEM = 0.79). When a mixture model was applied, the mean guess rate was extremely low (0.3%, SEM = 0.01) and the mean precision was quite high (κ = 57.82, SEM = 7.05). However, the precision was significantly lower in this experiment than in Experiment 1 (t₍₃₀₎ = 2.29, p = 0.029; two-sample t test). This difference could indicate that location-specific information is useful in maintaining precise orientation representations, leading to poorer memory when this information cannot be used (i.e., when the sample and test stimuli are at different locations). However, it could also reflect other factors, such as poorer sensory acuity at the peripheral locations used in the present experiment.

Experiment 2: scalp distributions

Figure 5 shows the grand average scalp topography for each teardrop orientation (averaged across the location of the teardrop) and each teardrop location (averaged across the orientation of the teardrop). As in Experiment 1, the alpha band maps show a suppression of alpha power over posterior scalp sites (relative to the prestimulus period), whereas the ERP maps show a positive voltage over posterior scalp sites and a negative voltage over anterior scalp sites.

Figure 5.

Scalp topography of (a) instantaneous alpha power and (b) ERP activity relative to prestimulus baseline for each of the 16 orientations of the sample teardrop, averaged across the delay interval and participants. The position of each scalp map corresponds to the orientation of the sample teardrop. Topography of (c) alpha power and (d) ERP activity for each of the 16 locations of the sample teardrop tip, averaged across the delay interval and participants. The position of each scalp map corresponds to the location of the tip of the sample teardrop. Both alpha power and ERP amplitude were computed relative to the prestimulus baseline period.

Experiment 2: decoding

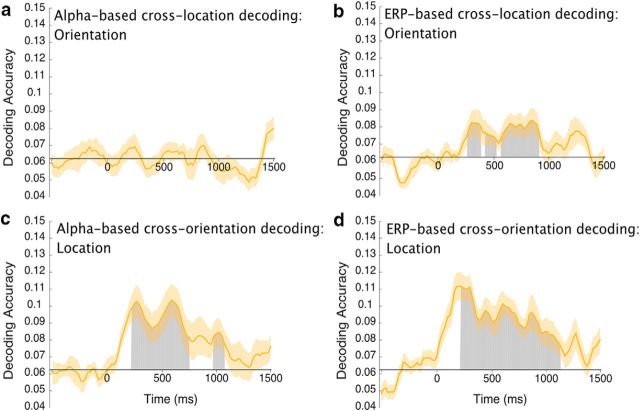
We decoded the orientation of the sample teardrop (collapsed across tip locations) using alpha-band activity in one analysis and ERP activity in another analysis. We also decoded the tip location (collapsed across orientations) in a separate pair of analyses. Figure 6 shows decoding accuracy for each of these analyses. Alpha-based decoding for orientation was extremely weak, remaining within 0.01 of chance accuracy at all time points, and the accuracy did not exceed chance except for a small cluster of significant time points (1 cluster, p = 0.026) at ∼700 ms (Fig. 6a, shaded region). By contrast, alpha-based decoding of location was well above chance (1 cluster; p < 10⁻⁴) from the beginning of the delay interval until ∼1000 ms but then fell to chance by the end of the delay interval. Location decoding was significantly more accurate than orientation decoding (1 cluster; p < 10⁻⁴) from the beginning of the delay period until ∼1250 ms (Fig. 6c, red horizontal bar). The same pattern of results was obtained when we used eye-movement rejection instead of correction. Specifically, alpha-based decoding of orientation was near chance (t₍₁₅₎ = 1.2225, p = 0.2404; one-sample t test), but alpha-based decoding of location was greater than chance (t₍₁₅₎ = 3.2954, p = 0.0049; one-sample t test).

Figure 6.

Alpha-based decoding accuracy for (a) the orientation of the sample teardrop and (c) the location of the sample teardrop tip. ERP-based decoding accuracy for (b) the orientation of the sample teardrop and (d) the location of the sample teardrop tip. Each gray area shows a cluster of time points for which the decoding was greater than chance after correction for multiple comparisons. The red lines in c and d indicate clusters of time points in which the decoding was significantly greater for location than for orientation. The orange shading indicates ±1 SEM. Note that the first 200 ms following stimulus onset were excluded from the statistical analysis to minimize any contributions of sensory activity to the decoding.

In contrast to the alpha-based decoding, the ERP-based decoding of orientation was robust and significantly greater than chance (1 cluster; p < 10⁻⁴) for almost the entire delay period. ERP-based location was also significantly above-chance (1 cluster; p < 10⁻⁴) for most of the delay period. The ERP-based decoding was significantly more accurate (1 cluster; p < 10⁻⁴) for location than for orientation for the first ∼600 ms of the delay period, but decoding accuracy for location and orientation was similar for the last ∼500 ms of the delay period (Fig. 6d). The same pattern of results was observed when we used eye-movement rejection instead of correction. Specifically, ERP-based decoding was significantly greater than chance for both orientation (t₍₁₅₎ = 4.03, p = 0.001; one-sample t test) and location (t₍₁₅₎ = 5.4763, p < 10⁻⁴; one-sample t test). These results demonstrate that sustained ERPs contain information about the specific orientation being maintained in WM, but alpha-band oscillations do not.

Experiment 2: cross-feature decoding

As described in Materials and Methods, it is unlikely that the above-chance decoding of orientation we observed in this experiment was based on the location of the tip of the teardrop or any other part of the teardrop. To provide a further test of this claim, we conducted an even more stringent test of the location-independence of the orientation decoding, in which the decoder was trained with the data from three of the four quadrants of the display and then tested on the data from the remaining quadrant (Fig. 7a). In this analysis, the decoder had no opportunity to learn the spatial properties of the orientations used in the test set, providing an even more rigorous test of the location independence of the decoding. Given that this was a more stringent test with decreased statistical power, our main statistical analyses examined decoding accuracy averaged across the entire 1300 ms delay period.

As shown in Figure 7c, alpha-based cross-location decoding of orientation was almost exactly at chance (t₍₁₅₎ = 0.25, p = 0.60; one-sample t test). We computed the corresponding Bayes factor (Rouder et al., 2009) using the default JZS scaling factor of 0.707, and we found that the data were 3.8 times more likely to arise from chance decoding than from above-chance decoding. This provides positive support for the hypothesis that orientation cannot be decoded from alpha-band oscillations when a stringent test is used. In contrast, ERP-based cross-location decoding of orientation (Fig. 7d) was significantly above chance (t₍₁₅₎ = 2.99, p = 0.0046; one-sample t test). This decoding was greater than chance for all but two of the participants, and the Bayes factor indicated that the data were 5.9 times more likely to arise from above-chance decoding than to arise from chance decoding. Thus, although it may be impossible to completely dissociate location and orientation information, the present analyses provide strong evidence that the sustained ERPs contained location-independent information about orientation.

Figure 8 shows decoding accuracy at each individual time point. There was no sign of above-chance alpha-based decoding of orientation at any point during the delay period, whereas ERP-based decoding of orientation was significantly greater than chance for much of the delay period (3 clusters; p = 0.011, p = 0.035, p < 10⁻⁴). These results provide even stronger evidence that sustained ERP activity contains information about the orientation being held in WM, independent of object location, with no evidence of true orientation information in the alpha-band oscillations.

Figure 8.

Average cross-feature decoding accuracy at each time point. a, Average accuracy of alpha-based cross-location decoding of orientation. b, Average accuracy of ERP-based cross-location decoding of orientation. c, Average accuracy of alpha-based cross-orientation decoding of location. d, Average accuracy of ERP-based cross-orientation decoding of location. The orange shading indicates ±1 SEM. Gray areas represent clusters of points with significantly above-chance decoding accuracy after correction for multiple comparisons. Note that the first 200 ms following stimulus onset were excluded from the statistical analysis to minimize any contributions of sensory activity to the decoding.

For the sake of completeness, we conducted a parallel cross-orientation decoding analysis for location, in which the decoder was trained using three quarters of the orientations and then tested on the other quarter (Fig. 7b). When averaged over the entire delay period, cross-orientation decoding of location was significantly greater than chance for both alpha-based decoding (t₍₁₅₎ = 3.09, p = 0.0037; one-sample t test) and ERP-based decoding (t₍₁₅₎ = 5.01, p = 0.00008; one-sample t test; Fig. 7c,d). Analyses of each individual time point (Fig. 8) provided evidence of above-chance location decoding across most of the delay period for both ERP-based decoding (1 cluster; p < 10⁻⁴) and alpha-based decoding (2 clusters; p < 10⁻⁴, p = 0.026). Thus, as in the previous analyses, the location of the teardrop could be decoded independently of its orientation from both alpha-band activity and sustained ERP activity.

Note that the cross-feature decoding was somewhat less accurate than the original decoding for both orientation and location, which presumably reflects the fact that cross-feature decoding requires explicit generalization to stimuli that were not used for training. In addition, the reliability of the decoding may have been decreased by the fact that, unlike the main decoding analyses, we could not iterate over multiple random assignments of stimuli for these analyses. Thus, the lower accuracy in the cross-feature decoding analyses does not imply that the main analyses were contaminated by information from the other dimension.

Confusion matrices for Experiments 1 and 2

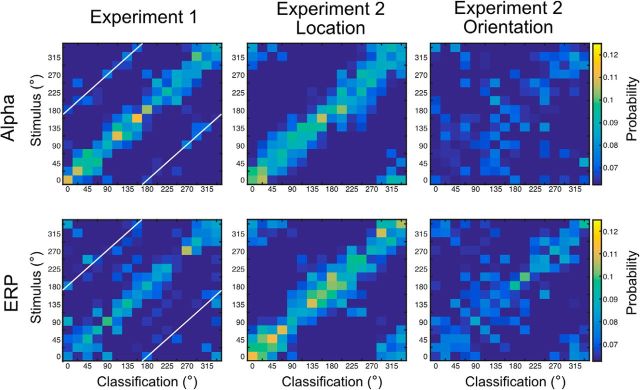
The main decoding analyses focused on accuracy for exact decoding of location and orientation, averaged across different stimulus values. Here, we provide the confusion matrix for each combination of stimulus value and classification response to provide a more detailed description of the results. Figure 9 shows the probability of a each possible classification response for each possible stimulus value, averaged over the delay interval and over participants. Separate panels are shown for each combination of signal type (alpha or sustained ERP) and decoded feature (orientation in Experiment 1, location in Experiment 2, and orientation in Experiment 2).

Figure 9.

Confusion matrices for alpha-based (top row) and ERP-based (bottom row) decoding for Experiment 1 (left column), Experiment 2 location (middle column), and Experiment 2 orientation (right column). Each cell shows the probability of a given classification response (x-axis) for given a stimulus value (y-axis), averaged over the entire delay interval and across observers. The white diagonal lines indicate classification responses that are 180° from the stimulus value. Note that the values in the top left and bottom right corners of each matrix represent stimulus–response combinations that are actually adjacent to the stimulus–response combinations in the bottom left and top right corners (because these matrices provide a linear representation of a circular stimulus space).

In Experiment 1, most of the classification responses were clustered around the true target value (the central diagonal) for both the alpha and ERP signals. Interestingly, a given target value in Experiment 1 was occasionally decoded as being 180° away from the true value (indicated by the white diagonal lines). This could reflect the fact that the orientation of an infinite-length line (as opposed to a ray) cannot be distinguished from an orientation that is 180° away. However, this result could also indicate that observers paid attention to the opposite end of the teardrop on some proportion of trials. In addition, these 180° decoding confusions were rare, and participants exhibited no evidence of 180° confusions in their behavioral responses (Fig. 4). In Experiment 2, both the alpha-based and ERP-based decoding of location exhibited a high probability of classification responses at or near the true value, with no obvious evidence of opposite-direction classification responses.

The ERP-based decoding of orientation in Experiment 2 showed a broader range of classification responses around the true value than was observed for orientation in Experiment 1 or for location in Experiment 2. However, there was still a clear cluster of classification responses around the true orientation value, and no obvious cluster of responses around the opposite orientation. This indicates that the decoding was primarily sensitive to ray orientation (with 360° of unique values) rather than line orientation (with only 180° of unique values). The confusion matrix for alpha-based decoding of orientation in Experiment 2 showed very little structure, consistent with the near-chance orientation decoding accuracy that was obtained for alpha-band activity in the main analyses.

Discussion

Human scalp EEG activity contains both sustained and oscillating activity during the delay period of WM tasks (van Dijk et al., 2010; Perez and Vogel, 2012; Fukuda et al., 2015), possibly reflecting the representation of information across the delay period. However, these signals might instead reflect support processes, such as attentional mechanisms that prevent interference, rather than the actual WM representations (Sauseng et al., 2009; Bonnefond and Jensen, 2012). The ability to decode the feature value being held in WM from a given neural signal provides much stronger evidence that the signal reflects the WM representation (Postle, 2016), and the present study therefore sought to determine whether orientation representations in WM could be decoded from scalp EEG activity. Given the close link between sustained ERP activity and WM capacity for objects (Vogel and Machizawa, 2004; Vogel et al., 2005), we predicted that the sustained ERP activity would reflect the features of the objects being maintained in WM. In contrast, given the close relationship between alpha-band activity and spatial attention (Worden et al., 2000; Rihs et al., 2007), we predicted that alpha-band oscillations would primarily reflect the location of the attended object. The results were consistent with these predictions.

Experiment 1 demonstrated that orientation information in a WM task could be decoded from the scalp distribution of both alpha-band oscillations and sustained ERP responses. Previous research has found that alpha-band activity can decode the location being maintained in spatial WM (Foster et al., 2016), but this is the first demonstration that sustained ERPs can decode delay-period activity in a WM task. However, it is quite plausible that participants focused their spatial attention on location of the teardrop's tip throughout the delay period as they prepared to reproduce the teardrop's orientation at the end of the trial. As a result, we may have been decoding the direction of spatial attention rather than a WM representation of orientation per se. This is especially plausible for the alpha-band activity, which has a scalp distribution that changes in a fine-grained manner as the location being attended varies (Rihs et al., 2007).

Distinguishing between spatial attention and the contents of WM

To distinguish between spatial attention and the contents of WM, the task used in Experiment 2 independently varied the location and orientation of the teardrop, and participants were instructed to remember the teardrop's orientation independently of its location. We found that the orientation being held in WM could be decoded from sustained ERP activity throughout the delay period, even though the orientation of the teardrop could not be predicted from its location. In an even more stringent test of location-independent orientation decoding, we found that orientation could be decoded when the decoder was trained with stimuli from one set of locations and tested with stimuli from a different set of locations. Thus, sustained ERP activity contains information about the feature value being held in WM beyond the location of the object. These results dovetail with previous studies showing that sustained ERP activity is closely tied to individual and group differences in WM capacity (Vogel and Machizawa, 2004; Leonard et al., 2013). However, additional research will be needed to determine whether the sustained activity that was responsible for the decoding in the present study is the same as the sustained activity that has been linked to WM capacity in previous research.

We also found that ERP activity could be used to decode the location of the teardrop, especially early in the delay interval. This likely reflects, at least in part, the N2pc component (Luck, 2012), which precisely tracks the location of attended objects (Fahrenfort et al., 2017).

The location of the teardrop could also be decoded from the scalp distribution of the alpha-band activity, but there was little or no evidence that alpha-band activity could be used to decode the orientation of the stimulus consistently throughout the delay period. Indeed, when we applied the stricter cross-location test of orientation decoding, alpha-based decoding of orientation was very close to chance throughout the delay period. Moreover, the Bayes factor for this analysis provided positive evidence that the data were more consistent with chance-level decoding than with above-chance decoding. These results are consistent with prior evidence that alpha-band activity is closely tied to attention in perceptual tasks (Adrian and Matthews, 1934; Worden et al., 2000; Sauseng et al., 2005) and serves to prevent interference in nonspatial WM tasks (Sauseng et al., 2009; Bonnefond and Jensen, 2012). The decoding methods used here go beyond the previous research, however, providing evidence that the scalp distribution of alpha-band activity contains decodable information about the location of an object but little or no decodable information about the other features of this object. However, it remains quite plausible that alpha-band activity is used to store object locations in WM, even when the task does not explicitly require location memory (Foster et al., 2017a).

Although we found little or no evidence of orientation information in alpha-band oscillations (or in any other frequency band), this should not be taken to indicate that neural oscillations have no role in object-based WM representations. The present decoding was based on differences in scalp distribution across feature values, and it is possible that scalp EEG oscillations (and LFP oscillations) contain information about feature values in a non-topographic manner (e.g., by means of phase-amplitude coupling; Sauseng et al., 2009). Because decoding provides important evidence that a neural signal actually reflects WM representations rather than support processes (Postle, 2016), it will be important for future research to determine whether these non-topographic features of scalp EEG oscillations contain information about the feature value being maintained in WM.

Orientation, space, and shape

As mentioned earlier, our task required perceiving ray orientation (360° of unique values) rather than line orientation (180° of unique values). Both behavioral performance and location-independent orientation decoding yielded no evidence of 180° confusions, which may indicate that participants were representing shape rather than orientation per se (Zhang and Luck, 2008). However, populations of end-stopped cells in early areas of visual cortex may be able to code ray orientation (Würtz and Lourens, 2000), so it is also possible that the present results reflect relatively low-level representations of orientation.

Note that the orientation representations in the present study may actually be conceived as object-centered spatial representations. Interestingly, fMRI-based decoding of orientation in primary visual cortex is not location-specific, and the orientation of a grating presented in one hemifield can be decoded from the pattern of activity in either hemisphere (Ester et al., 2009). This suggests that object-centered representations may involve early visual cortex and not just high-level areas.

Underlying neural activity

Although the present study found that sustained scalp-recorded ERP activity contained information about the orientation value being stored in WM, it is important to ask whether this could be the result of brief bursts of activity that create the appearance of a sustained response when averaged across neurons and/or trials. Our ERP-based decoding was based on data in which activity >6 Hz was filtered out, so oscillations in the alpha, beta, and gamma bands could not have contributed significantly to the decoding. This includes both the asymmetric alpha oscillations reported by Mazaheri and Jensen (2008) and van Dijk et al. (2010) and the gamma-band LFP bursts observed in monkeys by Lundqvist et al. (2016). However, the gamma bursts were accompanied by single-unit activity that carried information about the stimulus being represented; if these bursts of activity were accompanied by non-oscillating LFPs, the summed activity across a large population of neurons could have created sustained delay-period activity at the scalp. In this way, the sustained ERP-based decoding observed in the present study could reflect infrequent bursts of activity in individual neurons that produced sustained potentials when averaged across cells. In addition, it is possible that WM-related EEG signals were present during some portions of the delay period on some trials and other portions of the delay period on other trials rather than being sustained across the entire delay period on every trial (as observed in single-unit activity by Shafi et al., 2007).

Nonetheless, the present results put significant constraints on the neural signals that underlie decoding of WM content from scalp EEG signals. For example, the present results unambiguously demonstrate that the EEG contains decodable information about the remembered stimulus value that cannot be directly explained by oscillating LFPs, and they provide no evidence that the scalp distribution of alpha-band oscillations carries information about the contents of WM. Moreover, the present results imply that neural representation of orientation in WM is spatiotopically mapped at a sufficiently coarse cortical scale that it can be decoded even after the substantial spatial filtering that occurs when electrical potentials travel from the neurons that generate them through the brain and skull to the surface of the scalp. However, additional empirical research and modeling will be needed to determine the precise nature of the cellular activity that produces the scalp ERP signals that were decoded in the present study.