Long-range stress transmission guides endothelial gap formation

Abstract

In endothelial gap formation, local tractions exerted by the cell upon its basal adhesions are thought to exceed balancing tensile stresses exerted across the cell-cell junction, thus causing the junction to rupture. To test this idea, we mapped evolving tractions, intercellular stresses, and corresponding growth of paracellular gaps in response to agonist challenge. Contrary to expectation, we found little to no relationship between local tensile stresses and gap formation. Instead, we discovered that intercellular stresses were aligned into striking multicellular domains punctuated by defects in stress alignment. Surprisingly, gaps emerged preferentially not at stress hotspots, as predicted, but rather at stress defects. This unexpected behavior is captured by a minimal model of the cell layer as a jammed assembly of cohesive particles undergoing plastic rearrangements under tension. Together, experiments and model suggest a new physical picture in which gap formation, and its consequent effect on endothelial permeability, is determined not by a local stress imbalance at a cell-cell junction but rather by emergence of non-local, cooperative stress reorganization across the cellular collective.

Introduction

The pulmonary vascular endothelium forms a semi-selective barrier between circulating blood, pulmonary interstitium, and airspaces. Disruption of the endothelial monolayer leads to capillary leak, tissue flooding, and, ultimately, respiratory failure.[1, 2] Transit of fluid, solutes and cells across the disrupted endothelial barrier can occur through trans-cellular or paracellular routes, but, in the setting of acute inflammation, the paracellular route dominates.[3] The formation of a paracellular gap necessarily involves changes in the mechanical state of the endothelial cell-cell junction. At this site, cytoskeletal contractions tend to pull cells apart from one another. These contractile forces – manifested upon the substrate as tractions – are balanced by tension borne at junctional adhesion complexes. Tractions are generated by acto-myosin contractile units and supported by focal adhesions containing vinculin, paxillin, talin, and integrins.[4, 5] The balancing junctional tension is borne by peripheral cytoskeletal networks, and mechanosensory complexes[6, 7] containing VE-cadherin, VEGFRs, PECAM-1, α,β,γ-catenins and p120-catenin[4, 8–11] Therefore, formation of a paracellular gap has long been thought to result from a process in which local traction exceeds a yield threshold of the junctional complexes[12], leading to junction rupture. More recently, it has been suggested that local sub-cellular motions[13] or local traction fluctuations[14] are more predictive of gap formation than are the local tractions themselves. Associated changes in junctional tension, have received far less attention.

Existing techniques to measure intercellular tension during gap formation employ either simplified systems such as cell doublets[15, 16] that do not include the multi-cellular mechanical interactions characteristic of endothelial monolayers[17–21] or else are unable to localize inter-endothelial gaps in maps of cell-cell forces.[19] Here we overcome these limitations. We studied monolayers of primary human pulmonary artery endothelial cells (HPAECs) grown to confluence on a deformable, collagen-coated polyacrylamide substrate (700μm diameter circular islands, 4kPa stiffness Young’s modulus). We used Fourier Transform Traction Microscopy (FTTM)[20, 22] to map the spatial distribution of traction, and Monolayer Stress Microscopy (MSM)[19, 23] to map the spatial distribution of balancing intercellular tension. Importantly, we also mapped the location and growth of paracellular gaps in the same monolayer using Express Permeability Testing (XPerT).[24]

Materials and Methods

Preparation of gel substrates

Micropatterned cell substrates were prepared and ligated using polyacrylamide with a Young’s modulus of 4kPa similar to published protocols.[25] Following functionalization, the gel surface was ligated with biotinylated type-1 collagen within evenly spaced 700μm diameter islands.

Cell culture

Human Pulmonary Artery Endothelial Cells (HPAEC) were obtained from Lonza Inc., maintained in EGM-2 media with 5% FBS, and used as passages 5–8. Cells were plated on the micropatterned gel substrates as a dense drop (1 million cells/ml). They were maintained at 37 °C in humidified air containing 5% CO₂ for 48 hours prior to use.

Visualization of Paracellular Gaps

Gaps were visualized pre- and post-thrombin treatment with XPerT [24].

Traction and intercellular stress measurements

Cell-substrate forces were measured using Fourier Transform Traction Microscopy (FTTM), as previously described.[20, 22, 39] From the tractions, we computed intercellular stresses with Monolayer Stress Microscopy.[19, 23] Due to the assumptions inherent to the method, MSM is expected to be least accurate in the vicinity of a gap. For this reason we have confined our analysis of intercellular stress to the pre-thrombin stress map with its smaller and fewer gaps. A fuller discussion of this limitation to the application of MSM is contained in SI text2.

Orientation Ordering

MSM yields the local two-dimensional stress tensor at each point in the monolayer. This tensor is characterized by three variables: the maximum and minimum principal stresses, and the angle ϑ, taken on [0,π ], of the maximum principal stress relative to a laboratory coordinate system axis. For any region of the monolayer we can define an orientation order parameter, S:

$$S=\sqrt{Q_{xx}^2+Q_{xy}^2}$$

where Q_xx =< 2cos²ϑ − 1> and Q_xy= <2cosϑ sinϑ>, and the averages (<·>) are taken over a local region of the monolayer. Here we use 64x64 μm non-overlapping square regions. So constructed, S will vary between 1 (perfectly aligned) and 0 (not aligned).[27]

Correlating intercellular tension across the monolayer

The spatial correlation of intercellular tension is measured by the average angle between the orientation of neighboring principal stresses separated by a distance, r:

$$C(r)=\frac{1}{N}\sum _i\frac{1}{n_i}\sum _{j=1}^{n_i}\frac{{\overrightarrow{F}}_i·{\overrightarrow{F}}_j}{\left|{\overrightarrow{F}}_i\right|\left|{\overrightarrow{F}}_j\right|}$$

Where, F⃗_i, F⃗_j are the local maximal principal stresses, at locations r⃗_i, r⃗_j, taken as vector quantities (such that the angle between them is defined modulo π). The inner sum, for each i, runs over all n_i pixels j such that |r⃗_i − r⃗_j| ≈ r, where for r we use a bin width of 20 μm. The outer sum over i runs over all pixels in the field of view.

Computational model

The model is a disordered, cohesive assembly of disks that have both translational and rotational degrees of freedom and that interact via forces between the disks that act both radially and tangentially (Fig. 3a). For the attractive interactions, we use the Lennard-Jones potential, which has a repulsive and an attractive part and gives a convenient description of a potential well. When two disks i and j are bound through the attractive well, there is a rotational energy penalty (producing a torque) associated with changing the orientation of the rotational degrees of freedom with respect to the initial attractive force. The rotational energy depends on the rotational angles α_i and α_j with respect to the initial attractive force, as 2−(cos α_i+ cos α_j). To better mimic the type of structural disorder present in the cell assembly and avoid crystalline structures, the disks have different diameters, assigned with a uniform probability on [0.8a,1.2a], where a is the unit length.

Figure 3. Endothelial monolayer modeled as a tensed, disordered assembly of cohesive particles far from equilibrium.

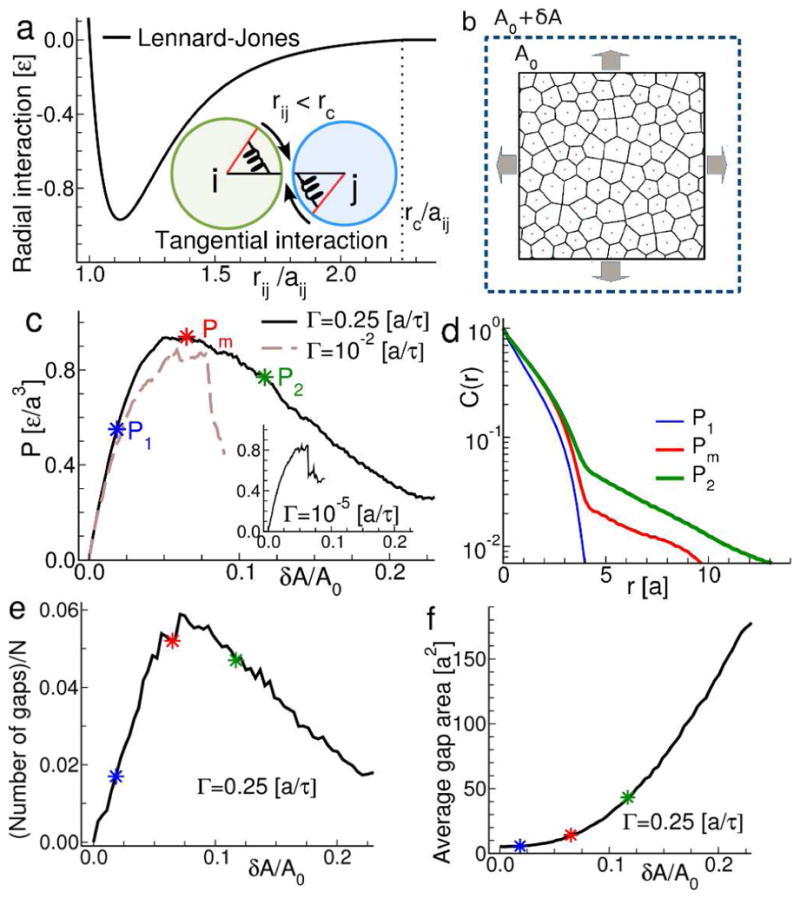
a. We construct a minimalist model of the monolayer as an assembly of particles, poly-disperse in size, joined by an attractive inter-particle interaction potential. The pair potential has components that act along the inter-particle contact radius and also tangential to it, to mimic the mechanics of actual cell-cell junctions. b. To mimic the action of contractile agonists such as thrombin, the model is strained by a symmetric, bi-axial expansion. The imposed external strain is balanced by a build-up of internal tensions. c. Load curve for the model monolayer subjected to biaxial strain. At slow rates of expansion, G, the stress-strain relationship is relatively linear (inset) and terminates with abrupt fracture. As G is increased the relationship changes, indicating the onset of plastic deformation and yielding rather than abrupt fracture. At the same time, the peak internal tension generated prior to failure is increased (solid and dashed lines). d. Spatial autocorrelation function of the model monolayer at different points on the load curves. The onset of plastic behavior is associated with the emergence of long-range correlations. e. Number of gaps (rescaled by the total number of particles N). f. Average gap area as a function of strain. In the yielding regime, permeability increases primarily by growth of existing gaps. Close to the maximum of the load curve, a few gaps of relatively small size are present. Further increasing the strain beyond the yielding threshold causes a rapid increase in gap area with a less dramatic increase in gap number. This is in contrast to the small and fairly constant average gap area measured in the linear regime, where the number of gaps rapidly increases.

We then use Molecular Dynamics (MD) as implemented in LAMMPS[40] to solve Newton’s equations of motion for each disk [41] as the assembly undergoes bi-axial expansions. We consider a void space between two particles as a gap when the distance between two particle-centers is at least 3/2 times the sum of their radii, i.e., the inter particle distance is at the tail of the Lennard-Jones potential. All codes and scripts used in the analysis may be obtained by email to Prof. Emanuela Del Gado (ed610@georgetown.edu).

Results and discussion

New gaps co-localize with pre-existing gaps

In all cell layers studied (n=13), phase contrast images revealed a typical cobblestone appearance, and the XPerT images revealed the presence of many small, nascent, paracellular gaps widely scattered throughout the monolayer (Fig. 1a). The corresponding distribution of tractions exerted by the layer upon its substrate was remarkably heterogeneous (Fig. 1b), with obvious traction hot-spots interspersed among regions of near-zero tractions, similar to previous reports on umbilical vein endothelial cell monolayers[25] and human pulmonary artery microvascular cell monolayers[14, 21] The corresponding spatial map of the intercellular stresses featured a similar degree of heterogeneity but over larger length scales (Fig. 1c). A more quantitative estimate of spatial heterogeneity was obtained by computing the probability density function of tractions and intercellular stresses. Consistent with previous reports[20, 21, 26], the distributions of tractions and of intercellular normal stresses (which is predominantly tensile) were found to be non-Gaussian with fat tails (SI text1, Fig. S1).

Figure 1. Agonist induced gaps co-localize with baseline gaps.

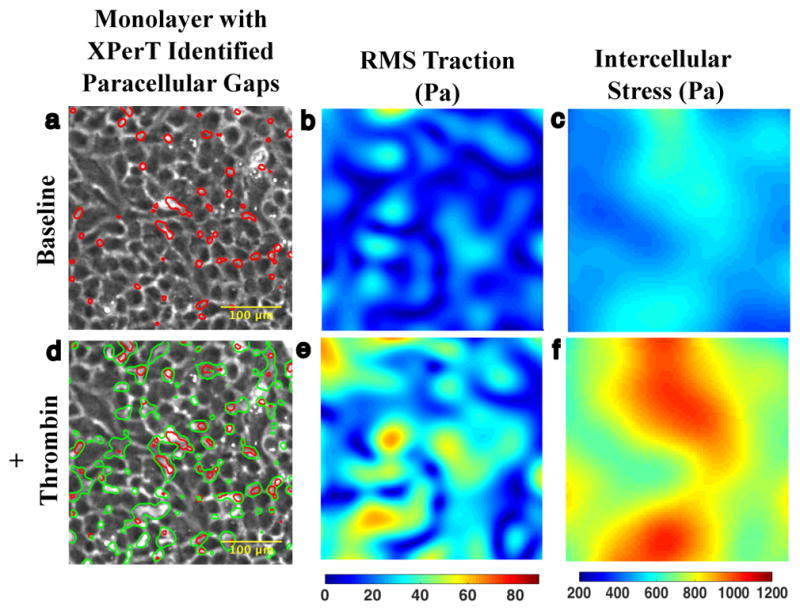
a. 10x phase contrast image of interior of micropatterned monolayer of Human Pulmonary Artery Cells adherent upon a polyacrylamide substrate. At baseline, the monolayer features an array of small XPerT identified paracellular gaps (red). b. The corresponding Fourier Transform Traction Microscopy (FTTM) map of tractions (Pa) is spatially heterogeneous. c. Monolayer Stress Microscopy (MSM) map of intercellular stress (Pa) is also heterogeneous but features larger spatial domains of similar tension. d. 15 minutes after treatment with 0.3 U/ml thrombin the monolayer permeability has increased as evidenced by the larger array of paracellular gaps (green contours). There is substantial overlap between the location of pre- and post-thrombin gaps indicating that much of the increase in permeability has occurred through gap growth rather than de novo gap formation. e. FTTM measured tractions 15 min after thrombin treatment demonstrate an increase in both traction magnitude and heterogeneity. f. MSM map of intercellular stress 15 min after thrombin treatment similarly shows an increase in tension and spatial heterogeneity.

Following the treatment of the monolayers with a hyper-permeability stimulus (thrombin, 0.3 U/ml, 15 min), both gap size and number of gaps increased (Fig. 1d). These changes resulted in increased permeability as assessed by the gap area as a fraction of monolayer area (from 0.05 ± 0.01 to 0.12 ± 0.01, p< 0.001). Comparison of post-thrombin gaps with the pre-thrombin gaps (Fig. 1d, green versus red outlines) revealed strong evidence of co-localization, suggesting that overall increases in permeability were largely attributable to growth of pre-existing gaps (Fig. S2). Tractions (root mean square (RMS) over the field) were seen to increase from 23.9 ± 17.5 to 39.8 ± 25.6 Pa (Fig.1e) and average normal stress (i.e., tension) increased from 689.7 ± 127.5 to 1161 ± 188.9 Pa (Fig. 1f).

Intercellular stresses reveal long-range order and orientation defects

When analyzed across the entire cellular layer, the values of intercellular tensions were strikingly correlated over distances of approximately 100–300μm, corresponding roughly to 10–20 cell diameters. This characteristic length increased somewhat after thrombin treatment (Fig. 2c). MSM provides not only the magnitude of local intercellular tension throughout the monolayer but also the full local stress tensor[19], from which we mapped the principal orientations of the stress tensor (see Materials and Methods). Large multi-cellular domains were evident in which principal stress orientations tended to align in parallel (Fig. 2a), reminiscent of nematic order in liquid crystals.[27] Between these orderly stress domains, were regions in which stress orientation changed rapidly over rather small distances; we call these more disordered regions stress orientational defects (SODs). Gaps were seen to grow preferentially not within the ordered domains but rather near the SOD (Fig. 2b).

Figure 2. Increases in monolayer permeability preferentially occur in vicinity of orientation defects.

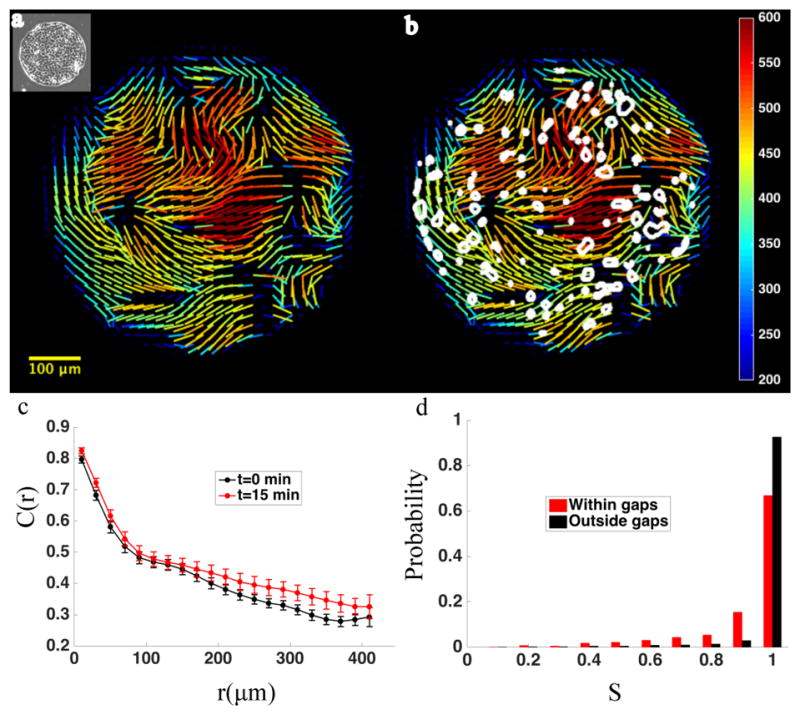
a. Cells are micropatterned into circular islands (inset, panel a). Within these islands, intercellular stress demonstrates regions of high orientational order. Lines representing orientation of maximal principal stress vectors tend to align in parallel over large domains. At domain boundaries, stress orientation ordering breaks down, creating regions of orientation defects. b. After treatment with thrombin (0.3 U/ml), the size and number of paracellular gaps increase. Contours of thrombin induced paracellular gaps are superimposed on map of baseline stress orientation (stress magnitude is in Pascals). Gaps (white outlines) tend to localize to areas that feature baseline orientation defects. c. The ordering of intercellular stress is reflected in a large spatial correlation length. The graph depicts the spatial autocorrelation function of intercellular stress before (black circles) and 15minutes after (red circles) thrombin treatment (n=13). Error bars represent standard error of the mean. Correlated domains of intercellular stress are 10–20 cells in diameter. d. Probability distribution of orientation order parameter, calculated for baseline monolayer, in areas which become disrupted by gaps (red) after thrombin treatment, compared with areas which do not become disrupted by gaps (black), illustrating the tendency of gaps to form in disordered regions.

To quantitatively assess the association between stress orientational defects and paracellular gaps, we computed an orientation order parameter[28], S (see Materials and Methods). Where regional stress orientations are mutually aligned, S approaches 1, and where regional stress orientations are uniformly random, S approaches 0. Across 13 monolayers, local gap formation was indeed found to vary systematically with S, with gaps forming preferentially in regions with lower values of S (Fig. 2d).

Gap formation in the endothelium is analogous to yielding of amorphous solids under tension

Simultaneous measurement of cell-generated forces and visualization of gap formation yields three significant observations: (1) intercellular stresses display a high degree of orientational order, (2) thrombin-induced permeability increases occur preferentially in regions of low orientational order, and (3) thrombin-induced increases in permeability occur to large degree by growth of pre-existing gaps rather than de novo junctional rupture. To rationale these findings, we developed a minimal computational model of the cell layer. The model is composed of a disordered assembly of cohesive particles. Each cell-cell junction in this assembly is represented by an attractive interaction potential that produces forces both radially and tangentially to particle-particle contact (Fig. 3a,). The tangential forces mimic the extended cohesive contact between two cells and the complexity of the junctional mechanics, beyond a simple spring or a Hertzian contact (SI text3). To mimic the mechanical state of the cell monolayer before and after the action of thrombin, we subjected the assembly to a biaxial tension (Fig. 3b). In response, the assembly remains mechanically stable but undergoes a stress relaxation. Higher strain leads to progressive gap formation and ‘rupture’ of pairwise interactions. Importantly, this process of yielding is coupled to the long-ranged stress correlation in the material (Fig. 3).

Like typical jammed amorphous solids, the energy landscape of our model solid is characterized by a wide distribution of local energy minima[29, 30] in which the system can become trapped (analogous to glass formation). The response to the imposed tensile strain when starting from such a non-equilibrium energy minimum, depends on the rate, Γ, at which the strain is imposed (Fig. 3e–f).[31] When Γ is fast (Fig. 3c, full and dashed lines; Fig. S3), the system displays a non-linear, non-monotonic dependence of the stress on the accumulated strain, similar to the yielding ductile response of soft glassy materials under shear.[29, 32, 33] In this regime, the system remains mechanically stable at higher stresses than those that could be attained in the low Γ regime (compare peak stress in Fig. 3c). The larger the Γ, the more extended was the yielding regime and the larger the strain prior to fracture.

In the yielding regime, gap formation is reminiscent of that seen in the experiments (Fig. 3e–f, Fig. 4a compare to Fig. 1a. and Fig. 1d). Strikingly, there spontaneously emerges large domains of aligned stresses wherein gaps tended not to form, interspersed among SODs wherein gaps tended to form preferentially (Fig. 4b–d, compare to 2a–d).

Figure 4. The model monolayer mimics endothelial gap formation.

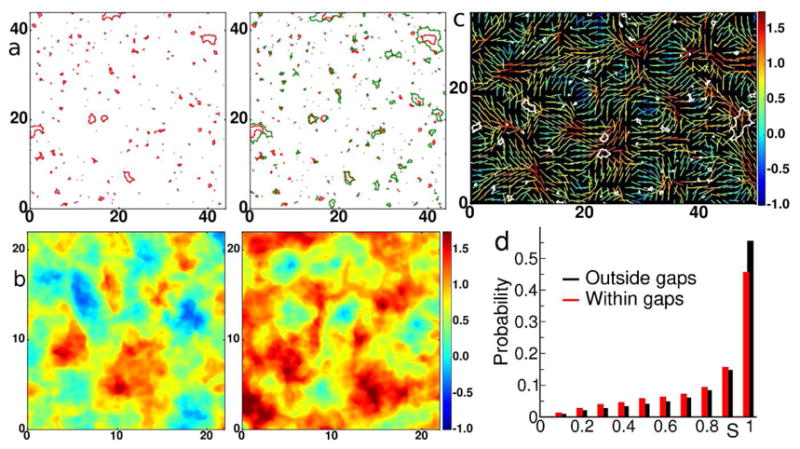
a. Red contours are the gaps at the yielding transition corresponding to the point labeled Pm in Figure 3c. Green contours are gaps with further increase of strain corresponding to moving from Pm to P2 in the yield curve of Figure 3c. The further increase in permeability preferentially occurs via gap growth as evidenced by comparing the maps of inter-particle gaps at the onset of the yielding regime (left panel) and after (right panel). b. Maps of average normal stress (in units of [ $\frac{\mathrm{\epsilon }}{{\mathrm{a}}^3}$]) in the model monolayer corresponding to P1 (left panel) and Pm (right panel) indicate that the yielding regime is associated with pronounced spatial heterogeneities in inter-particle stress. c. Lines represent orientation of maximal principal stress vectors at P1 and the color indicates the value of the local normal stress (measured in units of [ $\frac{\mathrm{\epsilon }}{{\mathrm{a}}^3}$]). Superimposed are the gaps (white contours) measured at Pm. d. Probability distribution of the orientation order parameter S in areas which become disrupted by gaps at Pm(red), compared to the overall distribution at P1 (black), illustrating the tendency of large gaps to grow in disordered regions.

What is the relationship between SODs and nascent gaps? Although the data presented here implicate SODs in gap growth, they do not determine whether the defects are a contributing cause or an effect of nascent gaps. It is conceivable that areas of disorder arise as a result of reorientation of stresses around a nascent gap and that the co-localization of thrombin induced gaps and SODs is therefore a result of nascent gaps. Ultimately, to definitively determine the direction of causality will require more comprehensive data on gap and stress dynamics. That the increase in permeability by gap growth and the co-localization of growing gaps with orientation defects emerge in the yielding regime of the model suggest that both are related to multi-cellular stress correlations and a non-equilibrium, jammed state of the monolayer.

The observed pattern of stress orientational order and SODs (Fig. 2a,b) are reminiscent of the nematic structural patterns seen in alignment of spindle-shaped cellular materials[34] or in the cell death and extrusion processes of epithelia.[35] Nevertheless, the topological defects identified here are strictly related to the stress alignment; we observed no tendency towards cell structural elongation or alignment. The time course of our experiment (15min) was chosen to include peak thrombin effects on cytoskeletal contraction[24] but is too short for significant cell migration or cell body realignment[36], hence the alignment and SODs discussed here may be precursors of the same nematic order and topological defects detected through cell shape reorientation. The stress alignment and the presence of SODs in our model (Fig. 4c), wherein each particle is symmetrical and thus possesses no potential for structural alignment, further suggest that the emergent stress alignment and SODs have a deeper, more general origin in the non-local mechanics of the monolayer.

From experiments and theory, we suggest that endothelial gap growth is similar to localized defects or strain localization in amorphous solids which undergo plastic re-arrangement under deformation.[30, 37, 38] The work described here, therefore, adds to the body of evidence that the biophysical mechanisms governing paracellular gap formation involve more than just the disruption of a local balance of forces at the cell-cell junction [14]. This revised picture will ultimately guide the development of more effective strategies for the prevention and treatment of endothelial barrier disruption.

Supplementary Material

2. Appendix A.

Supplementary data.