Using the Factor of Curves Model to Evaluate Associations Among Multiple Family Constructs Over Time

Abstract

Research in family psychology often focuses on understanding how multiple familial constructs develop over time. To examine these developmental processes, researchers frequently use a multivariate latent growth model (LGM) in which univariate LGMs are specified for each individual construct and then correlations are examined between the slopes and intercepts of different pairs of constructs. However, if the developmental associations among the constructs are hypothesized to derive from a higher-order common “cause” or factor, then a more appropriate model is the Factor of Curves (FOCUS) model. In this paper, we describe the FOCUS model for assessing the covariation among multiple developmental measures over time. We use empirical data to illustrate the benefits of the FOCUS model for testing whether a common factor, family academic orientation, is responsible for the interrelations among parental school perception, parental educational involvement, and children’s academic competence from elementary school to high school. Results support that a higher-order family academic orientation construct can be used to characterize the developmental associations among parental school perception, parental educational involvement, and children’s academic competence over time. We emphasize the importance of selecting a statistical model that matches one’s theory of developmental change.

Examining how relationships are established, changed, and sustained over time is an important objective of family research. Familial processes are multifaceted systems influenced by members of the collective unit and by aspects of the environmental context such as schools and neighborhoods. Under a structural equation modeling framework (SEM), multivariate latent growth models (LGMs; Meredith & Tisak, 1990) are often used to determine the extent to which several constructs (e.g., family values, hostility, parental practices) are interrelated over time. In family research, the associative LGM, a special case of the multivariate LGM, allows researchers to examine correlations between the model parameters for pairs of constructs over time.

However, if the associations among multiple familial processes are theorized to stem from a common “cause” or factor, then a statistical model that matches this theoretical model warrants consideration. The Factor of Curves (FOCUS; McArdle, 1988) evaluates whether a higher-order common factor is responsible for the relations among lower-order developmental processes. Although presented almost 30 years ago, and despite the benefits it provides for modeling multiple developmental constructs over time, its application has not been widely adopted across the psychological sciences.

The main objective of this article is to advocate the use of the FOCUS model for examining multiple trajectories of latent constructs involving family processes and settings. First, we discuss how multiple developmental processes are typically examined in longitudinal designs within SEM (i.e., associative LGMs) in family research. Then, we describe the FOCUS model, highlighting its methodological and theoretical advantages. We conclude with an empirical example in which we implement these methods, emphasizing the application of the FOCUS model for assessing the associations among parental school perception, parental educational involvement, and children’s perceived academic competence over time.

Modeling Change in Multiple Systems

As mentioned, an associative LGM permits researchers to assess the correlation among development parameters for pairs of constructs over time (Figure 1). This approach is common in family research, and can be seen, for example, in research modeling the development of parental support, stressful life events, and depressive symptoms in adolescents (Ge, Lorenz, Conger, Elder, & Simons, 1994); trends between teens, parent, and older sibling substance use (Duncan, Duncan, Hops, & Hyman, 1996); and parental support and adolescent physical health status (Wickrama, Lorenz, & Conger, 1997). Developing an associative LGM involves two steps (Duncan, Duncan, & Strycker, 2006). First, a univariate LGM is specified for each construct to determine the best form of the latent trajectory over time (e.g., flat, linear, quadratic). For instance, the following univariate LGMs would be specified to assess change independently in parental school perception X, parental educational involvement Y, and children’s academic competence Z across school grades (e.g., 5^th, 7^th, 9^th, and 11^th grades):

$$\begin{gathered} X_{ti}=x_{\mathit{0}i}+{\beta }_t{x}_{\mathit{si}}+e_{\mathit{xti}} \\ {Y}_{ti}=y_{\mathit{0}i}+{\beta }_t{y}_{\mathit{si}}+e_{\mathit{yti}} \\ {Z}_{ti}=z_{\mathit{0}i}+{\beta }_t{z}_{\mathit{si}}+e_{\mathit{zti}} \end{gathered}$$ (1)

where X_ti, Y_ti, Z_ti, represent an observed variable or indicator for each construct measured at time t for individual i. Each observed variable is a function of two corresponding growth factors, a latent intercept x_0i, y_0i, z_0i, that represents an individual’s level, and a latent slope x_si, y_si, z_si that denotes change across time. The mean structure provides information about the group’s average latent level ${\mu }_{x0}$, ${\mu }_{y0}$, ${\mu }_{z0}$ and the average rate of change over time ${\mu }_{xs}$, ${\mu }_{ys}$, ${\mu }_{zs}$.

Figure 1.

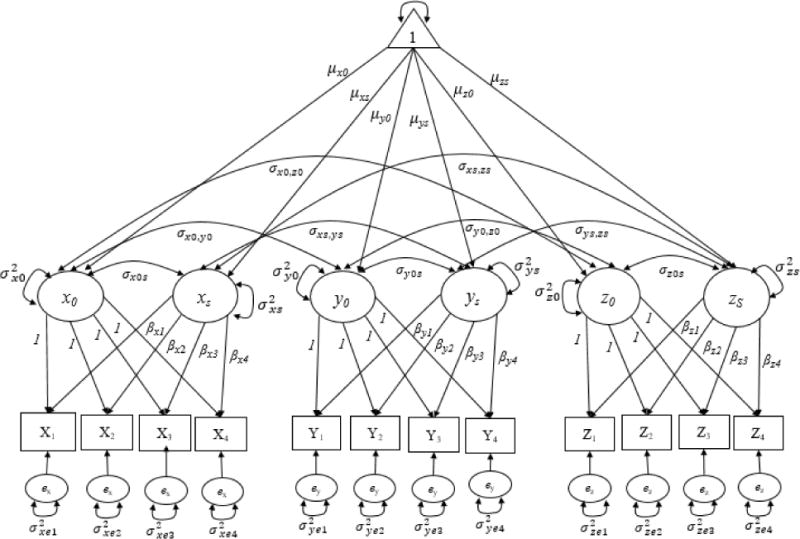
A path diagram of an Associative Latent Growth Model with three measures across four measurement occasions.

The mean of the latent level scaled at the first measurement occasion would be interpreted, for instance, as the average parental educational involvement score Y in 5^th grade. The mean of the latent slope scaled from the first to the last measurement occasion would be interpreted as the average change in parental educational involvement Y across school grades—i.e., 5^th to 11^th grades. The basis parameters β_t describe the shape of the latent trajectory. These parameters can be fixed at each time point to test different forms of change (e.g., linear: β_t = [0, 1, 2, 3], quadratic: β_t = [0, 1, 4, 9]) or estimated from the data using the latent basis method (e.g., β_t = [0, β₂, β₃, 1]). In a latent basis LGM, at least two basis coefficients are fixed to identify the model and to scale the latent intercept and slope factors. For example, β_t = [0, β₂, β₃, 1] designates the latent intercept factor to the initial assessment (i.e., β₁ = 0) and the latent slope factor represents the change from the first to last occasion (i.e., β₁ = 0 to β₄ = 1). The second and third basis coefficients signify the amount of change as a percentage of the overall change. Other scaling specifications can be used to test different forms of trajectories (Ram & Grimm, 2007).

Interindividual variability is assessed from the variance of the latent intercept ${\sigma }_{x0}^2$, ${\sigma }_{y0}^2$, ${\sigma }_{z0}^2$, and slope ${\sigma }_{xs}^2$, ${\sigma }_{ys}^2$, ${\sigma }_{zs}^2$. The latent intercept variance would be interpreted as individual differences among parental educational involvement scores in 5^th grade. The latent slope variance would be mean individual differences in change in parental educational involvement scores across school grades. The residual term e_xti, e_yti, e_zti represents the intraindividual variability over time. Residual terms would be interpreted, for example, as within-person differences in parental educational involvement scores at each grade level. The covariance between a construct’s latent intercept and slope ${\sigma }_{x0s}$, ${\sigma }_{y0s}$, ${\sigma }_{z0s}$, estimates the association between individuals’ initial status and rate of change across time. A positive correlation between the level and slope (e.g., ${\rho }_{x0s}$, ${\rho }_{y0s}$, ${\rho }_{z0s}$) would be interpreted, for example, as higher parental educational involvement in 5^th grade is associated with higher rates of change across school grades. A negative correlation among the latent level and slope would mean that higher parental educational involvement in 5^th grade is linked with lower rates of change across school grades.

Once the appropriate latent trajectory for each construct is selected and sufficient interindividual variability is detected in the latent growth factors, the second step is to covary the latent intercepts and slopes of the univariate LGMs. Suppose a multivariate representation of parental school perception, parental educational involvement, and children’s academic competence is hypothesized to follow an associative LGM (see Figure 1). This model will inform about the pattern of associations (strength and degree) among the latent intercepts (e.g., ${\sigma }_{0x,0y}$), the latent slopes or rates of change (e.g., ${\sigma }_{sx,sy}$), and the intercepts and slopes (e.g., ${\sigma }_{0x,sy}$) representing these familial processes over time. A positive correlation between the latent intercept of parental educational involvement and the slope of children’s academic competence (i.e., ${\rho }_{0y,sz}$), for example, could be interpreted, as higher parental educational involvement in 5^th grade is linked with higher rates of change in children’s academic competence from 5^th to 11^th grades. While the associative LGM is helpful in determining the extent to which pairs of family systems covary across time, this model cannot test whether these relations derive from an underlying factor. In addition, when the examined system includes multiple constructs, the number of possible associations increases, leading to a less than parsimonious representation.

McArdle (1988) presented two second-order LGMs designed to characterize different multivariate representations: the Curve of Factors (CUFFS) and the FOCUS models. The first level of a CUFFS model consists of a set of observed variables that are factor analyzed to define a hypothesized underlying construct at each measurement occasion. A series of longitudinal factorial invariance tests ensures that the same first-order factor is represented by the indicators across occasions. At the second-level of a CUFFS model, a latent growth model is specified to model the latent trajectory of the first-order factor. That is, the first-order common factor at each occasion is regressed onto second-order growth factors to summarize how the single construct changes (e.g., form of change, rate of change) over time. This method has been used to study, for example, to model change in individuals’ self-concept (Hancock, Kuo, & Lawrence, 2001), academic achievement (Hong & Ho, 2005), and general developmental research (Sayer & Cumsille, 2001). In contrast, the first level of a FOCUS model consists of individual univariate LGMs that characterize the independent developmental trajectory of each construct of interest. At the second level of a FOCUS model, second-order factors are specified to assess whether a higher-order factor structure drives the relation among the developmental trajectories of the lower-order constructs. A second-order common intercept factor represents what is shared among the lower-order functions at the initial time point and a second-order common factor slope represents the shared growth pattern among the constructs over time (i.e., they are growing, or changing over time, in a similar way) (see Figure 2). Thus, while the objective of a CUFFS model is to describe the quantitative growth of a single underlying construct defined by a set of indicators, the objective of a FOCUS model is to capture what is shared among different lower-order developmental processes over time. Although the CUFFS and FOCUS models were introduced at the same time, the latter model is underutilized in psychological research.

Figure 2.

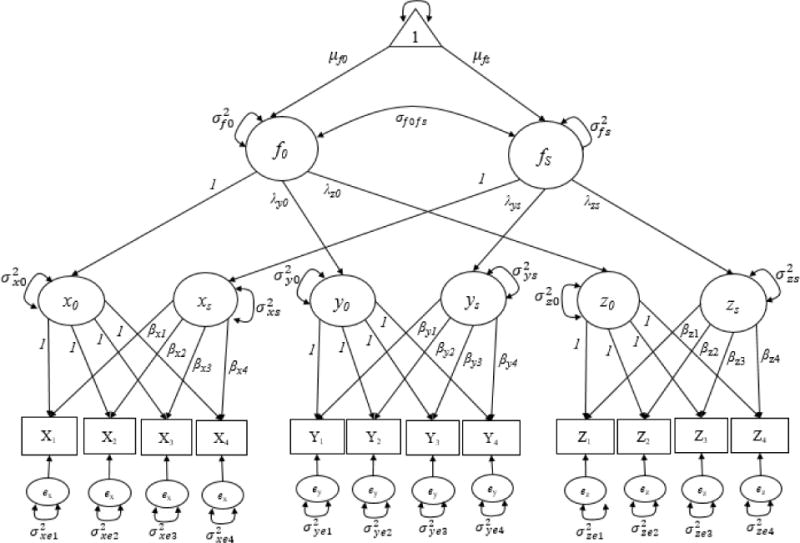
A path diagram of a Factor of Curves (FOCUS) model with three constructs across four measurement occasions.

Suppose that the developmental trajectories for parental school perception, parental educational involvement, and children’s academic competence are hypothesized to conjointly increase or decrease over time as a function of a family structure related construct, which we will term family academic orientation.¹ Specifically, as depicted in Figure 2, there are two higher-order common factors of interest, the intercept of family academic orientation f₀ and the slope or rate of development f_s of family academic orientation over time. For instance, the growth process for parental educational involvement Y can be expressed as:

$$y_0={\lambda }_{0y}{f}_0+{\alpha }_{y0}^2,$$ (2)

$$y_s={\lambda }_{sy}{f}_s+{\alpha }_{ys}^2.$$ (3)

Here y₀ and y_s represent the latent intercept and slope for construct Y, respectively. The lower-order latent intercept Y₀ is a function of a higher-order common factor f₀ (i.e., family academic orientation intercept), which captures the shared variance among all the lower-level latent intercepts, and residual variance ${\sigma }_{y0 }^2$, which represents the variance of the latent intercept not captured by the family academic orientation intercept factor. Likewise, the latent slope y_s is a function of a higher-order common slope factor f_s (i.e., family academic orientation slope), which accounts for the shared variance among all the lower-level growth models’ slopes or rate of change, and residual variance ${\sigma }_{ys }^2$, which represents the variance of the latent slope not captured by the family academic orientation slope factor. The mean for the family academic orientation intercept and family academic orientation slope informs about the participants’ average levels in the common initial status ${\mu }_{f0}$ and common average rate of change ${\mu }_{fs}$, respectively, in parental school perception, parental educational involvement, and children’s academic competence over time. The variance of the family academic orientation intercept ${\sigma }_{f0}^2$ and slope ${\sigma }_{fs}^2$ informs about the individual differences in these parameters. The covariance of the intercept and slope of family academic orientation ${\sigma }_{f0fs}$ can also be estimated. Equations 2 and 3 express the functions of construct Y, in this case, parental educational involvement, as it relates to the second-order factors—i.e., the intercept and slope of family academic orientation, but comparable functions would be specified for each lower order construct of interest.

Several criteria need to be met prior to modeling multiple measures with FOCUS models. First, data collected across repeated measurement occasions are necessary to examine both intraindividual change and interindividual differences. Second, sufficient variability in the lower-order growth factors (i.e., latent intercept and slope) is required before specifying a multivariate structure. Third, covariation among the growth factors representing the multiple constructs of interest is needed. Specifying a univariate LGM for each construct of interest will inform whether there is sufficient interindividual variability in the growth factors to warrant a multivariate representation of the data. Fourth, FOCUS models rely on SEM assumptions involving unobserved or latent variables. Thus, data issues such as continuous measures, normality of data, large sample size, and power are relevant to identify change and individual differences in growth trajectories (von Oerzen, Hertzog, Lindenberger, & Ghisletta, 2010).

The methodological benefits of second-order LGMs have been previously documented (e.g., Hancock, Kuo, & Lawrence, 2001; Murphy, Beretvas, & Pituch, 2011). The most salient benefits of examining change with a FOCUS model for family researchers include: (1) the ability to assess complex patterns of multivariate change simultaneously (Geiser, & Lockhart, 2012); (2) the observed score variance is further partitioned into reliable higher-order common factor variance ${\sigma }_{f0}^2$ and ${\sigma }_{fs}^2$, reliable growth construct variance ${\sigma }_{y0}^2$ and ${\sigma }_{ys}^2$, and random residual variance ${\sigma }_{\mathit{Yeti}}^2$. In an associative LGM, the reliable higher-order factor variance and growth variance are confounded. In contrast, a FOCUS model provides information about individual differences in the higher-order common factor and in each specified growth processes over time; (3) greater power to detect individual differences in change (von Oerzen et al., 2010); and (4) a more parsimonious representation of the data, relative to an associative LGM with comparable model fit (Duncan et al., 2006; Marsh, 1985). Note that when two analytical models account for the same relations among a set of measures, and there is no theoretical reason to do otherwise, the more parsimonious model is preferred as it has a higher possibility of generality (Epstein, 1984). Moreover, the FOCUS model aligns with a theoretical model that hypothesizes that a common source is responsible for the covariation over time among several family processes.

Modeling family processes with the FOCUS can produce results that would not otherwise be found with typical LGMs (e.g., associative LGM). Thus, this model can provide insight into understanding complex family relations over time. For example, factor analysis in parenting research has shown a strong relationship among parenting practices, including warmth, behavioral control, and autonomy support for their children (Castro-Schilo et al., 2013; Landry, Smith, Swank & Miller-Loncar, 2000). Application of the FOCUS model could determine whether parent's warmth, behavioral control, and autonomy support change together over time because of an underlying construct, such as positive parenting. The FOCUS model can also be used to better understand the time course of family beliefs and practices of immigrant families in the United States. For instance, relevant literature posits that over time, behaviors of families of Mexican-origin, such as gender roles, group activities, and language, collectively change over time to resemble those in the American culture (Arbona, Olvera, Rodriguez, Hagan, Linares, & Wiesner, 2010). Thus, the FOCUS model can test if a higher-order factor drives the simultaneous change in immigrant families’ culture and customs. Additionally, the FOCUS model can help research in the compound influence of ecological settings. For instance, research shows that psychological health, neighborhood support, and perceived safety vary across poor and affluent neighborhood environments (Cutrona et al., 2003). The FOCUS model can test whether a common factor (e.g., neighborhood culture) can characterize changes in individuals’ behaviors within their communities across occasions. In summary, the FOCUS model can help researchers understand why, when, and how related constructs develop over time.

To demonstrate the utility of the FOCUS model as a tool for examining multivariate processes in family research over time, we provide an empirical example. Specifically, we examine whether a higher-order factor that we label “family academic orientation”, can characterize the interrelations among parental school perception, parental educational involvement, and children’s academic competence from elementary school to high school.

Family Academic Orientation

Numerous studies support the positive association between family and school experiences (e.g., Becker & Epstein, 1982; Epstein, 1991; Izzo, Weissberg, Kasprow, & Fendrich, 1999; Hong & Ho, 2005). Germane to this study, prior research has found an interrelation between parents’ perception of school and educational involvement, as well as children’s academic competence. For example, positive parental attitudes and beliefs about their child’s teachers and school have been found to be linked to higher parental educational participation in the home, such as helping with homework assignments (Epstein, Simon, & Salinas, 1997) and attending school meetings or events (Dervarics & O'Brien, 2011; Neuman & Dickinson, 2011). Authors of existing literature on home and school connectedness have also asserted a positive association between parental educational involvement and children’s self-reported academic experience (Epstein, 1991). For instance, literacy research found children whose parents actively participate in reading and academic assignments have higher confidence in their literacy abilities which often transfers to other academic subjects (Neuman & Dickinson, 2011; Paratore, 2006). Also, research focused on child and parent relationships corroborate the association between parental involvement and children's reported self-concept measures (Patterson, 1986). Likewise, much has been documented about the parallels between children's academic attitudes and beliefs and that of their family (Delpit, 1995; Ogbu, 1993). For instance, students with optimistic views about their academic abilities are more likely to have parents with positive school perceptions (Hauser-Cram, Sirin, & Stipek, 2003). Finally, several studies have proposed that the relation among home and school connectedness is symbiotic in nature (Brophy, 1983; Jussim & Eccles, 1992; Wigfield, Galper, Denton, & Seefeldt, 1999).

Research on the development of family and academic constructs emphasizes the importance of environmental influences (Neuman & Dickinson, 2011). For instance, numerous studies have shown that settings which provide optimal academic support facilitate the development of positive educational behaviors from parents (e.g., surveillance of children’s school work) and children (perception of school competence) (Baumrind, 1971; Deci & Ryan, 1985; Ginsburg & Bronstein, 1993). Given that prevailing research has consistently reported a concurrent developmental relation between parental school perception, parental educational involvement and children’s academic competence, it is conceivable to hypothesize that there is some shared developmental process unfolding over time among these constructs. However, the underlying process through which these constructs develop over time has yet to be examined. Therefore, a model that can test this hypothesis should be explored. Next, we examine if a superordinate developmental factor, which we term family academic orientation and which we believe represents the broader orientation of the family toward the academic environment, is responsible for the shared developmental change among parental school perception, parental educational involvement, and children’s academic competence. As in any factor analysis, the researcher determines the theoretical and conceptual meaning of this superordinate factor.

The main objective of this paper is to illustrate the utility of the FOCUS model for family science. For this, we examine whether a common factor, family academic orientation, drives the interrelations among parental school perception, parental educational involvement, and children’s academic competence from elementary school to high school. Specifically, we examine the following: (a) the tenability of a longitudinal multivariate representation among parental school perception, parental educational involvement, and children’s self-perceived academic competence using the associative LGM; (b) whether a higher-order factor, family academic orientation, can describe the simultaneous development of these three constructs using the FOCUS model; and (c) the relative fit of these two models to the data.

Empirical Example

Data for this paper are from the California Families Project (CFP), a study of the development of Mexican-origin youth and their families in Northern California. Participants included 674 single (N = 125) and two-parent families (N = 549). Fifth-grade children (mean age = 10.8, SD = 0.60; 50% male) were randomly drawn from northern California school districts during the 2006-2007 and 2007-2008 school year and asked to participate. We used panel data collected when students were in the 5^th, 7^th, 9^th, and 11^th grades. The present study was exempt from Institutional Review Board review because it entailed secondary data analysis.

Measures

Children’s mothers completed the Parental School Perception and Parent Involvement in Child’s Education scales (Epstein & Salinas, 1993). To measure parental school perception, 15 items were rated on a 4-point Likert-type scale (1 = Not at all true to 4 = Very true; e.g., “This is a very good school”). Coefficient alpha reliability estimates for this scale were .83, .85, .86, and .87 in 5^th, 7^th, 9^th, and 11^th grade, respectively. To assess parental educational involvement, four items were rated on a 4-point Likert-type scale (1 = Never to 4 = Many times; e.g., “In the past year, you helped your child with homework or a school project”). Alpha reliability estimates for this scale were .66, .65, .67, and .68 in 5^th, 7^th, 9^th, and 11^th grade, respectively. To measure children’s perceived academic competence, we used the academic competence subscale of the Self-Description Questionnaire II-Short Form (Marsh, Ellis, Parada, Richards, & Heubeck, 2005), which assesses the degree to which children see themselves as effective, capable individuals who are proud and satisfied with the way they are. The academic competence scale includes four items that were rated using a 4-point Likert-type scale (1 = Not true for me to 4 = Really true for me; e.g., “You learn things quickly in most school subjects”). Alpha reliability estimates for this scale were .70, .74, .77, and .76 in 5^th, 7^th, 9^th, and 11^th grade, respectively. For all three scales, items at each occasion were averaged to form a composite indicator.

Estimation and Model Fit

Full Information Maximum Likelihood (FIML) was used to estimate all models. As common in most longitudinal studies, some participants were unavailable to participate or not know how to respond to a survey item on more than one occasion. We coded all these responses as missing. FIML adequately handles missing data when they are missing at random or completely missing at random, as we assumed to be the case, and estimates are adjusted based on all available data (Enders, 2001; Ferron & Hess, 2007). All models were fitted using the Lavaan package in the statistical software R 3.0.2 (R Development Core Team, 2013).

To evaluate the fit for each model, we used several fit indices: the chi-square test (χ²), the Comparative Fit Index (CFI) (Hu & Bentler, 1999), the Tucker-Lewis Index (TLI; Tucker & Lewis, 1973), the absolute model fit index Root Mean Square Error of Approximation (RMSEA; Browne & Cudeck, 1993), and the Standardized Root Mean Square Residual (SRMR; Hu & Bentler, 1999). To statistically compare the fit of the nested univariate LGMs, we used the likelihood ratio chi-square difference test (∆χ²). That is, we used this measure to determine whether the subsequent complex model was statistically different (i.e., ∆ ${\chi }^2$ in p < .05) than the former simpler model. The associative LGM and the FOCUS model cannot be statistically compared because they are not nested. Therefore, we used model fit indices that consider parsimony, as well as independent model fit, the Akaike information criterion (AIC; Akaike, 1974) and the Bayesian information criterion (BIC; Schwarz, 1978), to determine the most appropriate model (lower AIC and BIC values) for this data.

Analytical models

We ran a series of alternative univariate LGMs for each construct to determine the most adequate representation of the latent trajectory across all time points. For this, we sequentially tested a number of models: (a) no change, β_t = [0, 0, 0, 0]; (b) linear, β_t = [0, 0.33, 0.66, 1]; and (c) latent basis, β_t = [0, β₂, β₃, 1], in which β₂, and β₃ were estimated from the data.² The loadings of the latent intercept factor were set to 1.0. To identify all univariate LGMs, each indicator intercept was fixed to 0. The indicator residual variances were estimated.³ Finally, the following parameters were estimated for each univariate LGM: the latent intercept factor mean μ₀ and variance ${\sigma }_0^2$, the latent slope factor mean μ_s and variance ${\sigma }_s^2$, and their covariance ${\sigma }_{0s}$. The best fitting univariate LGM was included in the subsequent multivariate LGMs.

Given that prior research suggests a developmental relation between parental school perception, parental educational involvement, and children’s academic competence (e.g., Epstein, 1991; Patterson, 1986; Hong & Ho, 2005; Neuman & Dickinson, 2011), we found it appropriate to fit the associative LGM to these data. For this, we estimated the covariances between the latent intercepts and slopes of the univariate LGMs. Finally, given the plausibility that the reciprocal relation between parental school perception, parental educational involvement, and children’s academic competence can be characterized by a higher-order family academic orientation factor, we then specified a FOCUS model. To run this model, we fixed the covariances among the latent intercepts and slopes to 0, and specified these associations as part of two higher-order common factors. These factors represent the common family academic orientation intercept f₀ and the common family academic orientation slope f_s, and together, they account for the associations among the lower-order factors over time. To scale the family academic orientation factors, the reference variable method was used (Bollen & Curran, 2006). Specifically, we specified the parental school perception measure to serve as the referent construct from which to scale the superordinate factors. That is, we fixed the loadings connecting the latent intercept and slope factors of parental school perception to family academic orientation factors to 1.0 and estimated the remaining factor loadings (Duncan et al., 2006). The resulting parameter estimates in this model included a higher-order common intercept mean μ_f0 and variance ${\sigma }_{f0}^2$, a higher-order common slope mean μ_fs and variance ${\sigma }_{fs}^2$, and their covariance σ_f0fs. For each construct, we fixed the lower-order intercept and slope to 0 and estimated the variances.

Results

Table 1 presents the zero-order correlations, means, and standard deviations for parental school perception, parental educational involvement, and children’s academic competence across the 5^th, 7^th, 9^th, and 11^th-grade assessments. Each scale showed moderate stability over time, with correlations across occasions generally in the .30s to .50s. Correlations also indicated that the association among some pairs of indicators from different scales were moderate (e.g., parental school perception and parental educational involvement at time 1) while other pairings of indicators were small (e.g., parental educational involvement at time 1). Note that small correlations among indicators across occasions might indicate that the constructs of interest are not related over time. Researchers should use both theory and statistical methods to guide the selection of indicators. For illustrative purposes, we proceed to model the developmental link between these measures. Moreover, subsequent analyses would help decipher whether a complete multivariate representation of these constructs at the latent level (i.e., covariation among latent growth factors and/or underlying superordinate factor structure) will hold in the data. The means for parent school perception, parent educational involvement, and children’s academic competence showed small, gradual decreases over time. Figure 3 displays trajectories for all these measures across school grades. Figures reveal variability in within-person change and between-person differences over time.

Table 1.

Zero-order correlations, means, standard deviations (SD), and missing rates for measures across time

		Parental School Perception (PSP)				Parental Educational Involvement (PEI)				Child’s Academic Competence (CAC)
		t1	t2	t3	t4	t1	t2	t3	t4	t1	t2	t3	t4
PSP	t1	1.00
	t2	.47	1.00
	t3	.33	.43	1.00
	t4	.37	.39	.57	1.00
PEI	t1	.19	.10	.07	.09	1.00
	t2	.15	.20	.16	.09	.52	1.00
	t3	.15	.17	.19	.14	.40	.54	1.00
	t4	.17	.13	.14	.14	.39	.51	.61	1.00
CAC	t1	.14	.08	.08	.10	.09	.04	.06	−.02	1.00
	t2	.15	.08	.03	.10	.03	−.05	.02	−.03	.36	1.00
	t3	.12	.09	.18	.12	−.03	−.01	−.02	−.06	.36	.44	1.00
	t4	.16	.13	.10	.08	−.06	−.05	−.04	−.04	.28	.35	.49	1.00
PSP		t1	t2	t3	t4
	M	3.31	3.29	3.24	3.22
	SD	0.44	0.44	0.43	0.44
PEI	M	3.36	3.20	3.02	2.76
	SD	0.62	0.61	0.61	0.64
CAC	M	3.20	3.15	2.99	2.90
	SD	0.61	0.57	0.57	0.56

Note. t₁, t₂, t₃, and t₄ indicates measurement occasions.

Figure 3.

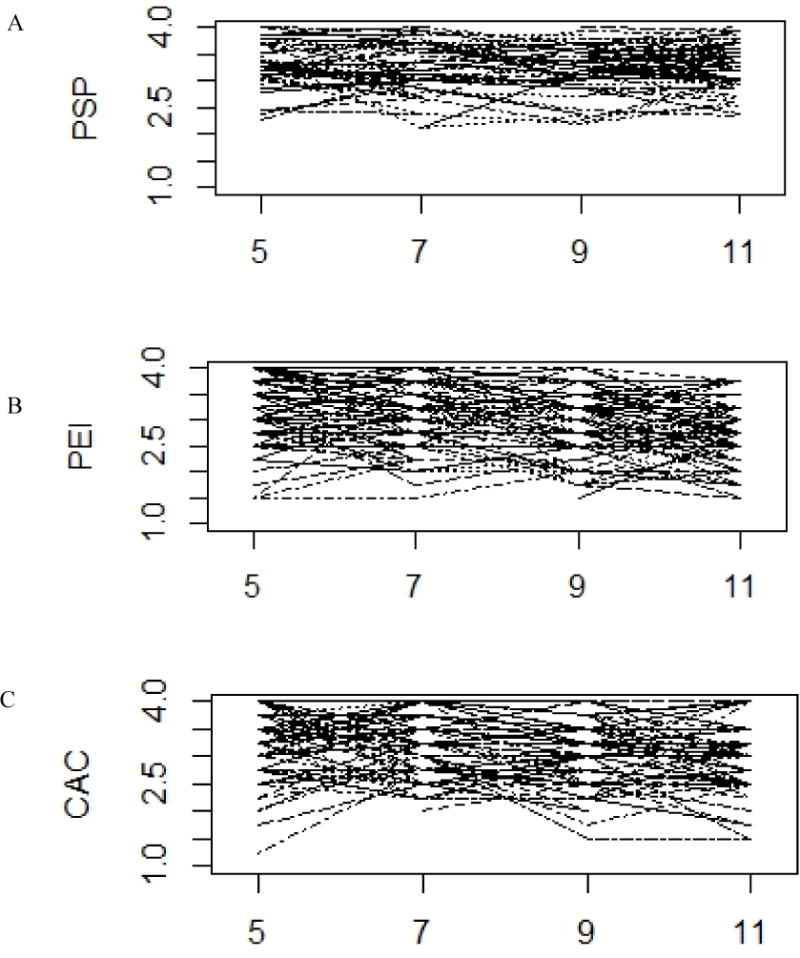
A random subsample (n = 100) of (a) parent school perception, (b) parent educational involvement, and (c) child’s academic competence scores (scores range 1 - 4) across school grades.

As frequently reported in longitudinal research, there was missing data for each scale across time. The missing rate for parental school perception across all four consecutive occasions were about 18%, 25%, 20%, and 15%. For parental educational involvement, the missing rates at each successive measurement were about 2%, 16%, 11%, and 14%. The missing rate for children’s academic competence across time points were about 5%, 14%, 10%, and 11%.

Univariate LGMs

Table 2 presents fit indices for each univariate LGM. For parental school perception, the linear LGM (CFI = .985, TLI = .982, RMSEA = .042, SRMR = .03) and the latent basis LGM (CFI = .989, TLI = .989, RMSEA = .03, SRMR = .027) had strong model fit. However, the ∆χ² test did not show a statistical difference between these two models (i.e., ∆ ${\chi }^2$ in p < .05), so the simpler model was selected, the linear LGM. Results showed a statistically significant mean in parental school perception at the initial status ( ${\mu }_{x0}$ = 3.30, p < .001) that varied across mothers ( ${\sigma }_{x0}^2$ = 0.09, p < .001), as well as significant overall change in parental school perception across time ( ${\mu }_{xs}$= −0.10, p < .001), which varied across mothers ( ${\sigma }_{xs}^2$ = 0.10, p < .001).

Table 2.

Assessment results of different forms of latent trajectories for each measure

	No Change	Linear	Latent Basis
Parental School Perception
${\chi }^2$/df	61/8	10/5	10/3
Δ ${\chi }^2$/Δdf	–	51/3b	0/2a
CFI	.856	.985	.989
TLI	.892	.982	.989
RMSEA (95% CI)	.10(.078, .125)	.042(.00, .077)	.03(.00, .065)
SRMR	.075	.03	.027
Parental Educational Involvement
${\chi }^2$/df	500/8	12/5	7/3
Δ ${\chi }^2$/Δdf	–	488/3b	5/2a
CFI	.285	.989	.994
TLI	.464	.986	.988
RMSEA (95% CI)	.303(.281, .326)	.048(.016, .082)	.045(.00, .089)
SRMR	.228	.03	.026
Child’s Academic Competence
${\chi }^2$/df	168/8	10/5	4/3
Δ ${\chi }^2$/Δdf	–	158/3b	6/2b
CFI	.605	.987	.995
TLI	.704	.984	.991
RMSEA (90% CI)	.173(.151, .196)	.04(.00, .075)	.031(.00, .078)
SRMR	.126	.031	.024

Note. Superscript a indicates model not statistically significant (i.e., Δ ${\chi }^2$ in p < .05) from previous fitted model. Superscript b indicates model statistically significant (i.e., Δ ${\chi }^2$ in p > .05) from previous fitted model. Bold text indicates overall best fitting model for each construct.

For parental educational involvement, both the linear LGM (CFI = .989, TLI = .986, RMSEA = .048, SRMR = .03) and the latent basis LGM (CFI = .994, TLI = .988, RMSEA = .045, SRMR = .026) had strong model fit. However, because the ∆χ² test did not indicate a statistical difference between these two models (i.e., ∆ ${\chi }^2$ in p < .05), we again selected the simpler model, the linear LGM. The mean in parental educational involvement at the initial measurement occasion was different from zero ( ${\mu }_{y0}$ = 3.38, p < .001) and varied across mothers ( ${\sigma }_{y0}^2$ = 0.21, p < .001). The overall change in parental educational involvement across time was negative ( ${\mu }_{ys}$= −0.60, p < .001), with differences across mothers ( ${\sigma }_{ys}^2$ = 0.20, p < .01).

Finally, for children’s academic competence, the latent basis LGM had the best fit (CFI = .995, TLI = .991, RMSEA = .031, SRMR = .024). This model was also statistically different (i.e., ∆ ${\chi }^2$ in p > .05) from the former simpler models. The latent basis coefficients indicated that the trajectory of this measure significantly changed nonlinearly across time. Specifically, the second basis coefficient was 0.17 (p < .05), which represents about 17% of the overall change in these scores. The third basis coefficient was 0.67 (p < .001), representing about 67% of the overall change or about 50% of the change from the second to third occasion in children’s academic competence. The mean in children’s academic competence at the initial time point was positive ( ${\mu }_{z0}$ = 3.19, p < .001) and varied across children ( ${\sigma }_{z0}^2$ = 0.13, p < .01), and the overall change in academic competence across time was negative ( ${\mu }_{zs}$= −0.30, p < .001), with variation across children ( ${\sigma }_{zs}^2$ = 0.10, p < .01). Given the variation in latent intercepts and slopes in each construct, we proceeded to fit the multivariate LGMs, the associative LGM and FOCUS model.

Multivariate LGMs

Table 3 presents model fit and correlation estimates among the latent intercepts and slopes from the associative LGM. This model had a good fit to the data (CFI = .983, TLI = .977, RMSEA = .028, SRMR = .03), indicating that a multivariate representation of these constructs was tenable. Per this model, results revealed statistically significant and positive correlations between the two intercepts ( ${\rho }_{0x,0y}$ = .337, p < .001) and the two slopes ( ${\rho }_{sx,sy}$ = .214, p < .01) of parental school perception and parental educational involvement. Results also indicated a positive correlation between the intercepts ( ${\rho }_{0x,0z}$ = .325, p < .001) and slopes ( ${\rho }_{sx,sz}$ = .343, p < .05) of parental school perception and children’s academic competence. Furthermore, the intercept of parental school perception correlated negatively with the slope of children’s academic competence ( ${\rho }_{0x,sz}$ = −.206, p < .05). Significant correlations were also found between the intercepts ( ${\rho }_{0y,0z}$ = .16, p < .05), slopes ( ${\rho }_{sy,sz}$ = .241, p < .05), and the intercept and slope ( ${\rho }_{0y,sz}$ = −.341, p < .01) of parental educational involvement and children’s academic competence. In the next modeling approach, we took these associations among the lower-order growth factors and characterized them in terms of two higher-order common factors.

Table 3.

Associative latent growth model parameter estimates and fit indices results

	Parental School Perception (PSP)		Parental School Involvement (PSI)		Child’s Academic Competence (CAC)
	Intercept	Slope	Intercept	Slope	Intercept	Slope
Mean	3.30(.01)***	−0.11(.02)***	3.38(.02)***	−0.60(.01)***	3.20(.01)***	−0.30(.02)***
Variance	0.09(.01)***	0.10(.02)***	0.21(.02)***	0.20(.02)***	0.13(.01)***	0.10(.03)**
	Intercept	Slope	Intercept	Slope	Intercept	Slope
PSP
Intercept	1.00
Slope	−.297*	1.00
PSI
Intercept	.337***	−.183*	1.00
Slope	−.06	.214**	−.303**	1.00
CAC
Intercept	.325***	−.167	.16*	−.153	1.00
Slope	−.206*	.343*	−.341**	.241*	−.218	1.00
Fit indices
${\chi }^2$/df		75/49
CFI		.983
TLI		.977
RMSEA (90% CI)		.028(.014, .04)
SRMR		.03
AIC		9548.061
BIC		9596.925

Note.

^*p < .05

^**p < .01

^***p < .001

Table 4 presents results from the FOCUS model. Overall, this model had good fit (CFI = .962, TLI = .959, RMSEA = .038, SRMR = .056), indicating that the specification of a higher-order factor structure (i.e., family academic orientation) was reasonable for representing change in the three constructs for this data. Results showed a statistically significant mean in the family academic orientation intercept ( ${\mu }_{f0}$ = 3.309, p < .001) and slope ( ${\mu }_{fs}$= −0.119, p < .001). This indicates that there was a significant average initial status and an overall decrease in the rate of change common to the three variables. There was also a significant variance for the family academic orientation intercept ( ${\sigma }_{f0}^2$ = 0.033, p < .001), but not in the slope ( ${\sigma }_{fs}^2$ = 0.002, p > .05). This indicates that, while there were individual differences in family academic orientation at the initial level, none existed at the slope. There was a statistically significant negative covariation between the intercept and slope of the family academic orientation factors ( ${\sigma }_{f0,fs}$ = −0.004, p < .05), which translated into a moderate negative correlation ( ${\rho }_{f0,fs}$ = −.516, p < .05). This shows that families who had higher scores on the family academic orientation factor at the initial level tended to have lower rates of change in the family academic orientation factor across time. In addition, the loadings for the intercept and slope family factors were statistically significant for parental educational involvement (λ_0y = 1.021, p < .001 and λ_sy = 4.977, p < .001) and children’s academic competence (λ_0z = 0.966, p < .001 and λ_sz = 2.509 p < .001), indicating that the lower-order intercepts and slopes contributed significantly to the definition of the second-order family academic orientation common factors. The standardized factor loadings of the latent intercept factors for parental school perception, parental educational involvement and children’s academic competence were .68, .43, and .49, respectively. These results support that all three lower-order intercepts adequately measured the family academic orientation intercept factor (i.e., λ > .30, Gorsuch, 1983). The standardized factor loadings of the latent slope factors for parental school perception, parental educational involvement and children’s academic competence were .17, .55, and .39, correspondingly. These findings indicate that while parental school perception did not properly measure the family academic orientation slope (i.e., λ < .30), parental educational involvement and children’s academic competence did (i.e., λ > .30). The proportion of variance explained by the two common factors of family academic orientation was 46%.

Table 4.

FOCUS model parameter estimates and fit indices results

	FOCUS
	Estimate	SE
Factor loadings
λ0x	1=	–
λ0y	.433***	.008
λ0z	.49***	.008
λsx	1=	–
λsy	.55***	.49
λsz	.384***	.419
Means
Intercept ${\mu }_0$	3.309***	.016
Slope ${\mu }_s$	−0.119***	.022
Variances	0.033***
Intercept ${\sigma }_0^2$	0.002	.006
Slope ${\sigma }_{\mathrm{s}}^2$	−0.004(−.516)*	.002
Covariance σ0s (ρ0s)		.002
Fit indices
${\chi }^2$/df	119/61
CFI	.962
TLI	.959
RMSEA (90% CI)	.038(.028, .048)
SRMR	.056
AIC	9561.85
BIC	9692.734

Note. Subscript X, Y, and Z indicate parental school perception, parental school involvement and child’s academic competence, respectively.

^*p < .05

^**p < .01

^***p < .001

Next, we compared the fit of the two competing multivariate models. For the associative LGM, the AIC was 9548.061 and the BIC was 9596.925. For the FOCUS model, the AIC was 9561.85 and the BIC was 9612.734. According to these two measures, the associative LGM fit the data better; however, the FOCUS model did not fit relatively worse.

Discussion

In this paper, we discuss multivariate change models for evaluating the association among several developmental processes over time in family research, with emphasis on the FOCUS model. Using empirical data, we first specified a series of univariate LGMs with varying forms of change (i.e., no change, linear, latent basis) to determine which shape best characterized the latent trajectory over time for parental school perception, parental educational involvement, and children's academic competence. These univariate LGMs also revealed important individual differences in the growth parameters to warrant specifying a multivariate model. Results from an associative LGM indicated that a multivariate representation of these constructs was tenable in the data. Results also showed that a FOCUS model fit the data. Thus, the tenability of a higher-order factor (i.e., family academic orientation) for characterizing the associations between these lower-order developmental processes was reasonable.

In our empirical example, we used the term family academic orientation as a broad label to capture the family’s general orientation toward the academic context. However, future research should attempt to identify the underlying causal factors that contribute to the shared growth patterns observed for parental school perception, parental educational involvement, and children's academic competence; such research could lead to a new conceptualization of, and therefore new label for, the superordinate common slope factor identified in the present study.

Comparing the two models in terms of statistical fit, both the AIC and BIC indicated that the associative LGM had slightly better fit than the FOCUS model. However, the FOCUS model was more parsimonious than the associative LGM, as it had fewer free parameters. Based on these statistical comparisons solely, selecting a model is challenging. Therefore, when deciding among competing models, researchers should use theory, knowledge of the data collection process, and fit indices to guide model selection.

The associative LGM limits a researcher’s effectiveness to answer questions about interrelated developmental processes, because it does not consider if there is a superordinate factor that explicates the change among such individual constructs. For instance, extant literature corroborates an interrelation between parental perception of school, parental educational involvement, and children’s academic competence (e.g., Epstein et al., 1997; Neuman & Dickinson, 2011). If we had only analyzed longitudinal change using an associative LGM, our understanding about the concurrent development of these constructs would have continued to be limited. We would have concluded that some pairs of growth parameters significantly covary over time (e.g., the initial status of parental school perception and rate of change of children's academic competence), while others do not (e.g., the initial status of parental school perception and rate of change of parental involvement). However, results from the FOCUS model support that the covariation among these constructs can be characterized by a common source.

Extensions to the FOCUS models can be specified to increase the capacity of researchers to test complex hypotheses of change among multiple processes over time in family science. Although we illustrated the application of the FOCUS model with three constructs reported by mothers and children, family researchers can apply this model to measures representing growth over time among various kinship groups (e.g., siblings, partners, grandparents), behaviors (e.g., family activities, daily routines), settings (e.g., households, neighborhoods), and cultural contexts (e.g., beliefs, rules), to name a few examples. Additionally, the higher-order factors specified in the FOCUS model (in the present case family academic orientation factors that represent parental school perception, educational involvement, and child’s academic competence) can be used as predictors or outcomes of change in other variables, thus allowing researchers to address a vast range of questions related to antecedents and consequences of family processes.

Despite the methodological benefits the FOCUS offers researchers, some limitations are worth mentioning. For example, because the FOCUS model is an extension of the typical LGM, it shares some of the same drawbacks. The most cited limitations of LGMs are the assumption of normality and large samples (Bollen & Curran, 2006). However, simulation studies indicate that moderate issues of nonnormality are adequately handled by FIML estimation (Forero, Maydeu-Olivares, & Gallardo-Pujol, 2009). Moreover, LGM within SEM partially relies on data that are collected when participants are measured at about the same measurement occasion, and spacing of observations are the same for all individuals (Duncan et al., 2006). Model constraints, however, can be imposed to adjust for irregular data collection designs (Bollen & Curran, 2006).

The FOCUS model offers family researchers a powerful tool for modeling change that is currently underused. Specifically, this model can be used to test whether an underlying family process hypothesized to drive the collective incline or decline of several variables over repeated occasions holds in the data. Thus, the FOCUS model can help family researchers understand the developmental relation among a set of multiple family systems over time. We hope that by providing model descriptions, parameterization, and interpretation of estimates, researchers in family psychology will be encouraged to include FOCUS models in their work.