Spin-orbit torques from interfacial spin-orbit coupling for various interfaces

Abstract

We use a perturbative approach to study the effects of interfacial spin-orbit coupling in magnetic multilayers by treating the two-dimensional Rashba model in a fully three-dimensional description of electron transport near an interface. This formalism provides a compact analytic expression for current-induced spin-orbit torques in terms of unperturbed scattering coefficients, allowing computation of spin-orbit torques for various contexts, by simply substituting scattering coefficients into the formulas. It applies to calculations of spin-orbit torques for magnetic bilayers with bulk magnetism, those with interface magnetism, a normal metal/ferromagnetic insulator junction, and a topological insulator/ferromagnet junction. It predicts a dampinglike component of spin-orbit torque that is distinct from any intrinsic contribution or those that arise from particular spin relaxation mechanisms. We discuss the effects of proximity-induced magnetism and insertion of an additional layer and provide formulas for in-plane current, which is induced by a perpendicular bias, anisotropic magnetoresistance, and spin memory loss in the same formalism.

I. INTRODUCTION

Broken inversion symmetry in magnetic multilayers allows for physics that is forbidden in symmetric systems, enriching the range of their physical properties and their relevance to spintronic device applications. Spin-orbit coupling combined with inversion symmetry breaking is a core ingredient of emergent phenomena, such as the intrinsic spin Hall effect [1–6], spin-orbit torques [7–17], Dzyaloshinskii-Moriya interactions [18–24], chiral spin motive forces [25, 26], perpendicular magnetic anisotropy [27–29], and anisotropic magnetoresistance [16, 30–34]. The contributions from an interface are frequently modeled by a two-dimensional Rashba model [35] while those from bulk are modeled by incorporating the spin Hall effect [6] into a drift-diffusion formalism [36] in three dimensions. Both interface and bulk contributions have the same symmetry since they originate from equivalent symmetry breaking making it difficult to distinguish mechanisms, particularly when different mechanisms are treated by different models.

Recent theoretical studies generalize the two-dimensional Rashba model in order to take into account three-dimensional transport of electrons near an interface. The two-dimensional Rashba model assumes electrons near the interface behave like a two-dimensional electron gas, thus allows only for in-plane electronic transport. Haney et al. [37] generalize this model to three-dimensions by including a delta-function-like Rashba interaction at the interface and compute interfacial contributions to in-plane-current-driven spin-orbit torques. They show that some results are qualitatively different from those of the two-dimensional model. Chen and Zhang [38] treat spin pumping with this model using a Green function approach. Studies of spin-orbit torques [39] and anisotropic magnetoresistance [40] in magnetic tunnel junctions under perpendicular bias give contributions that are at least second order in the spin-orbit coupling strength due to in-plane symmetry. Refs. [28] and [33] calculate respectively magnetic anisotropy and anisotropic magnetoresistance from the three-dimensional Rashba model in particular contexts. Refs. [41] and [42] incorporate interfacial spin-orbit coupling effects into the drift-diffusion formalism by modifying the boundary conditions. Doing so treats both interfacial and bulk spin-orbit coupling in a unified picture. Ref. [43] reports the solution of the drift-diffusion equation in the non-magnetic layer to capture the spin Hall effect coupled to a quantum mechanical solution in the ferromagnetic layer to capture the effects of interfacial spin-orbit coupling.

The results of each of these theories are model specific. Studying physical consequences for a variety of systems requires recomputing them for each system, such as metallic ferromagnets in contact with heavy metals, those with insulating ferromagnets, and topological insulators in contact with a magnetic layer. Even for a single system, a work function difference between the two layers forming the interface and possible existence of proximity-induced magnetism [44] at the interface may complicate the analysis. General analytic expressions that are applicable for a variety of interfaces would make it easier to understand trends within systems and differences between systems.

In this paper, we develop analytic expressions for interface contributions to current-induced spin-orbit torques by treating the interfacial spin-orbit coupling as a perturbation. The form of the analytic expression is independent of the details of the interface [Eq. (16)], written in terms of the scattering amplitudes of the interface. All details unrelated to spin-orbit coupling are captured by those scattering amplitudes, similarly to magnetoelectric circuit theory [45, 46]. This approach allows for the computation of spin-orbit torques either by computing scattering amplitudes for a given interface or using the scattering amplitudes as fitting parameters. It is possible to compute the scattering amplitudes through first-principles calculations or by solving the Schrödinger equation for toy models. Adopting the latter approach allows us to compute spin-orbit torques for various types of interfaces. We use the same formalism to find expressions for in-plane current, which is induced by perpendicular bias (like inverse spin Hall effect [47–49]), anisotropic magnetoresistance (like spin Hall magnetoresistance [50–55]), and spin memory loss [56] in terms of scattering amplitudes. These are presented in Appendix A.

The three-dimensional model for interfacial spin-orbit coupling reveals effects which are absent in the two-dimensional electron gas model. In the two-dimensional model, Rashba spin-orbit coupling generates mostly fieldlike component of spin-orbit torque [11, 12], while the dampinglike component becomes noticeable only when one considers an extremely resistive [13–16] system or a non-quadratic dispersion [17]. In contrast, the three-dimensional model of interfacial spin-orbit coupling reveals that in metallic magnetic bilayers a current flowing in the normal metal generates fieldlike and dampinglike components of spin-orbit torque of the same order of magnitude, and in some parameter regimes the dampinglike component can even be larger than the fieldlike component. The dampinglike contribution that we obtain here is distinct from those due to previously suggested mechanisms. For instance, an intrinsic mechanism is independent of the scattering time and vanishes for a quadratic dispersion [4, 5], while our result is proportional to the scattering time (thus the conductivity) and survives even for a quadratic dispersion. A detailed discussion of the distinctions is presented in Sec. VI A.

Another result is a generalization of previous approaches to systems with different-Fermi-surfaces, for example, a finite exchange interaction. Previous theories [33, 37, 41, 42], assume that all band structures are the same so that the wave vectors in the normal metal and the ferromagnet are identical, significantly simplifying the computation. However, even in the simplest model of bulk ferromagnetism, the exchange splitting Jσ · m introduces three different wave vectors; one defined in the normal metal and one each for the majority and minority bands in the ferromagnet. In this work, we carefully take into account the different Fermi surfaces and all the resulting evanescent modes, and demonstrate that proper treatment of the evanescent modes is crucial for accurate calculation of spin-orbit torques. Indeed, they can yield significant contributions since the amplitudes of reflected states are large at the interface and their velocities are slow where the energy is close to the barrier. This makes the interaction time for these electrons quite long so they can be more strongly affected by interfacial fields. We indeed demonstrate a significant contribution to spin-orbit torque from the evanescent modes with a toy model [See Fig. 4, Eq. (21), and related discussions]. In the previous theories, some of effects like the anisotropic magnetoresistance [33] originate from a difference between the relaxation times in majority and minority electrons in the ferromagnet, but we show that existence of the bulk magnetism by itself can also cause such effects.

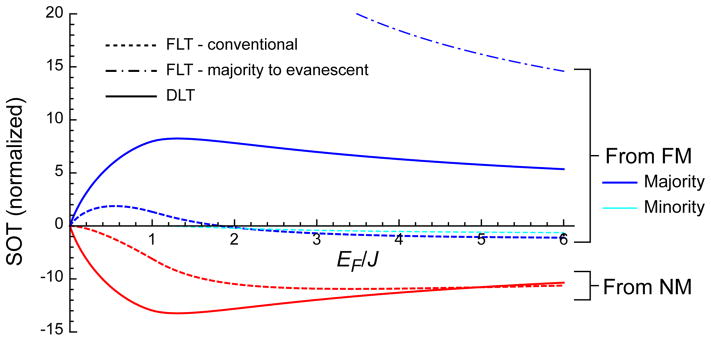
FIG. 4.

Spin-orbit torque (SOT) to the bulk magnetism in magnetic bilayer described by Eq. (17). The red lines are contributions from a current flowing in the normal metal, and the other lines are those from a current flowing in the ferromagnet. Among these, the blue lines are contributions from majority electrons flow and the cyan line represents contributions from minority electron flow. The dashed and dot-dashed lines are the real part, thus representing fieldlike torque (FLT), while the solid lines are the imaginary part, thus representing dampinglike torque (DLT). The dot-dashed line represents the third term in $Re[{\mathcal{T}}_R^{\mathrm{F}}]$ in Eq. (20), which originates from a nonzero value of J and transitions to resulting the evanescent states. The spin-orbit torque from electrons in normal metal, majority electrons, and minority electrons are divided by $2h_R\hslash e{E}_x\tau A{k}_F^3/\pi m_e,2h_R\hslash e{E}_x{\tau }^{\uparrow }A{k}_F^3/\pi m_e$, and $2h_R\hslash e{E}_x{\tau }^{\downarrow }A{k}_F^3/\pi m_e$, respectively, and the results are dimensionless. Thus, the total spin-orbit torque is given by the weighted sum of all the contributions with the weighting factors (τ, τ^↑, τ^↓).

We compute the current-induced contribution to the spin-orbit torque, in distinction to the electric-field-induced contribution. The former is proportional to the scattering time, thus is extrinsic. A recent paper [17] reports the existence of intrinsic spin-orbit torque from the Berry phase, which is perpendicular to the extrinsic component. This contribution can be an explanation for dampinglike spin-orbit torque for junctions with a ferromagnetic insulator or topological insulator (See Sec. V D). We leave the calculation of intrinsic spin-orbit torque (induced by the Berry phase) in the same formalism for future work.

This paper is organized as follows. In Sec. II, we summarize the core results. In Sec. III, we develop a general perturbation theory of scattering matrices. First we define scattering matrices (Sec. III A) and calculate them (Sec. III B). Then we derive expressions for modified scattering matrices due to interfacial spin-orbit coupling in a perturbative regime (Sec. III C). The resulting scattering matrices allow us to write down electronic eigenstates. In Sec. IV, we derive an expression for spin-orbit torque from these eigenstates, by calculating the angular momentum transfer (spin current) to the ferromagnet. We assume that an in-plane electrical current is applied along the x direction. Since the expression is written in terms of unperturbed scattering matrices, it allows us to compute spin-orbit torque by calculating unperturbed scattering matrices for a given interface. Therefore, in Sec. V, we apply our theory to various types of interfaces and various situations, such as magnetic bilayers with bulk magnetism, those with interface magnetism, a normal metal in contact with a ferromagnetic insulator, and topological insulator in contact with a metallic ferromagnet. Calculating unperturbed scattering matrices is straightforward by solving the one-dimensional Schrödinger equation. We plot fieldlike and dampinglike components of spin-orbit torque with varying parameters and discuss the results in each subsection. In Sec. VI, we make some general remarks on our theory. We compare our theory with the two-dimensional Rashba model. We also discuss how our result can be generalized when multilayer structures are considered. We discuss how proximity-induced magnetization can be considered in our theory. In Sec. VII, we summarize our results. Appendices include supplementary calculations that are not necessary for the main results.

II. SUMMARY OF THE RESULTS

The purpose of this section is to summarize the behavior of the spin-orbit torques presented in Sec. V A to Sec. V D, before showing the general perturbation theory. Here we focus on the existence and relative magnitudes of spin-orbit torques generated by interfacial spin-orbit coupling saving detailed discussions for later sections. The systems under consideration are normal metal/ferromagnetic metal junctions, normal metal/ferromagnetic insulator junctions, and topological insulator/ferromagnet junctions. Throughout this paper, we refer to these as magnetic bilayers, ferromagnetic insulators, and topological insulators in short, respectively. We describe the results below and summarize them in Table I.

TABLE I.

Behaviors of in-plane-current-induced spin-orbit torques for various systems. FLT and DLT refer to fieldlike torque and dampinglike torque respectively, and ✓(×) refers to their existence (absence). Our analytic calculation allows for the separation of contributions from a pure charge current (j_N) and a pure spin current (j_F) separately. A magnetic bilayer is a normal metal/ferromagnetic metal junction. Bulk magnetism originates from an exchange splitting in the ferromagnetic bulk and interface magnetism originates from a spin-dependent scattering at the interface. A ferromagnetic (topological) insulator is assumed to be attached to a normal (ferromagnetic) metal where the applied current flows. For all cases, interfacial spin-orbit coupling is present right at the interface. We present the behavior of the two-dimensional (2D) Rashba model as a reference. Since the intrinsic contribution to spin-orbit torque is not taken into account in our theory, the dampinglike component in 2D Rashba model is not considered here.

System	Source	FLT	DLT	Magnitude
2D Rashba model	jF	✓	×
Magnetic bilayer (bulk magnetism)	jN	✓	✓	FLT ≲ DLT
	jF	✓	✓	FLT ≫ DLT
Magnetic bilayer (interface magnetism)	jN	✓	✓	FLT ≳ DLT
	jF	✓	✓	FLT ≳ DLT
Ferromagnetic insulator	jN	✓	×
Topological insulator	jF	✓	×

When an in-plane current is applied to a bilayer junction, two components of spin-orbit torque can act on the magnetization m. Both are perpendicular to magnetization. When a torque is odd (even) in m, it is called fieldlike (dampinglike) [57]. For instance, for a constant vector y, m × y is fieldlike and m × (y × m) is dampinglike.¹ The names can be understood by their behaviors under time reversal: Fieldlike contributions are conservative while dampinglike contributions are dissipative. In fact, a dampinglike spin torque can act as an anti-dampinglike source, thus the terminology ‘dampinglike’ does not mean an energy loss but originates from irreversibility.

In contrast to the two-dimensional Rashba model, we show that magnetic bilayers show both fieldlike and dampinglike components even without the Berry phase [17] contribution and a spin relaxation mechanism [13–16]. The relative magnitude depends on the details of the system. We first consider a magnetic bilayer where the magnetism is dominated by an exchange splitting in the ferromagnetic bulk (not at the interface). In experiments, people usually apply a current in the normal metal side. We show that a current flowing in the normal metal (j_N) generates dampinglike and fieldlike spin-orbit torques that are of the same order of magnitude. The current also flows in the ferromagnet (j_F), generating a large field-like spin-orbit torque that can be the dominant contribution. Therefore, if j_N ≫ j_F, the dampinglike and fieldlike components are on the same order of magnitude. But if j_N ≈ j_F, the fieldlike component tends to dominate.

If magnetism at the interface plays a more important role than the bulk magnetism considered above, both components have similar orders of magnitude. As for the bulk magnetism case, there are two sources of spin-orbit torque, j_N and j_F. We demonstrate in Sec. V B that the dampinglike contributions are mostly subtractive and the fieldlike contributions are mostly additive. Therefore, the current in the ferromagnet tends not to change the total fieldlike spin-orbit torque, but tends to reduce the dampinglike spin-orbit torque.

For systems with a ferromagnetic insulator or a topological insulator, the dampinglike component is found to be absent.

III. PERTURBATION OF SCATTERING AMPLITUDES

A. Definition of the scattering matrices

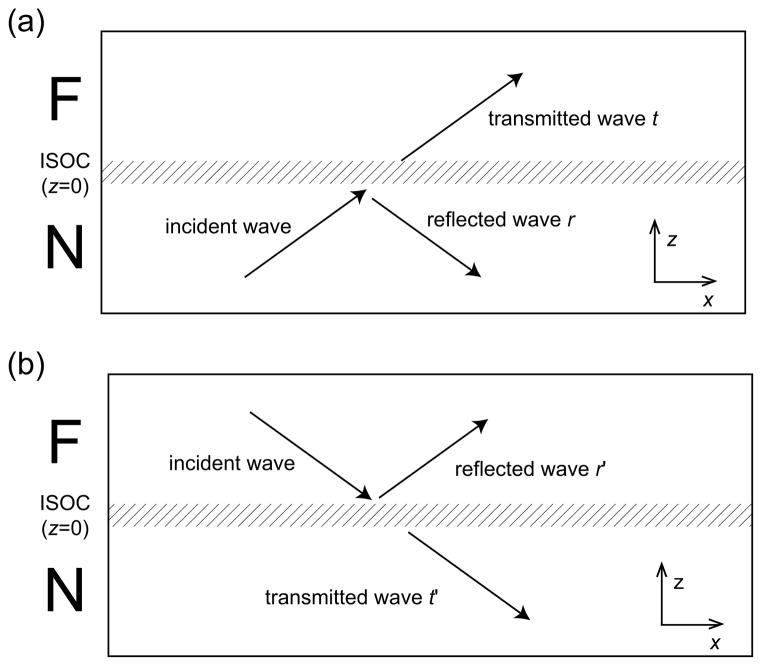
We consider a nonmagnet (z < 0)/ferromagnet (z > 0) interface at z = 0 where z is the interface normal direction. Either materials could be insulating. We define scattering amplitudes by Fig. 1. The scattering of electronic states incident from the normal metal define reflection and transmission amplitudes r and t. Those incident from the ferromagnet define r′ and t′. In the ferromagnet, there is an exchange splitting energy J > 0. At the interface, we assume an interface potential H_I = (ħ²/2m_e)κ̂δ(z), where κ̂ is a 2 × 2 matrix in spin space. The delta-function-like potential describes physics on a length scale shorter than the mean free path. The effects of lattice mismatch, interface magnetism [44], and interfacial spin-orbit coupling are examples. In our perturbative approach, we first ignore any interfacial spin-orbit coupling. After solving a boundary matching problem of the Schrödinger equation at z = 0, we obtain the scattering matrices in terms of the interface potential κ̂ [Eq. (6)]. We then add a Rashba-type interfacial spin-orbit coupling potential Δκ̂ = h_Rσ̂ · (k × z) to obtain a perturbative expansion of the scattering matrices, such as ${\widehat{r}}_{\mathbf{k}}={\widehat{r}}_{\mathbf{k}}^0+\mathrm{\Delta }{\widehat{r}}_{\mathbf{k}}$, where r̂_k is the 2 × 2 reflection matrix in spin space² for momentum k, ${\widehat{r}}_{\mathbf{k}}^0$ is the unperturbed reflection matrix (without interfacial spin-orbit coupling), and Δr̂_k is its correction due to interfacial spin-orbit coupling [Eq. (10)]. Then, the electronic eigenstates are computable analytically and play a crucial role in computing spin-orbit torque in Sec. IV.

FIG. 1.

Scattering matrices at the interface of a nonmagnet(z < 0, denoted by N)/ferromagnet (z > 0, denoted by F) structure. The interface is at z = 0. r and t refer to reflection and transmission matrices when the electronic state is incident from the normal metal layer. r′ and t′ are those when the electronic state is incident from the ferromagnetic layer. When the transverse mode is conserved, these are 2 × 2 matrices in spin space. In our model, the interfacial spin-orbit coupling (ISOC) is present only at z = 0 being delta-function-like, although the thickness of the region drawn with finite thickness for illustration.

We now mathematically write down electronic states as definitions of scattering amplitudes illustrated in Fig. 1. The wave incident from the nonmagnet having the momentum k = (k_x, k_y, k_z) and spin σ is $(1/\sqrt{V})e^{i\mathbf{k}·\mathbf{r}}{\xi }_{\sigma }$ where V is the volume of the system, r = (x, y, z) is the position vector, and ξ_σ is the spinor for the spin σ state. The spin quantization axis we use here is the direction of magnetization in the ferromagnet and σ = ±1 corresponds to the minority/majority bands (with the higher/lower exchange energy). When the plane wave hits the interface at z = 0, it scatters out. For simplicity, we assume translational symmetry over the xy plane. Then, the transverse momentum is conserved, thus the scattering matrices are diagonal in transverse modes. The reflected wave has the momentum k̄ = (k_x, k_y, −k_z). Here we denote the reflection amplitude $r_{\mathbf{k}}^{{\sigma }^{\prime }\sigma }$ by the amplitude of the scattering process (k,σ)_N → (k̄, σ′)_N, where the Roman subscript/superscript N refers to the nonmagnet. The scattering state in the nonmagnet is

$${\psi }_{\mathbf{k}\sigma }^{\mathrm{N}}(z<0)=\frac{1}{\sqrt{V}}{e}^{i\mathbf{k}·\mathbf{r}}{\xi }_{\sigma }+\frac{1}{\sqrt{V}}{e}^{i\overline{\mathbf{k}}·\mathbf{r}}\sum _{{\sigma }^{\prime }}{r}_{\mathbf{k}}^{{\sigma }^{\prime }\sigma }{\xi }_{{\sigma }^{\prime }}.$$ (1a)

The transmission matrix is defined in a similar way. Given the energy of the electronic state, the momentum k_z in the ferromagnet is different from that in the nonmagnet due to the exchange splitting J. We denote $k_z^{\sigma }$ for the corresponding momentum for spin σ band. For instance, if the kinetic energy is given by ħ²|k|²/2m_e and the exchange interaction is given by Jσ̂ · m where m is the unit vector along the magnetization, ${\hslash }^2{k}_z^2/2m_e={\hslash }^2{(k_z^{+})}^2/2m_e+J={\hslash }^2{(k_z^{-})}^2/2m_e-J$ defines the relation between k_z and $k_z^{\sigma }$. Then we denote the transmission amplitude $t_{\mathbf{k}}^{{\sigma }^{\prime }\sigma }$ by the amplitude of the scattering process (k, σ)_N → (k^σ′, σ′)_F, where the roman subscript/superscript F refers to the ferromagnet. Therefore, the scattering state in the ferromagnet is

$${\psi }_{\mathbf{k}\sigma }^{\mathrm{N}}(z>0)=\frac{1}{\sqrt{V}}\sum _{{\sigma }^{\prime }}\sqrt{\frac{\mid k_z\mid }{\mid k_z^{{\sigma }^{\prime }}\mid }}{e}^{i{\mathbf{k}}^{{\sigma }^{\prime }}·\mathbf{r}}{t}_{\mathbf{k}}^{{\sigma }^{\prime }\sigma }{\xi }_{{\sigma }^{\prime }}.$$ (1b)

Here the prefactor $\sqrt{\mid k_z\mid /\mid k_z^{{\sigma }^{\prime }}\mid }$ is introduced, in order to make the conservation of electrical charge equivalent to the unitarity of the scattering amplitudes [58]. The absolute value is introduced for cases where $k_z^{{\sigma }^{\prime }}$ is imaginary so that the transmitted wave function is evanescent. Since evanescent waves do not contribute to unitarity, this convention is arbitrary, but the choice should not affect the final expressions for physical quantities.

Now we introduce a compact matrix notation. Since the scattering amplitudes have two indices (σ′, σ), they are 2 × 2 matrices in spin space. We define the matrix ${\widehat{r}}_{\mathbf{k}}={\sum }_{{\sigma }^{\prime }\sigma }{\xi }_{{\sigma }^{\prime }}{r}_{\mathbf{k}}^{{\sigma }^{\prime }\sigma }{\xi }_{\sigma }^{†}$, and similarly t̂_k with $t_{\mathbf{k}}^{{\sigma }^{\prime }\sigma }$. The wave functions in this notation are

$${\psi }_{\mathbf{k}\sigma }^{\mathrm{N}}(z<0)=\frac{e^{i{k}_{x}x+i{k}_{y}y}}{\sqrt{V}}(e^{i{k}_{z}z}{\widehat{1}}_{\mathbf{k}}+e^{-i{k}_{z}z}{\widehat{r}}_{\mathbf{k}}){\xi }_{\sigma },$$ (2a)

$${\psi }_{\mathbf{k}\sigma }^{\mathrm{N}}(z>0)=\frac{e^{i{k}_{x}x+i{k}_{y}y}}{\sqrt{V}}\sqrt{{\mid k_z\Vert {\widehat{K}}_z\mid }^{-1}}{e}^{i{\widehat{K}}_{z}z}{\widehat{t}}_{\mathbf{k}}{\xi }_{\sigma },$$ (2b)

where ${\widehat{K}}_z=k_z^{+}{u}_{+}+k_z^{-}{u}_{-}$ is a diagonal 2 × 2 matrix consisting of momenta in the ferromagnet for each spin band and $u_{\sigma }={\xi }_{\sigma }{\xi }_{\sigma }^{†}$ is the projection matrix to the spin σ band. Equation (2) defines the electronic state depicted in Fig. 1(a). 1̂_k is essentially the identity matrix, but slightly different, as we explain in the next paragraph. In a similar way, the scattering states derived from waves incident from the ferromagnet define ${\widehat{r}}_{\mathbf{k}}^{\prime }$ and ${\widehat{t}}_{\mathbf{k}}^{\prime }$ matrices in Fig. 1(b).

$${\psi }_{\mathbf{k}\sigma }^{\mathrm{F}}(z<0)=\frac{e^{i{k}_{x}x+i{k}_{y}y}}{\sqrt{V}}\sqrt{{\mid k_z\mid }^{-1}}{e}^{-i{k}_{z}z}{\widehat{t}}_{\mathbf{k}}^{\prime }\sqrt{\mid {\widehat{K}}_z\mid }{\xi }_{\sigma },$$ (3a)

$${\psi }_{\mathbf{k}\sigma }^{\mathrm{F}}(z>0)=\frac{e^{i{k}_{x}x+i{k}_{y}y}}{\sqrt{V}}\sqrt{{\mid {\widehat{K}}_z\mid }^{-1}}(e^{-i{\widehat{K}}_{z}z}{\widehat{\mathrm{l}}}_{\mathbf{k}}^{\prime }+e^{i{\widehat{K}}_{z}z}{\widehat{r}}_{\mathbf{k}}^{\prime })\sqrt{\mid {\widehat{K}}_z\mid }{\xi }_{\sigma }.$$ (3b)

The matrices 1̂_k and ${\widehat{1}}_{\mathbf{l}}^{\prime }$ are the projection matrices to the Hilbert space. These matrices are introduced to prevent un-physical states (not in the Hilbert space) from contributing to any physical quantities that we compute. 1̂_k and ${\widehat{1}}_{\mathbf{k}}^{\prime }$ are the identity matrices (the scalar 1) in the Hilbert space, but are zero, out of the Hilbert space. An electronic state is out of the Hilbert space when the incident wave is evanescent. For instance, an electronic state written as Eq. (2a) with an imaginary k_z is not in the Hilbert space in the scattering theory, so it should not contribute to any physical quantity. Thus, we define 1̂_k by the following projection operator:

$${\widehat{1}}_{\mathbf{k}}=\{\begin{array}{ll}1\hfill & \text{if}{k}_z\text{is}\text{real},\hfill \\ 0\hfill & \text{if}{k}_z\text{is}\text{imaginary.}\hfill \end{array}$$ (4a)

In this paper, we define r̂_k = t̂_k = 0 if the electronic state is out of the Hilbert space. Then, one can see that r̂_k = r̂_k1̂_k and t̂_k = t̂_k1̂_k. In a similar way, ${\widehat{1}}_{\mathbf{k}}^{\prime }$ is defined by,

$${\widehat{1}}_{\mathbf{k}}^{\prime }=\{\begin{array}{ll}1\hfill & \text{if}\text{both}{k}_z^{\pm }\text{are}\text{real},\hfill \\ u_{-}\hfill & \text{if}\text{only}{k}_z^{-}\text{is}\text{real},\hfill \\ 0\hfill & \text{if}\text{both}{k}_z^{\pm }\text{are}\text{imaginary.}\hfill \end{array}$$ (4b)

${\widehat{1}}_{\mathbf{k}}^{\prime }=1$ if both majority and minority bands are propagating, ${\widehat{1}}_{\mathbf{k}}^{\prime }=u_{-}$ (projection to the majority band) if only majority band is propagating, and ${\widehat{1}}_{\mathbf{k}}^{\prime }=0$ if both bands are evanescent. Similarly, ${\widehat{r}}_{\mathbf{k}}^{\prime }={\widehat{r}}_{\mathbf{k}}^{\prime }{\widehat{1}}_{\mathbf{k}}^{\prime }$ and ${\widehat{t}}_{\mathbf{k}}^{\prime }={\widehat{t}}_{\mathbf{k}}^{\prime }{\widehat{1}}_{\mathbf{k}}^{\prime }$.

Defining the projection matrices is crucial when we consider the continuity of the wave functions at z = 0. If the Hilbert space is not properly considered, matching Eqs. (2a) and (2b) at z = 0 gives $1+{\widehat{r}}_{\mathbf{k}}=\sqrt{{\mid k_z\Vert {\widehat{K}}_z\mid }^{-1}}{\widehat{t}}_{\mathbf{k}}$. However, it does not hold when k_z is imaginary so r̂_k = t̂_k = 0. When we project this equation to the Hilbert space by multiplying 1̂_k, ${\widehat{1}}_{\mathbf{k}}+{\widehat{r}}_{\mathbf{k}}=\sqrt{{\mid k_z\Vert {\widehat{K}}_z\mid }^{-1}}{\widehat{t}}_{\mathbf{k}}$ is the correct continuity condition. In a similar way, the continuity at z = 0 of Eqs. (3a) and (3b) is given by ${\widehat{1}}_{\mathbf{k}}^{\prime }+{\widehat{r}}_{\mathbf{k}}^{\prime }=\sqrt{{\mid {\widehat{K}}_z\Vert k_z\mid }^{-1}}{\widehat{t}}_{\mathbf{k}}^{\prime }$. Therefore, with the projection matrices, we can write down a single equation which holds regardless of the reality of the perpendicular momenta.

Another place where the projection matrices are crucial is the unitarity relation of the scattering amplitudes. It holds only for physical states in the Hilbert space. Therefore, the unitarity relation in our notation can be subtle. We derive the unitarity relation for the scattering amplitudes in Appendix B.

B. Relation to the interface potential and introduction of extended scattering matrices

In this section, we derive explicit expressions for scattering matrices for a given interface potential. This allows defining extended scattering matrices (r̂_k,ex, t̂_k,ex, ${\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime },{\widehat{t}}_{\mathbf{k},\text{ex}}^{\prime }$) which even satisfy the continuity relation without projection. The extended scattering matrices remove the singularity of the scattering matrices,³ which is a main obstacle of our perturbation theory.

The explicit expressions for the scattering matrices are given by the interface potential. We start from the following interface potential at z = 0

$$H_I=\frac{{\hslash }^2}{2m_e}\widehat{\kappa }\delta (z),$$ (5)

where κ̂ is a 2×2 matrix in spin space and has the dimension of the inverse of length. Solving the Schrödinger equation gives the scattering matrices in terms of κ̂. The boundary condition for the delta-function-like potential is given by the derivative mismatching condition, κ̂ψ_z=0 = ∂_zψ_z=+0−∂_zψ_z=−0. After some algebra, we obtain the scattering matrices as

$${\widehat{t}}_{\mathbf{k},\text{ex}}=2i{k}_z\sqrt{{\mid {\widehat{K}}_z\Vert k_z\mid }^{-1}}{(i{\widehat{K}}_z+i{k}_z-\widehat{\kappa })}^{-1},$$ (6a)

$${\widehat{t}}_{\mathbf{k},\text{ex}}^{\prime }={(i{\widehat{K}}_z+i{k}_z-\widehat{\kappa })}^{-1}2i{\widehat{K}}_z\sqrt{{\mid k_z\Vert {\widehat{K}}_z\mid }^{-1}},$$ (6b)

$${\widehat{r}}_{\mathbf{k},\text{ex}}={(i{\widehat{K}}_z+i{k}_z-\widehat{\kappa })}^{-1}(i{k}_z-i{\widehat{K}}_z+\widehat{\kappa }),$$ (6c)

$${\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime }=\sqrt{\mid {\widehat{K}}_z\mid }{(i{\widehat{K}}_z+i{k}_z-\widehat{\kappa })}^{-1}(i{\widehat{K}}_z-i{k}_z+\widehat{\kappa })\sqrt{{\mid {\widehat{K}}_z\mid }^{-1}},$$ (6d)

where we call the matrices with the subscript ‘ex’ the extended matrices, discuss their meaning below. The expressions in Eq. (6) are nonzero even when the incident wave is evanescent. (For instance, r̂_k|_kz=iqz ≠ 0.) In our convention, the scattering matrices are zero if the electronic state is evanescent because the scattering matrices capture the asymptotic behavior of the scattering process. Therefore, the scattering matrices are obtained from the extended matrices by projecting the latter to the Hilbert space.

$$\begin{gathered} {\widehat{r}}_{\mathbf{k}}={\widehat{r}}_{\mathbf{k},\text{ex}}{\widehat{1}}_{\mathbf{k}},{\widehat{t}}_{\mathbf{k}}={\widehat{t}}_{\mathbf{k},\text{ex}}{\widehat{1}}_{\mathbf{k}}, \\ {\widehat{r}}_{\mathbf{k}}^{\prime }={\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime }{\widehat{1}}_{\mathbf{k}}^{\prime },{\widehat{t}}_{\mathbf{k}}^{\prime }={\widehat{t}}_{\mathbf{k},\text{ex}}^{\prime }{\widehat{1}}_{\mathbf{k}}^{\prime }. \end{gathered}$$ (7)

Now the expressions satisfy r̂_k = r̂_k1̂_k and similar relations for the others.

The introduction of the extended matrices is purely mathematical. As far as physical quantities are concerned, the parts of the extended matrices out of the Hilbert space are completely arbitrary and cannot affect any physical quantity. In this paper, there are three reasons why we choose the convention in Eq. (6). First, it provides a natural way to write down analytic expressions valid for any momenta (even imaginary). Equation (6) is the result from boundary matching at z = 0 of the Schrödinger equation whether or not all wave vectors are real. Second, it satisfies the generalized continuity relations $1+{\widehat{r}}_{\mathbf{k},\text{ex}}=\sqrt{{\mid k_z\Vert {\widehat{K}}_z\mid }^{-1}}{\widehat{t}}_{\mathbf{k},\text{ex}}$ and $1+{\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime }=\sqrt{{\mid {\widehat{K}}_z\Vert k_z\mid }^{-1}}{\widehat{t}}_{\mathbf{k},\text{ex}}^{\prime }$ even out of the Hilbert space. This supports the idea that Eq. (6) is the most natural way to define the extended matrices. Third and most importantly, the extended matrices have well-defined inverses. The singularity of 1̂_k and ${\widehat{1}}_{\mathbf{k}}^{\prime }$ for some momenta complicates the development of a perturbation theory, and the extended matrices give one way to resolve this difficulty.

Three remarks are in order. First, although we claim that Eq. (6) is the most natural form to extend out of the Hilbert space, this form depends on the normalization convention in Eqs. (2) and (3) for evanescent states. But we again emphasize that the mathematical convention cannot affect calculation of physical quantities. Second, the four matrices in Eq. (6) are not independent since they are defined by a single matrix κ̂. There are three relationships between the matrices. Two of them are the generalized continuity relations presented above. Another relationship that is derived from Eq. (6) is $(1+{\widehat{r}}_{\mathbf{k},\text{ex}})k_z^{-1}=\sqrt{{\mid {\widehat{K}}_z\mid }^{-1}}(1+{\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime })\sqrt{\mid {\widehat{K}}_z\mid }{\widehat{K}}_z^{-1}$. Third, if κ̂ is a spin-conserving Hamiltonian, κ̂ and K̂_z commute with each other. For instance, $\sqrt{{\mid \widehat{K}\mid }_z}$ and $\sqrt{{\mid \widehat{K}\mid }_z^{-1}}$ in ${\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime }$ cancel so that the expression becomes simpler. The last constraint becomes simpler $(1+{\widehat{r}}_{\mathbf{k},\text{ex}})k_z^{-1}=(1+{\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime }){\widehat{K}}_z^{-1}$. These features are useful for simplifying unperturbed contributions, which we consider spin conserving in the next section.

C. Perturbation of scattering matrices

To focus on the effects of interfacial spin-orbit coupling, we use a perturbative approach. Let the interface potential be

$$\widehat{\kappa }={\widehat{\kappa }}_0+h_R\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z}),$$ (8)

where the first term is the unperturbed interface potential and the second term is the interface Rashba interaction only present at z = 0. Here σ̂ is the vector of the spin Pauli matrices, z is the unit vector along the interface normal direction z, and h_R is the dimensionless Rashba parameter. We treat h_R perturbatively. Ref. [37] shows that the numerically computed spin-orbit torques are mostly linear in h_R, supporting this perturbative approach. We also assume that κ̂₀ is spin conserving in the sense that it is diagonal in spin space. Therefore, [κ̂₀, u_σ] = [κ̂₀, K̂_z] = 0. Examples of spin-conserving potentials are spin-independent barriers and interface exchange potentials in the form of u_mσ̂ · m. One interpretation of interface magnetism (u_m) is proximity-induced magnetism [44], which is discussed in Sec. VI C in more detail. The success of the conventional magnetoelectric circuit theory [45, 46] implies that assuming a spin conserving interface potential is reasonable.

To develop a perturbation theory, we denote unperturbed scattering matrices by a superscript 0. For instance from Eq. (6), ${\widehat{t}}_{\mathbf{k},\text{ex}}^0=2i{k}_z\sqrt{{\mid {\widehat{K}}_z\Vert k_z\mid }^{-1}}{(i{\widehat{K}}_z+i{k}_z-{\widehat{\kappa }}_0)}^{-1}$. It is straightforward after some algebra to show that the exact scattering matrix in the presence of h_R is related to the unperturbed scattering matrix as follows; ${({\widehat{t}}_{\mathbf{k},\text{ex}}^0)}^{-1}{\widehat{t}}_{\mathbf{k},\text{ex}}=1+(h_R/2i{k}_z)\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z})(1+{\widehat{r}}_{\mathbf{k},\text{ex}})$.⁴ By multiplying ${\widehat{t}}_{\mathbf{k},\text{ex}}^0$ on both sides,

$${\widehat{t}}_{\mathbf{k},\text{ex}}={\widehat{t}}_{\mathbf{k},\text{ex}}^0+\frac{h_R}{2i{k}_z}{\widehat{t}}_{\mathbf{k},\text{ex}}^0\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z})\sqrt{{\mid k_z\Vert {\widehat{K}}_z\mid }^{-1}}{\widehat{t}}_{\mathbf{k},\text{ex}},$$ (9)

which allows a perturbative expansion with respect to h_R in an iterative way. For instance, replacing t̂_k,ex in the right-hand side by ${\widehat{t}}_{\mathbf{k},\text{ex}}^0$ gives the first order perturbation result for t̂_k,ex. From t̂_k,ex, the three constraints mentioned in the previous section give the rest of the extended matrices immediately. Then, projecting to the Hilbert space by multiplying by 1̂_k and ${\widehat{1}}_{\mathbf{k}}^{\prime }$ gives our central result for the scattering matrices.

$${\widehat{t}}_{\mathbf{k}}={\widehat{t}}_{\mathbf{k}}^0+\frac{h_R}{2i{k}_z}{\widehat{t}}_{\mathbf{k},\text{ex}}^0\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z})({\widehat{1}}_{\mathbf{k}}+{\widehat{r}}_{\mathbf{k}}^0),$$ (10a)

$${\widehat{t}}_{\mathbf{k}}^{\prime }={\widehat{t}}_{\mathbf{k}}^{\prime 0}+\frac{h_R}{2i{k}_z}(1+{\widehat{r}}_{\mathbf{k},\text{ex}}^0)\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z}){\widehat{t}}_{\mathbf{k}}^{\prime 0},$$ (10b)

$${\widehat{r}}_{\mathbf{k}}={\widehat{r}}_{\mathbf{k}}^0+\frac{h_R}{2i{k}_z}(1+{\widehat{r}}_{\mathbf{k},\text{ex}}^0)\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z})({\widehat{1}}_{\mathbf{k}}+{\widehat{r}}_{\mathbf{k}}^0),$$ (10c)

$${\widehat{r}}_{\mathbf{k}}^{\prime }={\widehat{r}}_{\mathbf{k}}^{\prime 0}+\frac{h_R}{2i{k}_z}{\widehat{t}}_{\mathbf{k},\text{ex}}^0\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z}){\widehat{t}}_{\mathbf{k}}^{\prime 0}.$$ (10d)

With Eq. (10) in combination with Eqs. (2) and (3), one can write down the electronic wave functions for nonzero h_R. Then, physical quantities can be written in terms of unperturbed scattering matrices, as we present in the next section and Appendix A. These expressions in terms of reflection and transmission coefficients can be used for general interfaces with spin-nonconserving Hamiltonians of the Rashba type. ⁵ By computing the unperturbed scattering matrices with first-principles calculations or toy models, our theory enables computing interfacial spin-orbit coupling contributions for various types of interfaces. This approach is similar to the way that one computes the spin mixing conductance [45, 46] in magnetoelectric circuit theory.

Three remarks are in order. First, one may notice that Eq. (10) includes 1/2ik_z factors only, but there is no 1/2iK̂_z factor in ${\widehat{r}}_{\mathbf{k}}^{\prime }$ and ${\widehat{t}}_{\mathbf{k}}^{\prime }$. The absence of 1/2iK̂_z seems asymmetric since we consider all the waves incident from the normal metal and the ferromagnet. This is simply because we used the constraint ${(1+{\widehat{r}}_{\mathbf{k},\text{ex}})}^0{k}_z^{-1}={(1+{\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime })}^0{\widehat{K}}_z^{-1}$ to convert all 1/2iK̂_z to 1/2ik_z for simplicity. Therefore, our result does not break the symmetry in the expressions. Second, in the presence of interfacial spin-orbit coupling, a bound state that does not correspond to any unperturbed state could arise. In Appendix C, we demonstrate that a bound state is not present in the perturbative regime that we consider here. Third, the presence of the extended matrices in Eq. (10) is purely mathematical. This is similar to the Born approximation in scattering theory. In the Born approximation, the mathematical expression of scattering states contains virtual transitions which are not allowed due to the conservation of energy. However, such a treatment allows us to calculate the scattering states in a perturbative regime. Similarly, the presence of the extended matrices does not mean a physical transition but a mathematical artifact of the perturbative approach. Physical quantities do not depends on the extended space. The relation $(1+{\widehat{r}}_{\mathbf{k},\text{ex}}^0)k_z^{-1}=(1+{\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime 0}){\widehat{K}}_z^{-1}$ is helpful for this purpose. For instance, when we need to project r̂_k,ex by ${\widehat{1}}_{\mathbf{k}}^{\prime }$ to compute a physical quantity, the relation allows expressing r̂_k,ex in terms of ${\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime }$, so the projection by ${\widehat{1}}_{\mathbf{k}}^{\prime }$ is given by the natural relation ${\widehat{r}}_{\mathbf{k},\text{ex}}^{\prime }{\widehat{1}}_{\mathbf{k}}^{\prime }={\widehat{r}}_{\mathbf{k}}^{\prime }$.

IV. EXPRESSION OF SPIN-ORBIT TORQUE

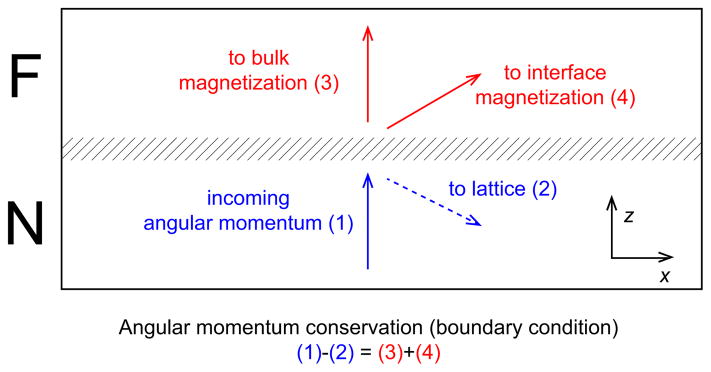
We consider a situation that an external current is applied. In the absence of spin-orbit coupling, angular momentum conservation suggests that the total angular momentum injected into the ferromagnet is equal to the spin current at the interface. However, in the presence of interfacial spin-orbit coupling, the spin current at z = +0 is not equal to the spin-orbit torque, because some of the angular momentum is transferred to the lattice. Thus, it requires a careful separation of the angular momentum flow [41, 42] (See Fig. 2).

FIG. 2.

Illustration of conservation of angular momentum at the interface. The incoming angular momentum (1) splits into three drains; to the lattice by interfacial spin-orbit coupling (2), to the bulk magnetism (3), and to the interface magnetism (4). The conservation of angular momentum implies that (1)=(2)+(3)+(4), which is captured by the boundary condition of the Schrödinger equation. Equation (16) is computed by (1)– (2), which is, by the conservation of angular momentum, (3)+(4), the total spin-orbit torque to magnetization.

To develop an expression for the torque, we first ignore magnetism at the interface and restore it later. Then, the total spin-orbit torque is computed by the spin current right at the interface in the ferromagnet, z = +0. For illustration, we first compute the spin current at z = −0 and how much angular momentum changes at the interface due to interfacial spin-orbit coupling. We compute the charge and spin current density at z = −0 by

$${\widehat{j}}_z(\mathbf{r})=-e{\text{Tr}}_{\mathbf{k}}Re[\rho \delta ({\mathbf{r}}_{\text{op}}-\mathbf{r})v_z],$$ (11)

where Re[A] = (A + A^†)/2 refers to the real part of the given matrix A, Tr_k is the partial trace over k only (the result is 2 × 2 matrix in spin space), ${\widehat{j}}_z=(j_z^e+\widehat{\mathit{\sigma }}·{\mathbf{j}}_z^s)/2,{\mathbf{j}}_z^s$ is the spin current flowing along z with the direction of the vector denoting the direction of spin, $j_z^e$ is the charge current along z, v_z = (ħ/m_ei)∂_z is the velocity operator, $\rho ={\sum }_{\mathbf{k}{\sigma }^{\prime }\sigma ,a=\mathrm{N}/\mathrm{F}}{f}_{\mathbf{k},{\sigma }^{\prime },\sigma }^{\mathrm{a}}\mid \mathbf{k}{\sigma }^{\prime };a\rangle \langle \mathbf{k}\sigma ;a\mid$; is the density matrix, $f_{\mathbf{k},{\sigma }^{\prime },\sigma }^{\mathrm{N}/\mathrm{F}}$ is the reduced density matrix for a given k, r_op is the position operator, and r is a c-number indicating the position at which the current density is evaluated. Here |kσ; N/F〉 refers to a scattering state incident from the nonmagnet (ferromagnet) that has momentum k in the nonmagnet and spin σ, that is, ${\psi }_{\mathbf{k}\sigma }^a(\mathbf{r})=\langle \mathbf{r}\mid \mathbf{k}\sigma ;a\rangle$. The current is written by ${\mathbf{j}}_z(\mathbf{r})=(-e/2){\sum }_{\mathbf{k}{\sigma }^{\prime }\sigma ,a=\mathrm{N}/\mathrm{F}}{f}_{\mathbf{k}{\sigma }^{\prime }\sigma }^a\langle \mathbf{k}\sigma ;a\mid \{v_z,\delta ({\mathbf{r}}_{\text{op}}-\mathbf{r})\}\widehat{\mathit{\sigma }}\mid \mathbf{k}{\sigma }^{\prime };a\rangle$, and similarly for the charge current. Since we know the electronic wave functions Eqs. (2a) and (3a), we can calculate this analytically. The delta function enables computing the matrix element without performing any integration. After some algebra,

$${{\widehat{j}}_z\mid }_{z=-0}=-\frac{eL}{hV}\sum _{{\mathbf{k}}_{\perp }}\int dE({\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}{\widehat{1}}_{\mathbf{k}}-{\widehat{r}}_{\mathbf{k}}{\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}{\widehat{r}}_{\mathbf{k}}^{†}-{\widehat{t}}_{\mathbf{k}}^{\prime }{\widehat{f}}_{\mathbf{k}}^{\mathrm{F}}{\widehat{t}}_{\mathbf{k}}^{\prime †}{\widehat{1}}_{\mathbf{k}}).$$ (12)

Here, ${\widehat{f}}_{\mathbf{k}}^{\mathrm{N}/\mathrm{F}}={\sum }_{{\sigma }^{\prime }\sigma }{\xi }_{{\sigma }^{\prime }}{f}_{\mathbf{k},{\sigma }^{\prime },\sigma }^{\mathrm{N}/\mathrm{F}}{\xi }_{\sigma }^{†}$ is the matrix representation of the reduced density matrix, L is the thickness of the system along z direction, h = 2πħ is the Planck constant, the summation over k_⊥ refers to the summation over all transverse momenta, and E is the energy of the electron. In order to compute the contribution from ${\widehat{f}}_{\mathbf{k}}^{\mathrm{F}}$, we assume that ${\widehat{f}}_{\mathbf{k}}^{\mathrm{F}}$ is diagonal in σ, so that the electrons in the ferromagnet has no spin component perpendicular to the magnetization, as assumed in the magnetoelectric circuit theory. In order to convert Σ_k to Σ_k⊥∫ dE, we use Σ_k = Σ_k⊥Σ_kz and Σ_kz = (L/2π) ∫ dk_z = (m_eL/2πħ²) ∫ dE/k_z. We use ${\widehat{1}}_{\mathbf{k}}{\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}\widehat{1}={\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}$ and ${\widehat{1}}_{\mathbf{k}}^{\prime }{\widehat{f}}_{\mathbf{k}}^{\mathrm{F}}{\widehat{1}}^{\prime }={\widehat{f}}_{\mathbf{k}}^{\mathrm{F}}$ by their definition.⁶ These relations play a role in projecting the extended matrices in Eq. (10) when computing physical quantities.

Equation (12) has the same form as the core result of the conventional magnetoelectric circuit theory [45, 46]. An evanescent contribution from a wave incident from the ferromagnet with σ = −1 cannot contribute to ĵ_z|_z=−0 (see additional 1̂_k factor in the last term). But in Appendix A, we show that an evanescent contribution plays an important role in an in-plane current flow in the presence of interfacial spin-orbit coupling.

Applying an external field shifts the distribution function. In linear response regime, we approximate the Fermi surface contribution by defining chemical potentials $\mathrm{\Delta }{\widehat{f}}_{\mathbf{k}}^{\mathrm{N}/\mathrm{F}}=e\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}/\mathrm{F}}\delta (E-E_F)$ where E_F is the Fermi level. The delta function allows us to perform integration over E in Eq. (12) by taking E = E_F. In the presence of an electrical (charge) current along x direction, it shifts the electron distribution function with a finite momentum relaxation time τ^N in the non-magnet, τ^↑/↓ in the ferromagnet. Here ↑ and ↓ refer to the majority (σ = −1) and minority (σ = 1) bands. That is, Δμ̂^N = (E_x/m_e)ħk_xτ^N1̂_k and $\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}=(E_x/m_e)\hslash k_x{\widehat{\tau }}^{\mathrm{F}}{\widehat{1}}_{\mathbf{k}}^{\prime }$ where E_x is the applied electric field, and τ̂^F = τ^↓u₊ + τ^↑u₋ is a 2 × 2 matrix of the relaxation times in the ferromagnet. Then the nonequilibrium current is

$$\begin{gathered} {{\widehat{j}}_z\mid }_{z=-0}=-\frac{e^{2}L}{hV}\sum _{{\mathbf{k}}_{\perp }}{\left[\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{1}}_{\mathbf{k}}-{\widehat{r}}_{\mathbf{k}}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{r}}_{\mathbf{k}}^{†}-{\widehat{t}}_{\mathbf{k}}^{\prime }\mathrm{\Delta }{\mu }^{\mathrm{F}}{\widehat{t}}_{\mathbf{k}}^{\prime †}{\widehat{1}}_{\mathbf{k}}\right]}_{E=E_F} \\ =\frac{e^{2}L{E}_x}{2\pi m_{e}V}\sum _{{\mathbf{k}}_{\perp }}{\left[k_x{\widehat{r}}_{\mathbf{k}}{\tau }^N{\widehat{r}}_{\mathbf{k}}^{†}+k_x{\widehat{t}}_{\mathbf{k}}^{\prime }{\widehat{\tau }}^F{\widehat{t}}_{\mathbf{k}}^{\prime †}{\widehat{1}}_{\mathbf{k}}\right]}_{E=E_F}. \end{gathered}$$ (13)

Since the expression is given by quantities at the Fermi level, we from now on omit [···]|_{E= EF} and implicitly assume that the nonequilibrium current is evaluated at the Fermi level. The simple formula Eq. (13) gives the nonequilibrum spin and charge currents right at the interface in the nonmagnet. Without spin-orbit coupling, the system has the rotational symmetry around z, so r̂_k is an even function of k_x and k_y. Therefore, Eq. (13) vanishes identically after summing up over all transverse modes. Thus, we reproduce the well-known result that there is no conventional spin-transfer torque induced by an in-plane charge current.

However, the existence of interfacial spin-orbit coupling changes the situation drastically. Since Eq. (10) includes a term which is odd in k, Eq. (13) gives rise to a finite contribution. Putting Eq. (10) into Eq. (13), we obtain

$${{\widehat{j}}_z\mid }_{z=-0}=-h_R\frac{e^{2}L{E}_x}{4\pi m_{e}V}Im\sum _{{\mathbf{k}}_{\perp }}\frac{k_{\perp }^2}{k_z}({\widehat{1}}_{\mathbf{k}}+{\widehat{r}}_{\mathbf{k}}^0){\widehat{\sigma }}_y{\widehat{t}}_{\mathbf{k}}^{\prime 0}({\widehat{\tau }}^{\mathrm{F}}-{\tau }^{\mathrm{N}}){\widehat{t}}_{\mathbf{k}}^{\prime 0†},$$ (14)

where Im[A] = (A − A^†)/2i refers to the imaginary part of the given matrix A and $k_{\perp }=\sqrt{k_x^2+k_y^2}$. Here we use the unitarity relation ${\widehat{r}}_{\mathbf{k}}^0{\widehat{r}}_{\mathbf{k}}^{0†}+{\widehat{t}}_{\mathbf{k}}^0{\widehat{t}}_{\mathbf{k}}^{\prime 0†}{\widehat{1}}_{\mathbf{k}}={\widehat{1}}_{\mathbf{k}}$ which is derived in Appendix B. In addition, we perform an angular average of the summand: For any unit vector u, ${\sum }_{{\mathbf{k}}_{\perp }}(\mathbf{k}·\mathbf{u})\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z})={\sum }_{{\mathbf{k}}_{\perp }}(k_{\perp }^2/2)\widehat{\mathit{\sigma }}·(\mathbf{u}\times \mathbf{z})$ after taking average of contributions from all directions of k_⊥ = k_xx + k_yy with the same magnitude. Taking u = x yields σ̂_y in Eq. (14).

Now we compute the discontinuity at the interface. The derivative mismatch condition h_Rσ̂ · (k × z)ψ_z=0 = ∂_zψ_z=+0 − ∂_zψ_z=−0, allows us to compute Δĵ_z ≡ ĵ_z|_z=+0 − ĵ_z|_{z= −0} in terms of the wave function at z = 0. From Eq. (11), j_z|_z=+0 − j_z|_z=−0 = −h_R(eħ/m_e) Tr_k Im[ρδ(r_op − r)σ̂σ̂ · (k ×z)], and similarly for the charge current. Here r is the position at the interface, so it does not have a z-component. Since the expression is already proportional to h_R, we can replace r̂_k in the wave function by ${\widehat{r}}_{\mathbf{k}}^0$ . After some algebra,

$$\mathrm{\Delta }{\widehat{j}}_z=h_R\frac{e^{2}L{E}_x}{4\pi m_{e}V}Im\sum _{{\mathbf{k}}_{\perp }}\frac{k_{\perp }^2}{\mid k_z\mid }{\widehat{\sigma }}_y[({\widehat{1}}_{\mathbf{k}}+{\widehat{r}}_{\mathbf{k}}^0){\tau }^{\mathrm{N}}({\widehat{1}}_{\mathbf{k}}+{\widehat{r}}_{\mathbf{k}}^{0†})+{\widehat{\tau }}_{\mathbf{k}}^{\prime 0}{\widehat{\tau }}^{\mathrm{F}}{\widehat{\tau }}_{\mathbf{k}}^{\prime 0†}].$$ (15)

The physical meaning of Eq. (15) is the angular momentum absorption or emission at the interface due to spin-orbit coupling. Therefore, Eq. (15) amounts to how much angular momentum is transferred from the lattice at the interface.

The expression for the spin-orbit torque is given by the Pauli components of ĵ_z|_z=+0 perpendicular to the magnetization m, and ĵ_z|_z=+0 is given by the sum of Eqs. (14) and (15). Explicitly, T_R = −(ħV/2eL) Tr_σ[σ̂_⊥ĵ_z|_z=+0], where σ̂_⊥ = σ̂ − m(σ̂ · m) is the transverse part of the Pauli matrix vector to m and Tr_σ is the trace over the 2 × 2 spin space. After some algebra,

$${\mathbf{T}}_R=Im[{\mathcal{T}}_R]\mathbf{m}\times (\mathbf{y}\times \mathbf{m})+Re[{\mathcal{T}}_R]\mathbf{m}\times \mathbf{y},$$ (16a)

$${\mathcal{T}}_R={\mathcal{T}}_R^{\mathrm{N}}+{\mathcal{T}}_R^{\mathrm{F}},$$ (16b)

$${\mathcal{T}}_R^{\mathrm{N}}=h_R\frac{\hslash e{E}_x\tau }{8\pi m_e}\sum _{{\mathbf{k}}_{\perp }}\frac{k_{\perp }^2}{k_z}(1-r_{\mathbf{k}}^{\uparrow \ast }{r}_{\mathbf{k}}^{\downarrow })(r_{\mathbf{k}}^{\uparrow }-r_{\mathbf{k}}^{\downarrow \ast })$$ (16c)

$${\mathcal{T}}_R^{\mathrm{F}}=-h_R\frac{\hslash e{E}_x}{8\pi m_e}\sum _{{\mathbf{k}}_{\perp }}\frac{k_{\perp }^2}{k_z}(r_{\mathbf{k}}^{\downarrow }{\mid t_{\mathbf{k}}^{\prime \uparrow }\mid }^2{\tau }^{\uparrow }-r_{\mathbf{k}}^{\uparrow \ast }{\mid t_{\mathbf{k}}^{\prime \downarrow }\mid }^2{\tau }^{\downarrow })+h_R\frac{\hslash e{E}_x}{8\pi m_e}\sum _{{\mathbf{k}}_{\perp },k_z^2<0}\frac{k_{\perp }^2}{\mid k_z\mid }({\mid t_{\mathbf{k}}^{\prime \uparrow }\mid }^2{\tau }^{\uparrow }-{\mid t_{\mathbf{k}}^{\prime \downarrow }\mid }^2{\tau }^{\downarrow }),$$ (16d)

where we expanded ${\widehat{r}}_{\mathbf{k}}^0=r_{\mathbf{k}}^{\downarrow }{u}_{+}+r_{\mathbf{k}}^{\uparrow }{u}_{-}$ and ${\widehat{t}}_{\mathbf{k}}^{\prime 0}=t_{\mathbf{k}}^{\prime \downarrow }{u}_{+}+t_{\mathbf{k}}^{\prime \uparrow }{u}_{-}$

as done in magnetoelectric circuit theory. Here ↑ is assigned for σ = −1 since σ = −1 is majority in our model. Equation (16) is the central result of this paper. The terms in Eq. (16) are the dampinglike spin-orbit torque and fieldlike spin-orbit torque respectively. ${\mathcal{T}}_R^{\mathrm{N}}$ is the contribution from a current flowing in the non-magnet. By the Drude model, the applied current is written as n_Ne² E_xτ/m_e where n_N is the electron density in the non-magnet. Therefore, τ multiplied by E_x is proportional to the applied current. Similarly, ${\mathcal{T}}_R^{\mathrm{F}}$ is the contribution from the current flowing in the ferromagnet. Especially, the second term in ${\mathcal{T}}_R^{\mathrm{F}}$ is an evanescent contribution in the nonmagnet (see $k_z^2<0$). Although the wave function in the nonmagnet is evanescent, incident waves from the ferromagnet can be propagating, giving rise to a finite amount of spin-orbit torque. Such a contribution is crucial for topological insulators where the nonmagnet is insulating. We also demonstrate in Sec. V A that this contribution can also be the dominant contribution in magnetic bilayers.

In the case of torques due to the spin Hall effect in the interior of the layer, the spin Hall current proportional to θ_SHE_x creates a spin current into the ferromagnet, where θ_SH is the spin Hall angle. For this mechanism, the real part of the spin mixing conductance G^↑↓ contributes to the damping-like torque and the imaginary part contributes to the fieldlike torque [45, 46]. Comparing this result to Eq. (16) suggests that θ_SH E_xG^↑↓ in the spin Hall effect contribution corresponds to i𝒯_R in the interfacial spin-orbit coupling contribution (up to a constant factor).

Now we restore the possibility of interface magnetism at the interface and argue that Eq. (16) is unchanged. When we add interfacial magnetism u_mσ̂ · m, the boundary condition changes to u_mσ̂ · mψ_z=0 +h_Rσ̂ · (k×z)ψ_z=0 = ∂_zψ_z=+0 −∂_zψ_z=−0. This is nothing but the angular momentum conservation relation at the interface. The terms in the left-hand side correspond to the angular momenta transferred from the interface magnetization and the lattice. The terms in the right-hand side correspond to the incoming and outgoing angular momenta. The first term in the left-hand side and the first term in the right-hand side correspond to the (negative of) spin-transfer torque to the interfacial magnetism and the spin-transfer torque to the bulk. Therefore, the total spin-transfer torque is computed by the sum of the interfacial spin-transfer torque and the bulk spin-transfer torque, which corresponds to ∂_zψ_z=+0 − u_mσ̂ · mψ_z=0. This is the same as ∂_zψ_z=−0 + h_Rσ̂ · (k×z)ψ_z=0, which is exactly what we express in Eq. (16). Conservation of angular momentum is summarized in Fig. 2.

V. SPIN-ORBIT TORQUE FOR VARIOUS TYPES OF INTERFACES

In this section, we use Eq. (16) to compute spin-orbit torques for various types of interfaces. Examples includes magnetic bilayers, ferromagnetic insulators, and topological insulators as presented in Table I.

A. Magnetic bilayers - Bulk magnetism

We start from the following unperturbed Hamiltonian.

$$H=-\frac{{\hslash }^2}{2m_e}{\nabla }^2+J\widehat{\mathit{\sigma }}·\mathbf{m}\mathrm{\Theta }(z),$$ (17)

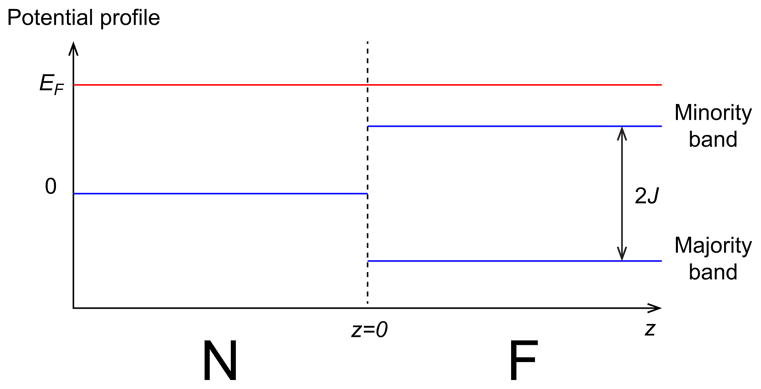
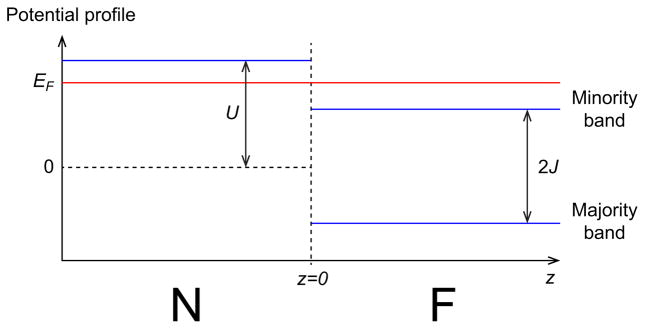
where Θ(z) is the Heaviside step function representing that the bulk ferromagnetism J is present only in z > 0. The potential energy profile is presented in Fig. 3. Here we assume E_F > 0, otherwise the normal metal is insulating.

FIG. 3.

The potential profile (blue lines) for the model Eq. (17). The energy profile is spin-independent for z < 0 while it has a 2J gap between the majority and minority bands for z > 0. Here the red line denotes the Fermi level. The figure shows a typical situation where E_F > J so that the spin polarization at the ferromagnet is incomplete, but the theory covers the whole range of positive E_F.

Since we have no interface potential other than spin-orbit coupling, we use Eq. (6) by putting κ̂ = 0.

$$r_{\mathbf{k}}^{\uparrow /\downarrow }=\{\begin{array}{ll}\frac{k_z-k_z^{\mp }}{k_z+k_z^{\mp }}\hfill & \text{if}{k}_z\text{is}\text{real},\hfill \\ 0\hfill & \text{if}{k}_z\text{is}\text{imaginary},\hfill \end{array}$$ (18a)

$$t_{\mathbf{k}}^{\prime \uparrow /\downarrow }=\{\begin{array}{ll}\frac{2i\sqrt{k_z^{\mp }\mid k_z\mid }}{i{k}_z+i{k}_z^{\mp }}\hfill & \text{if}{k}_z^{\mp }\text{is}\text{real},\hfill \\ 0\hfill & \text{if}{k}_z^{\mp }\text{is}\text{imaginary},\hfill \end{array}$$ (18b)

When we define $k_F^2=2m_e{E}_F/{\hslash }^2$ and Δ² = 2m_eJ/ħ², each momentum has the following relations: $k_{\perp }^2+k_z^2=k_F^2$ and $k_{\perp }^2+{(k_z^{\pm })}^2\pm {\mathrm{\Delta }}^2=k_F^2$. There always are evanescent contributions from any scattered wave regardless of E_F and J, since k_⊥ can be arbitrarily close to k_F.

The total spin-orbit torque is given by the sum of Eq. (16c) and Eq. (16d). Putting Eq. (18a) into Eq. (16c) gives spin-orbit torque generated by a current flowing in the normal metal.

$$Re[{\mathcal{T}}_R^{\mathrm{N}}]=-h_R\frac{\hslash e{E}_x\tau }{2\pi m_e}\sum _{k_{\perp }^2<k_F^2}{k}_{\perp }^2{k}_z\frac{{(k_z^{-})}^2-{\mid k_z^{+}\mid }^2}{{(k_z+k_z^{-})}^2{\mid k_z+k_z^{+}\mid }^2},$$ (19a)

$$Im[{\mathcal{T}}_R^{\mathrm{N}}]=-h_R\frac{\hslash e{E}_x\tau }{2\pi m_e}\sum _{k_{\perp }^2<k_F^2}{k}_{\perp }^2{k}_z\frac{2k_z^{-}Im[k_z^{+}]}{{(k_z+k_z^{-})}^2{\mid k_z+k_z^{+}\mid }^2},$$ (19b)

where ${\mathrm{\sum }}_{k_{\perp }^2<k_F^2}$ refers to the summation over all transverse mode satisfying $k_{\perp }^2<k_F^2$ thus making k_z real. Here, k_z and $k_z^{-}$ are real and positive. The evanescent contribution $Im[k_z^{+}]$ is crucial for the dampinglike component $Im[{\mathcal{T}}_R^{\mathrm{N}}]$. We remark that the real and imaginary parts of Eq. (19) have the same sign. This implies that the dampinglike and the fieldlike component of Eq. (16c) in this model have the same sign.

Putting Eq. (18b) into Eq. (16d) gives spin-orbit torque generated by a current flowing in the ferromagnet. Although the situation is slightly more complicated than above, the explicit expressions are similar:

$$\begin{gathered} Re[{\mathcal{T}}_R^{\mathrm{F}}]=-h_R\frac{\hslash e{E}_x{\tau }^{\uparrow }}{2\pi m_e}\sum _{k_{\perp }^2<k_F^2}{k}_{\perp }^2{k}_z\frac{k_z^2-{\mid k_z^{+}\mid }^2}{{(k_z+k_z^{-})}^2{\mid k_z+k_z^{+}\mid }^2}, \\ -h_R\frac{\hslash e{E}_x{\tau }^{\downarrow }}{2\pi m_e}\sum _{k_{\perp }^2+{\mathrm{\Delta }}^2<k_F^2}{k}_{\perp }^2{k}_z^{+}\frac{k_z^{-}-k_z}{{(k_z+k_z^{+})}^2(k_z+k_z^{-})} \\ +h_R\frac{\hslash e{E}_x{\tau }^{\uparrow }}{2\pi m_e}\sum _{k_F^2<k_{\perp }^2<k_F^2+{\mathrm{\Delta }}^2}\frac{k_{\perp }^2{k}_z^{-}}{{\mathrm{\Delta }}^2}, \end{gathered}$$ (20a)

$$Im[{\mathcal{T}}_R^{\mathrm{F}}]=h_R\frac{\hslash e{E}_x{\tau }^{\uparrow }}{2\pi m_e}\sum _{k_{\perp }^2<k_F^2}{k}_{\perp }^2{k}_z^{-}\frac{2k_{z}Im[k_z^{+}]}{{(k_z+k_z^{-})}^2{\mid k_z+k_z^{+}\mid }^2}.$$ (20b)

Here, terms proportional to τ^↑ and τ^↓ are contributions from majority and minority electron flows respectively. We remark that evanescent modes are crucial for the existence of damp-inglike components. The first two terms of the real part are majority and minority counterparts of $Re[{\mathcal{T}}_R^{\mathrm{N}}]$. The imaginary part has also the same form as $Im[{\mathcal{T}}_R^{\mathrm{N}}]$, but only majority electrons contribute because minority electrons do not make any transition to an evanescent state in this model. The last term in the real part has no counterpart in Eq. (19) since it originates from the imbalance between majority and minority states due to a nonzero J. This term originates from transition of majority electrons in the ferromagnet to evanescent states in the normal metal. We show below that this contribution is very large and can dominate the other contributions making the consideration of a finite J and the resulting evanescent modes very important.

Converting the summations in Eqs. (19) and (20) to integrations allows us to compute the spin-orbit torque as a function of E_F /J. To do this, we convert ${\mathrm{\sum }}_{k_{\perp }^2<k_F^2}$ to $(A/4\mathrm{\pi }){\int }_0^{k_F^2}d{(k_{\perp })}^2$, where A = V/L is the are of the interface, and similarly for the other summations. To express all momenta in terms of k_⊥, we use $k_z^2=k_F^2-k_{\perp }^2$ and ${(k_z^{\pm })}^2=k_F^2\mp {\mathrm{\Delta }}^2-k_{\perp }^2$. There are two regimes. For E_F ≤ J, $k_z^{+}$ is imaginary for the whole interval of the integration $0<k_{\perp }^2<k_F^2$. On the other hand, for E_F > J, it is necessary to consider the intervals $0<k_{\perp }^2<k_F^2-{\mathrm{\Delta }}^2$ and $k_F^2-{\mathrm{\Delta }}^2<k_{\perp }^2<k_F^2$ separately, since $k_z^{+}$ is imaginary for the former and is real for the latter. Thus, it has different properties when taking the absolute value. In both cases, $k_z^{-}$ is always real, and k_z is imaginary only when $k_F^2<k_{\perp }^2<k_F^2+{\mathrm{\Delta }}^2$. The integration can be performed fully analytically, however, we present only numerical results due to complexity of the expressions.

Figure 4 presents (normalized) contributions of spin-orbit torques as a function of E_F /J. The values are divided by factors proportional to E_xτ, E_xτ^↑, and E_xτ^↓ for electrons in normal metal, majority electrons in the ferromagnet, and minority electrons in the ferromagnet, respectively. In most experimental situations, people apply an electrical current mainly in the normal metal. Thus we discuss the spin-orbit torque originating from a current in the normal metal first and consider the effects of a current leaking to the ferromagnet.

Red lines in Fig. 4 represent fieldlike (dashed line) and dampinglike (solid line) components of spin-orbit torque induced by a current flowing in the normal metal. Unlike the two-dimensional Rashba model [11, 12], the damping-like component has the same order of magnitude as the field-like component and even larger for wide range of E_F. As we remark above, each component has the same sign. If the current leaking to the ferromagnet is sufficiently small or the ferromagnet is more resistive than the normal metal, we can consider the current to flow mainly in the normal metal. In this case, the dampinglike torque is comparable or even larger than fieldlike torque implying that experimental results for the dampinglike spin-orbit torque due to the spin Hall effect [8–10, 59–61] should be carefully analyzed due to the possibility of the contributions from interfacial spin-orbit coupling [62, 63].

Now we consider the contributions from the current flowing in the ferromagnet. Neglecting the unconventional term from a finite J (dot-dashed line in Fig. 4), the dampinglike component (solid blue line) has the opposite sign of the normal metal contribution because the dampinglike component is generated by angular momentum carried by a spin current, which has opposite directions for these two contributions. On the other hand, since the fieldlike component originates from the current-induced spin-orbit field, the contributions from currents in both sides can act additively. Thus, the dashed blue line and the cyan line have the same sign as the dashed red line in wide range of E_F/J.⁷

One remarkable result of this calculation is that the third term in $Re[{\mathcal{T}}_R^{\mathrm{F}}]$ in Eq. (20) is larger than the other contributions. It is around five times larger than the dampinglike components (solid lines) at E_F ≈ J (not shown). The origin of this term is the finite magnitude of J and the resulting evanescent states. If τ^↑ has the same order of magnitude as τ, this term can be the dominant contribution, illustrating the importance of accounting for the different Fermi surface. If the current flowing in the ferromagnet is at least comparable to that in the normal metal, the total spin torque is approximated by the third term in $Re[{\mathcal{T}}_R^{\mathrm{F}}]$. The summation is performed in a simple analytic form:

$${\mathcal{T}}_R\approx h_R\frac{\hslash e{E}_x{\tau }^{\uparrow }}{2\pi m_e}\sum _{k_F^2<k_{\perp }^2<k_F^2+{\mathrm{\Delta }}^2}\frac{k_{\perp }^2{k}_z^{-}}{{\mathrm{\Delta }}^2}=h_R\frac{e{E}_x{\tau }^{\uparrow }A\mathrm{\Delta }}{15\pi h}(5E_F+2J).$$ (21)

Since the number of electrons in the majority band remains finite when E_F → 0, the contribution does not vanish in this limit, unlike the other contributions in Fig. 4.⁸

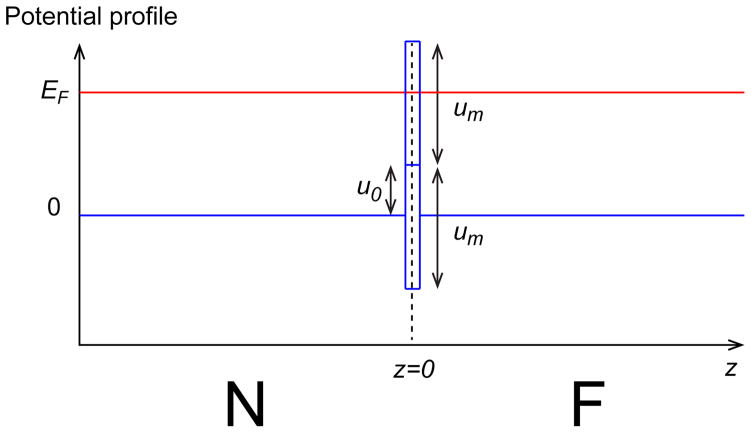
B. Magnetic bilayers - Interface magnetism

We start from the following unperturbed Hamiltonian.

$$H=-\frac{{\hslash }^2}{2m_e}{\nabla }^2+\frac{{\hslash }^2}{2m_e}(u_0+u_m\widehat{\mathit{\sigma }}·\mathbf{m})\delta (z),$$ (22)

where u₀ and u_m are parameters for spin-independent and spin-dependent interface potentials. The former refers to an interface barrier and the latter refers to an interface magnetism. The interface magnetism is a possible simple model for the proximity-induced magnetism at the interface [44]. Since all the Fermi wave vectors are the same, there are no evanescent waves. The potential energy profile is presented in Fig. 5. Each side around z = 0 is symmetric, so there is no explicit difference between the normal metal and the ferromagnet. Here we model the ferromagnet by assigning different τ^↑ and τ^↓ values and assuming that angular momentum right at z = +0 are absorbed into the ferromagnet and make a contribution to spin-orbit torque. In other words, we implicitly assume a vanishingly small magnitude of magnetism in the ferromagnetic bulk.

FIG. 5.

The potential profile (blue lines) for the model Eq. (22). Here the spin-independent potential u₀ and spin-dependent potential u_m are present at z = 0. The red line denotes the Fermi level. In this figure, a delta functions is represented as a square function with a finite height and a finite width for illustration.

We use Eq. (6) by putting K̂_z = k_z and κ̂ = u₀ + u_mσ̂ · m, to obtain

$$r_{\mathbf{k}}^{\uparrow \downarrow }=\frac{u_0\mp u_m}{2i{k}_z-(u_0\mp u_m)},t_{\mathbf{k}}^{\prime \uparrow \downarrow }=1+r_{\mathbf{k}}^{\uparrow \downarrow }.$$ (23)

Putting this into Eq. (16),

$$Re[{\mathcal{T}}_R]=h_R\frac{\hslash e{E}_x}{\pi m_e}\sum _{k_{\perp }^2<k_F^2}\frac{2u_0{u}_m(\tau +{\tau }_{\mathrm{F}}^e)+(u_0^2+u_m^2){\tau }_{\mathrm{F}}^s}{D_{\mathbf{k}}(u_0,u_m)},$$ (24a)

$$Im[{\mathcal{T}}_R]=-h_R\frac{\hslash e{E}_x}{\pi m_e}\sum _{k_{\perp }^2<k_F^2}{k}_z\frac{2u_0(\tau -{\tau }_{\mathrm{F}}^e)-2u_m{\tau }_{\mathrm{F}}^s}{D_{\mathbf{k}}(u_0,u_m)},$$ (24b)

where $D_{\mathbf{k}}(u_0,u_m)=[4k_z^2+{(u_0-u_m)}^2][4k_z^2+{(u_0+u_m)}^2]/k_{\perp }^2{k}_z$. ${\tau }_{\mathrm{F}}^{e/s}=({\tau }^{\uparrow }\pm {\tau }^{\downarrow })/2$ amounts to charge/spin current flowing in the ferromagnet.

We observe the following features. First, considering only charge current contributions, the fieldlike component is additive [ $\tau +{\tau }_{\mathrm{F}}^e$ in Eq. (24a)] and the dampinglike component is subtractive [ $\tau -{\tau }_{\mathrm{F}}^e$ in Eq. (24b)]. This observation is consistent with the discussion in Sec. V A. We can observe it here more clearly since there are no evanescent contributions in this model. Second, the charge current contributions are all zero when u₀ = 0. This means that, if an applied current is mostly flowing in the normal metal, interfacial spin-orbit torque induced by the current is proportional to the spin-independent barrier at the interface. Third, the spin-orbit torque does not vanish even when there is no magnetism; u_m = 0. The spin-orbit torque contribution without magnetism is attributed to our assumption that there is a vanishingly small magnetism in the ferromagnetic bulk. When angular momentum is transferred from the lattice through interfacial spin-orbit coupling, a finite amount of spin current at z = +0 is generated. In our approach, we assume, even when exchange in the bulk is not explicitly included, that dephasing transfers the spin angular momentum from the spin current to the bulk magnetism, giving rise to a torque. The size of the spin-orbit torque to the bulk is then determined by the conservation of angular momentum, so that the total spin torque absorbed into the ferromagnet is determined by the spin current at z = +0, no matter how small the bulk exchange coupling strength is in the model. In conclusion, the contributions proportional to u_m are spin-orbit torque to the interface magnetism u_m, while the other contributions are spin-orbit torque to the ferromagnetic bulk.

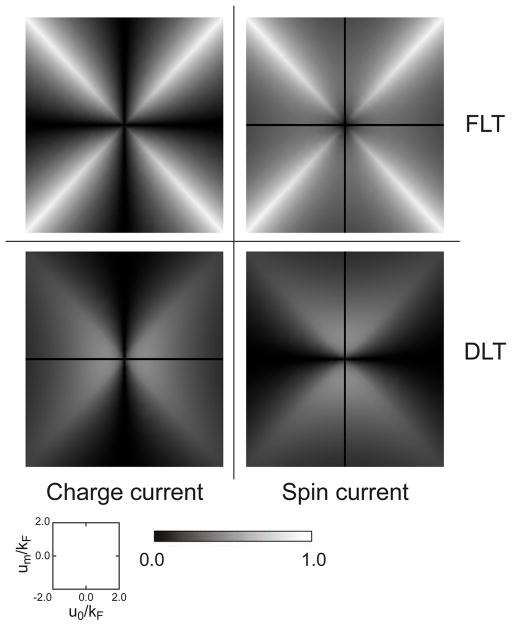
To compare the relative magnitude of the fieldlike and dampinglike components, we convert the summations in Eq. (24) to integrations as in Sec. V A. We plot the absolute values of each contribution in Fig. 6. Normalization factors, $\propto E_x(\tau \pm {\tau }_{\mathrm{F}}^e)$ or $E_x{\tau }_{\mathrm{F}}^s$, are introduced. The total spin-orbit torque is given by the weighted sum of each panel. We observe that the fieldlike and dampinglike components are on the similar order of magnitude, but the fieldlike component is in general larger than dampinglike component in wide range of parameters. The spin-current-induced fieldlike contribution is the largest. The same model has been studied by Haney et al. [37] without a perturbative approach. They show that the fieldlike component is in general larger than the dampinglike component, which is consistent with our approach.

FIG. 6.

Magnitude of spin-orbit torque in the presence of interface magnetism. We plot spin-orbit torque as a function of u₀/k_F and u_m/k_F. To compare magnitude clearly, we plot absolute values, discarding the signs. The upper two panels represent fieldlike components [Eq. (24a)] and the lower two panels represent damping-like components [Eq. (24b)]. The left two panels represent charge-current-induced contributions (proportional to $\tau \pm {\tau }_{\mathrm{F}}^e$). The right two panels represent spin-current-induced contributions (proportional to ${\tau }_{\mathrm{F}}^s$). The values are divided by h_RħeE_xA/24πm_ek_F for all panels, and additionally divided by $\tau \pm {\tau }_{\mathrm{F}}^e$ for the charge-current-induced contributions (+ for FLT and −for DLT) and ${\tau }_{\mathrm{F}}^s$ for the spin-current-induced contributions. The resulting values are dimensionless. The black lines near u₀ = 0 or u_m = 0 are regions where spin-orbit torque is not computed due to numerical instability.

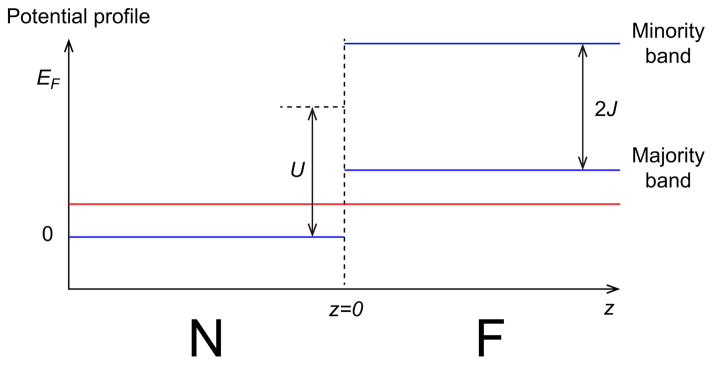
C. Ferromagnetic insulators

We start from the following unperturbed Hamiltonian.

$$H=-\frac{{\hslash }^2}{2m_e}{\nabla }^2+(U+J\widehat{\mathit{\sigma }}·\mathbf{m})\mathrm{\Theta }(z),$$ (25)

where U is a spin-independent potential that makes the ferromagnet (z > 0) insulating. Thus, the Fermi level should be below U − J. Without loss of generality, we can assume U > J, otherwise there are no occupied electronic states. The potential energy profile is presented in Fig. 7.

FIG. 7.

The potential profile (blue lines) for the model Eq. (25). In the ferromagnet, there is a spin-independent barrier U that makes the ferromagnet insulating. The Fermi level (red line) is less than U − J, thus both majority and minority bands are evanescent.

Since the ferromagnet is insulating, $k_z^{\pm }$ are all imaginary. We define $q_z^{\pm }=-i{k}_z^{\pm }$, which is real and positive. The reflection amplitudes are given by the same formula as in Sec. V A.

$$r_{\mathbf{k}}^{\uparrow \downarrow }=\frac{i{k}_z+q_z^{\mp }}{i{k}_z-q_z^{\mp }}.$$ (26)

Since all the other momenta are imaginary, there is no contribution from ${\mathcal{T}}_R^{\mathrm{F}}$. Thus, we only need to compute Eq. (16c):

$${\mathcal{T}}_R=h_R\frac{{\hslash }^{3}e{E}_x\tau }{2\pi m_e^2}\frac{J}{U^2-J^2}\sum _{k_{\perp }^2<k_F^2}{k}_{\perp }^2{k}_z.$$ (27)

Since 𝒯_ℛ is real, only fieldlike spin-orbit torques can survive.

We now perform the summation in the same way described in Sec. V A. After some algebra,

$${\mathcal{T}}_R=h_R\frac{8\sqrt{2m_e}e{E}_x\tau A}{15{\pi }^2{\hslash }^2}\frac{J{E}_F^{5/2}}{U^2-J^2}.$$ (28)

The spin-orbit torque vanishes at E_F = 0 since there are no occupied states. It increases as E_F increases. Equation (28) has a singularity at J = U, but it does not diverges at J = U because as J approaches U, E_F approaches to zero since E_F < U − J. The maximum of Eq. (28) occurs at E_F = U − J; 𝒯_R ∝ J(U − J)^5/2/(U²−J²), which has a maximum at J = U/3. Therefore,

$${\mathcal{T}}_R\le h_R\frac{8\sqrt{m_e}e{E}_x\tau A}{45\sqrt{3}{\pi }^2{\hslash }^2}{U}^{3/2},$$ (29)

which is finite.

To see the numerical behavior of 𝒯_R, we parameterize E_F, U, and J with two parameters. Since U > J and 0 < E_F ≤ U − J, we put J = αU and E_F = β(U − J) with dimensionless parameters α and β satisfying 0 ≤ α, β ≤ 1. Then,

$${\mathcal{T}}_R=h_R\frac{8\sqrt{2m_e}e{E}_x\tau A}{15{\pi }^2{\hslash }^2}\times \frac{{\beta }^{5/2}}{U^{3/2}}\times \frac{\alpha {(1-\alpha )}^{3/2}}{1+\alpha }.$$ (30)

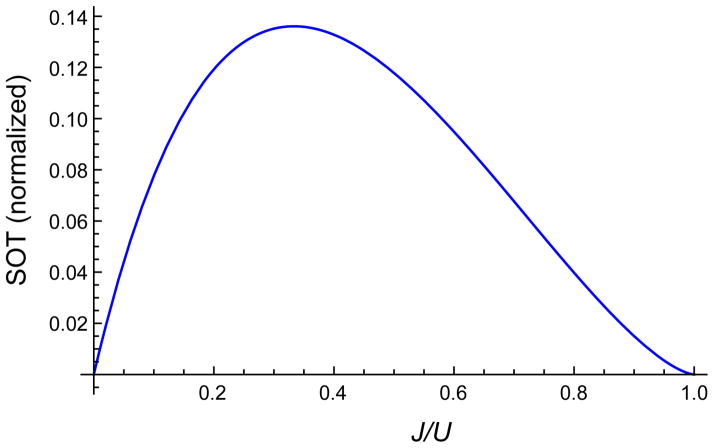
The first factor is an overall factor proportional to the applied current. The second factor shows a simple dependence of spin torque as a function of β and U. We plot the last factor in Fig. 8. As we discuss above the maximum occurs at J/U = 1/3. This plot confirms again that the spin-orbit torque is finite even when J approaches U.

FIG. 8.

Fieldlike spin-orbit torque in ferromagnetic insulators divided by $8h_R\sqrt{2m_e}e{E}_x\tau A/15{\pi }^2{\hslash }^2\times {[E_F/(U-J)]}^{5/2}/U^{3/2}$. The result is dimensionless.

We add the interface potential (u₀ + u_mσ̂ · m)δ(z) at z = 0 and briefly see how results change. The reflection amplitudes change to

$$r_{\mathbf{k}}^{\uparrow \downarrow }=\frac{i{k}_z+(q_z^{\mp }+u_0\mp u_m)}{i{k}_z-(q_z^{\mp }+u_0\mp u_m)}.$$ (31)

The spin-orbit torque is then

$${\mathcal{T}}_R=h_R\frac{\hslash e{E}_x\tau }{2\pi m_e}\sum _{{\mathbf{k}}_{\perp }}\frac{k_{\perp }^2{k}_z(q_z^{-}+q_z^{+}+2u_0)(q_z^{-}-q_z^{+}-2u_m)}{D_{\mathbf{k}}(u_0,u_m)},$$ (32)

where $D_{\mathbf{k}}(u_0,u_m)=[k_z^2+{(q_z^{-}+u_0-u_m)}^2][k_z^2+{(q_z^{+}+u_0+u_m)}^2]$. 𝒯_R is still real. It is consistent with the observation in Sec. VA that evanescent waves in the nonmagnet are crucial to get a dampinglike component. In this model, since the ferromagnet is insulating, there are no evanescent waves in the nonmagnet, thus only the fieldlike component can survive, regardless of an additional interface potential.

D. Topological insulators in contact with a ferromagnet

For the case of topological insulators in contact with a ferromagnet, the nonmagnet is insulating. Thus a current flows along the ferromagnet only and the Rashba-type interaction at the interface z = 0 gives rise to spin-orbit torque. Thus, we start from the following unperturbed Hamiltonian [64, 65]. ⁹

$$H=-\frac{{\hslash }^2}{2m_e}{\nabla }^2+U\mathrm{\Theta }(-z)+J\widehat{\mathit{\sigma }}·\mathbf{m}\mathrm{\Theta }(z).$$ (33)

Here the barrier U(> E_F) makes the nonmagnetic layer insulating. Without loss of generality, we can assume that U > J and E_F > −J, otherwise there are no occupied states. The potential profile of Eq. (33) is presented in Fig. 9. In the non-magnet, the wave vector is imaginary, so we define q_z = −ik_z. Then, $q_z^2+{(k_z^{\pm })}^2=2m_e(U\mp J)/{\hslash }^2$. From Eq. (6), the transmission amplitude is given by

FIG. 9.

The potential profile (blue lines) for the model Eq. (33). Here the spin-independent potential u₀ and spin-dependent potential u_m are present at z = 0. The Fermi level (red line) is below the barrier U.

$$t_{\mathbf{k}}^{\prime \uparrow \downarrow }=\frac{2i\sqrt{Re[k_z^{\mp }]q_z}}{i{k}_z^{\mp }-q_z}.$$ (34)

Since the normal metal is insulating, Eq. (16d) gives spin-orbit torque. Since there is no incident wave in normal metal, $r_{\mathbf{k}}^{\uparrow \downarrow }=0$, so the second term in Eq. (16d) contributes only. After some algebra,

$${\mathcal{T}}_R=h_R\frac{{\hslash }^{3}e{E}_x}{4\pi m_e^2}\sum _{{\mathbf{k}}_{\perp }}{k}_{\perp }^2\left(\frac{Re[k_z^{-}]}{U+J}{\tau }^{\uparrow }-\frac{Re[k_z^{+}]}{U-J}{\tau }^{\downarrow }\right).$$ (35)

Here $k_z^{-}$ is real since majority waves should be propagating. But $k_z^{+}$ can be imaginary depending on k_⊥.

To perform the summation, we convert it to an integration as in Sec. VA. After some algebra,

$${\mathcal{T}}_R=\frac{h_R\sqrt{2m_e}e{E}_{x}A}{15{\pi }^2{\hslash }^2}Re\left[\frac{{(E_F+J)}^{5/2}{\tau }^{\uparrow }}{U+J}-\frac{{(E_F-J)}^{5/2}{\tau }^{\downarrow }}{U-J}\right].$$ (36)

Here taking the real part (Re) eliminates contribution from states out of the Hilbert space. Explicitly, Re[(E_F − J)^5/2] = (E_F −J)^5/2Θ(E_F −J), thus the second term does not contribute when E_F < J.

Equation (36) shows that spin-orbit torques exist even when τ^↑ = τ^↓. A similar observation is made in Appendix A that an anisotropic magnetoresistance can arise even without difference between τ^↑ and τ^↓, unlike Ref. [33]. This is because, in our theory, $k_F^{+}\ne k_F^{-}$. Since we break a symmetry, we obtain a torque originating from the asymmetry. As a passing remark, similarly to Sec. VC, U − J in the denominator in the second term in Eq. (36) does not yield any singularity at J = U. This is because E_F ≤ U. When J approaches to U, there must be a point where J becomes equal or larger than E_F at which the second term does not contribute.

Since Eq. (36) is real, only a fieldlike component can survive. This is not an artifact of the particular Hamiltonian that we choose [Eq. (33)]. We remark that the second term in Eq. (16d) is always real, regardless of any detail of a model. On the other hand, recent experiments [66–68] report sizable dampinglike spin-orbit torques in topological insulators in contact with a ferromagnetic layer, contrary to our results. One possible cause of the dampinglike torque is that in real materials, the location of topological surface states is shifted on a nanometer scale when attached to a ferromagnet [69–71]. This displacement can be a cause of a finite dampinglike torque. Another possible cause is intrinsic spin-orbit torque. In our theory, we only consider extrinsic contributions that are proportional to scattering times. However, in the two-dimensional Rashba model, the intrinsic spin-orbit torque is perpendicular to extrinsic spin-orbit torque [17]. If similar contributions exist in our three-dimensional model, they could cause a dampinglike component.

VI. DISCUSSION

A. Comparison to the two-dimensional Rashba model

Magnetic bilayers with bulk magnetism can behave quite differently from two-dimensional Rashba models. The two-dimensional Rashba model shows only fieldlike components [11, 12] unless one takes into account intrinsic spin-orbit torque from the Berry phase [17] or a spin relaxation mechanism [13–16]. However, in our approach, a dampinglike spin-orbit torque with a similar order of magnitude arises if the current mostly flows in the normal metal layer. If a current flowing in the ferromagnet has a similar order of magnitude to that in the normal metal, the result shows mostly fieldlike contributions, dominated by the dot-dashed line in Fig. 4. However, the behavior is still very different from the two-dimensional model. The contribution only comes from the majority electrons in the ferromagnet and thus is proportional to τ^↑ only. On the other hand, the fieldlike spin-orbit torque derived by the two-dimensional Rashba model is proportional to the spin polarization ∝ (τ^↑ − τ^↓)/(τ^↑ + τ^↓). Therefore, the dominant contribution is not the counterpart of the fieldlike spin-orbit torque from the two-dimensional Rashba model.

Magnetic bilayers with interface magnetism behave similarly to the two-dimensional Rashba model. As in Fig. 6, the fieldlike spin-orbit torque from spin current is the largest. In the two-dimensional Rashba model, the imbalance between the numbers of electrons in majority and minority is the primary source of spin-orbit field and the resulting fieldlike spin-orbit torque. In our model, it is modeled by τ^↑ ≠ τ^↓ since we do not have a finite exchange splitting explicitly. Therefore, the upper right panel in Fig. 6 corresponds to the traditional contribution from the two-dimensional Rashba model. However, the spin-orbit torque contributions driven by pure charge currents ${\tau }_{\mathrm{F}}^e$ (left panels in Fig. 6) is a unique feature of the three-dimensional model.

Systems with a ferromagnetic insulator or a topological insulator show only fieldlike spin-orbit torques. This is similar to the two-dimensional Rashba model. We observe that a current flowing at z = 0 (where the Rashba interaction exists) results in fieldlike spin-orbit torque while a current across z = 0 results in dampinglike spin-orbit torque. If one of the layers is insulating, there is no propagating wave from one to another. The situation is the same as the two-dimensional Rashba model. In the two-dimensional model, the Rashba interaction is present over the whole sample, and only in-plane electron transport is allowed. Hence, there is no possibility for electrons to cross a Rashba region, eliminating the possibility of a dampinglike contribution.

We do not consider intrinsic contributions from the Berry phase [17]. In general, spin torques have two different contributions; extrinsic and intrinsic. The former is proportional to scattering times, while the latter is independent of scattering times. In this sense, the latter is an electric-field-induced spin torque, not a current-induced one. Ref. [72] highlights the subtle difference between them. The origin of an extrinsic spin torque is the change of distribution functions in the presence of an applied electric field. On the other hand, the origin of an intrinsic spin torque is the change of electronic wave functions due to an applied electric field. In the two-dimensional Rashba model, intrinsic spin torque was found to be larger than the extrinsic one in some contexts. But, it was also shown that intrinsic contributions are completely canceled out by vertex corrections [4, 5] in metallic systems with an ideal quadratic dispersion. Therefore, the relative magnitude of the extrinsic and intrinsic spin torques depends on the situation. Similar studies would be possible in the three-dimensional model, but is beyond the scope of this paper. We defer this question for future work.

B. Multilayer generalization

The starting point of our approach is a normal metal(z < 0)/ferromagnet(z < 0) bilayer. In metallic systems consisting of layers of thicknesses larger than the mean free path, one can describe each interface separately and solve the bulk property by the spin drift-diffusion equation. Therefore, a bilayer model is sufficient to describe a multilayer system. However, if any of the layers has a thickness not much greater than the mean free path, or the system includes an insulating insertion layer at which the spin drift-diffusion equation cannot be written down, one needs to consider a multilayer situation quantum mechanically. The results of our theory will change depending on the situation. However, we here show that when we consider a normal metal (z < 0)/any underlying structure (0 < z < L) with a Rashba interaction at z = 0, the reflection matrix r̂_k is independent of the details of the structure underneath.

We start from the interface Hamiltonian Eq. (5) with κ̂ = κ̂₀ + h_Rσ̂ · (k × ẑ). Since we do not know any details for z > 0, we use the transfer matrix formalism to focus on the interface at z = 0 only. We write the wave function near z = 0 by

$${\psi }^0(z<0)=\frac{e^{i{k}_x+i{k}_{y}y}}{\sqrt{V}}\sum _{\sigma }(e^{i{k}_{z}z}{a}_{\sigma }^R{\xi }_{\sigma }+e^{-i{k}_{z}z}{a}_{\sigma }^L{\xi }_{\sigma }),$$ (37a)

$${\psi }^0(z>0)=\frac{e^{i{k}_x+i{k}_{y}y}}{\sqrt{V}}\sum _{\sigma }(e^{i{k}_z^{\sigma }z}{b}_{\sigma }^R{\xi }_{\sigma }+e^{-i{k}_z^{\sigma }z}{b}_{\sigma }^L{\xi }_{\sigma }),$$ (37b)

where R and L refer to right-going and left-going states respectively. Here and from now on we neglect subscripts kσ indicating electronic states for simplicity. We define column vectors ${\widehat{a}}^{R/L}={(a_{+}^{R/L},a_{-}^{R/L})}^T$ and ${\widehat{b}}^{R/L}={(b_{+}^{R/L},b_{-}^{R/L})}^T$. Applying the boundary conditions at z = 0 given by ψ⁰(+0) = ψ⁰(−0) and ψ⁰′(+0) − ψ⁰′(−0) = (2m_eħ²)H_Iψ⁰(0), we obtain the following linear relation between b̂^R/L and â^R/L:

$$\left(\begin{array}{c}{\widehat{b}}^R\\ {\widehat{b}}^L\end{array}\right)=M_0\left(\begin{array}{c}{\widehat{a}}^R\\ {\widehat{a}}^L\end{array}\right),$$ (38a)

$$M_0^{-1}=\frac{1}{2i{k}_z}\left(\begin{array}{cc}i{k}_z+i{\widehat{K}}_z-\widehat{\kappa }& i{k}_z-i{\widehat{K}}_z-\widehat{\kappa }\\ i{k}_z-i{\widehat{K}}_z+\widehat{\kappa }& i{k}_z+i{\widehat{K}}_z+\widehat{\kappa }\end{array}\right).$$ (38b)

Here the physical meaning of M₀ is the transfer matrix at z = 0 (from z = −0 to z = +0). We now express the wave function at z = L+0 by the matrices ĉ^R/L with a suitable basis determined by the structure in z < L. By solving the Schrödinger equation, we can also write down the following transfer matrix.

$$\left(\begin{array}{c}{\widehat{c}}^R\\ {\widehat{c}}^L\end{array}\right)=M_{0\to L}\left(\begin{array}{c}{\widehat{b}}^R\\ {\widehat{b}}^L\end{array}\right).$$ (39)

Here M_0→L is the transfer matrix from z = 0 to z = L + 0 of which the detailed form is unnecessary here.

We consider a situation that a wave ψ̂_i is incident from z < 0 and it splits up to reflected (ψ̂_r) and transmitted (ψ̂_t) parts. In the language of the transfer matrices,

$$\left(\begin{array}{c}{\widehat{\psi }}_t\\ 0\end{array}\right)=M_{0\to L}{M}_0\left(\begin{array}{c}{\widehat{\psi }}_i\\ {\widehat{\psi }}_r\end{array}\right).$$ (40)

Inverting this,

$$\begin{gathered} \left(\begin{array}{c}{\widehat{\psi }}_i\\ {\widehat{\psi }}_r\end{array}\right)=\frac{1}{2i{k}_z}\left(\begin{array}{cc}i{k}_z+i{\widehat{K}}_z-\widehat{\kappa }& i{k}_z-i{\widehat{K}}_z-\widehat{\kappa }\\ i{k}_z-i{\widehat{K}}_z+\widehat{\kappa }& i{k}_z+i{\widehat{K}}_z+\widehat{\kappa }\end{array}\right)M_{0\to L}^{-1}\left(\begin{array}{c}{\widehat{\psi }}_t\\ 0\end{array}\right) \\ \equiv \frac{1}{2i{k}_z}\left(\begin{array}{c}{\widehat{m}}_i\\ -{\widehat{m}}_r\end{array}\right){\widehat{\psi }}_t, \end{gathered}$$ (41)

where m̂_i/r are 2 × 2 matrices. Now the reflection matrix is given by ${\widehat{r}}_{\text{ex}}=-{\widehat{m}}_r{\widehat{m}}_i^{-1}$.

To expand ${\widehat{m}}_{r/i}={\widehat{m}}_{r/i}^{(0)}+{\widehat{m}}_{r/i}^{(1)}$, we split κ̂ = κ̂₀+κ̂_R. Here κ̂_R is essentially the Rashba Hamiltonian, but written in the ·̂ space where the magnetization direction is along z. Explicitly,

$${\widehat{\kappa }}_R=h_R\left(\begin{array}{cc}{\xi }_{+}^{†}\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z}){\xi }_{+}& {\xi }_{+}^{†}\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z}){\xi }_{-}\\ {\xi }_{-}^{†}\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z}){\xi }_{+}& {\xi }_{-}^{†}\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z}){\xi }_{-}\end{array}\right).$$ (42)

Then,

$$\left(\begin{array}{c}{\widehat{m}}_i^{(0)}\\ {\widehat{m}}_r^{(0)}\end{array}\right)=\left(\begin{array}{cc}i{k}_z+i{\widehat{K}}_z-{\widehat{\kappa }}_0& i{k}_z-i{\widehat{K}}_z-{\widehat{\kappa }}_0\\ -i{k}_z+i{\widehat{K}}_z-{\widehat{\kappa }}_0& -i{k}_z-i{\widehat{K}}_z-{\widehat{\kappa }}_0\end{array}\right)M_{0\to L}^{-1}\left(\begin{array}{c}1\\ 0\end{array}\right),$$ (43a)

$$\left(\begin{array}{c}{\widehat{m}}_i^{(1)}\\ {\widehat{m}}_r^{(1)}\end{array}\right)=-{\widehat{\kappa }}_R\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)M_{0\to L}^{-1}\left(\begin{array}{c}1\\ 0\end{array}\right).$$ (43b)

Equation (43) allows us to compute ${\widehat{m}}_{r/i}^{(1)}$ in terms of unperturbed quantities. A typical way would be expressing $M_{0\to L}^{-1}{(1,0)}^T$ in terms of ${\widehat{m}}_{i/r}^{(0)}$ by inverting the matrix in front of it. Putting this into Eq. (43b) will give ${\widehat{m}}_{i/r}^{(1)}$ in terms of ${\widehat{m}}_{i/r}^{(0)}$. However, the matrix inversion is very complicated. Instead, it is useful to observe from Eq. (43a) that

$$\left(\begin{array}{cc}1& -1\\ 1& -1\end{array}\right)\left(\begin{array}{c}{\widehat{m}}_i^{(0)}\\ {\widehat{m}}_r^{(0)}\end{array}\right)=2i{k}_z\left(\begin{array}{cc}1& 1\\ 1& 1\end{array}\right)M_{0\to d}^{-1}\left(\begin{array}{c}1\\ 0\end{array}\right).$$ (44)

Comparing with Eq. (43b), we obtain

$${\widehat{m}}_i^{(1)}={\widehat{m}}_r^{(1)}=-\frac{1}{2i{k}_z}{\widehat{\kappa }}_R({\widehat{m}}_i^{(0)}-{\widehat{m}}_r^{(0)}).$$ (45)

Note that this expression is not perturbative since we have not assumed a small h_R up to this point.

From Eq. (45), we calculate ${\widehat{r}}_{\text{ex}}=-{\widehat{m}}_r{\widehat{m}}_i^{-1}$. First, we perturbatively expand r̂_ex by ${\widehat{r}}_{\text{ex}}={\widehat{r}}_{\text{ex}}^{(0)}+{\widehat{r}}_{\text{ex}}^{(1)}+{\widehat{r}}_{\text{ex}}^{(2)}\cdots$, where ${\widehat{r}}_{\text{ex}}^{(n)}$ is the n-th order Rashba contribution. After some algebra, we obtain

$${\widehat{r}}_{\text{ex}}^{(n)}=2i{k}_z\widehat{G}{({\widehat{\kappa }}_R\widehat{G})}^n,$$ (46a)

$$\widehat{G}=\frac{1}{2i{k}_z}(1+{\widehat{r}}_{\text{ex}}^{(0)}).$$ (46b)

Here we used ${\widehat{m}}_i^{-1}={({\stackrel{\sim }{m}}_i^{(0)})}^{-1}-{({\stackrel{\sim }{m}}_i^{(0)})}^{-1}{\stackrel{\sim }{m}}_i^{(1)}{({\stackrel{\sim }{m}}_i^{(0)})}^{-1}+{({\stackrel{\sim }{m}}_i^{(0)})}^{-1}{\stackrel{\sim }{m}}_i^{(1)}{({\stackrel{\sim }{m}}_i^{(0)})}^{-1}{\stackrel{\sim }{m}}_i^{(1)}{({\stackrel{\sim }{m}}_i^{(0)})}^{-1}+\cdots$ and ${\widehat{\kappa }}_R\widehat{G}=-{\widehat{m}}_i^{(1)}{({\widehat{m}}_i^{(0)})}^{-1}$ actively. Taking n = 1 gives the same result as Eq. (10c). Since we do not assume anything about the underlying structure in z > 0, our result on the reflection matrix holds for arbitrary underlying structures.

Three remarks are in order. First, although the same expression holds only for the reflection matrix, it is very useful for some situations. If one looks into a response of the normal metal induced by a current flow in the normal metal, the expression only includes r̂_k. The anisotropic magneto-resistance calculated in Appendix A is an example. Second, this derivation is a mathematical result, so the results holds in the extended space. Projecting Eq. (46a) by 1̂ does indeed give Eq. (10c). Third, the derivation by the transfer matrix is somewhat more abstract than the scattering formalism in Sec. III, but it allows easily generalizing our result up to any higher order contributions from h_R. The second order term is used in Appendix A.

C. Effects of proximity-induced magnetism

We model proximity-induced magnetism as magnetism right at the interface in Sec. VB and VC. In this section, we present how one can treat effects of interface magnetism more generally.

We first consider a situation without interface magnetism, and then treat u_m separately. Let ${\widehat{r}}_{\text{ex}}^{u_m=0}$ be the reflection matrix in the absence of interface magnetism. Then, it would be valuable to see how the scattering coefficients change in the presence of u_m. The transfer matrix formalism in Sec. VI B allows calculating the contributions from u_m perturbatively. When we replace κ̂_R in Eq. (46a) by u_mσ̂_z, we obtain ${\widehat{r}}_{\text{ex}}={\widehat{r}}_{\text{ex}}^{u_m=0}+{\widehat{r}}_{\text{ex}}^{(1)}+{\widehat{r}}_{\text{ex}}^{(2)}+\cdots$ where ${\widehat{r}}_{\text{ex}}^{(n)}=-2i{k}_z\widehat{G}{(u_m{\widehat{\sigma }}_z\widehat{G})}^n$ and $G=(-1/2i{k}_z)(1+{\widehat{r}}_{\text{ex}}^{u_m=0})$. Here we use the fact that any two diagonal matrices commute with each other. The result is given by the sum of a geometric series. After some algebra,

$${\widehat{r}}_{\text{ex}}={\widehat{r}}_{\text{ex}}^{u_m=0}=\frac{1+{\widehat{r}}_{\text{ex}}^{u_m=0}}{2i{k}_z{u}_m^{-1}{\widehat{\sigma }}_z{(1+{\widehat{r}}_{\text{ex}}^{u_m=0})}^{-1}+1}.$$ (47)

This expression is of course consistent with Eqs. (23) and (31). The other scattering matrices are given by the constraints $1+{\widehat{r}}_{\text{ex}}=\sqrt{{\mid k_z\Vert {\widehat{K}}_z\mid }^{-1}}{\widehat{t}}_{\text{ex}},1+{\widehat{r}}_{\text{ex}}^{\prime }=\sqrt{{\mid {\widehat{K}}_z\Vert k_z\mid }^{-1}}{\widehat{t}}_{\text{ex}}^{\prime }$, and $(1+{\widehat{r}}_{\text{ex}})k_z^{-1}=(1+{\widehat{r}}_{\text{ex}}^{\prime }){\widehat{K}}_z^{-1}$.

Equation (47) allows for the exploration of interface magnetism effects up to any higher order in u_m or 1/u_m. By focusing on consequences of second term in Eq. (47), one can look into the effects of proximity-induced magnetism on a given expression.

VII. CONCLUSION

In summary, we develop a perturbation theory for scattering matrices to compute interfacial spin-orbit coupling effects in magnetic bilayers. We extend the two-dimensional Rashba model by embedding it in three-dimensional transport of electrons. We explicitly show that spin or charge current can be generated perpendicularly to an applied bias. Using this fact, we calculate current-induced (extrinsic) spin-orbit torque in terms of scattering amplitudes. For a given spin-orbit coupling Hamiltonian (like the Rashba form in our study), the resulting expressions from our theory are independent of details of the interface, so they are easily applicable for wide range of contexts. As demonstrations, we apply our formulas to various types of interfaces such as magnetic bilayers with bulk magnetism, those with interface magnetism, ferromagnetic insulators in contact with a nonmagnet, and topological insulators in contact with a ferromagnet.

For magnetic bilayers, we show that a dampinglike component can be on the same order of or larger than a fieldlike component, even without taking into account the Berry phase contribution and spin relaxation mechanisms. For the systems with insulating layers, we found that only a fieldlike component can arise, since a dampinglike component originates from a current across the interface. We also demonstrate that for finite bulk exchange coupling, the evanescent states that become important for the mismatched Fermi surfaces can give rise to the dominant contribution to spin-orbit torque.

Although we express the systems by analytic toy models, combining with first-principles calculations would enrich the implications of our theory significantly. We provide some remarks on possible generalization of our theory and future directions. Furthermore, we present other spin-orbit coupling phenomena, such as an in-plane current generation by a perpendicular bias (similar to the inverse spin Hall effect), a spin memory loss at the interface, and an anisotropic magnetoresistance (similar to the spin Hall magnetoresistance) in the appendices below. Our theory helps to characterize features of spin-orbit coupling phenomena for a given interface and further it provides insight on separating the roles of multiple sources of spin-orbit coupling effects such as spin Hall effect, interfacial spin-orbit coupling, and the magnetic proximity effect.

Note During preparation of the manuscript, we found a recent report [73] which uses a similar scattering formalism to our theory and describes several interface spin-orbit coupling phenomena, but focuses on a particular context, metallic bilayers without interface magnetism.

Appendix A: Other physical consequences of interfacial spin-orbit coupling

1. In-plane current induced by a perpendicular bias

The spin-orbit torque derived in the main text is essentially perpendicular spin current generation by in-plane charge current flow. Here we derive its Onsager counterpart. When a perpendicular bias (chemical potential difference) is applied, an in-plane current can be generated.

Suppose first that there is no spin-orbit coupling and note that the current operator is proportional to k. If the system has rotational symmetry around xy plane, all the scattering matrices must satisfy r̂_k = r̂_−k for any in-plane k vector and similar relations for r̂′, t̂, and t̂′. Thus, even if there is a perpendicular bias, any contribution from k to an in-plane current is canceled out by the opposite state −k. Therefore, there is no in-plane current generation by a perpendicular bias.

However, the situation drastically changes when interfacial spin-orbit coupling is introduced. Here we present the perturbation result in the main text again.

$${\widehat{t}}_{\mathbf{k}}={\widehat{t}}_{\mathbf{k}}^0+\frac{h_R}{2i{k}_z}{\widehat{t}}_{\mathbf{k},\text{ex}}^0\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z})({\widehat{1}}_{\mathbf{k}}+{\widehat{r}}_{\mathbf{k}}^0),$$ (A1a)

$${\widehat{t}}_{\mathbf{k}}^{\prime }={\widehat{t}}_{\mathbf{k}}^{\prime 0}+\frac{h_R}{2i{k}_z}(1+{\widehat{r}}_{\mathbf{k},\text{ex}}^0)\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z}){\widehat{t}}_{\mathbf{k}}^{\prime 0},$$ (A1b)

$${\widehat{r}}_{\mathbf{k}}={\widehat{r}}_{\mathbf{k}}^0+\frac{h_R}{2i{k}_z}(1+{\widehat{r}}_{\mathbf{k},\text{ex}}^0)\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z})({\widehat{1}}_{\mathbf{k}}+{\widehat{r}}_{\mathbf{k}}^0),$$ (A1c)

$${\widehat{r}}_{\mathbf{k}}^{\prime }={\widehat{r}}_{\mathbf{k}}^{\prime 0}+\frac{h_R}{2i{k}_z}{\widehat{t}}_{\mathbf{k},\text{ex}}^0\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z}){\widehat{t}}_{\mathbf{k}}^{\prime 0}.$$ (A1d)

The Rashba contributions are odd in k. When they are multiplied by the current operator, the contributions from k and −k are no longer canceled out, thus an in-plane current can arise. Since the Rashba contribution is also proportional to the Pauli matrix vector, a charge bias will generate an in-plane spin current and a spin bias will generate an in-plane charge current. The latter has the same symmetry as the inverse spin Hall effect, implying that one needs to be careful when analyzing experiments [47, 49, 56, 74–76] using the inverse spin Hall effect as highlighted in Ref. [63].

Here we derive explicit expressions of the current density at the interface. We do not assume k to be in-plane, thus our result will also recover the results of the magnetoelectric circuit theory. The current density at the normal metal along a unit vector u is calculated by

$${\stackrel{\sim }{j}}_{\mathbf{u}}(z<0)=-\frac{e}{2}{\text{Tr}}_{\sigma }[\rho \{v_u,\delta ({\mathbf{r}}_{\text{op}}-\mathbf{r})\}\widehat{\stackrel{\sim }{\sigma }}],$$ (A2)

where v_u = (ħ/m_ei)∂_u and ρ is the density matrix, r_op is the position operator, and r is the position c-number. σ̃ = (1,σ) is the four-dimensional Pauli matrix vector. j̃_u is a four-dimensional vector whose zeroth component is the charge current along u and the other three components are the spin current along u with spin x, y, z directions. Here and from now on, we denote any four-dimensional vector by the ·̃ notation. As we develop in the main text, each of the eigen-states is written by a wave incident from the normal metal or a wave incident from the ferromagnet. Thus, they allow writing down the density matrix by a block-diagonal form. Using the notation of direct summation, ρ = ρ^N + ρ^F, where ρ^N/F are the density matrices block consisting of electrons incident from the normal metal/ferromegnet side. Thus we split the current into two terms: ${\stackrel{\sim }{j}}_{\mathbf{u}}={\stackrel{\sim }{j}}_{\mathbf{u}}^{\mathrm{N}}+{\stackrel{\sim }{j}}_{\mathbf{u}}^{\mathrm{F}}$, where ${\stackrel{\sim }{j}}_{\mathbf{u}}^{\mathrm{N}/\mathrm{F}}=-\frac{e}{2}{\text{Tr}}_{\sigma }[{\rho }^{\mathrm{N}/\mathrm{F}}\{v_u,\delta ({\mathbf{r}}_{\text{op}}-\mathbf{r})\}\widehat{\stackrel{\sim }{\sigma }}]$.

Let ${\rho }^{\mathrm{N}}={\sum }_{\mathbf{k}{\sigma }^{\prime }\sigma }{f}_{\mathbf{k},{\sigma }^{\prime }\sigma }^{\mathrm{N}}\mid \mathbf{k}{\sigma }^{\prime }\rangle \langle \mathbf{k}\sigma \mid$ where $f_{\mathbf{k},{\sigma }^{\prime }\sigma }^{\mathrm{N}}$ is the 2 × 2 reduced density matrix. In a matrix form ${\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}$, each component is given by $f_{\mathbf{k},{\sigma }^{\prime }\sigma }^{\mathrm{N}}={\xi }_{{\sigma }^{\prime }}^{†}{\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}{\xi }_{\sigma }$. Since we consider a noncollinear spin injection from the normal metal, we allow for ${\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}$ having an off-diagonal component. By its definition, ${\widehat{1}}_{\mathbf{k}}{\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}{\widehat{1}}_{\mathbf{k}}={\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}$, since there is no incident electrons out of the Hilbert space. The current at the normal metal from ρ^N is then calculated by the wave function Eq. (2a). After some algebra,

$${\widehat{j}}_{\mathbf{u}}^{\mathrm{N}}(z<0)=-\frac{e\hslash }{m_{e}V}\sum _{\mathbf{k}}(\mathbf{k}·\mathbf{u}{\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}+\mathbf{k}·\overline{\mathbf{u}}{\widehat{r}}_{\mathbf{k}}{\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}{\widehat{r}}_{\mathbf{k}}^{†}),$$ (A3)

where ū = (u_x, u_y, −u_z). ${\widehat{j}}_{\mathbf{u}}^{\mathrm{N}/\mathrm{F}}$ is a 2 × 2 matrix whose Pauli components are $(1/2){\stackrel{\sim }{j}}_{\mathbf{u}}^{\mathrm{N}/\mathrm{F}}$, that is, ${\stackrel{\sim }{j}}_{\mathbf{u}}^{\mathrm{N}/\mathrm{F}}={\text{Tr}}_{\sigma }[\widehat{\stackrel{\sim }{\sigma }}{\widehat{j}}_{\mathbf{u}}^{\mathrm{N}/\mathrm{F}}]$.

When a perpendicular bias is applied, the distribution function shifts. In the linear response regime, the distribution shift occurs only near the Fermi surface. To focus on the nonequilibrium current, we replace ${\widehat{f}}_{\mathbf{k}}^{\mathrm{N}}=e\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{1}}_{\mathbf{k}}\delta (E-E_F)$ where Δμ̂^N is the shift of the chemical potential of the normal metal due to the bias. To deal with the delta function easily, we convert the summation in Eq. (A3) to an integration: Σ_k → (L/2π)Σ_k⊥ ∫dk_z. By using dE = (ħ²/m_e)k_zdk_z, we convert the summation to an integration over energy. Due to the delta function, the energy integration is nothing but the integrand evaluated at the Fermi level. As a result, we obtain

$${\widehat{j}}_{\mathbf{u}}^{\mathrm{N}}(z<0)=-\frac{e^{2}L}{hV}\sum _{{\mathbf{k}}_{\perp }}\frac{1}{k_z}{[\mathbf{k}·\mathbf{u}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{1}}_{\mathbf{k}}+\mathbf{k}·\overline{\mathbf{u}}{\widehat{r}}_{\mathbf{k}}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{r}}_{\mathbf{k}}^{†}]}_{E=E_F},$$ (A4)

where L is the length along z direction.

We use a similar method to obtain ${\widehat{j}}_{\mathbf{u}}^{\mathrm{F}}$. There are three differences. First, we assume that there are no off-diagonal elements in ${\widehat{f}}_{\mathbf{k}}^{\mathrm{F}}$ due to strong dephasing. Second, when we convert the summation by an integration, ${\mathrm{\sum }}_{\mathbf{k}}\to (L/2\pi ){\mathrm{\sum }}_{{\mathbf{k}}_{\perp }}\int d{k}_z^{\sigma }$, instead of dk_z, because the wave function is normalized by the incident wave. And then, we use $({\hslash }^2/m_e)k_z^{\sigma }d{k}_z^{\sigma }=dE$. Third, the intervals of the integrations are different. The integral interval for ${\widehat{j}}_{\mathbf{u}}^{\mathrm{N}}$ is 0 < E < E_F. However, in this case, the integral interval is σJ < E < E_F. However, since we focus on the Fermi surface contributions only, the lower bound of the energy does not matter. Omitting the algebra, we obtain

$${\widehat{j}}_{\mathbf{u}}^{\mathrm{F}}(z<0)=-\frac{e^{2}L}{hV}Re\sum _{{\mathbf{k}}_{\perp }}{\left[\frac{\mathbf{k}·\overline{\mathbf{u}}}{\mid k_z\mid }{e}^{2Im[k_z]z}{\widehat{t}}_{\mathbf{k}}^{\prime }\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{\widehat{t}}_{\mathbf{k}}^{\prime †}\right]}_{E=E_F}.$$ (A5)

Now, the current right in the normal metal near the interface is given by the Pauli components of

$${\widehat{j}}_{\mathbf{u}}(z<0)={\widehat{j}}_{\mathbf{u}}^{\mathrm{N}}(z<0)+{\widehat{j}}_{\mathbf{u}}^{\mathrm{F}}(z<0).$$ (A6)

In a similar way, we obtain the expression of the current in the ferromagnet near the interface.

$${\widehat{j}}_{\mathbf{u}}(z>0)={\widehat{j}}_{\mathbf{u}}^{\mathrm{N}}(z>0)+{\widehat{j}}_{\mathbf{u}}^{\mathrm{F}}(z>0),$$ (A7a)

where

$${\widehat{j}}_{\mathbf{u}}^{\mathrm{N}}(z>0)=-\frac{e^{2}L}{hV}Re\sum _{{\mathbf{k}}_{\perp }}{\left[\widehat{\mathbf{K}}·\mathbf{u}\frac{e^{i{\widehat{K}}_{z}z}}{\sqrt{\mid {\widehat{K}}_z\mid }}{\widehat{t}}_{\mathbf{k}}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{t}_{\mathbf{k}}^{†}\frac{e^{-i{\widehat{K}}_z^{\ast }z}}{\sqrt{\mid {\widehat{K}}_z\mid }}\right]}_{E=E_F},$$ (A7b)

$${\widehat{j}}_{\mathbf{u}}^{\mathrm{F}}(z>0)=-\frac{e^{2}L}{hV}Re\sum _{{\mathbf{k}}_{\perp }}\widehat{\mathbf{K}}·{\{\frac{e^{i{\widehat{K}}_{z}z}}{\sqrt{\mid {\widehat{K}}_z\mid }}\left[\overline{\mathbf{u}}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{\widehat{1}}_{{\mathbf{k}}^{\prime }}+\mathbf{u}{\widehat{r}}_{\mathbf{k}}^{\prime }\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{\widehat{r}}_{\mathbf{k}}^{†}{e}^{-2Im[{\widehat{K}}_z]z}+(\overline{\mathbf{u}}{e}^{-2i{\widehat{K}}_{z}z}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{\widehat{r}}_{\mathbf{k}}^{\prime †}+\mathbf{u}{\widehat{r}}_{\mathbf{k}}^{\prime }\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{e}^{2i{\widehat{K}}_{z}z})\right]\frac{e^{-i{\widehat{K}}_{z}z}}{\sqrt{{\widehat{K}}_z}}\}}_{E=E_F},$$ (A7c)

where K̂ = (k_x, k_y, K̂_z) is a vector consisting of 2 × 2 matrices. From Eqs. (A4)–(A7), one can compute the current near the interface for given (spin/charge) chemical potential excitation. As in the main text, we from now on omit the [⋯]_E=EF and implicitly assume that the expressions are evaluated at the Fermi level.

We now simplify the expressions more. In Eq. (A5), the Im[k_z] contribution originates from transmitted evanescent waves incident from the ferromagnet. For perpendicular transport, since k · ū/|k_z| is imaginary, there is no contribution from evanescent modes to a perpendicular current, consistently with the conservation of charge current. However, for in-plane transport, such a contribution can be nonzero. Note that the evanescent contribution dies after 1/k_z length scale. Since 1/k_F is shorter than the mean free path scale, the current is almost unmeasurable in experimental resolution. Thus, we neglect decaying contributions in Eqs. (A5) and (A7). ^10,11 We also neglect highly oscillating terms in Eq. (A7). This is a common approximation to take into account dephasing of a transverse component to m in the ferromagnet. Then, we obtain

$${\widehat{j}}_{\mathbf{u}}(z<0)=-\frac{e^{2}L}{hV}\sum _{{\mathbf{k}}_{\perp }}\frac{{\widehat{1}}_{\mathbf{k}}}{k_z}[\mathbf{k}·\overline{\mathbf{u}}({\widehat{r}}_{\mathbf{k}}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{r}}_{\mathbf{k}}^{†}+{\widehat{t}}_{\mathbf{k}}^{\prime }\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{\widehat{t}}_{\mathbf{k}}^{\prime †})+\mathbf{k}·\mathbf{u}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}].$$ (A8a)

$${\widehat{j}}_{\mathbf{u}}(z>0)=-\frac{e^{2}L}{hV}\sum _{{\mathbf{k}}_{\perp }}\frac{{\widehat{1}}_{{\mathbf{k}}^{\prime }}}{{\widehat{K}}_z}[\widehat{\mathbf{K}}·\mathbf{u}\text{Diag}[{\widehat{r}}_{\mathbf{k}}^{\prime }\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{\widehat{r}}_{\mathbf{k}}^{\prime †}+{\widehat{t}}_{\mathbf{k}}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{t}}_{\mathbf{k}}^{†}]]+\widehat{\mathbf{K}}·\overline{\mathbf{u}}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}},$$ (A8b)

where Diag[⋯] = Σ_s u_s[⋯]u_s is the spin-diagonal part of a matrix. Physical meaning of this operation is the dephasing of a transverse component of spin in the ferromagnet.

We first take u = z to see that Eq. (A8) is consistent with the conventional magnetoelectric circuit theory. It is easy to show that

$${\widehat{j}}_{\mathbf{z}}(z<0)=-\frac{e^{2}L}{hV}\sum _{k_{\perp }^2<k_F^2}[\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}-({\widehat{r}}_{\mathbf{k}}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{r}}_{\mathbf{k}}^{†}+{\widehat{t}}_{\mathbf{k}}^{\prime }\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{\widehat{t}}_{\mathbf{k}}^{\prime †})],$$ (A9)

which is exactly the result of the magnetoelectric circuit theory. One can also show with Eq. (A8) and the unitarity constraint developed in Sec. B that ĵ_z(z > 0) = Diag[ĵ_z(z < 0)]. This implies the continuity of electrical current across the interface, thus we do not need to keep (z > 0) or (z < 0). Following the procedure of the magnetoelectric circuit theory [45, 46], we take $\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}=\mathrm{\Delta }{\mu }_0^{\mathrm{N}}-\widehat{\mathit{\sigma }}·\mathbf{s}\mathrm{\Delta }{\mu }_s^{\mathrm{N}}$ where s is the direction of spin magnetic moment in the normal metal. s can be deviated from m when one considers noncollinear spin injection. We also take $\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}=\mathrm{\Delta }{\mu }_0^{\mathrm{F}}-\widehat{\mathit{\sigma }}·\mathbf{m}\mathrm{\Delta }{\mu }_s^{\mathrm{F}}$.¹² The scattering matrices are taken by Eq. (A1). However, all the first order Rashba contributions are canceled out after summing over all transverse modes. They are odd in in-plane momentum k_x or k_y, thus are canceled by an opposite contribution from −k_x or −k_y. Therefore, we can discard the Rashba contributions and take only unperturbed scattering matrices, which are expanded by ${\widehat{r}}_{\mathbf{k}}^0=r_{\mathbf{k}}^{\downarrow }{u}_{+}+r_{\mathbf{k}}^{\uparrow }{u}_{-}$ and so on. Then, spin and charge currents are given by

$$\frac{V}{L}{\text{Tr}}_{\sigma }[{\widehat{j}}_z]=(G^{\uparrow \uparrow }+G^{\downarrow \downarrow })(\mathrm{\Delta }{\mu }_0^{\mathrm{F}}-\mathrm{\Delta }{\mu }_0^{\mathrm{N}})+(G^{\uparrow \uparrow }-G^{\downarrow \downarrow })(\mathrm{\Delta }{\mu }_s^{\mathrm{F}}-\mathbf{m}·\mathbf{s}\mathrm{\Delta }{\mu }_s^{\mathrm{N}}),$$ (A10a)

$$-\frac{V}{L}{\text{Tr}}_{\sigma }[\widehat{\mathit{\sigma }}{\widehat{j}}_z]=(G^{\uparrow \uparrow }-G^{\downarrow \downarrow })(\mathrm{\Delta }{\mu }_0^{\mathrm{F}}-\mathrm{\Delta }{\mu }_0^{\mathrm{N}})\mathbf{m}+(G^{\uparrow \uparrow }+G^{\downarrow \downarrow })(\mathrm{\Delta }{\mu }_s^{\mathrm{F}}-\mathbf{m}·\mathbf{s}\mathrm{\Delta }{\mu }_s^{\mathrm{N}})\mathbf{m}-2Re\left[G^{\uparrow \downarrow }[\mathbf{m}\times (\mathbf{s}\times \mathbf{m})+i\mathbf{s}\times \mathbf{m}]\right]\mathrm{\Delta }{\mu }_s^{\mathrm{N}},$$ (A10b)

where $G^{s{s}^{\prime }}=(e^2/h){\sum }_{k_{\perp }^2<k_F^2}(1-r_{\mathbf{k}}^s{r}_{\mathbf{k}}^{s^{\prime }\ast })$. G^{↑↑/↓↓} is the interface conductance for spin majority/minority electrons and G^↑↓ is the spin mixing conductance. Eq. (A10) recovers all the results in the traditional theory.

We now take an in-plane u. As we discuss above, non-Rashba contributions cannot generate an in-plane current. Using Eq. (A1) and collecting the first order contributions to h_R,

$${\widehat{j}}_{\mathbf{u}}(z<0)=-h_R\frac{e^{2}L}{hV}Im\sum _{k_{\perp }^2<k_F^2}\frac{\mathbf{k}·\mathbf{u}}{k_z^2}(1+{\widehat{r}}_{\mathbf{k}}^0)\widehat{\mathit{\sigma }}·(\mathbf{k}\times \mathbf{z})\times [(1+{\widehat{r}}_{\mathbf{k}}^0)\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{r}}_{\mathbf{k}}^{0†}+{\widehat{t}}_{\mathbf{k}}^0\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{t}_{\mathbf{k}}^{\prime 0†}].$$ (A11)

When summing up over all transverse modes, one should consider all possible angles of k_⊥ for a given magnitude. If the system has rotational symmetry, we can take an angle average of (k · u)[σ̂ · (k × z)] by integrating over the in-plane angle from −π to π and dividing the result by 2π. Then, we obtain $(k_{\perp }^2/2)\widehat{\mathit{\sigma }}·(\mathbf{u}\times \mathbf{z})$. After the angle average,

$${\widehat{j}}_{\mathbf{u}}(z<0)=-h_R\frac{e^{2}L}{2hV}Im\sum _{k_{\perp }^2<k_F^2}\frac{E_{\perp }}{E_F-E_{\perp }}(1+{\widehat{r}}_{\mathbf{k}}^0)\widehat{\mathit{\sigma }}·(\mathbf{u}\times \mathbf{z})\times [(1+{\widehat{r}}_{\mathbf{k}}^0)\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{r}}_{\mathbf{k}}^{0†}+{\widehat{t}}_{\mathbf{k}}^0\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{F}}{\widehat{t}}_{\mathbf{k}}^{\prime 0†}].$$ (A12)

Here $E_{\perp }={\hslash }^2{k}_{\perp }^2/2m_e$ and we used $k_{\perp }^2/k_z^2=E_{\perp }/(E_F-E_{\perp })$. Then, the in-plane spin and charge currents are given by its Pauli components.

$$\frac{V}{L}{\text{Tr}}_{\sigma }[{\widehat{j}}_u(z<0)]=-\frac{(\mathbf{u}\times \mathbf{z})}{2i}·\left[(G_{Rt}^{\uparrow \uparrow \uparrow }-G_{Rt}^{\downarrow \downarrow \downarrow })(\mathrm{\Delta }{\mu }_0^{\mathrm{F}}-\mathrm{\Delta }{\mu }_0^{\mathrm{N}})\mathbf{m}+(G_{Rt}^{\uparrow \uparrow \uparrow }+G_{Rt}^{\downarrow \downarrow \downarrow })(\mathrm{\Delta }{\mu }_s^{\mathrm{F}}-\mathbf{m}·\mathbf{s}\mathrm{\Delta }{\mu }_s^{\mathrm{N}})\mathbf{m}+(G_{Rr}^{\uparrow \downarrow \downarrow }-G_{Rr}^{\downarrow \uparrow \uparrow \ast })\mathrm{\Delta }{\mu }_s^{\mathrm{N}}[\mathbf{m}\times (\mathbf{s}\times \mathbf{m})+i\mathbf{s}\times \mathbf{m}]\right]+\text{c.c.},$$ (A13a)

$$\begin{gathered} -\frac{V}{L}{\text{Tr}}_{\sigma }[\widehat{\mathit{\sigma }}{\widehat{j}}_u(z<0)]=-\mathbf{m}\frac{(\mathbf{u}\times \mathbf{z})}{2i}·[(G_{Rt}^{\uparrow \uparrow \uparrow }+G_{Rt}^{\downarrow \downarrow \downarrow })(\mathrm{\Delta }{\mu }_0^{\mathrm{F}}-\mathrm{\Delta }{\mu }_0^{\mathrm{N}})\mathbf{m}+(G_{Rt}^{\uparrow \uparrow \uparrow }-G_{Rt}^{\downarrow \downarrow \downarrow })(\mathrm{\Delta }{\mu }_s^{\mathrm{F}}-\mathbf{m}·\mathbf{s}\mathrm{\Delta }{\mu }_s^{\mathrm{N}})\mathbf{m}-(G_{Rr}^{\uparrow \downarrow \downarrow }+G_{Rr}^{\downarrow \uparrow \uparrow \ast })\mathrm{\Delta }{\mu }_s^{\mathrm{N}}[\mathbf{m}\times (\mathbf{s}\times \mathbf{m})+i\mathbf{s}\times \mathbf{m}]] \\ -\frac{1}{2i}\left[(G_{Rt}^{\uparrow \downarrow \downarrow }-G_{Rt}^{\downarrow \uparrow \uparrow \ast })\mathrm{\Delta }{\mu }_0^{\mathrm{F}}-(G_{Rt}^{\uparrow \downarrow \downarrow }+G_{Rt}^{\downarrow \uparrow \uparrow \ast })\mathrm{\Delta }{\mu }_s^{\mathrm{F}}+(G_{Rr}^{\uparrow \downarrow \downarrow }-G_{Rr}^{\downarrow \uparrow \uparrow \ast })\mathrm{\Delta }{\mu }_0^{\mathrm{N}}-\mathbf{m}·\mathbf{s}(G_{Rr}^{\uparrow \downarrow \downarrow }+G_{Rr}^{\downarrow \uparrow \uparrow \ast })\mathrm{\Delta }{\mu }_s^{\mathrm{N}}\right] \\ \times \{\mathbf{m}\times [(\mathbf{u}\times \mathbf{z})\times \mathbf{m}]-i\mathbf{m}\times (\mathbf{u}\times \mathbf{z})\}-\frac{(\mathbf{u}\times \mathbf{z})·\mathbf{m}}{2i}(G_{Rr}^{\uparrow \uparrow \downarrow }+G_{Rr}^{\downarrow \downarrow \uparrow \ast })\mathrm{\Delta }{\mu }_s^{\mathrm{N}}[\mathbf{m}\times (\mathbf{s}\times \mathbf{m})+i\mathbf{s}\times \mathbf{m}]+\text{c.c.} \end{gathered}$$ (A13b)

where c.c. refers to complex conjugate of all terms in front of it. In the conductances $G_{Rr}^{s{s}^{\prime }{s}^{″}}$ and $G_{Rt}^{s{s}^{\prime }{s}^{″}}$, the subscript R refers to Rashba contributions, and r and t refer to contributions from reflection and transmission. The explicit expressions in terms of unperturbed scattering matrices are

$$G_{Rr}^{s{s}^{\prime }{s}^{″}}=-h_R\frac{e^2}{2h}\sum _{{\mathbf{k}}_{\perp }}\frac{E_{\perp }}{E_F-E_{\perp }}(1+r_{\mathbf{k}}^s)(1+r_{\mathbf{k}}^{s^{\prime }})r_{\mathbf{k}}^{s^{″}\ast },$$ (A14a)

$$G_{Rt}^{s{s}^{\prime }{s}^{″}}=-h_R\frac{e^2}{2h}\sum _{{\mathbf{k}}_{\perp }}\frac{E_{\perp }}{E_F-E_{\perp }}(1+r_{\mathbf{k}}^s)t_k^{\prime s^{\prime }}{t}_{\mathbf{k}}^{\prime s^{″}\ast }.$$ (A14b)

Equation (A13a) clearly demonstrates a charge current is generated by a spin chemical potential bias. For the case of collinear transport (s = m), the charge current along u = x is proportional to m_y. Since the inverse spin Hall effect is also dependent on m_y, it requires a careful analysis. Simultaneous description of the inverse spin Hall effect and interfacial spin-orbit coupling would be a future challenge.

As passing remarks, we present some properties of $G_{Rr/t}^{s{s}^{\prime }{s}^{″}}$. First, there are three indices. This is because there is interfacial spin-orbit coupling as an additional spin scattering source. A complete description requires three indices; first one for the incident spin, second one for the scattering due to interfacial spin-orbit coupling, and third one for the transmitted spin. Second, $G_{Rr/t}^{s{s}^{\prime }{s}^{″}}$ is symmetric under exchange between s and s′. Third, the unitarity constraint in Sec. B implies $Im[G_{Rr}^{\mathit{sss}}]+Im[G_{Rt}^{\mathit{sss}}]=0$. This is shown by using ${\mid r_{\mathbf{k}}^s\mid }^2+{\mid t_{\mathbf{k}}^{\prime s}\mid }^2=1$ to derive $G_{Rr}^{\mathit{sss}}+G_{Rt}^{\mathit{sss}}=-(h_R{e}^2/2h){\sum }_{k_{\perp }^2<k_F^2}[(E_{\perp })/(E_F-E_{\perp })]{\mid 1+r_{\mathbf{k}}^s\mid }^2$. This constraint guarantees the absence of a charge current generation at equilibrium.

We also remark that in-plane current can be discontinuous at the interface in the presence of interfacial spin-orbit coupling. To see this, we define a discontinuity matrix by Δĵ_u = ĵ_u(z > 0) − Diag[ĵ_u(z < 0)]. This is zero for u = z, not for an in-plane u. After some algebra, we obtain

$$\frac{V}{L}{\text{Tr}}_{\sigma }[\mathrm{\Delta }{\widehat{j}}_{\mathbf{u}}]=\frac{(\mathbf{u}\times \mathbf{z})}{2i}·\left[(\mathrm{\Delta }{G}_h^{\uparrow \uparrow }-G_{R\mathrm{\Delta }}^{\downarrow \downarrow })(\mathrm{\Delta }{\mu }_0^{\mathrm{F}}-\mathrm{\Delta }{\mu }_0^{\mathrm{N}})\mathbf{m}+(G_{R\mathrm{\Delta }}^{\uparrow \uparrow }+G_{R\mathrm{\Delta }}^{\downarrow \downarrow })(\mathrm{\Delta }{\mu }_s^{\mathrm{F}}-\mathbf{m}·\mathbf{s}\mathrm{\Delta }{\mu }_s^{\mathrm{N}})\mathbf{m}-2G_{R\mathrm{\Delta }}^{\uparrow \downarrow }\mathbf{m}\times (\mathbf{s}\times \mathbf{m})\mathrm{\Delta }{\mu }_s^{\mathrm{N}}\right]+\text{c.c.},$$ (A15a)

$$-\frac{V}{L}{\text{Tr}}_{\sigma }[\widehat{\mathit{\sigma }}\mathrm{\Delta }{\widehat{j}}_{\mathbf{u}}]=\frac{(\mathbf{u}\times \mathbf{z})}{2i}·\left[(G_{R\mathrm{\Delta }}^{\uparrow \uparrow }+G_{R\mathrm{\Delta }}^{\downarrow \downarrow })(\mathrm{\Delta }{\mu }_0^{\mathrm{F}}-\mathrm{\Delta }{\mu }_0^{\mathrm{N}})\mathbf{m}+(G_{R\mathrm{\Delta }}^{\uparrow \uparrow }-G_{R\mathrm{\Delta }}^{\downarrow \downarrow })(\mathrm{\Delta }{\mu }_s^{\mathrm{F}}-\mathbf{m}·\mathbf{s}\mathrm{\Delta }{\mu }_s^{\mathrm{N}})\mathbf{m}+2i{G}_{R\mathrm{\Delta }}^{\uparrow \downarrow }\mathbf{s}\times \mathbf{m}\mathrm{\Delta }{\mu }_s^{\mathrm{N}}\right]+\text{c.c.},$$ (A15b)

where

$$G_{R\mathrm{\Delta }}^{s{s}^{\prime }}=-h_R\frac{e^2}{2h}\sum _{k_{\perp }^2<k_F^2}\frac{E_{\perp }}{E_F-E_{\perp }}(1+r_{\mathbf{k}}^s)(1+r_{\mathbf{k}}^{s^{\prime }}).$$ (A16)

Before closing the section, we mention that the currents are proportional to L, the size of the system. In reality, the contributions will relax on the length scale of the mean free path λ. Thus, if L ≫ λ, L in the above expressions should be replaced by λ when one takes into account the bulk scattering.

In the main text and this section, we have demonstrated that a bias can generate a current perpendicular to the applied bias direction, not affecting its longitudinal transport. These results are first order perturbation theory. In the following two sections, we calculate second order effects in h_R to examine the effects of interfacial spin-orbit coupling on longitudinal transport. Each section deals with a perpendicular bias to the interface and an in-plane bias respectively.

2. Spin memory loss and spin torque from collinear spin injection

Equation (A10) describes the generation of a perpendicular current to the interface in the presence of a perpendicular bias. Spin flip at the interface due to interfacial spin-orbit coupling vanishes due to rotation symmetry around the xy plane. However, if we consider second order contributions, the result can change. Below we demonstrate, a spin-up (down) current can be generated by a spin-down (up) bias. This means that interfacial spin-orbit coupling flips the spin at the interface even when we consider a collinear transport. We interpret this as spin memory loss at the interface.

We start from Eq. (A9). The second order expansion is given by Eq. (46a). For simplicity, we consider only collinear transport with perpendicular magnetization (s = m = z). For s ≠ m, the coefficient of spin torque in Eq. (A10) will also change. For m ≠ z, the result will depend on the direction of the magnetization, leading to a current-perpendicular magnetoresistance. Below we make more remarks on this case.

Writing down the expression explicitly, one realizes that the Rashba contributions arises in the form of κ̂_RÂκ̂_R. For instance, there is a contribution proportional to $4k_z^2\widehat{G}[{\widehat{\kappa }}_R\widehat{G}\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}{\widehat{G}}^{†}{\widehat{\kappa }}_R]{\widehat{G}}^{†}$. The angle average over all transverse modes simplifies such expressions a lot. From Eq. (42) and some algebra, angle average of κ̂_RÂκ̂_R for an arbitrary diagonal matrix  is also diagonal:

$${\widehat{\kappa }}_R\left(\begin{array}{cc}{a}_1& 0\\ 0& a_2\end{array}\right){\widehat{\kappa }}_R\to h_R^2{k}_{\perp }^2\left(\begin{array}{cc}{a}_2& 0\\ 0& a_1\end{array}\right).$$ (A17)

We emphasize that the diagonal components are exchanged. As we show below, this exchange results in mixing of spin-up and spin-down components. As a result, a spin-up (down) bias can generate spin-down (up) current.

To see spin flip at the interface clearly, we use up/down (↑/↓) notations rather than the spin/charge (0/s) notations used in Sec. A1. We expand $\mathrm{\Delta }{\widehat{\mu }}^{\mathrm{N}}=\mathrm{\Delta }{\mu }_{\downarrow }^{\mathrm{N}}{u}_{+}+\mathrm{\Delta }{\mu }_{\uparrow }^{\mathrm{N}}{u}_{-}$ and similarly for Δμ̂^F.13 We also define I_↑↓ = (V/L) Tr_σ[u_Ŧ ĵ_z], which are spin-up/down currents. We simply denote Δμ_↑/↓, $\mathrm{\Delta }{\mu }_{\uparrow \downarrow }^{\mathrm{F}}-\mathrm{\Delta }{\mu }_{\uparrow \downarrow }^{\mathrm{N}}$, the spin chemical potential difference across the interface. After some algebra,

$$\left(\begin{array}{c}{I}_{\uparrow }\\ I_{\downarrow }\end{array}\right)=\left(\begin{array}{cc}{G}^{\uparrow \uparrow }-2h_{R}Re{G}_{Rr}^{\downarrow \uparrow \uparrow }& G_{\text{flip}}\\ G_{\text{flip}}& G^{\downarrow \downarrow }-2h_{R}Re{G}_{Rr}^{\uparrow \downarrow \downarrow }\end{array}\right)\left(\begin{array}{c}\mathrm{\Delta }{\mu }_{\uparrow }\\ \mathrm{\Delta }{\mu }_{\downarrow }\end{array}\right),$$ (A18a)

$$G_{\text{flip}}=h_R^2\frac{e^2}{2h}\sum _{k_{\perp }^2<k_F^2}\frac{E_{\perp }}{E_F-E_{\perp }}{\mid 1+r_{\mathbf{k}}^{\uparrow }\mid }^2{\mid 1+r_{\mathbf{k}}^{\downarrow }\mid }^2.$$ (A18b)

Here G^ss are the unperturbed interface conductances derived from the magnetoelectric circuit theory. The corrections to the diagonal terms are the second order corrections¹⁴ from interfacial spin-orbit coupling. These diagonal terms simply describes a spin-up/down current generation by a spin-up/down bias. On the other hand, G_flip describes spin-flipping contributions: A spin-up (down) bias generates spin down (up) current.

If m ≠ z, Eq. (A17) does not hold. Even the result is not diagonal.¹⁵ The existence of an off-diagonal element implies that one cannot use the two-current model and there arises a spin current whose spin direction is transverse to the magnetization. This means that a spin torque (depending on m_z) can be generated even for a collinear spin injection. Due to complexity of the expressions, we do now show it here, but the expression is given by exactly the same procedure [except Eq. (A17)]. Although this is a second order effect, it would be valuable if this spin torque is experimentally realized.

The spin memory loss and spin torque we illustrate above do not violate the conservation of angular momentum. The source of the angular momentum is nothing but the lattice at the interface. Spin-orbit coupling at the interface pumps orbital angular momentum from (to) the lattice to (from) the spin-magnetization system.

3. Anisotropic magnetoresistance

In the previous section, we examine second order effects for perpendicular transport to the interface. In this section, we consider in-plane transport. We below show that the electrical resistance depends on the direction of magnetization. When a charge current is flowing along x, the resistance includes terms proportional to $m_x^2$ and $m_y^2$. The former has the same symmetry with the conventional anisotropic magnetoresistance from ferromagnetic bulk, but can have the opposite sign. The latter has the same symmetry as the spin Hall magnetoresistance [50–55].

For simplicity we consider a current mainly flowing in the normal metal. When a charge current is flowing in the normal metal, the distribution function is shifted: $f_{\mathbf{k}}^{\mathrm{N}}=f_{\mathbf{k}}^{0,\mathrm{N}}+(eE\hslash /m_e)k_x\delta (E-E_F)$ where x is the direction of the current flow. Or equivalently, Δμ̂^N = (Eħτ/m_e)k_x. Putting this and u = x into Eq. (A4) and taking trace over the spin space gives the charge current due to the distribution shift.

$${\text{Tr}}_{\sigma }[{\widehat{j}}_x^{\mathrm{N}}]=-\frac{e^{2}E\tau L}{2\pi m_{e}V}{\text{Tr}}_{\sigma }\sum _{k_{\perp }^2<k_F^2}\frac{k_x^2}{k_z}(1+{\widehat{r}}_{\mathbf{k}}{\widehat{r}}_{\mathbf{k}}^{†}).$$ (A19)

The first term in the parenthesis (1) is the conventional electrical current and the second term ( ${\widehat{r}}_{\mathbf{k}}{\widehat{r}}_{\mathbf{k}}^{†}$) is the Rashba contribution. The second order expansion is given by Eq. (46a). First order Rashba contributions are odd in k_⊥ so are all canceled out after summing up over all transverse modes.

To compute second order contributions, by the same reason in Sec. A2, we take angle average of the expression κ̂_RÂκ̂_R for a diagonal Â.

$$k_x^2{\widehat{\kappa }}_R\left(\begin{array}{cc}{a}_1& 0\\ 0& a_2\end{array}\right){\widehat{\kappa }}_R\to h_R^2\frac{k_{\perp }^4}{2}\left(\begin{array}{cc}{a}_2& 0\\ 0& a_1\end{array}\right)+(a_2-a_1)\frac{h_R^2{k}_{\perp }^4{m}_z}{8m_{\Vert }}(m_x^2+3m_y^2){\widehat{\sigma }}_x+(a_2-a_1)\frac{h_R^2{k}_{\perp }^4}{4m_{\Vert }}{m}_x{m}_y{\widehat{\sigma }}_y+(a_2-a_1)\frac{h_R^2{k}_{\perp }^4}{8}(m_x^2+3m_y^2){\widehat{\sigma }}_z,$$ (A20)

after angle average. Here $m_{\Vert }=\sqrt{m_x^2+m_y^2}$.

In charge transport, the result is given by taking the trace. Thus the diagonal terms (the first and last terms) only matter. Due to the existence of ( $m_x^2+3m_y^2$) contribution in front of σ̂_z, a magnetoresistance proportional to ( $m_x^2+3m_y^2$) can arise. If the reflection matrix is spin independent, the magnetoresistance is zero since Tr[σ_z] = 0. However, if the reflection matrix is spin dependent, the contribution can survive. In a previous work [33], a magnetoresistance proportional to ( $m_x^2+3m_y^2$) is reported, but is proportional to τ^↑ − τ^↓, thus a current should flow in the ferromagnet. This is because their model assumes an equal-Fermi-surface model. On the other hand, we take into account more generalized situation and demonstrate that a magnetoresistance $\propto (m_x^2+3m_y^2)$ can arise if $r_{\mathbf{k}}^{\uparrow }\ne r_{\mathbf{k}}^{\downarrow }$.

Another remark is that the term $3m_y^2$ has the same symmetry as the spin Hall magnetoresistance. Therefore, the spin Hall magnetoresistance should also be carefully analyzed since there is an interface contribution. There are several theoretical and experimental reports [16, 32–34] that interface Rashba effect can give rise to a magnetoresistance having the same symmetry as the spin Hall magnetoresistance. Another difference is that the Rashba contribution has a $m_x^2$ contribution as well. The contribution has the same symmetry as the conventional anisotropic magnetoresistance, but below we show that it can have the opposite sign (we call it a negative magnetoresistance). Therefore, observing the spin-Hall-like magnetoresistance and a negative anisotropic magnetoresistance of a similar orders of magnitude will shed light on separating the bulk effects and the interfacial effects.

To complete our analysis, we explicitly calculate the current [Eq. (A19)] with Eqs. (46a) and (A20). After some algebra,

$${\text{Tr}}_{\sigma }[{\widehat{j}}_x^{\mathrm{N}}]=j_{\text{conv}}+j_{\text{nonMR}}+j_{\text{MR}}(m_x^2+2m_y^2),$$ (A21a)

$$j_{\text{conv}}=-\frac{e^{2}E\tau L}{4\pi m_{e}V}\sum _{k_{\perp }^2<k_F^2,s=\uparrow ,\downarrow }\frac{k_{\perp }^2}{k_z}(1+{\mid r_{\mathbf{k}}^s\mid }^2),$$ (A21b)

$$j_{\text{nonMR}}=-h_R^2\frac{e^{2}E\tau L}{8\pi m_{e}V}\times Re\sum _{k_{\perp }^2<k_F^2}\frac{k_{\perp }^4}{k_z^3}{\rho }_{\mathbf{k}}^{\uparrow }{\rho }_{\mathbf{k}}^{\downarrow }({\rho }_{\mathbf{k}}^{\uparrow \ast }{\rho }_{\mathbf{k}}^{\downarrow \ast }+{\rho }_{\mathbf{k}}^{\downarrow }{\rho }_{\mathbf{k}}^{\downarrow \ast }+{\rho }_{\mathbf{k}}^{\uparrow }{r}_{\mathbf{k}}^{\uparrow \ast }),$$ (A21c)

$$j_{\text{MR}}=-h_R^2\frac{e^{2}E\tau L}{32\pi m_{e}V}Re\sum _{k_{\perp }^2<k_F^2}[{({\mid {\rho }_{\mathbf{k}}^{\uparrow }\mid }^2-{\mid {\rho }_{\mathbf{k}}^{\downarrow }\mid }^2)}^2-2({\rho }_{\mathbf{k}}^{\uparrow }-{\rho }_{\mathbf{k}}^{\downarrow })({\rho }_{\mathbf{k}}^{\uparrow 2}{r}_{\mathbf{k}}^{\uparrow \ast }-{\rho }_{\mathbf{k}}^{\downarrow 2}{r}_{\mathbf{k}}^{\downarrow \ast })],$$ (A21d)

where ${\rho }_{\mathbf{k}}^{\uparrow \downarrow }=1+r_{\mathbf{k}}^{\uparrow \downarrow }$. Here j_conv is the non-Rashba contribution, j_nonMR is the second order Rashba correction that is independent of m, and j_MR is the magnetoresistance. If the summand in j_MR is positive, the magnitude of the current increases when $m_x^2$ increases, which is the negative magnetoresistance. Below we discuss when a negative magnetoresistance arises.

For magnetic bilayers, if bulk magnetism is dominant, the reflection matrix is real [See Eq. (18a)]. The reality of $r_{\mathbf{k}}^{\uparrow \downarrow }$ allows simplifying the summand in j_MR as

$$[{({\mid {\rho }_{\mathbf{k}}^{\uparrow }\mid }^2-{\mid {\rho }_{\mathbf{k}}^{\downarrow }\mid }^2)}^2-2Re[({\rho }_{\mathbf{k}}^{\uparrow }-{\rho }_{\mathbf{k}}^{\downarrow })({\rho }_{\mathbf{k}}^{\uparrow 2}{r}_{\mathbf{k}}^{\uparrow \ast }-{\rho }_{\mathbf{k}}^{\downarrow 2}{r}_{\mathbf{k}}^{\downarrow \ast })])={(r_{\mathbf{k}}^{\uparrow }-r_{\mathbf{k}}^{\downarrow })}^2(2-r_{\mathbf{k}}^{\uparrow 2}-r_{\mathbf{k}}^{\downarrow 2})\ge 0.$$ (A22)

For ferromagnetic insulators, one can deduce j_MR = 0. This is consistent with the Landauer-Büttiker formalism. Since the ferromagnet is insulating, the conductance (thus resistance) is determined by the number of transverse modes in the normal metal, and is independent of the magnetization direction. This is a general result which holds unless the translational symmetry along the current flowing direction is broken or there is a spin-dependent scattering source (for example, the spin Hall effect generating spin Hall magnetoresistance). The case for the topological insulators cannot be described by Eq. (A21) since we assume that a current is flowing in the normal metal. But we mention that it was studied in a previous report [33]. For complex $r_{\mathbf{k}}^{\uparrow \downarrow }$ in metallic magnetic bilayers, we found no a priori argument which guarantees the sign of j_MR.

Appendix B: Unitarity constraint of the scattering amplitudes

Provided that all waves are propagating, charge conservation implies the following unitarity constraint: For the following scattering matrix

$$S_{\mathbf{k}}=\left(\begin{array}{cc}{\widehat{r}}_{\mathbf{k}}& {\widehat{t}}_{\mathbf{k}}^{\prime }\\ {\widehat{t}}_{\mathbf{k}}& {\widehat{r}}_{\mathbf{k}}^{\prime }\end{array}\right),$$ (B1)

$S_{\mathbf{k}}^{†}{S}_{\mathbf{k}}=1$ holds. Up to this point, the expressions are conventional. However, this works only if all waves are propagating, thus it must be generalized to the extended space. In this section, we omit the subscript ‘ex’ for simplicity.

Let the σ = +1 band be evanescent in the ferromagnet. As far as unitarity is concerned, some of matrices should be projected into σ = −1. Note that S_k connects incoming waves to outgoing waves.

$$\left(\begin{array}{c}{\psi }_{\mathbf{k}}^{N,\text{out}}\\ {\psi }_{\mathbf{k}}^{F,\text{out}}\end{array}\right)=S_{\mathbf{k}}\left(\begin{array}{c}{\psi }_{\mathbf{k}}^{N,\text{in}}\\ {\psi }_{\mathbf{k}}^{F,\text{in}}\end{array}\right)$$ (B2)

The transmitted outgoing waves for σ = +1 electrons are dropped. Thus t̂_k → u₋t̂_k and ${\widehat{r}}_{\mathbf{k}}^{\prime }\to u_{-}{\widehat{r}}_{\mathbf{k}}^{\prime }$. In addition, there is no contribution incident from FM for σ = +1 electrons. Thus ${\widehat{t}}_{\mathbf{k}}^{\prime }\to {\widehat{t}}_{\mathbf{k}}^{\prime }{u}_{-}$ and $u_{-}{\widehat{r}}_{\mathbf{k}}^{\prime }\to u_{-}{\widehat{r}}_{\mathbf{k}}^{\prime }{u}_{-}$. Thus the projected scattering matrix is

$$S_{\mathbf{k}}^{\text{proj}}=\left(\begin{array}{cc}{\widehat{r}}_{\mathbf{k}}& {\widehat{t}}_{\mathbf{k}}^{\prime }{u}_{-}\\ u_{-}{\widehat{t}}_{\mathbf{k}}& u_{-}{\widehat{r}}_{\mathbf{k}}^{\prime }{u}_{-}\end{array}\right).$$ (B3)

Lastly, the unitarity constraint is given by the conservation of electrical charge. Neglecting σ = +1 in the ferromagnet, the unitarity constraint is given by

$${(S_{\mathbf{k}}^{\text{proj}})}^{†}{S}_{\mathbf{k}}^{\text{proj}}=\left(\begin{array}{cc}1& 0\\ 0& u_{-}\end{array}\right).$$ (B4)

Let only σ = −1 band be propagating. There is no contribution from r̂_k, t̂_k, and ${\widehat{t}}_{\mathbf{k}}^{\prime }$ for the unitarity constraint.

$$S_{\mathbf{k}}^{\text{proj}}=\left(\begin{array}{cc}0& 0\\ 0& u_{-}{\widehat{r}}_{\mathbf{k}}^{\prime }{u}_{-}\end{array}\right),$$ (B5)

and the unitarity constraint is given by

$${(S_{\mathbf{k}}^{\text{proj}})}^{†}{S}_{\mathbf{k}}^{\text{proj}}=\left(\begin{array}{cc}0& 0\\ 0& u_{-}\end{array}\right).$$ (B6)

The above relations also hold when the order of ${(S_{\mathbf{k}}^{\text{proj}})}^{†}$ and $S_{\mathbf{k}}^{\text{proj}}$ is reversed.

The three expressions can be combined by means of the projection matrices.

$$S_{\mathbf{k}}^{\text{proj}}=\left(\begin{array}{cc}{\widehat{1}}_{\mathbf{k}}{\widehat{r}}_{\mathbf{k}}& {\widehat{1}}_{\mathbf{k}}{\widehat{t}}_{\mathbf{k}}^{\prime }\\ {\widehat{1}}_{\mathbf{k}}^{\prime }{\widehat{t}}_{\mathbf{k}}& {\widehat{1}}_{\mathbf{k}}^{\prime }{\widehat{r}}_{\mathbf{k}}^{\prime }\end{array}\right),$$ (B7)

$${(S_{\mathbf{k}}^{\text{proj}})}^{†}{S}_{\mathbf{k}}^{\text{proj}}=S_{\mathbf{k}}^{\text{proj}}{(S_{\mathbf{k}}^{\text{proj}})}^{†}=\left(\begin{array}{cc}{\widehat{1}}_{\mathbf{k}}& 0\\ 0& {\widehat{1}}_{\mathbf{k}}^{\prime }\end{array}\right).$$ (B8)

Explicitly calculating each component gives the unitarity constraint of scattering matrices in our theory.

$${\widehat{r}}_{\mathbf{k}}^{†}{\widehat{1}}_{\mathbf{k}}{\widehat{r}}_{\mathbf{k}}+{\widehat{t}}_{\mathbf{k}}^{†}{\widehat{1}}_{\mathbf{k}}^{\prime }{\widehat{t}}_{\mathbf{k}}={\widehat{1}}_{\mathbf{k}},$$ (B9a)

$${\widehat{r}}_{\mathbf{k}}^{\prime †}{\widehat{1}}_{\mathbf{k}}^{\prime }{\widehat{r}}_{\mathbf{k}}^{\prime }+{\widehat{t}}_{\mathbf{k}}^{\prime †}{\widehat{1}}_{\mathbf{k}}{\widehat{t}}_{\mathbf{k}}^{\prime }={\widehat{1}}_{\mathbf{k}}^{\prime },$$ (B9b)

$${\widehat{r}}_{\mathbf{k}}^{†}{\widehat{1}}_{\mathbf{k}}{\widehat{t}}_{\mathbf{k}}^{\prime }+{\widehat{t}}_{\mathbf{k}}^{†}{\widehat{1}}_{\mathbf{k}}^{\prime }{\widehat{r}}_{\mathbf{k}}^{\prime }=0,$$ (B9c)

and

$${\widehat{1}}_{\mathbf{k}}({\widehat{r}}_{\mathbf{k}}{\widehat{r}}_{\mathbf{k}}^{†}+{\widehat{t}}_{\mathbf{k}}^{\prime }{\widehat{t}}_{\mathbf{k}}^{\prime †}){\widehat{1}}_{\mathbf{k}}={\widehat{1}}_{\mathbf{k}},$$ (B10a)

$${\widehat{1}}_{\mathbf{k}}^{\prime }({\widehat{r}}_{\mathbf{k}}^{\prime }{\widehat{r}}_{\mathbf{k}}^{\prime †}+{\widehat{t}}_{\mathbf{k}}{\widehat{t}}_{\mathbf{k}}^{†}){\widehat{1}}_{\mathbf{k}}^{\prime }={\widehat{1}}_{\mathbf{k}}^{\prime },$$ (B10b)

$${\widehat{1}}_{\mathbf{k}}({\widehat{r}}_{\mathbf{k}}{\widehat{t}}_{\mathbf{k}}^{†}+{\widehat{t}}_{\mathbf{k}}^{\prime }{\widehat{r}}_{\mathbf{k}}^{\prime †}){\widehat{1}}_{\mathbf{k}}^{\prime }=0.$$ (B10c)

Appendix C: Absence of a bound state

We show that the delta-function spin-orbit coupling potential at z = 0 does not create a bound state unless its magnitude is beyond a perturbative regime. For mathematical simplicity, we take a simpler model in which electrons are subject to the largest magnitude of the delta function. A bound state is most likely to exist in this situation. The maximum magnitude of the delta function is $({\hslash }^2/2m_e)h_R{k}_{\perp }^{max}$ where $k_{\perp }^{max}$ is the maximum value of $\sqrt{k_x^2+k_y^2}$. Then, the Hamiltonian becomes

$$H=-\frac{{\hslash }^2{\nabla }^2}{2m_e}\pm J\mathrm{\Theta }(z)-\frac{{\hslash }^2}{2m_e}{h}_R{k}_{\perp }^{max}\delta (z),$$ (C1)

where ± refers to each spin band. Let the bound state wave function be e^q₁z for z < 0 and e^−q₂z for z > 0. Then both q₁ and q₂ should be positive. The relation between q₁ and q₂ is $-{\hslash }^2{q}_1^2/2m_e=\pm J-{\hslash }^2{q}_2^2/2m_e$, or equivalently

$$(q_2-q_1)(q_2+q_1)=\pm \frac{2m_{e}J}{{\hslash }^2}.$$ (C2)

Now, the derivative mismatching condition from the delta-function potential is

$$\frac{{\hslash }^2}{2m_e}(q_2+q_1)=\frac{{\hslash }^2}{2m_e}{h}_R{k}_{\perp }^{max}.$$ (C3)

Combining the two conditions,

$$2q_{1/2}=h_R{k}_{\perp }^{max}\pm \frac{J{m}_e}{{\hslash }^2{k}_{\perp }^{max}{h}_R},$$ (C4)

where the choice of the sign ± that corresponds to 1 or 2 is ambiguous but it is not necessary to be determined.

A necessary condition for q₁ and q₂ being positive is that q₁q₂ is positive. Thus, we obtain

$$\mid h_R{k}_{\perp }^{max}\mid >\sqrt{\frac{2m_{e}J}{{\hslash }^2}}.$$ (C5)

For a perturbative h_R, this cannot be satisfied. For J ≈ 1 eV, the right-hand side is (0.14nm)⁻¹. On the other hand, $k_{\perp }^{max}$ is bounded by the order of the inverse lattice parameter, which is around (0.3nm)⁻¹. Therefore, h_R should be greater than one to satisfy Eq. (C5), which is beyond a perturbative regime.