Highlights
-
•
An experimental study on pulley-belt temperature measurement is presented.
-
•
The effects of torque, setting tension and angular speed on the belt.
-
•
A heat transfer model is proposed to calculate pulley-belt heat flux.
-
•
Validation based on experimental thermal surveys and thermocouple measures.
-
•
A comparative analysis between two heat fluxes (calculated and simulated) is done.
Keywords: Belt, Temperature, Pulley, Angular speed, Setting tension, Heat flux
Abstract
In most industrial applications, the re-use of belts in power transmissions continues to increase and invade the market especially in automobiles where various types of belts are used. For this purpose, the belt manufacturers are aware of the importance and the valuable advantages of this transmission member and put all their efforts to develop and improve its geometrical and mechanical characteristics in order to achieve an optimal service life. Indeed, this article is devoted to an experimental and numerical thermal study of a toothed belt transmission type AT10. The tests were carried out on an original derrick of test for the purpose of measuring belt and pulley temperatures, detector devices and data acquisitions will also be described. Further, we have developed a model that calculates the heat flux through our pulley-belt transmission. The results will be synthesized to make a comparison between two thermal fluxes. The first is determined from our mathematical model and the second is calculated using the thermal simulation of this belt pulley transmission. Finally, a discussion of the results, which will allow us to fully understand this thermal phenomenon.
Nomenclature
tangential force [N]
force transmissible per tooth [N]
admissible tensile load [N]
power [kW]
speed [m/s]
center distance [mm]
pulley width [mm]
crown diameter [mm]
pitch [mm]
number of belt teeth
number of teeth engaged on the driving pulley (max. 12 for calculation)
frequency [Hz]
number of teeth of the driving pulley and drive pulley
constant for measuring pretension
the heat flux of the belt tooth, heat flow of belt and global heat flux [W]
exchange surface of the tooth [mm2]
temperatures of the outer surface of the pulley and the belt [K]
setting tension [N]
thickness of the tooth [mm]
belt width [mm]
torque [N m]
winding angle [rd s−1]
angular speed [rpm]
temperatures of layers of a belt tooth [K]
the heat flux of the layers of a belt tooth [W]
the thermal conductivity of the layers of a belt tooth [W m−1 K−1]
the rays of the layers of the belt tooth [mm]
1. Introduction
Synchronous belt drives combine the advantages of single belt drives (flat, trapezoidal or ribbed) due to their low weight, low maintenance, large linear speed ranges and high transmission ratios with the advantages of chains that are no sliding, synchronized speed transmission and low installation tension, etc. Thanks to the toothing of the belt which penetrates into the synchronous pulleys, there is a direct transmission of the power without sliding as between two gears [1]. This transmission Fig. 1 is composed of a driving pulley, a belt, one or more driven toothed pulleys and optionally, smooth rollers making it possible, by rewinding the belt on the back, Contact arc on toothed pulleys. Most synchronous belts consist of an elastomer, or a thermoplastic material comprising the body of the belt in which is embedded the inextensible armature making it possible to transmit the force withdrawn from the driving pulley towards the receiving pulleys and a textile layer protecting the teeth. The inextensibility of the armature is necessary to ensure synchronism between the motor and receiver shafts (removal of the angular offset).
Fig. 1.

A power transmission by pulley belt.
The analysis of the work carried out on belt drives makes it possible to provide elements of response on the observed thermal and dynamic behavior. These belts are sensitive to the conditions of use; in fact it exists a variation of the values of the coefficient of friction and of the traction as a function of the temperature. Wurm et al. [2] concentrated their analysis on the heat transfer of continuously variable transmissions of rubber belts. They have developed a numerical model that is able to calculate the heat transfer effects in a closed belt continuously variable transmission using computational fluid dynamics. Sundararaman et al. [3] have studied the effect of temperature on the fatigue of V-ribbed serpentine belts. They developed a predictive model of fatigue crack growth to monitor the progressive deterioration of initial defects of small ribs Subjected to thermal and mechanical loads. This model is based on the mechanics of computational fractures and temperature dependent fatigue coupons.
Other research has investigated the operation of a serpentine belt system and pulley with ribs of an automobile. They created a three-dimensional dynamic finite element model consisting of a drive pulley, a receiving pulley and a V-belt with five full ribs. This model has been implemented in the ABAQUS/EXPLICIT code for simulation, which is used to determine the thermal stresses and temperature-dependent properties of rubber compounds: see Song et al. [4]. Krane et al. [5] obtained analytical expressions for the temperature distribution and heat transfer capacity of a belt-type radiator.
Moreover, other studies have gradually turned to the study of noise. Chen et al. [6] have studied and modeled the noise source differences of the synchronous belt by measuring the impact dynamics of the belt pinion contact, friction induced vibration, and friction induced teeth vibration and the noise induced by the air during the engagement. Chen et al. [7] analyzed the friction between the rubber belts and the pulley under cold conditions. And they presented the experimental characterization and analysis of the friction of the belt and the associated noise behavior on the basis of a belt pulley test bench. On the other hand, Tokoro et al. [8], [9] presented two studies. The first is the analyzed generation mechanism and the method of reducing high frequency noise for a timing belt that is installed on a real engine. The second study, they observed the mechanism of generation and the method of reducing the transverse vibration of the belt as a cause of the noise of the timing belt. In 1988, Koyama and Marshek [10] presented a technical paper on load distribution, service life, noise, transmission errors and toothed belt jump characteristics.
Since the amount of research on the dynamic behavior of belts is relatively limited, the work presented in this paper involves several original scientific contributions. Baltaa et al. [11] described an experimental study of the effects of belt drive parameters on the speed loss behavior of V-ribbed belt drives. Recently, Zhu et al. [12] have characteristics of hysteretic and dynamic damping of a serpentine belt.
They have developed a variable stiffness and variable damping model consisting of a variable stiffness spring and a variable damping damper to estimate these hysteretic and dynamic damping characteristics of the belt. In 2014, Manin et al. [13] presented a method for estimating a power loss map for any poly-v multi-pulley belt transmission. They identified and modeled power losses in a simple transmission consisting of two pulleys of V-shape and belt, focusing on belt losses due to the hysteretic behavior of the rubber and the sliding of the belt on the pulley. Yet, Ding and Zu [14] presented a study of the steady-state nonlinear response of a belt drive system with a one-way clutch. A dynamic model is established to describe the rotations of the drive pulley, the pulley and the auxiliary shaft. In addition, Čepon et al. [15] developed a poly-V belt drive model using an absolute nodal coordinate formulation, with the aim of introducing a damping mechanism into the belt model and verifying it using experimental data. In 2006, Nuttall and Lodewijks [16] proposed a model that describes the relationship between traction and sliding in the rolling contact roll of a belt conveyor driven by a wheel. On the other hand, Akehurst et al. [17] have presented a series of two documents detailing the loss mechanisms that occur in belt transmissions to obtain improvements in efficiency. A first article in which an analysis was made of the losses which occur due to the relative movement between the belts and the belt segments. The second article is devoted to the development of a number of models to predict slip losses in the drive system, based on the force distribution models developed in the first article. In 2004, Pellicano et al. [18] analyzed the nonlinear dynamic response of a power transmission belt excited by an eccentricity of the pulley. A theoretical model is developed to predict the response of the belt. This model is based on the theory of moving cords and the static effect of the elasticity of the belt. Kim [19] to develop an equation based on the classical Euler formula is driven to seek the distribution of normal and tangential forces on a flat belt drive when a concentrated contact load is applied to the pulley.
In the late eighties, Gerbert [20] describes two modes of failure of a flat belt. The first is a linear wear concept applied to the flat belt drive, this wear carried on the friction layer which causes a reduction in friction and a progressive malfunction. The second is the fatigue of the traction layer. This causes a sudden rupture and dysfunction of the belt. In 1987, Kim and Marshek [21], [22] presented two studies, the first theoretically devoted to the influence of the speed of a flat transmission belt on normal and tangential forces as well as the effect of Centrifugal forces on the tension of the belt. The second is a theoretical and experimental study of the characteristics of the friction between an abrasive belt and a driving or receiving pulley.
In this article, we used a test bench to measure the temperatures delivered by a belt pulley transmission type AT10. Several experiments were carried out with several parameters: the angular speed 500–3000 rpm with a pitch of 500 rpm, the torque of 0–100 N m with a pitch of 25 N m and setting tension of 400–600 N with a pitch of 100 N. In addition, we have developed a model that calculates the thermal flux by multi-layer radial conduction using the proposed contact formulation between the belt and pulley as well as the measured temperatures. This toothed belt is composed of four layers, three layers of polyurethane; hence the Thermal Conductivity and the fourth layer of alloy steel where . Although in this study we calculated a second heat flux with SOLIDWORKS software simulation using the same belt pulley characteristics and experimentally measured temperatures. Finally, we compared the results of these two heat fluxes. This document is organized as follows. Section 2 is devoted to the measurement of belt temperatures and the driving pulley per experimental bay. Section 3 presents the heat flux calculation model with contact formulation between the belt-pulley. Section 4 is that of determining this heat flux by simulation. Then, a comparison of the results between the simulations and the modelizations is given. Finally, in Section 5, the conclusions are drawn.
2. Measurement of belt and driving pulley temperature
2.1. Materials and test conditions
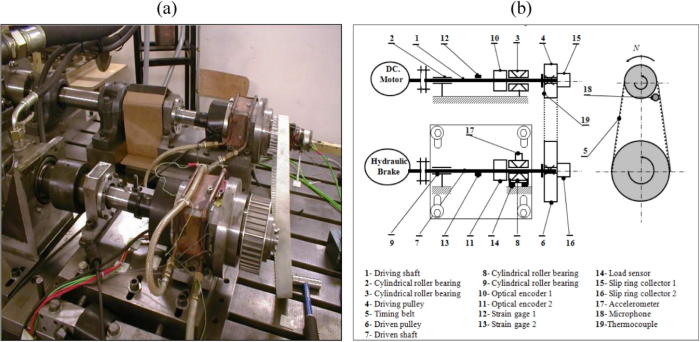
The general architecture of the belt [1] test bench is presented in Fig. 2. An AT10 type synchronous belt is mounted between two pulleys. The overall assembly can be moved perpendicular to the shaft axis for mounting and adjustment of the laying tension of this synchronous belt. Then, the set of elements is tight to a heavy rigid support. These two pulleys are mounted on two shafts with a diameter of 40 mm. For a test, the angular speed can be varied between 500 and 3000 rpm by the pitch of 500 rpm and it remains constant. By laying down a separate hydraulic circuit, it is possible to fix the pressure and thus the torque of resistance for a given angular velocity. The resistance to torsional moment can vary between 0 and 100 N m by the pitch of 25 N m. Of the same three setting tension 400, 500 and 600 N was considered.
Fig. 2.
Belt testing equipment: a – General view of the test rig, b – Belt test arrangement.
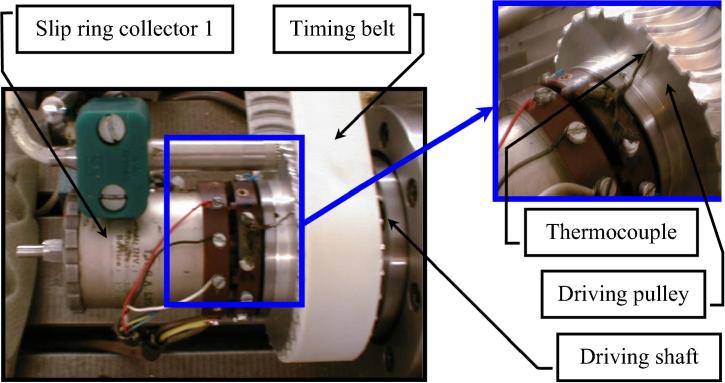
The general view of the test bench is given. The transmission belt evaluates the device is equipped with a maximum of conventional detectors. The driving pulley temperature is measured with a thermocouple placed in the middle of a pulley tooth and placed in the middle of the contact width Fig. 3. Our average belt temperature is measured with an infrared not coming into contact with the detector at the back of the belt. Each test condition requires approximately ten minutes of testing. The data were recorded on a digital data acquisition card. Only the temperature of the belt and the temperature of the drive pulley are given.
Fig. 3.
View of the thermocouple in the tooth of the driving pulley.
2.2. The method of calculating the parameters of the AT10 belt
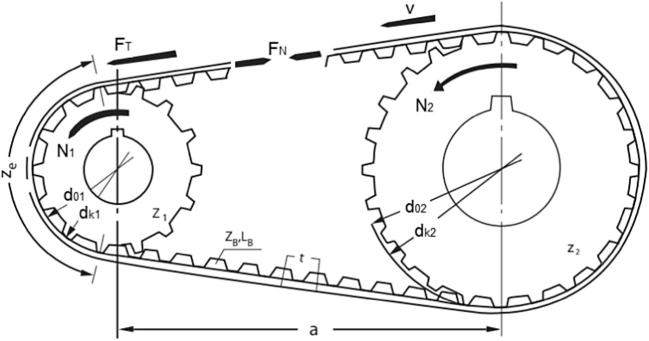
AT10 type transmission belts are the subject of numerous studies and research in order to optimize their behavior, their characteristic and in particular their lifetime. These toothed belts transmit a power or more exactly a torque by the teeth in engagement on the small driving pulley of diameter rotating at a speed .
Each tooth in mesh is capable of transmitting a maximum force of . To define a belt, it is therefore necessary to know the tangential force which will apply to the teeth in engagement and the reinforcement cables see Fig. 4. Eqs. (1), (2), (3), (4), (5), (6) are used to determine the torque , the power to be transmitted Tangential force , linear speed , number of toothed teeth on the drive pulley and resonant frequency to adjust the laying tension using the device TSM3 [23]:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
Fig. 4.
The parameters of the toothed belt type AT10.
According to the above equations, the values of the parameters of this belt AT10 are obtained as a function of angular speed, torque and initial tension by Table 1.
Table 1.
Parameters of a transmission belt AT10 type magnetic binder.
| Torque [N m] | Tangential force [N] | Angular speed [rpm] |
||||||
|---|---|---|---|---|---|---|---|---|
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | |||
| Power [kW] | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 25 | 534 | 1.3 | 2.6 | 3.9 | 5.2 | 6.5 | 7.8 | |
| 50 | 1068 | 2.6 | 5.2 | 7.8 | 10.4 | 13 | 15.8 | |
| 75 | 1602 | 3.9 | 7.8 | 11.7 | 15.6 | 19.5 | 23.4 | |
| 100 | 2136 | 5.2 | 10.4 | 15.6 | 20.8 | 26 | 31.6 | |
| Speed [m/s] | 1.21 | 2.43 | 3.65 | 4.87 | 6.08 | 7.30 | ||
| Setting tension [N] | 400 | 500 | 600 | |||||
| Frequency [Hz] | 48.2 | 53.9 | 59 | |||||
| Number of teeth | 14.67 « Maximum for calculation 12 » | |||||||
2.3. Measurement results
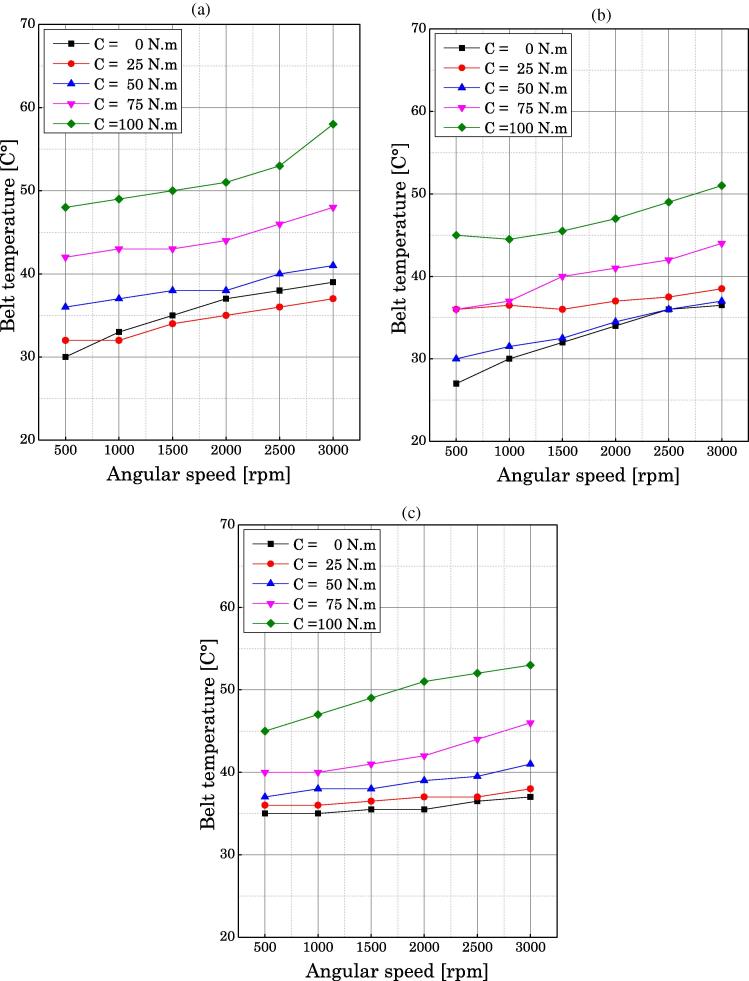
Numerous data have been gathered from tests and tables become within the scope of this article. It was decided to present major trends of curve visualizations. Each parameter is thus presented in relation to the angular velocity. Fig. 5, Fig. 6 summarized are the results for the transmission belt considered in this study.
Fig. 5.
A comparison between the variation of the belt temperature compared with the angular speed and motor torque: a – T0 = 400 N, b – T0 = 500 N and c – T0 = 600 N.
Fig. 6.
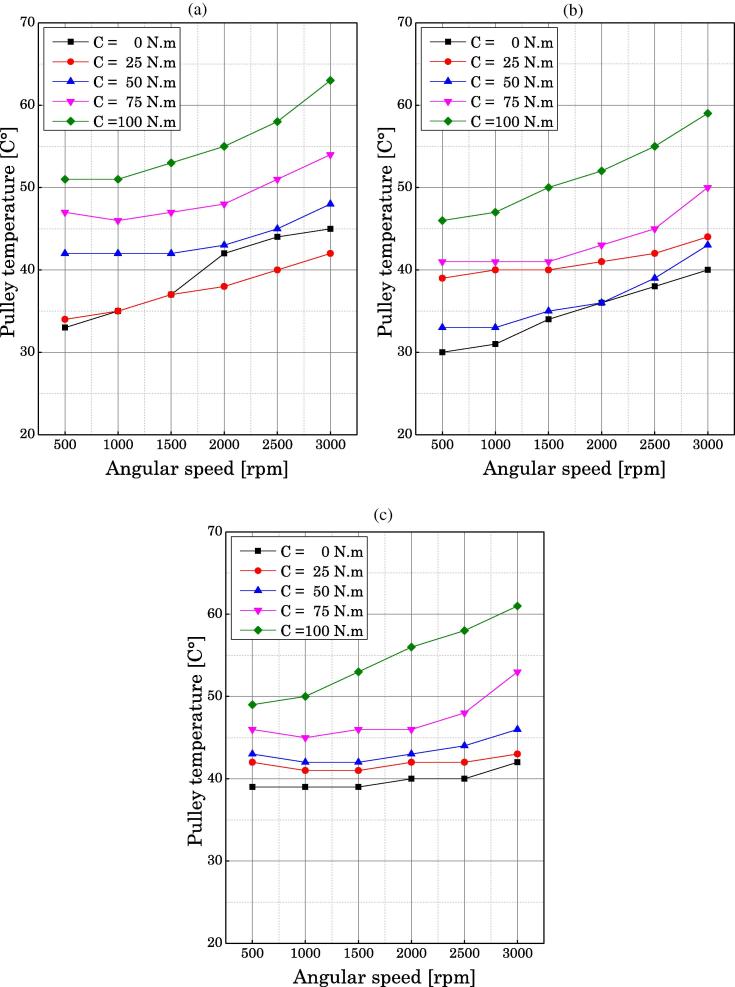
A comparison between variations of the pulley temperature Compared with the angular speed and motor torque: a – T0 = 400 N, b – T0 = 500 N and c – T0 = 600 N.
2.4. Discussion of results
The results illustrated in Fig. 5, have shown that the temperature of the AT10 belt is practically unchanged when the setting tension increases but increases with increasing torque. It is also observed that this temperature also increases with the increase of the angular speed. It is found that deviations in the temperature of the belt do not occur when the setting tension rises from 400 to 600 N (see Table 2).
Table 2.
Variation of the belts temperatures from to the setting tension.
| Type of belt | AT10 | ||
|---|---|---|---|
| Setting tension [N] | 400 | 500 | 600 |
| Temperature deviation from the angular speed [°C] | 10 | 9.5 | 8 |
| Temperature deviation from to the torque [°C] | 19 | 18 | 16 |
The analysis of Fig. 6 allows us to deduce that the driving pulley temperature increases when the angular speed and torque increases. And it can be seen that the deviations in temperature of the driving pulley with respect to the angular speed are almost noticed when the fitting tension increases. On the other hand, the variation in temperature of the drive pulley with respect to the torque decreases when the setting tension increases from 400 to 600 N (see Table 3).
Table 3.
Variation of the drive pulley temperatures from to the setting tension.
| Type of belt | AT10 | ||
|---|---|---|---|
| Setting tension [N] | 400 | 500 | 600 |
| Temperature deviation from the angular speed [C °] | 12 | 13 | 12 |
| Temperature deviation from to the torque [C °] | 18 | 19 | 19 |
From the analysis in Fig. 7, we have observed that the tooth temperatures of the drive pulley and the belt are suddenly increased to 80 °C as the speed of rotation and torque increases. The test was stopped and there was considerable wear of the belt. It is found that the increase in this temperature causes tooth wear and weight loss of this belt.
Fig. 7.
Evaluation of the wear of the AT10 belt tooth according to the angular speed: a – N = 500 rpm, b – N = 3000 rpm.
3. Development of mathematical model of heat flux in a belt-pulley
The heat flux delivered by a belt pulley transmission is a mode of heat transfer by conduction within an opaque environment, without displacement of material, under the influence of a temperature difference. This propagation of heat by conduction inside a body of the belt takes place according to two distinct mechanisms: a transmission by the vibrations of the atoms or molecules and a transmission by the free electrons. The theory of conduction is based on the Fourier hypothesis, ie the flux density is proportional to the temperature gradient.
In this paper, the heat flux developed between belt pulleys is considered as a heat transfer by multi-layer radial conduction which is composed of two fluxes Fig. 8. The first heat flux is that of the first layer of the belt tooth which is given by Eq. (7)
| (7) |
| (8) |
Fig. 8.
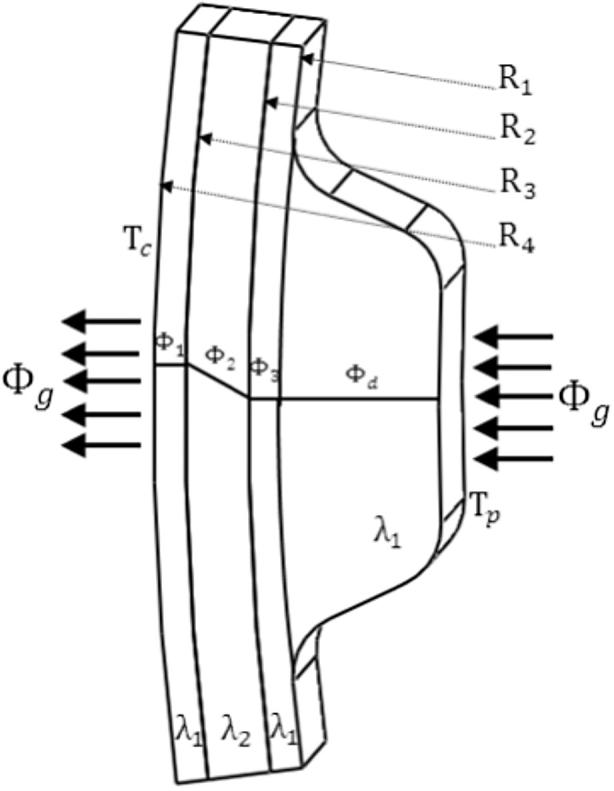
View of a tooth with a conduction flux.
After integration, we obtain:
| (9) |
The expression of the final heat flux of the belt tooth is deduced by Eq. (10)
| (10) |
where is exchange surface of the tooth, is flux density, is thickness of the tooth, is the thermal conductivity of the layers of a belt tooth, and are Temperatures of the outer surface of the pulley and temperature of the surface of the first belt tooth layer.
The second flux is that of the core of the belt which is composed of three layers. This flow is calculated by the law of FOURIER. See Eq. (11).
| (11) |
After integration, we obtain:
| (12) |
The expression of the heat flux is deduced therefrom:
| (13) |
According to Eq. (13), it is deduced that the thermal fluxes which pass through each layer of the core of the belt are presented by Eqs. (14), (15), (16)
-
•
Heat flux of layer 1
| (14) |
-
•
Heat flux of layer 2
| (15) |
-
•
Heat flux of layer 3
| (16) |
where and are temperatures of layers of a belt tooth, is winding angle, is the width of the belt.
This is the practical case of a belt tooth covered with several layers of different materials and where it is known only that the temperature of the air is in contact with the external face of the belt; H is the convective heat transfer coefficient between the air and the outer face (Fig. 8). In the steady state, the heat flux is preserved when the different layers are crossed by the addition of the formulas Eqs. (10), (14), (15), (16)
| (17) |
where and are the rays of the layers of the belt tooth, and are the thermal conductivity of the layers of a belt tooth, is temperatures of the outer surface of the belt.
In this article we used an AT10 type belt with a trapezoidal profile (the 20° angle, not 10 mm) of the teeth is combined with the different shape of wide. Note the tooth contact between the belt and the aluminum alloy pulley to take place at the top of the belt and 0.5 mm the clearance arrives in the hollow area. 0.4 mm. The clearance between the belt tooth and the pulley tooth is also defined; the disengaged position depends on the relative longitudinal position of the belt and the pulley teeth due to the torque. The distance between the primitive line given by the cables of the belt and the tooth tip is equal to 3.5 mm. Further, as the belt is made with 20 steel cords incorporated with polyurethane. All dimensions of this belt and two pulleys are given in Table 4, Table 5, Table 6.
Table 4.
Characteristics of the belt AT10.
| Belt layer | R [mm] | E [mm] | α [rd/s] | S [mm2] | λ [W/m K] |
|---|---|---|---|---|---|
| Tooth | 46.5 | 2.5 | 0872 | 4916 | 0.1 |
| Layer 1 | 47 | 0.5 | 0245 | 4606 | 0.1 |
| Layer 2 | 48 | 1 | 0245 | 4704 | 50 |
| Layer 3 | 48.5 | 0.5 | 0245 | 4753 | 0.1 |
Table 5.
Dimension of the driving pulley, driven pulley and belt AT10.
| Element | Tooth number | Diameter [mm] | Width [mm] | Pitch [mm] | Center Distance [mm] |
|---|---|---|---|---|---|
| Driving Pulley | 30 | 93 | 40–50 | 10 | 464 |
| Driven Pulley | 40 | 125 | 40–50 | 10 | |
| Belt AT10 | 128 | – | 32 | 10 |
Table 6.
Mechanical and thermal properties of a belt pulley transmission.
| Element | AT10 belt |
Driving Pulley and Driven Pulley | |
|---|---|---|---|
| Materials | Polyurethane | Alloy steel | Aluminum |
| Elastic Modulus [N/mm2] | 700 | 205000 | 74000 |
| Poisson's Ratio | 0.4 | 0.3 | 0.33 |
| Breaking strength [N/mm2] | 42–60 | 750–1300 | 390–420 |
| Tensile strength [N/mm2] | 8.5 | 500–900 | 260–320 |
| Hardness | 92 Shore A | HRC = 45 | HB = 111 |
| Shear Modulus [N/mm2] | – | 81,000 | 27,000 |
| Elongation% | 270 | 10–14 | 13 |
| Thermal conductivity [W/m K] | 0.1 | 50 | 121 |
According to the mathematical model developed previously by Eq. (17), the values of the heat flux are obtained as a function of the angular speed and the torque from to the initial tension values in the following Table 7.
Table 7.
Heat flux calculated from to the setting tension.
| Setting tension [N] | Torque [N m] | Angular speed [rpm] |
||||||
|---|---|---|---|---|---|---|---|---|
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | |||
| Flux [W] | 400 | 0 | 1.74 | 1.16 | 1.16 | 2.91 | 3.49 | 3.49 |
| 25 | 1.16 | 1.74 | 1.74 | 1.74 | 2.32 | 2.91 | ||
| 50 | 3.49 | 2.91 | 2.32 | 2.91 | 2.91 | 4.07 | ||
| 75 | 2.91 | 1.74 | 2.32 | 2.32 | 2.91 | 3.49 | ||
| 500 | 0 | 1.74 | 0.58 | 1.16 | 1.16 | 1.16 | 2.03 | |
| 25 | 1.74 | 2.03 | 2.32 | 2.32 | 2.61 | 3.20 | ||
| 50 | 1.74 | 0.87 | 1.45 | 0.87 | 1.74 | 3.49 | ||
| 75 | 2.91 | 2.32 | 0.58 | 1.16 | 1.74 | 3.49 | ||
| 600 | 0 | 2.32 | 2.32 | 2..03 | 2.61 | 2.03 | 2.91 | |
| 25 | 3.49 | 2.91 | 2.61 | 2.91 | 2.91 | 2.91 | ||
| 50 | 3.49 | 2.32 | 2.32 | 2.32 | 2.61 | 2.91 | ||
| 75 | 3.49 | 2.91 | 2.91 | 2.32 | 2.32 | 4.07 | ||
4. Simulation of the thermal behavior of a timing belt
4.1. Finite element model of the tooth of the AT10 belt
In thermal analysis, the finite element model of the belt tooth is generated by importing the geometric (solid) model of the structure modeled under SOLIDWORKS [24], [25]. We define the properties of the materials, the constraints (imposed displacements), the necessary loadings and the type of mesh. Thus, the global mesh of the system is generated by tetrahedral quadratic 3D elements of sizes 0.5908 mm. The system is discretized in 47822 elements linked to 69843 nodes.
4.2. Simulation results
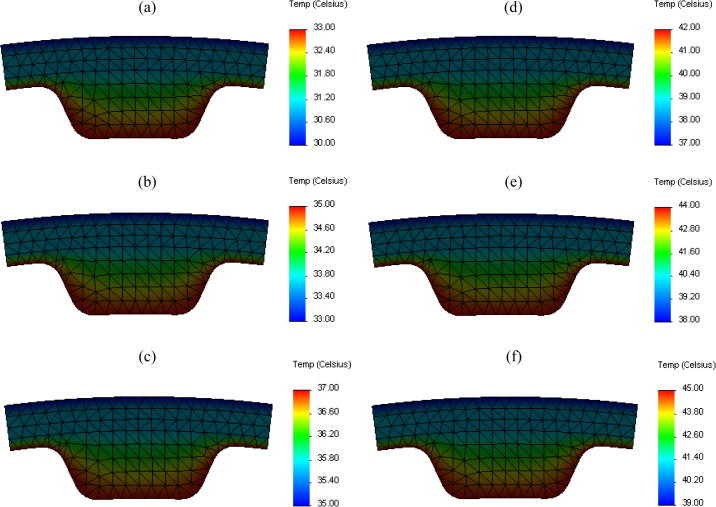
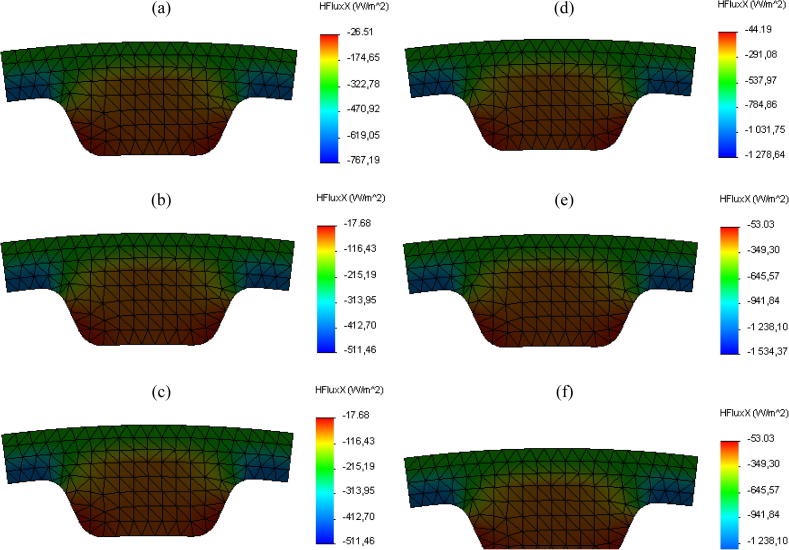
Fig. 9, Fig. 10 illustrate the simulation results of the thermal behavior of a toothed belt in this study. These figures show the variation of the temperature and heat flux of a tooth belt in function of the angular speed, engine torque and the setting tension.
Fig. 9.
Temperature distribution with respect to the angular speed for a setting tension 400 N: a – N = 500, b – N = 1000, c – N = 1500, d – N = 2000, e – N = 2500 and f – N = 3000 rpm.
Fig. 10.
Heat flux distribution with respect to the angular speed for a setting tension 400 N: a – N = 500, b – N = 1000, c – N = 1500, d – N = 2000, e – N = 2500 and f – N = 3000 rpm.
4.3. Discussion of results
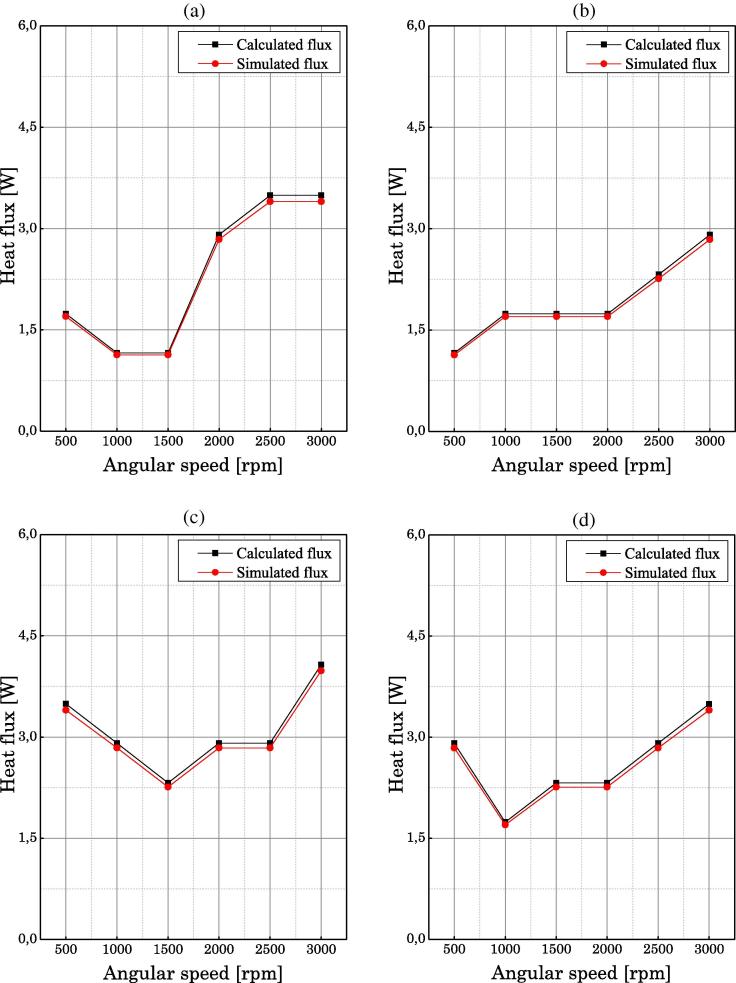
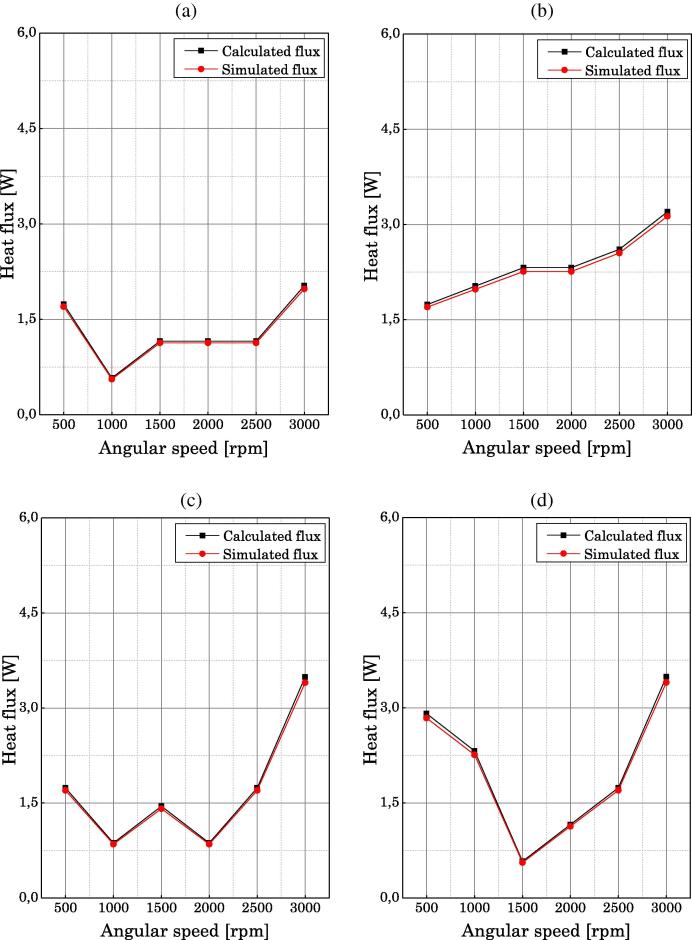
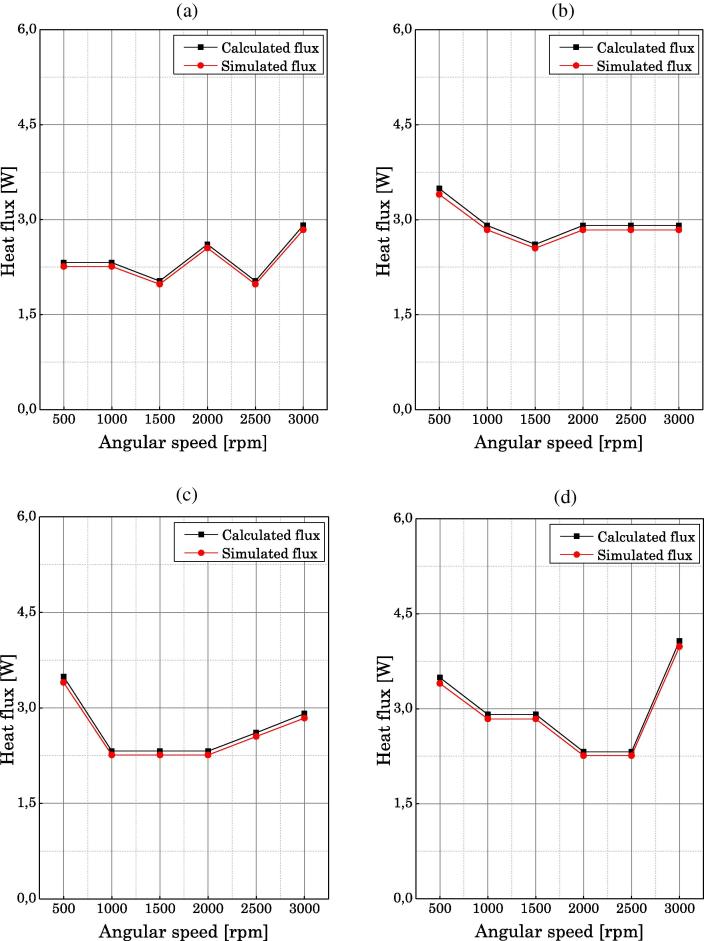
Fig. 11, Fig. 12, Fig. 13 illustrate a comparison between the calculated heat flux and the simulated heat flux with respect to the angular speed, motor torque and the setting tension.
Fig. 11.
A comparison between the variation of the heat two flux (calculated and simulated) in function to angular speed for a setting tension T0 = 400 N: a – C = 0, b – C = 25, c – C = 50, d – C = 75 N m.
Fig. 12.
A comparison between the variation of the heat two flux (calculated and simulated) in function to angular speed for an setting tension T0 = 500 N: a – C = 0, b – C = 25, c – C = 50, d – C = 75 N m.
Fig. 13.
A comparison between the variation of the heat two flux (calculated and simulated) in function to angular speed for a setting tension T0 = 600 N: a – C = 0, b – C = 25, c – C = 50, d – C = 75 N m.
The graphs illustrated in Fig. 11a, c and d show that for the heat flux decreases when the speed of rotation varies from 500 to 1500 rpm and increases when the speed varies between 1500 and 3000 rpm. On the other hand, the analysis of the curves represented by Fig. 11b allows us to deduce that the heat flux increases when the angular speed varies from 500 to 1000 rpm and from 2000 to 3000 rpm. It remains constant when the angular speed varies from 100 to 2000 rpm.
According to the graphs represented in Fig. 12a, it is found that the heat flux is decreased when the angular speed varies from 500 to 1000 rpm, since it increases between 1000 and 1500 rpm and 2500–3000 rpm. But, it remains constant between 1500 and 2500 rpm. For Fig. 12c and d, this heat flux decreases between 500 and 1500 rpm also is increased between 1500 and 3000 rpm. On the other hand for Fig. 12b, it can be seen that the flux increases between 500 and 1500 rpm and 2000–3000 rpm, as it remains constant between 1500 and 2000 rpm.
The graphs illustrated in Fig. 13a, show that, when the rotation speed varies between 500 and 1000 rpm, the heat flux remains almost stable. On the other hand, this flux increases when the angular speed varies from 1500 to 2000 rpm and from 2500 to 3000 rpm. And it decreases in the angular speed range from 1500 to 2000 rpm and from 2000 to 2500. However, the graphs shown in Fig. 13b show that the flux is decreasing in the angular speed range 500–1500 rpm and increasing in the angular speed range 1500–3000 rpm. Finally, for the graphs illustrated in Fig. 13c and d, the flux decreases between 500 and 1500 rpm. On the other hand, it increases in the 1500–3000 rpm range from 1500 to 2000 rpm and remains stable between 1000 and 1500 rpm.
Comparing Fig. 11, Fig. 12, Fig. 13 which represents the calculated flux values and the simulated flux values, it is noted that there is a difference of 2.18–3.21% between the simulated flux and the calculated flux (Table 8). This difference is caused by experimental conditions such as the temperature of the external environment and errors of the experiment in general.
Table 8.
Heat flux error from to the setting tension.
| Setting tension [N] | Torque [N m] | Angular speed [rpm] |
||||||
|---|---|---|---|---|---|---|---|---|
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | |||
| Heat flux error [%] | 400 | 0 | 2.45 | 3.21 | 3.21 | 2.30 | 2.45 | 2.45 |
| 25 | 3.21 | 2.45 | 2.45 | 2.45 | 2.64 | 2.30 | ||
| 50 | 2.45 | 2.30 | 2.64 | 2.30 | 2.30 | 2.24 | ||
| 75 | 2.30 | 2.45 | 2.64 | 2.64 | 2.30 | 2.45 | ||
| 500 | 0 | 2.61 | 3.21 | 3.21 | 3.21 | 3.21 | 2.88 | |
| 25 | 2.45 | 2.88 | 2.64 | 2.64 | 2.45 | 2.18 | ||
| 50 | 2.45 | 2.45 | 2.75 | 2.45 | 2.45 | 2.45 | ||
| 75 | 2.30 | 2.64 | 3.21 | 3.21 | 2.45 | 2.45 | ||
| 600 | 0 | 2.64 | 2.64 | 2.88 | 2.45 | 2.88 | 2.30 | |
| 25 | 2.45 | 2.30 | 2..45 | 2.30 | 2.30 | 2.30 | ||
| 50 | 2.45 | 2.64 | 2.64 | 2.64 | 2.45 | 2.30 | ||
| 75 | 2.45 | 2.30 | 2.30 | 2.64 | 2.64 | 2.24 | ||
5. Conclusion
In this article, we have highlighted a comparative analysis between two thermal fluxes. The first is calculated by a thermal model that was developed in this study, the second is simulated by a software. To validate this analysis, an experimental test bench study simulates significant working conditions of the industrial transmission belt by measuring pulley belt temperatures. Firstly, the experimental results obtained allow us to say that the temperature of the driving pulley is always greater than the temperature of the AT10 belt. It can also be deduced that the temperature of this belt is constant along its length, the pulley and belt gradients are practically identical. In addition, the increase in temperature and torque cause’s teeth wear and weight loss of the belt. Secondly, the deviation of the two heat fluxes increases linearly with the increase in temperature. This research shows that the simulated flow is more precise than the calculated flow, with a gap of between 2.18% and 3.21%. This difference between the results of two heat flows is caused by the experimenter conditions such as the temperature of the external medium, the speed of rotation, the engine torque and the setting tension, as well as the errors of the experiment in general.
Acknowledgments
This research was supported by the Thermal Energy and Applied (ETAP) Laboratory approved in 2012 by Ministerial Order N° 145 on 14 April 2012, a laboratory of excellence at the University of Tlemcen. The support and interest of our sponsors are gratefully acknowledged.
References
- 1.Merghache S., Ghernaout A. Influence of temperature on the performance toothed belts-binder magnetic. Eur. Sci. J. 2013;9(33):206–212. [Google Scholar]
- 2.Wurm J., Gumpesberger M., Väisänen E., Hochenauer C. Advanced heat transfer analysis of continuously variable transmissions (CVT) Appl. Therm. Eng. 2016;114:545–553. [Google Scholar]
- 3.Sundararaman S., Hu J., Chen J., Chandrashekhara K. Temperature dependent fatigue-failure analysis of V-ribbed serpentine belts. Int. J. Fatigue. 2009;31(8–9):1262–1270. [Google Scholar]
- 4.Song G., Chandrashekhara K., Breig W.F., Klein D.L., Oliver L.R. Analysis of cord-reinforced poly-rib serpentine belt drive with thermal effect. J. Mech. Des. 2005;127(6):1198–1206. [Google Scholar]
- 5.Krane R.J., Jischke M.C., Rasmussen M.L. The thermal analysis of a belt type radiator by the method of matched asymptotic expansions. Int. J. Heat Mass Transf. 1973;16(6):1165–1174. [Google Scholar]
- 6.Chen G., Zheng H., Qatu M. Decomposition of noise sources of synchronous belt drives. J. Sound Vib. 2013;332(9):2239–2252. [Google Scholar]
- 7.Chen G., Lee J.H., Narravula V., Kitchi T. Friction and noise of rubber belt in low temperature condition: the influence of interfacial ice film. Cold Reg. Sci. Technol. 2012;71:95–101. [Google Scholar]
- 8.Tokoro H., Nakamura M., Sugiura N., Tani H., Shuku T. Analysis of high frequency noise in engine timing belt. JSAE Rev. 1998;19(1):33–38. [Google Scholar]
- 9.Tokoro H., Nakamura M., Sugiura N., Tani H., Shuku T. Analysis of transverse vibration in engine timing belt. JSAE Rev. 1997;18(1):33–38. [Google Scholar]
- 10.Koyama T., Marshek K.M. Toothed belt drives-Past, present and future. Mech. Mach. Theory. 1988;23(3):227–241. [Google Scholar]
- 11.Baltaa B., Sonmezc F.O., Cengizd A. Speed losses in V-ribbed belt drives. Mech. Mach. Theory. 2015;86:1–14. [Google Scholar]
- 12.Zhu H., Hu Y., Pi Y. Transverse hysteretic damping characteristics of a serpentine belt: modeling and experimental investigation. J. Sound Vib. 2014;333(25):7019–7035. [Google Scholar]
- 13.L. Manin, X. Liang, C. Lorenzon, Power losses prediction in poly-v belt transmissions: application to front engine accessory drives, in: International Gear Conference, 2014, pp. 1162–1171. doi:10.1533/9781782421955.1162.
- 14.Ding H., Zu J.W. Effect of one-way clutch on the nonlinear vibration of belt-drive systems with a continuous belt model. J. Sound Vib. 2013;332(24):6472–6487. [Google Scholar]
- 15.Čepon G., Manin L., Boltežara M. Introduction of damping into the flexible multibody belt-drive model: a numerical and experimental investigation. J. Sound Vib. 2009;324(1–2):283–296. [Google Scholar]
- 16.Nuttall A.J.G., Lodewijks G. Traction versus slip in a wheel-driven belt conveyor. Mech. Mach. Theory. 2006;41(11):1336–1345. [Google Scholar]
- 17.Akehurst S., Vaughan N.D., Parker D.A., Simner D. Modelling of loss mechanisms in a pushing metal V-belt continuously variable transmission: Part 2: Pulley deflection losses and total torque loss validation. Proc. Inst. Mech. Eng., Part D: J. Automob. Eng. 2004;218(11):1283–1293. [Google Scholar]
- 18.Pellicano F., Catellani G., Fregolent A. Parametric instability of belts: theory and experiments. Comput. Struct. 2004;82(1):81–91. [Google Scholar]
- 19.Kim H. Force distribution for a flat belt drive with a concentrated contact load. Mech. Mach. Theory. 1990;25(6):667–677. [Google Scholar]
- 20.Gerbert B.G. Power rating of flat belt drives – a wear approach. Tribol. Des. Mach. Elem. 1989;14(2):143–147. [Google Scholar]
- 21.Kim H., Marshek K.M. The effect of belt velocity on flat belt drive behavior. Mech. Mach. Theory. 1987;22(6):523–527. [Google Scholar]
- 22.Kim H., Marshek K.M. Forces between an abrasive belt and pulley. Mech. Mach. Theory. 1987;22(1):97–103. [Google Scholar]
- 23.BINDER MAGNETIC, Catalogue for timing belt choice.
- 24.R. Ginestou, Learn how to use SolidWorks, Dassault Systèmes - SolidWorks Corporation 300 Baker Avenue Concord, Massachusetts 01742 USA.
- 25.M. Eltaief, A. Chouchene, Course on Solidworks, Higher Institute of Technological Studies of Sousse, 2012.