Skip to main content
PMC home page
Plant Physiology logoLink to Plant Physiology
. 2017 Sep 26;176(1):450–462. doi: 10.1104/pp.17.00605

Predicting Dynamic Metabolic Demands in the Photosynthetic Eukaryote Chlorella vulgaris1

Cristal Zuñiga a, Jennifer Levering a, Maciek R Antoniewicz b, Michael T Guarnieri c, Michael J Betenbaugh d, Karsten Zengler a,2
PMCID: PMC5761767  PMID: 28951490

Constraint-based modeling gives insights into dynamic metabolic demands and compartmentalization in a photosynthetic eukaryote.

Abstract

Phototrophic organisms exhibit a highly dynamic proteome, adapting their biomass composition in response to diurnal light/dark cycles and nutrient availability. Here, we used experimentally determined biomass compositions over the course of growth to determine and constrain the biomass objective function (BOF) in a genome-scale metabolic model of Chlorella vulgaris UTEX 395 over time. Changes in the BOF, which encompasses all metabolites necessary to produce biomass, influence the state of the metabolic network thus directly affecting predictions. Simulations using dynamic BOFs predicted distinct proteome demands during heterotrophic or photoautotrophic growth. Model-driven analysis of extracellular nitrogen concentrations and predicted nitrogen uptake rates revealed an intracellular nitrogen pool, which contains 38% of the total nitrogen provided in the medium for photoautotrophic and 13% for heterotrophic growth. Agreement between flux and gene expression trends was determined by statistical comparison. Accordance between predicted flux trends and gene expression trends was found for 65% of multisubunit enzymes and 75% of allosteric reactions. Reactions with the highest agreement between simulations and experimental data were associated with energy metabolism, terpenoid biosynthesis, fatty acids, nucleotides, and amino acid metabolism. Furthermore, predicted flux distributions at each time point were compared with gene expression data to gain new insights into intracellular compartmentalization, specifically for transporters. A total of 103 genes related to internal transport reactions were identified and added to the updated model of C. vulgaris, iCZ946, thus increasing our knowledgebase by 10% for this model green alga.

Microalgae are responsible for approximately 40% of the photosynthetic carbon fixation on Earth (Geider et al., 2001). Besides their critical role in global carbon fixation, phototrophs are attractive cell factories due to their flexible metabolism and polytrophic growth capacities (i.e. phototrophic, mixotrophic, or heterotrophic growth), which allow for cost-effective production of various chemicals, including biofuels, fragrances, dyes, pigments, pesticides, as well as food additives (Geider et al., 2001; Hussain et al., 2012). Differences in growth conditions, i.e. growth during day and night cycles, require phototrophs to shift their proteome demands and therefore adjust their metabolism. The complex interplay between energy and carbon metabolism and its dynamics in phototrophs is still not fully understood (Stitt, 2013). Available genome-scale models for phototrophic organisms have provided valuable insights into their metabolic capabilities and helped to improve yields and growth rates by determining optimal environmental conditions (Baroukh et al., 2015; Levering et al., 2016; Zuñiga et al., 2016). These genome-scale models associate metabolic reactions with the organism’s genome and enable the prediction of complex phenotypes based on the organism’s genomic information (Palsson, 2006). Flux balance analysis (FBA) is a widely used tool for interrogating metabolic models and to calculate an optimal network state given by a determined flux distribution while maximizing an objective function (Orth et al., 2010). Commonly, the production of biomass is used as objective function. The biomass objective function (BOF) is implemented into the model as a reaction that pulls resources from the metabolic network and defines all known cellular components (such as amino acids, nucleotides, fatty acids, carbohydrates, vitamins, ions, and cofactors) and their fractional contributions. Ideally, the BOF should be established based on experimental measurements from a given culture condition (Feist and Palsson, 2010; Thiele and Palsson, 2010). To assist in these efforts, new protocols for measuring biomass compositions have been established (Cordova et al., 2015, 2016; McConnell and Antoniewicz, 2016; Gonzalez et al., 2017). However, it is often time consuming to determine such detailed biomass composition for the organism of interest, and thus the vast majority of models are based on estimated biomass compositions (King et al., 2016). Several algorithms have been developed to define or to best-fit the BOF in the absence of experimental data (Feist and Palsson, 2010); examples of such algorithms include ObjFind, BOSS, or GrowMatch (Burgard and Maranas, 2003; Gianchandani et al., 2008; Kumar and Maranas, 2009). Various omics data, e.g. transcriptomics or proteomics, can help to define the BOF if experimental measurements of biomass components are missing (Montezano et al., 2015). Previous studies have used random sampling to correlate differentially expressed genes with fluxes to estimate the composition of the BOF (Bordbar et al., 2010). Random sampling is a statistically meaningful tool to explore the genome-scale model solution space. This unbiased assessment provides the possible flux distributions of the network at given constraints (Megchelenbrink et al., 2014; De Martino et al., 2015). Each stoichiometric coefficient associated to a certain metabolite in the BOF is a constraint and affects the reaction activity in the network as well as the final flux distribution and solution space (Bordbar et al., 2010; Bordel et al., 2010).

While the proportions in the biomass composition (carbohydrates, lipids, amino acids, and nucleotides) of heterotrophs such as Escherichia coli does not change significantly with changing growth conditions and growth stages (Feist and Palsson, 2008; Thiele and Palsson, 2010; Long et al., 2016), phototrophs exhibit more dramatic changes in biomass composition because of their inherent lifestyle (i.e. day-night cycle; Khoeyi et al., 2012). The biomass composition of phototrophic organisms thus changes drastically according to growth in the light or in the dark. However, automated reconstruction tools (e.g. ModelSEED; Henry et al., 2010) generally assemble an organism-specific draft biomass reaction independent of the culture stage, thus failing to account for a dynamic biomass composition. Here, some of the conditions considered include progression of biomass composition in both phototrophic and heterotrophic growth with gradual nitrogen depletion. The experimentally determined biomass compositions were used to constrain the genome-scale model iCZ843 recently constructed for C. vulgaris (Zuñiga et al., 2016) and to predict differences in growth rate and flux distribution for various culture conditions and stages. The constraint model captures the dynamic metabolic processes and accurately predicts differences in the growth rate of C. vulgaris over time. Furthermore, this theoretical study supported by omics data (RNA-seq and proteomics) provide insights into the dynamic proteome demands under photoautotrophic conditions and exemplifies how genome-scale metabolic models can be used to predict trends in gene expression. The study highlights how simulated flux trends can help improving genome annotation and emphasizes the importance of constraining the BOF in genome-scale models using accurate biomass composition.

RESULTS

Biomass Composition Is Highly Dynamic in Phototrophs

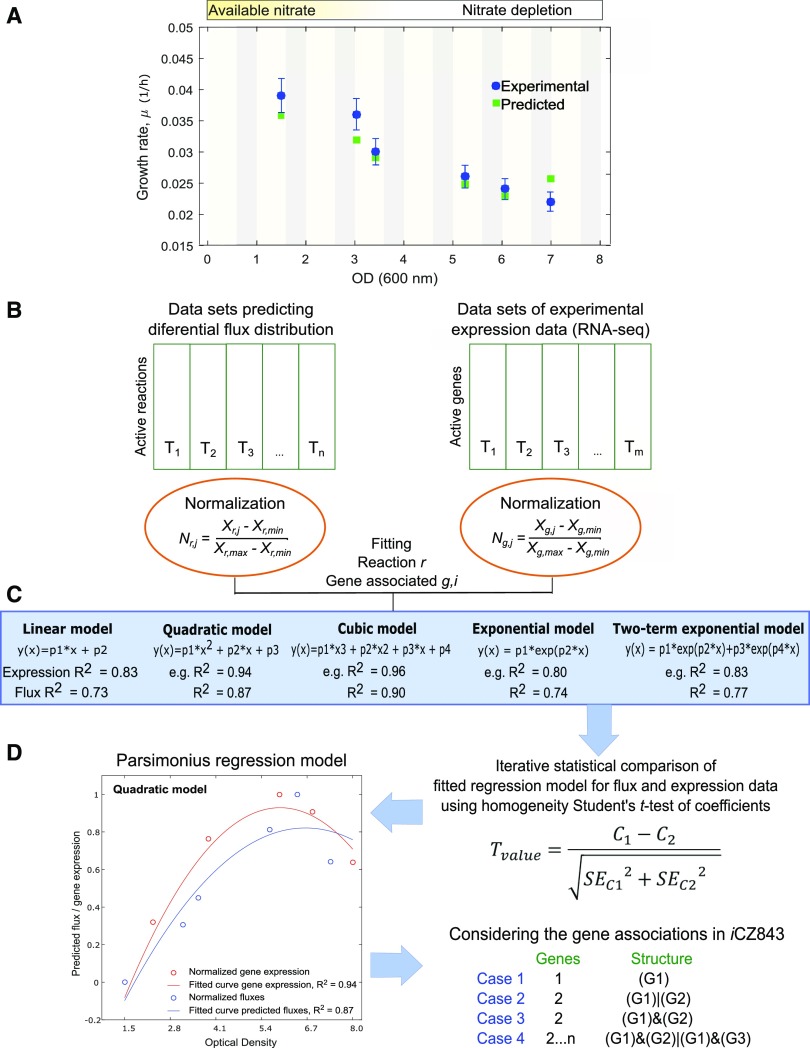
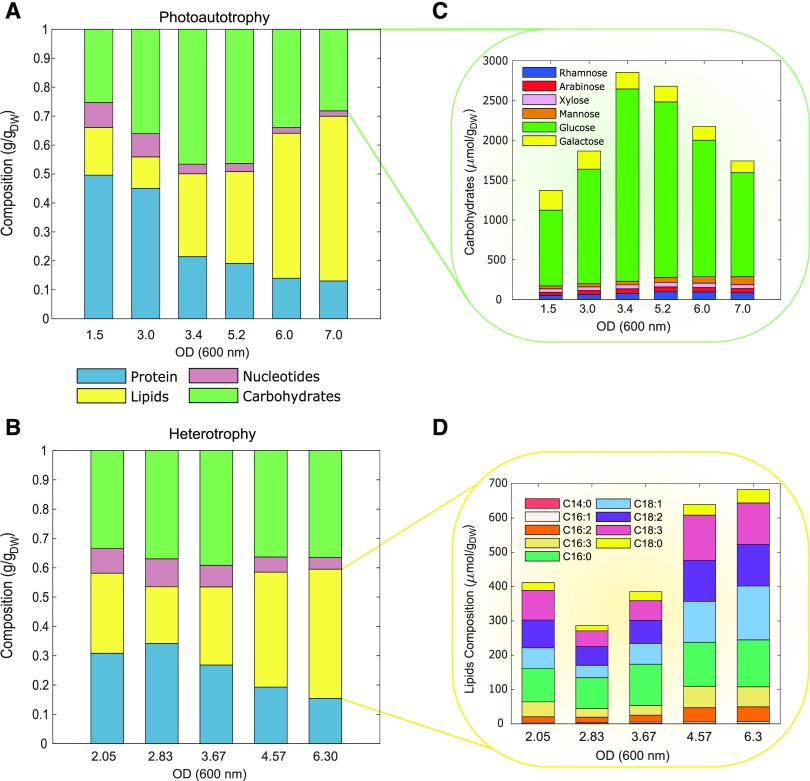
The green algae C. vulgaris can thrive under diverse environmental conditions and grow photoautotrophically, heterotrophically, and mixotrophically (Perez-Garcia et al., 2011). A model-based comparison of experimentally derived BOFs and in silico BOF revealed significant differences in the biomass composition (see Supplemental Text and Supplemental Table S1), highlighting the importance of biomass measurements for accurately predicting biomass production and growth rate as shown in Figure 1A. We determined the effect of a dynamic biomass composition of C. vulgaris UTEX 395 in terms of total amino acids, nucleotides, carbohydrates, and lipids on the cells’ growth rate under photoautotrophic or heterotrophic conditions over time (Figs. 2 and 3). For each time point, the concentration of 30 different biomass components was determined (Fig. 2). We found that macromolecular content (Fig. 2, A and B) but also the metabolite breakdown in each macromolecular class is highly dynamic and shows variation between photoautotrophic and heterotrophic growth (Figs. 2, C and D, and 3). However, under heterotrophy (Fig. 2B), changes in the macromolecular content are less pronounced over the growth course as compared to those under photoautotrophic conditions (Fig. 2A).

Figure 1.

Figure 1.

Open in a new tab

Overview and workflow diagram of data analysis. A, Experimental and predicted growth rates under photoautotrophic growth. B, Flux distributions and gene expression data sets were independently normalized. Nr,j represents the flux distribution normalized value of reaction r at j time point. Ng,j is the normalized value for the g gene at time j. The normalized values ranged between zero and one in each data set. C, Iteratively fitted regression models (linear, quadratic, cubic, exponential, and two-term exponential regression model). D, Statistically identical models were extracted using a homogeneity test of coefficients to define the agreement between the predicted flux and expression data. C1 and C2 correspond to the two coefficients being compared, and SEC1 and SEC2 to the se of coefficients calculated by least-squares fitting method. The number of fitted coefficients depends of the regression model (i.e. linear has two fitted coefficients [p1 and p2] and two-term exponential model has four). G1..n represents the number of genes associated with specific reaction.

Figure 2.

Figure 2.

Open in a new tab

Overview of experimental data breakdown. A, Growth course biomass composition (proteins, nucleotides, lipids, and carbohydrates) under photoautotrophy. B, Biomass composition under heterotrophy. C, Carbohydrate composition under photoautotrophy. D, Lipid distribution under heterotrophy. Experimental and predicted growth rates for C. vulgaris in heterotrophy (McConnell and Antoniewicz, 2016; Zuñiga et al., 2016).

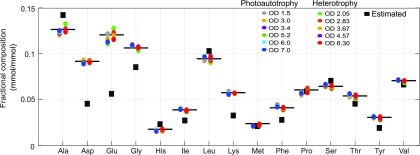
Figure 3.

Figure 3.

Open in a new tab

Comparison of experimental and estimated protein composition. Experimentally determined protein composition for C. vulgaris for photoautotrophic or heterotrophic growth in comparison to estimated protein composition based on genome annotation. Arg, Cys, Gln, and Trp were discarded because measurements over time were not found.

The experimental biomass measurements were used to define a BOF for each time point and growth condition. These BOFs for C. vulgaris account for carbohydrates (rhamnose, arabinose, Xyl, Man, Glc, and Gal), fatty acids (C14:0, C16:1, C16:2, C16:3, C16:0, C18:1, C18:2, C18:3, C18:0), amino acids (Ala, Asn, Gly, Val, Leu, Ile, Pro, Met, Ser, Thr, Phe, Asp, Glu, Lys, His, Tyr), and nucleotide composition. The condition-specific BOFs and models are provided in Supplemental File 1. Additionally, we estimated a universal BOF computationally from the genome sequence using an established protocol (Thiele and Palsson, 2010). Deploying the experimentally derived BOFs in conjunction with condition-specific constraints (i.e. carbon uptake rate and light) were sufficient to accurately simulate growth and nitrogen uptake rates (Fig. 4).

Figure 4.

Figure 4.

Open in a new tab

Nitrogen uptake and intracellular storage. Circles represent experimental measurements (Zuñiga et al., 2016; A and B) and squares the predicted uptake rates (B and C). Every letter represents an experimental point in which all biomass compounds were collected. A, Experimental nitrogen concentration in the supernatant under photoautotrophy (green solid line) and heterotrophy (red solid line). Dashed lines represent the nitrate concentration over time (top x axis). B, Predicted uptake rate of NO3 using the C. vulgaris genome-scale model iCZ843. Shaded areas show the experimental nitrate uptake rate under photoautotrophy (green) and heterotrophy (red). D, Predicted nitrogen consumption rates from the intracellular pool. The shaded areas are equivalent to the volumetric pool concentration and indicate nitrogen depletion from the culture medium. The first point of the definite integral was point b.

We used these biomass-specific models to investigate nitrogen uptake rates under photoautotrophic and heterotrophic growth conditions and to determine the interplay between intracellular metabolite pools and growth-limiting nutrients in C. vulgaris. Figure 4 shows the experimentally determined nitrate concentrations in the supernatant for both growth conditions as a function of biomass and time (Fig. 4A) and the simulated nitrogen uptake rates at different biomass concentrations (Fig. 4B) and time (Fig. 4C). The predicted uptake rates are in good agreement with previously reported data and our experimentally determined nitrate uptake rates (Taziki et al., 2016). Under photoautotrophic and nitrogen-replete conditions, the average predicted nitrogen uptake rate was 0.175 ± 0.02 mmolNO3/gDW/h, and our experimental estimation was 0.15 ± 0.02 mmolNO3/gDW/h. Both values are in sync with the previously reported nitrate uptake rate of 0.17 ± 0.05 mmolNO3/gDW/h (Taziki et al., 2016). Uptake rates of nitrate were decreasing over time for photoautotrophy while they were maintained more or less constant during heterotrophic growth (Fig. 4B). Model simulations predict nitrate utilization even after nitrate has been depleted from the culture medium, suggesting consumption of nitrogen from a so-far-uncharacterized intracellular pool. The hypothesis that nitrogen can be stored intracellularly by Chlorella and other algae is corroborated by simulations based on experimental data (Flynn and Fasham, 1997; Flynn, 1999). The simulated uptake rates after nitrogen depletion were integrated to estimate the total intracellular concentration of nitrogen required to account for the experimentally determined biomass production, while the experimental data set also encompasses other possible nitrogen storage sources, such as mainly amino acids and pigments.

By integrating the uptake rates and assuming that nitrogen is stored inside the cell in the form of ammonium (Smith, 1977), the total required ammonium for growth from this pool (considering the total biomass) was 4.2 mm under photoautotrophy and 1.6 mm under heterotrophy. The predicted pool concentrations after nitrate was depleted from the medium corresponded to 38% of the total nitrogen provided in the medium for photoautotrophic and 13% for heterotrophic growth.

Growth-Course Fluxes Predict Proteome Demands

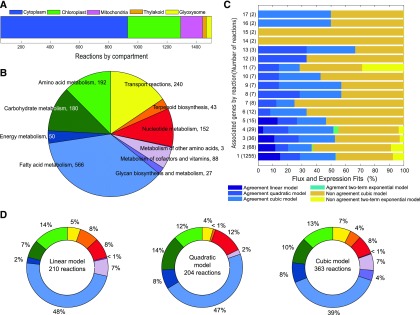
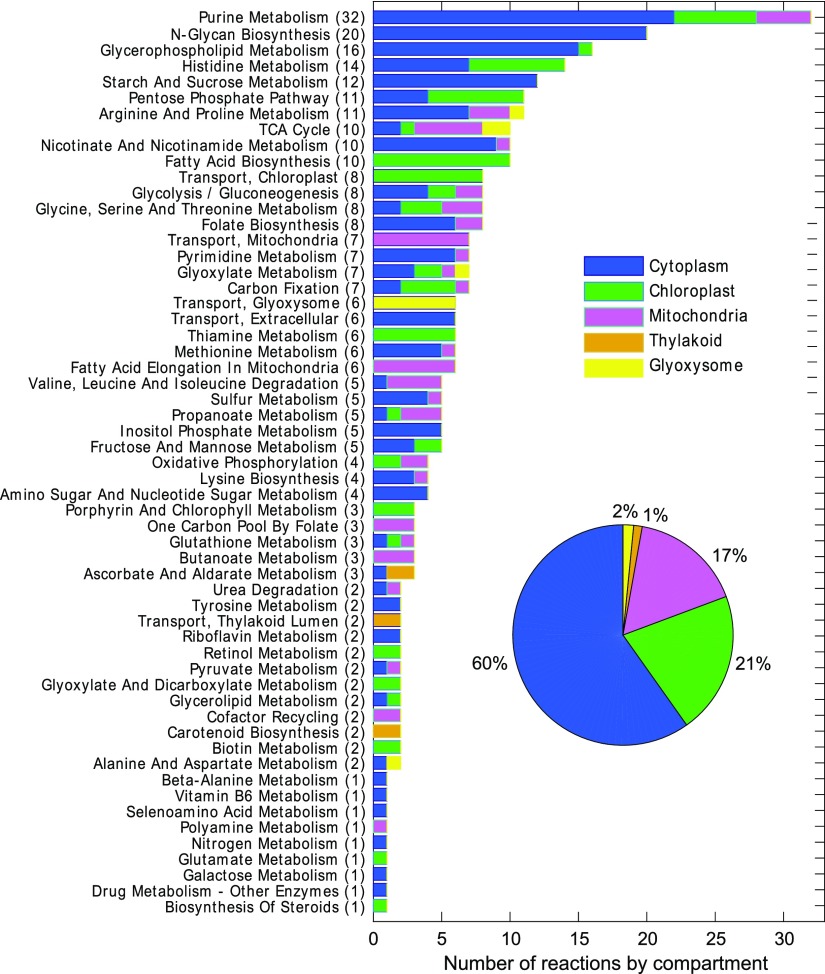
The number of all active reactions in every growth condition and at each time point was determined using the model iCZ843 (Zuñiga et al., 2016). Reactions carrying flux were defined as active, i.e. reactions with minimal or maximal possible flux value (as determined by flux variability analysis [FVA]) is not zero (Mahadevan and Schilling, 2003). Under photoautotrophic growth, 1,542 out of 2,294 reactions, equaling 69%, carried flux. Figure 5 shows the subcellular localization (Fig. 5A) and main subsystem associations (Fig. 5B) for all active internal reactions and genes under this condition. The list of predicted active reactions was identical for almost all of the time points (Supplemental Table S2), except reaction ACP1819ZD9DS (encoding the NADPH-dependent Stearoyl-[acyl-carrier-protein] delta9-desaturase), which was inactive at the 3 days time point. However, our simulations indicate that the list of active reactions for heterotrophic growth changed between time points. According to our FVA analysis, 1,506 and 1,507 reactions were able to carry flux for the first two time points (optical density, OD 2.05 and 2.82), respectively, and 1,504 reactions were active at each of the remaining three time points (OD 2.82, 3.67, and 4.57). There were 12 reactions differentially active across all sampled points. These reactions are involved in the transport and the biosynthesis of pantothenate, lipids, and CoA (Supplemental Table S3). The models predict a specific utilization of the enzymes O-acetyl-l-homo-Ser, hydrogen sulfide S-(3-amino-3-carboxypropyl) transferase, O-acetyl-l-homo-Ser succinate-lyase, and O-succinyl-l-homo-Ser succinate-lyase at OD 3.67. These enzymes are involved in Met and Cys metabolism but are also drivers in the synthesis of secondary metabolites during nutrient limitation (Shen et al., 2002), which is consistent with the depletion of nitrogen during that time.

Figure 5.

Figure 5.

Open in a new tab

Active reactions and expression data match. A, Compartmental distribution of the active reactions and genes under photoautotrophy. B, Distribution of the reactions and genes along the main subsystems in the metabolism. C, Differential expression fits versus predicted flux distribution fits. D, Pie charts of reactions with significant correspondence between differential expression and flux distribution. Color match between B and D.

We compared the active reactions for each growth condition to gain insight into the metabolic response of C. vulgaris to changing environmental conditions. A total of 1,489 reactions were active under both photoautotrophic and heterotrophic growth conditions; 27 were active in heterotrophic but not autotrophic conditions, and 93 reactions were only active under photoautotrophy (Supplemental Fig. S1). A list of these reactions and their associated subsystem is given in Supplemental Table S4. Under photoautotrophic conditions, reactions involved in light metabolism such as light conversion (EX_photonVis(e)), efflux (demand reactions needed for modeling purposes, e.g. DM_photon298(c)), and spectral decomposition (PRISM_solar_litho) are active and expectedly inactive under heterotrophic growth. Additionally, we found the highest number of active reactions involved in carbon fixation, photosynthesis, porphyrin and chlorophyll metabolism, and light-dependent retinol production from rhodopsin under photoautotrophy. Under this condition, C. vulgaris secretes formate and glycolate (Krampitz and Yarris, 1983) and, consequently, exchange reactions for secretion (EX_for(e), EX_glyclt(e)), reactions involved in glycolate production (GCLDH, PGLYCPH, HDAO10x, PGLYCPx, HYDAm), and transport reactions between the cellular compartments and out of the cell (2PGLYCth, GLYCLTth, FORti, GLYCLTt, 2PGLYCtx, GLYCLTtx, PItx, GLYCLTtm, H2tm) are active. Also, two starch-degrading reactions (STARCH300DEGRA, STARCH300DEGRB) are active under light conditions. These starch-degrading reactions differ from the ones used in the absence of light (STARCH300DEGR2A, STARCH300DEGR2B) in the stoichiometric coefficients. Under heterotrophic growth, the model simulates the degradation of internally stored starch by importing starch using the exchange reaction (EX_starch(h)). This reaction is manually blocked under photoautotrophic growth, since no starch is stored internally during this condition (Zuñiga et al., 2016). Under heterotrophic growth, the model predicts that light-independent reactions required for retinol and chlorophyll a production (CAROMO, CAROtu, PCHLDR) are active. We also found that three reactions involved in chloroplastic carbon metabolism (FBAh, G6PADHh, G6PBDHh) carry flux exclusively in the dark.

Predicting Expression Profiles

In the previous section, we determined the differences in active reactions at different time points and conditions. Here, the models containing each BOF were used to extract the active genes based on the predicted flux distributions. Although the model accounts for only annotated metabolic genes, which represent a fraction of all genes (843 out of 7,100 total genes), these metabolic genes approximate the same trends in gene expression as genome-wide expression trends based on the level of raw counts and corresponding normalized trends (Supplemental Fig. S2). The genes predicted to be differentially active were confirmed by gene expression data over time under photoautotrophic conditions (Guarnieri et al., 2011). Based on the model iCZ843, we identified 1,542 metabolically active internal reactions associated with 651 genes (see “Materials and Methods”). The behavior profiles of fluxes and the corresponding gene expression over time can be represented as trends. Each experimental and predicted trend was fitted to five different regression models as described in detail in the “Materials and Methods” with the quality of the fit measured as R2. For each regression model, the distribution of R2 values was calculated for expression data (Supplemental Fig. S3, A–E) and for predicted flux trends (Supplemental Fig. S3, F–J). The quadratic regression model accurately describes a higher number of trends than the linear model. The cubic and two-term exponential models reconcile with most of the data (expression and flux trends) at R2 > 0.6. The agreement between predicted and experimental trends was performed by statistically comparing (Student’s t test α = 0.05) the homogeneity of the fitted coefficients in each regression model (Fig. 5, C and D). We found over 50% (777) agreement between predicted flux and expression data for all active reactions. These 777 reactions have gene-protein-reaction (GPR) associations enclosing 75% of all active metabolic genes. Alternatively, 169 genes of the total active genes did not show significant agreement between predicted flux and expression data at any time point. These 169 genes belong to 57 different subsystems (Fig. 6). Forty percent of those genes are associated with reactions that are located in compartments other than the cytoplasm; for example, 35 are associated with duplicated or triplicate reactions located in the chloroplast, mitochondria, glyoxysome, or thylakoid (Supplemental Table S5).

Figure 6.

Figure 6.

Open in a new tab

Reactions with no agreement between flux and expression trends. More than 40% of reactions without agreement due to lack of knowledge at the metabolic level and subcellular localization are present in compartments different from the cytoplasm.

The model predicted that 142 allosteric reactions were active under photoautotrophic conditions. Out of those reactions, 91 could be explained by the expression data (Supplemental Fig. S4). Besides, 65 active reactions are catalyzed by multisubunit enzymes, out of which 49 showed positive results in the homogeneity test, resulting in a predicted percentage of 75% (Supplemental Table S6). Thus, for most of these multisubunit enzymes, the flux and expression trends coincide.

Identification of Putative Transporters

Reconstruction of genome-scale metabolic models for eukaryotic microorganisms is a challenge due to their compartmental complexity. Conventionally, the network connectivity in multicompartment organisms is kept by adding transport reactions within organelles. Given our lack of knowledge about intracellular transport, those transport reactions are often not associated with a gene. Here, the predicted flux trend for each non-gene-associated transport reaction in iCZ843 was compared to all expression trends of the genes in the genome. The list of tentative associated genes for each reaction was automatically created based on statistically similar significant trends (Fig. 1). The predictions pointed to 217 genes that could be related to transporters (e.g. channels, facilitators, ABC transporters, etc). Blast results against the transporter classification database (TCDB) (Saier et al., 2014) identified 190 of these 217 genes with transport capabilities. Some examples of automatically generated GPR are the association between the transporter of ammonia in the chloroplast (NH4th) and the gene genemark_Scaffold_87-abinit-gene-0.4, according with the TCDB. Importantly, this gene is annotated as a hypothetical protein for Chlorella but as an ammonia transporter for Arabidopsis (Arabidopsis thaliana). Similar results were obtained for the gene maker_Scaffold_995-augustus-gene-0.92, which was associated with the transport of Glu in the mitochondria (GLUNA1tm). After manual curation, 103 new genes, associated with 51 transport reactions, were added to the reconstruction of C. vulgaris (Supplemental Table S7), reducing the number of transport reactions without GPR to 86. The updated model now contains 946 genes, 2,294 reactions, and 1,770 metabolites (iCZ946; Supplemental File 2).

DISCUSSION

We used the genome-scale metabolic network of C. vulgaris UTEX 395 iCZ843 (Zuñiga et al., 2016) to analyze dynamic metabolism and biomass composition under photoautotrophic and heterotrophic conditions. Until now, highly dynamic biomass compositions as found in phototrophs have not been exploited to constrain genome-scale models. The dynamic growth-course data represent varying macromolecular compositions including carbohydrates, fatty acids, and proteins obtained by measuring intracellular metabolite concentrations. The experimental growth rates, lipid composition, and lipid speciation correspond to that determined from omics data sets (Guarnieri et al., 2013); however, here the fatty acid speciation was expanded to include detected levels of C16:3 and C18:2. The experimental data set was then used to time-specific constrain the metabolic network iCZ843 (Supplemental File 1).

Each constraint model provides a snapshot of metabolism, yielding a dynamic characterization of the solution space over time. We compared the average flux distributions at each time point, comprised of a different biomass, to growth-course expression data. The condition-specific constraint models were used to study the effect of varying biomass compositions on the growth rate, proteome demands, and flux-to-expression relationships. The resulting flux distribution of each model represents a steady-state metabolic phenotype, enabling the identification of metabolic bottlenecks and activity of pathways in different subcellular compartments in the network (Orth et al., 2010). On the other hand, intracellular metabolite pools, which are common in cellular systems, are not considered in single constraint-based modeling approaches, although changes in these pools can affect metabolism, and thus, metabolic flux distributions obtained from genome-scale metabolic models (Nikolaev et al., 2005; Feist and Palsson, 2008).

Microalgae, such as C. vulgaris, exhibit complex and intertwined metabolic networks. Organelle-specific metabolism and internal metabolite pools have to be adjusted when environmental conditions, such as light conditions and nitrogen availability, change over time (Fig. 4). Storage and consumption of nitrate in microalgae has been modeled previously (Flynn and Fasham, 1997; Flynn, 1999), but to our knowledge never before at the genome-scale. It has been hypothesized that C. vulgaris takes up all nitrogen (i.e. nitrate) from the culture medium, and stores it intracellularly in form of ammonium (Smith, 1977) or potentially other minor nitrogen compounds, such as amino acids or pigments (Li et al., 2015; Paes et al., 2016). By using the experimentally derived BOFs, this pool was quantitatively characterized through the interplay between predicted nitrogen uptake rates and nitrate concentration in the supernatant. According to the predicted flux distributions, the way to overcome nutrient depletion in the supernatant is to create an intracellular pool of ammonium (Fig. 4). This pool is 2.6 times larger during photoautotrophic growth than under heterotrophic conditions, 4.2 and 1.6 mm respectively, which agrees with prior observations (5–10 mm; Smith, 1977; Paes et al., 2016). The model predicts an ammonium consumption rate of 0.009 ± 0.0003 mmol/L/h independent of the growth condition, which could be due to strong regulation and interconnectivity of carbon and nitrogen metabolism in microalgae (Machado et al., 2015).

To date, systems biology approaches at genome-scale have enabled theoretical identification of the functional or active proteome required to support growth in heterotrophs (O’Brien et al., 2013; Yang et al., 2015; Steffani-Vallejo et al., 2017). Additionally, mechanistic analysis to correlate high-throughput data such as transcriptomics and proteomics with predicted growth rates and flux distributions have been successfully performed (Lewis et al., 2012; Yang et al., 2015; Zielinski et al., 2015; Barenholz et al., 2016). Here, the condition-specific constraint metabolic model predicts flux distributions revealing proteome demands over a growth course under heterotrophic or photoautotrophic conditions. The increase, decrease, presence, or absence of flux through reactions gives insights into enzyme activities in photoautotrophic cells. Experimental expression data were compared to predicted flux trends under photoautotrophic conditions. We found over 75% agreement between RNA-seq expression data and predicted flux distributions trends (Fig. 5). Interestingly, these reactions are spread throughout most of the subsystems in the reconstruction (64/86). The percentage of explained reactions by main subsystems (Fig. 5B) was calculated showing that energy metabolism, terpenoid biosynthesis, and gluthathione, amino sugar, and nucleotide sugar metabolism can be predicted using dynamic BOFs. Over 60% of reactions in the fatty acid and nucleotide metabolism can be explained, and over 44% of reactions in amino acid, carbohydrate, and cofactor and vitamin metabolism are captured accurately by the model. Reactions in subsystems without agreement between expression and flux predictions (25% total) included specific amino acids (Tyr and Met) and glyoxylate metabolism. The results suggest that nutrient availability, in this case nitrogen, is one of the main factors that drive a highly dynamic biomass composition. The experimental data showed balanced growth (as determined by OD), in which the built-in metabolites of the biomass are synthesized at its maximum rate. Balanced growth is characterized by a high protein content (∼50%) achieved by C. vulgaris around mid-log phase under photoautotrophy (OD = 3.0) and heterotrophy (OD = 2.8). The biomass composition adjustments among protein, carbohydrate, nucleotide, and lipid composition occurred after nitrogen was depleted in mid-log phase. This adjustment allowed for an increase in biomass (final OD = 6.6 ± 0.3). Nitrogen limitation causes a cascade of metabolic responses in algae that are associated with the synthesis of carbon-rich compounds; the exact nature of these responses, however, is currently not fully understood (Henard et al., 2017).

Discordant trends (expression versus simulations) can be grouped into four different categories: (1) reaction compartmentalization, (2) multisubunit enzymes, (3) allosteric reactions, and (4) other regulatory mechanisms. Most of these categories are out of the scope of constrain-based modeling and require alternative advanced modeling approaches (Liu et al., 2014). In the following, we will discuss the four categories in detail: (1) identical reactions in different compartments (Fig. 6). This category points to the fact that we currently lack basic information regarding intracellular transport and duplicated organelle-specific reactions or pathways (Giordano et al., 2005). For example, since the discovery of the chloroplast in 1905, very few chloroplast-related channels and transporters have been characterized (Hanson, 1985; Pottosin and Shabala, 2016). New tools have recently been deployed to quantitatively understand the interplay of metabolites between organelles (Itzhak et al., 2016). Integration of these tools with genome-scale models may help to elucidate metabolic traffic inside compartmentalized cells. (2) Multisubunit enzymes (Supplemental Table S6): These enzymes are commonly related to promiscuous activities that are not well understood on the genome-scale level (Nobeli et al., 2009). The trend analysis deployed here enabled predictions of expression and activity of these multisubunit enzymes. Genes of multisubunit enzymes and complexes are often expressed differently and posttranscriptionally regulated, generating a disagreement of 25% in the active multisubunit enzymes during our comparison. This could be circumvented by directly measuring translation, translation efficiency, and subunit stoichiometry, e.g. by Ribo-seq (Latif et al., 2015; Henard et al., 2017). (3) Allosteric reactions (Supplemental Fig. S4): This type of reaction has been challenging to predict by metabolic models (Machado et al., 2015; Du et al., 2016) and requires kinetic models (Saa and Nielsen, 2016), which currently exist on a genome-scale only for E. coli (Khodayari and Maranas, 2016). We found statistical agreement between gene expression trends and predicted flux distributions trends, making progress toward the understanding of the performance of 91 allosteric reactions in Chlorella’s metabolism over growth course by considering the tendency of the fluxes over time instead of single snapshots. However, some allosteric reactions still could not be predicted. Our results hint at a lack of knowledge in the glyoxylate and dicarboxylate metabolism that could improve model predictions. We also found that further research is needed in order to interpret the metabolic regulation at light and dark conditions of allosteric enzymes in oxidative phosphorylation, polyamine metabolism, riboflavin, selenoamino acid, ubiquinone biosynthesis, and photosynthesis. (4) Posttranscriptional or posttranslational regulation, expression of constitutive genes, and RNA and protein turnover: To address these discrepancies, the data were used to match the corresponding unpredicted genes with proteomics information (Guarnieri et al., 2013). Due to the reduced coverage inherent to proteomics data, only 102 out of 169 genes without agreement (flux-to-expression) contained peptide counts. Forty-seven percent of these 102 genes had a low Pearson correlation (R2 < 0.3) or negative correlation between transcriptomics and proteomics, indicating nonlinear correlation between flux (enzyme activity) and expression. This discrepancy explains why these genes cannot be accurately predicted by comparing the tendencies of predicted reactions rates (fluxes) with the expression of those enzymes. Ribo-seq data could help delineate nonlinear relationships between transcriptomics and proteomics (Latif et al., 2015; Henard et al., 2017). Furthermore, recent evidence has indicated highly active posttranslational mechanisms in C. vulgaris, which may also impact the discrepancy observed between gene and protein expression levels (Henard et al., 2017).

Predicting the interaction between nutrient availability and a dynamic biomass composition requires a nonstatic BOF. We evaluated quantitatively how the determination of the BOF varies based on experimental measurements in comparison to an estimated biomass composition based on genome sequence alone. We compared these two protein profiles (measured and estimated) using highly curated models of the proteobacterium E. coli and the microalgae Chlamydomonas reinhardtii and C. vulgaris (see Fig. 3; Supplemental Table S1). The estimated and measured profiles for C. vulgaris (Fig. 3) differ substantially for eight amino acids over time. In contrast, most of the amino acid composition in E. coli and C. reinhardtii was similar over time. Interestingly, Gly composition over time differed in all cases between estimated relative fraction obtained from estimation or experimental measurements. Thus, the macromolecular biomass composition is crucial for flux and growth rate simulation accuracy.

Currently, constraint-based modeling methods to contextualize omics data are limited to a single growth condition not reflecting the highly dynamic lifestyle of phototrophic organisms. We successfully compare experimental and predicted flux-to-gene trends over the course of growth (Figs. 1 and 5). Reconstructing a highly curated and validated genome-scale model is a time-consuming process and depends on the complexity of the organism’s genome and available data. One of the most time-consuming steps of the reconstruction process is the refinement of the model (Thiele and Palsson, 2010), during which the GPR of every reaction is verified. We successfully used our workflow to guide the GPR association, passing from predicted flux trends to formulation of possible GPR by scanning expression trends of all genes in the genome. Increasing the GPR associations in a metabolic model using omics data has not been applied before, and we argue that this workflow can substantially improve the reconstruction process. The non-GPR transport reactions were used as input to the workflow; thus, a GPR list was automatically created for these reactions and enabled the identification of new intercompartment transport genes. After a manual curation step, the number of genes in the reconstructions for C. vulgaris UTEX 395 was increased by over 10% from 843 to 946, resulting in an updated and improved model iCZ946. The increased scope of the model resulted in predictions of exchanges between specific subcellular compartments and yielded greater insights into the general compartmentalization nature of microalgae.

MATERIALS AND METHODS

Experimental Biomass Composition and Omics Data

Biomass composition (lipid, protein, carbohydrates, and nucleic acid [RNA]) was determined over a growth course as described previously (McConnell and Antoniewicz, 2016; Zuñiga et al., 2016; Rosenberg et al., 2014). In brief, Chlorella vulgaris UTEX 395 was grown photoautotrophically using Bold’s basal medium at 24°C with cycling of 14/10 h light/dark at 10,000 l× and 1% CO2. Under heterotrophy, C. vulgaris was grown under dark conditions in the above medium with the addition of 55 mm of Glc. Amino acids, carbohydrates, RNA, and lipids were measured by gas chromatography/mass spectrometry analysis (Long and Antoniewicz, 2014). Experiments were carried out in quadruplicate. Average se among these experiments varied from the mean between 7% and 14%. The amino acid content information was completed with data from the literature. Data for Arg, Cys, Gln, and Trp under photoautotrophy were obtained from Faheed and Fattah (2008), and Cys content in heterotrophy was taken from Wu et al. (2015). At the highest biomass protein content (46%), those metabolites (Arg, Cys, Gln, Trp) represented 1% of the total amino acid mass. Thus, biomass stoichiometric coefficients for these amino acids were considered constant over the course of growth. Similar assumptions were made for the 10 pigments (i.e. antheraxanthin, chloprophyll A and B, loroxanthin, lutein, neoxanthin, violaxanthin, zeaxanthin, α-carotene, β-carotene). Pigments represent less than 10% of the total biomass mass in C. vulgaris. Information about pigments was obtained from previous work (Safi et al., 2014). The photoautotrophic growth course contained six sample points at 3, 4, 5, 6, 7, and 8 d, corresponding to an OD600 of 1.5, 3.03, 3.42, 5.24, 6.05, and 6.98, respectively. The heterotrophic experiment was sampled at 4.24, 4.75, 5.24, 5.75, and 6.25 d (OD600 = 2.0, 2.82, 3.67, 4.57, 6.29). RNA-seq and proteomics data over the growth course for photoautotrophic growth were obtained from Guarnieri et al. (2011) at five time points corresponding to optical density of 2, 4, 6, 7, and 8. All samples under this condition, except sample with OD 2, were depleted in nitrogen (Supplemental File 1).

Determination of Biomass Composition In Silico

Biomass composition to define the BOFs was determined either based on experimental data or estimated based on a previously described protocol (Thiele and Palsson, 2010), in which the fraction of protein, DNA, and RNA components were estimated from the organism’s genome. Accuracy of the growth predictions using growth course measured BOFs, and an in silico determined BOF was evaluated and compared to two controls obtained for the heterotroph Escherichia coli and the green algae Chlamydomonas reinhardtii.

For C. vulgaris, we estimated the fractions of the amino acids using the available genome sequence (GenBank LDKB00000000.1) and the measured protein content (Zuñiga et al., 2016). For C. reinhardtii, the fractional contribution of amino acids to the protein biomass was determined using the published genome (chloroplast genome, GenBank BK000554.2; mitochondrial genome, GenBank U03843.1; nuclear genome, C. reinhardtii v5.5 from Joint Genome Institute) and from published protein content measurements (Boyle and Morgan, 2009). For E. coli, the fractions of the amino acids and RNA were estimated using NCBI NC_000913.3 and protein and RNA biomass content from the literature (Feist et al., 2007). The estimated fractional contributions were compared to the experimentally determined ones as reported in the corresponding genome-scale reconstructions for C. vulgaris (Zuñiga et al., 2016), C. reinhardtii iRC1080 (Chang et al., 2011), and E. coli iJO1366 (Orth et al., 2011). To facilitate the comparison, the amount of estimated stoichiometric coefficients was scaled to resemble the total experimental macromolecular amount of the coefficients (e.g. protein, nucleotides) in the corresponding model.

Metabolic Network Simulations and Solution Space Sampling

The experimentally and in silico determined biomass compositions were used to constrain the model for C. vulgaris iCZ843. The Glc and nitrate uptake rates were calculated from the experimental data by adjusting time-course nitrate measurements to the Gompertz model (Acuña et al., 1999) using MATLAB (The MathWorks Inc.). To simulate heterotrophic conditions, Glc uptake rate was 0.3025 mmol/gDW/h. Experimental nitrate uptake rates are shown in Figure 4B. To simulate photoautotrophic conditions, CO2 uptake was constrained to 15.3 mmol/gDW/h, and the photosynthetic oxygen evolution to 8.31 mmol/gDW/h (Zuñiga et al., 2016). Under both growth conditions, the nitrate uptake rate was not constrained. Supplemental Table S8 summarizes the applied constraints at each condition.

Genome-scale model simulations were performed using the Gurobi Optimizer Version 5.6.3 (Gurobi Optimization Inc.) solver in MATLAB (The MathWorks Inc.) with the COBRA Toolbox (Schellenberger et al., 2011). FBA was used to simulate the genome-scale model (Orth et al., 2010). To scan the solution space, to calculate flux ranges for each reaction, and to determine active reactions under the simulated conditions in the metabolic model, FVA (Mahadevan and Schilling, 2003) and random sampling of the metabolic model solution space were used. To uniformly sample the solution space of iCZ843, optGpSampler (Megchelenbrink et al., 2014) for MATLAB with Gurobi Optimizer Version 6.5.0 was used. The BOF was fixed to 90% and 100% of the predicted growth rates to better characterize the solution space. Before sampling, all reactions that could not carry flux under the simulated conditions were removed from the models using FVA. The reduced models were sampled with 50,000 sample points and a step count of double the number of reactions in the corresponding model. Reactions carrying an absolute flux lower than 10−10 were set to zero.

Comparison of Expression Data with Flux Distributions

There is an emerging interest in developing methods to analyze nonlinear relationships in big biological data sets (Székely and Rizzo, 2009; Chen et al., 2010; Reshef et al., 2011). Currently, omics data are often analyzed using simple mathematical methods, such as correlations (i.e. Pearson). However, complications with correlations arise when different data sources are obtained at different time points. Furthermore, conventional linear comparisons may not detect nonlinear trends, risking inaccurate interpretation of data (Pernet et al., 2013). To address these issues, we applied an iterative regression-based statistical approach applicable for both pairwise and nonpairwise linear and nonlinear tendencies, which can describe a number of possible behaviors observed in biological systems. This approach is able to reveal complex relationships between flux and gene expression using time-course observations, which can be sampled at equal or different time points within the same timeframe. Figure 1 and Supplemental Figure S5 depict a case example and flow diagram of the proposed approach.

Computational Approach and Data Preparation

To determine the agreement between predicted flux distributions and RNA-seq data under photoautotrophic growth conditions, the model iCZ843 (Zuñiga et al., 2016) was constrained with the biomass composition measurements. The trends of the resulting flux distributions over the six different time points were then compared to the trends of the expression data over the five collected samples using a statistical approach as described schematically in Figure 1.

For each time point, all active reactions in iCZ843, i.e. reactions that can carry flux under the simulated conditions, were determined using FVA (Mahadevan and Schilling, 2003). Based on the FVA result, the reactions active under all studied time points were collected in a master file. Since we were only interested in internal reactions, demand, exchange, and biomass reactions were removed from this list. To quantitatively describe the flux ranges for each active reaction, minimal, maximal, and median value were determined based on the sampling results. Although only the median value is used in the subsequent steps, the minimal and maximal values were kept to indicate the possible flux ranges. For each active reaction, the associated genes were obtained from iCZ843 and used to obtain the corresponding expression values for all time points.

Normalization and Fitting

First, we independently normalized (1) the predicted fluxes for each reaction over all six time points and (2) the time series expression data for each gene associated with the active reactions over all five time points. Note that we created models with each biomass composition measurement taken for six different time points, whereas the RNA-seq data were collected at five time points. Although the number of samples for both data sets is different, the time points and ODs at which the physiological and expression data were sampled correspond to each other.

For each active reaction r, the flux value for each time point i = 1,...,6 was normalized within a range between 0 and 1 using the median flux value Xr,i for reaction r, at time point i and the minimal (Xr,min) and maximal (Xr,max) flux values for reaction r over all six time points as shown in Equation 1.

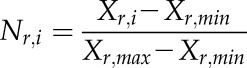graphic file with name PP_PP2017RA00605R2_equ1.jpg (1)

To normalize the expression values for each gene g at time point j = 1,...,5 within a range between 0 and 1, the average expression value Xg,j for gene g at time point j and the minimal (Xg,min) and maximal (Xg,max) average expression value for gene g over all five time points was used as shown in Equation 2.

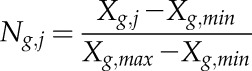graphic file with name PP_PP2017RA00605R2_equ2.jpg (2)

Subsequently, the normalized trends for fluxes and expression were iteratively fitted to linear, quadratic, cubic, exponential, and two-term exponential regression models. We used the coefficient of determination, R2, as a measure of the quality of the fit. The R2 was determined by least-minimum squares fitting using MATLAB (The MathWorks Inc.).

Testing the Consistency between Expression and Predicted Flux Trends

The Statistics and Machine Learning Toolbox of MATLAB (The MathWorks Inc.) was used to fit all regression models (see Fig. 1; Supplemental Fig. S5). The toolbox uses a least-squares method as standard approach to obtain the coefficient and se estimates. There are two important assumptions that are usually made for this method. First, the difference between an observed value and the fitted value provided by a model exists only in the response data. Second, the errors follow a normal (Gaussian) distribution with zero mean and constant variance. Regression-based approaches, such as linear, quadratic, cubic, exponential, and two-term exponential models applied in this study, require at least three observations for linear regression and four observations for the others (Simonton, 1977). Our study consists of five (experimental expression trends) and six observations (predicted flux), respectively. The significance of the regression fitted coefficients was taken into account as well as the experimental and predicted uncertainty before performing the fitting.

The iterative fitting of each gene trend or reaction trend started by selecting the less complex model or parsimonious model (R2 > 0.6.) to avoid over fitting. If R2 was below the threshold, the next higher order regression model was taken into account. Once the regression model with R2 > 0.6 for fluxes and expression was determined, the homogeneity Student’s t test α = 0.05 for each coefficient fitted in the regression model was determined. The homogeneity test of coefficients was performed by estimating the T-value, where the null hypothesis (H0) is that the coefficients are equal, while the alternative hypothesis (Ha) is that the coefficients are different (Montgomery, 2012). The chosen value or significance level was 0.05, corresponding to a critical T-value of 1.83 at 9 degrees of freedom (degree of freedom for expression data = 4, degree of freedom of flux distributions = 5). The decision rule was as follows: H0 is rejected if T-calculated is less than the critical T-value of 1.83 (Steel and Torrie, 1960). The agreement between the trend of gene expression over time and predicted flux values over time was defined by full agreement of the significant coefficients under the decision rule. Note that nonsignificant coefficients were not considered during the analysis. In case the coefficients are not similar (H0 is rejected), the test was repeated for the next higher-order regression model. When the hull hypothesis was rejected for all regression models, the accordance flux-to-expression was detonated as nonagreement.

The R2 value of 0.6 used in the selection of a regression curve was chosen as a common guideline when analyzing biological data (Cook and Weisberg, 2009). To investigate any effect of varying this parameter, we performed a robustness analysis of the R2 parameter by varying the minimum R2 allowed to start the iterative comparison of the fitted coefficients in each regression model. Reducing the R2 results in more linear regression being chosen more often, since this regression type is the first iteration tested. However, the total number of genes with agreement flux-to-expression only varied from 58% to 87% for an R2 varied range from 0.1 to 0.9, indicating that identified relationships were relatively consistent with respect to this parameter (see Supplemental Fig. S6).

Considerations and Decision Making

Twenty-five percent of the active internal reactions (n = 395) are associated with more than one gene. These genes are either isozymes, i.e. they are connected by an OR relationship, or form multisubunit enzyme complexes, meaning that they all are required to catalyze the reaction and are connected by an AND relationship. If the reaction is catalyzed by two or more isozymes, the first gene for which the homogeneity test was positive was selected to describe the reaction flux; the other isozymes were not taken into account for further analyses. In the case of multienzyme complexes, the flux trend was said to be in agreement with the expression data profile over time if the homogeneity test was positive for all genes participating in the multisubunit enzyme.

Feedback Validation Methods: Omics Data Correlation and Allosteric Information

An analysis of how the transcription values (fragments per kilobase million values) of the metabolic genes correlate with proteomics data (normalized spectral abundance factors; Guarnieri et al., 2011) was performed by calculating the Pearson correlation coefficient between transcriptomic and proteomic data. A bidirectional BLAST analysis was done to match the proteins originating from this transcriptome study and the genome-based transcriptome as used in the metabolic model iCZ843 (Zuñiga et al., 2016). The reactions without statistical agreement (flux-to-expression) were linked to the available allosteric reactions information. Because of the current lack of knowledge about allosteric regulation in Chlorella species as well as for other phototrophs (Krusteva et al., 1984; Weinstein and Beale, 1985), mapping was based on the available list of known allosteric reactions in the database ASD v3.0 (Shen et al., 2016).

Predicting Gene-Protein-Reaction Association Based on Flux-to-Expression Trend Matching

The constraints applied to the model resulted in the prediction of flux through reactions that are necessary to produce biomass. Within these active reactions, there are 137 transport reactions that have no GPRs associated. In order to provide gene annotation for those reactions and increase the knowledge of the so far poorly understood exchange between organelles in Chlorella, we performed a reverse identification, in which predicted flux trends of the active reactions were compared to expression trends of all genes in the genome by following the methodology depicted in Figure 1B. Using trends of statistical similarity between their expression and flux across conditions, putative GPRs were assigned to these transport reactions. After the identification of putative GPRs, manual curation and quality control (i.e. bidirectional BLAST) was performed.

Accession Numbers

Sequence data from this article can be found in the GenBank/EMBL data libraries under accession numbers LDKB00000000.1, U03843.1, and NC_000913.3.

Supplemental Data

The following supplemental materials are available.

Acknowledgments

The authors are thankful to Obdulia Gonzalez (UAM-Iztapalapa) for guidance of statistical analysis and Joanne Liu (UCSD) for fruitful discussions. This material is based upon work supported by the National Science Foundation under grant no. 1332344 and the US Department of Energy (DOE), Office of Science, Office of Biological & Environmental Research Award DE-SC0012658. C.Z. is in part supported by Mexican National Research Council, CONACYT, fellowship no. 237897.

Footnotes

1

This material is based upon work supported by the National Science Foundation under Grant no. 1332344 and the U.S. Department of Energy, Office of Science, Office of Biological & Environmental Research Award DE-SC0012658. C.Z. is in part supported by Mexican National Research Council, CONACYT, fellowship no. 237897.

References

  1. Acuña ME, Perez F, Auria R, Revah S (1999) Microbiological and kinetic aspects of a biofilter for the removal of toluene from waste gases. Biotechnol Bioeng 63: 175–184 [DOI] [PubMed] [Google Scholar]
  2. Barenholz U, Keren L, Segal E, Milo R (2016) A minimalistic resource allocation model to explain ubiquitous increase in protein expression with growth rate. PLoS One 11: e0153344. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Baroukh C, Muñoz-Tamayo R, Steyer J-P, Bernard O (2015) A state of the art of metabolic networks of unicellular microalgae and cyanobacteria for biofuel production. Metab Eng 30: 49–60 [DOI] [PubMed] [Google Scholar]
  4. Bordbar A, Lewis NE, Schellenberger J, Palsson BO, Jamshidi N (2010) Insight into human alveolar macrophage and M. tuberculosis interactions via metabolic reconstructions. Mol Syst Biol 6: 422. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bordel S, Agren R, Nielsen J (2010) Sampling the solution space in genome-scale metabolic networks reveals transcriptional regulation in key enzymes. PLOS Comput Biol 6: e1000859. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Boyle NR, Morgan JA (2009) Flux balance analysis of primary metabolism in Chlamydomonas reinhardtii. BMC Syst Biol 3: 4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Burgard AP, Maranas CD (2003) Optimization-based framework for inferring and testing hypothesized metabolic objective functions. Biotechnol Bioeng 82: 670–677 [DOI] [PubMed] [Google Scholar]
  8. Chang RL, Ghamsari L, Manichaikul A, Hom EFY, Balaji S, Fu W, Shen Y, Hao T, Palsson BO, Salehi-Ashtiani K, et al. (2011) Metabolic network reconstruction of Chlamydomonas offers insight into light-driven algal metabolism. Mol Syst Biol 7: 518. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Chen YA, Almeida JS, Richards AJ, Müller P, Carroll RJ, Rohrer B (2010) A nonparametric approach to detect nonlinear correlation in gene expression. J Comput Graph Stat 19: 552–568 [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cook D, Weisberg S (2009) Applied Regression Including Computing and Graphics. John Wiley & Sons, New York, NY [Google Scholar]
  11. Cordova LT, Long CP, Venkataramanan KP, Antoniewicz MR (2015) Complete genome sequence, metabolic model construction and phenotypic characterization of Geobacillus LC300, an extremely thermophilic, fast growing, xylose-utilizing bacterium. Metab Eng 32: 74–81 [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cordova LT, Lu J, Cipolla RM, Sandoval NR, Long CP, Antoniewicz MR (2016) Co-utilization of glucose and xylose by evolved Thermus thermophilus LC113 strain elucidated by (13)C metabolic flux analysis and whole genome sequencing. Metab Eng 37: 63–71 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. De Martino D, Mori M, Parisi V (2015) Uniform sampling of steady states in metabolic networks: heterogeneous scales and rounding. PLoS One 10: e0122670. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Du B, Zielinski DC, Kavvas ES, Dräger A, Tan J, Zhang Z, Ruggiero KE, Arzumanyan GA, Palsson BO (2016) Evaluation of rate law approximations in bottom-up kinetic models of metabolism. BMC Syst Biol 10: 40. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Faheed AF, Fattah ZA (2008) Effect of Chlorella vulgaris as bio-fertilizer on growth parameters and metabolic aspects of lettuce plant. J Agric Soc Sci 4: 165–169 [Google Scholar]
  16. Feist AM, Henry CS, Reed JL, Krummenacker M, Joyce AR, Karp PD, Broadbelt LJ, Hatzimanikatis V, Palsson BO (2007) A genome-scale metabolic reconstruction for Escherichia coli K-12 MG1655 that accounts for 1260 ORFs and thermodynamic information. Mol Syst Biol 3: 121. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Feist AM, Palsson BO (2008) The growing scope of applications of genome-scale metabolic reconstructions using Escherichia coli. Nat Biotechnol 26: 659–667 [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Feist AM, Palsson BO (2010) The biomass objective function. Curr Opin Microbiol 13: 344–349 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Flynn K. (1999) Nitrate transport and ammonium-nitrate interactions at high nitrate concentrations and low temperature. Mar Ecol Prog Ser 187: 283–287 [Google Scholar]
  20. Flynn KJ, Fasham MJ (1997) A short version of the ammonium-nitrate interaction model. J Plankton Res 19: 1881–1897 [Google Scholar]
  21. Geider RJ, Delucia EH, Falkowski PG, Finzi AC, Grime JP, Grace J, Kana TM, La Roche J, Long SP, Osborne BA, et al. (2001) Primary productivity of planet earth: biological determinants and physical constraints in terrestrial and aquatic habitats. Glob Change Biol 7: 849–882 [Google Scholar]
  22. Gianchandani EP, Oberhardt MA, Burgard AP, Maranas CD, Papin JA (2008) Predicting biological system objectives de novo from internal state measurements. BMC Bioinformatics 9: 43. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Giordano M, Beardall J, Raven JA (2005) CO2 concentrating mechanisms in algae: mechanisms, environmental modulation, and evolution. Annu Rev Plant Biol 56: 99–131 [DOI] [PubMed] [Google Scholar]
  24. Gonzalez JE, Long CP, Antoniewicz MR (2017) Comprehensive analysis of glucose and xylose metabolism in Escherichia coli under aerobic and anaerobic conditions by (13)C metabolic flux analysis. Metab Eng 39: 9–18 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Guarnieri MT, Nag A, Smolinski SL, Darzins A, Seibert M, Pienkos PT (2011) Examination of triacylglycerol biosynthetic pathways via de novo transcriptomic and proteomic analyses in an unsequenced microalga. PLoS One 6: e25851. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Guarnieri MT, Nag A, Yang S, Pienkos PT (2013) Proteomic analysis of Chlorella vulgaris: Potential targets for enhanced lipid accumulation. J Proteomics 93: 245–253 [DOI] [PubMed] [Google Scholar]
  27. Hanson J. (1985) Membrane transport systems of plant mitochondria. Encycl Plant Physiol 18: 248–275 [Google Scholar]
  28. Henard CA, Guarnieri MT, Knoshaug EP (2017) The Chlorella vulgaris S-nitrosoproteome under nitrogen-replete and -deplete conditions. Front Bioeng Biotechnol 4: 100–105 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Henry CS, DeJongh M, Best AA, Frybarger PM, Linsay B, Stevens RL (2010) High-throughput generation, optimization and analysis of genome-scale metabolic models. Nat Biotechnol 28: 977–982 [DOI] [PubMed] [Google Scholar]
  30. Hussain MS, Fareed S, Ansari S, Rahman MA, Ahmad IZ, Saeed M (2012) Current approaches toward production of secondary plant metabolites. J Pharm Bioallied Sci 4: 10–20 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Itzhak DN, Tyanova S, Cox J, Borner GH (2016) Global, quantitative and dynamic mapping of protein subcellular localization. eLife 5: e16950. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Khodayari A, Maranas CD (2016) A genome-scale Escherichia coli kinetic metabolic model k-ecoli457 satisfying flux data for multiple mutant strains. Nat Commun 7: 13806. [DOI] [PMC free article] [PubMed] [Google Scholar]
  33. Khoeyi ZA, Seyfabadi J, Ramezanpour Z (2012) Effect of light intensity and photoperiod on biomass and fatty acid composition of the microalgae, Chlorella vulgaris. Aquacult Int 20: 41–49 [Google Scholar]
  34. King ZA, Lu J, Dräger A, Miller P, Federowicz S, Lerman JA, Ebrahim A, Palsson BO, Lewis NE (2016) BiGG Models: A platform for integrating, standardizing and sharing genome-scale models. Nucleic Acids Res 44(D1): D515–D522 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Krampitz LO, Yarris CE (1983) Glycolate formation and excretion by Chlorella pyrenoidosa and Netrium digitus. Plant Physiol 72: 1084–1087 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Krusteva NG, Tomova NG, Georgieva MA (1984) Allosteric regulation of NAD(NADP)-dependent glyceraldehyde-3-phosphate dehydrogenase from Chlorella by α-amino acids, dithiothreitol and ATP. FEBS Lett 171: 137–140 [Google Scholar]
  37. Kumar VS, Maranas CD (2009) GrowMatch: An automated method for reconciling in silico/in vivo growth predictions. PLOS Comput Biol 5: e1000308. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Latif H, Szubin R, Tan J, Brunk E, Lechner A, Zengler K, Palsson BO (2015) A streamlined ribosome profiling protocol for the characterization of microorganisms. Biotechniques 58: 329–332 [DOI] [PubMed] [Google Scholar]
  39. Levering J, Broddrick J, Dupont CL, Peers G, Beeri K, Mayers J, Gallina AA, Allen AE, Palsson BO, Zengler K (2016) Genome-scale model reveals metabolic basis of biomass partitioning in a model diatom. PLoS One 11: e0155038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Lewis NE, Nagarajan H, Palsson BO (2012) Constraining the metabolic genotype-phenotype relationship using a phylogeny of in silico methods. Nat Rev Microbiol 10: 291–305 [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. Li YX, Zhao FJ, Yu DD (2015) Effect of nitrogen limitation on cell growth, lipid accumulation and gene expression in Chlorella sorokiniana. Braz Arch Biol Technol 58: 462–467 [Google Scholar]
  42. Liu JK, O’Brien EJ, Lerman JA, Zengler K, Palsson BO, Feist AM (2014) Reconstruction and modeling protein translocation and compartmentalization in Escherichia coli at the genome-scale. BMC Syst Biol 8: 110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Long CP, Antoniewicz MR (2014) Quantifying biomass composition by gas chromatography/mass spectrometry. Anal Chem 86: 9423–9427 [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Long CP, Gonzalez JE, Sandoval NR, Antoniewicz MR (2016) Characterization of physiological responses to 22 gene knockouts in Escherichia coli central carbon metabolism. Metab Eng 37: 102–113 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Machado D, Herrgård MJ, Rocha I (2015) Modeling the contribution of allosteric regulation for Flux control in the central carbon metabolism of E. coli. Front Bioeng Biotechnol 3: 154. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Mahadevan R, Schilling CH (2003) The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. Metab Eng 5: 264–276 [DOI] [PubMed] [Google Scholar]
  47. McConnell BO, Antoniewicz MR (2016) Measuring the composition and stable-isotope labeling of algal biomass carbohydrates via gas chromatography/mass spectrometry. Anal Chem 88: 4624–4628 [DOI] [PubMed] [Google Scholar]
  48. Megchelenbrink W, Huynen M, Marchiori E (2014) optGpSampler: An improved tool for uniformly sampling the solution-space of genome-scale metabolic networks. PLoS One 9: e86587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Montezano D, Meek L, Gupta R, Bermudez LE, Bermudez JCM (2015) Flux balance analysis with objective function defined by proteomics data—metabolism of Mycobacterium tuberculosis exposed to mefloquine. PLoS One 10: e0134014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Montgomery DC. (2012) Design and Analysis of Experiments, Ed 8 John Wiley & Sons, New York, pp 24–55 [Google Scholar]
  51. Nikolaev EV, Burgard AP, Maranas CD (2005) Elucidation and structural analysis of conserved pools for genome-scale metabolic reconstructions. Biophys J 88: 37–49 [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Nobeli I, Favia AD, Thornton JM (2009) Protein promiscuity and its implications for biotechnology. Nat Biotechnol 27: 157–167 [DOI] [PubMed] [Google Scholar]
  53. O’Brien EJ, Lerman JA, Chang RL, Hyduke DR, Palsson BO (2013) Genome-scale models of metabolism and gene expression extend and refine growth phenotype prediction. Mol Syst Biol 9: 693. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Orth JD, Conrad TM, Na J, Lerman JA, Nam H, Feist AM, Palsson BØ (2011) A comprehensive genome-scale reconstruction of Escherichia coli metabolism. Mol Syst Biol 7: 535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Orth JD, Thiele I, Palsson BØ (2010) What is flux balance analysis? Nat Biotechnol 28: 245–248 [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Paes CRPS, Faria GR, Tinoco NAB, Castro DJFA, Barbarino E, Lourenco SO (2016) Growth, nutrient uptake and chemical composition of Chlorella sp. and Nannochloropsis oculata under nitrogen starvation. Lat Am J Aquat Res 44: 275–292 [Google Scholar]
  57. Palsson BO. (2006) Systems Biology: Properties of Reconstructed Networks. Cambridge University Press, New York [Google Scholar]
  58. Perez-Garcia O, Escalante FME, de-Bashan LE, Bashan Y (2011) Heterotrophic cultures of microalgae: Metabolism and potential products. Water Res 45: 11–36 [DOI] [PubMed] [Google Scholar]
  59. Pernet CR, Wilcox R, Rousselet GA (2013) Robust correlation analyses: False positive and power validation using a new open source Matlab toolbox. Front Psychol 3: 606. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Pottosin I, Shabala S (2016) Transport across chloroplast membranes: Optimizing photosynthesis for adverse environmental conditions. Mol Plant 9: 356–370 [DOI] [PubMed] [Google Scholar]
  61. Reshef DN, Reshef YA, Finucane HK, Grossman SR, McVean G, Turnbaugh PJ, Lander ES, Mitzenmacher M, Sabeti PC (2011) Detecting novel associations in large data sets. Science 334: 1518–1524 [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Rosenberg JN, Kobayashi N, Barnes A, Noel EA, Betenbaugh MJ, Oyler GA (2014) Comparative analyses of three Chlorella species in response to light and sugar reveal distinctive lipid accumulation patterns in the Microalga C. sorokiniana. PLoS One 9: e92460. [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Saa PA, Nielsen LK (2016) Construction of feasible and accurate kinetic models of metabolism: A Bayesian approach. Sci Rep 6: 29635. [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. Safi C, Zebib B, Merah O, Pontalier P-Y, Vaca-Garcia C (2014) Morphology, composition, production, processing and applications of Chlorella vulgaris: A review. Renew Sustain Energy Rev 35: 265–278 [Google Scholar]
  65. Saier MH Jr., Reddy VS, Tamang DG, Västermark A (2014) The transporter classification database. Nucleic Acids Res 42: D251–D258 [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Schellenberger J, Que R, Fleming RMT, Thiele I, Orth JD, Feist AM, Zielinski DC, Bordbar A, Lewis NE, Rahmanian S, et al. (2011) Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox v2.0. Nat Protoc 6: 1290–1307 [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Shen B, Li C, Tarczynski MC (2002) High free-methionine and decreased lignin content result from a mutation in the Arabidopsis S-adenosyl-L-methionine synthetase 3 gene. Plant J 29: 371–380 [DOI] [PubMed] [Google Scholar]
  68. Shen Q, Wang G, Li S, Liu X, Lu S, Chen Z, Song K, Yan J, Geng L, Huang Z, et al. (2016) ASD v3.0: Unraveling allosteric regulation with structural mechanisms and biological networks. Nucleic Acids Res 44(D1): D527–D535 [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Simonton DK. (1977) Cross-sectional time-series experiments: Some suggested statistical analyses. Psychol Bull 84: 489–502 [Google Scholar]
  70. Smith T. (1977) Recent advances in the biochemistry of plant amines. In Reinhold N, Harbone JB, Swain T, eds, 1st Edition Pergamon Press, Oxford, pp 27–81 [Google Scholar]
  71. Steel R, Torrie J (1960) Principles and Procedures of Statistics with Special Reference to the Biological Sciences. McGraw-Hill Book Company, New York. [Google Scholar]
  72. Steffani-Vallejo JL, Zuñiga C, Cruz-Morales P, Lozano L, Morales M, Licona-Cassani C, Revah S, Utrilla J (2017) Draft genome sequence of Sphingobacterium sp. CZ-UAM, isolated from a methanotrophic consortium. Genome Announc 5: e00792-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Stitt M. (2013) Progress in understanding and engineering primary plant metabolism. Curr Opin Biotechnol 24: 229–238 [DOI] [PubMed] [Google Scholar]
  74. Székely GJ, Rizzo ML (2009) Brownian distance covariance. Ann Appl Stat 3: 1236–1265 [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Taziki M, Ahmadzadeh HA, Murry M (2015) Growth of Chlorella vulgaris in high concentrations of nitrate and nitrite for wastewater treatment. Curr Biotechnol 4: 441–447 [Google Scholar]
  76. Thiele I, Palsson BØ (2010) A protocol for generating a high-quality genome-scale metabolic reconstruction. Nat Protoc 5: 93–121 [DOI] [PMC free article] [PubMed] [Google Scholar]
  77. Weinstein JD, Beale SI (1985) Enzymatic conversion of glutamate to δ-aminolevulinate in soluble extracts of the unicellular green alga, Chlorella vulgaris. Arch Biochem Biophys 237: 454–464 [DOI] [PubMed] [Google Scholar]
  78. Wu C, Xiong W, Dai J, Wu Q (2015) Genome-based metabolic mapping and 13C flux analysis reveal systematic properties of an oleaginous microalga Chlorella protothecoides. Plant Physiol 167: 586–599 [DOI] [PMC free article] [PubMed] [Google Scholar]
  79. Yang L, Tan J, O’Brien EJ, Monk JM, Kim D, Li HJ, Charusanti P, Ebrahim A, Lloyd CJ, Yurkovich JT, et al. (2015) Systems biology definition of the core proteome of metabolism and expression is consistent with high-throughput data. Proc Natl Acad Sci USA 112: 10810–10815 [DOI] [PMC free article] [PubMed] [Google Scholar]
  80. Zielinski DC, Filipp FV, Bordbar A, Jensen K, Smith JW, Herrgard MJ, Mo ML, Palsson BO (2015) Pharmacogenomic and clinical data link non-pharmacokinetic metabolic dysregulation to drug side effect pathogenesis. Nat Commun 6: 7101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Zuñiga C, Li C-T, Huelsman T, Levering J, Zielinski DC, McConnell BO, Long CP, Knoshaug EP, Guarnieri MT, Antoniewicz MR, et al. (2016) Genome-scale metabolic model for the green alga Chlorella vulgaris UTEX 395 accurately predicts phenotypes under autotrophic, heterotrophic, and mixotrophic growth conditions. Plant Physiol 172: 589–602 [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Plant Physiology are provided here courtesy of Oxford University Press

RESOURCES