MRI-Related Geometric Distortions in Stereotactic Radiotherapy Treatment Planning: Evaluation and Dosimetric Impact

Abstract

In view of their superior soft tissue contrast compared to computed tomography, magnetic resonance images are commonly involved in stereotactic radiosurgery/radiotherapy applications for target delineation purposes. It is known, however, that magnetic resonance images are geometrically distorted, thus deteriorating dose delivery accuracy. The present work focuses on the assessment of geometric distortion inherent in magnetic resonance images used in stereotactic radiosurgery/radiotherapy treatment planning and attempts to quantitively evaluate the consequent impact on dose delivery. The geometric distortions for 3 clinical magnetic resonance protocols (at both 1.5 and 3.0 T) used for stereotactic radiosurgery/radiotherapy treatment planning were evaluated using a recently proposed phantom and methodology. Areas of increased distortion were identified at the edges of the imaged volume which was comparable to a brain scan. Although mean absolute distortion did not exceed 0.5 mm on any spatial axis, maximum detected control point disposition reached 2 mm. In an effort to establish what could be considered as acceptable geometric uncertainty, highly conformal plans were utilized to irradiate targets of different diameters (5-50 mm). The targets were mispositioned by 0.5 up to 3 mm, and dose–volume histograms and plan quality indices clinically used for plan evaluation and acceptance were derived and used to investigate the effect of geometrical uncertainty (distortion) on dose delivery accuracy and plan quality. The latter was found to be strongly dependent on target size. For targets less than 20 mm in diameter, a spatial disposition of the order of 1 mm could significantly affect (>5%) plan acceptance/quality indices. For targets with diameter greater than 2 cm, the corresponding disposition was found greater than 1.5 mm. Overall results of this work suggest that efficacy of stereotactic radiosurgery/radiotherapy applications could be compromised in case of very small targets lying distant from the scanner’s isocenter (eg, the periphery of the brain).

Introduction

In recent years, the use of magnetic resonance (MR) images in radiation treatment planning has drawn considerable attention.¹ This is majorly attributed to the superior soft tissue contrast of MR images compared to computed tomography (CT), which results in more accurate and (time) efficient structure delineation, as well as to the availability of dose delivery techniques with increased conformity which inspire greater accuracy in tumor delineation.

However, although the extent of a tumor can be determined in great detail on MR images, the geometric accuracy of these images is limited by distortions stemming from the inhomogeneity of the static background magnetic field, the nonlinearity of the applied gradient magnetic fields, the magnetic susceptibility of the imaged tissues, and chemical shift artifacts.^2,3 The magnitude of the observed distortions depends on the MR unit as well as on the parameters of the specific sequence used for patient imaging.² Distortions are minimal at the center of a closed bore magnet and increase gradually toward the radial edges of the scanning volume.^1–4 As the static magnetic field strength increases, geometric distortions are also increased. Even for a brain scan (where a limited field of view [FoV] is used), these distortions can be more than 3 mm.^5,6 In agreement with previous studies,⁷ it was recently showed that in stereotactic radiosurgery (SRS) applications, relatively small distortions of up to 1.3 mm in MR images may result in a significant underdosage (up to 30%) of specific very small targets.⁸ Distortion magnitude increases as one moves away from the center of the magnetic field resulting in increased localization uncertainties for targets lying at the periphery of the brain. Therefore, the specific magnetic resonance imaging (MRI) protocol employed for radiotherapy treatment planning should be evaluated in terms of geometric accuracy, especially in applications delivering highly conformed dose distributions to irradiate targets lying at the periphery of the brain.^9–11 Although no specific tolerance in geometric uncertainty exists, since the impact of geometric distortion on dose delivery depends on several parameters including the target volume and the conformity of the irradiation technique, it is generally acknowledged that SRS/stereotactic radiotherapy (SRT) applications require high geometric accuracy and precision.^12–16 Since MRI-related distortion has been recognized as one of the major contributors to geometric accuracy degradation in the entire dose delivery process, the implementation of MR distortion detection and assessment techniques could be of great importance.^2,15,16

In this work, we used a recently published phantom and methodology¹⁷ to evaluate spatial accuracy of 3 MR protocols clinically used for SRS/SRT treatment planning implemented in 2 different MR models with static magnetic fields of 1.5 and 3.0 T. The acquired images were processed to assess and compare the total geometric accuracy of the employed protocols, as well as derive detailed distortion maps in various orientations. In an effort to determine specific spatial accuracy tolerance for SRS/SRT applications, the dosimetric impact of the geometric uncertainties was investigated by simulating distortions and studying their impact on dose–volume histograms (DVHs) and plan quality metrics clinically used for plan evaluation in highly conformal SRS/SRT applications.

Materials and Methods

The Phantom

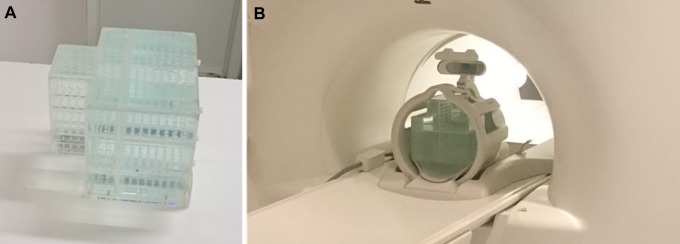
A custom-made phantom, recently developed by our group, was utilized (Figure 1A). Since the phantom has been extensively described in our previous work,¹⁷ its key characteristics will be presented in short. Control points (CPs) for distortion detection are determined as the centers of mass of 947 three-mm-diameter holes. The holes are distributed over 3 axial, 1 sagittal, and 1 coronal acrylic planes. On every plane, there is 1 CP every 10 ± 0.1 mm. The phantom’s total size and shape were carefully designed so that it can fit in a typical head coil (Figure 1B)—in order to simulate an intracranial MR scan for SRS/SRT treatment planning—while CP distribution ensures that an extended space is monitored and evaluated. In terms of imaging, the phantom is both CT and MR compatible provided for the latter case that it is filled with standard copper sulfate solution, commonly used in MR phantoms.^7,17,18

Figure 1.

A, The phantom utilized in this study filled with copper sulfate solution. B, The phantom being MR scanned using the head coil. MR indicates magnetic resonance.

Distortion Detection

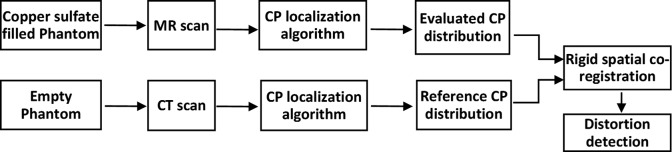
The procedure for distortion detection followed in this work is summarized in Figure 2. First, the phantom is filled with copper sulfate solution and MR scanned using the clinical protocol for SRS/SRT in order to obtain the evaluated CP distribution. Control point locations are determined in the 3-D DICOM coordinate system using the same CP localization algorithm as the one presented in the study by Pappas et al.¹⁷ Briefly, it consists of 3 steps (1) 3-D edge detection, (2) intensity thresholding, and (3) center of mass calculation and was implemented using in-house MATLAB (The MathWorks, Inc, Natick, Massachusetts) routines. Next, the phantom is CT scanned empty, and the same procedure is followed to provide the reference CP distribution (Figure 2). The resulting CP distributions are registered to the same coordinate system after performing a rigid spatial co-registration. More specifically, a rigid transformation is established after 4 CPs lying in the vicinity of the MR isocenter (where scanners are optimized to exhibit minimum geometric distortion^1,3) are selected and manually matched with the corresponding ones in the CT data set. This is a commonly adopted approach.^3,19–21 As a last step, identified CPs in the reference and evaluated data sets are paired by following their known design template. Geometric distortion is reflected as CP disposition on every axis and calculated as $d_i=i_{MR}-i_{CT}$, where i = x, y, z. The overall disposition was also calculated as $d_{tot}^R=\sqrt{d_x^2+d_y^2+d_z^2}$. Finally, by using interpolation methods, relevant distortion maps can be created on any orientation within the mapped area.

Figure 2.

Overview of the workflow for distortion detection implemented in this study.

Image Acquisitions

Two MR scanners were included in this study: a GE Optima MR450w (GE Healthcare, Little Chalfont, UK) with a static magnetic field of 1.5 T and a Siemens Skyra 3.0 T (Siemens Medical Solutions, Erlangen, Germany). Emphasis was given to evaluate the clinical protocols used specifically for SRS/SRT treatment planning. In particular, 3 sequences are employed in clinical routine labeled as “FSPGR BRAVO,” “FSPGR 3D T1w,” and “T1w MPRAGE.” The corresponding clinically used head coils were also utilized.

All specific details and imaging parameters were kept to their default values for SRS/SRT treatment planning and are summarized in Table 1. Pixel size was always 0.9375 × 0.9375 mm². Prior to scanning, the phantom was filled with standard copper sulfate solution.

Table 1.

Protocol Parameters of all the Performed MR Image Acquisitions Using Both Scanners Included in This Study.

MR Scanner Model	Protocol Name	Slice Thickness (mm)	TE/TR/FA (milliseconds/milliseconds/°)	Bandwidth (Hz/mm)	Frequency Encoding Direction
GE Optima MR450w 1.5 T	FSPGR BRAVO	1	3.46/8.29/12	260.4	A-P (y-axis)
GE Optima MR450w 1.5 T	FSPGR 3D T1w	1	2.18/6.60/15	260.4	A-P (y-axis)
Siemens Skyra 3.0 T	T1w MPRAGE	1	2.13/2300/8	213.3	A-P (y-axis)

Abbreviations: FA, flip angle; MR, magnetic resonance; TE, echo time; TR, repetition time.

To obtain the reference CP distribution, the phantom was also CT scanned. Images were acquired by a Siemens Somatom Definition scanner with a reconstruction pixel size of 0.45 × 0.45 mm², slice thickness of 0.6 mm, operated at 120 kVp.

No stereotactic frame, localization box, or any other apparatus was mounted on the phantom during MR (nor CT) scanning in order to avoid frame-induced distortions¹⁷ or susceptibility-related artifacts.

Dosimetric Effect

Furthermore, in order to quantify the dosimetric effect of the detected distortion, a highly conformal volumetric modulated arc therapy (VMAT) technique using multiple noncoplanar arcs^11,22,23 was utilized to irradiate targets of different diameters (5-50 mm). In specific, the Monaco v. 5.1.1 (Elekta Instrument AB, Stockholm, Sweden) treatment planning system based on X-ray voxel Monte Carlo and constraint optimization algorithms with biological cost functions was used to plan a 4 noncoplanar arc arrangement (1 full arc with couch angle 0° and 3 half arcs with couch angles 315°, 45°, and 90°) with the 6 MV photon beam energy setting of an ELEKTA Axesse linear accelerator equipped with beam modulator (4 mm Multi-Leaf Collimator leaves width). Dose calculations were performed on a rectangular grid of 1 mm³ voxel size requiring Monte Carlo statistical uncertainty of 1% (normalized standard deviation). A dose of 20 Gy was prescribed to cover the 95% of the volume of each target. Dose–volume histograms and plan quality metrics commonly used in the clinical setting were calculated for the different diameter targets and exported to form a reference data set. Reference data set included—inter alia—(1) the dose received by at least 95% of the target volume (D₉₅) used for target coverage evaluation, (2) the Paddick’s conformity index²⁴ (CI) used to evaluate the conformity of the prescription dose to the target volume, (3) the dose received by at least 50% of the target (D₅₀), (4) the minimum dose (D_min), and (5) the mean dose (D_mean). Spatial offsets of 0.5 up to 3 mm toward either the x (left–right), y (anterior–posterior), or z (superior–inferior) axes were deliberately added to the target locations, and dose distributions were recalculated. Dose–volume histograms and the aforementioned metrics were calculated for the plans with the mispositioned target locations, then exported and compared with the reference data set.

Results

Distortion Magnitude

Table 2 summarizes the detected CP offset between the MR and CT data sets on the 3 MR coordinate axes, d_i, as well as the total offset $d_{tot}^R$. In addition to minimum, maximum, and mean detected distortion, Table 2 gives the percentage of CPs that were dispositioned by more than 1 mm. Mean absolute distortions are well below 0.5 mm on any axis for all 3 protocols.

Table 2.

Detected Total Distortion for the 3 Imaging Protocols of the GE and SIEMENS Scanners Included in This Study.^a

Axis		GE 1.5 T		Siemens 3.0 T
		FSPGR BRAVO	FSPGR 3DT1w	T1w MPRAGE
x axis (mm)	Range	−0.44 to 0.46	−0.57 to 0.54	−1.12 to 1.16
	Mean	−0.04	0.00	0.05
	Mean absolute	0.18	0.28	0.36
	% CPs > 1 mm	0.00%	0.00%	0.63%
y axis (mm)	Range	−0.70 to 0.55	−0.64 to 0.79	−1.16 to 1.84
	Mean	−0.14	0.00	0.03
	Mean absolute	0.29	0.23	0.46
	% CPs > 1 mm	0.00%	0.00%	4.13%
z axis (mm)	Range	−1.36 to 0.75	−1.93 to 1.02	−1.05 to 0.57
	Mean	−0.16	−0.06	−0.34
	Mean absolute	0.31	0.46	0.41
	% CPs > 1 mm	0.08%	4.22%	0.21%
R (mm)	Range	0.04 to 1.37	0.05 to 1.99	0.06 to 1.92
	Mean	0.54	0.66	0.82
	% CPs > 1 mm	1.06%	5.07%	10.37%

Abbreviation: CPs, control points.

^aPercentage of CPs detected with more than 1 mm of absolute distortion (% CPs > 1 mm) is also given.

Regarding the 1.5 T GE scanner, increased distortion was detected on the z-axis (possibly due to increased z-gradient magnetic field nonlinearity, which could stem from a less effective performance of the automated distortion correction algorithms integrated in the scanner), while minimal distortion was observed on x and y axes, for both protocols investigated. The 3.0 T SIEMENS scanner is characterized by systematically higher mean distortion values (for the examined sequences) than the 1.5 T GE scanner. However, due to phantom repositioning, CP distribution within the imaged areas was not identical for the 2 scanners.

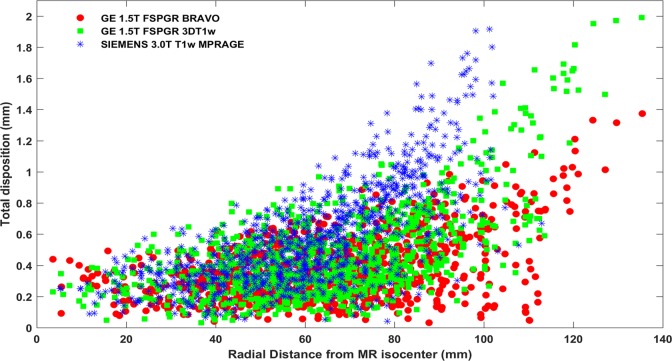
Figure 3 highlights the effect of increasing distortion magnitude with respect to increasing radial distance from the MR scanners’ isocenter. In particular, total distortion magnitude detected with all 947 CPs is presented against radial distance from the scanners’ origin for both scanners and for all 3 imaging protocols. The mean as well as the spread of the detected CP disposition significantly increases with distance from the isocenter (Figure 3). Note that the range of radial distances investigated (up to approximately 135 mm) exceeds the typical size of a head. CP distribution within the phantom extended to the far off of the available space within the employed MR head coils.

Figure 3.

Total geometric distortion detected at all 947 CP locations for the 3 clinically used imaging protocols. Results are presented against radial distance from the corresponding MR scanner’s isocenter. CP indicates control point; MR, magnetic resonance.

Figure 3 also allows for a qualitative comparison of distortion magnitude between the 3 clinically used protocols. As seen, the “FSPGR BRAVO” sequence is slightly less prone to distortion compared to the other 2 protocols investigated.

Distortion Distribution and Directionality

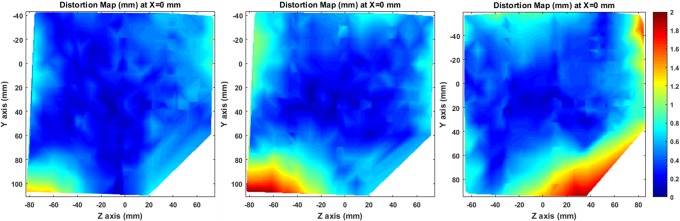
A series of 3-D total distortion maps ($d_{tot}^R$) have been created for all acquired image series. Inevitably, due to the interpolation procedure involved, accuracy of distortion maps deteriorates in regions distant from the CPs. Given that, y-z central planes carefully selected to lie in areas of high CP density (ie, at x = 0 mm) are presented in Figure 4. For all 3 MR protocols, detected distortion is minimal around the magnet’s isocenter and greatly increases at the corners of the examined space.

Figure 4.

Total distortion maps (d^R _tot) on a sagittal plane at x = 0 mm for FSPGR BRAVO (left), FSPGR 3DT1w (middle), and T1w MPRAGE (right).

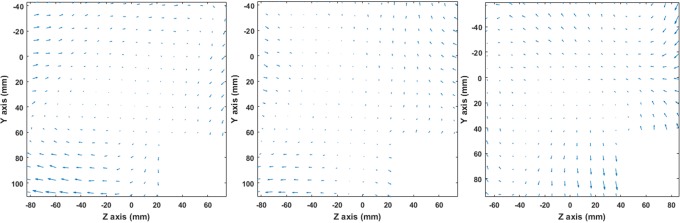
Figure 5 provides an insight into the spatial distribution and directionality of the detected distortion. The distortion vectors’ initial points correspond to CT-identified CP locations (ie, “reference” locations), while terminal points correspond to MRI-detected ones. Distortion vectors are projected on the y-z plane. The vectors’ lengths are proportional to the detected distortion magnitude. As also shown in Table 2, distortion for the GE 1.5 T scanner is excessive on the negative z-axis, while for the 3.0 T scanner, distortion magnitude exhibits an almost symmetrical spatial distribution in all 3 axes.

Figure 5.

Distortion vectors on a sagittal plane at x = 0 mm for FSPGR BRAVO (left), FSPGR 3DT1w (middle), and T1w MPRAGE (right). Vectors’ lengths have been magnified by a factor of 3 to increase visibility.

Dosimetric Impact

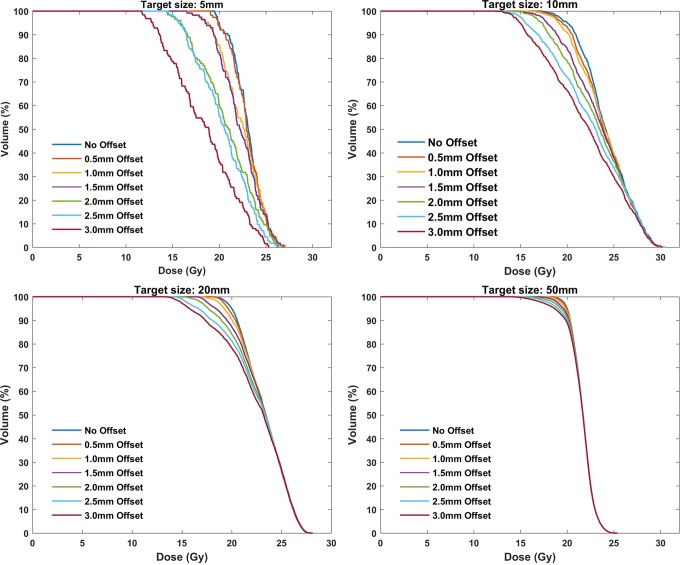
Figure 6 presents the impact of simulated geometric distortion (indicatively, along x-axis) on calculated DVHs for 4 representative target sizes (5, 10, 20, and 50 mm) and the highly conformal VMAT plans created using the 4 noncoplanar arcs technique. For the smallest target (5-mm diameter), the effect is considerable even for a spatial offset of 1 mm. As seen, target coverage deteriorates with increasing geometric offset, with the effect being more pronounced for smaller target sizes. Corresponding findings are also highlighted in Table 3. The D₉₅ and the Paddick’s CI²⁴ are tabulated for the original and x-axis mispositioned target locations. Both indices are very sensitive on both geometric distortion and target size, with their values rapidly decreasing as distortion magnitude increases and/or target size decreases. This trend is clearly shown in Figure 7 where the magnitude of the geometric uncertainty (distortion) resulting in D₉₅ differences greater than 5% is plotted against target diameter. The D_min index is even more sensitive to distortion than the D₉₅, while D_mean and D₅₀ are only affected for target sizes up to 10 mm. Similar DVH results were obtained for target misposition on y and z axes. However, the D₉₅ value was found slightly more sensitive to distortion on z-axis for the smallest target sizes due to the increased dose gradient on this direction. This is illustrated in Figure 7 where target misposition that yields 5% difference on D₉₅ is systematically lower for z-axis results.

Figure 6.

Calculated DVHs for the original plan (no offset) as well as for the deliberately mispositioned targets toward the x direction (0.5 up to 3 mm offset) for 4 representative target sizes. DVHs indicate dose–volume histograms.

Table 3.

Effect of Spatial Offset Toward the X Direction on Plan Quality Metrics for 5 Target Sizes.

Target Size	X-Offset (mm)	D95 (Gy)	Difference (%)	Paddick’s CI	Difference (%)
5 mm	0.0	20.0	-	0.65	-
	0.5	19.8	−0.8	0.63	−2.4
	1.0	18.7	−6.7	0.53	−18.6
	1.5	18.5	−7.5	0.48	−26.3
	2.0	15.9	−20.6	0.26	−59.7
	2.5	15.6	−22.0	0.23	−65.1
	3.0	12.8	−36.1	0.10	−85.2
10 mm	0.0	20.0	-	0.77	-
	0.5	19.5	−2.7	0.74	−3.3
	1.0	19.1	−4.4	0.70	−8.5
	1.5	17.8	−10.9	0.60	−21.9
	2.0	17.3	−13.5	0.53	−31.2
	2.5	15.5	−22.4	0.44	−42.7
	3.0	14.9	−25.3	0.38	−51.1
20 mm	0.0	20.0	-	0.93	-
	0.5	19.7	−1.8	0.88	−4.7
	1.0	19.2	−3.8	0.84	−9.4
	1.5	18.4	−8.0	0.78	−15.4
	2.0	17.6	−11.8	0.73	−21.4
	2.5	16.7	−16.7	0.68	−26.6
	3.0	15.7	−21.3	0.63	−32.0
30 mm	0.0	20.0	-	0.93	-
	0.5	19.9	−0.5	0.92	−1.7
	1.0	19.7	−1.4	0.90	−3.8
	1.5	19.3	−3.5	0.86	−7.7
	2.0	18.7	−6.3	0.83	−11.2
	2.5	17.8	−11.1	0.79	−15.6
	3.0	17.3	−13.7	0.75	−19.0
50 mm	0.0	20.0	-	0.94	-
	0.5	19.9	−0.3	0.93	−1.0
	1.0	19.8	−0.9	0.91	−3.2
	1.5	19.6	−2.0	0.89	−5.5
	2.0	19.3	−3.4	0.87	−7.7
	2.5	19.0	−5.0	0.85	−10.3
	3.0	18.7	−6.7	0.83	−12.4

Abbreviation: CI, conformity index.

Figure 7.

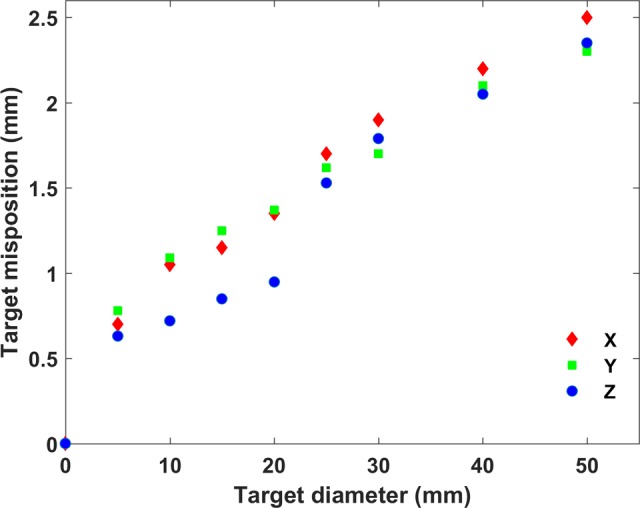
Geometric uncertainty on x, y, and z axes resulting in difference greater than 5% in D₉₅ value as a function of target diameter.

Discussion

The phantom and CP localization algorithm used in this study are similar to those employed in the study by Pappas et al.¹⁷ In this work, in contrast to our previous studies^8,17,25 where the reversed gradient technique^{3,4,17,19,20,25–27} was used to distinguish and characterize different sources of system-related geometric distortion (including those induced by stereotactic accessories such as the immobilization frame used in Gamma Knife SRS applications¹⁷), distortion assessment relied entirely on 1 MR scan, as has been demonstrated elsewhere.^5–7,28,29 Consequently, both sequence-independent (ie, arising from gradient nonlinearity) and sequence-dependent distortions^3,25,30,31 (ie, distortions related to B₀ inhomogeneity, chemical shift artifacts, and susceptibility differences) were taken into account. However, chemical shift artifacts are not relevant in a phantom study, while susceptibility-induced distortions (stemming from acrylic-copper sulfate solution susceptibility difference) are uniform throughout the entire geometry and, inevitably, cancel out during the spatial registration step. Effectively, the approach followed in this study mainly takes into account machine-related distortions⁵ (ie, B₀ inhomogeneity and gradient nonlinearity). According to our previous study,¹⁷ uncertainty in CP disposition detection is approximately 0.2 mm.

Three MR protocols used in SRS/SRT treatment planning (at 1.5 and 3.0 T) were evaluated in terms of geometric accuracy. Although mean absolute distortion was found less than 0.5 mm in any orientation, CP total dispositions of up to 2 mm were observed at the edges of the imaged area. This suggests that regions of interest lying within an FoV relative to the size of a large head exhibit considerable levels of distortion and may compromise dose delivery accuracy.⁸ Since distortion magnitude and orientation strongly depend on the imaging parameters used as well as the volume of interest and CP distribution within the imaged area, results cannot be directly compared with the previously published studies. However, detected distortion of more than 1 mm (related to gradient nonlinearity alone) is generally acknowledged^17,21,26,31 for volumes similar to the one examined in the present study. In the study of Yu et al,⁶ a total geometric distortion of approximately 3 mm was reported for brain MRI scans used in Gamma Knife SRS. For larger FoVs (used in extracranial stereotactic body radiotherapy), MR-related geometric accuracy is studied using body-sized phantoms,^{4,5,19–21,32–34} with distortions reported reaching up to 25 mm. In a review article,² a total of 11 studies investigating system-dependent geometric distortions were identified, with 5 of them reporting maximum detected distortion of less than 2 mm.

In addition to system-related distortion, patient-induced spatial inaccuracies should also be considered.^2,3 Several studies^8,17,35 have reported patient-related geometric uncertainties ranging up to 1.9 mm for MR protocols used in SRS treatment planning. In a simulation study, Stanescu et al ³⁶ reported susceptibility-induced distortion reaching up to 3.40 and 2.02 mm (for a 3.0 T MR scanner employing 5 mT/m gradient strength) in air cavities and bone structures, respectively, in intracranial patient MR images. Depending on B₀ strength, bandwidth used, anatomical site investigated, and orientation relative to B₀, susceptibility-induced distortion greatly varies.³⁶ Moreover, patient-induced distortion cannot be accurately predicted a priori since each patient is characterized by different magnetic susceptibility distributions which may also vary in time.² Therefore, a significant source of additional spatial uncertainties and potential dosimetric impact should be considered when defining margins for planning target volume determination.

To the best of our knowledge, no specific guidelines have been proposed with respect to the tolerance of geometric uncertainty in MRI series used in SRS/SRT treatment planning. Outdated guidelines³⁷ for radiotherapy Quality Assurance suggest that geometric distortion of more than 2 mm requires consideration. Weygand et al ² suggest that MR-related geometric distortions should be measured and accounted for when defining margins for determination of the planning target volume in MRI-guided radiotherapy applications. In this work, effort was made to quantitively assess what could be considered unacceptable distortion. Therefore, an investigation of the induced dosimetric error with respect to target dose delivery was conducted by applying geometric offsets of 0.5 up to 3 mm for several spherical targets irradiated using a highly conformal VMAT technique with multiple noncoplanar arcs. It is clearly shown that the required geometric accuracy depends significantly on target size. Target coverage, expressed by the D₉₅ value and in a greater extent by Paddick’s CI (which takes into account both target coverage and the conformity of the prescription dose to the target volume²⁴) is deteriorated (decreased) as the magnitude of geometric distortion increases and target size decreases. For targets less than 2 cm in diameter, a spatial disposition of the order of 1 mm could significantly affect both D₉₅ and Paddick’s CI values, with differences being greater than 5% compared to the reference (nondistorted) plan. For targets with diameter up to 3 cm, D₉₅ could be affected by spatial distortions of the order of 1.5 mm. For larger target diameters, geometric distortions greater than 2 mm are required to considerably (>5%) affect plan evaluation indices (Figure 7). Nevertheless, SRS applications are usually applied to irradiate multiple targets with diameters less than 3 cm, such as in multiple brain metastases cases,^11,22,23,38 where small-sized targets could lie on the periphery of the brain where distortion greatly increases. If all sources of geometric uncertainties are considered (MRI system-related, MRI patient-induced, spatial registration, patient setup, and mechanical accuracy) and no margins are applied in treatment planning (a practice that is commonly followed in SRS applications^16,38) deterioration of plan evaluation indices could reach unacceptable levels.

Knowledge of the MR distortions with the scanning parameters used for target delineation in the 3-D space could provide information for the margins required to ensure target coverage. In the current practice, geometric distortions are commonly checked at a specific plane (2-D distortion assessment) using the ACR phantom^39,40 for a typical T1w sequence using a passing criterion of 2 mm. In this work, a 3-D distortion detection phantom coupled with a suitable methodology was implemented for the specific clinical protocols at 1.5 and 3.0 T used for target localization, and distortions of up to 2 mm were identified in an area covering an extended region of the FoVs used in brain SRS/SRT applications. It is noted however that patient-induced distortions are not taken into account when phantoms are used to derive distortion maps. Another limitation of this study is that the analysis of the dosimetric impact was not comprehensive. As an example, the spatial offsets investigated were only toward one axis, while target shapes were always spherical. Induced dosimetric effects could considerably vary in case of nonuniform or different dose gradients and irregular target shapes. Furthermore, in a more realistic case, total distortion distribution is not uniform in the entire target volume, resulting to a deformable transformation of the structure. In the present study, only rigid transformations were applied, corresponding to uniform distortions. Moreover, MR-related geometric distortions do have a dosimetric impact to organs at risk as well, which is expected to depend on the magnitude and direction of distortion vectors at the location of each organ. However, this is beyond the scope of this work, which emphasizes in the corresponding impact on the target delivered dose distributions.

Nevertheless, this study reveals that the steep dose gradients along with high conformity plans used in SRS/SRT applications constitute the dose delivery very sensitive to spatial errors. Therefore, an evaluation of MR-related geometric distortions for the corresponding clinical protocols and parameters becomes paramount, especially when they are used for the delineation of small targets in the periphery of the brain, where MR geometry accuracy deteriorates even in the relative small FoVs involved (eg, multiple brain metastases cases). Further work is still needed to fully characterize MR-related distortions and determine the acceptable levels of spatial error that do not considerably compromise dose delivery and target coverage. Toward that direction, future work will focus on patient-induced distortions^3,36,41–43 which should also be considered an additional source of geometric degradation.

Conclusion

Spatial distortions of up to 2 mm were detected for clinical MR protocols (at 1.5 and 3.0 T) used in SRS/SRT treatment planning in regions away from scanner’s isocenter. Such distortions were found to significantly affect DVHs and plan quality metrics in realistic high conformal VMAT plans simulating SRS/SRT applications. Effort was made to determine levels of acceptable geometric distortion with corresponding results being strongly dependent on target size but the analysis was not comprehensive. Overall results of this work suggest that efficacy of SRS applications could be compromised in case of very small targets lying at the periphery of the brain, especially for MRI-alone treatment protocols employing high-dose gradients.

Abbreviations

CI

conformity index

CP

control point

CT

computed tomography

DVH

dose–volume histogram

FoV

field of view

MR

magnetic resonance

MRI

magnetic resonance imaging

SRS

stereotactic radiosurgery

SRT

stereotactic radiotherapy

VMAT

volumetric modulated arc therapy