Monitoring reservoir response to earthquakes and fluid extraction, Salton Sea geothermal field, California

Seismic interferometry provides insights into in situ reservoir response to stress changes.

Abstract

Continuous monitoring of in situ reservoir responses to stress transients provides insights into the evolution of geothermal reservoirs. By exploiting the stress dependence of seismic velocity changes, we investigate the temporal evolution of the reservoir stress state of the Salton Sea geothermal field (SSGF), California. We find that the SSGF experienced a number of sudden velocity reductions (~0.035 to 0.25%) that are most likely caused by openings of fractures due to dynamic stress transients (as small as 0.08 MPa and up to 0.45 MPa) from local and regional earthquakes. Depths of velocity changes are estimated to be about 0.5 to 1.5 km, similar to the depths of the injection and production wells. We derive an empirical in situ stress sensitivity of seismic velocity changes by relating velocity changes to dynamic stresses. We also observe systematic velocity reductions (0.04 to 0.05%) during earthquake swarms in mid-November 2009 and late-December 2010. On the basis of volumetric static and dynamic stress changes, the expected velocity reductions from the largest earthquakes with magnitude ranging from 3 to 4 in these swarms are less than 0.02%, which suggests that these earthquakes are likely not responsible for the velocity changes observed during the swarms. Instead, we argue that velocity reductions may have been induced by poroelastic opening of fractures due to aseismic deformation. We also observe a long-term velocity increase (~0.04%/year) that is most likely due to poroelastic contraction caused by the geothermal production. Our observations demonstrate that seismic interferometry provides insights into in situ reservoir response to stress changes.

INTRODUCTION

Geothermal energy is a source of renewable energy, providing an increasingly important contribution to the global energy supply (1, 2). The Salton Sea geothermal field (SSGF) located in the Salton Trough of southernmost California is one of the largest geothermal reservoirs in the world and is characterized by hot fluids (~350°C) at a depth of ~2 km (3). Operations at the SSGF started in 1980s and consist of 10 operational geothermal plants [based on the Department of Oil, Gas, and Geothermal Resources (DOGGR) database (4)] that extract and inject water at depths between 1 and 3 km (5). The SSGF experiences seismicity associated with the southernmost extension of the southern San Andreas fault, the Brawley seismic zone, and the geothermal system. It has also been suggested that changes in the net fluid volume (total fluid injected – total fluid withdrawn) dominate the background seismicity in the SSGF (6).

Earthquakes induced by geothermal injection and production have been observed in other geothermal systems (7, 8), attracting public attention in the past several years (9, 10). Because the magnitude of induced earthquakes can exceed 4 (11), there is thus a need for continuous monitoring of geothermal reservoirs to identify and understand changes in reservoir characteristics that might induce earthquakes. Seismic interferometry with ambient noise has become a powerful seismological approach to continuously monitor temporal behaviors of fluids in the subsurface, for example, at volcanoes (12–15) and after earthquakes (16–18). Although there are few studies that have applied ambient noise–based imaging to identify time-dependent geothermal reservoir characteristics (19, 20), they have focused on about 1 year of data, making it difficult to isolate any possible seasonal changes in velocity (21).

Here, we systematically explore changes in seismic velocity at the SSGF by analyzing ~6 years of continuous seismic recordings (December 2007 to January 2014) of the vertical component of ground motion collected from eight borehole short-period seismic sensors (fig. S1). We use an ambient noise–based seismic interferometry approach to obtain noise-derived empirical Green’s functions or noise cross-correlation functions (NCFs) for pairs of seismic stations (12) and apply a moving window cross-spectral approach (22) with MSNoise software (23) to measure a frequency-dependent relative time delay between a reference and 5-day stack of NCFs (Materials and Methods). The resultant time delay measurements were stacked over all possible pairs of stations to determine average surface wave seismic velocity changes at the SSGF.

RESULTS

The time evolution of fractional seismic velocity change (dv/v) exhibits two types of velocity changes (Fig. 1A). The first type of velocity change is a sudden reduction. The second is a long-term increase. A notable velocity drop was observed at the beginning of April 2010 and was registered in all frequency bands except for the lowest frequency range, 0.25 to 1.0 Hz. The onset time of this temporal reduction coincides with the occurrence of the 4 April 2010 M_w (moment magnitude) 7.2 El Mayor–Cucapah (EMC) earthquake (the location of the EMC hypocenter shown in the figure inset in fig. S1). The stack of time delay (dt) over all pairs of seismic stations used displays a clear change after the EMC earthquake (fig. S2). The magnitude of velocity reduction was found to gradually increase with decreasing frequency (Fig. 1B). The largest reduction (~0.25%) was observed in the frequency band 0.5 to 2.0 Hz, implying that the velocity change likely occurred at depths of ~0.5 to 1.5 km, assuming that coda of NCFs are mainly composed of scattered surface waves (Rayleigh waves) (fig. S3). Note that our data do not have the capability of exploring velocity changes below ~2.0 km because of the poor signal-to-noise ratio of NCFs at frequencies lower than 0.5 Hz for the CalEnergy borehole geophone data (Materials and Methods). Because each CalEnergy site was equipped with a three-component geophone, we also evaluated the velocity changes by averaging all nine combinations of NCFs (fig. S4). We found that the temporal variation in dv/v inferred from the nine components of NCFs is comparable to that obtained by the vertical-vertical (ZZ) component of NCFs (Fig. 1A). Although the nine-component inferred velocity change reduces uncertainties in dv/v measurements, the resultant velocity change would be sensitive to both Rayleigh and Love waves. To simplify the analysis of depth extent of velocity change, we used the velocity changes inferred from the ZZ component in which scattered Rayleigh waves dominate.

Fig. 1. Time-lapse measurements of seismic velocity changes.

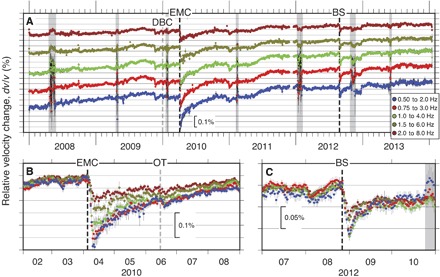
(A) Time history of seismic velocity (dv/v) with two-sigma SDs at five different frequency bands during December 2007 to January 2014. (B and C) Same as (A), but with time interval between February to August 2010 and July to October 2012. EMC, BS, DBC, and OT represent the 2010 M_w 7.2 El Mayor–Cucapah earthquake, the 2012 Brawley seismic swarm, the 30 December 2009 M 5.8 Delta, Baja California, Mexico, and the 15 June 2010 M 5.7 Ocotillo earthquake, respectively (vertical dashed lines). Gray areas indicate time windows in which we were not able to recover empirical Green’s functions (fig. S2 and Materials and Methods).

There appears to be another noticeable velocity reduction at the end of August 2012, during which the 2012 Brawley seismic (BS) swarm occurred 15 km south of the SSGF (the figure inset in fig. S1). This swarm consists of two M_w ~5 earthquakes occurring on 26 August 2012 and an elevated rate of seismicity (over 600 earthquakes) that lasted for about 1 month (24, 25). A frequency-dependent velocity change was observed (Fig. 1C), in which the velocity reduction is greater in lower-frequency bands. We obtained a velocity decrease of about 0.1% in the frequency bands 0.5 to 2.0, 0.75 to 3.0, and 1.0 to 4.0 Hz, whereas the velocity reductions in the frequency bands 1.5 to 6.0 and 2.0 to 8.0 Hz were ~0.05 to 0.07%.

It is commonly suggested that the stress changes from local earthquakes alter seismic velocities through opening or closing of cracks (16–18, 26). Dilatational static stress changes are expected at the SSGF from the EMC mainshock and the BS swarm, which would lead to reductions in velocity through opening of cracks that is consistent with our observations. The magnitude of dilatational static stress changes is, however, less than 0.01 MPa, similar to those from barometric pressure changes and tides (figs. S5A and S6A and Materials and Methods). On the other hand, the dynamic stress changes from the EMC earthquake and the BS swarm (the largest M_w 5.4 earthquake) are estimated to be 0.45 and 0.18 MPa, inferred from peak ground velocity (PGV) measurements of 7.47 and 2.91 cm/s, respectively (Fig. 2, figs. S5B and S6B, and Materials and Methods), which are an order of magnitude larger than the volumetric static stress changes. An increase in the local microearthquake activity was also identified at the SSGF immediately after the EMC earthquake, which is most likely due to dynamic stress changes from the EMC mainshock (27). Given the magnitudes of volumetric static and dynamic stress changes, we infer that the dynamic stresses are more likely to be responsible for the sudden velocity reductions, although it cannot be ruled out that the volumetric static stress changes also contribute to the velocity reductions. The geodetic measurements observe permanent static offsets of ~1.5 cm and ~2.0 mm at the SSGF after the EMC earthquake and the BS swarm, respectively (fig. S7).

Fig. 2. Stress sensitivity of seismic velocity change.

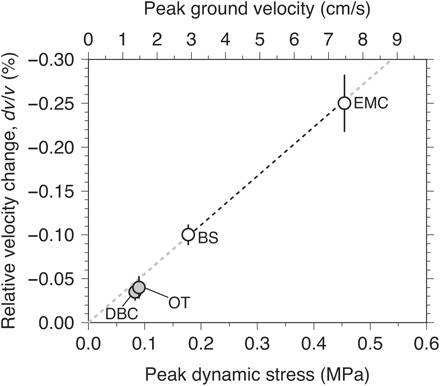
Velocity change measured with two-sigma SDs in a frequency range of 0.5 to 2.0 Hz as a function of stress changes inferred from PGV at station RHX. The two-sigma SDs plotted were the median two-sigma SDs in the first 10 days after the target earthquakes (for example, the EMC earthquake). To estimate dynamic stress changes, we used an S-wave velocity of 2.3 km/s and the rigidity of 14 GPa (Materials and Methods). The resultant mean stress sensitivity is −0.0056 MPa⁻¹ (black dashed line), inferred from the EMC earthquake and BS swarm (solid circles). Gray circles show the velocity changes from the DBC and OT earthquakes, and they are not used to compute the stress sensitivity. The inferred stress sensitivity (black dashed line) is extrapolated to the dashed gray lines.

The second type of velocity change is a long-term velocity increase. A steady increase in velocity was observed over the entire analysis period (Fig. 1A), although this long-term velocity increase was interrupted by earthquake-induced velocity reductions and might include increases in velocity associated with postseismic recovery processes. It is confirmed that there was no large (M > 6) earthquake (within 300 km from the SSGF at least 5 years before our analysis time period from the U.S. Geological Survey ComCat earthquake catalog) that might induce a long-term (>year) postseismic deformation causing a change in seismic velocity (fig. S8). In addition, some velocity fluctuations appear to be correlated with earthquake swarms (Fig. 3). As with the sudden velocity reductions associated with earthquakes, the long-term increase in velocity exhibits clear frequency dependence. The larger velocity increase was identified in lower frequency bands. An increase in velocity of ~0.25% was found in the frequency band 0.5 to 2.0 Hz during a 6-year period, which corresponds to a 0.04%/year increase in velocity. On the other hand, the high-frequency dv/v time series shows a weak long-term velocity increase (0.017%/year).

Fig. 3. Seismic velocity changes temporally correlated with earthquake swarms.

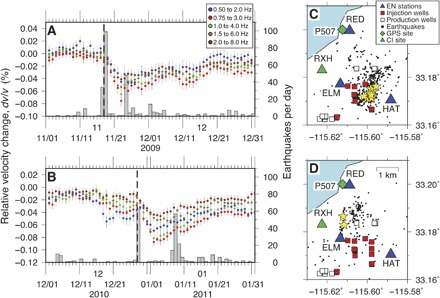
(A and B) Inferred seismic velocity changes in the time intervals (A) November to December 2009 and (B) December 2010 to January 2011. Gray bars represent the number of earthquakes per day that occurred within the regions shown in (C) and (D). Dashed lines indicate origin times of M 3+ earthquakes. (C and D) Map views of earthquake swarms. The blue triangles are the locations of the CalEnergy seismic network (EN network). Also shown are the locations of the geothermal injection (red squares) and production wells (white squares) obtained from the California Department of Conservation. Green triangle and diamond are the locations of seismic station RXH [Southern California Seismic (CI) Network] and continuous Global Positioning System (GPS) site P507, respectively. Black dots are relocated earthquake locations with a waveform cross-correlation analysis (77). Yellow stars are locations of M 3+ earthquakes. Earthquakes in the first 100 days from the first earthquake of the earthquake swarms were plotted.

To explore the underlying mechanism of the long-term velocity increase observed at the SSGF, we analyzed continuous waveforms collected from 13 broadband seismic sensors in and around the SSGF with a single-station cross-correlation analysis, in which ambient seismic noise recordings in different components from a single station are cross-correlated (that is, vertical-north, vertical-east, and north-east components) (fig. S9) (28). Following previous studies (28, 29), the long-term velocity changes at individual stations were evaluated by curve fitting (Materials and Methods). The largest long-term velocity change (~0.06%/year in the frequency band 0.5 to 2.0 Hz) was found at the SSGF (station RXH) among broadband seismic stations used for the single-station cross-correlation analysis (Fig. 4, fig. S10, and table S1). Station GLA shows the same order of magnitude negative velocity change. This site is a bedrock site located at Black Mountain near Glamis in southern California. We explored a correlation between the long-term velocity and topography (as a proxy of local geological condition) and find that there is no clear correlation between the long-term velocity change and topography (fig. S11). It remains an open question as to what mechanism is responsible for this long-term velocity decrease.

Fig. 4. Long-term linear trend of velocity change.

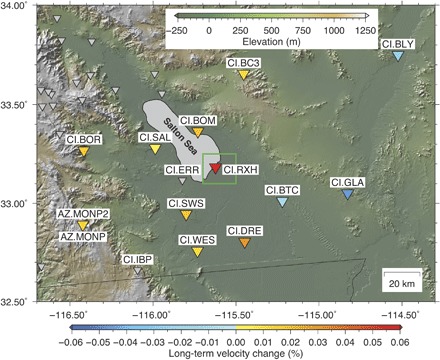
Values of long-term linear trend of velocity changes in a frequency range of 0.5 to 2.0 Hz obtained from curve fitting (table S1 and Materials and Methods) are shown by the color code in the bottom of the figure. Green rectangle is the SSGF region shown in fig. S1. Background color represents topography.

DISCUSSION

The largest velocity reduction was observed in the frequency range of 0.5 to 2.0 Hz for both the EMC earthquake and the BS swarm. The time history of seismic velocity change inferred from the single-station cross-correlation analysis of station RXH (located inside the SSGF) also supports this observation (fig. S12 and Materials and Methods). Considering the Rayleigh-wave sensitivity kernels, this observation suggests that the external stress transients preferentially affect the permeable geothermal reservoir at depths of ~0.5 to 1.5 km rather than the uppermost few hundred meters of cap rock (26, 30, 31). Because the majority of geothermal wells extend to similar depths of about 1 to 3 km (5), there would be high fractured/permeable layer at this depth range. A possible interpretation of our observation is that this fractured and permeable reservoir is particularly sensitive to external stress changes; seismic activity in the Salton Trough has been invoked to maintain the fracture permeability of the reservoir (32). Within this geothermal environment, a plausible mechanism is that the ground shaking leads to an increase of apparent crack density through unclogging of fractures due to pore pressure fluctuations (33) and reduces seismic velocity. A temporal increase in gas discharge (fig. S13) was also observed at the Davis-Schrimpf mud volcanoes (~4.5 km northeast from station ELM; the purple diamond shown in fig. S1) after the EMC earthquake (34), and a plausible mechanism of this increased gas discharge rate is a temporal enhancement of fracture permeability because of strong ground shaking by the EMC earthquake (34).

We attribute decreases in seismic velocities to increases in crack opening induced by stress transients. Under this assumption, the sensitivity of velocity changes to external stress transients (η) was evaluated through the ratio of relative seismic velocity change (Δv = dv/v) and external stress transient (Δσ), η = (Δv/Δσ) (15, 35, 36). If crack density (ρ_c) governs the velocity reduction, this stress sensitivity can be decomposed into two terms expressed as η = (Δv/Δρ_c)(Δρ_c/Δσ) (37). The first and second terms characterize the seismological properties (38, 39) and stress sensitivity (40) of the poroelastic medium, respectively. The crack density is expected to decrease exponentially with increasing depth because of increasing confining pressure (40), and consequently, the stress sensitivity decreases (41). Previous work mapped out the stress sensitivity with ambient noise cross-correlation analysis in eastern Japan and found that areas of higher stress sensitivity (−0.0005 to −0.001 MPa⁻¹) are spatially correlated with hydrothermal and volcanic fields (35), suggesting that pressurized hydrothermal fluids reduce the effective confining pressure and hence lead to an enhancement of the crack density, which, in turn, increases the stress sensitivity at depth.

The two sudden velocity reductions induced by earthquakes at the SSGF provide a rare opportunity to perform a repeatable measurement of stress sensitivity. It should be noted, however, that the BS swarm involved two M_w ~5 earthquakes. The largest M_w 5.4 earthquake occurred about 90 min after the M_w 5.3 earthquake. At the SSGF, the dynamic stress change from this M_w 5.3 earthquake is about half of that from the largest M_w 5.4 earthquake. However, the first M_w 5.3 earthquake would have also produced a change in seismic velocity. Because at least a 5-day stack of NCFs is required to stabilize the velocity change measurements, our analysis does not have the capability of separating the two possible velocity changes. The velocity reduction during the BS swarm may have been a combination of two distinct velocity changes. However, these two dynamic stress transients occurred within 90 min. Healing is unlikely to be significant within this 90-min time interval, and we speculate that velocity changes would be further promoted if an additional stress transient exceeds previous stress changes. With this assumption, we relate the velocity reduction of about 0.1% during the BS swarm to the largest dynamic stress change (or PGV) from the M_w 5.4 earthquake.

The stress sensitivities for the EMC earthquake and the BS swarm are −0.0055 and −0.0056 MPa⁻¹, respectively (Fig. 2). This consistency of the stress sensitivity measurements from two different earthquakes suggests a proportionality of seismic velocity to earthquake-induced dynamic stress transients at least for the range of velocity changes and dynamic stresses observed at the SSGF. The mean SSGF stress sensitivity (−0.0056 MPa⁻¹) is comparable to or at a slightly higher level than those at hydrothermal and volcanic regions in Japan (about −0.001 MPa⁻¹) obtained by Brenguier et al. (35). The single-station analysis yields a stress sensitivity of −0.0031 MPa⁻¹ at the SSGF (station RXH) for the EMC earthquake, which is the highest level of the stress sensitivity in the SSGF and surrounding region for the single-station cross-correlation analysis (fig. S14 and table S2). It should be noted, however, that the single-station analysis used a 60-day running median filter to obtain stable temporal change measurements (fig. S10). The sudden velocity reductions associated with the EMC earthquake were likely underestimated because of this median filter, which yields lower levels of stress sensitivity for the single-station cross-correlation analysis. It should also be noted that we used an S-wave velocity of 2.3 km/s and rigidity of 14 GPa for all broadband seismic stations that were used for the single-station cross-correlation analysis (Materials and Methods).

Using the measured stress sensitivity, we searched for additional velocity changes induced by other recent earthquakes. Expected dynamic stress changes at the SSGF for individual earthquakes were estimated using the ShakeMap products of Southern California Earthquake Data Center (SCEDC) (Materials and Methods) (42). During our observation period, PGVs from two earthquakes, the 30 December 2009 M 5.8 Delta, Baja California, Mexico (DBC) and the 15 June 2010 M 5.7 Ocotillo (OT), California earthquakes, exceed 1 cm/s (dynamic stress of ~0.08 MPa) that would induce velocity reductions of ~0.035 to 0.040% based on our stress sensitivity estimate.

Our dv/v time series shows velocity reductions around the origin times of these two earthquakes (Fig. 1B and fig. S15). The observed velocity reductions are in good agreement with the decrease expected from the stress sensitivity (Fig. 2), supporting the empirical relationship between the velocity change and stress change. It also suggests that the magnitude of velocity change is linearly proportional to the magnitude of the stress transient at least in the range of velocity change and dynamic stresses examined in this study. If the velocity reductions at the SSGF are the result of opening fractures because of dynamic stress transients, a temporary increase in permeability is also expected from the same process. Both field studies (43) and laboratory experiments (44) have documented a linear relation between the dynamic stress and permeability changes, at least in some settings and for some materials.

We observe two prominent reductions in seismic velocity in the middle of November 2009 and the end of December 2010 (Fig. 3, A and B), and they are not temporally correlated with strong ground shaking from earthquakes. There are a number of similarities in the two velocity reductions. First, the magnitudes of both velocity reductions are about 0.04 to 0.05% (dv/v in a frequency range of 0.5 to 2.0 Hz). It is also confirmed that these velocity changes were not caused by precipitation (fig. S16). Second, they appear to correspond to moderate earthquake swarms at the SSGF. The total number of earthquakes was about 150 to 200 for a 1-month period (Fig. 3, A and B), and the seismic activity was localized within a 2 km × 2 km area (Fig. 3, C and D).

No local M > 4 earthquakes occurred during the earthquake swarms. Instead, earthquakes with magnitudes ranging from 3 to 4 (hereafter referred to as M 3+ earthquakes) occurred in the early stage of the earthquake swarms. In the 2009 earthquake swarm, five M 3+ earthquakes (focal depths are ~3 km) occurred within a 2-hour time period on 17 to 18 November 2009. Expected velocity changes inferred from ground shaking (PGVs of 0.31 to 0.65 cm/s at station RXH) from individual five M 3+ earthquakes range from 0.01 to 0.02% based on our stress sensitivity estimate. Again, we assume that the velocity change was further enhanced when an external stress transient oversteps the previous level of stress change during this 2-hour time period. Because M 3+ earthquakes occurred inside our target area, an evaluation of static stress change is more complicated because of a spatial heterogeneity of stress changes (that is, mixing of dilatational and compressional stress areas) (fig. S17A). We compute the median value of the highest 10% of dilatational stress changes obtained at a depth of 1 km in the SSGF (Materials and Methods). This median value would be an upper bound of the dilatational stress change that might contribute to a decrease of seismic velocity through an opening of cracks.

The resultant dilatational static stress change from five individual M 3+ earthquakes ranges from 0.010 to 0.015 kPa at a depth of 1 km. With these small dynamic and static stress estimates, it appears that these M 3+ earthquakes may not be solely responsible for the velocity reduction, although there might be some contributions from those earthquakes. The same argument is applied to the 2010 earthquake swarm that has two M 3+ earthquakes at a depth of 6 km (PGVs are 0.31 to 0.46 cm/s at station RXH). It should be noted, however, that about 6 days after these M 3+ earthquakes, two other M 3+ earthquakes occurred ~3 km far from the 2010 earthquake swarm area (fig. S17D). It is unclear whether they were a part of the same earthquake swarm.

Alternatively, aseismic deformation might have induced these velocity changes (45). Recent field study shows that aseismic crustal deformation induces a rapid velocity reduction during a fluid injection experiment at an underground facility, Tournemire, France (46). Another study shows that a decrease in seismic velocity (up to ~0.2%) was observed at upper and mid-crustal depth in response to a large slow slip event in the Guerrero segment of the Middle America subduction zone (47). At the SSGF, geodetic measurements identified a notable aseismic slip transient (the total moment release is equivalent to M_w 5.75) at depths of 1 to 2 km during a more energetic earthquake swarm in 2005 (over 1000 earthquakes) (48). This aseismic slip has been suggested to trigger the 2005 earthquake swarm including a M_w 5.1 earthquake. The time history of velocity changes at station RXH suggests a possible velocity reduction of ~0.65% associated with the 2005 earthquake swarm (fig. S18 and Materials and Methods). We hypothesize that similar aseismic deformation episodes may have occurred with the 2009 and 2010 earthquake swarms, although there is no clear evidence of aseismic slip from geodetic observations (fig. S16, C and D).

Another possible explanation is that changes in pore pressure lead to earthquake swarms (49, 50) and velocity reductions by opening of cracks (51, 52). There are a number of studies documenting earthquake swarms in and around the SSGF (53, 54) that suggest that both aseismic deformation and pore pressure diffusion are the most likely drivers of earthquake swarms. The 2009 swarm occurred near the injection wells (Fig. 3C), and fluid pressure transients may be caused by this injection. It should be noted that detailed time history of injections from nearby geothermal wells is not known. There is no clear migration of seismicity in the 2009 and 2010 earthquake swarms (figs. S19 and S20), which suggests that pore pressure diffusion is not the primary underlying mechanism of these earthquake swarms.

The temporal evolution of dv/v shows a steady long-term increase, which can be attributed to a gradual closing of fluid-filled cracks over time. Fluid withdrawal consistently exceeds the volume reinjected since 1990s, except for periods of several months (4), which leads to long-term water depletion at the SSGF. Net fluid extraction leads to ground subsidence (fig. S8) and poroelastic contraction in the geothermal reservoirs (55). This poroelastic contraction will close cracks and increase seismic velocity. Poroelastic contraction at depths of 1.0 to 2.4 km is consistent with a long-term subsidence (up to ~50 mm/year) (56), similar to depths where we document the long-term velocity change.

We argue that the long-term velocity changes would be primarily controlled by the poroelastic stress changes induced by geothermal energy production. This hypothesis is supported by the observation of the largest long-term velocity increase at the SSGF (Fig. 4). Thus, we explore stress perturbations induced by the poroelastic contraction, assuming that opening and closing of cracks is proportional to changes in applied stress. During our observation period, the average velocity increase is about 0.04%/year at depths of 0.5 to 1.5 km (dv/v in a frequency range of 0.5 to 2.0 Hz). Geodetic measurements suggest a long-term poroelastic deformation due to extraction-induced reservoir compaction, yielding an increase of effective lithostatic stress ranging from ~0.1 to 0.3 MPa/year (compression is positive) (55, 56). By combining our velocity monitoring and the geodetic modeling, an inferred lithostatic stress sensitivity of seismic velocity changes for the poroelastic deformation is estimated to be ~0.0013 to 0.0040 MPa⁻¹, which is of the same order of magnitude as the stress sensitivity of ~0.007 MPa⁻¹ determined for the slow slip event for a shorter time scale (~3 months) and greater depths (47). If we assume that velocity changes by possible 2009 and 2010 aseismic deformation also reflect an induced pressure change in the reservoir, the resultant reductions in lithostatic changes are 0.10 to 0.37 MPa. Poroelastic deformation is one of the primary driving mechanisms for induced seismicity (57, 58). Time-lapse measurements of stress changes with seismic interferometry at geothermal reservoirs would thus provide additional important insights into the nucleation process of induced earthquakes.

MATERIALS AND METHODS

Seismic data and preprocessing

The temporal behaviors of seismic velocity at the SSGF were determined through temporal variations in the coda of noise NCFs obtained from seismic records collected at the eight stations of the CalEnergy network (EN; fig. S1). Each EN station is equipped with a three-component short-period (4.5 Hz) geophone (Mark Products L15B), and seismic data are sampled at 100 Hz (42). The interstation distance ranges from 2.3 to 10 km. All available seismic data (December 2007 to January 2014) were retrieved from the SCEDC (42). Seismic waveforms collected after January 2014 are not available to the public (42). To investigate possible depth variation in seismic velocity changes, NCFs were computed with six different frequency bands (0.25 to 1.0, 0.5 to 2.0, 0.75 to 3.0, 1.0 to 4.0, 1.5 to 6.0, and 2.0 to 8.0 Hz) in the vertical-vertical components using MSNoise software (23).

Our data processing for obtaining NCFs is similar to those by Brenguier et al. (16) and Taira et al. (18). First, the instrument response was corrected on 1-day long continuous seismic data to obtain ground displacement, and then a bandpass filter between 0.08 and 8.0 Hz was applied. Daily bandpass-filtered waveforms were down-sampled into 20 Hz and split into 30-min-long data. To suppress seismic signals associated with local and teleseismic earthquake signals, a spectral whitening process and subsequently 1-bit normalization were applied at frequency bands of interest. NCFs were computed for all station pairs in the vertical-vertical component. Daily NCFs were obtained by stacking NCFs of 30-min-long data. NCFs with good signal-to-noise ratio were not recovered in the lowest frequency range, 0.25 to 1.0 Hz, and were excluded from further analysis.

Seismic velocity (dv/v) measurement

Temporal variation in seismic velocity (dv/v) was determined through the time delay measurement (dt) for a pair of NCFs with the moving window cross-spectral technique (22), assuming a homogeneous velocity change that predicts dv/v = −dt/t (12, 17, 59). A 20-s-long coda of NCFs (−40 to −20 s and 20 to 40 s) was used for the dv/v measurement to avoid including direct surface waves that would be more sensitive to the seasonal variations of noise source (60, 61). This early coda window will predominantly consist of scattered surface waves (19, 20). The length of the moving widow (overlapped by 50%) was fixed to be the longest period of the frequency band used, for example, a 2-s time moving window was used for NCFs in the passband 0.5 to 2.0 Hz.

The dv/v was obtained from time delays (dt) between the 5-day stacks of NCFs and reference NCFs averaged over the entire ~6-year period. For each station, we used the measured dt in moving windows for which the value of cross-correlation between the 5-day stack and reference NCFs exceeds 0.85. The time history of dv/v was computed by averaging dt measurements over all station pairs (28 pairs) in the five frequency bands (0.5 to 2.0, 0.75 to 3.0, 1.0 to 4.0, 1.5 to 6.0, and 2.0 to 8.0 Hz) (Fig. 1). We manually checked the continuous seismic recordings in a number of time periods (about several weeks) during which the values of cross-correlations between 5-day stack of NCFs and reference NCFs dropped (fig. S2). It remains unclear why the majority of station pairs did not recover empirical Green’s functions. We excluded those time periods from our analysis. This cross-correlation ambient noise analysis for the CalEnergy stations is referred to as the two-station cross-correlation analysis to clearly differentiate it from a single-station cross-correlation analysis described next.

We also analyzed continuous seismic data collected by 13 broadband sensors surrounding the SSGF by using a single-station cross-correlation analysis (28). Broadband seismic waveforms were retrieved from SCEDC except for stations MONP and MONP2. Data for these two stations were downloaded from the Incorporated Research Institutions for Seismology Data Management Center (http://ds.iris.edu/ds/nodes/dmc), and the locations of two stations were essentially the same. We retrieved all available waveforms for 2004 to 2014, although some of the stations were not operational during the entire 11-year period. The single-station cross-correlation analysis involved a cross-correlation for different components collected from a single station (that is, vertical-north, vertical-east, and north-east components). Two stations (stations ERR and IBP) located near the SSGF were not used for our single-station cross-correlation analysis because of their shorter operational period.

All processes for the seismic velocity change estimate were the same as those for two-station cross-correlation analysis of the CalEnergy network, except for station MONP, in which the reference NCF was obtained from all available NCFs obtained from January 2004 to November 2007. In contrast to the CalEnergy borehole geophone data, continuous seismic data from the 13 broadband stations enabled us to retrieve NCFs with relatively good signal-to-noise ratio in the lowest frequency band, 0.25 to 1.0 Hz (fig. S12).

The single-station cross-correlation analysis allows us to explore spatial variations of temporal velocity changes without using an inversion (28). However, we needed to use a 60-day running median filter to obtain stable temporal variations of seismic velocity changes because only 3 independent NCFs were available for each station (whereas the total 28 NCFs were used for the two-station cross-correlation analysis for the CalEnergy network). Therefore, we mainly used the single-station analysis to characterize the long-term velocity changes.

Long-term velocity change estimate

To evaluate the long-term velocity changes including seasonal velocity variations, coseismic velocity reduction, and postseismic velocity recovery, we assumed the following fit function, f (T)

$$\begin{array}{cc}\hfill \mathit{f}(\mathit{T})=& \mathit{A}+\mathit{B}\mathit{t}+[\mathit{C} \text{exp}(-(\mathit{T}-{\mathit{T}}_{\text{eq}})/\mathit{D})]\mathit{H}(\mathit{T}-{\mathit{T}}_{\text{eq}})\hfill \\ & +\mathit{E} \text{sin}(\mathrm{\omega }\mathit{T})+\mathit{F} \text{cos}(\mathrm{\omega }\mathit{T})+\mathit{J} \text{sin}(2\mathrm{\omega }\mathit{T})\hfill \\ & +\mathit{K} \text{cos}(2\mathrm{\omega }\mathit{T})\hfill \end{array}$$ (1)

where A is a constant offset, B is a linear trend of velocity change, C is a coseismic velocity change due to the EMC earthquake, and D is a characteristic recovery time. E, F, J, and K are annual and semiannual velocity variations, and ω in the sine and cosine terms were fixed to be 2π year⁻¹. H(T) is the Heaviside step function and T_eq is the occurrence time of the EMC earthquake; T is an elapsed time (year). Our fit function was slightly modified from previous works (28, 29) to include the linear trend of velocity change.

Before estimating all free parameters listed in Eq. 1, we removed velocity change measurements with uncertainties (two-sigma SDs) larger than 0.1% and applied a 60-day running median filter to the time history of seismic velocity changes obtained through the single-station cross-correlation analysis. This running median filter was required to stabilize temporal change measurements. To evaluate the long-term linear trend of velocity change for each station, we made use of seismic velocity measurements obtained between December 2007 and January 2014. This time period was based on the data availability of the CalEnergy station data. Because station MONP was permanently closed in November 2007, we excluded this station for the long-term velocity change estimate. A nonlinear curve fitting with SciPy (62) was used to determine all free parameters, and the resultant free parameters are summarized in table S1. A goodness of fit to the observed velocity change was evaluated by calculating variance reduction (VR).

For the two-station cross-correlation analysis, we observed additional velocity reduction related to the BS swarm. The following additional term was included in f (T)

$$[{\mathit{C}}_2 \text{exp}(-(\mathit{T}-{\mathit{T}}_{\text{eq}2})/{\mathit{D}}_2)]\mathit{H}(\mathit{T}-{\mathit{T}}_{\text{eq}2})$$

where C₂ is a coseismic velocity change due to the 2012 M_w 5.4 earthquake and D₂ is a characteristic recovery time; T_eq2 is the occurrence time of this M_w 5.4 earthquake. There was no median filter involved for the curve fitting of the two-station cross-correlation analysis because the 5-day average values are very stable.

Static stress estimate

The volumetric static stress change (Δσ_s) was evaluated from dilatational strain estimate with Coulomb 3.4 software (63). The coseismic slip models for the EMC earthquake and the 26 August 2012 M_w 5.4 earthquake of the BS swarm (the largest earthquake of the BS swarm) were obtained from previous finite-fault modeling studies (64, 65). We used a rigidity of 14 GPa based on S-wave velocity (V_s) of 2.3 km/s and the rock density of 2.6 kg/m³ to compute the stress from the computed strain. This V_s value was determined as the mean value of the S-wave velocity in the top depth of 5 km with a one-dimensional P-wave velocity (V_p) model (66), with V_p/V_s ratio of 1.60 (67). The rock density was obtained from a borehole measurement at SSGF (68). Grid sizes for the static stress estimates for the EMC earthquake and the BS swarm were 10 and 0.5 km, respectively.

For earthquakes with magnitudes ranging from 3 to 4 (hereafter referred to as M 3+ earthquakes) involved in the 2009 and 2010 earthquake swarms and the 2 September 2005 M_w 5.1 earthquake [the largest earthquake during the 2005 Obsidian Butte (OB) earthquake swarm], their focal mechanisms were obtained from a refined focal mechanism catalog (69). The fault length and width were computed with an empirical relationship between the earthquake magnitude and the faulting style (70). The grid size was set to be 0.5 km. The volumetric stress changes show strong spatial heterogeneities (mixing dilatational and compressional stress changes) for those local earthquakes because the earthquakes occurred inside the target area (fig. S17, A and B). We obtained a median value of the highest 10% of dilatational stress changes over the SSGF (shown in fig. S1) to explore an effect of dilatational stress changes from those M 3+ earthquakes on the velocity reductions obtained during the 2009 and 2010 earthquake swarms.

Dynamic stress estimate

Earthquake-induced dynamic stress changes (Δσ_d) were computed with observed PGV at station RXH (the location of this site is shown as green triangle in Fig. 1) with Δσ_d = (PGV/V_s)μ, where V_s and μ are the shear wave velocity and the rigidity, respectively (71, 72). Station RXH was selected because this site has been equipped with strong-motion and/or broadband sensors since 2004 and registered ground motions from both local and regional earthquakes over a broad range of magnitudes (3.0 ≤ M ≤ 7.2) on scale with good signal-to-noise ratios. As with the static stress estimate, we used V_s = 2.3 km/s and μ = 14 GPa for our dynamic stress change estimate. It should be noted that the dynamic stress is predominantly related to surface waves (73). However, the surface wave velocity in the shallow crust (depth up to 10 km) at SSGF is estimated to be 2.0 to 2.5 km/s (74), which is comparable to the S-wave velocity. We used the same set of shear wave velocity and rigidity to obtain the static and dynamic stress. It should be noted that the dynamic stress estimate (and stress sensitivity measurements) depends on the choice of model parameters (S-wave velocity and rigidity).

From SCEDC ShakeMap products, the observed PGVs for the EMC earthquake and the 2012 M_w 5.4 earthquake of the BS swarm were 7.47 and 2.91 cm/s, respectively, and they yield Δσ_d of 0.45 and 0.18 MPa. It should be noted, however, that these PGV measurements represent the shaking level at a single location at station RHX. There should be spatial variability of ground motions over the SSGF. SCEDC ShakeMap products provide interpolated/smoothed ground motions nearby epicenters. The median PGVs over the SSGF (the entire region shown in fig. S1) are 9.11 and 4.70 cm/s for the EMC earthquake and the BS swarm, respectively, which are about 1.2 to 1.6 times higher than those observed at station RXH. However, the median PGV estimate will strongly depend on the spatial smoothing of the PGV observations by the ShakeMap products. Therefore, we used the observed PGVs by seismic sensors for the dynamic stress estimate.

We also extracted all available PGV measurements at station RXH from SCEDC ShakeMap products to compute expected dynamic stress changes from local and regional earthquakes. Two earthquakes produce PGVs exceeding 1.0 cm/s, and they are the 30 December 2009 M 5.8 Delta, Baja California, Mexico (DBC) and the 15 June 2010 M 5.7 Ocotillo (OT), California earthquakes. The RHX PGVs are 1.18 and 1.37 cm/s for the DBC and OT earthquakes, respectively, whereas the median PGVs over the SSGF are 2.57 and 1.84 cm/s.

For M 3+ earthquakes involved in the 2009 and 2010 earthquake swarms, the PGV ranges from 0.31 to 0.65 cm/s at station RXH, which are slightly higher than the median PGVs (0.11 to 0.39 cm/s) because station RXH is located near the epicenters (~2 km distance). Note that the smoothed PGV maps were not available at the SCEDC ShakeMap products for five M 3+ earthquakes.

Station RXH was not equipped with a strong-motion sensor until June 2008, and there is no on-scale seismic record for the 2 September 2005 M_w 5.1 earthquake (the largest earthquake during the 2005 earthquake swarm). The SCEDC smoothed PGV map suggests that the level of PGV is about 18 cm/s at the location of station RXH.

As shown in fig. S9, there are a number of broadband seismic sites displaying a velocity reduction associated with the EMC earthquake. All sites were equipped with a collocated strong-motion sensor. However, PGVs at several sites were not listed in the SCEDC ShakeMap products. We manually computed PGVs for all sites for the stress sensitivity estimate (fig. S14 and table S2).

Possible seismic velocity change related to the 2005 OB earthquake swarm

The 2005 OB earthquake swarm involves more than 1000 earthquakes, including 9 earthquakes with magnitudes greater than 4. These large earthquakes occurred over ~1-day time period. The seismicity was localized near station RXH (within ~5 km) at depths of 4 to 6 km. The intense seismic activity started around 28 to 29 August 2005 and lasted about 3 weeks. The largest earthquake (M_w 5.1) occurred on 2 September 2005. Geodetic measurements identified an aseismic slip event (M_w 5.75) and suggested that this aseismic slip event triggered the 2005 OB earthquake swarm (48).

The single-station cross-correlation analysis for station RXH shows large variability in seismic velocity that might be related to the aseismic slip event and the 2005 OB earthquake swarm (fig. S18). However, the uncertainty (two-sigma SDs) exceeded 0.1% during September to December 2005. We checked velocity changes for individual channel pairs (that is, vertical-north, vertical-east, and north-east NCF components). It appears that larger uncertainties were obtained when the vertical component was involved (fig. S18). The source of the large uncertainty for this 4-month period remains unclear.

Because of this large uncertainty in velocity change measurements, we were not able to perform detailed analysis to relate temporal variations in seismic velocity to the aseismic slip or the largest M_w 5.1 earthquake. However, the time evolution of the velocity changes inferred from the north-east NCF component suggests a systematic velocity reduction (~0.65%) starting from 1 to 2 September 2005. As with the BS swarm, we considered stress changes from this largest M_w 5.1 earthquake.

The dynamic stress was estimated to be ~1 MPa (PGV is ~18 cm/s). The level of the dynamic stress was at least one to two orders of magnitude larger than that of the volumetric static stress change at station RXH. An expected velocity reduction for this dynamic stress was about ~0.56% by using the stress sensitivity of seismic velocity changes for the dynamic stress (−0.0056 MPa⁻¹), which was slightly lower than that observed on the north-east NCF component. Additional stress change from the aseismic slip event may have contributed to the velocity reduction.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/1/e1701536/DC1

fig. S1. Map view of the seismicity at the SSGF.

fig. S2. Time delay measurements obtained from EN network at the SSGF.

fig. S3. Frequency-dependent Rayleigh-wave phase velocity sensitivity.

fig. S4. Time-lapse measurements of seismic velocity changes inferred from nine components of NCFs.

fig. S5. Stress changes imparted by the 4 April 2010 M_w 7.2 El Mayor–Cucapah earthquake.

fig. S6. Stress changes imparted by the 26 August 2012 M_w 5.4 Brawley earthquake.

fig. S7. Seismic velocity changes, geodetic line-length change, and precipitation measurements around occurrence times of the 2010 M_w 7.2 El Mayor–Cucapah earthquake and the 2012 Brawley seismic (BS) swarm.

fig. S8. Seismic velocity changes, net production, and geodetic line-length change measurements.

fig. S9. Time history of velocity changes with the single-station cross-correlation analysis.

fig. S10. Long-term velocity change estimate with curve fitting.

fig. S11. Long-term velocity change as a function of site elevation.

fig. S12. Time-lapse measurements of seismic velocity changes at station RXH with the single-station cross-correlation analysis.

fig. S13. Response of hydrothermal vents to stresses.

fig. S14. Stress sensitivity for the 2010 M_w 7.2 El Mayor–Cucapah earthquake.

fig. S15. Seismic velocity changes, geodetic line-length change, and precipitation measurements around occurrence times of the 30 December 2009 M 5.8 Delta, Baja California, Mexico and the 15 June 2010 M 5.7 Ocotillo, California earthquakes.

fig. S16. Seismic velocity changes, geodetic line-length change, and precipitation measurements around occurrence times of the 2009 and 2010 earthquake swarms.

fig. S17. Volumetric static stress change and seismicity map.

fig. S18. Possible velocity change during the 2005 OB earthquake swarm.

fig. S19. The November 2009 earthquake swarm.

fig. S20. The December 2010 earthquake swarm.

table S1. Parameters of the best-fitting curve to observed seismic velocity changes with Eq. 1 and variance reduction (VR).

table S2. PGV from the SCEDC and stress sensitivity estimate for the 4 April 2010 M_w 7.2 El Mayor–Cucapah earthquake.

References (78–80)