Multiple responses optimization in the development of a headspace gas chromatography method for the determination of residual solvents in pharmaceuticals

Abstract

An efficient generic static headspace gas chromatography (HSGC) method was developed, optimized and validated for the routine determination of several residual solvents (RS) in drug substance, using a strategy with two sets of calibration. Dimethylsulfoxide (DMSO) was selected as the sample diluent and internal standards were used to minimize signal variations due to the preparative step. A gas chromatograph from Agilent Model 6890 equipped with flame ionization detector (FID) and a DB-624 (30 m×0.53 mm i.d., 3.00 µm film thickness) column was used. The inlet split ratio was 5:1. The influencing factors in the chromatographic separation of the analytes were determined through a fractional factorial experimental design. Significant variables: the initial temperature (IT), the final temperature (FT) of the oven and the carrier gas flow rate (F) were optimized using a central composite design. Response transformation and desirability function were applied to find out the optimal combination of the chromatographic variables to achieve an adequate resolution of the analytes and short analysis time. These conditions were 30 °C for IT, 158 °C for FT and 1.90 mL/min for F. The method was proven to be accurate, linear in a wide range and very sensitive for the analyzed solvents through a comprehensive validation according to the ICH guidelines.

1. Introduction

Residual solvents (RS) are volatile organic chemicals (VOCs) that are used or produced during the manufacturing process of active pharmaceutical ingredients (APIs) or excipients and cannot be completely removed. RS analysis of pharmaceutical products is necessary not only because they represent a potential risk for human health, due to their toxicity and their undesirable side effects, but also because they may affect the physicochemical properties of pharmaceutical products. Therefore, it is a mandatory requirement for health authorities in the world to accurately determine the levels of RS that are present in APIs or excipients [1], [2], [3].

The International Conference on Harmonization (ICH) in their guideline Q3C (R5) [4] classifies the regularly used solvents into three different classes based on their toxicity: Class 1 (solvents that should be avoided due to their known carcinogenic effect on human), Class 2 (solvents that should be limited in order to protect patients from potential adverse effects), and Class 3 (solvents regarded as less toxic and of a lower risk for human health). According to ICH guidelines, the levels of Class 1 and 2 solvents should be restricted to the concentration limits established by the guideline. As regard to Class 3 solvents, amounts of up to 0.5% (w/w) are considered acceptable. Moreover, the European Pharmacopoeia (Ph. Eur.) and the United States Pharmacopoeia (USP) establish the maximum allowable limits of the RS in the APIs and excipients, in accordance with the ICH guidelines.

The most appropriate analytical technique to determine RS and organic volatile impurities is the capillary gas chromatography (GC). The reasons why GC is highly recommended to this purpose are its excellent separation ability, low detection limits and the possibility of analyzing liquid or solid samples of variable and complex nature. Most of the detectors used in GC are developed specifically for this technique. There are probably more than 60 detectors that have been used in GC, and most of them are based on the formation of ions by one means or another. Among them, the flame ionization detector (FID) becomes the most popular [5]. Mass spectrometers can also be used as detectors, properly coupled to the chromatograph. The combination of GC with mass spectroscopy has become a very popular and powerful tool [6].

Sampling techniques such as static headspace gas chromatography (SHGC) have gained ground against direct injection, mainly because of the many disadvantages associated with the direct injection of sample solution into the GC system [7]. In the SHGC procedure, the liquid or solid sample is placed in a sealed vial and thermostated until a thermodynamic equilibrium between the sample and the gas phase is reached. A known aliquot of the gas phase is then injected into the gas chromatograph and analyzed. Therefore, any potential interference, from non-volatile substances, is removed or minimized.

It is worth noting that sample diluent has an important influence on SHGC, affecting sensitivity, equilibration temperature and time. In addition, the diluent should be able to dissolve a large variety of samples, present a high boiling point and an acceptable stability [8]. There are several commonly used sample diluents for HSGC analyses, such as water, dimethylsulfoxide (DMSO), N,N-dimethylformamide (DMF), N,N-dimethylacetamide (DMA), benzyl alcohol (BA), 1,3-dimethyl-2-imidazolidinone (DMI) and mixtures of water/DMF or water/DMSO [9]. Water is a good diluent for water soluble samples, because it is clean, stable and inexpensive. However, many organic synthetic drug substances and drug products have low water solubility. When mixtures of water/DMF or water/DMSO are used as sample diluent, the solubility of many drug substances or drug products increases and the partition coefficient of the analytes decreases, resulting in a better transfer of analytes from the liquid to the gas phase. However, if the sample solution is equilibrated at or above the boiling point of the diluent, the inner pressure of the vial is dangerously increased [8]. This means that if water or water mixtures are chosen, the head space (HS) equilibration temperature must be below 100 °C, leading to poor volatilization of a large number of solvents with higher boiling points. In contrast, the use of pure solvents such as DMSO, DMF, DMA or DMI generally provides an adequate solubilization of most of drug substances, and gives the possibility to incubate at temperatures above 100 °C.

The sample pre-treatment involved in the SHGC procedure is a critical step that may lead to experimental errors that can invalidate the results of the analysis. A strategy used to overcome errors in the preparative step is the addition of an internal standard (IS) [5]. The IS may be used for two different purposes. On the one hand, it can be a substance or substances added to the sample solution prior to injection in order to minimize the variability due to the volume injected into the column. On the other hand, this substance or substances is added to the sample at the earliest possible point in an analytical scheme to compensate any loss during the extraction step [10]. The IS must meet several criteria: it should elute near the peaks of interest, but it must also be well resolved from them; it should be chemically similar to the analytes of interest, but it must not react with any sample component; and it must be available in high purity.

The IS is added to the sample in a concentration similar to that of the analyte(s) of interest. When several components are analyzed, it may not be possible to fulfill this condition and a concentration of IS between higher and lower concentrations of the analytes to be analyzed must be chosen. Moreover, if many analytes are to be determined simultaneously, several internal standards may be used to meet the preceding criteria [10]. The development of such a complex analytical method requires an appropriate optimization procedure.

When attempting to find the factors (k) that have a significant influence on the system under study and then optimize such a system, experimental design is a powerful tool that is increasingly being used [11]. The advantages of experimental design are well known by chemometricians in particular and, increasingly, by the scientific community in general. Especially, its use in separation science has increased in the last few years [12], [13], [14], [15], [16], [17].

Response surface methodology (RSM) is a collection of statistical and mathematical techniques used to develop, improve and optimize processes. One of the strengths of RSM is that it may work well in cases where there is incomplete knowledge about the state and behavior of the system under study as long as the system is stable and there is reasonable correspondence between set points and actual conditions [18]. There are several experimental designs suitable for this purpose, which vary in the number of experiments required and in the complexity of the mathematical models that can be built to describe the relationship between the factors and the responses under study [11]. Using a factorial design in the screening phase followed by a central composite design (CCD) in the optimization stage is an effective tool in the optimization of a process with several parameters [19].

In addition, when different objective functions (responses) have to be optimized simultaneously, the so-called “Derringer׳s desirability function” is a useful strategy. This function is based on the idea that the quality of a product or process that has many features is completely unacceptable if one of them is outside a “desirable” limit. Its aim is to find operating conditions that ensure compliance with the criteria of all the involved responses and, at the same time, to provide the best value of compromise in the desirable joint response. This is achieved by converting the multiple responses into a single one, combining the individual responses into a composite function followed by its optimization [20], [21]. In the first step of this methodology, a partial desirability function (di) must be created for each individual response using the fitted models and establishing the optimization criteria. The most desirable ranges for each design factor or response are selected by the user, based on the prior knowledge of the system including the researcher׳s priorities during the optimization procedure. This involves deciding if these factors or responses have to be maximized, minimized, maintained in the range or reach a target value. In addition, a weight (wi) or emphasis is given to each goal. After that, the global desirability function (D) is obtained using the following equation:

$$D={(d_1^{r_1}x{d}_2^{r_2}x...x{d}_n^{r_n})}^{1/\sum ri}={\left(\prod _{i=1}^n{d}_1^{ri}\right)}^{1/\sum ri}$$ (1)

where n is the number of variables included in the optimization procedure, and r_n is the importance of each factor or response relative to the others.

The n variables, transformed in desirability functions, are combined in a unique function (D) to find out the best joint responses. The optimization procedure implies maximizing D.

Derringer׳s desirability function allows the analyst to find the experimental conditions (factor levels) to reach simultaneously the optimal value for all the evaluated variables. When D reaches a value other than zero, all the variables which are being simultaneously optimized can be considered having a desirable value. Meanwhile, if one of the responses is completely undesirable, D will be zero.

In this work, an SHGC method was developed, optimized and validated for the simultaneous determination of methanol, ethanol, ethyl ether, acetone, 2-propanol, acetonitrile, methylene chloride, hexane, isopropyl ether, ethyl acetate, 2-butanone, chloroform, tetrahydrofuran, cyclohexane, benzene, heptane, isooctane, triethylamine, 1-butanol, trichloroethylene, 1,4-dioxane, propyl acetate, pyridine, toluene, ethylene glycol, carbon tetrachloride, DMF, m-xylene, p-xylene, o-xylene and DMSO as RS in raw material.

2. Experimental

2.1. Apparatus and software

All experiments were performed using a gas chromatograph Model 6890 (Agilent, Wilmington, DE, USA) equipped with FID. The Chemstation version B 0103 was used for data acquisition and processing. The GC column was a DB-624 (30 m×0.53 mm i.d., 3.00 µm film thickness) from Agilent. The inlet split ratio was 5:1.

Experimental design, surface response modeling and desirability function calculations were performed using the Design-Expert 8.0.0 (Stat-Ease Inc., Minneapolis).

2.2. Chemicals and reagents

DMSO was purchased from TEDIA (Fairfield, Ohio, USA). Methanol, ethanol, ethyl ether, acetone, methylene chloride, hexane, isopropyl ether, ethyl acetate, 2-butanone, isooctane, chloroform, tetrahydrofuran, cyclohexane, triethylamine, 1-butanol, trichloroethylene, 1,4-dioxane, propyl acetate, pyridine, toluene, ethylene glycol, DMF, and total xylenes were supplied by Anedra (San Fernando, Argentina), and 2-propanol, acetonitrile, benzene, heptane and carbon tetrachloride by Cicarelli (San Lorenzo, Argentina). Metronidazole benzoate raw material and betamethasone-17 valerate raw material used as validation samples were supplied by Lafedar S.A. (Parana, Argentina).

2.3. Calibration curves and internal standard selection

To perform the calibration curves, the concentrations of each analyte were defined. In order to obtain the same parity, the solvents were separated, according to their concentration limits, into two groups: solvents with high limits and solvents with low limits. Another aspect that was considered was the overlapped peaks of some analytes for which no separation was achieved in the optimization procedure (ethyl acetate-2-butanone, chloroform-tetrahydrofuran, heptanes-isooctane-triethylamine, dioxane-propyl acetate and toluene-ethylene glycol). A particular case resided in the determination of three coeluting analytes: isooctane–heptane–triethylamine. In this case, a bibliographic study of the occurrence of these solvents in raw materials allowed us to decide to work with heptane–triethylamine.

In addition, two internal standards were selected in each calibration group, one in low concentration and the other in high concentration. To define the solvent used as IS, we considered the resolutions between the peaks and co-eluting analytes and the characteristics of the solvents. According to these issues, we decided to use benzene, trichloroethylene, acetone and hexane. Its reproducibility during the runs was an important parameter to consider in the choice of the IS.

2.4. Internal standard solutions

Two internal standard solutions were prepared by diluting appropriate volumes of pure solvents in DMSO. For internal standard solution 1 (IS1), 12 µL of benzene and 410 µL of trichloroethylene were transferred into a 10 mL volumetric flask. For internal standard solution 2 (IS2), 115 µL of hexane and 250 µL of acetone were transferred into a 10 mL volumetric flask.

2.5. Standard solutions

Two standard stock solutions (SSSs) were prepared by diluting appropriate volumes of pure solvents of each analyte in DMSO. Calibration standards were prepared at the moment of the analysis by diluting suitable volumes of the SSSs in DMSO. By proper dilutions, the first SSS calibration solutions were obtained yielding concentrations of analytes in the ranges described in Table 1. Then, 25 µL of IS1 was added into each calibration solution reaching concentrations of 2.0 µg/mL for benzene and 60 µg/mL for trichloroethylene. With the similar method, the second SSS calibration solutions were obtained yielding concentrations of analytes in the ranges described in Table 2. Then, 25 µL of IS2 was added into each solution obtaining concentrations of 0.4 µg/mL for hexane and 20 µg/mL for acetone. After incubation of the solutions (5.0 mL in a 20 mL headspace vial) at 105 °C for 45 min, 2.5 mL of the vapor phase was injected into the GC system.

Table 1.

Concentration ranges for analytes in the first calibration set.

Analyte	Range (µg/mL)
Propyl acetate	2.99–89.7
Acetone	3.00–90.1
1-Butanol	47.8–77.6
Cyclohexane	2.99–89.7
Ethanol	2.99–89.9
Ethyl ether	2.99–89.8
Methanol	15.1–90.3
Ethyl acetate	15.0–89.8
Heptane	3.00–90.3
Hexane	1.44–8.64
2-Propanol	15.0–90.1
Isopropyl ether	15.0–90.1
Tetrahydrofuran	0.46–13.9
Toluene	2.95–17.7
Xylene	3.01–90.3

Table 2.

Concentration ranges of analytes in the second calibration set.

Analyte	Range (µg/mL)
Acetonitrile	5.03–8.17
Methylene chloride	9.31–15.1
2-Butanone	47.8–77.6
Chloroform	0.95–1.54
Benzene	0.034–0.055
Triethylamine	0.79–1.28
Trichloroethylene	1.31–2.13
1,4-Dioxane	6.59–10.7
Pyridine	3.21–5.21
Ethylene glycol	9.29–15.1
Carbon tetrachloride	0.061–0.099
N,N-dimethylformamide	14.5–23.6

2.6. Sample preparation

500 mg of metronidazole benzoate or betamethasone-17 valerate raw material was transferred into a 25 mL volumetric flask and an amount of DMSO (15 mL) was added to dissolve the sample. In the case of betamethasone-17 valerate, the analytes to be identified and quantified were chloroform, trichlorethylene, dioxane, DMF and ethyl acetate, and the IS2 (25 µL) was used. In the case of metronidazole benzoate, the analytes to be identified and quantified were methanol, acetone, methylene chloride, ethylene glycol and toluene, and the IS1was used. After incubation of the sample (5.0 mL in a 20 mL headspace vial) at 105 °C for 45 min, 2.5 mL of the vapor phase was injected into the GC system.

2.7. Fortified samples for recovery and precision studies

Portions of 500 mg of metronidazole benzoate raw material or betamethasone-17 valerate raw material were transferred into 25 mL volumetric flasks and spiked with appropriate amounts of solvents yielding concentrations of analytes in the ranges described in Table 3, Table 4. After that, DMSO (15 mL) was added to dissolve the sample and 25 µL of IS (IS1 or IS2) was added. After incubation of the sample (5.0 mL in a 20 mL headspace vial) at 105 °C for 45 min, 2.5 mL of the vapor phase was injected into the GC system.

Table 3.

Concentration levels (μg/mL) for analytes of the first calibration set used for precision and recovery studies.

Analyte	Recovery study				Precision study		Repeatability study
	1a	2a	3a	4a	1b	2b
Propyl acetate	5.98	44.7	59.8	83.7	2.99	89.7	59.8
Acetone	6.00	45.0	60.0	84.1	3.00	90.1	60.0
1-Butanol	6.03	45.3	60.3	84.5	3.02	90.5	60.3
Cyclohexane	5.98	44.9	59.8	83.8	2.99	89.8	59.8
Ethanol	6.00	45.0	60.0	83.9	3.00	98.9	59.9
Ethyl ether	5.99	44.9	59.9	83.9	3.00	89.8	59.9
Methanol	6.02	45.1	60.2	84.3	3.01	90.3	60.2
Ethyl acetate	5.99	44.9	59.9	83.9	3.00	89.8	59.9
Heptane	6.02	45.1	60.2	84.3	3.01	90.3	60.2
Hexane	0.58	4.32	5.76	8.06	0.29	8.64	5.76
2-Propanol	6.01	45.1	60.1	84.1	3.00	90.1	60.1
Isopropyl ether	6.00	45.0	60.0	84.0	3.00	90.1	60.0
Tetrahydrofuran	0.93	6.95	9.26	13.0	0.46	13.9	9.26
Toluene	1.18	8.84	11.8	16.5	0.59	17.7	11.8
Xylene	6.02	45.2	60.2	84.3	3.01	90.3	60.2

^aFortification level in recovery study.

^bFortification level in precision study.

Table 4.

Concentration levels (μg/mL) for analytes of the second calibration set used for precision and recovery studies.

Analyte	Recovery study				Precision study		Repeatability study
	1a	2a	3a	4a	1b	2b
Acetonitrile	5.97	6.29	6.60	7.86	5.03	8.17	6.29
Methylene chloride	11.1	11.6	12.2	14.5	9.31	15.1	11.6
2-Butanone	56.7	59.7	62.7	74.6	47.8	77.6	59.7
Chloroform	1.12	1.18	1.24	1.48	0.95	1.54	1.18
Benzene	0.040	0.042	0.044	0.053	0.036	0.055	0.042
Triethylamine	0.94	0.99	1.04	1.23	0.79	1.28	0.99
Trichloroethylene	1.55	1.64	1.72	2.04	1.31	2.13	1.64
1,4-Dioxane	7.83	8.24	8.65	10.3	6.59	10.7	8.24
Pyridine	3.81	4.01	4.21	5.01	3.21	5.21	4.01
Ethylene glycol	11.0	11.6	12.2	14.5	9.29	15.1	11.6
Carbon tetrachloride	0.070	0.076	0.080	0.095	0.061	0.099	0.079
N,N-dimethylformamide	17.2	18.1	19.0	22.7	2.1	23.6	18.1

^aFortification level in recovery study.

^bFortification level in precision study.

2.8. Experimental design and optimization

The goal of using experimental design was to find the optimal analytical conditions for the chromatographic separation of 31 solvents with satisfactory performance and in a reasonable analysis time.

In the first instance, runs were performed using the USP 34 method for residual solvents. The column was a DB-624 (30 m×0.53 mm i.d., 3.00 µm film thickness) from Agilent. The inlet split ratio was 5:1, and the carrier gas was nitrogen at a velocity of 5.0 mL/min. The column temperature was maintained at 40 °C for 20 min, then raised at a rate of 10 °C per min to 240 °C and maintained at 240 °C for 20 min. Fig. 1 shows a typical chromatogram obtained from these conditions.

Fig. 1.

Chromatogram obtained following the conditions described in USP 34: (A) full chromatogram and (B) expansion of the critical zone.

These previous experiments showed low or none resolution between several of the analyzed solvents and in some cases large peaks widths. Thus, we built an experimental design to determine the factors that were influencing the separation and peaks performance. A factorial design with six factors was used: (a) initial temperature of the GC oven in the range of 40–60 °C; (b) final temperature of the GC oven in the range of 100–150 °C; (c) time period of initial temperature in the range of 1–3 min; (d) time period of final temperature in the range of 1–3 min; (e) variation of the ramp in the range of 5–10 °C/min; and (f) carrier gas flow in the range of 2.5–10 mL/min.

Several responses were selected for optimization purposes: (R1) resolution between peaks of ethanol and ethyl ether, (R2) resolution between peaks of acetone and 2-propanol, (R3) resolution between peaks of 2–propanol and acetonitrile, (R4) resolution between peaks of acetonitrile and methylene chloride, and (R5) resolution between peaks of pyridine and toluene. These resolutions were selected based on the fact that in none of the runs these analytes had resolutions higher than 1.5.

Table 5 shows the fractional factorial design (6–1) built with 32 runs and blocked in 4 days. The analysis of the effects of the variables over the responses was concluded that the factors with no significant influence on the chromatography resolution of analyte were ramp rate (RR), time at final temperature (T FT) and time at initial temperature (T IT). While factors influencing the resolution of the peaks were initial temperature (IT), final temperature (FT) and flow (F).

Table 5.

Experiments of the factorial design.

Stda	Runa	Block	Factors (k)
			ITb	FTb	T ITc	T FTc	°C/min	Fd
8	1	1	60	150	3	1	5	10
1	2	1	40	100	1	1	5	2.5
14	3	1	60	100	3	3	5	2.5
20	4	1	60	150	1	1	10	2.5
26	5	1	60	100	1	3	10	10
21	6	1	40	100	3	1	10	10
31	7	1	40	150	3	3	1	2.5
11	8	1	40	150	1	3	5	10
29	9	2	40	100	3	3	10	10
16	10	2	60	150	3	3	5	10
23	11	2	40	150	3	1	10	2.5
9	12	2	40	100	1	3	5	2.5
18	13	2	60	100	1	1	10	10
6	14	2	60	100	3	1	5	2.5
3	15	2	40	150	1	1	5	10
28	16	2	60	150	1	3	10	2.5
24	17	3	60	150	3	1	10	10
15	18	3	40	150	3	3	5	2.5
10	19	3	60	100	1	3	5	10
5	20	3	40	100	3	1	5	10
4	21	3	60	150	1	1	5	2.5
27	22	3	40	150	1	3	10	10
30	23	3	40	150	1	3	10	10
17	24	3	40	100	1	1	10	2.5
7	25	4	40	150	3	1	5	2.5
22	26	4	60	100	3	1	10	2.5
13	27	4	40	100	3	3	5	10
32	28	4	60	150	3	3	10	10
25	29	4	40	100	1	3	10	2.5
12	30	4	60	150	1	3	5	2.5
2	31	4	60	100	1	1	5	10
19	32	4	40	150	1	1	10	10

^aStd refers to the standard order in the design. Run refers to the experiment order.

^bIT and FT in °C.

^cT IT (time at initial temperature) and T FT (time at final temperature) in minutes.

^dF in mL/min.

With this information, we proceeded to build a central composite design to find out the optimal values of the factors under study. Levels for each factor corresponding to –1 and +1 coded value were: 30.0 and 40.0 °C for IT, 150 and 160 °C for FT and 1.0 and 2.0 mL/min for F. The other chromatographic factors were kept constant at the following values: 1.50 min for T IT, 1.50 min for T FT and 5 °C/min for RR. The α-value used in the design was compatible with rotatable distribution of prediction variance. Experiments were divided into two blocks, with 10 runs on day one and 14 runs on day two, which are shown in Table 6 in their actual values.

Table 6.

Experiments and responses of the central composite design.

Stda	Runa	Block	Factors (k)			Responses
			ITb	FTb	Fc	R1	R2	R3	R4	R5
9	1	1	35.0	155.0	1.50	2.41	1.28	2.37	2.84	1.87
3	2	1	30.0	160.0	1.00	2.46	0.76	2.38	2.52	1.42
2	3	1	40.0	159.0	1.00	2.33	0.32	1.84	2.31	1.41
5	4	1	30.0	150.0	2.00	2.16	1.83	2.08	2.94	2.02
8	5	1	40.0	160.0	2.00	2.11	1.26	2.12	2.66	1.96
6	6	1	40.0	150.0	2.00	2.10	1.25	2.1	2.64	1.95
10	7	1	35.0	155.0	1.50	2.36	1.27	2.36	2.81	1.87
7	8	1	30.0	160.0	2.00	2.22	1.85	2.11	3.00	1.99
1	9	1	30.0	150.0	1.00	2.45	0.75	2.39	2.53	1.43
4	10	1	40.0	160.0	1.00	2.36	0.28	1.80	2.34	1.41
21	11	2	35.0	155.0	2.21	1.85	1.53	1.82	2.55	1.95
11	12	2	27.9	155.0	1.50	2.16	1.63	2.39	3.04	1.89
16	13	2	35.0	147.9	1.50	2.29	1.25	2.31	2.75	1.87
14	14	2	42.1	155.0	1.50	2.15	0.84	2.17	2.48	1.81
19	15	2	35.0	155.0	0.97	2.06	0.00	1.90	1.93	0.00
23	16	2	35.0	155.0	1.50	2.30	1.25	2.31	2.77	1.86
15	17	2	35.0	147.9	1.50	2.26	1.23	2.29	2.73	1.88
18	18	2	35.0	162.1	1.50	2.29	1.24	2.30	2.74	1.87
24	19	2	35.0	155.0	1.50	2.35	1.28	2.37	2.80	1.86
22	20	2	35.0	155.0	2.21	2.00	1.55	1.95	2.72	1.98
20	21	2	35.0	155.0	0.79	2.06	0.00	1.96	1.95	0.00
12	22	2	27.9	155.0	1.50	2.48	1.65	2.39	3.05	1.88
13	23	2	42.1	155.0	1.50	2.10	0.83	2.10	2.42	1.82
17	24	2	35.0	162.1	1.50	2.30	1.24	2.30	2.76	1.87

^aStd refers to the standard order in the design. Run refers to the experiment order.

^bIT and FT in °C.

^cF in mL/min.

The experiments were performed in a randomized order to ensure the independence of the results, minimizing the effects of uncontrolled factors. Then, the responses were evaluated and the models were built.

2.9. Method validation

In order to study the linearity, calibration standards were prepared in triplicate in DMSO. The central point of the calibrations was chosen as the upper limit allowed by USP for each solvent in raw material. In all cases, we used two sets of IS to maintain constant their concentrations during the construction of the curve. The headspace vapor of these solutions was introduced into the instrument in a randomized way and calibration plots were built by plotting concentration vs. relative areas (RA).

Limit of detection (LOD) and limit of quantification (LOQ) were calculated by the linear regression analysis and by using the signal/noise ratio criterion as described in the results.

To evaluate the trueness of the method, recovery experiments were made with the fortified sample solutions described in Section 2.7.

The instrumental repeatability was assessed by repetitive measurements (n=6) of standard solutions at the central point of the calibration, whereas the intermediate precision was evaluated by performing measurements (n=5) of fortified samples at two different concentrations (lower and upper levels of the curve) prepared by spiking metronidazole benzoate with a volume of an adequately standard solution through two days. Then, the relative standard deviation was calculated in all the cases.

The method was finally applied to the determination of RS in raw material.

3. Results and discussion

3.1. Optimization of the chromatographic separation

3.1.1. Models

In each model, the terms were evaluated by analysis of variance (ANOVA) and a backward regression procedure was applied to eliminate the insignificant factors (α=0.10). This probability value, α is used to limit the selection so that the terms with p-values larger than 0.10 were excluded from the model. In this way, simplified models, including only significant terms and those necessary to maintain hierarchy, were obtained. ANOVA is a collection of statistical models used to analyze the differences between group means. It estimated three sample variances: a total variance based on all the observation deviations from the grand mean, an error variance based on all the observation deviations from their appropriate treatment means and a treatment variance. Treatment considered in this case is the level of the factor. To determine the statistical significance of the term, the F-test was used to compare the variance between treatments with the variance within treatment. Resulting models are shown in Table 7.

Table 7.

Models fitting.

Response (y)	Model	Transformation	Significant terms (xi)	ANOVA p-valuea
				Model	Lack of fit
R1	Quadratic	None	A–C–C2	<0.0001	0.855
R2	Quadratic	Power. Lambda: 0.77	A–B–C–AB–BC – A2–B2–C2	<0.0001	0.572
R3	Quadratic	None	A–C–AC–A2–C2	<0.0001	0.567
R4	Quadratic	None	A–C–C2	<0.0001	0.158
R5	Quadratic	None	A–C–AC–A2–C2	<0.0001	0.238

A=Initial temperature (IT), B=Final temperature (FT), C=Flow (F).

^ap-Values less than 0.050 indicate significance.

3.1.2. Transformation of the responses

Generally, transformation of the responses is used for three different purposes: to stabilize the response variance, to do the distribution of the response variable closer to the normal distribution, and to improve the fit of the model to the experimental data. The last objective includes model simplification by eliminating interaction terms. Sometimes a transformation will be reasonably effective in simultaneously accomplishing more than one of these objectives.

Transformations apply a mathematical function to all the response data needed in order to meet the assumptions that make the ANOVA valid: residuals must be normally distributed, independent and with a constant variance.

There was a broad range of possible response transformations, and the Box Cox graphical strategy was used in this work [22]. Table 7 shows the transformation of the responses made after analyzing experimental results.

3.1.3. Optimal conditions achieved through desirability function

Table 8 shows the criteria chosen for the optimization of each response. Due to the fact that they were the most critical parameters, an importance of 5 was assigned to R2 and R5 when constructing the global desirability. The importance of the other variables was kept in an intermediate value.

Table 8.

Criteria followed for the optimization of individual factors and responses.

Variable	Goal	Range		Weight		Importance
		Lower limit	Upper limit	Lower	Upper
IT	Is in range	30	42	1	1	3
FT	Is in range	148	162	1	1	3
F	Is in range	0.80	2.48	1	1	3
R1	Maximize	1.85	2.48	0.5	1	3
(R2)0.77	Maximize	0.38	1.61	5	1	5
R3	Maximize	1.80	2.39	0.5	1	3
R4	Minimize	1.93	3.05	0.5	1	3
R5	Maximize	1.93	2.02	1	1	5

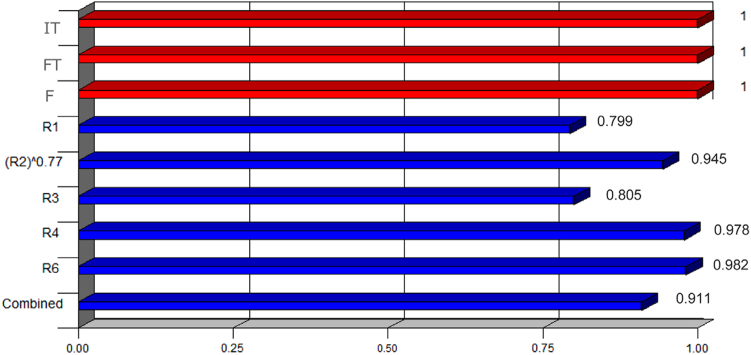
The global desirability function produced a maximum value (D=0.912) for IT of 30 °C, FT of 158 °C, and F of 1.90 mL/min in the separative method.

Fig. 2 shows the partial desirability reached by each variable in the system under the optimized conditions. Fig. 3 shows the global desirability three-dimensionally represented as a function of two of the influential variables in the system, depending on the flow rate and the final temperature.

Fig. 2.

Individual desirability obtained for each variable.

Fig. 3.

Desirability depending on flow (F) and final temperature (FT).

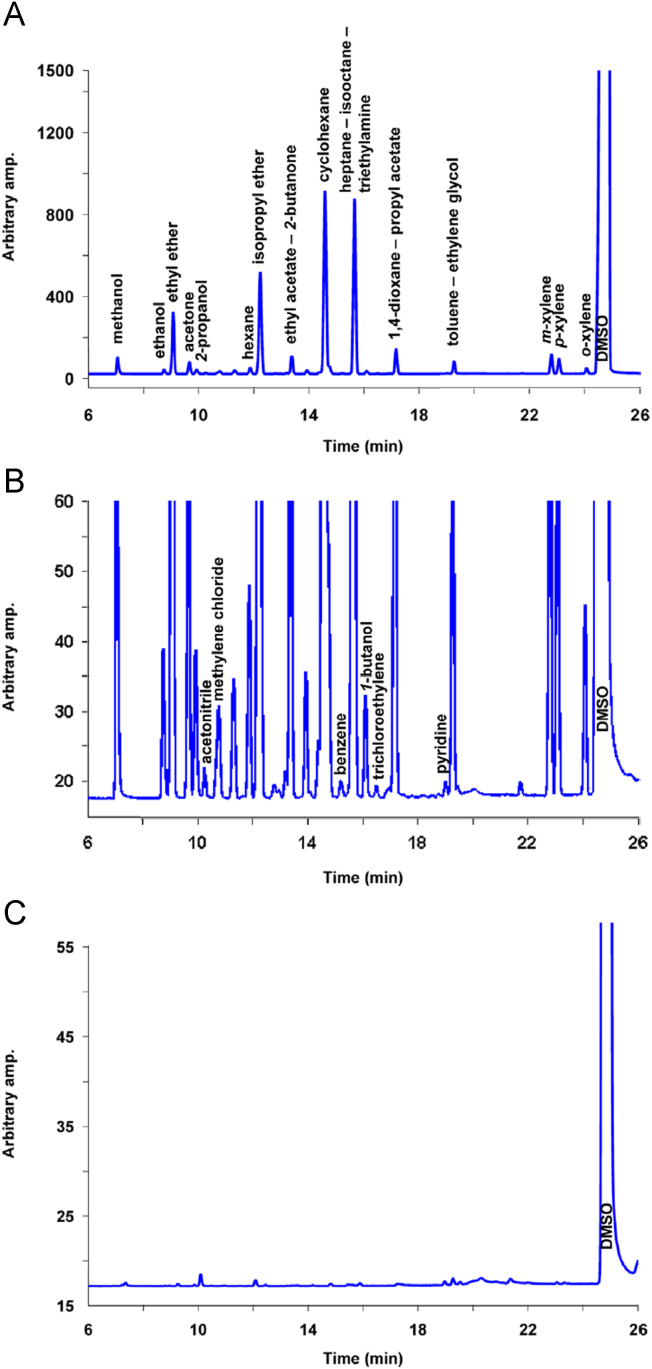
In setting the values that were assigned to the factors, the following confidence interval values (95% CI) for the five responses were predicted by the fitted models: R1=2.19–2.31, R2=1.40–1.43, R3=2.14–2.22, R4=2.96–3.05 and R6=2.00–2.02. The suggested optimal conditions were then experimentally corroborated, obtaining chromatographic signals like the one presented in Fig. 4.

Fig. 4.

Chromatogram corresponding to a standard solution: (A) full chromatogram; (B) expansion of the critical zone and (C) DMSO blank.

3.2. Sample diluent selection

First, we used mixtures of water–DMSO and water–DMF according to USP guide and then we used pure solvent (DMF and DMSO). In the case of solvent–water mixtures, the equilibrium temperature was maintained at 80 °C. In these experiments, a remarkable decrease in the sensitivity of the analytes was observed. For this reason, the incubation time was increased above 60 min in order to achieve satisfactory recoveries for the analytes at concentrations of 1 μg/mL or less.

In addition, we considered the stability and solubility of the raw materials to be analyzed. In this sense, DMF showed low stability at high temperature and susceptibility to degradation when exposed to ultrasonic during sample preparation. As the degradation products may interfere with the determination, we discarded the use of this solvent. Since DMSO is more stable at high temperature and has a higher capacity of dissolving drug substances and drugs products, it was chosen as the HS diluent.

3.3. Method validation and figures of merit

3.3.1. Specificity

In order to identify each analyte and their retention times in our GC system with FID, we ran the pure solvents individually. As it was previously described (Section 2.3) that several solvents have the same retention time, we took the initiative to separate them into two groups. The problem arose when a raw material had as residual solvents a couple that overlap. In these cases, we either changed the column using the same method or we developed a new method for separating the analytes in question.

3.3.2. Linearity and range

According to Taverniers et al. [22], linearity is defined as the ability of the method to obtain test results proportional to the concentration of analyte (within a given range) and linear range, and, working range or linearity limits is defined as the range of concentrations (or amounts) of analyte over which the method gives test results proportional to the concentration of analyte, or a linear calibration model can be applied with a known confidence level.

Calibration curves were obtained with six standards covering the selected range and each point in triplicate. Relative areas (analyte area/internal standard area) of each RS were calculated to get the curve, plotting concentration vs. relative area (RA). All of RS showed a good linear relationship (r²>0.99). The range and the calibration parameters are listed in Table 9. However, for assessment of the linearity of an analytical method, linear regression calculations are not enough. Therefore, the goodness of fit was tested by comparing the variance of the lack of fit against the pure error variance [23], [24]. The adequacy of the model was estimated by an F-test which uses the pure error variance (SS_PE/ν_PE) and the variance of the lack of fit (SS_LOF/ν_LOF):

$$F=({\mathrm{SS}}_{LOF}/{\nu }_{LOF})/({\mathrm{SS}}_{PE}/{\nu }_{PE})$$ (2)

where SS_PE is the sum of squares corresponding to pure error, SS_LOF is the sum of squares corresponding to the lack of fit, ν_LOF=ν_R–ν_PE, and ν_PE and ν_R are the degrees of freedom for estimating the sum of squares of pure error and residuals, respectively [25].

Table 9.

Linearity range results and figures of merit (in all case the F_tab=5.112).

Analyte	Linearity range (µg/mL)	Intercept	Slope	Fexpb	r2	Lack of fit (p-value)c
Propyl acetate	2.99–89.72	0.59 (0.23)	0.154 (0.004)	1.121	99.999	0.255
Acetone	3.00–90.06	0.077 (0.018)	0.122 (0.0003)	1.206	99.999	0.189
1-Butanol	3.02–90.51	−0.59 (0.18)	0.115 (0.003)	1.089	99.395	0.306
Cyclohexane	2.99–89.75	0.22 (0.17)	0.337 (0.003)	1.097	99.934	0.296
Ethanol	2.99–89.94	–0.098 (0.027)	0.060 (0.0004)	0.837	99.945	0.837
Ethyl ether	2.99–89.84	0.144 (0.098)	0.111 (0.002)	1.276	99.797	0.143
Methanol	15.05–90.29	−0.044 (0.017)	0.024 (0.0002)	1.330	99.914	0.126
Ethyl acetate	14.97–89.34	0.165 (0.029)	0.153 (0.0005)	1.154	99.994	0.237
Heptane	3.01–90.29	−0.669 (0.212)	0.465 (0.004)	1.253	99.946	0.157
Hexane	1.44–8.64	−0.024 (0.036)	0.917 (0.006)	1.987	99.125	0.361
2-Propanol	15.02–90.09	−0.179 (0.058)	0.066 (0.0009)	0.932	99.868	0.570
Isopropyl ether	15.01–90.09	0.405 (0.284)	0.193 (0.005)	1.373	99.621	0.109
Tetrahydrofuran	0.46–13.89	0.023 (0.009)	0.196 (0.001)	0.932	99.972	0.589
Toluene	2.95–17.69	0.254 (0.039)	0.363 (0.0003)	1.319	99.948	0.130
Xylene	3.01–90.30	−0.026 (0.019)	0.054 (0.003)	1.195	99.969	0.198
Acetonitrile	5.03–8.17	−0.078 (0.005)	0.032 (0.0006)	1.090	99.640	0.305
Methylene chloride	9.31–15.12	−0.048 (0.004)	0.020 (0.0003)	0.907	99.798	0.652
2-Butanone	47.75–77.60	−0.041 (0.0005)	0.004 (0.0007)	1.178	99.728	0.212
Chloroform	0.95–1.54	−0.332 (0.006)	0.428 (0.005)	0.978	99.905	0.496
Benzene	0.034–0.055	−0.107 (0.006)	7.56 (0.12)	1.134	99.788	0.255
Triethylamine	0.79–1.28	−1.46 (0.02)	1.86 (0.02)	1.308	99.929	0.126
Trichloroethylene	1.31–2.13	−1.98 (0.03)	1.74 (0.02)	1.346	99.927	0.109
1,4-Dioxane	6.59–10.71	−0.130 (0.007)	0.038 (0.0008)	1.239	99.627	0.166
Pyridine	3.21–5.21	−0.269 (0.009)	0.123 (0.002)	1.064	99.748	0.341
Ethylene glycol	9.29–15.09	−0.155 (0.008)	0.028 (0.0006)	1.174	99.580	0.215
Carbon tetrachloride	0.061–0.099	−0.113 (0.004)	3.47 (0.005)	0.862	99.822	0.773
DMF	14.50–23.56	−1.51 (0.05)	0.119 (0.002)	1.242	99.693	0.273

^aValues between parentheses indicate SD.

^bF-test for linearity determination.

^cSince the p-value for the lack of adjustment is greater than or equal to 0.10, the model seems to be adequate for the observed data.

The calibration model is considered suitable if F_exp is less than the one–tailed tabulated value F_tab(ν_R–ν_PE, ν_PE, p) at a p confidence level. In our case, the calibration model can be considered adequate as the F_exp, in all cases, lower than F_tab (Table 9).

3.3.3. LOD and LOQ

The LOD is the lowest concentration of analyte that can be detected and reliably distinguished from zero (or the noise level of the system), but not necessarily quantitated [22]. This parameter was calculated using standard solutions prepared in solvent, applying different criteria.

First, the LOD was computed from the linear regression analysis using the standard deviation of the regression (s_y) using the expression LOD=3.3s_y/b [26].

Additionally, the LOD was calculated as the concentration of analyte giving a signal three times of the noise level (S/N=3), using standard solutions prepared in solvent. The signal to noise ratio was calculated using the Chemstation software version B.

The LOD values obtained by these criteria are displayed in Table 10.

Table 10.

LOD and LOQ values computed according to different criteria.

Analyte	LODa		LOQa
	Calibration curve	S/R	Calibration curve	S/R
Propyl acetate	9.1	8.2	28	27
Acetone	0.89	0.19	2.7	0.63
1-Butanol	9.2	8.7	28	29
Cyclohexane	3.0	2.0	9.1	6.7
Ethanol	2.7	1.3	8.2	4.3
Ethyl ether	5.3	5.0	16	17
Methanol	3.6	2.2	11	7.3
Ethyl acetate	0.96	0.91	2.9	3.0
Heptane	2.7	2.0	8.2	6.7
Hexane	0.20	0.16	0.61	0.53
2-Propanol	4.4	3.9	13	13
Isopropyl ether	7.5	7.1	23	24
Tetrahydrofuran	0.30	0.13	0.91	0.43
Toluene	0.54	0.36	1.6	1.2
Xylene	2.1	1.1	6.4	3.7
Acetonitrile	0.53	0.24	1.6	0.80
Methylene chloride	0.74	0.50	2.2	1.7
2-Butanone	4.4	3.6	13	12
Chloroform	0.05	0.06	0.15	0.20
Benzene	0.003	0.002	0.009	0.007
Triethylamine	0.04	0.08	0.12	0.27
Trichloroethylene	0.06	0.08	0.18	0.27
1,4-Dioxane	0.71	0.27	2.2	0.90
Pyridine	0.28	0.46	0.85	1.5
Ethylene glycol	1.1	0.81	3.3	2.7
Carbon tetrachloride	0.005	0.006	0.015	0.020
N,N-dimethylformamide	1.5	1.1	4.5	3.7

^aConcentration in µg/mL.

According to different international regulatory bodies, the LOQ is the lowest concentration of analyte that can be determined quantitatively with an acceptable level of precision [22]. First, the LOQ was computed from the linear regression analysis using the standard deviation of the regression (s_y) as was done for the LOD but using a factor equal to 10. Additionally, it was calculated as the concentration of analyte giving a signal ten times of the noise level (S/N=10) using standard solutions prepared in solvent.

The LOQ values obtained by these criteria are displayed in Table 10.

3.3.4. Trueness

To assess the trueness of the method, recovery tests were made by adding different concentrations of the solvents of interest to a known mass of raw materials under study. The recoveries were examined by spiking raw materials of metronidazole benzoate and betamethasone-17 valerate with known amounts of standard solutions at the beginning of the sample preparation procedure (see Section 2.6). After analysis, the concentrations of the solvents were obtained from the regression parameters of the calibration curves and the recoveries were calculated. Four levels were evaluated (three replicates), and the results are displayed in Table 11, Table 12. It can be observed that excellent recoveries were achieved (between 85.7% and 113.1%).

Table 11.

Results of recoveries (%) for solvents of the first calibration set.

Analyte		Metronidazole benzoate				Betamethasone-17 valerate
		1a	2a	3a	4a	1a	2a	3a	4a
Propyl acetate		102.5	88.8	102.8	89.1	98.7	98.6	109.6	112.4
Acetone		97.6	102.7	90.1	89.5	87.6	94.5	88.3	90.3
1-Butanol		96.7	104.6	107.3	109.5	89.5	101.0	97.7	98.2
Cyclohexane		95.0	111.8	112.9	111.7	102.4	90.2	94.6	95.3
Ethanol		104.3	102.1	97.8	110.5	100.2	93.3	111.9	109.9
Ethyl ether		100.4	96.9	97.1	100.7	97.9	91.7	107.9	89.2
Methanol		98.1	94.2	100.4	104.4	99.3	100.8	92.3	108.7
Ethyl acetate		101.3	89.6	85.7	86.4	97.2	86.4	95.1	90.1
Heptane		106.9	95.8	86.5	86.6	102.6	91.4	103.4	102.6
Hexane		94.6	102.4	103.9	103.9	107.8	112.9	91.1	89.4
2-Propanol		99.1	105.9	93.7	91.2	102.3	88.3	103.9	97.1
Isopropyl ether		96.5	94.3	106.7	104.3	95.1	93.9	91.8	94.2
Tetrahydrofuran		111.3	91.6	90.0	102.2	91.1	99.7	91.7	90.3
Toluene		94.9	96.7	110.9	98.9	97.0	111.9	112.1	104.1
Xylene		110.1	101.7	108.5	98.7	106.3	109.1	111.8	108.5

^aFortification level.

Table 12.

Results of recoveries (%) for solvents of the second calibration set.

Analyte	Metronidazole benzoate				Betamethasone-17 valerate
	1a	2a	3a	4a	1a	2a	3a	4a
Acetonitrile	96.2	104.8	113.1	110.8	95.6	98.3	98.9	97.7
Methylene chloride	88.6	90.4	105.1	108.6	109.6	98.3	104.9	107.0
2-Butanone	92.0	93.8	93.6	93.1	91.5	100.1	96.9	105.1
Chloroform	86.2	89.2	87.2	90.4	88.5	90.5	90.8	88.0
Benzene	91.3	88.0	99.0	88.2	89.8	96.3	101.7	109.0
Triethylamine	106.5	102.5	108.6	111.3	102.2	105.1	110.4	103.8
Trichloroethylene	100.2	91.8	99.8	99.4	93.3	100.3	105.5	98.9
1,4-Dioxane	104.3	109.1	112.1	107.3	99.8	104.8	108.1	103.7
Pyridine	110.9	109.5	110.4	104.9	103.0	105.0	104.5	98.9
Ethylene glycol	106.0	112.3	110.1	96.8	95.3	94.6	93.9	103.1
Carbon tetrachloride	108.3	106.0	105.7	96.3	100.0	99.7	101.0	94.7
DMF	92.1	95.6	98.1	105.6	103.2	101.3	109.2	107.5

^aFortification level.

3.3.5. Precision

Two parameters were studied: repeatability or intra-assay variations and intermediate precision or inter-assay variations using fortified metronidazole benzoate raw material.

The relative standard deviation (RSD) of the obtained results was evaluated and an F-test (α=0.05) for comparison between series was performed showing acceptable precision parameters for the method. These results are displayed in Table 13.

Table 13.

Results of precision study.

Analyte	Level 1 (%RSD)		F between seriesa	Level 2 (%RSD)		F between Seriesa	Inter assay (%RSD)
	Day 1	Day 2		Day 1	Day 2
Propyl acetate	2.1	3.5	1.7	3.2	2.8	5.6	2.5
Acetone	4.0	3.2	1.1	2.7	3.6	8.2	2.4
1-Butanol	4.0	2.6	8.8	2.4	2.8	4.2	2.1
Cyclohexane	3.2	3.3	5.5	1.2	1.8	7.5	2.2
Ethanol	4.7	2.7	1.9	2.3	3.8	7.6	3.4
Ethyl ether	4.8	3.8	8.2	2.4	5.0	5.4	2.6
Methanol	6.2	3.6	2.1	2.1	3.4	7.5	3.7
Ethyl acetate	4.3	4.5	2.4	2.8	3.8	2.7	1.9
Heptane	4.7	4.7	2.1	2.2	2.9	5.3	2.4
Hexane	5.6	3.6	2.3	2.2	2.5	6.7	2.3
2-Propanol	5.8	3.0	2.3	2.0	3.8	4.8	2.8
Isopropyl ether	5.8	4.2	2.3	1.6	2.3	3.6	2.5
Tetrahydrofuran	3.2	2.9	2.2	3.6	3.2	3.8	2.5
Toluene	2.7	2.9	3.1	3.7	2.5	5.8	2.2
Xylene	4.2	3.3	1.7	2.2	3.0	9.0	2.1
Acetonitrile	3.9	3.4	1.1	3.0	3.0	1.3	2.8
Methylene chloride	3.5	3.1	2.5	2.9	2.4	3.4	2.5
2-Butanone	3.5	2.3	3.4	4.1	3.5	1.1	3.1
Chloroform	4.7	3.9	1.8	3.7	3.6	1.4	4.3
Benzene	4.3	3.0	1.6	2.3	3.0	1.0	3.3
Triethylamine	3.8	2.3	7.4	3.9	3.7	3.1	3.5
Trichloroethylene	2.9	2.7	4.8	2.4	3.3	1.9	2.3
1,4-Dioxane	3.8	2.3	1.2	2.4	3.6	1.0	2.0
Pyridine	2.9	3.0	1.2	3.9	3.4	3.1	2.6
Ethylene glycol	4.8	3.0	2.4	2.5	2.6	1.1	2.4
Carbon tetrachloride	3.6	3.2	1.9	5.5	3.2	4.3	3.5
DMF	3.0	3.4	5.0	4.8	2.6	4.8	2.8

^aF-values. F_{crit(4,4); α=0.05}=9.605.

3.4. Applications

The developed method was applied to residual solvents determination in several commercial samples of metronidazole benzoate and betamethasone-17 valerate raw material. In all cases, we analyzed not only the solvents stated by manufacturer to be used during the manufacturing process, but also the solvents that were calibrated. In the great majority, the analyzed samples met specifications containing solvents below allowable limits. However, there were cases in which the analyzed substances did not meet specifications. An example of each case is shown in Table 14, Table 15.

Table 14.

Concentration of analytes found in betamethasone-17 valerate raw material.

Analyte	Class	Concentration (µg/g)	Individual limit (µg/g)	Requested by the manufacturer
Chloroform	2	<LOD	60	Yes
Trichlorethylene	2	<LOD	80	Yes
Dioxane	2	390	380	Yes
DMF	2	<LOD	880	Yes
Ethyl acetate	3	<LOD	5000	Yes
Methanol	2	1850	3000	No
2-Propanol	3	2440	5000	No
Methylene chloride	2	57	600	No
Benzene	1	12	2	No

Table 15.

Concentration of analytes found in metronidazole benzoate raw material.

Analyte	Class	Concentration (µg/g)	Individual limit (µg/g)	Requested by the manufacturer
Toluene	2	<LOD	890	Yes
Acetone	3	<LOD	5000	Yes
Ethylene glycol	2	<LOD	620	Yes
Methanol	2	2270	3000	Yes
2-Propanol	3	<LOD	5000	Yes
Methylene chloride	2	<LOD	600	Yes
Pyridine	2	307	200	No
Chloroform	2	364	60	No
Dioxane	2	1450	380	No
Ethyl acetate	3	188	5000	No

As it can be seen, through the developed method, it was possible to determine the solvents required by the manufacturer and to identify and quantify other solvents that were not requested by the manufacturer, and exceeded the permitted limits, such as benzene in betamethasone-17 valerate and chloroform, dioxane and pyridine in metronidazole benzoate [4]. Several solvents are used in traditional betamethasone synthesis procedures, such as methanol, chloroform, tetrahydrofuran, dioxane and pyridine. Later, valerate is made from betamethasone and methyl ortovalerate as starting materials, using benzene as solvent [27]. Regarding metronidazole, dioxane is commonly used as a dehydrogenating agent in order to produce the precursors nitroimidazole drugs, in an efficient and economical manner [28]. Chloroform and ethyl acetate are used as extractant and recristalization solvents in the synthesis of metronidazole starting from nitroimidazole [27]. Finally, in the combination of benzoyl chloride and metronidazole to obtain the benzoate form of metronidazole, pyridine is usually employed as a deacid reagent to promote the reaction [29]. These solvents are typically removed by evaporation under vacuum, but it is clear that their removal from the raw material is sometimes inadequate. In Fig. 5A and B the chromatograms obtained from the analysis of these raw materials are shown.

Fig. 5.

Chromatograms corresponding to samples: (A) betamethasone-17 valerate raw material (IS: acetone and hexane) and (B) metronidazole benzoate raw material (IS: benzene and trichloroethylene).

4. Conclusions

A systematic analytical approach for identification and quantification of VOCs: methanol, ethanol, ethyl ether, acetone, 2-propanol, acetonitrile, methylene chloride, hexane, isopropyl ether, ethyl acetate, 2-butanone, chloroform, tetrahydrofuran, cyclohexane, benzene, heptane, isooctane, triethylamine, 1-butanol, trichloroethylene, 1,4-dioxane, propyl acetate, pyridine, toluene, ethylene glycol, carbon tetrachloride, DMF, m-xylene, p-xylene, o-xylene and DMSO in raw material is described in this article. A simple general method utilizing static headspace capillary gas chromatography coupled with FID was developed and provided an effective means for rapid screening of VOCs. The use of chemometric tools such as the experimental design and the multiple response optimizations showed to be of great help to achieve a fast and efficient optimization of the chromatographic conditions.

A systematic study of VOCs in raw materials from various sources is beyond the scope of this work. However, it is expected that the presence and amount of VOCs in commercial materials will vary from manufacturer to manufacturer and a comprehensive study using the presented methodology should be guaranteed.