Optimization of wavelength range and data interval in chemometric analysis of complex pharmaceutical mixtures

Abstract

The performance of different chemometric approaches was evaluated in the spectrophotometric determination of pharmaceutical mixtures characterized by having the amount of components with a very high ratio. Principal component regression (PCR), partial least squares with one dependent variable (PLS1) or multi-dependent variables (PLS2), and multivariate curve resolution (MCR) were applied to the spectral data of a ternary mixture containing paracetamol, sodium ascorbate and chlorpheniramine (150:140:1, m/m/m), and a quaternary mixture containing paracetamol, caffeine, phenylephrine and chlorpheniramine (125:6. 25:1.25:1, m/m/m/m). The UV spectra of the calibration samples in the range of 200–320 nm were pre-treated by removing noise and useless data, and the wavelength regions having the most useful analytical information were selected using the regression coefficients calculated in the multivariate modeling. All the defined chemometric models were validated on external sample sets and then applied to commercial pharmaceutical formulations. Different data intervals, fixed at 0.5, 1.0, and 2.0 point/nm, were tested to optimize the prediction ability of the models. The best results were obtained using the PLS1calibration models and the quantification of the species of a lower amount was significantly improved by adopting 0.5 data interval, which showed accuracy between 94.24% and 107.76%.

1. Introduction

Spectrophotometric analytical techniques are widely used in the pharmaceuticals and food quality controls during the batch production or stability controls. This choice is justified by the simplicity of sample preparation and execution as well as by the short analysis time and relatively lower cost than other analytical techniques [1], [2]. However, the techniques based on ordinary spectrophotometry are affected by low resolution and are often unsatisfactory in the analysis of complex mixtures [3], [4], [5], [6]. Several pharmaceuticals are multicomponent mixtures and often are difficult to be analyzed because of overlapping signals or the presence of components in much lower concentration than the others. In recent years, the advent of computerized instrumentation coupled to multivariate analysis techniques has allowed to increase the potential of the spectrophotometric analysis with the ability to simultaneously process a large number of spectral data recorded in turn by a high number of samples [7], [8]. Analysis of complex pharmaceutical mixtures by applying different chemometric procedures on spectral data has been reported in many papers [9], [10], [11], [12], [13]. Multivariate curve resolution-alternating least squares (MCR–ALS) has been applied to the study of complex mixtures to resolve different components in pharmaceutical formulation [14], [15], [16], [17], [18], [19].

In building a calibration sample set, an appropriate design of experiments (DOE) can affect the prediction ability of the multivariate models. In the present work, a simple latex design (SLD) distributed on five concentration levels was applied in order to select sets of reference mixtures covering the entire experimental domain corresponding to the content of the commercial pharmaceutical specialties [8]. Moreover, in the chemometric treatment of complex data sets, it is usually preferable to reduce the data in order to select those that carry useful analytical information and at the same time minimize those that carry redundant or useless information. In many cases, the choice of the most useful data influences the predictive ability of the multivariate models and this procedure can be very useful in the determination of the components at very low concentration that are often hidden by the more concentrated components [8].

In the first step of a multivariate regression method, principal component analysis (PCA) identifies orthogonal directions of maximum variance of the original data, and places the data in a space of lower dimensionality made from the components that have the highest variance. PCA combines the original variables into a smaller number of orthogonal variables called principal components (PCs). The first PCs are considered in the modeling because of containing the most useful information, whereas the last ones can be discarded [20], [21], [22], [23].

The principal component regression (PCR), partial least square 1 (PLS1), partial lest squares 2 (PLS2) and multivariate component analysis (MCR) models were applied to two pharmaceutical formulations, the first one containing three active pharmaceutical ingredients (APIs) and the other four APIs, which are very difficult to be analyzed by means of conventional spectrophotometric methods for the presence of some components in quantities much lower than the others. The increase in the predictive power of the models was studied by varying the instrumental parameter “data interval” between 0.5 and 2 nm in the recording of the spectra used in calibration.

The ternary formulation consisted of paracetamol (PAR), sodium ascorbate (ASC) and chlorpheniramine maleate (CHL), with a ratio of 150:140:1 (m/m/m). The quaternary mixture contained paracetamol (PAR), caffeine (CAF), phenylephrine hydrochloride (PHE) and chlorpheniramine maleate (CHL) with a ratio of 125:6.25:1.25:1 (m/m/m/m). Both mixtures are commonly used as analgesics and antipyretic specialties.

The analytical performance of the applied algorithms was tested on the data matrices from synthetic mixtures and commercial pharmaceutical preparations.

2. Materials and methods

2.1. Chemicals

The active pharmaceutical ingredients ASC (98%), CAF (99%), CHL (99%), PAR (100%), and PHE (98%) were purchased from Sigma-Aldrich (Milan, Italy) and used as received. The pharmaceutical specialties Dequa-Flu^® (Aspen Pharmacare SpA) and Zerinolflu^® (Boehringer Ingelheim SpA) were obtained commercially. Pure water and ethanol were of instrumental purity grade (J. T. Baker, Holland). All other reagents were of the highest purity commercially available.

2.2. Instruments

Absorption spectra were recorded on a Perkin-Elmer Lambda 40P spectrophotometer under the following conditions: quartz cell 10 mm; wavelength range 200–350 nm; scan rate 1 nm/s; time response 1 s; spectral band 1 nm; data density 0.5, 1.0 and 2.0 point/nm. Spectral acquisition and elaboration were performed by the software package UV Winlab 2.79.01 (Perkin-Elmer). Application of PCR and PLS algorithms was supported by the software package ‘The Unscrambler X 10.3’ (Camo Process As., Oslo, Norway). MCR-ALS routines were performed under Matlab computer environment and implemented as MATLAB functions. They were used as described in previous works [24], [25]. Source files containing these algorithms are available on the website “www.mcrals.info”.

2.3. Standard solutions

Stock solutions of the single compounds were prepared in ethanol by dissolving nearly 20.0 mg of each drug in 100 mL calibrated flasks. A calibration set of 18 ternary mixtures was prepared with PAR concentration in the range of 5.05–30.3 mg/L, ASC in the range of 2.04–30.60 mg/L and CHL in the range of 0.20–5.05 mg/L. A second calibration set of 38 quaternary solutions was prepared with the drugs in the following concentration ranges: PAR 5.10–30.60 mg/L, CAF 0.50–5.00 mg/L, CHL 0.20–2.01 mg/L, and PHE 0.21–2.10 mg/L.

The calibration mixtures were prepared by adopting an SLD distributed on five concentration levels. Two further independent validation sets, comprising 15 ternary mixtures and 15 quaternary mixtures, respectively, were then prepared to validate the calibration models. Statistical analysis was performed on data from analysis of three replicates for sample.

2.4. Pharmaceutical samples

Five tablets for each pharmaceutical specialty were reduced to fine powder and suspended in 100 mL of ethanol. The suspension was sonicated for 10 min and then filtered through a 45 μm membrane filter. Samples for analysis were obtained after proper dilution with ethanol.

3. Chemometric elaboration

PCR and PLS are known as factor analysis methods. In the first step of calibration, concentrations and analytical signals from reference samples are used to build a mathematical model. In the following prediction step, this model is used to evaluate the concentration of an unknown sample.

PCR considers all spectral data simultaneously (X variables) and correlates the concentration components (Y variables) with these data in the second phase of multiple regression. On the other hand, PLS modeling processes information from both spectral and concentration data (X and Y) and projects information in the new space of principal components.

In applying multivariate calibration to spectrophotometry, X variables or descriptors are represented by the absorptivity values of the samples at various wavelength values, whereas the Y variables or responses consisted of concentration values. In building multivariate models, PCs have to reach the optimal number because the prediction error decreases with them until they reach an optimal value. The most known validation procedure is full-cross validation, in which one reference is removed from the calibration set at a time and the same sample is predicted by using the calibration built with the remaining references. The number of PCs was chosen by adopting the root mean square error of cross validation (RMSECV), which estimates the error when unknown samples are predicted with the calibration model. The best prediction ability of the models corresponds to the lowest RMSECV.

$$\mathit{RMSECV}=\sqrt{\frac{{\sum }_{i=1}^n{\left(\widehat{c}-c_i\right)}^2}{n}}$$ (1)

where ĉ is the predicted value for the references; c_i is the real value for the references; and n is the number of references.

External validation was performed by adopting the parameter mean square error of prediction (RMSEP) and relative error (RE) in prediction:

RMSEP=RMSECV calculated for external samples

$$\mathit{RE}(\%)=100\sqrt{\frac{{\sum }_{i=1}^n(c_i-{\widehat{c}}_i)}{{\sum }_{i=1}^n{c}_i^2}}$$ (2)

MCR–ALS provides the decomposition of the experimental data matrix describing the chemical system into the contributions of the single species as a bilinear relation between the concentrations and the pure spectra, following the generalized law of Lambert–Beer in multi-sample and multivariable version [11], [12]. In matrix form, the bilinear model is expressed in the following way:

$$\mathbf{D}=\mathbf{C}{\mathbf{S}}^{\mathrm{T}}+\mathbf{E}$$ (3)

where D is the matrix of experimental data; C is the matrix of concentrations values of the different n species present in the samples; S^T is the spectra matrix; and E is the matrix associated to the error. MCR–ALS algorithm is run by applying an iterative optimization procedure under a suitable set of constraints until estimation of C and S^T matrices is given. This iteration procedure is stopped when convergence is achieved by fixing a preselected number of cycles or when the value of lack of fit (LOF) does not change significantly between consecutive iterations:

$$\%\mathrm{LOF}=100\times \sqrt{\frac{{\sum }_{ij}{(d_{ij}-d_{ij}^{*})}^2}{{\sum }_{ij}{d}_{ij}^2}}$$ (4)

where d_ij and $d_{ij}^{*}$ are respectively the experimental and calculated (by MCR–ALS) absorbance values. Another parameter used to indicate the quality of MCR–ALS modeling results is the percentage of explained variance (r²):

$$r^2=100\times \frac{{\sum }_{ij}{d}_{ij}^{2*}}{{\sum }_{ij}{d}_{ij}^2}$$ (5)

4. Results and discussion

4.1. Spectrophotometric analysis and construction of the models

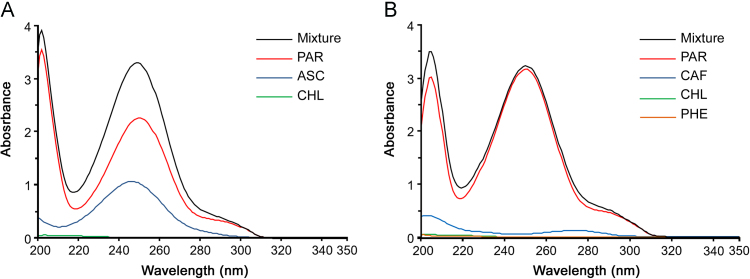
Absorption spectra for each calibration set were recorded in the range of 200–350 nm by fixing the value of data density at 1.0 point/nm. Fig. 1 shows the UV spectra of the single components and their mixtures for both ternary and quaternary studied pharmaceutical formulations. The mixtures contained the drugs with the same ratio of the commercial specialties.

Fig. 1.

Full absorption spectra (data interval 1.0 point/nm) of the single components and their cumulative spectra. Ternary mixtures (A): PAR 25.25 μg/mL, ASC 23.46 μg/mL, CHL 0.20 μg/mL. Quaternary mixtures (B): PAR 30.60 μg/mL, CAF 1.52 μg/mL, PHE 0.30 μg/mL, CHL 0.25 μg/mL.

The determination of CHL in both formulations and PHE in the quaternary formulation showed particular complexity because their concentrations were very low compared to the concentrations of the other components. The conventional spectrophotometric methods appear difficulties in application as they use only a limited number of wavelengths. In both mixtures, the spectra of the individual compounds overlapped along the full spectral range and no signal proportional to the components was singled out. In contrast, the multivariate calibration methods, which simultaneously use all the spectral data or at least a large number, seemed more suitable for resolving these mixtures.

The wavelengths below 210 nm and over 320 nm were discarded. The first ones are usually affected by high variability that can make the model unstable; the others were useless for the absence of signals due to the components. The 220–320 nm spectral data were used to build the data matrices for the ternary and quaternary samples, respectively. In the matrix of descriptors (X), each reference was described by n variables, corresponding to the absorbance values for all wavelengths; in the matrix of response variables (Y), the samples were described by the concentrations of the drugs.

The algorithms, namely, PCR, PLS1, PLS2 and MCR, were applied to these data matrices and the models carried out were validated by full-cross validation. RMSECVs were re-calculated when a new PC was added to the models every time. Table 1 summarizes the optimal PCs and the corresponding statistical parameters.

Table 1.

Statistical parameters from full-cross validation of all the chemometric models for ternary and quaternary mixtures in the range of 210–320 nm, data interval of 1 nm.

Model	Analyte	PCs	RMSECV	RE (%)	r2	Slope	Offset
PCR	PAR	3	0.1842	1.17	0.9998	0.9988	0.0012
	ASC	3	0.1953	6.43	0.9971	0.9752	0.0313
	CHL	4	0.3488	56.30	0.7416	0.6458	0.0700
	PAR	4	0.0733	0.7987	0.9999	0.9999	−0.0031
	CAF	4	0.1036	9.7120	0.9933	0.9623	0.0201
	CHL	5	0.1602	32.1449	0.9207	0.8437	0.0371
	PHE	5	0.2733	54.8336	0.7490	0.6105	0.0974
PLS1	PAR	3	0.4823	3.08	0.9988	1.0086	−0.1246
	ASC	3	0.2233	7.36	0.9961	0.9802	0.0391
	CHL	4	0.0551	13.32	0.9853	0.9939	−0.0035
	PAR	4	0.0733	0.7980	0.9999	0.9980	0.0169
	CAF	4	0.1078	10.1029	0.9927	0.9612	0.0224
	CHL	5	0.1621	26.5193	0.9187	0.8467	0.0371
	PHE	5	0.1130	25.7415	0.9173	0.7854	0.0453
PLS2	PAR	3	0.7184	4.5819	0.9971	0.9877	0.1237
	ASC	3	0.4330	14.2579	0.9857	0.9330	0.1174
	CHL	4	0.4506	72.7338	0.6012	0.5966	0.0961
	PAR	4	0.0738	0.8039	0.9999	1.0000	−0.0033
	CAF	4	0.1078	10.1029	0.9927	0.9612	0.0224
	CHL	5	0.1671	33.5223	0.9135	0.8264	0.0398
	PHE	5	0.1694	33.9903	0.9125	0.8792	0.0452

RMSECV values could be considered satisfactory for most of the components and all the models. In contrast, the values of r² and RE(%) were significantly worse than those of the other components, for CHL in the ternary mixture and for both CHL and PHE in the quaternary mixture. The bad results for CHL and PHE could be surely imputed to the relative low content of these drugs in the respective mixtures. The number of PCs also showed the highest values for CHL and PHE. As regards to the MCR method, the percentage value of LOF resulted in 7.92 and 42.21 for the ternary and quaternary mixtures, and r² was 0.9128 and 0.8521, respectively.

However, the statistics indicated a preliminary substantial equivalence between the multivariate techniques tested and none of them showed a higher sensitivity than the others.

4.2. Analysis of prediction sets

The prediction ability of the models built was tested on a series of ternary and quaternary synthetic mixtures. Two prediction sets of 15 samples, containing the drugs in the same concentration ranges used in the calibration sets, were randomly prepared. The calibration models defined above were applied to the prediction samples and the accuracy and precision results were compared in terms of percentage recovery and standard deviation. The results of PAR and ASC quantification by all the chemometric methods were good, showing recovery within the range of 97.14%–103.27% and cumulative standard deviation under 2.65. The high absorbance values of these drugs were surely essential in the success of their determination. Determination of CAF, in the quaternary mixtures, gave good results too, despite of its relative low concentration (recovery 96.78%–102.58%; SD≤3.10).

In contrast, less good results in terms of recovery (83.42%–129.42%) and SD (≤15.37) of CHL and PHE were confirmed also in this prediction step. An optimization procedure in the processing of data was necessary to increase the prediction power of the models for these drugs.

4.3. Optimization of the models

Two approaches were tried to optimize the models in order to emphasize the spectral characteristics of the individual components. The number of data interval was varied to provide a smaller or greater number of data in the processing of algorithmic patterns, and a recent procedure to select the wavelength regions containing the most useful information for the single components was applied.

Two additional series of spectra of the calibration samples were recorded by fixing the data interval at 0.5 and 2.0 nm, respectively. The number of spectral data for each sample in the new matrices thus passed from 120 to 240 and 60. The wavelength selection was performed by a mathematical procedure recently proposed [8], using the absolute values of the component regression coefficients. In a regression algorithm, the concentration of each component is correlated with all the wavelengths through the following equation:

$$C_i=b_o+b_1{\lambda }_1+b_2{\lambda }_2+\dots +b_n{\lambda }_n$$ (6)

where C_i is the component concentration (analytical response), λ the wavelengths (predictors), and b the regression coefficients. b values higher than 0.2 indicated wavelengths rich in useful information, while values below 0.1 indicated a negligible contribution [26]. Along the full range of wavelengths, the absolute values of b for each component were summed up to give a new parameter B, called cumulative coefficient:

$$B_{\lambda j}=\sum _{i=1}^n\left|b_i\right|$$ (7)

After that, the average value of B of all components ($\overline{B}$) was adopted as a cutoff value and the wavelengths presenting values of B over the cutoff line were selected to build the new model [8].

$$\overline{B}=\frac{1}{n}\sum _{j=1}^n{B}_j$$ (8)

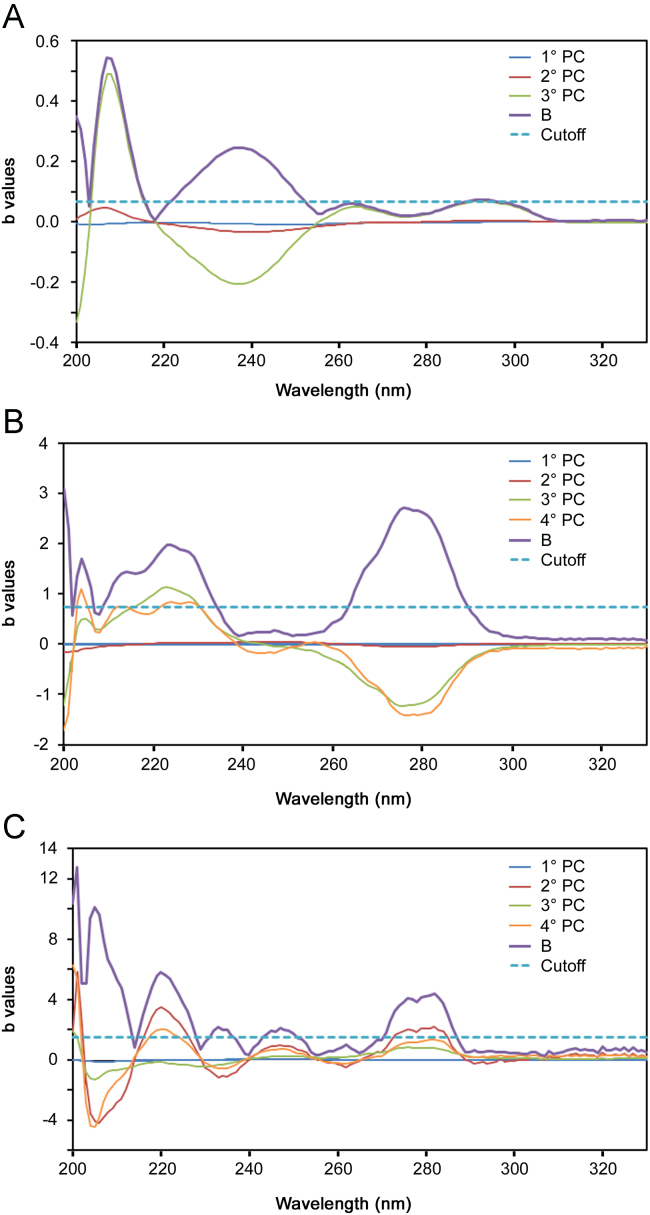
The spectral regions selected by this procedure were used for the determination of PHE in the quaternary mixture and CHL in both mixtures. Fig. 2 shows the distribution of the regression coefficients in the range of 210–320 nm for CHL in the ternary mixture (A) and quaternary mixture (B) and for PHE in the quaternary mixture (C). The wavelength ranges, selected by the procedure regression coefficient which produced a better prediction of CHL in the ternary mixtures without significantly affecting the prediction of the other components, were 222–252 nm and 289–296 nm. For the analysis of the quaternary mixtures, the results improved significantly for both CHL and PHE by selecting the ranges of 211–250 nm and 264–290 nm.

Fig. 2.

Distribution of regression coefficients for CHL in the ternary mixture (A), CHL in the quaternary mixture (B) and PHE in the quaternary mixture (C). The curve of the cumulative coefficients B and the cutoff lines are also plotted.

The regression models were re-built by adopting the selected spectral data of the samples recorded at the various data intervals (0.5–1.0–2.0 nm). There was a significant decrease of PCs in these new models, and especially in the models using a data interval of 0.5 nm. Both values of RMSECV and r² were improved, demonstrating such an increase in useful information from the adjustment of this instrumental parameter. The new models were applied to assay the samples of the prediction sets, giving the results summarized in Table 2.

Table 2.

Statistical parameters from external validation of the models for ternary and quaternary mixtures by adopting optimized wavelength ranges and 0.5 data interval.

Model	Analyte	PCs	RMSEP	RE (%)	r2	Slope	Offset
PCR	PAR	3	0.7268	4.6353	0.9971	0.9871	0.1345
	ASC	3	0.2414	3.2432	0.9961	0.9581	0.0154
	CHL	3	0.0374	9.1643	0.9933	0.9881	0.0013
	PAR	4	0.0725	0.7894	0.9999	1.0000	−0.0012
	CAF	4	0.1028	5.6284	0.9934	0.9826	0.0194
	CHL	4	0.1036	20.7917	0.9876	0.9505	0.0140
	PHE	4	0.1154	23.1650	0.9701	0.9397	0.0182
PLS1	PAR	3	0.3707	2.3643	0.9992	0.9969	−0.0032
	ASC	3	0.0907	2.9851	0.9994	0.9899	−0.0015
	CHL	3	0.0136	3.2816	0.9991	0.9937	0.0017
	PAR	4	0.1942	2.1152	0.9996	0.9982	0.0023
	CAF	4	0.0894	3.3802	0.9951	0.9752	0.0195
	CHL	4	0.0589	4.8168	0.9897	0.9716	0.0026
	PHE	4	0.0636	3.6352	0.9913	0.9885	−0.0019
PLS2	PAR	3	0.7017	3.4754	0.9983	0.9944	−0.0178
	ASC	3	0.0894	2.9423	0.9994	0.9962	−0.0012
	CHL	3	0.0360	5.7047	0.9936	0.9914	0.0024
	PAR	4	0.1707	1.8594	0.9997	0.9982	0.0007
	CAF	4	0.1721	6.1228	0.9907	0.9817	0.0328
	CHL	4	0.0739	5.8295	0.9840	0.9720	0.0132
	PHE	4	0.0667	5.3928	0.9969	0.9869	−0.0015
MCR	PAR	3	0.6921	4.4141	0.9974	0.9940	−0.0120
	ASC	3	0.0844	3.7808	0.9984	0.9962	−0.0013
	CHL	3	0.0145	5.5077	0.9990	0.9928	0.0025
	PAR	4	0.1598	1.7400	0.9998	0.9989	−0.0076
	CAF	4	0.1007	6.4332	0.9976	0.9655	0.0179
	CHL	4	0.0607	8.1726	0.9921	0.9903	0.0029
	PHE	4	0.0372	7.4667	0.9960	1.0021	−0.0070

The good values of RMSEP and r², already reached for PAR, ASC and CAF, were confirmed and further improved, especially for CAF. Recovery values were in the range of 96.21%–105.86% and precision was calculated within 3.14%–3.75% with no significant differences between the various models.

The dosage of CHL and PHE was greatly improved after optimization, giving values of RMSEP significantly lower than previous ones. PLS1 proved the method mostly benefiting from the selection of spectral regions and data interval. Recovery was between 94.53% and 106.92% and SD not above 3, representing a remarkable achievement considering the difficulties inherent to the two analytical systems in the dosage of these components.

4.4. Analysis of commercial formulations

Commercial pharmaceutical specialties containing the studied drugs were analyzed by using the final chemometric models. The assay results are summarized in Table 3. The experimental results coincided with the values reported on the label of the formulations.

Table 3.

Recovery (%) (±RSD) from application of optimized PCR, PLS and MCR–ALS models on the pharmaceutical formulations.

	Zerinolflu®			Dequa-Flu®
Model	PAR	ASC	CHL	PAR	CAF	PHE	CHL
PCR	97.01±3.25	99.04±4.99	101.00±2.21	103.07±2.74	104.64±4.77	96.80±6.25	96.00±5.28
PLS1	107.37±2.23	98.95±3.25	106.93±5.32	101.96±2.01	98.32±3.25	105.79±5.57	111.46±6.21
PLS2	100.06±3.60	101.06±3.11	90.74±4.25	94.29±3.25	102.02±5.21	94.53±7.25	92.52±8.96
MCR-ALS	98.87±2.57	101.38±5.25	106.12±7.25	98.93±4.35	96.19±6.34	111.57±8.22	102.02±9.57

Recovery values for PAR, ASC and CAF were in the range 94.29% – 107.37% and precision was calculated within 2.01% – 6.34% for all the methods. For the assay of CHL and PHE, application of the PLS1 models gave recovery between 105.79% and 111.46% and SD below 6.21.

5. Conclusion

A comparative study on the application of the most known chemometric techniques to the spectral data of complex pharmaceutical formulations was performed. The PCR, PLS1, PLS2 and MCR algorithms were applied to assay ternary and quaternary mixtures of drugs characterized by a very high ratio in their content. Elaboration of the models was stressed by varying the value of the instrumental data interval and selecting the most useful wavelengths by means of a procedure based on the regression coefficients. The selection of the analytical information brought a significant advantage to the predictive power of all models. However, the best assay results were obtained from the application of PLS1 models to both the data matrices built with the spectra at 0.5 nm⁻¹ data point. The satisfactory results showed significant contribution of the parameter data interval in improving the construction of multivariate models. Similarly, a suitable selection of the spectral regions characteristics can greatly contribute to the determination of the components that have low or superimposed absorbance than that of other components.