Stability and anisotropy of (Fe_xNi_1−x)₂O under high pressure and implications in Earth’s and super-Earths’ core

Abstract

Oxygen is thought to be an important light element in Earth’s core but the amount of oxygen in Earth’s core remains elusive. In addition, iron-rich iron oxides are of great interest and significance in the field of geoscience and condensed matter physics. Here, static calculations based on density functional theory demonstrate that I4/mmm-Fe₂O is dynamically and mechanically stable and becomes energetically favorable with respect to the assemblage of hcp-Fe and $R\overline{3}m$-FeO above 270 GPa, which indicates that I4/mmm-Fe₂O can be a strong candidate phase for stable iron-rich iron oxides at high pressure, perhaps even at high temperature. The elasticity and anisotropy of I4/mmm-(Fe_xNi_1−x)₂O at high pressures are also determined. Based on these results, we have derived the upper limit of oxygen to be 4.3 wt% in Earth’s lower outer core. On the other hand, I4/mmm-(Fe_xNi_1−x)₂O with high AV _S is likely to exist in a super-Earth’s or an ocean planet’s solid core causing the locally seismic heterogeneity. Our results not only give some clues to explore and synthesize novel iron-rich iron oxides but also shed light on the fundamental information of oxygen in the planetary core.

Introduction

Earth’s core is widely accepted to be dominantly composed of iron-nickel alloys. Light elements, which are cosmically abundant and soluble in iron at high pressures such as H, C, O, Si, S and P, are required to explain the 8~10% and 4~5% density deficit of Earth’s outer and inner core from pure iron, respectively^1–3. Additionally, the positive density jump from Earth’s liquid outer core to the solid inner core at the inner-outer core boundary (ICB) is too large to be explained by the solidification across the ICB alone⁴. Therefore, both suggest that there should be more light elements in Earth’s liquid outer core.

Oxygen is thought to be an important candidate for compensating the density deficit of Earth’s core. Previous ab initio calculations and models have shown that oxygen strongly partitions into Earth’s liquid outer core from the solid inner core^5,6. Therefore, much attention has been paid to explore oxygen in the outer core. For example, shockwave data in the Fe-S-O system demonstrated that adding oxygen into the liquid iron could not match the density and velocity profiles of the outer core simultaneously and indicated an oxygen-depleted outer core⁷. In contrast, ab initio molecular dynamic calculations found no oxygen-free iron alloy that fitted the seismological observations well⁸. This finding leads to the conclusion that oxygen is required as a major light element in Earth’s outer core and the best fitting result is 3.7 wt% O and 1.9 wt% Si without S or C in iron-nickel alloys⁸. Recent melting experiments have shown that O and Si could not exist at high concentrations simultaneously under outer core conditions and that SiO₂ saturation sets limits on O and Si concentrations in Earth’s outer core⁹. These different results indicate that the amount of oxygen in the outer core remains elusive. On the other hand, investigations into the Fe-FeO system at high pressures give direct clues to determine the temperature at ICB and provide an alternative method to estimate the amount of oxygen in the outer core^10–12. Melting experiments showed that the Fe-FeO system remains eutectic to at least 93 GPa¹⁰. However, the end member, FeO undergoes a series of transitions under higher pressure and temperature conditions, which will affect the phase relation of the Fe-FeO system^13–16. This raises the question as to whether the Fe-FeO system keeps eutectic under core conditions.

In addition to oxygen-bearing iron alloys in Earth’s core, iron oxides have a widespread occurrence in Earth’s crust and mantle, which have a significant influence on the oxidation state and the phase balance of Earth’s interior. Therefore, extensive experiments have been conducted at relevant P-T conditions of Earth’s interior to investigate structural and physical properties of iron oxides^13,16–21. In particular, recent studies have successfully synthesized a series of iron oxides with new stoichiometries at high P-T conditions such as Fe₄O₅, Fe₅O₆, Fe₅O₇, Fe₇O₉ and FeO₂ ^21–26. These findings have revealed a complex phase diagram of the Fe-O system at extreme conditions and indicated different scenarios in Earth’s interior. For example, Fe₄O₅ and Fe₅O₆ as well as those well-known iron oxides are stable and some of them are likely to coexist from 10 GPa to 20 GPa resulting in a complicated oxygen buffer in Earth’s transition zone^23,27,28. However, it is obvious that these newly synthesized compounds are all oxygen-rich iron oxides with Fe/O < 1. Heretofore, investigations into iron-rich iron oxides with Fe/O > 1 are rare. Although some theoretical studies have been performed to explore iron-rich iron oxides under high pressure^29–32, their structural and physical properties as well as thermodynamic stability with respect to other components in the Fe-O system are poorly understood.

Here we investigate the stability, elastic and seismic properties of (Fe_xNi_1−x)₂O under high pressure by first-principle calculations based on density functional theory (DFT). According to present results and previous data, we further discuss the existence of (Fe_xNi_1−x)₂O and its potential effect on geochemical and geophysical processes in Earth’s and a super-Earth’s interior.

Results

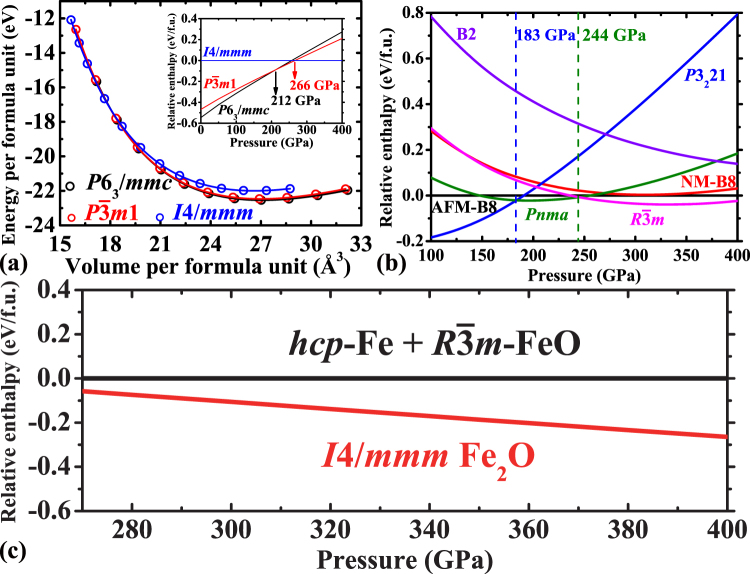
The static calculation results of Fe₂O are displayed in Fig. 1(a) and the corresponding Equation of State (EoS) parameters are listed in Table S1. This figure illustrates that Fe₂O undergoes structural transitions from P6₃/mmc to $P\overline{3}m1$ at 212 GPa and further to I4/mmm at 266 GPa, consistent with previous simulations³². The later transition is accompanied by an increase of the coordination number of oxygen from six to eight. To investigate the dynamic stability of the I4/mmm-type Fe₂O, ab initio lattice-dynamics calculations are performed [see Supplementary Fig. S2]. The phonon spectrum without any imaginary frequency implies that the I4/mmm structure is dynamically stable at 320 GPa.

Figure 1.

(a) The total energy vs. volume for Fe₂O with P6₃/mmc (black circles), $P\stackrel{\circledR }{3}m1$ (red circles) and I4/mmm (blue circles). The inset refers to calculated enthalpy differences as a function of pressure among the aforementioned structures. (b) Calculated enthalpy differences as a function of pressure for FeO with antiferromagnetic-B8 (black line), nonmagnetic-B8 (red line), P3₂21 (blue line), Pnma (olive line), $R\stackrel{\circledR }{3}m$ (pink line) and B2 (purple line). (c) Calculated relative enthalpy of I4/mmm-Fe₂O as a function of pressure compared with the assemblage of hcp-Fe and $R\stackrel{\circledR }{3}m$-FeO.

In order to evaluate the relative stability of Fe₂O versus FeO at pressures corresponding to Earth’s core, the following chemical reaction is considered in the present study:

$$\mathrm{FeO}+\mathrm{Fe}\to \mathrm{Fe2O}$$ 1

For FeO five candidate structures (P6₃/mmc (B8), (B2), P3₂21, Pnma and $R\overline{3}m$) are considered above 100 GPa in our simulations [see Supplementary Table S1]. Our simulations predict phase transitions form P3₂21 to Pnma and further to $R\overline{3}m$ at 183 GPa and 244 GPa, respectively [Fig. 1(b)]. These results are inconsistent with previously experimental observations, where B8 is the most stable structure above 100 GPa at moderate temperatures and will transform into B2 above 240 GPa at high temperatures^{13–15,33,34}. However, our results are in good agreement with previous theoretical calculations³². The present calculations are performed at 0 K (static calculations) while previous experiments were conducted at high temperatures. In addition, the ideal chemical stoichiometric compound FeO is considered in our simulations but the non-stoichiometric Fe_1−xO was often used in experiments. For Fe the hcp structure is predicted to be stable at high pressures corresponding to Earth’s core compared with the fcc structure [see Supplementary Table S1]. Based on these parameters, we have calculated the relative enthalpy of I4/mmm-Fe₂O as a function of pressure compared with the assemblage of hcp-Fe and $R\overline{3}m$-FeO [Fig. 1(c)]. Figure 1(c) demonstrates that I4/mmm-Fe₂O becomes energetically favorable above ~270 GPa and is likely to be stable at least up to 400 GPa. Additionally, the enthalpy difference between I4/mmm-Fe₂O and the assemblage of hcp-Fe and $R\overline{3}m$ $-$FeO increases with increasing pressure indicating that I4/mmm-Fe₂O becomes more stable upon compression.

The compression of volumes as a function of pressure displayed in Fig. S3 illustrates a marginal volume change across the chemical reaction (1). The volume reduction of reaction (1) is about 1.45% at 260 GPa and increases with increasing pressure. Previous experiments have detected B2-FeO under ultra-high pressure and temperature conditions¹⁵ and therefore calculated results of the assemblage of hcp-Fe and B2-FeO are also included for comparison [see Supplementary Fig. S3]. Similarly, I4/mmm-Fe₂O has a smaller volume compared with that of hcp-Fe + B2-FeO. Though the volume reduction of reaction (1) is marginal, generally smaller than 1.60% up to 400 GPa, it may have important contributions to stabilize the I4/mmm-type Fe₂O at high pressures.

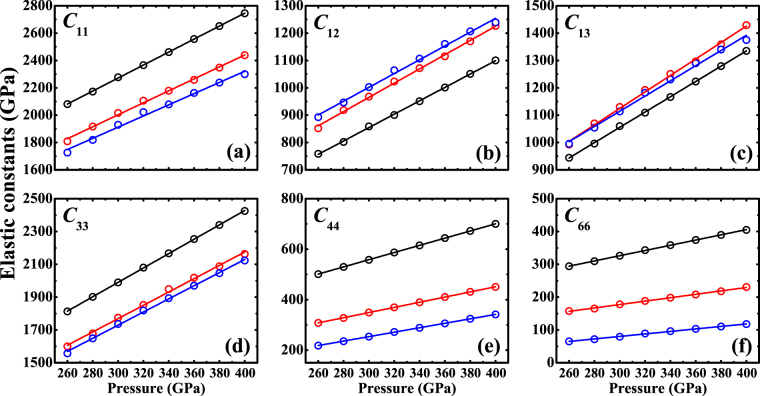
In order to evaluate the effect of Ni on elastic and seismic properties of Fe₂O at high pressures, the components Ni₂O and (Fe_0.5Ni_0.5)₂O are also included in present simulations [see Supplementary Fig. S1(b) and Table S1]. (It is worth mentioning that different arrangements of Ni in (Fe_0.5Ni_0.5)₂O were considered but they were unstable. When the atomic positions and unit-cell parameters were allowed to relax at each given volume, the I4/mmm structure would destroy.) The zero-pressure bulk modulus (K ₀) of (Fe_xNi_1−x)₂O decreases with the Ni content [see Supplementary Fig. S4]. The elastic constants of (Fe_xNi_1−x)₂O increase monotonically with pressure [Fig. 2 and see Supplementary Table S2]. These three components all present mechanically stable in the calculated pressure range supported by the Born-Huang criterion³⁵. The substitution of Ni for Fe in (Fe_xNi_1−x)₂O tends to significantly decrease C ₁₁, C ₃₃, C ₄₄ and C ₆₆ and increase C ₁₂ and C ₁₃. Figure 2 also reveals a moderate anisotropy in the axial incompressibility along a axis and c axis. The c axis is more compressible than a axis with C ₁₁ > C ₃₃ for (Fe_xNi_1−x)₂O.

Figure 2.

Calculated single-crystal elastic constants of I4/mmm-(Fe_xNi_1−x)₂O as a function of pressure. The black, red and blue open circles represent Fe₂O, (Fe_0.5Ni_0.5)₂O and Ni₂O, respectively. The black, red and blue lines are obtained by linear fitting.

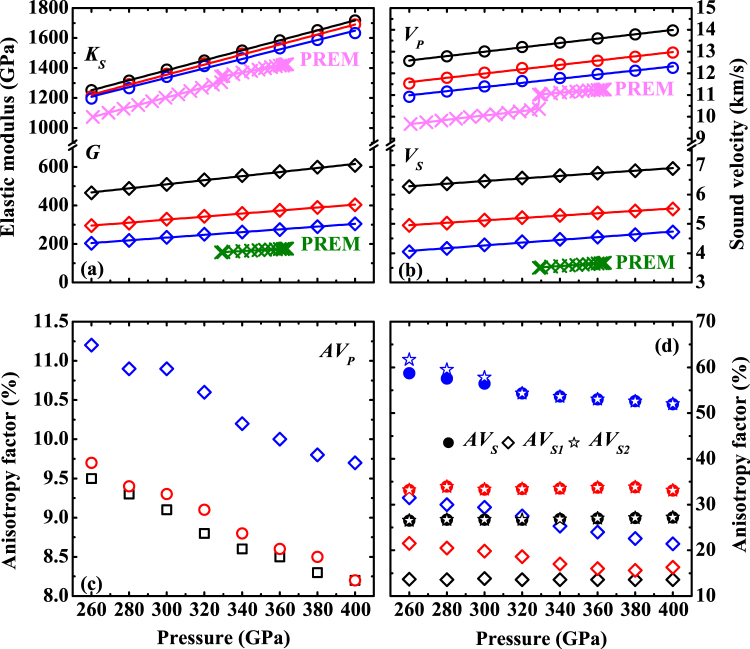
Using the aforementioned C _ij of (Fe_xNi_1−x)₂O, the adiabatic bulk and shear moduli (K _S and G) at high pressures are calculated according to the Voigt-Reuss-Hill averages³⁶ [Fig. 3(a) and see Supplementary Table S2]. The Ks and G of I4/mmm-(Fe_xNi_1−x)₂O increase monotonically with pressure and are all greater than PREM³⁷. The substitution of Ni in (Fe_xNi_1−x)₂O slightly affects the K _S but significantly reduces the G. Furthermore, the aggregate V _P and V _S of (Fe_xNi_1−x)₂O are obtained from their moduli and densities [Fig. 3(b) and see Supplementary Table S2]. In contrast to the moduli of (Fe_xNi_1−x)₂O, the substitution of Ni in (Fe_xNi_1−x)₂O largely reduces V _P and V _S because both of them are partially controlled by the G.

Figure 3.

(a) Bulk and shear moduli (K _S and G) and (b) aggregate velocities (V _P and V _S) of I4/mmm-(Fe_xNi_1−x)₂O as a function of pressure. (c) Variation of P wave anisotropies (AV _P) and (d) shear wave splitting factors (AV _S) and anisotropy factors of two polarized S waves (AV _S1 and AV _S2) for I4/mmm-(Fe_xNi_1−x)₂O at high pressures. The black, red and blue marks represent Fe₂O, (Fe_0.5Ni_0.5)₂O and Ni₂O, respectively. The lines in (a) and (b) are obtained by linear fitting. The elastic and seismic profiles of PREM (pink and olive crosses) (ref ³⁷) are plotted for comparison.

To understand the evolution of velocity anisotropies of the I4/mmm-type (Fe_xNi_1−x)₂O as a function of pressure, the percentage of velocity anisotropies and their distributions are calculated based on C _ij and density at each given pressure^38,39 [Fig. 3(c), (d) and see Supplementary Fig. S5, Table S2]. The AV _P of Fe₂O is 9.5% at 260 GPa and decreases to 8.2% at 400 GPa [Fig. 3(c) and see Supplementary Table S3]. The AV _P of (Fe_0.5Ni_0.5)₂O is similar to that of Fe₂O while the AV _P of Ni₂O is about 1.7% larger than that of Fe₂O at each pressure point. These results indicate that the small substitution of Ni for Fe will not change the AV _P of (Fe_xNi_1−x)₂O significantly in the calculated pressure range. At 320 GPa, the fastest P wave (13.82 km/s) propagates along a axis direction and the slowest P wave (12.65 km/s) distributes in the (110) plane in Fe₂O. The fastest and slowest P waves both reduce with the increasing amount of Ni in (Fe_xNi_1−x)₂O. It is worth mentioning that (Fe_xNi_1−x)₂O has a high AV _S, i.e., the AV _S are 26.5%, 33.2% and 58.7% for Fe₂O, (Fe_0.5Ni_0.5)₂O and Ni₂O at 260 GPa, respectively [Fig. 3(d)]. The high AV _S mainly results from the high anisotropy of V _S2, though AV _S1 is, in fact not small. The layered I4/mmm structure consists of OX₈ blocks (X: Fe or Ni) along c axis contributing to a high AV _S, which is similar to that of post-perovskite⁴⁰.

Discussion and Implications

Previous static simulations calculated the stability of $\mathit{Pm}\stackrel{\circledR }{3}m$-Fe₃O and $\mathit{Pm}\stackrel{\circledR }{3}m$-Fe₄O compared with the assemblage of hcp-Fe and B8-FeO under Earth’s core conditions²⁹. The results have shown that the chemical combination of Fe and FeO into Fe₃O or Fe₄O is energetically unfavorable under Earth’s core pressures. Additionally, the enthalpy difference increases with pressure indicating the large instability of Fe₃O or Fe₄O even at higher pressures. A BiI₃-like triclinic Fe₃O was later found to possess much lower enthalpy than that of Fe₃O with previously predicted structures³⁰. But the enthalpy of this new phase was still over 1 eV higher than that of the assemblage of hcp-Fe and B8-FeO. The present results demonstrate that the I4/mmm-type Fe₂O is energetically favorable than the hcp-Fe + $R\stackrel{\circledR }{3}m$-FeO assemblage. And the $R\stackrel{\circledR }{3}m$-FeO is more stable than B8-FeO based on our simulations. Thus, the I4/mmm-type Fe₂O will be much more stable than the triclinic Fe₃O at 0 K. Recent static calculations investigated the stability of $P\stackrel{\circledR }{6}m2$-Fe₃O and P4/nmm-Fe₃O at 350 GPa and 500 GPa, respectively by ab initio random structure searching³². These structures are still unstable with respect to the dissociation, though they are very close to the convex hull. Furthermore, the $P\stackrel{\circledR }{6}m2$ structure of Fe₃O is found to be a mixture of phases consisting of Fe and Fe₂O and the P4/nmm structure is found to consist of Fe, Fe₂O and FeO. Therefore, combining previous data with our results, we propose that it is unlikely to form Fe₃O or Fe₄O by the chemical combination of Fe and Fe₂O under Earth’s core pressures. Our static calculations indicate that the I4/mmm-type Fe₂O is a stable phase in iron-rich iron oxides at 0 K.

The present static calculations have shown that the I4/mmm-type Fe₂O is dynamically stable and has the smaller enthalpy and volume than those of the assemblage of Fe and FeO at high pressures, which all favor the formation of Fe₂O by the combination of Fe and FeO. However, our high-pressure simulations are limited at 0 K in contrast to the high P-T conditions of Earth’s core. As shown in Fig. 1(c), the enthalpy difference between the I4/mmm-type Fe₂O and the Fe + FeO assemblage at high pressure of the ICB is of the order of 0.15 eV corresponding to ~1750 K. In terms of B2-FeO, which has been experimentally confirmed at high P-T conditions, the enthalpy difference is of the order of 0.35 eV (~4100 K). Thus it is likely that the I4/mmm-type Fe₂O can be stable at high P-T conditions. On the other hand, the entropy is going to play an important role at high temperature but its effect on the relative stability of the target system is not considered in the present study. Previous ab initio simulations have found that when the entropic effect is included in the calculation, the Gibbs free energy of the reaction, 62Fe + FeO → Fe₆₃O, can be substantially reduced by ~3 eV³¹. As for the present target system, the introduction of entropic effect may correspondingly favor the combination of Fe and FeO at high P-T conditions. But, on the contrary, it can have an opposite effect causing the reaction energetically unfavorable. That means it might change our conclusion significantly and invalidate our further interpretations for the deep Earth at ultra-high temperature. Further investigations on the present target system by either ab initio molecular dynamics methods or high P-T experiments are definitely required to verify the reaction, Fe + FeO → Fe₂O. It is to be noted that Earth’s core contains diverse light elements. The present of one light element can affect the relative stability and the amount of the other one in Earth’s core^8,9. Thus, the relative stability and physical properties of the iron-rich iron oxide or oxygen-bearing iron alloys should be investigated as a function of not only pressure and temperature but also compositions in order to comprehensively elucidate the nature of oxygen in Earth’s core. But they are beyond the scope of the present study and we will work on them in the future.

In terms of phase relations of the Fe-FeO system, Sherman ²⁹ indicated there should be no solid solution between Fe and FeO under Earth’s core conditions due to the aforementioned reasons. In contrast, later simulations implied that oxygen dissolved in iron might be stabilized at concentrations up to a few mol% under core conditions because of the significant entropic effect in the dilute solution³¹. Recent thermodynamic simulations suggested the feasibility of the ideal solution model to calculate the Fe-FeO liquid property under outer core conditions and yielded the eutectic compositions of Fe-7.2~9.1 wt% O¹². Based on their thermodynamic simulations, they concluded that an overall oxygen-rich bulk outer core model should be excluded. In the present study, it is proposed that Fe₂O can be a strong candidate phase for stable iron-rich iron oxides at high pressure, perhaps even at high temperature, which can potentially change phase relations of the Fe-FeO system at pressures corresponding to Earth’s lower outer core.

The accurate measurement of the sound velocity of liquid iron alloys at high pressure is very challenging. Previous studies have discussed the sound velocity of the liquid phase can be addressed from the bulk sound velocity of the solid phase with identical compositions⁷. In addition, theoretical calculations have shown that the bulk sound velocity (V _φ) of the solid phase is comparable to V _P of the liquid phase (the difference is about 2.5%) and both are marginally dependent of temperature at a given high pressure^41,42. Indeed, recent experiments have presumed V _φ of the solid FeS₂ is equivalent to V _P of the liquid counterpart and thus estimated the sulfur content in Earth’s outer core⁴³. Furthermore, in the I4/mmm-type Fe₂O, the coordination number of oxygen is eight and each iron is surrounded by four oxygen and nine iron, which is similar to the recent report of structural properties of the liquid oxygen-bearing iron alloys by first-principles molecular dynamics⁴⁴. Thus, it is reasonable that the target system can be used to roughly derive the amount of oxygen in the lower outer core. We obtain V _φ of (Fe_xNi_1−x)₂O as a function of pressure [Fig. 4 and see Supplementary Table S2] and estimate the volume fraction of Fe₂O by the following relation:

$$V_{P(PREM)}=\frac{0.975V_{\varphi (solid-Fe2O)}{V}_{P(liquid-Fe)}}{\left(1-t\right)\cdot 0.975V_{\varphi (solid-Fe2O)}+t{V}_{P(liquid-Fe)}}$$ 2

where t is the volume fraction of Fe₂O. We find a volume fraction, t ~ 35% [Fig. 4]. Then, if oxygen is the only light element in Earth’s lower outer core, the maximum possible oxygen content is ~4.3 wt%. However, thermoelastic parameters of (Fe_xNi_1−x)₂O at realistic outer core conditions are not well constrained, which certainly warrants further explorations.

Figure 4.

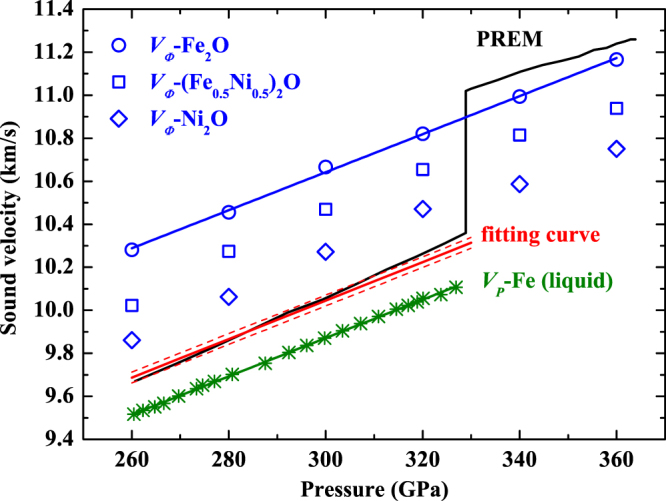
Bulk sound velocity of I4/mmm-(Fe_xNi_1−x)₂O (blue marks) as a function of pressure. The seismic profile of PREM (black line) (ref ³⁷) and V _P profile of liquid iron (olivine stars) (ref ⁴²) are plotted for comparison. The red fitting curve is calculated from 35 vol% I4/mmm-Fe₂O + 65 vol% iron.

On the other hand, for a terrestrial super-Earth, unlike Earth, the metal core is mainly composed of solid iron alloys and only a small portion of the core is liquid because of its high mass. Therefore, there will be more oxygen in a super-Earth’s solid core than that in Earth’s inner core assuming that they have similar cosmochemical compositions. There also exist a type of so-called ocean planets, where a thick layer of ice covers the rocky materials and the center temperature can be much lower than that of super-Earths’^45,46. Based on current results at 0 K, above 270 GPa, it is energetically favorable for the formation of the I4/mmm-type Fe₂O. The enthalpy difference becomes larger upon further compression, which can stabilize the I4/mmm-type Fe₂O even at high temperature. Thus, it is likely that I4/mmm-(Fe_xNi_1−x)₂O could exist in the solid core of a super-Earth or an ocean planet. In addition, Fig. 3(d) demonstrates that I4/mmm-(Fe_xNi_1−x)₂O has a high AV _S in the calculated pressure range due to its layered structure. If (Fe_xNi_1−x)₂O can accumulate in the solid core locally, it will cause the locally seismic anisotropy in the solid core, which might be even observed by advanced instruments.

Conclusions

In conclusion, the high-pressure behavior of (Fe_xNi_1−x)₂O has been studied based on first-principle density functional calculations. The end member Fe₂O, is predicted to undergo structural transitions from P6₃/mmc to $P\stackrel{\circledR }{3}m1$ at 212 GPa and further to I4/mmm at 266 GPa, consistent with previous simulations. The dynamically and mechanically stable I4/mmm-Fe₂O becomes energetically favorable with respect to the assemblage of hcp-Fe and $R\stackrel{\circledR }{3}m$-FeO above 270 GPa. These results indicate that I4/mmm-Fe₂O can be a strong candidate phase for stable iron-rich iron oxides at high pressure, perhaps even at high temperature, which requires further investigations by ab initio molecular dynamics methods or high P-T experiments. The elastic and seismic properties of I4/mmm-(Fe_xNi_1−x)₂O at high pressures have been discussed in detail. Combining previous data with present results, we roughly estimate that if oxygen is the only light element in Earth’s lower outer core, less than 4.3 wt% oxygen content is required to match the seismic observations. On the other hand, I4/mmm-(Fe_xNi_1−x)₂O may exist in a super-Earth’s or an ocean planet’s solid core. If (Fe_xNi_1−x)₂O can accumulate in its solid core locally, it is likely to cause the locally seismic heterogeneity because of its high AV _S.

Methods

Three candidate structures (P6₃/mmc, $P\stackrel{\circledR }{3}m1$ and I4/mmm [see Supplementary Fig. S1(a)]) for Fe₂O were considered in the present study and structural details could be found in Table S1. First-principle calculations were performed based on density functional theory with the projected augmented wave method (PAW) implemented in Vienna ab-initio simulation package (VASP)^47–49. The Perdew-Burke-Ernzerhof (PBE) version of the generalized gradient approximations (GGA) was selected to treat the exchange correlation potential⁵⁰. The kinetic energy cut-off was set to 1000 eV. The energy convergence criterion for the electronic self-consistent calculation was 10⁻⁶ eV. The total energy difference was converged to 1×10⁻⁵ eV/formula unit (f.u.) with respect to the energy cutoff and k-points, respectively. The force difference was converged to 1×10⁻³ eV/Å (less than 0.1 GPa). The spin-polarization of iron of Fe₂O with various structures was not included because the existence of magnetic moments under Earth’s core conditions could be safely ruled out. For each crystalline phase, the atomic positions and unit-cell parameters were allowed to relax at each given volume to obtain the minimum total energy. Once the minimum total energies of each phase were obtained at different volumes, they were fitted to the third-order Birch-Murnaghan EoS^51,52. Additionally, the enthalpy (H = E + PV) of each phase was compared with each other to identify the most stable structure at the given pressure.

The phonon dispersions were calculated using the Phonopy Code by the supercell method⁵³ and a 2×2×2 supercell was constructed for the I4/mmm-type Fe₂O. Single crystal elastic constants of I4/mmm-(Fe_xNi_1−x)₂O were computed from the stress-strain relations (σ _ij = c _ijkl ε _kl, where σ _ij stands for the stresses, c _ijkl for the elastic moduli and ε _kl for the strains)⁵⁴. For the I4/mmm symmetry, we derived six independent elastic constants (C ₁₁, C ₁₂, C ₁₃, C ₃₃, C ₄₄ and C ₆₆). We applied positive and negative strains of magnitude of 0.5% in order to accurately determine the stresses in the appropriate limit of zero strain.

Author Contributions

X.W. and S.H. conceived the research. S.H. performed the theoretical calculations. S.H., X.W. and S.Q. analyzed the data. S.H., X.W. and S.Q. wrote the manuscript. All authors reviewed the manuscript.

Competing Interests

The authors declare that they have no competing interests.