Determination of pKa values of alendronate sodium in aqueous solution by piecewise linear regression based on acid-base potentiometric titration

Abstract

As a mono-sodium salt form of alendronic acid, alendronate sodium presents multi-level ionization for the dissociation of its four hydroxyl groups. The dissociation constants of alendronate sodium were determined in this work by studying the piecewise linear relationship between volume of titrant and pH value based on acid-base potentiometric titration reaction. The distribution curves of alendronate sodium were drawn according to the determined pKa values. There were 4 dissociation constants (pKa₁=2.43, pKa₂=7.55, pKa₃=10.80, pKa₄=11.99, respectively) of alendronate sodium, and 12 existing forms, of which 4 could be ignored, existing in different pH environments.

Graphical abstract

1. Introduction

Alendronate sodium, an important bone absorption inhibitor, is often used for treating osteoporosis in postmenopausal women clinically [1], [2], [3]. It helps prevent fractures effectively by inhibiting the activity of bone cell and increasing bone density, which can be explained by retarding the formation of hydroxyapatite crystals for its combination with bone surface [4], [5]. In recent years, studies on alendronate sodium have been mainly focused on the pharmacological effects, especially for the expansion of its clinical indications and consolidation of the effect reducing fracture risk [6], while those on its physical and chemical properties are relatively fewer.

As a kind of bisphosphonates containing four hydroxyl groups that can all be dissociated, alendronate sodium has four dissociation constants, which leads to its different electrochemical states existing in aqueous solution with different pH values [7]. Dissociation constants are considered as vital physicochemical parameters from which we could get important information about drug properties such as solubility [8], acidity [9], [10], biological uptake [11], and metabolism [12]. Moreover, pKa values are important for estimating the charged state of analytes and the retention order in the development of chromatographic and electrophoretic methods. For polyprotic acid and base like alendronate sodium, dissociation constants are essential information of their accurate existing forms under different pH conditions.

To date, we have only found that Cornelio et al. [13] and Ribeiro et al. [14] reported the pKa values of alendronate sodium. Both of them cited the data from the Merck Index [15]. However, the method for measuring them has not been reported in the Merck Index or elsewhere. Consequently, we have established a method to determine the pKa values of alendronate sodium, and compared the measured pKa values with the Merck Index data.

Dissociation constants are determined by various methods such as spectroscopy [16], [17], electrophoresis [18], [19], [20], and potentiometric titration [11], [21], [22]. It is worth noting that UV-based method including ultraviolet visible spectrophotometry (UV–Vis), high performance liquid chromatography (HPLC) and capillary electrophoresis (CE) can not be used for determining the pKa values of alendronate sodium for its lack of absorbing chromophores [23] when ultraviolet absorption or fluorescence detectors were used. If ultraviolet or fluorescence derivatization was employed in the methods mentioned above, the measured pKa values would be its derivatives’ instead of alendronate sodium's. Although some other methods achieved by indirect UV method or non-UV detection, such as evaporative light scattering detection technique (ELSD) and mass spectrometry (MS), can be used to ensure its detectability, these methods are not straight or simple enough in the determination. Potentiometric titration in aqueous solutions is a simple and effective method and considered to be the most precise method for the determination of equilibrium constants, once a right model has been chosen [8]. Therefore, potentiometric titration was selected in this work.

Piecewise linear regression is a general method in statistical analysis, in which the independent variable is segmented according to its value, and the linear regression is performed separately on these segments [24]. The boundaries between the segments are called breakpoints. In this work, the method was applied to determine the pKa values of alendronate sodium based on the data obtained from acid-base potentiometric titration. According to the following deduction, the whole curve of lgV-pH is just like several intersecting lines and there is a good linear relationship between lgV and pH in each line. In this special case of piecewise linear regression where all segments are linear, the equation of piecewise regression is expressed as [25]:

$${\mathrm{Y}=\mathrm{a}}_1{+\mathrm{b}}_1\mathrm{X},\mathrm{X}\le {\mathrm{J}}_1$$

$${\mathrm{Y}=\mathrm{a}}_2{+\mathrm{b}}_2{\mathrm{X},\mathrm{J}}_2\ge \mathrm{X}\ge {\mathrm{J}}_1$$

$$\dots$$

$$\mathrm{Y}={\mathrm{a}}_{\mathrm{n}}{+\mathrm{b}}_{\mathrm{n}}\mathrm{X},\mathrm{X}\ge {\mathrm{J}}_{\mathrm{n}}$$

where Y is the dependent variable, X is the independent variable; a₁ to a_n and b₁ to b_n are the intercepts and slopes of the linear segments, respectively. J₁ to J_n are the breakpoints, which represent the pK_a values of alendronate sodium.

In this study, acid-base potentiometric titration and Origin 9.0 software were used to build a linear relationship between the logarithm of titration volume and pH values. According to the results, we drew the distribution curve by deducing the relational expression between distribution fraction at different forms and the dissociation constants of alendronate sodium.

2. Material and methods

2.1. Apparatus and materials

Alendronate sodium was purchased from Ruide Pharmaceutical Factory (Lanzhou, China). Sodium hydroxide and potassium hydrogen phthalate were of analytical grade and used without further purification. Distilled water was from the GLP lab of Lanzhou University (Lanzhou, China).

Acid-base potentiometric titration was performed using FE20 pH meter (Mettler Toledo Instrument Co., Ltd., Shanghai, China) and a base buret. A constant temperature magnetic agitator was needed to stir the solutions and control the titration temperature constant at 25.0±0.1 °C. The combination pH electrode was calibrated by the buffer solutions of pH 4.00 and pH 6.86 respectively before use.

2.2. Method of determination of pKa values

Alendronate sodium solution (0.01 mol/L) and sodium hydroxide titrant (0.1 mol/L) were prepared by distilled water respectively, and the latter was calibrated by potassium hydrogen phthalate that had been dried to constant weight at 105 °C before use.

The acid dissociation constants were determined by titrating 20.00 mL of alendronate sodium solution with standardized NaOH solution. The pH value of alendronate sodium solution was adjusted to 1.38 using HCl solution (0.1 mol/L) before titration. When a few drops of NaOH solution were dropped into the beaker, the volume and the pH value were recorded when they were unchangeable. The procedures mentioned above were repeated until the pH value rose to 13. Finally, 98 of the titration data were obtained for each experiment.

2.3. Theory of piecewise linear regression based on acid-base potentiometric titration

The dissociation process of alendronate sodium is shown in Fig. 1.

Fig. 1.

Dissociation process of alendronate sodium.

Origin9.0 software was used to fit a linear relationship between logarithm of titration volume and pH value according to the experimental data. The lgV-pH curve was obtained as shown in Fig. 2.

Fig. 2.

The lgV-pH curve of potentiometric titration.

First, the first ionization of alendronate sodium was taken as an example.

V was used to represent the volume of NaOH solution (C_T mol/L), and V₀ is the volume of alendronate sodium solution (C₀ mol/L). The dissociation constant is Ka₁,

$$[H^{+}][H_3{A}^{2-}]=[H_4{A}^{-}]K{a}_1$$ (1)

$$[H_4{A}^{-}]\iff [H_3{A}^{2-}]+[H^{+}]$$ (2)

The hydrolysis of alendronate sodium could be ignored for the existence of co-ions effect. Then,

$$[H_4{A}^{-}]=\frac{CoVo-C_{T}V}{V+Vo}$$ (3)

$$[H_3{A}^{2-}]=\frac{C_{T}V}{V+Vo}$$ (4)

In formula (1), when $[H^{+}]=K{a}_1$, then

$$[H_4{A}^{-}]=[H_3{A}^{2-}]$$ (5)

Under this condition, if V=V_T, then

$$CoVo=2C_T{V}_T$$ (6)

Eq. (6) was plugged into Eq. (1) and changed to logarithm form,

$$\lg V=pH-pK{a}_1+\lg (2V_T-V)$$ (7)

Information can be obtained from Eq. (7) that lgV-pH curve has an inflection point where V=V_T, and here pH=pKa₁. Thus, pKa₁ value could be obtained.

The whole curve was just like several intersecting lines and lgV verse pH has a good linear relationship in each line. According to the method above, the rest of pKa values can be deduced by analogy.

Therefore, all the pKa values of alendronate sodium can be obtained.

2.4. Data processing

Piecewise linear regression has been employed to the curve of lgV-pH from the 19th data point (V=5.3 mL) to the last one (V=62.0 mL) using Origin9.0 software. The linear correlation of the each trend line should be the highest in the piecewise areas we chose.

3. Results and discussion

3.1. Treatment of the potentiometric data

It was more notable that the natural pH of alendronate sodium in aqueous solution was measured to be 4.46. In order to expand the pH range in titration process, the pH value of alendronate sodium solution was adjusted to 1.38 using 0.1 M HCl solution before titration. In this condition, both alendronic acid and alendronate sodium exist in the solution. When pH=pKa±1 (pKa₁=0.8 for alendronic acid [7], [15]), the ratio of distribution coefficient between conjugate acid and base was 10:1 or 1:10 [26], that is, most of the alendronate acid has been transformed into alendronate sodium at pH=1.81, so linear relationship fitting was started from the 19th data point (pH=1.81) instead of the 1st one (pH=1.38), which ensures the accuracy of regression results.

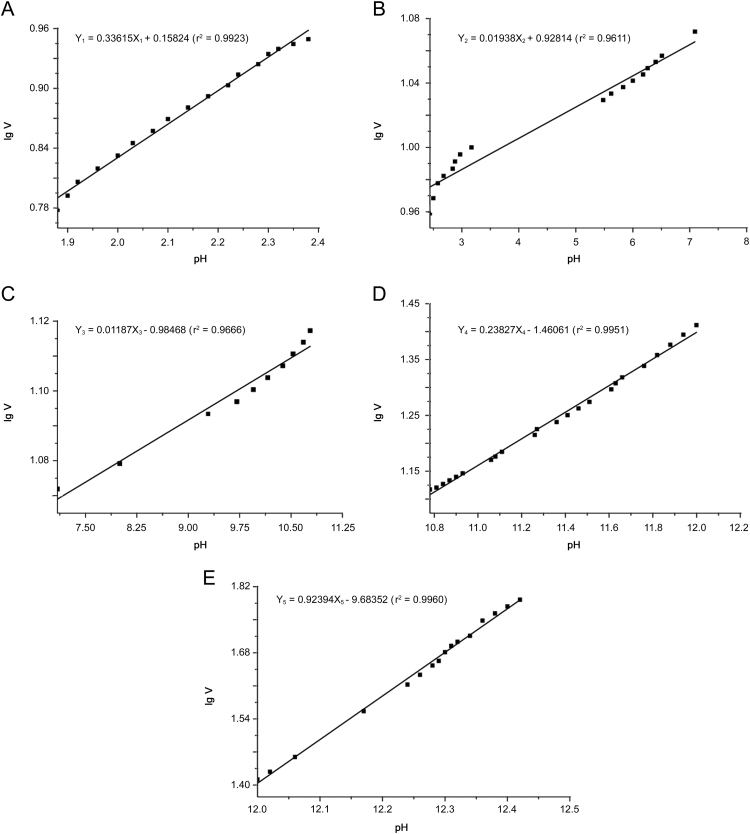
Regression results are shown in Fig. 3 and Table 1. One group of the five different lines obtained by fitting linear relationship piecewise is shown in Fig. 4.

Fig. 3.

Piecewise linear regression results of the lgV-pH curve.

Table 1.

Regression equations of lines.

Lines	Equation	r2	RSS	MS	F	P
Line 1	Y1=0.33615X1+0.15824	0.9923	0.0004	0.0498	2057.1034	0.0000
Line 2	Y2=0.01938X2+0.92814	0.9611	0.0007	0.0192	396.5566	0.0000
Line 3	Y3=0.01187X3+0.98486	0.9666	0.0001	0.0019	261.4822	0.0000
Line 4	Y4=0.23827X4−1.46061	0.9951	0.0009	0.1952	4439.3698	0.0000
Line 5	Y5=0.92394X5−9.68352	0.9960	0.0008	0.2208	3726.1033	0.0000

RSS: residual sum of squares; MS: mean square; F: F value. P: p-value.

Fig. 4.

One group of five different lines obtained by fitting linear relationship piecewise (A) 19–36; (B) 36–52; (C) 52–62; (D) 62–83; (E) 83–98 (the serial number of fitting data points).

The lgV-pH curve was divided into five segments. The p-values obtained for these segments models were all less than 0.05, which indicated that there were statistically significant relationships between pH values and lgV at the 95% confidence level. Line Y₂ (r²=0.9611) and line Y₃ (r²=0.9666) had a relatively poorer linear relationship compared to others. The possible reason may be that the data points of these two fitting lines were less and discontinuous. The steeper titration curve made pH value change sensitively in these two segments, which caused the fitting points to be reduced, especially only 10 points for line Y₃. So the error increased and linear relationship became poorer.

Four boundaries among the five segments, named breakpoints, represent the four pKa values of alendronate sodium as deduced above. Four pKa values were calculated using simultaneous every two equations of them. The determined pKa values are shown in Table 2. It can be seen that pKa values in this work are similar to the values in the literature except that the pKa₂ differs in value by ±1.18. The possible reason may be the lower accuracy of fitting results of Line Y₂ and line Y₃ caused by the relatively poorer linear relationship of them, from which the pKa₂ value was calculated directly. In addition, errors in method, operation and instrument may cause the difference in results between this work and the literatures.

Table 2.

Dissociation constants of alendronate sodium.

Source	pKa1	pKa2	pKa3	pKa4
This work	2.43±0.16	7.55±0.14	10.80±0.02	11.99±0.08
Literaturea	2.72±0.05	8.73±0.05	10.50±0.10	11.60±0.10
Difference	±0.29	±1.18	±0.30	±0.39

^aThe pKa values are from the Merck Index.

3.2. Distribution curve of different existing forms

The knowledge of distribution fraction is important in getting the equilibrium concentration of one of the solute forms in total concentration. H₅A was used to simply define alendronate acid, then,

$$\left[H_{5}A\right]\iff \left[H_4{A}^{-}\right]+\left[H^{+}\right]{10}^{-0.8}=\left[H_4{A}^{-}\right]\left[H^{+}\right]/\left[H_{5}A\right]$$

$$[H_4{A}^{-}]\iff [H_3{A}^{2-}]+[H^{+}]K{a}_1=[H_3{A}^{2-}][H^{+}]/[H_4{A}^{-}]$$

$$[H_3{A}^{2-}]\iff [H_2{A}^{3-}]+[H^{+}]K{a}_2=[H_2{A}^{3-}][H^{+}]/[H_3{A}^{2-}]$$

$$[H_2{A}^{3-}]\iff [H{A}^{4-}]+[H^{+}]K{a}_3=[H{A}^{4-}][H^{+}]/[H_2{A}^{3-}]$$

$$[H{A}^{4-}]\iff [A^{5-}]+[H^{+}]K{a}_4=[A^{5-}][H^{+}]/[H{A}^{4-}]$$

$$\mathrm{Distribution}\mathrm{fraction}\mathrm{of}{H}_{5}A:\frac{{[H^{+}]}^5/{10}^{-0.8}}{a}$$

$$\mathrm{Distribution}\mathrm{fraction}\mathrm{of}{H}_4{A}^{-}:\frac{{[H^{+}]}^4}{a}$$

$$\mathrm{Distribution}\mathrm{fraction}\mathrm{of}{H}_3{A}^{2-}:\frac{{[H^{+}]}^{3}K{a}_1}{a}$$

$$\mathrm{Distribution}\mathrm{fraction}\mathrm{of}{H}_2{A}^{3-}:\frac{{[H^{+}]}^{2}K{a}_{1}K{a}_2}{a}$$

$$\mathrm{Distribution}\mathrm{fraction}\mathrm{of}H{A}^{4-}:\frac{[H^{+}]K{a}_{1}K{a}_{2}K{a}_3}{a}$$

$$\mathrm{Distribution}\mathrm{fraction}\mathrm{of}{A}^{5-}:\frac{K{a}_{1}K{a}_{2}K{a}_{3}K{a}_4}{a}$$

where a=${[H^{+}]}^5/{10}^{-0.8}+{[H^{+}]}^4+{[H^{+}]}^{3}K{a}_1+{[H^{+}]}^{2}K{a}_{1}K{a}_2+[H^{+}]K{a}_{1}K{a}_{2}K{a}_3+K{a}_{1}K{a}_{2}K{a}_{3}K{a}_4$ The protonation of amino was taken into consideration, and pKb=4.1

$$[RN{H}_2]+H_{2}O\iff [RN{H_3}^{+}]+[O{H}^{-}]\dots Kb=[RN{H_3}^{+}][O{H}^{-}]/[RN{H}_2]$$

$$\mathrm{Distribution}\mathrm{fraction}\mathrm{of}RN{H}_2:\frac{[O{H}^{-}]}{[O{H}^{-}]+Kb}=\frac{Ka}{[H^{+}]+Ka}$$

$$\mathrm{Distribution}\mathrm{fraction}\mathrm{of}RN{H_3}^{+}:\frac{Kb}{[O{H}^{-}]+Kb}=\frac{[H^{+}]}{[H^{+}]+Ka}$$

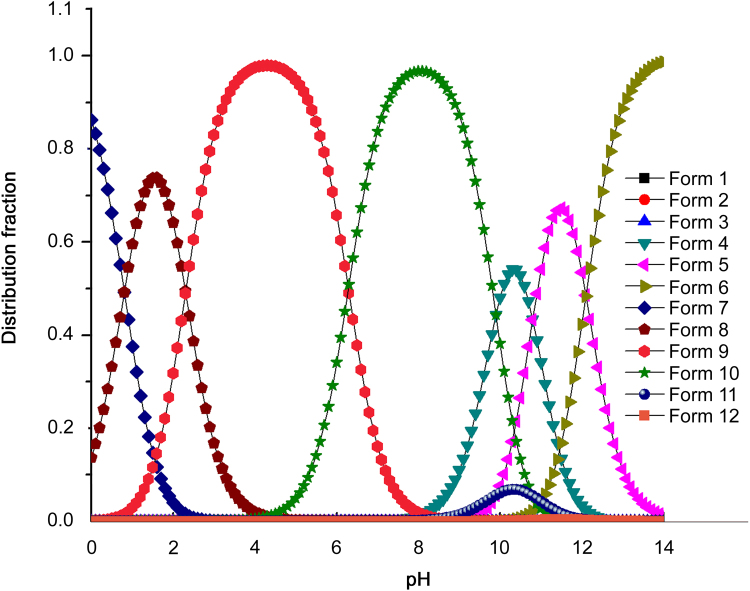
Therefore, there are 12 different existing forms of alendronate sodium as Table 3 shows. The four dissociation constants (pKa values) of alendronate sodium obtained in this work and pKb of amino were taken into the formulas. Then the distribution curves were simulated by computer software when changing the pH values varying from 0 to 14 with 0.1 increments.

Table 3.

Distribution fraction of 12 different forms of alendronate sodium.

Forms	$\delta H_{5}A$	$\delta H_4{A}^{-}$	$\delta H_3{A}^{2-}$	$\delta H_2{A}^{3-}$	$\delta H{A}^{4-}$	$\delta A^{5-}$
δ$RN{H}_2$	δ Form 1	δ Form 2	δ Form 3	δ Form 4	δ Form 5	δ Form 6
δ$RN{H}_3^{+}$	δ Form 7	δ Form 8	δ Form 9	δ Form 10	δ Form 11	δ Form 12

where δ represents distribution fraction

δ Form X represents the distribution fraction of the form that contains the two ion types in its corresponding row and column. e.g. δ Form 1=$\delta H_{5}A$*$\delta RN{H}_2$.

The distribution curve (Fig. 5) shows that form2 (δ$H_4{A}^{-}$*δ$RN{H}_2$) and form10 (δ$H_2{A}^{3-}$*δ$RN{H}_3^{+}$) are the main existing forms of alendronate sodium in aqueous solution. It means that the molecular form of alendronate sodium exists in the range of 0<pH<8, and when the pH=4.4±0.1, molecular form is the only one existing in solution. In this pH area, the amino group is mainly in its protonated form, which is consistent with the actual situation. When pH >8, ionic forms of alendronate sodium are in dominant positions.

Fig. 5.

Distribution curves of 12 forms of alendronate sodium in aqueous solution.

4. Conclusion

Potentiometric titration coupled with piecewise linear regression methods has several advantages such as being highly sensitive, accurate, and easy to operate. Due to the unavoidable random errors in the traditional graphing method, the data points in the method are more dispersed, and the error is larger. While piecewise linear regression overcomes the weakness of graphing method, making the results accurate and reliable. Besides, compared to programming method, piecewise linear regression is faster and simpler. In this work, we used the method to determine the dissociation constants of alendronate sodium and got a reliable result. Meanwhile, distribution curves of the 12 forms of alendronate sodium under different pH conditions were also obtained, of which 4 forms could be ignored. The work provides an important basis for exploring the drug properties of alendronate sodium.