Reaction Mechanism for Direct Proton Transfer from Carbonic Acid to a Strong Base in Aqueous Solution I: Acid and Base Coordinate and Charge Dynamics

Abstract

Protonation by carbonic acid H₂CO₃ of the strong base methylamine CH₃NH₂ in a neutral contact pair in aqueous solution is followed via Car–Parrinello molecular dynamics simulations. Proton transfer (PT) occurs to form an aqueous solvent-stabilized contact ion pair within 100 fs, a fast time scale associated with the compression of the acid–base hydrogen-bond (H-bond), a key reaction coordinate. This rapid barrierless PT is consistent with the carbonic acid-protonated base pK_a difference that considerably favors the PT, and supports the view of intact carbonic acid as potentially important proton donor in assorted biological and environmental contexts. The charge redistribution within the H-bonded complex during PT supports a Mulliken picture of charge transfer from the nitrogen base to carbonic acid without altering the transferring hydrogen’s charge from approximately midway between that of a hydrogen atom and that of a proton.

Graphical abstract

1. INTRODUCTION

Carbonic acid H₂CO₃ has long been discussed as a component of a buffer along with bicarbonate and CO₂ that stabilizes the pH in the human body^1–5 as well as the pH of the seas and oceans.⁶ However, the acid is unstable and decomposes reversibly in aqueous solution to CO₂ and H₂O with a room temperature lifetime of ∼60 ms.^7–15 Indeed, carbonic acid was only recently directly observed in aqueous solution,¹⁶ and relatively little is known about the chemical and biochemical reactivity of the intact H₂CO₃ molecule. In the present work, we present and analyze the results of Car–Parrinello molecular dynamics (CP MD) simulations of proton transfer (PT) in an aqueous solution from carbonic acid H₂CO₃ to a strong methylamine base in a neutral acid–base hydrogen (H)-bonded complex to give the product complex of the H-bonded bicarbonate-protonated methylamine ions,

$$\text{HOCOOH}\cdots {\text{NH}}_2{\text{CH}}_3\to {\text{HOCOO}}^{-}{\cdots }^{+}{\text{HNH}}_2{\text{CH}}_3$$ (1)

We wish to determine theoretically (a) if carbonic acid, whose reactivity is relatively little studied, is a viable proton-donor on the time scale that it remains intact, and (b) whether the acid behaves, both in rate and mechanism, like a normal acid consistent with its pK_a at a biologically relevant temperature 310 K (37 °C), and begin this effort here for the case where initially the acid and base are “in contact” in a hydrogen-bonded complex. A strong base is chosen to employ a strong thermodynamic driving force for the PT, which would favor a barrierless reaction, more readily studied. The precise value of the equilibrium constant K_a of aqueous H₂CO₃ has been a subject of debate for many decades and is still under consideration.¹⁷ H₂CO₃’s pK_a was recently experimentally determined to be ∼3.49;^16,18 this is a value quite different from the one sometimes reported in textbooks,¹⁹ but is, for example, consistent with the range of values subsequently found in computational studies of H₂CO₃’s PT to water in aqueous solution.^20–22 Our rationales above, as well as the choice of a strong nitrogen base, derive especially from our proposal, described in more detail elsewhere,¹⁸ is that H₂CO₃ has the potential of being a major protonating agent of, for example, nitrogen bases in the blood.

The eq 1 carbonic acid–methylamine PT reaction is a component of the overall bimolecular protonation of methylamine by carbonic acid in aqueous solution, which should be a diffusion-controlled process, that is, controlled by the rate for the relative diffusive approach of the acid and base reactants rather than the rate of the on-contact PT eq 1.¹⁸ This statement is supported by the rapid, activationless character of the PT reaction that we will find within. Nonetheless, the intrinsic PT reaction for H₂CO₃ with nitrogen bases such as methylamine is key for its chemistry in a biochemical context. In addition, the activated PT process has often been studied from a theoretical perspective,^23–30 but little is known about the molecular level details of the PT mechanism for such an activationless case. Further, the activationless character of the on-contact H₂CO₃−CH₃NH₂ PT reaction that we find should be consistent with H₂CO₃’s pK_a, in line with one of our motivations detailed above. We pause to examine that issue here.

The on-contact rate constant for PT within a general acid–base complex AH⋯B has been shown to primarily depend on ΔpK_a=pK_a(HB⁺) − pK_a(HA), the difference of the acid AH’s pK_a value and that of the base B’s conjugate acid HB^+16,31–33 (and has been exploited to determine the pK_a of H₂CO₃^16,18). For larger ΔpK_a values, the pK_a difference is sufficiently large that the acid’s protonation of the base is barrierless i.e. not activated. PT within an on-contact complex AH⋯B occurs so rapidly that a PT rate constant cannot be defined, and the overall aqueous solution reaction is diffusion-controlled. As we have already stated, we will find this to be the case for the on-contact H₂CO₃⋯CH₃NH₂ PT reaction, and that this can be readily understood from carbonic acid’s pK_a ∼ 3.5¹⁶ as compared to the pK_a of protonated methylamine ∼10.6.^34,35 Thus, ΔpK_a ∼ 7 for the reaction: H₂CO₃ is a far stronger acid than is CH₃NH₃⁺. This ΔpK_a is already past the transition, near ΔpK_a∼ 5^{16,18,31–33} between activated and activation-less PT. This ΔpK_a ∼ 7 acidity difference corresponds to a strongly favorable reaction free energy asymmetry ∼ −10 kcal/mol for the PT reaction. Since these pK_a and free energy values refer to the production of the separated carboxylate anion and protonated methylamine species, the reaction free energy for the PT within the complex should be even more favorable, given the electrostatic cost to separate the H-bonded product ions to infinite separation.

We pause to place in a more general perspective our choice of an initial investigation of the “on contact” reaction, in an equilibrated acid–base complex (as described in section 2). If the PT reaction were only possible in this situation, then the standard theory of diffusion-influenced reactions gives the overall reaction rate constant by k = (k_eqk_D)/(k_eq + k_D),³⁶ where k_D is the diffusion-controlled rate constant and k_eq is the rate constant for the in contact, equilibrated reacting pair. The latter describes reasonably approximately the situation considered within, in our focus on the chemistry rather than the diffusion aspects of the reaction. Of course it is possible for the PT reaction to also occur through the intermediacy of one or more water molecules, via some sort of proton relay;³⁷ indeed, we have found that this is the case, as will be reported elsewhere. Nonetheless, the present on contact case is important to study for at least two reasons (beyond those mentioned previously in this section). First, this on contact route can occur along with the more complex routes, and the relative efficacy of these routes needs to be established. Second, the on contact reaction affords the simplest opportunity of a detailed study of the electronic aspects of the PT reaction, which will greatly assist future assessment of the electronic aspects of more complex PT routes, for example, reaction involving a single water molecule between the acid and base.

The outline for the remainder of this paper is as follows. The simulation methods, including the construction of the H₂CO₃−CH₃NH₂ acid–base system, are detailed in section 2. Section 3 presents the temporal behavior for the nuclear coordinates during the PT reaction, that is, the H-bond separation and proton stretch, and examines the change in charge character associated with the transition of the neutral acid–base pair to the bicarbonate-protonated base ion pair in solution. Concluding remarks are offered in section 4.

2. SIMULATION DETAILS

Nonequilibrium CP³⁸ ab initio MD simulations have been performed for the carbonic acid-methylamine pair on-contact in a box of 100 water molecules. In the following, we describe the construction of the simulation box containing the aqueous solution of the H-bonded acid–base pair complex with the aid of gas phase quantum chemistry calculations and classical solution phase MD simulations. CP MD simulation details, including the required equilibration are then presented. Finally, simulations to obtain reference water solvent structures are described for isolated species (carbonic acid, bicarbonate, methylamine, and protonated methylamine) in an aqueous solution; these provide comparison with the water solvent structure surrounding the acid–base pair.

2.1. Aqueous System Construction and CP MD Simulation Details

The carbonic acid-methylamine H-bonded complex was first optimized in the gas phase at the B3LYP/6-311+G** level of theory^39,40 and basis set with the GAMESS package.⁴¹ In order to avoid waiting on diffusion time scales for the complex to form prior to the PT reaction eq 1, the acid–base H-bond length (see Scheme 1) is constrained to the O_A−N distance $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}=2.9$ Å during the optimization. This separation is small enough such that no waiting is required for strong H-bond formation, but is large enough for observation of subsequent PT on a reasonable time scale.

Scheme 1. Neutral On-Contact Carbonic Acid–Methylamine Pair with the Atoms Labeled^a.

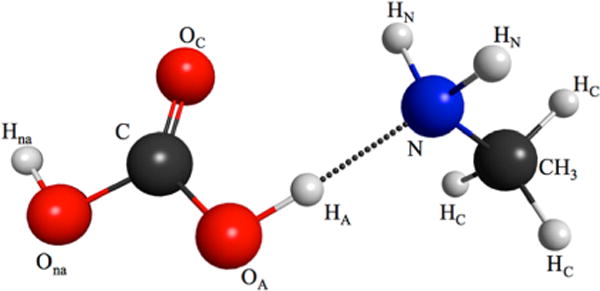
^aLabels are maintained throughout the PT reaction producing the contact ion pair products. The cis–cis H₂CO₃ conformer studied here is the most stable one in aqueous solution.²¹

The complex is then solvated in 100 water molecules in a periodic cubic box maintaining the density at the neat liquid water value 1 g/cm³, appropriate for the dilute 310 K solution considered here. The 310 K temperature is employed in view of the interest in the carbonic acid activity in vivo (37 °C), as discussed in the Introduction. As an initial equilibration of this aqueous system, classical simulations are performed with the acid–base complex fixed at the above calculated gas phase geometry; this avoids the requirement of intramolecular force-field parameters, which are unavailable for carbonic acid. The simulation is carried out for 100 ps in the constant volume and temperature ensemble using the GROMACS package.⁴² The H-bonded complex-solvent intermolecular interactions are defined by their atomic charges and the Lennard–Jones (LJ) parameters. The complex’s atomic charges have been obtained as ESP charges from our quantum chemically optimized gas phase structure.⁴³ The LJ parameters for atoms of methylamine are taken from previous simulations,⁴⁴ while those of carbonic acid are taken from a bicarbonate study.⁴⁵ Solvent molecules are modeled as rigid SPC/E water.⁴⁶ The last configuration resulting from this classical simulation is taken as the starting point for the CP MD simulations, now described.

The CP MD simulations are performed with the CPMD package⁴⁷ and the density functional theory (DFT) formalism with the gradient-corrected Becke, Lee, Yang, and Parr (BLYP) functional.^39,40 The interactions of the valence electrons with the nuclei and core electrons are represented by Vanderbilt ultrasoft pseudopotentials,^48–50 as have been used in previous studies.^50–53 The plane wave basis set cutoff is set to 40 Ry.^20,51–53 An electronic mass of 600 au and a 4 au (≈0.1 fs) time step were used, consistent with other relevant studies.^20,51–53 In order to account for long-ranged electron correlations, a van der Waals correction proposed by Grimme^54,55 is incorporated in the CPMD package,⁴⁷ which improves the description for PT. Further, periodic boundary conditions in all three directions have been applied throughout the simulation. Trajectories have been saved every after 10 steps (∼1 fs) both during and postequilibration. An initial 500 step CP MD simulation is performed (again with the O_A−N and O_A−H_A distances constrained) to obtain a system temperature of 310 K by temperature scaling. The Nosé–Hoover thermostat is employed to maintain the temperature at 310 K for the CP MD trajectories.⁵⁶ (It is shown in Figure S4 of the Supporting Information (SI) that fixed NVE simulations yield very similar results.) Trajectory details are given in the next subsection.

2.2. CP MD Trajectory Details and Solvent Structure Equilibration

The classical MD results presented above for the aqueous solution of the frozen H₂CO₃−CH₃NH₂ complex provide the initial system configuration for the CP MD trajectories now discussed. As stated in subsection 2.1, the 2.9 Å O_A⋯N H-bond separation allows observation of PT occurrence on a reasonable time scale.

Prior to the simulation of PT events, proper equilibration of the solvent structure surrounding the acid–base pair is critical to provide a proper solvent structure around the complex prior to PT, and to afford a reasonable sampling of initial possible solvent configurations. This equilibration is performed with constraints to prevent PT; these are subsequently released. These comprise harmonic restraints for the O_A−H_A and O_A⋯N separations at 1 and 2.9 Å respectively, with a spring constant of 10 kcal/mol/Ų for each. These separations help to ensure that the surrounding water solvent molecules are in a configuration that does not favor PT, that is, that favors the neutral pair reactant (cf. eq 1).

Ten CP MD reaction trajectories are examined in this work, in which the constraints are removed after an equilibration period (becoming increasingly longer with each trajectory). While a duration of tens of picoseconds is typically chosen for equilibrium CP MD simulations for a single trajectory,⁵⁷ this is not practical for each trajectory within such a significant, 10-member, set of trajectories. In order to deal with this situation, the initial configurations for each of these 10 trajectories are thus taken from certain branch points within a single long CP MD equilibration trajectory; the ten reaction trajectories are then independent branches from this equilibration trajectory. The 10 different branch points serve two purposes. First, they progressively increase the length of the equilibration process; this also allows confirmation that the water solvent structure remains close to equilibrium throughout, providing proper starting structures for the reaction trajectories. They also provide sampling of different initial solvent environments, a feature critical for a set of such reaction trajectories.

The first reaction trajectory is initiated by releasing the constraints. The reaction trajectory is followed for ∼1 ps, with its initial configuration given by that of the first branch point, which is located at 3 ps from the beginning of the equilbration trajectory. This location choice is explained at the end of this subsection. The initial configuration for the second reaction trajectory is taken from the second branch point on the long equilibration trajectory; this point is located at 1 ps past the first branch point, that is, at 4 ps after the beginning of the equilibration trajectory, and the duration of the reaction trajectory is ∼1 ps. The initial configurations for each of the remaining eight reaction trajectories are chosen in a similar manner: the n + 1 trajectory is initiated by releasing, in the equilibration trajectory, the constraints at 1 ps after the previous reaction trajectory’s (n’s) branching point on the equilibration trajectory, and, as with all reaction trajectories, is of ∼1 ps duration. The 10th reaction trajectory is thus initiated 9 ps past the time of the first branch point. The entire equilibration trajectory is 12 ps long, since it is 9 ps past the time up to the first branch point, which was located at 3 ps past the trajectory’s commencement.

Since each one of these 10 reaction trajectories is followed for ∼1 ps after releasing the constraints, and the PT occurrence times are <100 fs (see below), ∼900 fs of each trajectory is related to post-PT processes. (The product ion pair production is always affected in under much less than a few hundred femtoseconds so extended 1 ps trajectories are not displayed here.) We note in passing that, as detailed in the following paper,⁵⁸ on the detailed solvent participation in the reaction mechanism, such a reaction trajectory time interval precludes observation of solvent exchange around the complex but includes solvent librational and H-bond compression motions, with a typical time scale less than 200 fs.^59–65

We have yet to explain our choice of 3 ps as the first branch point’s location on the equilibration trajectory. This is determined by the minimum time required for the initial CP MD equilibration period in order to commence the first reaction trajectory. To determine that minimum time, we have analyzed the radial distribution g(r) functions governing the separation between the carbonic acid O (O_A) and water Hs from a simulation of an aqueous solution of isolated carbonic acid (simulation details for the isolated systems are discussed in the next subsection) with differing equilibration times. The results, provided in the Supporting Information (see Figure S1), indicate that this minimum equilibration time required is ∼2.5 ps; we then select the first branch, for the start of the first reaction trajectory, to be located at 3 ps after the start of the equilibration trajectory. The equilibration time preceding the inception of the nth reaction trajectory is thus (n + 2) ps, which is thus 12 ps for the last, 10th trajectory.

Finally, in order to confirm that the equilibrated system’s water solvent structure is consistent throughout the equilibration process, we have examined in section S1 of the SI the water–water (O⋯H) g(r) (Figure S2) calculated at all branching points. The determined water solvent structure is consistent with that obtained from bulk water CP MD simulations,^15,57,66,67 and remains so throughout the entire 12 ps equilibration trajectory.

2.3. Simulation of Isolated Species

The CP MD simulations for the reference systems of isolated (i) carbonic acid, (ii) methylamine, (iii) bicarbonate anion, and (iv) protonated methylamine in aqueous solution are now described. These simulations provide the appropriate comparison of the water solvation structure for key sites for the H-bonded acid–base pair complex with the reference situation in the complex’s absence. For example, equilibrium solvent structures around the carbonic acid and methylamine base, each isolated in aqueous solution, provide a solvent structure surrounding O_A and N which can be used as a reference for comparison with the corresponding water solvent structure for the on-contact pair before PT. Any deviation in solvation from that in the complex indicates solvent rearrangements specific to the acid–base pair. These trajectories also determine reference bond lengths, for example, O_A−H_A and H_A−N, those are keys in defining a useful reduced coordinate to follow the PT, discussed in the next section.

Constructions of these four aqueous systems are similar to that for the on-contact complex, discussed in subsection 2.1. The systems are first equilibrated with classical MD in a periodic simulation box containing the isolated species plus 100 water molecules, with the same force-field as used in the complex case. CP MD simulations of the system were then run without any constraints for 6 ps, the first 3 ps serving as the equilibration period and trajectory analysis made during the latter 3 ps. CP MD simulation details are as those described in subsection 2.1 for the H-bonded complex case. No counterions are added for the ionic systems, since CP MD uses a neutralizing uniformly distributed charge in the simulation cell.³⁸

3. PROTON TRANSFER RESULTS

We begin our investigation of the mechanism for the H₂CO₃⋯NH₂CH → HCO₃⁻⋯⁺HNH₂CH₃ eq 1 PT reaction by analyzing the progression of several key nuclear coordinates within the reactive acid–base complex: the proton stretch and the O_A−N H-bond length (see Scheme 1). The accompanying progression of atomic charges is then discussed. Certain important qualitative aspects of the water solvent rearrangements associated with the PT will be noted. A detailing of such rearrangements in terms of a solvent coordinate, as well as the connection to reaction coordinates of this coordinate and the H-bond complex’s nuclear coordinates and change in charge character, will be presented in the following paper.⁵⁸

3.1. H-bond Complex Nuclear Coordinates

We commence with the proton coordinate, defined as the difference of the O_AH_A and H_AN stretch coordinates ( $q_{{\mathrm{O}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}}$ and $q_{{\mathrm{H}}_{\mathrm{A}}\mathrm{N}}$, respectively)

$$X_{\text{PT}}=q_{{\mathrm{O}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}}-q_{{\mathrm{H}}_{\mathrm{A}}\mathrm{N}}$$ (2)

Accordingly, negative and positive values of X_PT correspond to proton positions closer to the proton donor O_A and the proton acceptor N, respectively. Figure 1a displays X_PT and the O_A−N separation $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$ versus time for the fourth reaction trajectory, which serves as a sample for our collection of 10 trajectories. In Figure 1a, t = 0 is the time when the nuclear constraints used during the CP MD equilibration trajectory are released for this particular reaction trajectory. The reaction proceeds via a compression in the H-bond, with X_PT following $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$. The negative to positive passage of X_PT indicates the PT process. The ensuing fast X_PT product oscillations with a period of ∼10–15 fs are consistent with a proton stretch vibration in an H-bond ν_NH ∼ 2800 cm⁻¹⁶⁸. The ∼100 fs $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$ oscillation period visible in Figure 1a is due to the product ion pair H-bond vibrational mode with frequency ∼200 cm⁻¹; there is an impact of this vibration present in X_PT as the slower oscillation, visible after ∼50 fs.

Figure 1.

(a) Proton coordinate eq 2 X_PT (solid line) and (b) the normalized proton coordinate eq 3 x_PT (solid line) versus time for the fourth reaction trajectory. The H-bond coordinate $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$ (dashed blue line) is also indicated for comparison. Here t = 0 is the time at which the $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$ and $q_{{\mathrm{O}}_{\mathrm{A}}\mathrm{H}}$ constraints were removed. The vertical red dashed line in (a) indicates the PT occurrence time t_PT for that trajectory. (c) Ten trajectory-averaged x_PT values (solid line) and the O_A−N H-bond separation $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$ (dashed blue line) versus time, with t = 0 set for x_PT = 0, our definition of the PT occurrence. x_PT = 0 is indicated in both (b) and (c) as the red dashed line.

It is much more useful in following the PT in detail to define, following,^69–72 a normalized version of eq 2,

$$x_{\text{PT}}=\frac{(q_{{\mathrm{O}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}}-{\overline{q}}_{{\mathrm{O}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}})-(q_{{\mathrm{H}}_{\mathrm{A}}\mathrm{N}}-{\overline{q}}_{{\mathrm{H}}_{\mathrm{A}}\mathrm{N}})}{(q_{{\mathrm{O}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}}-{\overline{q}}_{{\mathrm{O}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}})+(q_{{\mathrm{H}}_{\mathrm{A}}\mathrm{N}}-{\overline{q}}_{{\mathrm{H}}_{\mathrm{A}}\mathrm{N}})}$$ (3)

where ${\overline{q}}_{{\mathrm{O}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}}$ and ${\overline{q}}_{{\mathrm{H}}_{\mathrm{A}}\mathrm{N}}$ are the average $q_{{\mathrm{O}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}}$ and $q_{{\mathrm{H}}_{\mathrm{A}}\mathrm{N}}$ values evaluated in the neutral reactant HOCOOH⋯NH₂CH₃ and the ionic product HOCOO⁻⋯⁺HNH₂CH₃, respectively. The reactant ${\overline{q}}_{{\mathrm{O}}_{\mathrm{A}}{\mathrm{H}}_{\mathrm{A}}}=1.02$ Å and product ${\overline{q}}_{{\mathrm{H}}_{\mathrm{A}}\mathrm{N}}=1.05$ Å values were obtained from the isolated species CP MD simulations, as discussed in subsection 2.3. The structure of eq 3 describes x_PT as a PT “order parameter” indicating whether the neutral or ionic H-bond complex is present:^69–72 x_PT is close to −1 for the neutral pair and is close to 1 for the ion pair. This motivates our definition of the PT occurrence time t_PT as the time that x_PT first crosses 0, the midpoint between the neutral and ion H-bonded complex pairs; t_PT for each trajectory is given in Table 1.

Table 1.

Proton Transfer Occurrence Times t_PT for the 10 Reaction Trajectories

reaction trajectory	1	2	3	4	5	6	7	8	9	10
tPT (fs)	41	61	40	58	60	49	33	65	75	53

Figure 1b displays x_PT and the O_A−N separation $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$ versus time for the fourth reaction trajectory (the results for all 10 reaction trajectories are presented in SI Figure S3). With the aid of x_PT, one sees that the first minimum in H-bond coordinate $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$ coincides with PT, which occurs (x_PT ∼ 0) at t_PT = t ∼ 60 fs. As indicated in Table 1, the PT occurrence times for all trajectories are similar: t_PT ∼ 40–75 fs. (In SI section S3, it is shown that a smaller initial O_A−N separation leads to a somewhat smaller PT occurrence time.)

In Figure 1b, there is a direct transition across the dividing line x_PT = 0 between the neutral pair reactant and the ion pair product, without any recrossing. Such a transition indicates that there is sufficient stabilization of the incipient carboxylate-protonated methylamine ion pair to avoid any immediate attempt at a return in the direction of the carboxylic acid-methylamine reactant pair. One interesting signature of the initial aspects of this stabilization apparent in Figure 1a and b is the larger period of the proton oscillations present in x_PT just after PT, which subsequently shortens. This basic stabilization is due to the combination of a slight increase in H-bond separation and especially a fast water solvent response stabilizing the contact ion pair; this stabilization is explicitly reflected in Figure 2 below for the proton potential energy curves.

Figure 2.

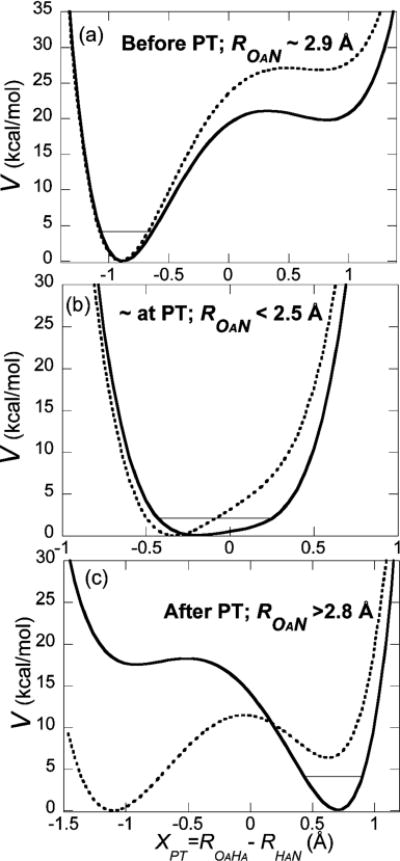
Proton potentials evaluated at three different time points along the fourth reaction trajectory: (a) before PT, (b) near the PT occurrence time t_PT, and (c) after PT occurrence. Solid bold lines are proton potentials with interactions with the water solvent (not including any solvent self-energy), while for reference the dotted lines are the vacuum proton potentials obtained by deleting the solvent contributions. Thin lines indicate the quantum ground vibrational level for the proton stretch of the proton potentials with water solvent, provided for discussion. The minima of both sets of potentials are set to zero to place them on the same scale. The H-bond length value or range is indicated for each case. (The relative energies of the potential minima with solvent (including solvent self energy) are given as (a) 0, (b) −12.5, and (c) −76.9 kcal/mol.) Note that the exothermic character of the aqueous phase reaction only becomes visible in panel (c), after H-bond and aqueous solvent changes.

The no-recrossing character of the proton coordinate transition in Figure 1b is repeated in the majority of the 10 trajectories in SI Figure S3. But for a minority of four trajectories there, the initial stabilization is evidently insufficient and there is recrossing of a mild character, i.e. just after x_PT reaches ∼1, it briefly drops to slightly below the x_PT = 0 line. But quickly after this recrossing, the proton again reaches x_PT ∼ 1 and is now successfully stabilized within the ion pair. Figure 1c shows that these slight recrossing events do not impact the overall behavior averaged over the 10 trajectories, and we continue to focus on the Trajectory 4 as our example trajectory before presenting averaged results. (Details of the ion pair stabilization, including the key water solvent motions involved, will be revisited in the following paper.⁵⁸)

Since the proton stretch vibration is typically faster than other nuclear vibrations, activated PT reaction is effected via the average proton position following the slower rearrangement of other nuclei, that is, that of the H-bond mode and the solvent.^{23–28,73,74} The stated time scale separation is confirmed for the classical treatment of the proton coordinate here by the many x_PT oscillations in the product within the period of H-bond compressions visible in Figure 1a and b. But a critical aspect of the present reaction is that it is barrierless, as will be seen explicitly in Figure 2 below, and is perforce more facile. One consequence of this is that there is a significant response of the heavier nuclear modes (e.g., the H-bond separation) and the water solvent to PT that primarily occurs after the PT occurrence.

The time scale separation leading to our ability to define a PT occurrence time has a useful consequence in that it allows an ensemble average of the trajectories referenced to the point of that PT occurrence, now discussed.

In order to present an ensemble picture for all ten reaction trajectories (in SI Figure S3), the time-dependent nuclear coordinates (cf. Figure 1b) are averaged over all these trajectories using a common reference time point, the PT occurrence time t_PT defined below eq 3, i.e. when x_PT = 0. All trajectories are synchronized at t_PT by shifting each trajectory in time, such that t = 0 occurs when x_PT = 0. The nuclear coordinates’ values for all trajectories are then averaged at every time point relative to t_PT, before and after PT.

Figure 1c presents this average picture for the H-bond nuclear coordinates. The H-bond compression after the release of the O_A−H_A and O_A⋯N constraints is evident, and inspection of SI Figure S3 shows that it is common to each trajectory, with PT occurring near the compression minimum. The x_PT oscillations visible in Figure 1b have averaged out, but the initial effective stabilization of the ion pair, that is, lack of recrossing of the x_PT = 0 transition line after the PT occurrence time t_PT, is dominant in the averaging, as we have already pointed out. Finally, the O_A⋯N H-bond vibration remains apparent, as is evident with the second $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$ minimum at ∼100–150 fs after PT.

3.2. Trajectory Analysis

In order to put these results into perspective, we now consider several key aspects of how the proton potential varies in a reaction trajectory and the important impact of the water solvent thereupon. Figure 2 displays proton potentials for three different time points along the fourth reaction trajectory, which are representative of before PT (at the Figure 1b trajectory’s starting point), during PT (near x_PT ∼ 0), and after PT (where $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$ first reaches ∼2.8 Å after PT occurrence at ∼50 fs post PT). These potentials were evaluated via quantum chemistry calculations (B3LYP/6-311+G**) for the carbonic acid-nitrogen base pair at various O_A-H_A and H_A-N separations, keeping all other nuclei fixed, with the surrounding water molecules treated as point charges (SCP/E charges: −0.8476 for O_W and 0.4238 for H_W). In order to elucidate the critical aqueous solvent effect on the proton potential, the potentials are calculated both with and without the presence of the water solvent point charges. We term the latter potential the vacuum proton potential and the former the proton potential with solvent. LJ parameters are not required for the present purposes: the van der Waals interactions with the proton-donor or proton-acceptor cancel out between the two potentials as the proton position is varied while the other nuclei are fixed; the van der Waals interactions with an H in an H-bond are negligible.⁷⁵

In general, the H-bond is not linear, that is, the O_A−H_A direction does not coincide with the H_A−N direction. Hence, the Figure 2 one-dimensional potentials are generated to best indicate the potential in the respective proton stretching direction: for the reactant complex, the Figure 2a potential was generated by moving the proton along the O_A−H_A direction, while in the product complex the Figure 2c potential is generated by moving the proton along the H_A−N direction. However, the H-bond is linear for short H-bonds, such that the proton potential is fairly independent of which proton direction is chosen; the short H-bond case Figure 2b was generated by moving along the H_A-N direction, even though its minimum is consistent with the reactant complex. The solid lines are the proton potentials in the field of the solvent water molecules, that is, the proton potential with solvent, while the dotted lines are the vacuum proton potentials. Both sets of potentials have their minimum set to zero to place them on the same scale.

The very considerable impact of the water solvent on the PT reaction is clearly evident in Figure 2. The asymmetry of the proton potentials including the aqueous solvent’s effect shifts from having the potential minimum near the carbonic acid’s O_A before PT occurrence to a minimum near the nitrogen base’s N after PT, with an evident strong correlation with the proton dynamics seen in Figure 1. Water solvent stabilization of the PT-transferred carboxylate-protonated methylamine is clearly essential for the reaction: the vacuum PT is unfavorable without this extensive solvent stabilization of the contact ion pair product. It must be pointed out however that the Figure 2 potentials without the solvent interaction, but which have been established via the solvation and the H-bond compression evident in Figure 1 already suggest that the H-bond compression plays a major role in establishing, for example, the central barrierless potential in Figure 2b and a potential well for the product in Figure 2c. In the detailed investigation of the aqueous solvent effects in the following paper,⁵⁸ we find that the major motion from reaction to proton transfer occurrence is the O_A-N H-bond compression rather than motion in the solvent. Evidently there is little water solvent preorganization from the solvation already existing for the reactant pair that is required for this exothermic reaction: its necessity is obviated by the energetic driving force, and most of the solvent motion occurs after the formation of an incipient carboxylate anion-protonated methylamine base ion pair complex.

We have also included in Figure 2, for perspective, the quantum ground vibrational level for the proton stretch coordinate at various points in the reaction (i.e., a quantum description which would replace a classical proton trajectory description). These levels were calculated as in this group’s previous PT work.^27–29,76 While we obviously do not present a full quantum treatment of the reaction, these levels would depict a quantum adiabatic PT reaction (rather than a quantum tunneling reaction)^23–29,77 for the eq 1 PT, although of a barrierless, nonactivated type, consistent with H₂CO₃’s acid strength and the reaction’s ΔpK_a difference, as anticipated in the Introduction.

However, the classical proton coordinate dynamics evident in Figure 1 indicates that there is proton vibrational excitation in the product compared to the reactant, which would not be consistent with adiabaticity in the sense of maintaining vibrational quantum number. We estimate that there is ∼11 kcal/mol in the product NH vibration; with estimated ground and first two excited NH vibrational levels in the product well of Figure 2c at 3.8, 10.7, and 16.2 kcal/mol above the potential minimum, this suggests that the first product vibrational level is excited in the PT reaction. Unfortunately, a fully quantum treatment for both protonic and other vibrations in the complex and the solvent would be required to deal accurately with this excitation and its decay, an aspect far beyond the capability of this first effort.

It is worthwhile pausing to note that the features emphasized in the preceding two paragraphs for the present exothermic PT reaction, vibrational excitation in the product and small requirement of solvent preorganization, with time, together with the subsequent, post-PT relaxation mentioned below, should also be central features of very exothermic excited electronic state, photoacid PT reactions.³¹

A key feature of the PT reaction, from either a classical or a quantum proton motion perspective, is a rapid shift in proton position at the time of PT occurrence. Figure 2b shows that near t_PT, the potential with solvent is fairly symmetric and characterized by a short H-bond length $R_{{\mathrm{O}}_{\mathrm{A}}\mathrm{N}}$, such that no barrier exists in the proton potential. This lack of a barrier allows the proton position to readily shift toward the product. For the classical proton motion involved in all the MD simulations of this paper, this proton shift is fast, following the slower H-bond motion. The proton becomes localized in the product H-bond complex at a larger ion pair H-bond separation, with attendant solvation by the polar water solvent, whose consequence is apparent in Figure 2. Further details of this stabilization, such as the timing and time scale of this solvation and the particular water molecules contributing to it, will be discussed in the following paper.⁵⁸

3.3. Charge Characterization for Proton Transfer

We now characterize the electrostatic charges and their change during the PT reaction for key atomic sites in the complex (see Scheme 1): the carboxylic oxygens O_A, O_C, and the remaining carbonic acid oxygen O_na, the nitrogen base atoms N, H_N, and of course the transferring proton H_A. The evolution of these charges is of course connected to the water solvent-assisted formation of the ion pair from the neutral pair complex and to the evolving proton potentials in the reaction (cf. Figure 2).

We have obtained the atomic charges for these sites via a natural population analysis (NPA)⁷⁸ during the course of the equilibration trajectory as well as each of the ten reaction trajectories. The averages of these NPA charges over these trajectories are displayed in Figure 3a as a function of time during the PT process. In order to highlight the ion pair formation, the time dependence of the total charges of the bicarbonate, methylamine and the transferring H during PT occurrence are shown in Figure 3b. The trajectory averaging is effected in a manner similar to that for Figure 1c. The equilibrium-averaged values of these charges are summarized in Table 2.

Figure 3.

(a) Trajectory-averaged NPA charges of the key atoms (H_A, H_N, N, O_A, O_C, and O_na) for the PT reaction in the HOCOOH⋯NH₂CH₃ H-bonded complex (see Scheme 1 for the atom labeling). t = 0 denotes the PT occurrence at x_PT = 0. The trajectory-averaged normalized proton coordinate x_PT (see Figure 1c) is also plotted versus time, right ordinate. The green dashed vertical line indicates when x_PT first reaches 1. (b) Total charges of bicarbonate, methylamine, and the transferring H as a function of time.

Table 2.

Averaged NPA Charges of the Key Atoms (O_A, O_na, O_C, H_A, N & H_N) and the Net Charge of the Carbonic Acid/Bicarbonate Anion and the Methylamine/Protonated Methylamine Moieties before/after PT^a

atoms/molecules	charge (e) before PTb	charge (e) after PTb	charge difference (e) (after – before)
OA	−0.73	−0.83	−0.10
Ona	−0.73	−0.80	−0.07
OC	−0.73	−0.85	−0.12
HA	0.53	0.47	−0.06
N	−0.89	−0.74	+0.15
${\overline{H}}_{\mathrm{N}}$ c	0.37	0.44	+0.07
carbonic acid/bicarbonated	−0.08	−0.93	−0.85
methylamine/protonated methylamined	0.09	0.91	0.82

^aAtom labeling is as in Scheme 1.

^bThe charges before PT are obtained from an average over configurations from the equilibration trajectory, while those after PT are obtained from an average over configurations from reaction trajectories for t > 100 fs (t = 0 corresponds to PT occurrence).

^cThe overbar indicates an overage over the two nitrogen hydrogens, both before and after PT. This number needs to be multiplied by 2 in order to arrive at the totals listed at the bottom of the table.

^dFor the X/Y notation, X and Y are respectively the species before and after PT. Due to an averaging over a finite number of configurations, the carbonic acid/bicarbonate charges are not exactly equal and opposite of the methylamine/protonated methylamine.

An initial glance at Figure 3a indicates a distinct transition at t ∼ 5 fs, that is, slightly after the PT occurrence; this transition occurs when the normalized proton coordinate x_PT (eq 3) first approaches its product value of 1 (green vertical line in Figure 3), consistent with the formation of the product ion pair. This transition is most pronounced for the acid carboxylate oxygens and the base nitrogen; it is less significant for the transferring proton H_A, since this proton’s charge remains fairly constant, ending up at a slightly smaller value in the ion pair product (see also Table 2). (We will return to this important near constancy below.) The bicarbonate moiety’s increase in anionic character in the product (see Table 2) is evident in Figure 3b, reflecting the increased magnitude of the negative charges on its carboxylate oxygens O_A and O_C, whose near equality reflects resonance in the anion (see Figure 3a and Table 2). The noncarboxylic oxygen O_na exhibits a smaller increase in negative charge magnitude.

Turning to the base, the proton-accepting N’s hydrogens are also reasonably constant, with the (average of the two amine hydrogens) H_N charge ending up slightly increased in the ion pair product. The final average H_N charge becomes nearly equivalent to that of the transferring proton H_A, since the latter is becoming the third hydrogen of the incipient NH₃ group. H_A remains slightly more positive than the average H_N charge, because it is still polarized in the H-bond with the bicarbonate anion. The combination of the N charge becoming less negative and the slight increase in the two H_N positive charges reflects the loss of electron density by the base. The base’s net charge change after PT to generate the protonated base, seen in Figure 3b and Table 2, involves the combination of this positive charge change with the ∼0.5e proton charge.

The Table 2 total charge values indicate a net charge change (acid’s loss and base’s gain) of ∼0.8. This includes the transferring proton H_A charge during PT with its approximately constant value ∼ + 0.5e; the difference ∼0.3e is the net negative charge flow from the nitrogen base toward the incipient bicarbonate anion. That the increase of the bicarbonate moiety’s negative charge properly mirrors the increase of methylamine’s positive charge is especially clear in the time dependence displayed in Figure 3b. As will be seen in ref⁵⁸., this evolution is strongly coupled to the solvation dynamics of the nearby water molecules surrounding the H-bonded ion pair complex.

It is important to point out that this detailed charge flow picture for PT in the acid–base complex is consistent with the Mulliken charge transfer picture for PT.^{23–25,73,79–82} In that picture, electronically adiabatic PT in an H-bond is primarily viewed as an adiabatic electron transfer from the base to the acid very strongly concerted with H transfer from the acid to the base (hence the H_A charge close to 0.5); as is appropriate for this strong H-bond, the process is characterized by a very large electronic coupling between the two VB states associated with the reactant and product forms in eq 1.^23–25,73 We will present elsewhere a detailed electronic orbital analysis which demonstrates that this charge transfer is from a nonbonding orbital of the methylamine base to an antibonding orbital of the carbonic acid.

4. CONCLUDING REMARKS

We have presented here a study, focused largely on the evolving acid and base coordinates and charges, of the proton transfer (PT) from carbonic acid H₂CO₃ to the methylamine base CH₃NH₂ in a contact hydrogen-bonded pair H₂CO₃⋯CH₃NH₂ in aqueous solution using Car–Parrinello (CP MD) molecular dynamics simulation. The observed times for PT occur after the trajectory start from an intact acid–base H-bonded complex varies from 33 to 75 fs over the ten trajectories examined. The occurrence of the PT is strongly correlated with compression of the H-bond in the acid–base complex, and the contact ion pair product is strongly stabilized by the aqueous solvent, as shown by calculated proton potential energies in the presence of the water solvent. The PT event itself is extremely rapid and requires only ∼1 fs. The extremely short PT times (33–75 fs) associated with the PT process observed here are consistent with a markedly downhill in free energy process, that is, a large positive ΔpK_a for the carbonic acid–methylamine base pair. In particular, it is consistent with the current assessment of the pK_a (3.49 ± 0.05) for the intact carbonic acid H₂CO₃.^16,18 These results support the proposition that carbonic acid is a potentially important proton donor in, for example, human blood and in the oceans,¹⁸ an issue raised in the Introduction.

The time-dependent analysis of the charges of the atoms of the complex, which confirms the formation of a contact ion pair due to the PT reaction, also demonstrates carboxylate group resonance within the carboxylate group of the bicarbonate ion in that ion pair. The PT is shown to occur via charge transfer from the methylamine base to carbonic acid without any change in the transferring proton’s charge, which remains approximately midway between that of an H atom and that of H⁺; these results support a Mulliken CT picture for the reaction.^{23–25,73,79–82}

Further aspects of the PT reaction, including discussion of reaction coordinates and further elaboration of the role of the water solvent in the reaction, in particular the participation of water solvent dynamics and local hydration stabilization, will be presented in the following paper.⁵⁸

As with any simulation methodology, especially one involving electronic structure aspects, it is useful to also consider other results in addition to those in the present work carried out in Boulder. In particular, results of QM/MM simulations with the MP2/dzv level of theory for the electronic structure of the H-bonded complex carried out in the Miller group will be presented separately elsewhere.