Explaining the Transition from Diffusion Limited to Reaction Limited Surface Assembly of Molecular Species through Spatial Variations

Abstract

Surface assembly is often decomposed into two classes: diffusion and reaction limited processes. The transition between the two cases is complex because the dynamics are so different. In this article, we simulate, explain, and experimentally discuss the evolution of the spatial distribution for surface assemblies with diffusion limited and reaction limited processes. Explicitly, we demonstrate that diffusion limited and reaction limited processes show some temporal differences, but more importantly, we show that the spatial arrangements are different enough to discriminate between the two cases. Using fundamental properties, such as the diffusion constant, we calculate the evolution of the spatial profile and derive from physical, heuristic models the assembly rate for reaction and diffusion limited processes based on the individual particle’s interactions with the surface. Finally, we confirm the spatial profile differences between diffusion and reaction limited cases by experimentally measuring the surface assembly between two molecules of similar size, but having different assembly routes. Unique to our description is that we have derived and simulated everything through the particle picture in place of ensemble descriptions such as the diffusion equation, and we show the equivalence between our heuristic formulas and those derived from the diffusion equation.

Introduction

The dynamics, both temporal and spatial, of surface assembly are important for the optimization and prediction of limitations for processes.^1,2 By understanding and accurately modeling the surface reactions and assembly, new architectures can be implemented to improve upon existing technologies and to push assay-based sensors to higher sensitivities.^3,4 In general, there are two limiting agents to the speed of a surface reaction or assembly: the diffusion of the reactants to the surface and the chemical or physical kinetics of the analyte’s interaction with the underlying substrate.^5,6 As such, the surface reactions and surface assembly are decomposed into two classes: diffusion limited and reaction limited processes. The former is typically understood as scenarios in which the reaction/assembly barrier is low, such that the rate is set by the transportation of the particulates in solution; meanwhile, the latter is the process in which there is a significant chemical barrier for deposition.

The temporal dynamics of diffusion limited versus reaction limited processes are treated differently. In the diffusion limited or barrier-less adsorption, the governing equation is the diffusion equation; whereas in reaction limited scenarios, the problem is decomposed into a two compartment model: an “inner” and an “outer” compartment.^7,8 The focus of these works has been dedicated to the temporal dynamics, but this two compartment model fails to explain the spatial difference between a diffusion and reaction limited process.

Recently, we showed that the probabilistic interpretation of the diffusion equation correctly predicts the spatial flux of particles assembling onto a circular patch.⁹ We measured that during particle adsorption onto a circular patch, there is a bias of particle assembling at the rim. The analytic form of the flux with the same boundary conditions shows a divergence at the rim, and we successfully and quantitatively compared the theoretical flux against our experiments. This divergence has been discussed previously,^4,10 but was never quantitatively measured until recently. The key to our recent work is the barrier-less nature of the deposition—there was no energetic cost to the particles adsorbing. Many assembly processes, however, have a barrier to deposition, and it stands to reason that if the temporal dynamics are different, so too must the spatial. Indeed, there is some experimental and simulation evidence to corroborate this spatial evolution,¹¹ but explaining and mapping out the evolution remains unsolved, particularly from the individual particle picture.

In this article, we offer a description of the transition from diffusion to reaction limited processes. Using simulations, we show that we can accurately map out both the spatial and the temporal dynamics of processes between the two extreme cases by accounting for the average behavior of individual particles. Furthermore, we derive through heuristic arguments a formula for the temporal dynamics, and we show that it is functionally equivalent to rates derived from the diffusion equation using boundary conditions known as Collins–Kimball method,¹² to describe diffusively influenced reactions. Finally, we experimentally confirm that diffusion limited and reaction limited processes have exceedingly different spatial profiles by comparing the assembly of the two fluorescent dyes. The two dyes have approximately the same size, but different modes of binding to the surface.

Methods and Materials

Simulations Details

Simulations were carried out using in-house developed software in MATLAB. We used Langevin dynamics (LD) assuming a Gaussian distribution Brownian force for a fixed period of time. Details on the LD are further described in the Supporting Information (Figure S2). In the simulations, particles were free to move under the influence of Brownian motion in a box; the particles were assumed to have no interactions among themselves. The box was designed such that five of the six walls were perfectly reflecting and connected to a reservoir. The sixth wall was designed with a concentric circular patch, such that anywhere outside the patch, particles would perfectly reflect, and anywhere inside the patch, any particle would bind with an efficiency parameter given by p. We refer to anytime a particle that interacts with the patch as a strike event, and anytime a binding event occurred, we refer to it as a successful strike.

To determine the information about the flux, the spatial location and temporal information of 10⁴ successful strikes were recorded for every p value. The spatial information was translated into a distribution by binning the radial information and properly normalizing each by the respective area given by the radial annulus defining each bin. To keep the particle number fixed, once a particle successfully struck the patch, a new particle was randomly added at one of the five reservoir walls.

Materials and Preparations

For this work, two thermally activated polymeric materials were used: an amine polymer and a polyphthalaldehyde (PPA) polymer. Details on the polymers can be found in the literature.^13,14 Under applications of heat, the amine polymer cleaves a protection group, leaving behind an exposed functional amine group while the PPA unzips from its polymeric form to its monomeric units.

Silicon samples of the amine polymer were prepared as previously described;^14,15 a brief description along with the chemical structures is provided in the Supporting Information (Figure S1). The samples had approximately 70 nm of the amine polymer. Just before the experiment, PPA was layered (∼7 nm) on top of the amine polymer.

Two fluorophores were used as a comparison between the diffusion and reaction limited process: N-hydroxysuccinimide ester-modified Alexa 488 (NHS-Alexa) and pyranine (trisodium 8-hydroxypyrene-1,3,6-trisulfonate). Prior to the experiments, diluted solutions of 10 nM in 0.1 mM phosphate buffer or 100 nM in 0.1 mM phosphate buffer were prepared.

Chemical Patterning and Labeling

To pattern the polymer materials, we employed thermos-chemical scanning probe lithography (tc-SPL). tc-SPL provides a means to remove the top layer of PPA and activate the underlying amine by locally heating the surface and causing a chemical or physical transformation on the surface.^13,16,17 All patterning were performed in the air. To average over a set, a 2 by 2 matrix of 5 μm radius patches spaced 40 μm apart was written into the sample. To minimize the topographic edge effects, the patterns were written at a fixed depth and a fixed temperature, see refs (9) and (15).

After tc-SPL patterning was completed, the samples were ready for fluorophore labeling. For each fluorophore, we do a low-concentration labeling and a high-concentration labeling. Between the low- and high-concentration labeling, fluorescent images were captured. The low-concentration labeling was attained by placing the samples into the separate baths containing low concentrations of the respective fluorophore for 1 min. The samples were then rinsed with phosphate-buffered solution and water and imaged with a Nikon TE eclipse epi-fluorescence microscopy equipped with a digital camera (Hamamatsu CMOS Digital Camera ORCA-Flash 4.0). Fluorescence images were taken with an exposure setting of 500 ms. All imaging were performed in deionized H₂O.

For high-concentration labeling to saturate the patterned areas, the samples were placed into high concentration solutions of their respective fluorophores for ∼45 min. They were rinsed and imaged with the same microscope as previously described. In addition, background images for each fluorophore illumination were collected.

Image Processing

Image processing was carried out using a combination of ImageJ and MATLAB. To correct for uneven illumination, the respective images were divided by the respective background images. The images were treated to an in-house developed tracking program to find the center of the patches. Using the computed center, the image intensities were collected as a function of radial distance (as measured from the pixels center), binned, and averaged. The bins were normalized by the annulus area. Processing was performed in this way to avoid interpolation and to average over the entire circle in the place of a single cross section. Finally, the background signal was subtracted from the data set. The averaged profiles were normalized against the saturated pattern intensity as measured after the exposure to high fluorophore concentration. Figure 4 shows the final plotted values as a function of radial distance for both the unsaturated patch and the saturated patch images.

Figure 4.

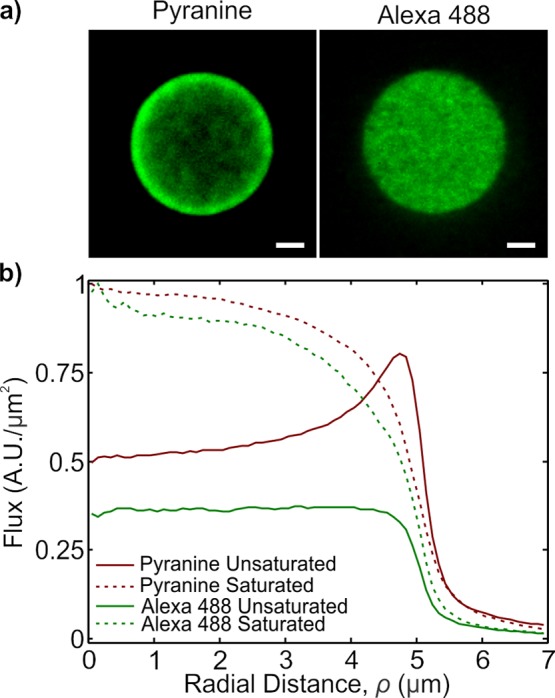
(a) Fluorescence image of pyranine and Alexa 488 before the surface reaction has saturated. Pyranine, which will have a low barrier to deposit onto the patterned area shows a divergence at the rim, in agreement with the diffusion equation; Alexa 488, which requires a chemical reaction to deposit onto the patterned areas, does not show a divergence. Scale bars 2 μm. (b) Plots of the fluorescence as a function of the radial distance (normalized by the area). This semiquantitative plot demonstrates the spatial differences between adsorption in a reaction limited process vs a barrier-less, diffusion limited adsorption. The plots are normalized against signals obtained from a saturated pattern; the dashed lines show the fluorescence signal for the saturated pattern.

Results and Discussion

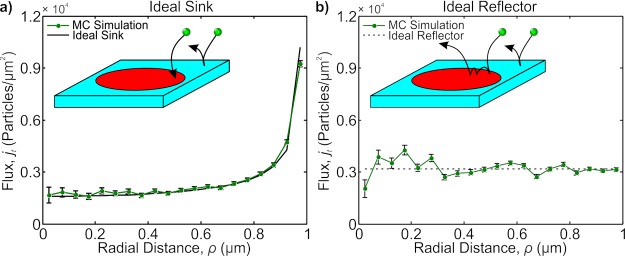
To understand the difference between diffusion limited and reaction limited processes, two ideal cases are shown in the insets of Figure 1a,b: an ideal sink and an ideal reflector. In both cases, particles undergoing Brownian motion are free to diffuse in a box; individual trajectories of the particles are calculated from the Langevin equations. Five walls of the box act as a reservoir, and the sixth wall is a surface with a concentric circular patch on it (R = 1 μm). We refer to a particle hitting the patch as a strike event; moreover, we call a strike successful if the particle sticks to the patch. The chance that a particle will successfully strike the patch is given by the efficiency parameter p. We define the flux, j(ρ), as the distribution of successful strikes per unit area per second (ρ is the radial distance from the patch’s center).

Figure 1.

(a) Monte Carlo (MC) simulation of the position-dependent flux. The solid line is the theoretical curve obtained from a perfectly adsorbing patch; the MC simulations correctly estimate the divergence theoretically predicted. Inset shows a schematic representing the perfectly adsorbing patch (red), whereas the rest of the surface (blue) is perfectly reflecting. (b) MC simulation of the position-dependent “flux” for a perfectly reflecting patch. Here, flux means the position the particle reflected from the patch. The solid line represent the theoretical curve for a uniform distribution. Inset shows a schematic of a perfectly reflecting patch (red) with a perfectly reflecting background (blue). In the schematic, the particle is shown bouncing along the patch to indicate how the divergence seen and simulated in (a) is smeared out.

To simplify the discussion, we decompose the patch’s flux into a magnitude component, 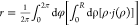, and a spatial distribution component, ι(ρ), such that we can write the flux as

1

We interchangeably refer to ι(ρ) as the spatial flux or the flux’s spatial distribution.

In the ideal sink case (p = 1), each strike event is successful, and with each successful strike event, the position and time of the strike are recorded. We concern ourselves with the high friction limit of the Langevin equations, and using the Smoluchowski equation,¹⁸ we expect the flux to be well-approximated from the diffusion equation. For these boundary conditions, the spatial flux, as defined in eq 1, is well-approximated by¹⁹

2

where R is the radius of the patch.

As shown in Figure 1a, eq 2 accurately predicts the particle distribution on the patch extracted from simulations. We note, the functional form in eq 2 diverges at the patch’s rim. The infinite divergence is not physically real; the derivation of eq 2 comes from the assumption of continuous media which has an infinitesimally small mean free path (MFP). Realistically, particles have a finite (albeit small) MFP. The MFP acts to smear out the divergence, and so eq 2 is only valid over length scales greater than the MFP. For this work, we always present plots with averaging over length scales several times larger than the simulated MFP (here we use ∼12 nm to expedite simulations, but the results presented here can be applied to smaller MFPs).

In the ideal reflector (p = 0), we measure the distribution of all strike events for a patch which perfectly reflects (i.e., all strike events are unsuccessful). We refer to this distribution of these unsuccessful strike events as the reflecting flux. Given that the patch is not biased in anyway, we expect the reflecting flux for the ideal reflector to be uniform. Figure 1b confirms this with simulations by showing a flat spatial flux.

The key difference between the ideal sink and the ideal reflector is the nature of the particle–patch interaction and subsequently how frequently an unbound particle interacts with the surface. The ideal sink is an averaged measure of a particle’s first encounter with the patch in solution, whereas the ideal reflector also accounts for the second, third, fourth strikes, and so on (see Figure 1b inset). These subsequent hits blur out the rim’s divergence measured in the ideal sink, and ultimately these additional encounters cause the reflecting flux to be uniform across the patch. We refer to this sequential hitting mechanism as bouncing. It may seem counterintuitive that the particles would continuously return to the surface quickly and repeatedly; however, the explanation comes from a problem in probability known as the Gambler’s Ruin.^20,21 In the particle picture, the Gambler’s Ruin mathematically guarantees that any freely diffusing particle, which is any distance away from the surface, will always return back to the surface. The Gambler’s Ruin analogy applies to every particle, independent of the particle’s history; this independence guarantees that reflected particles continuously return to the surface. Moreover, if we treat the problem discretely, one expects the particle to return with a time distribution given approximately by²²

3

where q_d is the discrete return time distribution function, τ is the discrete time step, and t is time. Introducing a more continuous model, we can use the fact that the particle has an MFP, l, and assuming the particle moves approximately that far upon reflecting from the surface, we can calculate the continuous return time distribution through first passage time theories as²³

4

where D is the diffusion constant. The long-time functional form of eqs 3 and 4 are equivalent (∼t^–3/2).

Physically real situations are somewhere between the ideal sink and ideal reflector. In a binding situation,²⁴ there is a certain probability, p, that a particle/molecule will react with the substrate. What determines p is a combination of physical (e.g., electrostatic repulsion), chemical (e.g., activation energy), and structural (e.g., orientation) interactions between the particle and an activated surface. We treat p as a representation of a barrier imposed by the various interactions between the particle and the surface. For a chemical reaction, it can be related to fundamental chemical and physical constants.²⁴

With a high p ≈ 1, we expect the particles to bind with high efficiency, corresponding to a low barrier case or a diffusion limited process. Conversely, a small p ≈ 0 is indicative of a large binding barrier case or a reaction limited process. Naively, one may assume the boundary conditions for the diffusion equations proportional to p. This is equivalent to decomposing the solution into two classes: those particles that can overcome the barrier and those that cannot. This assumption fails because each interaction between the surface and particles must be treated independently. Rescaling the problem only provides information about the first encounter between the particles and the patch while neglecting the subsequent independently treated interactions between the surface and particles not binding. In light of the bouncing mechanism described for the ideal reflector, particles not binding at the first encounter with the patch further diffuse until they eventually bind. As a result, we cannot expect a simple rescaling of the solution to hold. This is especially apparent if one thinks in terms of a structural barrier caused by a particle needing the correct orientation to bind. On first strike, the particle may be incorrectly oriented, but with each subsequent hit, the orientation changes, until ultimately there is a successful strike event.

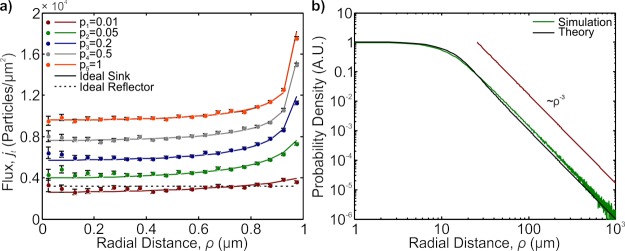
Understanding that we have to treat the strike events as independent, we expect the flux to act as somewhere between the flux for an ideal sink and reflecting flux when p is between 0 and 1. As p gets closer to 1, the divergence associated with the ideal sink will have little chance to smear out, and the flux will look more similar to the ideal sink. As p gets smaller, the divergence will smear out and if p is low enough, the flux will exhibit spatial behavior closer to the ideal reflector. To test this hypothesis, we ran simulations with our particles in a box. For each value of p, we ran the simulation subject to the strike events having a probability p for success. In Figure 2, we plot the results for five different probability values (p = 0.01, 0.05, 0.2, 0.5, and 1). We observe that as p changes from high-efficiency values (p = 1, 0.5) to low-efficiency values (p = 0.05, 0.01), the spatial flux goes from looking similar to the ideal sink to exhibiting a more uniform flux as associated with the ideal reflector, confirming our hypothesis.

Figure 2.

(a) MC simulation of the position-dependent flux for various probabilities of adsorption (p = 0.01, 0.05, 0.2, 0.5, and 1). The solid black line is the theoretical curve obtained from a perfectly adsorbing patch (overlaps with p = 1 curve); the dashed black line represents the distribution of particle reflections for a perfect reflecting patch. As the p value changes from an ideal sink (p = 1) to an ideal reflector (p = 0.01), the divergence predicted from a perfect sink disappears and the distribution approached that of a uniform one. The solid colored lines represent the curves calculated from eq 7. The curves are offset to help distinguish different p values. (b) log–log plot of the tRFD (green) along with the approximate curve (black) described in detail in the Supporting Information. The ρ^–3 curve is provided as a guide.

The evolution of the spatial flux as a function of p can be mapped out by properly accounting for all attempts that the particles make to bind to the patch. As determined by simulation, the first strike attempt distribution (ι₁) is well-mapped by the diverging flux analytically represented in eq 2. The chance that a particle survives the first strike is given by the survival, s = 1 – p, and we need to only consider the surviving particles’ average trajectories. The Gambler’s Ruin predicts that the surviving particles will return to the surface and by using the return time distributions such as those approximated in eqs 3 and 4, we can compute the temporally averaged return displacement distribution function (tRDF). The tRDF is a measure of the lateral displacement upon returning to the surface given that a Brownian particle initially started at the surface. In Figure 2b, we show a log–log plot of a tRDF’s simulation along with an analytic approximation. To get the approximate curve, we used the fundamental solution of the diffusion equation weighted against the continuous return time distribution in eq 4. We provide the full details for calculating the approximate tRDF in the Supporting Information. We note that the distribution’s tail asymptotically scales as ρ^–3, decisively not Gaussian. This tail is similar to those observed and discussed in the anomalous surface diffusion, the nature of which is not present in our simulations²⁵⁻²⁷ (i.e., our simulations assume the particles perfectly reflect, with no short-termed adsorption). This heavy-tail is a consequence of averaging temporally in conjunction with the return time distribution’s functional form.

We calculate the average lateral distribution for the surviving particles after the first strike (h₂) as a convolution (NB: We slightly abuse the term convolution here; this is a cross-correlation with a negative argument but because of symmetry, we can replace this with a convolution) of the first strike distribution, ι₁, with the tRDF

5

where S is the weighted survival probability 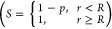, ⊗⁽²⁾ is the 2D convolution, and g is the tRDF. The distribution h₂ relates the lateral information about where, on average, the particles will return to the surface after surviving the first strike; it includes the particles that survive the first strike attempt and return to the surface either inside or outside the patch. For subsequent bounces, those outside the patch always survive (S = 1, r < R) but those inside the patch have a survival probability given by 1 – p. We call this the second bounce distribution, distinguishing it from ι₁ which is the first strike distribution.

To determine the third bounce distribution, h₃, we can use eq 5 substituting h₂ in place of ι₁. For each subsequent bounce, there is a contribution to the patch’s spatial flux, and we calculate the total distribution as the sum of each of these contributions

6

where P is the probability distribution for binding (P = 1 – S), and

In Figure 2, we show these results plotted against the simulation as the solid lines. The agreement between the theoretical and simulated curves confirms the validity of eq 6. Effectively, what we have computed is the flux’s spatial profile for a particle which has a certain probability of binding to the surface. Coupling this profile with the information about the flux’s magnitude provides a complete description for the average boundary condition on the patch.

We can determine the magnitude of the flux, by measuring the deposition rate; the rate is the total flux on the patch. In Figure 3, we show how the rate (number of particles/s) changes as a function of p. We observe that as p goes up, the rate increases up to some maximal level set by the diffusion. We can estimate this bound with the help of the diffusion equation, which for an ideal sink in an infinite medium goes as r_s = 4DC_BulkR; using values from the simulation, we get a rate given by ∼96 particles/s. The simulation revealed at a magnitude of approximately 105 particles/s. The discrepancy between the theoretical and simulated values comes from the fact that we are working with a finite-sized system. To compensate for this, we need to rescale C_Bulk to an effective bulk concentration, C_Bulk^eff. We describe in the Supporting Information how to calculate the effective concentration. Upon substitution with the effective concentration, we estimate the rate as 105 particles/s, which is in good agreement with the simulated values. We note that this rate represents the first strike rate, and as a result, it is the limiting time scale on the deposition process, a fact previously discussed.⁴

Figure 3.

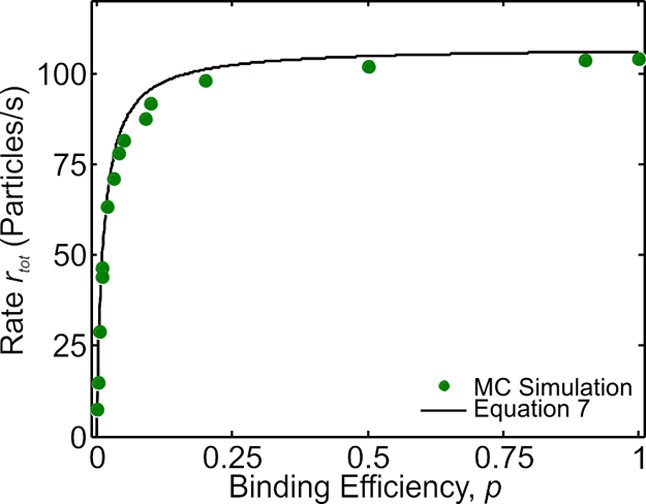
Plot of overall rate as a function of the adsorption rate value (p). The points represent values extracted from simulation, whereas the line represents the heuristic eq 7 discussed in the text. We note, the rate does not change drastically for significant changes in p because the effect from the increased attempts at adsorption from “bouncing” particles at deposition compensates for losses against an increased barrier.

Interestingly, Figure 3 shows that over 2 orders of magnitude of change in p, the rate only decreases by a factor of ∼2. Physically, this is a manifestation of the particles continuously bouncing against the patch subject with a return rate which is much faster than the first strike rate. To account for the rate change as a function of p, we propose to compute the average time for a successful strike ⟨τ_tot⟩ = 1/r. The first strike on average takes τ_s = 1/r_s = 1/4DC_Bulk^effR; with a survival probability given by 1 – p, the particle will strike again with some effective revisiting frequency r_d and consequently an effective revisiting time step τ_d = 1/r_d. For each subsequent strike, the survival probability scales by a factor 1 – p with approximately the same repeating frequency. Because the first profile is spatially biased, the revisiting frequency should change very slightly as a function of time, but this change is negligible for a decent approximation. We can estimate the average total rate as

7

where we have used the geometric series to simplify the above equation. To find a good estimate for r_d, we can either use simulation results obtained from the ideal reflection or with the formula derived in the Supporting Information: 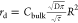(where τ is a small time step during which the particle’s motion is unaltered and R is the patch radius). In Figure 3, we have plotted eq 7 against the simulated data. The agreement suggests that eq 7 is a very good approximation to the rate.

There is an attractive and physically intuitive nature about eq 7. At p ≈ 1 values, the rate is proportional to the diffusion limited rate, but at small p (p ≈ 0), the rate is given by r_tot ≈ p·r_d, that is, the reaction limited rate. Equation 7 fills in the gaps between these two extreme cases. Furthermore, the spatial difference between the diffusion and reaction limited process is embedded in eq 7. We know that r_s ∝ R and the collision frequency is proportional to R². The extreme limits (p ≈ 1 and p ≈ 0) reveal the rates as proportional R and R², respectively. The only way for the rate to be proportional to R is with a nonuniform flux, but with a uniform flux, the rate is automatically proportional to R². This is exactly the results we show in Figure 2. Moreover, this tells us physically how to differentiate between a diffusion and reaction limited surface reaction: by examining how different-sized spatial elements will fill. If we take the number of binding sites, N, as proportional to R², the time scales for a diffusion limited process, t_diff ≈ N/r_s ≈ R²/R ≈ R, implying that the smaller the patch, the less time it takes to fill. For a reaction limited process, t_rxn ≈ N/r_d ≈ R²/R² ≈ 1, meaning the time scale is size-independent.

Finally, we observe and note the equivalence between this formula and formulas derived through the Collins–Kimball method. The Collins–Kimball method attempts to rectify the boundary conditions by equating the flux to the local concentration; it predicts the rate for diffusively influenced depositions. If we define r_rxn = p·r_d, then eq 7 can be rewritten as

8

where in the last step we have assumed r_rxn ≫ 0 (meaning it only contributes when p ≈ 0). The right-hand side of eq 8 is equivalent to formulas derived from the Collins–Kimball boundary conditions.^12,28,29 Here, however, we have derived the equation through the individual particle picture, not the ensemble picture.

Figure 4 shows the experimental evidence that the spatial distribution changes as a function of binding efficiency. We measure the fluorescence signal from two probes that have different modes of deposition. The first fluorophore is pyranine, which is a negatively charged UV-excited dye. There is no chemical functionality associated with pyranine, implying that the only binding forces are electrostatic or van der Waals in nature. To eliminate long-range electrostatic forces, we buffered pyranine with a Debye length of ∼30 nm in 0.1 mM phosphate buffer (pH ≈ 7.5); this Debye length is short in comparison with the patch diameter (10 μm). The second fluorophore we introduce is Alexa 488. To bind to the patch, the NHS group must undergo a chemical reaction.¹⁶ This chemical reaction is fairly efficient, requiring some buffering (0.1 mM phosphate buffer).

Both dyes are relatively small (pyranine molecular weight (MW) ≈ 524.4; Alexa 488 MW ≈ 643.4). On the basis of their sizes, we estimate the diffusion constant for both dyes to be fairly similar and on the order of 100 μm²/s. The key difference between the dyes is the different binding efficiencies of the dyes. Pyranine is a barrier-less deposition process, which should allow it to deposit in a fashion closer to that of an ideal sink. Alexa 488, however, has a barrier caused by the structural and chemical effects: the ester group must correctly face the amine group to react and the molecule itself must have enough energy to overcome the activation energy barrier for the reaction to take place. As a result of these effects, we expect the Alexa fluorophore has a lower efficiency in deposition, causing the first strike’s divergence to smear out, until ultimately the profile looks uniform.

To deposit the dyes onto a circular patch (R = 5 μm), we use tc-SPL^17,30 to write chemical patterns into a polymer stack consisting of a PPA layer on top of an amine polymer layer. The details of tc-SPL and the polymer can be found elsewhere.^13,17 Briefly, tc-SPL uses thermal probes to locally heat a surface and under appropriate conditions, the induced temperature profile can decompose or activate the underlying substrate. In particular, under applications of heat, PPA unzips from its polymeric structure into its monomeric units,¹³ whereas the amine polymer cleaves a protecting chemical group, leaving behind an exposed, functional primary amine.^14,16 We note, the activated primary amine in water solutions protonates, creating positively charged patterned areas. PPA acts as a passivating agent to help prevent nonspecific adsorption of the dyes, whereas the activated amine polymer acts as the binding agent.

To ensure the reaction is not saturated, short times (∼1 min) and a low concentration of fluorophore (10 nM) were employed. These values came from the “back-of-the-envelope” calculation based on the ideal sink solution and an estimated functional amine density of ∼0.1/nm² (i.e., ∼1 amine in a 3 × 3 nm² square). With these assumptions, the maximum number of sites available for deposition is N_max ≈ 7.5 × 10⁷, and the ideal deposition rate is 1.2 × 10⁴ molecules/s, which requires about 1 min to fill approximately 10% of the patch. Fluorescence images were taken with an epifluorescence microscope, and Figure 4a,b shows the acquired fluorescence images; we observe the clear difference in the spatial distribution of pyranine versus Alexa 488. Pyranine exhibits preferential deposition at the rim, whereas Alexa 488 deposits uniformly across the patch. This is consistent with our argument that pyranine’s deposition will be similar to the ideal sink, whereas Alexa 488 will be closer to the ideal reflector.

To verify that we had not saturated the binding reaction, we placed the samples back into higher concentration of their respective analyte (100 nM in 0.1 mM phosphate buffer for ∼45 min). We then measured the saturated patch’s fluorescence signal as a standard for normalization. In Figure 4c, we semiquantitatively plot the fluorescence signal for both dyes as a function of radial distance. These curves have been background subtracted and normalized with respect to the fluorescence signal measured from the final saturated patterns (dashed lines in Figure 4c). As qualitatively seen from the fluorescence images, the semiquantitative data show a clear, measureable difference between the two spatial adsorption profiles.

Conclusions

In this article, we have presented a series of simulations and thought experiments to help understand the difference between diffusion limited and reaction limited processes. We introduced a binding efficiency parameter, allowing us to map out how the spatial profile and temporal scales evolve. We experimentally verified that under cases of highly efficient deposition akin to a diffusion limited process, the molecules on average act as expected from the diffusion equation. With a less-efficient (reaction limited) process, the deposition of molecules deviates from the ideal sink and deposits in an increasingly uniform manner. In the reaction limited case, the molecules require a finite number of binding events for the deposition to occur. Using mathematical and physical arguments, we can predict not only the spatial profile but also how the rate changes as a function of efficiency. What is attractive about our presented approach is that both the profile and the rate can be solved for in-real situations using only fundamental properties of a molecule such as the diffusion constant and reaction kinetics buried in the Arrhenius equation. Furthermore, the method developed here can be used for other geometries and is not limited to the 2D case discussed.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.7b03050.

• Chemical structure of the amine polymer and the PPA passivating layer and schematic of the layering of the polymer materials; simulation of 3D motion of an ensemble of particles; schematic of a particle leaving the surface and eventually returning some lateral displacement away; plots showing the comparison of data extracted from simulation with temporally averaged return displacement distribution function and simulated and estimated tRDF for large displacement; log–log plots of the relative tRDF for different mean free path values; and cross section of the concentration profile for an infinite system (PDF)

Author Present Address

^† Now at SwissLitho AG, Technoparkstrasse 1, Zurich 8005 (U.D.).

The authors declare no competing financial interest.