Skip to main content
NCBI home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2017 Dec 28;51(1):204–212. doi: 10.1021/acs.macromol.7b01795

Force and Scale Dependence of the Elasticity of Self-Assembled DNA Bottle Brushes

Márcio Santos Rocha †, Ingeborg M Storm ‡, Raniella Falchetto Bazoni †, Ésio Bessa Ramos †, Armando Hernandez-Garcia §, Martien A Cohen Stuart ‡, Frans Leermakers ‡, Renko de Vries ‡,*
PMCID: PMC5763285  PMID: 29339838

Abstract

graphic file with name ma-2017-01795s_0010.jpg

As a model system to study the elasticity of bottle-brush polymers, we here introduce self-assembled DNA bottle brushes, consisting of a DNA main chain that can be very long and still of precisely defined length, and precisely monodisperse polypeptide side chains that are physically bound to the DNA main chains. Polypeptide side chains have a diblock architecture, where one block is a small archaeal nucleoid protein Sso7d that strongly binds to DNA. The other block is a net neutral, hydrophilic random coil polypeptide with a length of exactly 798 amino acids. Light scattering shows that for saturated brushes the grafting density is one side chain per 5.6 nm of DNA main chain. According to small-angle X-ray scattering, the brush diameter is D = 17 nm. By analyzing configurations of adsorbed DNA bottle brushes using AFM, we find that the effective persistence of the saturated DNA bottle brushes is Peff = 95 nm, but from force–extension curves of single DNA bottle brushes measured using optical tweezers we find Peff = 15 nm. The latter is equal to the value expected for DNA coated by the Sso7d binding block alone. The apparent discrepancy between the two measurements is rationalized in terms of the scale dependence of the bottle-brush elasticity using theory previously developed to analyze the scale-dependent electrostatic stiffening of DNA at low ionic strengths.

Introduction

A type of nonlinear polymer architectures that occurs regularly in biology is the bottle-brush polymer architecture, in which a main chain is grafted with side chains. Natural examples of bottle-brush polymers are aggrecan,1,2 lubricin,3 and neurofilaments.4,5 Bottle-brush polymers with side-chain spacings down to less than 1 nm have been prepared synthetically, and their physical properties have been studied using various methods.6,7 Some specific applications that seem to benefit from the bottle-brush polymer architecture are surface modification and lubrication. Synthetic bottle brushes with hydrophilic side chains and adsorbing main chains self-assemble into nonfouling polymer brushes.8,9 Surface layers of bottle-brush polymers with hydrophilic side chains have very good lubrication properties,10 especially if the side chains are highly charged.11 Fredrickson predicted that grafting side chains to a flexible main chain should dramatically increase the effective stiffness of the main chain and lead to the possibility of nematic ordering of bottle-brush polymers.12 Induced stiffening in bottle-brush polymers is indeed qualitatively obvious from the amply available experimental data on both natural and synthetic bottle brushes.1−7 However, quantitative understanding of the configurational statistics of bottle-brush polymers is still lacking.

Various scaling approaches for the induced main chain stiffening have been proposed, but they have significant limitations that restrict them from being applicable to most experimental systems. A first limitation is that the scaling theories are only valid in the limit of extremely long side chains (at least hundreds, but preferably thousands of monomers13−15), grafted on main chains that should be even (much) longer than the side chains. This scaling limit is unaccessible for both experimental bottle-brush systems and computer simulations, although it can be shown to exist in numerical self-consistent field calculations.13

A second limitation relates to the fact that stiffening is usually expressed in terms of an effective persistence length for the whole bottle brush. Such a description applies only for main-chain deformations with length scales or wavelengths that are much longer than the thickness of the bottle brush. This implies, for example, that for bottle brushes with flexible main chains (Figure 1a) and which are not extremely long the whole concept of an effective persistence length is not very useful, as has been clearly shown in recent computer simulations.14,15

Figure 1.

Figure 1

Open in a new tab

Different types of bottle brushes. (a) Flexible main chain, side chains consist of N monomers of diameter a, side-chain spacing is h, brush diameter is D. (b) Semiflexible main chain, main-chain persistence length Lp,0. (c) Self-assembled bottle brush with semiflexible main chain. Side chains attach via equilibrium binding of binding block to the main chain.

In order to gain insight, we have recently introduced a versatile experimental model system for self-assembled bottle brushes with semiflexible main chains (Figure 1c). As the semiflexible main chain we employ double-stranded DNA, which can be obtained in monodisperse form from very small up to extremely long contour lengths. Rather than chemically attaching the side chains, we have developed diblock polypeptides, produced via recombinant DNA technology, consisting of long hydrophilic block and a small DNA binding block. Hydrophilic blocks are based on a previously developed, de novo designed 98 amino acid long polypeptide with a high proportion of glycines, prolines, and other hydrophilic residues. These polypeptides adopt a random coil configuration for a wide range of (aqueous) solvent conditions.16 Initially, we have used a tetramer of the hydrophilic block (C4) and, for physical attachment to DNA, a simple cationic binding block B consisting of 12 lysine residues (BK12). The C4–BK12 diblock polypeptides very precisely coat double-stranded DNA molecules, leading to the formation of well-defined supramolecular DNA–protein bottle brushes.17 The reason that well-defined supramolecular DNA–protein bottle brushes are formed rather than larger aggregates is the extreme assymmetry in the lengths of the two blocks of the diblock polypeptide and the fact that the template is semiflexible.17,18 Note that a similar supramolecular approach to bottle-brush formation was recently developed by Mezzenga and co-workers,19 who used rigid β-lactoglobilin amyloid fibrils as a main chain.

The bottle-brush coating leads to significant induced stiffening, increasing the persistence length by an amount ΔP ≈ 200 nm for DNA fully saturated with C4-BK12 at low ionic strength.20 The C4–BK12 DNA bottle brushes form nematic phases at low weight concentrations,21 but at high concentrations, excess C4-BK12 acts to screen excluded volume interactions,22 such that the bottle brushes become more flexible and the nematic ordering decreases.23

The nonspecific DNA binding by the oligolysine BK12 binding block may be disadvantageous in applications in which components other than DNA are also present. With this in mind, a new diblock was developed in which the oligolysine binding block was replaced by the small (7 kDa) basic DNA binding protein B = Sso7d, a highly stable and well-characterized nucleoid protein24−26 from the thermophile Sulfolobus solfataricus. Additionally, the length of the side chain was doubled to C8, resulting in the new diblock polypeptide C8-BSso7d. This new diblock has proven to be very useful for modifying and stabilizing DNA nanostructures.27,28

Rather than focusing on the technological implications of the new the new diblock polypeptide C8-BSso7d, we here focus on the physics of the induced stiffening effect, which we quantify using both atomic force microscopy (AFM) imaging and single molecule force extension measurements using optical tweezers (OT). While AFM shows there is significant induced stiffening due to the bottle brush in the absence of external forces, the OT experiments show that the induced stiffening disappears under applied force (with deformations occurring at short length scales), signaling the breakdown of the concept of an effective persistence length for deformations at short length scales, as expected on theoretical grounds.

Experimental Section

Chemicals

NoLimits DNA fragments of 300 bp, 2 kbp, and 3 kbp were obtained Thermo Scientific. λ-DNA was obtained from New England Biolabs. Nucleotides dATP, dTTP, dGTP, and biotin 14-dCTP were obtained from Invitrogen. Streptavidin-coated beads were obtained from Bang Laboratories. Klenow fragment was obtained from Promega Corp., and streptavidin-coated coverslips were obtained from Xenopore Corp.

Protein Polymer Production and Purification

The production and purification of the recombinant C8-BSso7d diblock protein polymer were done essentially as described before.26 In short, we used a Pichia pastoris strain harboring a gene for the secreted expression of the diblock protein C8-BSso7d. For the fermentation process, we used a 2.5 L Bioflo3000 fermentor. Fed-batch fermentation was done for 2 days, from the moment of induction. During fermentation, the pH was kept at pH 3 by the controlled addition of ammonium hydroxide. The methanol content of the broth was maintained at 0.2% (w/v). When the fermentation was completed, the protein containing supernatant was separated from the yeast cells by centrifugation at 16000g for 30 min at 20 °C (SLA-rotor) and subsequent filtration using 0.2 μm AcroPak 200 capsules with a Supor membrane (Pall Corp.). After acquiring the cell-free protein solution, medium salts were precipitated by NaOH addition until a pH of 8 was reached. The protein solution was separated from the precipitated medium salt by centrifugation (16000g, 30 min, 4 °C, SLA-1500 rotor). The C8-BSso7d protein was selectively precipitated from secreted Pichia pastoris proteins by the addition of ammonium sulfate (45% saturation) for 30 min at 4 °C and subsequent centrifugation (16000g, 30 min, 4 °C, SLA-1500 rotor). This precipitation step was repeated, and the precipitate was resuspended in 10% of the original cell-free broth volume of 50 mM formic acid and extensively dialyzed against 50 mM formic acid. After refreshing the formic acid for four times, the protein solution was dialyzed once against 10 mM formic acid and subsequently frozen and freeze-dried.

Static Light Scattering (SLS)

SLS experiments were performed at a scattering angle of 173° on a Malvern Instrument zetasizer nanoseries, using a small volume quartz cell. A light scattering titration was performed by adding successive small aliquots of concentrated protein solution to a solution of dsDNA and measuring the light scattering intensity. From the light scattering intensities, we calculated the ratio of the scattering intensities of the samples with complexed protein and the free DNA sample, Icomplex/IDNA, correcting for the sample dilution caused by the additions of the titrant. Previously18 we showed that in the limit of small scattering angles and low concentrations it is reasonable to neglect the scattering of excess free diblock protein polymers, such that the scattering ratio is directly proportional to the mass ratio of the complexes and the free DNA. The length of the DNA template for this experiment is deliberately chosen to be small (300 bp) such that qR < 1, where q is the magnitude of the wave vector and R is the solution size of the complexes. For this case we have to a good approximation18

graphic file with name ma-2017-01795s_m001.jpg 1

where the mass ratio Γbound is

graphic file with name ma-2017-01795s_m002.jpg 2

with c and M being the molar concentrations and molar mass, and the indices refer to (bound) protein and DNA, respectively. ζ is the ratio of the respective refractive index increments of protein and DNA:

graphic file with name ma-2017-01795s_m003.jpg 3

where we use the same values we have previously used to analyze similar experiments:22 (dn/dC)prot = 0.18 and (dn/dC)DNA = 0.165, giving ζ = 1.091. We obtain the number of proteins cprot,b/cDNA bound per DNA molecule versus the total number of proteins per DNA molecule, cprot,t/cDNA, from the experimentally determined mass ratio Γbound, by using the molar masses of the protein and the DNA, Mprot = 80.37 kDa and MDNA = 182.38 kDa.

Small-Angle X-ray Scattering (SAXS)

SAXS experiments were performed at MAXlab II, Lund, Sweden, on the I911-4 beamline. The detector distance was chosen such that the range of the wavevector q covered was 0.008 < q < 0.550 Å–1, for a wavelength of the incident radiation of 1.2 Å. For detection, a PILATUS 1M detector (Dectris) was used. The sample environment was a high throughput solution scattering setup, for which the acquisition time was typically 20 min per sample. Scattering data were analyzed using SASview 3.0.0 software.

Atomic Force Microscopy (AFM)

For AFM of DNA–protein complexes on mica, 20 μL of DNA–protein complex was deposited on freshly cleaved mica. After 1 min, the substrate was carefully dipped deionized water filtered with into a 0.22 μm cutoff syringe filter and gently dried using N2(g). AFM imaging was performed on the mica substrates in air, at ambient temperatures, and controlled humidity (RH 30–35%), using a model NTEGRA AFM (NT-MDT-Russia) in tapping mode, using NanoWorld Supersharp Silicon tips with a reported force constant of 100 N/m and tip radius of 2 nm. Images were analyzed manually to extract end-to-end distances for the estimation of persistence lengths. For AFM on silica wafers, 5 μL of the DNA–protein complexes was deposited on pieces of plasma-cleaned silicon wafer. After 10 min, samples were washed by the careful application of 0.3 mL of Milli-Q water, followed by gentle drying of the sample with N2(g). Samples on pieces of silica wafer were analyzed using a Digital Instrument Nanoscope V, with a silicon tip on a nitride lever (Bruker) with a reported spring constant of 0.4 N/m. For the imaging process the ScanAsyst mode in air was used with a scanning speed of 0.977 Hz and a resolution of 512 samples/line (each scan line has 512 pixels). AFM images were produced using Nanoscope Analysis 1.4 software. These images were analyzed using “Easyworm” software29 to extract persistence-length estimates from end-to-end distances. At least 50 complexes were analyzed for each persistence length estimate.

Optical Tweezer Experiments

For the optical tweezer experiment, λ-DNA molecules (New England Biolabs) are end-labeled with biotin attached by one end to a streptavidin-coated bead of 3 μm diameter (Bangs Laboratories) and by the other end to a streptavidin-coated coverslip (Xenopore Corp.). An O-ring is glued onto the coverslip to form a sample chamber. The optical tweezers consist of a 1064 nm ytterbium-doped fiber laser (IPG Photonics) mounted on a Nikon Ti–S inverted microscope with a 100× N.A. 1.4 objective. DNA molecules are stretched by moving the microscope stage and consequently the coverslip with controlled velocity (100 nm/s) using a piezoelectric device (PINano P-545, Physik Instrumente). Each optical tweezer experiment with added protein is preceded by the recording of 5–7 stretching curves on the same DNA molecule without added protein. By analyzing these experiments, we obtain mean values of the persistence and contour lengths for the bare DNA, by fitting the experimental force–extension curves measured in the low-force entropic regime (f < 2.5 pN) to the Marko–Siggia wormlike chain (WLC) expression.30 Average results obtained for various λ-DNA molecules are 45 ± 3 nm for the persistence length and 16.5 ± 1 μm for the contour length, which are within the expected values for λ-DNA. Next we change the surrounding buffer solution, introducing the protein at a certain chosen concentration. We wait about 30 min for protein–DNA equilibration and then repeat the stretching experiments, performing 5–7 measurements and thus obtaining the average values and the error bars of the mechanical parameters for each protein concentration. Note that we do not remove unbound DNA from the sample chamber. Using UV spectrophotometry, the bulk DNA concentration in the OT sample chamber (which was constant for all OT experiments) was determined to be CDNA = 1.58 μg/mL.

Results

Grafting Density from Light Scattering

Previously26 we have qualitatively characterized the amount of bound C8-BSso7d diblock using an agarose electrophoresis mobility assay, which indicated that dsDNA templates become saturated with C8-BSso7d diblock at a protein-to-DNA ratio of about 0.3 pt/bp (protein per basepair). This is consistent with the reported size of the binding site of Sso7d at saturation of about 4 bp.25 Here we use light scattering to also estimate the grafting density of C8-BSso7d diblocks along the DNA main chain. As explained previously,21,18 we obtain the binding isotherms from the ratio of the scattering intensities of the bare and coated DNA templates. Results for the mole ratio [C8-BSso7d]bound/[DNA(bp)] of bound proteins bound per basepair as a function of the mole ratio [C8-BSso7d]/[DNA(bp)] of total proteins per basepair are shown in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Grafting density as deduced from light scattering. Mole ratio [C8-BSso7d]bound/[DNA(bp)] of bound proteins per DNA basepair as a function of the mole ratio [C8-BSso7d]/[DNA(bp)] of total proteins per DNA basepair. Scattering experiments were performed in 10 mM Tris-HCl buffer at pH 7.6, using 300 bp DNA at an initial concentration of 100 μg/mL, by titration with a 4 mg/mL solution of C8-BSso7d.

As in a previously published electrophoretic mobility shift assay,26 we observe saturation of binding for protein to DNA mole ratio’s larger than about 0.3 ptn/bp. Full saturation of the DNA template with C8-BSso7d protein polymers would imply a grafting density of about 0.25 ptn/bp, in view of the reported binding site of Sso7d. We observe a substantially (4-fold) lower saturation binding, of around 0.06 ptn/bp, corresponding to a grafting density of one side chain for every 5.6 nm of DNA main chain. Possibly, the binding strength of the Sso7d domain is not sufficient to overcome the strong steric repulsion that is associated with adding additional side chains to a high-density bottle brush.

Brush Thickness from Small-Angle X-ray Scattering

In order to determine the solution diameter D of C8-BSso7d-coated DNA, we have performed small-angle X-ray scattering (SAXS) for values of the magnitude q of the wavevector in the range of 0.1 < q < 2 nm–1. Scattering curves I(q) are shown in Figure 3 for both the free C8-BSso7d protein polymer (30 mg/mL in 10 mM Tris-HCl buffer, pH 7.6) and for its complexes with DNA (100 μg/mL ds λ-DNA and 0.5 ptn/bp of C8-BSso7d protein polymer in a 10 mM Tris-HCl buffer, pH 7.6). Data for the free protein polymers can be fitted with a polymer coil with excluded volume model,31 resulting in an estimated radius of gyration of 6.9 nm.

Figure 3.

Figure 3

Open in a new tab

Bottle-brush thickness from small-angle X-ray scattering. Scattering intensity (arbitrary units, a.u.) versus magnitude q of the wavevector in nm–1. Solution conditions are 10 mM Tris-HCl, pH 7.6. Blue squares are the scattering intensities for 100 μg/mL λ-DNA coated with the C8-BSso7d diblock protein polymer at a protein to DNA ratio of [C8-BSso7d]/[DNA(bp)] of 0.5 ptn/bp; black circles are the scattering intensities for 30 mg/mL free C8-BSso7d protein polymer. In the figure, the scattering intensity for the free C8-BSso7d protein polymer is scaled to match the high-q scattering of the of C8-BSso7d/DNA bottle-brush complex. The red line is a fit to a polymer coil model with excluded volume; the orange line is the sum of a contribution due to excluded volume polymer coils (representing the excess unbound protein polymers) and a contribution due to randomly oriented rigid cylinders. Separate contributions of polymer coils and cylinders are indicated in gray.

In order to make the bottle brushes, protein polymers had to be added in excess; consequently, there will also be free protein polymers in the solution, and I(q) reflects a mixture of the two objects. In fitting the data for the complexes, we therefore assume two independent contributions to the scattering: one due to randomly oriented cylindrical rods,31 representing the bottle brushes, and one due to excluded volume polymer chains, representing the free protein in solution. Parameters for the free proteins were taken from the fit for the pure C8-BSso7d protein polymers. We find that at large wavevectors (0.1 < q < 2 nm–1) the scattering due to the cylindrical rods is masked by the scattering of the free proteins. Only at low wavevectors (0.1 < q < 0.3 nm–1) the scattering of the mixture has a major contribution from the rods. By fitting the low wave vector data, we can extract an estimated value for the diameter of the cylindrical rods, for which we find D = 16.8 nm. This is more than twice the gyration radius for the free protein. Hence, the C8 chains decorating the DNA are moderately stretched and form a true “bottle brush” around the central DNA chain. The moderate stretching that we find from SAXS is also consistent with our conclusion from light scattering that side chain binding by Sso7d is not so strong that it can lead to full coverage and to the concomitant strong side-chain stretching.

Atomic Force Imaging of Dried Complexes

For unperturbed DNA bottle brushes with a main chain contour length L ≫ D, we expect that the end-to-end distance is mainly governed by the effective bottle-brush persistence length Peff. In order to estimate this effective persistence length, we have measured contour lengths L and end-to-end distances R for DNA bottle brushes adsorbed on mica and silica wafers using atomic force microscopy. Typical images of the coated DNA deposited on mica as a function of the protein concentration are shown in Figure 4.

Figure 4.

Figure 4

Open in a new tab

Representative AFM images (in air) of 3 kb linear dsDNA complexed with C8-BSso7d diblock protein polymer, adsorbed on mica. DNA concentration CDNA = 1 μg/mL. Buffer conditions: 10 mM Tris HCl pH = 7.4. Mole ratios [C8-BSso7d]/[DNA(bp)] are (a) 0, (b) 1/32 ptn/bp, (c) 1/16 pt/bp, (d) 1/8 ptn/bp, (e)1/4 ptn/bp, and (f) 1/2 ptn/bp.

At higher and higher protein concentrations it is clear that the background is showing more and more roughness that we believe is caused by the excess protein sticking to the mica. As a consequence, with mica as a substrate, we have not been able to extend the measurements to protein to DNA mole ratio’s higher than 1 protein per 2 basepairs. In further experiments we found that for silicon wafers as a substrate the problem of protein polymer background adsorption is much less severe, which allowed us to also explore higher protein to DNA ratios. Typical images are shown in Figure 5. In all cases complexes have a contour length roughly equal to that expected for the bare DNA, indicating that the C8-Sso7d proteins are indeed coating individual DNA molecules.

Figure 5.

Figure 5

Open in a new tab

Representative AFM images (in air) of complexes of C8-BSso7d with 2 kbp linear dsDNA, adsorbed on silicon wafers. Complexes were prepared at a DNA concentration CDNA = 25 μg/mL in 10 mM Tris-HCl solution, pH 7.6, and incubated 24 prior to deposition onto the silicon wafer and imaging. Protein to DNA mole ratios [C8-BSso7d]/[DNA(bp)] are (a) 1 ptn/bp and (b) 2 ptn/bp.

As has been shown in great detail by Rivetti et al.,32 obtaining accurate DNA persistence lengths by analyzing end-to-end distances from AFM images of adsorbed and dried DNA is possible but requires great care. Specifically, it requires an explicit demonstration that, under the given experimental conditions, the adsorption process leads to either 2D equilibrated states or to a 2D projection of 3D configurations (if adsorption is very rapid and essentially irreversible). In addition, the magnitude of excluded volume effects needs to be quantified or shown to be negligible.32 Instead of repeating the elaborate tests performed by Rivetti for the case of DNA bottle brushes adsorbing on mica and silicon wafers, we take a more pragmatic approach and simply assume that the adsorbed DNA bottle brushes are in a 2D equilibrated state and that (given the fact that rather short DNA is used) excluded volume interactions can indeed be neglected. Then, the expected mean-square end-to-end distances ⟨Re2⟩ according to the wormlike chain model are given by

graphic file with name ma-2017-01795s_m004.jpg 4

Experimental results for the effective persistence lengths (estimated using eq 4) as a function of the protein to DNA ratio are shown in Figure 6.

Figure 6.

Figure 6

Open in a new tab

Effective persistence lengths of C8-BSso7d-coated DNA as a function of the C8-BSso7d protein to DNA ratio, as deduced from analysis of end-to-end distances of complexes imaged using AFM assuming 2D equilibrated configurations (eq 4), versus protein to DNA mole ratio (ptn/bp). Dashed line is a guide to the eye.

In the limit of low protein concentration, we find values for Peff that are close to the expected value, P0 = 50 nm, which lends some support to the assumptions of 2D equilibrated configurations and negligble excluded volume interactions. It appears that upon progressively coating the DNA with more diblock copolymers there is initially a small decrease in the persistence length, possibly as a consequence of static bends, which the Sso7d and homologous binding blocks are known to induce.24−26 At higher densities, as the polymer brush starts to build up around the DNA, the persistence length increases and saturates at values of Peff ≈ 95 nm at high protein to DNA mole ratios.

Single-Molecule Force–Extension Curves

We measured force–extension curves f(z) for bottle-brush DNA using an optical tweezer (OT) setup, as described previously.33,34 The force range for which accurate force–extension data can be obtained with the setup is approximately 0.2–2.5 pN. This is not particularly broad, but as has been shown by other authors, it is enough to obtain reliable values of persistence lengths by fitting to models such as the worrmlike chain model.35,36 For ligand-induced changes of the nanomechanical properties of DNA it is well-known that the effective persistence length Peff may become force dependent.37 To check for possible force dependence of Peff over the range of forces probed in our OT experiments, we follow the analysis of Marko and Siggia in their treatment of the force-dependent electrostatic stiffening of DNA that occurs at low ionic strengths.30 Their analysis starts from the analytical approximation for the force–extension curve for the full wormlike chain (WLC) model:

graphic file with name ma-2017-01795s_m005.jpg 5

where kBT is the thermal energy. By inverting the high-force limit of eq 5 (for z/L > 0.5), the effective persistence length Peff(f) is expressed as a function of the force f:

graphic file with name ma-2017-01795s_m006.jpg 6

By computing Peff versus f from this equation using experimental force–extension data, one can test to which degree the assumption of a constant Peff is justified for a certain force range. Experimental values for Peff as a function for f (for z/L > 0.5) for the force curves of Figure 7a are shown in Figure 7b. We find very little force dependence of Peff, both for bare DNA (as expected) and for the same DNA molecule incubated with 7000 nM of the C8-BSso7d protein. This means that within the range of forces probed by our OT measurements we can neglect force dependence of Peff and use the WLC equation, eq 5, to estimate a single Peff valid at forces on the order of pN. Representative force–distance curves for DNA with and without the C8-BSso7d protein with associated fits to the WLC model, eq 5, are given in Figure 7a. Values of the effective persistence lengths versus the mole ratio [C8-BSso7d]/[DNA(bp)] of protein per basepair derived from the fits are shown in Figure 8.

Figure 7.

Figure 7

Open in a new tab

Force–extension curves from optical tweezer experiments. (a) Representative force–extension curve (averaged over Brownian motion to remove thermal fluctuations at low forces33) for bare DNA (open squares) and the same DNA molecule incubated with 7000 nM C8-BSso7d (corresponding to a mole ratio [C8-BSso7d]/[DNA(bp)] = 2.88). Solid lines are fits to the WLC equation, eq 5, for a contour length L = 16.7 ± 0.03 μm and effective persistence length Peff = 52 ± 1.6 nm (bare DNA, open squares) and for a contour length L = 16.2 ± 0.05 μm and persistence length Peff = 19.3 ± 0.5 nm (DNA + 7000 nM C8-BSso7d, open squares). (b) Force-dependent effective persistence lengths for z/L > 0.5, according to eq 6.

Figure 8.

Figure 8

Open in a new tab

Effective persistence lengths of C8-BSso7d-coated λ-DNA versus the mole ratio [C8-BSso7d]/[DNA(bp)] of protein to DNA basepairs, as deduced by fitting optical tweezer force extension curves with the wormlike chain model (eq 5). Solution conditions: 10 mM Tris-HCl, pH 7.4, DNA concentration CDNA = 1.58 μg/mL. Note that the upper x-axis shows the protein concentration in nM. Dashed line is a guide to the eye.

Note that in this experiment there is a known background DNA concentration CDNA = 1.58 μg/mL of nonimmobilized DNA, which ensures control over the protein polymer to DNA ratio so that we can directly compare to the AFM experiments.

We find again that estimated persistence lengths are close to the expected P0 = 50 nm at low protein concentrations. A control experiment with no added protein gave P = 48 ± 3 nm. At protein to DNA mole ratios between 0.1 and 0.3 ptn/bp (corresponding to C8-BSso7d protein concentrations between 300 and 700 nM), there is a sharp drop in the effective persistence length down to a value Peff ≈ 15 nm. This behavior is very similar to that found by Driessen et al.26 for the archaeal DNA binding proteins Sac7d and Sul7d that are heterologous to Sso7d and which was attributed to the introduction of static bends into the DNA helix by the binding of the proteins. Hence, it appears that the C8 tail does not at all contribute to the measured effective persistence length in the OT experiment, and we only observe the effect induced by the Sso7d binding domain that reduces the measured apparent persistence length by the introduction of static bends.

Discussion

The complete disappearance of DNA bottle-brush stiffening at pN forces should not have been a big surprise: it is well-known that at high forces f the typical wavelengths λ of thermal undulations of stretched DNA are very small, as illustrated in Figure 9a. Given a persistence length P, the typical wavelength of its thermally induced deformations is the Odijk deflection length38 λ:

graphic file with name ma-2017-01795s_m007.jpg 7

For example, for P = 50 nm and f = 1 pN, we find λ ≈ 14 nm, which is on the order or smaller than the brush thickness D, which from the SAXS experiment we estimated to be D ≈ 17 nm. Earlier theoretical treatments of bottle-brush elasticity13 have already pointed out that a description of bottle-brush elasticity in terms of an effective persistence length only makes sense if the length scale of the deformation is much larger than the thickness of the brush. For deformations at shorter length scales, the elasticity is expected to become scale-dependent, where the relevant length scale ξ should be on the order of the thickness of the brush. Eventually, for very short wavelength ripples, with wavelengths λ ≪ ξ, there will be no impact on the configurations of the polymers making up the brush, and hence in this limit, the brush elasticity is expected to vanish.

Figure 9.

Figure 9

Open in a new tab

Scale-dependent elasticity of DNA bottle brushes results in different apparent persistence lengths measured in optical tweezer and AFM experiments. (a) In optical tweezer experiments forces f are so high that the typical wavelength λ of the thermal deformations is of the order of the brush thickness or less, such that the stiffening due to the bottle brush is negligble. (b) In the AFM experiment there is no external force and the end-to-end distance is governed by the large-length scale effective bottle-brush persistence length, Peff.

The whole situation is very analogous to that of the scale-dependent electrostatic stiffening of polyelectrolytes at low ionic strength. This problem has been studied in great detail, both theoretically and experimentally.30,39 Electrostatic stiffening only operates at deformation wavelengths and length scales λ ≫ κ–1, where κ–1 is the Debye screening length, the thickness of the electric double layer, surrounding the polyelectrolytes. At very low ionic strengths, the Debye length can be quite large, such that there is quite a large range of deformation wavelengths where the stiffening does not operate.

Single molecule force–extension measurements for DNA at low ionic strength were analyzed in detail by Marko and Siggia,30 and we can follow their treatment of scale-dependent polymer elasticity in terms of a wave-vector-dependent persistence length P(q). In the high-force limit, z/L > 0.5, where the chain configurations can be described in terms of small undulations around an average straight configuration (Figure 9a), the extension z at a force f is

graphic file with name ma-2017-01795s_m008.jpg 8

In the absence of a detailed model for the scale-dependent elasticity of bottle brushes, we postulate that there is full stiffening due to side chains only above a certain wavelength ξ of the thermal deformations and no stiffening at shorter wavelengths:

graphic file with name ma-2017-01795s_m009.jpg 9

The resulting force–extension relation is

graphic file with name ma-2017-01795s_m010.jpg 10

The correction factor γ accounts for the stiffening that only occurs for long wavelength deformations:

graphic file with name ma-2017-01795s_m011.jpg 11
graphic file with name ma-2017-01795s_m012.jpg 12
graphic file with name ma-2017-01795s_m013.jpg 13

Following Marko and Siggia,30 for z/L > 0.5, an apparent, force-dependent persistence length Papp(f) can then again be calculated from eq 6. Plots for the predicted apparent persistence length Papp as a function of the force f, computed from eqs 10–13, are shown in Figure 10.

Figure 10.

Figure 10

Open in a new tab

Force dependence of the apparent persistence length Papp according to eq 6 and eqs 10–13, for different values of the crossover wavelength, ξ, and for P0 = 15 nm and ΔP = 80 nm. From top to bottom: ξ = 10, 25, 50, and 100 nm. The dotted horizontal lines enclose the values of the high-force persistence length found in the OT experiments, Peff = 15 ± 5 nm (Figure 8), while the dotted vertical lines enclose the range of forces f = 0.2–2.5 pN probed in the OT experiment. Hence, we conclude that an approximate lower bound for ξ is ξ > ξmin ≈ 100 nm.

At low force, the apparent persistence length has the limiting value Papp = P0 + ΔP, whereas at high forces, it approaches the limiting value Papp = P0. The force or scale dependence of the bottle-brush elasticity is governed by the characteristic length scale ξ. For large values of ξ, the apparent persistence length Papp already deviates from the limiting value Papp = P0 + ΔP at very low forces, on the order of than fξ = kBT/ξ.

In the absence of a force, as is the case in our AFM experiments (Figure 9b), the enhanced flexibility at short length scales merely leads to small corrections to the mean-square end-to-end distance R2 of the bottle brushes. These corrections vanish if the contour length of the main chain is sufficiently long (L ≫ ξ). An ad hoc approximation for this effect is obtained by postulating that correlations between the unit tangents û(s) along the contour s = 0 to L of the semiflexible bottle brush are governed by a scale-dependent rather than by a constant persistence length, as follows:

graphic file with name ma-2017-01795s_m014.jpg 14

where for the scale-dependent persistence length we make a similar assumption as done in the case of an applied force:

graphic file with name ma-2017-01795s_m015.jpg 15

The mean-square end-to-end distance can then be calculated in the usual way:

graphic file with name ma-2017-01795s_m016.jpg 16

For example, suppose we take L = 1 μm, P0 = 50 nm, ΔP = 50 nm, and ξ = 50 nm. Then, if we calculate the root-mean-square distance ⟨R2⟩ using an effective persistence length Peff = 100 nm, the error that we make in the mean-square end-to-end distance by neglecting the enhanced flexibility at short length scales, is only 5%.

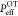From the AFM experiments, we obtain as limiting value for the effective persistence length at high protein concentrations, Inline graphic ≈ 95 nm. From the OT we found Inline graphic ≈ 15 nm, which is equal to the value found by Driessen et al.26 for the DNA-binding domain alone. In order to compare with eq 13 for Peff(f), we set P0 = 15 nm and ΔP = 80 nm. Plots of Peff(f) for this case are shown in Figure 9. The only unknown parameter in the comparison with the experiments is the crossover wavelength ξ, and curves for various values of ξ are presented in Figure 10. As follows from this figure, the OT observation that Inline graphic ≈ 15 ± 5 nm for forces f = 0.2–2.5 pN implies an approximate lower bound ξ > ξmin ≈ 100 nm. Unfortunately, at present we have no way to obtain an upper bound or to otherwise more precisely fix the value of the crossover wavelength ξ. However, we may expect ξ to scale with the thickness of the bottle brush, ξ ∝ D. For saturated C8-BSso7d bottle brushes we have found D ≈ 17 nm, and we would expect the crossover length scale to be at most a few times the bottle-brush thickness D, which is not very different from the lower bound of ξmin ≈ 100 nm following from from the above analysis.

Conclusions

We have shown experimentally that the main chain stiffening effect of bottle brushes vanishes for deformations at length scales below a crossover length ξ ∝ D, where D is the thickness of the bottle brush. Because at a force f the typical length scale λ for thermal deformations is λ ≈ kBT/f, the main chain stiffening effect of bottle brushes disappears at forces larger than fξ = kBT/ξ, where ξ ∝ D is the crossover wavelength. Since we considered a bottle brush for which D = 17 nm, the estimated critical force for our case is than fξ = 0.2 pN, and only for forces much smaller than this we can expect significnat stiffening due to the bottle-brush coating. Forces in our optical tweezer experiment were quite high, f = O(pN), such that we were indeed above the critical force fξ. More sensitive magnetic tweezer experiments could possible quantify forces in both regimes f > fξ and f < fξ as well the transitional regime where the main-chain stiffening effect starts to disappear.

The Sso7d binding domain also binds to single-stranded DNA (ssDNA), albeit with a somewhat lower affinity than to double-stranded DNA (dsDNA). Since the intrinsic persistence length of ssDNA is much lower than that of dsDNA, sensitive magnetic tweezer experiments with ssDNA as a template41 could elucidate many details for bottle brushes with flexible main chains.

For the low force and low stretching regime for which z/L < 0.5, Marko and Siggia30 also noted that dealing theoretically with the effect of scale-dependent elasticity is much more difficult. Possibly, one may take inspiration from theories previously developed for the force–extension curves of excluded volume chains—a case that has been worked out in significant detail42,43 and that has also been subjected to detailed experimentation using single-molecule experiments using flexible ssDNA.41 In that case, there is a low force regime with full excluded volume interactions and a high force regime in which excluded volume interactions no longer operate. One would hope that the similar transition from full bottle-brush elasticity at low forces to only main-chain elasticity at higher forces can also be quantified experimentally in the near future.

Acknowledgments

R.D.V. and A.H.G. thank John van Noort for preliminary optical tweezer studies on self-assembled DNA bottle-brush stiffening. M.A.C.S. and I.M.S. acknowledge financial support of the EU through ERC Advanced Grant 267254 (“Biomade”). R.D.V. acknowledges financial support of CNPq through Grant 303495/2014-6 in the program “Science without Borders”. M.S.R. acknowledge financial support from CNPq and FAPEMIG. R.D.V. acknowledges useful discussions with M. Rubinstein, M. Ballauf, and O. Saleh.

Author Contributions

M.S.R. and I.M.S. contributed equally.

The authors declare no competing financial interest.

References

  1. Ng L.; Grodzinsky A. J.; Patwari P.; Sandy J.; Plaas A.; Ortiz C. Individual cartilage aggrecan macromolecules and their constituent glycosaminoglycans visualized via atomic force microscopy. J. Struct. Biol. 2003, 143, 242–257. 10.1016/j.jsb.2003.08.006. [DOI] [PubMed] [Google Scholar]
  2. Ng L.; Grodzinsky A. J.; Patwari P.; Sandy J.; Plaas A.; Ortiz C. Persistence Length of Cartilage Aggrecan Macromolecules Measured via Atomic Force Microscopy. Macromol. Symp. 2004, 214, 1–4. 10.1002/masy.200451001. [DOI] [Google Scholar]
  3. Zappone B.; Greene G. W.; Oroudjev E.; Jay G. D.; Israelachvili J. N. Molecular Aspects of Boundary Lubrication by Human Lubricin: Effect of Disulfide Bonds and Enzymatic Digestion. Langmuir 2008, 24, 1495–1508. 10.1021/la702383n. [DOI] [PubMed] [Google Scholar]
  4. Deek J.; Chung P. J.; Kayser J.; Bausch A. R.; Safinya C. R. Neurofilament sidearms modulate parallel and crossed-filament orientations inducing nematic to isotropic and re-entrant birefringent hydrogels. Nat. Commun. 2013, 4, 2224. 10.1038/ncomms3224. [DOI] [PubMed] [Google Scholar]
  5. Beck R.; Deek J.; Choi M. C.; Ikawa T.; Watanabe O.; Frey E.; Pincus P.; Safinya C. R. Unconventional Salt Trend from Soft to Stiff in Single Neurofilament Biopolymers. Langmuir 2010, 26, 18595–18599. 10.1021/la103655x. [DOI] [PubMed] [Google Scholar]
  6. Zhang M.; Müller A. H. E. Cylindrical Polymer Brushes. J. Polym. Sci., Part A: Polym. Chem. 2005, 43, 3461–3481. 10.1002/pola.20900. [DOI] [Google Scholar]
  7. Potemkin I. I.; Palyulin V. V. Comblike Macromolecules. Polym. Sci., Ser. A 2009, 51, 123–149. 10.1134/S0965545X09020011. [DOI] [Google Scholar]
  8. Kenausis G. L.; Vörös J.; Elbert D. L.; Huang N.; Hofer R.; Ruiz-Taylor L.; Textor M.; Hubbell J. A.; Spencer N. D. Poly(L-lysine)-g-Poly(ethylene glycol) Layers on Metal Oxide Surfaces: Attachment Mechanism and Effects of Polymer Architecture on Resistance to Protein Adsorption. J. Phys. Chem. B 2000, 104, 3298–3309. 10.1021/jp993359m. [DOI] [Google Scholar]
  9. Perrino C.; Lee S.; Choi S. W.; Maruyama A.; Spencer N. D. A Biomimetic Alternative to Poly(ethylene glycol) as an Antifouling Coating: Resistance to Nonspecific Protein Adsorption of Poly(L-lysine)-graft-dextran. Langmuir 2008, 24, 8850–8856. 10.1021/la800947z. [DOI] [PubMed] [Google Scholar]
  10. Goren T.; Spencer N. D.; Crockett R. Impact of chain morphology on the lubricity of surface-grafted polysaccharides. RSC Adv. 2014, 4, 21497–21503. 10.1039/C4RA01087F. [DOI] [Google Scholar]
  11. Raviv U.; Giasson S.; Kampf N.; Gohy J.-F.; Jerome R.; Klein J. Lubrication by charged polymers. Nature 2003, 425, 163–165. 10.1038/nature01970. [DOI] [PubMed] [Google Scholar]
  12. Fredrickson G. H. Surfactant-Induced Lyotropic Behavior of Flexible Polymer Solutions. Macromolecules 1993, 26, 2825–2831. 10.1021/ma00063a029. [DOI] [Google Scholar]
  13. Feuz L.; Leermakers F. A. M.; Textor M.; Borisov O. Bending Rigidity and Induced Persistence Length of Molecular Bottle Brushes: A Self-Consistent-Field Theory. Macromolecules 2005, 38, 8891–8901. 10.1021/ma050871z. [DOI] [Google Scholar]
  14. Hsu H.-P.; Paul W.; Binder K. Estimation of Persistence Lengths of Semiflexible Polymers: Insight from Simulations. Polym. Sci., Ser. C 2013, 55, 39–59. 10.1134/S1811238213060027. [DOI] [Google Scholar]
  15. Binder K.; Hsu H.-P.; Paul W. Understanding the stiffness of macromolecules: From linear chains to bottle-brushes. Eur. Phys. J.: Spec. Top. 2016, 225, 1663–1671. 10.1140/epjst/e2016-60017-5. [DOI] [Google Scholar]
  16. Werten M. W. T.; Wisselink W. H.; Jansen-van den Bosch T. J.; de Bruin E. C.; de Wolf F. A. Secreted production of a custom designed, highly hydrophylic gelatin in Pichia Pastoris. Protein Eng., Des. Sel. 2001, 14, 447–454. 10.1093/protein/14.6.447. [DOI] [PubMed] [Google Scholar]
  17. Hernandez-Garcia A.; Werten M. W. T.; Stuart M. C.; de Wolf F. A.; de Vries R. Coating of Single DNA Molecules by Genetically Engineered Protein Diblock Copolymers. Small 2012, 8, 3491–3501. 10.1002/smll.201200939. [DOI] [PubMed] [Google Scholar]
  18. Golinska M. D.; de Wolf F.; Cohen Stuart M. A.; Hernandez-Garcia A.; de Vries R. Pearl-necklace complexes of flexible polyanions with neutral–cationic diblock copolymers. Soft Matter 2013, 9, 6406. 10.1039/c3sm50536g. [DOI] [Google Scholar]
  19. Rühs P. A.; Adamcik J.; Bolisetty S.; Sánchez-Ferrer A.; Mezzenga R. A supramolecular bottle-brush approach to disassemble amyloid fibrils. Soft Matter 2011, 7, 3571–3579. 10.1039/c0sm01253j. [DOI] [Google Scholar]
  20. Zhang C.; Hernandez-Garcia H.; Jiang K.; Gong Z.; Guttula D.; Ng S. Y.; Malar P. P.; van Kan J. A.; Dai L.; Doyle P. S.; de Vries R.; van der Maarel J. R. C. Amplified stretch of bottlebrush-coated DNA in nanofluidic channels. Nucleic Acids Res. 2013, 41, e189. 10.1093/nar/gkt783. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Storm I. M.; Kornreich M.; Hernandez-Garcia A.; Voets I. K.; Beck R.; Cohen Stuart M. A.; Leermakers F. A. M.; de Vries R. Liquid Crystals of Self-Assembled DNA Bottlebrushes. J. Phys. Chem. B 2015, 119, 4084–4092. 10.1021/jp511412t. [DOI] [PubMed] [Google Scholar]
  22. Bolisetty S.; Airaud I. C.; Xu Y.; Müller A. H. E.; Harnau L.; Rosenfeldt S.; Lindner P.; Ballauff M. Softening of the stiffness of bottle-brush polymers by mutual interaction. Phys. Rev. E 2007, 75, 040803R. 10.1103/PhysRevE.75.040803. [DOI] [PubMed] [Google Scholar]
  23. Storm I. M.; Kornreich M.; Voets I. K.; Beck R.; de Vries R.; Cohen Stuart M. A.; Leermakers F. A. M. Soft Matter 2016, 12, 8004–8014. 10.1039/C6SM01227B. [DOI] [PubMed] [Google Scholar]
  24. Gao Y.-G.; Su S.-Y.; Robinson R.; Padmanabhan S.; Lim L.; McCrary B. S.; Edmondson S. P.; Shriver J. W.; Wang A.H-J. The crystal structure of the hyperthermophile chromosomal protein Sso7d bound to DNA. Nat. Struct. Biol. 1998, 5, 782–786. 10.1038/1822. [DOI] [PubMed] [Google Scholar]
  25. Krueger J. K.; McCrary B. S.; Wang A.H.-J.; Shriver J. W.; Trewhella J.; Edmondson J. P. The Solution Structure of the Sac7d/DNA Complex: A Small-Angle X-ray Scattering Study. Biochemistry 1999, 38, 10247–10255. 10.1021/bi990782c. [DOI] [PubMed] [Google Scholar]
  26. Driessen R. P. C.; Meng H.; Suresh G.; Shahapure R.; Lanzani G.; Priyakumar U. D.; White M. F.; Schiessel H.; van Noort J.; Dame R. T. Crenarchaeal chromatin proteins Cren7 and Sul7 compact DNA by inducing rigid bends. Nucleic Acids Res. 2013, 41, 196–205. 10.1093/nar/gks1053. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Hernandez-Garcia A.; Estrich N. A.; Werten M. W. T.; van Der Maarel J. R. C.; LaBean T. H.; de Wolf F. A.; Cohen Stuart M. A.; de Vries R. Precise Coating of a Wide Range of DNA Templates by a Protein Polymer with a DNA Binding Domain. ACS Nano 2017, 11, 144–152. 10.1021/acsnano.6b05938. [DOI] [PubMed] [Google Scholar]
  28. Estrich N. A.; Hernandez-Garcia A.; de Vries R.; LaBean T. H. Engineered Diblock Polypeptides Improve DNA and Gold Solubility during Molecular Assembly. ACS Nano 2017, 11, 831–842. 10.1021/acsnano.6b07291. [DOI] [PubMed] [Google Scholar]
  29. Lamour G.; Kirkegaard J. B.; Li H.; Knowles T. P. J.; Gsponer J. Easyworm: an open-source software tool to determine the mechanical properties of worm-like chains. Source Code Biol. Med. 2014, 9, 16. 10.1186/1751-0473-9-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Marko J. F.; Siggia E. D. Macromolecules 1995, 28, 8759–8770. 10.1021/ma00130a008. [DOI] [Google Scholar]
  31. Hammouda B. SANS from Homogeneous Polymer Mixtures: A Unified Overview. Adv. Polym. Sci. 1993, 106, 87–133. 10.1007/BFb0025862. [DOI] [Google Scholar]
  32. Rivetti C.; Guthold M.; Bustamante C. Scanning Force Microscopy of DNA Deposited onto Mica: Equilibration versus Kinetic Trapping Studied by Statistical Polymer Chain Analysis. J. Mol. Biol. 1996, 264, 919–932. 10.1006/jmbi.1996.0687. [DOI] [PubMed] [Google Scholar]
  33. Silva E. F.; Bazoni R. F.; Ramos E. B.; Rocha M. S. DNA-doxorubicin interaction: New insights and peculiarities. Biopolymers 2017, 107, e22998. 10.1002/bip.22998. [DOI] [PubMed] [Google Scholar]
  34. Crisafuli F A P.; Cesconetto E. C.; Ramos E. B.; Rocha M. S. DNA–cisplatin interaction studied with single molecule stretching experiments. Integr. Biol. 2012, 4, 568–574. 10.1039/c2ib00183g. [DOI] [PubMed] [Google Scholar]
  35. Lipfert J.; Klijnhout S.; Dekker N. H. Torsional sensing of small-molecule binding using magnetic tweezers. Nucleic Acids Res. 2010, 38, 7122–7132. 10.1093/nar/gkq598. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Salerno D.; Brogioli D.; Cassina V.; Turchi D.; Beretta G. L.; Seruggia D.; Ziano R.; Zunino F.; Mantegazza F. Magnetic tweezers measurements of the nanomechanical properties of DNA in the presence of drugs. Nucleic Acids Res. 2010, 38, 7089–7099. 10.1093/nar/gkq597. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Bazoni R. F.; Lima C. H. M.; Ramos E. B.; Rocha M. S. Force-dependent persistence length of DNA–intercalator complexes measured in single molecule stretching experiments. Soft Matter 2015, 11, 4306–4314. 10.1039/C5SM00706B. [DOI] [PubMed] [Google Scholar]
  38. Odijk T. On the Statistics and Dynamics of Confined or Entangled Stiff Polymers. Macromolecules 1983, 16, 1340–1344. 10.1021/ma00242a015. [DOI] [Google Scholar]
  39. Li H.; Witten T. A. Fluctuations and Persistence Length of Charged Flexible Polymers. Macromolecules 1995, 28, 5921–5927. 10.1021/ma00121a031. [DOI] [Google Scholar]
  40. Hardy C. D.; Martin P. K. Biochemical characterization of DNA-binding proteins from Pyrobaculum aerophilum and Aeropyrum pernix. Extremophiles 2008, 12, 235–246. 10.1007/s00792-007-0120-z. [DOI] [PubMed] [Google Scholar]
  41. Saleh O. A.; McIntosh D. B.; Pincus P.; Ribeck N. Nonlinear Low-Force Elasticity of Single-Stranded DNA Molecules. Phys. Rev. Lett. 2009, 102, 068301. 10.1103/PhysRevLett.102.068301. [DOI] [PubMed] [Google Scholar]
  42. Pincus P. Excluded Volume Effects and Stretched Polymer Chains. Macromolecules 1976, 9, 386–388. 10.1021/ma60051a002. [DOI] [Google Scholar]
  43. Dobrynin A. V.; Carrillo J.-M. Y.; Rubinstein R. Chains Are More Flexible Under Tension. Macromolecules 2010, 43, 9181–9190. 10.1021/ma101860t. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Macromolecules are provided here courtesy of American Chemical Society

RESOURCES