Automatic methyl assignment in large proteins by the MAGIC algorithm

Abstract

Selective methyl labeling is an extremely powerful approach to study the structure, dynamics and function of biomolecule systems by NMR. Despite spectacular progress in the field, such studies are still rather limited in number. One of the main obstacles remains the assignment of the methyl resonances, which is labor intensive and error prone. Typically, NOESY crosspeak patterns are manually correlated to the available crystal structure or an in silico template model of the protein. Here, we propose Methyl Assignment by Graphing Inference Construct (MAGIC), an exhaustive search algorithm with no peak network definition requirement. In order to overcome the combinatorial problem, the exhaustive search is performed locally, i.e. for a small number of methyls connected through-space according to experimental 3D methyl NOESY data. The local network approach drastically reduces the search space. Only the best local assignments are combined together to provide the final output. Assignments that match the data with equivalent – or slightly lower - scores are made available to the user for cross-validation by additional experiments such as methyl-amide NOEs. Several NMR datasets for proteins in the 25–50 kDa range were used during development and for performance evaluation against the manually assigned data. We show that the algorithm is robust, reliable and greatly speeds up the methyl assignment task.

Introduction

Deuteration and selective methyl labeling give superior sensitivity and resolution in multidimensional NMR spectra of large proteins^1–3. The effect known as ‘methyl TROSY’ has expanded the scope and applicability of liquid state NMR to proteins and complexes up to several hundred kiloDalton (kDa). This technology, pioneered by the group of Lewis Kay and co-workers^4,5, has yielded new insights in the function of large proteins^6,7. In spite of advances in labeling technology that significantly simplify the task^8–19, the chemical shift assignment of methyl groups in highly deuterated proteins remains a significant bottleneck in the study of large systems. If amide assignments are available, methyl assignment can be carried out manually with a combination of through-bond and NOESY experiments²⁰. In the absence of backbone assignments, alternative strategies have been reported, such as the divide-and-conquer approach^10,21,22 or the systematic mutagenesis of all methyl-labeled residues²³. The former mainly suffers from the extensive ambiguities encountered during the assignment transfer. The latter is costly, time consuming and suffers from local mutated residue-induced conformational changes that scramble the position of several peaks in addition to the desired mutated residues.

Two computational model-based approaches were also proposed in which the assignment is inferred by matching the nuclear Overhauser effect spectroscopy (NOESY) data with the connectivity expected from a known structure or structure model via a Monte Carlo-based swapping procedure to reach convergence according to a matching function^24,25. Stochastic iterative swapping is implemented to overcome the computationally unfeasible exploration of the full assignment universe, which grows with the factorial of methyl number. This approach produces a single assignment per peak but does not immediately provide information about ambiguity and accuracy.

Graph theory and exhaustive search were previously applied to backbone amides assignment from 3D ¹⁵N-edited NOESY-HSQC ^26,27 and during the preparation of our manuscript a method appeared that used McGregor graph matching algorithm and exhaustive search to address the methyl assignment problem²⁸. The success of these approaches is highly dependent upon accurate a priori NOE-based peak network selection that is labor intensive to construct. The network definition step can easily approach complexity of direct expert manual assignment since hundreds of NOESY crosspeaks need to be manually examined and labeled.

Here we propose Methyl Assignment by Graphing Inference Construct (MAGIC), an exhaustive search algorithm that uses raw NMR data. The program is designed with the Nuclear Overhauser Effect (NOE) network density approach to bypass the manual network-definition step. The combinatorial problem is reduced to manageable levels by identifying local, high-density networks and prioritizing their assignment via a local exhaustive search protocol. The algorithm utilizes 2D ¹H,¹³C-heteronuclear multiple quantum coherence (2D ¹H,¹³C-HMQC) and 3D ¹H,¹³C-HMQC-NOESY-HMQC (CCH-NOESY or methyl NOESY)²⁹ unassigned peak lists directly and requires very limited expert curation of the data prior to running. Providing methyl residue type information in the 2D HMQC spectrum greatly decreases computation time, dramatically increases accuracy and is highly recommended. The code, implemented in python, is designed to handle all methyl-bearing amino acid residues (Ala, Ile, Leu, Met, Thr, and Val). The program is distributed with accompanying scripts (generate.py and pdb2noe.py) that aid in peak list preparation and manual verification of the results after the run. The pdb2noe.py validation script has already been added to the NMRFAM distribution of the program Sparky (T.D. Goddard and D.G. Kneller, University of California, San Francisco, CA)³⁰.

Theory

Peak clustering: the concept of NOE network density matrix

An exhaustive search method that considers and tests all possible assignments, allows for the ranking of assignments according to a scoring function that compares simulated and experimental NOESY data. In MAGIC, the assignment universe is reduced by taking into account that the NOE correlations are distance-limited and contain only local connectivity information. As a result, the exhaustive swapping procedure can be carried out locally, i.e. only for few peaks close in space that form peak clusters in the NOESY spectrum. The best assignments for each peak cluster are then combined to generate the full protein methyl assignments. Another important point to consider is that methyl-methyl networks occur in different sizes and ‘densities’ within the core of the protein. The presence of intercalating residues, i.e. aromatics, breaks the methyl network continuity at the core. In addition, methyl residues in loops or termini may be isolated or form isolated pairs. Ranking the connectivity and prioritizing assignments of high-density networks significantly reduces the combinatorial problem.

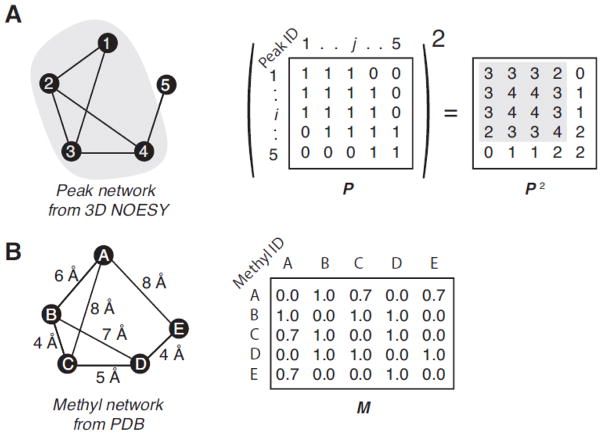
As in classic graph theory, the connectivity ‘construct’ is built from the user-independent analysis of the 3D methyl NOESY peak list as vertices in a square matrix of N × N elements called the adjacency or peak network matrix P where N is the number of edges, i.e. the number of peaks of the reference 2D HMQC spectrum (Fig. 1). Each matrix element represents a connection between two peaks and has nonzero value when a connection is present. Instead of searching for graph isomorphs the MAGIC protocol relies on exhaustive search to conduct peak matching at local and global levels. The peak network density matrix P² is computed which describes the density of the NOE connectivity network. A simple example of peak network is shown within Fig. 1A along with its related P and P² matrices. In order to define the cluster surrounding each peak, i.e. the local peak neighborhood of each peak in the two-dimensional spectrum, a clustering threshold (T_C) factor is introduced. T_C defines the minimal (i, j) element value in the P² for which the peak j belongs to the peak cluster surrounding the peak i (or the so-called i^th-cluster). The starting value of T_C corresponds to the highest off-diagonal (i, j) element value in the P² or maximum density. The basis of the MAGIC algorithm is to iteratively decrease the T_C value, re-define the peak clusters accordingly and repeat the exhaustive search step to find the accurate match to the methyl network in the 3D structure Fig 1B. For instance, taking in account the simple network within Fig. 1, if T_C = 3, the 1^st-, 3^rd- and 4^th-peak can be recruited to define the local peak neighborhood of the 2^nd-peak. This simple procedure enables one to define peak clusters according to both the network density and direct connection criteria. Due to the imperfect and incomplete nature for the experimental NMR data, automated peak-peak network generation can result in false positives and careful ranking of each peak-peak connection based on a confidence score needs to be conducted. In order to deal with the problem, a connectivity scoring protocol was implemented in which each element of the P matrix is converted into a confidence score. By evaluating connections using a confidence score, the peak clustering is then defined according to both high-confidence and high-density peak-peak connection criteria. Hereafter, we will demonstrate that the scoring of each peak-peak connection allows to bypass the manual network definition step and to achieve high accuracy automated assignment from raw data.

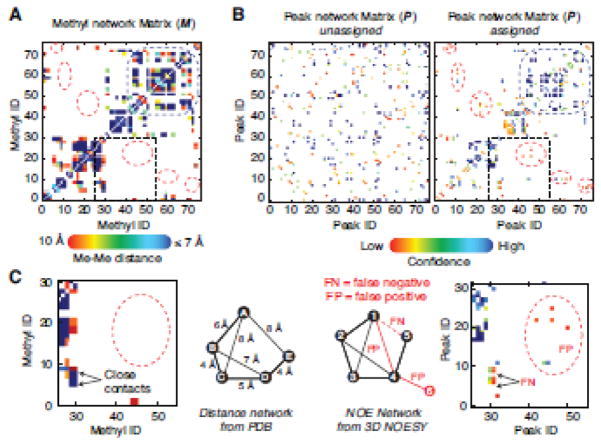
Figure 1. The peak network density matrix and the methyl network matrix.

Given the simple network (A) composed by five peaks and their connections, which are depicted by nodes and segments, respectively, the adjacency matrix, P, is built by all the non- zero value peak-peak interactions (here all set to one for simplicity) and the i^th-row/column corresponding to the i^th-peak. The square of P is the peak network density matrix used to define the peak cluster surrounding each peak. For instance, the second row of P² describes the network density surrounding the 2^nd-peak. Higher number indicates denser network, i.e. larger amount of connections per peak. The P² elements that describe the association between the 2^nd-peak and 3^rd-peak are high because both peaks are closely involved in the same network, i.e. both have connections with the 1^st- and the 4^th-peaks. It is worth noting that the values describing the networking between the 1^st- and 4^th-peaks, which are not directly connected, are not null because both are connected to the 2^nd- and the 3^rd-peak. Then the 4×4 sub-matrix (highlighted in grey) is the dense portion of this simple network. Conversely, the P² row corresponding to the 5^th-peak contains only low values and is not involved in high-density networking. Considering the simple methyl-methyl network (B) composed by five methyls and their connections, which are depicted by nodes and segments, respectively, the adjacency matrix, M, is built with all connections having non-zero value and the i^th-row/column corresponding to the i^th-methyl.

Peak clustering: the connectivity confidence score

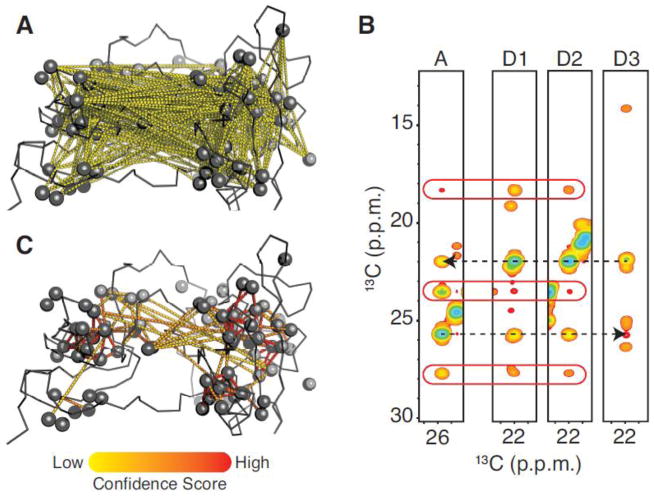
A connection between two peaks is determined by the 3D NOESY data. For each peak in the 2D HMQC or autocorrelation (diagonal) peak of the 3D NOESY (NOE acceptor), the connected peaks (NOE donors) are selected on the basis of ¹³C frequency matching between NOE crosspeaks and HMQC peaks within a defined chemical shift tolerance (typically +/− 0.1 and 0.01 ppm for δ_13C and δ_1H respectively). All connections, defined by this very simple criterion, are mapped into the test-case 3D structure (Fig. 2A). The majority of those connections are low likelihood because they correspond to distances beyond what is observable by NOE transfer (>10 Å). A first sorting method is implemented to retain only NOE contacts in which the symmetric crosspeak is also identified (i→j and j→i types) in the 3D data. As the result, the number of unlikely peak-peak connections is significantly reduced (Fig. S1A). However, unlikely connections are still pervasive in the data. The situation is improved further by ranking the connections via a confidence score: the higher the score, the more likely the connection. The source of wrong connections in NOE data was carefully scrutinized to define this score. The first source of error is peak overlap in the 2D HMQC reference spectrum. The connections between HMQC peaks that are subject to overlap are displayed into the test-case 3D structure (Fig. S1B). The overlap is defined according to the aforementioned chemical shift tolerance. It appears that most of wrong connections involve overlapped 2D peaks. Another source of error is the selection of wrong donors. For one NOE acceptor strip (Fig. 2B), both correct (D1 and D2) and incorrect (D3) donors can be identified that satisfy the aforementioned sorting criteria. We found that, for each NOE crosspeak, the probability of selecting a wrong donor increases with the number of putative donors. The mapping of the number of donors into the test-case 3D structure shows that unlikely connections tend to be extracted from NOE crosspeaks that have multiple donors (Fig. S1C).

Figure 2. Peak-peak connection confidence score.

(A) The peak-peak connections extracted from 3D CCH-NOESY data using the simple criterion of carbon frequency matching between NOE crosspeaks and 2D HMQC peaks are mapped as yellow dashed line into a test case 3D structure. Most of them represent unlikely methyl-methyl (carbon-carbon) distances beyond 10 Å. (B) The basis of confidence score calculation is illustrated with a series of strips corresponding to four 2D-HMQC reference peaks. The first strip represents the NOE acceptor 2D reference peak and the remaining three the putative NOE donor peaks. The two dashed arrows depict mirrored NOE connectivities between methyls. The red racetracks highlight the NOE crosspeaks with equivalent carbon frequencies among the three first strips. (C) All selected peak connections are mapped as dashed line into a test-case 3D structure with their calculated confidence scores, which are depicted with a color scale from yellow to red for low to high confidence score, respectively. Both structures are represented as ribbon with methyls as spheres.

Most of the incorrect connections can be discriminated via a penalty score for 2D HMQC overlap and for multiple donor selection. To further increase confidence another criterion is introduced that is based on the fact that two methyls showing NOESY correlations often share NOEs with other nearby methyls (Fig. 2B). This idea forms the basis of expert manual assignment strategies. In Fig. 2B, the first two NOESY strips that correspond to correct donors, three additional NOE crosspeaks are also found in the acceptor strip. Conversely, the wrong donor strip does not contain any NOE crosspeak at the frequencies corresponding to NOE crosspeaks within the acceptor strip. The number of shared NOEs for each connection was mapped into the test-case 3D structure (Fig. S1D), illustrating that, in contrast to wrong connections, correct pairings tend to have more than one NOE shared between donor and acceptor.

Taking into consideration all the criteria outlined above, the algorithm calculates the confidence score for each pairing, i.e. the P element values, according to the following equation:

$${\mathrm{P}}_{ij}=\sqrt{\frac{{\mathrm{\varphi }}_{\text{over}}^{\text{ij}}}{{\mathrm{\varphi }}_{\text{CS}}^{\text{ij}}}{\left(\frac{1+{\mathrm{N}}_{\text{noe}}^{\text{ij}}}{{\mathrm{N}}_{\text{donor}}^{\mathrm{i}}}\right)}^2}$$ (1)

with P_ij, the P element value at the position (i, j) that corresponds to the confidence score of the connection between the i^th- and j^th-peaks; ${\mathrm{\varphi }}_{\text{over}}^{\text{ij}}$ and ${\mathrm{\varphi }}_{\text{CS}}^{\text{ij}}$, the 2D peak overlapping and the carbon chemical shift deviation penalties, respectively; ${\mathrm{N}}_{\text{nos}}^{\text{ij}}$ and ${\mathrm{N}}_{\text{donor}}^{\mathrm{i}}$, respectively, the number of NOE crosspeaks shared between the 2D i^th- and j^th-peaks, and the number of possible donors for the NOE crosspeak connecting the 2D i^th- and j^th-peaks. The chemical shift root mean square deviation is calculated according to the equation $<\mathrm{\Delta }\delta {>}_{ij}=\sqrt{{\left({\delta }_i^{\mathit{noe}}-{\delta }_j^{\mathit{hmqc}}\right)}^2+{\left({\delta }_j^{\mathit{noe}}-{\delta }_i^{\mathit{hmqc}}\right)}^2}$, where ${\delta }_i^{\mathit{noe}}$ and ${\delta }_j^{\mathit{hmqc}}$, are the ¹³C frequencies of the NOE crosspeak related to the 2D i^th-peak and to the 2D HMQC j^th-peak, respectively. The ${\mathrm{\varphi }}_{\text{CS}}^{\text{ij}}$ penalty is applied to favor better frequency matching within the frequency tolerance. However, considering the intrinsic variation of peak maxima due to digital resolution limitations, the minimum value of <Δδ>_ij is limited to 0.05 ppm in order to avoid misleading score fluctuations. The penalty is then defined as ${\mathrm{\varphi }}_{\text{CS}}^{\text{ij}}=20<\mathrm{\Delta }\delta {>}_{ij}$ such as <Δδ>_ij = 0.05 leading to ${\mathrm{\varphi }}_{\text{CS}}^{\text{ij}}$. During the peak cluster buildup protocol, ${\mathrm{\varphi }}_{\text{over}}^{\text{ij}}$ is equal to 0 if the donor is overlapped with another peak, otherwise equal to 1. Confidence scores are then high for reliable connections and low for unlikely ones (Fig. 2C).

The confidence scores that define elements of P, and consequently P², contain information of both network density and peak connection reliability. Hence, the clusters of peaks defined for high T_C values are part of the more reliable and dense NOE networks. These highly curated peak clusters can then be assigned by an exhaustive search-based procedure resulting in very reliable assignments. As the highly reliable clusters become assigned, the possible assignment search space for the lower density and lower reliability networks is reduced.

The iterative protocol

The assignment consists in matching the peak network to the model-based methyl network. The algorithm extracts from 3D structure the distances between all methyl carbons and builds a square matrix of methyl-methyl connections (M) with each element defined by a scalar varying from 0 to 1 according to the corresponding methyl-methyl distance. The functions of methyl-methyl distance that define the elements of M have been tested and optimized to achieve the most accurate assignments possible based on the input data (see Fig. S2). The elements of M are equal to 1 for methyl-methyl distances (carbon-carbon distance) below 7 Å and to linearly decreasing values from 1 to 0 for distances from 7 to 10 Å (illustrating within Fig. 1B with a simple methyl network). Since the stereospecific assignment is beyond the scope of our algorithm, we introduced a pseudo-methyl per Val/Leu residues. The combined pseudo-methyl contains the sum of all methyl-methyl connections from each of the geminal Leu/Val methyl.

Additionally, a score matrix S is defined, which includes scores for all peak-peak connections (see Fig. S3B) according to the following equation:

$${\mathrm{S}}_{\text{ij}}={\mathrm{P}}_{ij}\frac{{\mathrm{I}}_i^j}{{\mathrm{\sum }}_k^n{\mathrm{I}}_i^k}$$ (2)

with S_ij and P_ij, the assignment and the confidence scores (eq. 1), respectively, associated to the connection between the i^th- and j^th-peaks; ${\mathrm{I}}_i^j$, the height of the NOE crosspeak that is related to the 2D i^th-peaks and that defines the correlation between the i^th- and j^th-peaks; and ${\mathrm{\sum }}_k^n{\mathrm{I}}_i^k$, the sum of the n NOE crosspeak intensities related to 2D i^th-peaks. Hence, the score for each connection corresponds to the product of the confidence score with the relative intensity of the associated NOE crosspeak. For score calculation purposes, the confidence score is slightly modified so as not to impose 2D peak overlapping penalty ( ${\mathrm{\varphi }}_{\text{over}}^{\text{ij}}=1$ in all cases).

The algorithm calculates the score for each assignment by adding all connection scores only if the peak-peak connection matches a methyl-methyl connection, i.e. by summing all elements of the S ∘ M Hadamard product (Fig. S3B). As a consequence of using relative NOE intensities in score calculation, the algorithm tends to assign high confidence and intense NOEs to connection between methyls separated by less than 7 Å (i.e. M element values set to 1, see Fig S2). Confidence scores of 2 and above are considered acceptable. The intensity of each NOE crosspeak is normalized according to the overall intensity of its individual NOESY strip to compensate for intrinsic differences in intensities of the autocorrelation peaks within the 3D spectrum. Thus, NOE intensities are used to prioritize the assignment of the most intense NOE crosspeaks in each individual strip that are considered most reliable (mimicking the expert manual analysis). The correlation between NOE and distance is very relaxed (see Fig S2) and not used to infer methyl-methyl distances directly.

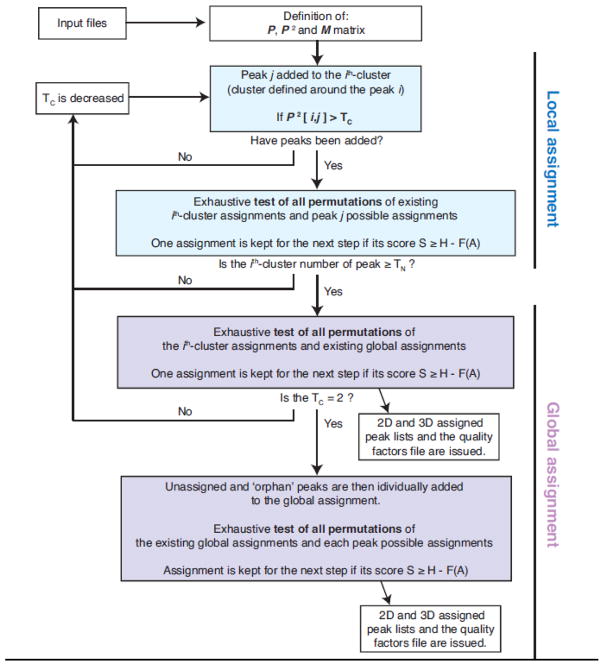
The flowchart for MAGIC is shown in Fig. 3. At the beginning of the calculation, the P², S and M are defined according to the input files (Fig. S4) and the iterative process can start (see Fig. S3 for a simple example). The first step is the local assignment that consists in exhaustively testing all possible permutations of individual assignments within each peak cluster. The individual assignment choice for each peak are defined according to their methyl type information (which can be ambiguous). The algorithm iteratively builds peak clusters according to the aforementioned T_C value and P² elements. The T_C value is minimized iteratively, starting from the highest value of P² down to 2 (which corresponds to the density network matrix value associated with an isolated peak-peak connection). Decreasing the T_C value recruits additional peaks and increases the peak cluster size. Once a cluster reaches the size threshold, i.e. a certain number of peaks, defined as T_N (from 3 to 5, depending on T_C value), the cluster is added to the global assignment process which consist in computing the total matching scores of all permutations between cluster assignments and global assignments. At each step, either local or global, only assignments with high score are promoted to the next step. Because the network is underdetermined at the beginning of the calculation, the correct assignment will likely not exhibit the highest score. Consequently, it is important not to discard potentially correct assignments and allow the algorithm to match not only the assignment with the highest score (defined as H), but to also keep a number of assignments with similar scores under consideration. A score tolerance function, ℱ(A), is introduced for that purpose. An assignment is kept only if the difference between its score and the highest score is within the score tolerance acceptance range. ℱ(A) depends on the ratio of unassigned peaks and a user-defined parameter ‘A’ (see details on the score tolerance function ℱ(A) in Supplementary Materials). ℱ(A) decreases all along the calculation trajectory while the network becomes more determined. The adjustable parameter ‘A’ controls the computing resources and the calculation time by controlling the allowed amplitude of score tolerance. Higher ‘A’ values extend the tree search by relaxing the cutoff criteria, increasing computing time and potential accuracy of the results, while a low value increases the rejection rate, shortens the calculation time while increasing the probability of rejecting a potentially correct assignment. The function ℱ(A) has been set such that A=1 gives rise to correct assignment for all our test cases within a reasonable time. However, the appropriate ‘A’ parameter can be adjusted based on the specific system, the data quality and the available computing facilities.

Figure 3. The MAGIC algorithm flowchart.

The schematic of the MAGIC algorithm subdivided into two main trunks of local and global assignment. The local assignment involves the isolated peak cluster growing with decreasing T_C, while global assignment produces peak cluster assignment merged with decreasing T_C. Briefly, the j^th-peak is added to the i^th-cluster if P²[i,j] > T_C. The i^th-cluster is added to the global assignment if its number of peak, n_i, is > T_N. Each time a peak is added to a cluster, or a cluster is added to the global assignment, the new calculated assignments are carried to the next step if their scores, S, is closed enough to the highest score (H) of the on-going calculation, such as H – S < ℱ(A).

Testing datasets

The input includes the structure coordinate file (pdb file), both 2D HMQC and a 3D CCH-NOESY peak lists and the parameters file (Fig. S4 and Fig S5). The HMQC peak list is prepared using a script to include information about methyl type and geminal pairs. Geminal pair information is optional and can be established via a short mixing time (~40 ms) version of the 3D methyl NOESY spectrum. The methyl type information for each peak is derived from chemical shifts statistics from BioMagResBank (http://www.bmrb.wisc.edu/ref_info/statsel.htm). The assigned 2D HMQC peak list can then be reviewed by the user and edited as needed in order to add additional experimentally derived information such as methyl types (M), manually assigned resonances or geminal pairs (G). The parameters file (Fig S5) is a simple text file including all input files location, the labeling type and some parameters that are discussed below.

Our algorithm was tested on 8 different datasets originated from proteins in the 25–50 kDa size range for which 2D ¹³C,¹H-HMQC and 3D ¹³C-HMQC-NOESY-¹³C,¹H-HMQC (CCH-NOESY) spectra were recorded (Fig. S6) in our group: i) The kinase domain of Abelson kinase 1b (Abl-KD, 33 kDa) [¹³C,¹H]-labeled on Ala-β, Met-ε, Ile-δ1, dimethyl Leu-δ1/2 and Val-γ1/2 methyls; ii) The N-terminal regulatory module of Abl kinase 1b (Abl-RM, 24 kDa), which was [¹³C,¹H]-labeled on Ala-β, Ile-δ1, dimethyl Leu-δ1/2 and Val-γ1/2 methyls; iii) The Colicin-M protein (ColM, 30 kDa) [¹³C,¹H]-labeled on Ala-β, Met-ε, Ile-δ1, dimethyl Leu-δ1/2 and Val-γ1/2 methyls; iv) the FlhA cytoplasmic domain (Flha CD, 37 kDa) [¹³C,¹H]-labeled on Ala-β, Met-ε, Ile-δ1, Thr-γ2, mono-methyl Leu-δ1/2 and Val-γ1/2 methyls; v) same as iv) but with [¹³C,¹H]-labeled on Met-ε, Ile-δ1, and Leu-δ2/Val-γ2 methyls (LV proS); vi) The N-terminal domain of heat shock protein 90 (Hsp90, 27 kDa) [¹³C,¹H]-labeled on Ala-β, Met-ε, Thr-γ2, Ile-δ1, dimethyl Leu-δ1/2 and Val-γ1/2 methyls; vii) The maltose binding protein (MBP, 42 kDa), either [¹³C,¹H]-labeled on Ala-β, Met-ε, Ile-δ1, dimethyl Leu-δ1/2 and Val-γ1/2 methyls or on Ala-β, Met-ε, Ile-δ1, Leu-δ2 and Val-γ2 methyls; viii) The VASA helicase C-terminal domain (VASA-C, 20 kDa) [¹³C,¹H]-labeled on Ala-β, Met-ε, Thr-γ2, Ile-δ1, dimethyl Leu-δ1/2 and Val-γ1/2 methyls.

MATERIALS AND METHODS

Protein isotope labeling for NMR studies

Highly deuterated, methyl labeled Abl-KD, Abl-RM, ColM, Hsp90, MBP, MBP (Leu, Val-proS) and VASA-CD samples for NMR study were prepared by growing the cells in minimal (M9) media. Cells were typically harvested at OD₆₀₀ ~1.0–1.2. U-[¹³C,¹⁵N]- or U-[²H,¹³C,¹⁵N]-labeled samples were prepared by supplementing the growth medium with 1 g·l⁻¹ of ¹⁵NH₄Cl and 2 g·l⁻¹ of [¹³C]- or [²H₇, ¹³C₆]-glucose in H₂O or 99.9%-²H₂O (CIL and Isotec). Methyl-protonated samples were prepared as described before⁷ using 50 mg·L⁻¹ of α-ketobutyric acid, 85 mg·L⁻¹ of α-ketoisovaleric, 50 mg·L⁻¹ of ¹³CH₃-Met, 50 mg·L⁻¹ of ²H₂, ¹³CH₃-Ala, and 50 mg·L⁻¹ U-²H, Thr-γ2[¹³CH₃]. MBP-cyclodextrin complex was prepared as previously described ⁴ and stereo-specific labeling of Val/Leu was achieved using 300 mg·L⁻¹ of methyl-labeled acetolactate ⁹.

NMR Spectroscopy

All NMR data were collected on Bruker AVANCE III 700, 850 or 900 MHz equipped with 5-mm TCI cryoprobes. All recorded spectra were processed with NMRPipe³¹ and analyzed with NMRFAM-Sparky³⁰. Spectra were recorded at 25, 32 or 37 °C. TROSY-based triple resonance experiments were recorded for backbone resonance assignment. Assignments for selectively [¹H,¹³C]-labeled methyl-bearing residues were obtained using a combination of 3D ¹³C,¹⁵N SOFAST-NOESY-HMQC and SOFAST-HMQC-NOESY-¹³C,¹⁵N-HMQC with 300 ms mixing time³². The 3D SOFAST version of the methyl-NOESY (3D ¹H-¹³C-HMQC-NOESY-HMQC) for automated assignment was acquired with 256 × 128 × 2k complex points and recycle delay of 0.2 s (Fig. S6). The 3D methyl-methyl peak lists for MAGIC run were picked automatically based on the peaks in the 2D-HMQC plane using ‘kr’ command in Sparky and then the autocorrelation (diagonal), artifacts and noise peaks were manually removed.

Computation

Test runs were conducted using two different computers: a 2013 iMac desktop with single CPU Intel i7 (4-core, 8-threads, 3.1 GHz and 8 GB 1600 MHz DDR3 RAM) and a dual-CPU Intel XEON E5-2687W (10-core, 20-threads V3 3.10 GHz and 64 GB of 2400 MHz DDR4 RAM). The score factor, A, was set to 1 and the methyl distance threshold to 7–10 Å. Assignment calculation was performed using either geminal pairs (G), methyl type (M), both M and G, or no information as specified in the input script (Fig S5). The output includes computing time, accuracy, 2D HMQC assignment completeness and ambiguity (i.e. the average number of alternative assignment), along with the starting number of 2D HMQC peaks, the number of NOEs and the number of connections defined out of the automatic NOESY analysis. Accuracy is evaluated against manually assigned peaks using amide-methyl data in addition to methyl NOESY data. The program output includes the assigned 2D HMQC and 3D CCH-NOESY peak lists in Sparky format for one of the assignment having the highest score (Fig. S4B). In addition the algorithm generates a PyMOL script file (.pml extension) that maps the confidence score of each peak-peak connection confidence and the completeness of NOE assignment for each 2D assigned peak onto the 3D structure (Fig. 5 for Abl-RM and Fig. S7 for all datasets) when opened for viewing in PyMOL (PyMOL Molecular Graphics System, Version 1.8 Schrödinger, LLC). The output files are continuously updated during the run. The 2D HMQC peak list also includes, for each peak, the list of alternative assignments, the sum of all confidence scores associated to each peak and the NOESY assignment completeness. The assigned 3D CCH-NOESY peak list also enumerates both confidence score and associated distance from the 3D structure for each NOE assignment (Fig. S4B). If backbone amides assignments are available, the results from automated run can be independently validated for consistency by simulating the methyl amide region in a 3D ¹H-¹³C NOESY-HMQC spectrum based on the 2D HMQC and the starting coordinates. Our ‘pdb2noe’ script already distributed in NMRFAM-Sparky can be used for that task. Manual validation can be done in minutes. If ambiguous in 2D assignment are present swapping can be done using several types of NOESY data until ambiguity is resolved (see example in Fig. S8). Software and demo files can be obtained here: https://github.com/NMRsoftware/MAGIC.

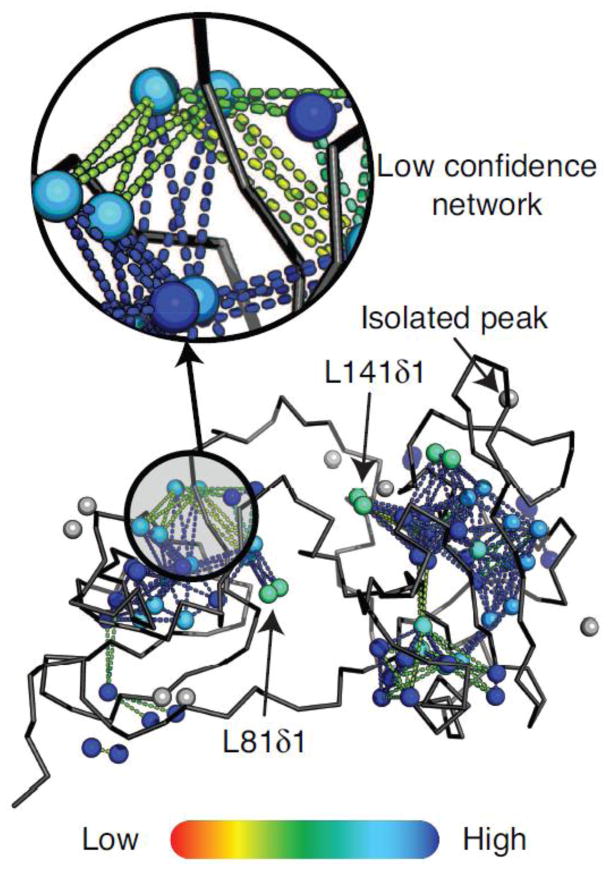
Figure 5. The quality factors mapping onto Abl regulatory domain structure.

Each set of output files is composed of a script to map into the 3D structure the quality factors using PyMOL and the 2D HMQC and 3D CCH-NOESY assigned peak list. The structure of the test case Abl-RM is displayed as a ribbon with methyls as spheres. Each methyl/peak pair is displayed as a sphere with a color code ranging from 0 to 1 (red to blue) for the NOE assignment completeness of the related NOESY strip. The methyl-methyl connections, depicted as dashed-lines, are also colored according to their associated peak-peak connection confidence score (red to blue color gradient from confidence 0 to 2, and blue above 2). Grey spheres indicate unassigned methyls due to low or no NOE crosspeaks. The inset highlights an example area of the protein in which the peak-peak connection network has a low confidence and needs further user verification. L141δ1 or L81δ1 are peaks involved in reliable network that display low NOE assignment completeness. This is due to strong overlap in the 2D HMQC. The assignment of those hidden peaks can be achieved by a second run with bootstrapped assignments.

RESULTS AND DISCUSSION

The algorithm was tested on 8 mid-sized proteins (25–42 kDa) for which high-quality data and accurate backbone and methyl assignments were available or determined by expert analysis. The results are summarized in Table 1. Single assignments in 4 out of 8 targets were 100% correct. On average, the automatic assignments were >95% correct while methyl type was specified and peaks received single assignment in ~60% of cases with >95% accuracy. Computation time depends on both the number of 2D HMQC peak to assign and on data quality (Table S1). Geminal information helps to decrease computation time by more than 4-fold, while the accuracy increased by a small but significant 2.3%, so acquiring a short mixing time NOESY is helpful in most cases.

Table 1.

Summary of MAGIC assignment results on a set of highly deuterated methyl labeled samples.

Protein (Labeling scheme)	Methyls	Input information1	Overall Assignment (%)2	Accuracy3 (%)	Single assignments4 (Incorrect)	Average assignments per 2D peaks	Time (min)
Abl-KD (AILMV)	133	M, G	85	96	68 (1)	2.9	15
		M	85	95	64 (2)	3.0	102
Abl-RM (AILV)	84	M, G	86	100	45 (0)	2.1	1
		M	86	100	40 (0)	2.2	2
		G	85	98	47 (1)	2.1	4.5
		-	86	98	35 (2)	2.5	10
Col-M (AILMV)	117	M, G	93	100	79 (0)	1.9	3
		M	93	98	69 (2)	2.1	8
		G	92	97	60 (0)	2.4	38
		-	93	92	75 (5)	2.2	75
FlhA-CD (AILMTV)5	209	M	32	97	19 (0)	4.9	5700
FlhA-CD (ILsMVs)6	102	M	97	90	56 (4)	2.2	270
Hsp90-ND (AILMTV)	111	M, G	88	94	82 (5)	2.2	4
		M	89	92	81 (9)	2.3	6.5
		G	88	90	83 (8)	2.8	20
MBP (ILMV)	120	M, G	94	96	90 (3)	1.7	11
		M	94	94	71 (5)	2.2	89
MBP (ILsMVs)6	76	M	95	100	60 (0)	1.3	1
		-	95	99	52 (0)	1.6	2
VASA-CD (AILMTV)	76	M, G	83	100	34 (0)	2.7	1
		M	83	93	21 (3)	2.8	2.5

¹Starting methyl input information: geminal pairs (G), methyl type (M) and no information (−). Note that methyl type and geminal pairs can be ambiguously specified.

²Overall percent assignments (assigned/2D peaks).

³Overall accuracy versus manual assignment independently cross-validated with H_N NOESY data.

⁴Number of methyls with single assignment and number of incorrect assignments in parenthesis.

⁵Leu and Val were labeled using mono-methyl labeled precursors.

⁶Ls and Vs refer to stereospecific (proS) methyl labeling for valine and leucine.

The validity of the network density approach is apparent when looking at the propensity for methyl residues to occur in clusters in the protein core. In fact, 78% of the 2D peaks are assigned as part of high-density clusters (i.e. peaks 1–4 in Fig 1A). In addition, 12% more peaks are assigned thanks to their connections to high-density clusters (i.e. peak 5 in Fig 1A). The challenge then becomes to accurately define clusters of peaks with minimal expert manual analysis. Our program automatically analyzes raw NOESY data and ranks NOE-based peak-peak connections according to their degree of confidence. Experimental data contains both false positive (FP) and false negative (FN) connections (Fig. 4). False positives, at least in our hands, hampered classic graph theory algorithmic approaches with raw NOESY data while false negatives underscored incomplete nature of NOESY data (see M vs. assigned P matrix in Fig. 4) quantified by the difference between the number of connections per methyl vs. the number of connection per peak (see Table S1). Mimicking the manual expert approach, MAGIC prioritizes the assignment of high-density networks, handling low connectivity methyls in later cycles. As a result, incorrect assignments tend to collect in low connectivity regions, in which even a single incorrect connection has a major statistical impact. Another consequence of the incomplete nature of the NOESY data is the assignment ambiguity. When ambiguity cannot be resolved based even on high confidence score values, the software will output multiple alternate assignments.

Figure 4. Peak network matrices in experimental data set.

The structure-based methyl network matrix (A) and the experimental 3D NOESY peak network matrix (B) for protein Abl-RM. The color grade (from red to deep blue) varies from 0 to 1 for the M matrix elements and from 0 to 4 for the confidence score or P matrix. For (B) both the starting and final peak network are shown. The P matrix starts from randomly distributed and converges during calculation to resemble M at the end of the run (left and right panel, respectively. The dotted red circles highlight discrepancies between the M and P that can be schematically represented by the simple networks shown in (C). M shows much higher density and represents the true connection pattern, while the P matrix shows several false negatives (FN) and false positive (FP). FN connectivities are those present in the structure but not in the data (due to dynamics or low s/n data or incomplete peak selection) and FP connectivities are those present in the data but not actually represented in M. The latter category indicates noise, incorrectly selected peaks or discrepancies between the structure and the data for example crystal vs. solution structure. The MAGIC algorithm deals with both by ranking FP and FN connections via the confidence score (S) matrix. For instance, FP connections receive a low confidence score in this example while FN connections do not impact the assignment in the high confidence portion of the network.

In rare cases, swapped assignments are observed in reliable NOE networks. These assignment swapping involve methyls that are very close in space and share the same methyl neighborhood. Leu clusters are particularly problematic in that regard, even manual assignment often requires additional data to validate the accuracy. Consequently, the software can interconvert those assignments because their connectivity maps are very similar. FP peaks in all forms, such as inconsistencies between crystal and solution structures, noisy data, or overlapped NOE crosspeaks can trigger the swapping by giving a score advantage to the incorrect assignment: for instance, if one area of the protein displays a high b² factor, such as for ColM data set, or if crystal structure includes ligand binding, such as for VASA-CT data set, it would suggest that these areas are poised for rearrangement in solution. In other cases, the side chains pack in a completely different way whereto the peak pattern in the NOESY cannot be reconciled with the high-resolution structure and will cause any automatic assignment software to fail without careful manual examination (Fig S9).

The MAGIC algorithm provides useful feedback that helps the user complete and verify the assignments. Simple metrics, such as NOE assignment completeness or confidence of peak-peak connection can be used to quickly identify areas of potentially inaccurate assignments. As an example, the quality factors issued for the automatic assignment of Abl-RM data set are mapped onto its 3D crystal structure (Fig. 5). The user then can focus on area of the protein where the assignment relies on low confidence connections (Fig. 5). In addition to the quality factors, wrong assignment can be detected by visually inspecting the assigned NOE crosspeaks.

We examined performance differences between our program and the exhaustive search, classic graph theory-based program MAGMA²⁸. Extensive comparison with the Monte Carlo-based algorithms^24,25 is already conducted in the MAGMA manuscript. MAGMA completes assignment for a proS-Leu/Val and Ile labeled MBP sample (VsLsI, 73 peaks) in 56 hours. Reportedly, 47/70 peaks have one assignment and those assignments are 100% correct, the remaining 23/70, have multiple assignments (see Table S2). MAGIC completes assignment of a proS-Leu/Val, Ile and Met labeled MBP sample (VsLsIM, 76 peaks) in 1 minute, for 60/76 peaks one assignment was found; 16/72 peaks have multiple assignment but overall accuracy is 100%. Moreover, our dataset enables the MAGIC algorithm to automatically extract 5.4 connections per peak while the MAGMA program has been used on a dataset containing 4.1 manually curated connections per peak, i.e. ambiguous or erroneous connections have been manually identified and discarded. In our sample, additional labeling of Met undoubtedly helps reducing NOE network redundancy. Nonetheless, MAGIC provides more complete LsVs assignment. Hsp90-ND samples dataset had major differences in labeling. Indicatively the performance reflects the number of methyls 120 in our case vs. 47 in the case of the sample used for MAGMA. When scaled to the number of observable methyls, MAGIC and MAGMA run time is similar for Hsp90.

The MAGIC algorithm produces accurate results from raw NMR data when the methyl type is known (Table 1). The methyl type can be easily obtained by specific methyl-labeling methods using small volume cultures and rapid 2D data acquisitions^13–15,34, however, it is of interest to establish the program accuracy in the case the methyl type information is only inferred from chemical shifts. We developed a setup script (generate.py) that determines putative methyl types for each peak according to ¹H-¹³C chemical shift averages and standard deviations extracted for the BMRB database and, if a short mixing time NOESY peak list is provided, also matches and labels the geminal peaks pairing. This script also provides ambiguous methyl type information to avoid mistyping errors at the calculation onset. The geminal pairing helps the software discriminate Leu and Val methyl type from the Ala and Thr containing pool of 2D crosspeaks. The Abl-RM and proS-methyl-labeled MBP data sets assignments completed within minutes, reaching >98% correct assignment. For these simple cases, methyl type and geminal information are clearly not required. Using geminal information, ColM and Hsp90-ND data set assignments were achieved within a much longer time with a drop in accuracy (90% for Hsp90-ND). Assays were also conducted without initial geminal pairing for ColM, raising 92% correct assignments within 75 min. These latter examples illustrate that as sample get larger and more complex, the information requirements become more stringent.

Based on our test cases, we propose reasonable labeling strategies to achieve automatic assignment. Ile and Met can be easily inferred from chemical shift analysis, however Ala, Leu, Thr and Val have highly overlapping chemical shift ranges. Understandably, the automatic methyl type definition according to the chemical shift is prone to failure in overlap regions and in the case of unusually shifted methyl groups and indeed that was the main source of errors in our tests. Additionally, we found that across the tested targets, the propensity for each methyl type to occur in a high-density cluster varies significantly as follows: Ala, 43% (27/63); Ile, 88% (91/104); Leu, 92% (213/232); Met, 77% (20/26); Thr, 75% (18/24) and Val, 82% (137/168). Ala is generally less than 50% assigned from local peak cluster assignment. This is because Ala tends to have low NOE connectivity compared to other amino acids. In all our tests, Ala drove up ambiguity and increased calculation time.

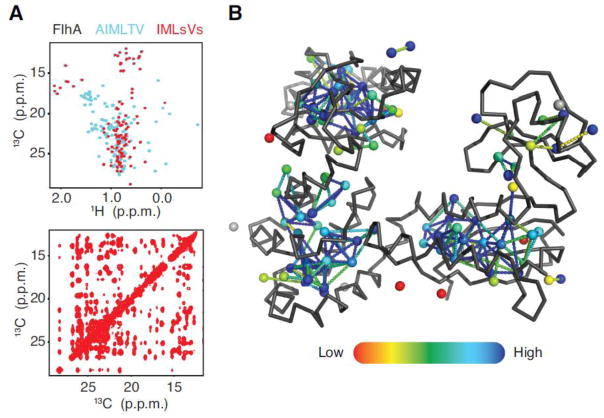
The safest labeling strategy would be to combine Ile, Leu, Met, and Val. If Ala and Thr are targets of interest, the problem could be addressed by recording 2D spectra on two different alternate samples: an Ala, Ile, Met, Thr and a Leu, Val sample. In the case of high molecular weight proteins, the preferred strategy is to use stereospecific Leu and Val labeling^9,15. The labeling scheme gives high signal to noise data while significantly reducing the combinatorial problem and NOE crosspeak overlapping. The FlhA dataset, which contains >200 methyl peaks, represents the upper limit to what MAGIC can handle at this time with just a 3D CCH-NOESY data and full methyl complement. The Leu region is highly overlapped and even manual assignment requires additional through-bond and 3D ¹⁵N,¹³C-edited NOESY data to resolve. A Leu/Val proS and (or) proR are generally required for similar samples. The strategy was implemented for FlhA by producing an Ile, Met and Leu/Val proS sample that was subsequently assigned with MAGIC resulting in ~97% completeness and 89% accuracy (Fig. 6) with ~3 hours of expert work for data processing and peak picking.

Figure 6. FlhA assigned by proS Leu and Val labeling.

The superposition of 2D ¹H-¹³C HMQC from alternative labeling schemes (A top panel) full complement (cyan) and stereospecific methyl labeling (red) are displayed, along with the ¹³C-¹³C plane of 3D ¹H-¹³C HMQC-NOESY-HMQC from stereospecifically-labeled sample (A bottom panel). Assignments (>94%) are mapped on FlhA coordinates. Each methyl and peak pair is displayed as a sphere with a color code ranging from 0 to 1 (red to blue) for the NOE assignment completeness of the related NOESY strip. The methyl-methyl connections, depicted as dashed-lines, are also colored according to their associated peak-peak connection confidence score (red to blue color gradient from confidence 0 to 2, and blue above 2). Unassigned methyls shown as grey spheres.

CONCLUSIONS

We have outlined the MAGIC computational approach for methyl ¹H and ¹³C resonance assignment in highly deuterated and selectively methyl labeled proteins that relies on 3D methyl-NOESY data and an existing experimental or model structure. The algorithm features a local exhaustive search algorithm that combines the advantage of full exploration of the possible assignment universe with a reasonable computational expense. Most notably, the program requires minimal raw data preparation that is limited to peak picking and simple labeling of amino acid types check. The program supports partially pre-assigned data, geminal connectivity definitions for Leu/Val and different labeling schemes such as mono- or di-methyl and stereospecific Leu/Val. Using actual experimental data of decent quality, the software can complete the assignment task on medium-sized proteins within a few minutes, while it can take much longer for more complicated data that may exhibit sparser or more overlapped methyl-methyl contacts. MAGIC was tested and performed reliably in system containing up to ~200 methyl residues in 2D ¹H-¹³C-HMQC with all methyl-containing residues labeled.

Supplementary Material

10858_2017_149_MOESM1_ESM

Figure S1. Mapping of elements of the confidence score parameter. The selected peak connections (dashed lines) have been mapped on the 3D structure thanks by the preliminary known assignment. Protein backbone (wireframe) and methyl carbons (spheres) are displayed. (A) The peak connections are selected using the two basic criteria: i) carbon frequencies matching and ii) presence of the symmetric NOE. Thereafter, the aforementioned connections are colored according to different criteria: (B) in red if at least one of the two 2D HMQC peaks is overlapped, otherwise in yellow; (C) low to high color gradient bar represents increasing number of putative donors associated to the NOE from which is defined the connections; (D) low to high color gradient bar represents increasing number of NOE crosspeaks with overlapping carbon frequencies in both donor and acceptor strips.

Figure S2: Input and output data of the MAGIC algorithm. (A) The input files are the PDB coordinate file, the 2D HMQC peak list and the NOE-only (no diagonal crosspeak) 3D ¹³C-HMQC-NOESY-¹³C,¹H-HMQC peak list. The insets show the peak lists format and needed information: for the NOESY peak list, from left to right, are the assignment, the ¹³C-¹³C-¹H chemical shifts and the intensity columns. The peak height column is mandatory as the score calculation is based on NOE crosspeak intensity. The 2D HMQC peak list is unassigned, however is preferable to name peak (arbitrary ID number) for result analysis purpose and it is mandatory to inform the methyl type – even if ambiguous (fourth column, LV for instance for leucine/valine peak). Moreover, the user can hold manually assigned or verified peaks with the flag ‘−’ in the fourth column. The last column is dedicated to geminal methyl pairing. This peak list is automatically generated using an included preparation script called generate.py. (B) The output files are the assigned 3D NOESY peak list including, for each assigned NOE in addition to the assignment and chemical shifts columns, from left to right, the confidence score and the methyl-methyl distance for critical analysis purposes. The 2D HMQC peak list is assigned according to the global assignment with the highest score. For each peak, the list includes in addition to the assignment and chemical shifts columns, from left to right, the total confident score (the sum of all P matrix i^th-row elements), the NOE strip assignment completeness, and the list of alternative methyl assignments, along with the associated global score. A quality factor-included script to map into 3D structure using PyMol the NOE completeness associated with each peak/methyl pair and the confidence score for each connection that has been assigned (red to blue color gradient from confidence 0 to 2, and blue above 2).

Figure S3. Example of the MAGIC automatic assignment procedure.​

(A) The iterative automatic assignment procedure is illustrated according to the simple networks introduced in Fig. 1. All peak clusters are defined for iteratively decreasing T_C values (here from 4 to 2). The assignment of such clusters constitutes the local assignment step of the algorithm. Before merging local cluster assignments with global assignments, a cluster has to meet a minimum size requirement, for the purpose of this example T_N = 4. The iteration process starts at T_C = 4, the 2^nd-cluster and the 3^rd-cluster recruit one peak each and their assignments are calculated. None of the 2^nd- and 3^rd-cluster does reach the T_N threshold. Then, the T_C is decreased to 3 and all cluster, except the 5^th-cluster, recruit new peaks and new local assignment calculations are performed. The 2^nd- and the 3^rd-clusters reach the minimal cluster size (>T_N) and consequently their assignments are transferred to the global assignment set for global assignment. However, because the cluster assignments are incorporated in a stepwise fashion, once the assignments of the 2^nd-cluster is achieved, those of the 3^rd-cluster can no longer be added because all peaks have already been assigned. At T_C = 2, the 1^st-cluster meets the minimum size requirement but all of its peaks have also already been assigned. The 4^th-cluster has now reached T_N, and contains assignments for the 5^th-peak, which is still not assigned. The 5^th-peak assignments obtained from the local assignment around 4^th-peak is then combined with the global assignments to complete assignments for the entire system. (B) Details of matrix manipulation and score calculation for two different assignments of the 2^nd-cluster at T_C=3 from the panel A (dotted circle): the methyl connection matrix and the peak connection matrix have been defined according to the simple networks introduced in Fig. 1. At the beginning of the algorithm run, the score matrix is computed using equation (2) within the main text. This equation can be written in matrix form as following: S = P ∘ I, with the element of I defined as ${\mathrm{I}}_{ij}=\frac{{\mathrm{I}}_i^j}{{\mathrm{\sum }}_k^n{\mathrm{I}}_i^k}$ with ${\mathrm{I}}_i^j$, the height of the NOE crosspeak that is related to the 2D i^th-peaks and that defines the correlation between the i^th- and j^th-peaks; and ${\mathrm{\sum }}_k^n{\mathrm{I}}_i^k$, the sum of the n NOE crosspeak intensities related to 2D i^th-peaks. The resulting S matrix contains the score for each individual peak-peak connection. The assignment calculation is then performed as follows: the square 4 × 4 sub-matrix of S corresponding to the peaks 1, 2, 3 & 4 and the square 4 × 4 sub-matrix of M corresponding to the methyls are extracted. The elements are re-arranged as the rows and columns of the sub-matrix M are aligned to those of the sub-matrix S. Then the Hadamard product is performed and the sum of all elements of the resulting matrix becomes the score of that particular assignment. The score of each individual peak assignment are the sum of all elements of the corresponding row (or column).

Figure S4. Testing of different functions used to define methyl matrix elements. M matrix elements correspond to methyl-methyl connections that are selected from the 3D structure according to methyl carbon-carbon distances. (A) Four different functions were defined to set M matrix values according to the distances. The minimal distance is set to 2.4 Å and upper limit is variable: i) below either 8 or 10 Å, matrix elements were set to 1, and beyond to 0 (settings 1 and 2, respectively); ii) below either 8, 7, 6 or 5 Å, matrix elements were set to 1, and for distances beyond, up to 10 Å, to linearly decreasing values from 1 to 0 (settings 5–8, respectively); iii) below 7 Å, matrix elements were set to 1, and for distances beyond, up to either 15 or 12 Å, to linearly decreasing values from 1 to 0 (setting 3 and 4, respectively); iv) matrix elements were set to linearly decreasing values from 1 to 0 for distance from 0 to either 10, 20, 30 or 40 Å (settings 9–12, respectively). (B) The Abl-RM dataset was used to assess the impact of different settings. The accuracy (solid bars) and the average number of assignments per 2D HMQC peak (hatched bars) are displayed for each M matrix elements defining function. The accuracy remained higher that 95% for all functions for which the scale factor is equal to 1 (or closed to 1 for setting 11 and 12) for distances below 7 Å (setting 1, 3, 4, 5, 6, 11 and 12). This can be understood considering that the relationship between NOE intensities and the r⁻⁶ distance is not homogeneous in all methyl-methyl pairs. In other words, it is worth to assign high-intensity NOE according to methyl-methyl distance between 2.5 and 7 Å. If the distance threshold is too low (setting 7, 8 and 9), too many methyl-methyl connections are missed or associated to very low factor, and consequently, the methyl-methyl network loses correlation to peak-peak networks and automated assignment fails. With longer distance thresholds (setting 11 and 12), the automated assignment usually keeps the correct assignment but with lower percentage of single assignments. For all our test cases, the setting 6 works properly and efficiently.

Figure S5. Input parameter start.txt script.​

The simple text file is placed in a directory containing the magic.py program, the sequence, peak and structure files. At the terminal prompt, the command (>python magic.py start.txt) starts the run and generated a time-stamped directory with the results. The code requires python 2.7 and several libraries that are freely available (https://www.anaconda.com/download/).

Figure S6. NMR spectra of all test cases.​

The 2D [¹³C,¹H]-HMQC spectra and the 2D ¹³C-¹³C projections of the 3D [¹³C,¹H]-HMQC-NOESY-[¹³C,¹H]-HMQC are displayed for all test cases. Below each protein name is displayed the labeling scheme.

Figure S7. The quality factors mapping into all test case 3D structures.​

The 3D structures of all test cases are displayed as a ribbon with methyls as spheres. Below each protein name is displayed the labeling scheme. Each methyl/peak pair are displayed as a sphere with a color code ranging from 0 to 1 (red to blue) for the NOE assignment completeness of the related NOESY strip. The methyl-methyl connections, depicted as dashed-lines, are also colored according to their associated peak-peak connection confidence score (red to blue color gradient from 0 to 2, and blue above 2). Grey methyls are unassigned due to low number of NOE connections.

Figure S8. Peak simulation and validation script ‘pdb2noe’.​

The graphic interface for ‘pdb2noe’ launches from the most recent NMRFAM sparky distribution by typing the two-keys stroke ‘SN’. A variety of methyl-methyl and methyl amide experiments such as CCH, HCH, HNH, NCH, CNH can be simulated according to two letter codes flags and the assigned 2D peak lists and a starting PDB structure. For example, ‘mm’ flag will simulate CCH (or 3D ¹³C-HMQC-NOESY-HMQC) peak list, while ‘.m’ will create a HCH (or 3D ¹³C NOESY-HMQC) peak list.

Figure S9. Rotamers discrepancy between 3D model and solution structure.​

(A) Detail from a 1.9 Å resolution crystal structure of FlhA (unpublished data) and (B) with readjusted rotamers. Structure (A) would exhibit no crosspeaks in the 3D NOESY strip (C, left strip) while the readjusted rotamers show the correct pattern (using pdb2noe script) that correspond to the true rotamer conformation in solution (C, right panel).

Table S1. Summary of data set quality.

Table S2. Performance comparison between MAGIC and MAGMA algorithms.