Computational Membrane Biophysics: From Ion Channels Interactions with Drugs to Cellular Function

Abstract

The rapid development of experimental and computational techniques has changed fundamentally our understanding of cellular-membrane transport. The advent of powerful computers and refined force-fields for proteins, ions, and lipids has expanded the applicability of Molecular Dynamics (MD) simulations. A myriad of cellular responses is modulated through the binding of endogenous and exogenous ligands (e.g. neurotransmitters and drugs, respectively) to ion channels. Deciphering the thermodynamics and kinetics of the ligand binding processes to these membrane proteins is at the heart of modern drug development. The ever-increasing computational power has already provided insightful data on the thermodynamics and kinetics of drug-target interactions, free energies of solvation, and partitioning into lipid bilayers for drugs. This review aims to provide a brief summary about modeling approaches to map out crucial binding pathways with intermediate conformations and free-energy surfaces for drug-ion channel binding mechanisms that are responsible for multiple effects on cellular functions. We will discuss post-processing analysis of simulation-generated data, which are then transformed to kinetic models to better understand the molecular underpinning of the experimental observables under the influence of drugs or mutations in ion channels. This review highlights crucial mathematical frameworks and perspectives on bridging different well-established computational techniques to connect the dynamics and timescales from all-atom MD and free energy simulations of ion channels to the physiology of action potentials in cellular models.

1. Introduction

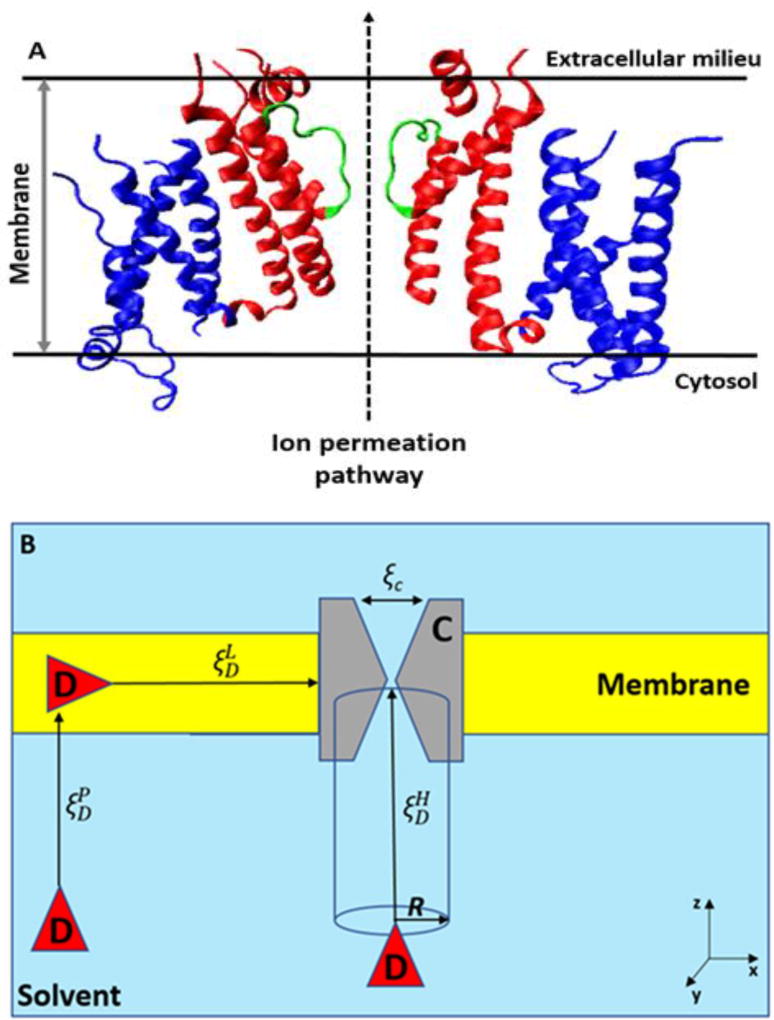
Large families of integral membrane proteins known as ion channels (Fig. 1 A) control the flux of ions through cellular membranes to enable many crucial physiological processes such as cell-cell communication and signaling, osmotic stress responses, muscle contraction and neuron firing. Their dysfunctions is directly implicated in a number of human diseases known collectively as channelopathies. Various channellopathies are associated with atrial fibrillation, congenital heart failure and potentially lethal heart rhythm aberration known as Torsades des Pointes, neonatal epilepsy, several forms of congenital blindness, asthma, hypertension, diabetes, and various cancers[1, 2]. Unsurprisingly, ion channels have been among the most common drug targets for decades of treatment efforts and novel drug development. While many ion channel targets are known (for example pace-maker channels: HCNs), the development of drugs that act as highly ion channel specific modulators remains challenging[3]. High-throughput technologies, animal models, detailed biochemical and biophysical explorations are all dispatched to identify potential leads with high specificity to a transmembrane protein. Nevertheless, even novel anti-arrhythmic agents designed specifically to block HCN channels were shown to have an overlapping concentration block of other channels in the heart (e.g. hERG) leading to the reported cases of drug-induced cardiac arrhythmias[4]. Another infamous example of very expensive drug development failure could be found in one of the most promising anti-retroviral agents BMS-986094 [5]. The lead molecule passed all regulatory stages and made it to the human clinical trials, but was discontinued due to severe cardiotoxicity, at least in part owing to highly specific interactions with cardiac ion channels[6, 7].

Figure 1.

Ion permeation and drug binding pathways in ion channels. A) The ion permeation pore in ion channels. The structure corresponds to the hERG potassium channel (PDBID: 5VA1). The voltage sensing and pore domains are colored in blue and red, respectively. The ion selectivity filter is colored in green. Only two subunits of the tetramer are shown for clarity. The extracellular and cytoplasmic sides of the plasma membrane are represented by solid black lines. B) Typical pathways for drug (D) - channel (C) binding mechanisms. ${\xi }_D^H$, ${\xi }_D^P$ or ${\xi }_D^L$ represent the reaction coordinate for hydrophilic, partition, and lipophilic pathways, respectively. Drug-induced conformational changes in the channel may be described by a set of reaction coordinates (ξ_c).

What are the greatest challenges in deciphering the molecular mechanisms of drug-ion channel interactions, which may help to further enable high-affinity/high-specificity development of ligands targeting ion channels?

The fine balance between drug lipophilicities and binding affinities is one of the greatest challenges for formulating a robust rational drug-design. Many drugs target ion channels via lipophilic routes, e.g., a ligand partitions first into lipid bilayers and subsequently diffuses to binding pockets, which are imbedded in hydrophobic environments (Fig. 1 B). The complex interaction mechanisms modulated by the composition of lipid bilayers, gender- and age-dependent fluctuations in concentration of endogenous substances, and co-therapies are all known to impact how drugs interact with ion channels[8–10]. Furthermore, these transmembrane proteins adopt multiple intermediate conformational states, one of those which might be preferentially targeted by drugs. It is difficult to identify one of the states on the physiological scale to understand and simultaneously monitor the effects of drug-binding and how ion permeation is altered. Selective ion permeation is fine-controlled by various ion channels located in the membranes of excitable cells. The ability to move ions selectively from one side of the membrane to another rapidly changing local ionic concentrations and hence electrochemical potentials on the surface is central for the generation of specific cellular response known as Action Potentials (AP). The APs are membrane-depolarizing waves, whose patterns and durations are critical for normal physiology [3]. Therefore, various mutations or drug binding that impact selective permeation or gating process may potentially be harmful. For example, drug that stabilize only closed states of a certain ion channel is potentially life-threatening because they have a potential to severely alter AP.

A complete ensemble of structures involved in drug association pathways must be sampled for retrieving and analyzing the thermodynamics and kinetics of binding. However, only a small set of experimental (either closed or open, or very few intermediate) structures is available for an ion channel, thus hindering the study of the state-dependence binding of drugs. Ion Channels do exist in multiple states with rapid (μs-ms) conformational changes triggered by membrane voltage changes and other ligand stimuli[3]. But the interconnections among all metastable states, on which specific drug bindings and cellular responses can be connected, are missing. In this regard, computational models at different levels of complexity can help elucidating missing pieces in the mechanism of drug-ion channel interactions and consequently guide rational drug design strategies[11]. Furthermore, many drugs often have complex multi-channel interactions, thus creating hurdles to regulate a specific channel type by inhibition or activation[11, 12].

The molecular modelling field has been benefited in the last decade from new theories, techniques, and rapid surge in computational power. The main goal of protein-ligand simulations is to map reaction coordinates involved in ligand-target binding and the assessment of the energy changes involved in this process. This means deciphering complex interrelationships between protein dynamics and ligand association; and then using this information to reconstruct ligand-binding thermodynamics and kinetics for a specific or intuitively known pathway. But the question arises whether this valuable information is adequately sufficient to predict the impacts of drug-ion channel binding at the physiological level? The answer, in our opinion, is “Not Yet”. Some studies may focus on drug binding processes for a certain type of ion channel (e.g., potassium-selective channels). However, these proteins are part of the complex network involving multiple inward/outward currents with different ionic types (e.g., sodium and calcium ions) that regulate cellular functions.

Ideally, the thermodynamics (free-energy differences) and kinetic information (rate constants, barriers) obtained at the single channel level from MD simulation of different types of ion channels may provide the basis for ion-current models developed for either single-channel or cellular levels. Then, action potentials can be generated in silico from these models, via a set of flux equations with different intermediate states of drug-ion channel binding. In this approach, the computed binding affinities and rate constants should be constrained by experimental data to produce key observables of drug-binding effects on ion channels. While the multi-scale connections among different branches of computational biophysics studying ion channels are still evolving, we believe that a combination of such multi-scale approaches will provide a fresh impetus for connecting the modulation of these transmembrane proteins by drugs with the corresponding cellular responses[13].

In this mini-review, we first discuss how to effectively sample the binding of drugs/ligands to ion channels via MD simulations. Since current atomistic simulations are able to produce a vast amount of data, a need of extracting the most relevant and comprehensible data has led to a rapid development of the Markov State Model (MSM) formalism[14]. This method allows rigorous estimation of the relevant dynamics and kinetics from all-atom MD simulations of channel-ligand binding. Finally, we outlined how to integrate the information derived from MD simulations (molecular level) into kinetic models (single channel, cell and tissue levels) to build predictive models for rational drug design[15].

2. Thermodynamics and Statistics of Drug Binding from MD Simulations

The thermodynamics and statistical data on drug binding to ion channels are crucial to quantitatively describe how drugs can disturb the functions of these proteins. This data may include, for instance, relative binding free energies, occupancy probabilities, and correlations between conformational states of ion channels and various binding modes of drugs. The accurate calculation of these quantities from MD simulations requires a thorough sampling of phase-space. But except for small molecules (e.g. soluble proteins of ~80 amino acids), there is a practical limit on the size of all-atom systems that can be thoroughly simulated to millisecond time-scales within a reasonable time with the most advanced technology[16–18]. For ion channels, which must be imbedded in some model lipid bilayers and solvated by explicit aqueous solutions, simulated system sizes can be much larger than the soluble-protein systems. As a result, thoroughly simulating ion channel systems can become exceedingly expensive. Consequently, millisecond MD simulations[19–21] remain unreachable for most of these proteins. Furthermore, drug binding events and their couplings to conformational dynamics and functions of ion channels take milliseconds or longer to have measurable physiological effects. In spite of this formidable sampling task, there are promising methodologies to enhance the sampling in MD simulations. These approaches could provide insights into the thermodynamics and intermediate states of drug-ion channel association process. As will be shown in Sec. 5, the thermodynamic properties and statistics of relevant functional states can be used to build kinetic models and rationalize experimental observations in terms of specific gating and drug binding mechanisms.

2.1 Biased MD simulations

Many simulations often implement a biased potential that drives systems for sampling rare but functionally relevant events, allowing the identification of global free-energy minima and transition pathways within affordable timescales. Biased MD simulations require a prior knowledge of viable reaction coordinates, along which the binding/unbinding pathways of drugs can be easily described. Typical sampling pathways for drug binding to ion channels are depicted in Figure 1 B. In the simplest case, drugs simply diffuse to the pore domain of these proteins, either from extracellular or intracellular sides and directly block the ion-permeation pathways. However, for most sampling problems, the selection of reaction coordinates is not trivial. In fact, it is difficult to reduce a large number of degrees of freedom into a comprehensive set of collective variables or reaction coordinates that would best represent a drug binding pathway or conformational transitions in many biological systems. In this case, some approximations may be necessary. For example, an approximation of drug binding to ion channels may require the truncation of unnecessary parts of the proteins, usually supported by mutagenesis data[22]. Sampling these approximate reaction coordinates (ξ) returns a useful thermodynamic quantity, referred as the Potential of Mean Force (PMF), which can be computed by

$$W(\mathit{\xi })=-k_B\mathit{\text{Tln}}[\rho (\mathit{\xi })]+C,$$ (1)

where ρ is an unbiased probability distribution of systems computed along ξ; and C is an arbitrary constant.

To compute ρ or PMF, many effective biasing sampling techniques have been developed such as adaptive biasing[23], steered/pulling MD[24, 25], conformational flooding[26, 27], and metadynamics[28, 29] methods. In this review, we focus on crucial aspects of umbrella sampling (US) as one of the most widely used methods for re-constructing unperturbed free-energy landscapes from biased data[30, 31]. In principle, one can use arbitrary external potentials for biasing purposes as long as sampled biasing distributions are ‘as wide and uniform as possible’ to have an accurate connection between perturbed and unperturbed distributions[30]. For example, Roux[31] showed that a wide and uniform biasing distribution can be achieved from combining a series of separated windows, which focus on sampling particular regions of a reaction coordinate coupled to an external harmonic potential. It can be proved that the distributions of reaction coordinate between consecutive biasing windows need to have sufficient overlapping for accurately reconstructing free-energy landscapes[32]. The resultant free-energy values are sensitive to the tails of windowed distributions and the overlap extend [31, 32]. So, it is advised to post-process umbrella sampling data via Weighted Histogram Analysis Method, which solve a set of non-linear equations to return optimal unperturbed free-energy profiles[33]. Then, uncertainty analysis of free-energy profiles can be performed via Bootstrap method[34] or assessing data correlations and mutual entropies [35] to identify unsatisfactorily sampled data points. It might be also very useful to perform force-decomposition analysis[36] to extract contributions from electrostatic and Van de Waals forces to PMFs.

Based on PMFs, one can estimate effective binding/dissociation constants or kinetic rates (κ) via Kramer’s theory[37, 38], as follows

$$\kappa =\frac{D\sqrt{K_b{K}_w}}{2\pi k_{B}T}\mathit{\text{exp }}\left(\frac{-\mathrm{\Delta }W}{k_{B}T}\right)$$ (2)

where K_b and k_w are the curvatures at the barrier and well, respectively; D is a diffusion coefficient, which can be estimated from MD data by various methods[39–41]; and ΔW is a free energy difference between the barrier and local minimum. As will be discussed in Sec. 5, these kinetic rates can be used to build kinetic models. Furthermore, relative free energy of drug binding is computed by

$$\Delta G_b=-k_B{T}^{\ast }\mathit{\text{ln}}({K_{\mathit{\text{eq}}}}^{\ast }{C}^{\mathit{0}})$$ (3)

where C⁰ is the standard concentration (1 M) and K_eq can be calculated from W(x, y, z) as follows

$$K_{\text{eq}}={\int }_{z1}^{z2}S(x,y)e^{-W(x,y,z)/k_{B}T}\mathit{\text{ dxdydz}}$$ (4)

where S(x,y) is a cross-section area in the xy-plane that influence the binding pathways, and z₁ and z₂ are the lower and upper bounds of z, respectively[42, 43]. If a binding process can be solely described by the pathway of ${\xi }_D^H$, W(x, y, z)~ W(z) and S(x,y) is approximated as πR², in which R is often chosen as an effective radius of ion channels[44–46]. However, if binding pathways involve the lateral fenestration by diffusion of drugs in lipid membranes (Figure 1 B), the estimation of S(x,y) may not be trivial. Sampling these pathways may become exponentially demanding, as additional dimensions of drug binding plus more rotational degrees of freedom than sampling the directly-blocking pathway must be considered[47]. In this case, we need a sampling strategy to both optimize sampling resources and ensure reliable outcomes (see below).

2.2 Unbiased MD simulations

For many ion channels, either the binding sites or binding pathways for drugs are rarely known. To get the least biased insight into the binding of drugs, standard MD simulations may be revealing if they can produce sufficient data. For example, using Anton simulation-dedicated supercomputer[19], Boiteux et. al.[11] performed multi-microsecond unbiased all-atom MD simulations of the antiepileptic drug benzocaine (BZC) and the anesthetic phenytoin (PHT), which bind to the bacterial NavAb channel, a homolog of the human Nav channels [48]. In these simulations, the system is saturated with many drug molecules to increase the probability of drug binding events. This study is one of the few reports that have pushed all-atom MD simulations of drug-ion channel systems into physiological time-scales[19, 49–53]. It showed that there are up to seven binding sites for BZC, leading to the determination of a high-affinity pore-blocking site through fenestrations, and an interesting site between the pore and voltage sensor domain of NavAb[11]. Note that this study used only one specific conformational state of NavAb for the sampling of the binding sites, thus it is not clear if the observed binding pathways for BZC and PHT are dependent on other conformational states. This methodology has also been used to study the binding pathways of the anesthetic drug isoflurane to both the nicotinic-acetylcholine receptor (nAChR)[54], and the bacterial voltage-gated sodium channel (NaChBac)[55] in simulations of ~0.5 μs, and also the binding pathways of ethanol to the glycine receptor (GlyR)[56].

There is another strategy to run standard MD simulations, which can cover many areas of phase space. For example, Folding@Home[57, 58], which is a network of desktop computers volunteered to run MD simulations, has been used to massively run a few hundred thousand of independent short straightforward MD simulations on protein complexes. To implement this simulation strategy, it is critical to prepare uncorrelated initial states so that several simulations sufficiently capture as many binding modes as possible. However, it is often tricky to know how many of these simulations would be needed to produce significant and reliable statistics, particularly for drug-ion channel binding events.

2.3 Accelerated/Enhanced/Guided/Weighted-Ensemble MD Simulations

Whenever the statistical quality of thermodynamic data is under thorough scrutiny, both biased and unbiased simulations can be applied with enhanced sampling techniques[47, 59–62] to provide a more ascertain justification to the convergence of MD data. Depending on whether well-defined reaction coordinates are available or not, additional layers of algorithms can be dispatched on top of normal Newton-based MD integrators to accelerate the exploration of a broader phase space. Tempering (T-REMD)[63] and Hamiltonian (H-REMD)[64] replica exchange simulations are typical algorithms available in many MD softwares to enhance the statistics of drug binding/unbinding events to ion channels. The essence of T-REMD and H-REMD is to exchange relatively higher-energy with lower-energy states and vice versa by means of the Metropolis criterion[65]. These methods can offer a sampling of about 50–100 times more relevant data than standard MD simulations started from the same initial configurations[66, 67]. These techniques can be expensive, since they may require few thousands of CPUs or hundreds of GPUs to distribute among many replicas of ion channel systems. A practical criterion for ‘good’ replica exchange sampling is to achieve an average exchange rate of 20–23% among all T-REMD or H-REMD replicas, or 30–50% among all solute replicas in REST2[15]. Using this criterion, a typical number of replicas of small soluble proteins for T-REMD with a temperature range between 275 and 400 K is around 64, and for H-REMD is one replica per about 0.5-Å incremented window. However, it should be noted that there is no clear justification for a “good” exchange rate because there may be still some aggregations of replicas in the temperature space[68]. In this case, an adaptive T-REMD can be implemented to avoid such aggregations[69]. Note that T-REMD or REST2 are particularly useful for simulation systems with unknown reaction coordinates for describing binding/unbinding events or correlation between binding/unbinding and conformational changes of ion channels. On the other hand, H-REMD simulations are likely affordable for a number of known reaction coordinates typically less than 3.

Other techniques, which might be also useful for efficiently guiding the drug-ion channel simulations, are string methods and weighted ensemble simulations. On-the-fly[70] and swarm-trajectory[71, 72] string methods[73] were designed to find minimum free-energy pathways (MFEP) between two known end-states more efficiently than simply sampling a sufficiently large free-energy landscapes and then identifying MFEP via, e.g., US sampling. It is suggested to be particularly powerful for studying systems without a prior knowledge of reaction coordinates, and has been proven to be effective in many systems[54, 74, 75]. The challenge of delineating data obtained via string methods in protein systems is how to reduce a large number of collective variables into a small and comprehensible set of major transformations. String methods have often been carried out to produce many initial configurations of proteins and tentative drug-binding pathways for running a massively large number of independent simulations[54, 74, 75]. Similar strategies could be carried out for studies of drug binding to ion channels, in which string methods could be performed to drive certain movements of gating domains or voltage-sensing domains to obtain a series of initial critical configurations of these proteins for running a large number of independent straightforward simulations. String methods can be combined with the weighted ensemble approach[76] to further enhance the sampling of drug binding. This weighted ensemble (WE)[77] approach utilizes an on-the-fly protocol of removing or dividing simulation replicas[78] to achieve a convergence probability distribution of states. It scales very well with a large number of CPUs to sample a ten thousand of trajectories per iteration[79]. Another advantage of this method is that it works with both equilibrium and non-equilibrium steady states, in which one might sample conformational states in equilibrium fashion while sampling of ion permeation in a steady state. This WE-string-method approach to study ion channels might be worth further exploring to compare with other sampling techniques.

Another viable approach for simulations of drug-ion channel binding is to incorporate critical experimental data like X-ray or NMR properties in simulations. For example, MELD (Modeling by Employing Limited Data)[80] can use ‘loose and vague’ or limited information from experiments to enhance sampling in MD simulations. It was developed for estimating relative binding affinities of peptide-protein complexes by ordering MD sampling to achieve some structural properties such as hydrophobic contacts or secondary structures via some evolutionary information[81]. In the simulations of the binding of p53 epitope on MDM2 (Mouse Double minute 2 homolog) as a factor contributing to cancer growth, MELD was used with replica exchange to swap binding and unbinding configurations of the complex[81]. So, a similar simulation approach can be carried out for the drug binding to ion channels.

3. How to decipher correlations between drug binding events and channel conformational states?

Many ligands (e.g. full- and partial- agonists, antagonists) are known to induce conformational changes at the ligand-binding domain (LBD) that trigger the opening or closing of distant conducting pores through allosteric mechanisms[82, 83]. For example, in ionotropic Glutamate Receptor (iGluR), the binding of agonist molecules to LBD induces the opening of its transmembrane pore domain to enable nerve impulses to propagate in the post-synaptic neuron. Through MD simulations approaches, it has been possible to decompose the complex relationships between ligand binding and conformational changes involving the opening and closure of LBD in iGluR[22, 82–87]. To correlate ligand binding with transition states of the LBD in GluA2, the free-energy contributions to the total LBD-ligand binding free energy were computed using a combination of different approaches (see Ref. [22] for details). This study only considered the LDB domain, not the entire channel. So, the precise allosteric mechanism for GluRs pore opening, triggered by the binding of agonists to the LBD, remains incomplete. It is indeed difficult and expensive to use the same approach to unravel the couplings between drug-binding events and channel conformational transitions. In this regard, the major questions are: (1) Which conformational states are the most crucial for drug bindings and ion permeations? (2) How are these states connected?

Logically, a systematic approach based on a combination of large datasets generated by computer simulations and interpreted with established kinetic approaches, such as Markov-State-Models (MSM), is currently the best strategy to shed light on these questions. Conceptually, the complex dynamics involving all states for a specific ion channel can be mapped out from exhaustively sampled atomistic simulations. With tetraflops supercomputers, simulations can produce a large sum of trajectories, in which drugs bind to ion channels in various locations with different probabilities among an enormous number of ‘noisy’ (non-relevant) structures. From these trajectories, it is a must to have a systematic and robust strategy to extract the most representative states and any possible coupling between drug binding and conformational dynamics of ion channels. A popular strategy to filtering out relevant conformational states is to construct MSMs from MD trajectories[88–92]. Conceptually, MSM assumes a Markovian network of labeled states, which are clustered from MD trajectories. One can cluster structural data and build MSM via various structural metrics or features including RMSD[93, 94], angles, dihedrals, relevant distances, contact maps and other internal coordinates[14, 95, 96]. MSM can be combined with time-structure independent component analysis (tICA)[97] to estimate the timescales of the slowest motion and correlated movements, or principle component analysis[98] to classify, project and optimize metastable states[99–101] in MD data. The so-called implied timescales, which are proportional to the inversed eigenvalues obtained from MSM-transition probability matrix, can be used to identify if the slow dynamic modes of the system occur in the time-scales for physiological events[47, 89, 96]. Simulation times may be few orders of magnitude smaller than implied timescales. As a result, one may obtain a handful of principal or slowest components and metastable states that are much more comprehensible than original MD data. Importantly, a cross-validation of any resultant MSM models can be also performed to identify any possible uncertainty[102]. One can then use the transitional matrix obtained from MSM to estimate a net flux of transitions between any product and reactant states[96, 103]. This transition matrix and the resultant transition fluxes among those states can be particularly useful for kinetic modeling (see Sec. 5).

Generally, when applying MSM to ion channel dynamics, it is necessary to use different sets of features and cluster algorithms to unravel relevant states that are important for both drug binding and also ion-selective transport[95]. For instance, subtle flexibility such as flip-flopping of carbonyl oxygen atoms and sidechains, which are crucial for ion permeation and selectivity[104], may be coupled with different gating modes [105, 106]. In a general case, one might have to use, for example, a set of distances among carbonyl oxygen atoms in a selectivity filter, relative positions of ions, and native contacts for the ion channel and drug as a feature for analysis. While MSM has been widely used to study the folding, ligand binding, and native conformational states of soluble proteins[107], there are only a few applications of MSM to membrane proteins. Among them, the studies by Kohlhoff et al. on b2-adrenergic receptor (b2AR)[58] and Choudhary et al. on VDAC1 channel, a cylindrical beta-barrel anion channel[108]. The dynamics of b2AR were simulated from the crystal structures of the active and inactive states, in which a partial inverse agonist and a full agonist were bound. As a result, a MSM model was built to map the influences of the agonist for modulating the structural changes of the receptor. Then, docking small molecules to those kinetically relevant states was carried to identify chemotypes for b2AR. In VDAC1[108], MSM was used to identify the permeation pathways of ATP along the interior of VDAC1. For this type of problems, MSM shown to be useful in ranking the different binding poses of ATP along the permeation pathways and link dynamical data generated by a large set of short (~50–200 ns/trajectories) simulations with open/closure transitions which occur in much longer timescales (~ seconds). Currently, python-based MSM software packages MSMBuilder[89] and PyEMMA[90] are freely available with insightful tutorials. PyEMMA is built based on MSMBuilder but generalized to include data from all replicas in T-REMD and H-REMD simulations[91, 92], thus robust to perform MSM analysis.

It is worth noting that MSM is based on the Markovian assumption among all possible clustering states, i.e., no memory among distant states. It is, however, known that some states of ion channels usually display a non-Markovian behavior, i.e., a significantly long history of initial states[109, 110]. Particularly, there is direct evidence of non-Markovian behavior ranging from gating in VDACs to polymer/ligand escape[53, 111, 112]. Therefore, it might be necessary to apply a non-Markovian State Model[113] to identify how drugs influence the conformational transitions of ion channels in individual trajectories, which are simulated from different initial states. It means that certain simulation protocols may be applicable to study the non-Markovian dynamics in these proteins, others may not. For example, a number of straightforward unbiased or individual biased MD trajectories contain possible long histories of initial states, but those sampled by tempering replica-exchange approaches may diminish the effects of initial states after just few iterations because of Metropolis exchanges with multiple distant states at different temperatures.

As discussed further below, the conceptual challenge of kinetic modeling lies in the consideration of multiple “hidden” states for fitting to electrophysiology data[4, 114–116]. The mathematic assumption of using hidden variables is that there may be more than one set of variables and connections among them that would fit few outcomes of so many unknowns. There is, however, a mathematically optimal set of variables (hidden and known) that would best describe and predict the outcomes within some constraints[117]. In the kinetic modeling of ion channels, many of the physiologically hidden states are “silent”, e.g., they are not resulting in directly measurable signals (for example, inactivated or some intermediate states). Yet, these states could be critical for drug binding and overall channel functions[7, 118]. Obviously, it is necessary to justify these hypothetically hidden states: how many are sufficient for describing physiological data? These states could be justified based on structural data of open, closed, and inactive states from experiments, if available. From the perspective of MD simulations, there is no hidden state if thorough sampling is reached. However, due to a limited amount of MD data, some intermediate states are likely not properly sampled. In this case, the concept of hidden variables or states could be also applied to MSM modeling, so-called Hidden Markov Modeling (HMM)[117, 119]. In fact, HMM could be used to smoothen out discrete states found in MSM model to potentially provide a better interpretation of transition pathways. HMM may be, therefore, useful to provide more insights into the hidden states hypothesized in the kinetic scheme or whether they are in fact not “hidden”.

4. Kinetic modeling of ion channels’ gating, drug interactions and cellular processes from Electrophysiology data

The original idea of modeling ion currents or channels gating and drug-induced perturbations could be dated back to the pioneering work of Hodgkin and Huxley on the Action Potential. Hodgkin and Huxley (HH)[120] formulated the first mathematical model of channel gating and AP generation and propagation. Their model is based on the inward (Na⁺) and outward (K⁺, leakage) currents in giant-squid axons at different membrane potentials (V_m) upon depolarization. These currents are calculated by the Ohm’s law:

$$I_x=g_x(V_m-E_x)$$ (5)

where x is an ionic type (i.e., Na⁺ or K⁺), I_x is a macroscopic transmembrane current [μA/cm²], E_x is an equilibrium potential (mV), and g_x is the conductance (mS/cm²). The conductance is estimated as $g_x=P_o\overline{g_x}$, where $\overline{g_x}$ is the maximum conductance for ion x and P_o is an opening probability that was modeled empirically by assuming independent gating and as a function of gating particles or gating parameters[120]. Although the HH formalism has been successful and is still widely used in many applications[121], the gating particles or parameters considered in HH model do not represent specific kinetic states of ion channels. For instance, the inactivation probability of the Na⁺ channel was found to be higher when the channel is open[122], which invalidates the HH assumption of independent gating.

Since the development of single channel recording techniques[123], a much more detailed picture of the mechanisms underlying membrane excitation has emerged over the years and the gating kinetics of several ion channels in excitable cells are better described by Markov Models[124, 125]. These models have been very useful as they involve well defined channel states and assume that transitions are interconnected by rate constants dependent on external variables like the membrane potential, ligand concentration, etc. The essence of Markov Models is that, for any single step in the gating mechanism, the transition probability (i.e. the microscopic equivalent of the rate constant) is time independent. This is also the main assumption for building MSM from MD simulations as pointed in the previous section. The state probabilities in the model are calculated by solving the following equation (eq. 6):

$$\frac{d\overrightarrow{p}}{\mathit{\text{dt}}}=Q\overrightarrow{p}$$ (6)

Where p⃗ is is the vector of state probabilities (P_O…P_i) and Q is the system matrix of the transition rate constants (α_kl, eq. 7), corresponding to the transition between states k and l. The transition rate constants of the system are assumed to have the following expression[126]:

$${\alpha }_{\mathit{\text{kl}}}(V_m)={\alpha }_{0\mathit{\text{kl}}}{e}^{{\beta }_{\mathit{\text{kl}}}{V}_m}$$ (7)

Where V_m is the external electric potential in mV, α_0kl is the voltage independent rate constant (α_0kl=α_kl (0 mV) in ms⁻¹ units) and β_kl (mV⁻¹ units) has the following expression:

$${\beta }_{\mathit{\text{kl}}}=\frac{{\theta }_{\mathit{\text{kl}}}{z}_{\mathit{\text{gkl}}}F}{\mathit{\text{RT}}}$$ (8)

Where θ_kl is the fraction of the gating charge z_gkl moved to reach the rate-limiting barrier in the forward direction. The fraction in the reverse direction would be 1- θ_kl. F is the Faraday constant, T is the temperature in Kelvin and R is the gas constant. In practice, initial values of α_kl and β_kl are guessed and then optimized to fit the outcomes of kinetic models to experiments. Once eq. 6 is solved, the probability of being in the open state (P_O: conducting state) is found and the current is calculated using the eq. 5.

The Markovian kinetic models for ion channels contain a number of hidden states, many of which, however, are nearly impossible to observe experimentally. Although the states are not directly visible, the output –ion channel gating behaviour- which is dependent on the hidden states, is visible. It is important to stress that all developed Markov Models for channel gating kinetics are constrained by experimental measurements to ensure reproducibility of key metrics[127]. Experimental data used to constrain the models might come either from voltage-clamp single channel recordings or whole cell measurements. The current measured in “whole cell” configuration belongs to many channels of the same type and is isolated from currents due to other type of channels in the cell. There are several software packages available to simulate ion channel currents and fit Markov Models to them. Those include NEURON[128, 129] and QuB[130–132] among others. Both provide a powerful platform for simulating single-channel and whole cell currents in response to electrophysiological stimuli and pharmacological stimuli. Fredkin and Rice[133] have shown that ideal single channel data obtained from voltage-clamp steps provide all the information necessary for fitting ion channel models but, with real noisy data, the analysis is extremely difficult and many complications arise[134].

Since whole-cell current measurements are widely used to describe ion channel gating kinetics, drug effects and mutations under physiological conditions, we will discuss a few studies using those measurements to constrain the fit to Markov Models. For example, Perissinotti et al. [4] recently developed a kinetic model to explain the mechanism of the drug NS1643 (channel activator) effect on hERG WT and L529I mutant using the five-state model from Wang et al.[135] (Graphical illustration for common kinetic scheme is shown in Figure 2). Another example is the modeling of blockers to hERG channels[136]. In these studies, voltage-clamp data from whole cell experiments on hERG was used, rate constants for binding (k_on)/unbinding (k_off) were constrained via optimization to electrophysiological pacing protocols and IC₅₀ values for each drug[15, 136, 137]. To simulate the effects of the drug, different models that include two populations of hERG channels in drug-free and drug-bound states (see Fig. 3) were considered with state-dependent drug binding affinities and on/off rates as essentially free variables but constrained by the available experimental data. In the case of the NS1643 activating effect, the model shows that the drug should bind to the open state and at least two early closed states; and modify the voltage dependence of the transition rates among the states to reproduce the experimental behavior. Interestingly, these mechanistic findings together with mutagenesis experiments and MD structural analysis suggested a binding site around the voltage sensor domain of hERG imbedded in lipid membrane as a mechanism to alter the voltage-gated properties of hERG[138].

Figure 2.

Kinetic models describing the activator effect of NS1643 drug on hERG channel. Closed states (C1 to C3), Open state (O), Inactivated state (I) and drug bound states (D subindex) are connected and constrained by experimental data. k_on-_C, k_on-_O are the drug association rates constants in the closed, open states, respectively. k_off-_C, k_off-_O are the dissociation rate constants in the closed and open states, respectively. The rest of the rate constants describing transitions between the unbound/bound states were modeled according to the previously Markov Model proposed by Wang et al.[135].

Figure 3.

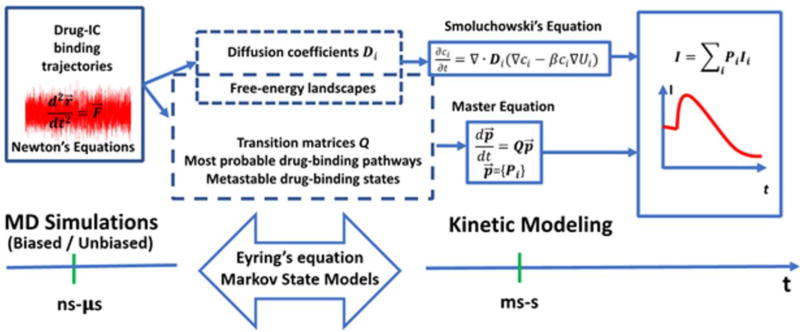
Schematic of MD-based kinetic modeling. Transition matrix Q can be generalized to include various ion-selective channels.

The examples presented above illustrate how the effect of drugs on a particular type of channel (hERG) can be rationalized in terms of a mechanism by fitting a proposed Markov Model to experimental data. In these examples, together with most studies in literature, the fitting is performed through the Global-Fitting procedure described by Balser et al.[127], which is the common methodology used when fitting Markov Models to whole cell electrophysiology data. The Global-Fitting Approach involves the use of comprehensive and extensive data sets of experimental information from a broad range of ion current responses to multiple voltage stimulations conditions (voltage protocols, membrane potentials, temperature, etc.) and is designed to reduce the universe of possible solutions to the model system mechanism, ensuring the robustness of the parameter set obtained for the model. Using that approach, a proposed kinetic model, which includes drug-free and drug-bound states attempts to explain and predict various effects of the drug on a particular ion channel. It is important to emphasise that those proposed models have limitations due to experimental uncertainties, type of cell line used, technical issues, and more importantly; they may still fail to explain the effect at the cellular or tissue level as other types of channels present in the cell may be involved in the observed side-effects.

5. Towards MD-based kinetic models for ion channels gating, drug interactions and cellular processes

The data obtained from all-atom simulations could form a basis for solid multi-scale platforms that allow the prediction of cellular responses from perturbations by drugs. In effect, these MD data could help to establish or discard hidden states in kinetic models, and replace them with MD-based metastable states. Ultimately, MD simulations can provide a molecular mechanism of drug-ion channel interactions, which underlie the cellular responses. The drug-induced cellular responses are results of perturbations propagated in a network of several ion channels that selectively translocate different ions. Thanks to advanced Cryo-EM techniques[139–141], a significant number of structures of mammalian ion channels recently resolved at a quality (~3–4 Å) suitable for MD simulations pave a way to rigorously understand the molecular basis of the cellular responses. Although sampling on individual channels itself is challenging and the cellular responses happen in a temporal-spatial scale that is not accessible by atomistic simulations, theoretically there are mathematical and physical frameworks to marry MD-sampled events with cellular responses. As will be shown below, the diffusion coefficients, relative free energies, barriers, and transition rates typically obtained from MD simulations of particular ion channels can supply kinetic models or even higher-level models like cells, tissues and organs, which are well established in the biomedical engineering field.

How can MD simulations be useful to restrain kinetic models? MD simulations with its current reach in time scales and the ability to incorporate effects of membrane potentials may provide missing parameters and states for kinetic models of ion channels. In a physical sense, the collection of parameters provided by kinetic models fitted (constrained) by experimental data should be sufficient to elucidate channel gating dynamics and to enable predictions for a variety of conditions (concentrations, temperatures, pH and voltages). Nevertheless, various models with different states or connectivity may provide a reasonable description for a complex phenomenon such as channels’ gating and at a higher level, AP propagation. Due to the complexity of the phenomena, there are usually components and processes that are neglected when trying to model cellular responses from kinetic models of ion channels. So, it is difficult to establish a cause when a prediction of drug effects from the models is proven wrong. We would like to argue that detailed atomistic models of state-specific drug interactions with ion channels might provide an additional level of validation for ion channel kinetics models, enabling self-consistent development of cellular models by incorporating restraints from a single protein level data and measurements of drug-induced perturbations at the cellular level. Essentially, a mathematical model that describes the channels’ gating and drug interaction could be proposed based on combined MD-MSM data. After fitting the model to experimental data and constrained it by MD data, the set of parameters obtained can then be plugged into a higher-level model like the whole cell, tissue or even organ and test how that ion channel drug- targeted effect interplays with the rest of currents in the cell.

The interplay between all-atom MD level and kinetic modeling could be illustrated with analysis of ion currents and dynamics of a single ion channel (the workflow is shown in Figure 3). As it was mentioned before, some of the simplest and successful kinetic models[142] for ion channel gating assumes the Markovian transition, i.e., the last probability does not have the memory from 0 to t but only the fact that the channel is open at t. As a result, an open probability of a single channel at time t is expressed as follows

$$P(t)={\sum }_i{\alpha }_i{\lambda }_i{e}^{-{\lambda }_{i}t},$$ (9)

where τ_i = 1/λ_i is a transition time and Σ_i α_i = 1. This probability function is in fact equivalent to an eigenstate obtained from time-structure independent component analysis (tICA)[97], which has been used as the most efficient way to extract maximal autocorrelation times among a large noisy data set of multi-dimensions in Markov Models. This probability is also a solution to the Eq. (6), and is equivalent to the matrix of metastable states that are extracted from a MSM built upon MD data. One can also estimate the transition rates (α_0kl) that will be used to build the transition matrix Q (eq. 6) via Eyring’s equation [126] as follow

$${\alpha }_{0\mathit{\text{kl}}}=\frac{k_{B}T}{h}{e}^{-\frac{\Delta G_{\mathit{\text{kl}}}}{\mathit{\text{RT}}}},$$ (10)

where the free-energy difference ΔG_kl between states k and l can be estimated from unperturbed free-energy landscapes obtained from unbiased or biased-MD simulations Then, the effects of the membrane voltage in the transition rates (α_kl(V_m)) can be simulated via equation 7. The transition rates (α_0kl) can also be obtained using MD-MSM, from the number of observed transitions between states k and l. Using these transition rates, ionic fluxes can be straightforwardly estimated (for example, see Refs. [142, 147]). Given such transition rates, various frameworks for simulating ion permeation can be found in Ref. [148]. Therefore, using transitional matrices obtained from either biased-MD or MSM-MD approaches, one would get all state-dependence probabilities via solving Eq. (6).

Once metastable states and their connectivity are available, it is possible to model ion permeation for an i-th intermediate state via Smoluchowski’s equation,

$$\frac{\partial c_i}{\partial t}=\nabla ·{\mathit{D}}_i(\nabla c_i-\beta c_i\nabla U_i),$$ (11)

where c_i(r,t) is a concentration of ions, ∇ is a gradient operator, D_i(r) is a spatial-dependence diffusion tensor, U_i(r) is equal to the sum of applied electric potentials and state-dependence potential of mean forces (W_i(r)) of single or multiple ions across ion channels obtained from MD simulations, and β is 1/(k_BT). Consequently, the average single-channel current can be computed from the probability of finding a channel in the i-th state (P_i) and the current, $I_i=\frac{\partial c_i}{\partial t}$, through the channel in this state as follows

$$I={\sum }_i{P}_i{I}_i.$$ (12)

This current can be measured in single-channel recordings and analysis for model testing. The entire procedure to marry MD simulations with kinetic modeling is schematically given in Figure 3.

It is also possible to extend the approach described above to the case of state-dependent drug blockade, which appears to be critical for understanding of many adverse drug effects. It has been shown that drugs with similar binding affinity but different binding kinetics can have diverse effects[3, 149, 150]. The most commonly used metric for drug blockade is IC₅₀, but it provides an average measure of drug potency to supress ion currents without any mechanistic insights. In that regard, state-dependent drug binding/unbinding kinetic rates, which are often impossible to measure experimentally, can be calculated from equilibrium or non-equilibrium MD simulations. This data can be used within the multiscale modeling strategy (Fig. 3) to better predict relationships between channel gating, drug binding, and altered cellular responses such as action potential duration.

For instance, MD-MSM can provide kinetic information on drug-ion channel binding through the mean-first-passage-time (MFPT) estimator. The MFPT, which can be solved from transition pathway theory, is defined as the average time taken for the transitions starting at state A until reaching state B for the first time.[107] For the case of a drug binding to an ion channel, the association (“on”) and dissociation (“off”) kinetic constants can be calculated as k_off = 1/MFPT_off and k_on = 1/(MFPT_onC^drug, where C^drug is the concentration of the drug[151]. Buch et al.[152] calculated the k_on and k_off kinetic constants for benzamidine-trypsin complex from the MFPT obtained from their MSM (see Section 3), although with one order of magnitude deviation with respect to experimental values. Moreover, coarse-grained models currently allow to build membranes that mimics the lipid composition of specific cell/organelle and to simulate the lateral distribution of the lipids[153]. This could be important to assess the influence of lipids in both the gating of ion channels and their association with drugs.

Clearly, the mathematical frameworks to obtain rates for channel gating transitions and drug binding/unbinding from MD simulations in single-channel modeling are connected (Fig. 3). As a result, detailed atomistic models of state-specific drug interactions with ion channels might provide additional levels of validation for the ion currents kinetic models, thus enabling self-consistent development of cellular models that are iterated between a single protein level data and measurements of drug-induced perturbations at the cellular levels. We believe that the knowledge resulting from this multi-scale modeling approach would significantly contribute to the molecular pharmacology.

Note that many challenges are to be solved including improvement of the force-field parameters[104], better modeling of physiologically relevant lipid mixtures[153], better models of membrane potentials controlling function of membrane proteins[154–156] among others. We foresee that fruitful structural information will be more easily derived from a number of experimental techniques such as Cryo-EM methodology[141] or X-ray laser serial crystallography[157]. Consequently, the MD-based kinetic modeling would become an inevitable and more accurate tool to predict the side effects of drugs targeting ion channels.

Highlights.

• Review present topical discussion on common strategies in studies ion channels-drug interactions

• Molecular and Cellular Models for Ion Channel Function are discussed

• The tentative multi-scale approach for integration of protein-level data with cellular kinetic models is presented

Abbreviations

AP

(Action Potential)

EM

(Electron Microscopy)

HH

(Hodgkin and Huxley model)

hERG

(human Ether-a-go-go channel)

HCN

(Hyperpolarization-activated Cyclic Nucleotide-gated channel)

H-REMD

(Hamiltonian-Replica Exchange Molecular Dynamics)

HMM

(Hidden Markov Model)

IC₅₀

(half-maximal inhibitory concentration)

MD

(Molecular Dynamics)

MELD

Modeling by Employing Limited Data)

(MFEP)

Minimum Free-Energy Pathways

MFPT

(Mean First Passage Time)

MSM

(Markov State Model)

NMR

(Nuclear Magnetic Resonance)

PMF

(Potential of Mean Force)

REST

(Replica-Exchange with Solute Tempering)

RMSD

(Root-Mean Square Deviation)

tICA

(time-structure Independent Analysis)

T-REMD

(Temperature-Replica Exchange Molecular Dynamics)

WHAM

(Weighted Histogram Analysis Method)