An Integrated Mathematical Epithelial Cell Model for Airway Surface Liquid Regulation by Mechanical Forces

Abstract

A robust method based on reverse engineering was utilized to construct the ion-channel conductance functions for airway epithelial sodium channels (ENaC), the cystic fibrosis transmembrane conductance regulator (CFTR), and calcium-activated chloride channels (CaCC). The ion-channel conductance models for both normal (NL) and cystic fibrosis (CF) airway epithelia were developed and then coupled to an adenosine triphosphate (ATP) metabolism model and a fluid transport model (collectively called the integrated cell model) to investigate airway surface liquid (ASL) volume regulation and hence mucus concentration, by mechanical forces in NL and CF human airways. The epithelial cell models for NL and CF required differences in Cl⁻ secretion (decreased in CF) and Na⁺ absorption (raised in CF) to reproduce behaviors similar to in vitro epithelial cells exposed to mechanical forces (cyclic shear stress, cyclic compressive pressure and cilial strain) and selected modulators of ion channels and ATP release. The epithelial cell models were then used to investigate the effects of mechanical forces and evaporative flux on ASL and mucus homeostasis in both NL and CF airway epithelia. Because of reduced CF ASL volumes, CF mucus concentrations increased and produced a greater dependence of ASL volume regulation on cilia-mucus-ATP release interactions in CF than NL epithelial nodules. Similarly, the CF model was less tolerant to evaporation induced ASL volume reduction at all ATP release rates than the NL model. Consequently, this reverse engineered model appears to provide a robust tool for investigating CF pathophysiology and novel therapies.

Introduction

ASL height (volume) regulation is critical to hydrate mucus sufficiently to maintain mucus transport and host defense. Cystic fibrosis (CF) patients are vulnerable to airways mucus hyperconcentration, mucus obstruction, and pulmonary infections. This vulnerability reflects the fact that CF subjects exhibit a dysfunction of cystic fibrosis transmembrane conductance regulator (CFTR) mediated ASL volume regulation. In series with submucosal gland secretion (Ballard & Spadafora, 2007; Widdicombe & Wine, 2015), ASL height is primarily governed by osmotic gradients generated by ion channels embedded in the apical membrane of superficial airway epithelia (Boucher, 2007). Multiple experiments have demonstrated that these channels are, in part, regulated by external and internal mechanical forces through adenosine triphosphate (ATP) release into the luminal compartment (Button et al., 2013; Button, et al., 2007; Tarran et al., 2005). Three different types of physical forces can trigger ATP release: cyclic shear stress, cyclic compressive stress, and cilial strain. Three distinct ion channels respond to the ATP release: epithelial sodium channels (ENaC), CFTR, and calcium-activated chloride channels (CaCC). However, ASL height homeostasis in the in vivo environment, reflecting the interactions between epithelia cells, mechanical forces, and thermodynamics, is not as easily characterized as ASL homeostasis in in vitro experiments. Thus, a numerical study of ASL height regulation may be useful to provide insights on ASL volume regulation in vivo in normal (NL) and CF lungs.

A high-fidelity computational fluid dynamics (CFD) method can accurately predict mechanical forces and water evaporative fluxes in the human airways and, consequently, could be coupled with a biophysical cell model of ion and water transepithelial transport to predict ASL height. Also available is an extracellular ATP metabolism model for airway epithelia (Zuo et al. 2008). However, this ATP model has not been coupled to ion transport models (Zuo, 2007). Herschlag et al. (2013) developed a cell model that predicted ASL height based on mechanical forces, but the model lumped all the interactions into three variables, i.e., ATP concentration ([ATP]), ion concentration, and ASL height. Without distinct variables and solving for individual regulatory pathways, the utility of the model was limited. Warren, Tawhai, and Crampin (2009) developed a cell model to predict ASL height by osmosis. Compared to reported ATP/ion/water transport models, their model solved the biophysical mechanisms for Na⁺, Cl⁻ and K⁺ transport with independent descriptions of the major ion channels, ion cotransporters, and ion pumps on both apical and basolateral membranes. They also included an ATP-trigged intracellular calcium component to model the activation of CaCC. However, they did not include other pathways required in ASL height regulation, e.g., extracellular ATP or its metabolites and their activation/inhibition of CFTR and ENaC. Garcia, Boucher, and Elston (2013) also developed a biophysical model for water and ion transport. Compared to Warren, Tawhai, and Crampin (2009)’s model that used conductance-voltage relations to simulate ion flux with conductances fitted to experimental data, Garcia et. al. used the Goldman-Hodgkin-Katz equation to simulate ion flux with permeabilities fitted to experimental data. Both methods showed good agreement with the experimental data.

In this study, we developed an ion-channel conductance model that coupled the previously developed fluid secretion model (Warren, Tawhai, and Crampin, 2009) with an ATP metabolism model (Zuo et al. 2008) to not only reproduce known steady state cellular responses reported experimentally, but to investigate the effects of mechanical forces and evaporative flux on the ASL volume homeostasis for NL and CF airway epithelia. The integrated model takes advantage of the two existing airway epithelial cell models that contain the fully described ATP metabolism and the ion-channel conductance/water transport descriptions of the known regulatory pathways for ASL volume homeostasis. The ultimate goal was to combine this integrated model with a thermo-fluid CFD lung mechanics model (Wu et al., 2015; Wu et al., 2014) that predicts in vivo local mechanical forces and water loss rates. The approach enables the prediction of ASL volume by accounting for CFD-predicted local evaporative fluxes and cellular responses to CFD-predicted local mechanical forces in a disease specific manner.

Method

An overview of the model

Figure 1 shows the schematic view of both normal (NL) and CF epithelial cells. The cell model elements reacting to mechanical forces are summarized into eight basic processes marked in Fig. 1 (a) (Zuo, 2007):

1. Mechanical forces trigger luminal ATP release from airway epithelial cells.

2. Extracellular ATP is metabolized into adenosine diphosphate (ADP), adenosine monophosphate (AMP), adenosine (ADO) and inosine (INO).

3. ATP binds to purinoceptor 2 receptor (P2Y2-R) and triggers phosphatidylinositol 4,5-bisphosphate (PIP₂) metabolism into inositol trisphosphate (IP₃) and diglyceride (DAG). IP₃ activates intracellular calcium release. Intracellular Ca²⁺ activates CaCC channel to increase Cl⁻ secretion.

4. ADO binds to the adenosine A_2b receptor and increases cyclic adenosine monophosphate (cAMP), which subsequently activates CFTR channel via protein kinase A to increase Cl⁻ secretion.

5. An increase of DAG concentration activates enzyme protein kinase C (PKC), which also activates the CFTR channel.

6. CFTR channel inhibits ENaC channels, decreasing Na⁺ absorption (Stutts et al., 1995). However, there exists contradictory evidence that CFTR does not inhibit ENaC (Nagel et al., 2005).

7. P2Y2-R-mediated depletion of PIP₂ inhibits ENaC channel, decreasing Na⁺ absorption.

8. As ion channels modulate extracellular ion concentrations, osmotic gradients are created that drive water flux through the epithelial cell membranes. For example, an increase of Cl⁻ secretion increases ASL height, whereas an increase of Na⁺ absorption decreases ASL height.

FIGURE 1.

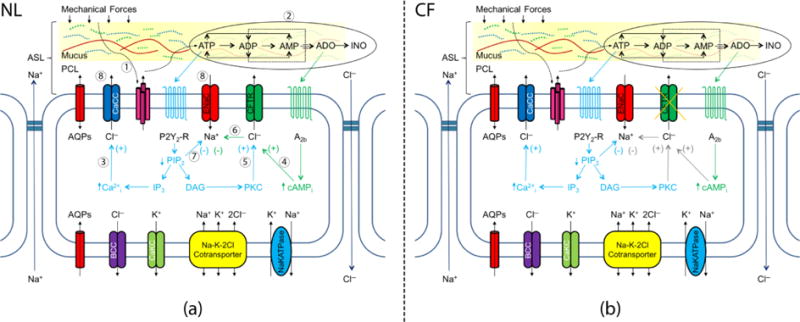
The Schematic View of the Mechanical Forces Regulated ASL Volume for (a) NL Cell Model and (b) CF Cell Model (Zuo, 2007; Warren, Crampin, and Tawhai, 2010): The eight processes described in the Method Section were marked with corresponding numbers. For each element illustrated in Figure 1: AQPs = aquaporin; CaCC = calcium activated Cl⁻ channel; ENaC = Epithelial Na⁺ channel; P2Y₂-R = purinoceptor 2 receptor; CFTR = cystic fibrosis transmembrane conductance regulator; A_2b = adenosine A_2b receptor; BCC = basolateral chloride channel; CaKC = calcium-activated potassium channel; Na⁺/K⁺-ATPase = active sodium-potassium adenosine triphosphatase. Mechanical forces = cyclic shear stress (CSS), cyclic compressive pressure (CCP), or cilial-mucus interactions. ASL = airway surface liquid; PCL = periciliary layer.

Thus, we present three models to predict the processes illustrated in Fig. 1: (a) an ATP model (processes 1 and 2); (b) an ion-channel conductance model (processes 3 to 7); and (c) a fluid transport model (FTM) (process 8). Note that these models do not account for: 1) the elements that regulate the extracellular pH (Coakley et al., 2003; Falkenberg & Jakobsson, 2010); 2) direct mechanical effects on CFTR (Zhang et al., 2010) or ENaC function (Althaus et al., 2007); or 3) the mass of mucins in the mucus layer. The differences between NL and CF epithelia cells are that steps 4, 5 and 6 in Fig. 1 (b) involving CFTR channels are dysfunctional in CF cells due to mutations in the CFTR gene.

ATP model and fluid transport model

The ATP model was developed and validated by Zuo et al. (2008) (see the reproduced result in Fig. 2 (a), which shows the hydrolysis of 100 μM ATP to its metabolites). The FTM was developed, extensively tested, and validated by Warren et al. (2009). As shown in Fig. 1, this model includes three apical membrane channels: CaCC, ENaC and CFTR, and two basolateral membrane channels; i.e., a basolateral chloride channel (BCC) and calcium-activated potassium channel (CaKC). It also includes a Na-K-2Cl cotransporter and an active sodium-potassium adenosine triphosphatase (Na⁺/K⁺-ATPase) on the basolateral surface. Figure 2 (b) shows the FTM prediction of 33% hypotonic challenge (reproduced as in Warren et. al. (2010)) compared to data from Okada et al. (2006). After hypotonic solution administration, water was driven by osmotic pressure and ions were driven by the electrochemical gradients across the membrane until equilibrium was again reached. The cell swelling and deswelling dynamics were modeled accurately by the FTM. More details of the ATP and FTM model are provided in the Supplementary Material.

FIGURE 2.

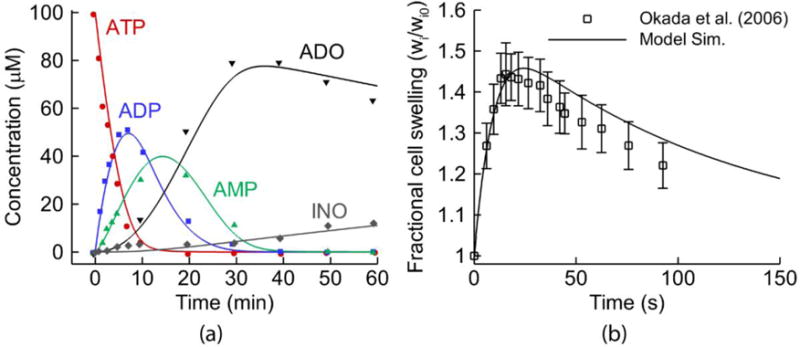
Models Combined into the Integrative Model: (a) The extracellular purinergic metabolism model describing the time response of 100 μM [ATP] addition to human airway surfaces. As in Zuo et al. (2008), the symbols are experimental data, while the solid lines are the reproduced result by the ATP model component in the integrative cell model. (b) The reproduced result of the fluid transport model from Warren et al. (2010): the predictions of 33% hypotonic challenge experimental data from Okada et al. (2006)

ATP release by mechanical forces

Extracellular ATP is released by cyclic shear stress, compressive stress, and cilial strain, which are the types of forces airway naturally experiencing during tidal breathing or coughing. Each type of stress was modeled as follows.

First, Tarran et al. (2005) found that ATP was released by cyclic shear stress (CSS) as given by J_{ATP_CSS} in Fig. 3 (a). As no single function described the relationship between [ATP] and cyclic shear stress, interpolation of measurement data was used. The ATP release range by CSS was approximately between [0, 130] nM.

FIGURE 3.

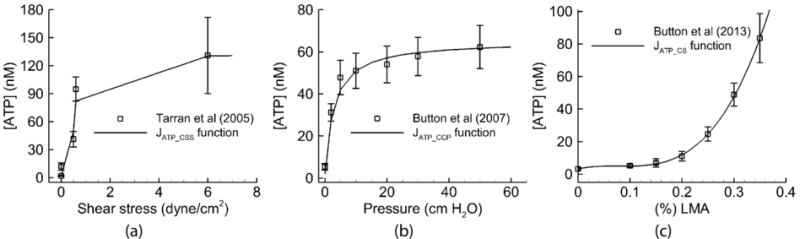
Fitting to Primary Experimental Data: (a) The ATP released due to cyclic shear stress, as in Tarran et al. (2005). (b) The ATP released due to cyclic compressive pressure, as in Button et al. (2007). (c) The ATP released due to cilia strain with mucus simulant concentration (% LMA), as in Button et al. (2013). The solid lines are produced from the functions in the model to describe the relationships between mechanical forces and ATP release for each experiment. The squares with error bars describe the experimental data.

Second, Button et al. (2007) found that ATP was released by cyclic compressive pressure (CCP), as denoted by J_{ATP_CCP} in Fig.3 (b). The release of ATP could be well described by the function $J_{\mathit{ATP}\_\mathit{CCS}}=P_{\mathit{max}}\frac{\mathrm{\Delta }P}{K_p+\mathrm{\Delta }P}$, where ΔP is the average change in CCP, K_p and P_max were fitted to match the data. The ATP release range by CCP was approximately between [0, 60] nM.

Third, Button et al. (2013) reported that cilial strain (CS) stimulated by mucus viscosity triggered the ATP release J_{ATP_CS}. They showed that the ATP release increases with mucus concentration (simulated by % LMA mucus simulant (see Table 1) in the experiments). In the model, we used a 3^rd order polynomial of % LMA to fit the experimental curve as shown in Fig.3 (c). The ATP release range by CS was approximately between [0, 100] nM.

Table 1.

Drug Information

Drugs	Description	Simulation Conditions
LMA	Low-melting point agarose, with different (%) concentration mimics mucus viscosity	Figure 3(c)
Apyrase	An enzyme that catalyzes ATP into AMP rapidly	Increase ATP reaction rate by 30 times in ATP model.
Bumetanide	An inhibitor of Cl secretion (affect both CaCC and CFTR)	The Cl− secretion is 0; GCaCC = 0 pSμm−2, GCFTR = 0 pSμm−2.
8-SPT	8 (p-sulfophenyl) theophylline; an ADO receptor antagonist	Equivalent to [ADO]=0 nM
Nystatin	An ionophore that significantly increases Na absorption rate through membrane, bypassing ENaC	GENaC = 40 pSμm−2; a large conductance to mimic the permeabilized membrane.
Aprotinin	ENaC inhibiting protein, decrease Na absorption	No effect to NL model; GENaC*0.25 in CF model.
Trypsin	ENaC activating protein, increase Na absorption	GENaC*1.25 in NL model; No effect to CF model.
DIDS	4,4 -diisothiocyanostilbene-2,2 -disulfonic acid; CaCC antagonist	GCaCC =0 pSμm−2.
CFTRinh172	CFTR antagonist	GCFTR =0 pSμm−2

Finally, we assumed that the ATP release due to mechanical forces generated by different types of stress in airways were additive to the basal ATP release rates (Herschlag et al., 2013). Therefore, total ATP release $J_{\mathit{ATP}}=J_{\mathit{ATP}\_\mathit{CSS}}+J_{\mathit{ATP}\_\mathit{CCP}}+J_{\mathit{ATP}\_CS}$ was added to the ATP values in ASL predicted by the ATP metabolism model, where a set of ODE equations were solved (Zuo, 2007).

Ion-channel conductance model

Although ASL height regulation by the three apical channels has been extensively investigated (Button et al., 2007; Herschlag et al., 2013; Tarran et al., 2005; Tarran et al., 2006; Zuo, 2007), the underlying complex biochemical reactions integrating the activity of these three channels have not yet been fully explored. In this study, as shown in Fig. 4 (a), the known conditions are the direct measurements a (Table 2) and b (Figure 3), predictions i (ATP model) and d (FTM), while the unknown conditions are c (activation of ion channels by ATP and its metabolites) and e (activation of ion channels directly by mechanical forces (Althaus et al., 2007; Zhang et al., 2010)). Condition a is the integral result of b, i, c, d and e. If we lump the unknown condition e into c, we can use the known condition a, b, i and d to solve c, namely the calibration of ion-channel conductance model. Therefore, we will first introduce the equations of this model, then we will use the known conditions to calibrate the parameters in these equations.

FIGURE 4.

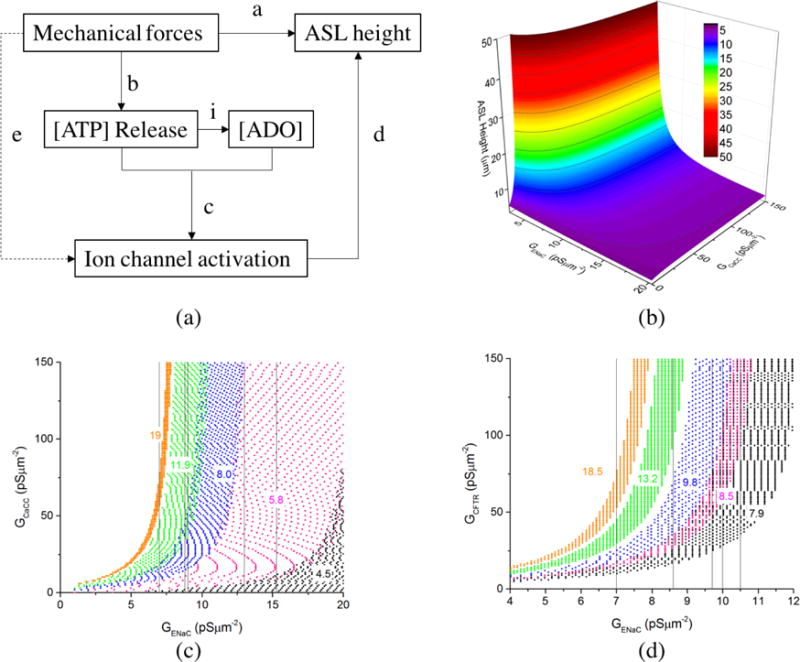
The construction of ion-channel conductance model: (a) Rationale: a. direct measurement; b. direct measurement; c. calibration of ion-channel conductance model; d. prediction by FTM; e. calibration of ion-channel conductance model; i. prediction by ATP model. (b) The data base of ASL height with different combination of G_ENaC and G_CaCC for CF model_. (c) The sample regions satisfy the experimental ASL data set of 2 (black), 3 (red), 4 (blue), 5 (green) and 6 (orange) in Table 2. Once G_ENaC function is chosen, the G_ENaC for each data set is determined. The vertical lines mark the values of G_ENaC for each data set, i.e. 15.3, 13, 9, 8.8 and 7 pSμm⁻². Then corresponding CaCC regions was extracted from fitting. (d) The sample regions satisfy the normal experimental data set of 2 (black), 3 (red), 4 (blue), 5 (green) and 7 (orange) in Table 2. The vertical lines mark the values of G_ENaC for each data set, i.e. 10.5, 10, 9.7, 8.6, and 7 pSμm⁻². Then corresponding CFTR regions were extracted from fittings.

Table 2.

Calibration Data Sets

Data set	Conditions	ATP (nM)*	ADO (nM)*	ASL(μm)	Ref**
NL
1	Apyrase+8-SPT	0	0	4.1±0.2	a
2	No force/additive	1.8	155.5	7.9±0.9	c
3	0.15% LMA	6.4	173.6	8.5±0.4	d
4	0.2% LMA	12.1	196.5	9.8±1.0	d
5	0.5 dynes/cm2 CSS	49.9	370.5	13.2±1.1	a
6	20 cmH2O CCP	57.2	409.5	13.2±1.7	c
7	Aprotinin+300 μM ATP (10 min)	34254	6836.9	18.5+2.2	b
8	Aprotinin+300 μM ADO (10 min)	1.8	123476.5	14.1+1.9	b
9	0.5 dynes/cm2 CSS + 8-SPT	49.9	0	7.5±1.0	a
CF
1	No force/additive	1.8	155.5	3.9±0.8	c
2	0.15% LMA	6.4	173.6	4.5±0.4	d
3	0.2% LMA	12.1	196.5	5.8±1.0	d
4	0.5 dynes/cm2 CSS	49.9	370.5	8.0±1.4	a
5	20 cmH2O CCP	57.2	409.5	11.9±3.4	c
6	Trypsin+300 μM ATP(10 min)	6187.3	8316.6	19.0+1.9	b

^*Calculated from ATP model

^**a. Tarran et al. (2005); b. Tarran et al. (2006); c. Button et al. (2007); d. Button et al. (2013).

Inspired by the method of lumping the five regulatory pathways in the processes 3 to 7 into the Na⁺ and Cl⁻ permeability functions in Zuo (2007), we lumped the five regulatory pathways (i.e. process 3 to 7 in Fig. 1(a)) into three ion-channel conductance functions with [ATP] and [ADO] as variables. With this strategy, our approach bypasses solving the actual biochemical reactions within each regulatory pathway, while the five regulatory pathways are independently described and fully accounted for. As illustrated in the schematic view of Fig. 1, the conductance functions can be written as G_CaCC = f (ATP), G_ENaC = f(ATP, ADO), G_CFTR = f (ATP, ADO) for the NL airway epithelial model, and G_CaCC = f (ATP), G_ENaC = f(ATP), G_CFTR = 0 for CF model. The G_CaCC is the same for both NL and CF models. Then, we used the form of Michaelis–Menten kinetic equation $G=G_{\mathit{max}}\frac{\left[L\right]}{K_G+\left[L\right]}$ to construct the conductance functions. The [L] represents the ligand binding to the receptors, where [L]_CF = [ATP] for CF model, while ${\left[L\right]}_{NL}=\left[\mathit{ATP}\right]+A_{\mathit{ADO}}\frac{\left[\mathit{ADO}\right]}{K_{\mathit{ADO}}+\left[\mathit{ADO}\right]}$ for NL model (the rationale for this equation form is in the Discussion section). Thus, the conductance equations read:

$$G_{\mathit{CaCC}}=\frac{A_{\mathit{CaCC}}\left[\mathit{ATP}\right]}{K_{\mathit{CaCC}}+\left[\mathit{ATP}\right]}$$ (1)

For CF Cells:

$$G_{\mathit{ENaC}}^{CF}=-\frac{A_{\mathit{ENaC}}^{CF}\left[\mathit{ATP}\right]}{K_{\mathit{ENaC}}^{CF}+\left[\mathit{ATP}\right]}+C_{\mathit{ENaC}}$$ (2)

For NL Cells:

$$G_{\mathit{CFTR}}^{NL}=\frac{A_{\mathit{CFTR}}^{NL}([\mathit{ATP}]+\frac{A_{\mathit{ADO}}[\mathit{ADO}]}{K_{\mathit{ADO}}+[\mathit{ADO}]})}{K_{\mathit{CFTR}}^{NL}+([\mathit{ATP}]+\frac{A_{\mathit{ADO}}[\mathit{ADO}]}{K_{\mathit{ADO}}+[\mathit{ADO}]})}$$ (3)

$$G_{\mathit{ENaC}}^{NL}=-\frac{A_{\mathit{ENaC}}^{NL}([\mathit{ATP}]+\frac{A_{\mathit{ADO}}[\mathit{ADO}]}{K_{\mathit{ADO}}+[\mathit{ADO}]})}{K_{\mathit{ENaC}}^{NL}+([\mathit{ATP}]+\frac{A_{\mathit{ADO}}[\mathit{ADO}]}{K_{\mathit{ADO}}+[\mathit{ADO}]})}+C_{\mathit{ENaC}}$$ (4)

Then, we proposed the following method to calibrate the parameters in conductance functions with the experiment data listed in Table 2. First, we created databases that gave the corresponding ASL heights with all the combinations of G_CaCC within [0 ~ 300] pS μm⁻², G_ENaC within [0 ~ 30] pS μm⁻², G_CFTR within [0 ~ 300] pS μm⁻² calculated by the FTM. Second, starting with the CF model, we extracted the regions that matched with experimental data, over which the luminal [ATP] and the resulting ASL heights were known (Fig. 4 (b)). As shown in Fig. 4 (c), we then generated a map of G_CaCC, $G_{\mathit{ENaC}}^{CF}$ with each color representing an experimental data set. Third, we guessed the values of $A_{\mathit{ENaC}}^{CF}$, $K_{\mathit{ENaC}}^{CF}$ and c_ENaC to determine $G_{\mathit{ENaC}}^{CF}$. Then, we obtained the corresponding regions for G_CaCC, at each [ATP] that reproduced the experimentally measured ASL height. Fourth, we found a pair of A_CaCC and K_CaCC that allowed G_CaCC to fall into these regions for the given [ATP]. Finally, with G_CaCC determined, we repeated the same process for $G_{\mathit{CFTR}}^{NL}$, $G_{\mathit{ENaC}}^{NL}$ for the NL model as shown in Fig. 4 (d). Note, before parameterizing $G_{\mathit{CFTR}}^{NL}$ and $G_{\mathit{ENaC}}^{NL}$, we needed to parameterize ${[L]}_{NL}=[\mathit{ATP}]+A_{\mathit{ADO}}\frac{[\mathit{ADO}]}{K_{\mathit{ADO}}+[\mathit{ADO}]}$, which required two equations for A_ADO and K_ADO. As shown in the NL data sets in Table 2, the data sets 2 and 9, and the data set 6 and 8 had similar ASL heights. In this case, we assumed that their ligand concentration [L] binding to the receptors was approximately the same, which gave [L]_{NL,Set 2} = [L]_{NL,Set 9} and [L]_{NL,Set 6} = [L]_{NL,Set 8}.

With the method presented here, the values selected for these parameters have certain flexibilities. As a result, we tested the sensitivity of the model predictions to the values of these parameters. The result showed that ±15% variation of all parameters, except for $A_{\mathit{ENaC}}^{NL}$ and $A_{\mathit{ENaC}}^{CF}$, had minor effects on the model predictions, as evidenced by the observations that variations in the simulation results were either negligible or within the standard deviations of the experiment data. The change of $A_{\mathit{ENaC}}^{NL}$ (or $A_{\mathit{ENaC}}^{CF}$) caused large variation in the simulated results of the NL (or CF) cell model. This result shows that the model predictions for both NL and CF cell model are sensitive to the modeling of EnaC channel activities. The selections of EnaC channel parameters $A_{\mathit{ENaC}}^{NL}$ for the NL cell model ( $A_{\mathit{ENaC}}^{CF}$ for CF cell model) affected the quality of model predictions. The values selected for the parameters and other details are shown in the Supplementary Material.

Results

We first validated the model predictions against experimental data, including the responses to selected pharmacologic agents or/and mechanical forces in NL and CF in vitro airway epithelial studies. Then, we investigated the variations of ASL height with respect to mechanical forces, and evaporative flux. All the pharmacologic/agents used in the Results Section are listed in Table 1.

Validation

Figure 5 (a) shows the NL model predictions for 24 hour time histories of ASL heights after 30 μl PBS addition (control), PBS with 20 cmH₂O CCP, and PBS with the adenosine receptor antagonist, 8-SPT. After PBS addition to control cultures, the equilibrium ASL height predicted by the NL model was 8.0 μm at 24h. We used this value as the reference value for the optimum ASL height in this study. The CCP exposure increased the ASL height to ~15μm, while the addition of 8-SPT by blocking ADO receptors, reduced the ASL height to a CF-like level (~4μm).

FIGURE 5.

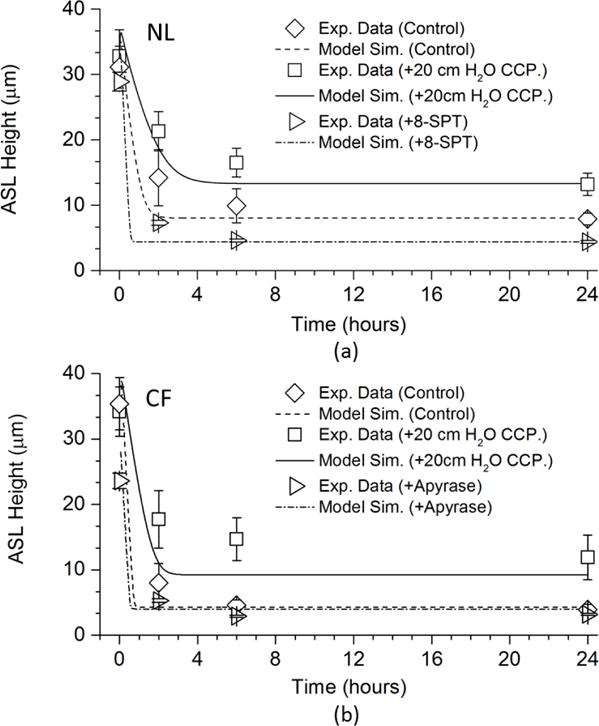
Model Simulations of Airway Surface Liquid Volume Additions to NL and CF Airway Epithelia: (a) The time series of predicted NL model responses to addition of 30 μl of PBS with and without 20 cmH₂O compressive pressure in comparison with the experimental data of Button et al. (2007), and with 8-SPT in comparison with the experimental data of Tarran et.al. (2005). (b) The time series of predicted CF cell responses to addition of 30 μl of PBS with and without 20 cmH₂O compressive pressure in comparison with the experimental data of Button et al. (2007), and with apyrase in comparison with the experimental data of Tarran et.al. (2005)

Figure 5(b) shows the similar tests for the CF model. After PBS addition under control conditions, the equilibrium ASL height predicted by the CF model was 4.3 μm at 24h. We used this value as the reference value for CF-like ASL heights in this study. CCP exposure increased ASL to ~12μm, a value consistent with normal mucus transport rates. In the absences of an adenosine-CFTR mechanism for ASL regulation in CF, the ATP-P2Y2-R system dominates nucleotide regulation of ASL volume. Apyrase is an enzyme that rapidly metabolizes ATP released in response to CCP exposure. The presence of apyrase in ASL during periods of CCP-induced ATP release blocked the CCP induced increase in CF ASL height, a response captured by our model.

Collectively, both NL and CF model predictions of the steady state values agreed well with the experimental data. The only discrepancies appeared in the 2–6h responses where the model simulations achieved steady state conditions faster than the experiments. This kinetic discrepancy likely reflects the absence of time mechanisms in the conductance functions in the ion-channel conductance model, i.e., we assumed that the ion channels would open/close instantly with the given conditions.

Next, we systematically tested NL model responses with manipulations of the Cl⁻ secretion pathway (Test 1 to 7) and Na⁺ absorption pathway (Test 9 to 12) (Fig. 6(a)). In the first of the seven Cl⁻ secretion test experiments, accelerated ATP release was trigged by CSS, which increased ASL height (Test 1 as control). In Test 2, a CFTR Cl⁻ channel inhibitor was added, with CSS regulated levels of [ATP] and [ADO] remaining unperturbed, and the ASL height was decreased by half. In Test 3, a CaCC Cl⁻ channel inhibitor was added to the CFTR inhibitor, and the ASL height further decreased to a CF-like level under CSS conditions. In Test 4, both Cl⁻ channels remained undisturbed, and apyrase was “added” to the apical solution of CSS stimulated cultures. ATP was metabolized into ADO at fast rate. Accordingly, the decrease in ATP activated CaCC mediated Cl⁻ secretion was compensated for by increased ADO-cAMP CFTR mediated Cl⁻ secretion. The acceleration of Na⁺ absorption due to apyrase relief of ATP mediated EnaC block reduced ASL to heights slightly below CSS controls in the stimulation. In Test 5, “addition” of 8-SPT to CSS stimulated cells reduced adenosine/cAMP regulated CFTR Cl⁻ secretion without upregulation of the ATP/P2Y2-R pathway. Accordingly, ASL height decreased almost by half. In Test 6, with both apyrase and 8-SPT “added”, total Cl⁻ secretion became very low, Na⁺ absorption was raised, and, consequently ASL height decreased to an almost CF-like level. In Test 7, bumetanide was “added” to deplete the intracellular Cl⁻, resulting in minimal/no Cl⁻ secretion and, the ASL height decreased to an almost CF-like level.

FIGURE 6.

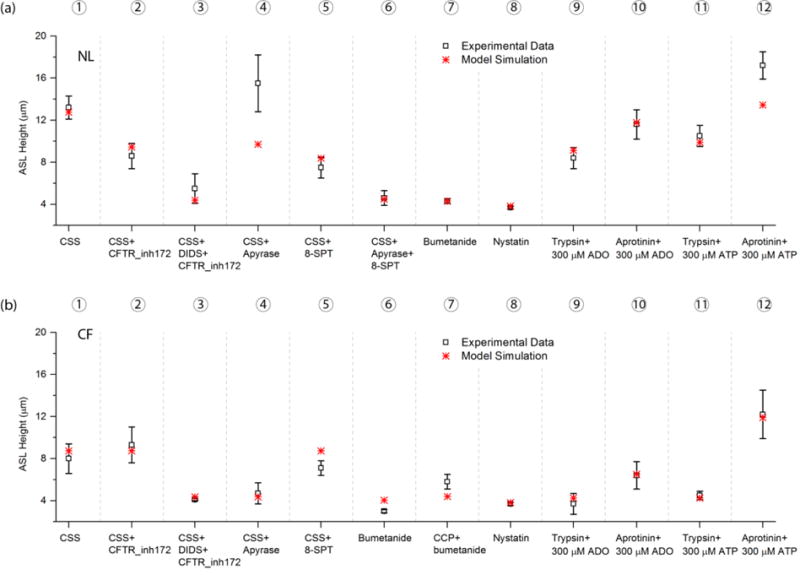
Model Simulations of Mechanical Forces and Pharmacologic Maneuvers in NL and CF Airway Epithelia: (a) 12 tests were performed to validate the NL model. The CSS was 0.5 dynes/cm². Experimental data in Test 1 to 6 is from Tarran et al. (2005), Test 7 to 12 from Tarran et al. (2006). (b) 12 tests were performed to validate the CF model. The CSS was 0.5 dynes/cm². The CCP was 20 cmH₂O. Experimental data in Test 1 to 6 is from Tarran et al. (2005), Test 7 from Button et al. (2007), and Test 8 to 12 from Tarran et al. (2006). The simulation conditions used to mimic the effect of the drugs are listed in Table 1.

The model closely predicted the NL experimental data measured change except for Test 4. We simulated the effect of apyrase by increasing the ATP metabolic rate 30 fold faster than under baseline conditions so that the luminal [ATP] was reduced to the reported 2.5 ± 0.3 nM (Tarran et al., 2005), and ATP model predicted a 368 nM [ADO]. The predicted ASL height was elevated to 9.7 μm, but still lower than the measured value.

Next, we focused on the NL Na⁺ absorptive pathway under basal conditions, i.e., without physical forces. Luminal nystatin was used to create unregulated pharmacologic Na⁺ permeable channels, aprotinin was used to block EnaC activating proteases, and trypsin was used to proteolytically activate EnaC. In Test 8, nystatin was added to the cells under normal conditions. Nystatin maximized Na⁺ absorption, reduced Cl⁻ secretory drives forces to zero, and reduced ASL height to CF-like conditions. The next series of simulations “added” trypsin or aprotinin with either 300 μM ADO or ATP (tests 9–12). Trypsin yielded an increase in EnaC Na⁺ absorption, as indicated by the lower ASL height compared to aprotinin addition in the presence of ADO (Test 9 vs. Test 10). Similarly, the ASL was lower with trypsin/ATP compared to aprotonin/ATP (Test 11 vs. Test 12). These results reflected the differential regulation of EnaC (trypsin activates aprotinin inhibits), and the simulations were consistent with experimental data.

The NL model predicted very similar cellular behaviors in response to regulation of the Na⁺ absorptive pathway similar to those observed in the experiments. The only discrepancy was in Test 12. The presence of ATP induced spikes Cl⁻ secretion that waned with ATP metabolism. In the model, the secretory spike waned faster than experimentally.

In Fig. 6 (b), we performed similar tests for the CF model. Tests 1 to 7 focused on the Cl⁻ secretion pathway. In Tests 1 to 5, ATP release was trigged by CSS (Test 1 served as control). For reference, the ASL heights with 20 cm H₂O CCP alone were 11.9 ± 3.4 μm experimentally in CF cells and 9.2 μm in the CF model as shown in Fig. 5(b). Note that in the CF model, the G_CFTR=0, and G_EnaC is not a function of [ADO]. Accordingly, the “addition” of the CFTR Cl⁻ channel inhibitor (Test 2) had no effect on the ASL height. In Test 3, the CaCC Cl⁻ channel inhibitor was added with CSS regulated [ATP] unperturbed, and the ASL height dropped to basal CF-like levels. In Test 4, apyrase was added with CaCC Cl⁻ channels unperturbed, and the ASL height fell to basal CF-like levels. In test 5, the addition of 8-SPT to CSS had little effect on CF ASL height, consistent with the absence of ADO-CFTR mediated Cl⁻ secretion in CF. In Test 6 and 7, we simulated the effect of bumetanide addition by minimizing Cl⁻ secretion. Without CCP (Test 6), the ASL height dropped below the basal CF-like levels. With 20 cmH₂O CCP (Test 7), the ASL height slightly increased from Test 6, which reflects EnaC channel inhibition by the ATP release due to CCP.

In Tests 8 to 12, we performed the same simulations as those in the NL model to test perturbations of the CF Na⁺ absorptive pathway. Neither nystatin nor trypsin affected ASL heights in CF cells, as CF cells already exhibited the maximum Na⁺ absorption rate (i.e., Tests 8 and 9) as compared to Test 3. In contrast, aprotinin inhibited EnaC channels in CF cells and raised ASL heights (Test 10). Adding ADO to activated (trypsin) or blocked (aprotinin) EnaC channels had no effect on CF ASL heights because of the absence of CFTR function. With the trypsin/ATP addition, ATP triggered a spike of Cl⁻ secretion that was rapidly terminated and the secreted fluid completely absorbed, producing low steady-state ASL heights (Test 11) similar to non-ATP treated cultures (Test 11 vs Test 8,9). With aprotinin inhibition of EnaC activation (Test 12), a higher ASL height was observed than with trypsin/ATP (Test 11), reflecting the aprotinin mediated EnaC failure to absorb Na⁺ secreted in response to ATP. Collectively, the CF model followed the exact same behaviors as reported for the experimental data.

In summary, we validated the responses of NL and CF models with/without mechanical forces and with manipulations of both Cl⁻ secretion and Na⁺ absorption as compared to the corresponding experiments (Button et al., 2013, 2007, Tarran et al., 2005, 2006). The overall agreement between experimental data and model simulations was good. With the model validated, we listed all the steady state values for both NL and CF models in Table 3. Of note, the depletion of ASL height in CF required the reduction in CFTR anion permeability to zero, an increase in CaCC Cl⁻ permeability, and a more than doubling of the apical membrane Na⁺ permeability.

Table 3.

Steady State Values Derived from Model: 1) Intracellular ion concentrations [Na⁺]_i, [Cl⁻]_i, [K⁺]_e; 2) Extracellular ion concentrations [Na⁺]_e, + [Cl⁻]_e, [K⁺]_e; 3) Membrane potentials V_a, V_b; 4) Na⁺ currents through ENaC, paracellular pathway; 5) Cl⁻ currents though CFTR, CaCC, and paracellular pathway; 6) Apical and paracellular Na⁺ permeability; 7) Apical and paracellular Cl⁻ permeability. Note: as we do not directly use permeabilities in the model, permeabilities are calculated through Goldman–Hodgkin–Katz flux equation.

Parameters	NL	CF	Units
ASL height	8.0	4.3	μm
[Na]i	23.2	24.4	mM
[K]i	79.6	79.5	mM
[Cl]i	42.4	44.4	mM
[Na]e	147.6	126.7	mM
[K]e	3.3	8.9	mM
[Cl]e	131.2	82.3	mM
Cell Volume	1450	1450	μm3
Va	−23.5	−22.8	mV
Vb	−34.0	−36.7	mV
IENaC	9.1	15.8	μA/cm2
IpNa	9.1	15.8	μA/cm2
ICFTR	19.4	0.0	μA/cm2
ICaCC	0.8	8.4	μA/cm2
IpCl	20.2	8.4	μA/cm2
PaNa	1.64E-08	3.72E-08	m/s
PpNa	1.70E-08	1.83E-08	m/s
PaCl	1.23E-08	9.23E-09	m/s
PpCl	2.99E-08	3.84E-08	m/s

ASL height vs. mechanical forces

In this section, we report the tests of model in response to the three types of mechanical forces applied experimentally to airway epithelia. Figures 7 (a) and (b) show the absolute ASL height increases for NL and CF epithelia in response to CSS or CCP, respectively. NL and CF models exhibited similar responses except that the ASL height in the NL model increased from the equilibrium height of 8.0 μm, while the ASL height in CF model increased from the equilibrium height of 4.3 μm. Both models responded rapidly to CSS from 0.0 to 0.6 dyne/cm² and to CCP from 0 to 20 cmH₂O. In Fig. 7 (c) we plotted the ASL height change (ASL height − equilibrium height) for the NL airway epithelia in response to mucus simulant concentrations (% LMA) from the data obtained from the NL cell experiments (Button et al., 2013) and plotted the model fit with a solid line. The increasing % LMA mimicked the increasing concentration of mucus on the airway surface, which stimulated higher cilial strain and ATP release. The NL model simulations agreed with experimental data. (Note: Though similar experiments were not done on CF cells, we showed the CF simulation results for comparison).

FIGURE 7.

Model Simulations of Mechanical Forces – Dependent ATP Release on ASL Height in NL and CF Airway Epithelia: (a) The relationships between the absolute ASL heights and CSS in NL and CF models. (b) The relationships between the absolute ASL heights and CCP in NL and CF models. (c) The relationship between the increase of mucus viscosity and the increase of ASL height in the NL model comparing with experimental data from Button et al. (2013). Also shown is simulation for CF airway epithelia. (d) The relationship between the increase of [ATP] triggered by increasing mechanical forces and the increase of ASL height for NL cells comparing with experimental data of Button et al. (2013). CF simulation is also shown.

As we assumed that ASL volume changes did not depend on the type of mechanical forces, but rather the rate of ATP release triggered by each force, the three types of forces produced almost the same linear relationships between change of ASL height and change of luminal [ATP] as shown in Fig. 7(d). The predicted curves agreed with experimental data from the LMA experiments (Button et al., 2013), from which both the range of [ATP] release and the ASL height increase were measured at different mucus simulant concentrations.

ASL height vs. evaporative flux

Evaporative water loss from airway surfaces and ATP release onto airway surfaces during tidal breathing are two important contributing factors with opposite predicted effects on ASL volumes. However, their relative roles/effects in ASL regulation during tidal breathing have not been quantified. In the cell model, ASL height is described by $\frac{d{w}_p}{dt}=A_a{J}_a^w-A_a{J}_{\mathit{evap}}-A_a{J}_p^w$, where the change of ASL volume w_p equals the apical water flux $A_a{J}_a^w$ (affected by ATP release) minus a constant paracellular water leak $A_a{J}_p^w$ and evaporative flux A_aJ_evap. (See Supplement for details). In Figures 8 (a) and (b), we present a series of the predicted ASL height-evaporative flux relationships versus ATP release rates corresponding to 0 to 190 nM ATP concentrations in ASL for NL and CF models. The x-axis “evaporative flux” increases from 0 to 800 nl/cm²/min. On each curve, ATP release from mechanical forces is the same, while ASL height changes with evaporative flux. From the red curve to the green curve, ATP concentrations increase from 0 to a maximum of 190 nM.

FIGURE 8.

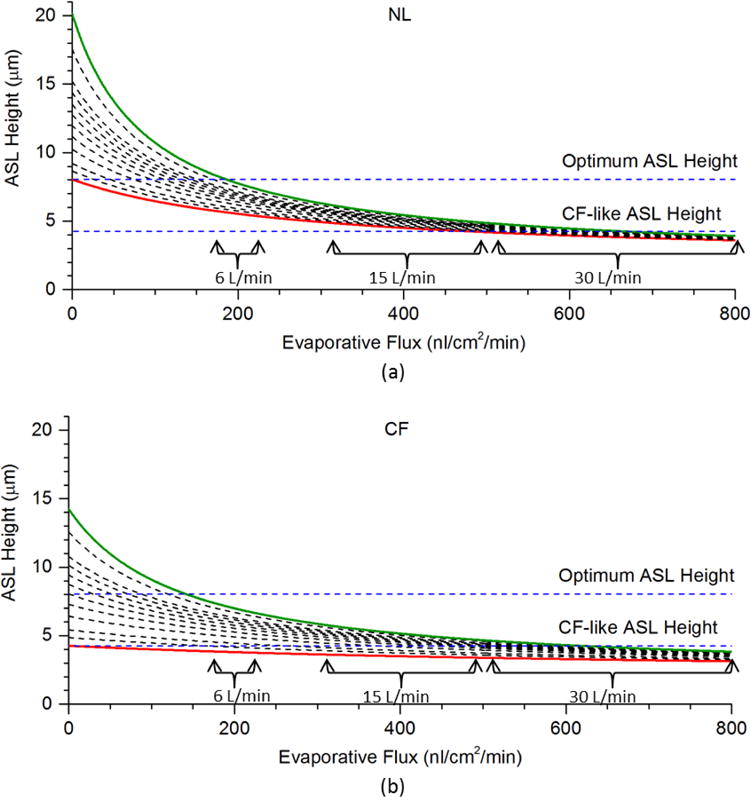
Model Simulations of the Relationships between Ventilation Induced Airway Surface Liquid Evaporation, Rates of ATP Release and ASL Height in NL and CF Airway Epithelia: The relationships between evaporative flux and ASL height with the [ATP] at 1.8 (0 ATP release: red solid line), 6.6, 11.4, 21, 30.6, 40.2, 50.0, 60.3, 72.6, 86.0, 130.4 and 193.6 (maximum ATP release: green solid line) nM for (a) NL model and (b) CF model. The range of predicted water loss rate at minute ventilation of 6 L/min, 15 L/min, and 30 L/min are marked.

In Wu et al. (2015), it was shown that average water loss rate (evaporation-condensation per cm² per minute) from the trachea to the 6^th generation bronchi is typically dominated by an evaporative loss of 200 nl/cm²/min for 6 L/min ventilation, 300~500 nl/cm²/min for 15 L/min ventilation, and 500~800 nl/cm²/min for 30 L/min ventilation, depending on factors such as regional geometry. At 200 nl/cm²/min, importantly, the ASL height would be ~ 5 to 8 μm for NL cell model and ~4 to 7 μm for CF cell model, depending on the local ATP release. At maximal ATP release rates/concentration (green lines), NL airways exhibit ~8μm ASL, whereas CF is ~7μm. These data suggest CF airways with sufficient ATP release can sustain MCC under normal breathing conditions, but they may be more vulnerable to insults that perturb ATP concentrations than normal subjects. Above 500 nl/cm²/min, the ASL height is predicted to decrease to around 3 μm over cell ranges of ATP release for normal and CF subjects.

These predictions indicate that the possibility that the mechanical-force-induced water secretion might not be able to balance the water loss rate at minute ventilation higher than 15 L/min. These considerations suggest active ion transport may not be sufficient to hydrate airway surfaces during maximal ventilation and other pathways such as additional cellular water fluxes are required (see Discussion).

Cilial strain vs. ASL recovery

Mucus concentration is dependent on the hydration status of ASL (indicated by ASL height). If ASL height decreases as excessive fluid being absorbed or evaporated, mucus concentration increases, exerting more stress on the cilia and, thus, triggering ATP release. The ATP release in turn increases ASL height and decreases mucus concentration (Button et al., 2013). Therefore, an important question is how effective is cilial strain in regulating ASL height in NL vs. CF epithelia.

To address this question, ASL height was decreased by evaporation. The increased mucus concentration triggered ATP release leading to an increase of ion and water fluxes onto the airway surface. Then, the percent $\mathit{ASL}\mathit{recovery}(\%)=\frac{AS{L}_{cs}-AS{L}_{\mathit{control}}}{AS{L}_{\mathit{control}}}\times 100\%$ was calculated as shown in Fig. 9 for NL model and CF models. (Note, ASL_cs is the ASL height with cilial strain, and ASL_control is the ASL height without cilial strain)

FIGURE 9.

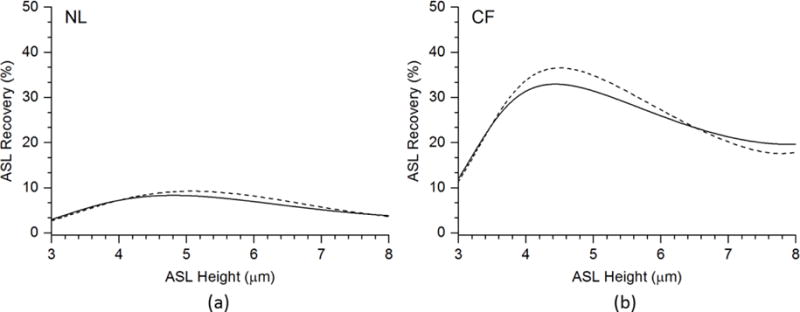
Cilia Mucus Interactions and Regulation of ASL Volume in NL and CF Respiratory Epithelia: ASL recoveries mediated by cilial-strain-induced ATP release for (a) NL model, (b) CF model. The solid line is the ASL recoveries (%) by simulating the mucus viscosity as a function of ASL osmotic pressure LMA_osm = 0.154(10^h/3.15)^1/3. The dash line is the ASL recoveries (%) by simulating the mucus viscosity as a function of ASL height LMA_h = 0.3 – 0.15(h − h_cf)/(h_opt − h_cf).

We tested two functions for cilial strain. For function LMA_h, we modeled mucus concentration increasing linearly with decreasing ASL height. For function LMA_osm, we tested the relationships when the mucus concentration is proportional to the mucus osmotic pressure to the power of 1/3 (Rubinstein & Colby, 2003). We also assumed mucus osmotic pressure is proportional to the PCL osmotic pressure, which is also a function of the PCL height (Button et al., 2012). Then, we used 0.3% LMA corresponding to a CF-like ASL height dependent concentration (h_cf) and 0.15% LMA corresponding to optimum ASL height and concentration (h_opt) to determine the coefficients of the functions. So we have function LMA_h(%) = 0.3 – 0.15(h−h_cf)/(h_opt − h_cf), and function LMA_osm(%) = 0.154(10^h/3.15)^1/3. Function LMA_osm is a better description to the biophysics of this situation, while function 1 serves as a simpler comparison.

In Fig. 9, the x-axis shows that the ASL height without cilial strain. The variation of ASL height from 3 to 8 μm was achieved by varying evaporative flux. The y-axis shows the ASL recovery (%) under the same evaporative flux with ATP released by cilial strain, which was predicted by the above cilial strain functions with respect to ASL height. As shown in Fig. 9, function LMA_h and function LMA_osm do not exhibit significantly different profiles. The peak recovery rate occurs at an ASL height in the 4.5 to 5 μm range for both NL and CF. Importantly, the dependence of ASL recovery is much greater in the CF model than the normal model. At the reported basal ASL heights of ~7μm and 4.5 μm for NL and CF respectively, the recovery cilialmucus interaction dependent rates are 5% and 30% for NL and CF epithelia, respectively.

In sum, cilial strain plays a greater role in ASL recovery in the CF model than in the NL model. This difference reflects the fact that in the normal model mucus concentration is lower (reflecting greater ASL height/hydration) so less cilial strain is required to transport mucus, with concomitantly less ATP release and fluid secretion generated by cilia interacting with normal mucus. Conversely, greater CF mucus concentration-dependent cilial strain increases the rate of ATP release ion transport balance and ASL height responses in the CF model. Consequently, the CF cells have a greater dependence of ASL volume regulation on cilia mucus interactions than normal.

Discussion

In this study, we first constructed a model integrating the existing ATP and fluid transport models to build comprehensive NL and CF cell models for ASL regulation that coupled to mechanical forces experienced in human airways to ASL homeostatic responses. Next, we assembled experimental data to calibrate and validate the NL and CF models. Finally, we utilized the NL and CF models to generate novel insights into mechanisms of local auto-regulation of ASL height by NL and CF airway epithelia as a function of mucus concentration and responses to the evaporative water losses that might occur at rest and exercise.

Overall, both the NL and CF models exhibited good agreement with experimental data (Figs. 5, 6, 7(c) and (d)). The integrated model captured the trends of the experimental data describing purinergic regulation of ENaC, CaCC and CFTR channels to set ASL height (volume). However, as time dependent mechanisms were not considered in the integrated model, the ASL time responses depended entirely on the ATP and FTM models. Generally, the time responses of the integrated model followed the trends observed in the experiments, but there existed deviations of the kinetic predictions from the measurements (Fig. 5). The deviation in time responses may be acceptable, however, as the steady state ASL valves were not affected (Fig. 5 and 6). Importantly, the approach served the purpose of predicting steady state ASL height responses to mechanical forces and evaporation during breathing (Figs. 7, 8 and 9), despite the fact that the detailed biochemistry reactions governing ion channel purinergic regulation remain unclear.

Note, the experiments used for calibration of the model have unavoidable biological variability, so the agreement of experiment data with model simulation may not necessarily be expected to yield perfect congruence. For example, even for NL epithelial basal ASL levels, ASL heights measured experimentally vary in different experiments, e.g., Button et al. (2013) measured 7.4 ± 0.3 μm while Tarran et al. (2005) measured 8.0 ± 1.0 μm. For most of ASL height measurements, the standard error reported across a spectrum of experimental studies varies roughly from 10% to 20%. In this study, in both calibration and testing processes, if the standard error was not provided by the original experiment data, we assumed an error of 5% standard deviation. However, any deviation within 20% of the value was considered acceptable as long as the model prediction exhibited the same trend with the experimental measurements.

Even though our integrated model does not solve detailed biochemical kinetics, the calibration process provided a thorough analysis of the model. For example, these functions satisfied the constraints inherent in the calibrating experimental data, despite certain flexibility in choosing the data ranges for each channel (Fig. 4). The ENaC conductance for NL cells under breathing conditions (i.e., ATP release within 100 nM) ranged from 8 to 10 pSμm⁻² (with 10 pSμm⁻² corresponding to 1.8 nM ATP), and the ENaC conductance for CF cells ranged from 8 to 20 pSμm⁻² (with 20 pSμm⁻² corresponding to 1.8 nM ATP). These data are consistent with the fact that the ENaC channel is strictly regulated in NL cells, but not so in CF cells (Tarran et al., 2005).

Another example is the integration of CFTR and ENaC function by ATP and ADO. In our NL model, the conductances of ENaC and CFTR were determined by the variable ${\left[L\right]}_{NL}=\left[\mathit{ATP}\right]+A_{\mathit{ADO}}\frac{\left[\mathit{ADO}\right]}{K_{\mathit{ADO}}+\left[\mathit{ADO}\right]}$, describing the ligands binding to the receptors that mediate CFTR function and ENaC inhibition. With this equation, the weight of [ADO] dominated [L]_NL only when [ATP] was at very low concentration. As [ADO] increases, its weight reached a plateau vs. ATP regulation. This relationship is indicated in Table 2, NL Data Sets, as follows. First, in Set 2, when [ATP] was at baseline, low levels (<2μM), 155 nM [ADO] was able to maintain ASL ~ 8 μm, showing [ADO] dominated in [L]_NL. Second, from Set 3 and 6, both [ATP] and [ADO] increased proportionally and ASL increased, showing [ATP] and [ADO] were equally weighted in [L]_NL. Similarly, when [ADO] was reduced to 0 in Set 9, ASL was reduced by half compared to Set 5. Third, Set 8 shows when [ADO] was extremely high, the correlative ASL was similar to Set 6, showing [ADO] reached a plateau with high doses. With reference to Set 7, with a high concentration of ATP, the resulting ASL was much higher, showing the dominance of ATP at high concentrations. Therefore, our model suggests that CFTR has a baseline inhibition on ENaC, i.e., at low [ATP], but this inhibition only reflects CFTR inhibition of ENaC up to certain levels. Namely, as [ATP] increases, the inhibition on ENaC through ATP-P2Y2-R mediated PIP₂ depletion becomes dominant.

The NL and CF model responses to mechanical forces were quite similar (Figs. 7 (a) to (c)), e.g., their ASL responses to increased [ATP] were almost identical. This notion is consistent with the data sets 4 and 5 in the CF model and the data sets 5 and 6 in the NL model. However, mechanical forces appear more important in CF than in NL for ASL regulation because the adenosine-CFTR secretory component can maintain ASL height at physiologically relevant levels at low static ATP release rates in NLs whereas ASL is pathologically low in CF in low ATP release rate (static) conditions (Tarran et al., 2005).

The contribution of an active, adenosine regulated CFTR mediated fluid secretion in normal airway epithelia provides an important buffer for ASL hydration. The importance of this buffer was revealed in our studies by the analyses of the interactions between NL vs. CF ion transport, ATP release rates, and ASL height responses to evaporative water loss (Fig. 8). At tidal ventilation (6L/min), NL airways have an increased likelihood of maintaining a physiologically-relevant ASL height at all ATP release rates compared to CF. An interesting observation was that ASL height can be dominated at high ventilation by evaporation with significant losses of ASL in both normal and CF subjects. This observation suggests that regulation of ASL volume (height) by active ion transport (ATP regulated) alone may not be sufficient to maintain airway surface hydration during exercise. Previous data have suggested that passive transepithelial water fluxes in response to evaporation induced luminal hyperconcentrated airway surface liquid may dominate this response (Willumsen, Davis, and Boucher, 1994). This evaporation-induced increase in ASL osmolality may also induce cell volume decreases which trigger increases in submucosal blood flow to restore water balance to the airway region (Matsui et al, 2000). In addition, reflex gland secretion may contribute as well. Thus, our simple models do not argue for cessation of exercise in CF (or NL) subjects.

The differences in resting ASL heights between NL and CF airway epithelia also imposed different contributions of the mucus-cilia ATP release mediated ASL auto-regulatory systems. Figure 9 shows that without vs. with cilial strain produced 30% differences in ASL height in CF, but only 8 % in NLs. This difference largely reflects the fact the NL model has tightly regulated ENaC and functioning CFTR to maintain the ion transport balance at low ATP release rates, which produces a normally concentrated mucus that yields relatively easily in response to ciliary motion. In contrast, activated ENaC and defective CFTR Cl⁻ secretion produce a more concentrated mucus that exhibits a higher yield stress in CF. Importantly, the more concentrated CF mucus yields less well in response to ciliary motion, imposes more stress on the cilia, and consequently produces higher ATP release rates. Thus, cilial strain might be an important contributor to ASL compensation in CF.

In summary, the integrated extracellular ATP metabolism/ion transport/evaporative water flux model exhibited utility with respect to simulating current experimental data exploring the roles of cilial beat and ventilation-induced evaporation in NL vs. CF ASL homeostasis. In the future, we can improve this model by adding time decay functions, adding direct regulation of ENaC and CFTR by mechanical forces, including more data to reduce noise from biological variability, and/or employing optimization algorithms to select the best fitting functions. With respect to data driven reverse engineering, this approach might also be used to add in other cell biophysical simulations relevant to airways host defense. For example, some studies suggested abnormal pH might also be a key contributor to the CF muco-obstructive phenotype (Shah et al., 2016; Tang et al., 2016). A more robust set of elements that control ASL pH, e.g., a luminal H-K ATPase, basolateral Cl⁻/HCO3⁻ and Na⁺/H⁺ exchangers, could be developed by the same method presented in this model to predict extracellular pH. Moreover, the integrated model currently developed also may potentially be applied in the study of hypertonic saline or ENaC blocker nebulization to predict therapeutic effectiveness in inducing ASL volume expansion in CF patients. Ultimately, the integrated model could be coupled with a mucus model to study the swelling and de-swelling in mucus in relationship to ASL volume (height) regulation and therapeutics. Collectively, these approaches may help optimize strategies to treat the ASL volume depletion characteristic of CF airways.

Highlights.

• An epithelial cell model for airway surface liquid(ASL) regulation was developed.

• The cell model reproduces various responses similar to in vitro epithelial cells.

• The cell model was tested with various mechanical forces and evaporative flux.

• ASL homeostasis in both normal and cystic fibrosis airway epithelia were studied.