Reversed graph embedding resolves complex single-cell trajectories

Abstract

Single-cell trajectories can unveil how gene regulation governs cell fate decisions. However, learning the structure of complex trajectories with two or more branches remains a challenging computational problem. We present Monocle 2, which uses reversed graph embedding to describe multiple fate decisions in a fully unsupervised manner. Applied to two studies of blood development, Monocle 2 revealed that mutations in key lineage transcription factors diverts cells to alternative fates.

Introduction

Most cell state transitions, whether in development, reprogramming, or disease, are characterized by cascades of gene expression changes. We recently introduced a bioinformatics technique called “pseudotemporal ordering”, which applies machine learning to single-cell transcriptome sequencing (RNA-Seq) data to order cells by progression and reconstruct their “trajectory” as they differentiate or undergo some other type of biological transition¹. Despite intense efforts to develop scalable, accurate pseudotime reconstruction algorithms (recently reviewed at²), state-of-the-art tools have several major limitations. Most pseudotime methods can only reconstruct linear trajectories, while others such as Wishbone³ or DPT⁴ support branch identification with heuristic procedures, but either are unable to identify more than one branch point in the trajectory or require that the user specify the number of branches and cell fates as an input parameter.

Here, we describe Monocle 2 (Supplementary Software and https://github.com/cole-trapnell-lab/monocle-release), which applies reversed graph embedding (RGE)^5,6, a recently developed machine learning strategy, to accurately reconstruct complex single-cell trajectories. Monocle 2 requires no a priori information about the genes that characterize the biological process, the number of cell fates or branch points in the trajectory, or the design of the experiment. Monocle 2 outperforms not only its previous version but also more recently developed methods, producing more accurate, robust trajectories.

Results

Monocle 2 begins by identifying genes that define biological process using an unsupervised procedure we term “dpFeature”. The procedure works by selecting the genes differentially expressed between clusters of cells identified with tSNE dimension reduction followed by density peak clustering. When applied to four different datasets^1,7–9 most of the genes returned by dpFeature were also recovered by a semi-supervised selection method guided by aspects of the experimental design and were highly enriched for Gene Ontology relevant to myogenesis, confirming that dpFeature is a powerful and general unsupervised feature selection approach. (Supplementary Figures 1–3)

We next sought to develop a pseudotime trajectory reconstruction algorithm that does not require the number of cell fates or branches as an input parameter. To do so, we employed reversed graph embedding^5,6, a machine learning technique to learn a parsimonious principal graph. Informally, a principal graph is like a principal curve¹⁰ that passes through the “middle” of a dataset but is allowed to have branches¹¹. However, learning a principal graph that describes a population of single-cell RNA-Seq profiles is very challenging because each expressed gene adds an additional dimension to the space. In general, learning geometry is dramatically harder in high-dimensional spaces¹². Reversed graph embedding solves this problem by finding a mapping between the high dimensional gene expression space and a much lower dimensional one while simultaneously learning the structure of the graph in this reduced space.

Monocle 2 uses DDRTree^5,6, a scalable RGE algorithm, to learn a principal tree on a population of single cells by default, asserting that it describes the sequence of changes to global gene expression levels as a cell progresses through the biological process under study (Figure 1A). In contrast to other methods^1,3,4,13, Monocle 2 identifies branch points that describe significant divergences in cellular state automatically. Monocle is also equipped with alternative RGE methods^5,6 including one that in principle can learn cyclical or disjoint trajectories, though doing so requires some degree of parameter optimization on behalf of the user.

Figure 1. Monocle 2 discovers a cryptic alternative outcome in myoblast differentiation.

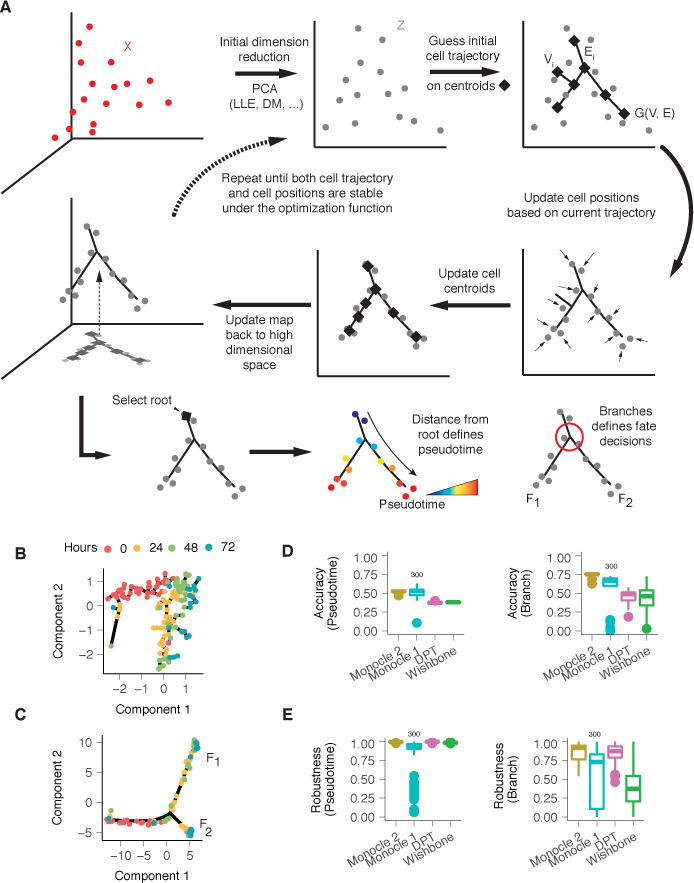
(A) Monocle 2 learns single-cell trajectories by reversed graph embedding. Each cell can be represented as a point in a high-dimensional space where each dimension corresponds to the expression level of an ordering gene. The high dimensional data are first projected to a lower dimensional space (Z) by any of several dimension reduction methods such as PCA (default), diffusion maps, etc. Monocle 2 then constructs a spanning tree on an automatically selected set of centroids of the data. The number of centroids (black diamonds) is determined using a formula that scales sublinearly in the number of cells. These centroids are chosen automatically using k-medoids clustering in the initialized low-dimensional space. The algorithm then moves the cells towards their nearest vertex of the tree, updates the positions of the vertices to “fit” the cells, learns a new spanning tree, and iteratively continues this process until the tree and the positions of the cells have converged (see Equation 3 in Methods). Throughout this process, Monocle 2 maintains an invertible map between the high-dimensional space and the low-dimensional one, thus both learning the trajectory and reducing the dimensionality of the data. In effect, the algorithm acts as soft K-means clustering on points Z that maps them to the centroids, and jointly learns a graph on the centroids. Once Monocle 2 learns the tree, the user selects a tip as the “root”. Each cell’s pseudotime is calculated as its geodesic distance along the tree to the root, and its branch is automatically assigned based on the principal graph. (B) Monocle 1 reconstructs a linear trajectory for differentiating human skeletal myoblasts (HSMM)¹. (C) Monocle 2 automatically learns the underlying trajectory and detects that cells from 24–72 hours are divided into two branches. The same genes selected with dpFeature (Supplementary Figure 1; Methods) were used for ordering for both of Monocle 1 and Monocle 2. (D) Accuracy of pseudotime calculation or branch assignments from each algorithm under repeated subsamples of 80% of the cells on the Paul dataset⁹. A marker based ordering (see Methods) is used as ground truth for results from each software in all downsamplings to compare with. (E) Consistency of pseudotime calculation or branch assignments from each algorithm under repeated subsamples of 80% of the cells on the Paul dataset⁹. All pairwise downsamplings are used to calculate the Pearson’s Rho and adjusted Rand index (ARI). Monocle 2, DPT, and Wishbone all use the full dataset for benchmark while Monocle 1 only uses a random downsampled 300 cells as for benchmarking.

To assess the Monocle 2’s accuracy, we first applied it to myoblasts, which we previously reported to differentiate along a linear trajectory¹ (Figure 1B). Surprisingly, Monocle 2 reconstructed a trajectory with a single branch point leading to two outcomes (Figure 1C). Some genes associated with mitogen withdrawal, such as CCNB2 showed similar kinetics on both branches, but a number of genes required for muscle contraction were strongly activated only on one of the two branches of the Monocle 2 trajectory (Supplementary Figure 4). A global search for genes with significant branch-dependent expression using Branch Expression Analysis Modeling (BEAM)¹⁴ revealed that cells along these two outcomes, F₁ and F₂, differed in the expression of 887 genes (FDR < 10%), including numerous components of the contractile muscle program. The BEAM analysis suggested that only outcome F₁ represented successful progression to fused myotubes (Supplementary Figure 4), consistent with immunofluorescence measurements of MYH2, which show a substantial fraction of isolated nuclei lacking MYH2 and that are not incorporated into myotubes (ref. Figures 1 and 4 of¹).

A simulation of differentiation driven by a set of stochastic differential equations controlled by a hypothetical gene regulatory network¹⁵ demonstrated that Monocle 2 robustly and accurately reconstructed trajectories with up to three fates (Supplementary Figure 5–8, Supplementary Data 1, 2)¹⁶. In contrast to other methods, Monocle 2 also accurately learned a complex tree with five branches in a fully automatic fashion (Supplementary Figure 6B, Supplementary Data 3).

We next sought to compare Monocle 2 to state-of-the art algorithms for inferring single-cell trajectories, including Monocle 1¹, Wishbone³, Diffusion Pseudotime (DPT)⁴, and SLICER¹³. Unlike Monocle 2, these methods do not construct an explicit tree. Instead they order cells based on pairwise geodesic distances between them as approximated by a nearest-neighbor graph (Wishbone and SLICER) or minimum spanning tree (Monocle 1) or calculated analytically (DPT). Wishbone, SLICER, and DPT identify branches implicitly by analyzing patterns in the pseudotime orderings that are inconsistent with a linear trajectory. Furthermore, Wishbone assumes the trajectory has exactly one branch point, while DPT can detect more than one, but provides no means of automatically determining how many genuine branches exist in the data. We hypothesized that Monocle 2’s explicit trajectory structure would yield more robust pseudotimes and branch assignments than alternative algorithms.

We tested each algorithm using data from Paul et al, who analyzed transcriptomes of several thousand differentiating blood cells⁹. Monocle 2, DPT, and Wishbone produced qualitatively similar trajectories, with CMP cells residing upstream of a branch at which GMP and erythroid cells diverge (Supplementary Figure 9–11). SLICER generated a branched trajectory in which the branch occurs within the erythroid population to bifurcate into either CMPs or GMPs. Monocle 2, Wishbone, and DPT produced orderings that were highly correlated with a “reference ordering”, constructed using a panel of markers similar to the approach introduced by Tirosh et al¹⁷, while SLICER and Monocle 1 were less so. Monocle 2 assigned cells to branches as or more accurately than other methods (Figure 1D, Supplementary Figure 10), but Monocle 2’s assignments were far more consistent when provided with subsampled fractions of the cells (Figure 1E, Supplementary Figure 9F,G). When run on the myoblast data, DPT positioned most fully differentiated cells along a major branch, with incompletely differentiated cells split along a minor branch or not assigned to either, while Wishbone failed to discriminate correctly between the two outcomes (Supplementary Figure 12). Although Monocle 2 can be tuned for several user-specified parameters, its results were similar to the defaults over widely varying values (Supplementary Figures 13–14). Monocle 2’s running time scaled linearly in the number of input cells, consistent with its linear algorithmic complexity, processing 8365 cells in 9 minutes (Supplemental Figures 13C) These benchmarks demonstrate that Monocle 2 produces trajectories that are as accurate and more robust than state-of-art methods and yet makes fewer assumptions regarding the number of cell fates generated by the trajectory.

We also assessed Monocle 2’s alternative algorithms for dimensionality reduction and graph learning. DDRTree, SimplePPT and SGL-tree, which implement RGE to learn principal trees reported highly concordant trajectories when the data was initially reduced with PCA, ICA, and diffusion maps (Supplementary Figure 15. LLE, a reduction technique known to be highly sensitive to tuning parameters, sometimes led to incorrect reconstructions with SimplePPT. L1-graph, an RGE algorithm that can learn graphs with multiple components or cycles, often reported less refined graphs with numerous minor branches, but captured the overall trajectory structure accurately.

Because Monocle 2 can in principle learn complex trajectories with many branches, we reanalyzed the data from Paul et al. in 10 dimensions (selected based on variance explained by PCs) rather than the default of two. This higher-dimensional trajectory contained five branching events leading to six different outcomes, with cells classified by Paul et al. as fully differentiated monocytes, neutrophils, eosinophil, basophils, dendritic cells, megakaryocytes, and erythrocytes confined to distinct outcomes (Supplemental Figure 16). Thus, Monocle 2 can resolve complex branching processes.

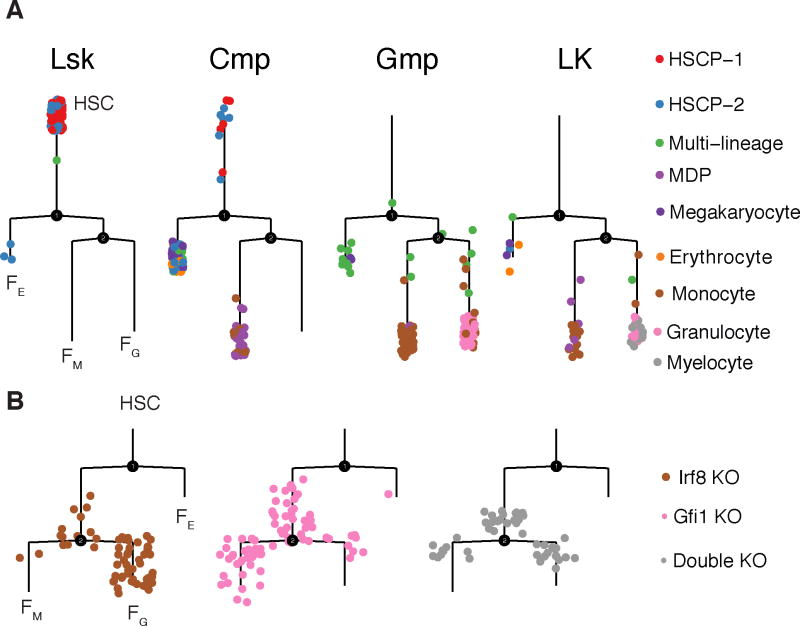
Although Monocle 2’s trajectories for differentiating myoblasts and common myeloid progenitors were broadly consistent with the known sequence of regulatory events governing those processes, we sought further experimental means of validating the structure of the algorithm’s trajectories. Recently, Olsson et al profiled several hundred FACS-sorted cells during various stages of murine myelopoeisis, i.e. LSK, CMP, GMP and LKCD34+ cells. We analyzed these cells with Monocle 2 and reconstructed a trajectory with two major branches and three distinct fates (Figure 2, Supplementary Figure 17, 18). Lin−/Sca1+/c-Kit+ (LSK) cells were concentrated at one tip of the tree, which we designated the root, with CMP, GMP, and LKCD34+ cells distributed over the remainder of the tree (Figure 2A, Supplementary Figure 17A).

Figure 2. Genetic perturbations divert cells to alternative outcomes in Monocle 2 trajectories.

(A) Monocle 2 trajectory of differentiating blood cells collected by Olsson et al⁸. Each subpanel corresponds to cells collected from a particular FACS gate in the experiment. Cells are colored according to their classification by the authors of the original study. (B) Cells with a single knockout of Irf8 or Gfi1 are diverted into the alternative granulocyte or monocyte branch, respectively. Double knockout cells are localized to both granulocyte and monocyte branches but concentrated near the branch point. Two branch points are identified, one that divides the erythroid or megakaryocyte outcome (F_E) from the granulocyte/monocyte progenitors (GMP), which then branches to the monocyte (F_M) and granulocyte (F_G) outcomes. All trajectories are reconstructed in four dimensions selected based variance explained by each PCA but rendered in two dimensions using layout_as_tree() from the igraph package.

Monocle 2 placed cells classified as erythrocytes or megakaryocytes on a path to outcome F_E, while granulocytes and monocytes by Olsson et al were confined to outcomes F_G and F_M respectively. Genes associated with the granulocytic and monocytic programs became progressively more differentially expressed following the second branch (Supplementary Figure 17B, C). Many of the genes with significantly branch-dependent expression (BEAM test¹⁴, FDR < 1%), were bound at their promoters by Irf8 or Gfi1, key activators of the monocytic and granulocytic expression programs, respectively (Supplementary Figure 17D, E).

Providing cells from mice lacking Gfi1 or Irf8 to Monocle 2 did not substantially alter the structure of the myeloid differentiation trajectory (Figure 2B). However, cells from Gfi1−/− mice were largely excluded from the branch occupied by wild-type granulocytes, and Irf8−/− cells were depleted from the wild-type monocyte branch. That is, the loss of a gene known to activate a fate-specific expression program appeared to divert cells to the opposite fate. Cells from double knockout mice (Gfi1−/− Irf8−/−) were present on both monocyte and granulocyte branches, but concentrated closer to the branch point and away from the tips of the tree, suggesting that they did not fully differentiate (Supplementary Figure 19A).

Testing whether Gfi1−/− or Irf8−/− had fully adopted the monocyte and granulocyte expression programs, revealed that Gfi1−/− cells on the branch to F_M express higher levels of genes from normally associated with granulocytes than wild-type monocytes (Supplementary Figure 19, Methods). Likewise, cells from Irf8−/− mice on the branch to F_G showed aberrantly high levels of monocytic genes. Analysis of genetic perturbations from the large-scale transcriptomic study of hematopoiesis reported by Paul et al also revealed diversions of cells onto specific branches of the trajectory, suggesting that diversion of cells from one fate to another may be a consequence of losing a key fate regulator (Supplementary Figure 19G, H).

In addition to known differentiated cell types, Olsson et al. detected cells that express a mix of genes specific to different terminal cell fates. They also reported rare, transient cell states that mix hematopoietic/multipotent markers with differentiated markers. They concluded that both types of “mixed lineage” cells reside in the developmental hierarchy downstream of long-term and short-term HSCs but upstream of cells that have committed to a lineage. Consistent with this interpretation, Monocle 2 positioned mixed-lineage cells and rare transient cells (Supplementary Figure 20) upstream of the the granulocyte-monocyte branch.

Discussion

Single-cell RNA-Seq has spurred an explosion of computational methods to infer the precise sequence of gene regulatory events that drive transitions from one cellular state to another. However, most current methods rely on strong assumptions about the structure of a biological trajectory. Many also require the user to supervise trajectory inference, inject large amounts of a priori biological knowledge, or both.

Monocle 2 learns complex cellular trajectories with multiple branches in a fully data-driven, unsupervised fashion with only limited assumptions regarding its structure. It employs a class of manifold learning algorithms that aim to embed a principal graph amongst the high-dimensional single-cell RNA-seq data. In contrast to previous methods that infer branch structure using heuristic analyses of pairwise distances between cells, Monocle 2 can use this graph to directly identify developmental fate decisions. We have demonstrated through extensive benchmarking that Monocle 2 compares favorably with other tools such as Wishbone without requiring the user to specify the structure of the trajectory.

Analysis of multiple real and synthetic datasets demonstrated that Monocle 2 reconstructs trajectories that faithfully characterize cellular differentiation. Previously, we showed that loss of interferon signaling can create a new branch in an otherwise linear trajectory that reflects the response of dendritic cells to antigen¹⁴. Here, we show that cells from mice that lack transcription factors required for establishing specific myeloid fates were diverted onto alternative fates of the same trajectory without altering its structure. Why some loss of function mutations create branches while others divert cells along existing ones is unclear, but this question underscores the increasing power of analyzing single-cell trajectories. We also anticipate that Monocle 2 will be useful not just for expression data, but for single-cell chromatin accessibility¹⁸ or 3D structure¹⁹ analysis as well. We are confident that Monocle 2 will help reveal how various layers of gene regulation coordinate developmental decision making within individual cells.

Online Methods

Reversed graph embedding

Monocle 2 uses a technique called reversed graph embedding^{5,6, 20} (RGE) to learn a graph structure that describes a single-cell experiment. RGE simultaneously learns a principal graph that represents the cell trajectory, as well as a function that maps points on the trajectory (which is embedded in low dimensions) back to the original high dimensional space. RGE aims to learn both a set of latent points $\mathcal{Z}=\{{\mathit{z}}_1,\dots ,{\mathit{z}}_N\}$ where $N$ is the number of the set (or cell numbers) and an undirected graph $\mathcal{G}$ that connects these latent points. The latent points $\mathcal{Z}$ in the low-dimensional space corresponds to the input data $\mathcal{X}=\{{\mathit{x}}_1,\dots ,{\mathit{x}}_N\}$ in the high-dimensional space. The graph $\mathcal{G}=(\mathcal{V},ℰ)$ contains a set of vertexes $\mathcal{V}=\{V_1,\dots ,V_N\}$ and a set of weighted, undirected edges $ℰ$, where each $V_i$ corresponds to latent point ${\mathit{z}}_i$, so the graph also resides in the latent, low-dimensional space.

In the context of the single-cell trajectory construction problem, ${\mathit{x}}_i$ is typically a vector of the feature genes’ expression values (for example, based on dpFeature selection, see Supplementary Notes) of the $i$th cell in a single-cell RNA-Seq experiment, $\mathcal{G}$ is the learned trajectory (for example, a tree) along which the cells transit, and ${\mathit{z}}_i$ is the principal point on $\mathcal{G}$ corresponding to the cell ${\mathit{x}}_i$.

RGE learns the graph $\mathcal{G}$ as well as a function that maps back to the input data space. Let $b_{\mathit{ij}}$ denote the weight of edge $(V_i,V_j)$, which represents the connectivity between ${\mathit{z}}_i$ and ${\mathit{z}}_j$. In other words, $b_{\mathit{ij}}>0$ means that edge $(V_i,V_j)$ exists in $\mathcal{G}$, and 0 otherwise. Define $f_{\mathcal{G}}$ as the projection function from ${\mathit{z}}_i$ to some point in the high-dimensional space. To learn $\mathcal{G}$, $\mathcal{Z}$ and $f_{\mathcal{G}}$, we need to optimize

$$\underset{\mathcal{G}\mathrm{\in }{G}_b}{\mathit{min}}\underset{f_{\mathcal{G}}\mathrm{\in }ℱ}{\mathit{min}}\underset{\mathcal{Z}}{\mathit{min}}{\displaystyle \sum }_{(V_i,V_j)\mathrm{\in }ℰ}{b}_{i,j}{\Vert f_{\mathcal{G}}({\mathit{z}}_i)-f_{\mathcal{G}}({\mathit{z}}_j)\Vert }^2$$

where ${\mathrm{G}}_{\mathrm{b}}$ is a set of feasible graph structures parameterized $\{{\mathrm{b}}_{\mathrm{i},\mathrm{j}},\mathrm{\forall }\mathrm{i},\mathrm{j}\}$, and $ℱ$ is a set of functions mapping a latent, low-dimensional point to a point in the original, high-dimensional space.

As shown in⁵, the above optimization will learn graph structures in the latent space, but it does not measure the deviations of latent points to the observed data. That is, no effort is made to ensure that the graph nodes are embedded in a way relevant to the cloud of observed data points. To ensure the graph describes the overall structure of the observed data, RGE aims to position the latent points such that their image under the function ${\mathrm{f}}_{\mathcal{G}}$ (that is, their corresponding positions in the high-dimensional space) will be close to the input data while also ensures neighbor points on low dimensional principal graph be “neighbors” in the input dimension. The optimization problem is formulated as

$$\underset{\mathcal{G}\mathrm{\in }{G}_b}{\mathit{min}}\underset{f_{\mathcal{G}}\mathrm{\in }ℱ}{\mathit{min}}\underset{\mathcal{Z}}{\mathit{min}}{\displaystyle \sum }_{i=1}^N{\Vert {\mathit{x}}_i-f_{\mathcal{G}}({\mathit{z}}_i)\Vert }^2+\frac{\lambda }{2}{\displaystyle \sum }_{(V_i,V_j)\mathrm{\in }ℰ}{b}_{i,j}{\Vert f_{\mathcal{G}}({\mathit{z}}_i)-f_{\mathcal{G}}({\mathit{z}}_j)\Vert }^2$$

where $\lambda$ is a parameter that adjusts the relative strength of these two summations. In practice, implementing reversed graph embedding requires that we place some constraints on $G_b$ and $f_{\mathcal{G}}$, as summarized briefly in the following sections.

SimplePPT: A simple principal tree algorithm

SimplePPT is the first RGE technique proposed by Mao et al for learning a tree structure to describe a set of observed data points. The tree can be learned in the original space or in some lower dimension retrieved by dimensionality reduction methods such as PCA²⁰. SimplePPT makes some choices that simplify the optimization problem. Notably, $f_{\mathcal{G}}({\mathit{z}}_i)$ is optimized as one single variable instead of two separate sets of variables. Moreover, the loss function in the reversed graph embedding is replaced by the empirical quantization error, which serves as the measurement between the $f_{\mathcal{G}}({\mathit{z}}_i)$ and its corresponding observed points ${\mathit{x}}_i$. The joint optimization of $f_{\mathcal{G}}({\mathit{z}}_i)$ is efficient from the perspective of optimization with respect to $\{b_{\mathit{ij}}\}$, which is solved by simply finding the minimum spanning tree.

The principal ${ℒ}_1$ graph algorithm

Mao et al later proposed an extension of SimplePPT that can learn arbitrary graphs, rather than just trees, which describes large datasets embedded in the same space as the input⁶. An ${ℒ}_1$ graph is a sparse graph which is based on the assumption that each data point (or cell) has a small number of neighborhoods in which the minimum number of points that span a low-dimensional affine subspace²¹ passing through that point. In addition, there may exist noise in certain elements of ${\mathit{z}}_i$ and a natural idea is to estimate the edge weights by tolerating these errors. In general, a sparse solution is more robust and facilitates the consequent identification of test sample (or sequenced single-cell samples). Unlike SimplePPT, this method learns the graph by formulating the optimization as a linear programming problem.

In the same work⁶, they also proposed a generalization of SimplePPT, which we term as SGL-tree (Principal Graph and Structure Learning for tree), to learn tree structure for large dataset by similarly considering clustering of data points as in DDRTree. Principal ${ℒ}_1$ graph and SGL-tree are all treated as SGL in this study.

DDRTree: Discriminative dimensionality reduction via learning a tree

DDRTree⁵, the default RGE technique used by Monocle 2, provides two key features not offered by SimplePPT learning framework. First, DDRTree does not assume the graph resides in the input space, and can reduce its dimensionality while learning the trajectory. Second, it also does not require that there be one node in the graph per data point, which greatly accelerates the algorithm and reduces its memory footprint.

Like SimplePPT, DDRTree learns a latent point for each cell, along with a linear projection function $f_{\mathcal{G}}({\mathit{z}}_i)={\mathit{Wz}}_i$, where $\mathit{W}=[{\mathit{w}}_1,\dots ,{\mathit{w}}_d]\mathrm{\in }{R}^{D\times d}$ is a matrix with columns that form an orthogonal basis $\{{\mathit{w}}_1,\dots ,{\mathit{w}}_d\}$ ( $D$ is the dimension of feature genes, $d$ is the dimension of latent space). DDRTree simultaneously learns a graph on a second set of latent points $\mathcal{Y}={\{{\mathit{y}}_k\}}_{k=1}^K$. These points are treated as the centroids of ${\{{\mathit{z}}_i\}}_{i=1}^N$ where $K\le N$ and the principal graph is the spanning tree of those centroids. The DDRTree scheme works by optimizing

$$\underset{\mathit{W},\mathit{B},\mathit{R},\mathcal{Y},\mathcal{Z}}{\min }{\displaystyle \sum }_{i=1}^N{\Vert {\mathit{x}}_i-{\mathit{Wz}}_i\Vert }^2+\frac{\lambda }{2}{\displaystyle \sum }_{k,k^{\prime }}{b}_{k,k^{\prime }}{\Vert {\mathit{Wy}}_k-{\mathit{Wy}}_{k^{\prime }}\Vert }^2+\gamma [{\displaystyle \sum }_{k=1}^K{\displaystyle \sum }_{i=1}^N{r}_{i,k}({\Vert {\mathit{z}}_i-{\mathit{y}}_k\Vert }^2+\sigma \log r_{i,k})]s.t.\{b_{i,j}\}\mathit{is}\mathrm{a}\mathrm{spanning}\mathrm{tree}{\mathit{W}}^T\mathit{W}=\mathit{I}$$

$${\displaystyle \sum }_{k=1}^K{r}_{i,k}=I,r_{i,k}\ge 0,\mathrm{\forall }i,k$$

In effect, the algorithm acts as soft $K$-means clustering on points $\mathcal{Z}$, and jointly learns a graph on the $K$ cluster centers. The matrix $\mathit{R}$ with the $(i,k)$th element as $r_{i,k}$ transforms the hard assignments used in $K$-means into soft assignments with $\sigma >0$ as a regularization parameter. The above problem contains a number of analytical steps, and can be solved by alternating optimization until convergence. Moreover, because some of the more expensive numerical operations involve matrices that are $K$ dimensional (instead of $N$ dimensional), they have complexity that is invariant of the size of the input data for a small fixed $K$. In Monocle 2, we provide a procedure to automatically chooses a value of $K$ that should work well for a wide range of datasets based on the number of cells $N$ in the experiment:

$$K=\{\begin{array}{c}N,\\ \frac{2\cdot 100\cdot \mathit{log}(N)}{\mathit{log}(N)+\mathit{log}(100)}\end{array}\begin{array}{c}\mathit{if}N<100,\\ \mathit{otherwise}\end{array}$$

During the first optimization iteration, these $K$ centroids are initialized by using $k$-mediods clustering in the low-dimensional space.

Pseudotime calculation and branch assignment

By default, Monocle 2 calls DDRTree to learn the principal tree describing a single cell experiment, and then projects each cell onto its nearest location on the tree. Monocle 2 allows users to conveniently select a tip of the tree as the root and then transverses the tree from the root, computing the geodesic distance of each cell to the root cell, which is taken as its pseudotime, and assign branch or segment simultaneously.

DDRTree returns a principal tree of the centroids of cell clusters in low dimension. To calculate pseudotimes, Monocle 2 projects the cell’s latent points $\mathcal{Z}$, to the principal graph formed by principal points, $\mathcal{Y}$. For latent points not near tip principal points (end nodes of the principal tree), Monocle 2 finds the nearest line segment on the principal tree and then project them to the nearest point on that segment. More formally, we can define a vector between a cell $c=(c_1,c_2,\dots )$, where $c_1,c_2,\dots$ denotes the coordinates of the cell in the latent space, to the nearest principal point $A$ by $\stackrel{\rightharpoonup }{\mathit{Ac}}$. The line segment formed by the two nearest principal points $(A=(A_1,A_2,\dots ),B=(B_1,B_2,\dots ))$ is $\stackrel{\rightharpoonup }{\mathit{AB}}$. Then we can calculate $t$ as $t=\frac{\stackrel{\rightharpoonup }{\mathit{Ac}}\cdot \stackrel{\rightharpoonup }{\mathit{AB}}}{\left|\right|\mathit{AB}\left|\right|}$. The projection can be calculated as:

$$p=\{\begin{array}{cc}A& \mathit{if}t<0\hfill \\ B& \mathit{if}t>1\hfill \\ A+t\cdot \stackrel{\rightharpoonup }{\mathit{AB}}& \mathit{if}0\le t\le 1\hfill \end{array}$$

For latent points near the tip principal points, we will orthogonally project the latent point to the line segment formed by extending the tip principal point and its nearest neighbor principal point in the graph to obtain the projection point, that is, $A+t\cdot \stackrel{\rightharpoonup }{\mathit{AB}}$.

We then calculate the distance between all the projection points and construct a minimal spanning tree (MST) on the projection points. To avoid zero values of distance between cells projected to the same principal points, which prevents the calculation of a MST, the smallest positive distance between all cell pairs is added to all distance values. This MST is used to assign pseudotime for each cell (See below).

To encode the position of each cell within the branching structure of the trajectory, Monocle 2 performs a depth-first traversal of the principal tree learned during RGE. Without loss of generality, we assume one principal point corresponds to one latent point (for example, in the case we set $\mathit{ncenter}=\mathit{NULL}$ or each cell corresponds to its own cluster). Following the definition introduced in¹, an ordering of cells (principal points) is obtained through a depth first search (DFS) of the learned principal tree starting from the root cell. We can then assign each cell to a trajectory segment, $b_x(G,\pi ,i)$ which specifies the segment $b_x$ by where the cell $i$ is located based on the ordering list, $\pi$, and the graph structure, $G$. We set $b_x=1$ at the root cell and increase a segment counter $b_x$ every time we reach a new branch point. More formally, we can write the formula of segment assignment as:

$$b_x(G,\pi ,i)=\{\begin{array}{c}1,\\ \mathit{max}(b_x(G,\pi ,j)),j\preccurlyeq i,\\ \mathit{max}(b_x(G,\pi ,j))+1,j\preccurlyeq i,\end{array}\begin{array}{c}\mathit{if}i=0\\ \begin{array}{c}\mathit{if}|E(G_j)|\le 2\\ \mathit{if}|E(G_j)|=3\end{array}\end{array}$$

where $j\preccurlyeq i$ represents all precedents $j$ of $i$ in the ordering $\pi$, $|E(G_i)|$represents the degree of cell $i$. T. For the general cases where the principal points is less than the cell numbers, cells will inherit the segment assignment of their nearest principal point.

Similar to our previous definition of pseudotime¹, Monocle 2 calculates pseudotime based on the geodesic distance of each cell to the root cells on the MST of the projection points. Define pseudotime of cell $i$ from a branching biological process $s$ with branches given by $b_x$ as ${\phi }_t(b_x,s_i)$, we can calculate its pseudotime recursively by adding the pseudotime of its parent cell on the MST of the projection points (closest cell on the same branch) with the Euclidean distance, ${\Vert \overrightarrow{p}(b_x,s_i),\overrightarrow{p}(\mathit{Parent}(b_x,s_i))\Vert }_2$, between current and the parent on the MST, by setting the root cell as pseudotime 0. That is,

$${\phi }_t(b_x,s_i)=\{\begin{array}{c}0,\\ {\phi }_t(\mathit{Parent}(b_x,s_i))+{\Vert \overrightarrow{p}(b_x,s_i),\overrightarrow{p}(\mathit{Parent}(b_x,s_i))\Vert }_2,\end{array}\begin{array}{c}\mathit{if}{b}_x=1,i=0\\ \mathit{if}i>0\end{array}$$

Assessing accuracy or robustness of pseudotime and branch assignments

We assessed the accuracy and robustness of each algorithm’s pseudotime assignment against the reference ordering by two measures of correlation (Pearson’s Rho (default) and Kendall’s Tau) between their pseudotime values.

We used adjusted Rand index (ARI)²², a common metric used for measuring clustering accuracy, to measure the accuracy or robustness of tree segment assignment. Given the number of common cells, denoted as $S$, between the reference ordering and the ordering based on an algorithm (Monocle 2, Monocle 1, DPT, Wishbone or SLICER (when available)), and corresponding trajectory segment assignments for reference ordering and ordering based on a different algorithm, $\mathcal{X}$ and $\mathcal{Y}$, namely, $\mathcal{X}=\{{\mathcal{X}}_1,{\mathcal{X}}_2,\dots ,{\mathcal{X}}_r\}$ and $\mathcal{Y}=\{{\mathcal{Y}}_1,{\mathcal{Y}}_2,\dots ,{\mathcal{Y}}_r\}$. The overlap between cells from segment $i$ ( ${\mathcal{X}}_i$) and cells from segment $j$ ( ${\mathcal{Y}}_j$) in each of the two orderings is represented by the number $n_{i,j}$ of cells in common, i.e. $n_{i,j}=\left|{\mathcal{X}}_i{\displaystyle \cap }{\mathcal{Y}}_j\right|$. Define the number of cells with segment $i$ from reference ordering is $a_i={\displaystyle \sum }_{j=1}^s{n}_{i,j}$ and the number of cells with segment $j$ from ordering based on an algorithm is $b_j={{\displaystyle \sum }}_{i=1}^r{n}_{i,j}$. The adjusted Rand Index is then formulated as

$$\mathit{ARI}(\mathcal{X},\mathcal{Y})=\frac{{{\displaystyle \sum }}_{\mathit{ij}}(\genfrac{}{}{0ex}{}{n_{\mathit{ij}}}{2})-[{{\displaystyle \sum }}_i(\genfrac{}{}{0ex}{}{a_i}{2}){{\displaystyle \sum }}_j(\genfrac{}{}{0ex}{}{b_j}{2})]/(\genfrac{}{}{0ex}{}{n}{2})}{\frac{1}{2}[{{\displaystyle \sum }}_i(\genfrac{}{}{0ex}{}{a_i}{2})+{{\displaystyle \sum }}_j(\genfrac{}{}{0ex}{}{b_j}{2})]-[{{\displaystyle \sum }}_i(\genfrac{}{}{0ex}{}{a_i}{2}){{\displaystyle \sum }}_j(\genfrac{}{}{0ex}{}{b_j}{2})]/(\genfrac{}{}{0ex}{}{n}{2})}$$

which is a measure of the similarity between two data clusterings (or segment assignment in this case). When ARI is closer to 1, the segment assignment is more consistent between the two orderings.

For calculating the accuracy of pseudotime and branch assignment of the simulation (neuron/astro-genesis) and Paul dataset, the reference ordering corresponds to the real simulation and branches assignment based on manual assessment (see Supplementary Notes) or the pseudotime and branch (or cell type suggested from the original study¹⁷) from the marker-based ordering (see next section).

For calculating the robustness, the reference ordering is defined in the context of downsampling. We apply two different downsampling strategies. First, we downsample the full dataset, including the simulation data for neuron/astro-genesis, Paul dataset and the lung dataset, selecting $80\%$ of the cells from the full dataset 25 times without replacement. Then we run Monocle 2, Monocle 1, DPT, and Wishbone to construct branched trajectory. SLICER was excluded from the downsampling analysis on account of its long running times and instability on occasional down-sample runs. Then we compare all pairs of downsamples by the metrics discussed above. We also progressively downsample all the full dataset over a range of increasing fractions of cells from the full dataset. Sampling is performed without replacement and three different subsets are generated for each proportion to serve as replicates. Then we run each software, including Monocle 1, Monocle 2, DPT, Wishbone, to construct branched trajectories for each fraction, which are compared to the corresponding trajectory built from the full dataset. ARI, Pearson’s Rho, Kendal’s Tau for all cases are then calculated as above.

In order to assess the robustness of Monocle 2 over different parameters choices, we run Monocle 2 and sample a large range for each parameter used in DDRTree, including, Dimension, lambda, maxIter, ncenter, param:gamm, sigma while keeping other parameters as default and compare the result to the ordering obtained by running Monocle 2 with all default parameters. Pearson’s Rho and ARI are used to calculate the robustness.

Comparing different algorithms to a marker-based ordering

In order to test the accuracy of each trajectory reconstruction algorithm, we compared their trajec-tories to an empirical ordering based on marker genes. Relying on results from Paul et al [8], we first select Pf4, Apoe, Flt3, Cd74 as CMP specific genes, Hba-a2, Car2, Cited4, Klf1 as MEP specific genes and Mpo, Prg2, Prtn3, Ctsg as GMP specific genes. Following the approach of Tirosh et al [9], we then select 100 other genes with expression correlated to these marker genes to calculate a stemness score and GMP or MEP lineage score. We define cells with stemness score larger than 0 as CMP cell and any cells with positive lineage score as MEP cells and negative score as GMP cells. This grouping of cells is used for branch assignment accuracy evaluation in Supplementary Figure 9. We then define the reference pseudotime for each cell as:

$${\phi }_t(b_x,s_i,l_i)=\{\begin{array}{c}d(C_i,\mathbf{0}),\\ {\mathit{Max}}_{j\mathrm{\in }\{\mathit{CMP}\}}[d(C_i,\mathbf{0})+d(C_i,\mathbf{0})],\end{array}\begin{array}{c}\mathit{if}i\mathrm{\in }\{\mathit{CMP}\}\\ \mathit{otherwise}\end{array}$$

where $\mathbf{0}$ corresponds to the origin $(0,0),$ $s_i$ corresponds to the stemness score and $l_i$ the lineage score for the lineage to which each cell is assigned, $d(\cdot ,\cdot )$represents the Euclidean distance between two points, and $\{\mathit{CMP}\}$ indicates the set of CMP cells.

Pseudotime correlations were computed on the paths from the root to each fate based on the reference ordering separately and then averaged. Since the empirical ordering based on marker genes is not perfect, we also investigate the accuracy of the ordering in terms of the absolute lag-1 autocorrelation of fitted spline curve for the selected marker genes. We first select the trajectory segments corresponding to the transition from the CMP cells to either MEP or GMP cells and then fit a kinetic curve for each marker gene for each transition with a spline curve with three degree of freedom. We then calculate the the absolute lag-1 autocorrelation r, which is defined as following:

$$r=\frac{{{\displaystyle \sum }}_{i=1}^{N-1}|(Y_i-\mu )(Y_{i+1}-\mu )|}{{{\displaystyle \sum }}_{i=1}^N{(Y_i-\mu )}^2}$$

where $Y_i$ represents the gene expression at time stamp $i,\mu$ is the mean expression across the pseudotime series for that gene. Higher autocorrelation value implies smoother gene expression dynamics based on the ordering. Those 300 cells are also used to calculate the accuracy of branch assignment with the branch assignment from the marker-based ordering.

Although a reference ordering based on markers from literature can serve as a reasonable gold-standard, it also introduces bias in a benchmarking analysis. Algorithms that order cells based on a small set of informative genes (which include or correlate the marker genes) will likely match it better than algorithms that order cells based on all genes. We therefore explored orthogonal means of measuring accuracy of each programs ordering based on the neuron simulation data (see Supplementary Notes).

Reconstruct complex haemopoiesis hierarchy

We check the scree plot to choose ten dimension as the intrinsic dimensions to reconstruct the developmental trajectory for the Paul dataset (cells used in Figure 1 of the original study⁹). Five branch points and six terminal lineages (monocytes, neutrophils or eosinophil, basophils, dendritic cells, megakaryocytes, and erythrocytes) are revealed. We ordered the cells using genes Paul et al. used to cluster their data rather than the genes from dpFeature, for the sake of consistency with their clusetering analysis. Similarly, we reconstruct Olsson datasets in four dimensions. The major bifurcation between the granulocyte and monocyte branch (GMP) as well as the intricate branch between GMP and megakaryocyte/erythrocyte (Ery/Meg) are revealed. Top 1, 000 genes from dpFeature based on WT cells are used in both of the WT and full datasets. The distribution (related to confusion matrix) of percentages of cells in each cluster from the original papers over each segment (state in Monocle 2) of the principal graph are calculated and visualized in the heatmap.

We applied BEAM analysis to identify genes significantly bifurcating between Ery/Meg and GMP branch on the Olsson wildtype dataset. We then calculate the instant log ratios (ILRs) of gene expression between Ery/Meg and GMP branch and find genes have mean ILR larger than 0.5. The ILRs are defined as:

$${\mathit{ILR}}_t=\log (\frac{Y_1^t}{Y_2^t})$$

So ${\mathrm{ILR}}_t$ is calculated as the log ratio of fitted value at interpolated pseudotime point $t$ for the Ery/Meg lineage and that for the GMP lineage. Those genes are used to calculate the lineage score (simply calculated as average expression of those genes in each cell, same as stemness score below) for both of the Olsson and the Paul dataset which is used to color the cells in a tree plot transformed from the high dimensional principal graph (see Supplementary Notes). The same genes are used to create the multi-way heatmap for both of the Paul and Olsson dataset (see plot multiple_branches_heatmap function). Critical functional genes from this procedure are identified. Car1, Car2 (important erythroid functional genes for reversible hydration of carbon dioxide) as well as Elane, Prtn3 (important proteases hydrolyze proteins within specialized neutrophil lysosomes as well as proteins of the extracellular matrix) are randomly chosen as example for creating multi-lineage kinetic curves in both of the Olsson and Paul dataset (see plot_multiple_branches_pseudotime function).

In addition, pseudotime dependent genes for the Ery/Meg and GMP branch are identified in the Olsson wildtype dataset. All genes that always have lower expression from both lineages than the average in the progenitor cells are selected. Those genes are used to calculate the stemness score for both of the Olsson and the Paul dataset which is used to color the cells in the tree plot.

Supplementary Material

1

Supplementary Data 1. Zipped file for the neuron simulation data.

2

Supplementary Data 2. Zipped file for the least action path data.

3

Supplementary Data 3. Zipped file for the complicate tree structure.