On the statistical analysis of single cell lineage trees

Highlights

Highlights

• •Statistical tool for single cell lineage tree analysis
• •Identification of stem cell-specific lineage trees
• •Statistically identified murine hematopoietic stem cells display known stem cell characteristics
• •First step towards novel accurate in-vitro hematopoietic stem cell identification

Abstract

Stem cells play a central role in the regeneration and repair of multicellular organisms. However, it remains far from trivial to reliably identify them. Despite decades of work, current techniques to isolate hematopoietic stem cells (HSCs) based on cell-surface markers only result in 50% purity, i.e. half of the sorted cells are not stem cells when functionally tested. Modern microscopy techniques allow us to follow single cells and their progeny for up to weeks in vitro, while recording the cell fates and lifetime of each individual cell. This cell tracking generates so-called lineage trees. Here, we propose statistical techniques to determine if the initial cell in a lineage tree was a HSC. We apply these techniques to murine hematopoietic lineage trees, revealing that 18% of the trees in our HSC dataset display a unique signature, and this signature is compatible with these trees having started from a true stem cell. Assuming 50% purity of HSC empirical datasets, this corresponds to a 0.35 power of the test, and the type-1-error is estimated to be 0.047. In summary, this study shows that statistical analysis of lineage trees could improve the classification of cells, which is currently done based on bio-markers only. Our statistical techniques are not limited to mammalian stem cell biology. Any type of single cell lineage trees, be it from bacteria, single cell eukaryotes, or single cells in a multicellular organism can be investigated. We expect this to contribute to a better understanding of the molecules influencing cellular dynamics at the single cell level.

Introduction

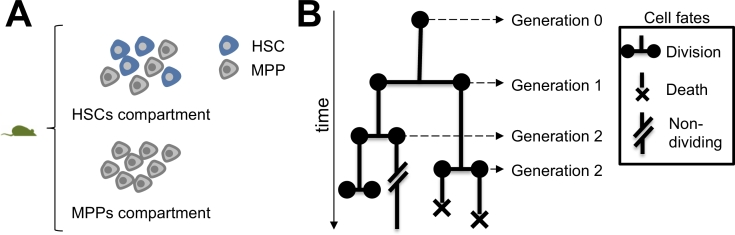
Adult stem cells have the unique ability to self-renew and differentiate into all cell types of a tissue during the organism’s lifetime to repair it in case of injury. Understanding the molecular mechanisms that govern the balance between self-renewal and/or lineage commitment is required for the advancement of stem-cell based therapeutic applications. However, the identification of the bona fide stem cells, rare cells within highly heterogeneous cell populations, remains challenging due to the lack of molecular markers for their isolation with high purity. As an example, a number of cell-surface markers have been utilized to prospectively isolate hematopoietic stem cells (HSCs) (Kiel, Yilmaz, Iwashita, Yilmaz, Terhorst, Morrison, 2005, Wilson, Laurenti, Oser, van der Wath, Blanco-Bose, Jaworski, Offner, Dunant, Eshkind, Bockamp, et al., 2008). Even though current fluorescence activated cell sorting (FACS) schemes result in a highly enriched population of HSCs, only  ∼ 50% of these cells demonstrate in vivo repopulation potential in transplantation assays, the only reliable assay to date to assess HSC potential (Kiel, Yilmaz, Iwashita, Yilmaz, Terhorst, Morrison, 2005, Kokkaliaris, Lucas, Beerman, Kent, Perié, 2016). It remains controversial whether the remaining  ∼ 50% cells in the HSCs compartment are cells that failed to engraft into recipient mice simply due to technical reasons (thus were not scored as HSCs), or whether they belonged to differentiated downstream cell populations (such as multipotent progenitors, MPPs). This controversy persists even though HSCs are among the best-studied adult stem cell systems. In contrast, purified MPP populations exclusively consist of non-stem cells (Fig. 1A). In what follows, we assume a purity of 50% in the HSC compartment, meaning we define an HSC as a cell which indeed shows in vivo repopulation potential, and thus we disregard technical issues. However, assuming a purity of higher than 50% will not affect our general conclusions, and will only decrease the power of one of our statistical tests in “Partitioning a dataset” as highlighted below.

Fig. 1.

(A) Population purity of HSCs and MPPs. While the MPPs compartment consists of non-stem cells exclusively, the HSCs compartment is heterogeneous. (B) Example of a lineage tree. At each generation, dividing mother cells give rise to two daughter cells. The lifetime of the cells is linked to the length of the branches and time axis on the left. Cells that did not divide until the end of the observation time are labelled “Non-dividing”.

While in vivo transplantations can reliably identify HSCs, they are retrospective functional assays. This means that cells with stem-cell properties can be classified as such only months after their transplantation, and thus do not allow us to directly isolate HSCs for molecular analysis. An attractive alternative is provided by single-cell time lapse imaging. Continuous long-term imaging with single-cell resolution allows to observe single cells and their progeny over many generations (Hilsenbeck, Schwarzfischer, Skylaki, Schauberger, Hoppe, Loeffler, Kokkaliaris, Hastreiter, Skylaki, Filipczyk, et al., 2016, Hoppe, Schwarzfischer, Loeffler, Kokkaliaris, Hilsenbeck, Moritz, Endele, Filipczyk, Gambardella, Ahmed, et al., 2016, Schroeder, 2011) and up to several weeks (Kokkaliaris et al., 2016a), while obtaining quantitative information about their division dynamics, phenotype and cell fate. Unlike other single-cell approaches where the cell is destroyed or its identity lost upon analysis, here the past, present and future of cells are known (Coutu, Schroeder, 2013, Schroeder, 2008, Schroeder, 2011, Skylaki, Hilsenbeck, Schroeder, 2016). Cellular pedigrees generated with this approach are represented as lineage trees, where each cell division is a branching event that generates two daughter cells, and cell death results in termination of a branch and the timing of these events is indicated via the branch lengths (Fig. 1B). In addition to the cell – lifetime dynamics, continuous single – cell imaging allows the quantification of a number of cellular characteristics ranging from cellular morphology, behavior or molecular dynamics, to name but a few, that can be linked to the branches of the lineage tree (Skylaki et al., 2016).

The aim of this paper is to provide a framework using lineage tree information to improve the identification of HSCs beyond the current purity of 50%. To enable continuous observation of HSCs and their progeny under ex vivo conditions favoring maintenance of stem-cell function, we co-cultured them with supportive stroma cells (Moore et al., 1997). By analyzing large collections of cell lineage trees we can investigate different patterns of cellular dynamics and fates and categorize cell populations with similar behaviors even when no additional molecular markers for the cells are available. The analysis of lineage trees therefore enables us to compare lineage trees within or between different cell populations, HSCs versus MPPs for example, and to obtain an estimate of impurity within a population. More specifically, in this work we develop statistical tools to analyze the tree sets obtained from HSC and MPP cell populations in order to assess:

• ST1Given two sets of lineage trees, are these sets significantly different in terms of their division dynamics and cell fate probabilities?
• ST2Given a set of lineage trees originating from cell type A (for example all cells are MPPs), and a set of lineage trees originating from an impure cell population of cell types A and B (for example  50% of cells are HSCs and  50% non-stem cells), can we determine the lineages trees characterized by cell type B?

We first show that we can determine a significant difference in division dynamics between the MPP dataset and the HSC dataset. Second, we determine a subset of cells within the HSC dataset (18%), which is significantly different from the MPP dataset and potentially represents the “true” HSC tree signature in vitro.

Methods

Three empirical datasets

We have used cell lineage trees generated by continuous long-term time-lapse imaging and single-cell tracking of murine HSCs and MPPs cultured under self-renewing condition for up to two weeks in vitro as described previously (Hilsenbeck, Schwarzfischer, Skylaki, Schauberger, Hoppe, Loeffler, Kokkaliaris, Hastreiter, Skylaki, Filipczyk, et al., 2016, Kokkaliaris, Drew, Endele, Loeffler, Hoppe, Hilsenbeck, Schauberger, Hinzen, Skylaki, Theodorou, et al., 2016). HSCs were isolated using FACS analysis and an established combination of markers (CD150+CD34-CD48-KSL) (Wilson et al., 2008). MPPs were divided in more primitive, early MPPs (CD150+ CD48- CD34+ KSL) and more differentiated late MPPs (CD150-CD48+CD34+ KSL). We have considered in total 292 HSCs lineage trees, 272 early-MPP lineage trees and 211 late-MPP lineage trees. The multipotent HSCs are found at the top of the hematopoietic hierarchy and when differentiating they give rise to the early and late MPPs, which have lost self-renewing capacity but they retain full lineage potential (Wilson et al., 2008).

Modelling the empirical data

A dataset consists of N lineage trees tracked for a given number of generations, here 3. This means that we track the lifetime of each cell in generation 0, 1 and 2 including its fate such as division or apoptosis. In maximum, we have trees with 4 cells in generation 2, each dividing at the end, so we know that the tree had 8 cells after termination of the third generation. In our datasets, we have N in the range 200–300.

We assume the following model for the growth of a lineage tree. Each new cell can have one of four different fates,

• 1.Division, leading to a new generation, which has probability p_D. The time from cell birth to division is assumed to be normally distributed with mean time μ_D and standard deviation σ_D.
• 2.Apoptosis which has probability p_A. The time from cell birth to apoptosis (cell death) is assumed to be normally distributed with mean time μ_A and standard deviation σ_A.
• 3.Non-dividing or slow-dividing cell, meaning the cell did not divide or die until the end of the observation period of up to two weeks, which has probability p_N.
• 4.Lost cells, meaning the cell could not be tracked any more, which we treat in the following way. We assume that a lost cell duplicated with probability p_D, underwent apoptosis with probability p_A, and was a non-dividing cell with probability p_N, with $p_D+p_A+p_N=1$.

We aim to estimate the 6 parameters $\theta =(p_D,{\mu }_D,{\sigma }_D,p_A,{\mu }_A,{\sigma }_A),$ and obtain $p_N=1-p_D-p_A$. In a given dataset with N trees, suppose we have n_D cells which eventually divide, n_A cells with apoptosis fate, n_N cells which are non-dividers, and n_L cells which become lost. The n_D cells divide after time $D_1,D_2,\dots ,D_{n_D}$. The n_A cells encounter apoptosis after time $A_1,A_2,\dots ,A_{n_A}$. The likelihood function, i.e. the probability of the data $\mathcal{D},$ given the parameters, is,

$$Lik\left(\theta \right|\mathcal{D})=p_D^{n_D}{p}_A^{n_A}{p}_N^{n_N}\prod _{i=1}^{n_D}\mathcal{N}(D_i,{\mu }_D,{\sigma }_D)\prod _{i=1}^{n_A}\mathcal{N}(A_i,{\mu }_A,{\sigma }_A)$$

with $\mathcal{N}(x,\mu ,\sigma )=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{(x-\mu )}^2}{2{\sigma }^2}}$ being the probability density of a normal distribution. The maximum likelihood parameter estimates for this likelihood function are,

$$\begin{array}{ccc}\hfill {\widehat{p}}_D& =& \frac{n_D}{n_D+n_A+n_N},\hfill \\ \hfill {\widehat{p}}_A& =& \frac{n_A}{n_D+n_A+n_N},\hfill \\ \hfill {\widehat{\mu }}_D& =& \frac{1}{n_D}\sum _{i=1}^{n_D}{D}_i,\hfill \\ \hfill {\widehat{\sigma }}_D& =& \sqrt{\frac{{\sum }_{i=1}^{n_D}{(D_i-{\widehat{\mu }}_D)}^2}{n_D}},\hfill \\ \hfill {\widehat{\mu }}_A& =& \frac{1}{n_A}\sum _{i=1}^{n_A}{A}_i,\hfill \\ \hfill {\widehat{\sigma }}_A& =& \sqrt{\frac{{\sum }_{i=1}^{n_A}{(A_i-{\widehat{\mu }}_A)}^2}{n_A}}.\hfill \end{array}$$

These equations are used to obtain all maximum likelihood estimates presented below.

ST1: Testing for difference between two datasets

We will use the maximum likelihood estimation method to test whether two given sets of trees, ${\mathcal{D}}_1$ and ${\mathcal{D}}_0,$ are significantly different. We will estimate the maximum likelihood parameters for ${\mathcal{D}}_1,$ denoted by ${\widehat{\theta }}_1,$ and the maximum likelihood parameters for ${\mathcal{D}}_0,$ denoted by ${\widehat{\theta }}_0$. We say that ${\mathcal{D}}_1$ is significantly different from ${\mathcal{D}}_0,$ if parameter ${\widehat{\theta }}_0$ is rejected in favor of parameter ${\widehat{\theta }}_1$ having generated ${\mathcal{D}}_1$.

Likelihood ratios

To test if we can reject ${\widehat{\theta }}_0$ (the null hypothesis) for dataset ${\mathcal{D}}_1$ in favor of its maximum likelihood estimate (the alternative hypothesis), we calculate the logarithm of the likelihood ratios,

$$\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0)=2(\log \left(Lik\right({\widehat{\theta }}_1\left|{\mathcal{D}}_1\right))-\log \left(Lik\right({\widehat{\theta }}_0\left|{\mathcal{D}}_1\right))).$$

The bigger $\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0),$ the more support we have for the maximum likelihood estimate ${\widehat{\theta }}_1$ providing a significantly better explanation for the data ${\mathcal{D}}_1$ compared to ${\widehat{\theta }}_0$. But how big does $\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0)$ have to be to reject ${\widehat{\theta }}_0$?

Given ${\mathcal{D}}_1$ was actually produced by parameters ${\widehat{\theta }}_0$ and its sample size is big enough, then $\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0)$ is χ² distributed with 6 degrees of freedom (i.e. the number of parameters), according to basic likelihood statistics (Wilks, 1938). It turns out that our sample sizes, meaning the number of trees in a dataset (here 200–300), is too small for the χ² distribution to be approached. For example, when randomly subdividing a dataset into two equally big datasets and again denoting these two datasets with ${\mathcal{D}}_1$ and ${\mathcal{D}}_0,$ then $\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0)$ is typically bigger than the 99th percentile of the χ² distribution. However, it would only be bigger in 1% of cases if $\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0)$ followed the χ² distribution.

Thus we need to determine the unknown distribution, $\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0),$ under the null hypothesis of ${\mathcal{D}}_1$ being generated by ${\widehat{\theta }}_0$. Further, we aim to determine $\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0),$ under the alternative hypothesis of ${\mathcal{D}}_1$ being generated by ${\widehat{\theta }}_1$. Together, this allows us to formulate a statistical test, based on calculating $\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0),$ in order to accept or reject ${\widehat{\theta }}_0$ for dataset ${\mathcal{D}}_1,$ with providing the type-1-error and power (i.e. (1- (type-2-error))) of this statistical test. The type-1-error is the probability of rejecting a parameter set ${\widehat{\theta }}_0$ for the generation of a dataset, when the dataset was in fact generated by ${\widehat{\theta }}_0$. The power is the probability to reject the parameter set ${\widehat{\theta }}_0$ in favor of parameter set ${\widehat{\theta }}_1,$ with parameter set ${\widehat{\theta }}_1$ indeed having generated the dataset. In all scenarios below, we approximate the unknown distributions Λ with 100 bootstrap treesets. We conclude from a rejection of ${\widehat{\theta }}_0$ that dataset ${\mathcal{D}}_1$ is significantly different from ${\mathcal{D}}_0$.

Bootstrapping to determine Λ

We use the concept of bootstrapping (Efron, 1979) to determine the distribution of Λ. For dataset ${\mathcal{D}}_k$ (k ∈ {0, 1}), we generate twice 100 bootstrap datasets (${\mathcal{D}}_{k_1,BS}^1,{\mathcal{D}}_{k_1,BS}^2,\dots ,{\mathcal{D}}_{k_1,BS}^{100},$ and ${\mathcal{D}}_{k_2,BS}^1,{\mathcal{D}}_{k_2,BS}^2,\dots ,{\mathcal{D}}_{k_2,BS}^{100}$), each with 250 trees (250 is a proxy for the number of trees in our empirical datasets). The 250 trees in each bootstrap dataset are sampled with replacement from the trees in the empirical dataset ${\mathcal{D}}_k$. Thus we have 400 bootstrap datasets, each with 250 trees.

Now for each of the 400 bootstrap datasets, we determine its maximum likelihood parameter estimates, ${\widehat{\theta }}_{1_1,BS}^i,{\widehat{\theta }}_{1_2,BS}^i,{\widehat{\theta }}_{0_1,BS}^i,{\widehat{\theta }}_{0_2,BS}^i$ ($i\in \{1,2,\dots ,100\}$). Then we calculate for $i\in \{1,2,\dots ,100\},$

$$\begin{array}{ccc}& & \Lambda ({\mathcal{D}}_{0_1,BS}^i,{\widehat{\theta }}_{0_1,BS}^i,{\widehat{\theta }}_{0_2,BS}^i)=2(\log \left(Lik\left({\widehat{\theta }}_{0_1,BS}^i\right|{\mathcal{D}}_{0_1,BS}^i)\right)\hfill \\ & & -\log \left(Lik\left({\widehat{\theta }}_{0_2,BS}^i\right|{\mathcal{D}}_{0_1,BS}^i)\right)),\hfill \\ & & \Lambda ({\mathcal{D}}_{1_1,BS}^i,{\widehat{\theta }}_{1_1,BS}^i,{\widehat{\theta }}_{1_2,BS}^i)=2(\log \left(Lik\left({\widehat{\theta }}_{1_1,BS}^i\right|{\mathcal{D}}_{1_1,BS}^i)\right)\hfill \\ & & -\log \left(Lik\left({\widehat{\theta }}_{1_2,BS}^i\right|{\mathcal{D}}_{1_1,BS}^i)\right)).\hfill \end{array}$$

These two bootstrap distributions, $\Lambda ({\mathcal{D}}_{0_1,BS},{\widehat{\theta }}_{0_1,BS},{\widehat{\theta }}_{0_2,BS})$ and $\Lambda ({\mathcal{D}}_{1_1,BS},{\widehat{\theta }}_{1_1,BS},{\widehat{\theta }}_{1_2,BS}),$ each represented by 100 samples (as $i=1,\dots ,100$), tell us how large we expect Λ to be under the null hypothesis. Based on this bootstrap distribution for Λ, we define a statistical test as follows.

Statistical test

For dataset ${\mathcal{D}}_1$ we reject the parameters ${\widehat{\theta }}_0$ (null hypothesis) in favor of the maximum likelihood estimate ${\widehat{\theta }}_1$ if $\Lambda ({\mathcal{D}}_1,{\widehat{\theta }}_1,{\widehat{\theta }}_0)$ is bigger than the 99th percentile of the bootstrap $\Lambda ({\mathcal{D}}_{0_1,BS},{\widehat{\theta }}_{0_1,BS},{\widehat{\theta }}_{0_2,BS})$ distribution, i.e. bigger than the second largest value of $\Lambda ({\mathcal{D}}_{0_1,BS}^i,{\widehat{\theta }}_{0_1,BS}^i,{\widehat{\theta }}_{0_2,BS}^i),$ $i=1,2,\dots ,100$.

Thus we reject wrongly with a 1% chance, meaning our type-1-error is 0.01. We further determine the power of the test (i.e. (1-(type-2-error))), i.e. how often we correctly reject the null hypothesis if the data was generated under the alternative hypothesis. For the power, we calculate,

$$\begin{array}{ccc}& & \Lambda ({\mathcal{D}}_{0_1,BS}^i,{\widehat{\theta }}_{0_1,BS}^i,{\widehat{\theta }}_{1_1,BS}^i)=2(\log \left(Lik\left({\widehat{\theta }}_{0_1,BS}^i\right|{\mathcal{D}}_{0_1,BS}^i)\right)\hfill \\ & & -\log \left(Lik\left({\widehat{\theta }}_{1_1,BS}^i\right|{\mathcal{D}}_{0_1,BS}^i)\right)),\hfill \\ & & \Lambda ({\mathcal{D}}_{1_1,BS}^i,{\widehat{\theta }}_{1_1,BS}^i,{\widehat{\theta }}_{0_1,BS}^i)=2(\log \left(Lik\left({\widehat{\theta }}_{1_1,BS}^i\right|{\mathcal{D}}_{1_1,BS}^i)\right)\hfill \\ & & -\log \left(Lik\left({\widehat{\theta }}_{0_1,BS}^i\right|{\mathcal{D}}_{1_1,BS}^i)\right)).\hfill \end{array}$$

The power of the test can be determined by counting how many samples $\Lambda ({\mathcal{D}}_{0_1,BS}^i,{\widehat{\theta }}_{0_1,BS}^i,{\widehat{\theta }}_{1_1,BS}^i)$ are bigger than the 99th percentile of $\Lambda ({\mathcal{D}}_{1_1,BS},{\widehat{\theta }}_{1_1,BS},{\widehat{\theta }}_{1_2,BS})$ (and analog, how many samples $\Lambda ({\mathcal{D}}_{1_1,BS}^i,{\widehat{\theta }}_{1_1,BS}^i,{\widehat{\theta }}_{0_1,BS}^i)$ are bigger than the 99th percentile of $\Lambda ({\mathcal{D}}_{0_1,BS},{\widehat{\theta }}_{0_1,BS},{\widehat{\theta }}_{0_2,BS})$).

Parameteric bootstrapping to determine Λ

As an alternative approach, we also performed parameteric bootstrapping to determine the distribution of Λ. This means that instead of (non-parametric) bootstrapping, meaning we sample 250 trees with replacement from the empirical dataset to obtain a bootstrap dataset, we now simulate 250 trees using the maximum likelihood parameters obtained from the empirical dataset. We call these datasets the simulated datasets. We then proceed as above to determine the error and power of the statistical test, notating the simulated datasets with Sim rather than BS.

ST2: Partitioning a dataset

Partitioning the HSC dataset

The markers for detecting HSC cells are only 50% accurate, meaning the HSC dataset consists of 50% HSCtrue trees, and 50% EarlyMPP trees. We want to use our statistical model to determine HSCtrue trees from the HSC dataset. For each tree T_HSC in the HSC dataset, we calculate

$$\Lambda (T_{\mathit{HSC}},{\widehat{\theta }}_{\mathit{HSC}},{\widehat{\theta }}_{\mathit{EarlyMPP}}).$$

Now, a Λ > 0 means that the HSC parameters are preferred, while a Λ < 0 means that the EarlyMPP parameters are preferred. We reject the null model of ${\widehat{\theta }}_{\mathit{EarlyMPP}}$ in favor or ${\widehat{\theta }}_{\mathit{HSC}}$ for $\Lambda (T_{\mathit{HSC}},{\widehat{\theta }}_{\mathit{HSC}},{\widehat{\theta }}_{\mathit{EarlyMPP}})>4.$ The trees rejecting the null model are denoted by HSCtrue, and the trees not rejecting the null model are denoted by HSCfalse. We obtain the maximum likelihood parameter estimates for these two sets, ${\widehat{\theta }}_{\mathit{HSCtrue}}$ and ${\widehat{\theta }}_{\mathit{HSCfalse}}$. The type-1-error of this test is obtained by determining the fraction of EarlyMPP trees T_EarlyMPP rejecting the null hypothesis ${\widehat{\theta }}_{\mathit{EarlyMPP}}$.

Given we are confident that 50% of the HSC trees are indeed HSCtrue, then we can work out the power of the test. We first determine the number of HSC trees rejecting the null hypothesis ${\widehat{\theta }}_{\mathit{EarlyMPP}}$ and multiply this number by (1- (type-1-error)). Then we divide by half the number of HSC trees (as we only expect half of the trees in the HSC dataset to be actual HSC trees).

Partitioning a simulated dataset

In order to explore if we can correctly partition a dataset, we simulated 250 trees using the maximum likelihood parameter estimates from the EarlyMPP trees (${\widehat{\theta }}_{\mathit{EarlyMPP}}$). Then we simulated a mixed dataset with 250 trees, of which 125 trees were simulated with the maximum likelihood parameter estimates from the EarlyMPP trees (${\widehat{\theta }}_{\mathit{EarlyMPP}}$), and 125 trees were simulated with the maximum likelihood parameter estimates from the HSCtrue trees (${\widehat{\theta }}_{\mathit{HSCtrue}}$). Then we used the approach described in the previous section to partition the two simulated datasets. We repeated this procedure 100 times.

Results

Testing for difference between HSC, EarlyMPP and LateMPP datasets

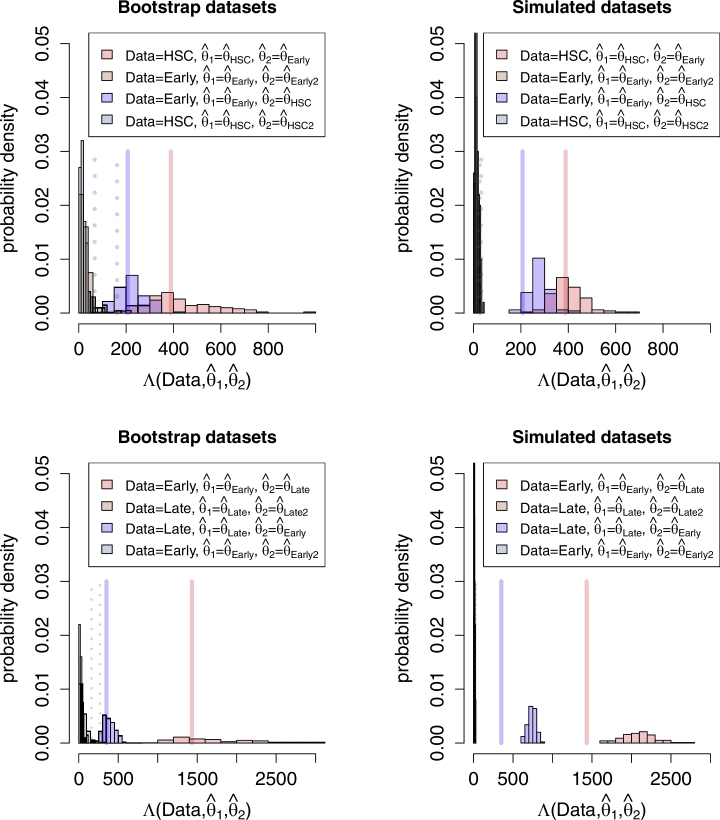
Fig. 2 shows the bootstrap and simulated log likelihood difference distributions Λ when comparing HSC to EarlyMPP, and comparing EarlyMPP to LateMPP. The solid lines show the log likelihood difference for the two empirical datasets, and the dashed lines show the 99th percentile of the bootstrap distribution. Since the empirical log likelihood differences are bigger than the 99th percentile (i.e. right of the dashed line), we conclude that the HSC is significantly different from the EarlyMPP dataset, and the EarlyMPP is significantly different from the LateMPP dataset.

Fig. 2.

Value of Λ for the empirical data (solid line) together with the bootstrap distributions (left panels) and simulated distributions (right panels). Dotted lines are .99 percentiles of the distributions.

We obtain a power of .99 and higher (i.e. we do not wrongly accept a false parameter or only accept it once) both when comparing HSC to EarlyMPP and EarlyMPP to LateMPP, using either the bootstrap or simulated distributions. In other words, given the two sets of empirical trees were generated under our statistical model with the parameters HSC and EarlyMPP (or if we were to generate simulated trees under these parameter combinations), we are able to distinguish the two sets of trees with a type-1-error of .01 and a power of  ≥ .99.

The parameter maximum likelihood estimates are provided in Table 1, row HSC, EarlyMPP, and LateMPP .

Table 1.

Parameter estimates for the three datasets HSC, EarlyMPP, and LateMPP, as well as the partitioned dataset HSC into HSCtrue and HSCfalse.

	pD	pA	pN	mD	σD	mA	σA
HSCtrue	0.67	0.13	0.20	3.62	2.28	3.30	3.07
HSC	0.71	0.20	0.09	2.31	1.54	2.00	2.09
HSCfalse	0.73	0.21	0.06	2.00	1.08	1.80	1.81
EarlyMPP	0.68	0.29	0.04	1.96	1.18	1.51	1.80
LateMPP	0.39	0.61	0.00	1.35	1.12	0.50	1.13

Partitioning a dataset

Partitioning the HSC dataset

We now determine the trees from the HSC dataset that are significantly different from the EarlyMPP dataset. The set of trees being different is called HSCtrue, the remaining trees from HSC are called HSCfalse. For each tree, we test if parameters ${\widehat{\theta }}_{\mathit{EarlyMPP}}$ are rejected in favor of the alternative hypothesis ${\widehat{\theta }}_{\mathit{HSC}}$. Fig. 3 summarizes these results, stratified for different tree size.

Fig. 3.

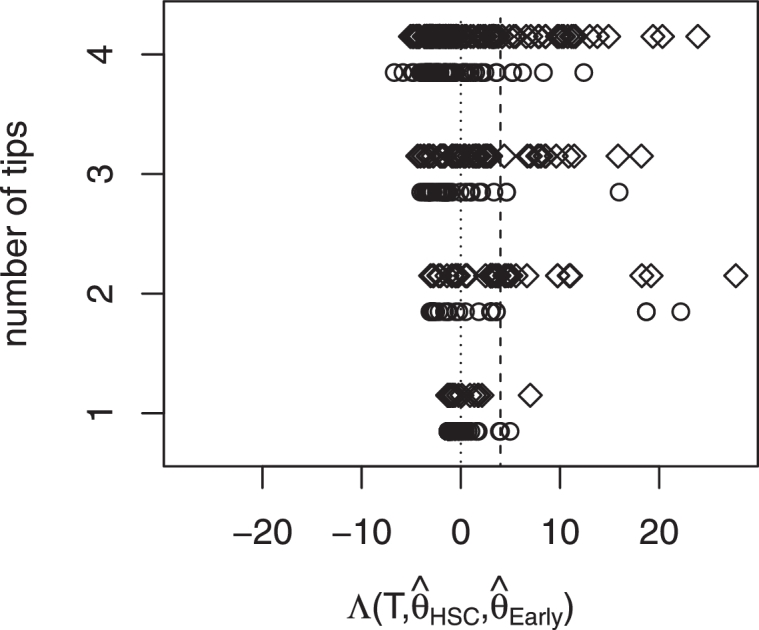
Each circle represents a tree T_EarlyMPP from EarlyMPP, each diamond represents a tree T_HSC from HSC. The x-axis displays $\Lambda (T,{\widehat{\theta }}_{\mathit{HSC}},{\widehat{\theta }}_{\mathit{EarlyMPP}}),$ seperated by the size of the tree via the y-axis. To the right of the dotted line are trees for which ${\widehat{\theta }}_{\mathit{HSC}}$ fits better than ${\widehat{\theta }}_{\mathit{EarlyMPP}},$ to the right of the dashed line are trees for which ${\widehat{\theta }}_{\mathit{HSC}}$ fits significantly better than ${\widehat{\theta }}_{\mathit{EarlyMPP}}$.

The type-1-error is determined by applying the test for the EarlyMPP trees. For the EarlyMPP trees, ${\widehat{\theta }}_{\mathit{EarlyMPP}}$ is wrongly rejected in 4.7% of the trees, meaning the type-1-error is .047. The test rejects ${\widehat{\theta }}_{\mathit{EarlyMPP}}$ in favor of ${\widehat{\theta }}_{\mathit{HSC}}$ for 18.2% of the trees. This means out of the 292 HSC trees, we have support for 53 actually being HSC trees. With an error of 4.7%, we expect 2.5 trees to incorrectly support HSC. The power of the test is .35, given 50% of the HSC trees are indeed HSC trees. The power of the test is lower if more than 50% of the HSC trees are indeed HSC trees, meaning if some in vivo-tested cells failed to engraft into recipient mice due to technical reasons but were indeed an HSC.

For the dataset HSCtrue and HSCfalse, we further determined the maximum likelihood parameter estimates for θ. Table 1 summarizes the parameter estimates for the different datasets.

Partitioning the simulated datasets

In the mixed simulated datasets, the median number of trees rejecting the null model was 17 with 95% interval [3,33]. From these 17 trees, we falsely rejected 1 tree [0,3]. Thus the power of the test is $16/125=0.128$. In the EarlyMPP simulated datasets, the median number of falesely rejected trees was 1 [0,4]. Thus the type-1-error is 1/250=0.004.

Discussion

We introduced a statistical test to determine if two sets of lineage trees are significantly different (ST1). Given they are different, we can further test which trees are in fact the ones being different within each set (ST2). These tests were applied to three sets of lineage trees from murine blood cells, cells which were potentially still stem cells (HSC), or more differentiated progenitors, EarlyMPP and LateMPP. These datasets were found to be significantly different. In particular the type-1-error, i.e. the probability of claiming statistical difference when they are identical, is 0.01. The power of the test, i.e. the probability of claiming difference in the datasets where difference is given, is  ≥ .99.

The HSC set is assumed to be a mix of trees representing the “true” HSC tree signature and non-stem cell trees which cannot be prospectively purified more accurately with available molecular markers, due to insufficient HSC-specific cell-surface markers and/or technical challenges (isolation impurities, stringent HSC criteria). Our statistical test suggests that 53 trees (18% of the trees) from the HSC set are significantly different from the differentiated non-stem trees and potentially “true” stem cell trees. Based on our simulations, we incorrectly claim that a tree is an HSC tree when it really is an MPP tree with probability 0.004 (type-1-error). However, we fail to detect many HSC trees within the HSC compartment, we only classify 12.8% of the HSC trees within the HSC compartment to be HSC trees, meaning the power is only .128.

It needs to be confirmed that these 53 trees are indeed HSC trees. This is tedious work for the experimentalist, implementing time-lapse imaging and single-cell tracking approaches followed by in vivo transplantations of colonies in primary and secondary recipient mice for 8 and 4 months, respectively. However, the parameter estimates for our datasets support the plausibility of these 53 trees being stem cell trees. In Table 1, from top to bottom, the probability of apoptosis increases, the mean time to division decreases, and the mean time to apoptosis decreases. These patterns are expected with increasing levels of specialization, meaning the HSCtrue set should be the least specialized cell set, arguably the true HSC compartment. Furthermore, in our simulation framework, we could detect the HSCtrue trees. Note that in the simulations, the power to detect HSCtrue trees as well as the type-1-error was lower compared to the empirical data.

The statistical tests proposed here are a major step towards detailed statistical analysis of lineage trees. They open the door for a number of future challenges. When we test if single trees from HSC belong to EarlyMPP, we do not explicitly acknowledge that HSC is produced by two processes (HSC and MPP lineage trees) but pretend that a process with parameters ${\widehat{\theta }}_{\mathit{HSC}}$ produced all 292 trees. Acknowledging that ${\widehat{\theta }}_{\mathit{EarlyMPP}}$ and the unknown parameter ${\widehat{\theta }}_{\mathit{HSCtrue}}$ produced the dataset may increase the power of the statistical test. The lifetime of cells is approximated by a normal distribution for statistical convenience. For understanding the cell lifetime and its variation in a more mechanistic way, age-dependent distributions such as the Weibull distribution will be appropriate. Furthermore, as outlined in the introduction, we know from in vivo assays that on average at least 50% of the HSC trees are indeed from HSC cells. Using Bayesian methods rather than the maximum likelihood framework here might allow us to use such information as a prior and also improve the power.

In this paper, we only use lifetime and fate of single cells as input data for our statistical tests. Using additional data such as continuous quantification of live reporter expression for the different cells may improve the power of our statistical tests. Furthermore, such data will allow us to investigate what factors determine gene expression levels. The potential of lineage trees towards understanding developmental biology processes has already been suggested in Mooers and Heard (1997). More than two decades later, with the increasing number of lineage trees obtained from empirical data, it is finally time to bring the appropriate statistical tools to the data. Sophisticated statistical analyses require care because of the non-independence of different cells due to shared ancestry. The field of phylogenetics may have appropriate tools to be adapted to lineage trees, meaning tools developed for macro-evolutionary processes happening over million of years may help us to understand microscopic processes on the level of cells.

Data availability

All analyzed datasets as well as the R code for processing this data and re-producing our results is available on xxx (so far submitted as “Data in Brief” along with this manuscript).