A TEST OF THE ADDITIVITY OF ACUTE TOXICITY OF BINARY-METAL MIXTURES OF NI WITH CD, CU, AND ZN TO DAPHNIA MAGNA, USING THE INFLECTION POINT OF THE CONCENTRATION–RESPONSE CURVES

Abstract

Mixtures of metals are often present in surface waters, leading to toxicity that is difficult to predict. To provide data for development of multimetal toxicity models, Daphnia magna neonates were exposed to individual metals (Cd, Cu, Ni, Zn) and to binary combinations of those metals in standard 48-h lethality tests conducted in US Environmental Protection Agency moderately hard reconstituted water with 3 mg dissolved organic carbon (DOC)/L added as Suwannee River fulvic acid. Toxicity tests were performed with mixtures of Ni and 1) Cd, which is considerably more toxic than Ni; 2) Cu, which is less toxic than Cd but more toxic than Ni; and 3) Zn, which has a toxicity threshold similar to Ni. For each combination of metals in the binary mixtures, the concentration of 1 metal was held constant while the second metal was varied through a series that ranged from nonlethal to lethal concentrations; then the roles of the metals were reversed. Inflection points of the concentration–response curves were compared to test for additivity of toxicity. Sublethal concentrations of Ni caused less-than-additive toxicity with Cd, slightly less-than-additive toxicity with Zn, and greater-than-additive toxicity with Cu. One explanation of these results might be competition among the metals for binding to biological ligands and/or dissolved organic matter. Therefore, models might have to incorporate sometimes competing chemical interactions to accurately predict metal-mixture toxicity.

INTRODUCTION

Surface waters can be contaminated by metals through a variety of pathways including point sources such as discharges from industries and municipal wastewater treatment plants, and nonpoint sources such as storm-water runoff, agricultural runoff, and mineral weathering [1]. Because of the variety of anthropogenic sources and the natural occurrence of combinations of metals in ore bodies, metals are rarely present alone in natural systems. Instead, metals usually occur as mixtures in soils, ground waters, and surface waters. However, metals usually are regulated on an individual basis instead of as mixtures, in part because current understanding does not allow accurate prediction of the toxicity of metal mixtures to aquatic organisms [2]. Therefore, to help develop more comprehensive approaches to water quality regulations, it is important to have a better understanding of metal-mixture toxicity that can lead to improved predictive models.

Numerous studies have demonstrated a relationship between water chemistry (e.g., pH, alkalinity, hardness, dissolved organic carbon [DOC] concentration) and the toxicity of metals to aquatic organisms [3,4]. In general, those water chemistry parameters can protect against metal toxicity either by complexing with the metals to form less bioavailable forms (e.g., as with HCO₃⁻, CO₃²⁻, and DOC) or by competing with the metals for binding at sites of toxic action on or in organisms (e.g., as with H⁺, Ca²⁺, and Mg²⁺) [5,6]. However, it is not currently well understood how the interactions of multiple metals with those water chemistry parameters and with aquatic organisms affect the toxicity of metal mixtures [2]. For example, metal–metal competition for binding to dissolved ligands such as DOC might increase the concentration of the free metal ion of 1 or more metals in the exposure water, thus potentially leading to more toxicity than would be expected. Metal–metal competition for binding at sites of toxic action might decrease the accumulation of 1 or more metals at those sites, thus potentially leading to less toxicity than would be expected [2]. Therefore, metal–mixture toxicity to a given organism might be less-than-additive (i.e., less than expected from a simple combination of the effects of the individual-metal exposures [2]), additive (i.e., as expected), or more-than-additive (i.e., more than expected), depending on the metals in the mixture. Meyer et al. [7] demonstrated examples of each of those possible situations with Daphnia magna exposed to binary mixtures of Cd, Cu, and Zn.

Bioavailability models such as the Biotic Ligand Model (BLM) [8] and the Windermere Humic Aqueous Model-Toxicity Function (WHAM-F_TOX) [9] are being developed to predict the effects of metal mixtures on aquatic organisms in a variety of water chemistry conditions, based on metal accumulation on a target tissue (i.e., the biotic ligand in the BLM) or a chemical surrogate (i.e., WHAM humic acid in WHAM-F_TOX) [10]. Both models assume that the aquo (free metal) ion is bioavailable and capable of causing toxic effects to an organism, but that it must compete with other cations (including the other metals in the mixture) to accumulate at sites of toxic action and potentially result in toxicity. However, only a small number of studies that have adequate water chemistry and toxicity data are currently available to parameterize such models [11–13].

Two general approaches are used to predict mixture toxicity from the toxicity of the individual components of the mixture: concentration additivity and response additivity [2]. Concentration addition is generally assumed to be appropriate when the chemicals have the same mechanism of toxic action (e.g., Cd and Zn impair Ca homeostasis [14]). Response addition is generally assumed to be appropriate when the chemicals have different mechanisms of action (e.g., impairment of Na homeostasis by Ag or Cu [14] vs impairment of Ca homeostasis by Cd and Zn). In the present study, response addition was chosen to evaluate the toxicity of the metal mixtures, because the exact mechanism of toxic action of 1 of the metals (Ni) that was included in each tested binary mixture is not known [14].

In response addition (also referred to as independent action [2]), 1 substance in a mixture does not change the determined outcome of another substance in the system [15], because the toxicants in a chemical mixture are assumed to act independently at different sites of toxicity [16]. As a result, substances in a mixture produce an effect that is the joint but independent probability of their individual effects. However, recent studies have shown that the toxicity of metal mixtures sometimes deviates from response-additive predictions [7]. Aqueous metal speciation, metal–metal competition for binding to dissolved ligands, and metal interactions within an organism can complicate this system to an extent that metal-mixture toxicity cannot be accurately explained using either a concentration-addition or a response-addition assumption if dissolved-metal concentrations are used as the predictor of toxicity [2]. This is important because the toxicity of more-than-additive metal mixtures will be underpredicted, thus potentially causing unanticipated ecological effects, whereas less-than-additive metal mixtures may be of concern to industrial and municipal dischargers because overpredicted toxicity may lead to overly restrictive and cost-ineffective regulation. Better understanding of metal-mixture toxicity should lead to improved, more accurate metal-mixture models that can then be used for more cost-effective regulation [2].

In the present study, results are presented from acute toxicity tests in which D. magna were exposed to binary mixtures of Ni combined with Cd, Cu, or Zn. These 4 metals were chosen because their toxicity to aquatic organisms has been studied extensively as individual metals and because they can also be found in association in surface waters that receive discharges from industry, municipalities, or mine drainage [17]. The present study extends an earlier study of the acute toxicity of binary mixtures of Cd, Cu, and Zn to D. magna [7] and provides additional evidence of the less-than-additive, additive, and more-than-additive toxicity interactions reported by those authors.

MATERIALS AND METHODS

Test organisms

Daphnia magna were used in all the toxicity tests. Neonates were obtained from Aquatic BioSystems, Inc., and kept in moderately hard reconstituted water [18] with the green alga Pseudokirchneriella subcapitata as food. The neonates were sent via same-day shipping to ensure that all organisms were less than 24 h old at the start of the toxicity tests. Because the toxicity tests were started as soon as a shipment arrived at the laboratory, the D. magna were not fed again.

Exposure water

The exposure water in the toxicity tests was moderately hard reconstituted water to which 3 mg DOC/L was added as Suwannee River fulvic acid obtained from the International Humic Substances Society. Fulvic acid was added to the exposure waters to provide a concentration of organic carbon that is more representative of surface waters than the low background concentration of ≤ 0.5 mg DOC/L in Milli-Q water [7,19]. Metals were added to that exposure matrix as acidified (2–5% nitric acid) standards that are used for atomic absorption and inductively coupled plasma spectroscopy analyses (EM Science, Merck). Exposure solutions were prepared 24 h to 36 h before the start of a toxicity test, to allow equilibration of the metals with the DOC [20].

Toxicity tests

The toxicity of individual metals and binary mixtures was determined in 48-h static, nonrenewal lethality tests, following procedures prescribed by the US Environmental Protection Agency [18]. The binary-metal tests comprised a series of either 6 combinations or 12 combinations of metal concentrations in a gradient designed to produce mortalities ranging between 0% and 100%. In the binary mixtures, the concentration of metal 1 was held constant throughout the entire series whereas the concentration of metal 2 was increased incrementally in the series; then the metals were reversed in separate tests (i.e., the former metal 2 became the constant-concentration metal, and the former metal 1 became the varied-concentration metal), as in the experimental design used by Meyer et al. [7]. Individual-metal toxicity tests were conducted concurrently with each binary mixture and comprised a dilution series of 6 concentrations (including a control) for each metal. For example, if the metals in the binary mixture were Ni and Zn, Ni-only and Zn-only toxicity tests were also conducted. In all tests, each metal concentration or mixture was tested in 4 replicate chambers, each containing 25 mL of exposure water and 5 organisms. Therefore, a total of 20 organisms were exposed to each concentration in the individual- or binary-metal gradient. The number of dead organisms was recorded at 24 h and 48 h, with immobilization as the indicator of mortality [18].

Testing of the binary-metal mixtures extended over a 14-mo period from September 2012 to November 2013. All tests were conducted in incubators (VWR International) at a temperature of 20 ± 2 °C, with a 16:8-h light:dark cycle.

Chemical analyses

At 0 h and 48 h, the pH, dissolved oxygen concentration, and temperature were recorded. Unfiltered water samples for analysis of total organic carbon (TOC) concentration were collected from the control and the highest metal concentration at the beginning of a test and preserved by addition of H₃PO₄ to pH < 2. The alkalinity of each batch of moderately hard reconstituted water was determined before testing. At the beginning of a test, unfiltered water from each treatment in the metal-concentration series was acidified to pH ≤ 2 with 2% Optima HNO₃ and then submitted for elemental analysis.

Water samples from all controls and exposure concentrations were analyzed at the beginning of the toxicity tests for total concentrations of metals (including Cd, Cu, Ni, and Zn), major inorganic cations (Ca²⁺, Mg²⁺, Na⁺, and K⁺), and sulfur using an Optima 5300 inductively coupled plasma–optical emission spectrophotometer (ICP–OES; PerkinElmer). The exposure waters were not filtered before analysis because particles were unlikely in these synthetic waters, and preliminary tests had demonstrated that commercial filters either sorb metals from, or leach metals into, initial volumes of water that are passed through the membranes [7]. Consequently, the small volumes (<100 mL) of exposure waters used in these D. magna toxicity tests were not sufficient to adequately rinse the filters or exceed their sorption capacity. Additional preliminary tests, in which sufficient sample was used to saturate the filter membrane, demonstrated that the metals added to moderately hard reconstituted water were >90% dissolved [7]. Therefore, the total-metal concentrations were assumed to closely approximate the dissolved-metal concentrations.

Temperature and dissolved oxygen were measured using a YSI 55 probe, and pH was measured using an Orion ROSS electrode and Orion 2 STAR meter (Thermo Fisher Scientific) calibrated with pH 4, 7, and 10 buffers. Alkalinity was analyzed in the moderately hard reconstituted water that was used to prepare all the exposure waters by titration with H₂SO₄ to the bromo-cresol green endpoint [21]. Changes in alkalinity at the various metal concentrations were modeled using WHAM VII software. Total organic carbon concentrations were analyzed by ultraviolet (UV)-catalyzed persulfate oxidation using a Sievers Model 900 TOC Analyzer (GE Analytical Instruments).

Sulfate concentrations in all controls and metal exposures were calculated by assuming that all the sulfur measured by ICP-OES was present as SO₄²⁻, and chloride concentrations were calculated by assuming that the molar Cl^– concentration equaled the measured molar K⁺ concentration (because the only Cl^– in the moderately hard reconstituted water recipe was added as KCl; [18]).

In all ICP-OES analytical runs, a Sc internal-calibration standard was continuously introduced into the plasma along with each sample, and samples were analyzed in triplicate. Quality assurance/quality control samples included deionized water blanks (Barnstead Nanopure system, Thermo Fisher Scientific) that contained trace-metal-grade HNO₃ (Thermo Fisher Scientific), and certified continuing calibration verification standards. The quality assurance samples were analyzed immediately after instrument calibration, after every 10 samples, and at the end of each set of samples. In addition, NIST certified standard reference materials 1640a and 1643e [22] were analyzed for trace elements before and at the end of each set of samples. All samples were reanalyzed in any analytical run in which acceptable quality assurance/quality control results were not obtained. Those unacceptable results could include: deviations of the internal Sc standard greater than 20% from the known concentration, deviations of the certified continuing calibration verification samples greater than 10% from the known concentrations, or relative standard deviations of triplicate analyses of a sample greater than 10%. The ranges of instrument detection limits for the metals, major cations, and sulfur during the present study were as follows: 3 µg/L to 14 µg/L Ca; 0.1 µg/L to 0.2 µg/L Cd; 0.3 µg/L to 0.4 µg/L Cu; 15 µg/L to 27 µg/LK (equivalent to 13–25 µg/L Cl); 0.1 µg/L to 0.2 µg/L Mg; 6 µg/L to 8 µg/L Na; 1.5 µg/L to 12.1 µg/L S (equivalent to 4.5–37 µg/L SO₄); 0.1 µg/L to 0.4 µg/L Ni; and 0.2 µg/L to 0.4 µg/L Zn.

Data analyses

Toxicity data were analyzed using OriginPro 9.1 Software (OriginLab). Although it is traditional to compare median effect concentrations (EC50 values) determined from 2 or more concentration–response series to quantitatively characterize and compare toxicity results, this approach was not appropriate in the present study when high background mortality was because of the constant-concentration metal (i.e., metal 1) in the binary-metal series. In such cases, it was more appropriate to ask what concentration of metal 2 was needed to immobilize 50% of the test organisms that would not have been immobilized by the background concentration of metal 1 (i.e., what concentration of metal 2 was needed to halve the residual survival). Therefore, for quantitative comparisons, it was necessary to determine an alternative to the traditional EC50 (i.e., the concentration at which 50% of all the organisms were immobilized). This alternative is denoted in the present study as the ECx_infl (i.e., the concentration at the inflection point of the binary-mixture concentration–response curve, at which a total of x% immobilization would occur) and was determined using normalized distributions of a probability density function for the predicted toxicities [23]. The probability density functions were established by taking the first derivative of the concentration– response curves that were fitted to the immobilization data using the least-squares log–logit regression (Equation 1). In this equation, y is the observed immobilization proportion; A₁ is the lower mortality limit; C is the metal concentration (either the concentration in an individual-metal test or the concentration of the varied metal in a binary-metal test); C₀ is the concentration at the center of the distribution (i.e., the ECx_infl); and p is the slope of the log–logit regression curve at C₀.

$$\mathrm{y}={\mathrm{A}}_1+\frac{(100-{\mathrm{A}}_1)}{1+{10}^{[\mathit{\text{log}}(C_0)-\mathit{\text{log}}(C)]p}}$$ (1)

The first derivative of these concentration–response curves is the change in immobilization proportion per unit change in the logarithm of the metal concentration. The maximum first derivative (i.e., the slope at the inflection point) in each binary-metal test series was scaled to a maximum possible value of 1.0 (i.e., the maximum first derivative in each test series was normalized by dividing it by the first derivative at the EC50 determined in the corresponding individual-metal toxicity test), from which an x% mortality at the inflection point (x_infl) was determined (Equation 2). In this equation, D is the maximum of the normalized derivative for each curve. This is akin to setting x_infl = 100 × [A₁+(100−A₁)/2] (i.e., akin to the mortality percentage at which the residual survival is halved).

$${\mathrm{x}}_{\text{infl}}=(1-\frac{\mathrm{D}}{2})\times 100$$ (2)

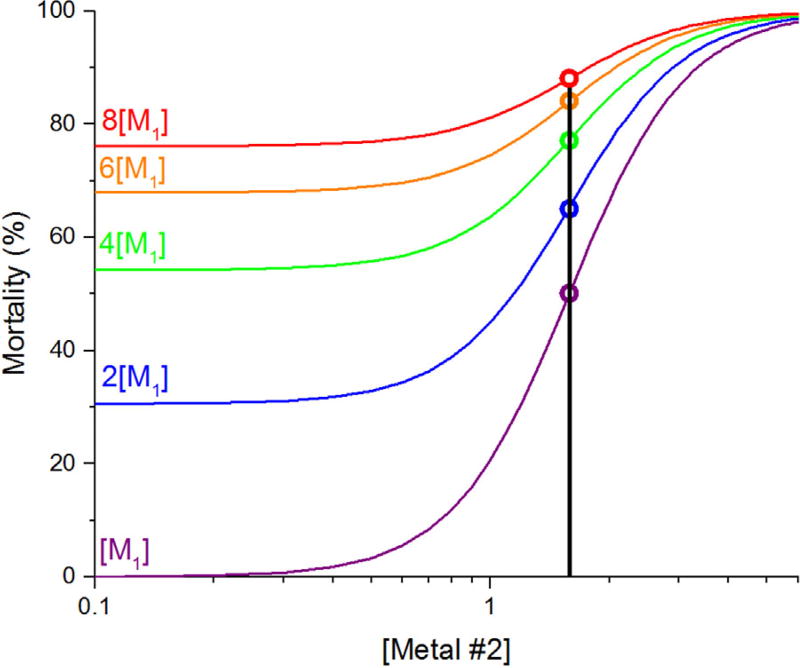
For a given binary-metal toxicity test, the concentration of metal 2 at the inflection point of the concentration–response curve (i.e., the ECx_infl) was then plotted on the vertical axis of a graph in which the concentration of metal 1 in the same toxicity test was plotted on the horizontal axis. As the concentration of metal 1 is increased in a sequence of separate binary-metal tests, a significant decrease or increase of the ECx_infl from the EC50 determined in the individual-metal test for metal 2 provides evidence for more-than-additive or less-than-additive toxicity, respectively, in mixtures containing those 2 metals. The statistical significance of those deviations was tested by determining whether the 84% confidence interval for a given ECx_infl was outside the 84% confidence interval determined for the EC50 values in all individual-metal toxicity tests that were conducted with metal 2. Overlap of 84% confidence intervals provides a more correct test of a significant difference between 2 mean values at the 95% confidence level than the more commonly used but overly conservative overlap of 95% confidence intervals [24]. In the present study, the widths of 95% confidence intervals on EC50 values calculated using OriginPro 9.1 were divided by the square root of 2 to estimate the widths of the corresponding 84% confidence intervals, as recommended by Meyer et al. [2]. The comparison of ECx_infl values with the individual-metal EC50 is valid because, assuming response-additive toxicity, 50% of the residual organisms that would survive exposure to metal 1 alone will be immobilized regardless of the percentage of the organisms that would be immobilized in the absence of metal 2 (i.e., 50% residual immobilization will always occur at the individual-metal EC50 (Figure 1); see Supplemental Data, Figures S1A and B for an explanation).

Figure 1.

Hypothetical example of response-additive toxicity of 2 metals in 5 different binary mixtures. In this example, metal 1 was held constant at 5 different background concentrations (represented by the 5 different colors; [Purple] < [Blue] < [Green] < [Orange] < [Red]) while metal 2 was increased along a concentration gradient at each background metal concentration. Higher concentrations of metal 1 cause higher initial mortality, but the inflection point of each curve will occur at the same concentration of metal 2 (at a concentration of ~1.6 in this example) if the toxicity of the metal mixture is response additive (see Supplemental Data, Equation S1). M₁ = metal 1.

RESULTS AND DISCUSSION

Water chemistry and toxicity data for all individual-metal and metal-mixture toxicity tests are available in the Supplemental Data, Tables S1–S4.

Individual metals

Based on the EC50 values in the individual-metal toxicity tests, Ni was the least toxic (i.e., it had the highest EC50) of the 4 metals tested in this moderately hard reconstituted water, followed by Zn, Cu, and Cd in sequence of increasing toxicity (Table 1). In the Ni-only, Cu-only, and Zn-only tests, the EC50 values among all tests conducted during the present 14-mo study had minimal variability around a steep concentration–response curve (Supplemental Data, Figure S2A–C; and see coefficients of variation in Table 1). In contrast, the concentration–response curves for Cd were shallower and more variable among the separate tests (Supplemental Data, Figure S2D; and see coefficient of variation in Table 1). Meyer et al. [7] reported similar results for Cd toxicity in a variety of organisms, indicating that Cd has a high variability in toxicity that is, as of yet, unexplained. The toxicity of Ni and Zn were more variable than for Cu, but less than for Cd. This intermediate variability of Zn toxicity to D. magna is similar to the ranking of toxicity variability among Cd, Cu, and Zn reported by Meyer et al. [7] in the same exposure-water recipe.

Table 1.

Average 48-h median effect concentration (EC50), standard deviation (SD), coefficient of variation (CV = standard deviation/average), and number of individual toxicity tests (n) performed for immobilization of Daphnia magna neonates exposed to Cd, Cu, Ni, or Zn in repeated individual-metal toxicity tests during the present 14-mo study

	Average EC50
Metal	(mg/L)	(µmol/L)	SD (mg/L)	CV	n
Cd	0.054	0.48	0.036	0.661	13
Cu	0.100	1.57	0.019	0.192	15
Ni	1.633	27.8	0.475	0.291	31
Zn	0.928	14.2	0.256	0.276	7

Ni and Cd binary mixtures

In moderately hard reconstituted water containing 3 mg DOC/L, Ni was approximately 2 orders of magnitude less toxic than Cd (Table 1), and concentrations of Ni in uncontaminated surface waters are generally more than 4 times greater than the concentrations of Cd [25]. For these reasons, the concentrations of Cd used in binary mixture toxicity tests were considerably lower than the Ni concentrations.

When the concentration of Cd was held constant as the Ni concentration was increased, increasing Ni concentrations depressed or, in some cases, wholly eliminated the initial Cd toxicity at Ni concentrations < 1 mg/L (Figure 2). For example, initial mortality in 0.1 mg Cd/L was nearly 100% (caused only by Cd toxicity, because the initial Ni concentration in the several repeat tests always was ~100 times to 1000 times less than the Ni-only EC50). As the added Ni concentration increased, the mortality steadily decreased to a minimum of 5% at approximately 0.5 mg Ni/L, demonstrating a large protection against Cd toxicity by Ni. However, mortality increased when Ni concentrations were high enough to cause Ni-induced toxicity (i.e., when the concentration– response curve of the Cd–Ni mixture became ~identical to the Ni-only concentration–response curve on the right half of Figure 2). These results are similar to the large protection against Cd toxicity to D. magna by Zn, until the Zn concentration became high enough to cause Zn-induced toxicity (see Figure 3B in Meyer et al. [7]).

Figure 2.

Mortality (determined by immobilization of Daphnia magna neonates) in 48-h exposures to Cd–Ni mixtures, in which a constant background concentration of Cd was maintained while Ni was varied along a concentration gradient. Different background concentrations of added Cd were used in different sets of toxicity tests, but with replicate tests conducted at each Cd concentration (k equals the number of replicate tests, indicated in the key). As the concentration of Ni was increased, the Cd-induced mortality decreased until Ni concentrations reached the range at which Ni-induced mortality began to increase, represented by the rising portion of the shaded Ni-only mortality band.

Figure 3.

Concentration–response curves of select binary-metal mixtures. (A) Concentration–response relationship when a constant concentration of Cu is present with increasing concentrations of Ni. The inflection points of the curves shift toward lower concentrations as the concentration of Cu is increased. Because less Ni is required to elicit mortality as the background Cu concentration is increased, the toxicity of this mixture is more-than-additive. (B) Mixtures of constant Ni concentrations with increasing concentrations of Cd. The inflection points of the curves shift to a higher concentration of Cd as the concentration of Ni is increased, thus illustrating less-than-additive toxicity.

When the roles of Cd and Ni were reversed in a test in which the Ni concentration was held constant and Cd was increased through a concentration series, the concentration–response curves shifted to the right (Figure 3B, Supplemental Data, Figure S3). These shifts also demonstrate a protective effect of Ni against Cd toxicity because, as Ni concentration was increased, higher Cd concentrations were needed to cause the same amount of Cd-induced immobilization. The results of these Cd–Ni toxicity tests are illustrated in Figure 4E, where the concentration of Cd at the inflection point of the Cd–Ni concentration–response curve (i.e., the ECx_infl) is plotted versus the constant Ni concentration in each test (Figure 4E). These ECx_infl concentrations can be compared with the solid horizontal line that represents the Cd-only EC50 (i.e., the Cd concentration at the inflection point of the Cd-only curve). If the 2 metals had acted independently of each other (and thus the toxicity of the Cd–Ni mixtures had been response-additive), the inflection point of each Cd–Ni toxicity curve should have occurred at approximately the Cd-only EC50. Instead, the Cd ECx_infl values increased as the Ni concentration in the exposure waters increased in the separate sets of Cd–Ni mixture tests, demonstrating less-than-additive toxicity.

Figure 4.

Toxicity of Cd–Ni, Cu–Ni, and Zn–Ni mixtures to Daphnia magna neonates in 48-h exposures in which the concentration of the metal that remained constant throughout a test is plotted on the horizontal axis versus the concentration at the inflection point of the varied metal’s concentration–response curve (the ECx_infl) plotted on the vertical axis. The solid horizontal line is the average median effect concentration (EC50) of the varied metal, as determined by single-metal toxicity tests run in conjunction with the mixture tests (Supplemental Data, Figure S2), and the dashed lines represent the 84% confidence limits. Open circles indicate that the ECx_infl of the binary mixture was not statistically different (p > 0.05) from the EC50 of the single-metal toxicity, based on overlap of the 84% confidence intervals for the single-metal EC50 and the mixture ECx_infl values (see text). Closed circles indicate trials in which the ECx_infl differed significantly from the single-metal EC50 (p ≤ 0.05). The tests represented in each graph are: (A) a constant background concentration of Cu while Ni was varied along a concentration gradient, (B) a constant background of concentration of Ni while Cu was varied along a concentration gradient, (C) a constant background concentration of Zn while Ni was varied along a concentration gradient, (D) a constant background concentration of Ni while Zn was varied along a concentration gradient, and (E) a constant background concentration of Ni while Cd was varied along a concentration gradient.

The literature contains few reports of Cd–Ni binary toxicity tests. However, our results differ from those of Martin et al. [26], who reported that reproduction of a terrestrial nematode (Caenorhabditis elegans) in a binary combination of Cd and Ni did not deviate from predictions of the independent action model. This lack of agreement between studies may be a result of differences in 1) bioavailability of the metals in the exposure media (growth-medium agar for the nematode, and water for D. magna); 2) the physiology of the organisms; 3) acute and chronic toxicity of Cd–Ni mixtures; and/or 4) geochemical interactions of the metals in the different concentration ranges in which the Cd–Ni mixtures were tested.

The mechanism(s) underlying the protective effects of 1 metal against the toxicity of another metal are difficult to determine. The lessening of toxicity may be the result of chemical interactions between the metals while in the bulk exposure water, chemical interactions between the metals at the biotic ligand site (e.g., competitive metal binding that alters the impairment of the organism’s uptake of major ions like Na⁺ and Ca²⁺), physiological interactions between the metals after they enter the organism, or any combination of those processes. However, the results of the present study are consistent with the hypothesis that chemical interactions between the metals at the biotic ligand caused the less-than-additive toxicity in the Cd–Ni mixtures, wherein Ni at sublethal concentrations outcompeted Cd at lethal concentrations for binding to the biotic ligand(s) and, as a result, decreased the Cd-induced toxicity. This is similar to the mechanism suggested by Meyer et al. [7] for D. magna exposed to Cd–Cu and Cd–Zn mixtures, and it is consistent with the suppression of Cd uptake by D. magna when the concentration of Ni in Cd–Ni mixtures is increased [27]. Bioavailability models like the BLM and WHAM-F_TOX account for chemical interactions of metals among each other and with major inorganic ions and dissolved organic matter, but they do not yet account for potential physiological interactions.

Ni and Cu binary mixtures

In moderately hard reconstituted water containing 3 mg DOC/L, Ni is approximately 1 order of magnitude less toxic than Cu (Table 1). Although the ratios of the concentrations of Cu and Ni used in these binary-metal toxicity tests do not necessarily reflect their natural abundance ratios, the concentrations produced a full range of immobilization percentage with emphasis on determining the inflection points on the concentration–response curves for the mixtures.

Each binary combination of Cu and Ni produced evidence of more-than-additive toxicity, because the inflection points of the concentration–response curves for the mixtures (i.e., the ECx_infl values) shifted to progressively lower concentrations than the individual-metal EC50 of the varied metal, as the concentration of the constant background metal was increased (Figures 3A, 4A and 4B, and Supplemental Data, Figure S4A and S4B). In mixtures in which the Cu concentration was held constant and the Ni concentration was varied, the Ni ECx_infl values should have remained constant at approximately 1.63 mg Ni/L if the mixture toxicity had been additive, but instead, the ECx_infl concentrations began decreasing at background Cu concentrations as low as approximately 0.02 mg to 0.04 mg Cu/L and eventually decreased to less than 0.1 mg Ni/L in the presence of background Cu concentrations greater than or equal to approximately 0.1 mg Cu/L (i.e., at greater than or equal to ~the Cu-only EC50; Figure 4A). Similarly, in mixtures in which the Ni concentration was held constant and the Cu concentration was varied, the Cu ECx_infl values should have remained constant at approximately 0.10 mg Cu/L if the mixture toxicity had been additive, but instead, the ECx_infl concentrations decreased to less than or equal to 0.06 mg Cu/L in the presence of background Ni concentrations greater than or equal to approximately 0.4 mg Ni/L (i.e., at greater than or equal to ~1/4 the Ni-only EC50; Figure 4B). This more-than-additive toxicity in mixtures of Cu and Ni supports results reported for Lebistes reticulatus [28] but is not consistent with the less-than-additive effect of Cu on Ni uptake in D. magna [27].

The results of the present study are consistent with the hypothesis that chemical interactions in the bulk exposure water caused the more-than-additive toxicity in the Cu–Ni mixtures. If hydrated free nickel ions (represented as Ni²⁺) competed with hydrated free Cu ions (represented as Cu²⁺) for binding to carboxylic or phenolic sites on the DOM, the concentrations of Cu²⁺ and/or Ni²⁺ (the purportedly most bioavailable forms of those metals) in the exposure water would have increased as the total dissolved concentration of either Cu or Ni was increased. Although Cu is generally assumed to have a higher affinity for DOM than Ni has [29,30], the outcome of competitive binding is determined by the mathematical product of the free-ion concentration and the binding affinity of the ion (i.e., the outcome is determined by [M²⁺] × K_M-DOM instead of only by K_M-DOM; where [M²⁺] is the molar concentration of the “free” ion, and K_M-DOM is the binding constant between the free ion and DOM) [2]. Therefore, the higher concentration of Ni than Cu could have allowed Ni to compete effectively with Cu. Because Cu is more toxic than Ni, increased Cu²⁺ concentrations in the exposure water (relative to the concentrations that would be expected in the absence of Ni) probably account for the more-than-additive toxicity in the Cu–Ni mixtures. This metal–metal competition for binding to DOM is similar to the mechanism suggested by Meyer et al. [7] for D. magna exposed to Cu–Zn mixtures.

Ni and Zn binary mixtures

In moderately hard reconstituted water containing 3 mg DOC/L, Ni and Zn had similar toxicity (Table 1). The EC50 values for Ni and Zn were 1.63 ± 0.48 mg/L and 0.93 ± 0.28 mg/L (average ± SD), respectively, which allowed the Ni±Zn mixture concentrations to be representative of concentrations possibly seen in heavily contaminated acid mine drainage sites [31,32]. Furthermore, Ni and Zn are used extensively in current technologies, which make them likely co-occurring constituents of industrial discharges into surface waters [33].

In mixtures in which the Ni concentration was held constant as the Zn concentration was increased, the toxicity was additive to less-than-additive (i.e., as the “background” Ni concentration was increased, the Zn ECx_infl values generally increased or did not differ significantly from the Zn-only EC50; Figure 4D, and Supplemental Data, Figure S5A). That pattern is consistent with a hypothesis that chemical interactions at the biotic ligand caused the less-than-additive toxicity in the Ni–Zn mixtures, wherein Ni at sublethal concentrations competed with Zn at lethal concentrations for binding to the biotic ligand(s). That pattern is also consistent with the slight inhibition of Zn uptake by D. magna in the presence of low Ni concentrations (0.1–0.25 µM) [27], although that decrease of Zn uptake rate was not statistically significant. Two of the 3 Ni–Zn tests in which the mixture toxicity was not significantly nonadditive had low background Ni concentrations (i.e., less than or equal to 0.2 mg Ni/L; Figure 4D), at which Ni–Zn competitive interactions might have been relatively small and thus more difficult to detect. Only 1 of the 9 Ni–Zn tests in which Ni was the constant-concentration background metal had a Zn ECx_infl that did not differ significantly from the Zn-only EC50 (i.e., the Zn ECx_infl was only 1.3 times the Zn EC50). That test had at a high background Ni concentration (2.0 mg Ni/L; Figure 4D), and the reason for that relatively low Zn ECx_infl is unknown (when all other Zn ECx_infl values in that range of background Ni concentrations from 1.5 Ni/L to 2.5 mg Ni/L were at least twice as high as the Zn-only EC50). However, in general, metal–metal competition likely decreased the Ni- or Zn-induced toxicity, which may be analogous to the mechanism hypothesized above for the less-than additive toxicity in Cd–Ni mixtures.

Although also suggesting less-than-additive toxicity, the response was more complicated in mixtures in which the Zn concentration was held constant as the Ni concentration was increased. In those mixtures, the Ni ECx_infl doubled at low Zn concentrations of 0.7 mg Zn/L and then tended to decrease but still remained greater than the Ni-only EC50 through Zn concentrations as high as 1.4 mg Zn/L (Figure 4C, and Supplemental Data, Figure S5B). The Ni ECx_infl values would be expected to gradually increase as occurred in the Cd–Ni mixtures (Figure 3B), if the only mechanism controlling the mixture toxicity was competition between Ni and Zn for binding to the biotic ligand(s). Therefore, an alternative or additional physiological process might have occurred in the mixtures in which the Zn concentration was held constant and the Ni concentration was varied. Previous studies on the toxicity of Ni–Zn binary mixtures in L. reticulatus [28] and D. magna [13] indicated that the interaction is difficult to classify. Khangarot [28] reported that in acute toxicity tests with L. reticulatus, the toxicity was less than additive at high Zn to Ni ratios but was greater than additive at low Zn to Ni ratios. In contrast, Nys et al. [13] reported that in chronic toxicity tests with D. magna, Ni and Zn did not have an interaction when each metal concentration was below its EC20, but the toxicity became more than additive when both metals were present at a concentration greater than their EC20.

A possible physiological explanation for the results in Figure 4C is the induction of metallothionein synthesis by Zn [34], which was also suggested by Meyer et al. [7] as a potential explanation for some unexpected results in Cd–Zn mixtures. If a near-maximal rate of metallothionein production was induced by 0.5 mg Zn/L, and higher Zn concentrations thus would not have induced higher rates of metallothionein production, the Ni ECx_infl values would remain approximately constant because the same concentration of Ni would be needed to exceed its sequestration by metallothionein. Analyses of metallothionein concentrations in D. magna exposed to various background Zn concentrations as Ni is increased through a concentration series would be needed to test this hypothesis.

Synthesis

Similar to the results reported by Meyer et al. [7] for binary mixtures of Cd, Cu, and Zn and in general similar to results of other metal-mixture studies [35,36], the toxicity of the Cd–Ni, Cu–Ni, and Ni–Zn mixtures in the present study was either less-than-additive, additive, or more-than-additive when based on dissolved-metal concentrations, depending on the combinations of metals and their concentrations. All of the tests were conducted in the same water chemistry, including the same DOC concentration and source, and replicate tests of the same mixture concentrations produced similar results, thus supporting the notion that the results were not the result of random variability.

The range of additive and nonadditive toxicity when the same metal (Ni) is used in binary mixtures with a variety of other metals (Cd, Cu, and Zn) demonstrates why a predictive model that can account for the various chemical interactions of metals with each other in a mixture, with various components of the exposure water (e.g., pH, alkalinity, major cations, and DOC), and with biotic ligands would help to improve water quality criteria and/or guidelines to incorporate metal mixtures instead of regulating on a metal-by-metal basis. However, physiological interactions between metals cannot be excluded as an alternative or complementary explanation for the nonadditive toxicity among some metals that is apparent when conclusions are based on dissolved-metal concentrations. Additional coordinated datasets with complete water chemistry and acute and/or chronic toxicity data for these and other metal mixtures will be needed to improve the mechanistic basis for predictive models. Acute and chronic toxicity data are needed because different regulatory jurisdictions use acute (e.g., United States) or chronic (e.g., Europe) results as the basis for most of their water criteria or guidelines for metals.

Although testing binary mixtures is a start, metal combinations in natural systems often contain more than just 2 metals and thus have almost unlimited possible combinations of metals and their concentrations. In addition, the types and extents of interactions among metals might vary as water chemistry varies. Because testing a large number of combinations of metals and their concentrations in a wide variety of water chemistries would be expensive and time consuming, many combinations of metals and water chemistry likely will never be evaluated. Nonetheless, the next logical steps to help parameterize metal-mixture toxicity models would be to systematically study a set of ternary-metal mixtures (e.g., comprising Cd, Cu, Ni, and Zn) and to determine the effects of varying water chemistry on the additivity or nonadditivity of the toxicity of the binary- and ternary-metal mixtures. In addition, testing at lower, more environmentally representative concentrations would be beneficial for modeling the potential chronic toxicity of metal mixtures.

CONCLUSIONS

Considerable work remains to fully understand the mechanisms underlying metal-mixture toxicity and thus to develop predictive, bioavailability-based models. Simple assumptions about additivity of toxicity in metal mixtures can sometimes be underprotective (e.g., more-than-additive toxicity demonstrated for Cu–Ni mixtures in the present study and for some Cu–Zn mixtures in Meyer et al. [7]) and can sometimes be overprotective (e.g., less-than-additive toxicity demonstrated for Cd–Cu, Cd–Ni, and Cd–Zn mixtures in the present study and in Meyer et al. [7]). Competitive chemical interactions of the metals with the components of the exposure water and with biotic ligands undoubtedly will play major roles in bioavailability-based models (e.g., multiple-metal BLMs and WHAM-F_TOX [10]), but metal interactions with physiological processes might also have to be incorporated. Simple reliance on dissolved-metal concentrations as predictors of metal-mixture toxicity leaves a cloudy picture, but measured or model-calculated concentrations of free metal ions and organism-accumulated metals [37] might help to clarify the picture. To that end, techniques to improve measurement of free-ion activities in metal mixtures and to measure metal accumulation at sites of toxic action (or to measure, for example, genetic markers of the bioavailability of metals in mixtures) could provide independent information for parameterization of metal-mixture models.