Surface based electrode localization and standardized regions of interest for intracranial EEG

Abstract

Intracranial recordings captured from subdural electrodes in patients with drug resistant epilepsy offer clinicians and researchers a powerful tool for examining neural activity in the human brain with high spatial and temporal precision. There are two major challenges, however, to interpreting these signals both within and across individuals. Anatomical distortions following implantation make accurately identifying the electrode locations difficult. In addition, because each implant involves a unique configuration, comparing neural activity across individuals in a standardized manner has been limited to broad anatomical regions such as cortical lobes or gyri. We address these challenges here by introducing a semi‐automated method for localizing subdural electrode contacts to the unique surface anatomy of each individual, and by using a surface‐based grid of regions of interest (ROIs) to aggregate electrode data from similar anatomical locations across individuals. Our localization algorithm, which uses only a postoperative CT and preoperative MRI, builds upon previous spring‐based optimization approaches by introducing manually identified anchor points directly on the brain surface to constrain the final electrode locations. This algorithm yields an accuracy of 2 mm. Our surface‐based ROI approach involves choosing a flexible number of ROIs with different spatial resolutions. ROIs are registered across individuals to represent identical anatomical locations while accounting for the unique curvature of each brain surface. This ROI based approach therefore enables group level statistical testing from spatially precise anatomical regions.

1. INTRODUCTION

Intracranial EEG (iEEG) recordings using subdural and depth electrodes are often used to evaluate candidates with Drug‐resistant focal epilepsy. The goal of these recordings is to identify regions of seizure activity for possible surgical resection (Cooper, Winter, Crow, & Walter, 1965; Penfield & Jasper, 1954). As such, it is important to identify the locations of these electrodes with high precision and accuracy. Besides their clinical utility, iEEG recordings also offer a natural opportunity to investigate the neural mechanisms underlying cognitive behavior, since participants are often monitored for an extended period of time (Crone, Boatman, Gordon, & Hao, 2001; Jacobs & Kahana, 2010; Lachaux, Rudrauf, & Kahane, 2003; Miller, Polyn, & Kahana, 2007). The high temporal resolution of these signals and their close proximity to the cortical surface offer researchers a powerful approach to directly assess neural signals underlying such behavior.

Although iEEG offers high spatial resolution, combining data across participants without losing this precision remains an important issue in the field. For both clinical and research purposes, comparing activity from similar anatomical regions across participants is necessary for making general claims about patterns of cortical activation. There are two major challenges for making such comparisons. First, identifying accurate electrode locations and comparing these locations to standard models is difficult due to the swelling and brain shift experienced following implantation; and second, comparing activity across participants is difficult since each participant is unique in their cortical anatomy and in the configuration of their implanted electrodes.

Numerous solutions addressing the challenge of electrode localization have been set forth (Dalal et al., 2008; Dykstra et al., 2012; Hermes, Miller, Vansteensel, & Ramsey, 2010; Pieters, Conner, & Tandon, 2013; Yang et al., 2012). In general, these approaches have found success by first defining the spatial configuration of the electrodes, and then warping the configuration so as to fit the surface anatomy determined by the preoperative MRI. Each approach fuses particular information from multiple imaging modalities acquired at different time points (pre‐, intra‐, and postoperative), including digital photography (Mahvash et al., 2007; Pieters et al., 2013; Wellmer et al., 2002), X‐ray radiography (Miller et al., 2007), computerized tomography (CT) (Dykstra et al., 2012; Grzeszczuk et al., 1992; Hermes et al., 2010; Hunter et al., 2005; LaViolette et al., 2011a; Sebastiano et al., 2006; Tao et al., 2009; Wang, Agrawal, Nguyen, Domocos, & Gotman, 2005; Winkler et al., 2000), and magnetic resonance imaging (MRI) (Bootsveld et al., 1994; Kovalev et al., 2005; Morris, O'Brien, Cook, Murphy, & Bowden, 1998; Schulze‐Bonhage et al., 2002; Yang et al., 2012).

Conversely, many methods for comparing data across participants either naively average and visualize data over broad anatomical regions such as cortical lobes or gyri, or forego group analysis altogether for individual participant analysis. Interestingly, functional imaging studies (fMRI) have largely addressed this issue by comparing activity among spatially defined voxels, standardized across participants to a template brain (Friston et al., 1995; Friston, Worsley, Frackowiak, Mazziotta, & Evans, 1994; Kriegeskorte, Goebel, & Bandettini, 2006; Worsley, Evans, Marrett, & Neelin, 1992). Creating a similar system of spatially defined regions could represent a tractable method of standardizing and then interpreting changes in neural iEEG activity across participants.

Here, we address these challenges by implementing a modified algorithm for electrode localization that builds upon previous approaches, and by creating standardized regions of interest (ROIs) that enable across participant analysis from analogous anatomical locations. We draw upon previous approaches for localizing electrode contacts by combining favorable elements into an algorithm that we demonstrate improves localization accuracy. Specifically, we identify electrode locations on a smoothed pial surface, defined in each participant by the preoperative MRI, using an adapted spring network optimization (Dykstra et al., 2012) guided with anchor points identified using intra‐operative photography (Dalal et al., 2008; Pieters et al., 2013; Yang et al., 2012). We compare the accuracy of localization between registration algorithms and confirm that the inclusion of anchor points enables accurate electrode localization. We then address the group level analysis problem by defining uniformly distributed ROI center points on a standard template brain, then normalizing each participant's brain to the template using surface‐based registration (Dykstra et al., 2012; Fischl, Sereno, & Dale, 1999; Kadipasaoglu et al., 2014) and a standardized mesh resampling (Saad & Reynolds, 2012). Consequently, each ROI center has a spatially analogous location across participants which is independent of a priori assumptions regarding function, and we are able to aggregate electrode data into ROIs for comparison across participants.

2. MATERIALS AND METHODS

2.1. Patient population

Seventeen participants (7 male; age 31.2 ± 2.6 years [mean ± SEM]) with medication‐resistant epilepsy underwent a surgical procedure in which platinum recording contacts (3 mm diameter) were implanted subdurally on the cortical surface. Participants were grouped into a primary cohort, S1‐S11, and a validation cohort, S12‐S17. Data from the validation cohort was held out from our initial analyses and was used solely to validate that our localization model did not overfit its parameters.

Data were collected at the Clinical Center at the National Institutes of Health (NIH; Bethesda, MD). The research protocol was approved by the Institutional Review Board, and informed consent was obtained from the participants and their guardians. Software packages used to implement electrode localization and the creation of standardized surface based regions of interest, as well as a sample data set, are available for public download at: https://neuroscience.nih.gov/ninds/zaghloul/downloads.html.

The available software package requires the publicly available software packages AFNI (http://afni.nimh.nih.gov) and FreeSurfer (http://surfer.nmr.mgh.harvard.edu) and takes as input the CT coordinates of each electrode.

2.2. Image acquisition and co‐registration

We acquired preoperative T1 weighted MPRAGE images for all participants using a 3.0T scanner (Philips Achieva; voxel size $0.83\times 0.83\times 1.4,\hspace{0.17em}1\times 1\times 1$, or $0.75\times 0.75\times 0.8$ mm [n = 9]; repetition time $3.1\le \text{TR}\le 4.3$ ms; echo time $6.9\le \text{TE}\le 8.9$ ms; field of view $\text{FOV}=240$ mm; flip angle 9 degrees). Following electrode implantation, all participants also received a postoperative clinical CT scan within four hours (GE LightSpeed Ultra, Siemens SOMATOM Definition Flass, or Siemens SOMATOM Force; voxel size $0.52\times 0.52\times 1,\hspace{0.17em}0.49\times 0.49\times 1$ [n = 4], or $0.59\times 0.59\times 1.25$ mm [n = 6]; 512 × 512 matrix).

We co‐registered MRI and CT images using AFNI (Cox, 1996). Specifically, we deobliqued the T1 MRI, then performed an affine transformation using a signed local Pearson correlation (LPC) cost function with AFNI's “align‐epi‐anat.py” (Saad & Reynolds, 2012). If this registration failed based on visual inspection, we repeated the procedure using an unsigned LPC cost function on an intensity‐inverted T1 MRI. This two‐tiered approach was successful for all attempted affine registrations.

2.3. Surface reconstruction and normalization

We reconstructed surfaces from preoperative MRI images using FreeSurfer (Fischl, 2012). We created surface models using “recon‐all.” After creating a surface for each participant, we created a smoothed pial surface using “localGI” that traverses cortical sulci (Figure 1b) (Kadipasaoglu et al., 2014; Schaer et al., 2008). The smoothed pial surface is a smoothed version of the surface which follows the gyral crowns and traverses cortical sulci. (Kadipasaoglu et al., 2014). Our goal was to localize electrode contacts to this smoothed pial surface.

Figure 1.

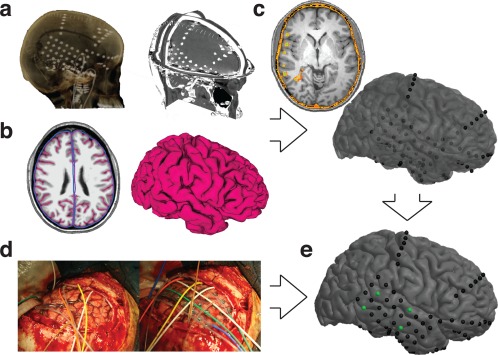
Pipeline Overview. (a) Electrodes localized on postoperative CT. (b) Pial surface and smoothed pial surface created from preoperative MRI. (c) CT‐MRI registration results in electrodes localized beneath the surface; the surface has been made translucent. (d) Intra‐operative photographs show cortical anatomy and electrode placement, allowing accurate identification of anchor points. (e) Result of our localization algorithm as guided by anchor points [Color figure can be viewed at http://wileyonlinelibrary.com]

Using FreeSurfer, we then normalized surfaces across participants (Figure 2). For each hemisphere of each participant, we inflated the surface and mapped its points onto a sphere. We then aligned the curvature patterns to a population average—the “fsaverage” template brain (Dale, Fischl, & Sereno, 1999; Fischl et al., 1999). To establish a correspondence between the vertices of different participants' surfaces, we resampled the warped spherical meshes into a standardized mesh grid with AFNI's “MapIcosahedron” command. The mesh grid is the inflation of a tessellated icosahedron to a sphere (Saad & Reynolds, 2012). We used a sampling with a linear depth of 141, where the linear depth is the number of divisions per icosahedral edge. Finally, we unwarped the resultant spheres to obtain resampled surfaces for each participant. As a result, each surface had the same number of mesh vertices (198,812), and these vertices corresponded to analogous anatomical locations across participants.

Figure 2.

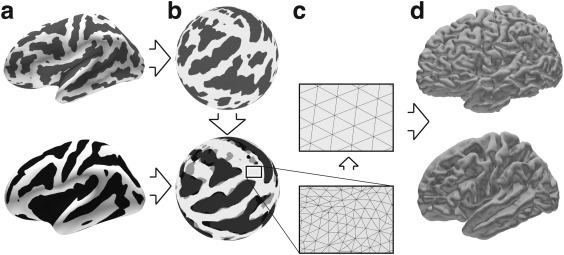
Surface Normalization. Surfaces are reconstructed for each individual participant (top row) and for a population average brain (bottom row). (a) A curvature measure is computed (brains inflated for illustrative purposes). (b) Surfaces are mapped onto a sphere, and subsequently individual participant curvature patterns are optimally aligned to the average curvature. (c) Surface meshes are resampled in a standardized manner using a recursively subdivided icosahedron template. (d) Surfaces are unfolded into their original geometries but retain their new aligned and corresponding surface meshes

2.4. Gold standard and anchor points

Intra‐operative digital photographs were taken of the exposed cortical surface before and after placement of subdural electrode contacts (Figure 1d). By matching vascular patterns visible on the photographs with gyral anatomy visible on the surfaces, we were able to identify anatomical landmarks and electrode locations (Hermes et al., 2010). To select anchor points, we chose only electrodes whose anatomical locations were clearly identified and were careful to select only electrodes that were positioned on the crown of a gyrus so as to best identify those locations on the brain surface reconstructions. For all clearly visible electrodes that could be confidently identified, we used the publicly available software package 3D Slicer (https://www.slicer.org) to mark locations on the smoothed pial surface of each participant's reconstructed preoperative surface. We defined a subset of these points as anchor points, which were used to inform the automated localization algorithm, and we used the remaining points as gold standard electrode locations to evaluate the success of localization (Table 1).

Table 1.

Participant summary

Participant	No. elec. implanted	No. elec. identified
S1	46	11
S2	48	14
S3	72	27
S4	78	11
S5	79	17
S6	60	20
S7	105	22
S8	70	15
S9	90	13
S10	132	22
S11	71	20
S12	68	22
S13	84	19
S14	134	19
S15	104	14
S16	74	17
S17	86	19

2.5. Electrode localization

We identified electrode locations in CT space using Curry Neuroimaging Suite (Compumedics USA, Charlotte, NC) through a combination of manual annotation and maximal intensity projection. We used the transformation matrix representing the successful co‐registration of CT and MR image sets to map coordinates identified in the postoperative CT space to the preoperative MRI space.

Due to the brain shift caused by the implantation procedure, transforming these electrode locations into the preoperative MRI space for each participant resulted in electrode locations that did not lie on the cortical surface (Figure 1c). To correct for this, we adapted a spring network optimization procedure that pulls electrode centers registered in MRI space to the preoperative smoothed pial surface (Dykstra et al., 2012). Conceptually, the spring network is iteratively relaxed from a strained initialization, with its total energy decreasing until it reaches target stability.

Importantly, we modified the optimization procedure in two ways. First, we constrained a subset of electrode contacts (anchors) to specific locations on the smoothed pial surface that were identified based on intra‐operative photography. We took all contacts that could be identified from these photographs but were not used as anchors to be our gold standard electrodes (Figure 3a,b; Table 1), and we used these to validate the performance of brain shift correction and final electrode localization. Second, the smoothed pial surface that we created for each participant is only an approximation of the true cortical surface upon which intracranial electrodes are placed. Using a spring optimization algorithm that strictly constrains electrodes to lie on this smoothed pial surface would therefore rely upon the accuracy of this approximation and on the assumption that the hardware follows the curvature of the smoothed pial surface. As such, we relaxed this constraint, and instead placed more emphasis on the information from the anchor points and registered geometry. The relative values of these constraints is reflected in the spring constants governing the optimization algorithm.

Figure 3.

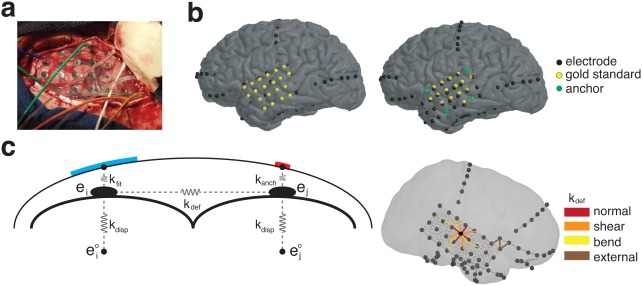
Localization Algorithm. (a) Intra‐operative photographs were used to visually identify electrode locations. (b) Identified electrodes are manually placed on the cortical envelope (left); a subset of these are used as anchor points (right), while the rest are used as the gold standard locations to validate the localization algorithm. (c) Final electrode localization is optimized based on a spring model (left). Springs governing the energy of displacement (k _disp) are placed between the final (e_i) location and CT‐registered location ( $e_i^0$), between the final electrode location and the cortical surface (k _fit) or anchor point (k _anch), and between neighboring electrodes (k _def). Neighboring electrodes (right) were chosen to model normal, bend, and shear forces, and external connections were made between hardware within 15 mm [Color figure can be viewed at http://wileyonlinelibrary.com]

To project electrodes to the smoothed pial surface, we constructed a spring network (Figure 3) and minimized the following energy function:

$$E_{\text{total}}=E_{\text{displacement}}+E_{\text{fitting}}+E_{\text{deformation}}$$ (1)

where E _displacement represents the energy of displacement and accounts for the displacement of electrode centers from their initial registered locations to their final location:

$$E_{\text{displacement}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N{k}_{\text{disp}}}\hspace{0.17em}\left|\right|e_i-e_i^0|{|}^2$$ (2)

where N is the total number of electrodes, $e_i^0$ is the coordinates of each initial registered electrode location, and e_i is its final determined location. We defined k _disp as the spring constant governing the energy of displacement.

E _fitting represents the energy of fitting, which pulls the electrode centers to either a constrained area on the smoothed pial surface, or to the identified anchor points:

$$E_{\text{fitting}}=\frac{1}{N}{\displaystyle \sum _{i=1}^N\{\begin{array}{ll}{k}_{\text{anch}}\left|\right|e_i-e_i^{\text{anch}}|{|}^2\hfill & \text{if} e_i \text{is} \text{an} \text{anchor},\hfill \\ k_{fit}\left|\right|e_i-e_i^{\text{near}}|{|}^2\hfill & \text{otherwise}.\hfill \end{array}}$$ (3)

where $e_i^{\text{anch}}$ is the coordinate of the i'th electrode's anchor point if one is defined, k _fit is the spring constant governing the energy of fitting, and $e_i^{\text{near}}$ is the coordinate of the nearest point on the smoothed pial surface to the electrode location e_i. We recalculated the nearest neighbor after every iteration of optimization to restrict electrode movement. We defined k _anch as the spring constant governing the energy of fitting to anchor points and used high values of k _anch to ensure that those designated electrodes were pulled to those specific locations.

E _deformation represents the energy of deformation, and accounts for changes in the original spatial arrangement of the electrode contacts:

$$\begin{array}{l}{E}_{\text{deformation}}=E_{\text{normal}}+E_{\text{shear}}+E_{\text{bend}}=\frac{1}{\left|\mathcal{N}\right|}{\displaystyle \sum _{i=1}^N{\displaystyle \sum _{j=i+1}^N{k}_{def}}}{\alpha }_{ij}{(d_{ij}-d_{ij}^0)}^2\\ {\mathrm{\alpha }}_{ij}=\{\begin{array}{l}1 \text{if}\hspace{0.17em}(i,j)\in \hspace{0.17em}\mathcal{N},\hfill \\ 0 \text{otherwise};\hfill \end{array}\end{array}$$

where k _def is the spring constant governing the energy of deformation, d_ij is the distance between electrodes i and j at their final determined locations, $d_{ij}^0$ is the original distance between electrodes i and j given their initial registered coordinates, and $\mathcal{N}$ is the set of all electrode pairs determined to be connected neighbors. The indicator function α_ij determines whether two electrodes, e_i and e_j are connected in the spring network. Within every grid or strip, we defined neighboring electrodes as connected if they were horizontally or vertically adjacent, if they were separated by two electrodes in the horizontal or vertical direction, or if they were separated by one electrode diagonally (Figure 3c). We directly identified neighbors within a grid or strip using the known layout of electrodes within that grid or strip. In this manner we captured normal, shear, and bend deformations (E _normal, E _bend, and E _shear, respectively). Electrodes on separate pieces of hardware were considered neighbors if their euclidean distance was within 15 mm, which is 1.5 times larger than the typical distance found between electrodes in the same grid or strip.

Because the initially registered locations give an accurate representation of electrode geometry but a poor position relative to the preoperative MRI surface, we wanted $k_{disp}\ll k_{def}$. This ensured that the overall geometry of the electrode grids and strips were retained, while allowing the position of the electrodes to move to the cortical surface. We wanted k _fit < k _anch since anchors, being based on intra‐operative photographs, yield more accurate electrode locations than naive projections (Pieters et al., 2013). But while we felt that the anchor points should play an important role in determining the final electrode locations, we did not feel it would be appropriate to set k _anch infinitely high since the locations of these anchor points are still subject to the inaccuracies of visual identification and therefore cannot be considered absolutely precise.

Searching the complete parameter space would be computationally intractable, and so we fixed k _disp and k _def. We reasoned that k _disp should be relatively low, since electrodes are known to shift from their CT coordinates and because the CT coordinates serve primarily as an initial estimate. We also reasoned that k _def should be relatively high since the geometry of the grid should remain mostly intact after implant. We therefore set these two parameters to be k _disp = 1 and k _def = 1,000, respectively. This established a limited space in which the remaining two parameters could be chosen. We used a sparse grid search over the remaining two parameters and evaluated the results on individual participants empirically, using visual inspection and error from the gold standard as metrics. We determined empirically that k _fit = 25 and k _anch = 200 yielded good results.

We performed optimization of Equation (1) using the fmincon function in MATLAB (The Mathworks Inc, Natick, MA). Optimization terminated when the change in total energy was less than 0.01. Electrode projection converged for all participants in an average of 110 ± 13 iterations (mean ± SEM) across participants with a maximum of 140 iterations.

2.6. Surface electrode mapping

To enable functional mapping within and across participants, we assigned mesh vertices to each electrode location on the smoothed pial surface surface to identify analogous electrode locations across participants. To do this, we defined a disk on the smoothed pial surface with a diameter equal to the exposed electrode diameter (3.0 mm) and centered at each electrode location. We then found the nearest vertex on the reconstructed brain surface to every point within the disc defined on the smoothed pial surface. We assigned all such identified vertices to that electrode (Kadipasaoglu et al., 2014).

2.7. Regions of interest

To conduct regions of interest (ROI) based analyses, we developed a method to generate a standard set of surface‐based ROIs which could be used across subjects. We first defined a set of ROI centers on an average template brain by sampling a subset of the surface's normalized mesh vertices. We ensured that the ROI centers were uniformly distributed by using a geodesic farthest point sampling algorithm (Peyré & Cohen, 2006). Conceptually, this procedure builds a subsampling such that each point added is the farthest geodesic distance from all previous points in the set, beginning with a random seed point. This method is flexible in that it allowed us to vary the number of ROIs simply by choosing when to terminate the procedure.

To evaluate the uniformity of the ROI centers' spatial distribution, we used the R‐statistic, given by $R=r_o/r_{CSR}$, which gives the observed average nearest neighbor (ANN) distance, r_o, as a fraction of the expected ANN distance of a completely spatially random distribution r _CSR (Clark & Evans, 1954). Note that a square lattice on a 2D plane has R = 2.00 and that the upper bound of R is 2.149. We found R = 2.06 for the fine sampling and R = 2.07 for the coarse grid, suggesting a uniform distribution of ROI centers on the average brain. However, due to the unique curvature patterns of individuals, we found that across participants, uniformity decreased to $R=1.72\pm 0.01$ and $R=1.76\pm 0.01$ for the fine and coarse grids, respectively. Although still highly uniform, this resulted in each participant's ANN distances between ROI centers being slightly below our targets (mean 4.7 ±0.07 mm, fine; $9.6\pm 0.12$ mm, coarse).

3. RESULTS

3.1. Electrode localization

We examined subdural strip and grid electrode locations in eleven participants with medication‐resistant epilepsy. We implemented an algorithm to accurately localize electrode contacts to the preoperative reconstructed cortical surface. In brief, we modified a previously described spring optimization algorithm (Dykstra et al., 2012) by using visually identified anchor points to guide localization (see Materials and Methods). We compared the final electrode locations to the locations of electrodes that were visually identified using intra‐operative photography, which we considered the gold standard. As such, because both the anchor point locations and the gold standard electrode locations rely upon the accuracy of intra‐operative photography, it is important to know how accurate we are in identifying these locations. To measure this, we compared the manually identified electrode locations in each participant between two independent raters and found that these locations differed by 2.25 ±0.12 mm. Moreover, it is also important to know to what extent electrodes may shift in the time between placement and recording. During the implantation procedure, electrode grids are routinely sewn to the overlying dura to prevent such shifts. Nevertheless, to confirm that electrode locations do not significantly shift during the monitoring period, in one case we had access to intra‐operative photographs taken during explantation of the hardware and could measure the displacement in electrode locations between placement and explantation. By identifying corresponding electrode contacts (n = 11) between images, we measured the average shift to be 1.90 ±0.10 mm (mean ± SEM).

For each participant, we calculated the distance between all gold standard electrode locations and the final electrode locations as determined by registration alone, by registration with the original optimization procedure, and by the modified, anchor‐based optimization procedure, in which we varied the number and spatial distribution of anchors. We used a Wilcoxon signed‐rank test for all of our statistical tests (which does not rely on assumptions of normality) and observed that the modified algorithm outperformed baseline registration and the original spring algorithm (Figure 4a). We found that using just a single anchor offers improvement over registration alone ( $T_{n=11,\hspace{0.17em}2-\text{tailed}}=66$; $p\le 0.001$) and over the original optimization procedure ( $T_{n=11,\hspace{0.17em}2-\text{tailed}}=66;p\le 0.001$). Moreover, using more anchors with higher inter‐anchor spacing yielded better results. Using five, maximally spaced anchors produced our best results (mean 2.01 ±0.15 mm), but even using two anchor points yielded an accuracy (2.64 ±0.25 mm) comparable to other approaches in the field.

Figure 4.

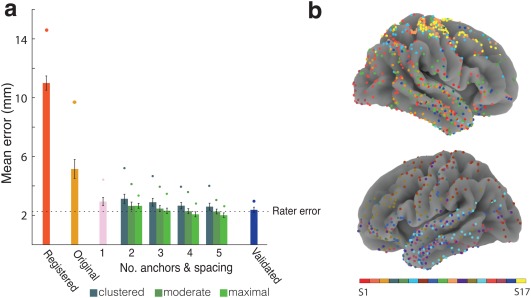
Algorithm Accuracy. (a) Mean distance between the location of the gold standard electrodes and localization by CT registration alone, original spring optimization without the use of anchor points, and optimization using one or more anchor points. When using more than one anchor point, mean distances are shown for different inter‐anchor distances. Each bar represents the average distance between final electrode locations and the locations of the gold standard electrodes averaged across the primary cohort of participants (with the exception of the “validated” bar, which reports the 5‐anchor, maximally spaced result across the validation cohort). Circles represent participants with maximum localization error, and error bars represent standard error. A dotted reference line is shown at the level of inter‐rater error. (b) Final location of subdural electrodes from all 17 participants color coded by participant and plotted on a population average brain [Color figure can be viewed at http://wileyonlinelibrary.com]

During the development of our localization procedure, we determined the spring constants in part by finding parameters that produced optimal localization results (see Materials and Methods). Therefore, it was critical to evaluate whether our localization algorithm performed equally well on an independent set of participants to ensure that the algorithm's success was not due to overfitting. We used six additional participants (S12‐S17) as a validation set and evaluated the results. Using a single anchor gave a mean error of 3.50 ± 0.35 mm, which was significantly lower than both the registered error (11.48 ± 0.56 mm, $T_{n=6,\hspace{0.17em}1-\text{tailed}}=21$; p = .016) and the original spring algorithm (6.03 ± 0.46 mm, $T_{n=6,\hspace{0.17em}1-\text{tailed}}=21$; p = .016). Using five anchors with maximum spacing produced a mean error of 2.29 ±0.36 mm.

There are several options for selecting which visually identified electrodes are to be used as anchor points. At one extreme, one could choose several neighboring electrodes as anchors, whereas at the other, one could select electrodes that are on opposite sides of the visible grid. We were interested in whether the spatial arrangement of the selected anchor points affects localization accuracy. To investigate this, we created three categories of anchor point arrangements: maximally‐spaced, moderately spaced, and clustered. The clustered category (and the separate, single‐anchor category) is based on identifying the centroid of all visible contacts and selecting anchor points only from neighboring contacts to that centroid. Conversely, for maximally spaced anchor points, we chose electrode contacts with the largest inter‐electrode distance. We found that as anchor points are spread further apart on the cortical surface, localization improves (ANOVA $F(2,3)=7.15$, p = .001), although a post hoc Tukey‐Kramer test did not suggest any significant difference between moderately and maximally spaced anchors. Increasing the total number of anchor points was also significantly helpful (ANOVA $F(2,3)=3.64$, p = .015). There was not a significant interaction between inter‐anchor distance and the number of anchors ( $F(6)=0.07$, p > .99).

3.2. Regions of interest

We were interested in developing a region of interest approach for aggregating and statistically analyzing iEEG activity from electrodes in analogous anatomical locations across participants. We intended to generate two grids of ROI centers with an average geodesic distance between ROI centers of 5 and 10 mm, allowing fine and coarse sampling of iEEG activity. By sampling 2,400 and 600 points, respectively, we generated uniformly distributed ROI centers (see Materials and Methods) with an average nearest neighbor (ANN) distance within 0.1 mm of our 5 mm and 10 mm targets (Figure 5a,c). Since the subsampling takes place on the normalized surface, the identified ROI centers correspond to analogous locations across participants (Figure 6a–c).

Figure 5.

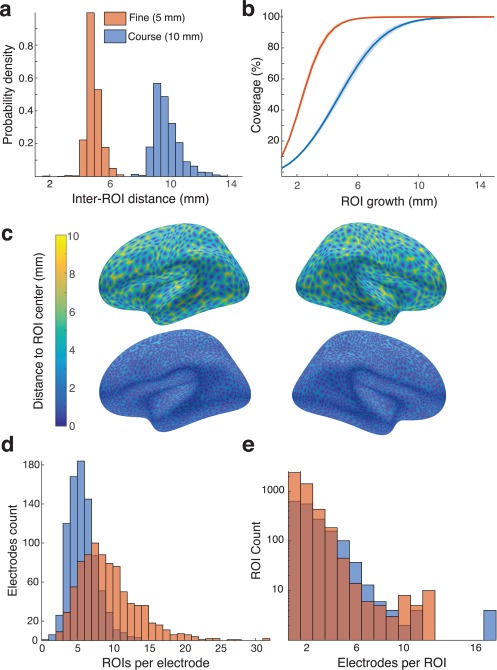
Regions of Interest. (a) Nearest‐neighbor distance was computed between all ROI centers on the average brain for fine and coarse spacing of the ROI centers. (b) ROIs were grown for each participant until 99.9 percent of the surface was covered. The geodesic radius needed to cover the standard brain is shown for both fine and coarse ROI centers. (c) ROI distribution on the average brain appeared uniform in the coarse (top) and fine (bottom) grids. (d) Each electrode was assigned to the nearest ROIs. Across all participants, the number of ROIs assigned to each electrode is shown as a distribution for both fine and coarse ROIs [Color figure can be viewed at http://wileyonlinelibrary.com]

Figure 6.

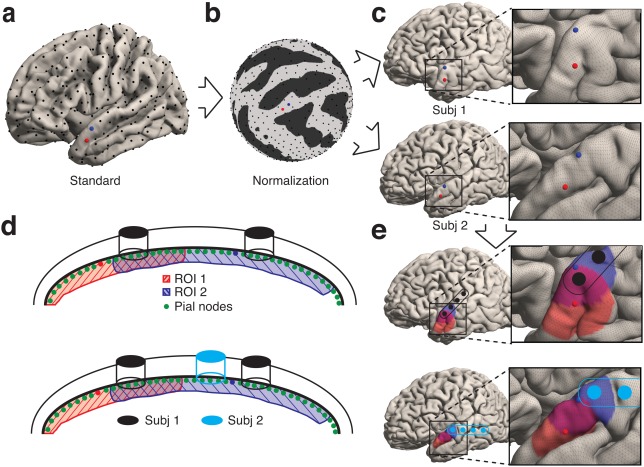
Electrode Mapping to ROIs. (a) ROI centers were chosen on the average brain with farthest point sampling until desired resolution was reached (coarse grid shown). (b) ROI center sampling was performed on the normalized pial mesh, allowing correspondence between participants. (c) ROI centers across participants are in analogous anatomical locations. (d) Each electrode is assigned to the nearest pial vertices and then to the closest ROIs. (e) ROIs are grown geodesically to cover the surface and frequently overlap. Each ROI detects activity from electrodes within its geodesically grown region [Color figure can be viewed at http://wileyonlinelibrary.com]

Having generated sets of ROI centers, we then radially grew geodesic, overlapping regions around each ROI center on each participant's surface to create a set of analogous ROIs for across‐participant analyses (Figure 5b). The radius of growth was increased until 99.9% of each surface was covered. Using the 5 mm inter‐ROI spacing, we found that we needed a geodesic radius of 8.8 ±0.3 mm around each ROI center. For the coarser 10 mm inter‐ROI spacing, the same coverage required a geodesic radius of 13.7 ±0.3 around each ROI center (Figure 5b). We assigned all surface vertices within an ROI's boundary to that ROI (Figure 6d,e). Consequently, ROIs may have overlapping coverage, and a surface vertex may be assigned to more than one ROI. As with the ROI centers, the vertices within each geodesically grown ROI are anatomically analogous across participants.

Finally, because we determined the location of each electrode on each participant's surface, we assigned all electrodes with any vertices within each ROI's boundary to that ROI (Figure 6d). In this manner, one ROI may be associated with more than one electrode, and one electrode may be associated with more than one ROI. However, because both electrode locations and ROIs are anatomically analogous across participants, iEEG electrode data aggregated into each ROI may be compared across participants. We observed that on average electrodes were assigned to 5.07 ±0.07 ROIs on the coarse grid and 9.31 ±0.13 ROIs on the fine grid while ROIs contained 2.40 ±0.05 electrodes on the coarse grid and 1.76 ±0.02 electrodes on the fine grid (Figure 5e,d).

To demonstrate how the constructed ROIs could be used to aggregate data across participants, we investigated changes in spectral power as three participants performed a simple motor task in which they were instructed to move either their hand or their foot (Figure 7a). When compared to a baseline period, we observed spatially localized effects in high frequency power (40–118 Hz) throughout the duration of movement. In each condition, these effects were observed in the expected sensorimotor cortices, both within individual participants (Figure 7b, bottom) and on the population average brain when aggregated into ROIs across participants (Figure 7b, top).

Figure 7.

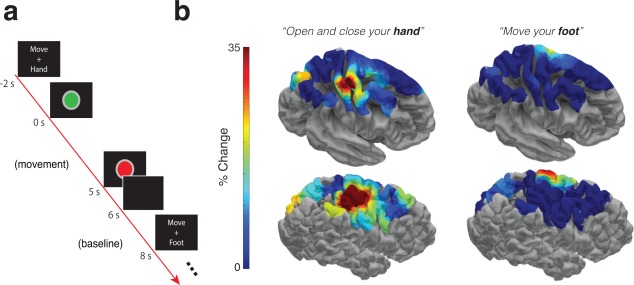
Motor Task Example. (a) Example trial from a task in which three participants were asked to move either their hand or their foot (contralateral to implant hemisphere). (b) Brain models depict the trial‐averaged increase in high frequency spectral power (40–118 Hz) during the five seconds of movement compared to a baseline period (left column hand, right column foot) plotted using the fine ROI resolution. We include the average response across participants depicted on an average brain surface (top), and the response of an individual example participant (bottom) [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

A necessary step for expanding the statistical tools available for the analysis of iEEG data is to develop a systematic way of comparing changes in neural activity across multiple participants. This requires accurately localizing iEEG electrodes and developing an approach for aggregating data from analogous anatomical locations across participants. We implement this goal here by first modifying previous electrode localization algorithms to additionally incorporate the use of manually identified anchor points (Dalal et al., 2008; Dykstra et al., 2012; Pieters et al., 2013; Yang et al., 2012). We then create evenly distributed and standardized ROIs that aggregate data from analogous cortical regions, enabling us to assess the consistency of activity at specific anatomical locations across multiple participants.

An important first step to attain this goal was localizing electrode contacts to each participant's smoothed pial surface, identified using the preoperative MRI. Implantation of subdural and depth electrodes routinely results in a parenchymal shift that makes it difficult to localize electrodes to the surface of the participant's brain. Several approaches have been proposed to address this issue (Dalal et al., 2008; Dykstra et al., 2012; Hermes et al., 2010; Pieters et al., 2013; Yang et al., 2012). Spring optimization algorithms are suitable for both grids and strips and offer the advantage of modeling inter‐electrode geometric relationships while simultaneously allowing for the nonuniform deformations often caused by brain shift. However, algorithms that take advantage of intra‐operative photography often outperform procedures that attempt to approximate locations without photographs. (Pieters et al., 2013).

We therefore built upon the spring optimization procedure (Dykstra et al., 2012) by including the additional use of anchor points identified using digital photography in the operating room. The use of intra‐operative photography to identify electrode locations has been well established (Dalal et al., 2008; Pieters et al., 2013; Yang et al., 2012). Our approach therefore combines the advantages of both spring optimization algorithms and manually identified anchor points, allowing accurate localization of grid and strip elements, as well as grids that are cut or arranged in an atypical arrangement. There are two limitations inherent in this approach, however. First, manually identifying electrode locations necessarily introduces some error, and therefore it is important that anchor points should only be selected if their visible location can be identified with high confidence. When we compared the manually identified locations between independent raters, we found that they were reassuringly consistent. Second, it is possible that the electrode locations may shift during the monitoring period following implantation, and because manual identification only relies on a single intra‐operative snapshot, it remains unknown whether the visual photograph represents the true electrode location. We were only able to verify that the electrode locations did not significantly shift in one case in which we captured an intra‐operative photograph during explantation. However, electrode grids are routinely sewn to the dura in multiple locations, which would minimize any such movement.

Despite these limitations, we found that our localization procedure identified accurate electrode locations when compared to those electrode locations manually identified. Accuracy minimally improved as we included more anchor points, but we were able to achieve sufficiently accurate localization with as few as two points. The optimization algorithm ensures that the designated anchor points inform the final position of nearby electrode locations, so many anchor points are unnecessary. In addition, accuracy improved as the space between anchor points increased, suggesting that the distributed locations of anchor points capture the overall geometry of the electrode locations. Of note, the accuracy that we attain using the addition of anchor points is comparable to the inter‐rater variability observed when manually identifying electrode contacts in the intra‐operative photographs. This suggests that localization using this semi‐automated algorithm approaches the upper limit of what is possible given the variability inherent in manual localization.

Recent approaches to the problem of localization have generally adopted two strategies: photography‐based labeling and projection algorithms (Table 2). On the one hand, intra‐operative photographs yield highly accurate information about electrode locations, but this approach is manually intensive (Dalal et al., 2008). On the other hand, projection algorithms are automated, but typically introduce inaccuracies (Dykstra et al., 2012; Hermes et al., 2010). The most accurate approaches combine both strategies, using procedures that manually identify two to four electrode locations at the corners and edges of the implanted strip or grid followed by a projection to the smoothed pial surface (Pieters et al., 2013; Yang et al., 2012). Studies using this hybrid approach, however, have based their localization procedure on the acquisition of a postoperative MRI. Hence, it is not clear whether the observed improvements are due to the combined hybrid approach, or whether the improved accuracy is due solely to the advantages offered by localization using a postoperative MRI.

Table 2.

Previously published methods

Author	Method	Postoperative MRI	Reported Error
Dalal et al. (2008)	photography	no	1.5 ± 0.5
Hermes et al. (2010)	projection	no	2.6 (median)
Dykstra et al. (2012)	spring model	no	2.53, 3.0
Yang et al. (2012)	projection with anchors	yes	0.95 ± 0.81
Pieters et al. (2013)	projection with anchors	yes	2.0

Indeed, many of the inaccuracies in localization can be partly resolved by using a transformation between the postoperative and preoperative MRIs. Using the postoperative MRI in this manner results in increased accuracy (LaViolette et al., 2011a; Pieters et al., 2013; Yang et al., 2012) and could also address the limitations related to manual identification of the electrode contacts and possible shifts in electrode locations. Here, we also adopt a hybrid approach, using electrode locations identified through intra‐operative photography to improve a projection algorithm. Importantly, however, in this case we extract initial electrode locations using a postoperative CT that is merged to the preoperative MRI. We were interested in achieving a high level of accuracy using the postoperative CT alone, and indeed find that the hybrid approach in this manner can offer significant improvements in accuracy that are comparable to the accuracy obtained with postoperative MRI. Obtaining postoperative CT images is standard in many epilepsy centers, and it is often the only imaging modality available during the postoperative period. Registration of the postoperative CT to the preoperative MRI requires co‐registering two separate imaging modalities, however, and risks introducing errors in localization. To minimize such errors, we used a previously validated registration algorithm, the LPC cost function (Saad et al., 2009), and found that this registration technique facilitated automation of the localization process without sacrificing accuracy.

To compare electrode activity from analogous anatomical locations across participants, we needed to standardize the anatomical space. Surface based normalization has been well established in functional imaging (Saad et al., 2009), and we borrow heavily from these methods. Normalizing surface anatomy in this manner has also been previously adapted in one study for iEEG data (Kadipasaoglu et al., 2014). We used surface based normalization to standardize all surfaces to a standard brain (Kadipasaoglu et al., 2014), then used icosahedral standardized sampling to establish an anatomical correspondence of vertex sets across patients (Saad et al., 2009). Hence, our approach is compatible with other methods of electrode localization as long as electrodes are assigned to nodes on participants' surfaces.

Although our localization approach projects electrodes to the smoothed pial surface, it is necessary to find each electrode's nearest points on the normalized surface so that these points can then be assigned to nearby ROIs. We represent each electrode as a disc on the smoothed pial surface, so the projection of all disc points results in a group of vertices on the participant's reconstructed surface. This allows an electrode that spans a small sulcus to potentially have points that are assigned to two different gyri (Kadipasaoglu et al., 2014). We note that projecting electrode contacts to the closest point on the surface introduces a small deviation from absolute location. This deviation, however, does not significantly affect inter‐electrode distances, how electrode contacts are anatomically defined, or how electrode contacts are aggregated into neighboring ROIs.

We were interested in creating standardized ROIs across participants to aggregate data from electrode contacts. Previous approaches for analyzing iEEG data across participants have relied on grouping electrodes into broad anatomical regions such as cortical lobes or gyri. Regions designated for comparison in these approaches are generally based on anatomical atlases, which require prior assumptions about function. However, atlases and even gyral regions can be coarse relative the spatial resolution offered by iEEG. Approaches that use surface based normalization have attempted to address this problem by aggregating data from different participants at the level of individual mesh vertices (Kadipasaoglu et al., 2014). Such an approach can certainly capture much of the variability between different participants. However, the size of the electrode contacts and the error in localization are both on the order of several millimeters. Thus, statistical analyses at the spatial resolution of the mesh indices (tenths of a millimeter) may at times be inappropriate. Indeed, data in these approaches are often either aggregated to the larger and coarser anatomical regions such as lobes or gyri or impose assumptions about cortical voltage propagation by using distance‐weighted decay functions.

Here, we offer an approach that takes advantage of surface based normalization to create a flexible set of standardized ROIs. Importantly, our approach creates a substrate for comparing activity at varying spatial scales across participants without making any a priori assumptions about the functional and anatomical architecture of the brain. We used farthest point subsampling to create ROIs uniformly spaced approximately every 5 and every 10 mm, but it is possible to aggregate iEEG data using ROIs with any degree of spatial precision that can more fairly represent the spatial resolution of the electrode contact and their localization. Appropriately spacing ROIs is an important factor in group analyses as the number of ROIs affects both the spatial resolution of interest and the number of multiple comparison tests needed in statistical analyses. By increasing the depth of subsampling, we were able to generate ROI centers that capture the spatial resolution of the relatively local iEEG sources while maintaining this balance. Furthermore, not only must these two competing factors be balanced, but given a desired spacing, it is important to evenly distribute ROIs over the cortex while minimizing their redundancy. We found that farthest point subsampling provided a uniformly distributed set of ROI centers.

By using geodesic growth around each ROI center on each participant's surface, we were able to identify cortical regions that are analogous across participants. Although electrical fields may spread as a function of euclidian distance, we implemented ROI growth using geodesic distance so that the aggregate activity represented in each ROI is derived from a single functional area of cortex (Kadipasaoglu et al., 2014; Oosterhof, Wiestler, Downing, & Diedrichsen, 2011). In this manner, no single ROI spans two different gyri, avoiding the possibility that functionally different areas of cortex would be averaged together in the same ROI. Indeed, an electrode contact may be localized to two different gyri if it lies on a sulcus between them. In these cases the activity of that electrode would map to two different ROIs. Moreover, ROIs constructed in this manner necessarily overlap to ensure complete coverage of the cortex. Depending on the size of the ROIs, more than one electrode may be assigned to an ROI, and a single electrode may be assigned to more than one ROI.

One concern when performing population analyses that is particular to iEEG data is the variability in the number of participants contributing data to different anatomical regions. For all group analyses, we can also calculate the number of participants with electrode locations contributing to each of our spatially defined ROIs. We can restrict drawing statistical conclusions across a population of participants to those ROIs that include data from a minimum number of participants. This number will depend on the statistical test and the size of the observed effect. Although the number of electrode contacts contributing data to each ROI will vary across participants, the aggregate data in each ROI from each participant is treated as an identical independent observation. Furthermore, because our ROIs are evenly spaced on the cortical surface, no individual electrode contact is over‐represented in contributing to the aggregate data for each ROI.

While our approach therefore enables comparisons in cortical activity across participants, one limitation is that the localization and aggregation of electrode data into standardized ROIs is strictly surface‐based. Hence, we do not account for depth electrodes. One possibility is to infer a deformation field from the output of our cortical localization process and apply this to depth electrodes. However, their locations will likely be misrepresented with this approach alone. Until better volumetric registration and standardization techniques are developed, identifying the location of depth electrodes may remain a manual process.

Nevertheless, the approach proposed here offers a number of advantages for systematically comparing neural activity across participants. First, aggregating data across participants is independent of the projection algorithm used to localize electrode contacts to the smoothed pial surface, as long as the surface and evenly spaced ROIs are standardized between participants. Second, the ROIs represent a well defined spatial region for which statistical results in individual participants can be aggregated. The size of these regions can be increased or decreased depending on the desired spatial resolution. Third, because each ROI is defined by a specific spatial location in a standard coordinate space, each ROI can be characterized by its three dimensional coordinates, Brodmann Area, gyrus, or lobe. This facilitates several other possible groupings for across‐participant analyses as alternatives to the ROIs themselves. Fourth, because both electrode locations and ROIs are identified in the individual surface, this approach enables inter‐modal comparisons with fMRI, for example, and other imaging techniques. And finally, this approach effectively allows us to treat every defined ROI in a manner similar to voxels defined for the standard brain in fMRI analyses. This opens up iEEG analysis to similar statistical tools available in the fMRI literature to assess the consistency of changes in neural activity across a population.

Trotta M, Cocjin J, Whitehead E, et al. Surface based electrode localization and standardized regions of interest for intracranial EEG. Hum Brain Mapp. 2018;39:709–721. 10.1002/hbm.23876