Abstract
A novel mega‐analytical approach that reduced methodological variance was evaluated using a multisite diffusion tensor imaging (DTI) fractional anisotropy (FA) data by comparing white matter integrity in people with schizophrenia to controls. Methodological variance was reduced through regression of variance captured from quality assurance (QA) and by using Marchenko–Pastur Principal Component Analysis (MP‐PCA) denoising. N = 192 (119 patients/73 controls) data sets were collected at three sites equipped with 3T MRI systems: GE MR750, GE HDx, and Siemens Trio. DTI protocol included five b = 0 and 60 diffusion‐sensitized gradient directions (b = 1,000 s/mm2). In‐house DTI QA protocol data was acquired weekly using a uniform phantom; factor analysis was used to distil into two orthogonal QA factors related to: SNR and FA. They were used as site‐specific covariates to perform mega‐analytic data aggregation. The effect size of patient‐control differences was compared to these reported by the enhancing neuro imaging genetics meta‐analysis (ENIGMA) consortium before and after regressing QA variance. Impact of MP‐PCA filtering was evaluated likewise. QA‐factors explained ∼3–4% variance in the whole‐brain average FA values per site. Regression of QA factors improved the effect size of schizophrenia on whole brain average FA values—from Cohen's d = .53 to .57—and improved the agreement between the regional pattern of FA differences observed in this study versus ENIGMA from r = .54 to .70. Application of MP‐PCA‐denoising further improved the agreement to r = .81. Regression of methodological variances captured by routine QA and advanced denoising that led to a better agreement with a large mega‐analytic study.
Keywords: DTI, mega‐analysis, multi‐site research, schizophrenia, QA
1. INTRODUCTION
Lower integrity of cerebral white matter (WM), quantified as reduced fractional anisotropy (FA) of water diffusion measured from diffusion tensor imaging (DTI), is a consistent finding in schizophrenia (Alba‐Ferrara & de Erausquin 2013; Ellison‐Wright & Bullmore 2009; Friedman et al., 2008; Glahn et al., 2013; Kelly et al., 2017; Kochunov & Hong 2014; Kubicki et al., 2007; Nazeri et al., 2012; Perez‐Iglesias et al., 2011; Phillips, Rogers, Barrett, Glahn, & Kochunov, 2012; Wright et al., 2015). FA deficits are hypothesized to be prominent in the associative WM fibers and responsible for neuropsychological deficits association with this disorder (Ellison‐Wright & Bullmore 2009; Friedman et al., 2008; Kochunov et al., 2017, 2016; Kubicki et al., 2007; Nazeri et al., 2012; Perez‐Iglesias et al., 2011). A challenge for evaluating regional WM deficits is the need for statistically powerful and representative samples that can be difficult to collect at a single site (Ioannidis 2014; Jahanshad et al., 2013). Multisite studies can collect larger and more representative samples but require pre‐processing steps to address site‐specific sources of methodological variance. The enhancing imaging genetics meta‐analysis (ENIGMA) consortium developed a multisite homogenization approach for DTI data to address methodological biases in multisite data (Jahanshad et al., 2013). We sought to improve upon this approach, by evaluating two new steps aimed at addressing site‐specific variances: (a) regression of the site‐specific variance captured through routine quality assurance (QA) program and (b) Marchenko–Pastur Principal Component Analysis (MP‐PCA)‐based noise reduction technique aimed at improving signal‐to‐noise ratio (SNR) and reporting potential artifacts that contribute to spatial nonuniformities of thermal noise. We tested these approaches in the data collected by the multicenter collaborative Social Processes Initiative In Neurobiology of the Schizophrenia(s) (SPINS) study.
We assessed the impact of regressing the site‐specific methodological variance and advanced denoising approach by comparing the effect size of schizophrenia on regional FA values to those published by the largest meta‐analytic analysis of regional FA deficits to date (N = 1,984/2,391 patients/controls, thirty independent cohorts worldwide) performed by ENIGMA (Kelly et al., 2017). The average effect size for regional FA values in ENIGMA was reported to be Cohen's d=∼.25 (Kelly et al., 2017). This suggested that a sample of N = 250 patients/250 controls is required to detect such an effect size. The SPINS sample (N = 192) is insufficiently powerful to reliably detect these regional differences. Therefore, the aim was to study the changes in the agreement in the pattern of regional difference between the SPINS and ENIGMA results. This study was focused on FA and did not explore other diffusion parameters (axial, radial, and mean diffusivities); FA was selected because it is the most commonly studied diffusion‐metric in schizophrenia research, and is the metric most consistently altered between schizophrenia patients and matched controls (Kelly et al., 2017).
2. METHODS
2.1. Subjects
The study was performed in N = 192 participants (average age =32.7 ± 10.1 years), including n = 119 schizophrenia patients (age = 33.6 ± 13.3) and n = 73 controls (age = 31.2 ± 10.2) collected at three sites (Table 1). Each site collected both patients and controls. Data for N = 84 participants were collected at the Centre for Addiction and Mental Health, Toronto (CAMH); N = 60 at the Maryland Psychiatric Research Center (MPRC), Baltimore; and N = 47 at the Zucker‐Hillside Hospital (ZHH), New York City. The demographic information is summarized in Table 1. Uniform clinical assessment and exclusion criteria were maintained across the three sites. The local Internal Review Boards approved the studies, and informed written consent was obtained from all participants. All participants had no current or past neurological conditions or major medical conditions. Patients were diagnosed with either schizophrenia or schizoaffective disorder as determined by the Structured Clinical Interview for DSM‐IV or IV‐TR (SCID). Controls had no Axis I psychiatric disorder as determined by the SCID. With the exception of nicotine, participants were excluded if they had DSM‐IV substance abuse in the last three months or substance dependence within the past six months. Other exclusion criteria included diagnosis with uncontrolled hypertension, type 2 diabetes, heart disorders, or a major neurological event such as stroke or transient ischemic attack.
Table 1.
Subject demographics for the Centre for Addiction and Mental Health (CAMH), Maryland Psychiatric Research Center (MPRC), and Zucker Hillside Hospital (ZHH) sites
| CAMH | MPRC | ZHH | ||||
|---|---|---|---|---|---|---|
| Patients (34M/17F) | Controls (17M/16F) | Patients (36M/8F) | Controls (13M/8F) | Patients (15M/14F) | Controls (9M/9F) | |
| Average Age, Range (years) |
28.9 ± 9.3 18–50 |
25.9 ± 6.7 18–47 |
37.9 ± 10.5 19–55 |
38.5 ± 11.1 20–55 |
36.6 ± 8.8 23–55 |
32.6 ± 9.4 20–50 |
|
BPRS (total) |
29.8 ± 6.8 | N/A | 33.5 ± 8.8 | N/A | 30.9 ± 9.2 | N/A |
| Age‐of‐Onset (years) | 21.3 ± 5.6 | N/A | 20.3 ± 6.3 | N/A | 18.9 ± 5.9 | N/A |
| Illness Duration (years) | 8.9 ± 7.2 | N/A | 15.4 ± 11.2 | N/A | 16.4 ± 11.3 | N/A |
|
Education (year) |
13.1 ± 7.2 | 15.5 ± 2.0 | 13.1 ± 2.8 | 15.7 ± 1.9 | 13.4 ± 3.2 | 15.2 ± 2.2 |
| IQ | 108.1 ± 16.2 | 116.5 ± 8.4 | 100.1 ± 20.6 | 115.5 ± 9.6 | 96.3 ± 20.6 | 107.5 ± 14.6 |
|
Handedness (% right) |
84% | 91% | 86% | 91% | 84% | 72% |
|
Medication Dose (CPZ) |
376.3 ± 270.1 | 543.3 ± 387.4 | 471.3 ± 426.5 | |||
| Current Smokers | 31% | 18% | 39% | 35% | 41% | 12% |
| FTND | 3.6 ± 3.0 | |||||
Severity of psychiatric symptoms was ascertained using the Brief Psychiatric Rating Scale (BPRS). Antipsychotic medication dose is provided in the chlorpromazine equivalent dose (mg/day). The severity of tobacco dependence was ascertained using the Fagerstrom Test for Nicotine Dependence (FTDN).
2.2. Diffusion tensor imaging
Imaging data were collected using 3T MRI systems and multichannel head coils. A homogenized diffusion imaging protocol was developed for this study and implemented on each site using a consistent set of 60 gradient vectors (b = 1,000 s/mm2) and five b = 0 volumes. Details of the implementation of the protocol at each site are summarized in Table 2.
Table 2.
DTI sequence parameters for Centre for Addiction and Mental Health (CAMH), Maryland Psychiatric Research Center (MPRC), and Zucker Hillside Hospital (ZHH) sites
| CAMH | MPRC | ZHH | |
|---|---|---|---|
| MRI system | GE MR750 Discovery | Siemens Trio | GE HDx |
| Year of Installation | 2010 | 2011 | 2004 |
| Head Coil | 8‐channel | 12‐channel | 8‐channel |
| Acceleration | Asset=2 | GRAPPA=2 | Asset=2 |
| Echo Time (ms) | 88 | 85 | 88 |
| Repetition Time (ms) | 8,800 | 8,800 | 17,000 |
| Flip Angle (degrees) | 90/180/180 | 90/180 | 90/180/180 |
| FOV (mm) | 256 | 256 | 256 |
| In‐plane resolution (mm) | 2.0 × 2.0 | 2.0 × 2.0 | 2.0 × 2.0 |
| Slice Thickness (mm) | 2.0 | 2.0 | 2.0 |
| Number of Slices | 66 | 66 | 66 |
Partial k‐space acceleration techniques, Array Spatial Sensitivity Encoding Technique (Asset), and Generalized Autocalibrating Partially Parallel Acquisitions (GRAPPA) were used on GE and Siemens scanners, respectively, to reduce effective TE and TE by undersampling k‐space along the phase encoding direction. A twice refocused spin‐echo EPI sequence was used on the GE scanners to improve spatial distortions. A refocused monopolar EPI sequence was used on the Siemens scanner to improve SNR.
2.3. Image processing
DTI data from the three sites was processed using the ENIGMA‐DTI analysis pipeline (http://enigma.ini.usc.edu/ongoing/dti-working-group/), which includes quality control and assurance QC/QA steps. One deviation from ENIGMA‐DTI protocol was inclusion of the principal component analysis (PCA)‐based approach for automatic removal of noise‐specific components, developed by Veraart, Fieremans, & Novikov (2016; Veraart, Novikov, et al., 2016). The MP‐PCA approach differs from traditional denoising approaches that improve SNR via spatial smoothing. Instead the MP‐PCA approach quantifies the principal components that are fundamentally associated with thermal noise signal in magnitude MRI data. Noise contributes randomly to voxel‐wise intensity values, but its contribution to the histogram of the eigenvalues of covariance matrix is deterministic (Veraart, Novikov, et al., 2016) and its eigenvalues are described by the Marchenko–Pastur (MP) distribution (Marchenko & Pastur 1967). The MP‐PCA approach estimates the noise level and the number of significant signal components and regresses eigenvalues related to noise while not affecting the temporal or spatial domains of the data (Veraart, Novikov, et al., 2016). Quantification and regression of thermal noise can both enhance SNR and identify the spatial patterns of noise distribution within data (Veraart, Novikov, et al., 2016) (Figure S1, see Supporting Information). The spatial distribution of thermal noise is independent of the underlying tissue type and, therefore, should have uniform spatial distribution(Veraart, Novikov, et al., 2016). Spatial heterogeneity in the noise component may serve as an important QA parameter that provides information regarding the linearity and noise properties of the receiving elements of the RF coil as shown by artifacts observed in the data from one of the sites (Figure S1, see Supporting Information). MP‐PCA denoising was applied to raw DTI data using the default filter setting. Both raw and MP‐PCA filtered data were processed using the ENIGMA‐DTI pipeline.
Next, DTI data were corrected for motion and eddy current distortions using the eddy correction tool distributed as a part of FMRIB Software Library (FSL, “eddy_correct”) package (Smith et al., 2006). FA maps were then generated by voxel‐wise fitting of the local diffusion tensor. Next, individual FA maps were warped to an ENIGMA‐DTI template and projected onto the ENIGMA‐DTI skeleton that represents the middle of the tract of major white matter structures. ENIGMA‐DTI per‐tract average values were calculated by averaging values along tract regions of interest in both hemispheres. Overall average FA values were calculated by averaging values for the entire white matter skeleton, including the tract regions of interest and peripheral white matter. DTI data is sensitive to artifacts brought about by subject's motion (Yendiki, Koldewyn, Kakunoori, Kanwisher, & Fischl, 2014). All data included in the analysis passed the ENIGMA‐DTI QA/QC adopted from the report by Acheson et al. (2017). The QA/QC steps included: visual inspection of raw and FA images, followed by calculating the frame‐wise displacement and the average projection distance onto the skeleton.
2.4. DTI quality assurance
DTI QA was performed one to two times per week following each scanner reboot. The details of the QA protocol are discussed elsewhere (Chavez et al., 2017). In short, the spherical (d = 17.5 cm) agar‐gel filled BIRN phantom (Biomedical Informatics Research Network) was used. The phantoms were stored in the scanner rooms to ensure temperature consistency. The QA protocol parameters matched imaging parameters used by the site. QA data were processed by a centralized automated QA pipeline (https://github.com/josephdviviano/qa-dti) (Chavez et al., 2017). The average signal‐to‐noise ratio (SNR) measurements for b = 0 and b = 1,000 s/mm2 images and the average and standard deviation of the fractional anisotropy (FA) measurements showed trending correlations with whole‐brain FA values in subjects. We included these measurements as potential explanatory variables for site‐specific methodological variance.
The QA sessions were matched‐in‐time to the human imaging session. For each site we chose the closest QA session to the human imaging session (average time interval = 2.5 ± 1.1 days). Factor analysis was performed on the QA measures to distill orthogonal measurements of scanner stability. Factor analysis used principal components analysis (PCA) to extract linear composites of correlated variables with eigenvalues > 1. MP‐PCA yielded eigenvalues describing the amount of variance among variables explained by a factor. A varimax rotation was used to remove collinearity (e.g., to orthogonalize individual eigenvectors). The factor analysis yielded factor loadings (correlations between a variable and a factor) and factor scores (a standardized score on each factor).
We compared the effect of the regression of the site‐specific QA factor scores by comparing effect sizes observed in this study to these published by the ENIGMA‐schizophrenia working group in the largest DTI study of patient‐control differences in this disorder (http://www.enigma-viewer.org) (Kelly et al., 2017). Specifically, we compared the regional FA differences observed here with ENIGMA's patient‐control effect sizes across white matter regions in the brain (Table 5). The SPINS data were collected past the deadline for the submission to ENIGMA project and, therefore, can be treated as an independent replication sample. The results provide a definitive and independent assessment of white matter regions most vulnerable to schizophrenia.
Table 5.
Effect size (Cohen's d) of patient‐control differences for whole‐brain and regional FA measurements
| Tract |
ENIGMA Cohen's d (p value) * |
Mega analysis (age and sex) Cohen's d (p value) |
Mega analysis (age, sex and qa factors) Cohen's d (p value) |
MP‐PCA mega analysis (age and sex) Cohen's d (p value) |
MP‐PCA mega analysis (age, sex, qa factors) Cohen's d (p value |
Fiber type | Connections |
|---|---|---|---|---|---|---|---|
| Whole‐Brain Average | .42 (4 × 10−24) | .55 (.0006) | .56 (.0005) | .57 (.0002) | .55 (.0002) | ||
| Regional | |||||||
| Genu (GCC) | .37 (1 × 10−18) | .39 (.015) | .37 (.0195) | .38 (.01) | .36 (.02) | C | Cerebral Hemispheres |
| Body (BCC) | .39 (3 × 10−18) | .24 (.12) | .34 (.0330) | .30 (.04) | .37 (.01) | C | Cerebral Hemispheres |
| Splenium (SCC) | .22 (4 × 10−6) | .31 (.049) | .29 (.0608) | .29 (.04) | .29 (.04) | C | Cerebral Hemispheres |
| Anterior CR (ACR) | .40 (9 × 10−19) | .37 (.021) | .35 (.0278) | .35 (.02) | .34 (.02) | A/P/C | Cortical/Subcortical |
| Superior CR (SCR) | .15 (7 × 10−6) | .00 (.98) | .03 (.8493) | .02 (.9) | .05 (.8) | A/P/C | Cortical/Subcortical |
| Posterior CR (PCR) | .25 (2 × 10−12) | .12 (.44) | .15 (.3455) | .14 (.36) | .20 (.18) | A/P/C | Cortical/Subcortical |
| Cingulum (CGC) | .27 (3 × 10−9) | .26 (.09) | .22 (.1812) | .26 (.08) | .36 (.02) | A | Cingulate Gyrus/Hippocampus |
| Cortico‐spinal tract (CST) | .04 (.3) | .18 (.25) | .07 (.6526) | .14 (.44) | .04 (.98) | P | Cortical/Spinal Cord |
| External Capsule (EC) | .21 (1 × 10−7) | .21 (.17) | .26 (.0915) | .19 (.17) | .20 (.12) | A | Frontal/Temporal/Occipital |
| Internal Capsule (IC) | .18 (2 × 10−5) | .37 (.020) | .33 (.0343) | .32 (.02) | .20 (.12) | P | Subcortical/Brainstem/Cortex |
| Fornix (FX) | .31 (7 × 10−12) | .32 (.043) | .36 (.0230) | .33 (.03) | .34 (.02) | P/C | Hippocampus/Thalamus |
| Inferior Fronto‐Occipital (IFO) | .11 (.003) | .25 (.10) | .25 (.1075) | .25 (.10) | .24 (.11) | A | Frontal/Temporal/Occipital |
| Superior Fronto‐Occipital (SFO) | .29 (4 × 10−8) | .14 (.38) | .16 (.3305) | .11 (.35) | .11 (.35) | A | Frontal/Parietal/Occipital |
| Superior Longitudinal Fasciculus (SLF) | .22 (6 × 10−8) | .29 (.06) | .21 (.1848) | .29 (.04) | .23 (.11) | A | Frontal/Temporal/Occipital |
| Sagittal Stratum (SS) | .30 (5 × 10−14) | .46 (.004) | .41 (.0095) | .43 (.004) | .38 (.01) | A/P | Subcortical/Temporal/Occipital |
| Uncinate Fasciculus (UNC) | .16 (9 × 10−7) | .25 (.12) | .23 (.1424) | .20 (.18) | .20 (.18) | P | Hypothalamus/Orbitofrontal |
First column shows ENIGMA effects sizes (Kelly et al., 2017). SPIN‐Mega analysis results are shown after correction for covariates, in parenthesis, including age, sex, and QA factors (second and third column) and following MP‐PCA denoising and correction for covariates.
2.5. Mega‐analysis
The ENIGMA‐DTI mega‐analysis algorithm was used to combine the data into a single population following regression of nuisance covariates and data homogenization. The goal of this analysis was to investigate the impact of the regression of QA‐related variance on the overall effect size of schizophrenia on the whole‐brain average and regional FA values. The ENIGMA‐DTI mega‐analysis uses two normalization steps: regression of covariates, per cohort, followed by the per‐cohort inverse Gaussian normalization of data (Kochunov et al., 2014). This produced the mega‐analytic sample to quantify the significance of the global and regional differences in the FA values and calculating effect size (Cohen's d). Four analyses were conducted: the first used the standard per‐site covariates (age, sex, age2, age × sex, age2 × sex), followed by the standard and QA covariates (FA and SNR factors), followed by denoising and the standard covariates and the final analysis combined denoising with the standard and QA covariates.
3. RESULTS
3.1. Extraction of QA factors
Temporal stability plots for the factorized and raw QA measures are provided in Supporting Information (Figures S2 and S3). Overall, all three system demonstrated a good stability (variance < 5%) across the 60 week period of data collection. Factor analysis in the SNR b = 0, SNR b = 1,000, average FA and standard deviation FA measures produced two orthogonal factors that explained 94%, 92%, and 97% of total variance in QA scores for the CAMH, MPRC and ZHH sites respectively (Table 3). The pattern of factor loading was similar for all three sites—with SNR and FA measurements loading on separate factors (Table 3).
Table 3.
Factor analyses using principal component extraction and orthogonalization were performed on QA data collected at the three sites
| SNR factor loading | FA factor loading | |
|---|---|---|
| CAMH | ||
| SNRb0 | .98 | –.06 |
| SNRdwi | .97 | –.05 |
| Average FA | –.64 | .72 |
| StdDev FA | .35 | .98 |
| MPRC | ||
| SNRb0 | .96 | –.12 |
| SNRdwi | .97 | –.06 |
| Average FA | –.10 | .93 |
| StdDev FA | .05 | .93 |
| ZHH | ||
| SNRb0 | .98 | –.17 |
| SNRdwi | .97 | –.14 |
| Average FA | –.89 | .41 |
| StdDev FA | –.18 | .98 |
3.2. Stability of QA factors
The scatter plot of QA factors over the week of scanning demonstrates that MPRC and ZHH sites experienced significant (p < .01) linear changes in QA factors with time on one or both factors (Supporting Information Figure S2). The MPRC site showed significant increase in both SNR and QA factors (r = .37 and .51, p < .02). The ZHH site showed significant increase in SNR factor (r = .71, p < .001).
3.3. Correlation between QA factors and average FA values
The two orthogonal QA factors explained ∼8.6% of the individual variance in the whole‐brain FA values and this was significant for the MPRC site (11% variance explained, p = .047) with the correlation coefficients shown in Table 4. Only the FA factor showed consistent negative correlation with FA values at all three sites (r=−.22, −.06, and −.24).
Table 4.
Pearson correlation coefficients between average FA values and two orthogonal QA factors and percent variance in average FA explained by two factors based on linear regression analysis
| Site | SNR factor | FA factor | % Variance explained (p value) |
|---|---|---|---|
| CAMH | .03 | –.22 | 11.0 (p=.047) |
| MPRC | .09 | –.04 | 7.5 (p=.11) |
| ZHH | –.08 | –.24 | 11.5 (p=.16) |
3.4. Effect of diagnosis before and after regression of QA factors
Patients showed lower average FA values than controls in each of three samples, after regression of age and sex effects (Figure 1, Table 5). This difference was only significant for MPRC and ZHH sites (Cohen's d = .82 and .60, p = .003 and .047 for MPRC and ZHH, respectively). The patient‐control difference for CAMH sample were not significant (Cohen's d = .25, p = .23).
Figure 1.
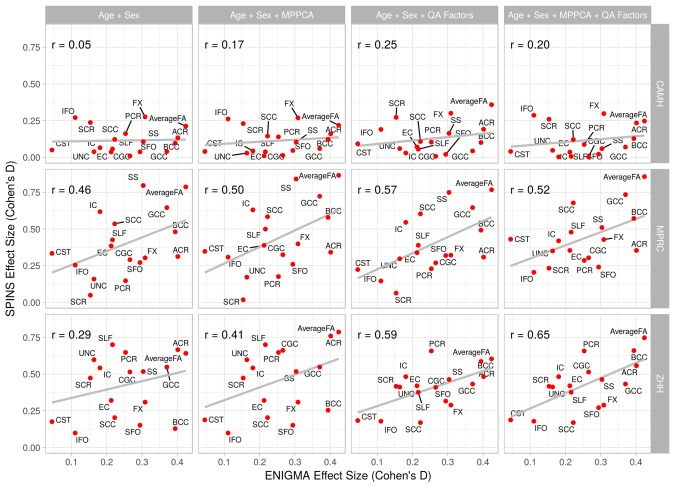
Correlation between regional effects of diagnosis (Cohen's d values) for each of the three sites versus ENIGMA effect sizes plotted after regression of age and sex, QA‐factors, and MP‐PCA denoising [Color figure can be viewed at http://wileyonlinelibrary.com]
The pattern of regional d values for each site was plotted versus effect sizes published by ENIGMA (Figure 1, Table 5). The correlation with ENIGMA pattern approached significance for MPRC sample (r = .46, p = .05). At CAMH and ZHH this correlation was not significant (r = .5, r = .29, p > .1).
Following inclusion of the QA factors Cohen's d values for CAMH improved from d = .25 to d = .31 but remained nonsignificant (p = .16). The effect sizes for MPRC and ZHH were unchanged (Cohen's d = .78 and .62, p = .004 and .048 for MPRC and ZHH, respectively). The correlation coefficients between per‐site effect size and ENIGMA were improved (Figure 1). Changes were observed for all three sites: CAMH (r = .05 to .25), MPRC (r = .46 to .57) and ZHH (r = .29 to .59). The correlation for both MPRC and ZHH became significant (p=∼.01). The correlation for CAMH remained nonsignificant (p = .13).
3.5. Effect of diagnosis after MP‐PCA‐denoising and regression of QA factors
PCA denoising led to improvements in the effect size for whole‐brain FA average for MPRC and ZHH sites (Cohen's d = .85 and .78, p = .002 and .020 for MPRC and ZHH, respectively). The patient‐control difference for CAMH sample remained nonsignificant (Cohen's d = .22, p = .25). Inclusion of QA factors did not cause a significant change (p > .5) in effect size for MPRC and ZHH sites (Cohen's d= .86 and .76, p = .002 and .020 for MPRC and ZHH, respectively).
The patterns of regional effect differences for each site were plotted versus effect sizes published by ENIGMA (Figure 1, Table 5). The MP‐PCA denoising improved correlation with ENIGMA pattern (r = .17, .50, and .41 for CAMH, MPRC, and ZHH) this correlation.
3.6. Mega‐analyses: Effect of diagnosis before and after MP‐PCA denoising and inclusion of QA factors
The mega‐analyses of schizophrenia‐related FA difference while accounting for age and sex demonstrated significantly reduced global FA values in patients compared to controls (Cohen's d = .55, p = .0006). MP‐PCA denoising led to a slight increase in the effect size and significance (Cohen's d = .57, p = .0002).
Regional pattern of mega‐analytical patient‐control FA difference was significantly correlated with that reported by the ENIGMA schizophrenia analysis (r = .54, p = .02; Figure 2). MP‐PCA denoising improved this correlation (r = .64, p = .004). Inclusion of QA factors in the regression of site‐specific parameters slightly improved the patient control difference for global FA values (r = .70, p = .001). The best agreement was observed following MP‐PCA and regression of QA factors (r = .81, p = .0001; Figure 2, Table 5).
Figure 2.
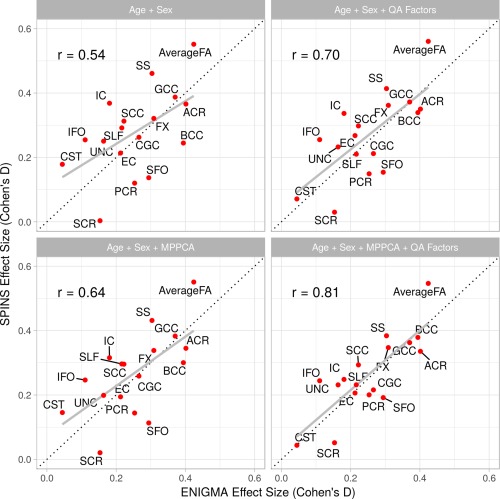
Comparison of regional mega‐analytic effect sizes following inclusion of the QA factors and MP‐PCA denoising [Color figure can be viewed at http://wileyonlinelibrary.com]
4. DISCUSSION
Many neuroimaging studies, such as the Social Processes Initiative in Neurobiology of Schizophrenia(s) (SPINS), use a multisite design to collect statistically powerful data sets across diverse sites, MRI scanners, or platforms. DTI places a heavy demand on the stability of the MRI hardware; we therefore proposed a quantitative DTI QA protocol and data analysis to capture potential methodological variances (Chavez et al., 2017). Quantitative metrics measured by this approach are sensitive to small drifts in hardware performance that do not produce detectable image artifacts (Chavez et al., 2017; Wang, Seo, Chia, & Rollins, 2011). We show that regression of this variance improves consistency of effect sizes across sites and makes the overall findings more agreeable with the findings of larger studies. In parallel, we show that a novel denoising technique that removes thermal noise from DTI images helps to improve the agreement of biological signal. Combining these two approaches produced the best outcome in terms of agreement between SPINS findings and those published in the largest cohort to date.
The two QA factors loaded on the SNR of the diffusion images and the average and standard deviation of FA values in the phantom. Longitudinal changes in SNR measurements may signify variability in the transmit/receive RF system, such as variance in the coil elements/pre‐amplifiers/amplifiers and other system instabilities. In a noise‐free, uniform agar‐gel phantom, water is expected to diffuse freely in all directions, leading to zero average FA values (Friedman, Glover, & Fbirn Consortium, 2006; Friedman, Glover, Krenz, & Magnotta, 2006). The measurement of FA from an agar‐gel phantom simultaneously captures the effect of noise, gradient instability, and gradient nonlinearity, as suggested by Wang and colleagues (Chavez et al., 2017; Wang et al., 2011).
Plots of factorized QA metrics over the two‐year period of data collection showed that all three sites demonstrated good stability (<5% variance) (Chavez et al., 2017). However, the time‐related trends of factorized QA metrics differed across sites. The SNR factor showed significant negative correlation with time for CAMH and a positive correlation for MPRC and ZHH (Figure 1). The FA factor showed significant positive correlation with time for MPRC and no changes for two other sites. Such deviations are expected for a multisite study, as system performances for different vendors/models are rarely consistent across sites or time.
Inclusion of the methodological variance captured from QA into the data analysis improved the agreement between the effect sizes among global and regional effect values observed in SPINS sample and those published by ENIGMA. Two orthogonal QA factors explained between 7.5 and 11.5% of the intersubject variance per site. Both QA factors contributed to explaining methodological variances observed in human FA values; the effect of removal of this variance was site‐specific and led to both higher and lower effect sizes. For instance, for all three sites, higher average FA values in the FBIRN phantom were associated with lower FA values in human subjects scanned the same week. Such an erroneous variance may both increase and decrease the observed effect sizes per site. The nonzero average FA values in the phantom is the consequence of mismatches between the recorded gradient direction/b value and these executed by the gradient system (Wang et al., 2011). Deviations between the expected and the executed gradients, as well contamination by noise may cause both reduced and increased voxel‐wise FA values in human participants by introducing fit error into the DTI model.
PCA denoising further improved agreement. DTI is an SNR‐limited technique but increasing SNR with longer scan time can lead to a diminishing return due to subject motion and other physiological artifacts (Hansen, Lund, Sangill, & Jespersen, 2013; Hansen et al., 2016; Poot, den Dekker, Achten, Verhoye, & Sijbers, 2010; Veraart, Novikov, et al., 2016). Spatial smoothing such as Gaussian kernel filtering are not appropriate for improving SNR in DTI as spatial averaging of the signal from nearby voxels may interfere with the fitting of the diffusion tensor model (Molloy, Meyerand, & Birn, 2014; Triantafyllou, Hoge, & Wald, 2006). Instead, advanced denoising techniques can improve SNR characteristics and fidelity of DTI‐derived parameters by taking advantage of the spatial and temporal redundancy of the data. We used a MP‐PCA‐based denoising technique to reduce signal fluctuations rooted in thermal noise and hence increase the SNR without altering the spatial resolution (Supporting Information Figure S2). The thermal noise‐selective nature is based on data redundancy in the MP‐PCA domain using universal properties of the eigenspectrum of random covariance matrices (Veraart, Novikov, et al., 2016). The MP‐PCA‐denoising brought the biggest improvements in the SNR‐limited ZHH data that was collected with an older MRI scanner (Supporting Information Figure S1). It also revealed regional inhomogeneity of the noise structure in that data set, which may be used as an important characteristic for future QA design. Conversely, MP‐PCA denoising only showed minor changes in the MPRC data set that was collected with the newest MRI scanner and a 32‐channel coil (Supporting Information Figure S2). The changes in CAMH data set were intermediate.
In summary, regression of site‐specific QA factors and application of MP‐PCA‐based denoising produced improved correlation between regional patterns of FA deficits observed in SPINS subjects and these published by the largest‐to‐date meta‐analysis study (N = 1,984/2,391 patients/controls). The observed improvements were modest but showed the outcomes of the SPINS study now more faithfully approximate the expected results. Our experiment demonstrates the importance of well‐powered samples in solving the problems of reproducibility in biomedical research. We used ENIGMA regional effect sizes as the “gold standard” to study the impact of data homogenization steps. The effect of diagnosis on FA values varied among the three sites due to differences in sample and methodological variance. The ZHH and MPRC samples showed higher effect sizes than ENIGMA, while CAMH sample showed only modest effect size. The mega‐analytic aggregation with regression of methodological and noise‐related variances improved the agreement between SPINS and ENIGMA findings. The SPINS sample was insufficiently powerful to detect regional findings and regression of methodological variance reduced significance of some of the regional effects despite providing a better agreement with ENIGMA. Therefore, the comparison with ENIGMA was used to show that smaller samples can achieve the expected patter of effect without achieving statistical significance.
Future directions should focus on quantifying regional site‐specific QA variance. Present assessment was aimed at overall quantification of the site‐specific variance. The spatial maps of the noise derived from the MP‐PCA approach indicated that methodological variance was regionally variable presumably due to nonlinearity in RF‐receiving elements of the coil or reconstruction algorithms or other scanner hardware or software related problems. Our observations should stimulate development of QA phantoms that approximate both the geometry of a typical human head and the nonanisotropy of human white matter for deriving regional QA indices.
5. CONCLUSION
Regressing methodological variances captured via a DTI‐specific QA program and reducing signal variances using an advanced denoising approach made the outcomes of a relatively smaller multicenter study more reproducible as judged by comparison with the largest meta‐analyses to date.
Supporting information
Additional Supporting Information may be found online in the supporting information tab for this article.
Supporting Information
ACKNOWLEDGMENTS
Support was received from NIH grants 1/3R01MH102324, 2/3R01MH102324, 3/3R01MH102324, R01EB015611. This work was also supported in part by the NIH Big Data to Knowledge (BD2K) Initiative (U54 EB020403).
Kochunov P, Dickie EW, Viviano JD, et al. Integration of routine QA data into mega‐analysis may improve quality and sensitivity of multisite diffusion tensor imaging studies. Hum Brain Mapp. 2018;39:1015–1023. 10.1002/hbm.23900
Funding information NIH, Grant/Award Numbers: 1/3R01MH102324, 2/3R01MH102324, 3/3R01MH102324, R01EB015611; NIH Big Data to Knowledge (BD2K) Initiative (U54 EB020403)
REFERENCES
- Acheson, A. , Wijtenburg, S. , Rowland, L. , Winkler, A. , Mathias, C. W. , Hong, L. , … Dougherty, D. D. (2017). Reproducibility of tract‐based white matter microstructural measures using the ENIGMA‐DTI protocol. Brain and Behavior, 7(2), e00615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alba‐Ferrara, L. M. , & de Erausquin, G. A. (2013). What does anisotropy measure? Insights from increased and decreased anisotropy in selective fiber tracts in schizophrenia. Frontiers in Integrative Neuroscience, 7, 9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chavez, S. , Viviano, J. , Zamyadi, M. , Kingsley, P. , Kochunov, P. , Strothers, S. , & Voineskos, A. (2017). A novel DTI‐QA tool: Automated metric extraction exploiting the sphericity of an agar filled phantom. Magnetic Resonance Imaging, 46, 28–39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellison‐Wright, I. , & Bullmore, E. (2009). Meta‐analysis of diffusion tensor imaging studies in schizophrenia. Schizophrenia Research, 108(1–3), 3–10. [DOI] [PubMed] [Google Scholar]
- Friedman, J. I. , Tang, C. , Carpenter, D. , Buchsbaum, M. , Schmeidler, J. , Flanagan, L. , … Davis, K. L. (2008). Diffusion tensor imaging findings in first‐episode and chronic schizophrenia patients. The American Journal of Psychiatry, 165(8), 1024–1032. [DOI] [PubMed] [Google Scholar]
- Friedman, L. , Glover, G. H. , & Fbirn Consortium. (2006). Reducing interscanner variability of activation in a multicenter fMRI study: Controlling for signal‐to‐fluctuation‐noise‐ratio (SFNR) differences. Neuroimage, 33(2), 471–481. [DOI] [PubMed] [Google Scholar]
- Friedman, L. , Glover, G. H. , Krenz, D. , & Magnotta, V. (2006). Reducing inter‐scanner variability of activation in a multicenter fMRI study: Role of smoothness equalization. Neuroimage, 32(4), 1656–1668. [DOI] [PubMed] [Google Scholar]
- Glahn, D. C. , Kent, J. W., Jr. , Sprooten, E. , Diego, V. P. , Winkler, A. M. , Curran, J. E. , … Blangero, J. (2013). Genetic basis of neurocognitive decline and reduced white‐matter integrity in normal human brain aging. Proceedings of the National Academy of Sciences of the United States of America, 110(47), 19006–19011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen, B. , Lund, T. E. , Sangill, R. , & Jespersen, S. N. (2013). Experimentally and computationally fast method for estimation of a mean kurtosis. Magnetic Resonance in Medicine, 69(6), 1754–1760. [DOI] [PubMed] [Google Scholar]
- Hansen, B. , Lund, T. E. , Sangill, R. , Stubbe, E. , Finsterbusch, J. , & Jespersen, S. N. (2016). Experimental considerations for fast kurtosis imaging. Magnetic Resonance in Medicine, 76, 1455–1468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ioannidis, J. P. A. (2014). How to make more published research true. PLoS Medicine, 11(10), e1001747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahanshad, N. , Kochunov, P. , Sprooten, E. , Mandl, R. C. , Nichols, T. E. , Almassy, L. , … Glahn, D. C. (2013). Multi‐site genetic analysis of diffusion images and voxelwise heritability analysis: A pilot project of the ENIGMA‐DTI working group. Neuroimage, 81, 455–469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly, S. , Jahanshad, N. , Zalesky, A. , Kochunov, P. , Hibar, D. , Chen, J. , … Donohue, G. (2017). Widespread white matter microstructural differences in schizophrenia across 4,375 individuals: Results from the ENIGMA Schizophrenia DTI Working Group. Molecular Psychiatry, In Press. https://www.ncbi.nlm.nih.gov/pubmed/29038599 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov, P. , Coyle, T. , Rowland, L. , Jahanshad, N. , Thompson, P. , Kelly, S. , … Le, H. (2017). White matter and core cognitive deficits in schizophrenia. JAMA Psychiatry, In Press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov, P. , Ganjgahi, H. , Winkler, A. , Kelly, S. , Shukla, D. K. , Du, X. , … Hong, L. E. (2016). Heterochronicity of white matter development and aging explains regional patient control differences in schizophrenia. Human Brain Mapping, 37, 4673–4688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov, P. , & Hong, L. E. (2014). Neurodevelopmental and neurodegenerative models of schizophrenia: White matter at the center stage. Schizophrenia Bulletin, 40(4), 721–728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov, P. , Jahanshad, N. , Sprooten, E. , Nichols, T. E. , Mandl, R. C. , Almasy, L. , … Glahn, D. C. (2014). Multi‐site study of additive genetic effects on fractional anisotropy of cerebral white matter: Comparing meta and megaanalytical approaches for data pooling. Neuroimage, 95C, 136–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubicki, M. , McCarley, R. , Westin, C. F. , Park, H. J. , Maier, S. , Kikinis, R. , … Shenton, M. E. (2007). A review of diffusion tensor imaging studies in schizophrenia. Journal of Psychiatric Research, 41(1–2), 15–30. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marchenko, V. A. , & Pastur, L. A. (1967). Distribution of eigenvalues for some sets of random matrices. Matematicheskii Sbornik, 114(4), 507–536. [Google Scholar]
- Molloy, E. K. , Meyerand, M. E. , & Birn, R. M. (2014). The influence of spatial resolution and smoothing on the detectability of resting‐state and task fMRI. NeuroImage, 86, 221–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nazeri, A. , Mallar Chakravarty, M. , Felsky, D. , Lobaugh, N. J. , Rajji, T. K. , Mulsant, B. H. , & Voineskos, A. N. (2012). Alterations of superficial white matter in schizophrenia and relationship to cognitive performance. Neuropsychopharmacology, 38, 1954–1962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez‐Iglesias, R. , Tordesillas‐Gutierrez, D. , McGuire, P. K. , Barker, G. J. , Roiz‐Santianez, R. , Mata, I. , … Crespo‐Facorro, B. (2011). White matter integrity and cognitive impairment in first‐episode psychosis. The American Journal of Psychiatry, 167(4), 451–458. [DOI] [PubMed] [Google Scholar]
- Phillips, K. A. , Rogers, J. , Barrett, E. A. , Glahn, D. C. , & Kochunov, P. (2012). Genetic contributions to the midsagittal area of the corpus callosum. Twin Research and Human Genetics, 15(3), 315–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poot, D. H. J. , den Dekker, A. J. , Achten, E. , Verhoye, M. , & Sijbers, J. (2010). Optimal experimental design for diffusion kurtosis imaging. IEEE Transactions on Medical Imaging, 29(3), 819–829. [DOI] [PubMed] [Google Scholar]
- Smith, S. M. , Jenkinson, M. , Johansen‐Berg, H. , Rueckert, D. , Nichols, T. E. , Mackay, C. E. , … Behrens, T. E. (2006). Tract‐based spatial statistics: Voxelwise analysis of multi‐subject diffusion data. Neuroimage, 31(4), 1487–1505. [DOI] [PubMed] [Google Scholar]
- Triantafyllou, C. , Hoge, R. D. , & Wald, L. L. (2006). Effect of spatial smoothing on physiological noise in high‐resolution fMRI. NeuroImage, 32(2), 551–557. [DOI] [PubMed] [Google Scholar]
- Veraart, J. , Fieremans, E. , & Novikov, D. S. (2016). Diffusion MRI noise mapping using random matrix theory. Magnetic Resonance in Medicine, 76, 1582–1593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veraart, J. , Novikov, D. S. , Christiaens, D. , Ades‐Aron, B. , Sijbers, J. , & Fieremans, E. (2016). Denoising of diffusion MRI using random matrix theory. NeuroImage, 142, 394–406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang, Z. J. , Seo, Y. , Chia, J. M. , & Rollins, N. K. (2011). A quality assurance protocol for diffusion tensor imaging using the head phantom from American College of Radiology. Medical Physics, 38(7), 4415–4421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wright, S. N. , Hong, L. E. , Winkler, A. M. , Chiappelli, J. , Nugent, K. , Muellerklein, F. , … Kochunov, P. (2015). Perfusion shift from white to gray matter may account for processing speed deficits in schizophrenia. Human Brain Mapping, 36, 3793–3804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yendiki, A. , Koldewyn, K. , Kakunoori, S. , Kanwisher, N. , & Fischl, B. (2014). Spurious group differences due to head motion in a diffusion MRI study. Neuroimage, 88C, 79–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Additional Supporting Information may be found online in the supporting information tab for this article.
Supporting Information


